Hybrid Aquila and Harris hawks optimization algorithm with dynamic opposition-based learning
-
摘要: 阿奎拉鹰优化算法(Aquila optimizer, AO)和哈里斯鹰优化算法(Harris hawks optimization, HHO)是近年提出的优化算法。AO算法全局寻优能力强，但收敛精度低，容易陷入局部最优，而HHO算法具有较强的局部开发能力，但存在全局探索能力弱，收敛速度慢的缺陷。针对原始算法存在的局限性，本文将两种算法混合并引入动态反向学习策略，提出一种融合动态反向学习的阿奎拉鹰与哈里斯鹰混合优化算法。首先，在初始化阶段引入动态反向学习策略提升混合算法初始化性能与收敛速度。此外，混合算法分别保留了AO的探索机制与HHO的开发机制，提高算法的寻优能力。仿真实验采用23个基准测试函数和2个工程设计问题测试混合算法优化性能，并对比了几种经典反向学习策略，结果表明引入动态反向学习的混合算法收敛性能更佳，能够有效求解工程设计问题。Abstract: In recent years, optimization algorithms such as the Aquila optimizer (AO) and Harris hawks optimization (HHO) have been proposed. Although AO has strong global optimization capabilities, its convergence accuracy is low, and it is susceptible to local optimization. While the HHO algorithm has a strong local development capability, it suffers from flaws such as limited global exploration capabilities and slow convergence speed. Given the limitations of the original algorithms, this paper combines the two algorithms and proposes a hybrid Aquila and Harris Hawks algorithm with dynamic opposition-based learning. It introduces a dynamic opposition-based learning strategy and proposes a hybrid Aquila and Harris Hawks algorithm with dynamic opposition-based learning. First, a dynamic opposition-based learning strategy is introduced in the initialization phase to improve the initialization performance and convergence speed of the algorithm. Second, the hybrid algorithm retains the exploration mechanism of AO and the exploitation mechanism of HHO, which improves the algorithm’s optimization ability. The simulation experiment compares several classical opposition-based learning strategies using 23 benchmark functions and two engineering design problems to test the optimization performance of the hybrid algorithm. The results show that the hybrid algorithm with dynamic opposition-based learning has better convergence performance and can effectively solve engineering design problems.
-
随着当代科技的飞速发展，工程领域的优化问题日益复杂，传统基于数学理论的优化方法（例如牛顿下山法、梯度下降法）已经无法有效解决此类问题。因此，众多学者将目光抛向了元启发式优化算法(meta heuristics, MAs)。MAs是一类受自然现象(例如生物群体行为、物理现象、进化法则)启发的优化算法。与传统优化方法相比，MAs不需要梯度信息，灵活且易于实现，被广泛应用于医学、计算机科学等领域的复杂优化问题[1-4]。常见的MAs有：遗传算法(genetic algorithm, GA)[5]、粒子群优化算法(particle swarm optimization, PSO)[6]、灰狼优化算法(grey wolf optimizer, GWO)[7]、多元宇宙优化算法(multi-verse optimizer, MVO)[8]、正余弦优化算法(sine cosine algorithm, SCA)[9]、鲸鱼优化算法(whale optimization algorithm, WOA)[10]、樽海鞘群优化算法(salp swarm algorithm, SSA)[11]、哈里斯鹰优化算法(Harris hawks optimization, HHO)[12]和阿奎拉鹰优化算法(Aquila optimizer, AO)[13]。上述MAs在某些领域内展示了出色的优化效果，但由于无免费午餐(no-free-lunch, NFL)定理[14]证实了没有一种MAs能够解决所有的优化问题，即每种MAs都有各自的优势和局限性，仅针对部分问题有效。这激励着众多学者提出各种新颖或改进的MAs来解决不同类型的优化问题。
AO是Abualigah等于2021年提出的一种新型MAs。该算法模拟了阿奎拉鹰针对不同猎物所采取的多种攻击行为。AO具有强大的全局寻优能力，搜索效率高，收敛速度快，但局部开发能力较弱，易受到局部极值的干扰。为了缓解上述问题，Al-qaness等[15]引入反向学习策略提高AO的搜索性能，并将其应用到自适应模糊神经推理系统，确定模型的最佳参数。Li等[16]引入自适应权重策略提高AO的局部开发能力，并将改进算法应用于冷热电联产系统，降低模型的运行成本。虽然上述文献提出的解决方案在一定程度上改善了AO的搜索性能，但上述研究均是通过改进策略提升算法的性能，忽略了混合算法所带来的优势特性(即利用多种算法实现搜索过程中的多样化信息交流)。此外，AO提出的时间较短，其性能有待进一步提升。HHO是在2019年由Heidari等提出的一种MAs。该算法模仿了哈里斯鹰捕食猎物的一系列行为。HHO根据猎物的逃逸能量，实现算法对全局探索阶段和局部开发阶段的过渡。开发阶段根据猎物的能量和逃跑概率采取4种不同的进攻策略。实验表明该算法局部寻优能力较强，采用4种不同的进攻策略的同时借助莱维游走使得HHO具有较强的抗局部最优值干扰能力，能够有效避免算法出现“早熟”现象，但前期全局探索能力较弱，无法快速找到全局最优所在的区域，导致算法收敛速度较慢。
基于上述分析，AO和HHO算法存在各自的优势和局限性。为了改善AO的寻优性能，本文利用混合算法的改进思路，分别汲取了AO和HHO在全局探索和局部搜索方面的优势，同时引入动态反向学习策略，提出了一种融合动态反向学习的阿奎拉鹰与哈里斯鹰混合优化算法(hybrid Aquila and Harris hawk optimization with dynamic opposition-based learning, DAHHO)。混合算法分别利用了AO的全局探索阶段和HHO的局部开发阶段进行迭代寻优，并且引入动态反向学习策略提升种群初始化性能，为后续的高效搜索奠定基础。仿真实验部分采用23个基准测试函数以及2个经典工程设计问题对改进算法进行性能测试，并探讨了其他反向学习策略所带来的优化效果，结果表明融合动态反向学习的混合算法寻优性能更优，收敛速度和收敛精度均有较大提高，为解决约束工程设计问题提供了一种行之有效的计算方法。
1. 阿奎拉鹰优化算法
阿奎拉鹰优化算法灵感来自阿奎拉鹰的捕食行为。阿奎拉鹰利用其极快的飞行速度与强有力的鹰爪攻击猎物，并且能够根据猎物的不同转换狩猎策略。AO通过迭代次数划分探索阶段和开发阶段，若
$t \leqslant \dfrac{2}{3}T$ 时，AO执行全局探索，否则执行局部开发。每个阶段的具体描述如下。1.1 探索阶段
阿奎拉鹰在搜索空间内通过2种不同的飞行方式搜索猎物，通过随机数r1平衡采用不同策略的概率。
1.1.1 高空飞行搜索
阿奎拉鹰在高空中探索，通过敏锐的眼睛观察位于其下方飞行的猎物，其位置更新公式为
$$ {\boldsymbol{X}}(t + 1) = {{\boldsymbol{X}}_{\rm best}}(t) \times \left(1 - \frac{t}{T}\right) + ({{\boldsymbol{X}}_{\rm{M}}}(t) - {{\boldsymbol{X}}_{\rm best}}(t) \times {r_2}) $$ (1) $$ {{\boldsymbol{X}}_{\rm{M}}}{\text{(}}t{\text{)}} = \frac{1}{N}\sum\limits_{i = 1}^N {{{\boldsymbol{X}}_i}{\text{(}}t{\text{)}}} $$ (2) 式中：Xbest(t)代表种群最佳位置；XM(t)代表种群平均位置；t为当前迭代次数；T为最大迭代次数；N为种群规模；r1和r2为分布在0到1之间的随机数。
1.1.2 环绕猎物飞行
确定猎物范围后，阿奎拉鹰会在目标上方盘旋，寻找合适的机会攻击猎物，数学模型为
$$ {\boldsymbol{X}}(t + 1) = {{\boldsymbol{X}}_{\rm best}}(t) \times {\rm{LF}}(D) + {{\boldsymbol{X}}_{\rm{R}}}(t) + (y - x) \times {r_3} $$ (3) 式中：D表示维度；XR(t)代表种群随机位置；r3是0到1的随机数；LF(D)表示莱维飞行函数，其公式为
$$ {\rm{LF}}(D) = s \times \dfrac{{u \times \sigma }}{{|v{|^{\frac{1}{\beta }}}}} $$ $$ \sigma = {\left( {\dfrac{{\Gamma (1 + \beta ) \times \sin \left(\dfrac{{{\text{π}} \beta }}{2}\right)}}{{\Gamma \left(\dfrac{{1 + \beta }}{2}\right) \times \beta \times {2^{\left(\frac{{\beta - 1}}{2}\right)}}}}} \right)^{\frac{{\text{1}}}{\beta }}} $$ 式中：s是取值为0.01的常数；u与v为[0,1]间的随机数；
$ \beta $ =1.5。$$ \left\{ \begin{aligned} &x = l \times \sin (\theta ) \\ &y = l \times \cos (\theta ) \\ &l = C + {\text{0.005\;65}} \times D \\ &\theta = - \omega \times D + \frac{{{\text{3}} {\text{π}}}}{{\text{2}}} \\ \end{aligned} \right. $$ 式中：C是取值为10的搜索空间系数；ω是取值为0.005的常数。
1.2 开发阶段
此时阿奎拉鹰已确定猎物位置，进而降低自身飞行高度以接近猎物，通过随机数r4采取不同的狩猎策略。
1.2.1 低空飞行攻击
阿奎拉鹰接近猎物并通过强壮的鹰爪攻击猎物背部或颈部，其数学模型为
$$ \begin{gathered} {\boldsymbol{X}}(t + 1) = ({{\boldsymbol{X}}_{\rm best}}(t) - {{\boldsymbol{X}}_M}(t)) \times \alpha - {r_5} +\\ (({\rm{UB}} - {\rm{LB}}) \times {r_{\text{6}}} + {\rm{LB}}) \times \delta \end{gathered} $$ 式中：α与δ是值为0.1的适应参数；UB和LB分别代表种群上下界；r5与r6为0~1的随机数。
1.2.2 地面近距离攻击
阿奎拉鹰在陆地游走接近猎物并发动攻击，数学模型为
$$ \begin{gathered} {\boldsymbol{X}}(t + 1) = {\rm{QF}} \times {{\boldsymbol{X}}_{\rm best}}(t) - ({G_1} \times {\boldsymbol{X}}(t) \times {r_{\text{7}}}) - \\ {G_2} \times {\rm{LF}}(D) + {r_{\text{8}}} \times {G_1} \\ {\rm{QF}}(t) = {t^{\frac{{2 \times {r_{\text{9}}} - 1}}{{{{(1 - T)}^2}}}}} \\ {G_1} = 2 \times {r_{{\text{10}}}} - 1 \\ \end{gathered} $$ $$ {G_2} = 2 \times \left(1 - \frac{t}{T}\right) $$ 式中：
${\rm{QF}}(t)$ 是质量函数，用于平衡其搜索策略；G1猎物的逃跑轨迹；G2是从2到0线性递减参数，表示阿奎拉鹰在空中追逐猎物的飞行斜率；r7、r8、r9、r10为分布在0到1之间的随机数。2. 哈里斯鹰优化算法
哈里斯鹰是美国南部地区的一种猛禽，它们的觅食方式取决于狩猎环境以及猎物的逃逸形式。算法主要分为探索阶段、探索与开发转换阶段、开发阶段[17]。
2.1 探索阶段
哈里斯鹰随机栖息在搜索空间中，通过两种策略搜寻猎物，利用随机数平衡使用策略的概率，数学表述为
$$ {\boldsymbol{X}}(t + 1) = \left\{ \begin{gathered} {{\boldsymbol{X}}_R}(t) - {r_{1{\text{2}}}}|{{\boldsymbol{X}}_R}(t) - 2{r_{1{\text{3}}}}{\boldsymbol{X}}(t)| \\ ({{\boldsymbol{X}}_{\rm best}}(t) - {{\boldsymbol{X}}_{{M}}}(t)) - {r_{1{\text{4}}}}({\rm{LB}} + {r_{1{\text{5}}}}({\rm{UB}} - {\rm{LB}})) \\ \end{gathered} \right. $$ 式中：r12、r13、r14、r15均为0~1的随机数。
2.2 探索与开发转换阶段
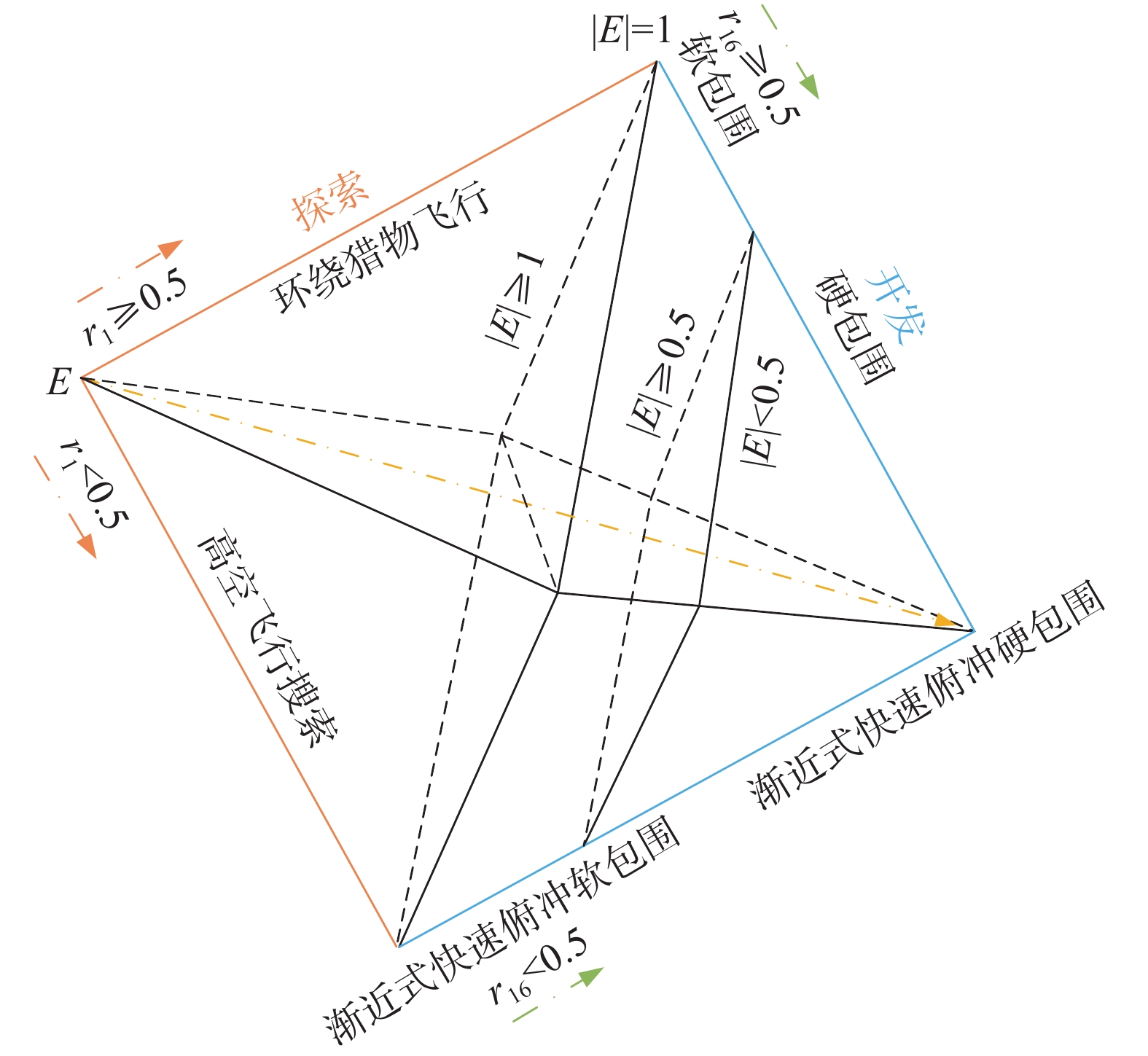
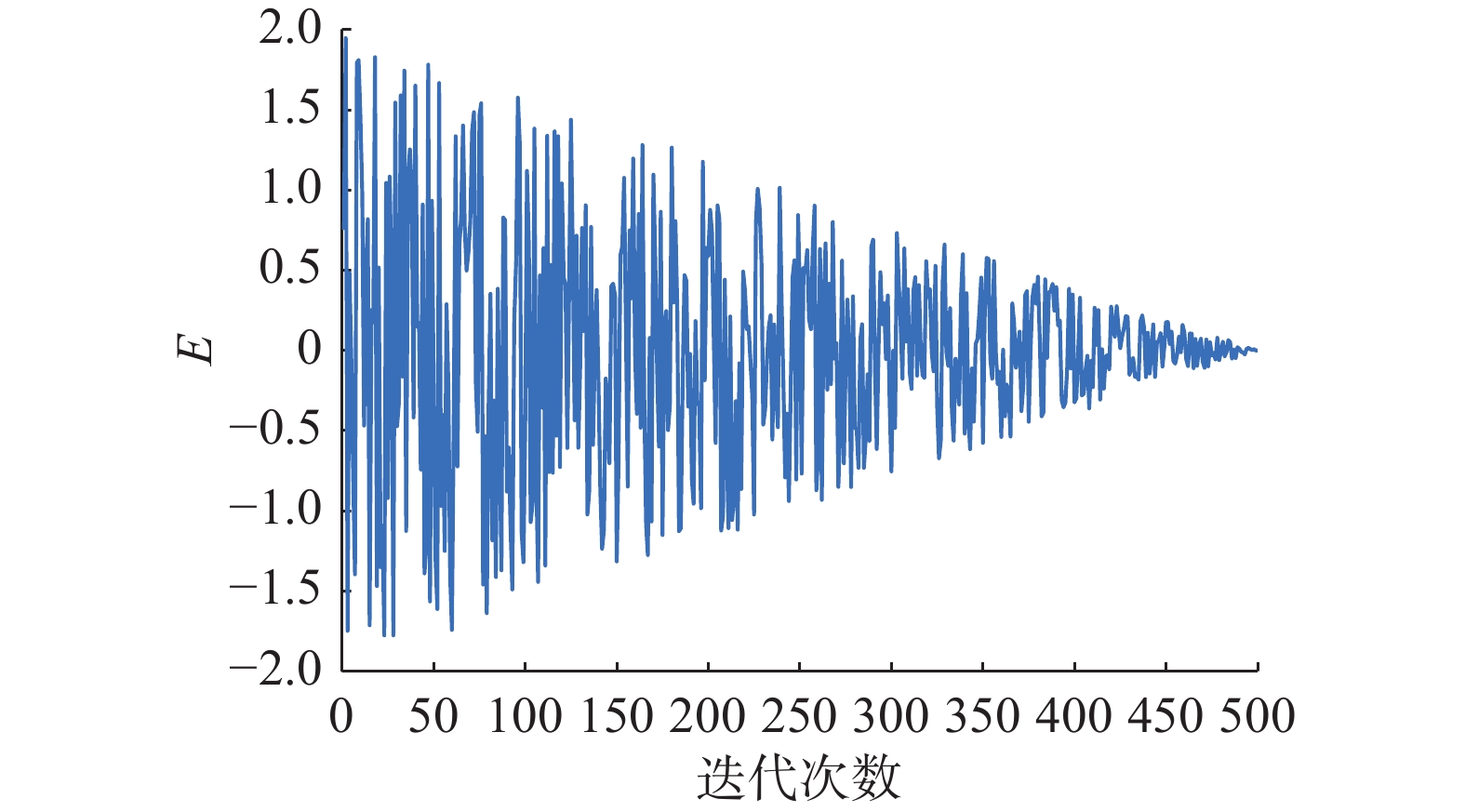
哈里斯鹰根据猎物的逃逸能量实现探索阶段与开发阶段的转换，猎物的逃逸能量E如图1所示，其计算公式为
图 1 能量逃逸因子曲线图Fig. 1 Curve of energy escape factor
下载:
全尺寸图片
$$ E = 2{E_0}\left(1 - \frac{t}{T}\right) $$ 式中：E0为−1~1之间的随机数；当
$ |E| \geqslant {\text{1}} $ 时，HHO执行探索模式；否则执行开发模式。2.3 开发阶段
2.3.1 软包围
当
$ {r_{1{\text{6}}}} \geqslant 0.5 $ 且$ |E| \geqslant {\text{0}}{\text{.5}} $ 时，猎物有足够的能量躲避追捕，此时哈里斯鹰通过软包围方式围捕猎物，计算公式为$$ {\boldsymbol{X}}(t + 1) = \Delta {\boldsymbol{X}}(t) - E|J{{\boldsymbol{X}}_{\rm best}}(t) - {\boldsymbol{X}}(t)| $$ $$ \Delta {\boldsymbol{X}}(t) = {{\boldsymbol{X}}_{\rm best}}(t) - {\boldsymbol{X}}(t) $$ $$ J = 2(1 - {r_{1{\text{7}}}}) $$ 式中：
$\Delta {\boldsymbol{X}}(t)$ 为最优解与当前解的差值；J为猎物随机跳跃的距离；r16、r17是0~1的随机数。2.3.2 硬包围
当
$ {r_{1{\text{6}}}} \geqslant 0.5 $ 且$ |E| < {\text{0}}{\text{.5}} $ 时，猎物的逃逸能量不足，此时哈里斯鹰通过硬包围方式进行狩猎，计算公式为$$ {\boldsymbol{X}}(t + 1) = {{\boldsymbol{X}}_{\rm best}}(t) - E|\Delta {\boldsymbol{X}}(t)| $$ (4) 2.3.3 渐近式快速俯冲的软包围
当
$ {r_{1{\text{6}}}} < 0.5 $ 且$ |E| \geqslant {\text{0}}{\text{.5}} $ 时，猎物有足够的能量逃出包围圈，因此哈里斯鹰需要在攻击前形成一个更加智能的软包围圈，并在莱维游走与快速俯冲突袭之间选取最佳进攻策略(根据适应度值评判)，计算公式为$$ {\boldsymbol{Y}} = {{\boldsymbol{X}}_{\rm best}}(t) - E|J{{\boldsymbol{X}}_{\rm best}}(t) - {\boldsymbol{X}}(t)| $$ (5) $$ {\boldsymbol{Z}} = {\boldsymbol{Y}} + {\boldsymbol{S}} \times {\rm{LF}}(D) $$ (6) $$ {\boldsymbol{X}}(t + 1) = \left\{ \begin{gathered} {\boldsymbol{Y}},\quad F({\boldsymbol{Y}}) < F({\boldsymbol{X}}(t)) \\ {\boldsymbol{Z}},\quad F({\boldsymbol{Z}}) < F({\boldsymbol{X}}(t)) \\ \end{gathered} \right. $$ (7) 式中：S为1×D的位于[0,1]间的随机向量。
2.3.4 渐近式快速俯冲的硬包围
当
$ {r_{1{\text{6}}}} < 0.5 $ 且$ |E| < {\text{0}}{\text{.5}} $ 时，猎物没有足够的能量逃逸，哈里斯鹰在攻击前形成一个硬包围圈，基于猎物位置和种群平均位置进行围捕，从而减小种群与猎物的距离。若突袭失效，则执行莱维游走(根据适应度值评判)，数学表述为$$ {\boldsymbol{Y}} = {{\boldsymbol{X}}_{\rm best}}(t) - E|J{{\boldsymbol{X}}_{\rm best}}(t) - {{\boldsymbol{X}}_M}(t)| $$ (8) 3. 动态反向学习策略
对于元启发式优化算法来说，种群初始化往往是在搜索空间内随机生成的，只能保证种群在搜索空间内的分散程度，无法保证初始解的质量。然而，研究表明初始化的好坏将直接影响算法的收敛速度和解的精度。基于此问题，国内外学者将多种策略引入初始化部分，以提高算法初始化性能，常见的有混沌初始化、反向学习和柯西随机生成等。文献[18]针对此问题提供了一种新思路，将个体分布在非对称动态搜索空间内，并利用贪婪策略选取最佳个体作为初始化种群，能够有效提高解的质量。因此，本文引入动态反向学习策略，提高初始化解的质量，计算方法如下为
$$ {{\boldsymbol{X}}_{\rm DOBL}} = {{\boldsymbol{X}}_{\rm init}} + {r_{1{\text{8}}}} \times ({r_{{\text{19}}}} \times ({\rm{LB}} + {\rm{UB}} - {{\boldsymbol{X}}_{\rm init}}) - {{\boldsymbol{X}}_{\rm init}}) $$ 式中：Xinit代表通过随机生成的初始化种群；r18与r19均为分布在0~1的随机数。首先，算法分别生成原始初始化种群Xinit与反向初始种群XDOBL，然后将两个种群合并为新种群Xnew={XDOBL∪Xinit}。计算新种群的适应度值，并利用贪婪策略使种群内部充分竞争，选取最佳的N个个体作为初始化种群。通过此方法能够让种群更快地靠近最优解，从而提升算法的收敛速度。
4. DAHHO算法
4.1 改进混合算法理论分析
根据第1节的阐述，阿奎拉鹰根据不同猎物会采取4种不同的捕食行为。在前期迭代中，根据随机数r1选择高空飞行搜索或环绕猎物飞行，这两种探索方式主要针对快速移动的猎物。因此位置更新中分别考虑了阿奎拉鹰种群的最佳位置、平均位置和随机位置，式(1)利用种群最佳位置和平均位置实现整体种群在搜索空间内的大范围搜索，式(3)利用莱维飞行配合最佳位置实现搜索空间的大范围随机扰动，体现算法较强的全局探索能力。当迭代次数
$t > (\dfrac{2}{3} \times T)$ 时，根据随机数r4选择低空飞行攻击或地面近距离攻击策略，这两种攻击方式主要针对移动速度较慢的猎物，体现算法的局部搜索能力。然而，根据生物特性来看，阿奎拉鹰倾向于单独狩猎，且地面移动能力较弱，无法对地面上猎物实行有效攻击。从数学描述来看，局部开发过程并没有对选定的搜索空间进行充分搜索，其中莱维飞行的作用也很弱，根据适应度进行位置更新加剧了局部最优停滞。此外，AO算法仅是根据迭代次数进行阶段划分，无法有效平衡算法全局阶段与局部阶段。因此，AO算法全局探索阶段随机性较强，种群在搜索空间覆盖面广，不易错失关键的搜索信息，而局部开发阶段容易陷入局部最优。HHO则根据猎物的能量衰减实现全局到局部搜索的过渡。探索过程主要依靠最优个体信息，没有与其他个体交流，引发种群多样性下降，导致收敛速度较慢。随着迭代次数的增加，猎物的能量下降，进入局部开发阶段，根据猎物能量和逃逸概率采取4种不同的捕食策略。当逃逸概率r16 ≥ 0.5时，通过猎物能量选择软包围或硬包围，分别根据自身与猎物的距离和猎物的位置进行位置更新。否则，通过猎物能量选择渐进式快速俯冲的软包围或硬包围，两种方式均加入了莱维飞行项，并根据适应度判断使用莱维游走还是快速俯冲攻击，使算法能够有效跳出局部最优。总的来说，AO的全局搜索和HHO的局部搜索分别是该两种算法的核心特点，本文将AO的全局探索阶段和HHO的局部探索阶段相结合，充分发挥两种算法的优势，保留算法的全局探索能力、较快的收敛速度和跳出局部最优的能力。此外，在初始化阶段引入动态反向学习策略，进一步提升算法初始化种群质量，使混合算法的收敛速度和精度都得到提高，增强了算法的整体寻优性能。DAHHO算法的不同阶段如图2所示。
图 2 DAHHO算法的不同阶段Fig. 2 Different phases of DAHHO下载:
全尺寸图片
DAHHO算法步骤如下：
1）初始化种群，计算动态反向学习种群，根据贪婪策略保留较优个体进入主程序迭代。
2）计算种群适应度值,记录较优个体。
3）如果 |E| ≥ 1，个体随机选择式(1)或式(3)开始探索行为。
4）如果 |E| < 1，种群根据逃逸猎物能量值与适应度值选择开发策略：
策略1 软包围。当r16 ≥ 0.5且|E| ≥ 0.5，子群个体采用式(11)更新位置。
策略2 硬包围。当r16 ≥ 0.5且|E| < 0.5，子群个体采用式(4)更新位置。
策略3 渐近式快速俯冲软包围。当r16 < 0.5且| E| ≥ 0.5，子群个体采用式（5）、（6）、（7）更新位置。
策略4 渐近式快速俯冲硬包围。当r16 < 0.5且| E| < 0.5，子群个体采用式（6）、（7）、（8）更新位置。
5）判断程序是否满足终止条件，满足则跳出循环，否则返回步骤2。
6）输出最佳位置及适应度值。
4.2 计算复杂度分析
DAHHO计算复杂度主要取决于以下3个过程：动态反向学习初始化，适应度评估以及种群位置更新。假设种群规模为N，则初始化计算复杂度为O(2×N)。评价最佳位置以及更新种群位置向量的计算复杂度为O(N×T+N×T×D)。综上所述，DAHHO的计算复杂度为O(N×(2+T+T×D))。考虑到NFL定理，增加一些额外的计算复杂度来获取更好的解决方案是可取的。
5. 实验仿真与分析
本文实验环境采用Intel(R) Core(TM) i5-9500 CPU，主频为3.00 GHz，内存24 GB的电脑，操作系统为64位Windows 10，编程语言为MATLAB ，版本R2020b。使用23个基准测试函数对算法进行性能测试，可有效验证本文所提算法的寻优能力[4]。其中，F1~F7为单峰测试函数，只有一个最优解，可评估算法的收敛速度与求解精度，F8~F24是多峰测试函数，具有多个局部最优值与一个全局最优值，用于评估算法的全局搜索能力与避免陷入局部最优能力。
5.1 实验环境与参数设置
为了确保实验的公平性与可对比性，本文采用两组对比算法进行实验。第1组：选取7种不同的优化算法作为对比算法，这些算法被证实具有良好的寻优能力，分别是：AO[13]、HHO[12]、SSA[11]、WOA[10]、SCA[9]、MVO[8]、GWO[7]和GA[5]。各算法参数设置如表1所示。第2组：以混合算法为主体，在初始化阶段引入不同的经典反向学习策略，如引入反向学习[19](OBLAHHO)、随机反向学习[4](ROBLAHHO)与准反向学习[20](QOBLAHHO)，以验证不同类型的反向学习策略对混合算法的改进效果。在实验设置方面，设定所有算法的种群规模N=30，维度D=30，最大迭代次数T=500,各算法独立运行30次。本文分别采用平均值、标准差与Wilcoxon秩和检验作为算法性能评价指标。其中，平均值越小代表算法收敛精度高，标准差越小代表算法波动小，稳定性高。
表 1 各算法参数设置Table 1 Parameter setting of each algorithm算法 参数名称 参数设置 AO[8] 搜索周期参数 C=10 HHO[7] 随机跳跃长度 J=[0,2] SSA[16] 平衡参数 c1=[1,0] 收敛因子 a=[2,0] WOA[6] 随机数 l=[−1,1] 螺旋常数 b=1 SCA[17] 移动系数 a=2 MVO[18] 蠕虫存在率 WEP=[0.2,1] 旅行距离率 TDR=[0.6450,0] GWO[19] 收敛因子 a=[2,0] GA[20] 交叉概率 Pc=0.7 变异概率 Pm=0.3 OBLAHHO 随机跳跃距离 J=[0,2] ROBLAHHO 随机跳跃距离 J=[0,2] QOBLAHHO 随机跳跃距离 J=[0,2] 5.2 求解精度分析
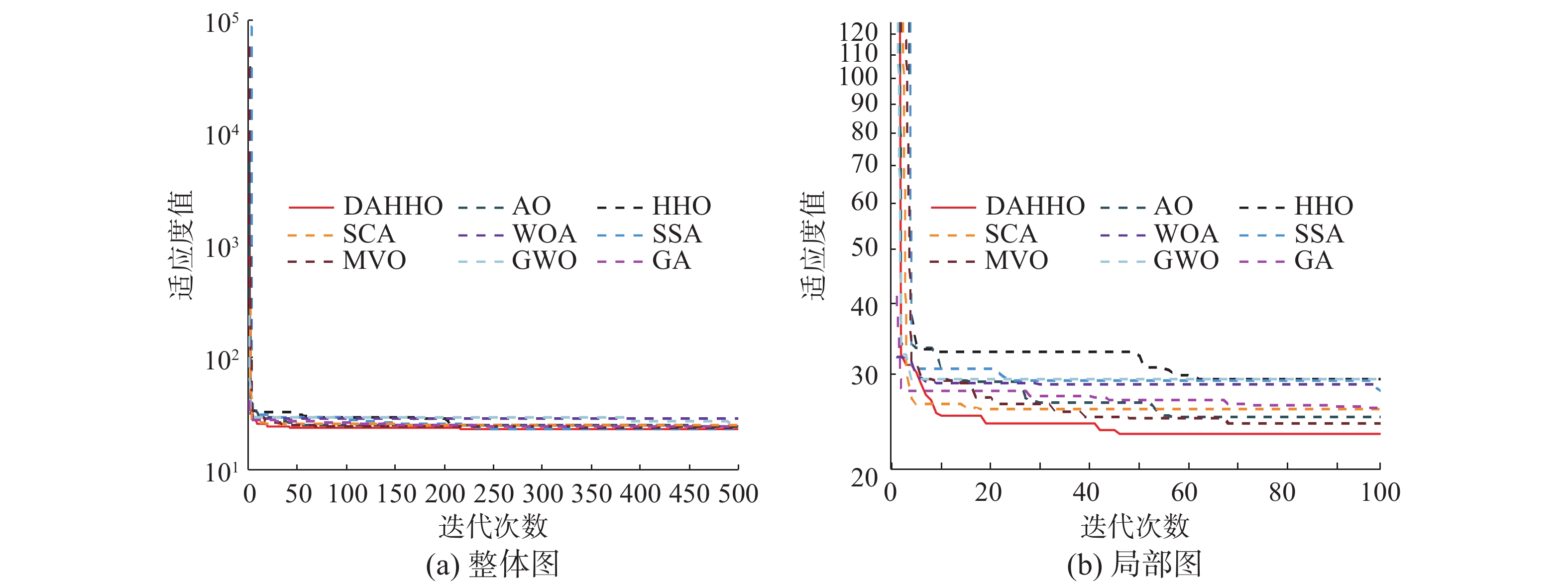
第1组实验结果如表2所示。其中，最佳结果用粗体显示。从单峰测试函数来说，DAHHO在测试函数F1~F5与F7表现最佳，不仅求解精度最高，而且稳定性也超过了其余对比算法。值得注意的是，在求解F1与F3时，DAHHO的标准差为0，表现出优秀的求解稳定性。对于函数F6，DAHHO优化效果仅次于SSA。在多峰测试函数中，DAHHO也能表现出不错的效果。对于函数F9~F11，DAHHO可直接搜寻到理论最优值，且方差最小。F8是最复杂的多峰测试函数，DAHHO虽不能寻到全局最优值，但结果也仅次于HHO算法。对于函数F12、13与F15，DAHHO寻优精度与标准差皆优于其他算法。对于F14，效果不及MVO。对于F20，GWO达到了理论最优值，但标准差不如MVO。对于函数F16~F19、F21和F23，DAHHO能够寻到全局最优值，寻优结果超过大部分对比算法，并且表现出不错的稳定性。从算法测试结果可以看出，DAHHO并不能在所有测试函数上跑赢对比算法，从侧面反映出本文选取的对比算法是具有可对比性与一定的参考价值。但DAHHO能够在大部分测试函数上表现出优秀的收敛精度以及稳定性。
表 2 DAHHO与对比算法的基准函数测试结果Table 2 Benchmark function results of DAHHO and contrast algorithm函数 统计值 DAHHO AO HHO SSA WOA SCA MVO GWO GA F1 平均值 1.068×10−231 6.400×10−99 8.200×10−98 1.667×10−7 7.250×10−74 1.882×101 1.210 8.881×10−28 7.103×103 标准差 0.000 2.650×10−98 4.330×10−97 1.752×10−7 3.560×10−73 4.216×101 4.300×10−1 1.838×10−27 2.784×103 F2 平均值 1.819×10−120 2.800×10−53 4.060×10−52 1.944 1.370×10−49 1.800×10−2 1.150 9.163×10−17 3.539×101 标准差 4.849×10−120 1.530×10−52 1.900×10−51 1.477 7.420×10−49 3.000×10−2 1.390 5.910×10−17 5.673 F3 平均值 4.982×10−192 3.040×10−109 5.060×10−69 1.257×103 4.663×104 8.659×103 2.405×102 9.791×10−6 9.976×103 标准差 0.000 1.660×10−108 2.770×10−68 7.937×102 1.357E×105 6.034×103 1.105×102 2.516×10−5 4.027×103 F4 平均值 1.464×10−117 7.100×10−55 1.290×10−47 1.076×101 4.983×101 3.364×101 2.080 8.978×10−7 2.747×101 标准差 7.860×10−117 3.880×10−54 6.140×10−47 3.439 2.536×101 1.124×101 8.000×10−1 1.000×10−6 4.449 F5 平均值 4.617×10−4 6.500×10−3 1.420×10−2 2.359×102 2.793×101 1.586×104 3.680×102 2.721×101 3.352×106 标准差 7.029×10−3 9.000×10−3 2.600×10−2 4.215×102 5.200×10−1 2.369×104 6.076×102 7.400×10−1 1.755×106 F6 平均值 7.443×10−6 1.500×10−4 1.400×10−4 1.508×10−7 4.010×10−1 2.506×101 1.260 8.188×10−1 7.327×103 标准差 1.300×10−5 4.000×10−4 1.900×10−4 1.290×10−7 2.340×10−1 6.332×101 3.603×10−1 3.573×10−1 2.203×103 F7 平均值 9.154×10−5 2.000×10−4 1.000×10−4 1.600×10−1 2.000×10−3 1.620×10−1 1.489×101 2.323×10−3 1.581 标准差 7.424×10−5 8.300×10−5 1.000×10−4 6.293×10−2 2.800×10−3 8.200×10−2 1.028×101 1.537×10−3 1.120 F8 平均值 −1.227×104 −8.154×103 −1.253×104 −7.544×103 −1.018×104 −3.775×103 −7.668×103 −5.702×103 −5.188×103 标准差 1.280×103 4.021×103 1.354×102 6.536×102 2.017×103 2.577×102 8.095×102 6.549×102 8.136×102 F9 平均值 0.000 0.000 0.000 4.663×101 0.000 4.168×101 1.198×102 3.852 1.911×102 标准差 0.000 0.000 0.000 1.363×101 0.000 3.315×101 3.638×101 4.545 2.379×101 F10 平均值 8.882×10−16 8.880×10−16 8.880×10−16 2.583 3.840×10−15 1.499×101 1.843 9.847×10−14 1.339×101 标准差 0.000 0.000 0.000 7.491×10−1 2.480×10−15 8.078 6.290×10−1 1.663×10−14 1.227 F11 平均值 0.000 0.000 0.000 1.590×10−2 1.500×10−2 9.300×10−1 8.500×10−1 5.621×10−3 6.088×101 标准差 0.000 0.000 0.000 1.224×10−2 4.200×10−2 3.330×10−1 8.000×10−2 1.033×10−2 1.687×101 F12 平均值 1.842×10−6 3.130×10−6 6.610×10−6 6.996 2.400×10−2 2.638×104 2.048 3.669×10−2 1.661×105 标准差 2.964×10−6 4.490×10−6 7.650×10−6 2.859 1.200×10−2 7.601×104 1.430 1.645×10−2 3.700×105 F13 平均值 1.119×10−5 3.880×10−5 8.040×10−5 1.902×101 4.499×10−1 8.043×104 2.242×10−1 7.337×10−1 3.813×106 标准差 2.121×10−5 4.540×10−5 1.000×10−4 1.356×101 2.272×10−1 2.348×105 1.196×10−1 2.986×10−1 3.227×106 F14 平均值 2.706 2.010 1.097 1.230 2.862 2.056 9.980×10−1 3.488 1.559 标准差 2.528 2.714 3.033×10−1 5.005×10−1 3.320 1.006 2.430×10−11 3.223 1.287 F15 平均值 3.543×10−4 5.000×10−4 4.000×10−4 2.170×10−3 6.000×10−4 1.000×10−3 4.300×10−3 3.701×10−3 2.223×10−3 标准差 6.154×10−5 1.000×10−4 1.000×10−4 4.955×10−3 4.000×10−4 3.000×10−4 1.100×10−2 7.579×10−3 4.953×10−3 F16 平均值 −1.032 −1.032 −1.032 −1.032 −1.032 −1.032 −1.032 −1.032 −1.032 标准差 2.580×10−13 3.000×10−4 4.830×10−9 2.899×10−12 2.170×10−9 6.630×10−5 2.640×10−7 2.065×10−8 6.454×10−10 续表 2 函数 统计值 DAHHO AO HHO SSA WOA SCA MVO GWO GA F17 平均值 3.980×10−1 3.980×10−1 3.980×10−1 3.979×10−1 3.980×10−1 3.996×10−1 3.980×10−1 3.979×10−1 3.979×10−1 标准差 1.073×10−13 1.000×10−4 6.490×10−6 1.437×10−11 1.320×10−5 1.646×10−3 1.880×10−7 6.391×10−7 2.875×10−10 F18 平均值 3.000 3.043 3.000 3.000 3.000 3.000 5.700 3.000 3.000 标准差 2.153×10−12 4.000×10−2 3.830×10−7 2.116×10−10 5.570×10−5 1.000×10−4 1.479×101 6.101×10−5 1.962×10−10 F19 平均值 −3.861 −3.860 −3.860 −3.860 −3.860 −3.870 −3.860 −3.860 −3.860 标准差 3.449×10−9 6.000×10−3 3.300×10−3 1.152×10−7 1.300×10−2 1.000×10−2 3.580×10−6 4.141×10−3 2.539×10−4 F20 平均值 −3.074 −3.170 −3.115 −3.220 −3.250 −2.910 −3.290 −3.268 −3.233 标准差 1.311×10−1 1.020×10−1 1.200×10−1 5.836×10−2 8.300×10−2 3.500×10−1 5.390×10−2 6.952×10−2 8.950×10−2 F21 平均值 −1.015×101 −1.015×101 −5.381 −8.240 −7.583 −2.729 −7.043 −9.476 −9.479 标准差 3.025×10−3 9.900×10−3 8.770×10−1 3.254 2.572 2.105 3.077 1.751 1.747 F22 平均值 −1.022×101 −1.040×101 −5.080 −7.978 −8.554 −3.171 −8.069 −1.011×101 −8.836 标准差 9.700×10−1 8.000×10−2 4.230×10−1 3.114 2.897 1.757 3.199 9.898×10−4 2.916 F23 平均值 −1.054×101 −1.054×101 −5.120 −8.723 −5.902 −3.975 −9.012 −1.026×101 −9.690 标准差 3.641×10−3 1.400×10−2 4.940×10−1 3.122 3.020 1.836 2.864 1.481 2.221 第2组实验结果如表3所示。从中可以看出，无论在求解单峰测试函数问题上还是多峰测试函数，引入动态反向学习策略的混合算法在求解精度和稳定性都强于其他反向学习策略。这是因为动态反向学习策略将个体扩展到非对称搜索空间中，更有利于个体充分探索目标区域，增加了总体寻到全局最优解的概率，从而有效提高算法寻优性能。
表 3 DAHHO与不同类型反向学习混合算法的基准函数测试结果Table 3 Benchmark function results of DAHHO and different types of opposition-based learning hybrid algorithms函数 统计值 DAHHO OBLAHHO ROBLAHHO QOBLAHHO F2 平均值 1.82×10−120 5.93×10−119 1.75×10−118 4.76×10−119 标准差 4.85×10−120 3.23×10−118 8.86×10−112 2.57×10−118 F3 平均值 4.98×10−192 5.64×10−189 7.76×10−190 8.19×10−173 标准差 0.00 0.00 0.00 0.00 F4 平均值 1.46×10−117 1.75×10−115 7.57×10−116 1.69×10−117 标准差 7.86×10−117 8.42×10−111 4.09×10−113 5.49×10−117 F6 平均值 1.87×10−5 1.96×10−5 3.42×10−5 6.35×10−6 标准差 3.72×10−5 3.84×10−5 7.64×10−5 9.73×10−6 F7 平均值 8.15×10−5 8.53×10−5 8.90×10−5 1.14×10−4 标准差 7.42×10−5 7.03×10−5 8.28×10−5 1.33×10−4 F8 平均值 −1.23×104 −1.23×104 −1.22×104 −1.22×104 标准差 1.28×103 1.38×103 1.47×103 1.52×103 F13 平均值 1.12×10−5 2.42×10−5 1.18×10−5 4.17×10−4 标准差 2.12×10−5 4.35×10−5 1.67×10−5 5.92×10−4 F19 平均值 −3.86 −3.86 −3.86 −3.86 标准差 3.45×10−3 7.20×10−3 3.82×10−3 4.36×10−3 续表 3 函数 统计值 DAHHO OBLAHHO ROBLAHHO QOBLAHHO F21 平均值 −1.02×101 −9.98 −1.01×101 −9.98 标准差 3.02×10−3 9.30×10−1 5.93×10−3 9.30×10−1 F23 平均值 −1.05×101 −1.05×101 −1.05×101 −1.05×101 标准差 3.64×10−3 5.50×10−3 8.70×10−3 1.15×10−2 5.3 收敛性分析
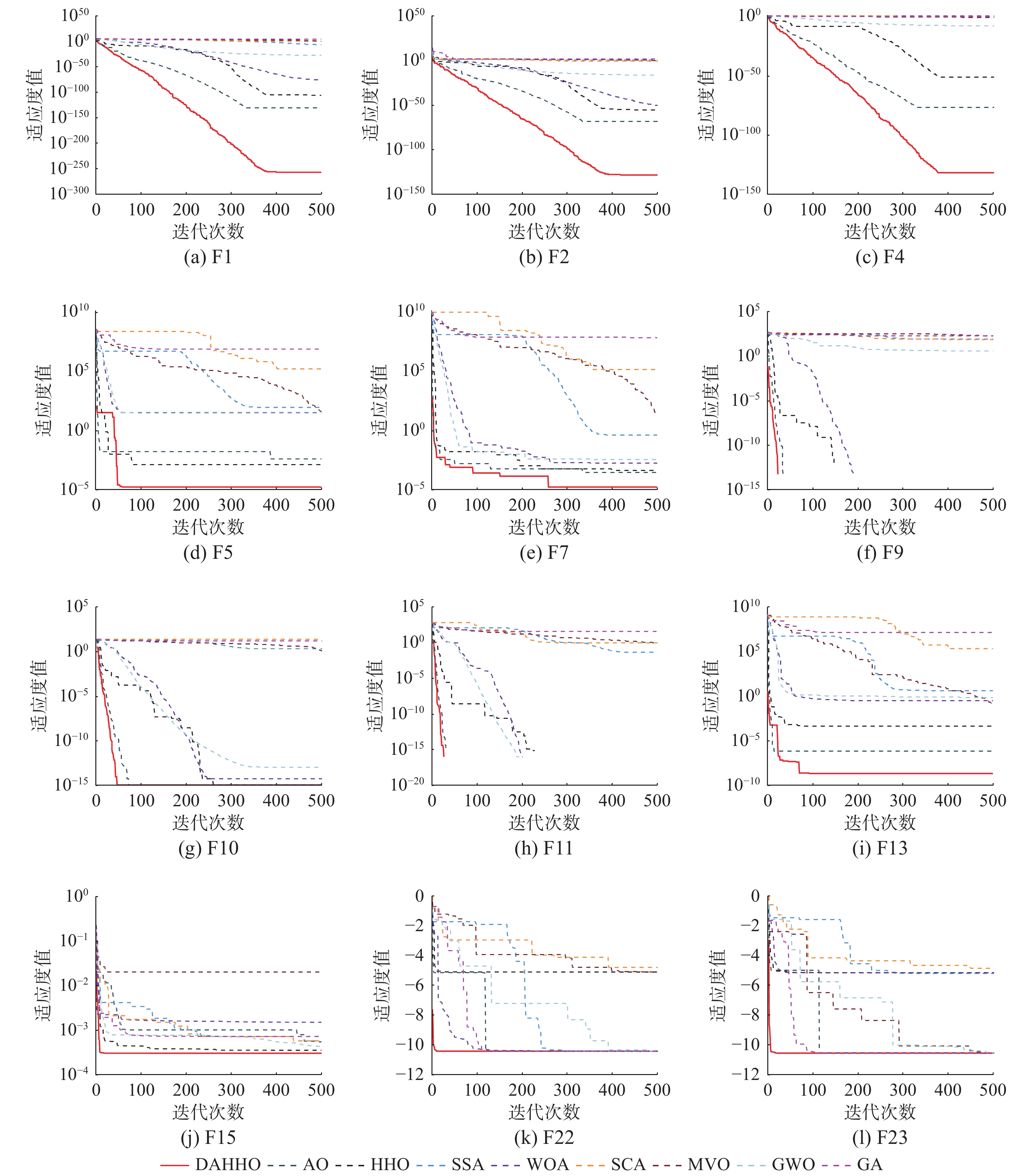
本文借助各算法求解基准测试函数的迭代曲线来验证DAHHO的收敛性。图3展示了各算法求解部分基准测试函数的收敛曲线。由图中可以看出，在求解单峰函数F1、F2和F4时，MVO、SSA、SCA和GA均过早收敛到局部最优解，而DAHHO随着迭代次数的增加，收敛精度不断提高，在迭代初期便超过了所有对比算法，在迭代末期收敛到更接近理论最优值的全局最优值。对于函数F5，可以看出DAHHO在迭代初期收敛精度便强于对比算法，可知引入动态反向学习策略成功提升算法收敛速度。对于F7，DAHHO算法的收敛曲线呈阶梯状下降，证明了本文所提算法均能跳出不同程度的局部最优解，也证明了HHO不错的开发能力。在函数F9和F11，AO、HHO与WOA均收敛到理论最优值，但收敛速度不及DAHHO。对于函数F10，仅有DAHHO、AO和HHO收敛到全局最优值，但AO和HHO的收敛速度不及DAHHO。对于函数F13，WOA、GWO、AO与HHO均陷入不同程度的局部最优值，MVO虽能不断跳出，但收敛精度太低，DAHHO在收敛前期就表现出优秀的寻优性能，具有较强的避免早熟收敛能力。对于函数F15、F22与F23，DAHHO均保持了最快的收敛速度和最佳的搜索精度。综上所述，混合算法有效利用了AO和HHO的优势特性，在基准测试函数上表现出更佳的优化性能，同时借助动态反向学习策略，提升了种群的初始化性能，为后续种群搜索奠定了基础，证实了DAHHO的收敛性。
图 3 各种算法收敛曲线Fig. 3 Convergence curves of various algorithm下载:
全尺寸图片
5.4 Wilcoxon秩和检验
上述仿真中，仅采用了平均值与标准差进行评价，为了进一步验证改进算法有效性，本文采用Wilcoxon秩和检验进行统计检验[21]。显著性水平设置为5%，若p值小于5%，则拒绝零假设，说明两种算法之间具有显著性差异，否则说明两种算法性能相差不大。Wilcoxon秩和检验p值结果如表4所示，因为算法无法与自身对比，故表中不再列出DAHHO的p值，其中p>0.05已用粗体展示，NaN表示数据无效，即实验样本数据相同，算法性能相当。
表 4 各算法Wilcoxon秩和检验结果Table 4 Wilcoxon rank sum test results of each algorithm函数 AO HHO SSA WOA SCA MVO GWO GA F1 3.392×10−6 3.392×10−6 3.392×10−6 3.392×10−6 3.392×10−6 3.392×10−6 3.392×10−6 3.392×10−6 F2 3.392×10−6 3.392×10−6 3.392×10−6 3.392×10−6 3.392×10−6 3.392×10−6 3.392×10−6 3.392×10−6 F3 3.392×10−6 3.392×10−6 3.392×10−6 3.392×10−6 3.392×10−6 3.392×10−6 3.392×10−6 3.392×10−6 F4 3.392×10−6 3.392×10−6 3.392×10−6 3.392×10−6 3.392×10−6 3.392×10−6 3.392×10−6 3.392×10−6 F5 2.628×10−2 1.356×10−4 3.392×10−6 3.392×10−6 3.392×10−6 3.392×10−6 3.392×10−6 3.392×10−6 F6 3.691×10−3 3.357×10−5 5.760×10−4 3.392×10−6 3.392×10−6 3.392×10−6 3.392×10−6 3.392×10−6 F7 4.450×10−2 3.615×10−2 3.392×10−6 7.477×10−6 3.392×10−6 3.392×10−6 3.392×10−6 3.392×10−6 F8 2.329×10−5 4.903×10−2 3.392×10−6 2.329×10−5 3.392×10−6 3.392×10−6 3.392×10−6 4.143×10−6 F9 NaN NaN 6.866×10−7 4.923×10−2 6.866×10−7 6.866×10−7 6.646×10−7 6.866×10−7 F10 NaN NaN 6.866×10−7 9.954×10−7 6.866×10−7 6.866×10−7 5.902×10−7 6.866×10−7 F11 NaN NaN 6.866×10−7 3.507×10−1 6.866×10−7 6.866×10−7 3.841×10−2 6.866×10−7 F12 2.253×10−2 3.230×10−3 3.392×10−6 3.392×10−6 3.392×10−6 3.392×10−6 3.392×10−6 3.392×10−6 F13 1.282×10−2 1.404×10−3 3.392×10−6 3.392×10−6 3.392×10−6 3.392×10−6 3.392×10−6 3.392×10−6 F14 2.808×10−1 4.902×10−2 1.611×10−3 2.290×10−1 5.897×10−1 2.823×10−3 6.700×10−4 1.102×10−3 F15 6.152×10−6 3.401×10−1 3.392×10−6 4.795×10−3 3.392×10−6 3.392×10−6 1.249×10−1 1.140×10−2 F16 3.392×10−6 5.202×10−1 1.140×10−2 4.450×10−2 3.392×10−6 3.392×10−6 3.392×10−6 2.739×10−6 F17 4.143×10−6 4.800×10−2 3.275×10−6 1.620×10−3 3.392×10−6 5.615×10−1 2.253×10−2 6.866×10−7 F18 3.392×10−6 2.808×10−1 6.152×10−6 1.892×10−4 6.152×10−6 2.329×10−5 1.935×10−5 2.668×10−6 F19 1.866×10−3 2.134×10−1 3.392×10−6 1.249×10−2 3.230×10−3 1.356×10−4 7.716×10−1 1.563×10−6 F20 4.197×10−2 3.401×10−2 4.225×10−4 5.452×10−3 1.140×10−2 4.806×10−5 9.662×10−5 2.622×10−4 F21 1.711×10−1 3.392×10−6 9.709×10−2 9.662×10−5 3.392×10−6 2.019×10−2 1.150×10−2 1.968×10−1 F22 2.019×10−2 3.192×10−6 6.709×10−4 1.330×10−5 3.392×10−6 4.150×10−2 6.187×10−1 6.115×10−4 F23 1.099×10−5 3.392×10−6 4.150×10−4 4.143×10−6 3.392×10−6 1.057×10−2 4.795×10−3 5.553×10−6 由表4可知，大部分p值均小于5%，表明DAHHO算法优越性在统计检验上是显著的。可以认为DAHHO算法相比于对比算法，表现出更好的寻优能力。
通过分析算法收敛精度、收敛曲线与统计性检验，可以得出结论：基于两种算法的优势特性、本文改进算法DAHHO的全局探索能力、局部开发能力与避免早熟收敛能力均得到增强，此外加入动态反向学习有效提升了算法的收敛速度，表现出更优秀的收敛性能及稳定性。
6. 工程设计优化问题
为了验证DAHHO对现实工程问题的优化性能，本文引入管柱设计问题和汽车碰撞设计问题对算法进行测试。实验参数设置5.1节所述相同。
6.1 管柱设计问题
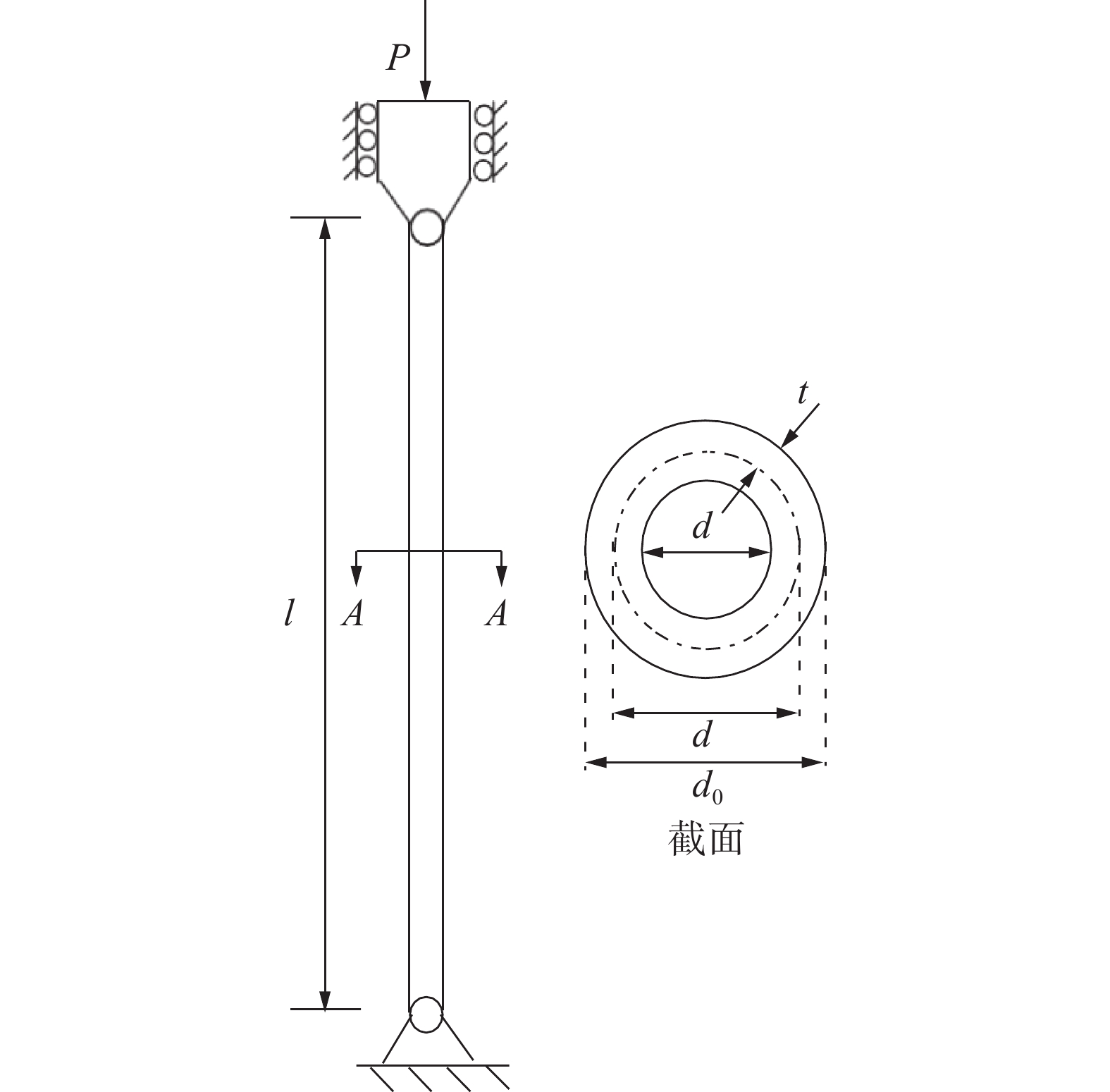
管柱设计问题[22]是一个常用的工程设计问题。模型如图4所示。该问题试图使管柱设计成本最小化，其需要优化的变量有两个，分别是直径d与厚度t。数学公式为
图 4 管柱设计问题Fig. 4 Tubular column design problem下载:
全尺寸图片
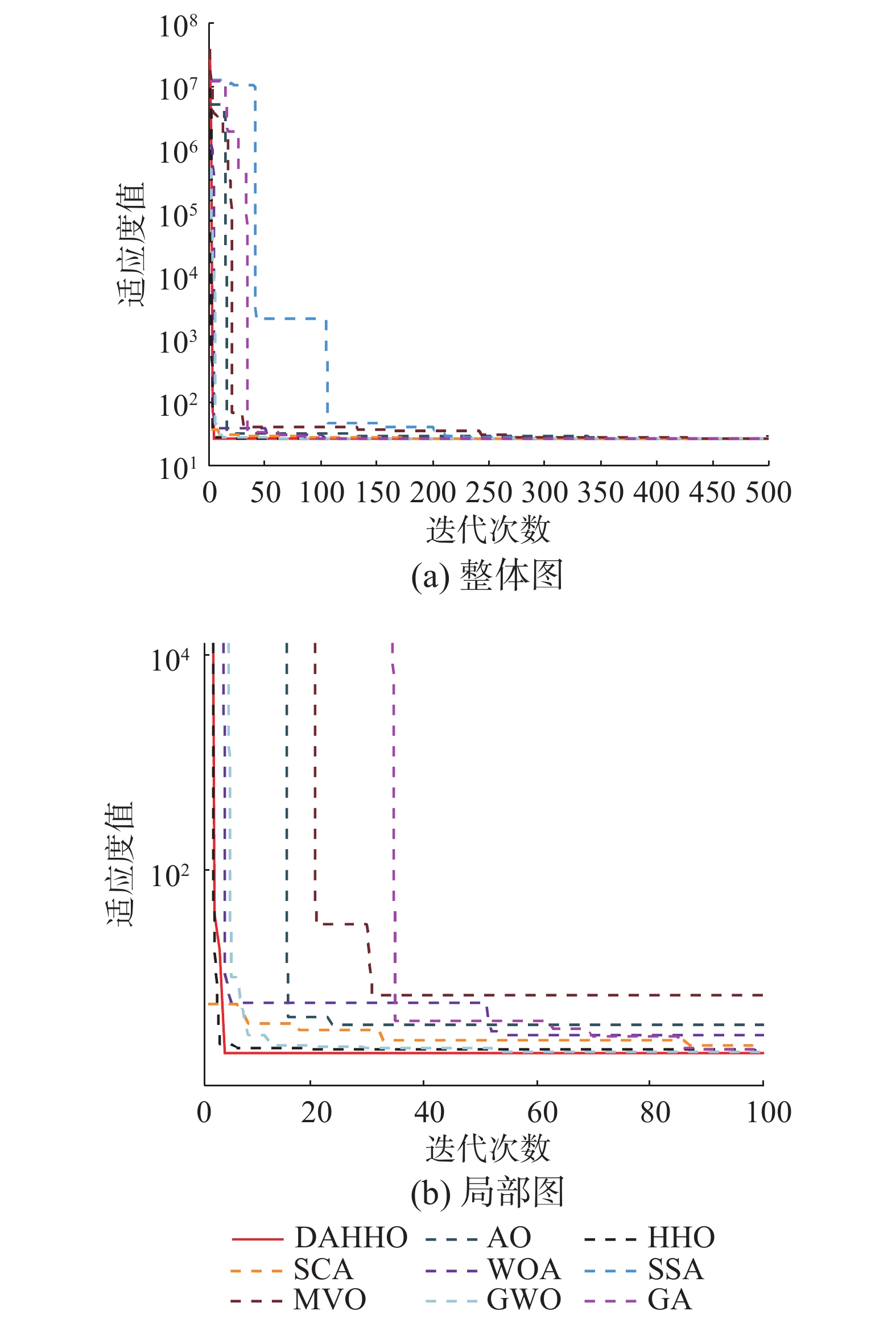
$$\left\{ \begin{gathered} f(d,t) = 9.8dt + 2d \\ {g_1} = \frac{P}{{{\text{π}} dt{\sigma _y}}} - 1 \leqslant 0,\\ {g_2} = \frac{{8P{L^2}}}{{{{\text{π}} ^3}Edt({d^2} + {t^2})}} - 1 \leqslant 0 \\ {g_3} = \frac{{2.0}}{d} - 1 \leqslant 0,\\ {g_4} = \frac{d}{{14}} - 1 \leqslant 0, \\ {g_5} = \frac{{0.2}}{t} - 1 \leqslant 0,\\ {g_6} = \frac{t}{{0.8}} - 1 \leqslant 0 \\ \end{gathered}\right. $$ 表5列出了DAHHO及对比算法求解管柱设计问题的实验结果。通过数据可以看出，DAHHO相比于WOA有较大提升。相比于其他算法，DAHHO也有不同程度的提升。图5展示了各算法求解管柱设计问题收敛曲线，可以看出DAHHO具有较快的收敛速度。总体来看，DAHHO在求解管柱设计问题时能够提供优秀的解决方案。
表 5 各算法求解管柱设计问题优化结果Table 5 Optimization results of each algorithm for tubular column design算法 d t 结果 DAHHO 5.4512 0.2920 26.5313 AO 5.4652 0.2934 26.6788 HHO 5.4998 0.2894 26.6285 SSA 5.4779 0.2906 26.5887 WOA 6.1227 0.2599 27.8744 SCA 5.523 0.2887 26.7019 MVO 5.4847 0.2909 26.6370 GWO 5.4536 0.2919 26.5375 GA 5.374 0.3092 27.0627 
图 5 各算法求解管柱设计问题收敛曲线Fig. 5 Convergence curve of each algorithm for tubular column design problem下载:
全尺寸图片
6.2 汽车碰撞设计问题
汽车碰撞设计问题是一个经典工程设计问题，与我们的日常生活息息相关[23]。设计模型如图6所示。该问题对汽车侧面进行撞击，若不断增强汽车侧面耐撞性能，则汽车重量也随之增加，从而提高汽车日常使用成本。因此，汽车碰撞设计问题试图使汽车安全性能与总重量达到一定的平衡。本问题需要最小化一个具有11个设计变量的目标函数，分别是：B柱内板厚度x1、B柱加强筋厚度x2、地板内侧厚度x3、横梁厚度x4、门梁厚度x5、车门腰线加固x6、车顶纵梁厚度x7、B柱内件材质x8、内板内侧材料x9、屏障高度x10和障碍物撞击位置x11，具体数学模型为
图 6 汽车碰撞设计问题Fig. 6 Car crash design problem下载:
全尺寸图片
目标函数：f(x)=1.98+4.90x1+6.67x2+6.98x3+4.01x4+1.78x5+2.73x7，
约束条件：
g1(x)=1.16−0.37170.00931x2x4−0.00931x2x10−0.484x3x9+0.01343x6x10 ≤ 1，
g2(x)=0.261−0.0159x1x2−0.188x1x8−0.019x2x7+0.0144x3x5 + 0.0008757x5x10 + 0.080405x6x9 +0.00139x8x11+0.00001575x10x11 ≤ 0.32，
g3(x)=0.214+0.00817x5−0.131x1x8−0.0704x1x9+0.03099x2x6 − 0.018 x2x7+0.0208x3x8 + 0.121x3x9 − 0.00364 x5x6 + 0.0007715x5x10 − 0.0005354 x6x10 +0.00121x8x11 ≤ 0.32，
g4(x)=0.074−0.061x2−0.163x3x8+0.001232x3x10−0.166x7x9+0.227
$x_2^2 $ ≤ 0.32，g5(x)=28.98+3.818x3−4.2x1x2+0.0207x5x10+6.63x6x9−7.7x7x8+0.32x9x10 ≤ 32，
g6(x)=33.86+2.95x3+0.1792x10−5.057x1x2−11.0x2x8−0.0215x5x10−9.98x7x8+22.0x8x9 ≤ 32，
g7(x)=46.36−9.9x2−12.9x1x8+0.1107x3x10 ≤ 32
g8(x) = 4.72 − 0.5x4 − 0.19x2x3 − 0.0122x4x10 +0.009325x6x10+0.000191
$x_{11}^2$ ≤ 4g9(x)=10.58−0.674x1x2−1.95x2x8+0.02054x3x10−0.0198x4x10+0.028x6x10 ≤ 9.9
g10(x)=16.45−0.489x3x7−0.843x5x6+0.0432x9x10−0.0556x9x11−0.000786
$x_{11}^2 $ ≤ 15.7变量范围：
$0.5 \leqslant {x_1} \sim {x_7}\leqslant 1.5,{x_8}, {x_9} \in (0.192,0.345), - 30 \leqslant {x_{10}},{x_{11}} \leqslant 30$ 。表6列出了各算法求解汽车碰撞设计问题所得实验结果，可以看出DAHHO得到的解决方案是最佳的。同时图7展示了各算法求解该问题的收敛曲线，可以看出DAHHO具有较快的收敛速度和跳出局部极值能力，说明本文算法DAHHO对于求解这类工程问题具有良好的性能。
表 6 各算法应用汽车碰撞设计问题优化结果Table 6 Algorithms applied to the optimization results of car crush design problem算法 x1 x2 x3 x4 x5 x6 x7 x8 x9 x10 x11 结果 DAHHO 0.5046 1.2507 0.5000 1.1138 0.5006 0.5009 0.5004 0.3427 0.2768 3.8389 6.9421 22.9975 AO 0.5901 1.2008 0.5189 1.1813 0.5137 0.7646 0.5853 0.3450 0.1920 0.8966 2.0208 23.7403 HHO 0.5000 1.3342 0.5000 1.1407 0.5483 0.5000 0.5000 0.2000 0.3052 1.7723 8.2050 23.7233 SSA 0.5000 1.2329 0.5000 1.1635 0.5000 1.2465 0.5000 0.3439 0.2696 0.4011 0.3779 23.0528 WOA 0.5000 1.3311 0.5000 1.2461 0.6878 0.5000 0.5526 0.1920 0.1920 0.2747 1.2092 24.5159 SCA 0.5000 1.3338 0.5000 1.5000 0.5000 0.5083 0.5000 0.1920 0.3450 0.1834 18.8321 25.0711 MVO 0.5000 1.2390 0.5000 1.1503 0.5000 0.8584 0.5023 0.3447 0.1986 1.5950 3.4810 23.0468 GWO 0.5000 1.2416 0.5000 1.1408 0.5000 0.5639 0.5003 0.3450 0.2956 2.0066 5.1117 23.0202 GA 0.5907 1.3087 0.5767 1.1444 1.0940 0.5000 0.9016 0.1920 0.2401 0.2869 8.1420 26.6149 通过对以上2种不同类型的经典工程问题进行测试，充分说明了本文改进算法DAHHO在求解此类工程问题上具有较好的应用潜力，能够提供优良可信的解决方案。
图 7 各算法求解汽车碰撞设计问题收敛曲线Fig. 7 Convergence curve of each algorithm for car crush design problem design problem下载:
全尺寸图片
7. 结束语
本文针对AO和HHO两种新型优化算法的优势互补特点，提出了融合动态反向学习的阿奎拉鹰与哈里斯鹰混合优化算法。DAHHO保留了原AO算法较强的全局探索能力，同时将HHO较强的局部开发能力融入AO的局部位置更新中，使算法有效避免局部最优。此外，初始化阶段引入动态反向学习策略，增加初始化种群多样性，提高算法的收敛速度。仿真实验部分对23个基准测试函数及2个工程设计问题进行了验证。同时，在混合算法的基础上引入其他经典反向学习策略进行对比，结果表明引入动态反向学习的混合算法DAHHO的寻优性能更佳，在整体上也明显优于GWO、WOA和SSA等经典MAs，具有更佳的收敛速度、收敛精度、鲁棒性和工程适用性，为解决约束工程问题提供了一种行之有效的计算方法。未来的研究考虑将DAHHO应用到图像多阈值分割或特征选择中，并结合实际问题作进一步研究。
-
图 1 能量逃逸因子曲线图
Fig. 1 Curve of energy escape factor
下载:
全尺寸图片
图 2 DAHHO算法的不同阶段
Fig. 2 Different phases of DAHHO
下载:
全尺寸图片
图 3 各种算法收敛曲线
Fig. 3 Convergence curves of various algorithm
下载:
全尺寸图片
图 4 管柱设计问题
Fig. 4 Tubular column design problem
下载:
全尺寸图片
图 5 各算法求解管柱设计问题收敛曲线
Fig. 5 Convergence curve of each algorithm for tubular column design problem
下载:
全尺寸图片
图 6 汽车碰撞设计问题
Fig. 6 Car crash design problem
下载:
全尺寸图片
图 7 各算法求解汽车碰撞设计问题收敛曲线
Fig. 7 Convergence curve of each algorithm for car crush design problem design problem
下载:
全尺寸图片
表 1 各算法参数设置
Table 1 Parameter setting of each algorithm
算法 参数名称 参数设置 AO[8] 搜索周期参数 C=10 HHO[7] 随机跳跃长度 J=[0,2] SSA[16] 平衡参数 c1=[1,0] 收敛因子 a=[2,0] WOA[6] 随机数 l=[−1,1] 螺旋常数 b=1 SCA[17] 移动系数 a=2 MVO[18] 蠕虫存在率 WEP=[0.2,1] 旅行距离率 TDR=[0.6450,0] GWO[19] 收敛因子 a=[2,0] GA[20] 交叉概率 Pc=0.7 变异概率 Pm=0.3 OBLAHHO 随机跳跃距离 J=[0,2] ROBLAHHO 随机跳跃距离 J=[0,2] QOBLAHHO 随机跳跃距离 J=[0,2] 表 2 DAHHO与对比算法的基准函数测试结果
Table 2 Benchmark function results of DAHHO and contrast algorithm
函数 统计值 DAHHO AO HHO SSA WOA SCA MVO GWO GA F1 平均值 1.068×10−231 6.400×10−99 8.200×10−98 1.667×10−7 7.250×10−74 1.882×101 1.210 8.881×10−28 7.103×103 标准差 0.000 2.650×10−98 4.330×10−97 1.752×10−7 3.560×10−73 4.216×101 4.300×10−1 1.838×10−27 2.784×103 F2 平均值 1.819×10−120 2.800×10−53 4.060×10−52 1.944 1.370×10−49 1.800×10−2 1.150 9.163×10−17 3.539×101 标准差 4.849×10−120 1.530×10−52 1.900×10−51 1.477 7.420×10−49 3.000×10−2 1.390 5.910×10−17 5.673 F3 平均值 4.982×10−192 3.040×10−109 5.060×10−69 1.257×103 4.663×104 8.659×103 2.405×102 9.791×10−6 9.976×103 标准差 0.000 1.660×10−108 2.770×10−68 7.937×102 1.357E×105 6.034×103 1.105×102 2.516×10−5 4.027×103 F4 平均值 1.464×10−117 7.100×10−55 1.290×10−47 1.076×101 4.983×101 3.364×101 2.080 8.978×10−7 2.747×101 标准差 7.860×10−117 3.880×10−54 6.140×10−47 3.439 2.536×101 1.124×101 8.000×10−1 1.000×10−6 4.449 F5 平均值 4.617×10−4 6.500×10−3 1.420×10−2 2.359×102 2.793×101 1.586×104 3.680×102 2.721×101 3.352×106 标准差 7.029×10−3 9.000×10−3 2.600×10−2 4.215×102 5.200×10−1 2.369×104 6.076×102 7.400×10−1 1.755×106 F6 平均值 7.443×10−6 1.500×10−4 1.400×10−4 1.508×10−7 4.010×10−1 2.506×101 1.260 8.188×10−1 7.327×103 标准差 1.300×10−5 4.000×10−4 1.900×10−4 1.290×10−7 2.340×10−1 6.332×101 3.603×10−1 3.573×10−1 2.203×103 F7 平均值 9.154×10−5 2.000×10−4 1.000×10−4 1.600×10−1 2.000×10−3 1.620×10−1 1.489×101 2.323×10−3 1.581 标准差 7.424×10−5 8.300×10−5 1.000×10−4 6.293×10−2 2.800×10−3 8.200×10−2 1.028×101 1.537×10−3 1.120 F8 平均值 −1.227×104 −8.154×103 −1.253×104 −7.544×103 −1.018×104 −3.775×103 −7.668×103 −5.702×103 −5.188×103 标准差 1.280×103 4.021×103 1.354×102 6.536×102 2.017×103 2.577×102 8.095×102 6.549×102 8.136×102 F9 平均值 0.000 0.000 0.000 4.663×101 0.000 4.168×101 1.198×102 3.852 1.911×102 标准差 0.000 0.000 0.000 1.363×101 0.000 3.315×101 3.638×101 4.545 2.379×101 F10 平均值 8.882×10−16 8.880×10−16 8.880×10−16 2.583 3.840×10−15 1.499×101 1.843 9.847×10−14 1.339×101 标准差 0.000 0.000 0.000 7.491×10−1 2.480×10−15 8.078 6.290×10−1 1.663×10−14 1.227 F11 平均值 0.000 0.000 0.000 1.590×10−2 1.500×10−2 9.300×10−1 8.500×10−1 5.621×10−3 6.088×101 标准差 0.000 0.000 0.000 1.224×10−2 4.200×10−2 3.330×10−1 8.000×10−2 1.033×10−2 1.687×101 F12 平均值 1.842×10−6 3.130×10−6 6.610×10−6 6.996 2.400×10−2 2.638×104 2.048 3.669×10−2 1.661×105 标准差 2.964×10−6 4.490×10−6 7.650×10−6 2.859 1.200×10−2 7.601×104 1.430 1.645×10−2 3.700×105 F13 平均值 1.119×10−5 3.880×10−5 8.040×10−5 1.902×101 4.499×10−1 8.043×104 2.242×10−1 7.337×10−1 3.813×106 标准差 2.121×10−5 4.540×10−5 1.000×10−4 1.356×101 2.272×10−1 2.348×105 1.196×10−1 2.986×10−1 3.227×106 F14 平均值 2.706 2.010 1.097 1.230 2.862 2.056 9.980×10−1 3.488 1.559 标准差 2.528 2.714 3.033×10−1 5.005×10−1 3.320 1.006 2.430×10−11 3.223 1.287 F15 平均值 3.543×10−4 5.000×10−4 4.000×10−4 2.170×10−3 6.000×10−4 1.000×10−3 4.300×10−3 3.701×10−3 2.223×10−3 标准差 6.154×10−5 1.000×10−4 1.000×10−4 4.955×10−3 4.000×10−4 3.000×10−4 1.100×10−2 7.579×10−3 4.953×10−3 F16 平均值 −1.032 −1.032 −1.032 −1.032 −1.032 −1.032 −1.032 −1.032 −1.032 标准差 2.580×10−13 3.000×10−4 4.830×10−9 2.899×10−12 2.170×10−9 6.630×10−5 2.640×10−7 2.065×10−8 6.454×10−10 续表 2 函数 统计值 DAHHO AO HHO SSA WOA SCA MVO GWO GA F17 平均值 3.980×10−1 3.980×10−1 3.980×10−1 3.979×10−1 3.980×10−1 3.996×10−1 3.980×10−1 3.979×10−1 3.979×10−1 标准差 1.073×10−13 1.000×10−4 6.490×10−6 1.437×10−11 1.320×10−5 1.646×10−3 1.880×10−7 6.391×10−7 2.875×10−10 F18 平均值 3.000 3.043 3.000 3.000 3.000 3.000 5.700 3.000 3.000 标准差 2.153×10−12 4.000×10−2 3.830×10−7 2.116×10−10 5.570×10−5 1.000×10−4 1.479×101 6.101×10−5 1.962×10−10 F19 平均值 −3.861 −3.860 −3.860 −3.860 −3.860 −3.870 −3.860 −3.860 −3.860 标准差 3.449×10−9 6.000×10−3 3.300×10−3 1.152×10−7 1.300×10−2 1.000×10−2 3.580×10−6 4.141×10−3 2.539×10−4 F20 平均值 −3.074 −3.170 −3.115 −3.220 −3.250 −2.910 −3.290 −3.268 −3.233 标准差 1.311×10−1 1.020×10−1 1.200×10−1 5.836×10−2 8.300×10−2 3.500×10−1 5.390×10−2 6.952×10−2 8.950×10−2 F21 平均值 −1.015×101 −1.015×101 −5.381 −8.240 −7.583 −2.729 −7.043 −9.476 −9.479 标准差 3.025×10−3 9.900×10−3 8.770×10−1 3.254 2.572 2.105 3.077 1.751 1.747 F22 平均值 −1.022×101 −1.040×101 −5.080 −7.978 −8.554 −3.171 −8.069 −1.011×101 −8.836 标准差 9.700×10−1 8.000×10−2 4.230×10−1 3.114 2.897 1.757 3.199 9.898×10−4 2.916 F23 平均值 −1.054×101 −1.054×101 −5.120 −8.723 −5.902 −3.975 −9.012 −1.026×101 −9.690 标准差 3.641×10−3 1.400×10−2 4.940×10−1 3.122 3.020 1.836 2.864 1.481 2.221 表 3 DAHHO与不同类型反向学习混合算法的基准函数测试结果
Table 3 Benchmark function results of DAHHO and different types of opposition-based learning hybrid algorithms
函数 统计值 DAHHO OBLAHHO ROBLAHHO QOBLAHHO F2 平均值 1.82×10−120 5.93×10−119 1.75×10−118 4.76×10−119 标准差 4.85×10−120 3.23×10−118 8.86×10−112 2.57×10−118 F3 平均值 4.98×10−192 5.64×10−189 7.76×10−190 8.19×10−173 标准差 0.00 0.00 0.00 0.00 F4 平均值 1.46×10−117 1.75×10−115 7.57×10−116 1.69×10−117 标准差 7.86×10−117 8.42×10−111 4.09×10−113 5.49×10−117 F6 平均值 1.87×10−5 1.96×10−5 3.42×10−5 6.35×10−6 标准差 3.72×10−5 3.84×10−5 7.64×10−5 9.73×10−6 F7 平均值 8.15×10−5 8.53×10−5 8.90×10−5 1.14×10−4 标准差 7.42×10−5 7.03×10−5 8.28×10−5 1.33×10−4 F8 平均值 −1.23×104 −1.23×104 −1.22×104 −1.22×104 标准差 1.28×103 1.38×103 1.47×103 1.52×103 F13 平均值 1.12×10−5 2.42×10−5 1.18×10−5 4.17×10−4 标准差 2.12×10−5 4.35×10−5 1.67×10−5 5.92×10−4 F19 平均值 −3.86 −3.86 −3.86 −3.86 标准差 3.45×10−3 7.20×10−3 3.82×10−3 4.36×10−3 续表 3 函数 统计值 DAHHO OBLAHHO ROBLAHHO QOBLAHHO F21 平均值 −1.02×101 −9.98 −1.01×101 −9.98 标准差 3.02×10−3 9.30×10−1 5.93×10−3 9.30×10−1 F23 平均值 −1.05×101 −1.05×101 −1.05×101 −1.05×101 标准差 3.64×10−3 5.50×10−3 8.70×10−3 1.15×10−2 表 4 各算法Wilcoxon秩和检验结果
Table 4 Wilcoxon rank sum test results of each algorithm
函数 AO HHO SSA WOA SCA MVO GWO GA F1 3.392×10−6 3.392×10−6 3.392×10−6 3.392×10−6 3.392×10−6 3.392×10−6 3.392×10−6 3.392×10−6 F2 3.392×10−6 3.392×10−6 3.392×10−6 3.392×10−6 3.392×10−6 3.392×10−6 3.392×10−6 3.392×10−6 F3 3.392×10−6 3.392×10−6 3.392×10−6 3.392×10−6 3.392×10−6 3.392×10−6 3.392×10−6 3.392×10−6 F4 3.392×10−6 3.392×10−6 3.392×10−6 3.392×10−6 3.392×10−6 3.392×10−6 3.392×10−6 3.392×10−6 F5 2.628×10−2 1.356×10−4 3.392×10−6 3.392×10−6 3.392×10−6 3.392×10−6 3.392×10−6 3.392×10−6 F6 3.691×10−3 3.357×10−5 5.760×10−4 3.392×10−6 3.392×10−6 3.392×10−6 3.392×10−6 3.392×10−6 F7 4.450×10−2 3.615×10−2 3.392×10−6 7.477×10−6 3.392×10−6 3.392×10−6 3.392×10−6 3.392×10−6 F8 2.329×10−5 4.903×10−2 3.392×10−6 2.329×10−5 3.392×10−6 3.392×10−6 3.392×10−6 4.143×10−6 F9 NaN NaN 6.866×10−7 4.923×10−2 6.866×10−7 6.866×10−7 6.646×10−7 6.866×10−7 F10 NaN NaN 6.866×10−7 9.954×10−7 6.866×10−7 6.866×10−7 5.902×10−7 6.866×10−7 F11 NaN NaN 6.866×10−7 3.507×10−1 6.866×10−7 6.866×10−7 3.841×10−2 6.866×10−7 F12 2.253×10−2 3.230×10−3 3.392×10−6 3.392×10−6 3.392×10−6 3.392×10−6 3.392×10−6 3.392×10−6 F13 1.282×10−2 1.404×10−3 3.392×10−6 3.392×10−6 3.392×10−6 3.392×10−6 3.392×10−6 3.392×10−6 F14 2.808×10−1 4.902×10−2 1.611×10−3 2.290×10−1 5.897×10−1 2.823×10−3 6.700×10−4 1.102×10−3 F15 6.152×10−6 3.401×10−1 3.392×10−6 4.795×10−3 3.392×10−6 3.392×10−6 1.249×10−1 1.140×10−2 F16 3.392×10−6 5.202×10−1 1.140×10−2 4.450×10−2 3.392×10−6 3.392×10−6 3.392×10−6 2.739×10−6 F17 4.143×10−6 4.800×10−2 3.275×10−6 1.620×10−3 3.392×10−6 5.615×10−1 2.253×10−2 6.866×10−7 F18 3.392×10−6 2.808×10−1 6.152×10−6 1.892×10−4 6.152×10−6 2.329×10−5 1.935×10−5 2.668×10−6 F19 1.866×10−3 2.134×10−1 3.392×10−6 1.249×10−2 3.230×10−3 1.356×10−4 7.716×10−1 1.563×10−6 F20 4.197×10−2 3.401×10−2 4.225×10−4 5.452×10−3 1.140×10−2 4.806×10−5 9.662×10−5 2.622×10−4 F21 1.711×10−1 3.392×10−6 9.709×10−2 9.662×10−5 3.392×10−6 2.019×10−2 1.150×10−2 1.968×10−1 F22 2.019×10−2 3.192×10−6 6.709×10−4 1.330×10−5 3.392×10−6 4.150×10−2 6.187×10−1 6.115×10−4 F23 1.099×10−5 3.392×10−6 4.150×10−4 4.143×10−6 3.392×10−6 1.057×10−2 4.795×10−3 5.553×10−6 表 5 各算法求解管柱设计问题优化结果
Table 5 Optimization results of each algorithm for tubular column design
算法 d t 结果 DAHHO 5.4512 0.2920 26.5313 AO 5.4652 0.2934 26.6788 HHO 5.4998 0.2894 26.6285 SSA 5.4779 0.2906 26.5887 WOA 6.1227 0.2599 27.8744 SCA 5.523 0.2887 26.7019 MVO 5.4847 0.2909 26.6370 GWO 5.4536 0.2919 26.5375 GA 5.374 0.3092 27.0627 表 6 各算法应用汽车碰撞设计问题优化结果
Table 6 Algorithms applied to the optimization results of car crush design problem
算法 x1 x2 x3 x4 x5 x6 x7 x8 x9 x10 x11 结果 DAHHO 0.5046 1.2507 0.5000 1.1138 0.5006 0.5009 0.5004 0.3427 0.2768 3.8389 6.9421 22.9975 AO 0.5901 1.2008 0.5189 1.1813 0.5137 0.7646 0.5853 0.3450 0.1920 0.8966 2.0208 23.7403 HHO 0.5000 1.3342 0.5000 1.1407 0.5483 0.5000 0.5000 0.2000 0.3052 1.7723 8.2050 23.7233 SSA 0.5000 1.2329 0.5000 1.1635 0.5000 1.2465 0.5000 0.3439 0.2696 0.4011 0.3779 23.0528 WOA 0.5000 1.3311 0.5000 1.2461 0.6878 0.5000 0.5526 0.1920 0.1920 0.2747 1.2092 24.5159 SCA 0.5000 1.3338 0.5000 1.5000 0.5000 0.5083 0.5000 0.1920 0.3450 0.1834 18.8321 25.0711 MVO 0.5000 1.2390 0.5000 1.1503 0.5000 0.8584 0.5023 0.3447 0.1986 1.5950 3.4810 23.0468 GWO 0.5000 1.2416 0.5000 1.1408 0.5000 0.5639 0.5003 0.3450 0.2956 2.0066 5.1117 23.0202 GA 0.5907 1.3087 0.5767 1.1444 1.0940 0.5000 0.9016 0.1920 0.2401 0.2869 8.1420 26.6149 -
[1] 贾鹤鸣, 李瑶, 孙康健. 基于遗传乌燕鸥算法的同步优化特征选择[J]. 自动化学报, 2022, 48(6): 1601–1615. JIA Heming, LI Yao, SUN Kangjian. Simultaneous feature selection optimization based on hybrid sooty tern optimization algorithm and genetic algorithm[J]. Acta automatica sinica, 2022, 48(6): 1601–1615. [2] 贾鹤鸣, 姜子超, 李瑶. 基于改进秃鹰搜索算法的同步优化特征选择[J]. 控制与决策, 2022, 37(2): 445–454. JIA Heming, JIANG Zichao, LI Yao. Simultaneous feature selection optimization based on improved bald eagle search algorithm[J]. Control and decision, 2022, 37(2): 445–454. [3] 贾鹤鸣, 姜子超, 李瑶, 等. 基于改进斑点鬣狗优化算法的同步优化特征选择[J]. 计算机应用, 2021, 41(5): 1290–1298. JIA Heming, JIANG Zichao, LI Yao, et al. Simultaneous feature selection optimization based on improved spotted hyena optimizer algorithm[J]. Journal of computer applications, 2021, 41(5): 1290–1298. [4] 贾鹤鸣, 刘宇翔, 刘庆鑫, 等. 融合随机反向学习的黏菌与算术混合优化算法[J]. 计算机科学与探索, 2022, 16(5): 1182–1192. doi: 10.3778/j.issn.1673-9418.2105016 JIA Heming, LIU Yuxiang, LIU Qingxin, et al. Hybrid algorithm of slime mould algorithm and arithmetic optimization algorithm based on random opposition-based learning[J]. Journal of frontiers of computer science and technology, 2022, 16(5): 1182–1192. doi: 10.3778/j.issn.1673-9418.2105016 [5] KATOCH S, CHAUHAN S S, KUMAR V. A review on genetic algorithm: past, present, and future[J]. Multimedia tools and applications, 2021, 80(5): 8091–8126. doi: 10.1007/s11042-020-10139-6 [6] KENNEDY J, EBERHART R. Particle swarm optimization[C]//Proceedings of ICNN’95 - International Conference on Neural Networks. Perth: IEEE, 1995: 1942−1948. [7] MIRJALILI S, MIRJALILI S M, LEWIS A. Grey wolf optimizer[J]. Advances in engineering software, 2014, 69: 46–61. doi: 10.1016/j.advengsoft.2013.12.007 [8] MIRJALILI S, MIRJALILI S M, HATAMLOU A. Multi-verse optimizer: a nature-inspired algorithm for global optimization[J]. Neural computing and applications, 2016, 27(2): 495–513. doi: 10.1007/s00521-015-1870-7 [9] MIRJALILI S. SCA: a sine cosine algorithm for solving optimization problems[J]. Knowledge-based systems, 2016, 96: 120–133. doi: 10.1016/j.knosys.2015.12.022 [10] MIRJALILI S, LEWIS A. The whale optimization algorithm[J]. Advances in engineering software, 2016, 95: 51–67. doi: 10.1016/j.advengsoft.2016.01.008 [11] MIRJALILI S, GANDOMI A H, MIRJALILI S Z, et al. Salp swarm algorithm: a bio-inspired optimizer for engineering design problems[J]. Advances in engineering software, 2017, 114: 163–191. doi: 10.1016/j.advengsoft.2017.07.002 [12] HEIDARI A A, MIRJALILI S, FARIS H, et al. Harris hawks optimization: algorithm and applications[J]. Future generation computer systems, 2019, 97: 849–872. doi: 10.1016/j.future.2019.02.028 [13] ABUALIGAH L, YOUSRI D, ABD ELAZIZ M, et al. Aquila optimizer: a novel meta-heuristic optimization algorithm[J]. Computers & industrial engineering, 2021, 157: 107250. [14] WOLPERT D H, MACREADY W G. No free lunch theorems for optimization[J]. IEEE transactions on evolutionary computation, 1997, 1(1): 67–82. doi: 10.1109/4235.585893 [15] AL-QANESS M A A, EWEES A A, FAN Hong, et al. Modified Aquila optimizer for forecasting oil production[J]. Geo-spatial information science, 2022, 25(4): 519–535. [16] LI Xiaoyan, MOBAYEN S. Optimal design of a PEMFC-based combined cooling, heating and power system based on an improved version of Aquila optimizer[J]. Concurrency and computation:practice and experience, 2022, 34(15): e6976. [17] 刘小龙, 梁彤缨. 基于方形邻域和随机数组的哈里斯鹰优化算法[J/OL]. 控制与决策, 2021. [2021−08−19]. https: //doi. org/10.13195/j. kzyjc. 2021.0478. LIU Xiaolong, LIANG Tongying. Harris hawk optimization Algorithm based on square neighborhood and random array[J/OL]. Control and decision, 2021. [2021−08−19].https://doi.org/10.13195/j.kzyjc.2021.0478. [18] SUN Pu, LIU Hao, ZHANG Yong, et al. An improved atom search optimization with dynamic opposite learning and heterogeneous comprehensive learning[J]. Applied soft computing, 2021, 103: 107140. doi: 10.1016/j.asoc.2021.107140 [19] HOUSSEIN E H, HUSSAIN K, ABUALIGAH L, et al. An improved opposition-based marine predators algorithm for global optimization and multilevel thresholding image segmentation[J]. Knowledge-based systems, 2021, 229: 107348. doi: 10.1016/j.knosys.2021.107348 [20] FAN Qian, CHEN Zhenjian, XIA Zhanghua. A novel quasi-reflected Harris hawks optimization algorithm for global optimization problems[J]. Soft computing, 2020, 24(19): 14825–14843. doi: 10.1007/s00500-020-04834-7 [21] TAHERI A, RAHIMIZADEH K, RAO R V. An efficient balanced teaching-learning-based optimization algorithm with individual restarting strategy for solving global optimization problems[J]. Information sciences, 2021, 576: 68–104. doi: 10.1016/j.ins.2021.06.064 [22] GANDOMI A H, YANG Xinshe, ALAVI A H. Cuckoo search algorithm: a metaheuristic approach to solve structural optimization problems[J]. Engineering with computers, 2013, 29(1): 17–35. doi: 10.1007/s00366-011-0241-y [23] YILDIZ B S, PHOLDEE N, BUREERAT S, et al. Enhanced grasshopper optimization algorithm using elite opposition-based learning for solving real-world engineering problems[J]. Engineering with computers, 2022, 38(5): 4207–4219.
