A genetic-firework hybrid algorithm oriented to maintenance resource distribution scheduling
-
摘要: 为减轻资源供应不及时对维修活动顺利开展的影响，本文针对配送式供应保障，基于带时间窗的多配送中心车辆路径规划问题提出了一种半开放式的协同配送调度模型，使得多个资源库存中心之间达成了协同合作与互相保障，从而减少了资源的供应时长和调度成本，提高了全局调度效率。为高效地求解该模型，本文提出了一种遗传–烟花混合算法，混合算法在经典遗传算法的基础上引入了烟花算法的爆炸算子以增加种群优秀个体的数量，丰富种群基因的多样性，从而提高算法的寻优能力。通过仿真实验对比，证明了爆炸算子对遗传算法容易“早熟”的缺点有所改善，且混合算法具有更高的求解效率。Abstract: In order to alleviate the impact of belated supply of maintenance resources on smooth maintenance activities, in this paper, a semi-open collaborative resource distribution scheduling model is established based on the multiple distribution centers’ vehicle routing problem (VRP) with time-windows to achieve collaboration and mutual guarantee among multiple depots. In this way, the delivery time and the scheduling cost are reduced and the overall resource supply efficiency is improved. In order to efficiently solve the model, this paper proposes a genetic-firework hybrid algorithm, which introduces the explosion operator of the firework algorithm into the classical genetic algorithm to increase the amount of good individuals and the diversity of the population, so as to improve its optimization capacity. And through comparison of simulative experiments, it is proved that the hybrid algorithm has higher solving efficiency and that the introduction of explosion operators can solve the problem that genetic algorithm is easy to converge.
-
自主维修保障模式是未来装备维修保障的发展方向[1]，但我军现有维修保障体系与自主维修保障模式还存在较大的差距，现行军队体制中各军区、各兵种以及各部队单位之间的维修资源的调度中存在很多不合理现象，这对我军装备维修保障的能力与速度都造成了不利的影响[2]。而资源供应的敏捷性会直接影响到维修保障的效率，我军自主维修保障研究中急需解决的问题之一就是如何根据设备健康管理(prognostics health management, PHM)系统的预测信息，联合多个资源库存中心，制定合理高效的配送调度方案，对多个部队维修基地进行快速可靠的资源供应保障。
在现代化自主维修保障系统中，对维修资源多采用配送式供应保障模式，将库存成本高的维修物资实行统一存储与管理，以缩短军需物资冗长的供应链，实现对各级部队单位的直达式供应[3]。其主要核心是根据PHM提供的预测信息，计算具体的资源需求，确定保障资源的配送时间，然后通过合理的供应路线设计，控制资源的调度成本，从而获得全局最优的资源保障渠道。
目前，对配送式资源供应保障模式的研究涉及交通运输、供应链优化以及物流管理等领域，并且在时间上存在一定的约束，因此属于带时间窗的多站点车辆路径问题问题(multi-depot vehicle routing problem with time-windows, MDVRPTW)。过去的几十年间，国内外的学者已对经典RCPSP (resource-constrained project scheduling problem)模型及其求解算法进行了深入的研究,由于大规模的调度[4-7]为NP-hard问题，目前对MDVRPTW问题的研究多集中在启发式算法的优化上[8-16]，本文将配送中心设为半开放式，然后在遗传算法和烟花算法的基础上，提出了一种混合算法，充分结合了两种算法在全局搜索和局部搜索的优点，具有更高的搜索效率，可以在短时间内得到更优的调度方案。
1. 问题描述
1.1 配送式资源供应
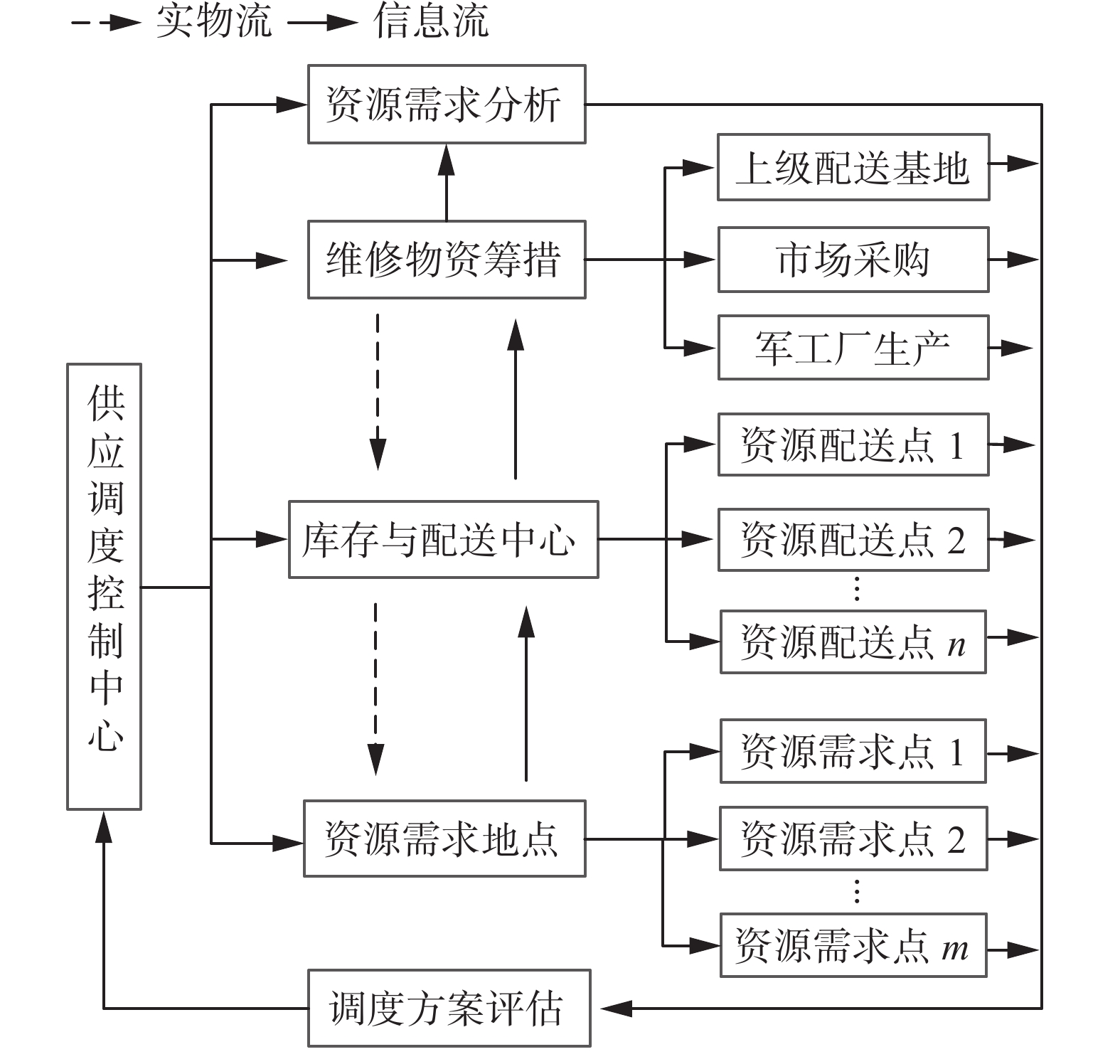
自主维修保障中为减小高技术装备维修资源的库存成本[17-19]，资源主要在库存配送中心集中存储，采用如图1所示的配送式供应模式：各级维修单位计划开展维修活动时，需向库存配送中心提出具体的资源需求，调度决策者会根据全局资源的分布情况，在满足需求数量和抵达时间的约束条件下，将各种资源供应至需求地点。
1.2 约束条件
1）时间约束
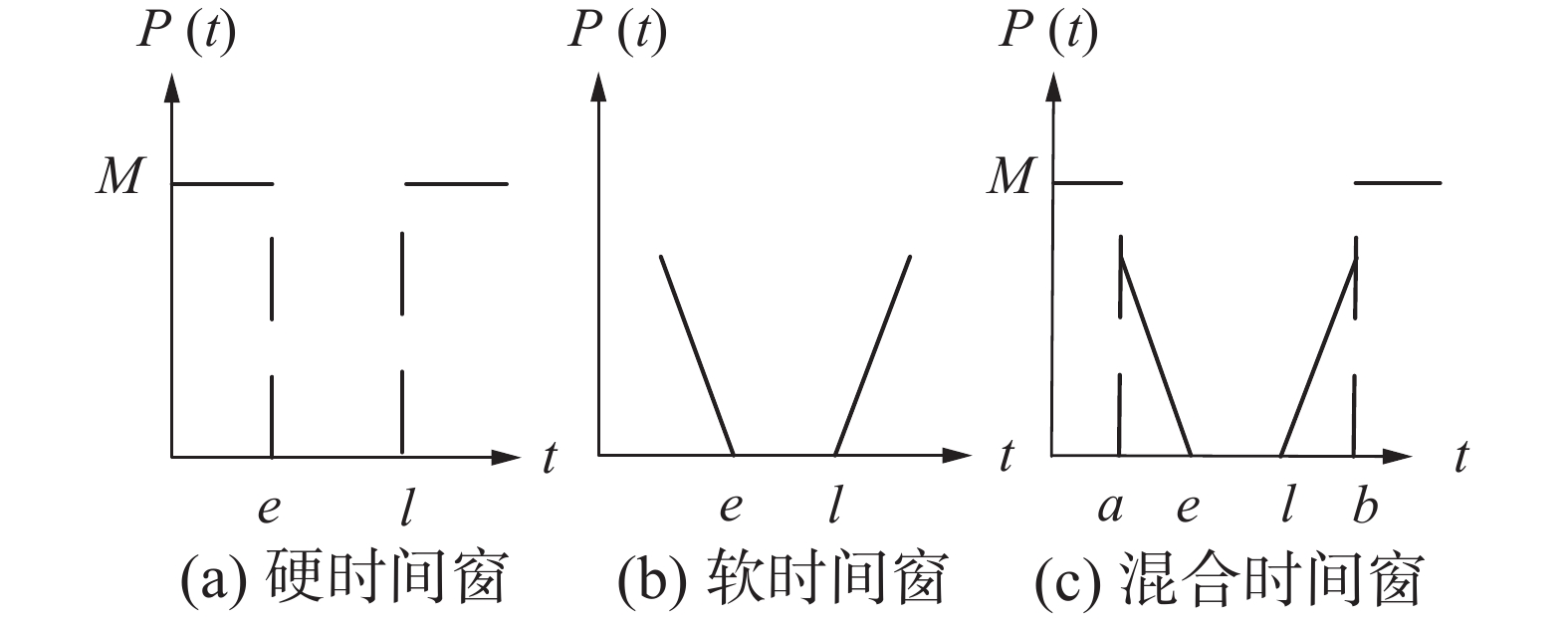
供应调度中的时间有效性约束一般采用时间窗口描述，根据决策者对供应时间准确性和供应成本之间的偏好，可以分为如图2所示的3种时间窗。图2(a)表示硬时间窗：车辆必须在规定时间段
$ (e,l) $ 之内将资源送达需求地点，需求地在这个时间段之外将拒绝接收资源，其中$ P(t) $ 为惩罚函数，在硬时间窗之外的惩罚值M是一个很大的值。图2(b)表示软时间窗：配送中各种突发情况可能导致配送车辆无法在规定时间内到达，但需求地点对此可以接受，不过需要按照一定规则处以一定的惩罚，图2(b)即一种可能的惩罚函数。图2(c)将硬、软两种时间窗相结合，形成了混合型时间窗：在规定的时间段$ (e,l) $ 之内将资源送达会直接接受，在规定时间段之外的一个较小的区间内送达，如$ (a,e) $ 或$ (l,b) $ ，则在加以一定惩罚后接受维修资源，但在$ (a,b) $ 之外将不再接受资源的供应。
图 1 配送式维修资源供应Fig. 1 Distribution type maintenance resource supply
下载:
全尺寸图片
图 2 时间窗分类Fig. 2 Time window classification下载:
全尺寸图片
2）车辆使用性约束
车辆是维修资源供应过程中调度的主要执行者，对于车辆本身的许多固有属性，常常存在一些硬性的约束，具体如下：
① 承载约束
每辆配送车辆的运载能力都是有限的，在配送的过程中，通常不允许实际的装载量超过车辆的承载限制，承载限制一般考虑为车辆的最大承重重量或车辆的最大资源容纳数量。
② 行驶上限约束
车辆在行驶过程中会产生成本与损耗，如油耗、器械磨损、人员体力损耗等，若这些成本或损耗达到一定的阈值，则车辆须返回进行保养与休整。此外，考虑到配送任务的均衡性，应该禁止超长配送路线的出现，需要对车辆设置行驶上限，车辆必须在行驶时间或行驶路程到达行驶上限之前返回配送中心。
③ 使用数量约束
实际配送中不可能存在无限多的配送车辆，因此需要对每个配送中心的实际可用车辆数目加以限制，车辆动用数量必须小于当前空闲的车辆数。
1.3 半开放配送中心
基本的配送式供应[20]保障中一般要求车辆回到其出发的配送中心，这种模式下车辆使用率不高，并且配送中心之间没有联系和互动，资源也无法共享。基于此，本文研究半开方式的配送中心：车辆从配送中心a出发并完成配送任务后，可以根据距离因素自行选择是否返回原配送中心a；若选择不返回原配送中心a，而是另一个配送中心b，则配送中心b在该车辆返回后，拥有该车辆的使用权，后续可以为该车辆安排配送中心b的配送任务。此外，配送中心自己也可以作为一个需求地点，从而可以实现配送中心之间的资源共享和互相保障，使得供应保障体系更加高效且可靠。由于配送中心的半开放性，本文引入了车位的概念，增加了如下两条约束原则：仅当配送中心拥有的车辆数目小于配送中心车位数目时，才允许新的车辆返回该配送中心；车辆应选择距离路线末端最近的，且具有多余停车位的配送中心返回。
2. 数学模型
考虑到计算的方便性以及仿真实验的可行性，模型采用如下基本假设：
1）资源数量充足，全局的维修资源库存能够满足全局的资源需求；
2）车辆由一个配送中心出发后返回到多个配送中心中的一个，每辆车不得重复调度；
3)采用同类型的配送车辆，车辆与需求地点之间为一对多的关系；
4)运输道路状况和车流量忽略不计，道路距离按直线距离计算，单位距离的行驶时间为单位时间；
5)每个配送中心存在固定数量的车位，可用车位数不足时，车辆不能在该配送中心停靠；
6)车辆到达需求地点的时间应在允许的时间范围内波动，如果车辆在规定时间之外到达，则会进行处罚，增加一定的供应成本；
7)车辆在每个节点存在装卸货物的时间，称为服务时间，服务时间在车辆到达后才能开始计时，服务结束后车辆才可以离开。
由于配送中心以及需求地点位置的分散性，协同供应调度模型可以看作一个完全无向图
$ G=(V,A)$ ，其中，${{V}} = \left\{ {{v_1}, \cdots {v_N},{v_{N + 1}}, \cdots {v_{N + M}}} \right\} $ 为节点集，代表了配送中心或需求地点，其位置用二维坐标$ (X, Y) $ 表示；$ A=\left\{\left(v_{i}, v_{j}\right) \mid v_{i}, v_{j} \in V_{t}, l \neq j\right\} $ 为弧集，代表了节点之间的距离长度。在节点集V中，
$C=\left\{c_{1}, c_{2}, \cdots, c_{N}\right\}=\left\{v_{1}, v_{2}, \cdots, v_{N}\right\}$ 代表N个需求地点,$D =\{ {{d_1},{d_2}, \cdots, {d_M}} \} = \{ {v_{N + 1}},{v_{N + 2}}, \cdots, $ $ {v_{N + M}} \}$ 代表M个配送中心。在弧集A中，每个弧$(v_i,v_j)\in A$ 代表两个节点之间的路径，与之对应的参数$ c_{11} $ 代表两者之间的距离。对于每个需求节点
$ v_{i} \in C $ ，有着与其对应的资源需求量$ q_{i} $ ，装卸服务时间$s_i$ ，以及供应时间窗口$ \left[e_{i}, l_{i}\right] $ ，其中$ e_i $ 是接受配送的最早开始时间，$ l_{i} $ 是接受配送的最晚时间。对于每个配送中心节点
$ v_{i} \in D $ ，有着于其对应的车辆数目$ \left|K_{d}\right| $ 和车位数目$ \left|P_{d}\right| $ ，在没有需求和配送服务时，配送中心的资源需求量和服务时间都为0，即$ q_{i}=s_{i}=0 $ 。每个配送中心的车辆集合表示为
$K=\{k_{1}, k_{2}, \cdots, $ $ k_{L}\}$ ，其中L是车辆数目，车辆有其对应的负荷量$ Q_{k} $ ，最大工作时间$ {T}_{{k}} $ ，动用成本$C_{k}^{\rm fix}$ 和单位距离行驶成本$C_{{k}}^{\rm run}$ 。记车辆k到达节点i的时间为$ k $ ，车辆在节点i的服务开始时间为$ a_{ki} $ ，车辆的累计工作时长为$ \pi_{k} $ 。由于采用了软时间窗进行建模，惩罚函数以时间的线性函数的形式表示，因此模型引入了早到单位时间惩罚成本
$C^{\rm earl}$ 和迟到单位时间惩罚成本$ C^{\text {lat }} $ ，以及提前、推迟到达节点i的时间差$T_{k i}^{\rm earl}$ 和$T_{k i}^{\rm lat}$ 。当车辆早于时间窗的开启时刻或晚于时间窗的关闭时刻到达时，会增加调度成本，增加的成本等于对应的单位时间惩罚成本与时差的乘积。最后，引入了本文供应调度模型中最重要决策变量
$ x_{kij} $ ，它用于判断车辆k的行驶路线，若车辆k从节点i驶向节点j，则$ x_{kij}=1 $ ；否则$ x_{kij}=0 $ 。根据以上的模型描述与符号定义，可对资源协同供应调度模型进行如下的公式化归纳：
$$ \begin{gathered} {\text{min}} {\text{Cost}} = \sum\limits_{k \in K} {\sum\limits_{i \in V} {\sum\limits_{j \in V} {{c_{ij}}} } } {x_{kij}}{C_k}^{{\text{run}}} + \sum\limits_{k \in K} {C_k^{{\text{fix}}}} + \\ \sum\limits_{k \in K} {\sum\limits_{i \in V} {(T_{ki}^{{\text{earl}}}{C^{{\text{earl}}}} + T_{ki}^{{\text{lat}}}} } {C^{{\text{lat}}}}) \\ \end{gathered} $$ (1) $$ {\text{s}}{\text{.t}}{\text{.}} \sum\limits_{k \in K} {\sum\limits_{j \in C} {{x_{kdj}}} } \leqslant \left| {{K_d}} \right|,\quad \forall d \in D $$ (2) $$ \sum\limits_{k \in K} {\sum\limits_{j \in V} {{x_{kij}}} } = \sum\limits_{k \in K} {\sum\limits_{j \in V} {{x_{kji}}} } = 1,\quad \forall i \in C $$ (3) $$ \sum\limits_{d \in D} {\sum\limits_{j \in C} {{x_{kdj}}} } = \sum\limits_{d \in D} {\sum\limits_{i \in C} {{x_{kid}}} } \leqslant 1,\quad \forall k \in K $$ (4) $$ \sum\limits_{i \in R} {\sum\limits_{j \in R} {{x_{kij}}} } \leqslant |R| - 1,\quad \forall R \subseteq C,k \in K $$ (5) $$ \sum\limits_{i \in D} {\sum\limits_{j \in D} {{x_{kij}}} } = 0,\quad \forall k \in K $$ (6) $$ \sum\limits_{k \in K} {\sum\limits_{i \in C} {{x_{kid}}} } \leqslant \left| {{P_d}} \right|,\forall d \in D $$ (7) $$ {x_{kij}}\left( {{b_{ki}} + {s_i} + {c_{ij}} - {a_{kj}}} \right) = 0,\quad \forall i,j \in V,k \in K $$ (8) $$ {b_{ki}} \geqslant {a_{ki}} \geqslant 0,\quad \forall i \in C,k \in K $$ (9) $$ \sum\limits_{i \in V} {\sum\limits_{j \in C} {{q_j}} } {x_{kij}} \leqslant {Q_k},\quad \forall k \in K $$ (10) $$ \begin{gathered} {\pi _k} = \sum\limits_{i \in C} {{x_{kid}}} \left( {{b_{ki}} + {s_i} + {c_{id}}} \right) - \sum\limits_{i \in C} {{x_{k{d^\prime }i}}} \left( {{a_{ki}} - {c_{i{d^\prime }}}} \right) \leqslant {T_k}, \\ \forall k \in K,d,{d^\prime } \in D \\ \end{gathered} $$ (11) $$ {x_{kij}} \in \{ 0,1\} ,\quad \forall i,j \in V,k \in K $$ (12) $$ {T}_{ki}^{\rm earl}=\left\{\begin{array}{l}{e}_{i}-{a}_{ki},\quad{a}_{ki} < {e}_{i}\\ \text{0}\text{，}{其他}\end{array} \right.$$ (13) $$ {T}_{ki}^{\rm lat}=\left\{\begin{array}{l}{a}_{ki}-{l}_{i},\quad{a}_{ki} > {l}_{i}\\ \text{0}\text{，}{其他}\end{array}\right. $$ (14) 其中：式（1）的目标函数为最小化调度总成本，等式右边第1项对所有车辆的行驶成本求和，第2项对所有车辆的固定成本求和，第3项计算总的时间成本；约束（2）要求从每个配送中心出发的车辆数量不超过可用车数；约束（3）确保每个需求地仅被一辆车服务一次；约束（4）表示每辆车从一个配送中心，并在一个配送中心结束；约束（5）确保了车辆k的行程路径上各个需求地点已连接；约束（6）表示车辆不能直接从配送中心i到配送中心j；约束（7）表示车辆数量返回每个配送中心的数量不超过配送中心的车位数量；约束（8）描述了节点的访问顺序，若车辆k直接从节点出发i到节点j，则节点j的到达时间必须等于上个节点的服务开始时间+服务时间+行驶时间；约束（9）确保车辆k在节点i处的启动服务时间晚于或等于其到达间；约束（10）确保车辆服务路径上的需求总数量小于车辆负载；约束（11）确保车辆实际工作时长（终点配送中心的到达时间–起始配送中心离开时间）小于最大工作时长；约束（12）表示决策变量的范围；约束（13）和约束（14）分别计算车辆k提前、推迟到达需求地点i的时间差。
3. 遗传–烟花混合算法
供应调度问题是经典的NP-hard问题，精确算法可以求得问题的最优解，但其时间复杂度却不适用大规模问题的求解，近年来的相关研究多集中在启发式算法的创新上。
遗传算法(genetic algorithm, GA)[21-23]是一种经典的群智能算法，针对建立的资源供应调度模型，本文提出了一种遗传–烟花混合算法为改善遗传算法容易“早熟”的缺陷，引入了烟花算法[24-25]中的爆炸操作，扩大了遗传算法的局部搜索范围，从而加快了对最优解的搜索速度，提高了算法的求解性能，下面对该算法进行详细的介绍。
3.1 染色体编解码
1）编码规则
对于资源协同供应调度模型，代表模型可行解的染色体应该含有资源配送中心信息、维修地点信息、车辆使用信息、车辆的路径信息等。因此，本文设计了如图3所示的编码方案，使用自然数表示的二维向量，其中第一维向量为需求地点ID的全排列，其元素不能存在重复，而第二维向量为需求地点对应的配送中心ID，其元素可以相同。
图 3 染色体编码方式示意Fig. 3 Chromosome coding method下载:
全尺寸图片
2）解码规则
由于染色体编码使用了需求地的直接排列，但却没有设置分割车辆信息的基因位置，因此需在解码阶段对车辆路径进行具体的划分。为了最大化车辆使用效率，应使用尽量少的车辆来完成资源的配送，染色体解码被分为了如下两个步骤：
① 整体调度路径提取。根据配送中心的ID，将同一配送中心对应的基因按照从左到右的顺序依次提取，然后组合成为一条新的“子染色体”，称为整体调度路径，该路径记录了该配送中心负责保障的所有需求地点的配送顺序。
② 车辆行驶路径划分。对于每一条整体调度路径，根据各种约束条件，按照从左到右的顺序，将其需求地向量的元素依次加入一个有序集合，该有序集合称为车辆行驶路径。在加入新需求地时，若违反了模型的约束条件（如车辆运载能力、行驶时间等），则设置当前车辆路径终点为最近的配送中心，然后另起一个新的有序集合，继续为剩余的需求地划分车辆路径，直至当前整体调度路径中所有需求地都归入了对应的车辆行驶路径。
3.2 算法基本要素
1）初始种群
根据上述编码方案，按照给定的配送中心和需求地信息，随机产生固定数量(Popsize)的染色体，即可作为混合算法的初始种群。Popsize的大小往往决定了算法的搜索性能，一般需根据模型输入数据的规模进行调整，从而保证种群基因的多样性。
2）适应度函数
对于本文的保障资源供应调度模型，其优化目标是使维修资源供应调度方案的总成本最小，算法的目标函数即是调度总成本，因此适应度函数可用倒数函数形式表示，即
$$ {\text{fit}}(i) = 1/{\text{Cost}}(i) $$ (15) 式中：
$ {\text{Cost}}(i) $ 为种群中个体i的目标函数值；$ {\text{fit}}(i) $ 即个体i的染色体所对应的适应度，$ {\text{fit}}(i) $ 越大，被选则的几率就越大。3）停止准则
对于本文提出的混合算法，其主体结构依旧是遗传算法，只需设置一个迭代次数的上限Maxgen，当算法的迭代次数达到该阈值时候，结束程序，输出当前的满意解即可。
4）选择操作
首先通过精英保留策略直接保留最优秀的个体：根据适应度的大小对当前种群中的个体降序排列，将一定数量的优秀个体直接放入子代种群。对于剩下的个体采用轮盘赌策略进行选择，具体流程为：先通过式（16）计算保留概率
$ P{\text{(}}{x_{\text{i}}}{\text{)}} $ ，然后对所有个体的保留概率累加，得到个体的累计概率分布刻度区间，最后在(0，1]区间内产生$ {\text{Gap}} \times {\text{Popsize}} $ 个随机数，根据随机数掉落的刻度区间确定被选中的染色体。$$ P{\text{(}}{x_i}{\text{) = }}\frac{{{\text{fit}}({x_j}){\text{ }}}}{{\displaystyle\sum_{j = {\text{1}}}^{{\text{Popsize}}} {{\text{fit}}({x_j})} }} $$ (16) 式中：
$ {\text{fit}}({x_i}){\text{ }} $ 表示个体$ {x_i} $ 的适应度；$ P{\text{(}}{x_{{i}}}{\text{)}} $ 表示个体$ {x_i} $ 的保留概率。5）交叉操作
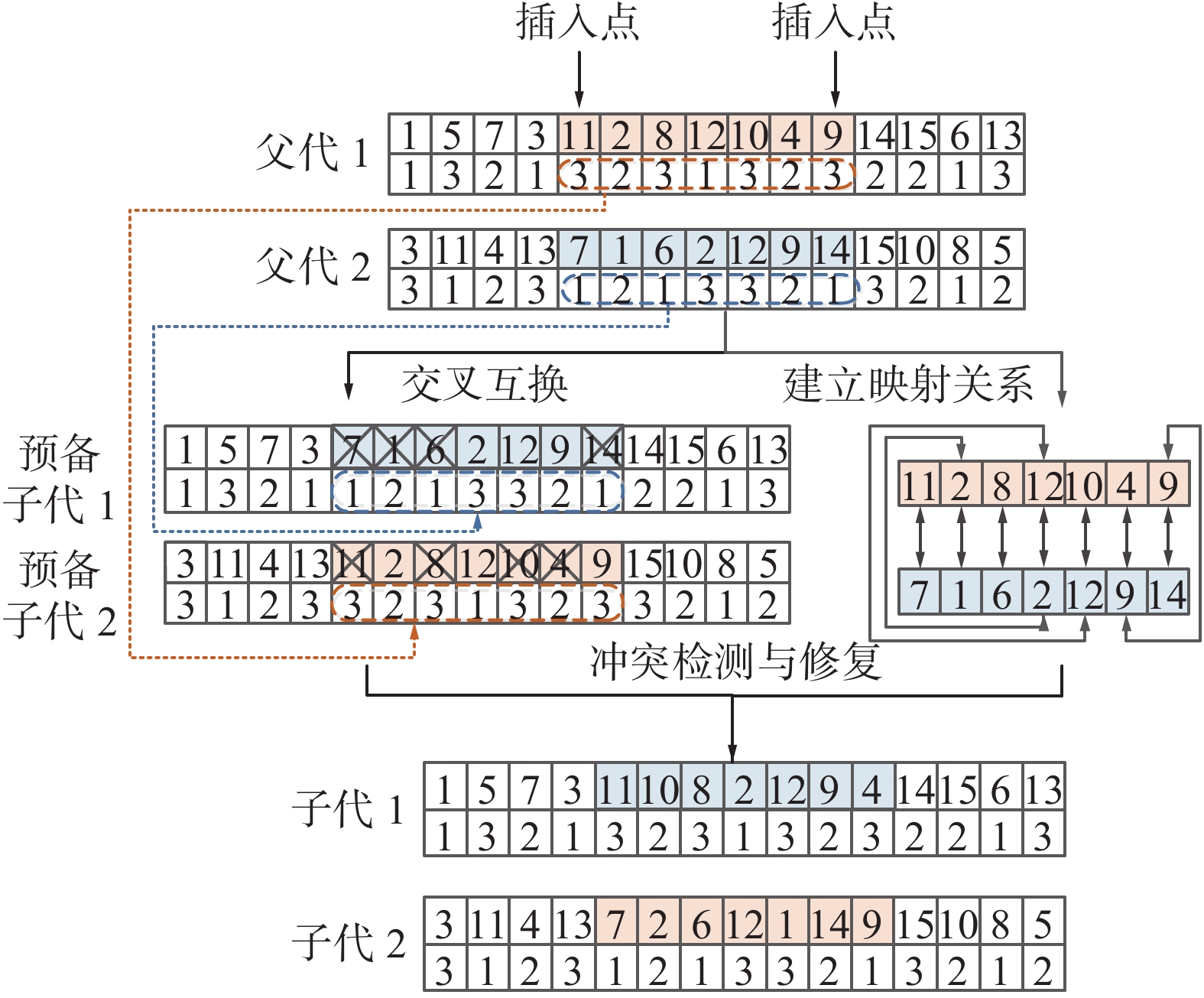
本文对染色体编码中的两个维度采用了不同的交叉方法。第一维编码向量是需求地编码的全排列，具有唯一性，简单的交叉方法非常容易产生不可行解，因此本文采用的交叉方法为部分匹配交叉法(partially matching crossover，PMX)。以图4为例，其具体步骤如下：
①随机选择一对染色体（父代1和父代2），在染色体上再随机选择两个插入点，作为交叉片段的起止位置；
②根据插入点的位置，交换两个父代中的基因片段，并根据交换的具体基因建立一个两两映射关系集合。例如，在图4交换的基因片段中，存在11-7、1-（2-12）-10、8-6、4-（9）-14 4个对应关系；
图 4 交叉操作流程示意Fig. 4 Cross-operation flow diagram下载:
全尺寸图片
③对交换基因片段后产生的预备子代进行冲突检测与修复。以预备子代1为例，交换之后存在重复基因7、1、6、14。而通过映射关系可知，这4个重复基因依次与基因11、10、8、14匹配，按照该映射规则进行替换，预备子代1中的基因7、1、6、14被替换为了基因11、10、8、14，从而得到了无重复基因的子代1。预备子代2也按照同样的方法根据映射关系进行修复即可。
编码第二维向量为配送中心信息，不具有唯一性，允许元素的重复出现。因此本文采用简单的两点交叉策略，将父代中虚线所指的配送中心编码片段两两交换即可，如图4中虚线所示。
6）变异操作
混合算法中变异操作采用简单的两点交换策略，在种群中以一定变异概率随机选择一定数量的个体进行基因交换，具体步骤十分简单：对选中的个体，随机选择其染色体上的两个基因作为交换点，然后交换它们的位置即可。
7）爆炸算子设计
在烟花算法中爆炸操作即为一次邻域搜索过程，且适应度值较好的烟花在较小的范围内产生较多的火花粒子，称为“局部烟花”，适应度值较差的烟花在较大的范围内产生较少的火花粒子，称为“全局烟花”。遗传算法种群中适应度最好的个体含有更为优秀的遗传信息，在很大程度上能够引导算法的收敛方向，因此可以看作一个产生“局部烟花”的最佳爆炸点；而适应度最差的个体由于其包含了和优秀个体差异程度最大的遗传信息，能够使得种群的遗传信息更加多样化，因此可以看作产生“全局烟花”的一个较好爆炸点。
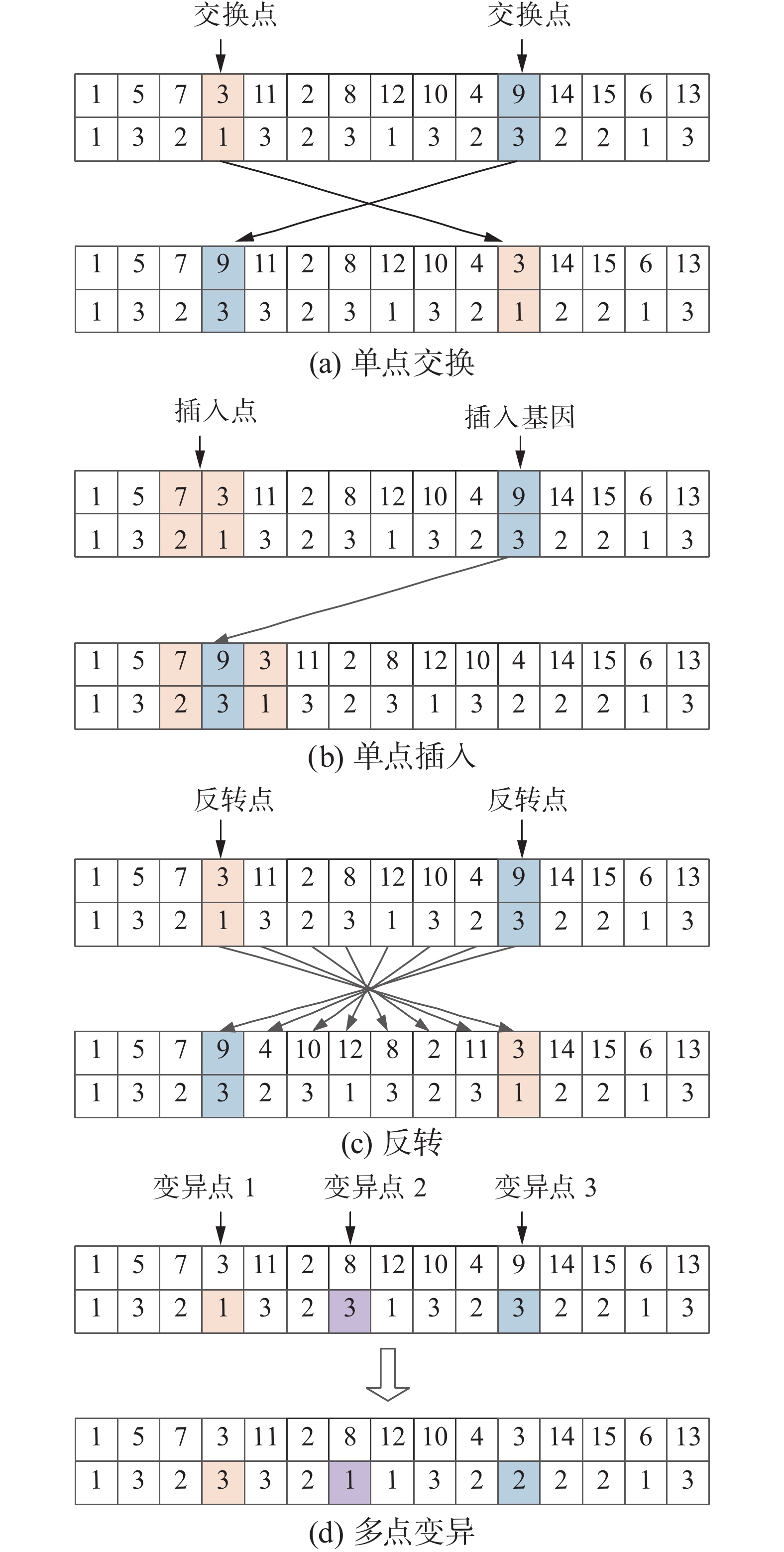
由于本文染色体中需求地和配送中心两个向量的生成规则不同，因此爆炸算子也需要对不同维度的向量分别进行操作，才能保证生成新个体的正确性，具体的操作分为图5所示的4种策略。对于第一维的需求地向量，爆炸算子采用一种随机混合方案，对每一次的爆炸操作，随机采用单点交换、插入与反转3种策略中的一种执行，如图5中(a)、(b)、(c)所示；而对于第二维的配送中心向量，由于无需考虑冲突检测，在上述3种策略之外，还加入了多点变异策略，如图5(d)。
图 5 爆炸算子示意Fig. 5 Flow chart of explosion operator下载:
全尺寸图片
爆炸算子中的爆炸数量
$ {S_i} $ 和爆炸半径$ {R_i} $ 的计算规则为$$ {S_i} = {S_{{\text{sum }}}} \cdot \frac{{{{\rm{fit}}_{\max }} - {\rm{fit}}\left( {{x_i}} \right)}}{{\displaystyle\sum\limits_{i = 1}^N {\left( {{{\rm{fit}}_{\max }} - {\rm{fit}}\left( {{x_i}} \right)} \right)} }} $$ (17) $$ {R_i} = A \times \frac{{{\rm{fit}}\left( {{x_i}} \right) - {{\rm{fit}}_{{\text{min }}}}}}{{\displaystyle\sum\limits_{i = 1}^N {\left( {{\rm{fit}}\left( {{x_i}} \right) - {{\rm{fit}}_{{\text{min }}}}} \right)} }} $$ (18) 式中：
$ {S_{{\text{sum }}}} $ 为预设的爆炸火花数；$ A $ 为爆炸半径的基值；${\rm{fit}}\left( {{x_i}} \right)$ 为个体$ {x_i} $ 的适应度；${{\rm{fit}}_{\max }}$ 与${{\rm{fit}}_{{\text{min }}}}$ 分别为进行爆炸操作的个体中的最大适应度值与最小适应度值；$ N $ 为进行爆炸操作的个体的数量。爆炸半径规定了爆炸操作时进行邻域搜索的范围，对于本文的自然数编码方案，爆炸半径可以对应为爆炸操作的最大执行次数，即对于烟花i，需要随机进行1~
$ {R_i} $ 次爆炸操作才可以得到一个新的火花。由于在遗传算法阶段进行了相关变异操作，为避免不必要的运算，本文爆炸算子没有考虑高斯变异火花。由于爆炸数量根据个体的适应度计算的，具有一定的不确定性，因此本文对
$ {S_i} $ 设置了上下界：$$ {\hat S_i} = \left\{ {\begin{array}{*{20}{l}} {{S_{\max }},}&{{S_i} > {S_{\max }}} \\ {{S_i},}&{{S_{\min }} < {S_i} < {S_{\max }}} \\ {{S_{\min }},}&{{S_i} < {S_{\min }}} \end{array}} \right. $$ (19) 式中：
$ {S_{\max }} $ 与$ {S_{\min }} $ 分别为的预先设置的最大、最小爆炸火花数量。最后为了保证种群规模不变，规定每次保留
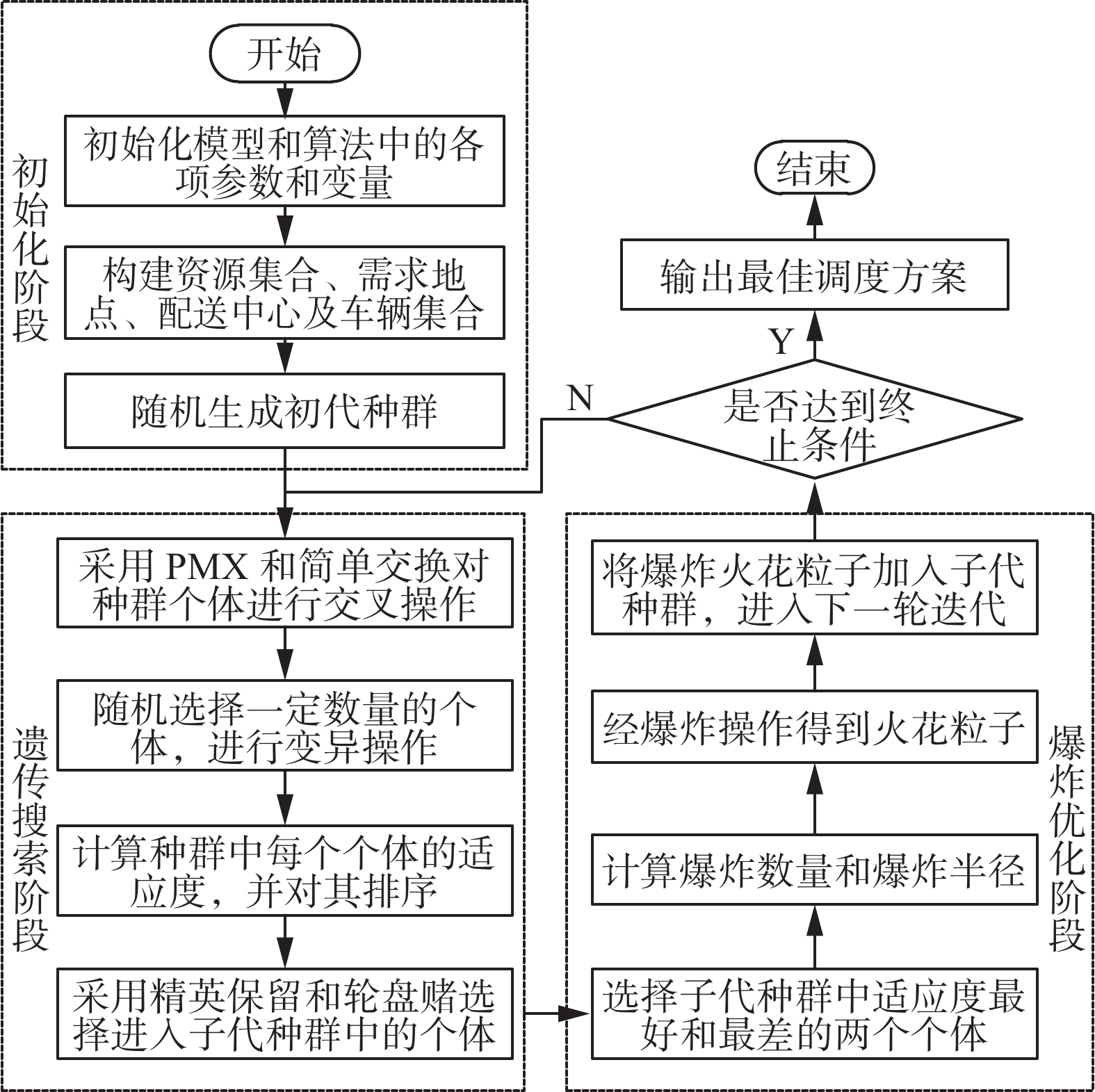
$ {S_{\min }} $ 个火花作为爆炸算子产生的新个体，加入遗传算法的种群中，进行混合算法的下一轮迭代。3.3 混合算法流程
混合算法的基本流程如图6所示，分为初始化、遗传进化和爆炸优化3个阶段。
图 6 遗传–烟花混合算法流程图Fig. 6 Flow chart of genetic-firework hybrid algorithm下载:
全尺寸图片
4. 实验结果与分析
4.1 实验数据与算法参数
由于本章建立的资源供应调度模型属于MDVRPTW模型的一个扩展，相较于原模型增加了许多新约束，目前还没有公开标准数据可用于测试验证。因此，本文引入了国际通用的MDVRPTW公开基准数据集[26]，并对其进行了补充与改造。
实验从Cordeau数据集中选择10个具有代表性的基础实例，为其增加了车辆、车位和工作时长限制，得到了A1~A5和B1~B5两组共10个实验算例，如表1。对于A、B两组数字序号相同的算例，其节点地理分布是完全相同的，但A组算例具有较窄的时间窗口，B组算例具有较宽的时间窗口。
表 1 实验算例基本信息Table 1 Basic information of experimental examples算例编号 Cordeau
实例号配送中心
数量/个需求地点
数量/个配送中心
车位数/个配送中心车
辆数/辆最大载资源
承载负荷/个最大工作
时长/minA1 pr01 4 48 4 2 200 1000 A2 pr07 6 72 4 2 200 1000 A3 pr02 4 96 6 3 196 960 A4 pr03 4 144 8 4 150 920 A5 pr08 6 144 6 3 190 850 B1 pr11 4 48 2 1 200 1000 B2 pr17 6 72 2 1 200 1000 B3 pr12 4 96 4 2 196 960 B4 pr13 4 144 6 3 150 920 B5 pr18 6 144 4 2 190 850 为了便于对比，相关变量及参数的取值如表2，参数测试候选值和最终取值见表3。
表 2 模型参数值设置Table 2 Model parameter value setting模型参数名称 参数值 车辆动用成本/元 1000 每千米行驶成本/元 10 提前到达每分钟惩罚成本/元 0.5 推迟到达每分钟惩罚成本/元 2 车辆行驶速/m·s−1 16.6 表 3 混合算法参数Table 3 Hybrid algorithm parameters算法参数名称 参数测试候选值 参数取值 遗传种群数量/个 50、100、200 100 遗传种群代沟 0.5、0.7、0.9 0.9 交叉概率 0.6、0.7、0.8 0.8 变异概率 0.1、0.2、0.3 0.1 预设爆炸数量/个 15、30、60 30 最大爆炸数量/个 12、24、30 24 最小爆炸数数/个 5、10、20 10 爆炸半径 10、20、30 20 遗传–烟花混合算法是一种启发式算法，启发参数的好坏往往决定了算法的性能。因此本文使用表1中的算例进行了参数评估。
4.2 算法性能对比
单个的算例的运行结果具有一定的局限性，为了进一步对比算法的求解性能，本文对遗传算法、烟花算法以及混合算法在同样的硬件条件下，对表1中的10个算例分别进行了对比实验。为了保障实验的公平性，对于相同的算例，3种算法的候选解规模、迭代次数以及初始种群都设置完全相同。
1）求解质量对比
为了综合对比算法的求解质量，记录3种算法10次运行结果中目标函数的最优值、平均值以及标准差分别如表4、表5和表6所示。
对比表4和5中的目标函数值可以明显看出，在绝大部分算例上，无论是最优值还是平均值，混合算法都比遗传算法和烟花算法要小，这说明混合算法具有最好的求解质量，得到的满意解更加逼近实际最优解，得到了调度成本最小的方案。
2）求解速度对比
为了综合对比算法的求解速度，分别统计3种算法在各算例上10次运行结果中初次找到满意解时的平均迭代次数及平均运行时长（单位：s），如图7所示。
表 4 目标函数最优值Table 4 Optimal value of objective function算例 A1 A2 A3 A4 A5 B1 B2 B3 B4 B5 GA 16072 22130 28327 42640 41351 14636 20484 24930 40823 39215 FWA 15474 21711 27634 41715 40700 13918 19420 23786 39601 38532 混合 14936 21322 27122 40067 39429 13565 19170 22973 38725 37783 表 5 目标函数平均值Table 5 Average value of objective function算例 A1 A2 A3 A4 A5 B1 B2 B3 B4 B5 GA 16892 22910 29138 43653 42564 15421 21180 26086 41970 40585 FWA 15725 22137 28354 42405 41638 14753 20187 24786 40533 39714 混合 15270 21634 27592 41517 40727 14195 19794 23553 39022 38372 表 6 目标函数标准差Table 6 Standard deviation of objective function算例 A1 A2 A3 A4 A5 B1 B2 B3 B4 B5 GA 384.3 339.9 442.6 485.1 552.3 340.7 327.6 532.5 673.4 472.9 FWA 207.4 208.2 337.5 349.2 362 327.7 308.2 411.8 479.2 512.0 混合 229.6 147.4 219.7 459.9 294.6 257.2 328.5 272.5 459.3 324.5 
图 7 初次找到满意解的平均迭代次数Fig. 7 Average number of iterations to find a satisfactory solution for the first time下载:
全尺寸图片
综合求解质量和求解速度的结果来看：混合算法求解质量是最好的，其收敛速度也快于烟花算法和遗传算法，但在运行时间上会略慢于遗传算法，即混合算法在略微增加了一些运算成本的情况下获得了更好的求解质量。而增加的运算成本可以通过硬件配置进一步缩小，但对于求解质量，其他两种算法却无法靠简单的硬件升级进行弥补，因此混合算法是3种算法中综合性能最强的算法。
从理论上对实验结果进行分析，由于遗传算法种群中适应度最好的个体其包含更为优秀的遗传信息，对其进行爆炸操作能在很大程度上能够引导算法的收敛方向，而适应度最差的个体由于包含了和优秀个体差异程度最大的遗传信息，能够使得种群的遗传信息更加丰富，从而扩大了局部搜索的范围。对两种算法进行混合，充分结合了遗传算法全局搜索能力强和烟花算法局部搜索能力强的特点，使得混合算法在收敛速度和搜索范围上都得到了改善，从而能够以更快的速度得到更小成本的调度方案，这对于实际的资源供应调度具有重要的经济效益。
5. 结束语
本文针对建立的维修资源供应调度模型，本文提出了一种遗传–烟花混合算法。混合算法在遗传算法的基础上，引入了烟花爆炸算子，使得种群优秀个体的数量增多，增强了算法的局部寻优能力。通过仿真对比实验，结果表明本文提出的混合算法可以得到成本更低的调度方案，同时具有更快的收敛速度，并且适用于各种规模的资源供应调度需求。 -
图 1 配送式维修资源供应
Fig. 1 Distribution type maintenance resource supply
下载:
全尺寸图片
图 2 时间窗分类
Fig. 2 Time window classification
下载:
全尺寸图片
图 3 染色体编码方式示意
Fig. 3 Chromosome coding method
下载:
全尺寸图片
图 4 交叉操作流程示意
Fig. 4 Cross-operation flow diagram
下载:
全尺寸图片
图 5 爆炸算子示意
Fig. 5 Flow chart of explosion operator
下载:
全尺寸图片
图 6 遗传–烟花混合算法流程图
Fig. 6 Flow chart of genetic-firework hybrid algorithm
下载:
全尺寸图片
图 7 初次找到满意解的平均迭代次数
Fig. 7 Average number of iterations to find a satisfactory solution for the first time
下载:
全尺寸图片
表 1 实验算例基本信息
Table 1 Basic information of experimental examples
算例编号 Cordeau
实例号配送中心
数量/个需求地点
数量/个配送中心
车位数/个配送中心车
辆数/辆最大载资源
承载负荷/个最大工作
时长/minA1 pr01 4 48 4 2 200 1000 A2 pr07 6 72 4 2 200 1000 A3 pr02 4 96 6 3 196 960 A4 pr03 4 144 8 4 150 920 A5 pr08 6 144 6 3 190 850 B1 pr11 4 48 2 1 200 1000 B2 pr17 6 72 2 1 200 1000 B3 pr12 4 96 4 2 196 960 B4 pr13 4 144 6 3 150 920 B5 pr18 6 144 4 2 190 850 表 2 模型参数值设置
Table 2 Model parameter value setting
模型参数名称 参数值 车辆动用成本/元 1000 每千米行驶成本/元 10 提前到达每分钟惩罚成本/元 0.5 推迟到达每分钟惩罚成本/元 2 车辆行驶速/m·s−1 16.6 表 3 混合算法参数
Table 3 Hybrid algorithm parameters
算法参数名称 参数测试候选值 参数取值 遗传种群数量/个 50、100、200 100 遗传种群代沟 0.5、0.7、0.9 0.9 交叉概率 0.6、0.7、0.8 0.8 变异概率 0.1、0.2、0.3 0.1 预设爆炸数量/个 15、30、60 30 最大爆炸数量/个 12、24、30 24 最小爆炸数数/个 5、10、20 10 爆炸半径 10、20、30 20 表 4 目标函数最优值
Table 4 Optimal value of objective function
算例 A1 A2 A3 A4 A5 B1 B2 B3 B4 B5 GA 16072 22130 28327 42640 41351 14636 20484 24930 40823 39215 FWA 15474 21711 27634 41715 40700 13918 19420 23786 39601 38532 混合 14936 21322 27122 40067 39429 13565 19170 22973 38725 37783 表 5 目标函数平均值
Table 5 Average value of objective function
算例 A1 A2 A3 A4 A5 B1 B2 B3 B4 B5 GA 16892 22910 29138 43653 42564 15421 21180 26086 41970 40585 FWA 15725 22137 28354 42405 41638 14753 20187 24786 40533 39714 混合 15270 21634 27592 41517 40727 14195 19794 23553 39022 38372 表 6 目标函数标准差
Table 6 Standard deviation of objective function
算例 A1 A2 A3 A4 A5 B1 B2 B3 B4 B5 GA 384.3 339.9 442.6 485.1 552.3 340.7 327.6 532.5 673.4 472.9 FWA 207.4 208.2 337.5 349.2 362 327.7 308.2 411.8 479.2 512.0 混合 229.6 147.4 219.7 459.9 294.6 257.2 328.5 272.5 459.3 324.5 -
[1] TADJDEH Y. F-35 logistics system faces challenges[J]. National defense, 2018, 102(772): 36–37. [2] 王蕾, 林涛. 新时期下装备维修保障模式研究[J]. 现代防御技术, 2020, 48(5): 86–91,104. doi: 10.3969/j.issn.1009-086x.2020.05.013 WANG Lei, LIN Tao. Research on equipment maintenance support mode in the new period[J]. Modern defence technology, 2020, 48(5): 86–91,104. doi: 10.3969/j.issn.1009-086x.2020.05.013 [3] 石文成, 杨西龙. 战备物资综合管理研究综述[J]. 军事交通学院学报, 2020, 22(12): 47–51. https://www.cnki.com.cn/Article/CJFDTOTAL-JSTO202012012.htm SHI Wencheng, YANG Xilong. On comprehensive management of war readiness materials[J]. Journal of military transportation university, 2020, 22(12): 47–51. https://www.cnki.com.cn/Article/CJFDTOTAL-JSTO202012012.htm [4] ZAMAN F, ELSAYED S M, SAKER R, et al. Resource constrained project scheduling with dynamic disruption recovery[J]. IEEE access, 2020, 8: 144866–144879. doi: 10.1109/ACCESS.2020.3014940 [5] CREEMERS S. The preemptive stochastic resource-constrained project scheduling problem[J]. European journal of operational research, 2019, 277(1): 238–247. doi: 10.1016/j.ejor.2019.02.030 [6] KANNIMUTHU M, RAPHAEL B, EKAMBARAM P, et al. Comparing optimization modeling approaches for the multi-mode resource-constrained multi-project scheduling problem[J]. Engineering, construction and architectural management, 2020, 27(4): 893–916. doi: 10.1108/ECAM-03-2019-0156 [7] OZTEMEL E, SELAM A A. Bees Algorithm for multi-mode, resource-constrained project scheduling in molding industry[J]. Computers & industrial engineering, 2017, 112: 187–196. [8] 滕尚儒, 何成铭, 丛彬. 装备维修器材军民融合供应保障模式探索[J]. 物流技术, 2020, 39(4): 117–124. doi: 10.3969/j.issn.1007-1059.2020.04.020 TENG Shangru, HE Chengming, CONG Bin. Exploration on military-civilian integrated supply and support mode for equipment maintenance materials[J]. Logistics technology, 2020, 39(4): 117–124. doi: 10.3969/j.issn.1007-1059.2020.04.020 [9] DANTZIG G B, RAMSER J H. The truck dispatching problem[J]. Management science, 1959, 6(1): 80–91. doi: 10.1287/mnsc.6.1.80 [10] SOEANU A, RAY S, BERGER J, et al. Multi-depot vehicle routing problem with risk mitigation: Model and solution algorithm[J]. Expert systems with applications, 2020, 145: 113099. doi: 10.1016/j.eswa.2019.113099 [11] KARAKATIČ S, PODGORELEC V. A survey of genetic algorithms for solving multi depot vehicle routing problem[J]. Applied soft computing, 2015, 27: 519–532. doi: 10.1016/j.asoc.2014.11.005 [12] STODOLA P. Hybrid ant colony optimization algorithm applied to the multi-depot vehicle routing problem[J]. Natural computing, 2020, 19(2): 463–475. doi: 10.1007/s11047-020-09783-6 [13] MIRABI M, SHOKRI N, SADEGHIEH A. Modeling and solving the multi-depot vehicle routing problem with time window by considering the flexible end depot in each route[J]. International journal of supply and operations management, 2016, 3(3): 1373–1390. [14] SUN Peng, VEELENTURF L P, HEWITT M, et al. Adaptive large neighborhood search for the time-dependent profitable pickup and delivery problem with time windows[J]. Transportation research part E:logistics and transportation review, 2020, 138: 101942. doi: 10.1016/j.tre.2020.101942 [15] 张家骅, 李爱平, 刘雪梅. 行驶时间区间不确定的装配线物料配送路径规划[J]. 中国机械工程, 2021, 32(18): 2239–2246. doi: 10.3969/j.issn.1004-132X.2021.18.013 ZHANG Jiahua, LI Aiping, LIU Xuemei. Routing planning for assembly line material distributions under interval uncertain travel TimeChinese full text[J]. China mechanical engineering, 2021, 32(18): 2239–2246. doi: 10.3969/j.issn.1004-132X.2021.18.013 [16] 马龙, 王春嬉, 张正义, 等. 多目标多时间窗车辆路径问题的鸽群-水滴算法[J]. 计算机工程与应用, 2021, 57(2): 237–250. doi: 10.3778/j.issn.1002-8331.2004-0034 MA Long, WANG Chunxi, ZHANG Zhengyi, et al. Pigeon-inspired optimization and intelligent water drops algorithm for multiple-objective vehicle routing problem with multiple time WindowsChinese full TextEnglish full text (MT)[J]. Computer engineering and applications, 2021, 57(2): 237–250. doi: 10.3778/j.issn.1002-8331.2004-0034 [17] 刘明德. 基于群体智能的动态需求车辆路径规划[D]. 哈尔滨: 哈尔滨工业大学, 2020. LIU Mingde. Research on vehicle routing problem with dynamic demands based on swarm intelligence[D]. Harbin: Harbin Institute of Technology, 2020. [18] ABED F, CHEN Lin, DISSER Y, et al. Scheduling maintenance jobs in networks[J]. Theoretical computer science, 2019, 754: 107–121. doi: 10.1016/j.tcs.2018.02.020 [19] TIRKOLAEE E B, GOLI A, HEMATIAN M, et al. Multi-objective multi-mode resource constrained project scheduling problem using Pareto-based algorithms[J]. Computing, 2019, 101(6): 547–570. doi: 10.1007/s00607-018-00693-1 [20] CHAKRABORTTY R K, ABBASI A, RYAN M J. Multi-mode resource-constrained project scheduling using modified variable neighborhood search heuristic[J]. International transactions in operational research, 2020, 27(1): 138–167. doi: 10.1111/itor.12644 [21] GARCÍA J M, ACOSTA C A, MESA M J. Genetic algorithms for mathematical optimization[J]. Journal of physics:conference series, 2020, 1448(1): 012020. doi: 10.1088/1742-6596/1448/1/012020 [22] ERMAKOV S M, SEMENCHIKOV D N. Genetic global optimization algorithms[J]. Communications in statistics - simulation and computation, 2019: 1–10. [23] TAN Ying, YU Chao, ZHENG Shaoqiu, et al. Introduction to fireworks algorithm[J]. International journal of swarm intelligence research, 2013, 4(4): 39–70. doi: 10.4018/ijsir.2013100103 [24] LI Junzhi, TAN Ying. A comprehensive review of the fireworks algorithm[J]. ACM computing surveys, 2020, 52(6): 1–28. [25] SETHANAN K, JAMRUS T. Hybrid differential evolution algorithm and genetic operator for multi-trip vehicle routing problem with backhauls and heterogeneous fleet in the beverage logistics industry[J]. Computers & industrial engineering, 2020, 146: 106571. [26] CORDEAU J F, GENDREAU M, LAPORTE G. A tabu search heuristic for periodic and multi-depot vehicle routing problems[J]. Networks, 1997, 30(2): 105–119. doi: 10.1002/(SICI)1097-0037(199709)30:2<105::AID-NET5>3.0.CO;2-G
