Multimodal function optimization based on DE algorithm of probabilistic evaluation mechanism
-
摘要: 多峰值优化问题要求算法同时找到一个问题的多个全局最优解。近年来,演化算法已被广泛用于求解多峰值优化问题。然而,如何在极其有限的适应值评估次数内找到问题的多个全局最优解依然为演化算法带来了巨大的挑战。通过分析个体的历史更新经验,为每个个体赋予双层适应值评估概率,对个体进行选择性评估,从而减少算法运行过程中无效或低效的适应值评估,提出了一种基于概率评估差分进化的多峰值优化算法。实验结果显示,概率评估机制可以为算法节省更多的适应值评估次数,增加迭代过程,效果远好于其他主流的多峰值优化算法。Abstract: Multimodal optimization problems (MMOPs) require algorithms to simultaneously determine multiple global optima. Recently, evolutionary algorithms (EAs) have been widely used to solve MMOPs. However, there is still a great challenge for EAs to determine multiple global optima within very limited fitness evaluation (FE) times. To solve the inefficient FE, this paper proposes a multimodal function optimization algorithm based on the differential evolution algorithm of the probabilistic evaluation mechanism for solving MMOPs. In this algorithm, each individual will be assigned with the two-level FE probability according to its historical update experience to determine whether it needs to be evaluated. The experimental results show that the probabilistic evaluation mechanism can reduce FE times for the proposed algorithm and increase its iterative process, and its effect is much better than that of other mainstream mechanisms.
-
许多实际优化问题中具有多个全局最优解,如蛋白质结构检测[1]、电磁系统设计[2]、结构优化[3]和多行人检测[4-6]等。例如,多行人检测通常要求算法在一张给定的图片中尽可能多地检测到多个行人。此类问题被称为多峰值优化问题。求解多峰值优化问题具有很多实际益处。如果能同时找到一个实际问题的多个最优解,就能用多种方式来保持系统的最优性能。当其中某个最优解因为实际物理条件无法实现时,可以很快地切换到另一个最优解。
演化算法[7-14]因其基于种群的进化机制,拥有多个候选解,在求解多峰值优化问题中具有潜在的优势。然而,传统的演化算法仅仅是寻求问题的一个最优解。为了求解多峰值优化问题,最主流的思想便是小生境策略[15-28],就是将整个种群划分为多个子种群,如Crowding[15]、Speciation[16]、聚类[17-18]、Hill-valley[23]等。但是,现有的小生境策略对它们各自的小生境参数特别敏感,以及为了提升种群划分的准确性,算法需要采样并评估足够多的中间点,消耗了大量的适应值评估次数(fitness evaluations, FEs)。
在我们先前发表于IEEE Transactions on Cybernetics的研究中[29],提出了一种自适应分布估计的差分进化算法(adaptive estimation distribution distributed differential evolution, AED-DDE),算法提出了一种基于自适应分布估计(adaptive estimation distribution,AED)的无参数小生境策略,并提出了概率局部搜索机制(probabilistic local search,PLS)来提升算法求解精度。AED-DDE算法在多峰值优化问题上已经取得了很好的实验效果。然而,如何在极其有限的适应值评估次数内找到问题的多个全局最优解,依然为AED-DDE以及其他演化算法带来了巨大的挑战。如果可以分析个体的历史更新经验,对个体进行选择性评估,减少算法运行过程中无效或低效的适应值评估,算法性能将会得到进一步的提高。
本文基于之前AED-DDE的工作,进一步提出了概率评估机制(probabilistic evaluation, PE),并将这个机制应用在AED-DDE算法中,称为PEDE。在PEDE算法中,每个个体会通过历史经验的学习,被赋予第一层的适应值评估概率,并根据该个体的适应值赋予第二层的适应值评估概率。每个个体在进化过程中会根据该个体的双层适应值评估概率进行选择性评估。被评估的个体更新个体的适应值,同时学习这个更新过程来调整自身的适应值评估概率;而未被评估的个体则直接根据该个体的历史经验进行个体更新。通过概率适应值评估机制,可以节省FEs来增加算法的迭代次数,从而提升算法求解精度。同时,通过概率评估机制,可以充分学习到个体的历史经验,更加方便种群的搜索。
在多峰值优化测试集IEEE CEC 2013上的实验结果显示,相比于其他的多峰值优化算法,PEDE算法取得了更好的实验结果。同时,将概率评估机制应用到了其他基于DE的多峰值优化算法中,算法效果都有了一定的提升。
1. 相关工作
1.1 差分进化算法
差分进化算法(differential evolution,DE)最初是由Storn和Price提出[30]。它通过群体内个体之间的差异来优化群体的搜索方向。DE算法在进化过程中有变异、交叉、选择等操作,具体来说:
1) 变异
在每一代中,每个个体xi称为目标向量,它通过变异操作产生它自身的变异向量vi。3种常用的变异策略如式(1)~(3)所示:
DE/rand/1:
$$ {\boldsymbol{v}}_{i}={\boldsymbol{x}}_{r_1}+F×({\boldsymbol{x}}_{r_2}–{\boldsymbol{x}}_{r_3}) $$ (1) DE/best/1:
$$ {\boldsymbol{v}}_{i}={\boldsymbol{x}}_{{\rm{best}},g}+F×({\boldsymbol{x}}_{r_1}–{\boldsymbol{x}}_{r_2}) $$ (2) DE/current-to-best/1:
$$ {\boldsymbol{v}}_{i}={\boldsymbol{x}}_{i}+F×({\boldsymbol{x}}_{\rm{best}}–{\boldsymbol{x}}_{i})+F×({\boldsymbol{x}}_{r_1}–{\boldsymbol{x}}_{r_2}) $$ (3) 其中,r1、r2和r3是3个不同的{1, 2, …, N}中的整数(N代表种群规模),并且都与i不同。放大系数F是一个正实数的控制参数,用来放大差分向量。xbest是指当前种群中适应值最好的个体。
2) 交叉
在变异操作后,DE通常会在个体xi和它自身的变异向量vi上执行二元交叉操作,来产生试验向量ui,如式(4)所示:
$$ {{\boldsymbol{u}}_{i,j,g}} = \left\{ \begin{aligned} &{{\boldsymbol{v}}_{i,j,g}},\quad{\text{ rand}} \leqslant {\rm{CR}}\;{或}\;j = {j_{\rm{rand}}} \\ &{{\boldsymbol{x}}_{i,j,g}},\quad{其他} \\ \end{aligned} \right. $$ (4) 其中,jrand是{1, 2, …, D}中的一个随机整数(D代表问题维度),用来保证试验向量ui至少有一维不同于xi。参数CR是交叉概率,用来决定试验向量ui从变异向量vi的继承比例。
3) 选择
为了判断试验向量ui是否可以进入下一代,试验向量ui会与个体xi进行比较。其中拥有较好适应值的个体进入下一代。例如,对于一个最大化问题来说,拥有较大适应值的个体会进入下一代,如式(5)所示:
$$ {{\boldsymbol{x}}_{i,g + 1}} = \left\{ \begin{aligned} &{{\boldsymbol{u}}_{i,g}},\quad{\text{ }}f({{\boldsymbol{u}}_{i,g}}) > f({{\boldsymbol{x}}_{i,g}}) \\ &{{\boldsymbol{x}}_{i,g}},\quad {其他} \\ \end{aligned} \right. $$ (5) 其中f(x)为适应值评估函数。
而在多数基于DE的多峰值优化算法中,普遍使用的选择操作是将试验向量ui与距离ui最近的个体xj进行比较,拥有较好适应值的个体进入下一代,如式(6)所示:
$$ {{\boldsymbol{x}}_{j,g + 1}} = \left\{ \begin{aligned} &{{\boldsymbol{u}}_{i,g}},\quad {\text{ }}f({{\boldsymbol{u}}_{i,g}}) > f({{\boldsymbol{x}}_{j,g}}) \hfill \\ &{{\boldsymbol{x}}_{j,g}},\quad {其他} \hfill \\ \end{aligned} \right. $$ (6) 1.2 多峰值优化算法
在求解多峰值优化问题中,最主流的思想便是小生境策略[15-28],就是将整个种群划分为多个子种群,每个子种群分别去寻找该问题的一个或多个全局最优解,如Crowding[15]、Speciation[16]、聚类[17-18]、Hill-valley[23]等。但是,现有的小生境策略对它们各自的小生境参数特别敏感,以及为了提升种群划分的准确性,算法需要采样并评估足够多的中间点,消耗了大量的FEs。
基于小生境策略,Zhang等[19]提出了一种基于局部敏感哈希的小生境技术用来减小算法运行过程中的计算复杂度。Zhao等[20]提出了基于局部二值模式的小生境技术,并设计了一种参数自适应的DE算法。Chen等[21]设计了一种基于个体的分布式框架,在每个个体周围产生虚拟个体来形成小生境。Wang等[22]设计了一种基于最小生成树拓扑结构的差分进化算法,充分捕捉个体进化过程中的全局信息和局部信息。此外,Wang等[24]还设计了一种基于AP聚类的无参小生境技术,在避免了小生境参数敏感度的同时,也免去了FEs的消耗。
除了研究小生境策略,许多研究人员尝试提出新的变异策略来提升多峰值优化算法的性能。Biswas等[25]提出了基于局部信息分享机制的DE算法(local information DE,LoICDE和LoISDE)。同时,Biswas等[26]进一步提出了基于邻近度和父代中心的DE算法(parent-centric normalized mutation with proximity-based crowding DE,PNPCDE),充分利用邻居的进化信息。Wang等[27]则针对多峰值优化问题中的选择操作,提出了一种基于AP聚类的概率选择操作技术。
除了DE,还有很多演化算法用来求解多峰值优化问题。例如,在文献[31]中,基于聚类的小生境技术被应用在了分布估计算法中,称之为局部多峰值分布估计算法(locally multimodal estimation of distribution algorithm,LMCEDA和LMSEDA)。
此外,也有一些研究人员通过使用多目标转化的方法来求解多峰值优化问题。Wang等[32]设计了一种独特的转化方式,在每个维度上都设计了两个互相冲突的目标,算法称之为(multiobjective optimization for multimodal optimization problem,MOMMOP)。
1.3 AED-DDE
1.3.1 基于AED的自适应无参小生境技术
AED-DDE算法提出了一种基于AED的自适应无参小生境技术,每个个体将找到一个适合该个体本身的小生境大小,并形成一个小生境来寻找一个全局最优解。具体来说,每个个体xi会首先选择距离该个体最近的3个个体来形成一个初始的小生境(个体xi的初始小生境大小Mi设置为3)。接着,算法采用高斯分布来估计该小生境的分布。小生境Ni的分布估计Di如式(7)所示:
$$ \begin{gathered} \quad\quad{{\boldsymbol{\mu}} _{i,j}} = \frac{1}{{{M_i}}}\sum\limits_{k = 1}^{{M_i}} {{{\boldsymbol{x}}_{k,j}}} \hfill \\ {{\boldsymbol{\sigma}} _{i,j}} = \sqrt {\frac{1}{{{M_i}}}\sum\limits_{k = 1}^{{M_i}} {({{\boldsymbol{x}}_{k,j}} - } {{\boldsymbol{\mu}} _{i,j}}{)^2}} \hfill \\ \end{gathered} $$ (7) 式中:μi和σi表示小生境Ni的各维度均值和方差;xk表示小生境Ni中的第kth个个体;Mi表示小生境Ni的大小(初始化中Mi =3)。
在估计完小生境Ni的分布Di后,AED使用范围μi±3σi来判断一个给定的个体是否可以被分布Di拟合。算法首先选择距离个体xi第4th近的个体xi4th来观察个体xi4th是否能落在范围μi±3σi中。如果个体xi4th不能落在范围μi±3σi中,这就意味着个体xi4th距离个体xi较远。这样,个体xi4th应当被小生境Ni排除,小生境Ni应当保持大小Mi=3,从而避免误导进化。
而如果个体xi4th落在范围μi±3σi中,小生境Ni的大小Mi加1,新的个体xi4th加入到小生境Ni中,算法继续使用式(7)来重新估计小生境Ni的分布Di。之后,算法继续来看距离个体xi第5th近的个体是否可以被分布Di所拟合。重复上述的过程,直到小生境的大小不再改变为止。完整的基于AED的小生境策略的伪代码如算法1所示。
算法1 基于AED的小生境技术
For种群中的每个个体xi;
选择距离个体xi最近的3个个体来形成 一个初始小生境Ni(个体xi的初始小生境 大小Mi设置为;
使用式(7)来估计小生境Ni的分布Di;
While (true);
If距离个体xi最近的第(Mi+1)th个个体 落在范围μi±3σi中;
将距离个体xi最近的第(Mi+1)th个个 体加入小生境Ni中;
Mi=Mi+1;
重新使用式(7)来估计小生境Ni的 分布Di;
Else
Break;
End If
End While
End For
经过基于AED的小生境技术后,每个个体将找到适合该个体本身的小生境大小,从而自适应地形成多个小生境。不同的小生境协同共进化,执行基本DE算法的变异和交叉操作来得到试验向量,而后使用式(6)执行选择操作。
1.3.2 基于PLS的局部搜索技术
为了进一步提高解的准确度,更加精确地找到问题的所有全局最优解,算法提出了概率局部搜索技术(probabilistic local search,PLS)。
在PLS中,算法使用了基于高斯分布的局部搜索技术,如式(8)所示:
$$ {\boldsymbol{x}}_{\rm{new}}= {{N}}({\boldsymbol{x}},\sigma ) $$ (8) 式中:xnew是高斯分布在个体x周围新采样的个体;高斯分布N(x, σ)表示以个体x作为均值,σ作为标准差。标准差σ的设置如式(9)所示:
$$ \sigma = {10^{ - 1 - \frac{{\left( {10/D + 3} \right) \times {\rm{FEs}}}}{\rm{MaxFEs}}}} $$ (9) 在PLS中,算法为适应值好的个体分配较高的局部搜索概率。首先,按照个体的适应值对个体进行由坏到好的排序。接着,算法设置第ith个个体执行局部搜索的概率为
$$ P_{i}=r_{i}/N $$ (10) 式中:ri表示第ith个个体在适应值排序中的位置;N表示种群规模。
在执行局部搜索操作时,每个个体在各自的周围采样2个点。完整的PLS算法伪代码如算法2所示。
算法2 PLS算法
使用式(9)确定高斯分布的标准差σ;
使用式(10)为个体设置局部搜索概率;
For 每个个体xi:
If rand<Pi;
使用式(8)在xi周围采样两个个体;
评估这两个个体,定义较好的个体为
${\boldsymbol{x}}'_i$ ;FEs=FEs+2;
If 个体
${\boldsymbol{x}}'_i $ 的适应值好于个体xi;用个体
${\boldsymbol{x}}'_i $ 替换掉个体xi;End If
End If
End For
2. 概率评估的差分进化算法(PEDE)
AED-DDE算法在多峰值优化问题上已经取得了很好的实验结果。然而,在极其有限的适应值评估次数内,AED-DDE算法的性能仍然可以进一步提高。本文提出的PEDE算法基于之前的研究工作AED-DDE[29],并在AED-DDE算法的基础上引入了概率评估机制。
2.1 概率评估机制PE
首先,在算法进化过程中,AED-DDE并没有考虑利用个体的历史进化信息。例如,如果一个个体xj持续被更新,就说明产生的试验向量ui可以经常性地替换个体xj,那么个体xj的适应值很有可能并不好或者处于非最优区域;相反,如果一个个体xj很久没有被更新,就说明产生的试验向量ui很难替换个体xj,那么个体xj的适应值很可能已经非常好或者已经找到了最优解。如果我们可以充分挖掘并利用这些个体的历史进化信息来帮助种群的搜索,算法性能会进一步地提高。
其次,在有限的适应值评估次数内,并没有必要对所有的个体都进行评估。例如,如果一个个体xj持续被更新,就说明产生的试验向量ui可以经常性地替换该个体,那么可以近似认为,在不评估试验向量ui的情况下,试验向量ui的适应值大概率是要好于个体xj的;同样地,如果一个个体xj很久没有被更新,就说明产生的试验向量ui很难替换个体xj,那么我们可以近似认为,在不评估试验向量ui的情况下,试验向量ui的适应值大概率是要差于个体xj的。也就是说,在这两种情况下,可以不去评估试验向量ui,直接利用个体的进化信息就可以近似选择出适应值更好的个体。这个历史经验信息的积累就当作为我们第一层适应值评估概率的基础。
2.1.1 第一层适应值评估概率
首先为每个个体赋予第一层适应值评估概率PFj和两个选择概率PXj和PUj,分别代表个体j的第一层适应值评估概率,选择自身xj进入下一代的概率,以及选择试验向量ui进入下一代的概率,三者均初始化为0.5。
在算法运行初期(在0.3×MaxFEs内),需要充分挖掘个体的历史进化信息,因此,在这个阶段里,所有的个体都要进行评估。每当产生一个试验向量ui后,如果试验向量ui的适应值要好于它最近的父代个体xj,则个体xj的选择概率PUj会适当地增加,而选择概率PXj会适当地减小;相反,如果试验向量ui的适应值要差于它最近的父代个体xj,则个体xj的选择概率PUj会适当地减小,而选择概率PXj会适当地增加。我们定义个体xj的选择概率PUj和PXj的范围为[0.2, 0.8],且PUj+PXj=1,二者更新式如(11)所示:
$$ \begin{gathered} {{\rm{PU}}_j} = \left\{ \begin{gathered} {{\rm{PU}}_j} + {\rm{max}}(0,{\rm{N}}(0.05,0.01)),{\text{ }}{\text{ }}f({{{u}}_{i,g}}) > f({{{x}}_{j,g}}) \\ {{\rm{PU}}_j} - {\rm{max}}(0,{\rm{N}}(0.05,0.01),\quad{其他} \\ \end{gathered} \right. \\ {{\rm{PX}}_j} = {\text{ }}1 - {{\rm{PU}}_j} \\ \end{gathered} $$ (11) 而个体的第一层适应值评估概率PFj则是根据选择概率PUj和PXj,选择二者中的最小值,如式(12)所示:
$$ {\rm{PF}}_{j} = {\rm{min}}({\rm{PX}}_{j }, {\rm{PU}}_{j}) $$ (12) 也就是说,假如个体xj的选择概率PUj很大而选择概率PXj很小,那么该个体的第一层适应值评估概率就会设置为PXj,即很小的值。因为xj的选择概率PUj很大,也就是说,根据前期经验,产生的试验向量ui是有很大概率可以替换掉个体xj的,那么即使不对试验向量ui进行评估,也可以近似认为试验向量ui是有很大概率可以替换掉个体xj,故而将个体xj的第一层适应值评估概率PFj设置为较小的值PXj。同理,假如个体xj的选择概率PUj很小而选择概率PXj很大,那么该个体的第一层评估概率就会设置为PUj。因为xj的选择概率PUj很小,也就是说根据前期经验,产生的试验向量ui是几乎不可能替换掉个体xj的,那么即使不对试验向量ui进行评估,我们可以近似认为试验向量ui是几乎不可能替换掉个体xj,故而将个体xj的第一层适应值评估概率PFj设置为较小的值PXj。很显然,个体的第一层适应值评估概率PFj的取值范围就是[0.2,0.5]。
PFj的取值越大,则说明个体xj前期的适应值评估经验越弱,选择概率越模糊。当PFj=0.5时,也就是个体xj前期的适应值评估经验几乎为0,此时如果仍然依赖个体xj前期的适应值评估经验,很有可能误导种群的进化。也就是说,我们希望当PFj=0.5时,个体xj必须被评估。所以进一步在PFj上增加了拉伸操作,如式(13)所示:
$$ {\rm{PF}}_{j} = 2×{\rm{PF}}_{j} $$ (13) 即将个体的第一层适应值评估概率PFj的取值范围由[0.2,0.5]线性拉伸到[0.4,1],增加前期适应值评估经验较弱个体的适应值评估概率。
2.1.2 第二层适应值评估概率
除了个体的历史经验信息以外,还需要考虑的就是个体当前的适应值。显然,当评估次数极其有限时,自然是希望将这有限的适应值评估次数用在更有可能寻找到问题最优解的个体上。适应值越好的个体,接近最优解的概率也相应越高。因此,在这里基于每个个体的适应值,为每个个体xj设计了第2层的适应值评估概率PSj。具体的设计思路与AED-DDE算法中的PLS策略类似,按照个体的适应值对个体进行由坏到好的排序。接着,设置个体xj的第二层的适应值评估概率PSj如式(14)所示:
$$ {\rm{PS}}_{j}=r_{j}/N $$ (14) 式中:rj表示第jth个个体在适应值排序中的位置。也就是说,适应值越好的个体就拥有更好的第二层的适应值评估概率PSj。
2.1.3 完整的概率评估机制流程
在我们的算法设计中,使用两个适应值评估概率的最大值作为个体最终的适应值评估概率Pj,如式(15)所示。
$$ P_{j}={\rm{max}}({\rm{PF}}_{j}, {\rm{PS}}_{j}) $$ (15) 具体来说,如果个体xj的第1层适应值评估概率PFj很小但是第2层的适应值评估概率PSj很高,这说明个体xj具有很好的适应值,寻找到最优解的概率也会很高,此时,即使个体xj的第一层适应值评估概率PFj很小,依然为个体xj设置较大的适应值评估概率,加快算法找到问题最优解的速率。同样,如果个体xj的第一层适应值评估概率PFj很高但是第2层的适应值评估概率PSj很小,这说明个体xj虽然适应值较差,但个体xj前期的适应值评估经验较弱,选择概率较为模糊,此时,为了提升算法的准确性,同样为个体xj设置较大的适应值评估概率,进一步丰富并优化个体xj的历史评估经验,方便后续算法性能的提升。这两个适应值评估概率的结合,可以进一步增强算法的优化性能。
在算法运行初期结束后,就开始采用概率评估机制。在这个阶段中,每个个体xj会根据自身的适应值评估概率Pj来选择性评估。如果该个体xj满足自身的适应值评估概率Pj,则对产生的试验向量ui进行适应值评估,通过比较ui与xj的适应值来判断是否对xj进行更新,并采用上述方法相应地更新个体xj的选择概率PUj和PXj以及第1层的适应值评估概率PFj。
若是该个体xj并不满足自身的适应值评估概率Pj,则不对产生的试验向量ui进行适应值评估,而是根据前期积累的历史经验,直接根据选择概率PUj和PXj来判断是否对xj进行更新,即如果个体xj满足自身的选择概率PXj,则直接忽略试验向量ui,不对个体xj进行更新。如果个体xj满足自身的选择概率PUj,则直接用试验向量ui替换掉个体xj。然而,由于此时并没有对试验向量ui进行适应值评估,试验向量ui没有相应的适应值,在这种情况下,即使个体xj更新了,依然使用它之前的适应值作为更新后个体的新适应值。同时,由于并没有对个体的适应值进行评估,此时个体xj的选择概率PUj和PXj以及第一层的适应值评估概率PFj不进行更新。
综上,概率评估机制所节省下来的FEs可以提供给那些更需要评估的个体,增加种群的迭代次数,提升算法的求解精度;同时,概率评估机制充分捕捉了算法运行过程中每个个体的历史经验信息,实现了信息的充分利用,有利于算法的进一步搜索;最后,双层概率的结合使用互为补充,从多方面决定个体的适应值评估概率,丰富了算法的设计,进一步提升了算法的优化性能。完整的概率评估机制PE的算法伪代码如算法3所示。
算法3 PE算法
If FEs
$\leqslant $ 0.3×MaxFEs:评估每个试验向量ui;
FEs=FEs+N;
For 每个试验向量ui;
找到与ui与最近的父代个体xj;
If ui的适应值好于xj;
xj = ui;xj的适应值更新为ui的适应值;
PUj=min(PUj + max(0, N(0.05,0.01)), 0.8);
Else:
PUj=max(PUj − max(0, N(0.05,0.01)), 0.2);
End If
PXj = 1−PUj;
PFj = min(PXj , PUj);
PFj = 2×PFj;
Else:
使用式(10)为个体设置第二层适应值评估概率PSj;
Pj = max(PFj , PSj);
For 每个试验向量ui:
找到与ui与最近的父代个体xj;
If rand
$\leqslant $ Pj:评估试验向量ui;
FEs=FEs+1;
If ui的适应值好于xj:
xj = ui;
PUj=min(PUj + max(0, N(0.05,0.01)), 0.8);
Else:
PUj=max(PUj - max(0, N(0.05,0.01)), 0.2);
End If
PXj = 1−PUj;
PFj = min(PXj , PUj);
PFj = 2×PFj;
Else:
If rand
$\leqslant $ PUj:xj = ui;xj的适应值保持不变;
End If
End If
End For
End If
2.2 完整的PEDE算法
结合AED-DDE算法与以上的概率评估机制PE,完整的PEDE算法伪代码如算法4所示。
算法4 PEDE算法
初始化种群;FEs=0;PF=0.5;PX=0.5;PU=0.5;
评估整个种群;
FEs=FEs+N;
While FEs
$\leqslant $ MaxFEs:使用算法1执行基于AED的自适应小生境技术;
每个小生境进行进化并产生试验向量ui;
使用算法3执行基于PE的概率适应值评估机制;
使用算法2执行基于PLS的概率局部搜索技术;
End While
1) 结合了AED-DDE算法中基于AED的小生境策略以及基于PLS的局部搜索策略,可以避免种群划分的困难以及小生境参数的敏感度,同时使得算法可以更加精确地找到所有的全局最优解。
2) 概率评估机制的提出为算法节省FEs,便于算法将及其有限的FEs提供给那些更需要评估的个体,同时增加种群的迭代次数,提升算法的求解精度。
3. 数值实验分析
3.1 实验设置
采用目前最主流的多峰值优化测试集IEEE CEC 2013[33]来测试PEDE的算法性能。
多峰值优化问题有两个重要的评估指标,分别是最优解寻找率(peak ratio,PR)和成功运行率(success rate,SR)。对于一个给定的最大适应值评估次数MaxFEs和一个准确度ε,PR指的是算法多次运行中,全局最优解的平均找寻率;SR指的是算法的成功运行比率,其中一次成功运行表示算法可以在当次运行中找到该问题的所有全局最优解。
PEDE的种群规模N的设置如表1所示,而MaxFEs的设置则是引用IEEE CEC 2013多峰值优化测试集的要求。此外,PEDE中使用的变异策略为 DE/rand/1,放大系数F与交叉概率CR分别设置为0.9和0.1。所有的算法独立运行51次,对比实验结果的均值。此外,采用准确度ε=10−4来测试算法性能,该准确度的使用最为普遍[15-28]。
表 1 参数设置Table 1 Parameters setting测试函数 N MaxFEs F1~F5 80 5.00×104 F6 100 2.00×105 F7 300 2.00×105 F8~F9 300 4.00×105 F10 100 2.00×105 F11~F13 200 2.00×105 F14~F20 200 4.00×105 比较PEDE与以下15个多峰值优化算法,它们分别是小生境策略算法CDE[15]、SDE[16]、NCDE[18]、NSDE[18]、Self-CCDE[17]、Self-CSDE[17]、AED-DDE[29];新变异策略算法LoICDE[25]、LoISDE[25]、R3PSO[34]、LIPS[35], PNPCDE[26]、LMCEDA[31]、LMSEDA[31];以及多目标优化算法MOMMOP[32]。这些算法都是近年来的多峰值优化中的代表性主流成果,时间跨度从2004年到2021年。所有的算法采用相同的MaxFEs设置,以此来保证比较的公平性。
3.2 实验结果
3.2.1 与主流多峰值优化算法实验结果对比
表2列举了PEDE与其他多峰值优化算法在准确度ε=10−4下PR与SR的实验结果。为了突出显示,最好的PR结果加粗显示。此外,Wilcoxon秩和检验在α=0.05下用来做不同算法之间PR结果的显著性分析[36]。符号“+”、“−”和“≈”分别表示算法PEDE要显著好于(+)、显著差于(−)以及无明显差异(≈)对比算法。从表2中可以看到,在函数F1~F6和F10~F12上,只有PEDE和AED-DDE可以在每一次运行中都找到所有的全局最优解,PR值与SR值均为1.000,而其他的任何一个算法都不能达到相同的效果。在函数F7~F9上,Self-CCDE和MOMMOP取得了令人非常满意的结果,甚至结果要好于PEDE,特别是MOMMOP,PR值与SR值均为1.000。然而,PEDE在函数F7~F9上也取得了很好的结果,要显著好于其他的多峰值优化算法。同时,Self-CCDE和MOMMOP在函数F11和F12上的结果要显著差于PEDE。在函数F13上,PEDE取得了与LIPS近似的实验结果,但要显著好于其他所有的多峰值优化算法。同时,LIPS在其他函数上的结果都不能优于PEDE。在函数F14~F20上,PEDE在函数F14、F16和F20上都取得了最好的实验结果。需要注意的是,F20是IEEE CEC 2013中最复杂、维度最高的测试函数,许多算法在F20上甚至不能找到任何一个全局最优解。即使PEDE在函数F15、F17和F19上的实验结果要略微逊色于LMCEDA 和LMSEDA,PEDE的实验结果依然要显著好于其他的多峰值优化算法。同时,与算法LMCEDA 和LMSEDA 相比,PEDE在其他函数上的效果要明显好于LMCEDA 和LMSEDA,尤其是在4个拥有着数量巨大的全局最优解的函数F6~F9上。
表 2 IEEE CEC 2013测试集在准确度ε=10−4下的PR与SR的实验结果Table 2 Experimental results of IEEE CEC 2013 in PR and SR at accuracy level ε=10−4测试
函数PEDE CDE SDE LIPS AED-DDE R3PSO NCDE NSDE PR SR PR SR PR SR PR SR PR SR PR SR PR SR PR SR F1 1.000 1.000 1.000(≈) 1.000 0.696(+) 0.431 0.892(+) 0.824 1.000(≈) 1.000 1.000(≈) 1.000 1.000(≈) 1.000 1.000(≈) 1.000 F2 1.000 1.000 1.000(≈) 1.000 0.773(+) 0.588 1.000(≈) 1.000 1.000(≈) 1.000 0.992(≈) 0.961 1.000(≈) 1.000 0.808(+) 0.726 F3 1.000 1.000 1.000(≈) 1.000 1.000(≈) 1.000 1.000(≈) 1.000 1.000(≈) 1.000 1.000(≈) 1.000 1.000(≈) 1.000 1.000(≈) 1.000 F4 1.000 1.000 0.995(≈) 0.980 0.284(+) 0.000 0.995(≈) 0.980 1.000(≈) 1.000 0.971(+) 0.902 1.000(≈) 1.000 0.255(+) 0.000 F5 1.000 1.000 1.000(≈) 1.000 0.961(+) 0.922 1.000(≈) 1.000 1.000(≈) 1.000 1.000(≈) 1.000 1.000(≈) 1.000 0.686(+) 0.373 F6 1.000 1.000 1.000(≈) 1.000 0.059(+) 0.000 0.209(+) 0.000 1.000(≈) 1.000 0.662(+) 0.000 0.324(+) 0.000 0.056(+) 0.000 F7 0.887 0.157 0.870(+) 0.000 0.055(+) 0.000 0.399(+) 0.000 0.838(+) 0.039 0.429(+) 0.000 0.873(+) 0.039 0.043(+) 0.000 F8 0.805 0.000 0.000(+) 0.000 0.017(+) 0.000 0.081(+) 0.000 0.747(+) 0.000 0.431(+) 0.000 0.001(+) 0.000 0.013(+) 0.000 续表 2 测试
函数PEDE CDE SDE LIPS AED-DDE R3PSO NCDE NSDE PR SR PR SR PR SR PR SR PR SR PR SR PR SR PR SR F9 0.406 0.000 0.472(−) 0.000 0.011(+) 0.000 0.104(+) 0.000 0.384(+) 0.000 0.129(+) 0.000 0.457(−) 0.000 0.005(+) 0.000 F10 1.000 1.000 1.000(≈) 1.000 0.144(+) 0.000 0.755(+) 0.083 1.000(≈) 1.000 0.869(+) 0.137 0.997(≈) 0.961 0.088(+) 0.000 F11 1.000 1.000 0.373(+) 0.000 0.301(+) 0.000 0.944(+) 0.686 1.000(≈) 1.000 0.650(+) 0.000 0.732(+) 0.020 0.226(+) 0.000 F12 1.000 1.000 0.000(+) 0.000 0.211(+) 0.000 0.586(+) 0.000 1.000(≈) 1.000 0.537(+) 0.000 0.238(+) 0.000 0.132(+) 0.000 F13 0.771 0.020 0.154(+) 0.000 0.307(+) 0.000 0.775(≈) 0.118 0.686(+) 0.000 0.654(+) 0.000 0.667(+) 0.000 0.219(+) 0.000 F14 0.667 0.000 0.059(+) 0.000 0.212(+) 0.000 0.660(≈) 0.000 0.667(≈) 0.000 0.644(+) 0.000 0.667(≈) 0.000 0.173(+) 0.000 F15 0.635 0.000 0.010(+) 0.000 0.110(+) 0.000 0.348(+) 0.000 0.637(≈) 0.000 0.206(+) 0.000 0.321(+) 0.000 0.123(+) 0.000 F16 0.667 0.000 0.000(+) 0.000 0.101(+) 0.000 0.281(+) 0.000 0.667(≈) 0.000 0.451(+) 0.000 0.667(≈) 0.000 0.170(+) 0.000 F17 0.412 0.000 0.000(+) 0.000 0.074(+) 0.000 0.164(+) 0.000 0.375(+) 0.000 0.120(+) 0.000 0.248(+) 0.000 0.096(+) 0.000 F18 0.654 0.000 0.167(+) 0.000 0.013(+) 0.000 0.128(+) 0.000 0.654(≈) 0.000 0.092(+) 0.000 0.534(+) 0.000 0.167(+) 0.000 F19 0.368 0.000 0.000(+) 0.000 0.098(+) 0.000 0.000(+) 0.000 0.375(−) 0.000 0.034(+) 0.000 0.306(+) 0.000 0.098(+) 0.000 F20 0.250 0.000 0.000(+) 0.000 0.000(+) 0.000 0.000(+) 0.000 0.250(≈) 0.000 0.066(+) 0.000 0.250(≈) 0.000 0.123(+) 0.000 + 12 19 14 5 16 10 18 − 1 0 0 1 0 1 0 ≈ 7 1 6 14 4 9 2 测试
函数PNPCDE Self-CCDE Self-CSDE LoICDE LoISDE LMCEDA LMSEDA MOMMOP PR SR PR SR PR SR PR SR PR SR PR SR PR SR PR SR F1 1.000(≈) 1.000 1.000(≈) 1.000 1.000(≈) 1.000 1.000(≈) 1.000 0.990(≈) 0.980 1.000(≈) 1.000 1.000(≈) 1.000 1.000(≈) 1.000 F2 1.000(≈) 1.000 1.000(≈) 1.000 1.000(≈) 1.000 1.000(≈) 1.000 0.263(+) 0.078 1.000(≈) 1.000 1.000(≈) 1.000 1.000(≈) 1.000 F3 1.000(≈) 1.000 1.000(≈) 1.000 1.000(≈) 1.000 1.000(≈) 1.000 1.000(≈) 1.000 1.000(≈) 1.000 1.000(≈) 1.000 1.000(≈) 1.000 F4 1.000(≈) 1.000 1.000(≈) 1.000 0.706(+) 0.333 0.971(+) 0.882 0.250(+) 0.000 1.000(≈) 1.000 1.000(≈) 1.000 1.000(≈) 1.000 F5 1.000(≈) 1.000 1.000(≈) 1.000 0.961(+) 0.922 1.000(≈) 1.000 0.706(+) 0.412 1.000(≈) 1.000 1.000(≈) 1.000 1.000(≈) 1.000 F6 0.559(+) 0.000 0.928(+) 0.431 0.707(+) 0.059 1.000(≈) 1.000 0.056(+) 0.000 0.991(+) 0.843 0.970(+) 0.529 1.000(≈) 1.000 F7 0.887(≈) 0.000 0.875(+) 0.000 0.695(+) 0.000 0.691(+) 0.000 0.029(+) 0.000 0.724(+) 0.000 0.668(+) 0.000 1.000(−) 1.000 F8 0.000(+) 0.000 0.997(−) 0.863 0.679(+) 0.000 0.000(+) 0.000 0.012(+) 0.000 0.350(+) 0.000 0.608(+) 0.000 1.000(−) 1.000 F9 0.470(−) 0.000 0.457(−) 0.000 0.272(+) 0.000 0.115(+) 0.000 0.005(+) 0.000 0.280(+) 0.000 0.247(+) 0.000 1.000(−) 1.000 F10 1.000(≈) 1.000 1.000(≈) 1.000 0.992(+) 0.922 1.000(≈) 1.000 0.083(+) 0.000 1.000(≈) 1.000 1.000(≈) 1.000 1.000(≈) 1.000 F11 0.634(+) 0.000 0.771(+) 0.118 0.415(+) 0.000 0.660(+) 0.000 0.167(+) 0.000 0.667(+) 0.000 0.853(+) 0.157 0.712(+) 0.000 F12 0.000(+) 0.000 0.375(+) 0.000 0.333(+) 0.000 0.529(+) 0.000 0.125(+) 0.000 0.750(+) 0.000 0.983(+) 0.863 0.936(+) 0.529 F13 0.438(+) 0.000 0.663(+) 0.000 0.324(+) 0.000 0.523(+) 0.000 0.167(+) 0.000 0.667(+) 0.000 0.667(+) 0.000 0.667(+) 0.000 F14 0.330(+) 0.000 0.657(+) 0.000 0.343(+) 0.000 0.660(≈) 0.000 0.167(+) 0.000 0.667(≈) 0.000 0.667(≈) 0.000 0.667(≈) 0.000 F15 0.029(+) 0.000 0.358(+) 0.000 0.208(+) 0.000 0.314(+) 0.000 0.125(+) 0.000 0.694(−) 0.000 0.743(−) 0.000 0.618(+) 0.000 F16 0.000(+) 0.000 0.657(+) 0.000 0.078(+) 0.000 0.546(+) 0.000 0.167(+) 0.000 0.667(≈) 0.000 0.667(≈) 0.000 0.647(+) 0.000 F17 0.000(+) 0.000 0.250(+) 0.000 0.037(+) 0.000 0.248(+) 0.000 0.074(+) 0.000 0.417(≈) 0.000 0.632(−) 0.000 0.502(−) 0.000 F18 0.154(+) 0.000 0.327(+) 0.000 0.007(+) 0.000 0.216(+) 0.000 0.160(+) 0.000 0.654(≈) 0.000 0.660(≈) 0.000 0.493(+) 0.000 F19 0.000(+) 0.000 0.103(+) 0.000 0.000(+) 0.000 0.049(+) 0.000 0.032(+) 0.000 0.471(−) 0.000 0.458(-) 0.000 0.221(+) 0.000 F20 0.000(+) 0.000 0.052(+) 0.000 0.000(+) 0.000 0.123(+) 0.000 0.088(+) 0.000 0.066(+) 0.000 0.250(≈) 0.000 0.125(+) 0.000 + 13 12 17 13 18 8 7 8 − 1 2 0 0 0 2 3 4 ≈ 6 6 3 7 2 10 10 8 总之,PEDE分别要在12、19、14、5、16、10、18、13、12、17、13、18、8、7和8个函数上好于CDE、SDE、LIPS、AED-DDE、R3PSO、NCDE、NSDE、PNPCDE、Self-CCDE、Self-CSDE、LoICDE、LoISDE、LMCEDA、LMSEDA和MOMMOP。相反,PEDE只在1、1、1、2、2、3和4个函数上要略微差于CDE、NCDE、PNPCDE、Self-CCDE、LMCEDA、LMSEDA和MOMMOP。同时,PEDE的效果要好于AED-DDE,说明了概率适应值评估机制的有效性。
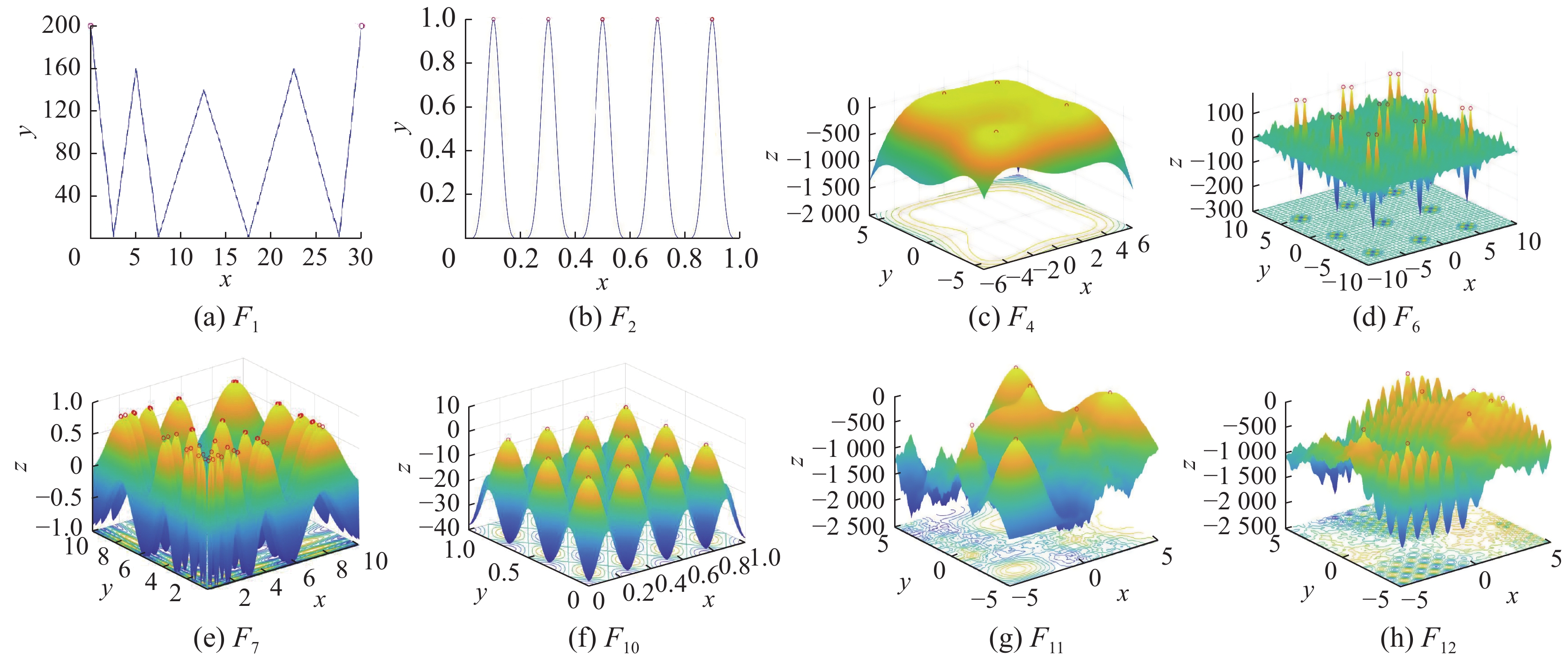
为了有一个更加直观的视角来看PEDE算法的求解效果,在8个可视化函数上将PEDE算法最终的种群分布展示出来。
如图1所示。
正如我们从图1中看到的,PEDE可以找到问题所有的全局最优解。即使当问题有数量巨大的全局最优解时,如图1(d)和图1(e),在函数F6和F7上,PEDE依然可以找到所有的全局最优解。当求解一些包含有数量巨大的局部最优解的复杂问题时,如图1(g)和图1(h),在函数F11和F12上,PEDE可以维持种群多样性和探索能力,有效地避开局部最优解,将所有的全局最优解找到。
3.2.2 与多峰值测试集冠军算法实验对比
为了进一步说明PEDE算法的优越性,在本节中,比较PEDE与多峰值优化测试集 IEEE CEC 2013的冠军算法(niching migratory multi-swarm optimizer, NMMSO[37])。为了公平比较,直接引用NMMSO算法在多峰值优化测试集IEEE CEC 2015上的实验数据。
PEDE与NMMSO在准确度ε=10−4下的PR与SR的详细对比结果如表3所示,其中最好的PR实验结果加粗显示。
从表3中可以看到,PEDE在7个函数上的实验结果要优于NMMSO,而在7个函数上的实验结果要略差于NMMSO。然而,可以看到,PEDE可以在9个函数上每一次运行中都找到问题所有的全局最优解(函数F1~F6和F10~F12),PR值与SR值均为1.000,而NMMSO仅可以在7个函数上找到问题所有的全局最优解(函数F1~F5、F7和F10)。同时,在PEDE差于NMMSO的测试函数上,PEDE也实现了与NMMSO近似的实验结果。例如,在函数F14、F17和F19上,NMMSO的PR实验结果分别是0.720、0.468和0.450,而PEDE也实现了近似的PR实验结果,分别是0.667、0.412和0.368。此外,在高维复合函数F16~F20上,PEDE在3个函数上要好于NMMSO,而NMMSO仅在2个函数上要好于PEDE。特别地,在函数F20上,也是多峰值优化测试集IEEE CEC 2013中最复杂的函数,PEDE的实验结果要好于NMMSO。
表 3 PEDE与NMMSO在准确度ε=10−4下的PR与SR的实验结果对比Table 3 Experimental results between PEDE and NMMSO in PR and SR at accuracy level ε=10−4测试函数 PEDE NMMSO PR SR PR SR F1 1.000 1.000 1.000(≈) 1.000 F2 1.000 1.000 1.000(≈) 1.000 F3 1.000 1.000 1.000(≈) 1.000 F4 1.000 1.000 1.000(≈) 1.000 F5 1.000 1.000 1.000(≈) 1.000 F6 1.000 1.000 0.992(+) 0.880 F7 0.887 0.157 1.000(−) 1.000 F8 0.805 0.000 0.899(−) 0.020 续表 3 测试函数 PEDE NMMSO PR SR PR SR F9 0.406 0.000 0.978(−) 0.120 F10 1.000 1.000 1.000(≈) 1.000 F11 1.000 1.000 0.990(+) 0.940 F12 1.000 1.000 0.993(+) 0.940 F13 0.771 0.020 0.983(−) 0.900 F14 0.667 0.000 0.720(−) 0.000 F15 0.635 0.000 0.632(+) 0.000 F16 0.667 0.000 0.660(+) 0.000 F17 0.412 0.000 0.468(−) 0.000 F18 0.654 0.000 0.650(+) 0.000 F19 0.368 0.000 0.450(−) 0.000 F20 0.250 0.000 0.172(+) 0.000 + 7 − 7 ≈ 6 总之,PEDE可以实现近似甚至好于多峰值优化测试集IEEE CEC 2013的冠军算法的实验结果,特别是在一些复杂度较高的函数上。
3.2.3 概率评估机制性能测试
从表2中可以看到,PEDE的效果要好于AED-DDE,说明了概率适应值评估机制的有效性。在本节中,进一步测试概率评估机制的性能。将概率评估机制应用在其他的多峰值优化算法中来测试其性能。由于我们的概率评估机制适用于DE算法,因此在这里,将概率评估机制应用在NCDE[18]、LoICDE[25]、Self-CCDE[17]、PNPCDE[26]这4个基于DE的多峰值优化算法中。这4个算法结合概率评估机制的算法变种命名为算法-PE,例如,NCDE算法结合概率评估机制的算法变种命名为NCDE-PE。这4个算法与它们相应的算法变种在准确度ε=10−4下的PR与SR的详细对比结果如表4所示。
表 4 多峰值优化算法及其在概率评估机制下的变种算法在准确度ε=10−4下的PR与SR的实验结果Table 4 Experimental results of multimodal optimization algorithms and their variants with PE in PR and SR at accuracy level ε=10−4函数 NCDE-PE NCDE LoICDE-PE LoICDE Self-CCDE-PE Self-CCDE PNPCDE-PE PNPCDE PR SR PR SR PR SR PR SR PR SR PR SR PR SR PR SR F1 1.000 1.000 1.000(≈) 1.000 1.000 1.000 1.000(≈) 1.000 1.000 1.000 1.000(≈) 1.000 PR SR 1.000(≈) 1.000 F2 1.000 1.000 1.000(≈) 1.000 1.000 1.000 1.000(≈) 1.000 1.000 1.000 1.000(≈) 1.000 1.000 1.000 1.000(≈) 1.000 F3 1.000 1.000 1.000(≈) 1.000 1.000 1.000 1.000(≈) 1.000 1.000 1.000 1.000(≈) 1.000 1.000 1.000 1.000(≈) 1.000 F4 1.000 1.000 1.000(≈) 1.000 1.000 1.000 0.971(+) 0.882 1.000 1.000 1.000(≈) 1.000 1.000 1.000 1.000(≈) 1.000 F5 1.000 1.000 1.000(≈) 1.000 1.000 1.000 1.000(≈) 1.000 1.000 1.000 1.000(≈) 1.000 1.000 1.000 1.000(≈) 1.000 F6 0.382 0.000 0.324(+) 0.000 1.000 1.000 1.000(≈) 1.000 0.936 0.529 0.928(+) 0.431 0.593 0.000 0.559(+) 0.000 F7 0.883 0.039 0.873(+) 0.039 0.702 0.000 0.691(+) 0.000 0.877 0.000 0.875(≈) 0.000 0.883 0.000 0.887(−) 0.000 F8 0.003 0.000 0.001(+) 0.000 0.002 0.000 0.000(+) 0.000 0.995 0.784 0.997(−) 0.863 0.003 0.000 0.000(+) 0.000 F9 0.454 0.000 0.457(≈) 0.000 0.121 0.000 0.115(+) 0.000 0.456 0.000 0.457(≈) 0.000 0.469 0.000 0.470(−) 0.000 F10 1.000 1.000 0.997(≈) 0.961 1.000 1.000 1.000(≈) 1.000 1.000 1.000 1.000(≈) 1.000 1.000 1.000 1.000(≈) 1.000 F11 0.718 0.000 0.732(−) 0.020 0.667 0.000 0.660(+) 0.000 0.781 0.157 0.771(+) 0.118 0.667 1.000 0.634(+) 0.000 F12 0.252 0.000 0.238(+) 0.000 0.525 0.000 0.529(≈) 0.000 0.375 0.000 0.375(≈) 0.000 0.012 0.000 0.000(+) 0.000 F13 0.667 0.000 0.667(≈) 0.000 0.500 0.000 0.523(−) 0.000 0.667 0.000 0.663(+) 0.000 0.457 0.000 0.438(+) 0.000 F14 0.667 0.000 0.667(≈) 0.000 0.667 0.000 0.660(≈) 0.000 0.667 0.000 0.657(+) 0.000 0.333 0.000 0.330(≈) 0.000 F15 0.306 0.000 0.321(−) 0.000 0.331 0.000 0.314(+) 0.000 0.346 0.000 0.358(-) 0.000 0.025 0.000 0.029(≈) 0.000 F16 0.667 0.000 0.667(≈) 0.000 0.565 0.000 0.546(+) 0.000 0.667 0.000 0.657(+) 0.000 0.000 0.000 0.000(≈) 0.000 F17 0.257 0.000 0.248(+) 0.000 0.250 0.000 0.248(≈) 0.000 0.250 0.000 0.250(≈) 0.000 0.020 0.000 0.000(+) 0.000 F18 0.529 0.000 0.534(≈) 0.000 0.235 0.000 0.216(+) 0.000 0.359 0.000 0.327(+) 0.000 0.167 0.000 0.154(+) 0.000 F19 0.318 0.000 0.306(+) 0.000 0.061 0.000 0.049(+) 0.000 0.098 0.000 0.103(≈) 0.000 0.000 0.000 0.000(≈) 0.000 F20 0.250 0.000 0.250(≈) 0.000 0.125 0.000 0.123(≈) 0.000 0.064 0.000 0.052(+) 0.000 0.000 0.000 0.000(≈) 0.000 + 6 9 7 7 − 2 1 2 2 ≈ 12 10 11 11 从表4中可以看到,概率评估机制都可以在一定程度上提升这4个算法的性能,分别在6、9、7、7个函数上提升了NCDE、LoICDE、Self-CCDE、PNPCDE的算法性能,尤其是在函数F6、F11~F14、F16~F20上,这4个结合概率评估机制的算法变种要显著好于原算法,进一步说明了概率评估机制的有效性与可拓展性。
4. 结束语
本文基于之前的自适应分布估计的差分进化算法这一研究工作,进一步提出了一种概率评估机制。概率评估机制技术的提出,充分挖掘了个体在搜索和学习过程中的历史经验信息,对个体进行选择性评估,节省算法的适应值评估次数,增加算法迭代次数,从而提升算法的求解精度。而对个体历史经验的充分学习也进一步促进了种群在搜索空间中的充分探索。
将自适应分布估计的差分进化算法与概率评估机制有机结合,充分利用了二者的优势,形成了本文中提出的新算法PEDE。PEDE不仅在多峰值优化测试集上取得了非常好的效果,同时,还将概率评估机制应用到其他的差分进化算法中,效果都有了一定的提升,也说明了概率评估机制的有效性与可拓展性。
在未来工作中,我们希望进一步增强PEDE算法在复杂多峰值优化问题上的求解性能,并将PEDE算法应用在多峰值实际优化问题当中。
-
表 1 参数设置
Table 1 Parameters setting
测试函数 N MaxFEs F1~F5 80 5.00×104 F6 100 2.00×105 F7 300 2.00×105 F8~F9 300 4.00×105 F10 100 2.00×105 F11~F13 200 2.00×105 F14~F20 200 4.00×105 表 2 IEEE CEC 2013测试集在准确度ε=10−4下的PR与SR的实验结果
Table 2 Experimental results of IEEE CEC 2013 in PR and SR at accuracy level ε=10−4
测试
函数PEDE CDE SDE LIPS AED-DDE R3PSO NCDE NSDE PR SR PR SR PR SR PR SR PR SR PR SR PR SR PR SR F1 1.000 1.000 1.000(≈) 1.000 0.696(+) 0.431 0.892(+) 0.824 1.000(≈) 1.000 1.000(≈) 1.000 1.000(≈) 1.000 1.000(≈) 1.000 F2 1.000 1.000 1.000(≈) 1.000 0.773(+) 0.588 1.000(≈) 1.000 1.000(≈) 1.000 0.992(≈) 0.961 1.000(≈) 1.000 0.808(+) 0.726 F3 1.000 1.000 1.000(≈) 1.000 1.000(≈) 1.000 1.000(≈) 1.000 1.000(≈) 1.000 1.000(≈) 1.000 1.000(≈) 1.000 1.000(≈) 1.000 F4 1.000 1.000 0.995(≈) 0.980 0.284(+) 0.000 0.995(≈) 0.980 1.000(≈) 1.000 0.971(+) 0.902 1.000(≈) 1.000 0.255(+) 0.000 F5 1.000 1.000 1.000(≈) 1.000 0.961(+) 0.922 1.000(≈) 1.000 1.000(≈) 1.000 1.000(≈) 1.000 1.000(≈) 1.000 0.686(+) 0.373 F6 1.000 1.000 1.000(≈) 1.000 0.059(+) 0.000 0.209(+) 0.000 1.000(≈) 1.000 0.662(+) 0.000 0.324(+) 0.000 0.056(+) 0.000 F7 0.887 0.157 0.870(+) 0.000 0.055(+) 0.000 0.399(+) 0.000 0.838(+) 0.039 0.429(+) 0.000 0.873(+) 0.039 0.043(+) 0.000 F8 0.805 0.000 0.000(+) 0.000 0.017(+) 0.000 0.081(+) 0.000 0.747(+) 0.000 0.431(+) 0.000 0.001(+) 0.000 0.013(+) 0.000 续表 2 测试
函数PEDE CDE SDE LIPS AED-DDE R3PSO NCDE NSDE PR SR PR SR PR SR PR SR PR SR PR SR PR SR PR SR F9 0.406 0.000 0.472(−) 0.000 0.011(+) 0.000 0.104(+) 0.000 0.384(+) 0.000 0.129(+) 0.000 0.457(−) 0.000 0.005(+) 0.000 F10 1.000 1.000 1.000(≈) 1.000 0.144(+) 0.000 0.755(+) 0.083 1.000(≈) 1.000 0.869(+) 0.137 0.997(≈) 0.961 0.088(+) 0.000 F11 1.000 1.000 0.373(+) 0.000 0.301(+) 0.000 0.944(+) 0.686 1.000(≈) 1.000 0.650(+) 0.000 0.732(+) 0.020 0.226(+) 0.000 F12 1.000 1.000 0.000(+) 0.000 0.211(+) 0.000 0.586(+) 0.000 1.000(≈) 1.000 0.537(+) 0.000 0.238(+) 0.000 0.132(+) 0.000 F13 0.771 0.020 0.154(+) 0.000 0.307(+) 0.000 0.775(≈) 0.118 0.686(+) 0.000 0.654(+) 0.000 0.667(+) 0.000 0.219(+) 0.000 F14 0.667 0.000 0.059(+) 0.000 0.212(+) 0.000 0.660(≈) 0.000 0.667(≈) 0.000 0.644(+) 0.000 0.667(≈) 0.000 0.173(+) 0.000 F15 0.635 0.000 0.010(+) 0.000 0.110(+) 0.000 0.348(+) 0.000 0.637(≈) 0.000 0.206(+) 0.000 0.321(+) 0.000 0.123(+) 0.000 F16 0.667 0.000 0.000(+) 0.000 0.101(+) 0.000 0.281(+) 0.000 0.667(≈) 0.000 0.451(+) 0.000 0.667(≈) 0.000 0.170(+) 0.000 F17 0.412 0.000 0.000(+) 0.000 0.074(+) 0.000 0.164(+) 0.000 0.375(+) 0.000 0.120(+) 0.000 0.248(+) 0.000 0.096(+) 0.000 F18 0.654 0.000 0.167(+) 0.000 0.013(+) 0.000 0.128(+) 0.000 0.654(≈) 0.000 0.092(+) 0.000 0.534(+) 0.000 0.167(+) 0.000 F19 0.368 0.000 0.000(+) 0.000 0.098(+) 0.000 0.000(+) 0.000 0.375(−) 0.000 0.034(+) 0.000 0.306(+) 0.000 0.098(+) 0.000 F20 0.250 0.000 0.000(+) 0.000 0.000(+) 0.000 0.000(+) 0.000 0.250(≈) 0.000 0.066(+) 0.000 0.250(≈) 0.000 0.123(+) 0.000 + 12 19 14 5 16 10 18 − 1 0 0 1 0 1 0 ≈ 7 1 6 14 4 9 2 测试
函数PNPCDE Self-CCDE Self-CSDE LoICDE LoISDE LMCEDA LMSEDA MOMMOP PR SR PR SR PR SR PR SR PR SR PR SR PR SR PR SR F1 1.000(≈) 1.000 1.000(≈) 1.000 1.000(≈) 1.000 1.000(≈) 1.000 0.990(≈) 0.980 1.000(≈) 1.000 1.000(≈) 1.000 1.000(≈) 1.000 F2 1.000(≈) 1.000 1.000(≈) 1.000 1.000(≈) 1.000 1.000(≈) 1.000 0.263(+) 0.078 1.000(≈) 1.000 1.000(≈) 1.000 1.000(≈) 1.000 F3 1.000(≈) 1.000 1.000(≈) 1.000 1.000(≈) 1.000 1.000(≈) 1.000 1.000(≈) 1.000 1.000(≈) 1.000 1.000(≈) 1.000 1.000(≈) 1.000 F4 1.000(≈) 1.000 1.000(≈) 1.000 0.706(+) 0.333 0.971(+) 0.882 0.250(+) 0.000 1.000(≈) 1.000 1.000(≈) 1.000 1.000(≈) 1.000 F5 1.000(≈) 1.000 1.000(≈) 1.000 0.961(+) 0.922 1.000(≈) 1.000 0.706(+) 0.412 1.000(≈) 1.000 1.000(≈) 1.000 1.000(≈) 1.000 F6 0.559(+) 0.000 0.928(+) 0.431 0.707(+) 0.059 1.000(≈) 1.000 0.056(+) 0.000 0.991(+) 0.843 0.970(+) 0.529 1.000(≈) 1.000 F7 0.887(≈) 0.000 0.875(+) 0.000 0.695(+) 0.000 0.691(+) 0.000 0.029(+) 0.000 0.724(+) 0.000 0.668(+) 0.000 1.000(−) 1.000 F8 0.000(+) 0.000 0.997(−) 0.863 0.679(+) 0.000 0.000(+) 0.000 0.012(+) 0.000 0.350(+) 0.000 0.608(+) 0.000 1.000(−) 1.000 F9 0.470(−) 0.000 0.457(−) 0.000 0.272(+) 0.000 0.115(+) 0.000 0.005(+) 0.000 0.280(+) 0.000 0.247(+) 0.000 1.000(−) 1.000 F10 1.000(≈) 1.000 1.000(≈) 1.000 0.992(+) 0.922 1.000(≈) 1.000 0.083(+) 0.000 1.000(≈) 1.000 1.000(≈) 1.000 1.000(≈) 1.000 F11 0.634(+) 0.000 0.771(+) 0.118 0.415(+) 0.000 0.660(+) 0.000 0.167(+) 0.000 0.667(+) 0.000 0.853(+) 0.157 0.712(+) 0.000 F12 0.000(+) 0.000 0.375(+) 0.000 0.333(+) 0.000 0.529(+) 0.000 0.125(+) 0.000 0.750(+) 0.000 0.983(+) 0.863 0.936(+) 0.529 F13 0.438(+) 0.000 0.663(+) 0.000 0.324(+) 0.000 0.523(+) 0.000 0.167(+) 0.000 0.667(+) 0.000 0.667(+) 0.000 0.667(+) 0.000 F14 0.330(+) 0.000 0.657(+) 0.000 0.343(+) 0.000 0.660(≈) 0.000 0.167(+) 0.000 0.667(≈) 0.000 0.667(≈) 0.000 0.667(≈) 0.000 F15 0.029(+) 0.000 0.358(+) 0.000 0.208(+) 0.000 0.314(+) 0.000 0.125(+) 0.000 0.694(−) 0.000 0.743(−) 0.000 0.618(+) 0.000 F16 0.000(+) 0.000 0.657(+) 0.000 0.078(+) 0.000 0.546(+) 0.000 0.167(+) 0.000 0.667(≈) 0.000 0.667(≈) 0.000 0.647(+) 0.000 F17 0.000(+) 0.000 0.250(+) 0.000 0.037(+) 0.000 0.248(+) 0.000 0.074(+) 0.000 0.417(≈) 0.000 0.632(−) 0.000 0.502(−) 0.000 F18 0.154(+) 0.000 0.327(+) 0.000 0.007(+) 0.000 0.216(+) 0.000 0.160(+) 0.000 0.654(≈) 0.000 0.660(≈) 0.000 0.493(+) 0.000 F19 0.000(+) 0.000 0.103(+) 0.000 0.000(+) 0.000 0.049(+) 0.000 0.032(+) 0.000 0.471(−) 0.000 0.458(-) 0.000 0.221(+) 0.000 F20 0.000(+) 0.000 0.052(+) 0.000 0.000(+) 0.000 0.123(+) 0.000 0.088(+) 0.000 0.066(+) 0.000 0.250(≈) 0.000 0.125(+) 0.000 + 13 12 17 13 18 8 7 8 − 1 2 0 0 0 2 3 4 ≈ 6 6 3 7 2 10 10 8 表 3 PEDE与NMMSO在准确度ε=10−4下的PR与SR的实验结果对比
Table 3 Experimental results between PEDE and NMMSO in PR and SR at accuracy level ε=10−4
测试函数 PEDE NMMSO PR SR PR SR F1 1.000 1.000 1.000(≈) 1.000 F2 1.000 1.000 1.000(≈) 1.000 F3 1.000 1.000 1.000(≈) 1.000 F4 1.000 1.000 1.000(≈) 1.000 F5 1.000 1.000 1.000(≈) 1.000 F6 1.000 1.000 0.992(+) 0.880 F7 0.887 0.157 1.000(−) 1.000 F8 0.805 0.000 0.899(−) 0.020 续表 3 测试函数 PEDE NMMSO PR SR PR SR F9 0.406 0.000 0.978(−) 0.120 F10 1.000 1.000 1.000(≈) 1.000 F11 1.000 1.000 0.990(+) 0.940 F12 1.000 1.000 0.993(+) 0.940 F13 0.771 0.020 0.983(−) 0.900 F14 0.667 0.000 0.720(−) 0.000 F15 0.635 0.000 0.632(+) 0.000 F16 0.667 0.000 0.660(+) 0.000 F17 0.412 0.000 0.468(−) 0.000 F18 0.654 0.000 0.650(+) 0.000 F19 0.368 0.000 0.450(−) 0.000 F20 0.250 0.000 0.172(+) 0.000 + 7 − 7 ≈ 6 表 4 多峰值优化算法及其在概率评估机制下的变种算法在准确度ε=10−4下的PR与SR的实验结果
Table 4 Experimental results of multimodal optimization algorithms and their variants with PE in PR and SR at accuracy level ε=10−4
函数 NCDE-PE NCDE LoICDE-PE LoICDE Self-CCDE-PE Self-CCDE PNPCDE-PE PNPCDE PR SR PR SR PR SR PR SR PR SR PR SR PR SR PR SR F1 1.000 1.000 1.000(≈) 1.000 1.000 1.000 1.000(≈) 1.000 1.000 1.000 1.000(≈) 1.000 PR SR 1.000(≈) 1.000 F2 1.000 1.000 1.000(≈) 1.000 1.000 1.000 1.000(≈) 1.000 1.000 1.000 1.000(≈) 1.000 1.000 1.000 1.000(≈) 1.000 F3 1.000 1.000 1.000(≈) 1.000 1.000 1.000 1.000(≈) 1.000 1.000 1.000 1.000(≈) 1.000 1.000 1.000 1.000(≈) 1.000 F4 1.000 1.000 1.000(≈) 1.000 1.000 1.000 0.971(+) 0.882 1.000 1.000 1.000(≈) 1.000 1.000 1.000 1.000(≈) 1.000 F5 1.000 1.000 1.000(≈) 1.000 1.000 1.000 1.000(≈) 1.000 1.000 1.000 1.000(≈) 1.000 1.000 1.000 1.000(≈) 1.000 F6 0.382 0.000 0.324(+) 0.000 1.000 1.000 1.000(≈) 1.000 0.936 0.529 0.928(+) 0.431 0.593 0.000 0.559(+) 0.000 F7 0.883 0.039 0.873(+) 0.039 0.702 0.000 0.691(+) 0.000 0.877 0.000 0.875(≈) 0.000 0.883 0.000 0.887(−) 0.000 F8 0.003 0.000 0.001(+) 0.000 0.002 0.000 0.000(+) 0.000 0.995 0.784 0.997(−) 0.863 0.003 0.000 0.000(+) 0.000 F9 0.454 0.000 0.457(≈) 0.000 0.121 0.000 0.115(+) 0.000 0.456 0.000 0.457(≈) 0.000 0.469 0.000 0.470(−) 0.000 F10 1.000 1.000 0.997(≈) 0.961 1.000 1.000 1.000(≈) 1.000 1.000 1.000 1.000(≈) 1.000 1.000 1.000 1.000(≈) 1.000 F11 0.718 0.000 0.732(−) 0.020 0.667 0.000 0.660(+) 0.000 0.781 0.157 0.771(+) 0.118 0.667 1.000 0.634(+) 0.000 F12 0.252 0.000 0.238(+) 0.000 0.525 0.000 0.529(≈) 0.000 0.375 0.000 0.375(≈) 0.000 0.012 0.000 0.000(+) 0.000 F13 0.667 0.000 0.667(≈) 0.000 0.500 0.000 0.523(−) 0.000 0.667 0.000 0.663(+) 0.000 0.457 0.000 0.438(+) 0.000 F14 0.667 0.000 0.667(≈) 0.000 0.667 0.000 0.660(≈) 0.000 0.667 0.000 0.657(+) 0.000 0.333 0.000 0.330(≈) 0.000 F15 0.306 0.000 0.321(−) 0.000 0.331 0.000 0.314(+) 0.000 0.346 0.000 0.358(-) 0.000 0.025 0.000 0.029(≈) 0.000 F16 0.667 0.000 0.667(≈) 0.000 0.565 0.000 0.546(+) 0.000 0.667 0.000 0.657(+) 0.000 0.000 0.000 0.000(≈) 0.000 F17 0.257 0.000 0.248(+) 0.000 0.250 0.000 0.248(≈) 0.000 0.250 0.000 0.250(≈) 0.000 0.020 0.000 0.000(+) 0.000 F18 0.529 0.000 0.534(≈) 0.000 0.235 0.000 0.216(+) 0.000 0.359 0.000 0.327(+) 0.000 0.167 0.000 0.154(+) 0.000 F19 0.318 0.000 0.306(+) 0.000 0.061 0.000 0.049(+) 0.000 0.098 0.000 0.103(≈) 0.000 0.000 0.000 0.000(≈) 0.000 F20 0.250 0.000 0.250(≈) 0.000 0.125 0.000 0.123(≈) 0.000 0.064 0.000 0.052(+) 0.000 0.000 0.000 0.000(≈) 0.000 + 6 9 7 7 − 2 1 2 2 ≈ 12 10 11 11 -
[1] WONG K C, LEUNG K S, WONG M H. Protein structure prediction on a lattice model via multimodal optimization techniques[C]//Proceedings of the 12th Annual Conference on Genetic and Evolutionary Computation. Portland, USA, 2010: 155-162. [2] WOO D K, CHOI J H, ALI M, et al. A novel multimodal optimization algorithm applied to electromagnetic optimization[J]. IEEE transactions on magnetics, 2011, 47(6): 1667–1673. doi: 10.1109/TMAG.2011.2106218 [3] 孙文新, 穆华平. 自适应群体结构的粒子群优化算法[J]. 智能系统学报, 2013, 8(4): 372–376. https://www.cnki.com.cn/Article/CJFDTOTAL-ZNXT201304020.htm SUN Wenxin, MU Huaping. Particle swarm optimization based on self-adaptive population structure[J]. CAAI transactions on intelligent systems, 2013, 8(4): 372–376. https://www.cnki.com.cn/Article/CJFDTOTAL-ZNXT201304020.htm [4] 陈丽, 马楠, 逄桂林, 等. 多视角数据融合的特征平衡YOLOv3行人检测研究[J]. 智能系统学报, 2021, 16(1): 57–65. https://www.cnki.com.cn/Article/CJFDTOTAL-ZNXT202101010.htm CHEN Li, MA Nan, PANG Guilin, et al. Research on multi-view data fusion and balanced YOLOv3 for pedestrian detection[J]. CAAI transactions on intelligent systems, 2021, 16(1): 57–65. https://www.cnki.com.cn/Article/CJFDTOTAL-ZNXT202101010.htm [5] 杨会成, 朱文博, 童英. 基于车内外视觉信息的行人碰撞预警方法[J]. 智能系统学报, 2019, 14(4): 752–760. https://www.cnki.com.cn/Article/CJFDTOTAL-ZNXT201904021.htm YANG Huicheng, ZHU Wenbo, TONG Ying. Pedestrian collision warning system based on looking-in and looking-out visual information analysis[J]. CAAI transactions on intelligent systems, 2019, 14(4): 752–760. https://www.cnki.com.cn/Article/CJFDTOTAL-ZNXT201904021.htm [6] 伍鹏瑛, 张建明, 彭建, 等. 多层卷积特征的真实场景下行人检测研究[J]. 智能系统学报, 2019, 14(2): 306–315. https://www.cnki.com.cn/Article/CJFDTOTAL-ZNXT201902016.htm WU Pengying, ZHANG Jianming, PENG Jian, et al. Research on pedestrian detection based on multi-layer convolution feature in real scene[J]. CAAI transactions on intelligent systems, 2019, 14(2): 306–315. https://www.cnki.com.cn/Article/CJFDTOTAL-ZNXT201902016.htm [7] WANG Zijia, ZHAN Zhihui, YU Weijie, et al. Dynamic group learning distributed particle swarm optimization for large-scale optimization and its application in cloud workflow scheduling[J]. IEEE transactions on cybernetics, 2020, 50(6): 2715–2729. doi: 10.1109/TCYB.2019.2933499 [8] 卢福强, 刘婷, 杜子超, 等. 模糊粒子群优化算法的第四方物流运输时间优化[J]. 智能系统学报, 2021, 16(3): 474–483. https://www.cnki.com.cn/Article/CJFDTOTAL-ZNXT202103016.htm LU Fuqiang, LIU Ting, DU Zichao, et al. Convergence fuzzy particle swarm optimization based transportation time optimization of 4PL[J]. CAAI transactions on intelligent systems, 2021, 16(3): 474–483. https://www.cnki.com.cn/Article/CJFDTOTAL-ZNXT202103016.htm [9] 陈强, 王宇嘉, 梁海娜, 等. 目标空间映射策略的高维多目标粒子群优化算法[J]. 智能系统学报, 2021, 16(2): 362–370. https://www.cnki.com.cn/Article/CJFDTOTAL-ZNXT202102027.htm CHEN Qiang, WANG Yujia, LIANG Haina, et al. Multi-objective particle swarm optimization algorithm based on an objective space papping strategy[J]. CAAI transactions on intelligent systems, 2021, 16(2): 362–370. https://www.cnki.com.cn/Article/CJFDTOTAL-ZNXT202102027.htm [10] 吴一全, 周建伟. 布谷鸟搜索算法研究及其应用进展[J]. 智能系统学报, 2020, 15(3): 435–444. https://www.cnki.com.cn/Article/CJFDTOTAL-ZNXT202003005.htm WU Yiquan, ZHOU Jianwei. Overview of the cuckoo search algorithm and its applications[J]. CAAI transactions on intelligent systems, 2020, 15(3): 435–444. https://www.cnki.com.cn/Article/CJFDTOTAL-ZNXT202003005.htm [11] 钱小宇, 葛洪伟, 蔡明. 基于目标空间分解和连续变异的多目标粒子群算法[J]. 智能系统学报, 2019, 14(3): 464–470. https://www.cnki.com.cn/Article/CJFDTOTAL-ZNXT201903009.htm QIAN Xiaoyu, GE Hongwei, CAI Ming. Decomposition and continuous mutation-based multi-objective particle swarm optimization[J]. CAAI transactions on intelligent systems, 2019, 14(3): 464–470. https://www.cnki.com.cn/Article/CJFDTOTAL-ZNXT201903009.htm [12] 裴小兵, 孙志卫. 改进区块遗传算法解决分布式车间调度问题[J]. 智能系统学报, 2021, 16(2): 303–312. https://www.cnki.com.cn/Article/CJFDTOTAL-ZNXT202102018.htm PEI Xiaobing, SUN Zhiwei. Solving distributed-shop scheduling problems based on modified genetic algorithm[J]. CAAI transactions on intelligent systems, 2021, 16(2): 303–312. https://www.cnki.com.cn/Article/CJFDTOTAL-ZNXT202102018.htm [13] ZHAN Zhihui, WANG Zijia, JIN Hu, et al. Adaptive distributed differential evolution[J]. IEEE transactions on cybernetics, 2020, 50(11): 4633–4647. doi: 10.1109/TCYB.2019.2944873 [14] WANG Zijia, ZHAN Zhihui, KWONG S, et al. Adaptive granularity learning distributed particle swarm optimization for large-scale optimization[J]. IEEE transactions on cybernetics, 2021, 51(3): 1175–1188. doi: 10.1109/TCYB.2020.2977956 [15] THOMSEN R. Multimodal optimization using crowding-based differential evolution[C]//Proceedings of the 2004 Congress on Evolutionary Computation. Portland, USA, 2004: 1382-1389. [16] LI Xiaodong. Efficient differential evolution using speciation for multimodal function optimization[C]//Proceedings of the 7th Annual Conference on Genetic and Evolutionary Computation. Washington, USA, 2005: 873-880. [17] GAO Weifeng, YEN G G, LIU Sanyang. A cluster-based differential evolution with self-adaptive strategy for multimodal optimization[J]. IEEE transactions on cybernetics, 2014, 44(8): 1314–1327. doi: 10.1109/TCYB.2013.2282491 [18] QU B Y, SUGANTHAN P N, LIANG J J. Differential evolution with neighborhood mutation for multimodal optimization[J]. IEEE transactions on evolutionary computation, 2012, 16(5): 601–614. doi: 10.1109/TEVC.2011.2161873 [19] ZHANG Yuhui, GONG Yuejiao, ZHANG Huaxiang, et al. Toward fast niching evolutionary algorithms: A locality sensitive hashing-based approach[J]. IEEE transactions on evolutionary computation, 2017, 21(3): 347–362. http://ieeexplore.ieee.org/iel7/4235/4358751/07556317.pdf [20] ZHAO Hong, ZHAN Zhihui, LIN Ying, et al. Local binary pattern-based adaptive differential evolution for multimodal optimization problems[J]. IEEE transactions on cybernetics, 2020, 50(7): 3343–3357. doi: 10.1109/TCYB.2019.2927780 [21] CHEN Zonggan, ZHAN Zhihui, WANG Hua, et al. Distributed individuals for multiple peaks: a novel differential evolution for multimodal optimization problems[J]. IEEE transactions on evolutionary computation, 2020, 24(4): 708–719. doi: 10.1109/TEVC.2019.2944180 [22] WANG Zijia, ZHAN Zhihui, ZHANG Jun. Distributed minimum spanning tree differential evolution for multimodal optimization problems[J]. Soft computing, 2019, 23(24): 13339–13349. doi: 10.1007/s00500-019-03875-x [23] URSEM R K. Multinational evolutionary algorithms[C]//Proceedings of the 1999 Congress on Evolutionary Computation. Washington, USA, 1999: 1633-1640. [24] WANG Zijia, ZHAN Zhihui, LIN Ying, et al. Automatic niching differential evolution with contour prediction approach for multimodal optimization problems[J]. IEEE transactions on evolutionary computation, 2020, 24(1): 114–128. doi: 10.1109/TEVC.2019.2910721 [25] BISWAS S, KUNDU S, DAS S. Inducing niching behavior in differential evolution through local information sharing[J]. IEEE transactions on evolutionary computation, 2015, 19(2): 246–263. doi: 10.1109/TEVC.2014.2313659 [26] BISWAS S, KUNDU S, DAS S. An improved parent-centric mutation with normalized neighborhoods for inducing niching behavior in differential evolution[J]. IEEE transactions on cybernetics, 2014, 44(10): 1726–1737. doi: 10.1109/TCYB.2013.2292971 [27] WANG Zijia, ZHAN Zhihui, LIN Ying, et al. Dual-strategy differential evolution with affinity propagation clustering for multimodal optimization problems[J]. IEEE transactions on evolutionary computation, 2018, 22(6): 894–908. doi: 10.1109/TEVC.2017.2769108 [28] STOEAN C, PREUSS M, STOEAN R, et al. Multimodal optimization by means of a topological species conservation algorithm[J]. IEEE transactions on evolutionary computation, 2010, 14(6): 842–864. doi: 10.1109/TEVC.2010.2041668 [29] WANG Zijia, ZHOU Yuren, ZHANG Jun. Adaptive estimation distribution distributed differential evolution for multimodal optimization problems[J]. IEEE transactions on cybernetics, 2020,DOI: 10.1109/TCYB.2020.3038694. [30] STORN R, PRICE K. Differential evolution–a simple and efficient heuristic for global optimization over continuous spaces[J]. Journal of global optimization, 1997, 11(4): 341–359. doi: 10.1023/A:1008202821328 [31] YANG Qiang, CHEN Weineng, LI Yun, et al. Multimodal estimation of distribution algorithms[J]. IEEE transactions on cybernetics, 2017, 47(3): 636–650. doi: 10.1109/TCYB.2016.2523000 [32] WANG Yong, LI Hanxiong, YEN G G, et al. MOMMOP: multiobjective optimization for locating multiple optimal solutions of multimodal optimization problems[J]. IEEE transactions on cybernetics, 2015, 45(4): 830–843. doi: 10.1109/TCYB.2014.2337117 [33] LI Xiaodong, ENGELBRECHT A, EPITROPAKIS M G. Benchmark functions for CEC’2013 special session and competition on niching methods for multimodal function optimization[R]. Australia: RMIT University, Evolutionary Computation and Machine Learning Group, 2013. [34] LI Xiaodong. Niching without niching parameters: particle swarm optimization using a ring topology[J]. IEEE transactions on evolutionary computation, 2010, 14(1): 150–169. doi: 10.1109/TEVC.2009.2026270 [35] QU B Y, SUGANTHAN P N, DAS S. A distance-based locally informed particle swarm model for multimodal optimization[J]. IEEE transactions on evolutionary computation, 2013, 17(3): 387–402. doi: 10.1109/TEVC.2012.2203138 [36] DERRAC J, GARCÍA S, MOLINA D, et al. A practical tutorial on the use of nonparametric statistical tests as a methodology for comparing evolutionary and swarm intelligence algorithms[J]. Swarm and evolutionary computation, 2011, 1(1): 3–18. doi: 10.1016/j.swevo.2011.02.002 [37] FIELDSEND J E. Running up those hills: multi-modal search with the niching migratory multi-swarm optimiser[C]//2014 IEEE Congress on Evolutionary Computation. Beijing, China, 2014: 2593−2600.























 下载:
下载:

