Research on mahjong game based on prior knowledge and Monte Carlo simulation
-
摘要: 针对内陆麻将缺乏统一平台和大量牌谱数据,难以设计出基于监督学习的博弈算法的问题,本文设计了一系列将规则、经验与蒙特卡罗方法相结合的博弈算法。首先,分别针对麻将博弈的弃牌模块、听牌模块、吃牌模块提出了弃牌优先级、听牌有效数、吃牌优先级的方法,完善了麻将AI的知识体系,设计了基础版博弈算法Fanfou_ba和优化版博弈算法Fanfou_op;其次,提出了利用蒙特卡罗方法模拟听牌对手手牌来降低己方点炮概率的提升版博弈算法Fanfou_mc;最后,将3种博弈算法进行对比实验。实验结果显示Fanfou_op相比Fanfou_ba胜率提高了9.76%,Fanfou_mc相比Fanfou_op胜率提高了0.13%且点炮率降低了0.47%,表明本文所提出的改进策略是可行并有效的。Abstract: In view of the difficulty in designing game algorithms based on supervised learning due to the shortage of a unified platform and a large amount of card score data for inland mahjong, ,this paper designs a series of game algorithms that combine rules, experience and the Monte Carlo method for inland mahjong game. Firstly, the fold priority, effective number of draws and the eating priority are proposed for the discard module, draw module, and card eating module of the mahjong game, respectively. The mahjong AI knowledge system is improved, and the basic game algorithm Fanfou_ba and the optimized game algorithm Fanfou_op are designed. Secondly, the game algorithm Fanfou_op is proposed that reduces the probability of firing a shot by using the Monte Carlo method to simulate the waiting opponent's hand. Finally, comparative experiments are conducted on these three kinds of game algorithms. The experimental results show that compared with Fanfou_ba, the Fanfou_op algorithm improves the win rate by 9.76%, and that compared with the Fanfou_op algorithm, the Fanfou_mc algorithm enhances win rate by 0.13% and reduces the shot rate by 0.47%, which proves that the improvement strategy proposed is feasible and effective.
-
Keywords:
- mahjong /
- game /
- prior knowledge /
- Monte Carlo /
- opponent’s hand /
- simulation /
- win by discard /
- win rate
-
计算机博弈是通过计算机给出着法,与人类选手或另一个计算机进行的各种游戏对弈,是人工智能领域中最具挑战性的研究方向之一,被称为人工智能科学的“果蝇”[1-3]。
近些年来,DeepMind团队开发的Alpha系列[4-7]使得人工智能在完备信息博弈中完全超越了人类。而以德州扑克为代表的Pluribus在无限制德州扑克的比赛中成功战胜五名专家级人类玩家,标志着人工智能在多人非完备信息博弈领域取得了重大突破[8-11]。
非完备信息博弈中隐藏信息对于博弈难度的影响较大,信息集数目和信息集平均大小与博弈复杂度成正比[12]。其中一对一德州扑克通过子博弈策略达到近似纳什均衡求解[13],而在多人扑克博弈中没有合适的策略。麻将隐藏信息的数量远远超过德州扑克,所以麻将博弈研究比德州扑克更加复杂。
麻将除了丰富的隐藏信息,复杂的计分规则和出牌规则,还需要考虑多种决策类型。任意一位玩家的吃、碰、杠动作都会改变后续玩家的摸牌顺序,因此我们很难为麻将构建一棵规则的博弈树。一些在围棋和德州扑克中表现很好的算法,如蒙特卡罗树搜索、蒙特卡罗反事实遗憾最小化等都无法直接应用于麻将博弈,导致麻将博弈中没有经典博弈算法可以对比,需要自行设计对比算法。
本文的研究以胜利局数和点炮次数作为算法效果的评价指标,不考虑复杂的计分规则。本文主要针对麻将博弈中的弃牌和听牌模块进行了设计,通过对比实验验证了所提出策略和算法的有效性。贡献及创新点总结如下:
1) 设计了基础版算法Fanfou_ba,以最快听牌、胡牌为目标,应用先验知识,针对弃牌模块细粒度地设计了弃牌的优先层级,并对吃牌模块作了简单的限制处理。Fanfou_ba在第十四届中国计算机博弈锦标赛麻将项目中获得冠军,取得了较好的效果。本文将Fanfou_ba作为基准算法与提出的其它算法进行对比。
2)在Fanfou_ba基础上设计了优化版算法Fanfou_op。首先,针对听牌模块提出了“听牌有效数”的设计方法;其次,完成了吃牌模块的优先级设计;最后,实现了补杠、特殊牌型(如七对和碰碰胡和连牌牌型)的弃牌选择处理。经第一组12000局对比实验,Fanfou_op领先Fanfou_ba 1171局,相比Fanfou_ba胜率提高了9.76%。
3)针对麻将多智能体博弈场景和麻将点炮让己方收益最小化的问题,不再局限于己方AI的设计,也为降低其他选手的胡牌概率采取措施,在Fanfou_op基础上设计了提升版算法Fanfou_mc,应用蒙特卡罗方法模拟听牌选手手牌。经第二组和第三组共计32000局对比实验,Fanfou_mc在胜率分别提升0.2%和0.13%的基础上,点炮率分别降低了0.4%和0.47%,验证了使用蒙特卡罗方法模拟听牌选手手牌对避免点炮的有效性。
1. 相关工作
麻将的胡牌规则基本一致,但由于地区文化差异,玩法稍有不同。例如,具体番数计算、牌的种类和数目。本文研究的麻将沿用2020年“竞技世界杯”中国大学生计算机博弈大赛暨第十四届中国计算机博弈锦标赛麻将项目规则[14],牌库只有序数牌,不考虑其他牌型种类。图1显示了27种序数牌,每种序数牌有4张,共108张牌。
目前关于麻将博弈的研究并不多,Cheng等[15]在2017年首次使用数学技术,通过基本组合理论研究麻将中一组特殊的牌型k-gate。例如:清一色的13张牌型T称为nine-gate (九门),如图2所示,可以向T中添加任意一张筒类牌实现胡牌。
来自悉尼科技大学和陕西师范大学的Li等[16]在2019年的论文中定义了“缺牌数”的概念,缺牌数代表当前牌面的好坏,缺牌数为0时代表胡牌。同时提出最优策略,在k次牌面变换(k ≥ 1)的条件下增加胡牌的概率,确定当前该打的牌。上述两篇论文的研究都是基于起手牌为13张的麻将,并且只考虑了萬条筒3种序数牌型。
关于麻将博弈算法的研究可以分为经验知识和深度学习两个视角。前者的研究主要集中在台湾麻将,以先验知识设计为研究重点,并结合一些经典算法[17-19];而后者主要被应用于日本麻将,通过大量的专家牌谱数据进行神经网络训练,其中最显著的成果是微软亚洲研究院研发的AI Suphx[20-24],内陆麻将博弈的研究总体上还处于起步阶段[25-27]。
2. 基于知识和手牌模拟的麻将AI
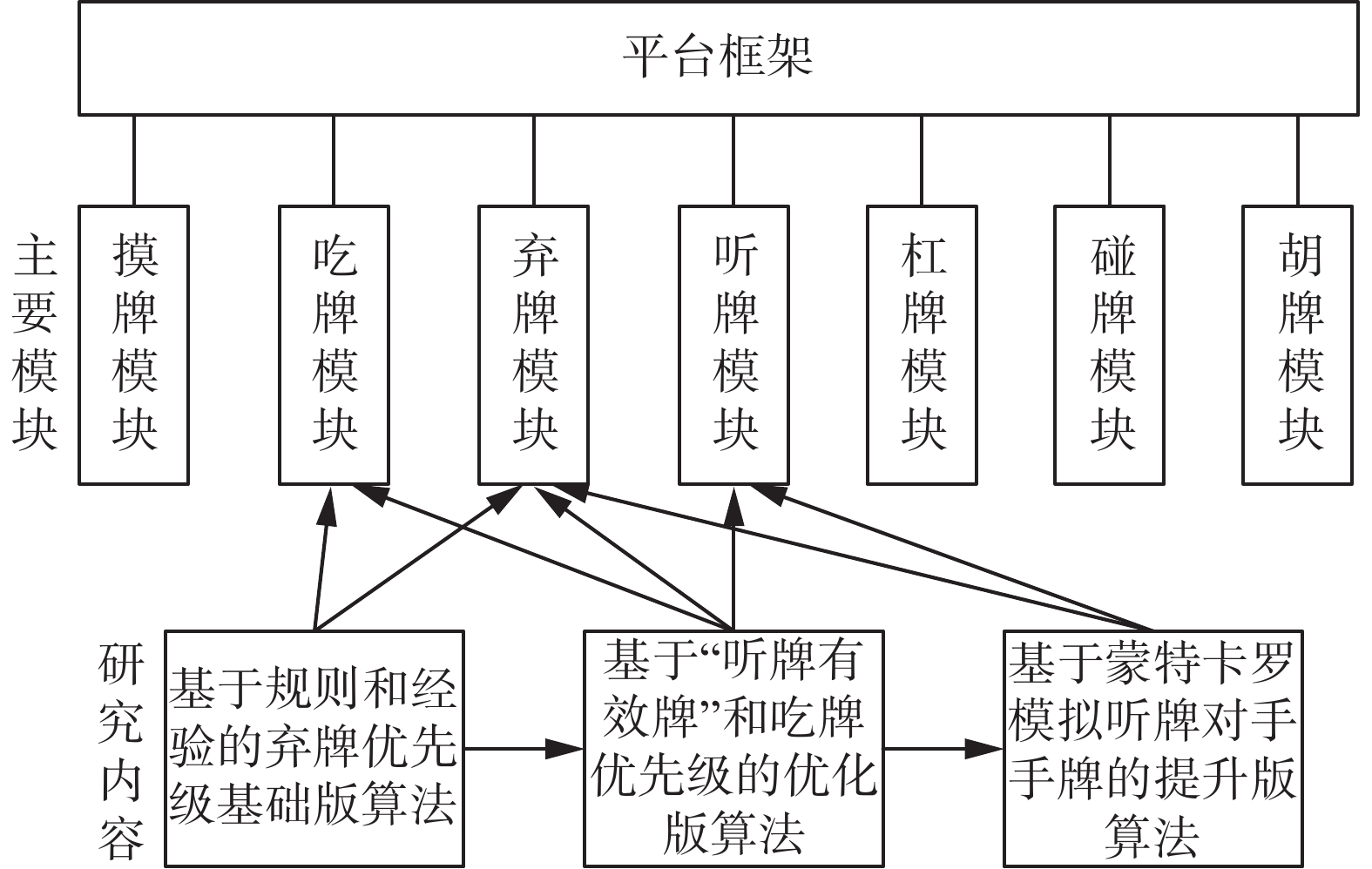
本文麻将博弈主要内容框架如图3所示,设计了3种麻将AI算法:基础版算法Fanfou_ba、优化版算法Fanfou_op和提升版算法Fanfou_mc。其中,Fanfou_ba考虑了弃牌模块的优先级设计和吃牌模块的限制处理;Fanfou_op针对听牌和吃牌模块提出了听牌有效数和吃牌模块的优先级;Fanfou_mc考虑到多智能体博弈场景和麻将点炮的特点,应用蒙特卡罗方法对听牌对手手牌进行了模拟。3种麻将AI算法的博弈水平呈现渐进式提升,下面分别对3种算法进行介绍。
2.1 弃牌优先级和吃牌限制
麻将中听牌是指缺少一张牌便能胡牌的状态,如图2的牌型,缺少任意一张筒字牌;胡牌是指形成特定的牌型(四个组合和一个对子,组合指顺子或刻子),分为自摸胡牌和点炮胡牌,自摸和炮胡的区别在于缺少的一张牌是由自己摸到还是对手打出。胡牌用式(1)表示:
$$ {\rm{Win}} = x(ABC) + y(AAA) + AA $$ (1) 式中:ABC代表顺子;AAA代表刻子;AA代表对子;x(.)和y(.)代表对应牌型的数目。本文研究的麻将起手牌是13张,此时
$ x + y = 4 $ ,而在起手牌16张的麻将博弈中,$ x + y = 5 $ 。Fanfou_ba要实现尽快听牌、胡牌的目标,每次弃牌处理时都要打出当前手牌中最不需要的牌,Li等[15]在论文中定义的缺牌数也说明了弃牌模块的重要性[16]。
Fanfou_ba针对弃牌模块总体设计了4个优先级,详见表1。假设摸到1张牌后的手牌如图4所示,分别对应4种类型的单牌:两边都不搭的单牌有1条和7萬(没有2条、3条和5萬、6萬、8萬、9萬);只搭一边的单牌有5条、7条和9条(没有4条、6条和8条);对子间隔搭的单牌有1萬和4萬(都没有3萬);对子旁边搭的单牌有4萬(没有2萬和5萬)。
表 1 弃牌优先层级Table 1 Priority level of discard优先级 具体牌型 第1层1、9:100、900 第1级 第2层2、8:0200、0800 第3层3–7:00300–00700 第2级 第1层9:987600、980、907、9886、986、9776、976 第1层1:123400、120、103、1224、124、1334、134 第2层2、8:if 对子数>1: 1223、7889 第3层2、9:2450、2450、5689、5689 第4层3–5:00356–00578、00356–00578 第4层5–7:23500–45700、23500–45700 第5层1:1220、122345、133、1244 第5层9:9880、988765、977、9866 第6层2、8:12230、07889 第7层1、9:1222、1333、9888、9777 第7层2、8:02333、77780 第8层3–8:003444–008999
第8层2–7:111200–666700第8层3–8、2-7:111030–666080、02444–07999 第9层2–4、6–8:24567–46789、12346–34568 第10层5:123500、005788 第11层2、8:0204、0806 第12层3–7、7–3:10305-50709、90705–50301 第3级 第1层2、8:11200、0244、99800、6680 第2层3–7:0030–0700、0030–0070 第3层3、4–7:0355、0466–0799、123466–456799 第3层7、3–6:5570、1130–4460、113456–446789 第4层1、9:11230、07899 第5层8、3–7:067889、112305–567709 第5层3–7:103345–507789、023340–067780 第4级 第1层2–8:1223–7889 第2层2、8:02330、07780 第3层3–7:3440–7880、0223–0667 表1中具体牌型是通过大量测试总结出来的,层序代表了同等优先级下单牌牌型弃牌的先后顺序。因为1和9的序数牌可搭的牌有2种(分别是2、3和7、8对应的序数牌),2和8的序数牌可搭的牌有3种,3、4、5、6、7的序数牌可搭的牌有4种,所以顺序分为:1和9对应的序数牌(1条/萬/筒和9条/萬/筒);2和8对应的序数牌;3、4、5、6、7对应的序数牌。数字下面的下划线代表这张牌不是0张,可能多张或1张,数字下面双划线代表这张牌不是1张,可能多张或0张,数字下面虚线代表这张牌数量不为2,可能0、1、3、4张。算法1描述了基于弃牌优先级的决策过程。
算法1 基于弃牌优先级的决策过程
输入 手牌,已经打过的牌HISTORY;
输出 最佳弃牌选择。
1) 手牌遍历23种层级牌型,更新4个等级弃牌列表 Di
2) FOR ALL EACH Di i
$ \in $ {1,2,3,4} DO3) FOR j IN len(Di) DO
4) IF HISTORY[Di[j]] >0:
5) RETURN Di[j]
6) END IF
7)
END FOR 8) END FOR
表1中的数字代表序数牌中对应的牌,0表示没有对应的序数牌,冒号后面的具体牌型代表弃牌时手牌需满足的条件,若满足条件则将对应的牌加入当前等级的弃牌列表。
因为比赛规则中规定吃牌获得分数低于碰牌和杠牌获得的分数,所以针对一些不合理的吃牌动作策略进行了优化处理。例如:限制了拆除手牌中刻子(3张一样的牌)或两个对子进行吃牌的动作策略,因为这样的吃牌处理可能会丢失碰牌或杠牌获得更高分数的机会。
2.2 听牌有效数和吃牌优先级
麻将规则中明确规定,AI一旦听牌后不能再更改手牌,只能打出摸到的牌或者做杠牌和胡牌处理。本节针对Fanfou_ba在设计时没有考虑到死听(听牌有效数为0)的问题,提出了应用听牌有效数的算法Fanfou_op。听牌有效数是听牌后所胡牌(胡张)的有效数量,也就是指牌库(未知牌)中剩余胡张的个数,不包含手牌和已经打出去的牌(已知牌)中的胡张,并将其应用在弃牌处理之前的判听模块。
首先,Fanfou_op获得一张牌后,轮流打出手牌中每一张牌,判断手牌是否达到听牌状态;其次,统计听牌有效数;再次,选择弃牌后听牌有效数最大的手牌打出;最后,鉴于听牌有效数与胡牌概率成正比,因此Fanfou_op在听牌有效数小于2时选择放弃听牌。假设听牌后能胡的牌有h种(
$ 0 \leqslant h \leqslant 9 $ ),已经打出去的牌中含有的胡张数有d张,手牌中含有的胡张数有m张,此时听牌有效数t_num的计算方法如公式(2)。$$ t\_{\rm{num}} = h \times 4 - d - m $$ (2) 算法2描述了基于听牌有效数的决策过程。Fanfou_op在每一次弃牌前都会调用判听方法,在能够听牌的条件下,计算所有胡牌张数h以及听牌有效数t_num,当t_num ≥2时选择对应的手牌打出,然后听牌;否则放弃听牌,按照弃牌优先级进行弃牌处理。
算法2 基于听牌有效数的决策过程
输入 手牌HAND;
输出 最佳弃牌选择(听牌有效数最大的弃牌)。
1) FOR i IN len(HAND) DO
2) TEMP_HAND = 复制(HAND)
3) TEMP_HAND.remove(HAND[i])
4)调用判听返回能否听牌和听牌结果得到CAN_TING和RESULT
5) IF CAN_TING THEN
6) 计算HAND[i]弃牌后的TING_NUM
7) END IF
8) END FOR
9) IF max(TING_LIST) > 1 THEN
10)返回 max(TING_LIST)对应的手牌HAND[i]
11) END IF
假设摸到一张牌后的手牌如图5所示,已打出去的胡张有
$ x $ 个。打出手牌中1萬后,将有3萬和6萬两种胡张,手牌中3萬和6萬各有1个,则此时的听牌有效数为$ 2 \times 4 - 2 - x $ ;打出手牌中3萬或6萬后,将有1萬一种胡张,手牌中1萬有一个,则此时的听牌有效数为$ 1 \times 4 - 1 - x $ ;选择打出牌后听牌有效数最大的手牌做弃牌处理。Fanfou_ba针对吃牌模块仅做了两种特殊牌型的限制处理,并不足以应对复杂的情况。例如:上家打出5萬,Fanfou_ba的手牌中有两张3萬、一张4萬和一张6萬,Fanfou_ba会选择3萬和4萬进行吃牌,但理想的动作策略应该是保留3萬的对子而选择4萬和6萬进行吃牌。
为解决上述问题,Fanfou_op提出了将吃牌处理模块划分为3个优先级的方法,详见表2。吃牌处理时,首先,考虑两个单牌的牌型;其次,考虑一个对子和一张单牌的牌型;最后,考虑两个对子的牌型,其中两个对子吃牌的情况可以细分为3种特定条件。
表 2 吃牌优先级Table 2 Priority of chow优先级 示例 第1级
两张单牌吃上家打5 萬,手牌中有一张3 萬和一张4 萬;或一张4 萬和一张6 萬,可以吃 第2级
一个对子吃上家打5 萬,手牌中有两张3 萬和一张4 萬;或一张4 萬和两张6 萬,可以吃 第3级
两个对子吃两个对子连着可吃:如上家打5 萬,手牌中有两张3 萬和两张4 萬;或两张6 萬和两张7 萬,可以吃
两个对子不连中间有牌可吃:如上家打5 萬,手牌中有两张4 萬和两张6 萬,且有一张5 萬,可以吃
两个对子不连中间无牌时只能吃4/5/6:如上家打5 萬,手牌中有两张4 萬和两张6 萬,且2 萬、3 萬和7 萬,或3 萬、7 萬和8 萬都只有一张,可以吃2.3 听牌对手的手牌模拟
麻将属于多人非完备信息博弈,Fanfou_ba和Fanfou_op均属于单智能体的范畴,仅考虑己方AI的设计而没有考虑到对手的手牌,忽略了多人博弈的特点,导致点炮概率较大,未能实现己方收益最大化。
文献[16]通过使用蒙特卡罗方法模拟整个牌局来降低点炮概率:首先,随机生成3个玩家的缺牌数;其次,检查缺牌数是否合理;最后,模拟选手手牌。但是这样模拟会产生两个问题:1)缺牌数的合理判断需要结合人类经验,具有较大的随机性;2)最后随机产生的手牌是经由牌型的组合划分(未知牌中顺子、刻子、对子和单牌的组合)产生的,人工划分的组合考虑不到所有的可能性。
针对上述问题,提出了通过蒙特卡罗方法模拟听牌选手手牌的算法Fanfou_mc。AI进行模拟需要满足己方没有听牌和对手有听牌两个条件,后者避免了考虑结合经验并且有较大随机性的缺牌数问题,只需要模拟出的手牌满足听牌条件;前者保证了AI追求最快听牌胡牌的目标不受影响。
通过模拟听牌选手手牌,计算弃牌列表中每张牌的点炮次数。若有3家对手听牌,则同时模拟3个玩家的手牌,选择优先级高的弃牌列表中点炮次数最少的牌打出,实现了通过模拟对手手牌降低点炮几率的目标。
Fanfou_mc包括两个参数:模拟手牌的种类数目和模拟听牌玩家手牌的数目。其中,模拟手牌种类数目与模拟消耗时间成正比、与点炮概率成反比,考虑比赛有出牌时间的限制,经反复实验后将模拟手牌种类数目设置为10,在尽可能降低点炮概率的同时出牌时间不超过比赛时间的限制,Fanfou_mc的方案流程如图6所示。
模拟听牌玩家手牌的数目(sim_num)由听牌玩家的吃、碰、杠数目决定,设一听牌玩家吃牌、碰牌、杠牌数目分别为C、P、K,则模拟手牌数目计算方法如式(3):
$$ {\rm{sim\_num}} = 13 - 3C- 3P- 3K $$ (3) Fanfou_mc模拟完所有听牌选手手牌后,选择弃牌列表中点炮次数为0的牌做弃牌处理时,点炮概率最小。若所有牌点炮次数都为0,则会按顺序选择弃牌列表中第一张点炮次数为0的牌打出;若弃牌列表中没有点炮次数为0的牌,则会选择点炮次数最少的牌打出。算法3描述了通过模拟听牌对手手牌降低点炮概率的决策过程。
算法3 基于对手手牌模拟的弃牌决策过程
输入 手牌HAND,已经打过的牌HISTORY;
输出 最佳弃牌选择。
1) 剩余未知牌CARD = 所有牌 − HAND − HISTORY
2) FOR ALL EACH OPPONENTi
$ \in $ {上家,对家,下家} DO3) IF OPPONENTi 听牌THEN
4) 计算OPPONENTi的手牌数目sim_num
5) WHILE (TRUE) DO
6) SIM_LIST = CARD中随机模拟sim_num个牌
7) IF SIM_LIST能够听牌 THEN
8) j++ // 模拟的听牌手牌数目
9) END IF
10) IF j = = 10 THEN // 模拟10种听牌手牌
11) BREAK
12) END IF
13) END WHILE
14) END IF
15) END FOR
16) 将弃牌列表中每张牌依次加入到模拟听牌选手的手牌
17) 统计弃牌列表中每张牌的点炮次数
18) 生成弃牌列表对应的点炮次数列表FIRE_LIST
19) IF min (FIRE_LIST) > 1 THEN
20) 选择FIRE_LIST中第一个min (FIRE_LIST)打出
21) END IF
22) RETURN min (FIRE_LIST)对应的牌
3. 实验设计与分析
基于弃牌优先级和吃牌限制设计的Fanfou_ba参加了2020“竞技世界杯”中国大学生计算机博弈大赛暨第十四届中国计算机博弈锦标赛麻将项目比赛,经过三轮初赛每轮50局,三轮决赛每轮100局比赛,获得了冠军,决赛最终成绩如表3所示,本文将此AI作为基准程序。
表 3 中国计算机博弈锦标赛首届麻将项目决赛成绩Table 3 Final result of the first Mahjong event of China Computer Game Championship机构 战队名称 总分 主要方法 沈阳航空航天大学 Fanfou_ba 454 经验与知识 北京信息科技大学 北信科大麻将 12 深度学习 微智娱 Dzmj-smzy −219 蒙特卡罗计算出
牌期望+知识重庆理工大学 骑士麻将1队 −247 知识 3.1 实验方案
实验环境是Pycharm2019,使用Python3.7实现本文方法,在一台Inter (R) Core (TM) i5-4210U 1.7 GHz,内存为4 GB,显卡为NVIDIA GeForce 820M的Window 10操作系统上进行实验。经测试模拟10种听牌手牌的平均模拟次数为6000次,平均消耗时间1.5 s,符合比赛出牌时间限制3 s的要求。
麻将属于多智能体博弈项目,为能够完整进行实验并增加麻将博弈中的不确定性,引入了随机出牌算法Robot,即弃牌处理时随机打出手牌。由于麻将博弈中吃、碰、杠的动作策略会打乱出牌顺序和加快博弈进程,所以Robot吃、碰、杠的动作决策完全沿用Fanfou_op的设计,更加符合真实比赛和线下博弈的场景。本文实验的博弈平台框架设计流程如图7所示,具体设计可参考[14]中名为“完整实验2.1”的文件。
本文以胜利场数和点炮次数作为评价指标,进行了3组对比实验。其中,第一组对比实验中Robot1、Robot2、Fanfou_ba和Fanfou_op进行比赛,验证Fanfou_op中的改进策略的有效性;第2组对比实验中Robot1、Robot2、Fanfou_op和Fanfou_mc进行比赛;第3组对比实验中Fanfou_op、Fanfou_op、Fanfou_mc和Fanfou_mc进行比赛。后两组实验是为了充分验证Fanfou_mc中通过蒙特卡罗方法模拟听牌对手手牌避免点炮的效果,第2组引入Robot是为增加比赛中的不确定性,对应多智能体博弈中有牌力较弱选手参与的场景,第3组对应多智能体都是牌力较强选手博弈的场景。
麻将规则表明,吃牌只能吃上家的牌,因此对比实验中需要考虑AI之间的顺序。经式(4)计算可知前两组对比实验顺序有12种,为确保实验的严谨性,每种排列方式要进行一轮比赛,每轮比赛有1000局非流局(一局比赛结束后有人胡牌)的测试结果;第三组对比实验顺序有4种,安排4轮比赛,每轮比赛有5000局非流局的测试结果。
$$ ^{ } n = A_4^2 = 12 ^{ } $$ (4) 3.2 实验结果与分析
实验数据中位置1、位置2、位置3、位置4分别代表麻将智能体的位置,局数是指在该轮比赛中进行的总场数(包括每轮比赛中产生的流局),A、B、C、D、E分别代表Fanfou_ba、Fanfou_op、Robot1、Robot2和Fanfou_mc五个智能体,炮数是指在该轮比赛中玩家的点炮总局数。第1组对比实验结果数据见表4。
以表4中第一轮比赛数据为例,在第1轮比赛中一共进行了1008场比赛,其中Fanfou_ba获胜472局,Fanfou_op获胜486局,Robot1和Robot2分别获胜22局和20局。
表 4 第1组Fanfou_ba、Fanfou_op和Robot对比实验结果Table 4 First set of Fanfou_ba, Fanfou_op and Robot comparative experiment results轮数 局数 位置1 位置2 位置3 位置4 1 1008 A(472) B(486) C(22) D(20) 2 1008 A(466) C(22) B(481) D(31) 3 1016 A(453) C(30) D(27) B(490) 4 1014 B(537) A(417) C(19) D(27) 5 1008 C(26) A(445) B(506) D(23) 6 1015 C(29) A(448) D(25) B(498) 7 1006 B(562) C(15) A(399) D(24) 8 1012 C(27) B(563) A(379) D(31) 9 1013 C(27) D(34) A(452) B(487) 10 1013 B(541) C(28) D(32) A(399) 11 1015 C(29) B(570) D(29) A(372) 12 1012 C(22) D(20) B(555) A(403) 在第1组对比实验中,Fanfou_ba获胜5105局,胜率为42.54%,Fanfou_op获胜6276局,胜率为52.3%;Fanfou_op相比Fanfou_ba胜率提升9.76%,验证了听牌有效数和吃牌优先级策略的有效性,胜利场数比较如图8所示。
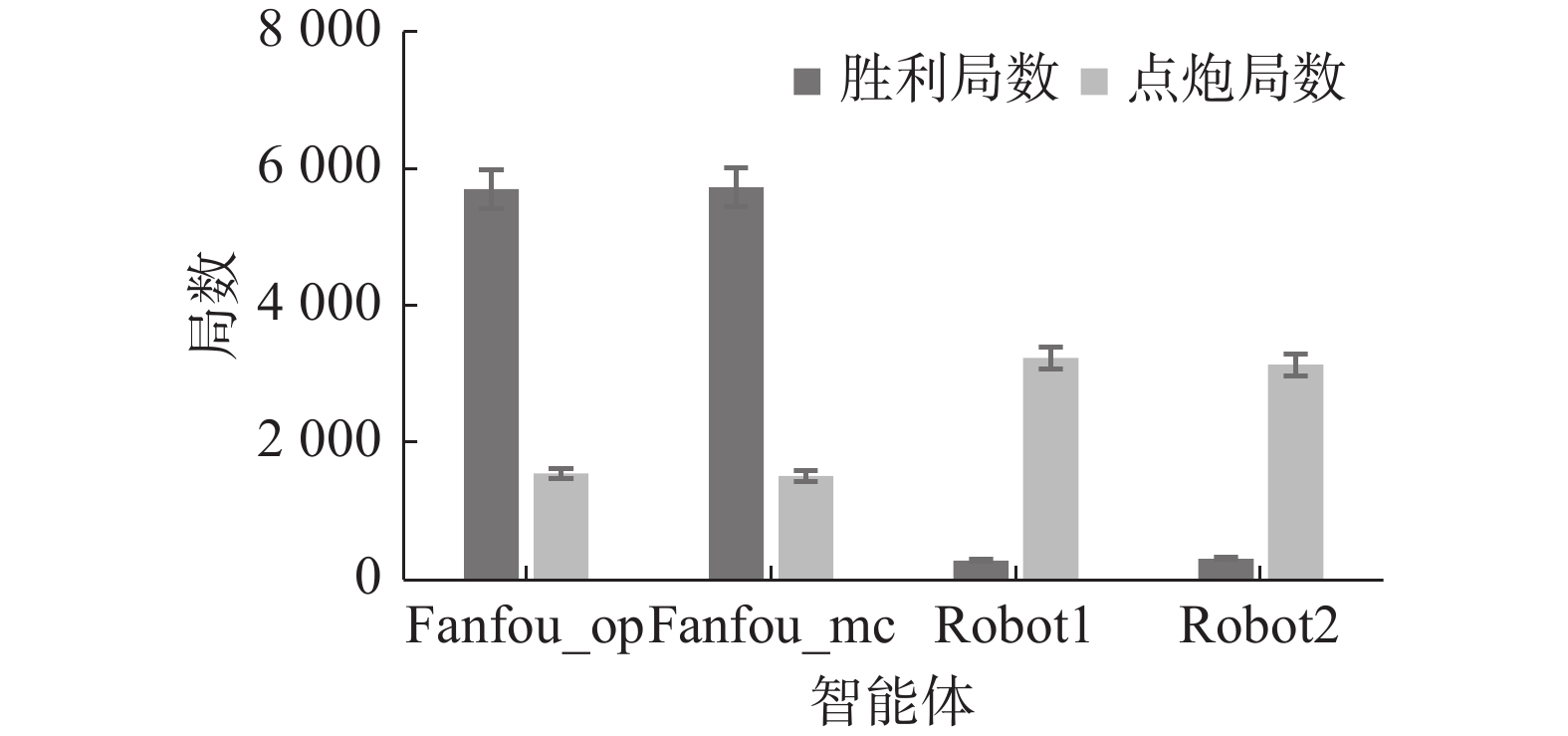
第2组对比实验结果数据见表5,以表5中第一轮比赛数据为例,在第1轮比赛中一共进行了1010场比赛,一共点炮787局;其中Fanfou_mc获胜480局,点炮128局,Fanfou_op获胜471局,点炮144局,Robot1获胜24局,点炮284局,Robot2获胜25局,点炮231局。
在第2组对比实验中,Fanfou_op获胜5698局,Fanfou_mc获胜6276局,Fanfou_mc的胜率相比Fanfou_op提升了0.2%;Fanfou_op点炮1547局,Fanfou_mc点炮1509局,Fanfou_mc的点炮率相比Fanfou_op降低了0.4%,胜利场数和点炮局数比较如图9所示。
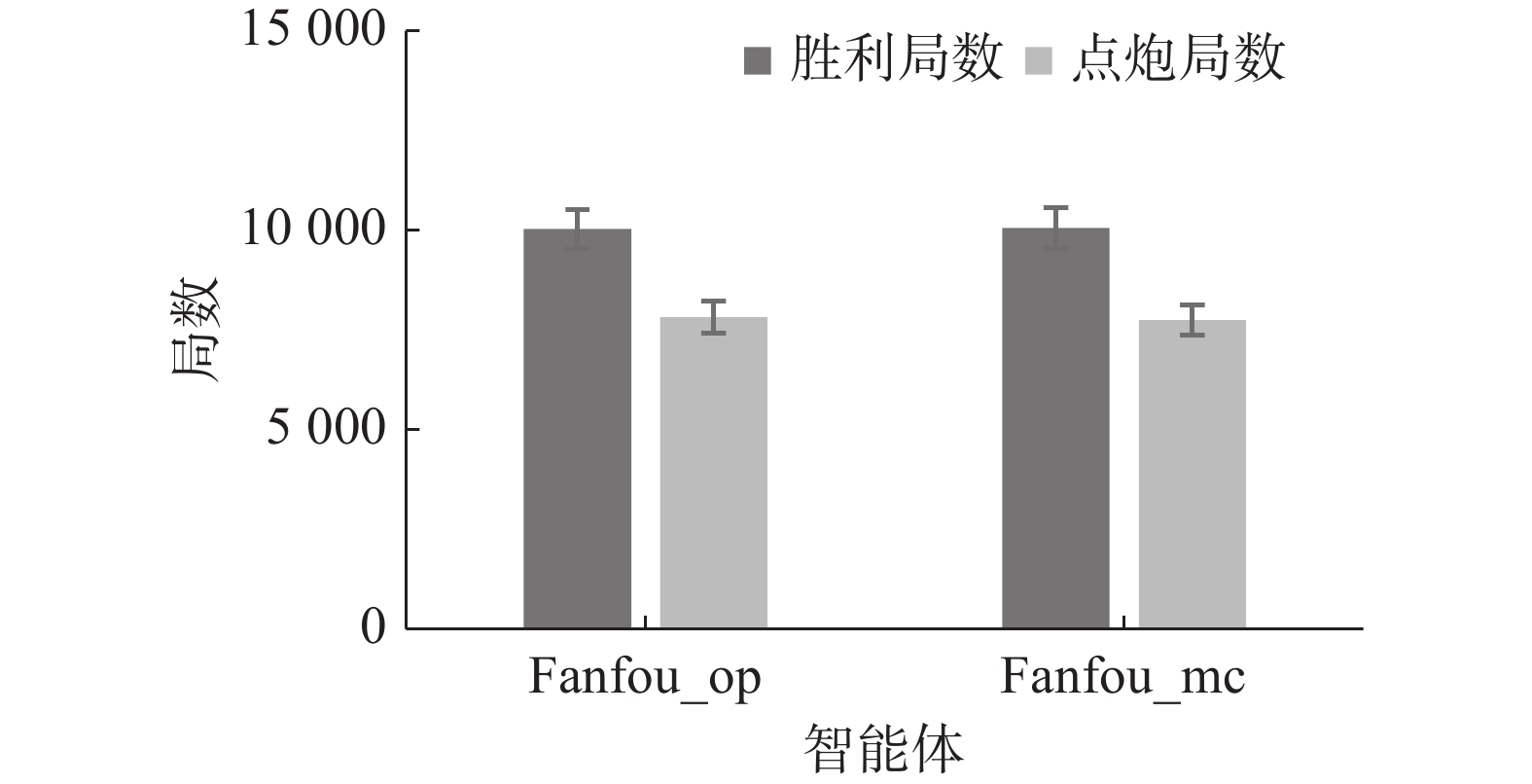
表 5 第2组Fanfou_op、Fanfou_mc和Robot对比实验结果Table 5 Second set of Fanfou_op, Fanfou_mc and Robot comparative experiment results轮数 局/炮数 位置1 位置2 位置3 位置4 1 1010/787 E(480/128) B(471/144) C(24/284) D(25/231) 2 1017/823 E(487/127) C(22/272) B(463/137) D(28/287) 3 1014/791 E(462/148) C(20/268) D(32/256) B(486/119) 4 1012/757 B(467/114) E(476/120) C(24/269) D(33/254) 5 1013/780 C(30/247) E(485/115) B(465/134) D(20/284) 6 1008/791 C(24/276) E(475/134) D(23/253) B(478/128) 7 1014/790 B(484/120) C(21/281) E(479/112) D(16/277) 8 1013/763 C(20/234) B(498/102) E(460/123) D(22/304) 9 1013/775 C(22/267) D(22/236) E(474/125) B(482/147) 10 1005/799 B(479/138) C(19/298) D(28/248) E(474/115) 11 1009/800 C(33/258) B(432/144) D(22/276) E(513/112) 12 1010768 C(18/278) D(32/230) B(493/120) E(457/140) 第3组对比实验结果数据见表6,经计算可以得出,Fanfou_mc的胜率相比Fanfou_op提升了0.13%,点炮率相比Fanfou_op降低了0.47%。后两组对比实验验证了模拟听牌对手手牌避免点炮策略的有效性,胜利场数和点炮局数比较如图10所示。
实验数据表明,完善的知识体系使Fanfou_op能够较快达到听牌状态,对麻将AI的博弈水平有显著的提升。由于Fanfou_mc中蒙特卡罗模拟策略无法在己方处于听牌状态时使用,所以Fanfou_mc没有明显提高胜率。
表 6 第3组Fanfou_op和Fanfou_mc对比实验结果Table 6 Third set of Fanfou_op and Fanfou_mc comparative experiment results轮数 局/炮数 位置1 位置2 位置3 位置4 1 5022/3909 E(1227/979) B(1271/967) E(1215/976) B(1287/987) 2 5022/3839 E(1283/938) E(1227/961) B(1266/945) B(1224/995) 3 5027/3868 B(1224/980) B(1254/992) E(1287/942) E(1235/954) 4 5031/3887 B(1214/916) E(1288/991) B(1247/1006) E(1251/974) 4. 结束语
本文以麻将为研究载体,提出了结合知识与蒙特卡罗模拟的博弈算法。首先,阐述了冠军AI智能体Fanfou_ba弃牌优先级和吃牌限制的设计思想;其次,以Fanfou_ba为基础设计了Fanfou_op,提出了听牌有效数和吃牌优先级的方法;再次,在Fanfou_op基础上设计了Fanfou_mc,应用蒙特卡罗方法模拟听牌对手手牌来降低点炮概率;最后,为完成实验引入了Robot1和Robot2,在个人平台上进行3组对比实验,前两组各12轮每轮1000局,第3组4轮每轮5000局,共44000局的比赛,实验的结果数据验证了本文所提算法的有效性,并对实验结果进行了分析。
为了保证完全随机性,在Fanfou_mc中使用的蒙特卡罗模拟方法,没有考虑到其他玩家的历史弃牌情况;未来可以在小批量样本对手建模角度和深度学习两个方面做进一步的研究,前者是根据对手的弃牌历史进行建模,以预测对手需要的牌,后者则是建立己方的模型,兼顾胜率和点炮率。深度学习视角是将4个Robot自对弈的牌谱数据进行训练,生成弃牌的模型,将该模型与Fanfou_ba、Fanfou_op和Fanfou_mc做对比实验,验证深度学习训练的弃牌模型的有效性。
-
表 1 弃牌优先层级
Table 1 Priority level of discard
优先级 具体牌型 第1层1、9:100、900 第1级 第2层2、8:0200、0800 第3层3–7:00300–00700 第2级 第1层9:987600、980、907、9886、986、9776、976 第1层1:123400、120、103、1224、124、1334、134 第2层2、8:if 对子数>1: 1223、7889 第3层2、9:2450、2450、5689、5689 第4层3–5:00356–00578、00356–00578 第4层5–7:23500–45700、23500–45700 第5层1:1220、122345、133、1244 第5层9:9880、988765、977、9866 第6层2、8:12230、07889 第7层1、9:1222、1333、9888、9777 第7层2、8:02333、77780 第8层3–8:003444–008999
第8层2–7:111200–666700第8层3–8、2-7:111030–666080、02444–07999 第9层2–4、6–8:24567–46789、12346–34568 第10层5:123500、005788 第11层2、8:0204、0806 第12层3–7、7–3:10305-50709、90705–50301 第3级 第1层2、8:11200、0244、99800、6680 第2层3–7:0030–0700、0030–0070 第3层3、4–7:0355、0466–0799、123466–456799 第3层7、3–6:5570、1130–4460、113456–446789 第4层1、9:11230、07899 第5层8、3–7:067889、112305–567709 第5层3–7:103345–507789、023340–067780 第4级 第1层2–8:1223–7889 第2层2、8:02330、07780 第3层3–7:3440–7880、0223–0667 表 2 吃牌优先级
Table 2 Priority of chow
优先级 示例 第1级
两张单牌吃上家打5 萬,手牌中有一张3 萬和一张4 萬;或一张4 萬和一张6 萬,可以吃 第2级
一个对子吃上家打5 萬,手牌中有两张3 萬和一张4 萬;或一张4 萬和两张6 萬,可以吃 第3级
两个对子吃两个对子连着可吃:如上家打5 萬,手牌中有两张3 萬和两张4 萬;或两张6 萬和两张7 萬,可以吃
两个对子不连中间有牌可吃:如上家打5 萬,手牌中有两张4 萬和两张6 萬,且有一张5 萬,可以吃
两个对子不连中间无牌时只能吃4/5/6:如上家打5 萬,手牌中有两张4 萬和两张6 萬,且2 萬、3 萬和7 萬,或3 萬、7 萬和8 萬都只有一张,可以吃表 3 中国计算机博弈锦标赛首届麻将项目决赛成绩
Table 3 Final result of the first Mahjong event of China Computer Game Championship
机构 战队名称 总分 主要方法 沈阳航空航天大学 Fanfou_ba 454 经验与知识 北京信息科技大学 北信科大麻将 12 深度学习 微智娱 Dzmj-smzy −219 蒙特卡罗计算出
牌期望+知识重庆理工大学 骑士麻将1队 −247 知识 表 4 第1组Fanfou_ba、Fanfou_op和Robot对比实验结果
Table 4 First set of Fanfou_ba, Fanfou_op and Robot comparative experiment results
轮数 局数 位置1 位置2 位置3 位置4 1 1008 A(472) B(486) C(22) D(20) 2 1008 A(466) C(22) B(481) D(31) 3 1016 A(453) C(30) D(27) B(490) 4 1014 B(537) A(417) C(19) D(27) 5 1008 C(26) A(445) B(506) D(23) 6 1015 C(29) A(448) D(25) B(498) 7 1006 B(562) C(15) A(399) D(24) 8 1012 C(27) B(563) A(379) D(31) 9 1013 C(27) D(34) A(452) B(487) 10 1013 B(541) C(28) D(32) A(399) 11 1015 C(29) B(570) D(29) A(372) 12 1012 C(22) D(20) B(555) A(403) 表 5 第2组Fanfou_op、Fanfou_mc和Robot对比实验结果
Table 5 Second set of Fanfou_op, Fanfou_mc and Robot comparative experiment results
轮数 局/炮数 位置1 位置2 位置3 位置4 1 1010/787 E(480/128) B(471/144) C(24/284) D(25/231) 2 1017/823 E(487/127) C(22/272) B(463/137) D(28/287) 3 1014/791 E(462/148) C(20/268) D(32/256) B(486/119) 4 1012/757 B(467/114) E(476/120) C(24/269) D(33/254) 5 1013/780 C(30/247) E(485/115) B(465/134) D(20/284) 6 1008/791 C(24/276) E(475/134) D(23/253) B(478/128) 7 1014/790 B(484/120) C(21/281) E(479/112) D(16/277) 8 1013/763 C(20/234) B(498/102) E(460/123) D(22/304) 9 1013/775 C(22/267) D(22/236) E(474/125) B(482/147) 10 1005/799 B(479/138) C(19/298) D(28/248) E(474/115) 11 1009/800 C(33/258) B(432/144) D(22/276) E(513/112) 12 1010768 C(18/278) D(32/230) B(493/120) E(457/140) 表 6 第3组Fanfou_op和Fanfou_mc对比实验结果
Table 6 Third set of Fanfou_op and Fanfou_mc comparative experiment results
轮数 局/炮数 位置1 位置2 位置3 位置4 1 5022/3909 E(1227/979) B(1271/967) E(1215/976) B(1287/987) 2 5022/3839 E(1283/938) E(1227/961) B(1266/945) B(1224/995) 3 5027/3868 B(1224/980) B(1254/992) E(1287/942) E(1235/954) 4 5031/3887 B(1214/916) E(1288/991) B(1247/1006) E(1251/974) -
[1] 王骄, 徐心和. 计算机博弈: 人工智能的前沿领域: 全国大学生计算机博弈大赛[J]. 计算机教育, 2012(7): 14–18. doi: 10.3969/j.issn.1672-5913.2012.07.003 WANG Jiao, XU Xinhe. Computer game: the frontier field of artificial intelligence: the national college student computer game competition[J]. Computer education, 2012(7): 14–18. doi: 10.3969/j.issn.1672-5913.2012.07.003 [2] 王亚杰, 邱虹坤, 吴燕燕, 等. 计算机博弈的研究与发展[J]. 智能系统学报, 2016, 11(6): 788–798. https://www.cnki.com.cn/Article/CJFDTOTAL-ZNXT201606008.htm WANG Yajie, QIU Hongkun, WU Yanyan, et al. Research and development of computer games[J]. CAAI transactions on intelligent systems, 2016, 11(6): 788–798. https://www.cnki.com.cn/Article/CJFDTOTAL-ZNXT201606008.htm [3] 徐心和, 邓志立, 王骄, 等. 机器博弈研究面临的各种挑战[J]. 智能系统学报, 2008, 3(4): 287–293. https://www.cnki.com.cn/Article/CJFDTOTAL-ZNXT200804004.htm XU Xinhe, DENG Zhili, WANG Jiao, et al. Challenging issues facing computer game research[J]. CAAI transactions on intelligent systems, 2008, 3(4): 287–293. https://www.cnki.com.cn/Article/CJFDTOTAL-ZNXT200804004.htm [4] SILVER D, HUANG A, MADDISON C J, et al. Mastering the game of Go with deep neural networks and tree search[J]. Nature, 2016, 529(7587): 484–489. doi: 10.1038/nature16961 [5] SILVER D, SCHRITTWIESER J, SIMONYAN K, et al. Mastering the game of Go without human knowledge[J]. Nature, 2017, 550(7676): 354–359. doi: 10.1038/nature24270 [6] SILVER D, HUBER T, SCHRITTWIESER J, et al. Mastering chess and shogi by self-play with a general reinforcement learning algorithm[J]. IEEE transactions on computational intelligence and AI in games, 2017, 3(2): 167–170. [7] SILVER D, HUBERT T, SCHRITTWIESER J, et al. A general reinforcement learning algorithm that masters chess, shogi, and go through self-play[J]. Science, 2018, 362(6419): 1140–1144. doi: 10.1126/science.aar6404 [8] 李翔, 姜晓红, 陈英芝, 等. 基于手牌预测的多人无限注德州扑克博弈方法[J]. 计算机学报, 2018, 41(1): 47–64. https://www.cnki.com.cn/Article/CJFDTOTAL-JSJX201801003.htm LI Xiang, JIANG Xiaohong, CHEN Yingzhi, et al. Game in multiplayer no-limit texas Hold'Em based on hands prediction[J]. Chinese journal of computers, 2018, 41(1): 47–64. https://www.cnki.com.cn/Article/CJFDTOTAL-JSJX201801003.htm [9] MORAVČÍK M, SCHMID M, BURCH N, et al. DeepStack: expert-level artificial intelligence in heads-up no-limit poker[J]. Science, 2017, 356(6337): 508–513. doi: 10.1126/science.aam6960 [10] BROWN N, SANDHOLM T. Superhuman AI for multiplayer poker[J]. Science, 2019, 365(6456): 885–890. doi: 10.1126/science.aay2400 [11] NOAM B. Equilibrium finding for large adversarial imperfect-information Games[D]. Pittsburgh: Carnegie Mellon University, 2020. [12] 微软亚洲研究院.哪类游戏AI难度更高? 用数学来分析一下[EB/OL]. (2019-8-16) [2021-07-17]. https://www.msra.cn/zh-cn/news/features/difficulty-of-ai-games. MSRA. Which game is more difficult for AI? Use math to analyze[EB/OL]. (2019-8-16) [2021-07-17]. https://www.msra.cn/zh-cn/news/features/difficulty-of-ai- games. [13] BROWN N, SANDHOLM T. Safe and nested subgame solving for imperfect-information games[J]. NIPS, 2017: 690–700. [14] XINGDREAM. 2020麻将项目比赛规则和本文完整实验源码[EB/OL]. (2021-06-01) [2021-07-17]. https://github.com/xingdream/mahjong. XINGDREAM. 2020 Mahjong competition rules and the complete experimental source code of this article[EB/OL]. (2021-06-01) [2021-07-17]. https://github.com/xingdream/mahjong. [15] CHENG Yuan, LI Chikwong, LI Sharon H. Mathematical aspect of the combinatorial game “Mahjong”[J]. Southeast asian bulletin of Mathematics, 2019, 43: 815–826. [16] LI Sanjiang, YAN Xueqing. Let's play mahjong[J]. IEICE transactions on fundamentals of electronics, communications and computer sciences, 2019, abs/1903.03294. [17] 林典馀, 吴毅成. 麻将之人工智慧研究[D]. 新竹: 国立交通大学, 2008. LIN Dianyu, WU Yicheng. The study of mahjong artificial intelligence[D]. Xinzhu: National Chiao Tung University, 2008. [18] 陈新飏, 林顺喜. 电脑麻将程序ThousandWind 的设计与实作[D]. 新竹: 国立台湾师范大学, 2013. CHEN Xinsi, LIN Shunxi. The design and implementation of the mahjong program ThousandWind[D]. Xinzhu: National Taiwan Normal University, 2013. [19] 曾海洋, 颜士净. 蒙特卡罗麻将程式设计与改良[D]. 新竹: 台湾计算机博弈学会, 2015. ZENG Haiyang, YAN Shijing. Monte Carlo Mahjong programming and improvement[D]. Xinzhu: Taiwan Computer Game Association, 2015. [20] HANDA H. Evolution of the weight vectors in Mahjong non-player characters[C]//2013 World Congress on Nature and Biologically Inspired Computing. New York, USA: IEEE, 2013: 147−152. [21] MIZUKAMI N, TSURUOKA Y. Building a computer Mahjong player based on Monte Carlo simulation and opponent models[C]//2015 IEEE Conference on Computational Intelligence and Games. New York, USA: IEEE, 2015: 275−283. [22] GAO Shiqi, OKUYA Fuminori, KAWAHARA Yoshihiro, et al. Supervised learning of imperfect information data in the game of mahjong via deep convolutional neural networks[J]. Information processing society of Japan, 2018(2018): 43–50. [23] GAO SHIQI, OKUYA F, KAWAHARA Y, et al. Building a computer mahjong player via deep convolutional neural networks[EB/OL]. (2019-06-00) [2021-07-17]. https://arxiv.org/abs/1906.02146. [24] LI JUNJIE, KOYAMADA S, YE QIWEI, et al. Suphx: mastering mahjong with deep reinforcement learning[EB/OL]. (2020-03-30) [2021-07-17]. https://arXiv preprint arXiv:2003.13590. [25] WANG Mingyan, YAN Tianwei, LUO Mingyuan, et al. A novel deep residual network-based incomplete information competition strategy for four-players Mahjong games[J]. Multimedia tools and applications, 2019, 78(16): 23443–23467. doi: 10.1007/s11042-019-7682-5 [26] 任航. 基于知识与树搜索的非完备信息博弈决策的研究与应用[D]. 南昌: 南昌大学, 2020. REN Hang. Research and application of imperfect information game decision based on knowledge and game-tree search[D]. Nanchang: Nanchang University, 2020. [27] 雷捷维, 王嘉旸, 任航, 等. 基于Expectimax搜索与Double DQN的非完备信息博弈算法[J]. 计算机工程, 2021, 47(3): 304, 310–320. https://www.cnki.com.cn/Article/CJFDTOTAL-JSJC202103040.htm LEI Jiewei, WANG Jiayang, REN Hang, et al. Incomplete information game algorithm based on expectimax search and double DQN[J]. Computer engineering, 2021, 47(3): 304, 310–320. https://www.cnki.com.cn/Article/CJFDTOTAL-JSJC202103040.htm


 下载:
下载: