Bearing only target tracking and observability control of a mobile robot
-
摘要: 为了解决未知环境下的单目视觉移动机器人目标跟踪问题，提出了一种将目标状态估计与机器人可观性控制相结合的机器人同时定位、地图构建与目标跟踪方法。在状态估计方面，以机器人单目视觉同时定位与地图构建为基础，设计了扩展式卡尔曼滤波框架下的目标跟踪算法；在机器人可观性控制方面，设计了基于目标协方差阵更新最大化的优化控制方法。该方法能够实现机器人在单目视觉条件下对自身状态、环境状态、目标状态的同步估计以及目标跟随。仿真和原型样机实验验证了目标状态估计和机器人控制之间的耦合关系，证明了方法的准确性和有效性，结果表明：机器人将产生螺旋状机动运动轨迹，同时，目标跟踪和机器人定位精度与机器人机动能力成正比例关系。Abstract: To address the object tracking issue of a mobile robot based on monocular vision in an unknown environment, a method for robotic simultaneous localization, map building, and object tracking is proposed, combining the object state estimation with the observability control of a mobile robot. Regarding state estimation, based on robot monocular visual simultaneous localization and mapping, a target tracking algorithm under the extended Kalman filtering framework is designed. Considering the observability control, an optimal control method based on updating the maximization of the target covariance matrix is designed. Using the monocular vision, this method can synchronously estimate the robot’s own state, environmental state, and target state, as well as the target following. The simulation and prototype experiments verify the coupling relationship between the target state estimation and robot control, demonstrating the effectiveness and accuracy of the method. The results indicate that by employing this method, the robot can generate a spiral maneuvering trajectory, and the accuracy of target tracking and robot positioning is directly proportional to its maneuvering ability.
-
智能移动机器人是一类能够通过传感器感知环境和自身状态，实现在有障碍物的环境中面向目标的自主运动，从而完成一定作业功能的机器人系统[1]。从该定义可见，机器人对自身和环境对象（包括：静态对象和动态对象）的感知在任务执行中起到关键性和基础性作用。
单目视觉传感器作为一种被动式传感器，凭借其体积小、耗能少、细节呈现度高等特点，正在机器人导航学中发挥着重要作用[2]。机器人和计算机视觉领域的相关学者已经展开了基于单目视觉的机器人同时定位、地图构建与目标跟踪(simultaneous localization , mapping and object tracking, SLAMOT)问题研究[3]。机器人领域的SLAMOT以SLAM为核心[4-6]，目标识别与跟踪目的是提供更好的环境特征观测值，通常假设目标为静止的结构性物体且不考虑平台可观性机动问题，Castler等[7]在PTAM (parallel tracking and mapping)方法[8]基础上提出了独立于摄像机SFM (structure from motion)的目标识别与跟踪方法，该方法在图像关键帧上通过特征点匹配识别环境目标并利用扎集优化方法(bundle adjustment, BA)实现对目标空间位置的估计，但其假设目标为静止的画像平面。De 等[9]将实际场景中运动物体融入地图构建以解决增强现实中虚拟物体投影参考缺失问题。Dai等[10]利用RGBD传感器解决了动态物体对SLAM的影响，但并未研究动态物体跟踪问题。Li等[11]研究了基于运动目标跟踪和静止物体识别的语义学SLAM方法，运功目标跟踪目的同样是为了减少对SLAM的干扰。Civera等[12]将目标识别与跟踪纳入到基于反转深度的全关联卡尔曼滤波框架[13]中，实现了环境物体的识别和空间位置的在线估计。同样，该方法假设目标为静止的平面物体。Wangsiripitak等[14]设计了单目SLAM与目标跟踪同步估计算法，该算法处理的是空间立体静止物体并未考虑目标运动问题。Migliore等[15]设计了一种单目SLAM和动态目标跟踪算法，该算法将传统的SLAM滤波器和纯方位角观测目标跟踪器相结合，实现了对摄像机、环境特征和动态目标状态的同时迭代估计，方法利用的平台为手持摄像机，因此并未考虑平台可观性机动对目标状态估计的影响。
Bescos等[16]设计了一种SLAM和多目标跟踪相结合的方法，验证了动态目标跟踪对SLAM的辅助作用。Liu等[17]提出了SLAM和目标跟踪强、弱耦合估计切换方法，有效结合了两者的有点。Sualehm等[18]采用多传感器融合方法实现动态环境下SLAM任务，能够完成对多个运动目标的跟踪。Liu等[19]研究了人造动态环境下的SLAM问题，提出了动态目标跟踪、视觉里程计和地图构建的多线程估计方法。计算机视觉领域的SLAMOT以基于单目视觉的目标跟踪为核心，又称为：纯方位角观测目标跟踪(bearing only object tracking)或目标运动分析(target motion analysis)，此类方法希望利用平台机动和目标纯方位角观测，实现运动目标的状态估计，通常假设移动平台状态已知。Oh等[20]提出了一种基于粒子群优化的解决方法，但未考虑平台的机动优化问题。Zhuk等[21]通过对比相邻帧中跟踪点实现运动物体检测，但并未实现目标状态估计。Watanabe等[22]提出了基于单目视觉的移动平台导航方法，该方法针对单目视觉传感器特点将导航控制和目标状态估计作为耦合问题处理，其假设移动平台状态已知。Kim等[23]针对纯方位角观测目标跟踪问题提出了“双重作用(dual effect)理论”认为由于观测深度信息缺失使得目标状态估计和平台机动运动之间存在关联作用，目标跟踪准确性极大依赖于平台机动方式，同样，其假设平台状态已知。
综上所述，学界已经开展了基于单目视觉的SLAMOT问题的相关研究，但通常将SLAM和OT相互割裂，并未考虑目标的移动性、机器人状态未知性以及平台的可观性优化控制问题。文章正是针对以上问题展开研究，提出了基于单目视觉的机器人同时定位、地图构建与目标跟踪及平台控制方法，该方法利用单目视觉SLAM实现对机器人状态估计，并结合目标观测模型进行基于扩展式卡尔曼滤波的目标状态估计。为了克服观测模型缺陷，提出了基于目标协方差阵更新最大化的机器人优化控制方法，最终实现了未知环境下基于单目视觉的移动机器人目标跟踪。
1. 问题描述和模型构建
1.1 问题描述
假设
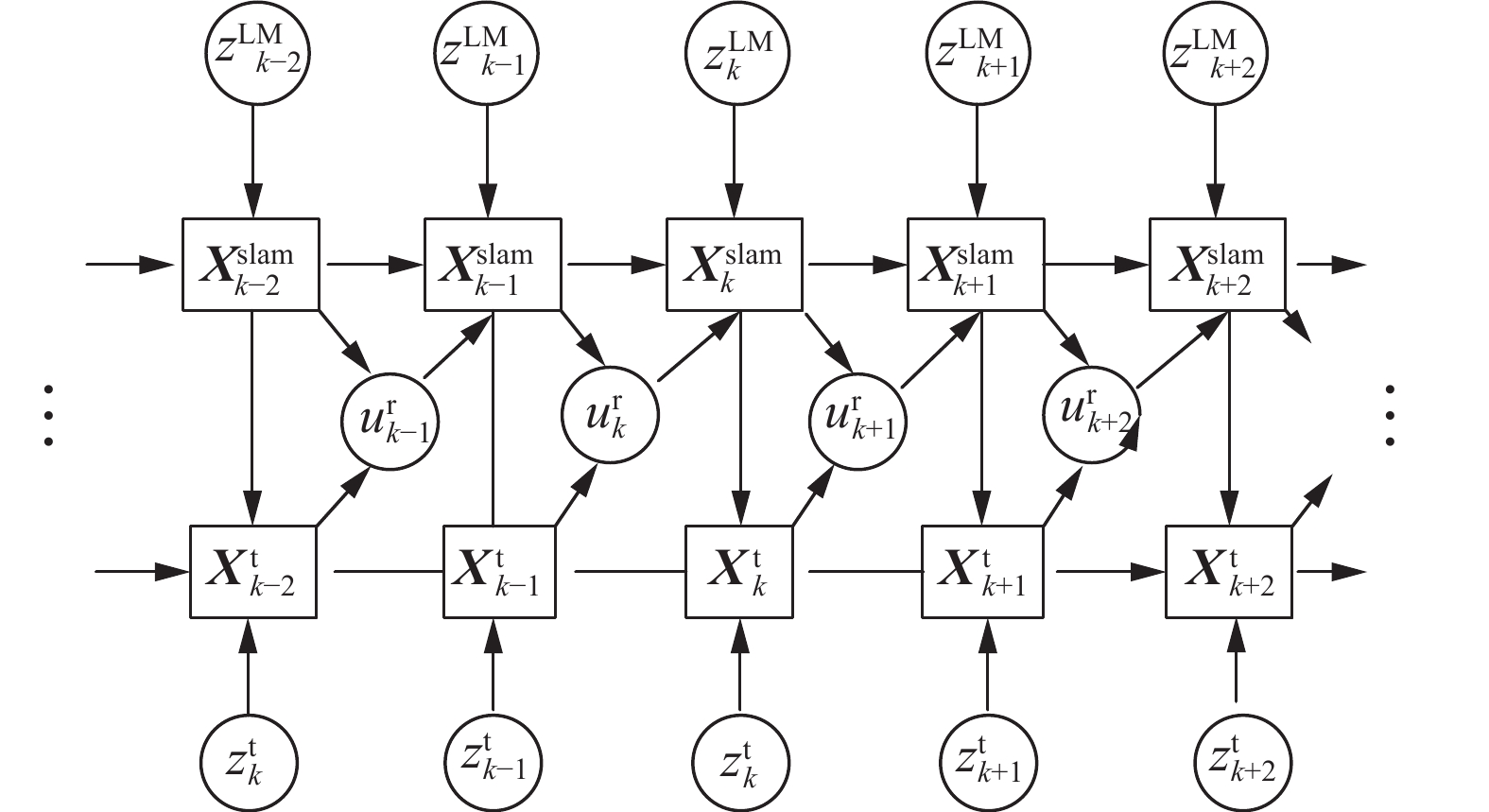
$ k $ 时刻机器人状态为${\boldsymbol{X}}_k^{\text{r}}$ ，环境特征状态为${\boldsymbol{X}}_k^{{\text{l}}{{\text{m}}_i}},i = 1,2,\cdots,m$ ，目标状态为${\boldsymbol{X}}_k^{\text{t}}$ ，机器人利用单目视觉传感器对目标和环境特征进行观测且观测值分别为${\boldsymbol{z}}_k^{\text{t}}$ 和${\boldsymbol{z}}_k^{{\text{l}}{{\text{m}}_i}}$ ，方法处理目的是在机器人端实现对${\boldsymbol{X}}_k^{\text{r}}$ ，${\boldsymbol{X}}_k^{\text{t}}$ 及${\boldsymbol{X}}_k^{{\text{l}}{{\text{m}}_i}},i = 1,2,\cdots,m$ 的在线估计。由于单目摄像机得到的观测量缺少距离信息，存在可观性问题。为了估计目标与机器人的相对距离，机器人需要根据目标不确定分布实时计算控制量${\boldsymbol{u}}_k^{\text{r}}$ ，以保证在该控制量作用下得到的前后时序目标观测值${\boldsymbol{z}}_{k{{ - }}1}^{\text{t}}$ 和${\boldsymbol{z}}_k^{\text{t}}$ 之间存在足够视差，从而为距离估计提供足够的信息。相关对象状态演变符合马尔可夫过程，其对应的贝叶斯网络模型如图1所示。其中
${\boldsymbol{X}}_k^{{\rm{slam}}} = \left[ {{\boldsymbol{X}}_k^{{\rm{r}}'}\;\;{\boldsymbol{X}}_k^{{\rm{LM}}'}} \right]'$ 为机器人状态和环境特征状态扩展构成的SLAM系统状态向量。系统的两条主线为${\boldsymbol{X}}_k^{{\text{slam}}}$ 估计流程和${\boldsymbol{X}}_k^{\text{t}}$ 估计流程，${\boldsymbol{X}}_k^{{\text{slam}}}$ 的估计采用基于反转深度的单目视觉SLAM方法[12]。${\boldsymbol{X}}_k^{\text{t}}$ 估计过程基于扩展式卡尔曼滤波，首先，根据目标运动模型预测目标状态${\boldsymbol{X}}_k^{\rm{t^-}}$ 和协方差阵${\boldsymbol{P}}_k^{\rm{t^-} }$ ，第二，利用SLAM环节得到的机器人状态${\boldsymbol{X}}_k^{\text{r}}$ 和协方差${\boldsymbol{P}}_k^{\text{r}}$ ，结合目标观测模型得到目标预测观测值${{\boldsymbol{z}}_k^{\rm{t^ -}}}$ 和观测残差阵${{\boldsymbol{S}}_k^{\rm{t^ - }}}$ ，最后，对预测状态${\boldsymbol{X}}_k^{\rm{t^ - }}$ 和协方差阵${\boldsymbol{P}}_k^{\rm{t^ - }}$ 进行更新，得到${\boldsymbol{X}}_k^{\text{t}}$ 和${\boldsymbol{P}}_k^{\text{t}}$ 。
图 1 贝叶斯网络模型Fig. 1 Bayesian network model
下载:
全尺寸图片
系统解决的关键问题有两点：1)设计
${\boldsymbol{X}}_k^{\text{r}}$ ，${\boldsymbol{X}}_k^{\text{t}}$ 及${\boldsymbol{X}}_k^{{\text{l}}{{\text{m}}_i}},i = 1,2,\cdots,m$ 在线估计方法；2)如何生成机器人优化控制量${\boldsymbol{u}}_k^{\text{r}}$ ，这两点将在第4和第5部分讨论。1.2 数学模型构建
1）目标运动模型
目标
$ k $ 时刻状态由各坐标轴分量及其速度构成，即，${\boldsymbol{X}}_k^{\rm t} = [x_k^{\rm t}{\text{ }}y_k^{\rm t}{\text{ }}z_k^{\rm t}{\text{ }}\dot x_k^{\rm t}{\text{ }}\dot y_k^{\rm t}{\text{ }}\dot z_k^{\rm t}]'$ 。假设目标运动模式为定速度模型(constant velocity model, CVM)[24]，则CVM模型的离散形式可表示成为$$ {\boldsymbol{X}}_k^{\rm t} = {f^{\rm t}}({\boldsymbol{X}}_{k - 1}^{\rm t},{\boldsymbol{A}}_{k|k - 1}^{\rm t},{\boldsymbol{q}}_{k|k - 1}^{\rm t}) = {\boldsymbol{A}}_{k|k - 1}^{\rm t} \cdot {\boldsymbol{X}}_{k - 1}^{\rm t} + {\boldsymbol{q}}_{k|k - 1}^{\rm t} $$ (1) 式中：
${\boldsymbol{A}}_{k|k - 1}^{\rm t}$ 为状态转移阵；${\boldsymbol{q}}_{k|k - 1}^{\rm t}$ 为高斯白噪声。2）机器人运动模型
机器人运动模型符合运动方向和线速度解耦的多旋翼无人机模型，设k时刻状态为
${\boldsymbol{X}}_k^{\rm{r'} } = [ {{\boldsymbol{x}}_k^{\rm{r'}}}\;\;{{\boldsymbol{q}}_k^{\rm{r'} }} ]$ 其中${\boldsymbol{x}}_k^{\text{r}}= [x_k^{\text{r}}\;\;y_k^{\text{r}}\;\;z_k^{\text{r}}]'$ 为空间位置向量，${\boldsymbol{q}}_k^{\text{r}} = [{q_{1,k}}\;\;{q_{2,k}}\;\;{q_{3,k}} \;\; {q_{4,k}}]'$ 为朝向4元组向量。假设k时刻机器人的控制量为
${\boldsymbol{u}}_k^{\text{r}} \;=\; [\Delta {\boldsymbol{x}}_k^{\text{r}}\;\;\Delta {\boldsymbol{\varphi}} _k^{\text{r}}]'$ ，其中$\Delta {\boldsymbol{x}}_k^{\rm{r}}\;{{ = [}}\Delta x_k^{\rm{r}}\;\;\Delta y_k^{\rm{r}}\;\;\Delta z_k^{\rm{r}}{{]'}}$ 为位移控制分量，$\Delta {\boldsymbol{\varphi}} _k^{\text{r}} = [\Delta \phi _k^{\text{r}}\;\; \Delta \theta _k^{\text{r}}\;\;\Delta \psi _k^{\text{r}}]'$ 为角度控制分量，则机器人的状态更新可分解位置和朝向更新，即：$$ {\boldsymbol{X}}_k^{\text{r}} = {\boldsymbol{f}}({\boldsymbol{X}}_{k - 1}^{\text{r}},{\boldsymbol{u}}_{k - 1}^{\text{r}})= \left[ {\begin{array}{*{20}{c}} {{\boldsymbol{x}}_{k - 1}^{\text{r}} + {\boldsymbol{R}}({\boldsymbol{q}}_{k - 1}^{\text{r}}) \cdot \Delta {\boldsymbol{x}}_{k - 1}^{\text{r}}} \\ {{\boldsymbol{q}}_{k - 1}^{\text{r}} + \dfrac{1}{2} \cdot {\boldsymbol{\varOmega}} (\Delta {\boldsymbol{\varphi}} _{k - 1}^{\text{r}}) \cdot {\boldsymbol{q}}_{k - 1}^{\text{r}}} \end{array}} \right] $$ (2) 其中，
${\boldsymbol{R}}({{\boldsymbol{q}}^{\text{r}}})$ 是世界坐标系到机器人坐标系的旋转矩阵，其值可根据${\boldsymbol{q}}_{}^{\text{r}}$ 计算，${\boldsymbol{\varOmega}} (\Delta {\boldsymbol{\varphi }}_{}^{\text{r}})$ 为朝向3元组到4元组的反对称矩阵，表示为$$ {\boldsymbol{\varOmega}} (\Delta {\boldsymbol{\varphi }}_{}^{\text{r}}) \left[ {\begin{array}{*{20}{c}} 0&{ - \Delta \phi _k^{\text{r}}}&{ - \Delta \theta _k^{\text{r}}}&{ - \Delta \psi _k^{\text{r}}} \\ {\Delta \phi _k^{\text{r}}}&0&{\Delta \psi _k^{\text{r}}}&{ - \Delta \theta _k^{\text{r}}} \\ {\Delta \theta _k^{\text{r}}}&{ - \Delta \psi _k^{\text{r}}}&0&{\Delta \phi _k^{\text{r}}} \\ {\Delta \psi _k^{\text{r}}}&{\Delta \theta _k^{\text{r}}}&{ - \Delta \phi _k^{\text{r}}}&0 \end{array}} \right] $$ 3）目标观测模型
目标观测模型实现从机器人状态
${\boldsymbol{X}}_k^{\text{r}}$ 、目标状态${\boldsymbol{X}}_k^{\text{t}}$ ，摄像机在机器人坐标系中的位姿${\boldsymbol{X}}_k^{{\text{R,c}}}$ 到图像观测值${\boldsymbol{z}}_k^{\rm{t}}{{ = [}}u_k^{\rm{t}}\;\;v_k^{\rm{t}}{{]'}}$ 的映射，其符合单目小孔成像模型[25]，可表示为$$ {\boldsymbol z}_{k}^{\text{t}}={\boldsymbol h}^{\text{t}}({\boldsymbol X}_{k}^{\text{t}},{\boldsymbol X}_{k}^{\text{r}},{\boldsymbol X}_{k}^{\text{R,c}},{\boldsymbol{d}},{\boldsymbol{s}})+{\boldsymbol{r}} $$ (3) 式中：
${\boldsymbol{s}} = [{s_u}\;\;{s_v}\;\;{u_0}\;\;{v_0}]'$ 为摄像机内参向量，${\boldsymbol{d}} = [{d_1}\;\;{d_2}]'$ 为摄像机畸变系数向量，$\boldsymbol s$ 和$\boldsymbol d$ 由文献[16]介绍的相机标定方法获得。$\boldsymbol r$ 是均值为0，标准差为$\sigma \boldsymbol r$ 的观测加性白噪声。2. 系统总体框架
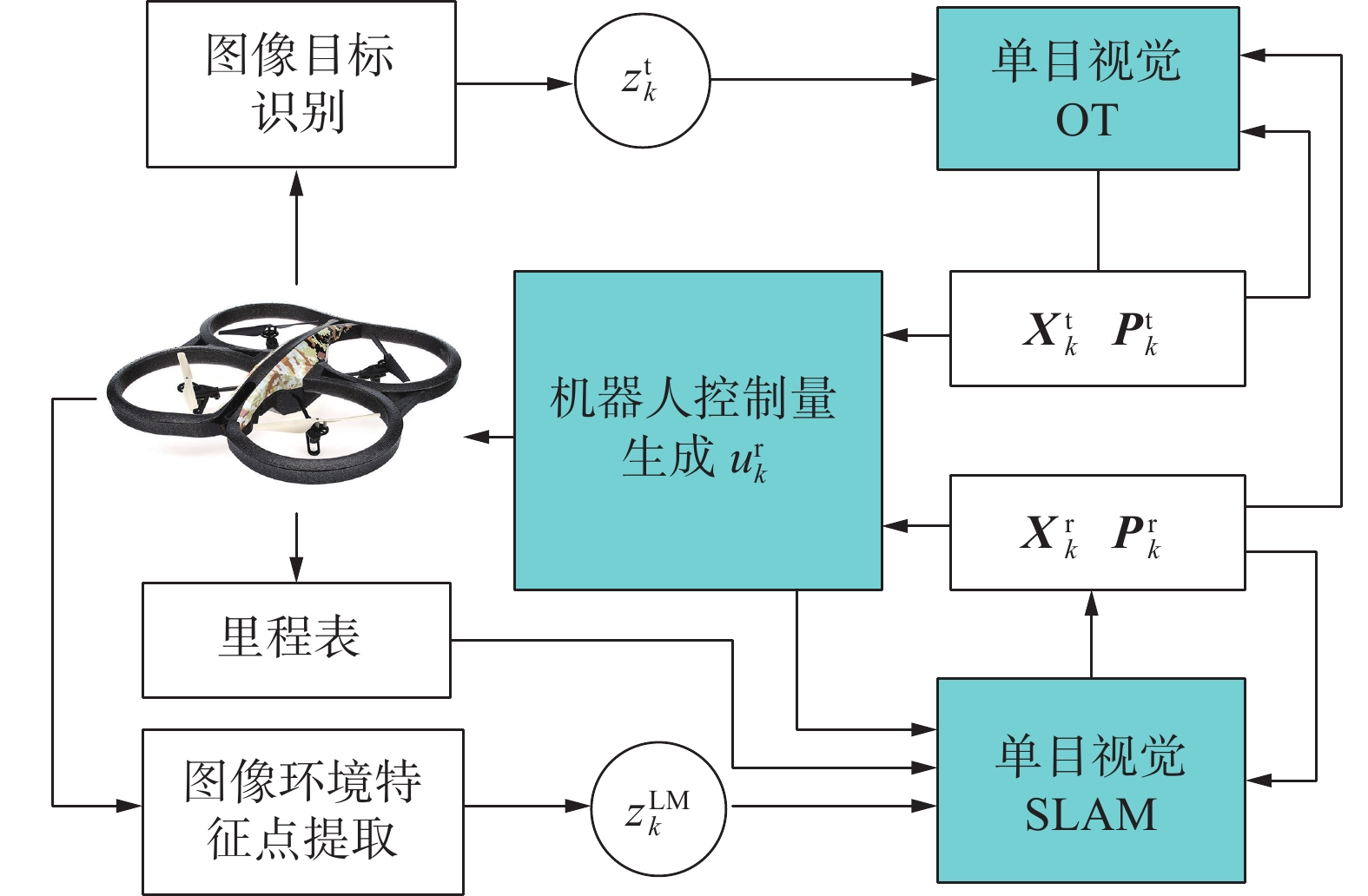
系统总体框架如图2所示。
图 2 系统总体框架Fig. 2 Overall framework of the system下载:
全尺寸图片
机器人外感传感器是前向单目摄像机，每轮观测对拍摄的图片进行环境特征提取以及目标识别进而获得目标观测值
${\boldsymbol{z}}_k^{\text{t}}$ 与环境特征观测值${\boldsymbol{z}}_k^{{\text{LM}}}$ 。系统包含3个核心处理模块：1)单目SLAM处理模块；2)单目视觉OT模块；3)机器人控制量生成模块。其中，单目SLAM处理模块采用基于反转深度参数表示法的全概率卡尔曼滤波方法实现机器人状态和协方差阵的估计；单目OT模块利用${\boldsymbol{X}}_k^{\text{r}}$ 和${\boldsymbol{P}}_k^{\text{r}}$ 结合此时目标观测值${\boldsymbol{z}}_k^{\text{t}}$ 进行基于扩展式卡尔曼滤波的目标跟踪得到目标状态${\boldsymbol{X}}_k^{\text{t}}$ 和协方差阵${\boldsymbol{P}}_k^{\text{t}}$ ；由于单目视觉传感器缺少深度观测值使目标状态估计出现可观性问题，即，目标状态无法利用机器人状态和观测值直接推导出，因此在机器人控制量生成环节，需要利用优化控制方法生成机器人控制量${\boldsymbol{u}}_k^{\text{r}}$ ，以保证机器人对目标的跟随和目标状态的有效估计。3. 机器人单目视觉SLAM
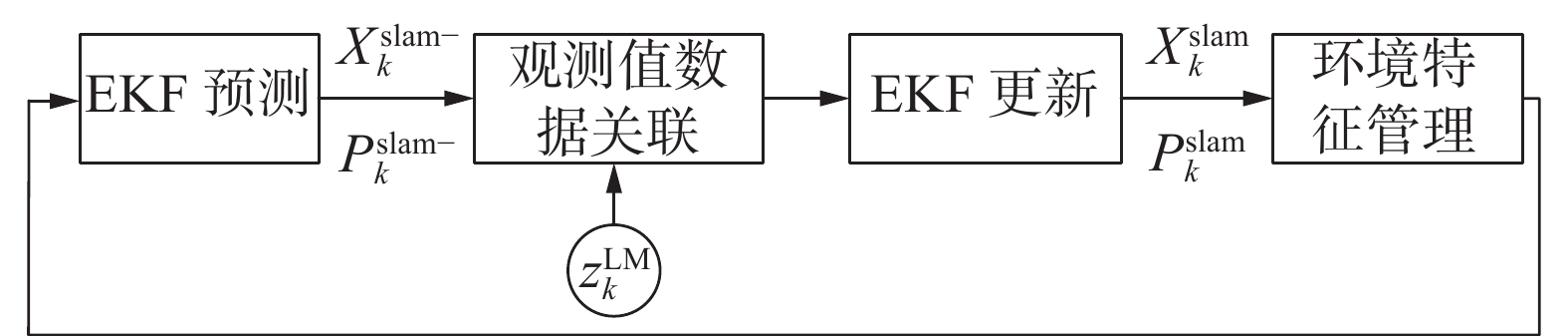
采用文献[9]提出的反转深度单目视觉SLAM方法，基本处理流程图3所示。
图 3 VSLAM处理流程Fig. 3 Processing flow of VSLAM下载:
全尺寸图片
系统状态为
${\boldsymbol{X}}_k^{{\rm{slam'}} } = [{\boldsymbol{X}}_k^{\rm{r'}}\;\;{\boldsymbol{X}}_k^{{\rm{LM'}} }]$ ，${\boldsymbol{X}}_k^{\text{r}}$ 和${\boldsymbol{X}}_k^{{\text{LM}}}$ 为机器人和环境特征状态向量，初始阶段利用反转深度参数法表示环境特征状态，当特征状态线性化程度达到预设门限时，在环境特征管理环节将特征的反转深度状态转换为笛卡尔状态。在每轮估计结束时，提取${\boldsymbol{X}}_k^{{\text{slam}}}$ 和${\boldsymbol{X}}_k^{{\text{slam}}}$ 中的机器人状态和协方差分量得到${\boldsymbol{X}}_k^{\text{r}}$ 和${\boldsymbol{X}}_k^{\text{r}}$ 用于后续目标状态估计。4. 单目视觉移动机器人目标跟踪方法
目标跟踪采用扩展式卡尔曼滤波框架，假设
$ k $ 时刻机器人的状态${\boldsymbol X}_k^{\text{r}}$ 和协方差${\boldsymbol P}_k^{\rm r}$ 由第3节介绍方法获得。目标跟踪的处理过程如下。1）目标状态、协方差预测
目标状态预测公式如下：
$$ {\boldsymbol{X}}_k^{{{\rm t}^{^ - }}} = {\boldsymbol{A}}_{k|k - 1}^{\rm t} \cdot {\boldsymbol{X}}_{k - 1}^{\rm t} $$ (4) $$ {\boldsymbol{P}}_k^{{{\rm t}^ - }} = {\boldsymbol{A}}_{k|k - 1}^{\rm t} \cdot {\boldsymbol {X}}_{k - 1}^{\rm t} \cdot {\boldsymbol{A}}_{k|k - 1}^{{\rm t}' } + {\boldsymbol{Q}} $$ (5) 式中：
${\boldsymbol{A}}_{k|k - 1}^{\rm t}$ 为目标定速模型状态转移矩阵；${\boldsymbol{Q}}$ 为状态误差阵。2）目标观测值及观测残差阵预测
将机器人状态
${\boldsymbol{X}}_k^{\text{r}}$ 和预测目标状态${\boldsymbol{X}}_k^{{\rm t^ - }}$ 代入式（3）得到目标预测观测值：$$ {\boldsymbol z}_{k}^{\rm{t^-}}={\boldsymbol h}^{\text{t}}({\boldsymbol X}_{k}^{\rm{t}^-},{\boldsymbol X}_{k}^{\text{r}},{\boldsymbol X}_{k}^{\text{R,c}},{\boldsymbol{d}},{\boldsymbol{s}}) $$ (6) 式中：
${\boldsymbol{X}}_k^{\rm{t^ - }}$ 为式（4）确定的预测目标状态；${\boldsymbol{X}}_k^{\text{r}}$ 为利用单目视觉SLAM环节得到的机器人位姿状态。利用误差传播公式链式产生目标观测残差阵
${\boldsymbol{S}}_k^{\rm{t^ - }}$ 如下：$$ \begin{gathered} {{\boldsymbol{S}}_k^{\rm{t^ - }} = {{\boldsymbol{H}}^{\rm t \to z}} \cdot {\boldsymbol{P}}_k^{{\rm t^ - }}} \cdot {{\boldsymbol{H}}^{\rm t \to z}}' + {{\boldsymbol{H}}^{\rm r \to z}} \cdot {\boldsymbol{P}}_k^{\rm r} \cdot {{\boldsymbol{H}}^{\rm r \to z}}' + {{\boldsymbol{H}}^{\rm c \to z}} \cdot {\boldsymbol{P}}_k^{\rm c} \cdot \\ {{\boldsymbol{H}}^{\rm c \to z}}' + {{\boldsymbol{H}}^{\rm s \to z}} \cdot {\boldsymbol{P}}_k^{\rm S} \cdot {{\boldsymbol{H}}^{\rm s \to z}}' + {{\boldsymbol{H}}^{\rm d \to z}} \cdot {\boldsymbol{P}}_k^{\rm d} \cdot {{\boldsymbol{H}}^{\rm d \to z}}' + {\boldsymbol{R}} \\ \end{gathered} $$ (7) 其中，
$$\begin{gathered} {{\boldsymbol{H}}^{\rm r \to z}} = {\left. {\frac{{\partial {{\boldsymbol{h}}^{\text{t}}}}}{{\partial {\boldsymbol{X}}_k^{\text{r}}}}} \right|_{{\boldsymbol{X}}_k^{\text{r}} = {\boldsymbol{X}}_k^{\rm{r^*}}}} ,{{\boldsymbol{H}}^{\rm t \to z}} = {\left. {\frac{{\partial {{\boldsymbol{h}}^{\text{t}}}}}{{\partial {\boldsymbol{X}}_k^{\text{t}}}}} \right|_{{\boldsymbol{X}}_k^{\text{t}} = {\boldsymbol{X}}_k^{\rm{t^ -}}}} , {{\boldsymbol{H}}^{\rm c \to z}} = {\left. {\frac{{\partial {{\boldsymbol{h}}^{\text{t}}}}}{{\partial {\boldsymbol{X}}_k^{{\rm{R,c}}}}}} \right|_{{\boldsymbol{X}}_k^{{\rm{R,c}}} = X_k^{{\rm{R,c^*}}}}}\\ {{\boldsymbol{H}}^{\rm d \to z}} = {\left. {\dfrac{{\partial {{\boldsymbol{h}}^{\text{t}}}}}{{\partial {\boldsymbol{d}}}}} \right|_{d = {d^{\text{*}}}}},{{\boldsymbol{H}}^{\rm s \to z}} = {\left. {\dfrac{{\partial {{\boldsymbol{h}}^{\text{t}}}}}{{\partial {\boldsymbol{S}}}}} \right|_{S = {S^*}}} \end{gathered}$$ 分别为式（3）对
${\boldsymbol{X}}_k^{\text{r}}$ 、${\boldsymbol{X}}_k^{\rm t}$ 、${\boldsymbol{X}}_k^{{\text{R,c}}}$ 、$\boldsymbol d$ 、$\boldsymbol s$ 的雅可比阵。${\boldsymbol P}_k^{{\rm t^ - }}$ 、${\boldsymbol{P}}_k^{\rm{r}}$ 、${\boldsymbol P}_k^{\rm c}$ 、${\boldsymbol P}_k^{\rm S}$ 、${\boldsymbol P}_k^{\rm d}$ ，$\boldsymbol R$ 分别为此刻${\boldsymbol{X}}_k^{\text{r}}$ 、${\boldsymbol{X}}_k^{\rm{t}}$ 、${\boldsymbol{X}}_k^{{\text{R,c}}}$ 、$\boldsymbol d$ 、$\boldsymbol s$ 、$\boldsymbol r$ 对应的协方差阵。3）目标状态、协方差更新
根据扩展式卡尔曼滤波原理，更新后的目标状态
${\boldsymbol{X}}_k^{\rm t^ + }$ 和协方差阵${\boldsymbol{P}}_k^{{\rm t^ + }}$ 分别为$$ {\boldsymbol{X}}_k^{{\rm t^ + }} = {\boldsymbol{X}}_k^{{\rm t^ - }} + {\boldsymbol{K}} \cdot ({\boldsymbol{z}}_k^{\rm{t}} - {\boldsymbol{z}}_k^{\rm{t^ - }}) $$ (8) $$ {\boldsymbol{P}}_k^{\rm{t^{^ + }}} = {\boldsymbol{P}}_k^{\rm{t^{^ - }}} - {\boldsymbol{K}} \cdot {\boldsymbol{S}}_k^{\rm{t}} \cdot {\boldsymbol{K}}' $$ (9) $$ {\boldsymbol{K}} = {\boldsymbol{P}}_k^{\rm{t^ - }} \cdot {\boldsymbol{H}}_k^{\rm t \to z} \cdot ({\boldsymbol{S}}_k^{\rm{t^ - }})$$ (10) 其中，
$\boldsymbol K$ 为卡尔曼增益阵，${\boldsymbol{H}}_k^{\rm t \to z}$ 为式（6）对${\boldsymbol{X}}_k^{\rm t}$ 的雅可比阵。5. 基于目标协方差阵更新最大化的机器人优化控制方法
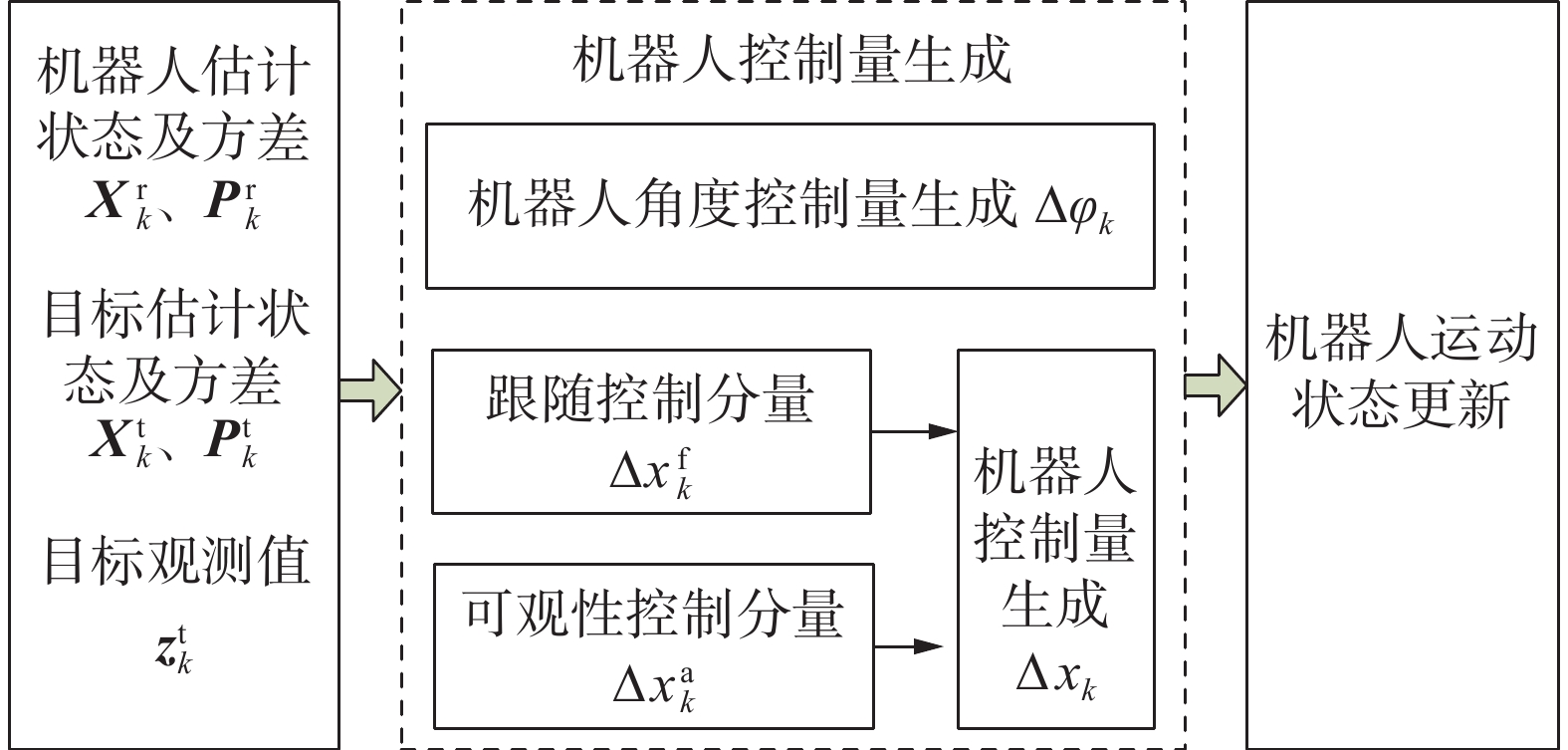
机器人控制要达到两个目的：首先，要确保机器人对目标的追踪，使目标始终在机器人视野内并保持一定距离；第二，保证机器人能够在纯方位角观测条件下对目标状态的准确估计。优化控制量生成过程如图4示。
图 4 优化控制量生成过程Fig. 4 Generation process of optimal control value下载:
全尺寸图片
机器人控制量包括角度控制3元组
$\Delta {{\boldsymbol{\varphi}} _k}$ 和位置控制3元组$\Delta {{\boldsymbol{x}}_k}$ ，首先，产生角度控制量$\Delta {{\boldsymbol{\varphi}} _k}$ ，该控制分量要保证机器人始终朝向目标。之后，产生位移控制量$\Delta {{\boldsymbol{x}}_k}$ ，$\Delta {{\boldsymbol{x}}_k}$ 由跟随控制分量$\Delta {\boldsymbol{x}}_k^{\text{f}}$ 和可观性控制分量$\Delta {\boldsymbol{x}}_k^{\text{a}}$ 组成。5.1 角度控制
$\Delta {{\boldsymbol{\varphi}} _k}$ 计算假设k时刻，目标观测值为
${\boldsymbol{z}}_k^{\text{t}} = [{u^{\text{t}}}{\text{ }}{v^{\text{t}}}]'$ ，根据摄像机小孔成像模型可知：$$ {\boldsymbol{x}}^{{\text{C,r}} \to {\text{t}}} = \left[ {\begin{array}{*{20}{c}} {x^{{\text{C,r}} \to {\text{t}}}} \\ {y^{{\text{C,r}} \to {\text{t}}}} \\ {z^{{\text{C,r}} \to {\text{t}}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {({u^{\text{t}}} - {u_0})/{s_u}} \\ {({v^{\text{t}}} - {v_0})/{s_v}} \\ 1 \end{array}} \right] $$ (11) $${\boldsymbol{u}}^{{\text{R,r}} \to {\text{t}}} = \left[ {\begin{array}{*{20}{c}} {x^{{\text{R,r}} \to {\text{t}}}} \\ {y^{{\text{R,r}} \to {\text{t}}}} \\ {z^{{\text{R,r}} \to {\text{t}}}} \end{array}} \right] = {{\boldsymbol{R}}^{{\text{C}} \to {\text{R}}}} \cdot {{\boldsymbol{x}}^{{\text{C,r}} \to {\text{t}}}} $$ (12) 式中：
${\boldsymbol{x}}^{{\text{C,r}} \to {\text{t}}}$ 为摄像机坐标系中，成像焦点指向目标的向量；$ {u_0} $ 、$ {v_0} $ 、$ {s_u} $ 、$ {s_v} $ 为摄像机内参；${{\boldsymbol{R}}^{{\text{C}} \to {\text{R}}}}$ 为机器人坐标系中摄像机相对于机器人的旋转矩阵。假设k时刻，机器人角度控制量为
$\Delta {{\boldsymbol{\varphi}} _k} = [\phi {\text{ }}\theta {\text{ }}\psi ]'$ ，分量表示机器人坐标系中绕X轴（旋转roll），Y轴（俯仰pitch）和Z轴（偏航yaw）的角度增量。$\Delta {{\boldsymbol{\varphi}} _k}$ 的计算公式为$$ \Delta {{\boldsymbol{\varphi}} _k} = \left[ {\begin{array}{*{20}{c}} \phi \\ \theta \\ \psi \end{array}} \right] = \left[ \begin{gathered} 0 \\ {\rm{ - arc}}(\sin (z^{{\text{R,r}} \to {\text{t}}})) \\ {\text{arc}}(\tan ({{y^{{\text{R,r}} \to {\text{t}}}} {/ {\vphantom {{y^{{\text{R,r}} \to {\text{t}}}} {x^{{\text{R,r}} \to {\text{t}}}}}} } {x^{{\text{R,r}} \to {\text{t}}}}})) \\ \end{gathered} \right] $$ (13) 其中
$ x_{}^{{\text{R,r}} \to {\text{t}}} $ 、$ y_{}^{{\text{R,r}} \to {\text{t}}} $ 、$ z_{}^{{\text{R,r}} \to {\text{t}}} $ 由式（12）确定。5.2 位移控制量
$ \Delta {x_k} $ 计算假设k时刻，机器人位置控制量为
$\Delta {{\boldsymbol{x}}_k}$ ，其计算公式为$$ \Delta {{\boldsymbol{x}}_k} = \left[ {\begin{array}{*{20}{c}} {\Delta {x_k}} \\ {\Delta {y_k}} \\ {\Delta {z_k}} \end{array}} \right] = V \cdot {\Delta {{\boldsymbol{u}}_k}}/{\Delta {{\boldsymbol{u}}_k}} $$ (14) 其中，
$$ \Delta {{\boldsymbol{u}}_k} = {\boldsymbol{R}}_{k}^{{\rm{W}} \to {\rm{R}}'} \cdot \left[\Delta {\boldsymbol{x}}_k^{\rm{f}} + \cdot \left(V - \left| {\Delta {\boldsymbol{x}}_k^{\rm{f}}} \right|\right) \cdot \frac{{\Delta {\boldsymbol{x}}_k^{\rm{a}}}}{{\left| {\Delta {\boldsymbol{x}}_k^{\rm{a}}} \right|}}\right] $$ $ V $ 为机器人速度常量，${\boldsymbol{R}}_k^{{\text{W}} \to {\text{R}}}$ 为世界坐标系到机器人坐标系的旋转矩阵，$\Delta {\boldsymbol{x}}_k^{\text{f}}$ 为跟随控制分量，$\Delta {\boldsymbol{x}}_k^{\text{a}}$ 为产生目标观测视差的可观性控制分量。由于机器人通过角度控制始终朝向目标，因此，
$\Delta {\boldsymbol{x}}_k^{\text{f}}$ 仅包含前向运动分量，即$$ \Delta {\boldsymbol{x}}_k^{\text{f}}= \left[ {\begin{array}{*{20}{c}} {\Delta x_k^{\text{f}}} \\ 0 \\ 0 \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{{ - }}V + \dfrac{{2 \cdot V}}{{1 + {{\rm{e}}^{\lambda \cdot ({D^{{\text{eq}}}} - \left| {d_k^{{\text{R}} \to {\text{T}}}} \right|)}}}}} \\ \begin{gathered} 0 \\ 0 \\ \end{gathered} \end{array}} \right] $$ (15) 其中
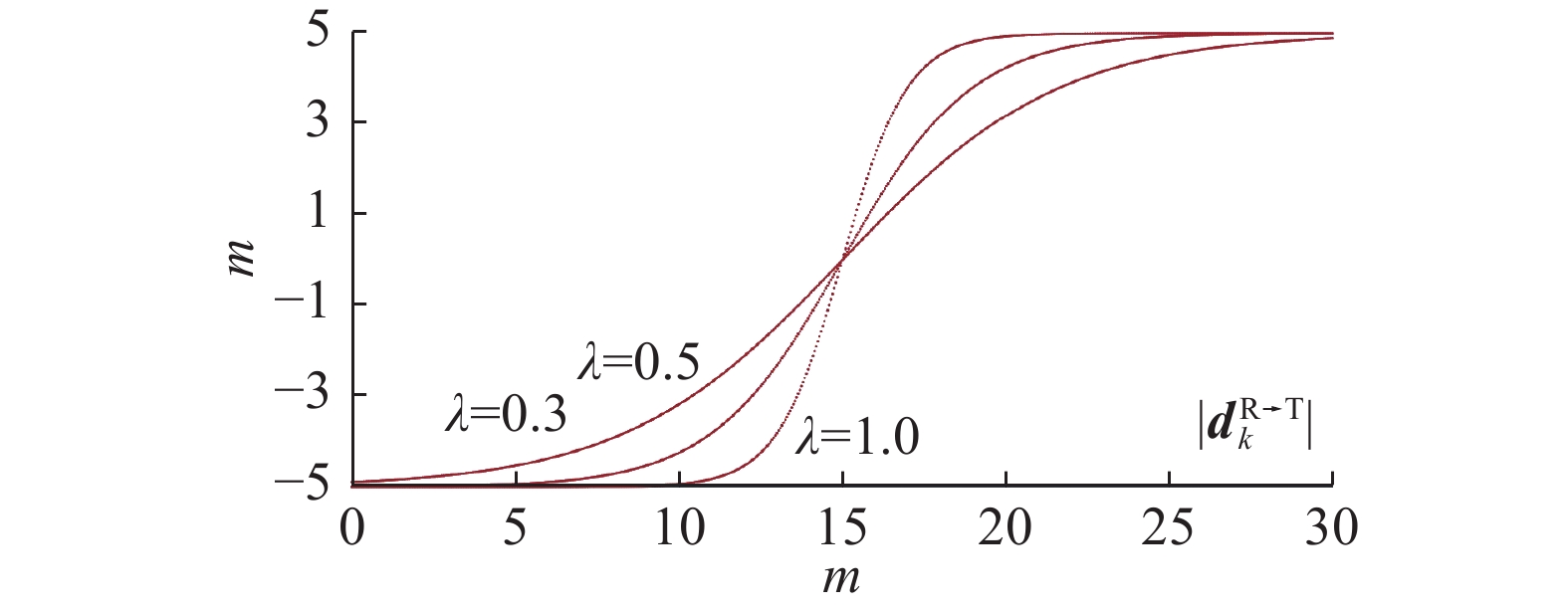
$ \lambda \in (0{\text{ }}1] $ 为转换速度参量，其值越大转换速度越快，$\left| {{\boldsymbol{d}}_k^{{\text{R}} \to {\text{T}}}} \right|$ 为k时刻机器人与目标之间的距离，$ {D^{{\text{eq}}}} $ 为机器人和目标间的平衡距离。图5为
$V = 5{\text{ m/s}}$ ，${D^{{\text{eq}}}}{{ = }}15{\text{ m}}$ ，$ \lambda $ 分别取0.3、0.5、 1，$\left| {{\boldsymbol{d}}_k^{{\text{R}} \to {\text{T}}}} \right|$ 为0~30连续变换时形成的$ \Delta x_k^{\text{f}} $ 曲线。
图 5$\Delta {\boldsymbol{x}}_k^{\text{f}}$ 随$\left| {{\boldsymbol{d}}_k^{{\text{R}} \to {\text{T}}}} \right|$ 变化曲线Fig. 5 Curve graph of$\Delta {\boldsymbol{x}}_k^{\text{f}}$ with$\left| {{\boldsymbol{d}}_k^{{\text{R}} \to {\text{T}}}} \right|$ 下载:
全尺寸图片
由图5可见，当机器人和目标距离小于平衡距离时，
$\Delta {\boldsymbol{x}}_k^{\text{f}}$ 为负值，以保证远离目标；当机器人和目标距离大于平衡距离时，$\Delta {\boldsymbol{x}}_k^{\text{f}}$ 为正值，以保证追随目标。在该值的控制下，能够实现机器人在恒定距离对目标的追随。若控制量只包含
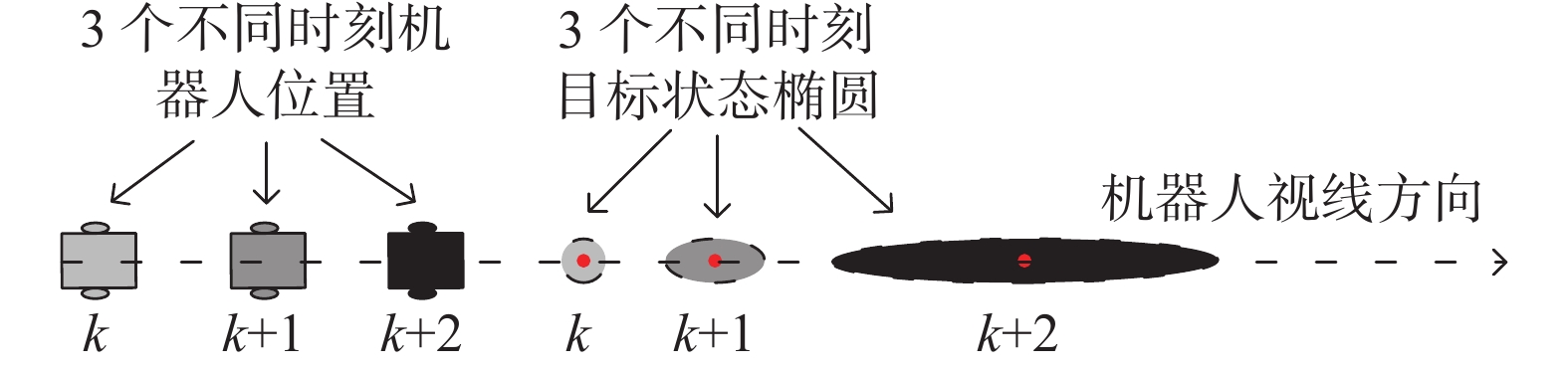
$\Delta {\boldsymbol{x}}_k^{\text{f}}$ 机器人将始终追随目标运动，由于单目视觉无法观测到距离信息，在机器人和目标的视线方向的目标不确定性将逐步增大，最终造成跟踪失败，如图6所示。图中显示了纯追随运动模式下3个时刻目标的不确定椭圆变化，目标在机器人视线方向上的不确定性逐步累积。为了克服该问题，机器人运动还需包含机动运动因素以产生足够的目标观测视差，从而实现深度估计，这种机动控制量称为可观性控制分量$\Delta {\boldsymbol{x}}_k^{\text{a}}$ ，下面介绍其生成方法。
图 6 纯追随模式下不同时刻，目标不确定椭圆变化图Fig. 6 Target uncertain elliptic change diagram at different times in pure follow-up mode下载:
全尺寸图片
$\Delta {\boldsymbol{x}}_k^{\text{a}}$ 优化有两点原则：首先，希望由式（9）更新后的目标协方差阵对应的分布椭圆体积最小；第二，希望$\left\| {\Delta {\boldsymbol{x}}_k^{\text{a}}} \right\|$ 最小以减少机动负担，因此，优化目标函数为Object:
$$\mathop {\min }\limits_{\Delta {\boldsymbol{x}}_k^{\rm{a}}} \left[\frac{1}{2} \cdot {V^t}(\Delta {\boldsymbol{x}}_k^{\rm{a}}) + \frac{1}{2} \cdot \Delta {\boldsymbol{x}}_k^{\rm{a'} } \cdot {\boldsymbol{B}} \cdot \Delta {\boldsymbol{x}}_k^{\rm{a}}\right] $$ (16) 其中，
$ {V^t} $ 为式（9）中${\boldsymbol{P}}_k^{\rm{t^ + }}$ 对应的位置不确定椭圆体积，${\boldsymbol{B}} > 0$ 为加权常量阵。因为：
$$\begin{gathered} \mathop {\min }\limits_{\Delta x_k^{\text{a}}} \left[\frac{1}{2} \cdot {V^t}(\Delta {\boldsymbol{x}}_k^{\text{a}})\right] \cong \mathop {\min }\limits_{\Delta {\boldsymbol{x}}_k^{\text{a}}} \left[tr({\boldsymbol{P}}_k^{\rm{t^ + }})\right] =\\ \mathop {\min }\limits_{\Delta {\boldsymbol{x}}_k^{\text{a}}} \left[{\rm{tr}}({\boldsymbol{P}}_k^{\rm{t^ - }} - {\boldsymbol{K}} \cdot {\boldsymbol{S}}_k^{\text{t}} \cdot {\boldsymbol{K}}')\right] \end{gathered}$$ (17) 又有：
$$\begin{gathered} \mathop {\min }\limits_{\Delta {\boldsymbol{x}}_k^{\text{a}}} \left[{\rm{tr}}\left({\boldsymbol{P}}_k^{\rm{t^ - }} - {\boldsymbol{K}} \cdot {\boldsymbol{S}}_k^{\text{t}} \cdot {\boldsymbol{K}}'\right)\right] = \\ \mathop {\min }\limits_{\Delta {\boldsymbol{x}}_k^{\text{a}}} \left[{\rm{tr}}\left({\boldsymbol{P}}_k^{\rm{t^ - }}\right) - tr\left({\boldsymbol{K}} \cdot {\boldsymbol{S}}_k^{\text{t}} \cdot {\boldsymbol{K}}'\right)\right] \end{gathered}$$ (18) 其中
${\boldsymbol{P}}_k^{\rm{t^ - }}$ 由式（5）确定，其值与机器人控制量无关，因此，式（18）可写成：$$\begin{gathered} \mathop {\min }\limits_{\Delta {\boldsymbol{x}}_k^{\text{a}}} \left[{\rm{tr}}({\boldsymbol{P}}_k^{\rm{t^ - }} - {\boldsymbol{K}} \cdot {\boldsymbol{S}}_k^{\text{t}} \cdot {\boldsymbol{K}}')\right] \cong - \mathop {\min }\limits_{\Delta {\boldsymbol{x}}_k^{\text{a}}} \left[{\rm{tr}}\left({\boldsymbol{K}} \cdot {\boldsymbol{S}}_k^{\text{t}} \cdot {\boldsymbol{K}}'\right)\right] =\\ \mathop {\max }\limits_{\Delta {\boldsymbol{x}}_k^{\text{a}}} \left[{\rm{tr}}\left({\boldsymbol{K}} \cdot {\boldsymbol{S}}_k^{\text{t}} \cdot {\boldsymbol{K}}'\right)\right] \end{gathered}$$ (19) 重写式（16）为
Object:
$$\begin{gathered} \mathop {\min }\limits_{\Delta {{x}}_k^{\rm{a}}} \left[\frac{1}{2} \cdot {V^t}(\Delta {\boldsymbol{x}}_k^{\rm{a}})\right] + \mathop {\min }\limits_{\Delta {{x}}_k^{\rm{a}}} \left[\frac{1}{2} \cdot \Delta {\boldsymbol{x}}_k^{\rm{a'} } \cdot {\boldsymbol{B}} \cdot \Delta {\boldsymbol{x}}_k^{\rm{a}}\right]\Rightarrow \\ \mathop {\max }\limits_{\Delta {{x}}_k^{\text{a}}} \left[{\rm{tr}}({\boldsymbol{K}} \cdot {\boldsymbol{S}}_k^{\text{t}} \cdot {\boldsymbol{K}}')\right] + \mathop {\min }\limits_{\Delta x_k^{\text{a}}} \left[\frac{1}{2} \cdot \Delta {\boldsymbol{x}}_k^{\rm{a'} } \cdot {\boldsymbol{B}} \cdot \Delta {\boldsymbol{x}}_k^{\text{a}}\right]\Rightarrow \\ \mathop {\max }\limits_{\Delta x_k^{\text{a}}} \left[{\rm{tr}}({\boldsymbol{K}} \cdot {\boldsymbol{S}}_k^{\text{t}} \cdot {\boldsymbol{K}}')\right] - \mathop {\max }\limits_{\Delta x_k^{\text{a}}} \left[\frac{1}{2} \cdot \Delta {\boldsymbol{x}}_k^{\rm{a'} } \cdot {\boldsymbol{B}} \cdot \Delta {\boldsymbol{x}}_k^{\text{a}}\right] \end{gathered}$$ 则最终可得目标函数为
Object:
$$ \mathop {\max }\limits_{\Delta x_k^{\text{a}}} \left[{\rm{tr}}({\boldsymbol{K}} \cdot {\boldsymbol{S}}_k^{\text{t}} \cdot {\boldsymbol{K}}')\right] - \mathop {\max }\limits_{\Delta x_k^{\text{a}}} \left[\frac{1}{2} \cdot \Delta {\boldsymbol{x}}_k^{\rm{a'} } \cdot {\boldsymbol{B}} \cdot \Delta {\boldsymbol{x}}_k^{\text{a}}\right] $$ (20) 根据式（10）有：
$$ \begin{gathered} {\rm{tr}}({\boldsymbol{K}} \cdot {\boldsymbol{S}}_k^{\text{t}} \cdot {\boldsymbol{K}}') =\\ {\rm{tr}}(({\boldsymbol{P}}_k^{\rm{t^ - }} \cdot {\boldsymbol{H}}_k^{\rm t \to z} \cdot {({\boldsymbol{S}}_k^{\rm{t^ - }})^{ - 1}}) \cdot {\boldsymbol{S}}_k^{\rm{t^ - }} \cdot ({\boldsymbol{P}}_k^{{t^ - }} \cdot {\boldsymbol{H}}_k^{\rm t \to z} \cdot {({\boldsymbol{S}}_k^{\rm{t^ - }})^{ - 1}})') = \\ {\rm{tr}}({\boldsymbol{P}}_k^{{t^ - }} \cdot {\boldsymbol{H}}_k^{\rm t \to z' } \cdot {({\boldsymbol{S}}_k^{\rm{t}})^{ - 1}} \cdot {\boldsymbol{H}}_k^{\rm t \to z} \cdot {\boldsymbol{P}}_k^{\rm{t^ - }}) \\ \end{gathered} $$ 其中
${\boldsymbol{S}}_k^{\text{t}} = {\boldsymbol{H}}_k^{\rm t \to z} \cdot {\boldsymbol{P}}_k^{\rm{t^ - }} \cdot {\boldsymbol{H}}_k^{\rm t \to z' } + {{\boldsymbol{R}}_k}$ ，则有：$$ \begin{gathered} {\rm{tr}}({\boldsymbol{K}} \cdot {\boldsymbol{S}}_k^{\text{t}} \cdot {\boldsymbol{K}}') =\\ {\rm{tr}}({\boldsymbol{P}}_k^{\rm{t^ - }} \cdot {\boldsymbol{P}}_k^{\rm{t^ - }} \cdot {\boldsymbol{H}}_k^{\rm t \to z'} \cdot {({\boldsymbol{H}}_k^{\rm t \to z} \cdot {\boldsymbol{P}}_k^{\rm{t^ - }} \cdot {\boldsymbol{H}}_k^{\rm t \to z' } + {{\boldsymbol{R}}_k})^{ - 1}} \cdot {\boldsymbol{H}}_k^{\rm t \to z}) \\ \end{gathered} $$ (21) 将式（21）代入式（20）可得目标函数最终形式为
Object:
$$ \begin{gathered} \mathop {\max }\limits_{\Delta x_k^{\text{a}}} \left[\frac{1}{2} \cdot {\rm{tr}}({({\boldsymbol{P}}_k^{\rm{t^ - }})^2} \cdot {\boldsymbol{H}}_k^{\rm t \to z' } \cdot {({\boldsymbol{H}}_k^{\rm t \to z} \cdot {\boldsymbol{P}}_k^{\rm{t^ - }} \cdot {\boldsymbol{H}}_k^{\rm t \to z' } + {{\boldsymbol{R}}_k})^{ - 1}} \cdot\right.\\ \left. {\boldsymbol{H}}_k^{\rm t \to z}) - \frac{1}{2} \cdot \Delta {\boldsymbol{x}}_k^{\rm{a'} } \cdot {\boldsymbol{B}} \cdot \Delta {\boldsymbol{x}}_k^{\text{a}}\right] \end{gathered}$$ (22) 对式（22）取
$\Delta {\boldsymbol{x}}_k^{\text{a}}$ 的偏导并令结果为0，整理可得$\Delta {\boldsymbol{x}}_k^{\text{a}}$ 的优化值为$$\begin{gathered} \Delta {\boldsymbol{x}}_k^{\text{a}} = \frac{1}{2} \cdot {{\boldsymbol{B}}^{ - 1}} \cdot \dfrac{\partial }{{\partial \Delta {\boldsymbol{x}}_k^{\text{a}}}}\left( {\rm{tr}}({{({\boldsymbol{P}}_k^{\rm{t^ - }})}^2} \cdot {\boldsymbol{H}}_k^{\rm t \to z' } \cdot \right.\\ \left.{{({\boldsymbol{H}}_k^{\rm t \to z} \cdot {\boldsymbol{P}}_k^{\rm{t^ - }} \cdot {\boldsymbol{H}}_k^{\rm t \to z' } + {{\boldsymbol{R}}_k})}^{ - 1}} \cdot {\boldsymbol{H}}_k^{\rm t \to z}) \right) \end{gathered}$$ (23) 下面给出式（23）的具体求解方法，在不产生歧义的情况下，将
${\boldsymbol{H}}_k^{\rm t \to z}$ 写成${\boldsymbol{H}}$ ，${\boldsymbol{P}}_k^{\rm{t^ - }}$ 写成${\boldsymbol{P}}$ 。假设k时刻机器人位置状态为
${\boldsymbol{x}}_k^{\rm W,r}$ ，目标位置状态为${\boldsymbol{x}}_k^{\rm W,t}$ ，机器人可观性控制量为$\Delta {\boldsymbol{x}}_k^{\rm W,a}$ ，则世界坐标系中从机器人到目标的向量${\boldsymbol{x}}_k^{\rm W,r \to t}$ 为$$ {\boldsymbol{x}}_k^{\rm W,r \to t} = {\boldsymbol{x}}_k^{\rm W,t} - ({\boldsymbol{x}}_k^{\rm W,r} + \Delta {\boldsymbol{x}}_k^{\rm W,a}) $$ (24) 此刻世界坐标系到机器人坐标系的旋转矩阵为
${\boldsymbol{R}}_k^{\rm W \to R}$ ，则机器人坐标系下指向目标的向量${\boldsymbol{x}}_k^{\rm R,r \to t}$ 为$$ {\boldsymbol{x}}_k^{\rm R,r \to t} = \left[ {\begin{array}{*{20}{c}} {x_k^{\rm R,r \to t}} \\ {y_k^{\rm R,r \to t}} \\ {z_k^{\rm R,r \to t}} \end{array}} \right] = {\boldsymbol{R}}_k^{\rm W \to R} \cdot {\boldsymbol{x}}_k^{\rm W,r \to t} $$ (25) 根据单目摄像机小孔成像模型有：
$$ {\boldsymbol{z}} = {\boldsymbol{h}}({\boldsymbol{x}}_k^{\rm R,r \to t}) = \frac{f}{{{z^{\rm R,r \to t}}}}\left[ {\begin{array}{*{20}{c}} {{s_u} \cdot {x^{\rm R,r \to t}}} \\ {{s_v} \cdot {y^{\rm R,r \to t}}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{u_0}} \\ {{v_0}} \end{array}} \right] $$ (26) 由偏导链式原则可知：
$$ {\boldsymbol{H}}(\Delta {\boldsymbol{x}}_k^{\text{a}}) = \frac{{\partial {\boldsymbol{h}}({\boldsymbol{x}}_k^{\rm R,r \to t})}}{{\partial \Delta {\boldsymbol{x}}_k^{\rm W,a}}} = \frac{{\partial {\boldsymbol{h}}({\boldsymbol{x}}_k^{\rm R,r \to t})}}{{\partial {\boldsymbol{x}}_k^{\rm R,r \to t}}} \cdot \frac{{\partial {\boldsymbol{x}}_k^{\rm R,r \to t}}}{{\partial {\boldsymbol{x}}_k^{\rm W,r \to t}}} \cdot \frac{{\partial {\boldsymbol{x}}_k^{\rm W,r \to t}}}{{\partial \Delta {\boldsymbol{x}}_k^{\rm W,a}}} $$ (27) 根据式（24）~（26）分别计算式（27）中各项整理可得：
$$ {\boldsymbol{H}}(\Delta {\boldsymbol{x}}_k^{\rm W,a}) = \frac{{\partial {\boldsymbol{h}}({\boldsymbol{x}}_k^{\rm R,r \to t})}}{{\partial \Delta {\boldsymbol{x}}_k^{\rm W,a}}}= - \frac{f}{{{z^{\rm R,r \to t}}}} \cdot {{\boldsymbol{H}}_{\text{1}}} \cdot {\boldsymbol{R}}_k^{\rm W \to R} $$ (28) 其中，
$$ {{\boldsymbol{H}}_{\text{1}}} = \left[ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {{s_u}}&0 \\ 0&{{s_v}} \end{array}}{ - \dfrac{1}{f} \cdot \left( {{\boldsymbol{h}}({\boldsymbol{x}}_k^{\rm R,r \to t}) - \left[ {\begin{array}{*{20}{c}} {{u_0}} \\ {{v_0}} \end{array}} \right]} \right)} \end{array}} \right] $$ (29) 将式（28）代入式（23）整理可得：
$$ \Delta {\boldsymbol{x}}_k^{\text{a}} = \frac{1}{2} \cdot {{\boldsymbol{B}}^{ - 1}} \cdot \dfrac{\partial }{{\partial \Delta {\boldsymbol{x}}_k^{\text{a}}}}\left( {{\rm{tr}}({{\boldsymbol{P}}_{\text{1}}} \cdot {{\boldsymbol{P}}_{\text{1}}} \cdot {{\boldsymbol{H}}_{\text{1}}}^\prime \cdot {{\boldsymbol{S}}_{\text{1}}}^{ - 1} \cdot {{\boldsymbol{H}}_{\text{1}}})} \right) $$ (30) 其中，
$$ {{\boldsymbol{S}}_{\text{1}}} = {{\boldsymbol{H}}_{\text{1}}} \cdot {{\boldsymbol{P}}_{\text{1}}} \cdot {{\boldsymbol{H}}_{\text{1}}}^\prime + {{\boldsymbol{R}}_{\text{1}}} $$ (31) $$ {{\boldsymbol{P}}_{\text{1}}} = {\boldsymbol{R}}_k^{\rm W \to R} \cdot {\boldsymbol{P}} \cdot {\boldsymbol{R}}_k^{\rm W \to R' } $$ (32) $$ {{\boldsymbol{R}}_{\text{1}}} = {{{{({z^{\rm R,r \to t}})}^2}} \mathord{\left/ {\vphantom {{{{({z^{R,r \to t}})}^2}} {{f^2}}}} \right. } {{f^2}}} \cdot {\boldsymbol{R}} $$ (33) 将式（30）表示的可观性控制量
$\Delta {\boldsymbol{x}}_k^{\text{a}}$ 写成分量形式并利用矩阵迹求导性质有：$$ \begin{gathered} \Delta x_{k,i}^{\text{a}} = \frac{1}{2} \cdot {{\boldsymbol{B}}^{ - 1}} \cdot \frac{\partial }{{\partial \Delta x_{k,i}^{\text{a}}}}\left( {{\rm{tr}}({{\boldsymbol{P}}_{{1}}} \cdot {{\boldsymbol{P}}_{{1}}} \cdot {{\boldsymbol{H}}_{{1}}'} \cdot {{\boldsymbol{S}}_{\text{1}}}^{ - 1} \cdot {{\boldsymbol{H}}_{\text{1}}})} \right)=\\ {\left. {{{\boldsymbol{B}}^{ - 1}} \cdot {\rm{tr}}\left( {{{\boldsymbol{P}}_{\text{1}}}^2 \cdot {{\boldsymbol{H}}_{\text{1}}'} \cdot {{\boldsymbol{S}}_{{1}}}^{ - 1} \cdot \frac{{\partial {{\boldsymbol{H}}_{{1}}}}}{{\partial \Delta x_{k,i}^{\text{a}}}}} \right)} \right|_{x_k^{W,r},x_k^{W,t}}} + \\ \frac{1}{2} \cdot {\left. {{{\boldsymbol{B}}^{ - 1}} \cdot {\rm{tr}}\left( {{{\boldsymbol{P}}_{\text{1}}}^2 \cdot {{\boldsymbol{H}}_{{1}}'} \cdot \frac{{\partial {{\boldsymbol{S}}_{{1}}}^{ - 1}}}{{\partial \Delta x_{k,i}^{\text{a}}}} \cdot {{\boldsymbol{H}}_{{1}}}} \right)} \right|_{x_k^{W,r},x_k^{W,t}}} \\ \end{gathered} $$ (34) 其中
$ \Delta x_{k,i}^{\text{a}} $ ，$ i{\text{ = 1,2,3}} $ 是控制向量$\Delta {\boldsymbol{x}}_k^{\text{a}}$ 的3个分量。计算式（29）对分量$ \Delta x_{k,i}^{\text{a}} $ 的偏导有：$$ \frac{{\partial {{\boldsymbol{H}}_{{1}}}}}{{\partial \Delta x_{k,i}^{\text{a}}}} = \left[ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} 0&0 \\ 0&0 \end{array}}\;\;{\dfrac{{- 1}}{f} \cdot {\boldsymbol{H}}(\Delta {\boldsymbol{x}}_k^{\rm W,a}) \cdot {{\boldsymbol{e}}_i}} \end{array}} \right] $$ (35) 同样，计算式（31）分量
$ \Delta x_{k,i}^{\text{a}} $ 的偏导有：$$\begin{gathered} \frac{{\partial {{\boldsymbol{S}}_{\text{1}}}^{ - 1}}}{{\partial \Delta x_{k,i}^{\text{a}}}} = \frac{1}{{{\rm det}\left({{\boldsymbol{S}}_{\text{1}}}\right)}}\left( {\rm det}\left(\frac{{\partial {{\boldsymbol{S}}_{\text{1}}}}}{{\partial \Delta x_{k,i}^{\text{a}}}}\right) \cdot {{\left(\frac{{\partial {{\boldsymbol{S}}_{\text{1}}}}}{{\partial \Delta x_{k,i}^{\text{a}}}}\right)}^{ - 1}} - \right.\\ \left.\left(\frac{{\partial {\rm det}\left({{\boldsymbol{S}}_{\text{1}}}\right)}}{{\partial \Delta x_{k,i}^{\text{a}}}}\right) \cdot {{\boldsymbol{S}}_{\text{1}}}^{ - 1} \right) \end{gathered}$$ (36) 将式（35）、（36）代入式（34）即可得到最优控制分量。
实现未知环境下基于单目视觉的机器人目标跟踪可观性控制需要完成以下3方面计算：首先，完成机器人同时定位于地图构建，第二，完成目标状态跟踪，第三，根据机器人和目标状态完成机器人控制量计算。计算复杂度主要集中在机器人SLAM过程中，由于机器人SLAM、目标跟踪和控制量生成在计算上是相互解耦的，因此可以选用运算效率较高的SLAM方法（FAST-SLAM等）。
6. 实验设计与验证分析
6.1 实验设计
1）仿真实验设计
下面通过仿真实验验证方法的有效性、准确性并分析影响目标跟踪准确性的因素。实验仿真环境为MATLAB2017，场景如图7所示。
图 7 仿真实验场景Fig. 7 Experiment scene of simulation下载:
全尺寸图片
实验场景为三维立体空间，其范围为：X: −25 m~25 m， Y: −25 m~25 m， Z: −10 m~10 m，在空间四周均匀地分布着环境特征点。相关实验参数配置如 表1所示。
表 1 实验参数配置表Table 1 Parameter configuration机器人控制标准差 摄像机内参/像素 图像像素尺寸/像素 观测标准差/像素 $\begin{gathered} \sigma \Delta \tilde x_k^{\text{r} }= [0.01{\text{ m } }\;0.01{\text{ m } }\;0.01{\text{ m } }\;0.01{\text{ m} }] \\ \sigma \Delta \tilde e_k^{\text{r} } = [0.02{\text{° } }0.02{\text{° } }0.02{\text{° } }] \\ \end{gathered}$ $ \begin{array}{l}{u}_{0}=320，{v}_{0}=240\\ {s}_{u}=320，{s}_{v}=320\end{array} $ $ \begin{gathered} u = 648 \\ v = 480 \\ \end{gathered} $ $ \sigma r{\text{ = }}[3{\text{ }}3] $ 2）实体机器人实验设计
实体机器人实验采用Turtlebot2型差动驱动平台，如图8所示。
图 8 Turtlebot2实体机器人平台Fig. 8 Turtlebot2 physical robot platform下载:
全尺寸图片
该平台配备单目摄像头，WiFi无线通信系统以及UWB（ultra wide band, UWB）室内定位系统。单目摄像头完成RGB图像获取，无线通信系统完成机器人端和服务器端的数据传输，UWB定位系统提供机器人和目标的定位真值。实验场景如图9所示。
图 9 实验场景Fig. 9 Experimental scene下载:
全尺寸图片
实验环境为室内环境，载有色块的机器人作为目标进行匀速直线运动，后方机器人作为跟踪机器人，环境中4个UWB基站作为定位标准点且位置已知。
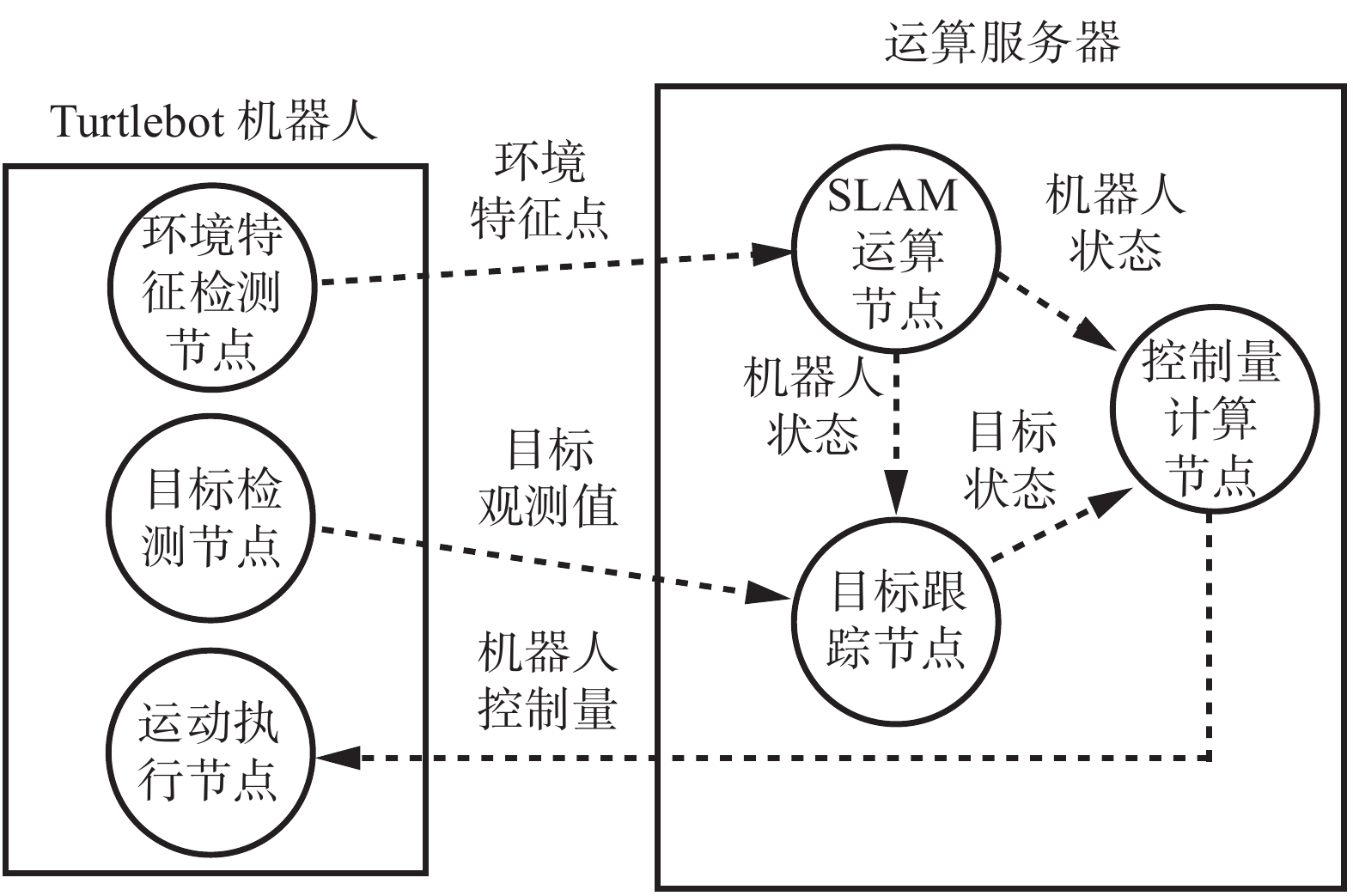
实验基于ROS（robot operating system, ROS）框架，节点及消息关系如图10所示。
图 10 ROS框架节点及消息关系实验场景Fig. 10 ROS framework node and message diagram下载:
全尺寸图片
考虑到图像数据量巨大不利于实时传输，以及Turtlebot上位机运算能力有限不利于计算等因素，系统将感知与执行，对象状态估计与控制量生成分别在机器人端和运算服务器端完成。Turtlebot机器人端包含感知节点和执行节点分别完成环境特征检测、目标检测和平台运动控制任务，其中环境特征为Sift特征点，目标检测利用Camshift方法实现。运算服务器端包含SLAM运算节点、目标跟踪节点和控制量计算节点分别利用第3、4、5节介绍方法实现机器人状态估计、目标状态估计和平台控制量生成任务。另外，由于该机器人运动学受非完整性约束限制，采用文献[26]所介绍的控制方法实现完整性约束到非完整性约束的转换控制。
6.2 仿真实验验证及分析
6.2.1 有效性实验分析
为了验证方法有效性，假设目标运动轨迹为直线，初始位置坐标为
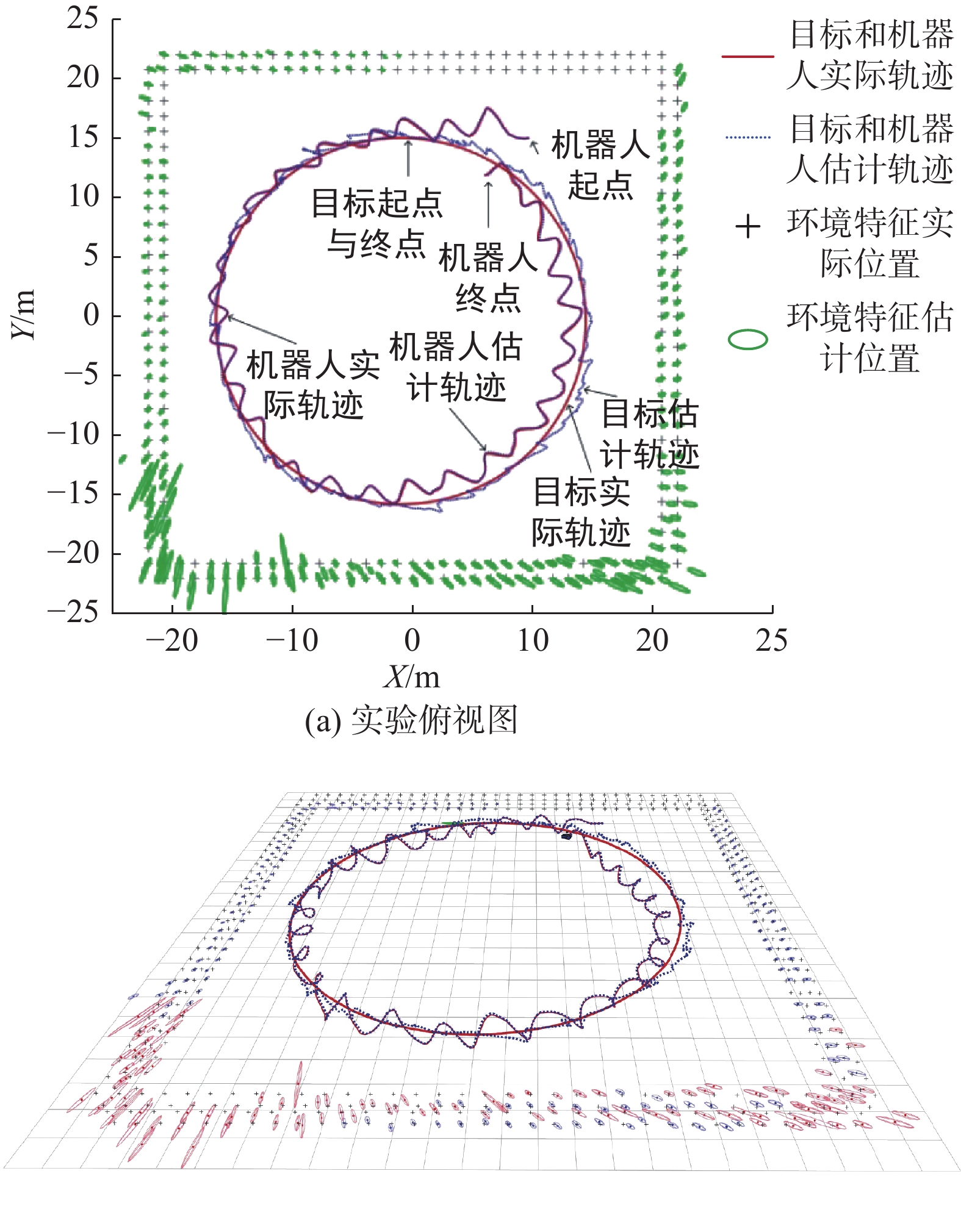
$ (15,15,1) $ ，速度恒定为2 m/s。机器人初始位置坐标为$ (15, - 15,1) $ 。机器人与目标的平衡距离设为$ {D^{{\text{eq}}}} = 10\;{\text{m}} $ ，机器人最大机动速度设为$ {v_{\max }} = 2.5\;{\text{m/s}} $ ，仿真共进行了300次迭代，时间步进为0.05 s。实验总体跟踪结果俯视图如图11所示。图中目标和机器人实际轨迹为实线，目标和机器人估计轨迹为虚线，十字点为环境特征实际位置，椭圆为环境特征状态估计分布椭圆。从图可见，实验开始时机器人距离目标较远，控制以追随为主，当机器人距离目标较近时可观性控制分量开始发挥作用，机器人做机动运动。从目标估计轨迹可见，刚开始由于机器人并未产生可观性机动，因此目标估计轨迹逐渐偏离实际轨迹，当机器人开始机动时，目标估计轨迹快速收敛到实际轨迹附近。
图 11 实验总体跟踪结果Fig. 11 Overall tracking results下载:
全尺寸图片
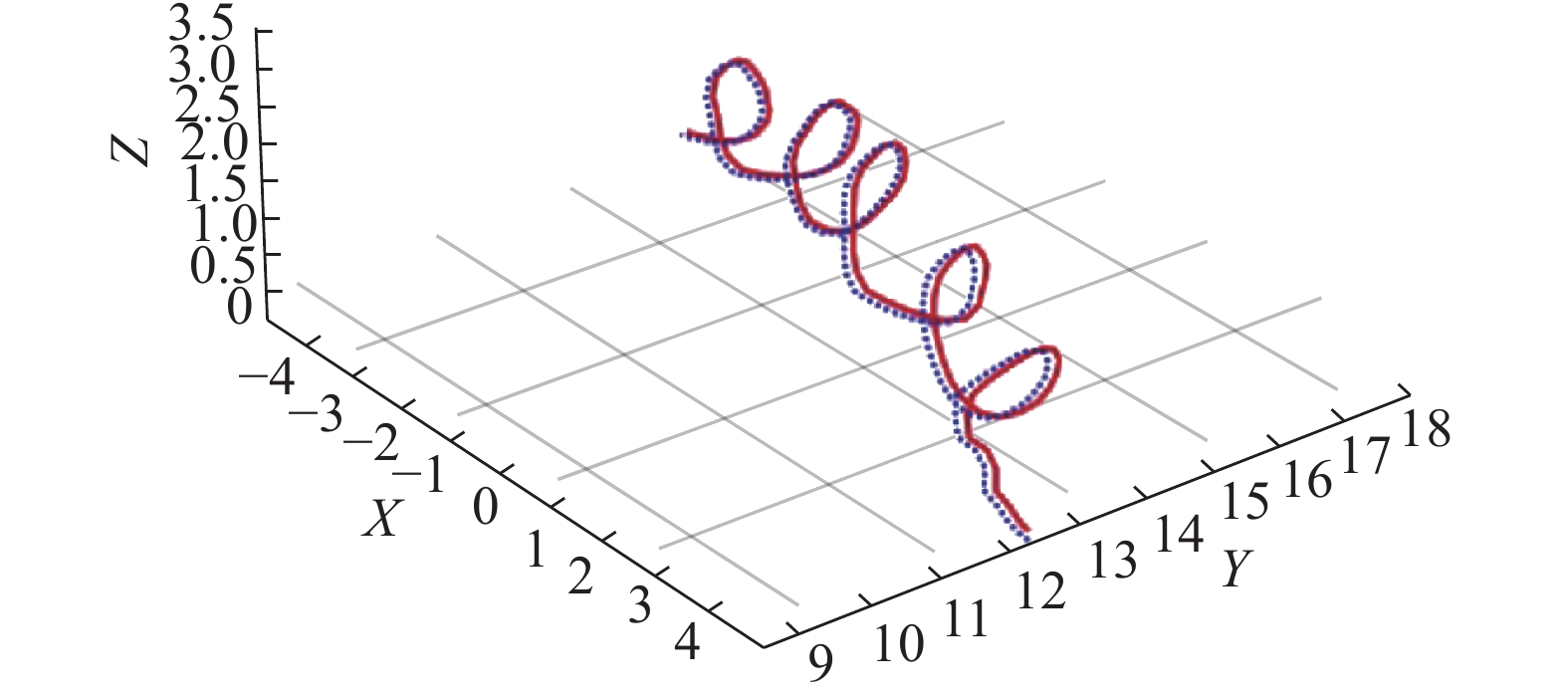
图12为三维空间中机器人实际和估计轨迹的局部放大图。由图可见，机器人的机动曲线为螺旋式曲线。机器人以此种轨迹对目标进行跟随有利于产生足够的单目观测视差，从而快速完成相对目标距离的估计。
图 12 三维空间机器人轨迹局部放大图Fig. 12 A local large robot trajectory in three dimensional space下载:
全尺寸图片
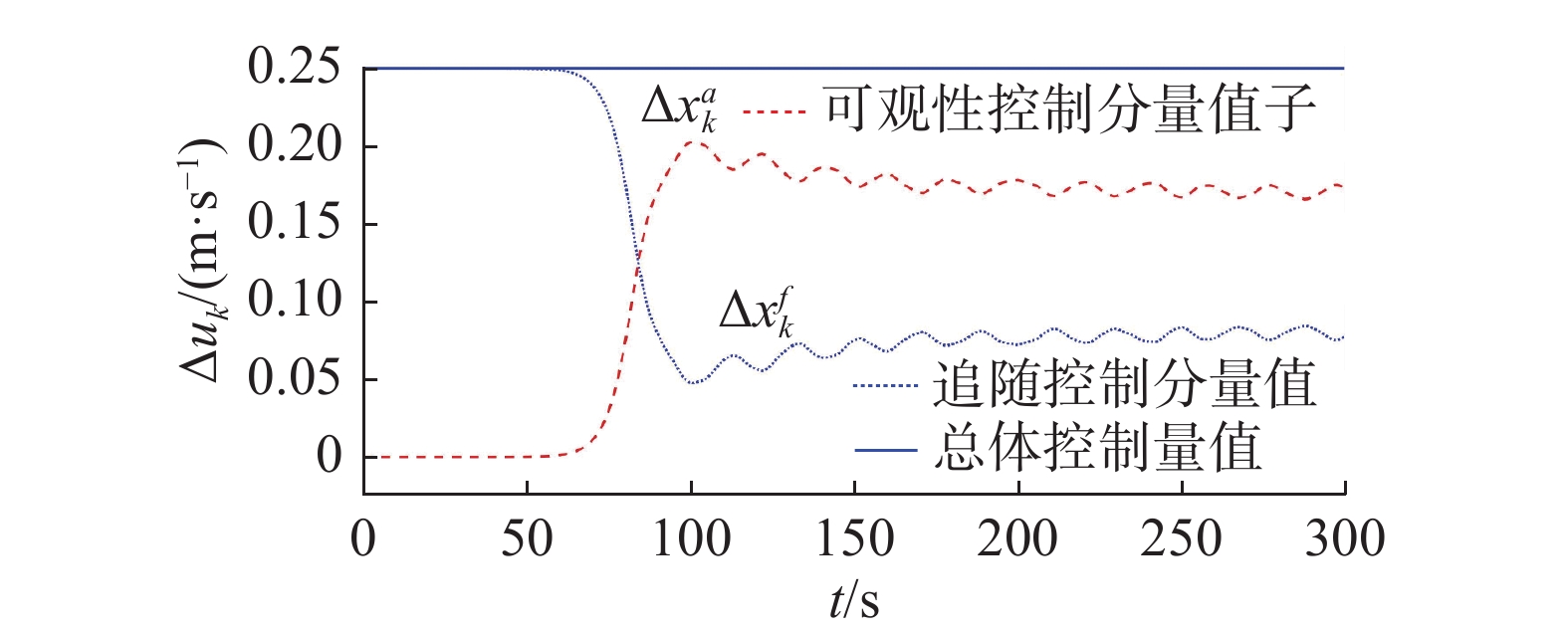
图13为实验中不同时刻机器人控制量成分值变化曲线。图中实线为不同时刻机器人速度控制值，细虚线为其中追随控制分量值，粗虚线为其中可观性控制分量值，由图可见，在跟踪初期0~85 s期间，机器人控制量的主要成分为追随控制分量。随着机器人靠近目标可观性控制分量开始发挥作用，在时段85~300 s期间，可观性控制成分大于追随控制成分，因此，在此期间机器人开始螺旋式机动运动，从而克服单目视觉深度观测值缺失的问题，快速实现目标位置状态估计。
图 13 不同时刻机器人控制分量变化曲线Fig. 13 The curve of control component of robot at different time下载:
全尺寸图片
图14为不同时刻机器人和目标各分量及位置估计误差曲线。
图 14 目标和机器人各分量及位置估计误差曲线Fig. 14 Estimation error curve of each components and position下载:
全尺寸图片
从图14(a)可见，在0~85 s期间，由于机器人并未进行可观性机动，因此，目标各分量及位置误差持续增加。在85~300 s期间，机器人开始机动运动，目标各分量及位置误差快速减小并始终保持在较低水平。从图14(b)可见，机器人各分量及位置估计始终较为准确，从图11可见，环境特征分布均匀且机器人在运动过程中有足够多的、准确性高的特征保持在其视野中，这些保证了较高的机器人定位精度。
图15为不同时刻，目标观测残差阵
${\boldsymbol{S}}_k^{\text{t}}$ 对应的不确定椭圆面积变化曲线。
图 15 不同时刻目标观测值不确定椭圆面积变化曲线Fig. 15 Target observation uncertain elliptical area change curve下载:
全尺寸图片
由图可见，在0~85 s期间，观测不确定椭圆面积变化很平稳，说明机器人对目标的前后时序观测视差变化较小，用来进行深度估计的信息量较少，因此，目标状态估计误差持续增大。在85 s，出现了一个较大跳变，此后机器人开始可观性机动运动，在此期间，观测不确定椭圆面积变化较为剧烈，这说明机器人在前后观测中存在较大视差，能够为目标深度估计提供足够多的信息量，从而保证了目标跟踪的准确性。
6.2.2 准确性实验及分析
为了验证方法的准确性，假设目标起点与终点均为
$ (0,15,1) $ ，目标实际运行轨迹为圆形，线速度为$ 2\;{\text{m/s}} $ 。机器人起点为$ (10,15,1) $ ，朝向为$(0,0,{\text{π}} )$ ，机器人与目标的平衡距离设为$ {D^{{\text{eq}}}}= 10\;{\text{m}} $ ，机器人最大机动速度设为$ {v_{\max }}= 2.5\;{\text{m/s}} $ ，仿真共进行了500次迭代，时间步进为0.05 s。实验总图跟踪结果如图16所示。
图 16 实验总体结果Fig. 16 Overall tracking results下载:
全尺寸图片
从结果可知，机器人和目标的估计轨迹和实际轨迹保持较高的一致性。
图17为机器人和目标轨迹及误差曲线。
图 17 机器人和目标轨迹及误差曲线Fig. 17 Robot , target trajectory and error curve下载:
全尺寸图片
上方两个子图为机器人和目标的实际与估计轨迹对比图，下方两个子图为不同时刻机器人和目标位置估计误差曲线图，从轨迹图可见，机器人和目标估计轨迹始终贴合实际轨迹。从误差曲线图可见，机器人和目标估计误差均保持在容差范围内。另外，在整个估计过程中机器人平均估计误差为0.202 m，目标平均估计误差为1.227 m，目标和机器人估计准确性相差一个数量级。
6.2.3 影响因素实验及分析
下面分别分析机器人定位精度、机器人机动程度两种因素对目标跟踪精度的影响。
假设机器人最大速度为
$ {v_{\max }} = 3.5\;{\text{m/s}} $ ，平衡距离$ {D^{{\text{eq}}}} = 10\;{\text{m}} $ 条件下，机器人位置估计在10种噪声干扰下得到的目标状态估计误差均值和方差曲线如图18所示。
图 18 机器人定位误差对目标定位精度影响曲线Fig. 18 Influence between robot and target localization accuracy下载:
全尺寸图片
由图可见，随着人为引入机器人定位噪声的增加，当加性机器人定位高斯白噪声的标准差为1时，目标定位误差均值为16.36，误差标准差为5.83。由此可见，目标定位精度与机器人定位精度呈现正相关性。
图19为假设平衡距离
$ {D^{{\text{eq}}}}{\text{ = }}10{\text{ m}} $ ，机器人最大速度$ {v_{\max }} $ 取10个不同值时对应的目标状态估计误差均值和方差曲线。
图 19 机动能力对目标定位精度影响曲线Fig. 19 Influence between robot maneuver ability and target localization accuracy下载:
全尺寸图片
由图可见，随着机器人最大运动速度
$ {v_{\max }} $ 的增大，目标状态估计准确性逐步提高并最终趋近于恒定值。说明目标定位精度与机器人机动能力成正相关性。6.3 实体机器人实验验证及分析
实体机器人实验中，目标初始位置坐标为
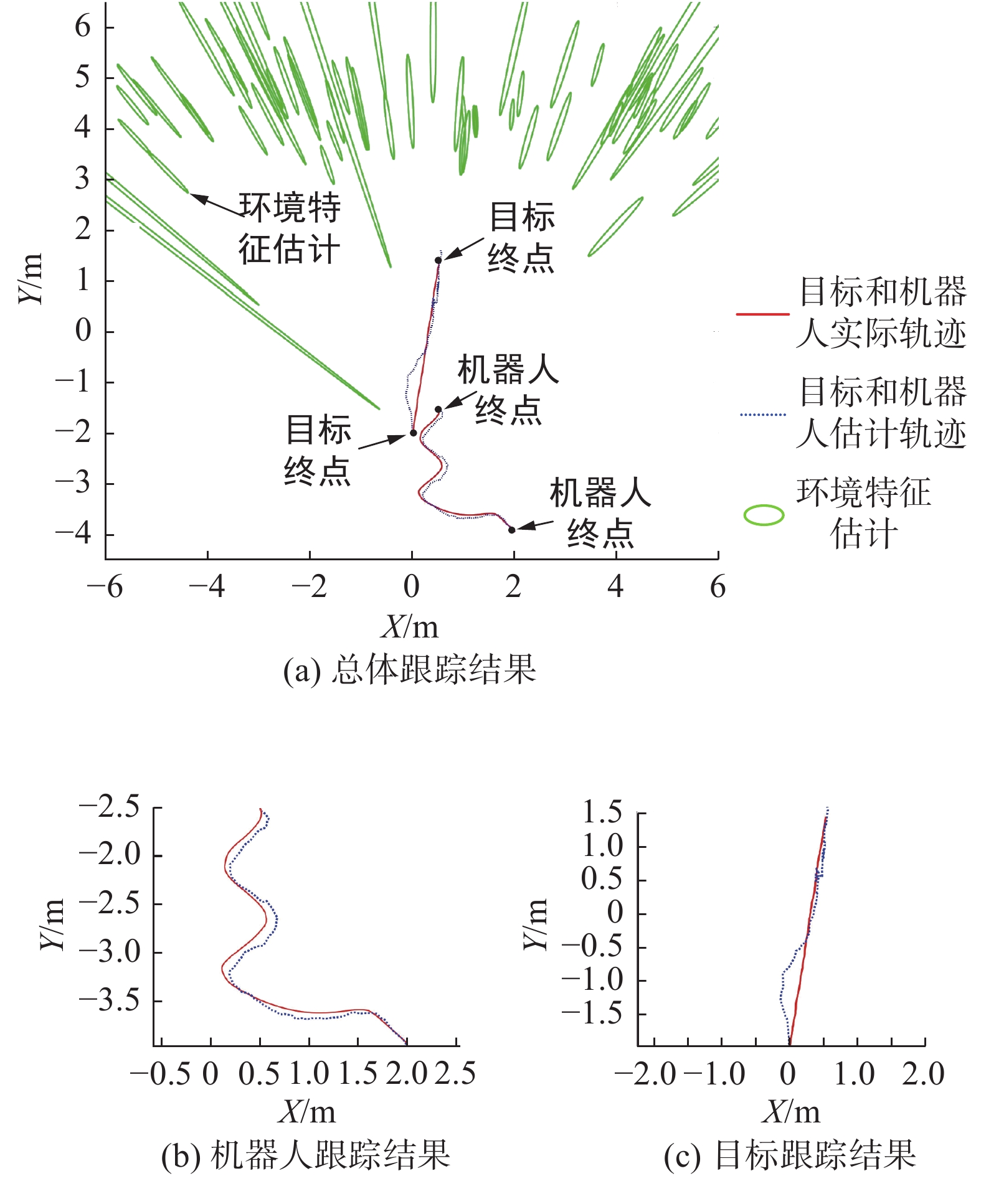
$ (0,{{ - }}2) $ ，速度恒定为0.07 m/s。机器人初始位置坐标为$ (2,{{ - }}4) $ 。机器人与目标的平衡距离设为${D^{{\text{eq}}}}{\text{ = }}1{\text{ m}}$ ，机器人最大机动速度为${v_{\max }}{\text{ = }}0.2{\text{ m/s}}$ ，实验共进行了60 s。需要说明的是，由于所选用的机器人平台较为简易，其单目摄像头视野狭窄，同时，易产生图像晃动问题。因此，在实验中有意将目标和机器人运动速度调慢，意在弱化条件，重点检验方法对目标状态，机器人状态估计的有效性和准确性。实体机器人跟踪结果如图20所示。
图 20 实体机器人跟踪结果Fig. 20 Physical robot tracking results下载:
全尺寸图片
由图20(b)可见，由于机器人和目标在相同平面运动，为了产生观测视差，机器人形成曲线运动轨迹，同时估计轨迹和实际轨迹一致。目标估计轨迹和实际轨迹开始一致性较差，之后逐步趋于一致，其原因在于初始阶段机器人以追随为主并未产生足够视差，当机器人接近目标后开始曲线运动，足够的视差使目标跟踪精度得以提高。
7. 结论
针对未知环境下基于单目视觉的移动机器人目标跟踪问题展开研究，提出了一种纯方位角观测条件下的机器人同时定位、地图构建与目标跟踪及控制方法。该方法在机器人单目视觉SLAM基础上，设计了扩展式卡尔曼滤波框架的目标跟踪算法，并将目标状态估计和机器人运动控制作为耦合问题进行处理，提出了基于目标协方差阵更新最大化的机器人优化控制方法。仿真和实体实验验证了方法的有效性和准确性，通过对实验数据的分析可知：目标跟踪准确性与机器人定位精度以及机器人机动能力大小成正相关性。接下来将针对障碍物条件下的估计和控制方法展开进一步研究。
-
图 1 贝叶斯网络模型
Fig. 1 Bayesian network model
下载:
全尺寸图片
图 2 系统总体框架
Fig. 2 Overall framework of the system
下载:
全尺寸图片
图 3 VSLAM处理流程
Fig. 3 Processing flow of VSLAM
下载:
全尺寸图片
图 4 优化控制量生成过程
Fig. 4 Generation process of optimal control value
下载:
全尺寸图片
图 5
$\Delta {\boldsymbol{x}}_k^{\text{f}}$ 随$\left| {{\boldsymbol{d}}_k^{{\text{R}} \to {\text{T}}}} \right|$ 变化曲线Fig. 5 Curve graph of
$\Delta {\boldsymbol{x}}_k^{\text{f}}$ with$\left| {{\boldsymbol{d}}_k^{{\text{R}} \to {\text{T}}}} \right|$ 下载:
全尺寸图片
图 6 纯追随模式下不同时刻，目标不确定椭圆变化图
Fig. 6 Target uncertain elliptic change diagram at different times in pure follow-up mode
下载:
全尺寸图片
图 7 仿真实验场景
Fig. 7 Experiment scene of simulation
下载:
全尺寸图片
图 8 Turtlebot2实体机器人平台
Fig. 8 Turtlebot2 physical robot platform
下载:
全尺寸图片
图 9 实验场景
Fig. 9 Experimental scene
下载:
全尺寸图片
图 10 ROS框架节点及消息关系实验场景
Fig. 10 ROS framework node and message diagram
下载:
全尺寸图片
图 11 实验总体跟踪结果
Fig. 11 Overall tracking results
下载:
全尺寸图片
图 12 三维空间机器人轨迹局部放大图
Fig. 12 A local large robot trajectory in three dimensional space
下载:
全尺寸图片
图 13 不同时刻机器人控制分量变化曲线
Fig. 13 The curve of control component of robot at different time
下载:
全尺寸图片
图 14 目标和机器人各分量及位置估计误差曲线
Fig. 14 Estimation error curve of each components and position
下载:
全尺寸图片
图 15 不同时刻目标观测值不确定椭圆面积变化曲线
Fig. 15 Target observation uncertain elliptical area change curve
下载:
全尺寸图片
图 16 实验总体结果
Fig. 16 Overall tracking results
下载:
全尺寸图片
图 17 机器人和目标轨迹及误差曲线
Fig. 17 Robot , target trajectory and error curve
下载:
全尺寸图片
图 18 机器人定位误差对目标定位精度影响曲线
Fig. 18 Influence between robot and target localization accuracy
下载:
全尺寸图片
图 19 机动能力对目标定位精度影响曲线
Fig. 19 Influence between robot maneuver ability and target localization accuracy
下载:
全尺寸图片
图 20 实体机器人跟踪结果
Fig. 20 Physical robot tracking results
下载:
全尺寸图片
表 1 实验参数配置表
Table 1 Parameter configuration
机器人控制标准差 摄像机内参/像素 图像像素尺寸/像素 观测标准差/像素 $\begin{gathered} \sigma \Delta \tilde x_k^{\text{r} }= [0.01{\text{ m } }\;0.01{\text{ m } }\;0.01{\text{ m } }\;0.01{\text{ m} }] \\ \sigma \Delta \tilde e_k^{\text{r} } = [0.02{\text{° } }0.02{\text{° } }0.02{\text{° } }] \\ \end{gathered}$ $ \begin{array}{l}{u}_{0}=320，{v}_{0}=240\\ {s}_{u}=320，{s}_{v}=320\end{array} $ $ \begin{gathered} u = 648 \\ v = 480 \\ \end{gathered} $ $ \sigma r{\text{ = }}[3{\text{ }}3] $ -
[1] 蔡自兴, 邹小兵. 移动机器人环境认知理论与技术的研究[J]. 机器人, 2004, 26(1): 87–91. doi: 10.3321/j.issn:1002-0446.2004.01.019 CAI Zixing, ZOU Xiaobing. Research on environmental cognition theory and methodology for mobile robots[J]. Robot, 2004, 26(1): 87–91. doi: 10.3321/j.issn:1002-0446.2004.01.019 [2] YANG Nan, WANG Rui, GAO Xiang, et al. Challenges in monocular visual odometry: photometric calibration, motion bias, and rolling shutter effect[J]. IEEE robotics and automation letters, 2018, 3(4): 2878–2885. doi: 10.1109/LRA.2018.2846813 [3] WANG C C, THORPE C, THRUN S, et al. Simultaneous localization, mapping and moving object tracking[J]. The international journal of robotics research, 2007, 26(9): 889–916. doi: 10.1177/0278364907081229 [4] 伍明, 李琳琳, 孙继银. 基于概率数据关联交互多模滤波的移动机器人未知环境下动态目标跟踪[J]. 机器人, 2012, 34(6): 668–679. doi: 10.3724/SP.J.1218.2012.00668 WU Ming, LI Linlin, SUN Jiyin. PDA-IMM based moving object tracking with mobile robots in unknown environments[J]. Robot, 2012, 34(6): 668–679. doi: 10.3724/SP.J.1218.2012.00668 [5] MUNARO M, LEWIS C, CHAMBERS D, et al. RGB-D human detection and tracking for industrial environments[M]//Intelligent Autonomous Systems 13. Cham: Springer International Publishing, 2015: 1655−1668. [6] ZHANG Rui, WANG Zhaokui, ZHANG Yulin. Astronaut visual tracking of flying assistant robot in space station based on deep learning and probabilistic model[J]. International journal of aerospace engineering, 2018, 2018: 1–17. [7] CASTLER O, MURRAYDW. Object recognition and localization while tracking and mapping[C]// Proceedings of 8th IEEE International Symposium on Mixed andAugmented Reality. Orlando, IEEE, 2009: 179−180. [8] KLEIN G, MURRAY D. Parallel tracking and mapping for small AR workspaces[C]// Proceedings of6th IEEE and ACM International Symposium on Mixed and Augmented Reality. Nara, IEEE, 2007: 225−234. [9] DE OLIVEIRA D CB, DE SOUZA DA SILVA R L. Moving object tracking for SLAM-based augmented reality[J]. Journalof mobile multimedia, 2021, 17(4): 577–602. [10] DAI W, ZHANG Y, ZHENG Y, et al. RGB-D SLAM with moving object tracking in dynamic environments[J]. IET cyber-systems and robotics, 2021, 3(4): 11. [11] LI Guihai, CHEN Songlin. Visual slam in dynamic scenes based on object tracking and static points detection[J]. Journal of intelligent & robotic systems, 2022, 104(2): 1–10. [12] CIVERA J, DAVISON A J, MONTIEL J M M. Inverse depth parametrization for monocular SLAM[J]. IEEE transactions on robotics, 2008, 24(5): 932–945. doi: 10.1109/TRO.2008.2003276 [13] DISSANAYAKE M W M G, NEWMAN P, CLARK S, et al. A solution to the simultaneous localization and map building (SLAM) problem[J]. IEEE transactions on robotics and automation, 2001, 17(3): 229–241. doi: 10.1109/70.938381 [14] WANGSIRIPITAK S, MURRAY D W. Avoiding moving outliers in visual SLAM by tracking moving objects[C]// Proceedings of IEEE International Conference on Robotics and Automation. Kobe, IEEE, 2009: 375−380. [15] MIGLIORE D, RIGAMONTI R, MARZORATI D, et al. Use a single camera for simultaneous localization and mapping with mobile object tracking in dynamic environments[C]//Proceedings of IEEE International Conference on Robotics and Automation, Kobe, Japan. IEEE, 2009: 889−895 [16] BESCOS B, CAMPOS C, TARDÓS J D, et al. DynaSLAM II: tightly-coupled multi-object tracking and SLAM[J]. IEEE robotics and automation letters, 2021, 6(3): 5191–5198. doi: 10.1109/LRA.2021.3068640 [17] LIU Yuzhen, LIU Jiacheng, HAO Yun, et al. A switching-coupled backend for simultaneous localization and dynamic object tracking[J]. IEEE robotics and automation letters, 2021, 6(2): 1296–1303. doi: 10.1109/LRA.2021.3056072 [18] SUALEH M, KIM G W. Semantics aware dynamic SLAM based on 3D MODT[J]. Sensors (Basel, Switzerland), 2021, 21(19): 6355. doi: 10.3390/s21196355 [19] LIU Jiacheng, MENG Ziyang, YOU Zheng. A robust visual SLAM system in dynamic man-made environments[J]. Science China technological sciences, 2020, 63(9): 1628–1636. doi: 10.1007/s11431-020-1602-3 [20] OH R, SHIYifang, CHOI J W. A hybrid Newton-raphson and particle swarm optimization method for target motion analysis by batch processing[J]. Sensors (Basel, Switzerland), 2021, 21(6): 2033. doi: 10.3390/s21062033 [21] ZHUK R S. Automatic detection and tracking the moving objects observed by an unmanned aerial vehicles video camera[J]. Informatics, 2021, 18(2): 83–97. doi: 10.37661/1816-0301-2021-18-2-83-97 [22] WATANABE Y. Stochastically optimized monocular vision-based navigation and guidance[D]. USA: Georgia Institute of Technology, 2008: 57. [23] KIM J, ROCK S. Stochastic feedback controller design considering the dual effect[J]//AIAA Guidance, Navigation, and Control Conference and Exhibit. Keystone, Colorado. Reston, Virginia: AIAA, 2006: 6090. [24] SCHÖLLERC, ARAVANTINOS V, LAY F, et al. What the constant velocity model can teach us about pedestrian motion prediction[J]. IEEE robotics and automation letters, 2020, 5(2): 1696–1703. doi: 10.1109/LRA.2020.2969925 [25] ZHANG Z. A flexible new technique for camera calibration[J]. IEEE transactionson pattern analysis and machine intelligence, 2000, 22(11): 1330–1334. doi: 10.1109/34.888718 [26] DAI Y, LEE S G. The leader-follower formation control of non-holonomic mobile robots[J]. International journal of control, automation and systems, 2012, 10(2): 350–361. doi: 10.1007/s12555-012-0215-x
