随着5G的普及和6G的开发，大带宽无线通信让大规模共位密集编队卫星群的组建成为了可能。甚至是原本只能依赖晶片通信总线和接线式的通信，在不久的未来也可以通过大带宽无线通信互联。人工智能技术的快速发展也让卫星群中的各个子卫星拥有的自主能力持续提高。共位密集编队卫星群将原来的一颗重型卫星的各个子系统拆分，分装进多个小型卫星中，利用大带宽无线通信互联，并且带宽和信号延迟不亚于实体IO。在无线通信快速发展的大背景下，课题将通过当前相关关键技术的研究进展，探讨共位编队卫星的智能系统特性与优势，并由此引出共位编队卫星群的可行性和大致开发方向。

共位密集编队技术的发展对未来的军事和商用航天领域有着重要的意义。当一颗重型卫星的各个子系统被拆分成为共位编队中分散布置并且可以随时替换的多个子卫星时，能够大大降低整个系统的发射成本和维护成本。小型的子卫星可以通过堆叠充分利用运载火箭的整流罩空间，战时可以快速补充在轨战斗力。故障的子卫星再入大气后，编队中的大部分功能任可以保留，并且随后即可补充。同时，编队内的子卫星也可以作为执行攻击等命令的单位，整个共位卫星编队有着很强的灵活性和可编辑性。模块化的系统也能够大幅度提高卫星的生产效率，短时间内就可以大量地发射。在商用领域这一技术也大大降低了企业的运营风险，不会因为一个子系统的故障而报废整个系统。

就共位编队本身来说，十米级间距的共位密集编队可以极大程度上改善以往因为间距较远所带来的问题。比如，距离较远各卫星轨道六根数不同、受到的摄动不同，因此随着时间的推移编队难以保持。小间距密集编队各卫星间的轨道根数相近、摄动几乎相同，所以保持编队所消耗的推进剂更少，有利于长时间执行任务。

1.   共位监测卫星星载智能系统研究现状及分析

1.1   智能星载芯片系统硬件设计研究现状及分析

在硬件方面，星载计算机由于受制于恶劣的使用环境普遍存在算力不足的问题，难以实现在轨深度学习等在轨复杂运算。不过近些年来随着半导体制程的不断进步，各种计算芯片的计算性能也随着增强。目前小型卫星的星载芯片系统大多基于FPGA+ARM开发，FPGA在航空航天领域有着极为广泛的应用。在航天领域，基于FPGA的姿态控制、卫星内部总线（如1553B、CAN等）控制、CNN网络的卷积计算加速、高分辨率图像处理、星间加解密通信及数据传输等方向有着大量的研究与应用。

相关行业的先进单位基于FPGA在航天领域的应用做了大量的研究，在姿态精确控制、通信、硬件运算加速、图像处理等领域都取得了令人瞩目的成果^[1-2]。FPGA芯片可以根据不同任务的需要进行深度定制，芯片内有大规模的逻辑门阵列，并行运算能力突出，相比单片机有着极强的IPC性能。FPGA芯片非常适合进行信号处理、元件桥接、人工智能运算等工作^[3]。

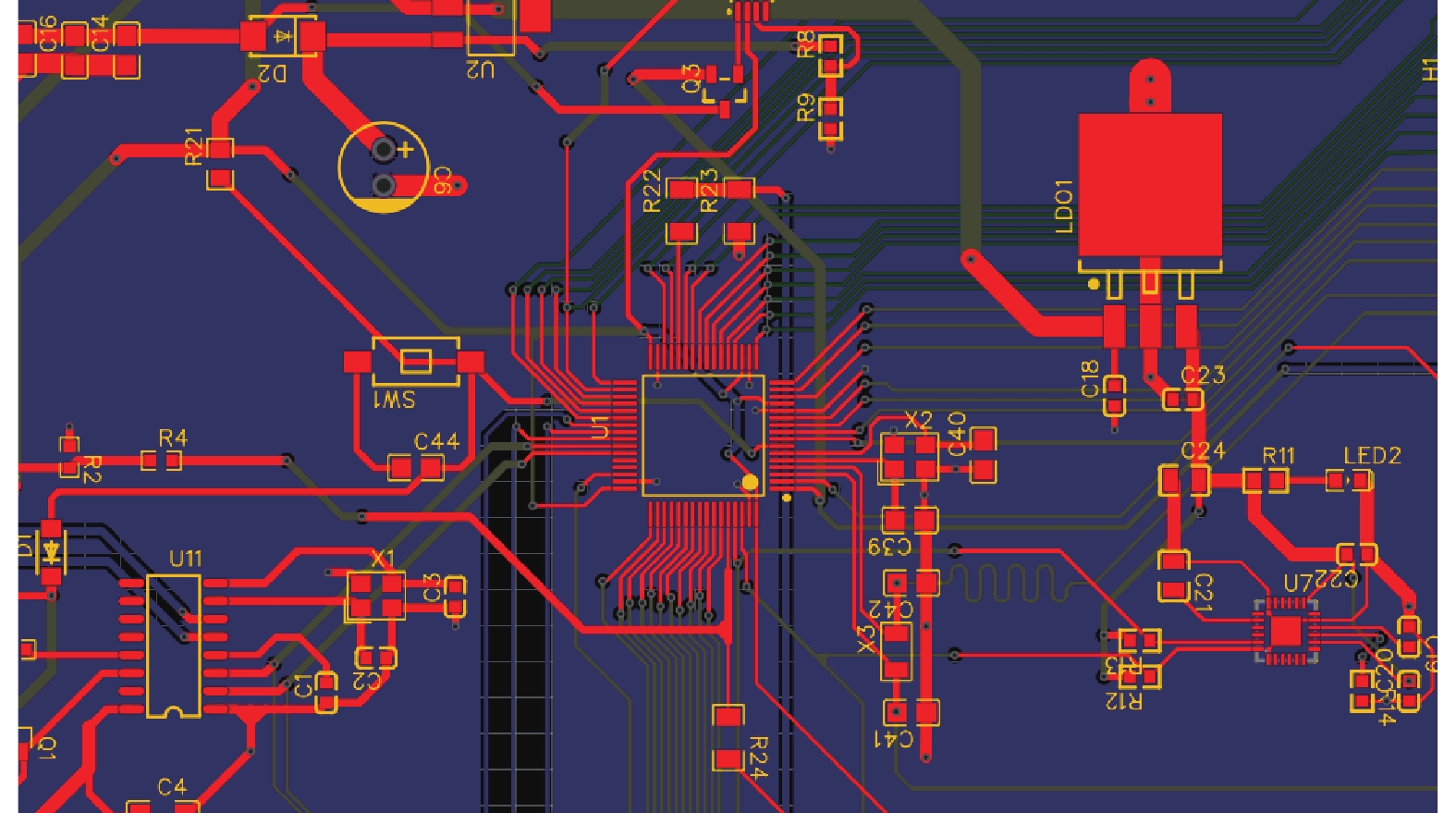
随着大规模集成电路制造技术的发展，精简指令集架构（如ARM）处理器的性能也随着增强。ARM处理器普遍有着IO资源丰富、逻辑运算能力强大的优点，并且能够集成大规模的流处理单元以提高并行计算能力，可拓展性极强。图1所示为ARM处理器与星载陀螺仪集成设计的PCB。其中Cortex-M系列内核以其高能耗比、开发便捷的特点被广泛应用于人工智能运算领域。尤其是2017年发布的Cortex-M7内核更是集成了L1缓存（指令及数据缓存）、分支预测单元等以往CPU上才有的模块，单片机的特性也越来越向高性能运算靠拢。德州仪器、意法半导体等都基于Cortex内核开发出了一系列性能优良价格低廉的单片机，这些单片机被广泛地应用于人工智能、航空航天、数控加工等大量高精尖领域。ARM处理器在航天领域的应用和研究更是在千禧年初就已经开始了，随着ARM处理器的发展和完善，其在星载计算领域的地位在近几年也越来越重要。

图  1  ARM处理器与星载陀螺仪集成的PCB

Fig.  1  PCB integrated with ARM processor and spaceborne gyroscope

下载: 全尺寸图片

2017年，Nvidia首次在Volta架构的GV100核心中将硬件张量计算单元Tensor Core整合到GPU中，并在之后的Turing架构和Ampere架构中沿用。以深度学习模型训练中常用的keras库为例，其核心的GEMM运算在Tensor Core的加速下相比上一代架构Pascal有着8~9倍的提升。在解决好功耗问题后，未来此类高性能GPU可以与ARM等架构整合并用于星上模型训练，让航天器获得更加高效的实时学习能力，大幅度地摆脱对地面的依赖。这也将是航天器未来在无测控协同深空探测任务中所需要具备的条件之一。

1.2   星载系统智能化研究现状及分析

人工智能在控制领域应用的重要性日渐凸显，以美国为代表的一些国家甚至直接将“保证人工智能领域领先状态”写入到行政命令中，大力扶持。当今，随着上述半导体行业的发展进步，星载计算机的算力随之快速增强。图2所示为星载芯片系统智能化发展历程。

图  2  星载芯片系统智能化发展历程

Fig.  2  Developmental history of the onboard chip system

下载: 全尺寸图片

以深度学习、强化学习为代表的下一代航天器人工智能控制技术势必能够由“地面训练，星上使用”逐步转向“星上学习，星上使用”。新一代智能自适应容错控制将具备更强的任务规划和姿轨跟踪及控制能力，胜任更加复杂的任务^[4-5]。现今世界上主流的各类型航天器控制模型普遍具有时变、非线性、多变量的特点。并且复杂的任务，执行任务的航天器具有更复杂的结构设计，其在调姿及变轨的时候也会有更加复杂的执行扰动和难以识别的耦合，人工智能控制高鲁棒性的优势就凸显出来了^[6-7]。

学习、推理、决策是人工智能控制系统所具备的基本能力。卫星能够主动适应任务环境的变化，仅依靠自身算力进行快速自适应控制策略调整是星载计算领域研究推进的大方向。人工智能飞控单元相比传统的飞控系统具备的优势如表1所示。

智能体的自主控制是一个智能感知、智能决策、智能控制的闭环，实现航天器的高度智能化先进的信号处理方法、计算系统设计以及控制策略等方面都是必不可少的，不然就会因为木桶效应使得整个系统应用某一部分的缺陷导致无法得到预期的效果。诸如强化学习这种机器学习的方法，主要用于解决智能体与环境的交互问题，描述和优化智能体在“实践”过程中的学习策略。航天器在执行任务时的环境是时变的，不合适的优化算法可能会导致系统陷入到局部最优解当中，致使后续的监测效果不佳甚至出错。因此近些年对智能算法的改进也成为了许多学者的工作方向。未来数年的航天器智能化也会依赖深度学习进行地面数据训练，利用先进通信技术实现地面−轨道的双向迁移学习是一项较为关键的技术。将地面预训练模型锁定后，发射入轨后在执行任务的过程中利用星上算力进行迁移学习，对全连接层以及部分解锁的卷积基等进行在轨训练。比如谷歌开发的超深卷积神经网络InceptionResNetV2深度高达572层，使用全球的互联网样本进行训练，其Top-1和Top-5精度分别可达0.803和0.953。这一类的预训练网络可以作为迁移学习模型对基础特征进行准确的判断，从而避免实际任务进行中可采集样本较少使模型在训练过程中出现过拟合。在轨训练所能采集的数据集较少，难以提取基础特征，因此需要拆分训练模型，分别在地面对基础任务特征以及在轨对具体任务特征进行训练。如图3所示为星载智能系统的架构简要示意图。

图  3  星载智能系统架构示意

Fig.  3  Onboard intelligent system architecture

下载: 全尺寸图片

根据上述的诸多问题，国内外许多机构、院所的学者们进行了大量的研究，提出了的开创性结论和相关解决方法。自2016年开始，美国商业航天公司SpaceX和美国国防高级研究计划局（DARPA）联合研制的猎鹰9号系列运载火箭实现了在线智能监测与轨迹规划，并利用该技术成功实现了芯一级和助推级的动力载入回收^[12-13]。智能控制系统让猎鹰9号系列运载火箭的发射成本和成功率实现了前所未有的突破。

2.   共位监测卫星星间智能协同控制研究现状及分析

2.1   智能共位协同编队卫星群的研究现状及分析

编队智能化这一课题主要有3点显著特征：1）抽象数据搜索引导；2）基于抽象数据做出判断；3）分布式智能体卫星间能够实现一定程度上任务并行处理。从计算机科学初的通用线性问题求解器到现如今的专家系统和智能决策支持系统，都利用了人类在任务领域的相关经验^[14-15]。然而所谓经验是一个模糊抽象、非线性、数据量庞大的概念。智能化共位协同编队的主要特征如表2所示。

未来共位卫星群任务的关键就是实现分布式多智能体协同控制技术的应用。而卫星智能协同控制的关键技术及技术难点主要包括任务协调调度、路径规划、多星协同状态监测3个主要方面^[16-18]。其关键技术主要依赖于超深网络的特征提取和任务规划以及高效算法在包含深度网络的系统中对协同控制策略的规划。

球场上运动员之间默契的配合，手术台上外科医生们的密切配合都依赖于个体之间的经验，能够将所谓经验数据化就是智能协同控制系统最显著的特征。在共轨位卫星编队中智能监测卫星的关键目标就是通过利用全局/局部信息共享和邻近代理分布式的方式来达到任务所需的多智能体协同行为。

共位编队中的卫星任务的协同调度是一大难点和关键技术。传统的任务调度方式主要有两种。其一是以BIE为代表的优先级分配。在一次任务中，编队监测卫星对每颗卫星预先的建模进行评估以确定其在任务协调中的权重，或者每颗卫星通过贪婪策略评估自身权重与其他卫星进行比对，以此来协调每颗卫星在任务中所需执行的最佳指令。这种策略的优势就在于在算力不足的星载系统上也能使各卫星有效地协同完成任务，较小的数据量也能够让该策略具有很好的通信时效性和容错能力，但是无论由监测星评估还是各星自身评估都会在不同程度陷入局部最优解，稳定性欠佳。其二是卫星网络调度协议，由优先级协调策略发展而来。这种策略不以预先建模为评估原点，而是任务调度分为监测卫星接收任务指令、编队各星对任务各项进行申请、指令下达3个阶段进行，在任务协调阶段建立临时能力集，以此为指标进行具体分配。作为优先级确定权重策略的一种改进，这种策略仍然在一定程度上存在容易陷入局部最优解的问题，但是其依赖先进网络协议的特性使其能够在中小规模的卫星编队中实现全局最优任务协同。

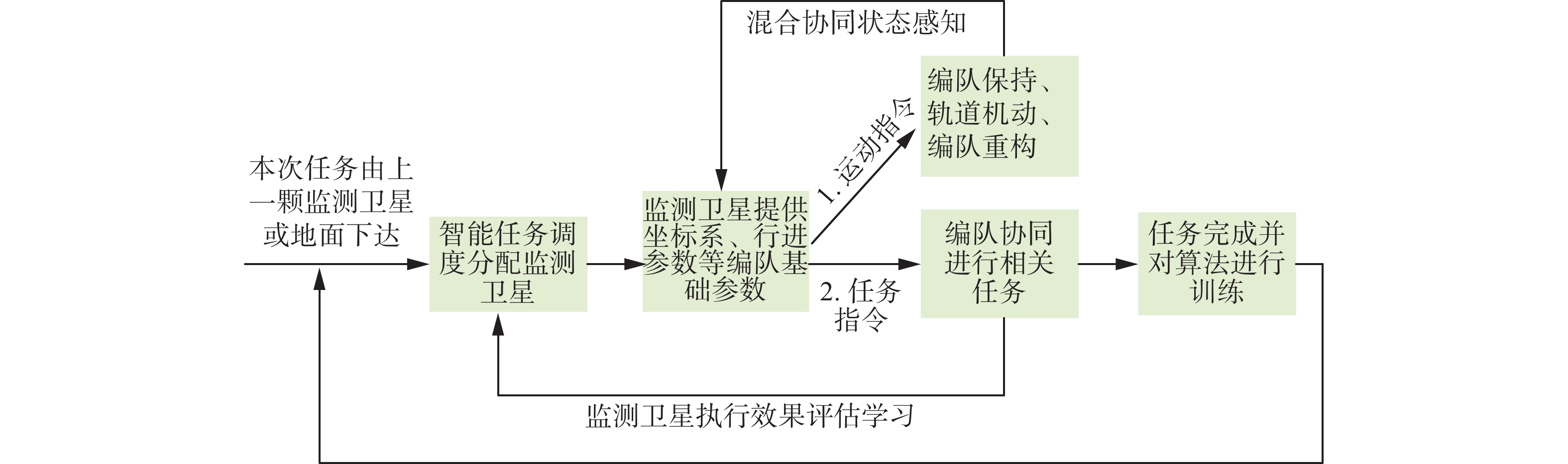
近年来随着积体电路技术和无线网络技术的快速发展，基于群体智能概念的自组织任务协同策略成为航天器编队协同控制中的一项重要课题。在自组织协同中，监测卫星所发挥的作用也与传统任务调度大有不同。这种任务协同方式通过编队卫星地面学习和长期的在轨学习，解决在轨编队任务自组织问题，极大地提高了编队任务执行过程中的鲁棒性也避免了传统算法策略中对既定任务局部最优解的约束^[19]。在编队完成任务分配后的指令执行阶段，共轨位卫星编队的协同控制路径规划计算中，编队结构往往存在诸多约束条件，需要对算法进行训练以让动作序列满足对应的约束条件。在耦合路径规划中存在空间维度大，难以在复杂环境中解析编队状态；而在解耦合状态下又存在星间路径冲突频繁，容易陷入局部最优解等问题。图4所示为当前主要的协同路径规划模式。针对这些问题，近年来一些学者提出了基于三角不等式的RRT-connect路径规划、改进麻雀搜索算法等解决办法^[20-21]。着重解决了规划时间、路径长度、任务动态性的问题。同时，在编队状态监测中，在轨的单个卫星由于搭载的载荷种类、通信感知能力、星载处理系统往往都各不相同，对自身状态与其他星状态的感知能力受限，对于轨道摄动与自身故障等问题普遍鲁棒性欠佳。而协同监测体系则能够有效地改善上述问题，整个编队依托星间链路作为一个大的系统对编队自身进行监测就能够实现1+1>2的效果^[22-23]。

图  4  协同路径规划示意

Fig.  4  Cooperative path planning mode

下载: 全尺寸图片

随着近二十多年的研究发展，航天器编队飞行的理论基础已经基本奠定。在100 km间距量级上通过选定特定的一条轨道，让在这条轨道上的卫星集群能够利用其摄动始终保持让整个卫星集群在一定的范围内而不需要携带推进剂^[24]。这样能够极大地简化卫星的设计，但是完全依靠特殊轨道上的摄动力保持一定的集群密度。缺点也是显而易见的，这种集群方式轨道太过特殊，并且也无法保持某种特定的队形，卫星分布靠摄动力粗略地维持在一定范围内，无法进行在轨协同任务。事实上，对多星共构卫星群的相关研究起步较早。NASA早在2003年就曾提出过类似的计划，将一组子卫星转移至地球火星轨道间的小行星带之后从容器内释放，组成一个编队，不同的卫星各有分工，不过时至今日这个项目由于技术原因没有上马。因为多星协同严重依赖地面测控，如果能突破卫星自主协同的技术难关，多星共构系统的应用范围将得到极大的扩展。由此，有人曾提出了一种改进的模拟退火算法，并将这种算法应用于卫星集群重构中，这种机动测策略能够在控制效率与燃料消耗之间找出良好的平衡点^[25]。不过卫星集群不等于共位编队，这是两个不同的概念。他提出的重构机动策略虽然具有高效快捷的优点，但是无法让多个卫星以一种特定的队形共位运行，应用于对系统响应能力要求较高的领域会有较大的局限性。

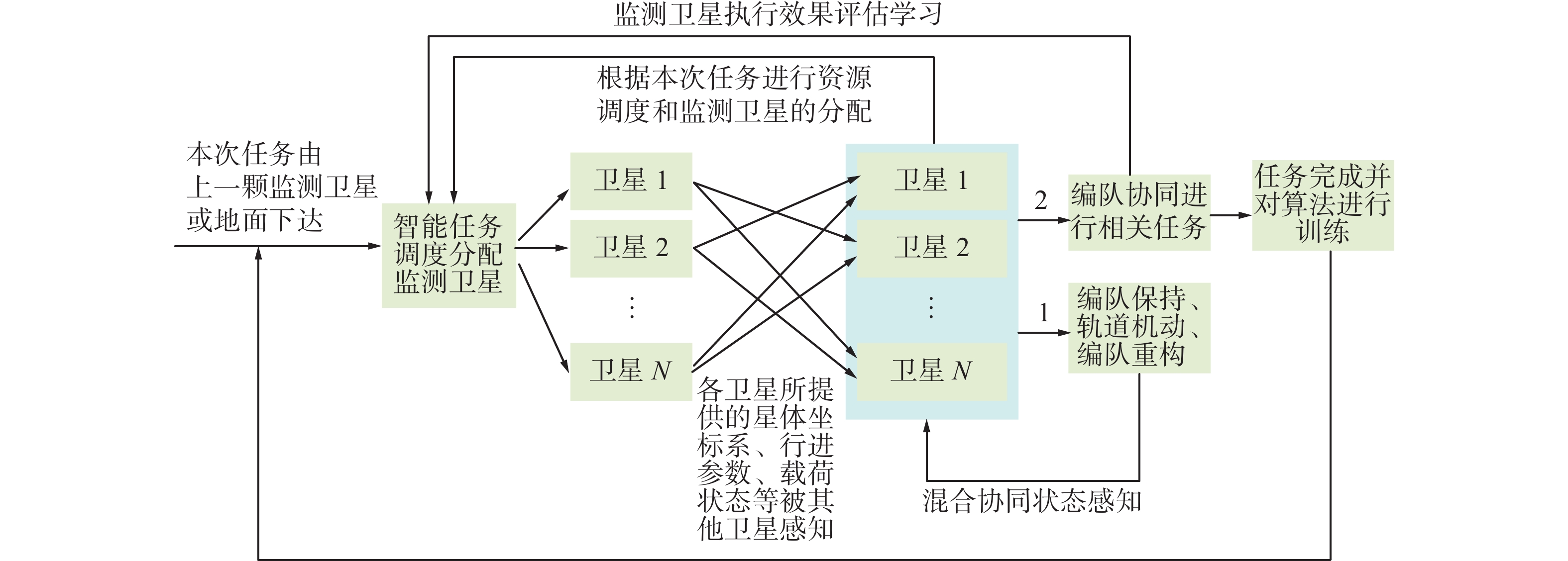
为此本文基于前文所述的协同控制策略加以改进搭建了一个较为简易的地面仿真+实验的平台，用于验证相关的智能共位编队在实现中较为关键的技术，架构如图5所示。

图  5  协同控制关键技术地面验证平台架构

Fig.  5  Architecture of the ground verification platform for key technologies of cooperative control

下载: 全尺寸图片

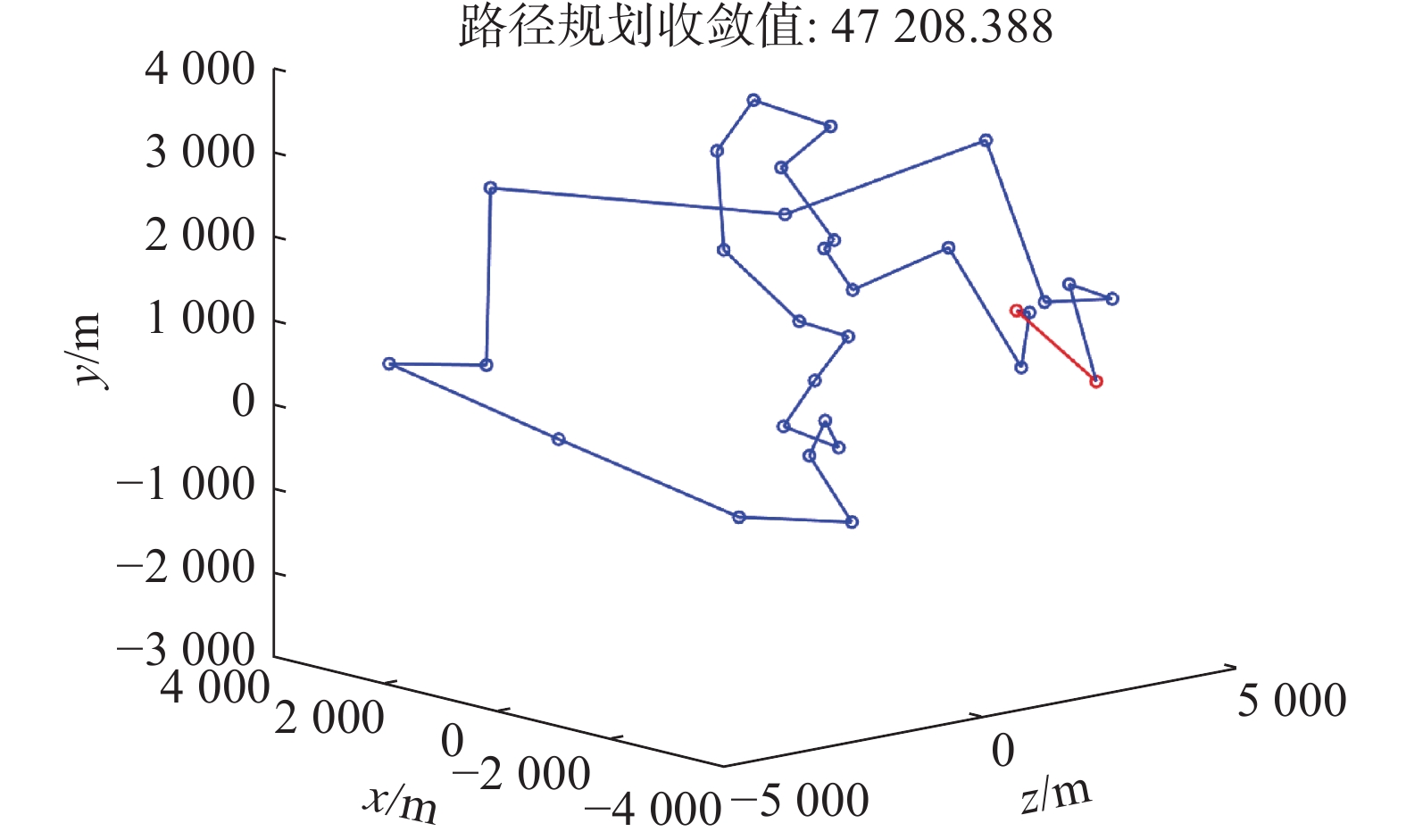
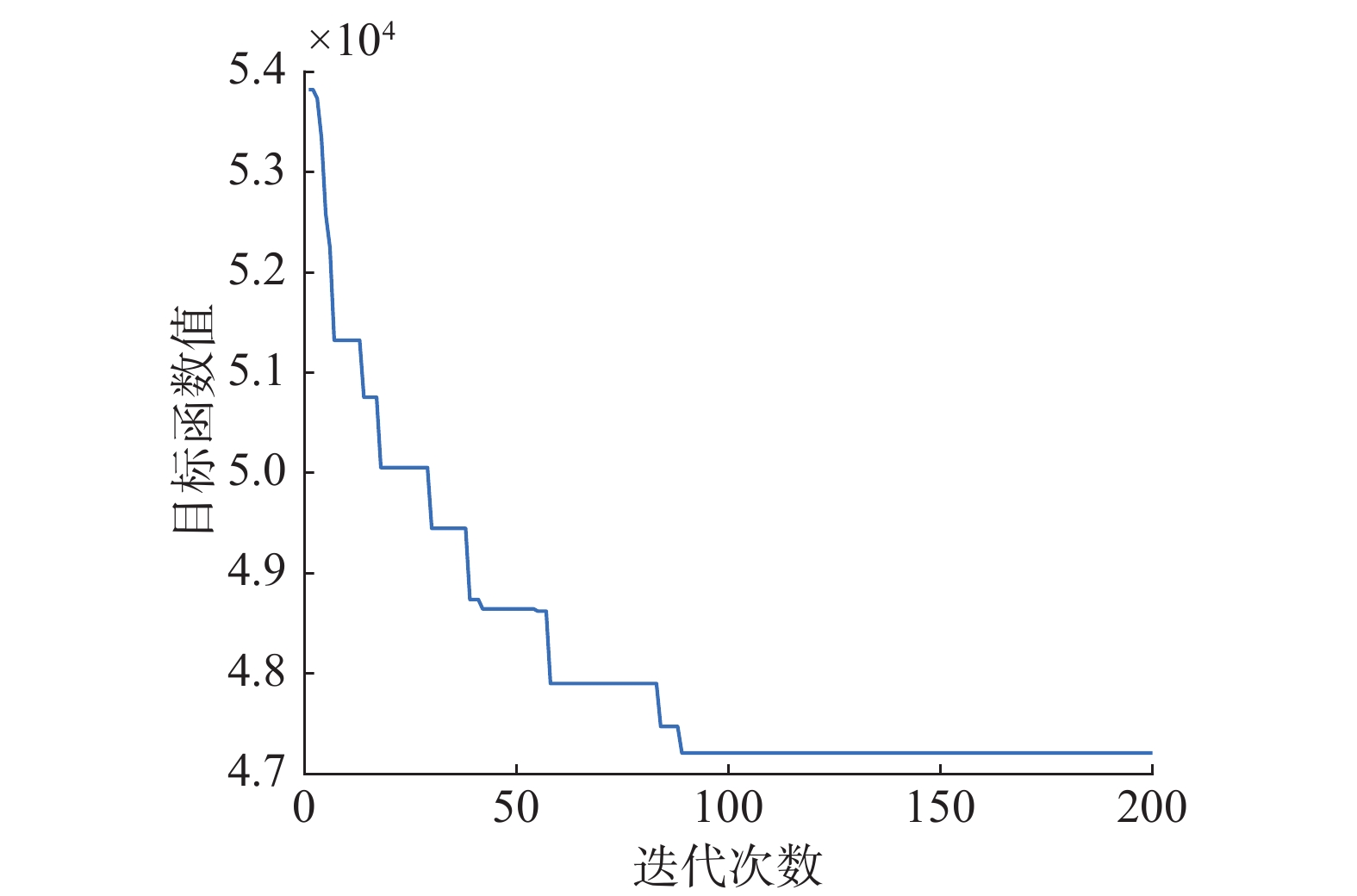
该平台以超深网络+浅网络机器学习的基本框架搭建了仿真的基本环境，通过超深网络训练和地面–轨道双向迁移学习使系统具有较强的拟合能力。在这个框架下，可以通过增减算法模块的方式调整仿真实验，具有较好的拓展性。在初步的技术验证中该平台的实验效果较为理想。图6、7分别是平台在子卫星协同清除在轨非合作目标中的路径规划效果和规划效率的示意图。实验证明该平台能够在较短时间内对非合作目标进行甄别和定点清除，在模型迁移后能够有效地提取特征，可以用于进一步的实验。在更换性能更强的后端技术验证平台后，将会有更高效的表现。

图  6  协同监测路径规划示意图

Fig.  6  Diagram of collaborative monitoring path planning

下载: 全尺寸图片

图  7  路径规划实验的学习曲线

Fig.  7  Learning curve of the path planning experiment

下载: 全尺寸图片

在之后的研究中，我们也能够根据这一技术路线和系统框架，逐步地完善编队在轨监测与协同控制系统，使其能够应用于实际任务当中。

未来航天器智能协同编队中至关重要的功能分化式子卫星相关技术，国内目前的研究主要集中在硬件支持和算法的研究、改进及应用上。虽然当前的研究处于起步阶段，不过可重构计算机近几年随着半导体制程的进步得到了快速发展，星载可重构计算机领域取得了长足的发展^[26]。西北工业大学将基于FPGA的可重构星载计算机应用在了一枚12U立方星上。不过这一可重构处理系统并不是以功能分化为目的设计的，仅是在系统部件出现故障的情况下，通过预设算法对系统进行重构以保证最低限度的性能来完成既定任务。当然这一成就仍然以后续以功能分化为目的的可重构系统具有相当的指导意义。算法相关的研究也自2017年以来快速增加，卫星的功能分化重构依赖于执行效率高、解集收敛性优秀的算法。针对这一目标，国内很多院所、学者对诸如NSGA-II、MOPSO为代表的多个多目标算法的应用进行了大量的研究^[27-31]。卫星通过计算得出并进行特定方式筛选解集，利用算法对星载计算机进行编码重构，有针对性地自主制定一系列策略。研究结果表明，现阶段卫星在一定程度上能够自主地对自身系统进行无地面指令优化，提高了系统的鲁棒性。

2.2   共位智能协同控制系统算法研究现状及分析

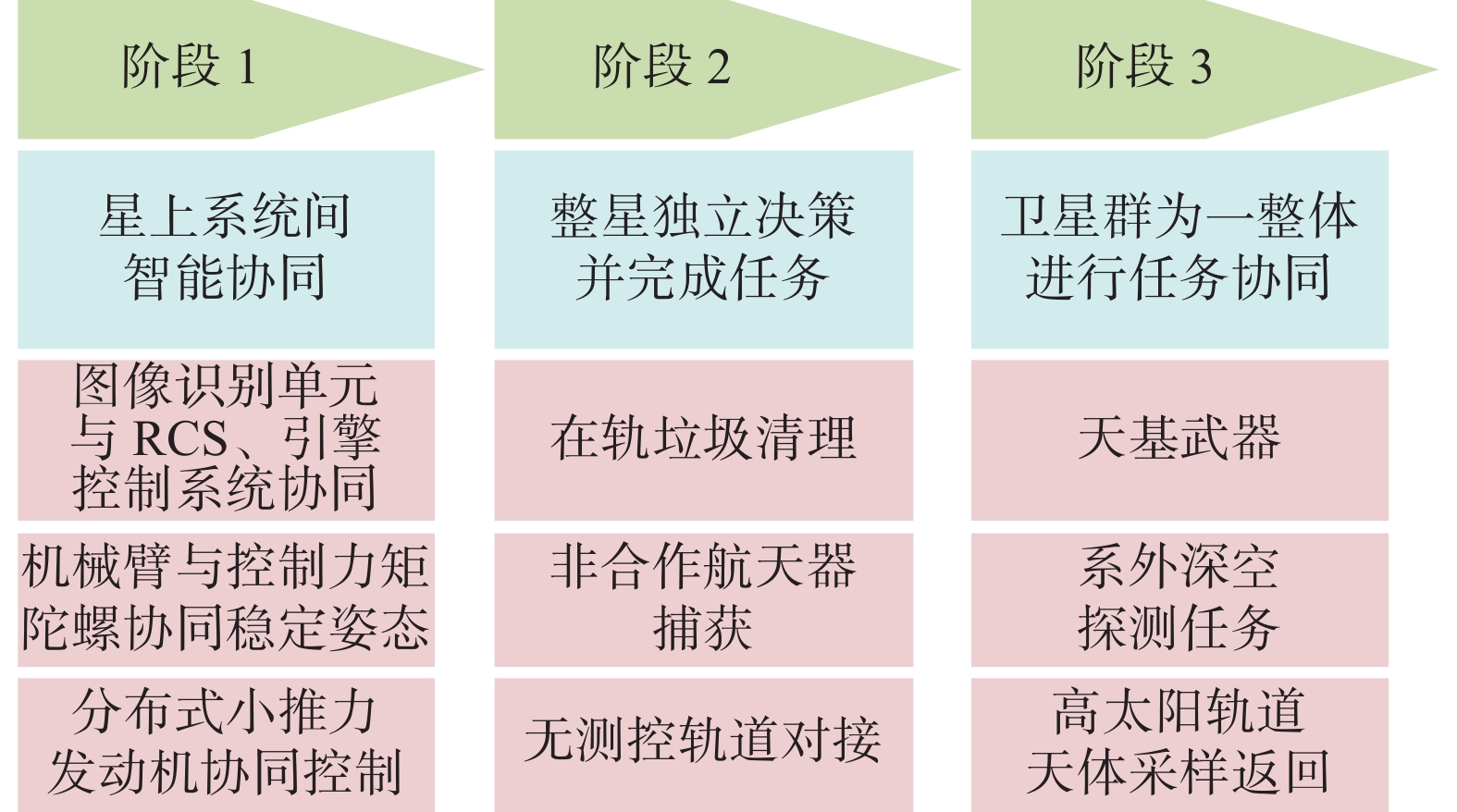
自然界中的群居生物普遍具有一种被称为自组织机制的社会行为，借鉴了这种机制的人工智能协同技术是实现大规模共位密集协同编队的关键所在。人工智能协同在航天领域的发展大致可以分为3个阶段，如图8所示：第一阶段，星上某个或某几个分系统实现智能化任务协同^[32]；第二阶段，单个整星可完全不依赖具体动作指令，以完成既定任务为目的进行自主决策。具体行为自主完成，并且整个系统有很强的鲁棒性,能够自主诊断纠错^[33-34]；第三阶段，在一个任务当中所有参与的单位全部实现智能化，各单位依赖先进通信技术协同配合，全程无人参与，自主决策^[35-36]。

图  8  航天器智能协同技术的发展阶段示意

Fig.  8  Development stages of spacecraft intelligent collaboration technology

下载: 全尺寸图片

当前的航天领域仍然处在第一阶段，航天器尚不能实现完全地自主决策，而是以某一分系统的以深度学习的方式实现航天器的部分智能化自主决策。当前诸如着陆自主避障，在轨自主交会对接、地形图像识别着陆等技术就是其中的典型，而这些先进的技术也将对航天器智能化迈向下一阶段起到关键的支撑作用。自主协同控制将是未来我国航天器的关键技术之一，未来将对我国的航天探测、轨道军事产生深远影响。航天器自主能力的提高将会在极大程度上减小对地面测控的依赖，航天领域下放到民用的门槛也将会降低。我国初步将人工智能应用于航天领域的是嫦娥3号、嫦娥4号、嫦娥5号、天问1号着陆器。这几个着陆器都通过人工智能算法在着陆最后阶段的悬停避障时自主地完成着陆。嫦娥系列任务，尤其是嫦娥5号任务环月轨道自主交会及对接的成功将对我国后续多星智能协同具有重要的指导意义。

航天器的协同控制算法近几年相关的研究发展迅速，控制算法多种多样各有优劣。实现方式大致都可以按照不同的协同方式分为一致性算法、蜂拥算法和基于优化算法的编队三类协同控制算法，如表3。

如图9所示的一致性算法与代码效率和网络分区容错性之间存在取舍，包括能够着重解决优化分布式缓存调度问题的一致性哈希算法、强一致性要求下监测卫星作为调度的二阶段提交算法、着重解决多星资源互斥问题的Lamport面包店算法、着重于解决星间交互容错问题的raft、Paxos算法等。

图  9  一致性算法下的编队协同监测模式示意图

Fig.  9  Formation cooperative monitoring mode under consensus algorithm

下载: 全尺寸图片

如图10所示的基于蜂拥算法的卫星协同集群中有两种基本的运动原则：规避和速度匹配。算法经过长期的训练能够高效地建立目标运动矢量与RCS等控制机构的映射^[40]，如式(1)可以简要地说明蜂拥算法对编队中任意一颗卫星的控制逻辑。

图  10  基于优化算法的协同监测模式示意图

Fig.  10  Cooperative monitoring model based on the optimization algorithm

下载: 全尺寸图片

式中：瞬时质心受力 ${F_{{\text{co}}}}$ 由RCS等推力机构产生； $ {F_{{\text{drg}}}} $ 为协同编队密度参数算法通过训练对其进行调整； $ {\hat \theta _{\text{c}}} $ 为瞬时航点角度； $ {K_{{\text{sat}}}} $ 表示单颗卫星的一项系数，可以表示如质量、质心位置等参数；N为该卫星规定邻域内的卫星数量，或者是除该卫星外的全部卫星数量 $({N_{{\text{com}}}} - 1)$ ； $\left\| {{l_{{I}}}} \right\|$ 、 ${\hat l_{{I}}}$ 分别为捕获到对应卫星的各项距离参数和角度参数； $ {l_{\bmod }} $ 为卫星碰撞模型参数。通过引入式(2)的参数捕获周期内的质心合力变量 $\Delta {F_{{\text{co}}}}$ 也可以对编队结构的刚性进行一定程度上的收敛控制。

式中： $\Delta {\theta _{\rm CoS}}$ 为当前卫星星体坐标系X轴在参数捕获周期内的指向变量； $\Delta {l_{{\text{cur}}}}$ 为当前卫星星体坐标系原点在参数捕获周期内的位移； ${A_{{\text{trans}}}}$ 为整个编队上一个参数捕获周期开始时的瞬时矢量在当前星体坐标系的转换值； ${K_1}$ 、 ${K_2}$ 、 ${K_3}$ 表示在通过模型深度学习训练收敛得到的权重值。

三类协同控制算法又有众多分支，相关研究者也深入地展开了一系列的挖掘。中国科学院软件研究所的许轲等^[41]致力于推进人工智能技术在航天信息处理领域的应用，他们的团队在2018年提出了一种以改进型PID控制为初始策略的深度强化学习姿态控制算法。该算法可以在航天器有效载荷、自身结构等各种参数未知的情况下通过深度学习以收敛出姿态控制的策略，并且在一定程度上可以随着任务的进行而对控制策略进行小幅度优化。这种算法实际上是一种为了简化代码而设计的贪心搜索算法，算法自身的局限性导致系统在航天器姿态控制、智能协同等复杂问题中倾向于得出局部最优解，随着时间的积累星载系统后续任务可能会出现预期之外的错误决策。海军大连舰艇学院长期承担舰艇指挥智能化方向的研究，多年来的研究对我国的军事指挥体系有着深远的影响。该校首次将Agent技术应用于反潜指挥系统当中。该系统目前在小型反潜无人艇上得到了初步的技术验证，单个无人艇的系统有着良好的自主型，与其他无人艇的信息共享能力与协同作战能力也表现良好^[42]。但是需要其中一个无人艇作为主艇进行全局干预，由其他无人艇实现半自主协同。相信未来几年随着芯片计算能力、可靠性以及国产自主流片等关键技术的突破，更先进的协同控制系统将能应用于军队建设和航天探测之中去。针对目前飞行器自主程度不足，需要主飞行器干预的现状，曾有专家在2016年提出了一种完全脱离个体间通信也能依靠外部综合传感器进行人工智能协同的控制策略,这样更加接近人类之间的协同工作关系^[43]。这种策略充分地考虑了视觉传感器延迟、计算延迟等对编队保持的影响，其仿真结果也证明这一策略拥有较高的控制效率与精度。北京控制工程研究所曾多次参与研发我国重大航天探测任务，如“嫦娥”系列探测器的综合控制系统等。他们的团队提出了一种基于神经网络的智能协同控制系统，该系统的控制策略的开创性实现了双组神经网络一致性协议下的协同控制，通过一组循环神经网络，根据其他卫星的状态进行高频次预测，预测结果收敛后再通过另一组循环神经网络将预先输入的二阶理想控制律转变为卫星姿控执行机构的输出量以完成协同控制。在他们的仿真实验中，这套协同控制策略能够有效地应对类似多卫星近距离协同这样的复杂指令环境，并且有着理论上良好的鲁棒性，对模型误差有着良好的适应性。

3.   结束语

本文主要着眼于未来数年人工智能技术在航天任务中的应用前景，梳理了共轨位智能监测协同控制的发展现状，总结了相关关键技术的开发和未来应用所面临的挑战。根据调研，各国的该领域学者已经针对航天器智能化进行了大量且深入的研究，研究取得了显著的成果。

智能化协同监测是航天测控的一大主要发展方向，其根本目的是提高航天器的任务效率并尽可能减小对地面测控的依赖，是未来大规模集群协同任务的关键所在。航天智能化领域不可避免地成为了国际竞争的又一新焦点。航天器协同任务的高度智能化将会深刻地影响包括轨道军事、航天基建、深空科研等诸多领域。