无人机可以应用于不同的场景，例如日常的便民生活应用^[1]，农业生产过程^[2]，矿场的侦探和挖掘过程^[3]等。单一的无人机不受地形的限制，但是由于携带电池能量的限制，执行任务时间短，并且难以承担较重的负载。无人车（船）移动范围受限于地形，难以到达特定的位置。无人机–无人车（船）的组合系统可以结合两者的优点，完成复杂的任务^[4-5]。在执行任务结束后，无人机如何移动到指定位置是协同系统实际应用的关键问题^[6]，因此本文聚焦于无人机的自主降落问题。

在文献[7-8]中，作者将多种传统的控制方法应用于无人机降落任务，这些方法具有稳定和低算力需求的优点，但是较难实现最优的控制效果。文献[9-12]将强化学习理论应用于无人机降落问题，并取得良好的效果。在文献[13-16]中，使用强化学习原理调整控制算法的参数，面对不同的控制情形，能够实现较优的控制效果，但是并没有进行真实无人机实验。

针对以上方法的不足，本文结合深度强化学习理论和比例积分微分(proportional-integral-derivative, PID)控制方法，解决无人机降落至移动平台的问题，本方法既有PID方法的稳定性，又能够发挥强化学习寻找最优控制策略的优点，迅速完成无人机降落到无人移动平台的任务。

1.   无人机降落问题描述

在多机器人无人系统中，无人机在完成特定任务后需要降落至特定平台，本文基于上述任务，针对无人机降落问题，提出一种结合深度强化学习算法和比例积分微分(proportional-integral-derivative, PID)原理的控制方法。文中首先介绍多机器人协同系统以及实现无人机降落任务的必要性，并详细介绍传统控制方法和机器学习方法在无人机降落问题上的应用现状。

1.1   关键的无人机降落问题

在如今的机器人学研究中，单一的机器人难以完成复杂任务。在所有的无人设备中，无人机有着多项优点，其他设备难以替代无人机执行任务。首先无人机运动不受地形限制，可以轻易地到达特定的位置，并且无人机在空中悬停可以为地面无人设备和工作人员提供高处视角的图像信息，为发现和定位目标物品提供可能。同时，无人机由于自身结构的原因也有特定的缺点，包括由于电池能量不足造成的执行任务时间短和无法携带较重负载的问题等。对单一的无人机设备添加无人车（船）组成协同系统可以有效地解决无人机的上述缺点。实际应用中，无人机完成任务，须自动返回，以备下次任务的执行。因此，在这些协同系统中，如何将无人机降落到特定的平台上是一项必须解决的任务。在文献[17]中，作者提出一种无人机和无人车的协同系统，该系统作业于建筑行业，收集建筑区域内的各种关键数据。该方法结合了两种机器人的优点，弥补单一机器人的不足，高效地实现建筑行业数据收集任务，不过在文中提到的无人机降落方法依然有进步的空间，难以在复杂的环境中实行降落任务。

1.2   传统控制方法应用

文献[18]提出一种比例微分(proportional-integral, PD)控制器，该控制方法针对无人机自主降落问题，实现了无人机降落到固定平台的任务。在文献[8]中，作者将模型预测控制方法应用于无人机降落问题，该方法结构轻量，响应迅速，能够在低算力的平台中运行。同时，作者在文中使用仿真环境进行验证，且效果良好，但是并没有在真实的场景中进行降落效果的测试。PID控制方法在控制任务中广泛使用，但是固定参数的PID控制方法对非线性问题适应性差，在文献[7]中，作者提出一种基于模糊逻辑的PID控制方法，结果显示，该方法优于传统的控制方法，不足之处在于该方法未考虑无人机降落到移动的平台的情形。

1.3   强化学习算法的应用

许多学者应用强化学习算法寻找解决问题的最优策略。强化学习算法能够实现在干扰和复杂情况下的最优控制，这是传统控制方法难以比拟的。理论上，基于马尔可夫过程的强化学习算法有潜力找到最优的控制策略，当算法训练充分后就可以实现对于无人机降落问题的最优控制。在文献[9,11]中，作者将确定性策略梯度方法^[19]应用于无人机降落问题中，该方法在虚拟环境中进行训练，并且可以在仿真和真实环境中，实现对无人机降落过程的控制。确定性策略梯度方法能够根据不同的状态输入输出不同的动作，进而完成当前的任务。文献[11]中，输入状态包含x、y两个方向上的位置信息，算法根据不同的位置信息控制无人机降落，以连续的状态作为输入并输出连续动作，有潜力实现精确控制，由于文章中的方法未使用z方向的位置信息，当面对不同高度的输入时可能有相同的输出，影响控制无人机降落的效果。文献[9]中，作者同样使用确定性策略梯度方法，该方法的输入包括三轴的位置信息，可根据无人机高度改变输出动作，从而实现精准控制，同上面的方法一样，此方法以连续的状态作为输入并输出连续的动作，保证无人机的精确控制。

在文献[16,20]中，一种结合PID理论和强化学习原理的方法被应用于移动机器人的路径规划问题，在仿真实验中，对比传统PID方法，文中提出的Q学习–PID方法在路径规划实验的结果中优势明显，面对不同环境和干扰时，表现出鲁棒性强的优点。文献[21-22]将参数自学习调节方法应用于无人机降落至静止平台的任务，由于控制器参数随当前状态自适应调节，因此取得的无人机路径控制效果均优于传统PID方法。目前类似的方法还没有应用于无人机降落至移动平台任务，在无人机降落问题中，使用结合PID理论和强化学习原理的方法，具有创新性和可行性。在文献[23]中，作者提出一种矫正纠偏（corrective advice communicated humans, COACH）框架，使用人类建议，用于帮助强化学习算法寻找最优的控制策略，效果显著，能优化获得的最终策略。

本文提出一种结合PID原理和强化学习理论的方法，完成无人机降落到移动平台的任务，应用矫正纠偏框架，优化最终训练得到的策略。上层的控制策略选择确定性策略梯度方法，该方法有着连续的输入和输出，在连续空间上，有潜力实现优秀的控制效果。下层应用PID方法，用于保证无人机降落的稳定性。

2.   强化学习算法描述

2.1   强化学习

人工智能领域中，强化学习通常根据特定的状态寻找最优动作，并将动作执行进而完成相应的任务。基于强化学习原理的方法已经在多个领域取得亮眼表现，包括围棋^[24]、电脑游戏^[25-26]等。在理论上，基于强化学习的方法在经过一定回合的训练后，所获得的智能体可以在不同场景实现特定的任务。一个标准的强化学习问题可以由S、A、P、r、γ定义。其中S 和A分别代表输入状态和输出动作的集合，s和a表示某一时间的状态和动作，P表示状态转移概率，r是奖励信息，γ是折扣因子，同时定义总体奖励 $ {R_t} =\displaystyle \sum\limits_{i = t}^f {{\gamma ^{i - t}}r} ({s_i},{a_i}) $ ，其中f是最后的回合数。

智能体在环境中进行训练，不断优化当前的策略，对于一个特定的策略π，本文以公式 ${V^\pi }({s_t}) = {\rm E}\left[ {{R_t}|s = {s_t},\pi } \right]$ 定义价值函数 $ {V^\pi } $ 。同样由公式 ${Q^\pi }({s_t},{a_t}) = {\rm{E}}\left[ {{R_t}|s = {s_t},a = {a_t},\pi } \right]$ 定义动作价值函数。同时本文使用 $J(\pi )$ 定义策略π的评价标准，具体为 $J(\pi ) = {\rm E}[{R_t}|\pi ]$ 。最后使用 ${\pi ^*}$ 来代表最优的控制策略，即，

智能体不断地在环境中训练，并使用贝尔曼方程：

不断更新状态价值函数，因此智能体在强化学习算法的规则下不断训练并获得最优的控制策略。

在强化学习的发展过程中，最具有代表性的算法^[27]是Q学习算法^[28]，算法本身结构简单，并为其后的算法带来启发，这些算法包括深度Q学习^[29]、双Q学习^[30]、决斗Q学习算法^[31]，但是Q学习算法由于其离散的输入和输出，只能解决复杂度低的低维度问题。

2.2   深度强化学习

在实际任务执行时，状态和动作的表示是连续的，由于维度爆炸的问题，在连续的动作状态空间中使用离散的状态和动作难以实现。因此，本文使用神经网络非线性拟合的特点，对动作价值函数进行估计，为了更好的表示动作价值函数，本方法定义损失函数 $L({\theta ^Q}) = {\rm E}[{({y_t} - Q({s_t},{a_t}|{\theta ^Q}))^2}]$ 来优化网络参数 $ {\theta ^Q} $ ，其中 $ {y_t} = r({s_t},{a_t}) + \gamma Q({s_{t + 1}},{a_{t + 1}}|{\theta ^Q}) $ 。如果策略是确定的，则可以将状态映射到动作上，即 $\mu :{{S}} \to {{A}}$ ，之后本文定义动作网络 $ {\theta ^\mu } $ ，其遵循 $J(\pi )$ 进行更新，使得 $J(\pi )$ 变大，即根据 ${\nabla _{{\theta ^\mu }}}J(\pi ) \approx { {\rm{E}}[{\nabla _{{\theta ^\mu }}}Q(s,a|{\theta ^Q}){|_{s = {s_i},a = \mu ({s_i}|{\theta ^\mu })}}]} { = {\rm{E}}[{\nabla _a}Q(s,a|{\theta ^Q}){|_{s = {s_i},a = \mu ({s_i})}}{\nabla _{{\theta ^\mu }}}\mu (s|{\theta ^\mu }){|_{s = {s_i}}}]}$ 进行更新。

确定性策略梯度方法^[19]是一种解决在连续状态空间和动作空间的无模型算法。此方法使用动作–评论家的结构，有两个主要的人工神经网络，一个用于拟合动作价值函数，称为价值网络 $ {\theta ^Q} $ ，另一个网络用于产生动作，成为动作网络 $ {\theta ^\mu } $ 。在这两个网络进行更新时，网络的迭代会不稳定和发散，因此，使用两个目标网络（目标价值网络 $ {\theta ^{Q'}} $ 和目标动作网络 $ {\theta ^{\mu '}} $ ）对更新的两个主网络进行软更新，提高其稳定性。两个目标网络分别与价值网络和动作网络有着相同的结构。在训练时，每个输出动作有随机的干扰，用于增加算法探索的空间，动作作用于环境后，智能体会将观察数组 $({s_{\rm step}},{a_{\rm step}},{r_{\rm step}},{s_{\rm step + 1}})$ 储存到记忆库中，记忆库达到一定数量后，按公式 $L{\text{ }} = \left( {\dfrac{1}{B}} \right)\cdot \displaystyle\sum\limits_i {{{({y_i} - Q({s_i},{a_i}|{\theta ^Q}))}^2}}$ 更新价值网络参数 $ {\theta ^Q} $ 使得L减小，其中 $ B $ 是样本取样个数， ${y_t} = r({s_t},{a_t}) + \gamma Q({s_{t + 1}},\mu ({s_{t + 1}}|\theta^{\mu '})|{\theta ^Q}')$ ，之后按照 ${\nabla _{\theta \mu }}J \approx \dfrac{1}{B}\displaystyle\sum\limits_i {{\nabla _a}Q(s,{\text{ }}a|{\theta ^Q}){|_{s = {s_i},a = \mu ({s_i})}}} {\nabla _{{\theta ^\mu }}}\mu (s|{\theta ^\mu }){|_{{s_i}}}$ 对动作网络 $ {\theta ^\mu } $ 进行更新，使得 $J$ 增大，接着，本方法对两个目标网络进行软更新，具体公式为： ${\theta ^{Q'}} = \tau {\theta ^Q} + (1 - \tau ){\theta ^{Q'}}$ 和 $ {\theta ^{\mu '}} = \tau {\theta ^\mu } + (1 - \tau ){\theta ^{\mu '}} $ 。最后经过不断地训练，会得到两个主网络，用于实际问题的解决。

2.3   使用矫正纠偏框架的强化学习方法

使用深度强化学习算法需要大量的时间进行训练，并且训练的时间随着动作空间维度的增加而显著增加。为了减少训练的时间并提升训练的效果，一种矫正纠偏框架用于提升训练的效率，在智能体输出动作时，使用人类的建议（一个二值化的量）对智能体产生的动作进行增强或者减弱。在矫正纠偏框架下的确定性策略梯度方法具体结构如图1所示，使用人类建议指导智能体探索，使用确定性策略梯度方法对网络进行更新，最终迅速获得最优策略。

图  1  使用矫正纠偏框架的确定性策略梯度方法

Fig.  1  DDPG with COACH

下载: 全尺寸图片

在本文提出的方法中，使用人类的建议增加或者减弱智能体生成的动作，最终动作作用于环境中，并储存在 $ ({{s}_{t}}{,}{{a}_{t}}{,}{r_{t}}{,}{{s}_{{t + 1}}}) $ 中，且与确定性策略梯度方法一致，对网络权重进行更新。总体来看，将人类的建议用于修正智能体产生的动作，会使得智能体在相同的训练回合下，获得更佳的策略。

3.   无人机降落控制策略

3.1   传统PID方法控制无人机降落

传统的PID方法结构如图2所示，误差信号 $e(t)$ 是设定值和测量值的差值，有比例、积分、微分3个环节，分别由 ${k_{\rm P}}$ 、 ${k_{\rm I}}$ 、 ${k_{\rm D}}$ 3个参数对输入的误差信号按公式 $u(t) = {k_{\rm P}}e(t){\text{ + }}{k_{\rm I}}\int_0^t {e(\tau )} {\rm{d}}\tau {\text{ + }}{k_{\rm D}}\dfrac{{{\rm{d}}e(t)}}{{{\rm{d}}t}}$ 处理，最终获得所需的输出控制量。

图  2  标准PID控制器

Fig.  2  Standard structure of a PID controller

下载: 全尺寸图片

3.2   深度强化学习算法控制无人机降落

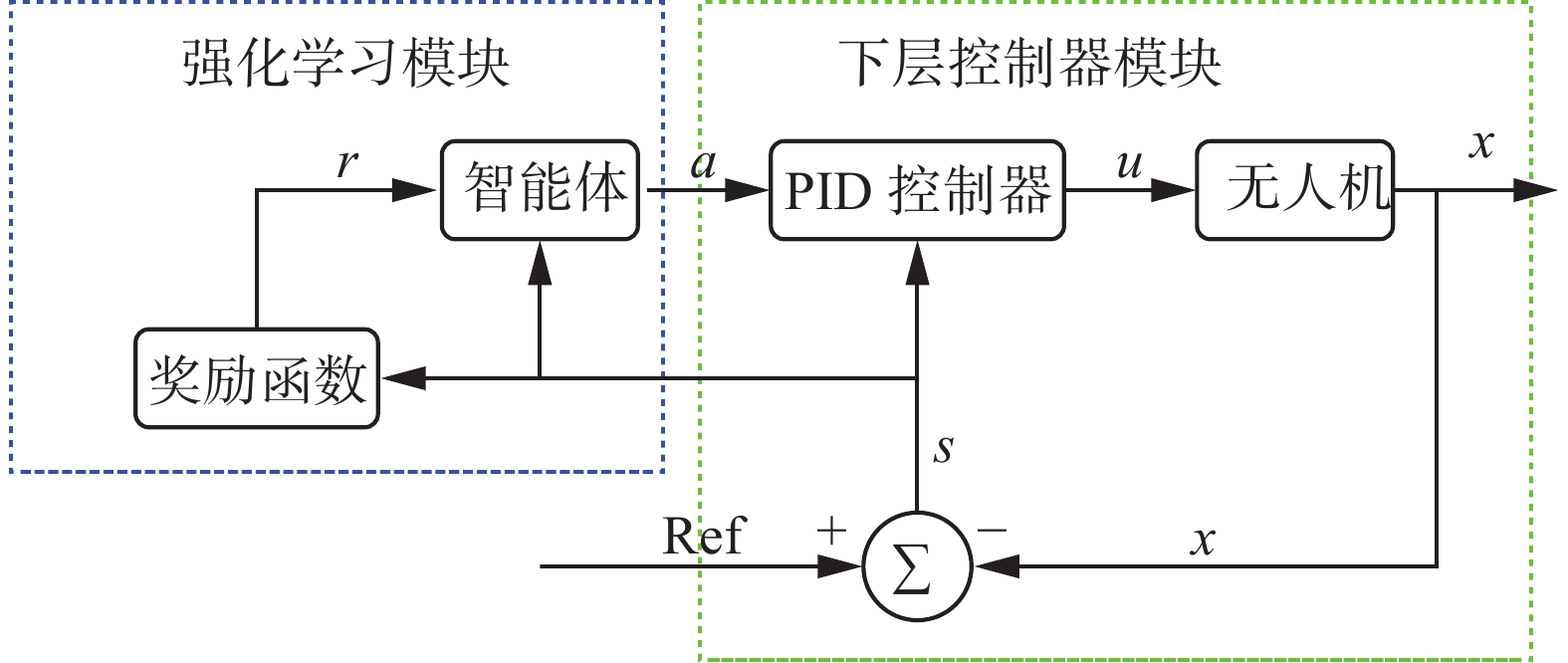
本文提出的方法将强化学习算法应用在PID控制算法的上层，方法的结构如图3所示，有两个控制模块，左边框为强化学习模块，右边框为PID控制模块，强化学习的输入状态由3个方向上的位置组成，输出a为PID控制模块的参数 ${k_{\rm P}}$ 、 ${k_{\rm I}}$ 、 ${k_{\rm D}}$ 。

图  3  强化学习与PID结合方法

Fig.  3  RL-based PID

下载: 全尺寸图片

强化学习模块时刻调节PID控制器的参数，具体的奖励函数由公式

定义，其中 $ {d_t} $ 是t时刻无人机与目标点的欧式距离。当无人机降落到指定的地点，奖励值为1，当降落失败（目标消失或未降落至目标点）时，奖励值为−1，其他情况下，奖励值为与上一时刻欧式距离和当前时刻欧式距离的差值。一旦记忆库存满，评价网络和动作网络便开始更新。

由于强化学习模块能时刻输出动作a对PID控制模块的参数进行调整，因此本方法可在多个场景控制无人机进行降落。PID模块输出控制命令u，包含x和y方向上的控制位置，无人机在z方向上的目标降落速度为0.3m/s保持不变，Ref代表无人机的目标位置，x是当前机器人的位置，s是无人机在图像中相对目标点的位置，包含x、y和z三轴的信息。由于强化学习算法的加入，本方法能够在复杂环境中更加有效地控制无人机降落。

3.3   应用矫正纠偏框架的深度强化学习算法控制无人机降落

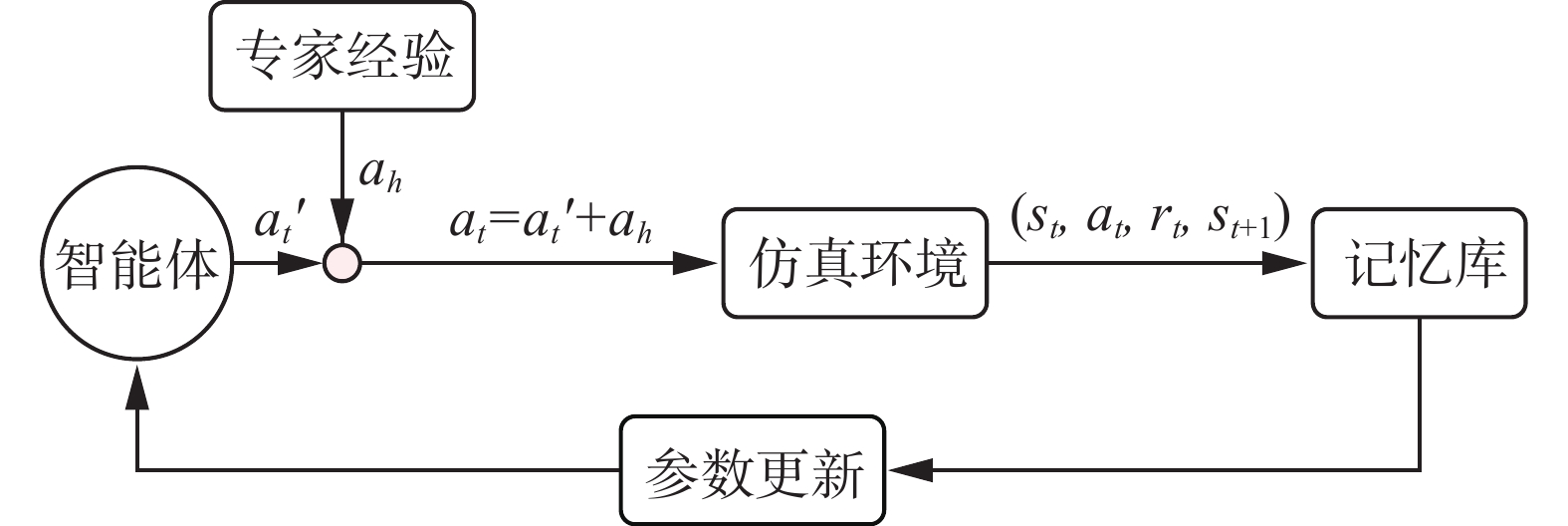
本文的方法使用矫正纠偏框架优化训练过程，强化学习算法和矫正纠偏框架的结构如图4所示，矫正纠偏框架使用人的建议代替干扰信号，用于智能体探索环节，因为人类建议的加入，所以增强了最终获得策略的鲁棒性。

图  4  使用矫正纠偏框架的强化学习方法

Fig.  4  RL with COACH

下载: 全尺寸图片

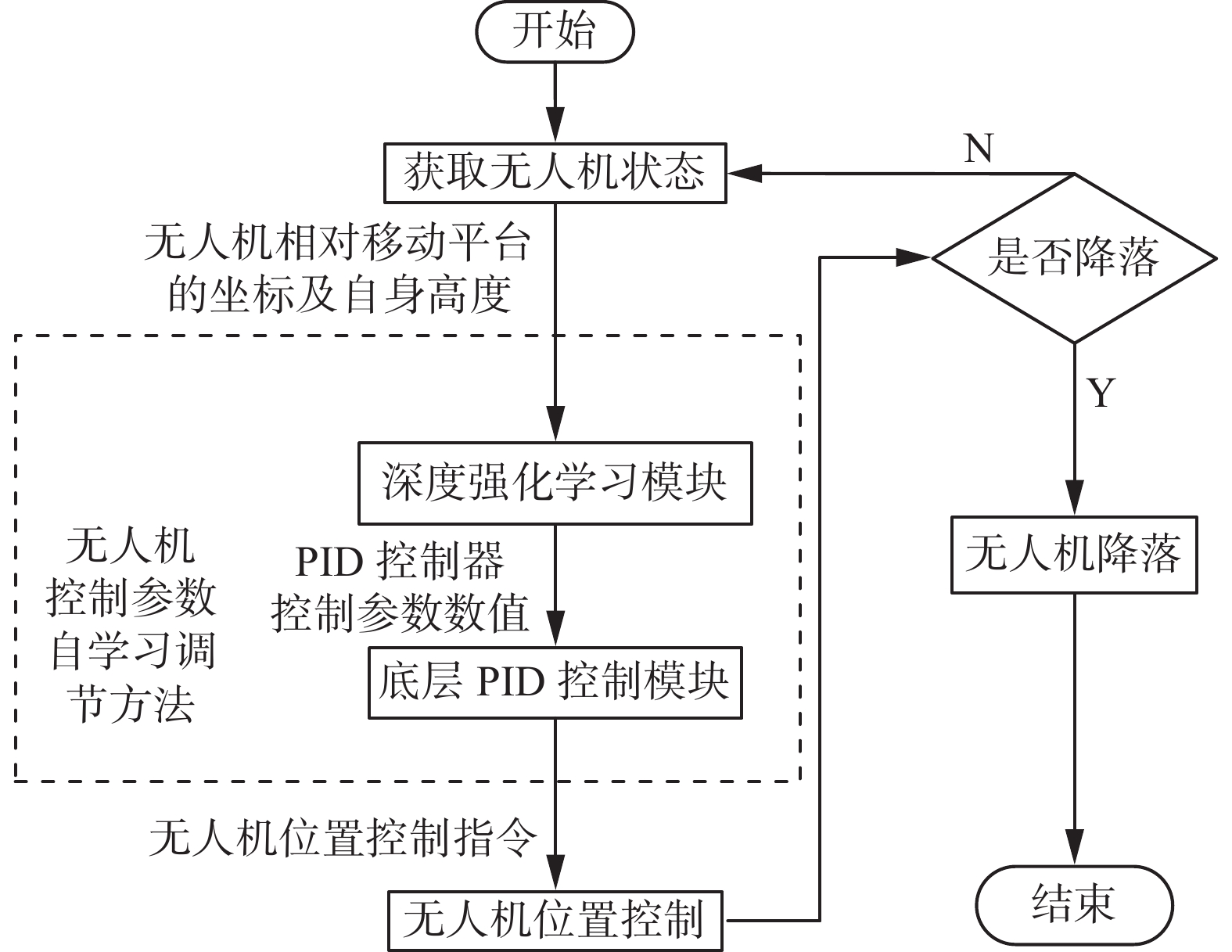
当智能体选择动作 $ {{a'}_{t}} $ ，然后根据人类当前指导获得最终的输出 $ {{a}_{t}} $ ，其中 ${{a'}_{t}}$ 的取值范围为 $[0,1.0]$ 叠加人类的经验 ${{a}_{h}}$ ，其取值为0.2或者−0.2，最终输出的结果 $ {{a}_{t}} $ 区间为 $[0,1.0]$ ，当 $ {{a}_{t}} $ 超出1.0时，认为输出结果为1.0，当 $ {{a}_{t}} $ 小于0时，认为输出结果为0。当误差范围较大时，人类经验认为可以增大比例参数，此时 ${{a}_{h}} = 0.2$ ，进而加速无人机到达目标点，当误差范围较小时，人类经验认为需减小比例参数，即取 ${{a}_{h}} = - 0.2$ ，进而实现精准的降落，对于积分和微分参数并没有使用人类的经验进行调节。

控制参数自学习调节方法具体流程如图5所示，由传感器获得无人机相对移动平台的坐标，深度强化学习模块对状态进行处理，输出底层控制器的x、y方向上的控制参数，之后底层控制模块根据当前误差和控制参数计算获得无人机位置控制指令并执行。无人机在降落过程中不断检测当前状态，若无人机位置合适，则旋翼停止运动，无人机降落至目标区域，否则无人机继续执行位置控制的步骤，直至无人机降落至目标区域。

图  5  无人机自主降落流程

Fig.  5  Autonomous landing process for an UAV

下载: 全尺寸图片

4.   实验及结果分析

本文提出的方法，在Gazebo仿真环境中训练并在仿真和真实环境中进行测试。此外，PID模块和强化学习模块之间的通信使用机器人操作系统(robot operation system)^[32]，如图6所示，图6(a)给出的是仿真环境，图6(b)给出的是真实降落的场景。

图  6  降落环境搭建

Fig.  6  Training and testing environment

下载: 全尺寸图片

4.1   无人机降落至静止平台

降落实验中，静止平台比无人机稍大，无人机具体尺寸为0.4 m×0.4 m，平台具体的尺寸为0.6 m×0.8 m，用于无人机降落。在仿真实验中，搭建了一个简单的环境，如图6（a）所示。为了得到无人机与目标位置的相对信息，在无人机的底部加装有摄像头传感器，并通过ROS框架进行信息交互。无人机在这个仿真环境中训练和测试，对于强化学习PID方法和应用矫正纠偏COACH方法的强化学习PID方法，本实验对智能体进行了200回合的训练。当无人机降落至平台并保持静止后，本实验认为无人机成功完成降落任务，经过共600次仿真实验测试表明，3种方法都能够有效地(>99%)实现无人机降落任务。

3种方法控制无人机降落的轨迹如图7所示。

图  7  3种方法的降落轨迹（仿真）

Fig.  7  Trajectories of three approaches for landing in a simulated situation

下载: 全尺寸图片

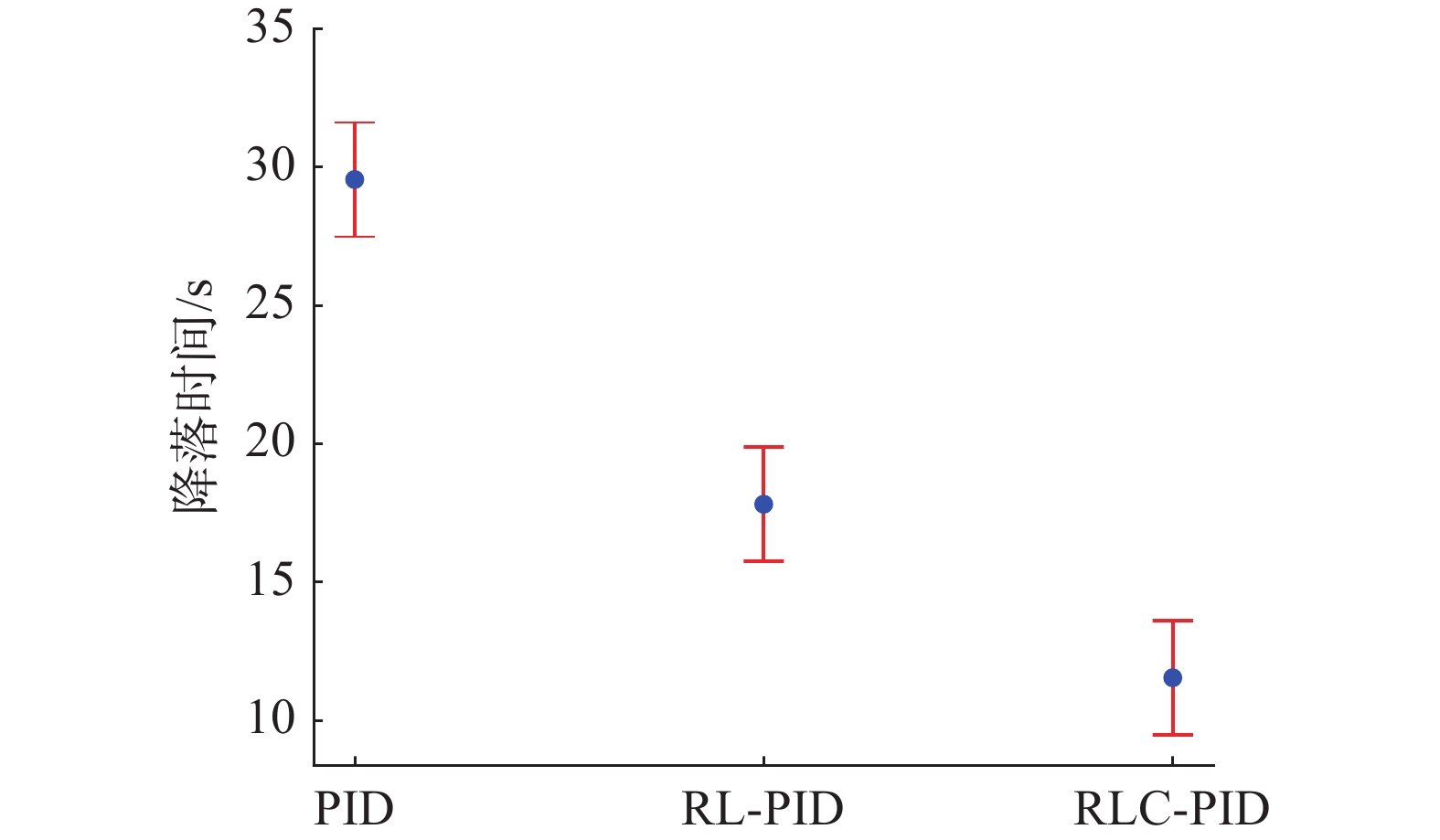
红色的轨迹为传统PID方法，本方法轨迹平滑，证明本方法的3个控制参数人工选择合理，能够有效完成无人机降落到固定平台的任务。绿色的轨迹是深度强化学习PID方法，本方法同样可以将无人机降落到规定的区域，但是在最终降落时，与静止平台中心的距离较大。蓝色轨迹曲线为应用矫正纠偏框架的深度强化学习PID方法，能迅速地对当前误差进行调整并且最终降落时与静止平台中心的距离较近，本方法有效应用了深度强化学习理论和PID控制方法，并使用矫正纠偏框架对两者进行结合，实现最佳的轨迹控制。无人机从坐标（0.3 m，0.3 m，3 m）出发，目标点为（0 m，0 m，0.2 m），3种方法在各200次的测试实验中都能够有着较高的成功率（>99%），稳定完成无人机降落的任务。图8给出了3种方法控制下，无人机执行降落任务的时间，从结果上看，两种结合强化学习原理的方法能够有效地减少无人机降落的时间（传统PID方法时间平均值为29 s，强化学习PID方法平均降落时间为17 s，使用矫正纠偏框架的强化学习PID方法平均时间为11 s），并且使用矫正纠偏框架，能够使得强化学习算法最终得到的策略控制效果更好，有效提升控制策略。最后，传统PID方法如果要达到控制要求，本身的参数是需要合理选择的，并且参数的选择是一个耗费时间的过程，在结合强化学习原理后，通过在虚拟环境中训练，可以实现智能体代替人类进行参数的选择，并且控制无人机降落效果比人类调节参数的PID方法效果更佳。

图  8  3种方法控制无人机至平台的时间（仿真）

Fig.  8  Time for UAV landing on a simulated static platform

下载: 全尺寸图片

4.2   无人机降落至移动平台

实验设置从静止的平台改变为移动的平台，移动平台前进和后退并不断循环，其他的设置同之前静止实验相同，且使用了先前实验的训练模型和参数设置。

无人机初始坐标为（0.3 m，0.3 m，3 m），降落目标点坐标为（0 m，0 m，0.2 m），在移动平台降落实验中，3种方法的成功率如表1所示。当平台移动后，由于各种不稳定性因素，无人机降落至平台的难度加大，固定参数PID方法的成功率在99%附近，结合强化学习原理的方法成功率分别是89%和100%，本结果表明在训练合适的情况下，强化学习原理能够提高无人机降落的稳定性。

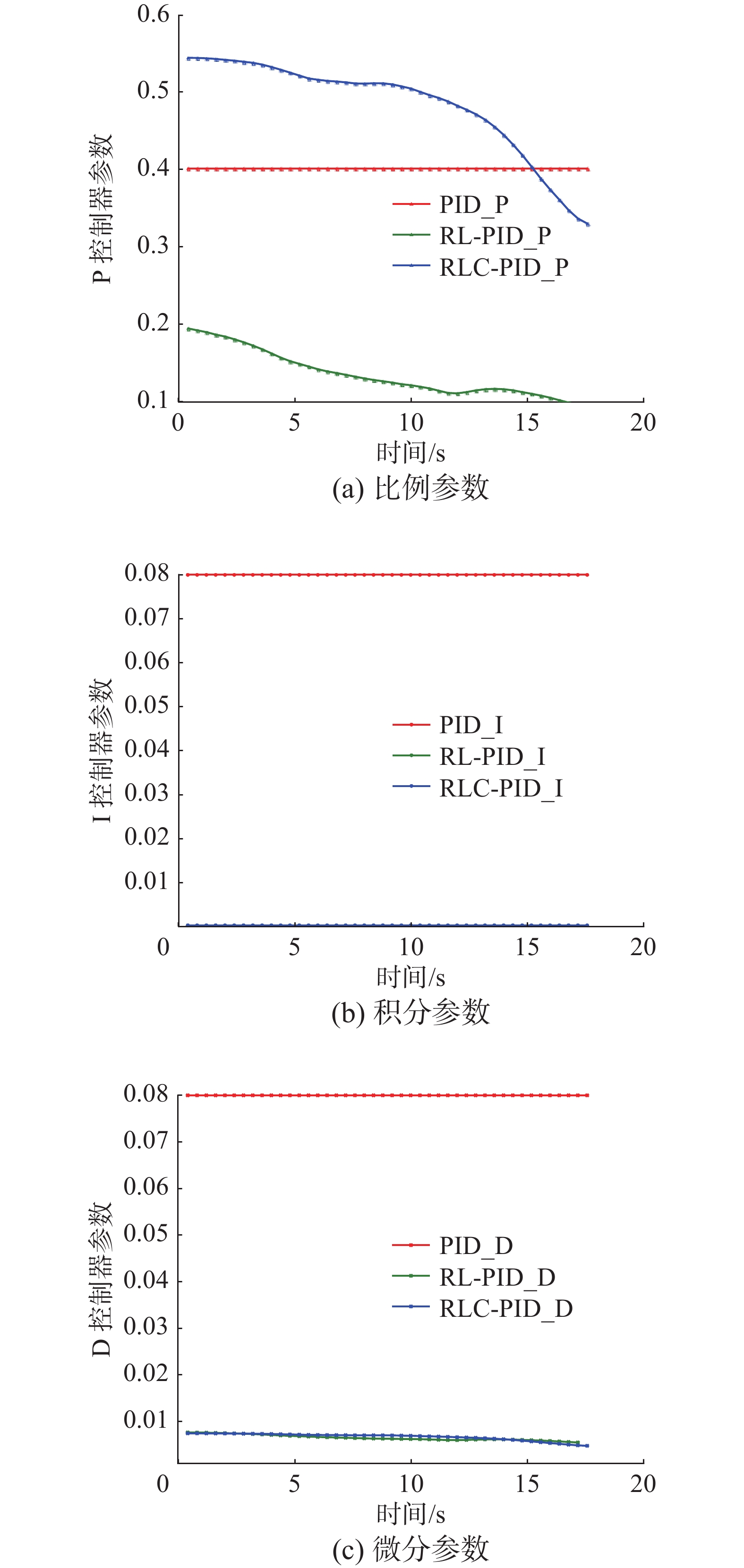
图9给出的是无人机降落过程中，3种方法PID参数的变化情况，传统PID方法的参数是固定的， ${k_{\rm P}}$ 、 ${k_{\rm I}}$ 、 ${k_{\rm D}}$ 分别是0.4、0.08、0.08。使用矫正纠偏COACH方法的强化学习PID方法， ${k_{\rm P}}$ 时刻改变，并且范围在区间（0.0，0.6）， ${k_{\rm I}}$ 、 ${k_{\rm D}}$ 也在不断地更新来适应不同的环境。对于强化学习PID方法， ${k_{\rm P}}$ 同样时刻改变，范围为区间（0.0，0.2）。

图  9  3种方法的PID参数

Fig.  9  PID control gains in every sample time of three approaches

下载: 全尺寸图片

两种基于强化学习原理的方法面对相同的降落问题，同样的训练过程，具有不同的效果，主要的原因在于输出的PID控制参数不同，应用矫正纠偏框架的强化学习方法能够在无人机处于高处时，输出大的比例参数，有助于跟随目标平台，在处于较低的高度时，输出较低的比例参数，有助于无人机实现精准降落。

图10给出的仿真环境中，无人机降落至移动平台的轨迹。如图10(a)、(b)、(c)所示，蓝色“×”表示无人机降落的初始位置，红色点线是3种方法控制下，无人机降落至移动平台的轨迹，紫色点表示无人机降落时，平台的位置，绿色线为移动平台的移动轨迹。无人机降落轨迹的终点与移动平台的终点距离是评判无人机降落效果的重要标准，两者距离近则认为降落的效果优。图10(b)和(c)中无人机轨迹终点与移动平台的距离更近，因此两种应用强化学习原理的方法有着更佳的控制效果。

图  10  3种方法降落至移动目标

Fig.  10  Trajectories of three approaches for landing on a moving platform

下载: 全尺寸图片

图10(d)是3种方法控制下无人机的降落轨迹对比图，在高处，使用矫正纠偏方法的强化学习PID方法控制无人机，控制无人机的动作幅度大，有助于无人机在高处跟随平台进行移动；在较低高度，本方法控制无人机的动作幅度小，从而实现精准降落。实验结果表明应用矫正纠偏框架的强化学习PID方法既能及时跟随平台移动，也能有比其他两种方法更高的降落精度，因此，使用矫正纠偏方法的强化学习PID方法在仿真环境中控制无人机降落的效果最佳。

4.3   无人机实体实验

在真实世界的设置与仿真环境中一致，并且模型的输入和输出也与仿真时相同。无人机降落的初始高度为3 m，并且初始位置偏离目标平台0.3 m。首先测试在静止平台上的降落，基于强化学习的方法不断输出动作，直到无人机降落至目标平台，具体轨迹如图11所示，无人机可以稳定地降落至目标平台的中心附近，在20次的测试中，无人机可以全部降落至目标点0.3 m半径内，认为无人机降落任务执行成功。

图  11  无人机（实体）降落至静止平台

Fig.  11  Trajectories of our approach for landing on a static platform

下载: 全尺寸图片

在协同系统执行任务时，大部分情况是移动或者不稳定的降落平台，因此，本文设置了无人机降落至移动平台的实验。实体实验设置为无人机降落的初始高度为3 m，并且初始位置偏离目标平台0.3 m，并且降落的平台在前后循环移动，速度在0.05~0.1 m/s范围内变化。如图12所示，实验结果证明使用矫正纠偏框架的深度强化学习方法能够控制无人机降落至移动的目标平台，有效完成移动平台在不稳定情况下的无人机降落任务。通过20次的测试，无人机都能够在平台移动的情况下，降落至偏离目标平台0.4 m半径内，认为无人机降落成功。综上，静止平台和移动平台的实验都证明了本文提出方法的有效性和稳定性。

图  12  无人机降落至速度为0.05~0.1m/s的平台

Fig.  12  Trajectories of our approach for landing on a moving platform

下载: 全尺寸图片

5.   结束语

本文提出一种用于无人机降落的深度强化学习方法。上层使用在矫正纠偏框架下的深度确定性策略梯度方法，用于不断输出PID参数，提高PID方法的实用性，在底层使用PID方法，直接输出控制量，用于控制无人机实现降落任务。强化学习模型在环境中不断训练，不断输出PID参数值，区别于固定PID方法，获得的模型有更优的控制效果。矫正纠偏框架将人类经验应用于强化学习模型训练中，在人类的指导下，得到的强化学习模型控制无人机降落时间更短，降落成功率更高。仿真实验和真实实验的实验结果都表明本文提出的结合矫正纠偏COACH框架的深度强化学习PID方法能有效完成无人机移动平台降落任务。