A hesitant fuzzy multi-attribute decision-making method with unknown attribute weights
-
摘要: 针对属性权重未知的犹豫模糊多属性决策，利用犹豫模糊元边界的确定性与边界内隶属度的犹豫性，把犹豫模糊元转换成集对分析中的三元联系数；再根据三元联系数的势函数和属性离差最大法确定属性权重，基此建立属性权重未知条件下的基于三元联系数的犹豫模糊多属性决策模型，利用模型中不同犹豫强度对备选方案进行排序。实例计算和对比分析结果表明，新模型不仅包含了其他模型得到的结果，还提供了更多潜在的排序方案信息，由此形成的有条件决策，是犹豫模糊多属性决策不确定性本质属性的映照，与犹豫模糊多属性决策实际应用情况吻合。Abstract: For hesitant fuzzy multi-attribute decision making (HFMADM) with unknown attribute weight, using the certainty of the hesitation fuzzy element boundary and the hesitation of the membership degree within the boundary, the hesitant fuzzy element is transformed into the ternary connection number (TCN) in set pair analysis. The attribute weight is then determined using the potential function of the TCN and the principle of maximum deviation of attributes. Furthermore, a hesitant fuzzy multi-attribute decision-making model based on TCN is established under the condition of unknown attribute weight. The possible ranking of alternatives is discussed by using different hesitant intensity values in the model. The results of case calculation and comparative analysis show that the new model not only contains the findings of other models but also provides other possible ranking alternatives. The conditional decision formed by this model reflects the essential attribute of uncertainty in HFMADM, which is consistent with its practical application.
-
多属性决策是有广泛应用背景的一类决策。但由于客观事物既有确定性一面又有不确定性一面，使得这一类决策问题通常受种种不确定性的困扰，决策者会因此在决策时产生一定的犹豫性，这使得Torra等[1-2]的犹豫模糊集（hesitant fuzzy set, HFS）理论应运而生。HFS理论允许元素属于集合的隶属度可以是若干个犹豫模糊值，一定程度上发展了Zadeh模糊集理论，吸引了不少学者基于HFS理论研究犹豫模糊环境下的多属性决策问题。Xia等[3]最早给出犹豫模糊集的数学表达式。在中国，张超等[4]研究了犹豫模糊图及其在多属性决策中的应用，武文颖等[5]给出了基于概率犹豫信息集成方法的群决策模型，王宝丽等[6]提出基于粒计算给出未知属性权重时的犹豫模糊多准则决策方法[7-10]等。集对分析理论能同时表示系统的确定性测度与不确定性测度以及两者之间的关系，把人们对事物的确定性与不确定性关系的辩证认识转换成一个具体的数学工具——联系数。集对分析自赵克勤[11]于1989年提出以来，已在人工智能和不确定性决策中得到应用[12-17]。文献[18]针对准则权系数信息不完全确定的多准则直觉模糊决策，将直觉模糊数转化为二元联系数，建立了基于二元联系数的多准则直觉模糊决策综合加权模型。文献[19-20]研究了区间数和联系数之间的关系，分别提出了准则值和准则权重为区间数的多准则决策方法。文献[21-22]中针对二元联系数信息的集成问题，定义了几种二元联系数信息集成的几何算子，提出了基于二元联系数的信息不完全的群决策方法。文献[23]通过将三角模糊数转化为二元联系数，提出了一种基于三角模糊数的二元联系数双重多属性决策方法。文献[24]将不确定语言变量转换为二元联系数，利用二元联系数的距离公式，建立了多目标规划模型。文献[25-26]利用二元联系数方法解决了区间直觉模糊多属性决策和犹豫模糊多属性决策问题。
本文利用犹豫模糊元边界的确定性与边界内隶属度取值的不确定性，把同样具有确定性与不确定性双重特性的集对分析理论中的三元联系数引入到属性权重未知的犹豫模糊多属性决策研究，建立了属性权重未知情况下的基于三元联系数的犹豫模糊多属性决策新模型，该新模型不仅包含了其他模型的结果，还提供了其他可能的方案排序结果，由此形成的有条件决策，是犹豫模糊多属性决策不确定性本质属性的映照，与犹豫模糊多属性决策实际应用情况吻合，且算法简明；此外，在第5节还介绍了经典势函数shi(μ)的扩展公式，使得本文给出的新模型有更好的潜力应对更为复杂的犹豫模糊多属性决策问题。
1. 权重未知的犹豫模糊多属性决策
1.1 犹豫模糊集
犹豫模糊集的基本特征在于用多个隶属度刻画给定元素对于给定集合的隶属程度。例如，3位科技专家在评估某科技项目创新程度时分别给出0.65、0.75、0.8三个隶属度，这3个隶属度用<0.65,0.75,0.8>表示，称之为犹豫模糊元。犹豫模糊元是犹豫模糊集理论的核心，一般用
$ {h_A}\left( x \right) $ 表示一个犹豫模糊元，定义如下。定义1 设X是一个非空集合，从集合X到
$ \left[ {0,1} \right] $ 区间上的一个函数称为犹豫模糊元（hesitant fuzzy element，HFE）。Xia等给出的犹豫模糊集的数学表达式为$$ M = \left\{ {\left\langle {x,{h_M}\left( x \right)} \right\rangle |x \in X} \right\} $$ (1) 式中：x代表某一属性；
$ {h_M}\left( x \right) $ 表示方案M对属性x的隶属程度,也称综合犹豫模糊元，它是方案M在n个属性上的n个犹豫模糊元${h_A}\left( x \right) ( A = 1, 2, \cdots, n )$ 的综合值。Torra给出犹豫模糊元的计算公式[2]：
$$\left\{\begin{aligned} &{h^c} = \bigcup\limits_{\gamma \in h} {\left\{ {1 - \gamma } \right\}}\\ &{h_1} \cap {h_2} = \bigcup\limits_{{\gamma _1} \in {h_1},{\gamma _2} \in {h_2}} {\min \left\{ {{\gamma _1},{\gamma _2}} \right\}}\\ &{h_1} \cup {h_2} = \bigcup\limits_{{\gamma _1} \in {h_1},{\gamma _2} \in {h_2}} {\max \left\{ {{\gamma _1},{\gamma _2}} \right\}}\end{aligned}\right.$$ 其中：h、h1、h2是3个犹豫模糊元。
熟悉模糊数学的人知道，对于两个和两个以上模糊隶属度作“取大取小”运算会丢失信息和导致误判。同理，对于两个和两个以上犹豫模糊元作“取大取小”运算也会丢失信息和导致误判。因此，如何科学地提取一个犹豫模糊元的犹豫模糊信息，又为后续的数学建模运算与决策提供方便，显然是犹豫模糊多属性决策研究的关键问题。
1.2 权重未知的犹豫模糊多属性决策问题
在犹豫模糊多属性决策问题中，属性权重对决策起着举足轻重的作用。通常，在给定的一个模糊多属性多方案决策问题中，属性权重由专家根据自身的知识和经验给定，但专家定权会有一定的主观性，简称主观定权；与主观定权法相反的有“客观定权法”，这是根据原始数据之间的关系来确定权重。在同一个多属性决策问题中，如何客观地给多个属性确定权重，是一个复杂的问题；为了界定本文要研究和解决的问题，下面对权重未知的犹豫模糊多属性决策问题先作一般性描述：设有四元组D=(S,Q,W,P)表示一个犹豫模糊多准则决策系统，其中S为评价对象集
$S = \left( {S_1},{S_2}, \cdots, \right. \left.{S_m} \right)$ ，$ m \geqslant 2 $ ；Q为评价属性集$Q = \left( {{Q_1},{Q_2}, \cdots, {Q_n}} \right)$ ，$ n \geqslant 2 $ ；且${Q_1},{Q_2}, \cdots, {Q_n}$ 都是越大越好的效益型属性；W为属性权重集$W = \left( {{w_1},{w_2}, \cdots, {w_n}} \right), \displaystyle\sum\limits_{k = 1}^n {{w_k} = 1,n \geqslant 2}$ ；P为评价函数$ P = f\left( {S \times Q} \right) \in \left[ {0,1} \right] $ 。要求在未知
$\left( {{w_1},{w_2}, \cdots ,{w_n}} \right)$ 具体数值，但$\displaystyle\sum\limits_{k = 1}^n {{w_k} = 1}$ 条件下，决断出S中的最优对象，并作出S中m个对象的优劣排序。当评价函数P为犹豫模糊元时，属性权重未知的犹豫模糊多属性决策问题可以进一步描述如下：
设有m个备用方案
$\left( {{S_1},{S_2}, \cdots, {S_m}} \right)$ ，每个方案各有n个相同的属性$({Q_1},{Q_2}, \cdots ,{Q_n} )$ ，但对每个属性的评价函数${P_{kt}}\left( {k = 1,2, \cdots, m;t = 1,2, \cdots, n} \right)$ 不同，且用犹豫模糊元$ {h_p}\left( {x{}_{kt}} \right) = \left( {{x_{kt1}},{x_{kt2}}, \cdots ,{x_{ktn}}} \right) $ 表示，属性权重${\boldsymbol{w}}={\left[ {{w_1}\;{w_2}\; \cdots \;{w_n}} \right]^{\text{T}}}$ ，${w_t} \in \left[ {0,1} \right], \displaystyle\sum\limits_{t = 1}^n {w_t} = 1$ ，但${w_1},{w_2}, \cdots , {w_n}$ 具体数值未知，为方便，约定各属性都是越大越好的效益型属性，要求在m个备用方案中决策出最优方案，并对这些方案在犹豫模糊环境下的优劣排序作犹豫模糊性分析。不难看出：属性权重未知的犹豫模糊多属性决策问题比属性权重已知的犹豫模糊多属性决策问题更为复杂。
2. 三元联系数
2.1 基于犹豫模糊元的三元联系数定义
三元联系数是集对分析理论中的一种结构函数，也称同异反联系数，其一般形式为
$\mu {\text{ = }}a + bi + cj$ ，但对应于不同的“反”有不同的类型，如“正负型‘反’（$ j = - 1,i \in \left[ { - 1,1} \right] $ ）”“有无型‘反’（$j = 0,i \in \left[ {0,1} \right]$ ）”等；为了把三元联系数用于未知属性权重的犹豫模糊多属性决策研究，重作定义：定义2 设
$ {h_A}\left( x \right) = \left( {{x_1},{x_2}, \cdots ,{x_n}} \right) $ 是一个犹豫模糊元，$0 < {x_1} < {x_2} < \cdots <{x_n} < 1$ ，$ {x_1},{x_2}, \cdots ,{x_n} \in \left[ {0,1} \right] $ ，并称x1是hA(x)的下界，xn是hA(x)的上界，令$$ a = {x_1} $$ (2) $$ b = {x_n} - {x_1} $$ (3) $$ c = 1 - {x_n} $$ (4) 称
$ \mu {\text{ = }}a + bi + cj $ ，$i = \left[ {0,1} \right] , j \in \left[ { - 1,0} \right] $ 为基于犹豫模糊元的三元联系数，或称犹豫模糊元联系数，也简称三元联系数。一般式为
$$\begin{gathered} \left\{\begin{aligned} &\mu = a + bi + cj, \\ & a + b + c = 1 , \end{aligned} \right. \\ \end{gathered}$$ (5) 式中：
$a \in \left[ {0,1} \right], b \in \left[ {0,1} \right], c \in \left[ {0,1} \right],i \in \left[ {0,1} \right] , j \in \left[ { - 1,0} \right] $ ，i称为犹豫模糊元联系数中偏于肯定的犹豫模糊强度系数，j称为犹豫模糊元联系数中偏于否定的犹豫模糊强度系数。统称i、j为犹豫模糊强度示性系数，简称示性系数。以上定义的三元联系数具有以下性质。
性质1 与犹豫模糊元具有等价性。
证明 根据定义2和式（5）可知，当三元联系数中的示性系数i，j取适当的数值时，可以得到由式（1）定义的犹豫模糊元中任意一个隶属度，例如前面提到的犹豫模糊元
${h_A}\left( x \right) = \left( 0.65,0.75,0.8 \right)$ ，由此按定义2得到犹豫模糊元三元联系数$$ \begin{gathered} \mu = 0.65+ \left( {0.8 - 0.65} \right)i + \left( {1 - 0.8} \right)j = \\ 0.65 + 0.15i + 0.2j \\ \end{gathered} $$ 显然有
$$ \mu {\text{ = }}0.65{\text{ + }}0.15i + 0.2j|_{j = 0}^{i = 0} = 0.65 $$ $$ \mu {\text{ = }}0.65 + 0.15i + 0.2j|_{j = 0}^{i = 0.667} = 0.75 $$ $$ \mu {\text{ = }}0.65 + 0.15i + 0.2j|_{j = 0}^{i = 1} = 0.8 $$ 性质2 系统性。
证明 首先，式（5）所示三元联系数具有整体性，这是因为相对于犹豫模糊元
${h_A}\left( x \right) = \left( {x_1},{x_2}, \cdots, {x_n} \right)$ ，多了hA(x)的补集$ \overline{\overline {{h_A}\left( x \right)}} $ ，也就是，有$ {h_A}\left( x \right) = cj $ ，${h_A}\left( x \right) = a + bi$ 。根据系统是由两个或两个以上要素组成的有机整体的定义，可知式（5）所示三元联系数是一个系统，所以具有系统性。
其次，三元联系数的系统性还体现在3个联系分量a，bi，cj的层次性，这种层次性由3个联系分量的示性系数1，i，j得到充分体现，因为
$ i \in \left[ {0,1} \right] $ ，$ j \in \left[ { - 1,0} \right] $ 。再次，在
$ \mu {\text{ = }}a + bi + cj $ 中a、bi、cj存在相互作用，例如当i、j有具体数值时，会对a起增减作用。第四，不确定性。不仅
$ i \in \left[ {0,1} \right] $ ，$ j \in \left[ { - 1,0} \right] $ 在各自的定义区间取哪一个具体数值具有不确定性，而且当i在[0,1]取定某个具体的数值时，是加大a还是减小c也具有不确定性；同理，当j在[−1,0]取定某个具体的数值时，是减小a还是减小b也具有不确定性。显然，上述不确定性说明了式（5）所示三元联系数不仅是一个不确定性系统，也同时说明应用三元联系数解决不确定性多属性决策问题时与实际不确定性环境的对应性与灵活性。
性质3 可比较性。
证明 情况1，示性系数效应结果比较。根据定义2，易知
$$ \left( {a + bi + cj|_{j = 0}^{i = 1}} \right) > \left( {a + bi + cj|_{j = - 1}^{i = 1}} \right) $$ $$ \left( {a + bi + cj|_{j = 0}^{i = 0}} \right) > \left( {a + bi + cj|_{j = - 1}^{i = 0}} \right) $$ 成立。
情况2，示性系数有确定值时的结果比较。由情况1进一步推知，当两个三元联系数
$\,{\mu_1}= a{}_1 + {b_1}{i_1} + {c_1}{j_1}$ 与$\, {\mu_2}= {a_2} + {b_2}i + {c_2}j$ 中的i1，j1与i2，j2各有确定的值时，$\,{\mu_1} $ 与$\,{\mu_2} $ 能比较大小。例如对于三元联系数
$\, {\mu_1}{\text{ = }}0.6{\text{ + }}0.3{i_1} + 0.1{j_1}$ 与$ {\mu_2}{\text{ = }}0.5{\text{ + }}0.25{i_2} + 0.25{j_2} $ ，当$ {i_1} = 0.3 $ ，$ {j_1} = - 0.5 $ ，$ {i_2} = 0.8 $ ，${j_2} = - 0.1$ 时，有$\,{\mu_1} = 0.6 + 0.09 - 0.05 = 0.64 $ ，$ \,{\mu_2}= 0.5 + 0.2 - 0.025 = 0.675$ 。显然，这时有$\,{\mu_2>\,{\mu_1}} $ 。情况3，同异反联系分量几何合成结果比较。把三元联系数
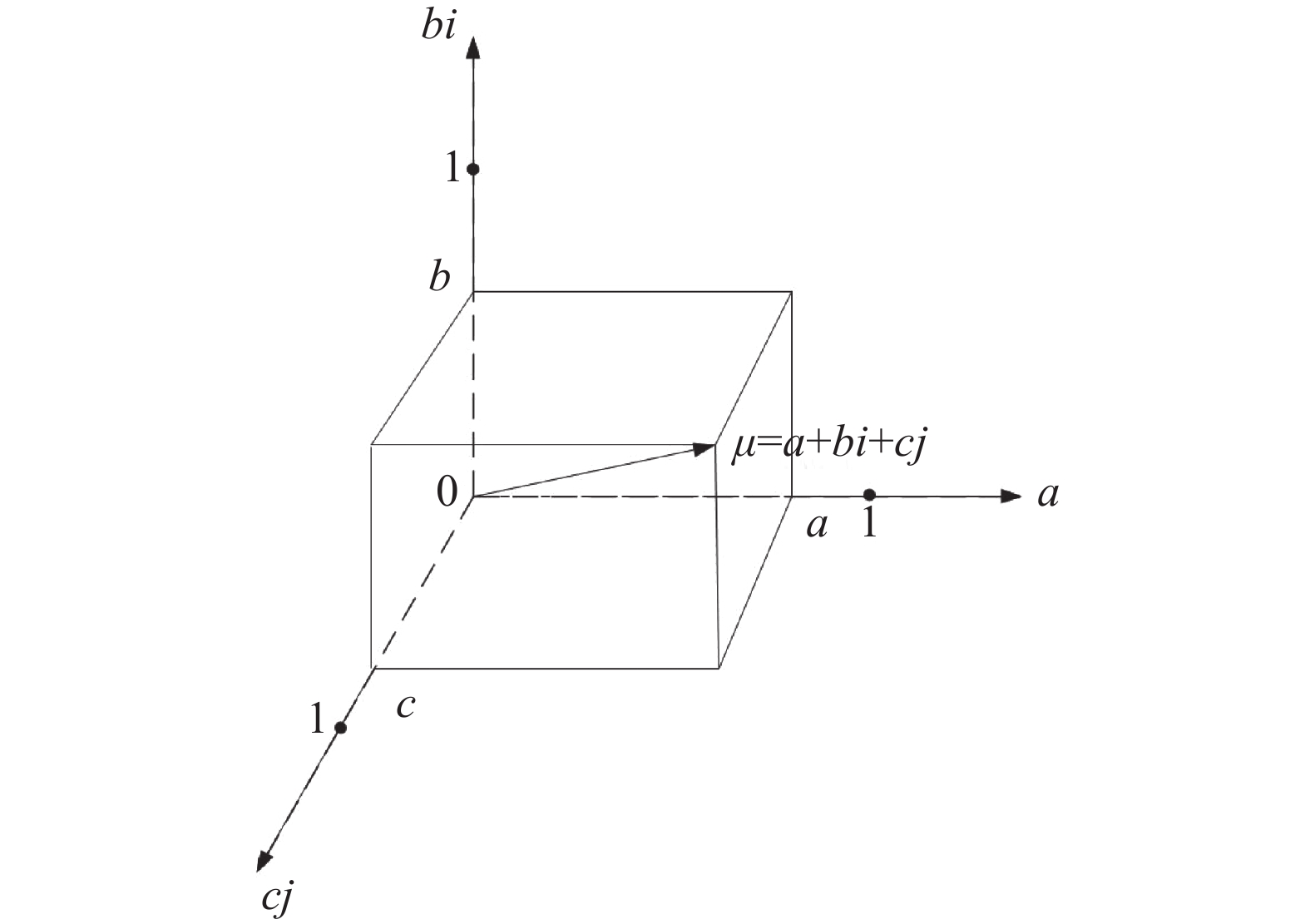
$\, {\mu _k} = {a_k} + {b_k}{i_k} + {c_k}{j_k}\left( {k = 1,2, \cdots ,n} \right) $ 映射到“同异反”三维空间见图1，计算三元联系数的“模”：$$ {r_k} = \sqrt {a_k^2 + b_k^2 + c_k^2} \;\;\left( {k = 1,2, \cdots ,n} \right) $$ 根据“模”rk的大小关系确定n个三元联系数
$ \,{\mu _k} = {a_k} + {b_k}{i_k} + {c_k}{j_k} $ 的大小关系。其原理是把三元联系数看成是一组三维向量，在“同异反犹豫模糊决策”空间中求这三组三维向量的合成，见图1。
图 1 同异反犹豫模糊空间中的同异反犹豫向量合成示意Fig. 1 Synthesis of identical discrepancy contrary vectors in identical discrepancy contrary hesitant fuzzy space
下载:
全尺寸图片
从图1看出，三元联系数
$ a + bi + cj $ 的“模”是正向（肯定的）确定性测度a与负向（否定的）确定性测度c和不确定的犹豫测度bi在$ i = 1 $ 时的一种几何合成。情况4，与完全非犹豫点的距离比较。
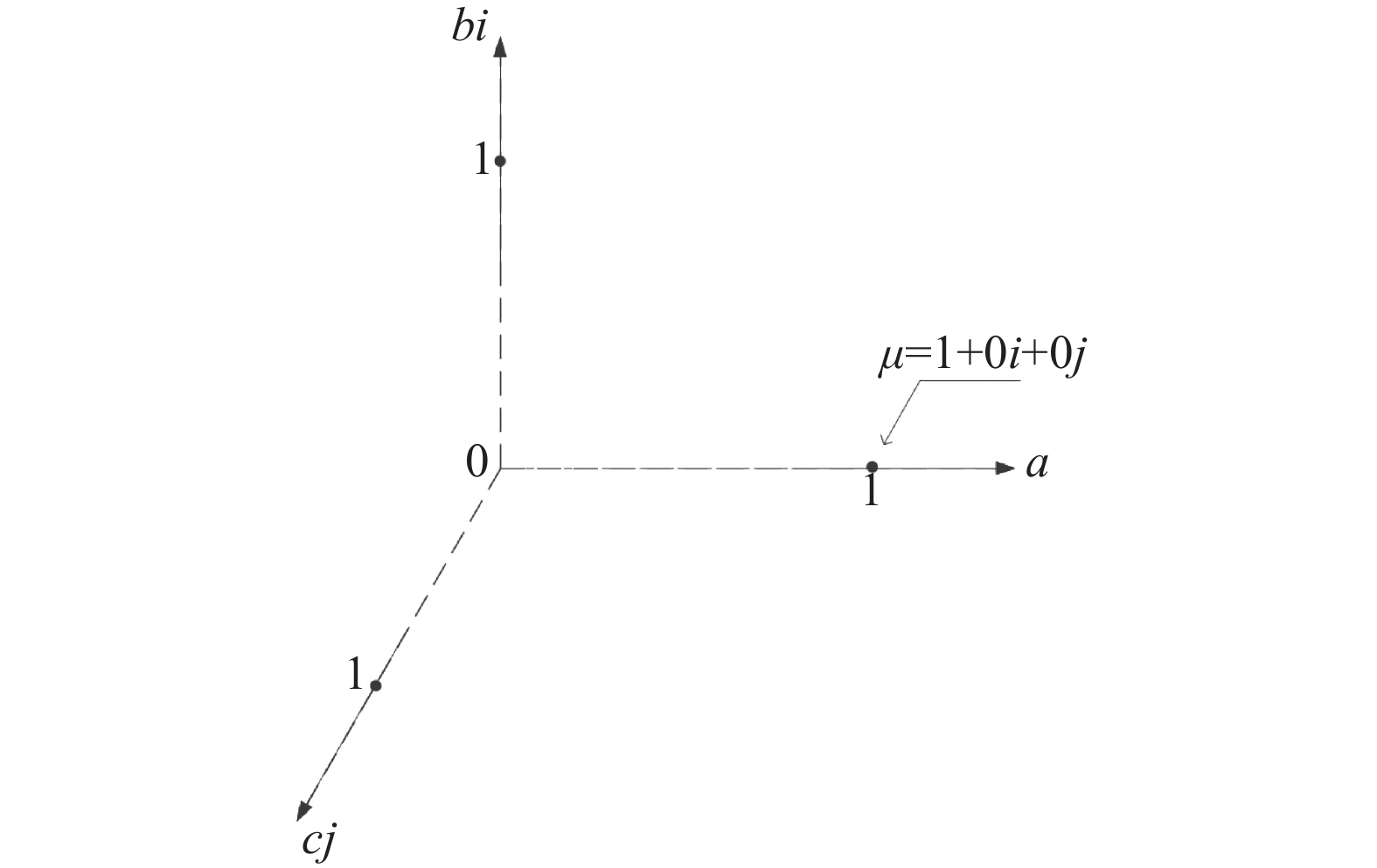
定义3 由定义1和定义2，可以进一步称犹豫模糊元三元联系数为
$ \,{\mu _{{h_A}\left( x \right)}} = 1 + 0i + 0j $ 在图1所示同异反犹豫模糊决策空间中的点为完全肯定点（完全非犹豫点），记为$\, {\mu _{\left( {1,0,0} \right)}} $ ，见图2。计算任意一个非完全不犹豫点
$\,{\mu _k} = {a_k} + {b_k}i + {c_k} j\left( {k = 1,2, \cdots ,n} \right)$ 与完全非犹豫点$ \,{\mu _{\left( {1,0,0} \right)}} $ 的海明距离ρ，即$$ \begin{gathered} \rho \left( {k \to 1,0,0} \right) = \sqrt {{{\left( {{a_k} - 1} \right)}^2} + {{\left( {{b_k} - 0} \right)}^2} + {{\left( {{c_k} - 0} \right)}^2}} =\\ \sqrt {{{\left( {{a_k} - 1} \right)}^2} + {b_k}^2 + {c_k}^2} \end{gathered}$$ 当有m个非完全不犹豫点时，可以根据它们与完全肯定点（完全非犹豫点）
$\, {\mu _{\left( {1,0,0} \right)}} $ 的距离大小作出肯定程度的比较，与$\, {\mu _{\left( {1,0,0} \right)}} $ 距离小的要比与$\, {\mu _{\left( {1,0,0} \right)}} $ 距离大的肯定。
图 2 同异反犹豫模糊决策空间中完全非犹豫点Fig. 2 Completely non-hesitant point in identical discrepancy contrary hesitant fuzzy space下载:
全尺寸图片
情况5，势函数比较。
定义4 当犹豫模糊三元联系数
$\,\mu = a + bi + cj$ 中的ck不是零时，定义$ {a \mathord{\left/ {\vphantom {a c}} \right. } c} $ 为犹豫模糊三元联系数$\, \mu {\text{ = }}a + bi + cj $ 的势函数，记为$$ {\text{shi}}\left( \mu \right) = {a \mathord{\left/ {\vphantom {a c}} \right. } c} $$ (6) 利用势函数可以比较两个犹豫模糊三元联系数势的大小。
2.2 三元联系数的运算
根据集对分析理论，三元联系数可以作普通的加减乘除四则运算，但本文仅用到其中的加法运算和乘法运算，定义如下：
定义5 设
$ {\mu _1} = {a_1} + {b_1}i + {c_1}j $ ，$\, {\mu _2} = {a_2} + {b_2}i + {c_2}j $ 是两个三元联系数，则它们的和是一个三元联系数$\, \mu {\text{ = }}a + bi + cj $ ，记作$$ \mu {\text{ = }}{\mu _1}{\text{ + }}{\mu _2}{\text{ = }}a + bi + cj $$ 式中：
$ a = {a_1} + {a_2} $ ，$ b = {b_1} + b{}_2 $ ，$ c = {c_1} + {c_2} $ 。从定义5看出，三元联系数的加法运算满足交换律，对于三个和更多个三元联系数相加满足结合律。
定义6 设
$ \,{\mu _1} = {a_1} + {b_1}i + {c_1}j $ ，$ \,{\mu _2} = {a_2} + {b_2}i + {c_2}j $ 是两个三元联系数，则他们的乘积是一个三元联系数$\, \mu {\text{ = }}a + bi + cj $ ，记作$$ \mu = {\mu _1} \times {\mu _2} = a + bi + cj $$ 式中：
$ a = {a_1}{a_2} + {c_1}{c_2} $ ，$ b = {b_1}{a_2} + {b_2}{a_1} + {b_1}{b_2} + {c_1}{b_2} $ ，$c = {a_1}{c_2} + {b_1}{c_2} + {a_2}{c_1}$ ，示性系数i，j在以上运算过程中的规则是$ ii = i $ ，$ ij = j $ ，$ jj = 1 $ 。从定义6看出, 三元联系数的乘法运算满足交换律，对于三个和更多个三元联系数相乘满足结合律。
定义7 一个不等于零的实数
$ k\left( {k \ne 0} \right) $ 与三元联系数$ \,\mu = a + bi + cj $ 相乘，其积仍然是一个三元联系数。记作$$ k\mu = k\left( {a + bi + cj} \right) = ka + kbi + kcj $$ 3. 算法步骤
1)将决策者对各方案在每个属性下的评价值进行数学表达形式转换。应用式(2~5)把专家给出的各属性评价值犹豫模糊元转换成三元联系数形式。
2)利用式(6)，即三元联系数
$\,\mu = a + bi + cj$ 的势函数$ {\text{shi}}\left( \mu \right) $ 计算公式，计算1)中得到的各三元联系数的势函数值。3)利用基于离差的属性权重计算公式计算各属性权重：
$$ {w_{kt}} = \dfrac{{\max {\text{shi}}\left( {{\mu _{kt}}} \right) - \min {\text{shi}}\left( {{\mu _{kt}}} \right)}}{{\displaystyle\sum\nolimits_{k = 1}^n {\left[ {\max {\text{shi}}\left( {{\mu _{kt}}} \right) - \min {\text{shi}}\left( {{\mu _{kt}}} \right)} \right]} }} $$ (7) 4)利用综合加权求和计算公式计算各评价对象的综合三元联系数：
$$ \mu \left( {{u_k}} \right) = \displaystyle\sum\limits_{k = 1}^n {\mu \left( {{c_k}} \right)} w\left( {{c_k}} \right) $$ (8) 5)犹豫性分析。利用犹豫示性系数i，j取不同值时各评价对象的三元联系数值，讨论犹豫性对初排序的影响。
6)给出决策建议。根据以上5步结果，提出决策建议，说明在何种犹豫模糊条件下的最优方案及其他方案的优劣排序。
4. 应用实例
为便于作对比分析，以下用2个实例来验证本文前述模型的有效性。其中实例1取自文献[6]，实例2取自文献[27]。
实例1 某企业为选拔一重要部门优秀管理人员，需要作多属性决策。企业负责人根据2位专家的建议，从5位备选管理人员u1~u5 中根据专业技能c1、理性技能c2、人际交往技能c3和设计技能c4四个方面选择1位部门经理。各个考核准则权重未知。一方面，由于两位专家来自不同部门，对各个备选人员在不同属性上的模糊评判可能不同，即产生犹豫模糊判断值；另一方面，可能有专家对部分备选人员在一些属性上的表现把握不准或了解不够，从而出现不能给出模糊值的情况，如人力资源部门的管理人员对备选人员u1的人际交往技能c3方面了解不够，因此未做出评价，仅有本部门2个评估专家给出的模糊判断值0.5。2位专家对备选人员的判断评价信息如表1所示。试给出5个排序对象的优劣次序。
1)根据式(2)、(3)、(4)、(5)把表1中的各个犹豫模糊元改写出成三元联系数的形式，得表2。
表 1 犹豫模糊决策系统Table 1 Hesitant fuzzy decision making system对象 c1 c2 c3 c4 u1 {0.4,0.6} {0.8} {0.5} {0.4} u2 {0.5} {0.4,0.9} {0.6} {0.7} u3 {0.3,0.7} {0.5,0.7} {0.5,0.7} {0.3} u4 {0.6} {0.6,0.8} {0.8} {0.6,0.8} u5 {0.6} {0.7} {0.55,0.65} {0.6} 表 2 用三元联系数表示的犹豫模糊决策系统Table 2 Hesitant fuzzy decision making system expressed TCN人员 μ(c1) μ(c2) μ(c3) μ(c4) u1 0.4+0.2i+0.4j 0.8+0i+0.2j 0.5+0i+0.5j 0.4+0i+0.6j u2 0.5+0i+0.5j 0.4+0.5i+0.1j 0.6+0i+0.4j 0.7+0i+0.3j u3 0.3+0.4i+0.3j 0.5+0.2i+0.3j 0.5+0.2i+0.3j 0.3+0i+0.7j u4 0.6+0i+0.4j 0.6+0.2i+0.2j 0.8+0i+0.2j 0.6+0.2i+0.2j u5 0.6+0i+0.4j 0.7+0i+0.3j 0.55+0.1i+0.35j 0.6+0i+0.4j 2)利用三元联系数
$ \mu = a + bi + cj $ 的势函数$ {\text{shi}}\left( \mu \right) $ 计算公式式(6)，计算表2中各三元联系数的势函数值，得表3。表 3 一个犹豫模糊决策系统三元联系数的势函数Table 3 Potential function of TCN in a hesitant fuzzy decision making system人员 $ {\text{sh}}{{\text{i}}_{{c_1}}}\left( \mu \right) $ $ {\text{sh}}{{\text{i}}_{{c_2}}}\left( \mu \right) $ $ {\text{sh}}{{\text{i}}_{{c_3}}}\left( \mu \right) $ $ {\text{sh}}{{\text{i}}_{{c_4}}}\left( \mu \right) $
u1 1.0000 4.0000 1.0000 0.6667 u2 1.0000 4.0000 1.5000 2.3333 u3 1.0000 1.6667 1.6667 0.4286 u4 1.5000 3.0000 4.0000 3.0000 u5 1.5000 2.3333 1.5714 1.5000 3)利用式(7)，得到各属性权重为
$$ {w_{{c_1}}} = 0.059\;5 $$ $$ {w_{{c_2}}} = 0.277\;6 $$ $$ {w_{{c_3}}} = 0.356\;9 $$ $$ {w_{{c_4}}} = 0.305\;9 $$ 4)利用式(8)，计算得u1、u2、u3、u4、u5 5个评价对象各自的综合三元联系数：
$$ \mu \left( {{u_1}} \right) = 0.546\;7 + 0.011\;9i + 0.441\;4j $$ $$ \mu \left( {{u_2}} \right) = 0.569\;1 + 0.138\;8i + 0.292\;1j $$ $$ \mu \left( {{u_3}} \right) = 0.426\;9 + 0.150\;7i + 0.422\;4j $$ $$ \mu \left( {{u_4}} \right) = 0.671\;4 + 0.116\;7i + 0.211\;9j $$ $$ \mu \left( {{u_5}} \right) = 0.609\;9 + 0.035\;7i + 0.354\;4j $$ 5)犹豫性分析。
分别考察犹豫示性系数i、j取不同值时的5个评价对象的三元联系数值，并给出优劣排序，结果见表4。
表 4 优劣排序比较Table 4 Comparison of ranking三元联系数 $ i = 0,j = 0 $ $ i = 0.5,j = 0 $ $ i = 1,j = 0 $ $ i = 1,j = - 0.5 $ $ i = 0.5,j = - 0.5 $ $ i = 0,j = - 1 $ $\mu \left( {{u_1}} \right) $ 0.5467 0.5527 0.5586 0.3380 0.3320 0.1054 $\mu \left( {{u_2}} \right) $ 0.5691 0.6385 0.7079 0.5619 0.4925 0.2771 $\mu \left( {{u_3}} \right) $ 0.4269 0.5023 0.5776 0.3664 0.2911 0.0045 $\mu \left( {{u_4}} \right) $ 0.6714 0.7297 0.7881 0.6822 0.6238 0.4595 $\mu \left( {{u_5}} \right) $ 0.6099 0.6278 0.6456 0.4684 0.4506 0.2555 序次与文献[6]比较 同
u4最好异
u4最好异
u4最好异
u4最好异
u4最好异
u4最好6)决策建议。
首先，从表4看出，无论是在哪一种犹豫情况下，u4最好。其次，由表4看出，5个评价对象在i=0，j=0时的排序与文献[6]得到的5个评价对象排序相同，提示文献[6]所用到的算法并没有从实质上计及决策者的犹豫模糊性；表4第3列到第7列在计及决策者的犹豫模糊性之后，显示出这5个评价对象的优劣排序跟随犹豫强度变化而变化，这符合犹豫模糊决策实际。
实例2 某企业董事会的5名成员计划制定未来5年内的战略计划。假设有4种可能的方案
$ {Y_i}\left( {i = 1,2,3,4} \right) $ 要进行评估。选择其中最重要的项目，并从其重要性的角度进行排序，考虑如下4个属性：G1财务支出，G2客户满意度，G3内部业务流程，G4学习与成长前景。企业董事会成员对各方案在不同属性下的评估值如表5所示。表 5 犹豫模糊决策信息表Table 5 Hesitant fuzzy decision information table方案 G1 G2 G3 G4 Y1 {0.2,0.4,0.7} {0.2,0.6,0.8} {0.2,0.3,0.6,0.7,0.9} {0.3,0.4,0.5,0.7,0.8} Y2 {0.2,0.4,0.7,0.9} {0.1,0.2,0.6,0.7,0.9} {0.3,0.4,0.6,0.9} {0.5,0.6,0.8,0.9} Y3 {0.3,0.5,0.6,0.7} {0.2,0.4,0.5,0.6} {0.3,0.5,0.7,0.8} {0.2,0.5,0.6,0.7} Y4 {0.3,0.5,0.6} {0.2,0.4} {0.5,0.6,0.7} {0.8,0.9} 1)根据式(2)~(5)将表6中专家对各个属性的评估值改写出成三元联系数的形式，得表6。
表 6 用三元联系数表示的犹豫模糊决策信息表Table 6 Hesitant fuzzy decision information table expressed by TCNs方案 G1 G2 G3 G4 Y1 0.2+0.5i+0.3j 0.2+0.6i+0.2j 0.2+0.7i+0.1j 0.3+0.5i+0.2j Y2 0.2+0.7i+0.1j 0.1+0.8i+0.1j 0.3+0.6i+0.1j 0.5+0.4i+0.1j Y3 0.3+0.4i+0.3j 0.2+0.4i+0.4j 0.3+0.5i+0.2j 0.2+0.5i+0.3j Y4 0.3+0.3i+0.4j 0.2+0.2i+0.6j 0.5+0.2i+0.3j 0.8+0.1i+0.1j 2)利用三元联系数的势函数
$ {\text{shi}}\left( \mu \right) $ 计算公式，计算表6各三元联系数的势函数值，得表7。3)根据式(7)计算得各属性权重为
$$ {w_{{G_1}}} = 0.123\;1 $$ $$ {w_{{G_2}}} = 0.061\;5 $$ $$ {w_{{G_3}}} = 0.138\;5 $$ $$ {w_{{G_4}}} = 0.676\;9 $$ 表 7 犹豫模糊决策信息中三元联系数的势函数Table 7 Potential function of TCN in hesitant fuzzy decision making information方案 $ {\text{sh}}{{\text{i}}_{{G_1}}}\left( \mu \right) $ $ {\text{sh}}{{\text{i}}_{{G_2}}}\left( \mu \right) $ $ {\text{sh}}{{\text{i}}_{{G_3}}}\left( \mu \right) $ $ {\text{sh}}{{\text{i}}_{{G_4}}}\left( \mu \right) $ Y1 0.6667 1.0000 2.0000 1.5000 Y2 2.0000 1.0000 3.0000 5.0000 Y3 1.0000 0.5000 1.5000 0.6667 Y4 0.7500 0.3333 1.6667 8.0000 4)利用式(8)计算出各方案的综合三元联系数：
$$ \mu \left( {{Y_1}} \right) = 0.267\;7 + 0.533\;8i + 0.198\;5j $$ $$ \mu \left( {{Y_2}} \right) = 0.410\;8 + 0.489\;2i + 0.100\;0j $$ $$ \mu \left( {{Y_3}} \right) = 0.226\;2 + 0.481\;5i + 0.292\;3j $$ $$ \mu \left( {{Y_4}} \right) = 0.660\;0 + 0.144\;6i + 0.195\;4j $$ 5)犹豫性分析。
计算犹豫示性系数i，j取不同值时4个方案的三元联系数值，并给出优劣排序，结果见表8。
表 8 4个方案的优劣排序比较Table 8 Comparison of the ranking for four schemes三元联系数 $i = 0, j = 0$ $i = 0.5, j = 0$ $i = - 0.5 , j = 0$ $i = 0.5, j = 0.5$
$i = 0.5 , j = - 0.5$ $i = 0, j = - 1$ $ \mu \left( {{Y_1}} \right) $ 0.2677 0.5346 0.0008 0.6338 0.4354 0.0692 $ \mu \left( {{Y_2}} \right) $ 0.4108 0.6554 0.1662 0.7054 0.6054 0.3108 $ \mu \left( {{Y_3}} \right) $ 0.2262 0.4669 −0.0146 0.6131 0.3208 −0.0662 $ \mu \left( {{Y_4}} \right) $ 0.6600 0.7323 0.5877 0.8300 0.6346 0.4646 序次与文献[27]比较 同
Y4最好同
Y4最好同
Y4最好同
Y4最好同
Y4最好同
Y4最好6)决策建议。从5)中看出，当4个方案联系数中的i和j同步取值时（同步犹豫），Y4最好。这与文献[27]中的决策建议一致。但是不同步取值（不同步犹豫）时，每个方案都有可能成为最优。
5. 讨论
5.1 模型的有效性
本文把集对分析中的三元联系数用于属性权重未知的犹豫模糊多属性决策研究，核心工作是把犹豫模糊元转换成三元联系数
$\, \mu = a + bi + cj $ ，继而利用三元联系数的势函数$ {\text{shi}}\left( \mu \right) $ ，按“离差最大法”计算得到各属性的权重，为处理未知属性权重的犹豫模糊多属性决策问题提供了一个新途径。实例应用表明，这一新思路可行且有效，其有效性首先源自把犹豫模糊元$ {h_A}\left( x \right) $ 转换成三元联系数$\, \mu=a+b i+c i $ 的过程，较为系统地保留了的犹豫模糊信息；其次是建立基于三元联系数的犹豫模糊多属性决策模型；三是从不同角度和不同算法提取三元联系数的系统信息；四是就各方案的各属性加权综合后的三元联系数$\, \mu \left( {{u_k}} \right) $ 作不同犹豫模糊强度下的不确定性分析，在数值上重现出犹豫模糊不确定性在决策空间中的真实犹豫模糊图景，从而保证了模型计算结果对各种犹豫模糊情况的总体覆盖，保证了犹豫模糊不确定性决策建议的客观合理性和科学性。从系统科学的角度看，本文介绍的基于三元联系数$\, \mu = a + bi + cj $ 的属性权重未知的犹豫模糊多属性决策模型，其有效性来自三元联系数系统地利用了问题给出的犹豫模糊结构信息。5.2 关于势函数
三元联系数
$\, \mu=a+b i+c i $ 的势函数$ \operatorname{shi}(\mu) $ 在本文研究中起着重要的作用，其所以有效，主要是规避了三元联系数中犹豫模糊不确定性的干扰且又在一定程度上映射出三元联系数中犹豫模糊不确定性与确定性关系的某种整合性，因为从数学上，由式（5）定义的三元联系数可以与其伴随的二元表达式等价，势函数$ {\text{shi}}\left( \mu \right){{{\text{ = }}a} \mathord{\left/ {\vphantom {{{\text{ = }}a} c}} \right. } c} $ 采用两个联系分量a和c相除的形式，表达了μ中肯定的犹豫模糊信息与否定的犹豫模糊信息之相互作用，根据三元联系数$\, \mu=a+b i+c i $ 与伴随函数$\,\mu = a + cj$ 的等价性，立即知道三元联系数$ \,\mu=a+b i+c i $ 的势函数$ \operatorname{shi}(\mu)=a / c $ 有代表性地表达了三元联系数μ中肯定的犹豫模糊信息与否定的犹豫模糊信息之间相互作用；从而使得后续利用势函数$ {\text{shi}}\left( \mu \right) $ 的最大离差原则确定属性权重能得到客观的结果，为保证模型结果的有效性提供了前提。但最近的研究表明，三元联系数$ \mu=a+b i+c i $ 的经典势函数$ \operatorname{shi}(\mu)=a / c $ 可以扩展成一种新的数学形式，记为${\text{shi}}\left( \mu \right) = \dfrac{a}{c} + \dfrac{b}{c}i$ ，$ \text { shi }(\mu) $ 能比$ \operatorname{shi}(\mu)=a / c $ 更完整地表达三元联系数$ \mu=a+b i+c i $ 的宏观趋势，这时，称$ \operatorname{shi}(\mu)=a / c $ 是$\operatorname{shi}(\mu)=\dfrac{a}{c}+\dfrac{b}{c} i$ 中的主势函数，我们称${\text{shi}}\left( \mu \right) = \dfrac{a}{c} + \dfrac{b}{c}i$ 与三元联系数$ \,\mu = a + bi + cj $ 是强等价，$ {\text{shi}}\left( \mu \right){\text{ = }}{a \mathord{\left/ {\vphantom {a c}} \right. } c} $ 与三元联系数$\, \mu = a + bi + cj $ 是弱等价。依此思路可知，本文前面仅仅是把$\operatorname{shi}(\mu)=\dfrac{a}{c}+ \dfrac{b}{c} i$ 中的主势函数用于属性权重未知的犹豫模糊多属性决策研究，当计及$\operatorname{shi}(\mu)=\dfrac{a}{c}+\dfrac{b}{c} i$ 中的次势函数$\dfrac{b}{c}i$ 时，由于i的犹豫模糊特性，将得到各属性的犹豫模糊权重，从而更加全面也更加真实地反映出犹豫模糊环境下未知属性权重本身的犹豫模糊性，但相应的决策算法也更复杂，限于篇幅，本文不做展开，待另文介绍。5.3 关于犹豫模糊条件决策
犹豫模糊条件决策是本文提出的一个新概念。从数学的角度看，犹豫模糊多属性决策是一类在犹豫模糊空间中展开的决策，这个空间本身具有犹豫模糊性，犹豫模糊多属性决策系统是该空间中的一个有限子空间，这个有限子空间与周围的空间有着信息的交换，所有这些信息构成了犹豫模糊决策条件集；显然，在犹豫模糊空间中展开的犹豫模糊决策，本质上离不开这些犹豫模糊条件的约束，这是犹豫模糊条件决策的空间几何解释。本文给出的基于三元联系数的犹豫模糊多属性决策模型则是犹豫模糊条件决策的一种简化了的数学模型，模型中的犹豫模糊示性系数i、j如实地把不同犹豫模糊条件下的犹豫模糊强度信息传递给有关决策参数，化解了由“犹豫”和“模糊”两类不确定因素叠加而致的复杂性，在保证模型计算结果客观合理的同时又让算法具有经济性、简明性和实用性。
另一方面，“犹豫模糊条件决策”也将是一个会引发争鸣的概念。因为，从犹豫模糊多属性决策文献[4-10]和文献[27]看，这些文献介绍的工作都是通过某种算法得到唯一确定的计算结果，进而给出基于这一确定的计算结果的决策建议。由此引出一个值得深思的问题：面对一个犹豫模糊多属性决策问题，研究结果是给出一个唯一确定的决策建议好，还是给出不同犹豫模糊强度条件下的决策建议集好。这需要有关犹豫模糊决策研究人员深思，也需要大量的决策实践检验。
6. 结束语
本文把集对分析中的三元联系数用于属性权重未知的犹豫模糊多属性决策研究，发现基于三元联系数的属性权重未知的犹豫模糊多属性决策模型的计算结果中，不仅包括了同一个属性权重未知的犹豫模糊多属性决策问题用粒计算得到的结果，还得到其他的方案优劣排序，真实地映照出属性权重未知的犹豫模糊多属性决策系统在犹豫模糊多属性决策空间中与犹豫模糊环境进行犹豫模糊信息交换，影响到决策结果的真实图景；文章对犹豫模糊环境中的“犹豫模糊条件决策”概念作出了几何解释和数量化解释；还介绍了三元联系数经典势函数
$ {\text{shi}}\left( \mu \right) $ 的扩展公式，使得本文给出的模型有更好的适用性；当然，作为一种新的属性权重未知的犹豫模糊多属性决策方法，仍然需要有更多的实例验证和决策实践检验，也需要在形式化和程序化处理上作进一步研究，以便于用计算机处理此类问题，这也是下一步的工作。 -
图 1 同异反犹豫模糊空间中的同异反犹豫向量合成示意
Fig. 1 Synthesis of identical discrepancy contrary vectors in identical discrepancy contrary hesitant fuzzy space
下载:
全尺寸图片
图 2 同异反犹豫模糊决策空间中完全非犹豫点
Fig. 2 Completely non-hesitant point in identical discrepancy contrary hesitant fuzzy space
下载:
全尺寸图片
表 1 犹豫模糊决策系统
Table 1 Hesitant fuzzy decision making system
对象 c1 c2 c3 c4 u1 {0.4,0.6} {0.8} {0.5} {0.4} u2 {0.5} {0.4,0.9} {0.6} {0.7} u3 {0.3,0.7} {0.5,0.7} {0.5,0.7} {0.3} u4 {0.6} {0.6,0.8} {0.8} {0.6,0.8} u5 {0.6} {0.7} {0.55,0.65} {0.6} 表 2 用三元联系数表示的犹豫模糊决策系统
Table 2 Hesitant fuzzy decision making system expressed TCN
人员 μ(c1) μ(c2) μ(c3) μ(c4) u1 0.4+0.2i+0.4j 0.8+0i+0.2j 0.5+0i+0.5j 0.4+0i+0.6j u2 0.5+0i+0.5j 0.4+0.5i+0.1j 0.6+0i+0.4j 0.7+0i+0.3j u3 0.3+0.4i+0.3j 0.5+0.2i+0.3j 0.5+0.2i+0.3j 0.3+0i+0.7j u4 0.6+0i+0.4j 0.6+0.2i+0.2j 0.8+0i+0.2j 0.6+0.2i+0.2j u5 0.6+0i+0.4j 0.7+0i+0.3j 0.55+0.1i+0.35j 0.6+0i+0.4j 表 3 一个犹豫模糊决策系统三元联系数的势函数
Table 3 Potential function of TCN in a hesitant fuzzy decision making system
人员 $ {\text{sh}}{{\text{i}}_{{c_1}}}\left( \mu \right) $ $ {\text{sh}}{{\text{i}}_{{c_2}}}\left( \mu \right) $ $ {\text{sh}}{{\text{i}}_{{c_3}}}\left( \mu \right) $ $ {\text{sh}}{{\text{i}}_{{c_4}}}\left( \mu \right) $
u1 1.0000 4.0000 1.0000 0.6667 u2 1.0000 4.0000 1.5000 2.3333 u3 1.0000 1.6667 1.6667 0.4286 u4 1.5000 3.0000 4.0000 3.0000 u5 1.5000 2.3333 1.5714 1.5000 表 4 优劣排序比较
Table 4 Comparison of ranking
三元联系数 $ i = 0,j = 0 $ $ i = 0.5,j = 0 $ $ i = 1,j = 0 $ $ i = 1,j = - 0.5 $ $ i = 0.5,j = - 0.5 $ $ i = 0,j = - 1 $ $\mu \left( {{u_1}} \right) $ 0.5467 0.5527 0.5586 0.3380 0.3320 0.1054 $\mu \left( {{u_2}} \right) $ 0.5691 0.6385 0.7079 0.5619 0.4925 0.2771 $\mu \left( {{u_3}} \right) $ 0.4269 0.5023 0.5776 0.3664 0.2911 0.0045 $\mu \left( {{u_4}} \right) $ 0.6714 0.7297 0.7881 0.6822 0.6238 0.4595 $\mu \left( {{u_5}} \right) $ 0.6099 0.6278 0.6456 0.4684 0.4506 0.2555 序次与文献[6]比较 同
u4最好异
u4最好异
u4最好异
u4最好异
u4最好异
u4最好表 5 犹豫模糊决策信息表
Table 5 Hesitant fuzzy decision information table
方案 G1 G2 G3 G4 Y1 {0.2,0.4,0.7} {0.2,0.6,0.8} {0.2,0.3,0.6,0.7,0.9} {0.3,0.4,0.5,0.7,0.8} Y2 {0.2,0.4,0.7,0.9} {0.1,0.2,0.6,0.7,0.9} {0.3,0.4,0.6,0.9} {0.5,0.6,0.8,0.9} Y3 {0.3,0.5,0.6,0.7} {0.2,0.4,0.5,0.6} {0.3,0.5,0.7,0.8} {0.2,0.5,0.6,0.7} Y4 {0.3,0.5,0.6} {0.2,0.4} {0.5,0.6,0.7} {0.8,0.9} 表 6 用三元联系数表示的犹豫模糊决策信息表
Table 6 Hesitant fuzzy decision information table expressed by TCNs
方案 G1 G2 G3 G4 Y1 0.2+0.5i+0.3j 0.2+0.6i+0.2j 0.2+0.7i+0.1j 0.3+0.5i+0.2j Y2 0.2+0.7i+0.1j 0.1+0.8i+0.1j 0.3+0.6i+0.1j 0.5+0.4i+0.1j Y3 0.3+0.4i+0.3j 0.2+0.4i+0.4j 0.3+0.5i+0.2j 0.2+0.5i+0.3j Y4 0.3+0.3i+0.4j 0.2+0.2i+0.6j 0.5+0.2i+0.3j 0.8+0.1i+0.1j 表 7 犹豫模糊决策信息中三元联系数的势函数
Table 7 Potential function of TCN in hesitant fuzzy decision making information
方案 $ {\text{sh}}{{\text{i}}_{{G_1}}}\left( \mu \right) $ $ {\text{sh}}{{\text{i}}_{{G_2}}}\left( \mu \right) $ $ {\text{sh}}{{\text{i}}_{{G_3}}}\left( \mu \right) $ $ {\text{sh}}{{\text{i}}_{{G_4}}}\left( \mu \right) $ Y1 0.6667 1.0000 2.0000 1.5000 Y2 2.0000 1.0000 3.0000 5.0000 Y3 1.0000 0.5000 1.5000 0.6667 Y4 0.7500 0.3333 1.6667 8.0000 表 8 4个方案的优劣排序比较
Table 8 Comparison of the ranking for four schemes
三元联系数 $i = 0, j = 0$ $i = 0.5, j = 0$ $i = - 0.5 , j = 0$ $i = 0.5, j = 0.5$
$i = 0.5 , j = - 0.5$ $i = 0, j = - 1$ $ \mu \left( {{Y_1}} \right) $ 0.2677 0.5346 0.0008 0.6338 0.4354 0.0692 $ \mu \left( {{Y_2}} \right) $ 0.4108 0.6554 0.1662 0.7054 0.6054 0.3108 $ \mu \left( {{Y_3}} \right) $ 0.2262 0.4669 −0.0146 0.6131 0.3208 −0.0662 $ \mu \left( {{Y_4}} \right) $ 0.6600 0.7323 0.5877 0.8300 0.6346 0.4646 序次与文献[27]比较 同
Y4最好同
Y4最好同
Y4最好同
Y4最好同
Y4最好同
Y4最好 -
[1] TORRA V, NARUKAWA Y. On hesitant fuzzy sets and decision[C]//2009 IEEE International Conference on Fuzzy Systems. Jeju: IEEE, 2009: 1378−1382. [2] TORRA V. Hesitant fuzzy sets[J]. International journal of intelligent systems, 2010, 25(6): 529–539. [3] XIA Meimei, XU Zeshui. Hesitant fuzzy information aggregation in decision making[J]. International journal of approximate reasoning, 2011, 52(3): 395–407. doi: 10.1016/j.ijar.2010.09.002 [4] 张超, 李德玉. 犹豫模糊图及其在多属性决策中的应用[J]. 模式识别与人工智能, 2017, 30(11): 1012–1018. doi: 10.16451/j.cnki.issn1003-6059.201711006 ZHANG Chao, LI Deyu. Hesitant fuzzy graph and its application to multi-attribute decision making[J]. Pattern recognition and artificial intelligence, 2017, 30(11): 1012–1018. doi: 10.16451/j.cnki.issn1003-6059.201711006 [5] 武文颖, 李应, 金飞飞, 等. 基于概率犹豫信息集成方法的群决策模型[J]. 模式识别与人工智能, 2017, 30(10): 894–906. doi: 10.16451/j.cnki.issn1003-6059.201710004 WU Wenying, LI Ying, JIN Feifei, et al. Group decision making model based on probabilistic hesitant fuzzy information aggregation operations[J]. Pattern recognition and artificial intelligence, 2017, 30(10): 894–906. doi: 10.16451/j.cnki.issn1003-6059.201710004 [6] 王宝丽, 梁吉业, 胡运红. 基于粒计算的犹豫模糊多准则决策方法[J]. 模式识别与人工智能, 2016, 29(3): 252–262. doi: 10.16451/j.cnki.issn1003-6059.201603007 WANG Baoli, LIANG Jiye, HU Yunhong. Granular computing based hesitant fuzzy multi-criteria decision making[J]. Pattern recognition and artificial intelligence, 2016, 29(3): 252–262. doi: 10.16451/j.cnki.issn1003-6059.201603007 [7] CHEN Na, XU Zeshui, XIA Meimei. Correlation coefficients of hesitant fuzzy sets and their applications to clustering analysis[J]. Applied mathematical modelling, 2013, 37(4): 2197–2211. doi: 10.1016/j.apm.2012.04.031 [8] YANG Xibei, SONG Xiaoning, QI Yunsong, et al. Constructive and axiomatic approaches to hesitant fuzzy rough set[J]. Soft computing, 2014, 18(6): 1067–1077. doi: 10.1007/s00500-013-1127-2 [9] ZHANG Chao, LI Deyu, YAN Yan. A dual hesitant fuzzy multigranulation rough set over two-universe model for medical diagnoses[J]. Computational and mathematical methods in medicine, 2015, 2015: 292710. [10] 张超, 李德玉, 翟岩慧. 双论域上的犹豫模糊语言多粒度粗糙集及其应用[J]. 控制与决策, 2017, 32(1): 105–110. doi: 10.13195/j.kzyjc.2015.1365 ZHANG Chao, LI Deyu, ZHAI Yanhui. Hesitant fuzzy linguistic multigranulation rough set over two universes and its application[J]. Control and decision, 2017, 32(1): 105–110. doi: 10.13195/j.kzyjc.2015.1365 [11] 赵克勤. 集对分析及其初步应用[M]. 杭州: 浙江科学技术出版社, 2000. [12] 刘秀梅, 赵克勤. 区间数决策集对分析[M]. 北京: 科学出版社, 2014. [13] 蒋云良, 徐从富. 集对分析理论及其应用研究进展[J]. 计算机科学, 2006, 33(1): 205–209. doi: 10.3969/j.issn.1002-137X.2006.01.057 JIANG Yunliang, XU Congfu. Advances in set pair analysis theorv and its applications[J]. Computer science, 2006, 33(1): 205–209. doi: 10.3969/j.issn.1002-137X.2006.01.057 [14] 蒋云良, 赵克勤, 刘以安. 信息处理集对分析[M]. 北京: 清华大学出版社, 2015. [15] 赵克勤. 二元联系数A+Bi的理论基础与基本算法及在人工智能中的应用[J]. 智能系统学报, 2008, 3(6): 476–486. ZHAO Keqin. The theoretical basis and basic algorithm of binary connection A+Bi and its application in AI[J]. CAAI transactions on intelligent systems, 2008, 3(6): 476–486. [16] 蒋云良, 赵克勤. 集对分析在人工智能中的应用与进展[J]. 智能系统学报, 2019, 14(1): 28–43. doi: 10.11992/tis.201803030 JIANG Yunliang, ZHAO Keqin. Application and development of set pair analysis in artificial intelligence: a survey[J]. CAAI transactions on intelligent systems, 2019, 14(1): 28–43. doi: 10.11992/tis.201803030 [17] 蒋云良, 赵克勤. 人工智能集对分析[M]. 北京: 科学出版社, 2017. [18] 王霞. 二元联系数的多准则直觉模糊决策[J]. 智能系统学报, 2010, 5(5): 454–457. doi: 10.3969/j.issn.1673-4785.2010.05.013 WANG Xia. The multi-criteria intuitionistic fuzzy decision-making based on a binary connection number[J]. CAAI transactions on intelligent systems, 2010, 5(5): 454–457. doi: 10.3969/j.issn.1673-4785.2010.05.013 [19] 江文奇, 王晨晨, 尚优, 等. 基于二元联系数的区间直觉模糊数多准则决策方法[J]. 控制与决策, 2017, 32(10): 1849–1854. doi: 10.13195/j.kzyjc.2016.1039 JIANG Wenqi, WANG Chenchen, SHANG You, et al. Method of interval-valued intuitionistic fuzzy multiple attribute decision making based on binary connection number[J]. Control and decision, 2017, 32(10): 1849–1854. doi: 10.13195/j.kzyjc.2016.1039 [20] 贺颖, 赵罡, 修睿. 一种区间数–二元联系数转换的模糊决策改进算法[J]. 控制与决策, 2020, 35(10): 2442–2448. HE Ying, ZHAO Gang, XIU Rui. An improved fuzzy decision making algorithm for interval number-binary connection number conversion[J]. Control and decision, 2020, 35(10): 2442–2448. [21] 汪新凡, 王坚强, 杨小娟. 基于二元联系数的信息不完全的群决策方法[J]. 管理工程学报, 2014, 28(1): 202–208,213. doi: 10.3969/j.issn.1004-6062.2014.01.027 WANG Xinfan, WANG Jianqiang, YANG Xiaojuan. Group decision making approaches based on binary connection number with incomplete information[J]. Journal of industrial engineering and engineering management, 2014, 28(1): 202–208,213. doi: 10.3969/j.issn.1004-6062.2014.01.027 [22] 汪新凡, 王坚强, 杨恶恶. 基于二元联系数集结算子的多准则群决策方法[J]. 控制与决策, 2013, 28(11): 1630–1636. WANG Xinfan, WANG Jianqiang, YANG Wue. Multiple criteria group decision making method based on binary connection number aggregation operators[J]. Control and decision, 2013, 28(11): 1630–1636. [23] 王海波, 陈彦萍. 一种基于三角模糊数的二元联系数双重多属性决策方法[J]. 计算机与数字工程, 2019, 47(4): 769–772,805. doi: 10.3969/j.issn.1672-9722.2019.04.006 WANG Haibo, CHEN Yanping. A dual attribute multiple decision making method based on triangular fuzzy number of two element connection number[J]. Computer & digital engineering, 2019, 47(4): 769–772,805. doi: 10.3969/j.issn.1672-9722.2019.04.006 [24] 刘卫锋, 王东晓. 基于二元联系数距离的不确定语言多属性决策模型[J]. 数学的实践与认识, 2012, 42(21): 148–153. doi: 10.3969/j.issn.1000-0984.2012.21.020 LIU Weifeng, WANG Dongxiao. An uncertain linguistic multi-attribute decision-making model based on binary connection number distance[J]. Mathematics in practice and theory, 2012, 42(21): 148–153. doi: 10.3969/j.issn.1000-0984.2012.21.020 [25] SHEN Qing, HUANG Xu, LIU Yong, et al. Multiattribute decision making based on the binary connection number in set pair analysis under an interval-valued intuitionistic fuzzy set environment[J]. Soft computing, 2020, 24(10): 7801–7809. doi: 10.1007/s00500-019-04398-1 [26] SHEN Qing, LOU Jungang, LIU Yong, et al. Hesitant fuzzy multi-attribute decision making based on binary connection number of set pair analysis[J]. Soft computing, 2021, 25(23): 14797–14807. doi: 10.1007/s00500-021-06215-0 [27] 张慧敏, 李小南. 基于冲突分析的犹豫模糊多属性决策[J]. 模式识别与人工智能, 2020, 33(7): 610–618. doi: 10.16451/j.cnki.issn1003-6059.202007004 ZHANG Huimin, LI Xiaonan. Hesitant fuzzy multi-attribute decision making based on conflict analysis[J]. Pattern recognition and artificial intelligence, 2020, 33(7): 610–618. doi: 10.16451/j.cnki.issn1003-6059.202007004
