Hand-eye coordination of robots based on the 3D object tracking algorithm
-
摘要: 为了适应环境的复杂性和多样性，增强机器人抓取任务的鲁棒性，本文从3D目标跟踪算法出发，提出了一种实现机器人手眼协调的新方法。该方法采用改进的基于区域的位姿追踪算法同时跟踪机械臂夹持器和目标物体的位姿，根据二者的相对位置关系引导机械臂运动。对基于区域的位姿跟踪算法，本文提出根据局部区域分割线构建分割模型并改进模型颜色似然的线性更新方式，使得算法能够准确跟踪机械臂夹持器与目标物体。基于ROS平台搭建了一套仿真实验环境，并分别在仿真环境和真实环境下验证了此手眼协调系统的有效性和鲁棒性。这种方式不仅不需要手眼标定，更接近于人类“Sensor-Actor”带反馈的闭环控制方式，同时赋予了机器人足够的灵活性来应对弹性的任务和多变的环境。Abstract: To adapt to the complexity and diversity of an environment and enhance the robustness of the robot grasping tasks, this paper suggests a novel method to realize the hand-eye coordination of a robot based on the 3D object tracking algorithm. In this method, an improved region-based pose tracking algorithm is used to track the poses of the manipulator and the target and simultaneously guide the manipulator movement according to its relative position. For the region-based pose tracking algorithm, a segmentation model is constructed as per the segmentation lines of the local region, and the linear updating method of the model color likelihoods is improved, to accurately track the gripper and the target. Simulation experiments are conducted based on the ROS platform, and the effectiveness and robustness of the hand-eye coordination system are verified in both the simulation and real environments. This method does not need hand-eye calibration and is closer to the human closed-loop control of the “Sensor-Actor” mode with feedback. Concurrently, it provides robots with enough flexibility to deal with versatile tasks in a modifiable environment.
-
机器人手眼协调[1-4]是指机器人感受器与控制器之间的协调控制策略。传统流水线上的工业机器人，它们面对固定不变的任务，因而其操作流程和动作序列在设定后就可以保持不变，因此即使是盲操作(无需反馈)也足以完成任务。而类似于服务机器人的非工业流水线机器人所面对的环境和任务是不可预知的，这就需要实时感知这些状态的变化，并做出正确的调整。高级哺乳动物，如人应对这种任务的能力就特别强。基于 Goodale和Milner提出的视觉双通路理论[5-6]，我们大脑是这样工作的，视觉信息经过腹侧通路产生知觉，然后背侧系统进行视觉引导。信息加工能够在短时间内完成，保证了由视觉引导的动作是实时且动态调整的。
因此，带反馈和闭环控制的手眼协调为完成这种具有各种可变性的机器人抓取任务提供了可能，使它们变得更加智能，不再局限于一成不变的环境和任务中。
机器人手眼协调的前提是准确的三维感知以获取目标对象的状态。物体跟踪[7]是机器人领域的核心技术，三维物体位姿追踪通过输入的图像序列分析确定目标物体在三维空间的位姿参数，该参数包括位置分量和姿态角。针对刚性物体位姿追踪已有多种研究思路，并取得很大进展。主要分为以下几类方法：
基于特征匹配[8-10]的方法，这种方法倾向于检测图像中的边缘、角点等基于梯度的特征，再将这些特征与3D模型匹配进行位姿估计。这种方法要求检测对象具有良好的纹理，同时受运动模糊、低光照条件以及与摄像机距离等条件的限制。
基于学习[11]的方法，目前深度学习技术在位姿估计[12-14]和目标跟踪领域已取得很大进展，但在位姿追踪领域的研究工作较少。 Crivellaro等[11]首次提出利用深度神经网络来实现姿态跟踪，其核心思想是根据物体的三维模型，选择模型的某些部件作为被追踪的目标。当跟踪器运行时，跟踪器会首先定位这些部件在图像中的二维投影位置，然后利用此二维投影估计被追踪部件的三维位姿，物体的位姿则通过被追踪部件的三维位姿来恢复。这种方法需要为每个物体的各个部件进行人工标记，同时需要单独训练多个网络。使用神经网络，不可避免要对特定环境收集和标注大量样本，使用大量的GPU资源用于训练，同时这种方法不具备足够的扩展性，只能用于特定的环境和物体。若将其用于机器人还要同时考虑算力、机器人成本、便携性、大量参数的易操作性能否满足神经网络模型的需求。
基于区域[15-19]的方法，更适应于复杂场景中的对象。此类方法假设目标和背景区域之间具有不同的图像统计信息，基于合适的统计外观模型和3D形状先验，使用分割模型在当前图像上提取目标对象轮廓，同时再对姿态预先参数化的形状先验渲染得到轮廓。通过不断改变用于合成投影的3D模型的位姿参数来最小化两个轮廓的差异，从而得到目标对象的位姿。
目前机器人手眼协调的实现大都基于标定的方法[2-4，20-25]，通过标定相机的内参数与外参数，得到机器人手眼关系，构建图像空间与机器人操作空间的映射。这种方式下，一旦标定工作完成，相机的位置也将固定，除非进行重新标定。标定工作是繁琐的，同时不符合人类“Sensor-Actor”的方式。
受人类手眼协调的启发，本文利用基于区域的位姿跟踪算法，同时跟踪机械臂夹持器和目标物体。在不进行手眼关系标定的前提下，我们基于位姿跟踪算法计算夹持器与目标物体的相对位置关系，根据它们的相对位姿，求解机械臂运动的目标位置，最后通过MoveIt模块规划机械臂运动路径，实时引导机械臂靠近目标物体。实验表明，本文改进的位姿跟踪算法能够应用于机械臂环境，并且具有足够的鲁棒性。
1. 基于区域的物体位姿跟踪
1.1 问题描述
基于区域的位姿追踪算法基于两个假设：1) 物体和背景具有不同的图像统计数据；2) 已知目标物体的3D模型，即形状先验。首先需要初始化模型的位姿，即对3D模型赋予初始姿态参数，进而得到模型在此位姿下的投影轮廓。基于区域的位姿跟踪算法通过定义能量函数来最小化目标物体真实轮廓和投影轮廓之间的差异，获得目标物体在相机坐标系下的真实位姿。
物体的位姿估计实质上是求解3D模型坐标系到相机坐标系的变换，该变换用齐次坐标可以表示为矩阵
${\boldsymbol{T}} = \left[ {{\boldsymbol{R}}|{\boldsymbol{t}}} \right]$ ，其中$\boldsymbol R$ 是描述空间旋转的矩阵，$\boldsymbol t$ 是描述空间位移的向量。通过相机标定可以得到相机内参矩阵：$$ {\boldsymbol{K}} = \left( {\begin{array}{*{20}{c}} {{f_x}}&0&{{c_x}} \\ 0&{{f_y}}&{{c_y}} \\ 0&0&1 \end{array}} \right) \in \mathop {\bf R}\nolimits^{3 \times 3} $$ (1) 根据式(1)将3D模型顶点
${\boldsymbol{X}}_{\bar{i}}=\left[X_{\bar{i}} \;\; Y_{\bar{i}} \;\; Z_{\bar{i}}\right]^{{\rm{T}}} \in {\bf{R}}^{3}, i=1, 2,\cdots, n$ 投影至图像：$$ x=\pi （K{(T\tilde{{\boldsymbol{X}}})}_{3\times 1}） $$ (2) 其中
$\pi (X) = {[X/Z,\;\;Y/Z]^{\rm T}}$ ，$\tilde {\boldsymbol X} = \left[ {X}\;\;{Y}\;\;{Z}\;\; 1 \right]$ 是$X$ 的齐次表示。3D目标位姿跟踪过程如下。
1) 结合相机内参矩阵
$\boldsymbol K$ 和物体3D模型$M$ ，利用Aruco marker初始化物体的位姿$T = {T_0}$ ；2) 将需要跟踪的物体的3D模型根据位姿
$T$ 投影到图像平面，然后根据投影轮廓构建区域分割线；3) 针对每组区域分割线，求解局部分割模型；
4) 通过高斯–牛顿法对物体进行位姿优化，得到物体优化后的位姿
$T$ ；5) 重新进行2)，直到停止跟踪。
1.2 初始位姿估计
算法开始阶段，需要粗略估计目标物体在相机坐标系下的位姿，本文借助Aruco marker[26] 来进行初始位姿估计。PnP（perspective-n-point）问题即根据几组已知坐标系下的3D空间点，及对应图像上的2D点，可以用于求解相机位于该坐标系下的位置和旋转角，即矩阵
${\boldsymbol{T}} = \left[ {{\boldsymbol{R}}|{\boldsymbol{t}}} \right]$ 。常见用于解决PnP问题的算法包括P3P、EPnP[27]、DLT、RPnP、OI等。其中EPnP算法通常设置4个控制点，即将3D坐标表示为一组虚拟的控制点的加权和。本文利用Aruco标志物的4个角点计算P4P 问题来估计ArUco二维码在相机坐标系下的位姿，从而粗略估计目标物体在相机坐标系下的初始位姿参数。1.3 分割模型
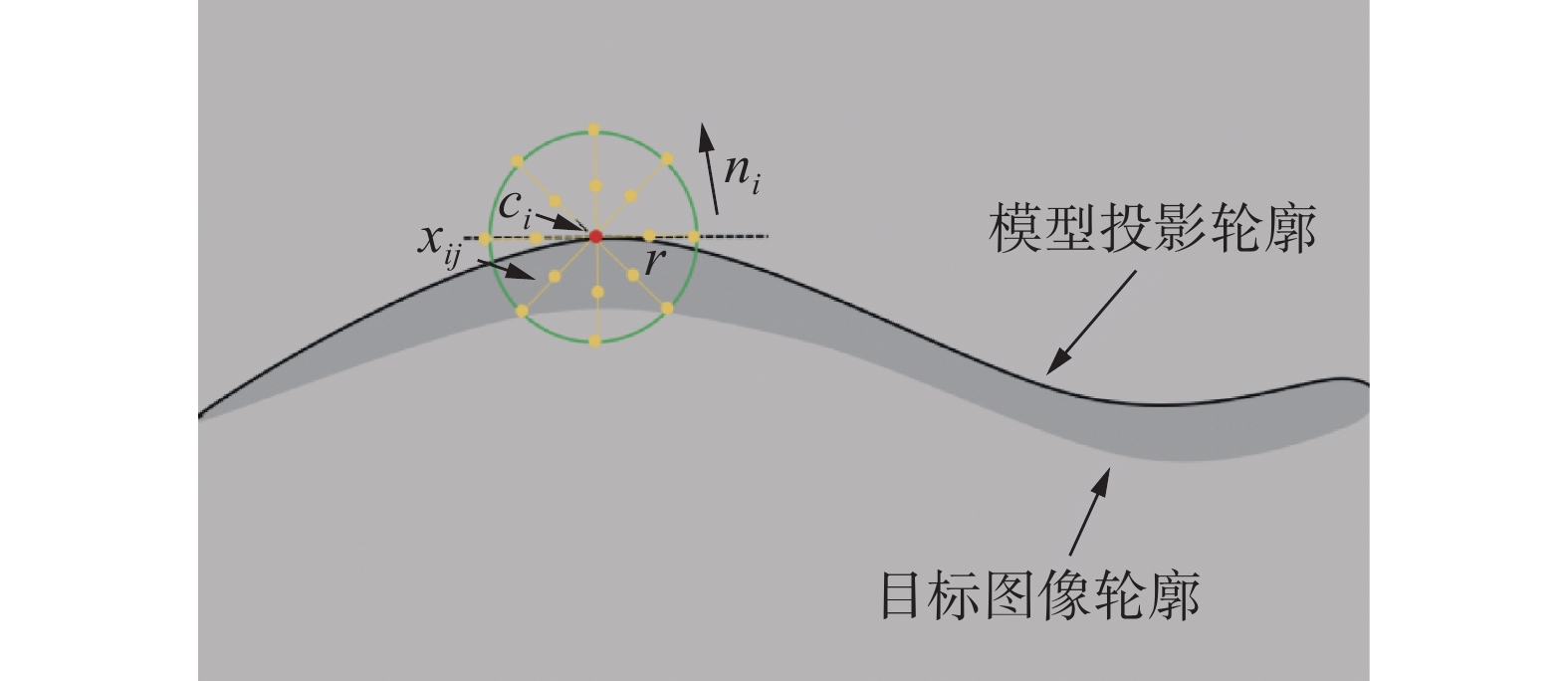
基于区域的位姿跟踪算法RBOT[18]对模型投影轮廓的每个点都建立半径为
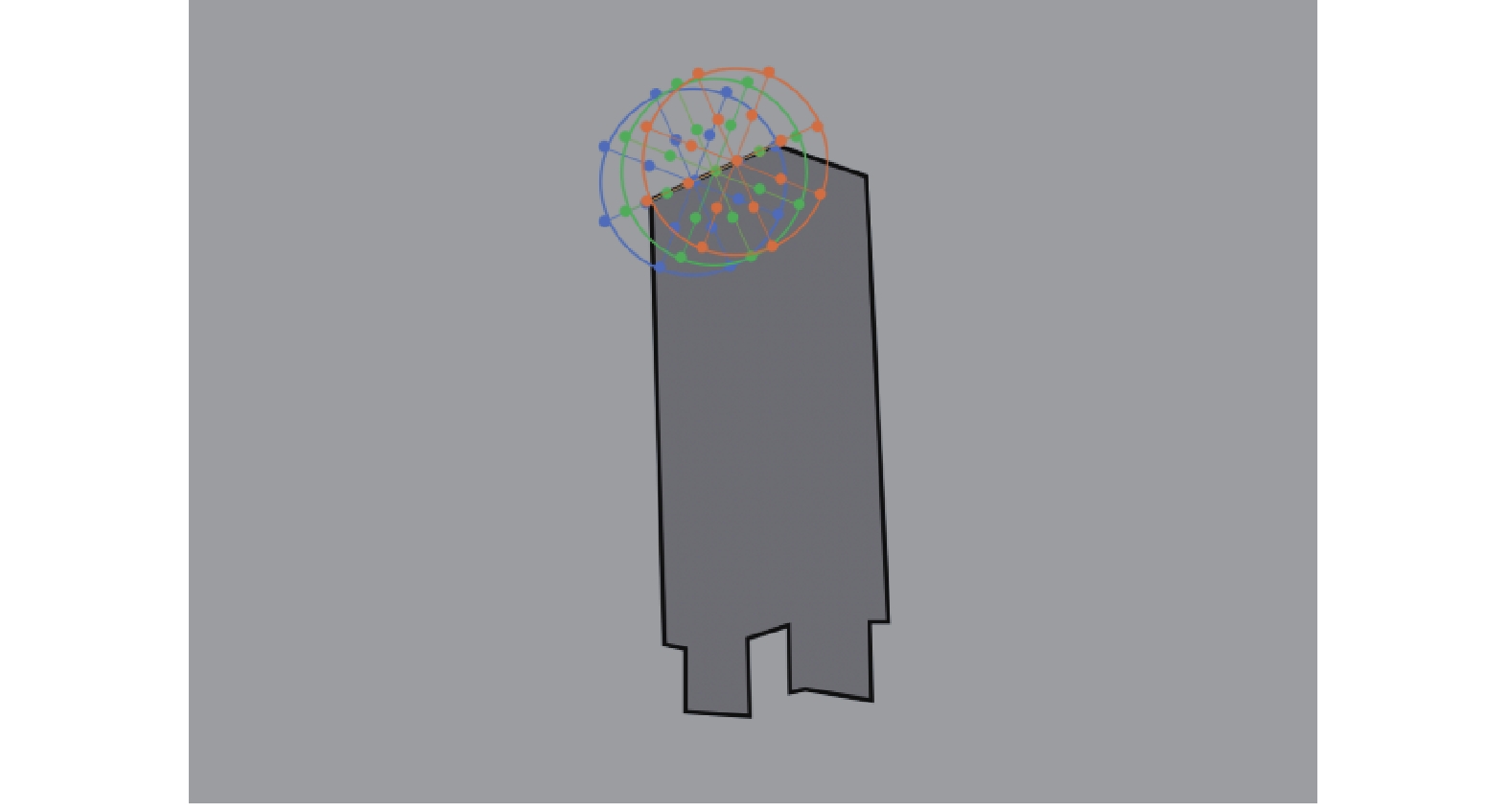
$r$ 的圆域，然后计算每个圆域的前景和背景颜色直方图，构建外观模型。以夹持器为例，如图1所示，在跟踪过程将计算大量重叠的圆域，这需要维护和更新大量的局部颜色直方图。若减小半径$r$ ，重叠域减小，每个局部区域计算的像素量也会减少。而由较少的像素计算出的局部颜色直方图会降低算法的稳定性，从而导致跟踪失败。
图 1 经典局部外观模型Fig. 1 Classic local appearance model
下载:
全尺寸图片
为了提高RBOT算法[18]的性能，在此基础上，本文提出在圆域的分割线上提取颜色特征的方法。如图2所示，建立以
${c_i}$ 为圆心，半径为$r$ 的圆域，然后以该点的法线为基础构建4条分割线，将圆域平均分块。以每个圆域及其相邻的左右两个圆域为一组，对12条分割线上的像素点分别统计前景和背景局部颜色直方图。由图3可以看到，相邻区域内计算的重复像素点大大减少。
图 2 局部区域分割线Fig. 2 Cutting line of local area下载:
全尺寸图片
图 3 基于分割线的局部外观模型Fig. 3 Local appearance model based on cutting line下载:
全尺寸图片
在像素独立的前提下，使用类似RBOT算法的局部能量函数：
$$ E = - \displaystyle \sum\limits_{x \in \varOmega } {\log [{H_\varepsilon }(\phi (x)){{\overline P }_f}(x) + (1 - } {H_\varepsilon }(\phi (x)){\overline P _b}(x)] $$ (3) 其中，
$$ {H_\varepsilon }(\phi (x)) = \dfrac{1}{{\text{π} }}\left( { - a\tan (s \cdot \phi (x)) + \frac{{\text{π} } }{2}} \right) $$ (4) $$ {\overline P _f}(x) = \dfrac{1}{{\displaystyle \sum\limits_{n = 1}^N {{B_n}(x)} }}\displaystyle \sum\limits_{n = 1}^N {{P_{fn}}(y){B_n}(x)} $$ (5) $$ {\overline P _b}(x) = \dfrac{1}{{\displaystyle \sum\limits_{n = 1}^N {{B_n}(x)} }}\displaystyle \sum\limits_{n = 1}^N {{P_{bn}}(y){B_n}(x)} $$ (6) $$ {B_n}(x) = \left\{ {\begin{array}{*{20}{c}} 1,&{x \in {L_n}} \\ 0,&{x \notin {L_n}} \end{array}} \right. $$ (7) 式中：
$N$ 表示分组个数；${B_n}$ 标识像素$x$ 是否在分割线上；${\overline P _f}(x)$ 和${\overline P _b}(x)$ 为所有局部颜色直方图的平均后验。其中，$$ \left\{ {\begin{array}{*{20}{c}} {{P_{fn}}(x) = P({M_f}|y) = \dfrac{{P(y|{M_{fn}})}}{{{\eta _{fn}}P(y|{M_{fn}}) + {\eta _{bn}}P(y|{M_{bn}})}}} \\ {{P_{bn}}(x) = P({M_b}|y) = \dfrac{{P(y|{M_{bn}})}}{{{\eta _{fn}}P(y|{M_{fn}}) + {\eta _{bn}}P(y|{M_{bn}})}}} \end{array}} \right. $$ (8) 这里，
${\eta _{{f_n}}} = \sum\nolimits_{x \in \varOmega } {{H_\varepsilon }(\phi (x))}$ ，${\eta _{{b_n}}} = \sum\nolimits_{x \in \varOmega } {1 - {H_\varepsilon }(\phi (x))}$ ，分别表示每个圆域$n$ 内统计的所有属于前景、背景的像素数目，$P(y|{M_{{f_n}}})$ 和$P(y|{M_{{b_n}}})$ 分别表示像素值为$y$ 的前景和背景先验概率。使用RGB颜色模型，对通道量化为32位。对每组分割线，我们利用颜色直方图，根据式(8)计算前景和背景的后验概率。1.4 迭代更新
对于每一帧图像，根据式(2)将物体模型的顶点投影到图像上，形成投影轮廓。在出现跟踪偏差或遮挡情况下，若只计算每帧图像的颜色直方图，算法将产生较大的误差并导致跟踪失败。如果上一帧图像的位姿估计结果正确，则可使用如下线性联合的方式来更新前景和背景模型：
$$ \left\{ {\begin{array}{*{20}{c}} {P(y|{M_f}) = (1 - {\alpha _f}){P^{t - 1}}(y|{M_f}) + {\alpha _f}{P^{t}}(y|{M_f})} \\ {P(y|{M_b}) = (1 - {\alpha _b}){P^{t - 1}}(y|{M_b}) + {\alpha _b}{P^{t}}(y|{M_b})} \end{array}} \right. $$ (9) 一般而言，
${\alpha _f} = 0.1$ ，${\alpha _b} = 0.2$ 。这种更新方式保证当前结果的准确性和时序的一致性。考虑以下情况：图像两帧之间由于光照等原因产生较大颜色差异。若更新时仍然以上一帧图像的统计模型为主，位姿更新时将会产生较大偏差，继而影响后续跟踪。针对此问题，本文提出如下的联合更新方式：
$$ \begin{array}{c} {P^{t}}(y|{M_{\rm in}}) = {\alpha _i}{P^{t - 1}}(y|{M_{\rm in}}) + {\beta _i}{P^t}(y|{M_{\rm in}}) + {\gamma _i}P{'^t}(y|{M_{\rm in}}) \end{array} $$ (10) 其中，
$i \in \left\{ {f,b} \right\},\alpha + \beta + \gamma = 1$ 。两帧图像之间物体的位姿变化微乎其微，但图像特征发生巨大差异。因此我们利用上一帧的位姿参数将模型投影到当前帧，计算其前景与背景的似然
$P{'^t}(y|{M_{\rm in}})$ 。这消除${P^{t - 1}}(y|{M_{\rm in}})$ 带来的错误引导，为了不丢失上一帧的颜色分布，我们保留了此项。2. 3D目标跟踪实现手眼协调
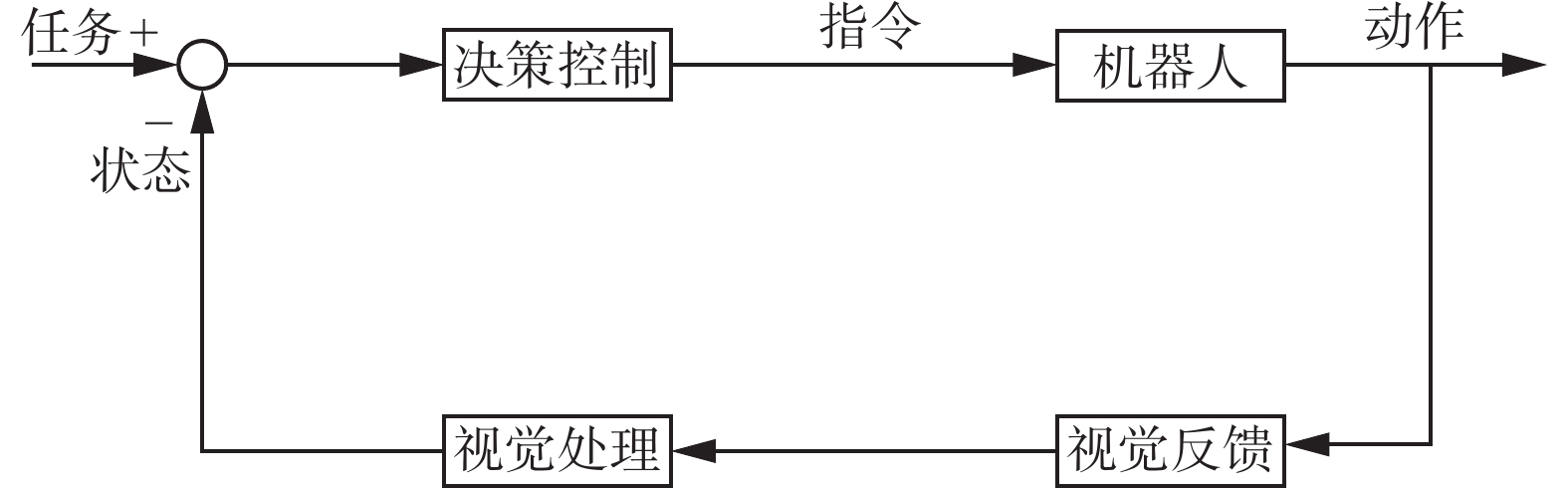
机器人手眼协调研究的是机器人感受器与控制器之间的协调控制策略，如图4所示。
图 4 手眼协调系统结构Fig. 4 Hand-eye coordination system architecture下载:
全尺寸图片
决策控制部分根据任务和当前机器人及目标物体的状态，进行运动规划，控制机器人运动；视觉反馈环节通过摄像机感知外界环境、机器人状态等的变化，进而通过视觉处理使机器人做出新的决策调整。
本文手眼协调系统由机械臂硬件系统、单目相机、夹持器和控制计算机构成。机械臂硬件系统包括控制柜、示教器和机械臂本体。在机械臂末端，我们安装了基于伺服电机的电动夹爪。实验环境如图5所示，SD700E机械臂本体固定在桌面，相机固定在桌面上方，桌面上放置待抓取物体，待抓取物体为易拉罐、犀牛玩具等物体。
图 5 手眼协调系统Fig. 5 Hand-eye coordination system下载:
全尺寸图片
首先机械臂的运动根据运动学方程，得到机械臂六轴的变换关系。由于本系统在原机器人的基础上，增加一截电动手爪，因此需要在运动学方程中添加机器人的连杆参数，使其可以被看做一个理想的笛卡尔元件。表1为SD700E机械臂D-H参数[28]。其中
$\theta $ 表示关节，$d$ 表示杆件长度，$a$ 表示杆件连接位移，$\alpha $ 表示杆件之间扭转角度。表 1 D-H参数Table 1 D-H parameters$i$ ${a_{i - 1}}$ $ {\alpha _{i - 1}} $ ${d_i}$ ${\theta _i}$ 1 0 0 基座 $ - {\theta _1}$ 2 0 $- {\text{π}} /2$ 0 $- {\theta _2}({\text{π}} /2)$ 3 ${l_2}$ 0 0 ${\theta _3}$ 4 0 $- {\text{π}} /2$ ${l_3}$ $ - {\theta _4}$ 5 0 ${\text{π}} /2$ 0 ${\theta _5}$ 6 0 $- {\text{π}} /2$ ${l_5}$ ${\theta _6}$ 根据改进的D-H表示法，利用式(11)的变换矩阵将坐标系
$\left\{ {i - 1} \right\}$ 变换到坐标系$\left\{ i \right\}$ ：$$ {}_i^{i - 1}{\boldsymbol T} = {\rm Rot}(x,{\alpha _{i - 1}}){\rm Trans}({a_{i - 1}},0,0){\rm Rot}(z,{\theta _i}){\rm Trans}(0,0,{d_i}) $$ (11) 将上述变换矩阵展开为
$$ {}_i^{i - 1}{\boldsymbol T} = \left[ {\begin{array}{*{20}{c}} {c{\theta _i}}&{ - s{\theta _i}}&0&{{a _{i - 1}}} \\ {s{\theta _i}c{\alpha _{i - 1}}}&{c{\theta _i}c{\alpha _{i - 1}}}&{ - s{\alpha _{i - 1}}}&{ - {d_i}s{\alpha _{i - 1}}} \\ {s{\theta _i}s{\alpha _{i - 1}}}&{c{\theta _i}s{\alpha _{i - 1}}}&{c{\alpha _{i - 1}}}&{{d_i}c{\alpha _{i - 1}}} \\ 0&0&0&1 \end{array}} \right] $$ (12) 式中：
$c{\theta _i}$ 表示${\theta _i}$ 的余弦值；$s{\theta _i}$ 表示${\theta _i}$ 的正弦值。机械臂末端坐标系与基坐标系的变换矩阵
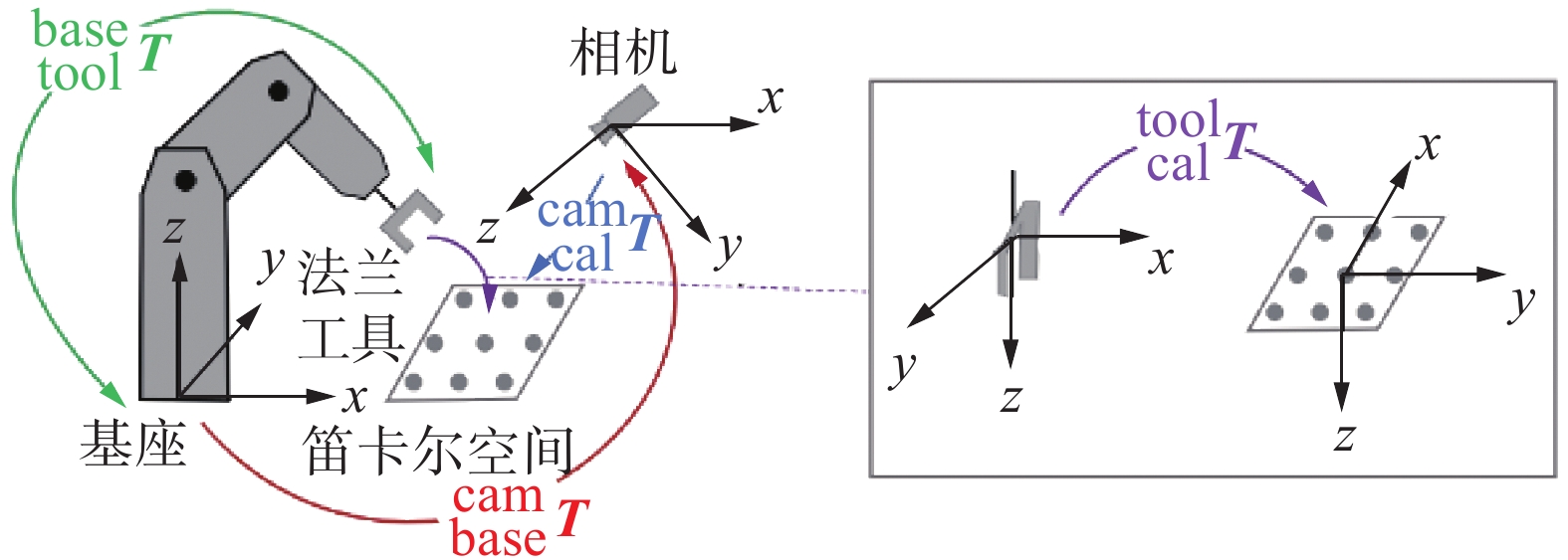
${}_6^0{\boldsymbol T}$ 可以表示为式(15)：$$ {}_6^0{\boldsymbol T} = {}_1^0{\boldsymbol T} ({\theta _1}){}_2^1{\boldsymbol T} ({\theta _2}){}_3^2{\boldsymbol T} ({\theta _3}){}_4^3{\boldsymbol T} ({\theta _4}){}_5^4{\boldsymbol T} ({\theta _5}){}_6^5{\boldsymbol T} ({\theta _6}) $$ (13) 手眼协调的实现通常以系统标定为前提，通过手眼关系标定，得到相机与机械臂坐标系的变换关系。如图6所示，通过标定得到相机坐标系与机械臂基坐标系的变换矩阵
${}_{\rm base}^{\rm cam}{\boldsymbol T}$ ，当视觉系统得到目标物体的状态${}_{\rm obj}^{\rm cam}{\boldsymbol T}$ 时，由${}_{\rm obj}^{\rm base}{\boldsymbol T} = {}_{\rm cam}^{\rm base}{\boldsymbol T} \cdot {}_{\rm obj}^{\rm cam}{\boldsymbol T}$ 获得物体在机械臂坐标空间的位置，进而控制机械臂运动。这种方式无法应对弹性任务，同时一旦标定成功之后，摄像机(眼)将永远被固定，除非重新进行标定。
图 6 手眼标定(眼在手外)Fig. 6 Hand-eye calibration (eye outside the hand)下载:
全尺寸图片
利用物体位姿跟踪算法，同时跟踪机械臂夹持器和目标物体，利用二者相对位置关系，实现机械臂边看边做的动态反馈控制。
$$ {}_{\rm obj}^{\rm base}{\boldsymbol T} = {}_{\rm tool}^{\rm base}{\boldsymbol T} \cdot {}_{\rm obj}^{\rm tool}{\boldsymbol T} = {}_{\rm tool}^{\rm base}{\boldsymbol T} \cdot {}_{\rm cam}^{\rm tool}{\boldsymbol T} \cdot {}_{\rm obj}^{\rm cam}{\boldsymbol T} $$ (14) 根据位姿跟踪算法可以实时获得夹持器在相机坐标系下的位姿
${}_{\rm tool}^{\rm cam}{\boldsymbol T}$ 以及目标物体在相机坐标系下的位姿${}_{\rm obj}^{\rm cam}{\boldsymbol T}$ ，利用${}_{\rm tool}^{\rm base}{\boldsymbol T}\cdot{}_{\rm cam}^{\rm tool}{\boldsymbol T}$ 代替标定获得的${}_{\rm cam}^{\rm base}{\boldsymbol T}$ 。3. 运动规划
ROS 为机器人开发提供了一个统一的开发和 测试平台，MoveIt 是 ROS 中集成的一个功能强大的软件开发包，使用它能够方便地进行运动规划，同时它兼备三维感知、控制、导航等功能。根据机器人的 URDF 模型，利用 MoveIt 可以在综合考虑场景信息基础上，完成机器人运动规划及避障的相关计算。我们利用ROS MoveIt结合实时位姿跟踪，完成机械臂自主导航任务。
ROS中还提供 Gazebo 物理仿真工具，它不仅能够模拟机器人的理想运动，还可以为机器人加入质量、惯性、摩擦系数等物理属性。因此我们针对实验的机械臂在Gazebo 环境下搭建了仿真实验平台，如图7所示。
图 7 Gazebo仿真环境Fig. 7 Gazebo simulation environment下载:
全尺寸图片
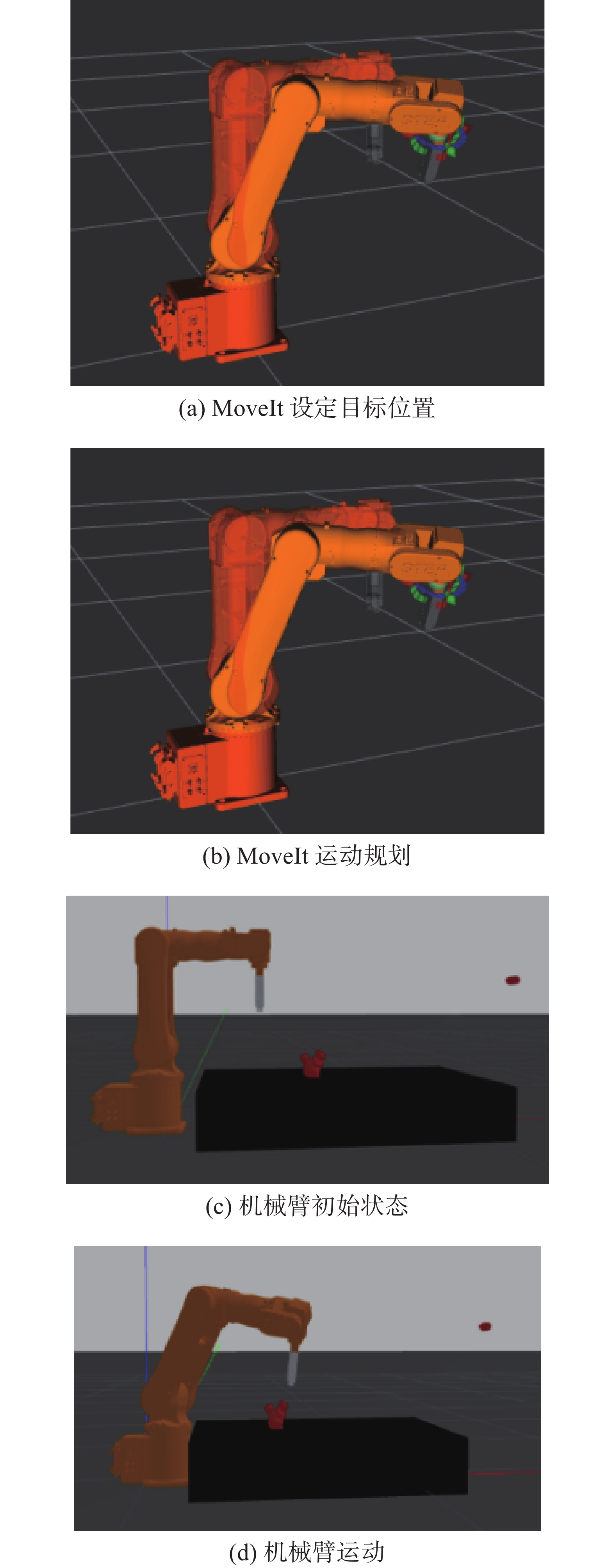
在ROS仿真环境下，利用MoveIt进行运动规划使机械臂根据规划的路径运动到目标位置。仿真结果如图8所示。
图 8 仿真环境运动规划Fig. 8 Motion planning in the simulation environment下载:
全尺寸图片
同时，利用MoveIt并结合机械臂底层通信实现真实环境下机械臂的运动规划与执行，主要流程和实验效果如图9所示。
图 9 真实环境运动规划Fig. 9 Motion planning in the real world下载:
全尺寸图片
1) 确定机械臂运动目标；
2) MoveIt完成运动规划得到目标关节轨迹；
3) 通过socket接口和控制器连接，将关节轨迹发送给控制器；
4) 控制器执行插补运算，将结果周期性发送给电机驱动器；
5) 驱动器完成闭环控制后，由电机跟随输入指令；
6) 控制器反馈实时状态到MoveIt。
4. 实验
4.1 位姿跟踪实验
为了验证改进后的跟踪算法的准确度，我们分别录制了机械臂运动的局部区域视频序列、完整跟踪测试序列以及目标物体的运动序列。视频序列分辨率为640×480，画面中包括物体的平移、旋转、运动模糊以及光照不均等现象。
对于图10(a)机械臂的局部区域视频序列，可以看到夹持器在运动时颜色特征发生了明显的变化，尤其体现在旋转过程，造成了上下两帧图像明暗、颜色差异较大。 对每一帧图像，将模型根据位姿估计结果渲染到图像上，模型渲染结果与图像中目标物体越吻合，则结果越准确。图10(b) 和图10(c) 展示了RBOT算法和本文算法的表现差异，当夹持器在空间中运动时，RBOT算法出现偏差，并导致后面的跟踪完全丢失。由于本文算法改进了用于提取颜色特征的局部区域以及颜色似然的更新方式，在整个夹持器旋转过程都能准确跟踪。
图 10 夹持器跟踪结果对比Fig. 10 Comparison of gripper tracking results下载:
全尺寸图片
图11给出了RBOT算法与本文算法在兔子模型上的跟踪结果对比。按照从左到右的顺序依次为相机采集的视频序列第20帧、第672帧、第780帧和第910帧。两个算法在该模型数据上的跟踪效果表现相对较好，但在第910帧时，从图11(b)最右图中的红色圆圈标注部分可以看出，RBOT[18]算法渲染的结果与真实模型偏差较大。主要原因是基于局部圆形区域的方法会导致圆域之间出现大量重叠，邻圆域内上下文信息相似性较高，无法准确分割物体轮廓。而本文提出的局部圆域分割线方法，可以在物体轮廓的法线、切线及对角线方向上构建局部分割线，可以对轮廓进行更精准的定位，充分捕获局部区域的上下文信息，实现更为精准的位姿跟踪。从图11(c)最右图可以看出本文提出的局部区域分割线位姿跟踪效果更优。
图 11 兔子跟踪结果对比Fig. 11 Comparison of rabbit tracking results下载:
全尺寸图片
图12(a)和12(b)分别给出了本文算法在企鹅模型和易拉罐模型上的跟踪效果。从图中可以看出，根据算法估计的位姿参数将模型渲染到图像上的效果与物体贴合紧密，较为准确地估计出物体的位姿，本文算法在物体跟踪过程具有较好的准确度和鲁棒性。
图 12 本文算法其他模型跟踪结果Fig. 12 Tracking results of other models with our algorithm下载:
全尺寸图片
为了定义位姿估计的误差
${E_p}$ ,我们将物体模型的顶点分别根据估计的位姿$[R,t]$ 和真实位姿$[{R^*},{t^*}]$ 进行变换，然后计算变换后坐标点的欧氏距离：$$ {E_p} = \frac{1}{m}\sum\limits_{i = 1}^m {||(R{x_i} + t) - ({R^*}{x_i} + {t^*})||} $$ (15) 式中：
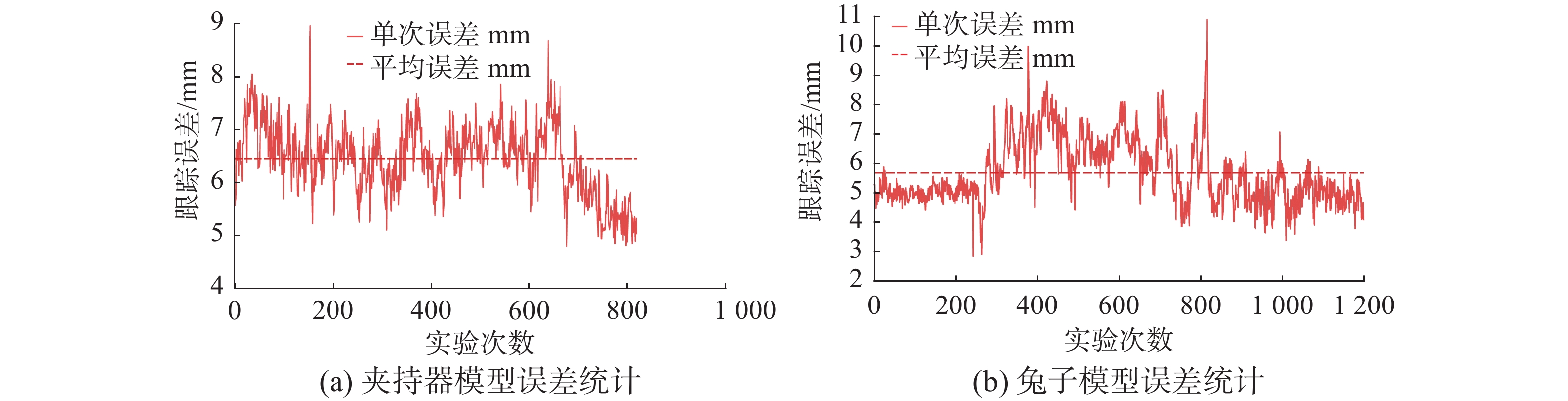
$ {x}_{i} $ 表示模型的顶点；$m$ 表示顶点总数。我们统计了夹持器位姿跟踪实验和兔子模型位姿跟踪实验位的姿估计误差。如图13所示，夹持器模型的位姿估计平均误差为6.43 mm，兔子模型的平均误差为5.68 mm。可以看出夹持器模型误差与兔子模型相比较大，且波动明显，这主要由于夹持器支架与夹持器具有相似的颜色特征。同时二者都存在一些误差较大的帧，主要由运动模糊或者遮挡导致。总体而言，本文算法满足实验精度需求。
图 13 位姿跟踪误差统计Fig. 13 Error statistics for pose tracking下载:
全尺寸图片
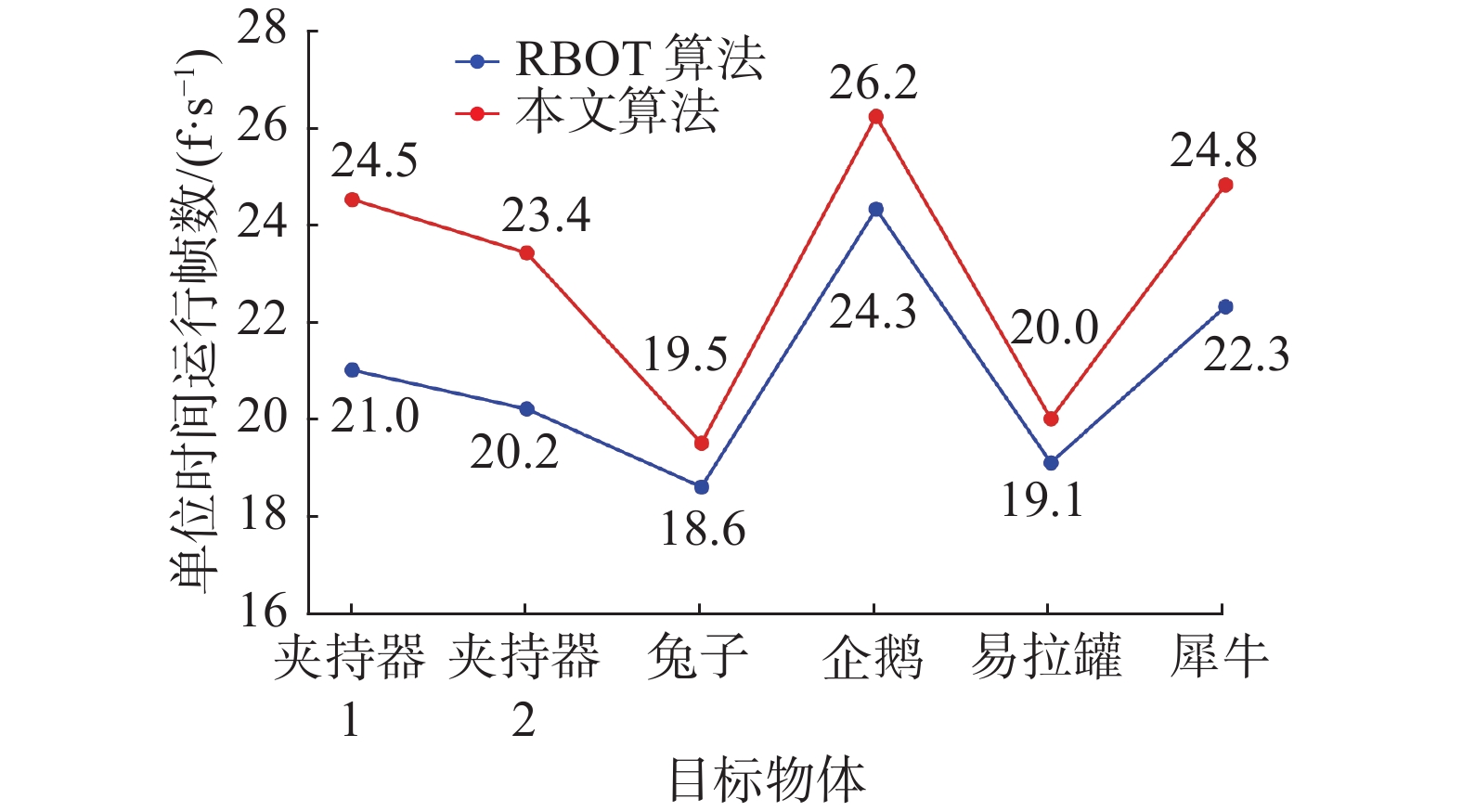
此外，由于本文提出的局部区域分割线算法减少了重复像素的计算，本文算法的跟踪速度也有了一定的提升，如图14所示，本文算法在性能一般的处理器上运行，与RBOT算法相比，每秒提升了0.9~3.5帧。
图 14 本文算法与RBOT算法速度对比结果Fig. 14 Speed comparisons between our algorithm and RBOT algorithm下载:
全尺寸图片
4.2 机器人手眼协调实验
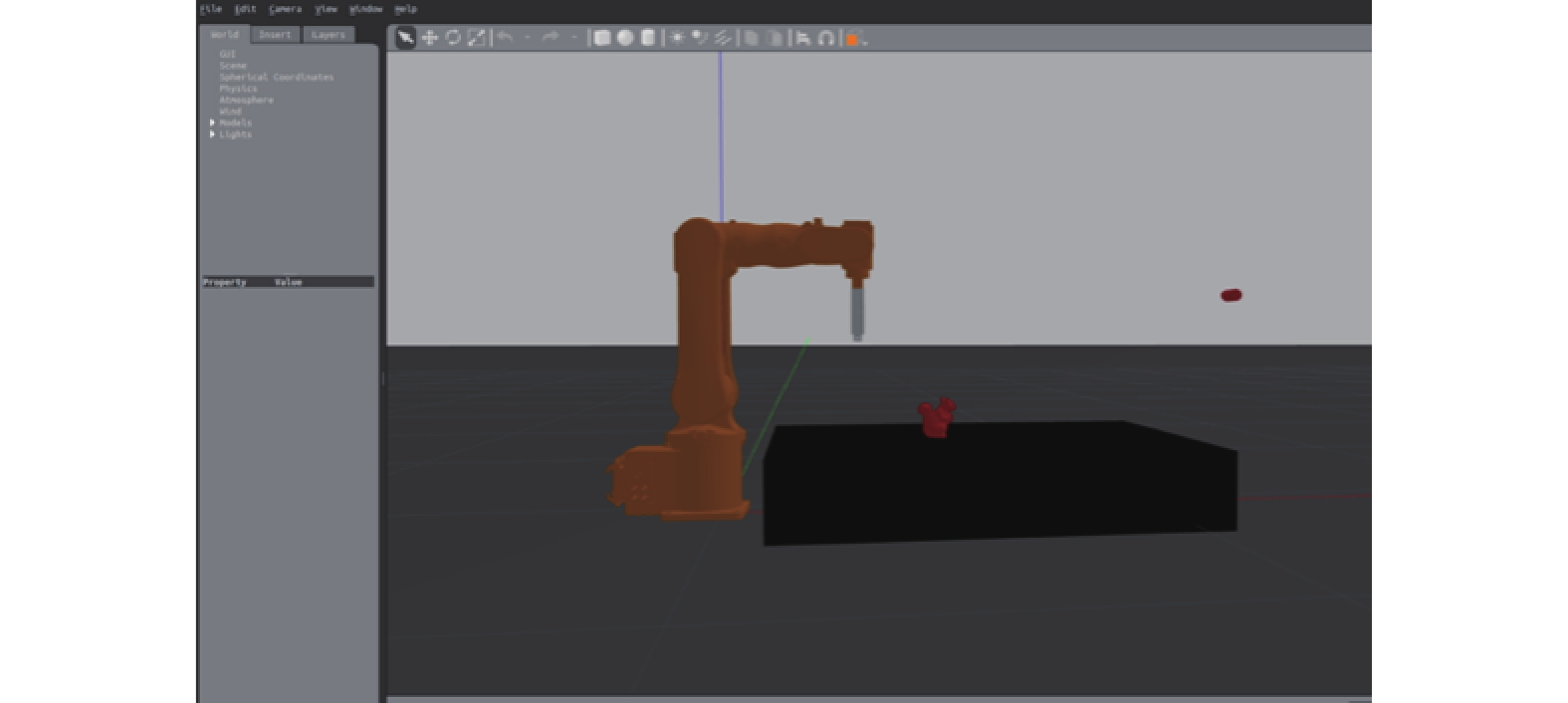
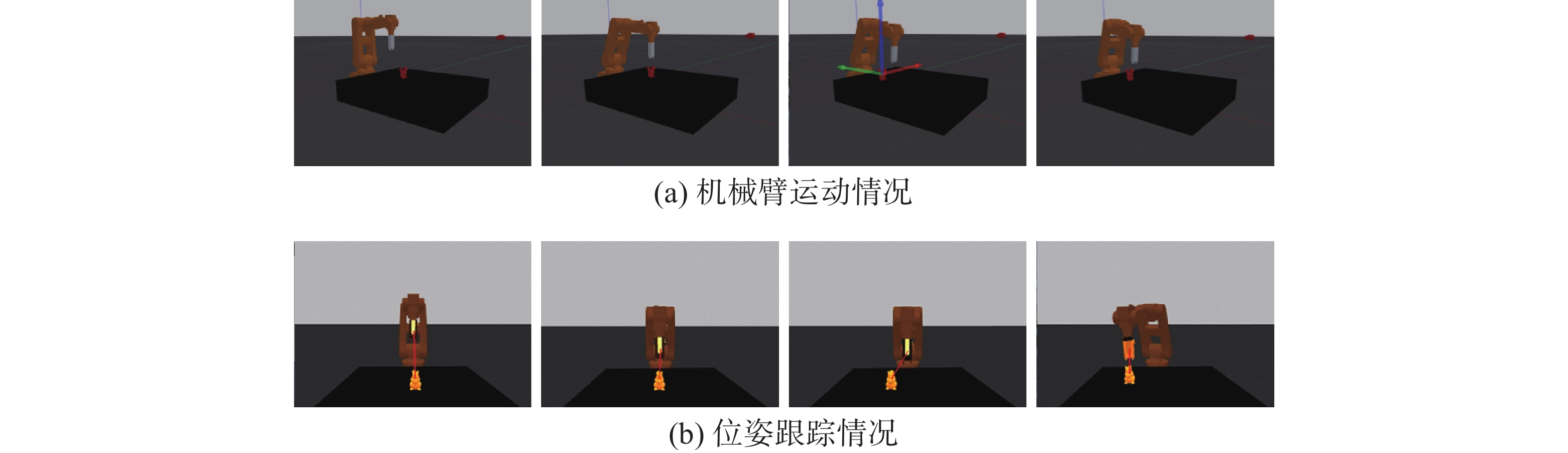
机器人手眼协调实验的目标是基于位姿跟踪算法完成机械臂自主导航任务，让夹持器自动靠近目标物体，实现手眼协调系统。 为了验证本文方法的可行性与准确度，在实验过程中我们多次改变物体的位姿，对物体进行平移、旋转操作，考察在仿真环境和真实环境下机械臂运动情况。图15为仿真环境下，机械臂靠近松鼠的运动过程。在此过程中人为改变了松鼠的位姿，可以看到机械臂也对应改变了运动方向。图16为真实环境下的实验，目标物体为易拉罐，实现了机械臂边看边靠近的动态反馈控制过程。
图 15 仿真环境实验结果Fig. 15 Experimental results in the simulation environment下载:
全尺寸图片
图 16 真实环境实验结果Fig. 16 Experimental results in the real environment下载:
全尺寸图片
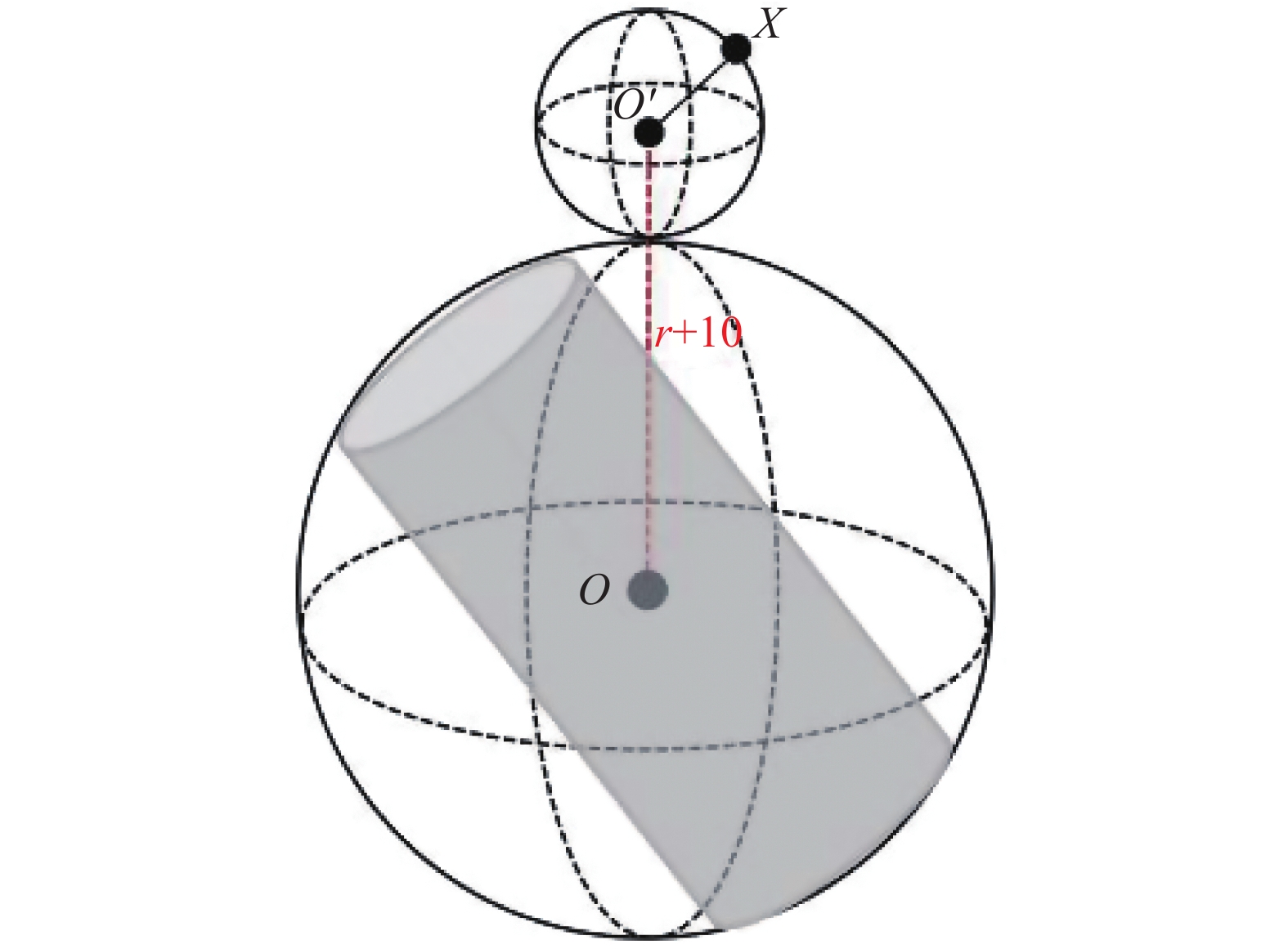
为了评估基于位姿估计的手眼协调系统的性能，我们定义对接近误差作了量化统计。如图17所示，我们以目标物体质心作为球心定义最小外接球，半径为r，机械臂运动的目标位置为
$X(x_0,y_0,z_0)$ 。在实际情况下，我们设置机械臂运动的目标位置在z轴正方向上平移10个单位，以避免机械臂误碰撞。我们定义误差$E = \dfrac{{{D_{{O'}X}}}}{{{r'}}}$ ，其中$D_{O'X}$ 表示机械臂运动的目标位置$X$ 到球心${O'}$ 之间的欧式距离，当$E \leqslant 1$ 时，表明实验成功。
图 17 误差模型示意图Fig. 17 Error model demonstration下载:
全尺寸图片
针对5种不同的物体模型，分别进行10组实验，并且每组实验中随机改变物体位姿5次，然后统计实验中的接近误差以及实验的成功率。如表2所示，兔子的成功率最高，而犀牛和易拉罐的成功率较低。由于犀牛模型体积较小，相机距离目标物体较远，且该模型的纹理信息欠缺，导致跟踪过程相对不稳定，成功率较低。而易拉罐模型轮廓单一，相似度较高，成功率接近90%。实验结果表明，我们的手眼协调系统对物体的平移、旋转、光照等具有足够的鲁棒性。
表 2 真实环境中不同物体的位姿跟踪过程中机械臂动态反馈能力验证Table 2 Dynamic feedback capability verification of the robotic arm during the pose tracking of different objects in the real environment目标
物体实验
次数运动方向
正确次数误差
$E \leqslant 1$次数成功率/% 兔子 50 49 47 94 易拉罐 50 47 44 88 犀牛 50 46 45 90 松鼠 50 48 46 92 企鹅 50 49 46 92 5. 结束语
本文提出了在不需要手眼标定的前提下实现机器人手眼协调的新方法，改进了基于区域的物体位姿跟踪算法，使其可以应用于真实场景。通过跟踪机械臂夹持器和物体的位姿，利用它们的相对位置关系以动态反馈的方式引导机械臂运动。最后，在仿真环境和真实环境下测试，表明这种手眼协调能力使机器人能够较好应对动态的任务和多变的环境，验证了方案的可行性。在未来，我们会构建快速三维重建平台，并继续改进物体跟踪算法的准确性以应对更加复杂的场景。
-
图 1 经典局部外观模型
Fig. 1 Classic local appearance model
下载:
全尺寸图片
图 2 局部区域分割线
Fig. 2 Cutting line of local area
下载:
全尺寸图片
图 3 基于分割线的局部外观模型
Fig. 3 Local appearance model based on cutting line
下载:
全尺寸图片
图 4 手眼协调系统结构
Fig. 4 Hand-eye coordination system architecture
下载:
全尺寸图片
图 5 手眼协调系统
Fig. 5 Hand-eye coordination system
下载:
全尺寸图片
图 6 手眼标定(眼在手外)
Fig. 6 Hand-eye calibration (eye outside the hand)
下载:
全尺寸图片
图 7 Gazebo仿真环境
Fig. 7 Gazebo simulation environment
下载:
全尺寸图片
图 8 仿真环境运动规划
Fig. 8 Motion planning in the simulation environment
下载:
全尺寸图片
图 9 真实环境运动规划
Fig. 9 Motion planning in the real world
下载:
全尺寸图片
图 10 夹持器跟踪结果对比
Fig. 10 Comparison of gripper tracking results
下载:
全尺寸图片
图 11 兔子跟踪结果对比
Fig. 11 Comparison of rabbit tracking results
下载:
全尺寸图片
图 12 本文算法其他模型跟踪结果
Fig. 12 Tracking results of other models with our algorithm
下载:
全尺寸图片
图 13 位姿跟踪误差统计
Fig. 13 Error statistics for pose tracking
下载:
全尺寸图片
图 14 本文算法与RBOT算法速度对比结果
Fig. 14 Speed comparisons between our algorithm and RBOT algorithm
下载:
全尺寸图片
图 15 仿真环境实验结果
Fig. 15 Experimental results in the simulation environment
下载:
全尺寸图片
图 16 真实环境实验结果
Fig. 16 Experimental results in the real environment
下载:
全尺寸图片
图 17 误差模型示意图
Fig. 17 Error model demonstration
下载:
全尺寸图片
表 1 D-H参数
Table 1 D-H parameters
$i$ ${a_{i - 1}}$ $ {\alpha _{i - 1}} $ ${d_i}$ ${\theta _i}$ 1 0 0 基座 $ - {\theta _1}$ 2 0 $- {\text{π}} /2$ 0 $- {\theta _2}({\text{π}} /2)$ 3 ${l_2}$ 0 0 ${\theta _3}$ 4 0 $- {\text{π}} /2$ ${l_3}$ $ - {\theta _4}$ 5 0 ${\text{π}} /2$ 0 ${\theta _5}$ 6 0 $- {\text{π}} /2$ ${l_5}$ ${\theta _6}$ 表 2 真实环境中不同物体的位姿跟踪过程中机械臂动态反馈能力验证
Table 2 Dynamic feedback capability verification of the robotic arm during the pose tracking of different objects in the real environment
目标
物体实验
次数运动方向
正确次数误差
$E \leqslant 1$次数成功率/% 兔子 50 49 47 94 易拉罐 50 47 44 88 犀牛 50 46 45 90 松鼠 50 48 46 92 企鹅 50 49 46 92 -
[1] HUTCHINSON S, HAGER G D, CORKE P I. A tutorial on visual servo control[J]. IEEE transactions on robotics and automation, 1996, 12(5): 651–670. doi: 10.1109/70.538972 [2] HAGER G D, CHANG W C, MORSE A S. Robot hand-eye coordination based on stereo vision[J]. IEEE control systems magazine, 1995, 15(1): 30–39. doi: 10.1109/37.341862 [3] HELLER J, HAVLENA M, PAJDLA T. Globally optimal hand-eye calibration using branch-and-bound[J]. IEEE transactions on pattern analysis and machine intelligence, 2016, 38(5): 1027–1033. doi: 10.1109/TPAMI.2015.2469299 [4] LI Wenlong, XIE He, ZHANG Gang, et al. Hand-eye calibration in visually-guided robot grinding[J]. IEEE transactions on cybernetics, 2016, 46(11): 2634–2642. doi: 10.1109/TCYB.2015.2483740 [5] GOODALE M A, MILNER A D. Separate visual pathways for perception and action[J]. Trends in neurosciences, 1992, 15(1): 20–25. doi: 10.1016/0166-2236(92)90344-8 [6] GOODALE M A. Transforming vision into action[J]. Vision research, 2011, 51(13): 1567–1587. doi: 10.1016/j.visres.2010.07.027 [7] YILMAZ A, JAVED O, SHAH M. Object tracking[J]. ACM computing surveys, 2006, 38(4): 13. doi: 10.1145/1177352.1177355 [8] KLEIN G, MURRAY D W. Full-3D edge tracking with a particle filter[C]//Proceedings ofthe British Machine Vision Conference 2006. Edinburgh. British Machine Vision Association, 2006: 1119–1128. [9] WAGNER D, REITMAYR G, MULLONI A, et al. Real-time detection and tracking for augmented reality on mobile phones[J]. IEEE transactions on visualization and computer graphics, 2010, 16(3): 355–368. doi: 10.1109/TVCG.2009.99 [10] KIM K, LEPETIT V, WOO W. Keyframe-based modeling and tracking of multiple 3D objects[C]//2010 IEEE International Symposium on Mixed and Augmented Reality. Seoul, IEEE, 2010: 193–198. [11] CRIVELLARO A, RAD M, VERDIE Y, et al. Robust 3D object tracking from monocular images using stable parts[J]. IEEE transactions on pattern analysis and machine intelligence, 2018, 40(6): 1465–1479. doi: 10.1109/TPAMI.2017.2708711 [12] HINTERSTOISSER S, LEPETIT V, ILIC S, et al. Model based training, detection and pose estimation of texture-less 3D objects in heavily cluttered scenes[M]//Computer Vision – ACCV 2012. Berlin: Springer Berlin Heidelberg, 2013: 548–562. [13] WANG Chen, XU Danfei, ZHU Yuke, et al. DenseFusion: 6D object pose estimation by iterative dense fusion[C]//2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR). Long Beach, IEEE, 2019: 3338–3347. [14] PENG Sida, LIU Yuan, HUANG Qixing, et al. PVNet: pixel-wise voting network for 6DoF pose estimation[C]//2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR). Long Beach, IEEE, 2019: 4556–4565. [15] PRISACARIU V A, REID I D. PWP3D: real-time segmentation and tracking of 3D objects[J]. International journal of computer vision, 2012, 98(3): 335–354. doi: 10.1007/s11263-011-0514-3 [16] TJADEN H, SCHWANECKE U, SCHÖMER E. Real-time monocular segmentation and pose tracking of multiple objects[M]//Computer Vision – ECCV 2016. Cham: Springer International Publishing, 2016: 423–438. [17] TJADEN H, SCHWANECKE U, SCHÖMER E. Real-time monocular pose estimation of 3D objects using temporally consistent local color histograms[C]//2017 IEEE International Conference on Computer Vision. Venice, IEEE, 2017: 124–132. [18] TJADEN H, SCHWANECKE U, SCHÖMER E, et al. A region-based Gauss-Newton approach to real-time monocular multiple object tracking[J]. IEEE transactions on pattern analysis and machine intelligence, 2019, 41(8): 1797–1812. doi: 10.1109/TPAMI.2018.2884990 [19] HEXNER J, HAGEGE R R. 2D-3D pose estimation of heterogeneous objects using a region based approach[J]. International journal of computer vision, 2016, 118(1): 95–112. doi: 10.1007/s11263-015-0873-2 [20] 张雪华, 刘华平, 孙富春, 等. 采用Kinect的移动机器人目标跟踪[J]. 智能系统学报, 2014, 9(1): 34–39. ZHANG Xuehua, LIU Huaping, SUN Fuchun, et al. Target tracking of mobile robot using Kinect[J]. CAAI transactions on intelligent systems, 2014, 9(1): 34–39. [21] 贺超, 刘华平, 孙富春, 等. 采用Kinect的移动机器人目标跟踪与避障[J]. 智能系统学报, 2013, 8(5): 426–432. HE Chao, LIU Huaping, SUN Fuchun, et al. Target tracking and obstacle avoidance of mobile robot using Kinect[J]. CAAI transactions on intelligent systems, 2013, 8(5): 426–432. [22] 韩峥, 刘华平, 黄文炳, 等. 基于Kinect的机械臂目标抓取[J]. 智能系统学报, 2013, 8(2): 149–155. HAN Zheng, LIU Huaping, HUANG Wenbing, et al. Kinect-based object grasping by manipulator[J]. CAAI transactions on intelligent systems, 2013, 8(2): 149–155. [23] 徐呈艺, 刘英, 贾民平, 等. 木板抓取冗余机械臂逆运动学求解[J]. 计算机集成制造系统, 2020, 26(12): 3368–3374. XU Chengyi, LIU Ying, JIA Minping, et al. Inverse kinematics solution of redundant robot arm in picking board[J]. Computer integrated manufacturing systems, 2020, 26(12): 3368–3374. [24] 臧雨飞. 基于机器视觉的机械臂半自主控制系统的研究[D]. 南京: 东南大学, 2018. ZANG Yufei. The research on semi-autonomous control system of mechanical arm based on machine vision[D]. Nanjing: Southeast University, 2018. [25] DU Guoguang, WANG Kai, LIAN Shiguo, et al. Vision-based robotic grasping from object localization, object pose estimation to grasp estimation for parallel grippers: a review[J]. Artificial intelligence review, 2021, 54(3): 1677–1734. doi: 10.1007/s10462-020-09888-5 [26] FERRÃO J, DIAS P, NEVES A J R. Detection of aruco markers using the quadrilateral sum conjuncture[M]//Lecture Notes in Computer Science. Cham: Springer International Publishing, 2018: 363–369. [27] LEPETIT V, MORENO-NOGUER F, FUA P. EPnP: an accurate O(n) solution to the PnP problem[J]. International journal of computer vision, 2008, 81(2): 155–166. doi: 10.1007/s11263-008-0152-6http://dx.doi.org/10.1007/s10462-020-09888-5 [28] MISRA A, SINGH G. Kinematic and dynamic analysis of an industrial six-axis robotic manipulator[C]// International Conference on Robotics, Automation and Non-destructive Evaluation. [S.l.]: 2019.
