Light graph convolutional collaborative filtering recommendation approach incorporating social relationships
-
摘要: 图卷积网络(graph convolution network, GCN)因其强大的建模能力得到了迅速发展，目前大部分研究工作直接继承了GCN的复杂设计（如特征变换，非线性激活等），缺乏简化工作。另外，数据稀疏性和隐式负反馈没有被充分利用，也是当前推荐算法的局限。为了应对以上问题，提出了一种融合社交关系的轻量级图卷积协同过滤推荐模型。模型摒弃了GCN中特征变换和非线性激活的设计；利用社交关系从隐式负反馈中产生一系列的中间反馈，提高了隐式负反馈的利用率；最后，通过双层注意力机制分别突出了邻居节点的贡献值和每一层图卷积层学习向量的重要性。在2个公开的数据集上进行实验，结果表明所提模型的推荐效果优于当前的图卷积协同过滤算法。Abstract: Graph convolutional network (GCN) has rapidly developed due to their powerful modeling capability. However, much of the research up to now has directly inherited the complex design of GCN (e.g., feature transformation and nonlinear activation), which lacks thorough ablation analysis on GCN. Additionally, implicit feedback is not fully utilized, and data sparsity is not well resolved, which are also shortcomings of current recommendation algorithms. This paper proposes a light graph convolutional collaborative filtering recommendation approach that incorporates social relationships to address such problems (F-LightGCCF). In GCN, the model abandons the design of feature transformation and nonlinear activation. Then it can generate a series of intermediate feedback from users’ implicit negative feedback by taking advantage of social networking, improving the utilization of implicit negative feedback. Lastly, the importance of the contribution values of neighboring nodes and the learning vectors of each layer of the graph convolution layer are aggregated separately using the dual attention mechanism. By conducting experiments on two publicly available datasets, the results show that the proposed model outperforms current graph convolutional collaborative filtering algorithms in the recommendation.
-
移动网络的普遍应用，为人们带来选择麻痹的困扰，推荐系统是解决信息过载问题的关键技术。推荐的重点在于推测用户偏好和拓展用户视野。推荐的核心在于预测用户是否会与某个项目进行交互，例如点击、评级、购买以及其他形式的交互。现有的推荐方法[1-2]大多单一利用可以直接反映用户偏好的显式反馈信息（如用户评分或评价）进行推荐。显式反馈的推荐模型，一般无法考虑用户对打分机制的宽容度差异，在一定程度上会造成数据误差，从而影响推荐结果。隐式反馈[3](如用户点击或浏览)也是影响推荐结果的重要因素。研究者在利用隐式反馈时，经常忽略那些用户不点击或不浏览的项目，这类数据被称为隐式负反馈数据。通常，这类数据信息更稠密，可以间接挖掘用户的隐藏偏好，缺点是不易获取，也更容易包含噪声数据。本文利用用户社交图的拓扑结构，通过分析用户行为和朋友亲密度间接捕获这类隐式负反馈，称为中间反馈。中间反馈相比于显/隐式反馈被视为弱偏好，而相比于隐式负反馈被视为强偏好。并且，本文利用注意力机制[4]对输入数据的噪声进行过滤，减少噪声数据对结果的消极影响，有助于选择最相关的信息，而不是所有可用的信息。
此外，数据稀疏性也影响着协同过滤推荐技术的准确性。最近，将信息网络嵌入到低维向量空间的图嵌入方法已被广泛应用于推荐领域[5-7]，这类低维表示比用户–项目交互矩阵更加稠密，有效缓解了数据稀疏性的消极影响。因此，本文模型的嵌入层利用图嵌入技术将用户、项目和朋友信息映射到低维稠密的向量的空间。图卷积网络因其强大的建模能力得到了快速发展，NGCF[8]、LightGCN[9]等均为典型的图卷积协同过滤技术。图卷积网络[10](graph convolution network, GCN)最初是为图分类任务设计的，“图像”每个节点都包含丰富的语义信息作为输入。然而，在协同过滤中，每个用户/项目只有一个ID作为输入，没有具体的语义。在这种情况下，进行特征变换和非线性激活可能对推荐效果的提升没有任何好处。换句话说，模型包含太多无用的操作，可能会增加模型的训练难度，降低模型性能。基于此猜想，提出的模型摒弃了图卷积网络中特征变换和非线性激活的设计。
1. 研究背景
1.1 用户社交图
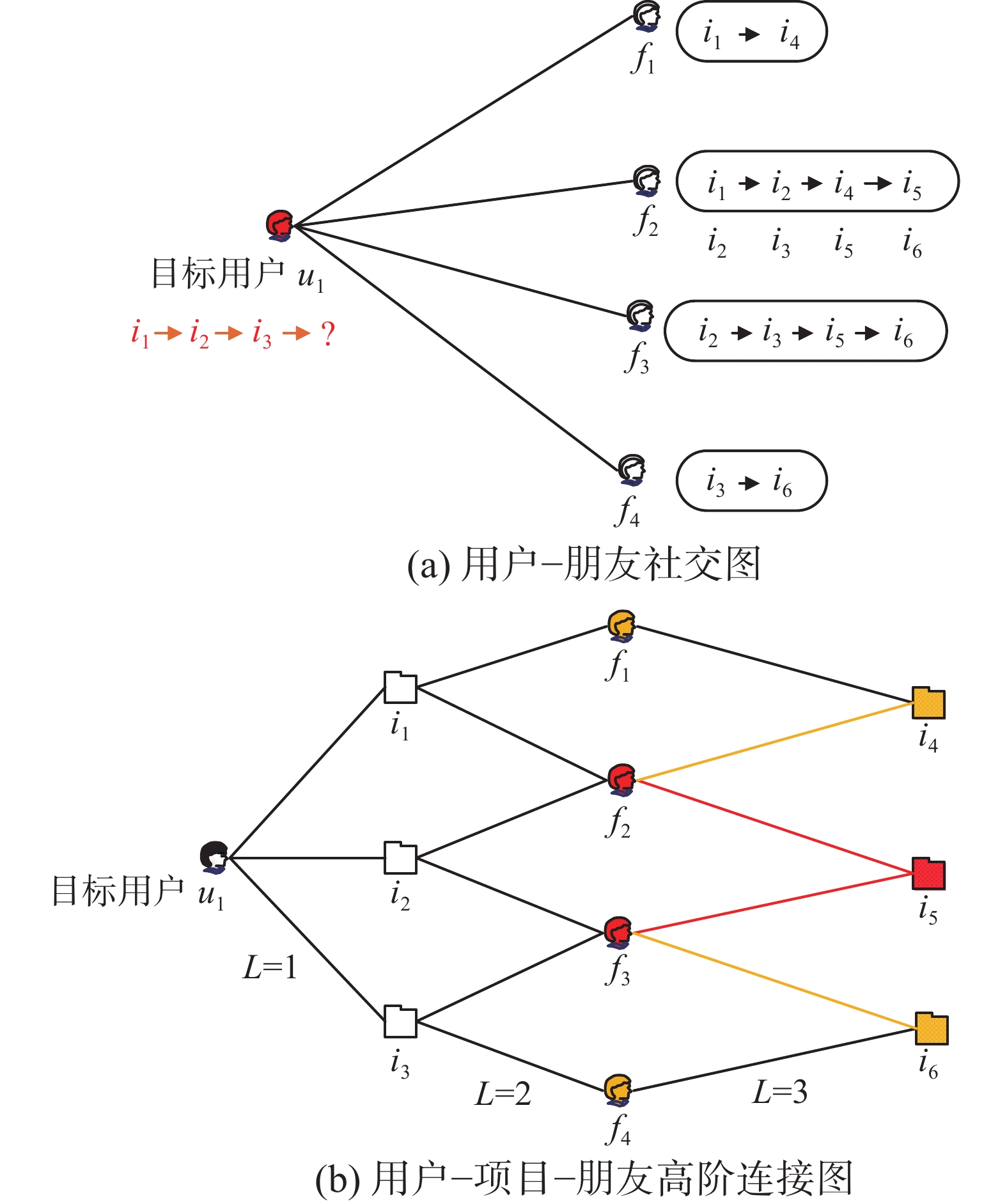
本文利用用户–朋友社交图和用户–项目–朋友高阶连接图从隐式负反馈中产生一系列的中间反馈。从图1(a)可知目标用户u1有4个朋友，分别为朋友f1、f2、f3、f4。从图1(b)可知路径长度L>1表示目标用户u1的高阶连接性，此类高阶连接性承载着u1的显/隐式反馈以及中间反馈的偏好信息。路径L=1表示目标用户u1直接交互的项目，路径L=2表示目标用户与其朋友的行为相似度（即亲密度）。例如， f2、f3与u1直接交互的项目有两次交互，而f1、f4与u1直接交互的项目仅一次交互，由此可以推断f2、f3与目标用户u1的行为相似度更高，对u1决策的影响更大。路径L=3预测更能引起目标用户u1感兴趣的项目。由路径L=2可知，f2、f3与目标用户u1有着更高的行为相似度，因此推断f2、f3共同交互的i5比i4、i6更能引起u1的兴趣。
图 1 用户社交图Fig. 1 User social graph
下载:
全尺寸图片
1.2 相关工作
随着深度学习的发展，研究者将其与推荐算法[11-13]结合，有效提高了推荐结果的准确性。图卷积网络使用卷积算子学习图结构的方法逐渐成为推荐新技术，通过平滑图上的特征来学习节点的表示。文献[14]提出了一种基于二分图的信息传递自动编码框架GC-MC，通过在用户–项目交互图上进行信息传递并产生用户/项目节点的潜在特征，但模型仅考虑了用户的一阶邻居，降低了训练数据的丰富性。文献[15]提出了一种联合矩阵分解和图卷积神经网络的推荐模型Hop-Rec，利用矩阵分解将用户–项目的交互信息因子化以获取用户偏好，显式的建模用户和项目之间的高阶偏好。此类高阶偏好尚未编码到消息传递机制中，仅仅丰富了训练数据。
注意力机制可以为不同的用户和项目分配权重，动态捕获更具代表性的用户/项目影响。文献[16]提出了一种引入双层注意力机制的DAML模型，联合卷积神经网络的局部注意力和相互注意力学习用户和评论之间所存在的潜在特征的相关性。模型仅利用了用户的显式反馈，忽略了隐式反馈的重要影响。文献[17]提出了一种联合反向传播与注意力机制的推荐模型，利用反向传播学习目标用户与邻居节点之间的信息传播，设计注意力机制捕获每个用户对所有最近邻居节点的总体影响。但模型尚未有效解决数据稀疏性对推荐结果产生的消极影响。
需指出的是，以往的推荐技术在不同程度上提高了推荐结果的有效性，但是在缓解数据稀疏性以及隐式负反馈的低利用率等方面尚有不足。本文提出的模型通过图嵌入技术将用户、项目以及朋友信息嵌入到低维向量空间中，利用高阶图卷积层学习用户、项目、朋友之间的高阶连接信息，从隐式负反馈中产生一系列的中间反馈，以统一的方式缓解了数据稀疏性和隐式负反馈利用率低下的局限。
2. 问题定义与解决方案
2.1 问题定义
定义1（用户与项目集合） 用户集
$U = \left\{ {u_1},\right. \left.{u_2}, \cdots ,{u_m} \right\}$ 包含M个用户，项目集$I = \left\{ {{i_1},{i_2}, \cdots ,{i_N}} \right\}$ 包含N个项目。定义2（用户–朋友社交图） 用户与朋友之间的交互构成了用户–朋友社交图，记为Guf={U∪F, Euf}，是一个社会关系图。其中F={f1, f2, …, fL}为朋友集包含了L个朋友，Euf是用户和朋友之间边的集合。
定义3（交互矩阵） 用户与项目之间的交互构成了交互矩阵，记为Rm×n，其中m和n分别为用户和项目的数量。R中的每个元素记为rmn，表示用户u与项目i是否交互；若用户u与项目i之间有过交互，则rmn记为1，否则rmn为0。
定义4（中间反馈） 通过分析用户行为和朋友亲密度而间接捕获的用户对项目的隐式偏好，称为中间反馈。中间反馈相比于显/隐式反馈被视为弱偏好，而相比于隐式负反馈被视为强偏好。
2.2 解决方案
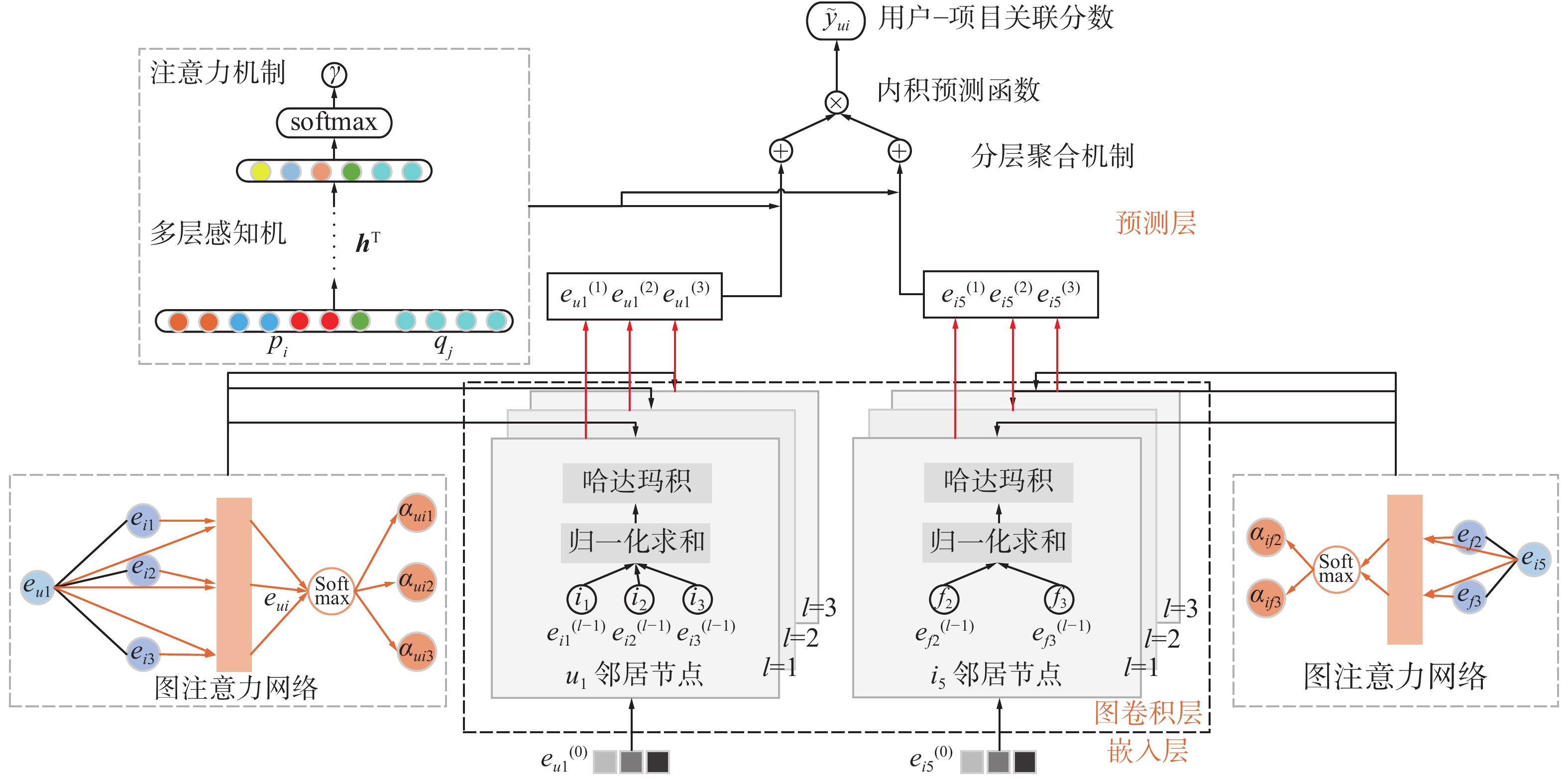
本文设计了一种融合社交关系的轻量级图卷积协同过滤模型，框架如图2，主要由3个模块组成。①嵌入层：初始化用户和项目的嵌入向量。②图卷积层：通过学习用户–朋友社交图和用户–项目–朋友高阶连接图的用户和项目嵌入，从隐式负反馈中产生一系列中间反馈，并利用高阶连接信息来细化嵌入向量。③预测层：采用内积交互函数，得到用户与项目之间的关联分数。
图 2 F-LightGCCF模型框架图Fig. 2 Framework of F-LightGCCF model下载:
全尺寸图片
2.2.1 嵌入层
根据图嵌入模型[5-7]，一个用户u（朋友f或项目i）的嵌入向量表示为cu∈Rd( cf ∈Rd 或 ci ∈Rd)，其中d表示嵌入向量的维度，用户、用户朋友以及项目等嵌入向量构成的初始嵌入向量查找表为
$$ {\boldsymbol{E}}_m = [e_{u1} e_{u2}\cdots e_{uM} e_{f1} e_{f2}\cdots e_{fL} e_{i1} e_{i2}\cdots e_{iN}] $$ 其中，嵌入查找表作为用户嵌入、用户朋友嵌入以及项目嵌入的初始状态，以端到端的方式进行传递和优化。
2.2.2 图卷积层
受GAT[4]、NGCF[8]、LightGCN[9]等模型的启发，在GCN[10]消息传递机制的基础上，从图结构中捕获协同过滤 (collaborative filtering，CF)信号，并细化嵌入向量。本文设计了由消息构建和消息聚合两部分构成的图卷积层。
1）消息构建
从图1(b)可知，当L=1时存在连接用户–项目对(u,i)，从项目i到用户u的消息传递定义为
$$ {\boldsymbol{m}}_{u \leftarrow i}{\text{ = }}f{\text{(}}{\boldsymbol{e}}_i{\text{,}}{\boldsymbol{e}}_u{\text{,}}p_{ui}{\text{)}} $$ 其中，u←i表示从项目到用户的方向传递交互信息， m为表示传递消息的嵌入向量，f()是一个消息编码函数，输入为该用户–项目节点对中用户u和项目i的嵌入向量eu和ei，以及相关系数pui，相关系数p用来控制(u，i)边上每次传播时的衰减因子。
本文中，消息编码函数f()的具体定义为
$$ {\boldsymbol{m}}_{u \leftarrow i}=\frac{1}{\sqrt{\left|N_{u} \| N\right|}}\left(\sigma\left(\sum_{i \in {N_u}} \alpha_{u} \varepsilon_{i}\right)+\left({{\boldsymbol{e}}_i}\odot {{\boldsymbol{e}}_u}\right)\right) $$ 其中，本文模型不仅考虑了ei的影响，还利用哈达玛积(
${\boldsymbol{e}}_i \odot {\boldsymbol{e}}_u$ )将用户与项目之间的交互信息编码到消息传递机制中，使得消息传递取决于ei与eu之间的亲密度值。相关性系数$ p_{u i}=1 / \sqrt{\left|N_{u}\right|\left|N_{i}\right|} $ 采用图卷积神经网络中常用的拉普拉斯范数，其中Nu和Ni表示用户u与项目i的一阶邻居。传统的聚合函数不能区分邻域的重要性，在更新节点时，所有邻域被赋予一个静态权重。因此，本文利用图注意力网络衡量邻域的贡献值，还使得模型更新邻域节点权重时仅依赖于节点之间的特征表达，独立于具体的图结构（图2展示了图注意力网络更新特征节点的方式），提高了模型的泛化能力。
依据图注意力网络原理，邻居节点i对目标节点u的影响，可由注意力相关分数表示：
$$ e_{ui} = {\text{LeakyRelu}}({\boldsymbol{e}}_u||{\boldsymbol{e}}_i) $$ 最后，使用softmax函数对输出结果进行归一化，得到目标用户u的所有邻居节点i的注意力权重，计算方法为
$$ \alpha_{ui} = {\text{softmax}}(e_{ui}) = \dfrac{{\exp (e_{ui})}}{{\left(\displaystyle\sum\nolimits_{k \in N_u} {\exp (e_{uk})} \right)^{\beta_1}}} $$ 其中，β1为一个平滑系数，防止softmax函数对活跃用户权重的过度惩罚，取值范围为[0,1]。
同理，当L=2时存在连接项目–用户朋友对(i,f)，从用户朋友f到用户直接交互项i的消息传递可定义为
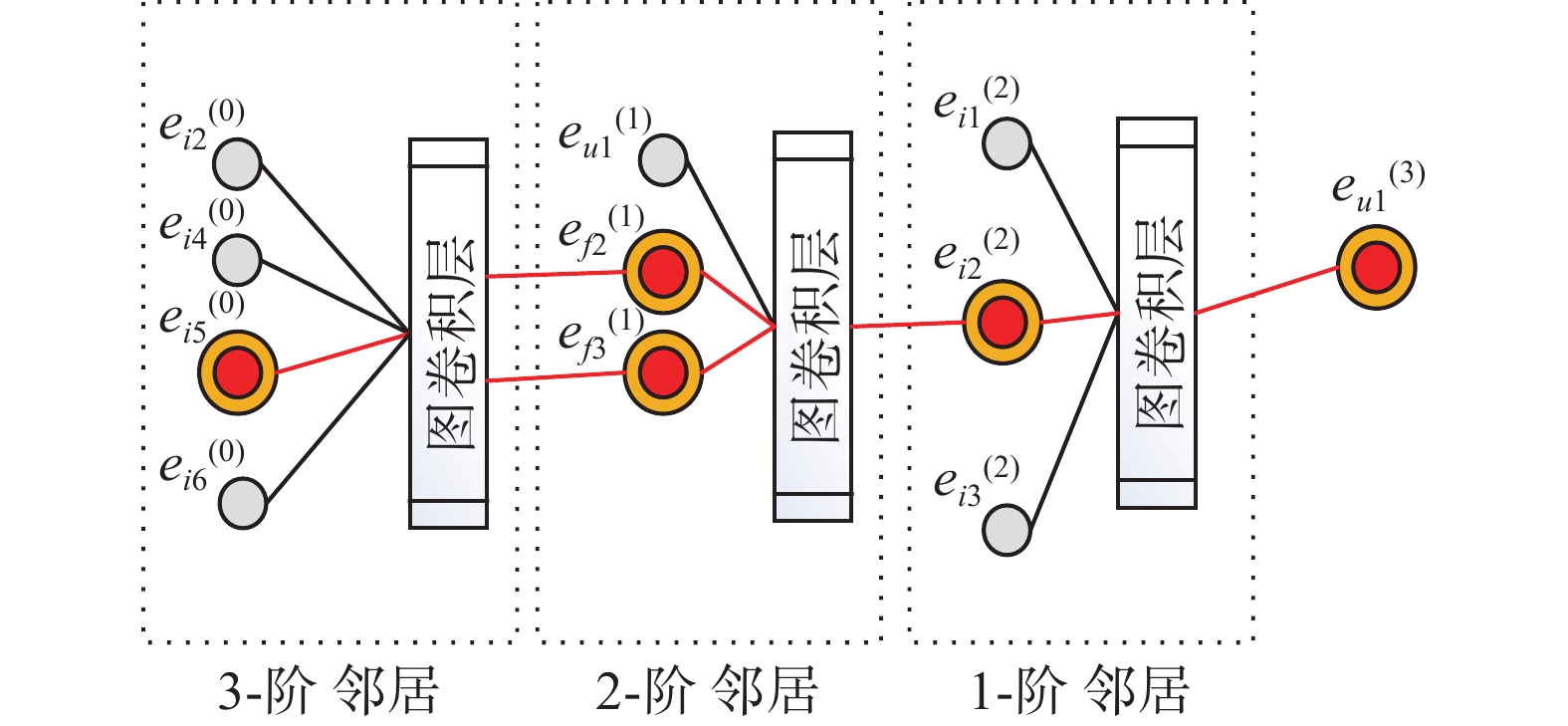
$m_{i \leftarrow f}^{(2)} = f({\boldsymbol{e}}_f,{\boldsymbol{e}}_i,p_{if})$ ，捕获了用户与朋友之间的亲密度。当L=3时存在连接用户朋友–项目对(f,i)，从用户未交互项i到用户朋友f的消息传递可定义为$m_{f \leftarrow i}^{(3)} = f({\boldsymbol{e}}_i,{\boldsymbol{e}}_f,p_{fi})$ ，从隐式负反馈中产生一系列的中间反馈。L=2与L=3消息构建原理与L=1相同。图3展示了目标用户u1的三阶图卷积传播过程，如i5→f2→i2→u1这条传播链上的交互信息被模型捕获，使得 i5上的信息被编码到$ e_{u1}^{(3)} $ 。由此，通过堆叠3层图卷积层，利用社交关系捕获隐式负反馈信息(即，中间反馈)。
图 3 三阶图卷积传播层Fig. 3 Third-order graph convolution propagation layers下载:
全尺寸图片
2）消息聚合
经过3层图卷积传播后，相应的得到了用户u的3个不同的嵌入向量表达，它们对用户偏好有不同的影响。通过聚合目标用户u的所有邻居节点特征来更新用户u的嵌入表达eu，聚合函数可定义为
$$ {\boldsymbol{e}}_u^* = m_{u \leftarrow i}^{(1)}||m_{i \leftarrow f}^{(2)}||m_{f \leftarrow i}^{(3)} $$ 式中：ǁ表示拼接运算。
2.2.3 预测层
同理，对经过3层图卷积传播后得到的3个不同的项目嵌入表达，最终的用户和项目的嵌入表达分别如式（1）、（2）所示：
$$ {\boldsymbol{e}}_u = \sum\limits_{l = 1}^3 {\gamma_l \times {\boldsymbol{e}}_u^{(l)}} $$ (1) $$ {\boldsymbol{e}}_i = \sum\limits_{l = 1}^3 {\gamma_l*{\boldsymbol{e}}_i^{(l)}} $$ (2) 式中：γl≥0表示第l层嵌入的重要程度，该参数采用注意力机制自动优化。
本文采用一个多层感知机来实现注意力机制：
$$ F({\boldsymbol{p}}_i,{\boldsymbol{q}}_j) = {{\boldsymbol{h}}^{\text{T}}}{\text{ReLU}}({\boldsymbol{w}}({\boldsymbol{p}}_i \odot {\boldsymbol{q}}_j) + {\boldsymbol{b}}) $$ 式中：pi通过图嵌入技术将one-hot稀疏向量转换为低维稠密向量表示，pi∈Rd×1；d为嵌入向量维度；qj为每个与用户交互过的项目嵌入表达，qj∈Rd×1；j∈Ru+，Ru+为与用户交互过的项目集合；wl×d、bd×1分别表示从输入层到隐藏层的权重矩阵和防止过拟合的偏置项；hT表示从隐藏层到输入层的权重向量。最后使用softmax函数对输出结果进行归一化处理：
$$ \gamma=\frac{\exp \left(F\left({\boldsymbol{p}}_{i}, {\boldsymbol{q}}_{i}\right)\right)}{\left[\displaystyle\sum_{j \in \pi_{\mathrm{r}}} \exp \left(F\left({\boldsymbol{p}}_{i}, {\boldsymbol{q}}_{i}\right)\right)\right]^{\beta_{2}}} $$ 式中：β2为一个平滑系数，防止过度平滑，取值范围为[0,1]。
最后，在模型预测部分，采用内积交互函数，通过内积运算得到用户对目标项目的偏好为
$$ \begin{gathered} \hat y_{ui} = {\boldsymbol{e}}_u^{\rm{T}}*{\boldsymbol{e}}_i \\ \end{gathered} $$ 2.2.4 模型优化
本文使用贝叶斯(Bayesian personalized ranking，BPR)损失函数[18]对模型进行优化，主要原因是贝叶斯损失函数考虑了观察到的交互和未观察到的交互之间的成对偏好比较。本文还利用用户的社交关系产生了一系列中间反馈，与BPR的基本假设相比，本文假设可以从用户的社交网络中，在未观察到的交互中挖掘出更多的用户偏好，优化目标为
$$ L_{\text {APA }}=\sum_{u, \lambda, j, k}-\ln \sigma\left(\hat{y}_{u}+\hat{y}_{u,}-\hat{y}_{u}\right)+\lambda\|\Theta\|^{2} $$ 式中：
$\Theta $ ={(u,i,j,k)|(u,i)∈R+,(u,j)∈R−,(u,k)∈R−+}表示数据集合，每一条数据都是一个四元组。R+表示观测到的用户–项目交互动作，R−表示未观测到的用户–项目交互动作，R–+表示挖掘出的中间反馈，σ()是sigmoid函数。$\lambda ||\Theta ||^2$ 为L2正则化项，$ \lambda $ 为正则化系数，控制L2正则化强度防止过拟合，$ \Theta $ ={E,β }表示所有可训练的模型参数。Dropout策略可以在模型训练时有效防止模型的过拟合，本文采用节点丢弃的Dropout策略。随机冻结一些特定节点，使其消息不向外传播，对于3层高阶传播，随机丢弃拉普拉斯矩阵中的(M+N)p个节点，其中p为Dropout率。
3. 实验
3.1 数据集
实验采用Gowalla和Yelp2018两个公开的数据集来评估提出的模型，表1给出了两个数据集的统计信息。
表 1 实验数据信息Table 1 Statistics of the datasets数据集 用户/个 项目/个 朋友/个 社交数据/条 稀疏度 Gowalla 7464 40981 22394 1027370 0.00084 Yelp2018 7958 40841 23873 1666869 0.00128 3.2 对比算法
本文提出的融合社交关系的轻量级图卷积协同过滤模型(light graph convolutional collaborative filtering recommendation approach incorporating social relationships，F-LightGCCF)，分别与以下4种先进的推荐模型比较：
1）GRMF[19]：该模型通过利用图拉普拉斯正则化算子来平滑矩阵分解，设计了图正则化交替最小二乘法对算法进行优化，利用加权核范数结构化矩阵分解框架。
2）Mult-VAE[20]：该模型将可变自动编码器应用于协同过滤算法，利用非线性概率模型挖掘用户–项目之间的隐式反馈。
3）NGCF[8]：该模型是基于图卷积神经网络的先进推荐模型，通过构建了k层嵌入传播层对交互信息进行嵌入传播学习，最终得到用户–项目之间的关联分数。
4）LightGCN[9]：该模型基于NGCF模型，摒弃了NGCF模型中特征变换和非线性激活2个复杂的设计，降低了模型的训练难度。
3.3 实验设置
本文模型和算法使用Python语言基于TensorFlow框架实现，机器配置为GPU i7-8700K 3.7 GHz，操作系统为Windows 10。在实验中，对于每一个数据集，随机选择每个用户的80%的交互历史构成训练集，剩余的20%作为测试集。随机选取训练集中的10%作为验证集，用于参数的调试。基于以往模型[9]的经验，正则化系数设置为1×10−4，每次处理的数据量大小为1024，迭代次数为100次时模型收敛。经验证集测试后，在Gowalla数据集和Yelp2018数据，Dropout率分别设置为0.3和0.1。学习率设置为0.0006，注意力网络的平滑系数β1和β2均设置为0.5。参数调整好之后，本文采用Adam[21]作为优化器，使用Xavier方式初始化模型参数，嵌入大小为64，使用3个64×64的图卷积层。
3.4 评价指标
在本文，每种模型均输出用户对所有项目的偏好分数，为了评估top-k推荐和偏好排序的有效性，实验使用召回率(Recall@k)、精确率(Precision@k)和归一化折现积累收益(NDCG@k)作为推荐效果方面的评价指标。默认情况下，设置k=20。召回率是所有“被正确推荐的项目”占所有“应该被推荐的正确的项目”的比例，精确率是“被正确推荐的项目”占“所有被正确推荐的项目”的比例，分别如式（3）和（4）所示。
$$ \text {Recall} @ {k}=\dfrac{\displaystyle\sum_{{u}}|R(u) \cap| T(u) \mid}{\displaystyle\sum_{{u}}|T({u})|} $$ (3) $$ \text {Prectaion} @ {k}=\dfrac{\displaystyle\sum_{{u}}|R(u) \cap T(u)|}{\displaystyle\sum_{{u}}| T(u)\cap {F}(u) \mid} $$ (4) 式中：R(u)是为用户推荐的项目集合；T(u)为测试集上用户感兴趣的项目的集合；F(u)为测试集上用户不感兴趣的项目的集合。
NDCG是一种基于排名的测试指标，排名靠前的项目得分更高。
$$ {\text{NDCG}}@ k = \frac{1}{n}\sum\limits_{l = 1}^k {\frac{{{2^{{\text{rel}}_i}} - 1}}{{\log_2(i + 1)}}} $$ 式中：reli表示用户对第i个项目的评分；log2(i+1)是一个位置递减权重。
3.5 实验结果
3.5.1 模型推荐效果
将本文模型与对比模型分别在2个相同的数据集上实验，实验结果如表2所示。从模型推荐效果的总体比较来看，本文提出的F-LightGCCF模型在2个数据集上的3方面表现优于其他方法，证明了模型的高效性和良好的泛化能力。
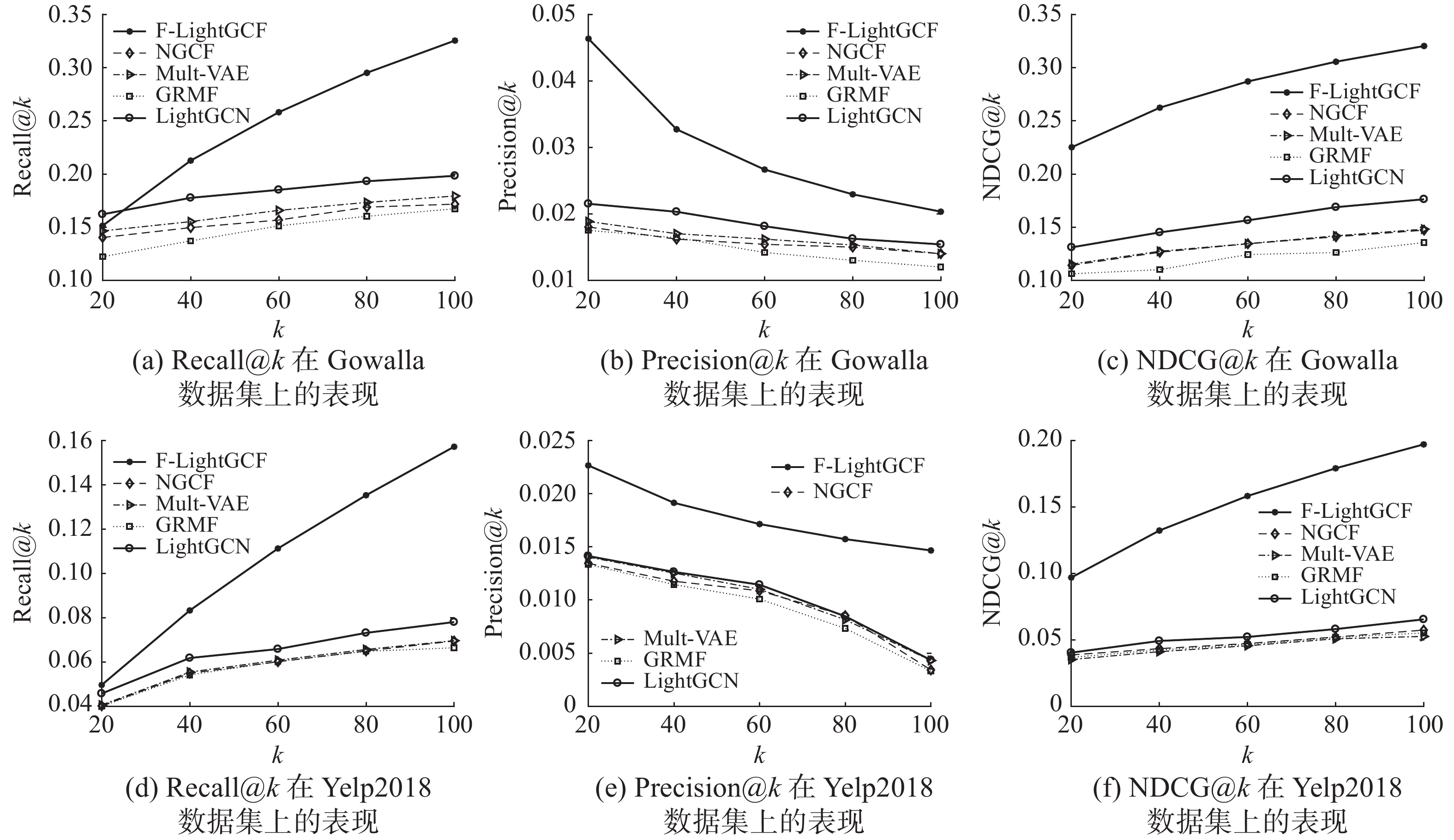
实验对模型的top-k推荐进行了Recall@k、Precision@k和NDCG@k 3方面评估以验证模型的有效性，其中k分别取值为20、40、60、80、100，结果如图4所示。本文模型的top-k推荐效果在全局和局部均有明显的提升，主要原因是采用图嵌入技术将用户、项目、朋友信息映射到低维稠密的向量空间，有效缓解了数据的稀疏性。通过堆叠3层图卷积层，利用社交关系捕获隐式负反馈信息，从而挖掘出能够间接反映用户偏好的中间反馈。另外，通过使用图注意力网络来衡量并更新邻居节点的贡献值。最后，将图卷积层学习到的多个嵌入向量通过分层聚合机制加权聚合，并引入注意力机制自动学习第l层嵌入向量的重要程度，有效提高了模型推荐效果。
表 2 总体比较Table 2 Overall performance comparison算法 Gowalla Yelp2018 Recall@20 Precision@20 NDCG@20 Racall@20 Precision@20 NDCG@20 GRMF 0.1477 0.0146 0.1205 0.0571 0.0091 0.0462 Mult-VAE 0.1641 0.0163 0.1335 0.0584 0.0100 0.0450 NGCF 0.1570 0.0157 0.1327 0.0579 0.0096 0.0477 LightGCN 0.1830 0.0183 0.1554 0.0649 0.0102 0.0530 F-LightGCF 0.2485 0.0306 0.2800 0.1073 0.0179 0.1527 Improve/% 35.79 67.21 80.18 65.33 75.49 188.11 
图 4 2个不同数据集上top-k推荐效果Fig. 4 Top-k recommendation performance on two different data sets下载:
全尺寸图片
3.5.2 图卷积层的影响
图卷积层对F-LightGCCF模型推荐效果中起决定性作用。本文分别了设计GC-MC图卷积层[14]和Hop-Rec图卷积层[15]，模型的推荐效果如表3所示。本文设计的图卷积层的推荐效果相比于其他两种设计均有明显提高，原因是本文图卷积层的设计使用哈达玛积(
${\boldsymbol{e}}_i \odot {\boldsymbol{e}}_u$ )，使得消息传递取决于ei与eu之间的亲密度值。在邻域聚合时，每个邻域嵌入采用对称归一化。经以往研究[9]证实，对称归一化可以使模型表现良好。此外，通过图注意力网络来衡量邻居的贡献值。而GC-MC和Hop-Rec图卷积层的设计并未对图卷积层进行简化操作，仅使用了线性变换，其次，它们的设计并没有考虑用户的社交关系，降低了训练数据的丰富性。此外，Hop-Rec层总体表现优于GC-MC层，原因是GC-MC层仅考虑了用户–项目连接性的一阶邻居影响，而Hop-Rec层利用高阶邻居来丰富训练数据，对用户和项目之间的高阶偏好进行建模。由表2与表3比较可知，更换了图卷积层的F-LightGCCF模型仍表现出很好的推荐效果，原因是本文模型设计了分层聚合机制，考虑了嵌入向量对最终向量表达的影响，融合注意力机制学习第l层嵌入的重要程度，验证了模型设计的合理性。
表 3 不同图卷积层模型的推荐效果Table 3 Recommendation effects of different graph convolution layer models算法 Gowalla Yelp2018 Recall@20 Precision@20 NDCG@20 Racall@20 Precision@20 NDCG@20 GC-MC 0.1811 0.0218 0.2037 0.0978 0.0163 0.1362 Hop-Rec 0.1853 0.0225 0.1967 0.0997 0.0165 0.1386 F-LightGCF 0.2485 0.0306 0.2800 0.1073 0.0179 0.1527 3.5.3 消融分析
以往的工作[22-23]遵循标准的GCN设计，包括特征变换和非线性激活。受LightGCN模型启发，对本文提出的模型进行消融工作。实验结果如表4所示，其中NF-GCCF为未消融的模型，F-LightGCCF为消融的模型。F-LightGCCF模型的推荐效果有明显提高，验证了之前的猜想。在协同过滤推荐中，对用户/项目的one-hot向量进行特征变换和非线性激活无助于特征学习，反而会增加模型的训练难度，降低模型性能。
表 4 消融分析Table 4 Ablation analyses算法 Gowalla Yelp2018 Recall@20 Precision@20 NDCG@20 Racall@20 Precision@20 NDCG@20 NF-GCCF 0.2316 0.0226 0.2158 0.1002 0.0167 0.1429 F-LightGCF 0.2485 0.0306 0.2800 0.1073 0.0179 0.1527 3.6 超参数学习
模型训练过程中，超参数直接影响模型学习的结果，为了使模型达到最佳的推荐效果，本文对模型的超参数学习如表5。
表 5 测试超参数Table 5 Test hyper-parameters超参数 测试参数值 lr {0.0001,0.0003,0.0005,0.0006,0.0007,
0.0008,0.0009,0.001,0.0015,0.002}node_dropout {0.1,0.2,0.3,0.4,0.5} β {0,0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1} 3.6.1 学习率影响
模型的学习率直接影响着神经网络模型的收敛状态，进而影响着模型的性能表现，因此选择一个合适的学习率对于一个神经网络模型的影响至关重要。在神经网络模型中，学习率可以被视为一个超参数来手动调整，也可以看作一个学习参数自动学习。在实验中，将其设置为一个超参数，通过手动调整训练得到最优的学习率大小，实验结果如图5。当学习率lr=0.0006时，模型推荐的总体效果达到最佳，当学习率lr=0.0001时，模型推荐的总体效果最差。
图 5 学习率测试Fig. 5 Learning rate test下载:
全尺寸图片
3.6.2 Dropout率
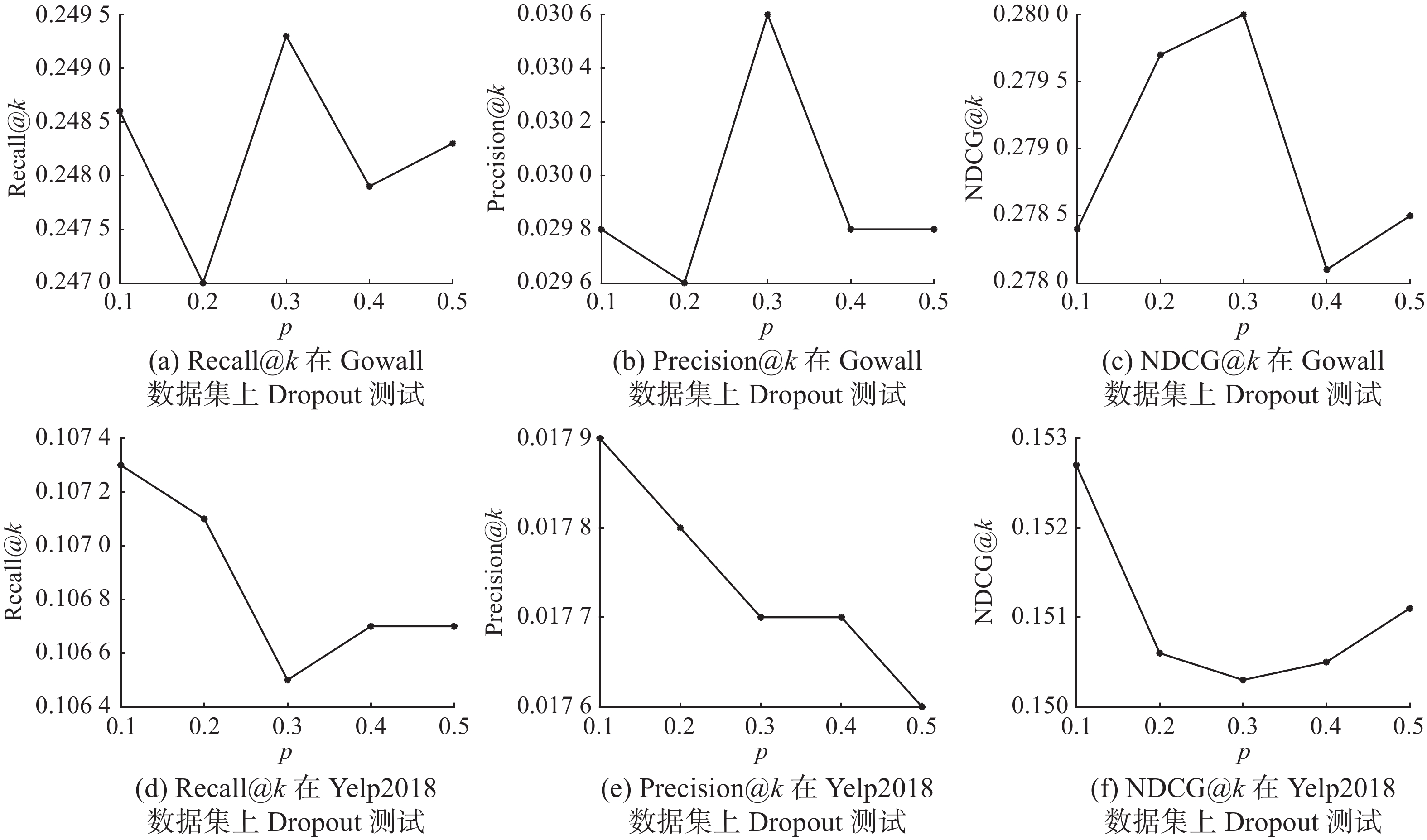
Dropout策略在模型训练时有效防止模型的过拟合，本文提出了一种Dropout策略为节点丢弃(node_dropout)。图6分别显示了节点丢弃率p取不同值作用于2个不同的数据集上产生的不同影响。当p=0.3时，模型在Gowalla数据集上的推荐效果最佳。当p=0.1时，模型在Yelp2018数据集上的推荐效果最佳。原因是Gowalla数据集的稀疏度低于Yelp2018数据集的稀疏度，故而Gowalla数据集更需要丢弃一些无用的数据节点。
3.6.3 平滑系数
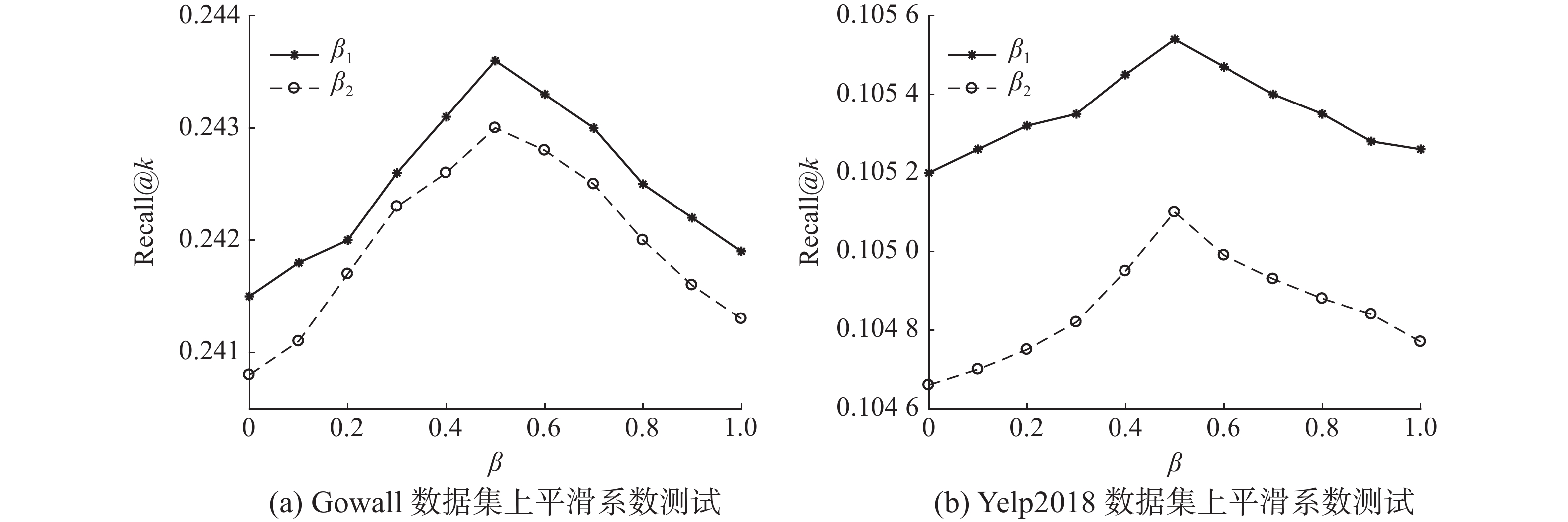
注意力网络的平滑系数用于防止过度平滑对推荐结果所产生的消极影响。本文将平滑系数设置为可手动训练的超参数，图7展示了平滑系数β1和β2分别作用于2个数据集上对召回率的影响。当β1=β2 =0.5时，取得最佳的推荐效果。
图 6 Dropout率测试Fig. 6 Dropout test下载:
全尺寸图片
图 7 平滑系数的影响Fig. 7 Effect of smoothing factor下载:
全尺寸图片
4. 结束语
本文提出了一种融合社交关系的轻量级图卷积协同过滤模型(F-LightGCCF模型)，首先，模型在嵌入层嵌入用户、项目和朋友信息，缓解了数据稀疏性的影响；在图卷积层引入注意力机制衡量邻居节点的贡献值，摒弃了图卷积网络中特征变换和非线性激活的设计，降低了模型的训练难度，提升了模型性能；其次，设计了分层聚合机制综合考虑嵌入学习向量对最终向量表达的影响，再次融合注意力机制学习第l层嵌入的重要程度；最后，模型预测层，利用内积运算预测用户与项目之间的关联分数。实验结果表明，与现有的主流协同过滤推荐模型相比，本文模型取得了更好的推荐效果。本文所构建的轻量级图卷积神经网络模型，是一种简单、线性模型，它更容易实现和训练，但是模型受线性的影响，可能无法有效地捕捉初始数据中的非线性结构。在未来的工作中，将采用更为丰富的训练数据，以缓解推荐模型的冷启动问题。与此同时，考虑影响推荐效果的更多属性，如用户兴趣的动态变化等，尝试通过设计更合理的协同过滤推荐模型来缓解推荐系统中数据稀疏性和隐式反馈的低利用率等问题，进一步提升推荐的准确性。
-
图 1 用户社交图
Fig. 1 User social graph
下载:
全尺寸图片
图 2 F-LightGCCF模型框架图
Fig. 2 Framework of F-LightGCCF model
下载:
全尺寸图片
图 3 三阶图卷积传播层
Fig. 3 Third-order graph convolution propagation layers
下载:
全尺寸图片
图 4 2个不同数据集上top-k推荐效果
Fig. 4 Top-k recommendation performance on two different data sets
下载:
全尺寸图片
图 5 学习率测试
Fig. 5 Learning rate test
下载:
全尺寸图片
图 6 Dropout率测试
Fig. 6 Dropout test
下载:
全尺寸图片
图 7 平滑系数的影响
Fig. 7 Effect of smoothing factor
下载:
全尺寸图片
表 1 实验数据信息
Table 1 Statistics of the datasets
数据集 用户/个 项目/个 朋友/个 社交数据/条 稀疏度 Gowalla 7464 40981 22394 1027370 0.00084 Yelp2018 7958 40841 23873 1666869 0.00128 表 2 总体比较
Table 2 Overall performance comparison
算法 Gowalla Yelp2018 Recall@20 Precision@20 NDCG@20 Racall@20 Precision@20 NDCG@20 GRMF 0.1477 0.0146 0.1205 0.0571 0.0091 0.0462 Mult-VAE 0.1641 0.0163 0.1335 0.0584 0.0100 0.0450 NGCF 0.1570 0.0157 0.1327 0.0579 0.0096 0.0477 LightGCN 0.1830 0.0183 0.1554 0.0649 0.0102 0.0530 F-LightGCF 0.2485 0.0306 0.2800 0.1073 0.0179 0.1527 Improve/% 35.79 67.21 80.18 65.33 75.49 188.11 表 3 不同图卷积层模型的推荐效果
Table 3 Recommendation effects of different graph convolution layer models
算法 Gowalla Yelp2018 Recall@20 Precision@20 NDCG@20 Racall@20 Precision@20 NDCG@20 GC-MC 0.1811 0.0218 0.2037 0.0978 0.0163 0.1362 Hop-Rec 0.1853 0.0225 0.1967 0.0997 0.0165 0.1386 F-LightGCF 0.2485 0.0306 0.2800 0.1073 0.0179 0.1527 表 4 消融分析
Table 4 Ablation analyses
算法 Gowalla Yelp2018 Recall@20 Precision@20 NDCG@20 Racall@20 Precision@20 NDCG@20 NF-GCCF 0.2316 0.0226 0.2158 0.1002 0.0167 0.1429 F-LightGCF 0.2485 0.0306 0.2800 0.1073 0.0179 0.1527 表 5 测试超参数
Table 5 Test hyper-parameters
超参数 测试参数值 lr {0.0001,0.0003,0.0005,0.0006,0.0007,
0.0008,0.0009,0.001,0.0015,0.002}node_dropout {0.1,0.2,0.3,0.4,0.5} β {0,0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1} -
[1] TANG Weitao, YU Dunhui, WEI Shiwei. Commodity recommendation algorithm fusing with knowledge graph and user comment[J]. Computer engineering, 2020, 46(08): 93–100. [2] ZHANG Su, LI Hui, SHI Jun, et al. Reaearch on recommendation algorithm combining user comments and rating information[J]. Journal of shaanxi normal university, 2020, 48(02): 84–91. [3] 印鉴, 王智圣, 李琪, 等. 基于大规模隐式反馈的个性化推荐[J]. 软件学报, 2014, 25(9): 1953–1966. YIN Jian, WANG Zhisheng, LI Qi, et al. Personalized recommendation based on large-scale implicit feedback[J]. Journal of software, 2014, 25(9): 1953–1966. [4] PETAR V, GUIKKEM C, ARANTXA C, et al. Graph attention networks. [C]//Proceedings of the 6th International Conference on Learning Representations. Vancouver: ICLR, 2018: 1710−1722. [5] PEROZZI B, AL-RFOU R, SKIENA S. Deepwalk: online learning of social representations[C]//KDD '14: Proceedings of the 20th ACM SIGKDD international conference on Knowledge discovery and data mining. New York: ACM, 2014: 701−710. [6] 周林娥, 游进国. 一种结合聚集图嵌入的社会化推荐算法[J]. 小型微型计算机系统, 2021, 42(1): 78-84. ZHOU Line, YOU Jinguo. Social Recommendation with Embedding of Summarized Graphs [J]Journal of Chinese computer systems. 2021, 42(1): 78−84. [7] 高海燕, 毛林, 窦凯奇, 等. 基于图嵌入模型的协同过滤推荐算法[J]. 数据采集与处理, 2020, 35(3): 483-493. GAO Haiyan, MAO Lin, DOU Kaiqi, et al. Graph embedding model based collaborative filtering algorithm [J]Journal of data acquisition and processing. 2020, 35(03): 483−493. [8] WANG Xiang, HE Xiangnan, WANG Meng, et al. Neural graph collaborative filtering[C]//Proceedings of the 42nd International ACM SIGIR Conference on Research and Development in Information Retrieval. New York: ACM, 2019: 165−174. [9] HE Xiangnan, DENG Kuan, WANG Xiang, et al. LightGCN: simplifying and powering graph convolution network for recommendation[C]//SIGIR’20: Proceedings of the 43rd International ACM SIGIR Conference on Research and Development in Information Retrieval. New York: ACM, 2020: 639−648. [10] KIPF T, WELLING M. Semi-supervised classification with graph convolutional networks[EB/OL]. New York: arXiv, 2016. (2016−09−09)[2021−07−17].https://arxiv.org/abs/1609.02907v4. [11] 刘荣辉, 张敬普. 基于深度学习的正则化矩阵分解推荐系统[J]. 西南师范大学学报(自然科学版), 2021, 46(7): 103–108. doi: 10.13718/j.cnki.xsxb.2021.07.014 LIU Ronghui, ZHANG Jingpu. Recommender system of regularization matrix decomposition based on deep learning[J]. Journal of Southwest China Normal University (natural science edition), 2021, 46(7): 103–108. doi: 10.13718/j.cnki.xsxb.2021.07.014 [12] 吴国栋, 查志康, 涂立静, 等. 图神经网络推荐研究进展[J]. 智能系统学报, 2020, 15(1): 14–24. doi: 10.11992/tis.201908034 WU Guodong, ZHA Zhikang, TU Lijing, et al. Research advances in graph neural network recommendation[J]. CAAI transactions on intelligent systems, 2020, 15(1): 14–24. doi: 10.11992/tis.201908034 [13] 刘方爱, 王倩倩, 郝建华. 基于深度神经网络的推荐系统研究综述[J]. 山东师范大学学报(自然科学版), 2021, 36(4): 325–336. LIU Fangai, WANG Qianqian, HAO Jianhua. A survey of recommendation system based on deep neural network[J]. Journal of Shandong Normal University (natural science edition), 2021, 36(4): 325–336. [14] RIANNE Van Den Berg, THOMAS N. KIPF M W. Graph convolutional matrix completion[EB/OL]. New York: arXiv, 2017. (2017−06−07)[2021−07−17].https://arxiv.org/abs/1706.02263. [15] YANG J H, CHEN C M, WANG Chuanju, et al. HOP-rec: high-order proximity for implicit recommendation[C]//RecSys’18: Proceedings of the 12th ACM Conference on Recommender Systems. New York: ACM, 2018: 140−144. [16] LIU Donghua, LI Jing, DU Bo, et al. DAML: dual attention mutual learning between ratings and reviews for item recommendation[C]//KDD’19: Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. New York: ACM, 2019:344−352. [17] XI Wudong, HUANG Ling, WANG Changdong, et al. BPAM: recommendation based on BP neural network with attention mechanism[C]//Proceedings of the 28th International Joint Conference on Artificial Intelligence. California: International Joint Conferences on Artificial Intelligence Organization, 2019: 3905−3911. [18] RENDLE S, FREUDENTHALER C, GANTNER Z, et al. BPR: Bayesian personalized ranking from implicit feedback[C]//UAI’09: Proceedings of the 25th Conference on Uncertainty in Artificial Intelligence. New York: ACM, 2009: 452−461. [19] RAO N, YU H F, RAVIKUMAR P, et al. Collaborative filtering with graph information: consistency and scalable methods[C]//NIPS’15: Proceedings of the 28th International Conference on Neural Information Processing Systems-Volume 2. New York: ACM, 2015: 2107−2115. [20] LIANG Dawen, KRISHNAN R G, HOFFMAN M D, et al. Variational autoencoders for collaborative filtering[C]//Proceedings of the 2018 World Wide Web Conference on World Wide Web. New York: ACM Press, 2018: 689–698. [21] KINGMA DIEDERIK, BA JIMMY. Adam: a method for stochastic optimization. [C]//Proceedings of the International Conference on Learning Representations. San Diego: [s. n. ], 2015: 1412−1427. [22] FU Sichao, LIU Weifeng, ZHANG Kai, et al. Semi-supervised classification by graph p-Laplacian convolutional networks[J]. Information sciences, 2021, 560: 92–106. doi: 10.1016/j.ins.2021.01.075 [23] 苏静, 许天琪, 张贤坤, 等. 基于图卷积与外积的协同过滤推荐模型[J]. 计算机应用研究, 2021, 38(10): 3044–3048. doi: 10.19734/j.issn.1001-3695.2021.02.0053 SU Jing, XU Tianqi, ZHANG Xiankun, et al. Collaborative filtering recommendation model based on graph convolution and cross product[J]. Application research of computers, 2021, 38(10): 3044–3048. doi: 10.19734/j.issn.1001-3695.2021.02.0053
