A clustering method based on the asymmetric convolutional autoencoder
-
摘要: 基于深度神经网络的非监督学习方法通过联合优化特征表示和聚类指派,大大提升了聚类任务的性能。但大量的参数降低了运行速度,另外,深度模型提取的特征的区分能力也影响聚类性能。为此,提出一种新的聚类算法(asymmetric fully-connected layers convolutional auto-encoder, AFCAE),其中卷积编码器结合非对称全连接进行无监督的特征提取,然后K-means算法对所得特征执行聚类。网络采用3×3和2×2的小卷积核,大大减少了参数个数,降低了算法复杂性。在MNIST上AFCAE获得0.960的聚类精度,比联合训练的DEC(deep embedding clustering)方法(0.840)提高了12个百分点。在6个图像数据集上实验结果表明AFCAE网络有优异的特征表示能力,能出色完成下游的聚类任务。Abstract: Unsupervised learning methods based on deep neural networks have synergistically optimized the feature representation and clustering assignment, thus greatly improving the clustering performance. However, numerous parameters slow down the running speed, and the discriminative ability of the features extracted by deep models also influences their clustering performance. To address these two issues, a new clustering algorithm is proposed (asymmetric fully-connected layers convolutional autoencoder, AFCAE), where a convolutional autoencoder combined with several asymmetric fully-connected layers is used to extract the features, and the K-means algorithm is subsequently applied to perform clustering on the obtained features. AFCAE adopts 3×3 and 2×2 convolutional kernels, thereby considerably reducing the number of parameters and the computational complexity. The clustering accuracy of AFCAE on MNIST reaches 0.960, almost 12% higher than that of the jointly trained DEC method (0.840). Experimental results on six image data sets show that the AFCAE network has excellent feature representation ability and can finish the subsequent clustering tasks well.
-
无监督聚类是机器学习的重要分支,根据数据自身的相似性揭示数据内部的隐藏结构。传统的聚类算法如K均值(K-means)[1-2]、高斯混合模型GMM (Gaussian mixture model)[3]、基于密度的聚类算法DBSCAN (density-based spatial clustering of applications with noise)[4]等简单易实现,得到广泛应用。但在图像、文本、语音等高维且无结构的数据上容易发生维度灾难,且需要为每个数据集和任务人工设计特征,从而使聚类性能大打折扣。主成分分析法(principal component analysis,PCA)[5]对高维数据进行降维并提取特征,其线性表征能力在应对某些特殊分布的数据时效果不佳。基于非监督学习的自编码器(auto-encoder,AE)[6-7]通过多层复合映射能得到数据的非线性特征。自编码器将原始高维数据映射到低维特征空间,在该空间中更容易依据特征的分布形态执行聚类分析。
深度聚类是用深度神经网络进行表征学习和聚类指派的过程,通常卷积神经网络(convolutional neural networks,CNN)[8]或堆叠自编码器自适应地学习特征表示,再使用传统聚类算法完成聚类指派。此类方法与非深度聚类算法相比,在基准测试图像数据集上都获得了较好的性能。而AE由此不断发展为稀疏自动编码器(sparse auto-encoder)[9-10]、降噪自动编码器(denoising auto-encoder)[11-12]以及卷积自动编码器(convolutional auto-encoder,CAE)[13]。
现有的聚类方法大多侧重于建模实例之间的相似或相异关系,而忽略了提取更有效的表示,这在很大程度上影响了聚类性能。受此启发,本文提出了一种基于非对称全连接层的卷积自编码器的深度聚类算法进行图像聚类分析。非对称全连接层的卷积自编码器学习输入图片的特征表示,然后经典的K-means算法对特征进行聚类划分,对应成原图像的聚类结果。该方法的主要贡献包括:
1)提出非对称全连接层的卷积网络;
2)使用小卷积核,降低算法的复杂性,加快运行速度;
3)在MNIST数据集上取得优于先进的深度聚类算法的聚类精度。
1. 相关工作
自动编码器是无监督表示学习中重要算法之一,由于隐藏层维度通常比数据层小,它可以帮助提取更显著的特征。DEC(deep embedding clustering)[14]先通过深度编码解码网络对数据进行降维,然后采用软分配确定样本点所属簇类,得到聚类结果。通过最小化软标签的分布和辅助目标分布之间的KL散度来迭代改善聚类。IDEC[15]基于DEC的这种思路,在表征学习步骤时使用重构损失和聚类损失联合训练聚类网络。使用欠完备自动编码器来学习嵌入特征。DCN[16]结合了自动编码器和K-means算法。DCN预先训练自动编码器,而后优化重建损失和K-means损失。精心设计了网络结构,以避免琐碎和无意义的解决方案,并提出了一个有效的优化程序来处理挑战性问题。DEN[17]利用自动编码器从原始数据中学习简化的表示。应用局部保留约束保留数据的局部结构属性,通过优化损失对网络进行微调实现聚类的精度的提高。
卷积自编码器中卷积核利用局部感受野抽取图像的局部特征和权值共享减少参数个数等优点,使得深度聚类方法DBC[18]在图像数据集上获得很好的聚类结果。DBC尝试学习深度卷积自编码器以端到端的方式进行训练,设计卷积层(卷积层和反卷积层)和池化层(池化层和反池化层)组成的全连接卷积自编码器(FCAE)网络。使用t分布嵌入算法(t-SNE)[19]分布去衡量特征点与特征聚类中心点的相似性。
CAE进行特征提取加快了网络训练的速度还提高了其下游应用任务的精度。基于深度特征表示的Softmax聚类算法(ASCAE-Softmax)[20]算法设计非对称自编码器网络进行无监督聚类,其中随机初始化网络权值替代层层预训练和全连接层的重构误差作为目标函数的正则约束。该方法为无监督聚类分析和特征表达提供了新思路。
2. AFCAE聚类算法
利用卷积自编码器进行无监督的特征提取,并应用在下游聚类任务中。与一些联合聚类算法不同,本文方法分阶段进行。
2.1 网络结构
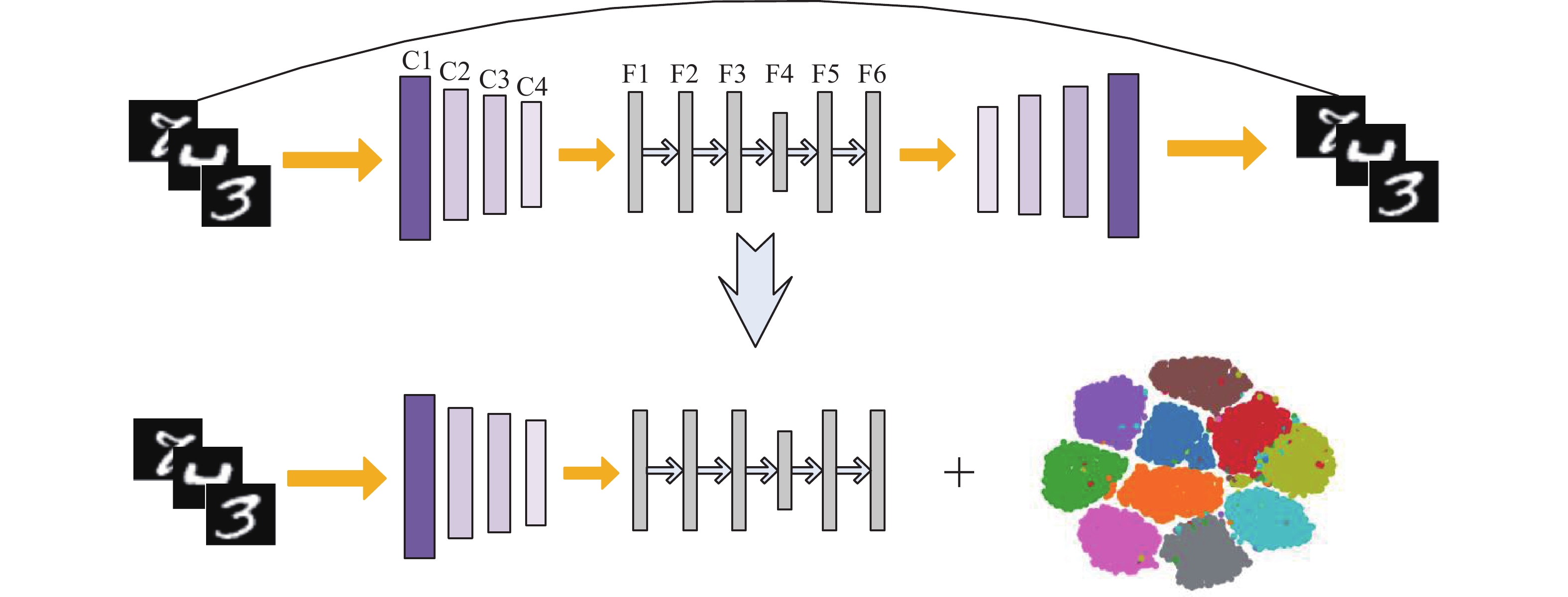
本文提出了一种非对称全连接的卷积自编码器(asymmetric fully-connected layers convolutional auto-encoder, AFCAE),网络结构如图1上半部分所示。网络的输入是28×28的图片,然后通过卷积网络(C1-C4)进行特征提取。受经典联合聚类算法DBC[18]的启发,卷积核多采用3×3。C1到C3的每个待提取特征图都使用3×3卷积核,而C4层上使用2×2的卷积核。在C1层使用步长为3的3×3卷积核,步长等于卷积核的尺寸相当于把图片分割成小片再做特征提取,便于在分辨率高的图像上捕捉丰富的局部特征信息。F1-F6是全连接层,其中F4层的神经元个数与数据集有关,其他层均设为50个。网络采用ReLU激活函数。AFCAE网络相对于对称式网络而言可以看成在F2-F6对称全连接部分前加入F1全连接层进行数据的整合,从而形成非对称网络。改善网络的非线性特征表示的能力。
这个AFCAE网络的端到端无监督预训练结束后,截取C1到F6层后接入K-means算法形成本文的深度聚类模型。为了减少名词的困扰,称其为AFCAE聚类算法,见图1的下半部分。后面实验用到的AFCAE聚类算法详细化为图2,对应的网络参数列于表1,其中(k,n)/s分别代表卷积核的大小、通道数和步长。
表 1 AFCAE网络参数详细表Table 1 The detailed description of AFCAE network parameters层 卷积核/步长 C1 (3,25)/3 C2 (3,50)/2 C3 (3,50)/1 C4 (2,50)/1 F1 50 F2 50 F3 50 F4 10 F5 50 F6 50 2.2 AFCAE方法
AFCAE网络损失函数为输入
$ {x_i} $ 与输出${\hat x_i}$ 之间的误差平方和,为防止网络过拟合,加入$ {L_2} $ 正则化约束:$$ J(W;X;\hat X)=\frac{1}{N}{\displaystyle \sum _{i=1}^{N}\left|\right|{x}_{i}-}{\widehat{x}}_{i}|{|}^{2}+\alpha {\displaystyle \sum _{}\left|\right|W|{|}^{2}} $$ (1) 式中:
$X = \{ {x_1},{x_2},\cdots,{x_N}\}$ 为图像数据集;$ N $ 为图片总个数。第1项损失为重构损失,输入$ {x_i} $ 通过自编码器得到重构后的输出${\hat x_i}$ 。第2项是${L_2}$ 正则化约束,$W$ 为网络参数。$ \alpha $ 为超参数,后面实验中设置$ \alpha = 0.01 $ 。训练好非对称全连接层卷积自编码器后,保留C1-F6层网络结构和参数,使用F6层输出作为特征信息进行聚类。
2.3 复杂性分析
卷积层的理论时间复杂性表示[21]为
$$ O\left(\sum\limits_{l = 1}^d {{n_{l - 1}}k_{_l}^2} {n_l}m_l^2\right) $$ (2) 式中:
$ d $ 为卷积层的数量;$ l $ 是卷积层的索引;$ {n_l} $ 是第$ l $ 层中卷积核的数量,也称为输出通道数;$ {n_{l - 1}} $ 称为第$ l $ 层的输入通道数;$ {k_l} $ 是卷积核的尺寸;$ {m_l} $ 为卷积核输出的特征图大小。全连接层的时间复杂性为输入通道和输出通道的乘积,表示为
$$ O\left(\sum\limits_{l = 1}^d {{n_{l - 1}}{n_l}} \right) $$ (3) 3. 实验结果与分析
本节主要通过K-means对特征表示进行聚类分析来验证AFCAE网络的特征表示能力。所有实验均在6个图像数据集上进行,3.1节详细介绍不同数据集。为了减少随机初始化对K-means算法性能的影响,每组实验都重复50次,选取最好的聚类精度。
实验环境:IntelCorei5-6300HQ处理器,NVIDIA 2.0GB显存,8.0GB RAM显卡;基于开源的Keras库搭建AFCAE网络。
3.1 实验数据集
1) MNIST:由70000个手写数字组成的灰度图像数据集。图像尺寸为28×28,属于10个不同的类(http://yann.lecun.com/exdb/mnist/)。
2) CAS-PEAL-R1:属于40个不同类的200幅灰度图像数据集。每张图片尺寸为480×360。是纯色背景下人脸有表情变化的正面视图。且每人有5幅图片(http://www.jdl.ac.cn/peal/JDL-PEAL-Release.htm)。
3) COIL-20:由日常生活物品组成的1440张尺寸为128×128的数据集。数据集类别为20类,是有角度、无形变的灰度图片(https://www.dazhuanlan.com/2019/10/06/5d999ded06295/)。
4) BioID-Face:数据集为23位人物组成的1521幅灰度图像,图片尺寸为384×286。每张图片为正面视图,具有较大的姿态变化和表情变化(https://www.bioid.com/facedb/)。
5) IMM-Face:属于40个类簇的240幅图片,图片尺寸为640×48,视图为纯色背景下有侧面和正面、有表情变化的图片,每人6幅彩色/灰度图片(http://www.imm.dtu.dk/~aam/aamexplorer/)。
6) UMISTS:包括20个人共564幅图像,图片尺寸为220×220,纯色背景下每个人具有不同角度、不同姿态的灰度图像(https://see.xidian.edu.cn/vipsl/database_Face.html)。
3.2 评价指标
本文使用评价聚类性能的数值指标是聚类精度(accuracy,ACC)和标准互信息(normalized mutual information,NMI)。两个指标值越近1,说明聚类准确度越高。
聚类精度(ACC):聚类精度定义为聚类指派对的数据个数与全部数据个数之比:
$$ {\rm{ACC }}= \dfrac{{\displaystyle\sum_{i = 1}^N {\delta ({s_i},{r_i})} }}{N} $$ (4) $$\delta ({s_i},{r_i}) = \left\{ \begin{aligned} &1,\quad{s_i} = {r_i} \\ &0,\quad{其他} \\ \end{aligned} \right.$$ 式中:
$ {s_i} $ 代表真实标签;$ {r_i} $ 是聚类指派的标签;$ N $ 为总的数据个数。经典匈牙利算法对聚类类标和真实类标进行匹配,通过最佳类别指派得到最优类别结果。ACC值越接近1,说明聚类准确度越高。标准互信息(NMI):将互信息归一化到[0,1],若互信息为0表示两者毫无关联;若为1表示完全相关。NMI可定义为
$$ {\rm{NMI}} = \dfrac{{2I({s_i},{r_i})}}{{H({s_i}) + H({r_i})}} $$ (5) 式中:
$ H $ 为信息熵;$ I $ 是真实标签和聚类标签之间的互信息。NMI衡量了样本标签的预测分布与真实分布的相关程度。3.3 消融实验
为证实AFCAE网络具有优异的特征提取能力,在MNIST和COIL-20数据集上从全连接层是否对称,瓶颈层参数选择以及聚类层数的选择这3方面进行详尽的实验分析。
3.3.1 全连接层的选择
AFCAE网络可以看成在F2-F6对称全连接部分前加入全连接层F1。卷积自动编码器中添加的全连接层是将提取的特征进行整合。为了证实合理增加全连接层数有助于提高网络的聚类精度。保持编码器和解码器网络结构不变,对全连接层部分尝试了不同深度以及对称和非对称式的设计。为了对比的公平性,选取全连接层F6层的特征输出进行聚类分析并比较聚类精度,实验结果列于表2,其中“d-50-c-50”中的数字代表全连接层的神经元个数,d是输入全连接层数据的维度,c是瓶颈层神经元的个数,括号中数值为进行20次实验取得的方差。黑体为本文选取网络全连接层结构以及对应的聚类精度。
表 2 全连接层部分的设计和对应的聚类精度Table 2 Design of fully connected layers and corresponding clustering accuracies全连接层的设计结构 MNIST(ACC) COIL-20(ACC) d-50-c-50 0.923(7.5×10−4) 0.688(6.4×10−4) d-50-50-c-50 0.935(6.9×10−4) 0.714(4.3×10−3) d-50-50-c-50-50 0.934(5.8×10−4) 0.737(6.5×10−3) d-50-50-50-c-50-50 0.960(4.6×10−4) 0.768(3.6×10−4) d-50-50-50-c-50-50-50 0.910(6.8×10−4) 0.751(5.7×10−4) d-50-50-50-50-c-50-50-50 0.896(7.9×10−4) 0.693(6.5×10−4) 根据表2可知,随着全连接层数的增加,聚类精度先增长后有所下降,说明全连接层的增加有助于网络提取有效的特征,使得K-means算法在MNIST上有0.960的聚类精度。实验发现不断地增加全连接层的深度,聚类精度呈下降趋势,说明不能盲目增加网络深度。故本文全连接部分选取d-50-50-50-c-50-50结构。
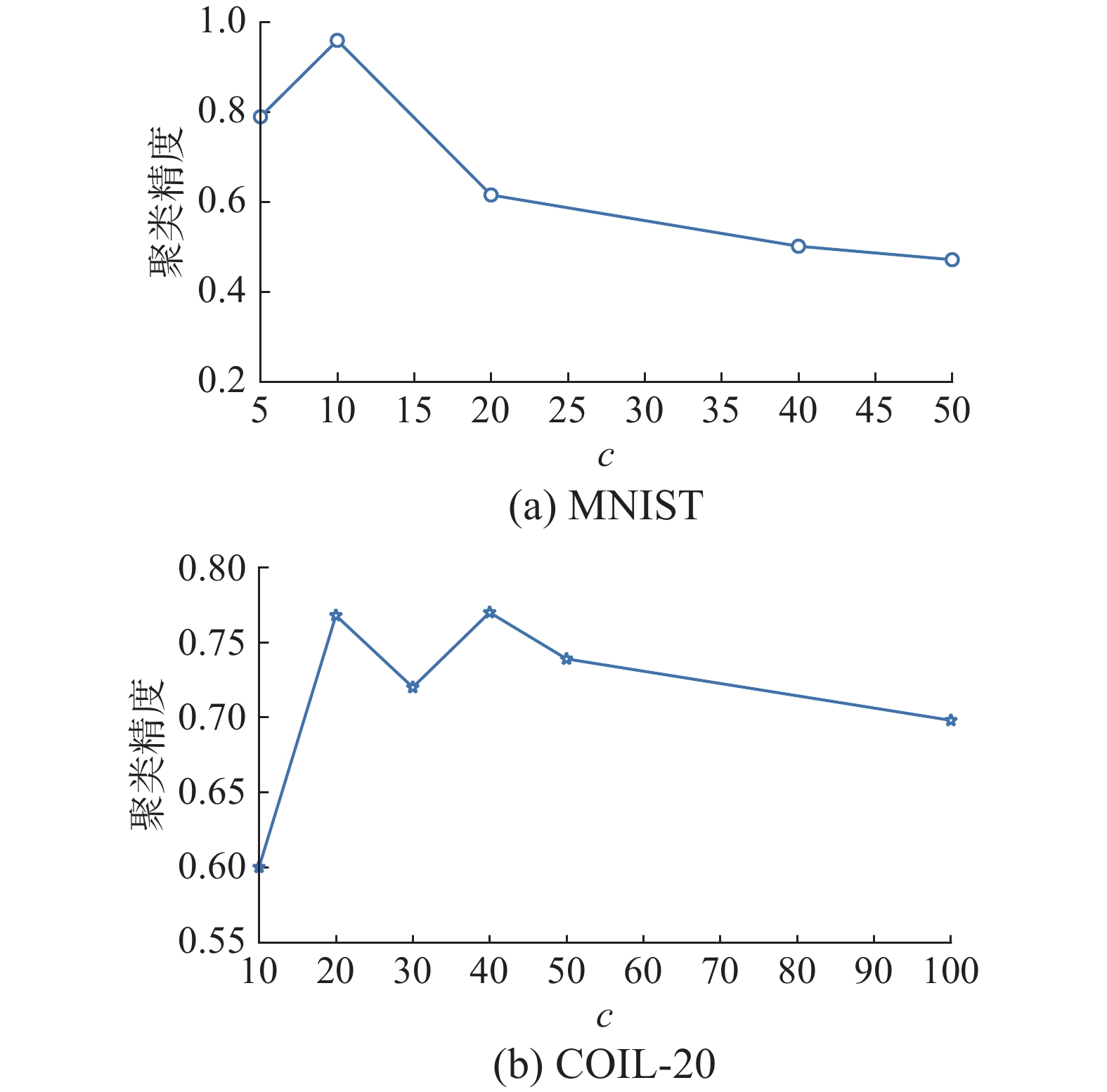
接着在MNIST和COIL-20数据集上验证瓶颈层神经元个数c的选择,结果见图3。
观察图3(a)和(b)不难发现,在简单的MNIST数据集上,随着神经元个数的增加,聚类精度先上升后一直呈下降趋势,c=10(基准类别数)时出现最高精度;而在相对复杂的COIL-20数据集上,随着神经元个数的增加,聚类精度并不稳定,c为20(基准类别数)和40时均出现最高聚类精度。可见瓶颈层神经元个数影响网络的抽象表达能力,也最终影响聚类性能。综合考虑,后续实验中设定AFCAE网络的瓶颈层神经元个数c为聚类簇数。
3.3.2 聚类输入层的选择
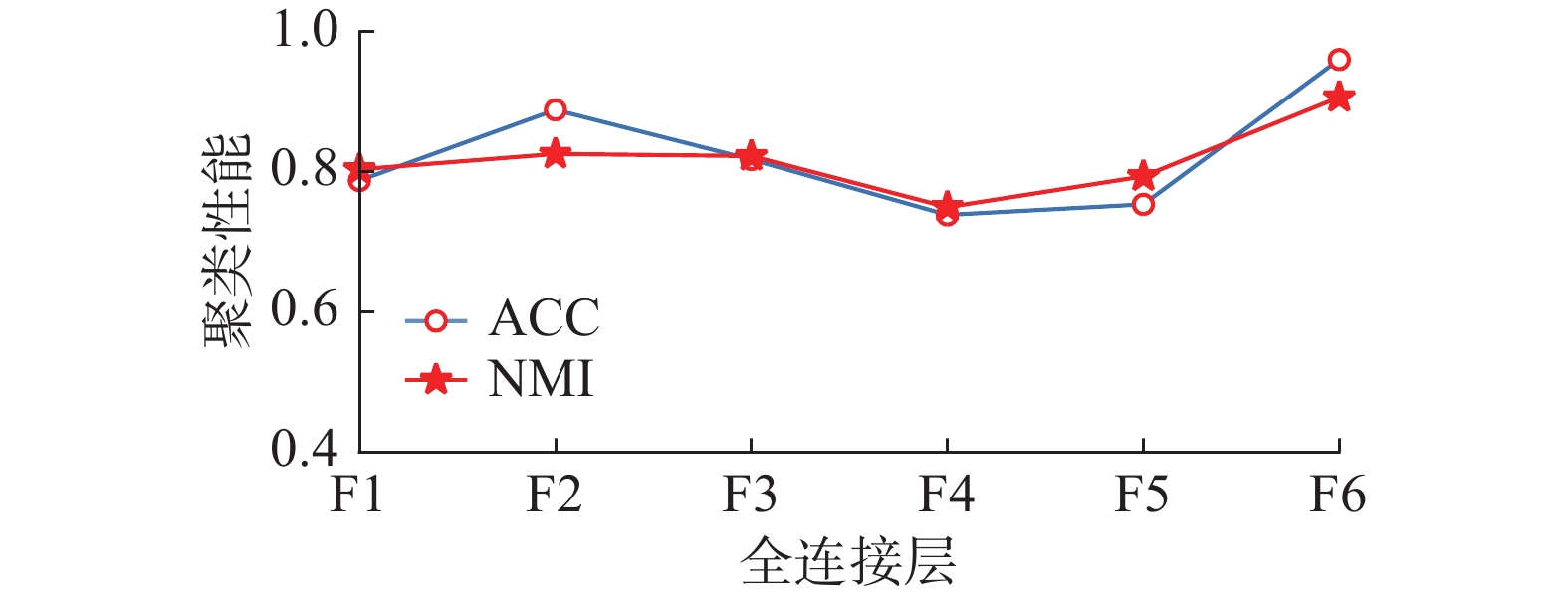
本组实验在MNIST数据集上测试AFCAE网络中不同的全连接层的输出特征在聚类性能上的差异。在某一全连接层后接K-means算法,进行深度聚类分析,所得聚类性能如图4所示。显然,F6层的特征使得聚类性能ACC(0.960)和NMI(0.916)均达到最优。在卷积层C4上获取的局部特征,全连接层通过权值矩阵将局部特征进行组合。随着全连接层数的增加,特征表示不断抽象组合,更趋向于全局特征的表示,因此F6层所提取的特征可看作聚类的输入,实验也证明了F6层上的聚类精度最高。
3.3.3 卷积部分的选择
本组实验在MNIST上验证卷积核与卷积层数对聚类性能的影响。全连接部分与前面的设置相同,只改变卷积核大小、数量和卷积层数,从而建立A、B、C、D和E共5个卷积部分,参数的详细信息见表3,其中(k,n)/s分别为卷积核的大小、数目和步长。
表 3 5个不同卷积网络结构对比Table 3 Comparison 5 different convolutional structures卷积层
网络C1 C2 C3 C4 C5 C6 A (25,3)/3 (50,3)/2 (50,3)/1 (50,3)/2 B (25,3)/3 (50,3)/2 (50,3)/1 (50,2)/2 C (25,3)/3 (25,2)/2 (25,3)/1 (50,2)/1 D (25,3)/3 (50,2)/2 (50,2)/1 (50,2)/1 (50,2)/1 E (25,3)/2 (25,3)/1 (25,3)/1 (25,3)/2 (50,3)/1 (50,2)/1 由于不同数据集的图片尺寸不统一,不考虑输入图像尺寸,仅考虑输入通道、输出通道以及卷积核大小时,理论时间复杂性用式子
$ {n_{l - 1}}k_l^2{n_l} $ 来计算。比如网络B上的理论运行时间为:1×32×25 + 25×32×50 + 50×32×50 + 50×22×50=43950。以网络B的理论时间为基准,定义网络的复杂性,计算公式为
$$ {\rm{Comp(net)}}=\frac{{\rm{net}}的理论运行时间}{B的理论运行时间} $$ (6) 这5个网络的运行时间、网络复杂性以及聚类精度列于表4。
表 4 卷积网络的运行时间,复杂性和聚类精度Table 4 Running time, complexity and clustering accuracy of the convolutional structures网络 运行时间/s 复杂性 精度 A 56475 1.284 0.900 B 43950 1 0.960 C 13350 0.303 0.930 D 35225 0.801 0.942 E 38350 0.872 0.935 由表3和表4可知,B网络C4的2×2卷积核被A网络的3×3替代,复杂性和运行时间增加了,而聚类精度却大大降低;而C网络只将B网络的C2和C3的卷积核数量减少为25个,复杂性和理论运行时间大大减少,同时聚类精度也降低;对比B网络,D网络多了一个2×2的卷积层,但是C2、C3的卷积核也替换成2×2,使得运行时间减少,复杂性降低,同时聚类精度也降低了;E网络变化比较大,将C2、C3和C4的卷积核个数减少为25个,又增加了C5和C6卷积层,运行时间和复杂性没有提高反而继续下降,聚类精度也降低了。
通过对比卷积部分的复杂性和聚类精度,发现小卷积核有利于网络提取适合聚类的特征,犹如网络A到B的转换,精度也随之增长。卷积核的数量对网络的特征提取也起到积极作用。但是一味地增加网络深度,会导致网络过拟合,从而精度下降。综上分析,本文选取卷积网络B作为AFCAE的卷积部分进行后续实验。
3.4 对比实验与分析
AFCAE与其他聚类方法在MNIST和COIL-20上的对比实验分析,包括经典将K-means算法应用于原始图像聚类方法KMS;使用深度自编码器进行特征提取后,使用K-means进行后续聚类的DAE-KMS算法,在此基础上同时优化了数据重建误差和表示紧凑性的AEC算法;以及深度表示和图像聚类的联合无监督学习DEC、IDEC、DBC、JULE和ASCAE-softmax算法。
AFCAE算法的最优聚类性能见表5和表6。同时,选取文献[20]中的DBC在MNIST和COIL-20上的聚类精度分别列于表5和表6。其中黑体字表示最优的性能。
表 5 MNIST数据集上各类聚类方法的对比Table 5 Comparison clustering performances of several clustering methods on MNIST dataset由表5可知,AFCAE网络的聚类精度达到0.96,超过联合训练的其他深度聚类算法,进一步证实了F6层的聚类效果。图5是AFCAE网络的F1层和F6层聚类簇的二维可视化图,F1全连接层的聚类簇大致可以区分开,但各簇类间距较小且分布杂乱。F6中仅有少量特征散乱分布,各簇间有明显的分界线。可视化图直观地证实了全连接层帮助卷积自编码器整合所提取的特征。
在COIL-20上,对AFCAE的F6层特征进行K-means聚类,仅得到0.624的聚类精度。在C1-C4层加入BN层改善网络梯度的变化范围,进而改善网络抽取局部特征的能力,微调结构后聚类精度达到了0.768。聚类可视化如图6所示。
根据表6不难发现,AFCAE的聚类精度0.768高于联合训练的DEC方法的0.731,也略高于ASCAE-softmax方法的0.755。但是NMI不及DEN方法的。由于COIL-20数据集由外形简单但不同角度的物品图片组成,实验过程中发现一些物品轮廓相似,导致的特征之间区分度较小,无法清晰地分成不同的类簇。因此对于轮廓相似的物品图像仍需进一步研究可辨识的特征。
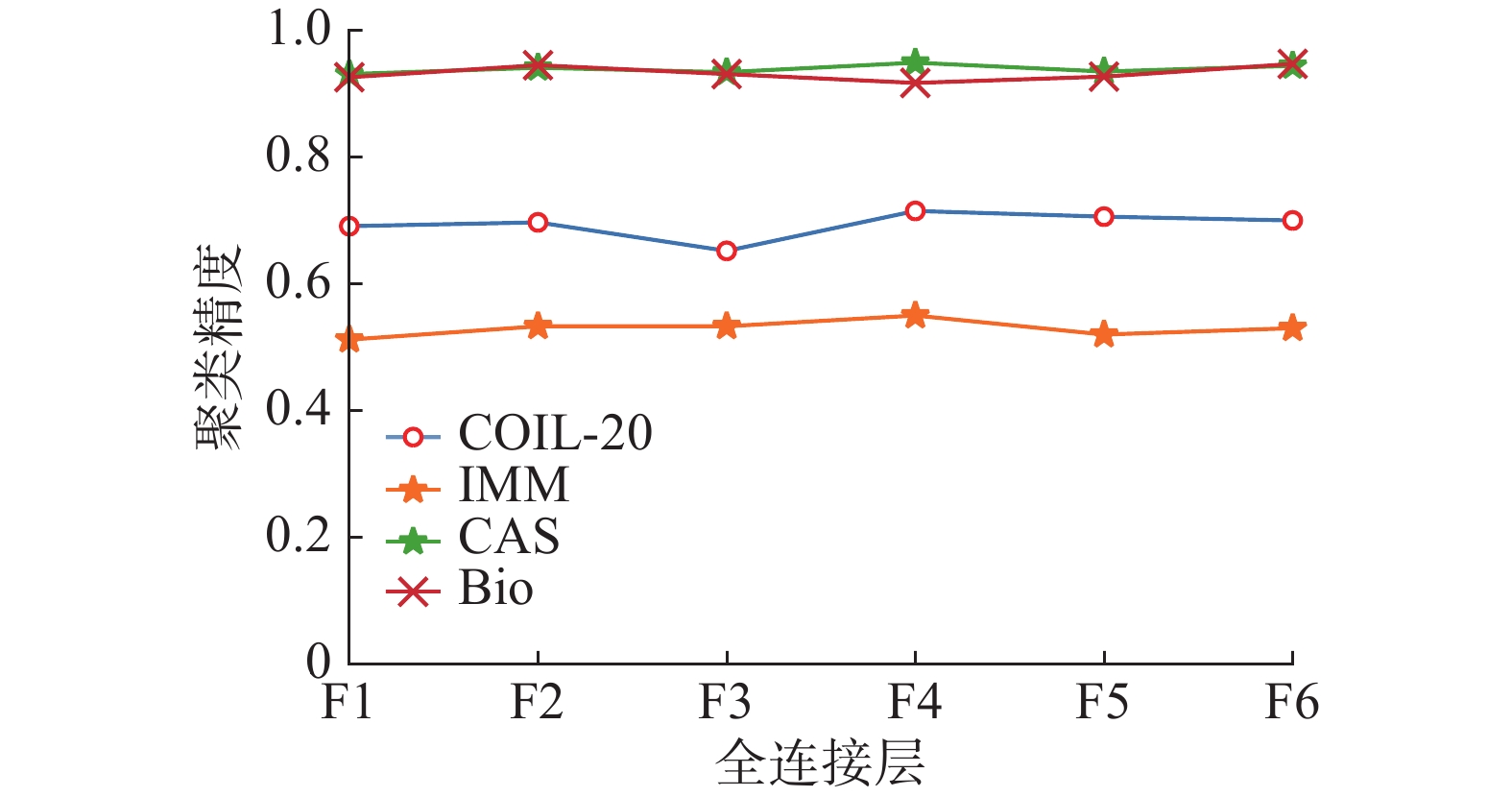
AFCAE网络在4个人脸数据集上也进行了2组实验。第1组验证了每个全连接层的聚类精度,见图7;第2组把F6层的特征输出后进行K-means聚类分析,聚类的ACC和NMI列于表7。
根据图7可知AFCAE网络具有较好的整体稳定性。表7显示在CAS-PEAL-R1和BioID-Face上AFCAE的聚类性能不错,而在IMM和UMISTS上不太令人满意,可能是这两个数据集的图片均有不同程度的表情和姿态,AFCAE网络没能捕获到合适的特征。这将是未来工作之一。
表 7 AFCAE算法在4个人脸数据集上的聚类性能Table 7 Clustering performances of AFCAE algorithm on four face datasets数据集 ACC NMI CAS-PEAL-R1 0.930 0.962 BioID-Face 0.882 0.960 IMM-Face 0.580 0.795 UMISTS 0.488 0.686 4. 结束语
本文提出一个非对称全连接层聚类网络AFCAE,结合K-means并由此提出一个AFCAE深度聚类方法。该方法通过改善网络结构,提取更有辨识力的聚类特征来提高聚类性能。在MNIST和COIL-20上通过详细对比和分析全连接部分,卷积部分包括卷积核大小和数目、卷积层数,特征输出层F6的选择。验证了本文的AFCAE方法降低运行时间的基础上提高聚类性能,而且还优于深度聚类算法DEC和ASCAE的聚类性能。但实验中也发现小卷积核网络对形变较大或类别不确定性较大的数据集的聚类效果不令人满意,这将是未来工作之一。
-
表 1 AFCAE网络参数详细表
Table 1 The detailed description of AFCAE network parameters
层 卷积核/步长 C1 (3,25)/3 C2 (3,50)/2 C3 (3,50)/1 C4 (2,50)/1 F1 50 F2 50 F3 50 F4 10 F5 50 F6 50 表 2 全连接层部分的设计和对应的聚类精度
Table 2 Design of fully connected layers and corresponding clustering accuracies
全连接层的设计结构 MNIST(ACC) COIL-20(ACC) d-50-c-50 0.923(7.5×10−4) 0.688(6.4×10−4) d-50-50-c-50 0.935(6.9×10−4) 0.714(4.3×10−3) d-50-50-c-50-50 0.934(5.8×10−4) 0.737(6.5×10−3) d-50-50-50-c-50-50 0.960(4.6×10−4) 0.768(3.6×10−4) d-50-50-50-c-50-50-50 0.910(6.8×10−4) 0.751(5.7×10−4) d-50-50-50-50-c-50-50-50 0.896(7.9×10−4) 0.693(6.5×10−4) 表 3 5个不同卷积网络结构对比
Table 3 Comparison 5 different convolutional structures
卷积层
网络C1 C2 C3 C4 C5 C6 A (25,3)/3 (50,3)/2 (50,3)/1 (50,3)/2 B (25,3)/3 (50,3)/2 (50,3)/1 (50,2)/2 C (25,3)/3 (25,2)/2 (25,3)/1 (50,2)/1 D (25,3)/3 (50,2)/2 (50,2)/1 (50,2)/1 (50,2)/1 E (25,3)/2 (25,3)/1 (25,3)/1 (25,3)/2 (50,3)/1 (50,2)/1 表 4 卷积网络的运行时间,复杂性和聚类精度
Table 4 Running time, complexity and clustering accuracy of the convolutional structures
网络 运行时间/s 复杂性 精度 A 56475 1.284 0.900 B 43950 1 0.960 C 13350 0.303 0.930 D 35225 0.801 0.942 E 38350 0.872 0.935 表 5 MNIST数据集上各类聚类方法的对比
Table 5 Comparison clustering performances of several clustering methods on MNIST dataset
表 6 COIL-20数据集上6个聚类算法的对比
Table 6 Comparison clustering performances with six methods on COIL-20 dataset
表 7 AFCAE算法在4个人脸数据集上的聚类性能
Table 7 Clustering performances of AFCAE algorithm on four face datasets
数据集 ACC NMI CAS-PEAL-R1 0.930 0.962 BioID-Face 0.882 0.960 IMM-Face 0.580 0.795 UMISTS 0.488 0.686 -
[1] LLOYD S. Least squares quantization in PCM[J]. IEEE transactions on information theory, 1982, 28(2): 129–137. doi: 10.1109/TIT.1982.1056489 [2] HAEUSSER P, PLAPP J, GOLKOV V, et al. Associative deep clustering: training a classification network with no labels[C]//German Conference on Pattern Recognition. Cham: Springer, 2019: 18−32. [3] REYNOLDS D. Gaussian mixture models[M]//Encyclopedia of Biometrics. Boston, MA: Springer US, 2009: 659−663. [4] LIU Peng, ZHOU Dong, WU Naijun. VDBSCAN: varied density based spatial clustering of applications with noise[C]//2007 International Conference on Service Systems and Service Management. Chengdu, China. IEEE, 2007: 1−4. [5] ABDI H, WILLIAMS L J. Principal component analysis[J]. Wiley interdisciplinary reviews:computational statistics, 2010, 2(4): 433–459. doi: 10.1002/wics.101 [6] ALQAHTANI A, XIE X, DENG J, et al. A deep convolutional auto-encoder with embedded clustering[C]//2018 25th IEEE International Conference on Image Processing. Athens, Greece. IEEE, 2018: 4058−4062. [7] YU Tianqi, WANG Xianbin, SHAMI A. UAV-enabled spatial data sampling in large-scale IoT systems using denoising autoencoder neural network[J]. IEEE Internet of things journal, 2019, 6(2): 1856–1865. doi: 10.1109/JIOT.2018.2876695 [8] LECUN Y, BOTTOU L, BENGIO Y, et al. Gradient-based learning applied to document recognition[J]. Proceedings of the IEEE, 1998, 86(11): 2278–2324. doi: 10.1109/5.726791 [9] MASCI J, MEIER U, CIREŞAN D, et al. Stacked convolutional auto-encoders for hierarchical feature extraction[M]//Lecture Notes in Computer Science. Berlin, Heidelberg: Springer Berlin Heidelberg, 2011: 52−59. [10] LEE Honglak, EKANADHAM C, NG A Y. Sparse deep belief net model for visual area V2[C]//Proc of Conf on Advances in Neural Information Processing Systems. Washington D. C. , USA: MIT Press, 2007: 873−880. [11] VINCENT P, LAROCHELLE H, BENGIO Y, et al. Extracting and composing robust features with denoising autoencoders[C]//Proceedings of the 25th international conference on Machine learning-ICML '08. Helsinki, Finland. New York: ACM Press, 2008: 1096−1103. [12] BENGIO Y, LAMBLIN P, POPOVICI D, et al. Greedy layer-wise training of deep networks[C]//Proc of Advances in Neural Information Processing Systems. Washington, USA: MIT Press, 2006: 153−160. [13] MA Xiaolei, DAI Zhuang, HE Zhengbing, et al. Learning traffic as images: a deep convolutional neural network for large-scale transportation network speed prediction[J]. Sensors, 2017, 17(4): 818. doi: 10.3390/s17040818 [14] XIE Junyuan, ROSS G, ALI F. Unsupervised deep embedding for clustering analysis[C]//Proc of ICML’16 Proc of the 33rd Int Conf on Int Conf on Machine Learning. New York City, NY: Semantic Scholar, 2016: 478−487. [15] GUO Xifeng, GAO Long, LIU Xinwang, et al. Improved deep embedded clustering with local structure preservation[C]//IJCAI'17: Proceedings of the 26th International Joint Conference on Artificial Intelligence. New York: ACM, 2017: 1753−1759. [16] YANG Bo, FU Xiao, NICHOLAS D S, et al. Towards K-means-friendly spaces: simultaneous deep learning and clustering[C]//Proc of ICML’17 Proc of the 34th Int Conf on Machine Learning. Sydney, Australia: TonyJebara, 2016: 3861−3870. [17] HUANG Peihao, HUANG Yan, WANG Wei, et al. Deep embedding network for clustering[C]//2014 22nd International Conference on Pattern Recognition. Stockholm, Sweden. IEEE, 2014: 1532−1537. [18] LI Fengfu, QIAO Hong, ZHANG Bo. Discriminatively boosted image clustering with fully convolutional auto-encoders[J]. Pattern recognition, 2018, 83: 161–173. doi: 10.1016/j.patcog.2018.05.019 [19] VAN L, MAATEN D, GEOFFREY H. Visualizing data using t-SNE[J]. Journal of machine learning research, 2008, 9(2605): 2579–2605. [20] 陈俊芬, 赵佳成, 韩洁, 等. 基于深度特征表示的Softmax聚类算法[J]. 南京大学学报(自然科学版), 2020, 56(4): 533–540. doi: 10.13232/j.cnki.jnju.2020.04.011 CHEN Junfen, ZHAO Jiacheng, HAN Jie, et al. Softmax clustering algorithm based on deep features representation[J]. Journal of Nanjing university (natural science edition), 2020, 56(4): 533–540. doi: 10.13232/j.cnki.jnju.2020.04.011 [21] HE Kaiming, SUN Jian. Convolutional neural networks at constrained time cost[C]//2015 IEEE Conference on Computer Vision and Pattern Recognition. Boston, MA, USA. IEEE, 2015: 5353−5360. [22] SONG Chunfeng, LIU Feng, HUANG Yongzhen, et al. Auto-encoder based Data clustering[C]//Iberoamerican Congress on Pattern Recognition. Berlin, Heidelberg: Springer, 2013: 117−124. [23] LIU Hongfu, SHAO Ming, LI Sheng, et al. Infinite ensemble for image clustering[C]//KDD '16: Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York: ACM, 2016: 1745−1754. [24] YANG Jianwei, PARIKH D, BATRA D. Joint unsupervised learning of deep representations and image clusters[C]//2016 IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas, NV, USA. IEEE, 2016: 5147−5156.

 下载:
下载: