A design of an improved self-organizing mapping method based on a knowledge reasoning framework
-
摘要: 随着互联网技术的快速发展，在智能制造过程中会伴随着出现海量的工艺知识数据，为了提升对工艺数据的充分利用和掌握，提出一种知识推理框架下的改进自组织映射算法。在协同训练的思想下，对于知识库当中的工艺知识数据进行自组织映射网络下的筛选优胜，提高优胜单元的抗局部最优能力；利用改进自组织映射算法对特征优胜单元进行知识推理准则判断，在向量空间的映射下，通过双曲空间距离公式优选出置信度高的样本数据进行更新子代样本集；为了进一步提升特征信息的利用率，在知识推理框架下多次循环筛选提高工艺知识数据的有效预测。通过对铣削过程中真实数据进行建模仿真，验证了所提方法在面对多样本数据情况下的良好预测优化的性能。Abstract: In the rapidly developing world of Internet technologies, a vast amount of process knowledge data is generated in the smart manufacturing process. To effectively utilize this data and master it, we propose an improved self-organizing mapping algorithm within the framework of knowledge reasoning. The improved algorithm screens and optimizes the process knowledge data in the knowledge base using collaborative training, enhancing the anti-localization ability of the winning unit. The improved self-organizing mapping algorithm judges the knowledge reasoning criteria of the winning feature unit and selects sample data with high confidence through the mapping of vector space and the use of the hyperbolic space distance formula. Multiple cycles of screening are carried out to further improve the utilization of feature information and enhance the effective prediction of process knowledge data. Through the modeling and simulation of actual milling process data, the proposed method demonstrates its strong predictive and optimized performance when faced with multi-sample data.
-
Keywords:
- knowledge reasoning /
- predicting /
- self-organized mapping /
- smart manufacturing /
- map matching /
- confidence /
- hyperbolic space /
- winning unit
-
自组织映射是一种无监督的神经网络，是知识提取和机器学习领域一个重要的研究方向，其本思想是对数据向量进行矢量化操作，从而减少数据的维度，以提高数据的优化效果[1-4]。现有的自组织映射方法将多个输入与单一的神经单元关联到一起，通过从搜索空间中搜索候选解决方案，对大量的搜索结果加以分析，以此减少计算的效率问题。现有的自组织映射方法根据学习方法大致可以分为两类：基于特征信息的动态自增长半监督协同方法[5]和基于历史特征信息的动态进化方法[6-7]。其中半监督协同方法大都着眼于样本本身的结构信息，完成绝大部分数据样本的标记，对于剩余的噪声数据放进子分类器进行投票输出标记，对于输出不一致的样本进行K均值的二分类判别。动态进化的主要思想是利用算法过程当中产生的不同种群解集，减少新数据的获取和内部属性的关系推理，采用新的知识搜索策略，提高算法的搜索能力，从而对非线性优化问题进行优化。此外，自组织映射思想也可以和其他典型的方法进行结合，充分发挥两者结合的优势和自组织映射思想的特点，在相关领域获取显著的成果研究[8-10]。
知识推理思想是机器学习领域的一个重要研究方向，一般结合其他的方法用来进行知识数据的上下关联推理[11-13]。通常用于知识图谱当中，基本可以分为逻辑推理[14-15]和非逻辑推理[16]，一般从已知的知识出发，结合头实体和尾实体之间的路径，通过已经存在的知识从而获取得到新的事实，实现知识图谱信息的扩充补全。文献[17]通过对实体集进行语义化生成路径表示，对路径采用有效推理的思想寻找了项目和用户之间的潜在关系。
上述方法有的考虑了迭代过程当中的历史信息，有的考虑了特征信息的自适应，有的考虑了规则推理问题，有的考虑了置信度问题。但是，当历史特征信息存在局部最优，上述方法的使用就会出现不足之处，没有进一步考虑到特征信息的优胜过程中采用知识推理的框架对多维历史信息进行上下关联推理。
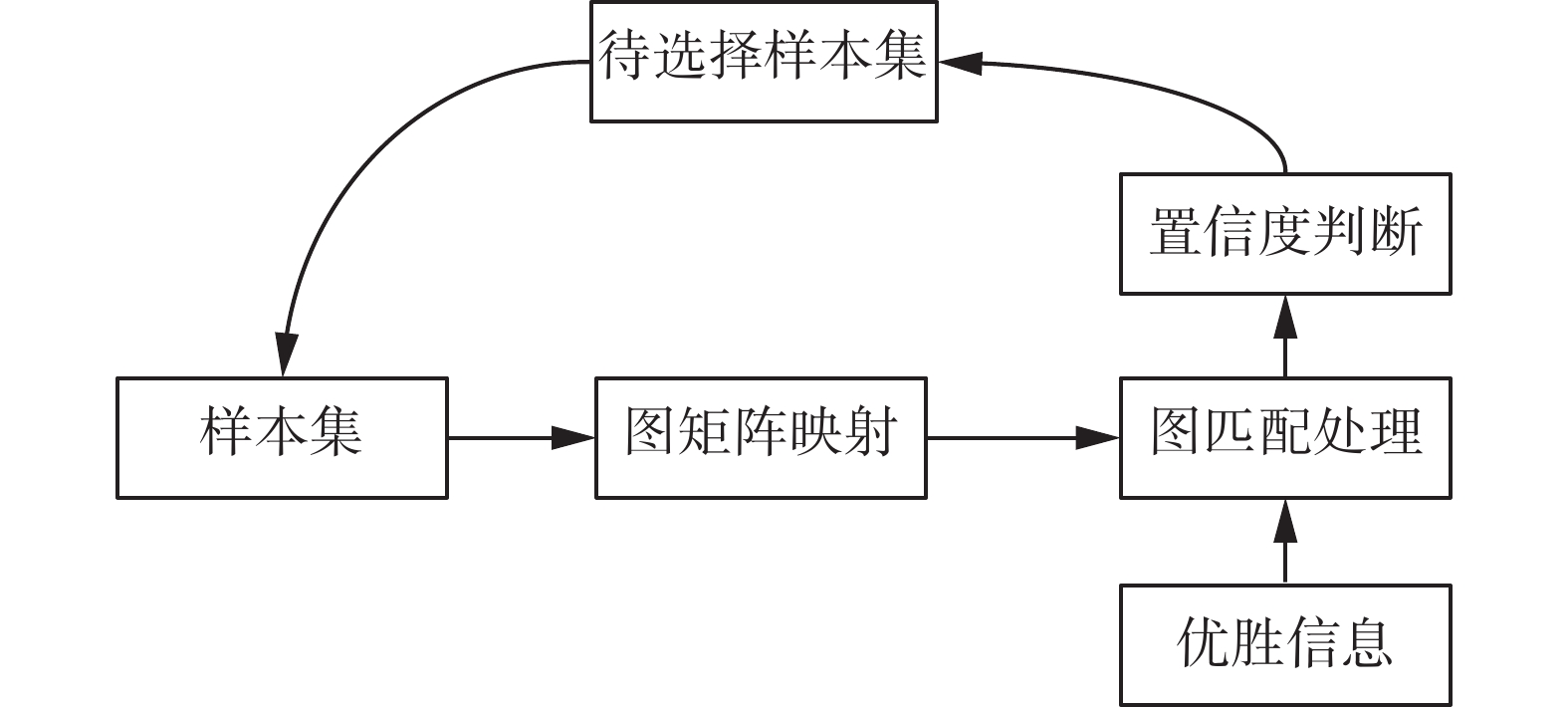
本文针对在特征信息比较多的情况下，综合考虑了以上各个方面对建模的影响，为了提升对特征历史信息利用的准确性和充分性，提出一种知识推理框架下的改进自组织映射优化算法。首先，利用协同训练的思想生成主辅自组织映射神经网络，对网络中优胜过程输入的特征信息进行优选，保证输入信息之间联系性，提高输入信息优化的准确性；其次将其映射为图节点矩阵，利用图匹配的方法对特征信息之间的联系进行匹配，优选出满足推理框架下的知识特征集；然后，通过对此框架下的知识特征集进行置信度判断，得到置信度高的优选样本集；最后，为了进一步提高优化的效果，在改进自组织优化算法下，多次循环筛选提高优化率。
1. 相关知识
1.1 图节点匹配
图节点匹配是一种利用图结构之间的相似度信息，进行寻找图结构之间节点与节点之间的匹配关系。图可以表示为
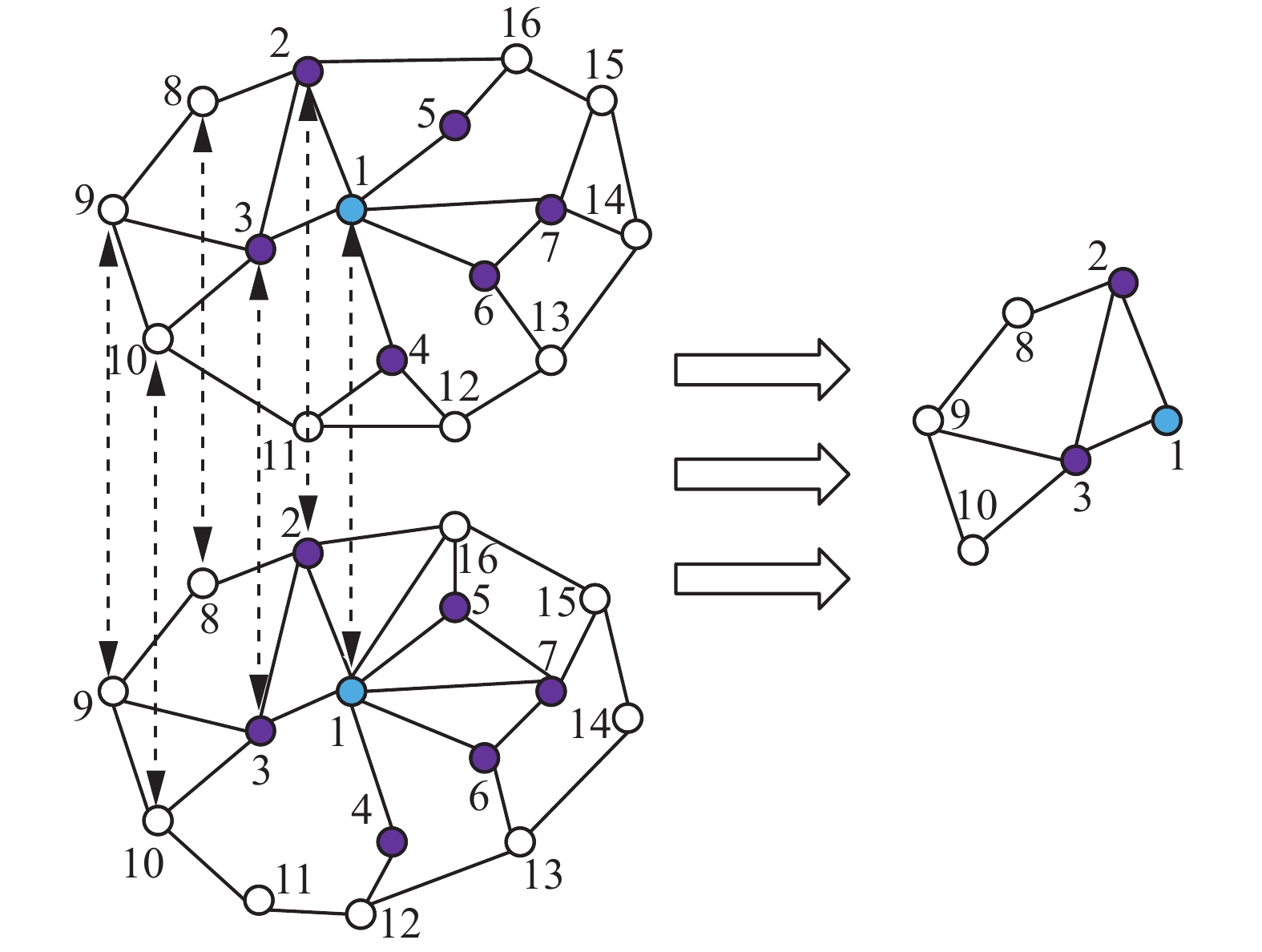
$ G = < H,R,E > $ 三元组表达式[18]，其中$ H $ 是头实体集，$ R $ 是一个关系集，$ E $ 是一个尾实体集，在这些实体集中，每个都是包含着特征和标签的。如图1所示，图节点匹配算法的基本思想：根据图的结构和属性特征用邻接矩阵等将其映射到双曲空间上面。此时不仅包含着图的节点内容、关系边以及权重，更多的是包含更多可挖掘的节点之间的隐含属性[19]。通过将向量空间的图信息嵌入到自组织映射神经网络当中，我们可以在一定程度上面提升算法的稳定性和精确度，从而完成特征集信息的推理优化[20-21]。
图 1 图节点信息匹配Fig. 1 Map information matching
下载:
全尺寸图片
1.2 图匹配置信度判断
置信度判断是用来进行判断知识信息的符合程度，筛选出可信的推理知识样本用于下一次迭代过程中的更新方向，直接影响改进自组织映射算法的优化性能。本文通过打分函数来实现置信度的判断[22]，打分函数表示为
$$ \begin{gathered}{f_{ r}}({\boldsymbol{ h, t}}) = - d_B^c{({{\boldsymbol{ h}}^r},{{\boldsymbol{ t}}^r})^2} + {b_h} + {b_t} = \\ - d_B^c{({\boldsymbol{R}}{ \otimes _c}{\boldsymbol{ h}},{\boldsymbol{ t}}{ \oplus _c}{\boldsymbol{ r}})^2} + {b_h} + {b_t} \end{gathered}$$ (1) 式中：
${{\boldsymbol{h}}^r}$ 、${{{ {\boldsymbol{t}}}}^r} $ 对应于三元组信息中实体嵌入，其对应的${{ {\boldsymbol{h}}}}，{ {\boldsymbol{t}}} \in {\boldsymbol{B}}_c^d$ ，${{{ {\boldsymbol{B}}}}}_c^d$ 表示为双曲空间；$ {b_h} $ 和$ {b_t} $ 是两个偏置，用来更好地拟合数据；$ {\boldsymbol{R}} $ 属于$ {\boldsymbol{B}}_c^d $ ，是一个关系对角矩阵；$ { \otimes _c} $ 表示莫比乌斯–向量乘法；$ { \oplus _c} $ 表示莫比乌斯−加法；$ d_B^c $ 表示双曲空间中的距离定义。双曲空间较之欧几里得空间通过模型当中额外的偏置$ b $ 来表达双曲空间中的信息影响范围距离。1.3 知识推理
知识推理思想是机器学习中一种重要的推理技术，一般结合其他算法用于逻辑或非逻辑推理当中，作用是利用已知的知识信息或者由上到下的规则样本，在向量空间中推理归纳得到新的知识样本。其工作流程：首先，根据已有的少量标签样本构建得到初始的知识图谱；然后，利用知识图谱建立其各个节点之间的关联存在，采用不同的知识推理模型选出推理的样本数据进行训练，搜寻存在的关系路径；通过置信度的判断获取到正确的推理结果。
将知识推理思想融入本文算法，能实现对历史特征信息的充分准确利用，算法思想如图2所示。
图 2 算法的基本思想Fig. 2 Basic concept of the algorithm下载:
全尺寸图片
2. 本文算法
2.1 算法分析
自组织映射算法是一种采用竞争策略的无监督双层神经网络，通过高阶数据的输入以及中间层的优胜策略，从而输出形成新的拓扑结构。自组织神经网络具有在处理信息数据的时候保留数据拓扑结构的特点，往往用于数据缩减和聚类方面[23]。在自组织映射神经网络的训练过程当中，通过将高维数据映射到二维网格状神经元空间，使神经元可以直接近似描述为一种模式的分布，具有高纬度数据处理的良好效果。一个自组织映射算法集成了两个不同的神经网络层：一个输入层和一个竞争层。
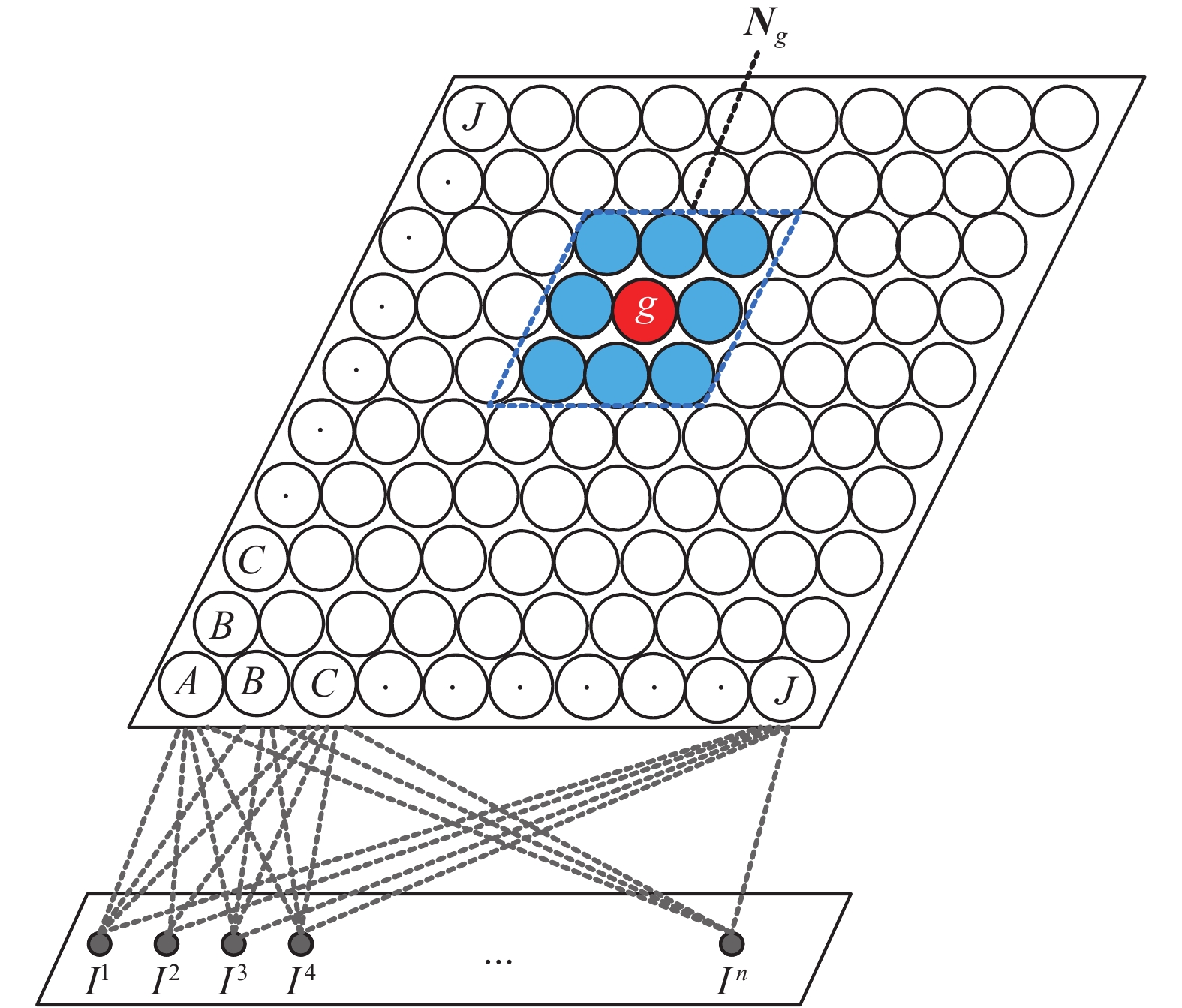
自组织映射神经网络的训练过程涉及两个重要的因素，权重的调整和神经单元的拓扑邻域定义。自组织映射算法的学习过程包含两个阶段，相似度的计算和权重适应调整。在训练开始的初始时段，用随机生成的值进行权重值的初始化，随后引入第一个数据向量，在相似度计算阶段，计算与神经单元有关联的权重和数据向量之间的欧氏距离，紧接着选择在
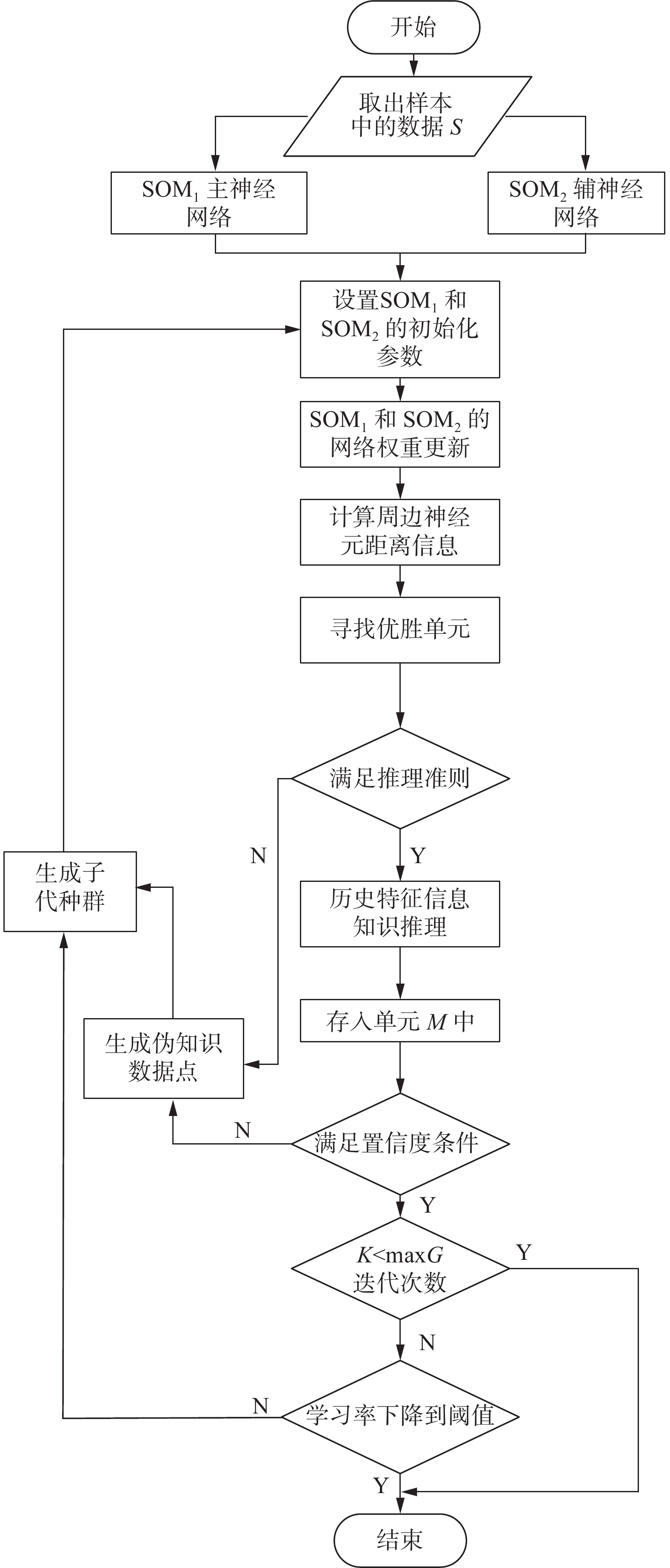
$ H $ 个神经单元中达到最小距离的神经单元$ g $ 作为赢家神经元；在权重调整阶段，获胜神经单元$ g $ 的权重$ {{\boldsymbol{w}}_g} $ 被调整，并且确定赢家神经单元$ g $ 邻域内神经单元的拓扑邻域结构；最后，调整拓扑结构$ {{\boldsymbol{N}}_g} $ 当中神经单元的权重，如图3所示。
图 3 自组织映射网络结构层Fig. 3 Self-organizing mapping network architecture layer下载:
全尺寸图片
图4为知识推理框架下的改进自组织映射算法的流程图，主要包含知识推理框架、置信度判断、样本筛选、迭代更新4个部分。本文在SOM(self-organizing feature map)算法的基础上通过添加协同训练的思想，在进化迭代过程当中利用知识推理思想进行包含特征信息的三元组知识的优化，便于针对不同样本类型，从而构成新的解决方案，优化算法的普适性。另外在避免数据多样性带来的局部优解的情况下，通过多个并行的SOM神经网络进行半监督实现特征数据样本的优化。通过优胜单元的寻取，找寻出不同神经网络当中的数据差异大的地方，在知识推理准则的判断下将带有更新信息的知识推理信息进行输入，根据推理准则的判断结果进行标记，利用知识推理进行二次推理判别，将其加入到待迭代的数据集中，通过双曲空间的距离计算来判别待筛选的样本，判断是否满足置信度条件，另外在整个协同训练的过程中，每确定一个推理样本，分别依次加入到不同的SOM神经网络当中，保证协同训练过程当中的各个子网络的学习均衡和公正。该算法一方面有效避免了陷入局部最优的情况，另一方面针对不确信的样本数据，通过知识推理，增加了算法的可信度。
图 4 改进自组织映射算法流程Fig. 4 Flow of improve self-organizing mapping algorithm下载:
全尺寸图片
2.2 知识推理及协同策略
本文提出的改进自组织映射算法，综合考虑进化过程当中的历史信息以及协同训练的思想，在迭代进化过程中使用知识来执行搜索策略方面的更新，提高优化能力。本文提出的知识推理准则，综合考虑了高维数据降维、历史信息知识推理、基于置信度判断的样本筛选等3方面问题，进而达到准确预测优化样本的目的，防止在迭代的过程中误差累积情况的发生。历史信息知识推理中对样本进行优选和推理不仅保证了初期仅仅挑选当次迭代样本分布范围内的样本，还包含了过往迭代中的优选知识信息，排除了样本中可能存在的离群点的影响，降低优化误差，避免产生过大的震荡。
2.2.1 协同训练策略
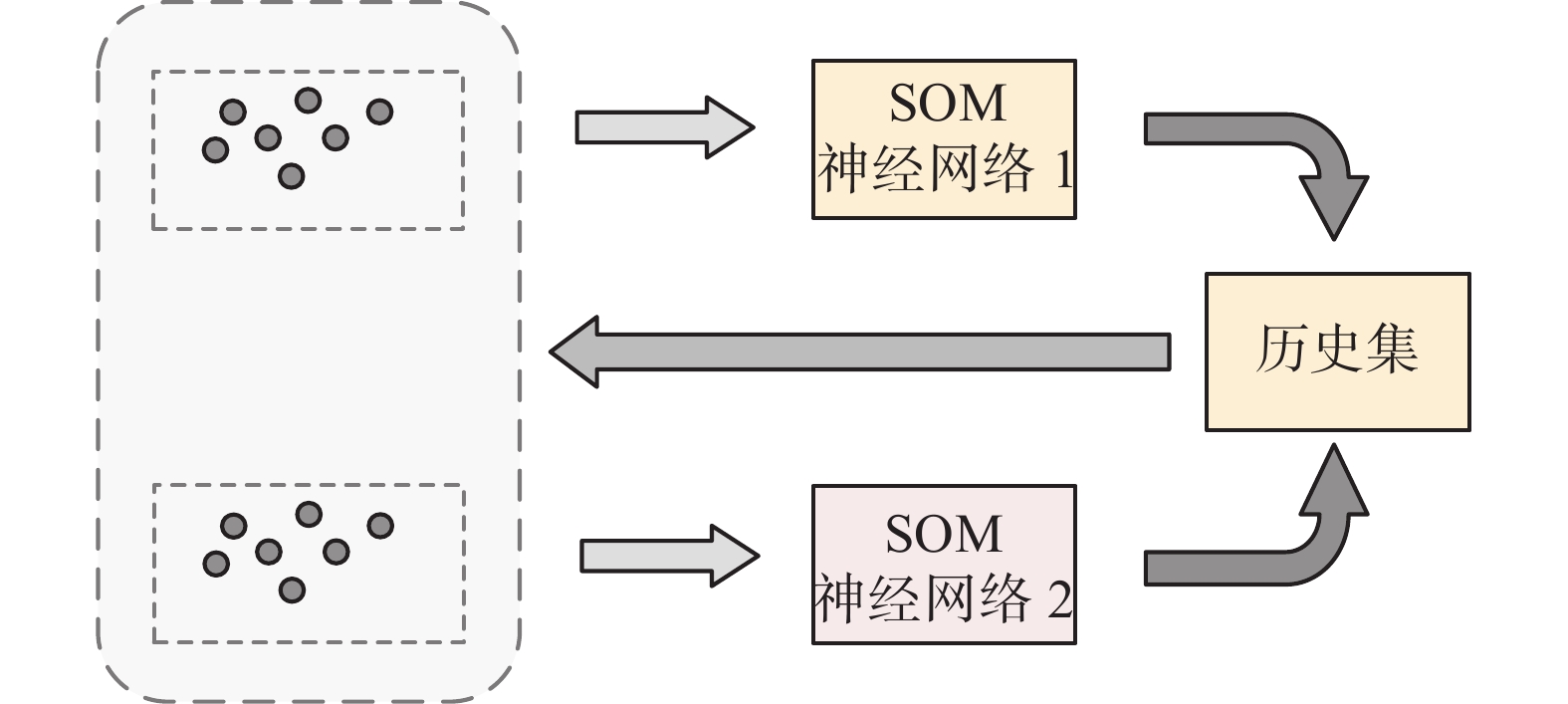
在协同训练思想基础上，将样本数据用来初始化训练2个并行的SOM神经网络，形成带有差别信息的类别中心，在数据多样性的表示基础上，更新更为优化的解集，返回到子代种群中。协同训练思想如图5所示。
图 5 SOM协同训练Fig. 5 SOM combined training下载:
全尺寸图片
2.2.2 知识推理准则
知识推理准则1 给定一个阈值
$ {y_1} $ ，利用双曲空间距离来进行度量当次样本$ x $ 与历史信息$ {x_1} $ 之间的相似度，如果$ x $ 和$ {x_1} $ 之间的距离大于阈值，那么$ x $ 满足知识推理的条件。知识推理准则2 给定一个阈值
$ {y_2} $ ，判断将历史信息样本加入建模过程中后对模型的优化效果的影响，如果模型对样本优化的方差小于阈值$ {y_2} $ ，那么历史信息可信，能够用于更新样本。知识推理准则3 给定一个阈值
$ {y_3} $ ，如果推理得出的信息与历史信息的总平均的双曲空间距离小于阈值的话，那么该条信息就是成功的，可以加入样本$ M $ 。上述3个知识推理准则，知识推理准则1通过双曲空间距离选出与历史信息中具有不相似度的样本点集，该准则有利于历史信息多样性。知识推理准则2利用双曲空间距离提出了每次迭代过程当中比较偏离的样本点，提升了知识推理的精确度。知识推理准则1和2的阈值采用工程经验进行设定，也可以通过采用枚举的方法进行获取，就是先固定阈值
$ {y_2} $ ，更改阈值$ {y_1} $ ，由其对模型优化效果的影响确定$ {y_1} $ 的最优阈值范围，同理也可以得到$ {y_2} $ 的最优范围，然后利用枚举法进行双向枚举得到最佳的阈值。知识推理准则3通过对推理得到的信息进行筛选，选出其中可靠的样本用于更新下一代子集，其基本思想是假设当前样本集为最优样本集合，那么利用阈值判断加入该信息后的影响结果，如果误差变小，那么可以更新子集，从而提升准确性。当前迭代中的信息样本与历史信息之间的双曲空间距离${d^c}({{ {\boldsymbol{x}}}},{ {\boldsymbol{y}}})$ 计算公式[24]为$$ {d^c}({{ {\boldsymbol{x}}, {\boldsymbol{y}}}}) = \frac{2}{{\sqrt c }}{\text{artanh}}\left(\sqrt c \left\| - {{ {\boldsymbol{x}}}}{ \oplus _c}{{ {\boldsymbol{y}}}}\right\|\right) $$ (2) $$ {{ {\boldsymbol{x}}}}{ \oplus _c}{{ {\boldsymbol{y}}}} = \dfrac{{\left(1 + 2c\langle {{ {\boldsymbol{x}}, {\boldsymbol{y}}}}\rangle + c{{\left\| {{{ {\boldsymbol{y}}}}} \right\|}^2}\right){{ {\boldsymbol{x}}}} + \left(1 - c{{\left\| {{{ {\boldsymbol{x}}}}} \right\|}^2}\right){{ {\boldsymbol{y}}}}}}{{1 + 2c\langle {{{\boldsymbol{x}},{\boldsymbol{y}}}}\rangle + {c^2}{{\left\| {{{{\boldsymbol{x}}}}} \right\|}^2}{{\left\| {{{{\boldsymbol{y}}}}} \right\|}^2}}} $$ (3) 式(2)中
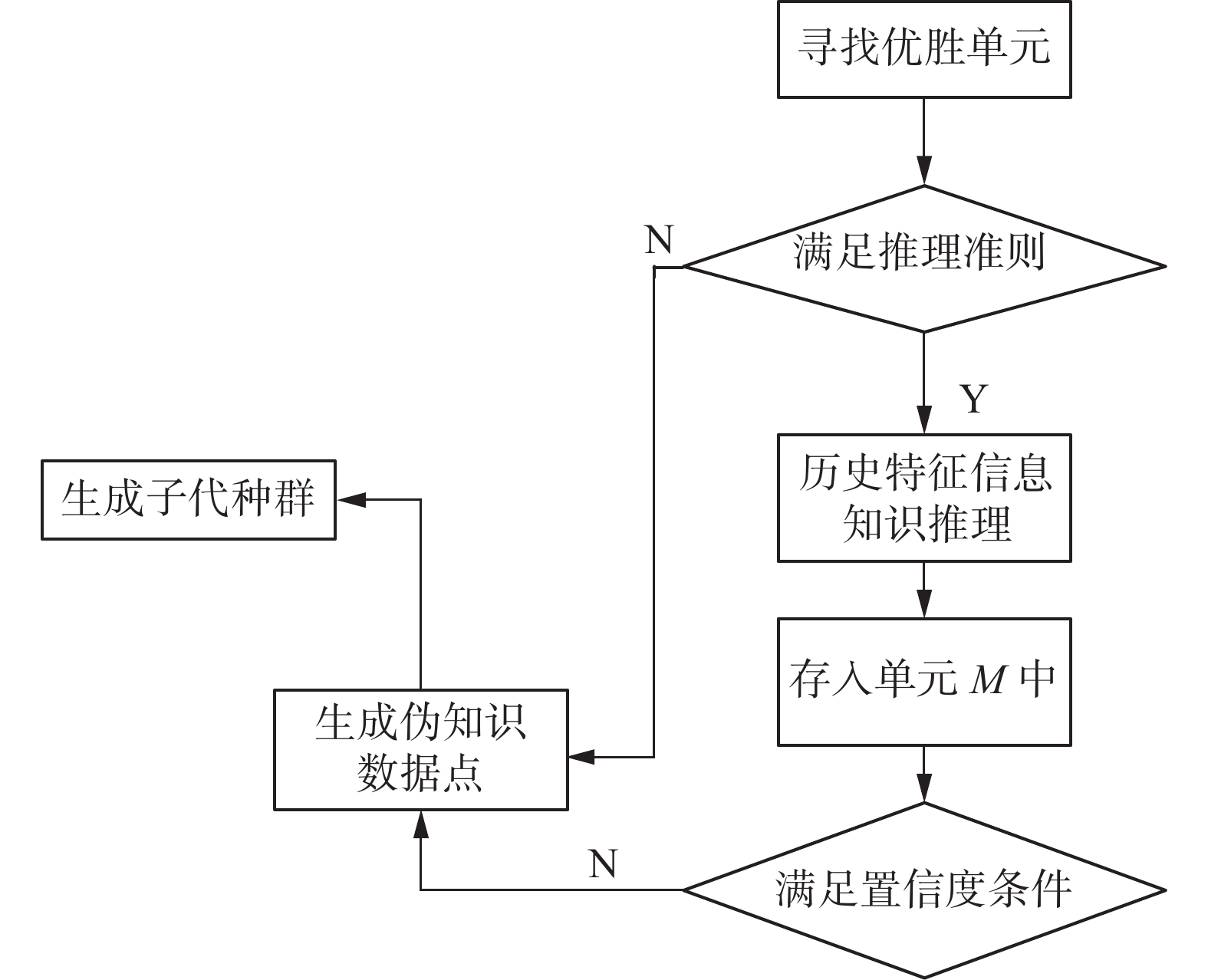
${{{\boldsymbol{x}}}}{ \oplus _c}{{ {\boldsymbol{y}}}}$ 是双曲空间当中的莫比乌斯加法，用来实现向量的加法，$ c $ 表示双曲空间的曲率，${{ {\boldsymbol{x}}}}$ 、${{ {\boldsymbol{y}}}}$ 表示双曲空间中的两个向量。式(3)中的$\langle {{{\boldsymbol{x}},{\boldsymbol{y}}}}\rangle$ 表示两个向量的内积，结果是标量。利用知识推理进行历史信息的筛选，算法流程如图6所示。
图 6 知识推理的过程Fig. 6 Knowledge reasoning process下载:
全尺寸图片
从图6流程图可知，按照流程，首先进行优胜单元的搜索，然后根据搜索的结果进行历史特征信息的知识推理，具体算法步骤：
1) 初始化参数。初始化阈值
$ {y_1} $ 、$ {y_2} $ 和历史样本信息$ {h_1} $ ；2) 依次取出其中的样本；
3) 由式(2)计算双曲空间的距离；
4) 根据推理准则进行判断样本取值的结果是否满足迭代要求，如果不满足跳转到8)；
5) 在满足推理准则的情况下进行特征信息的推理；
6) 存入单元M中，判断是否满足置信度条件；
7) 如果不满足跳转到8)，满足的情况下跳转到9)；
8) 生成伪数据知识点；
9) 放入子代解集中进行解集的迭代。
2.2.3 置信度判断
在改进自组织映射算法中，如果存在不准确的样本信息，容易造成SOM神经网络的误差累积，从而导致优化效果比较差，所以必须对知识推理完成的信息进行置信度判断，在知识推理准则3的基础上进行置信度的判断，具体步骤如下：
1) 初始化样本集，阈值
$ {y_3} $ ；2) 根据式（3）计算得到阈值
$ {y_3} $ ；3) 依次取出样本；
4) 计算平均方差；
5) 判断是否满足知识推理准则3，满足存入，否则跳转6)；
6) 判断是否取完样本，取完跳出循环，否则，跳转2)。
2.3 算法总体步骤
知识推理框架下的改进自组织映射算法总体步骤如下：
1) 初始化参数，包括样本集、循环次数、初始权重、学习率；
2) 更新网络权重值，计算距离，获取主副SOM神经网络当中的优胜神经单元；
3) 利用双曲空间距离进行阈值的计算和初始化；
4) 判断是否满足知识推理准则1和知识推理准则2；
5) 对历史特征信息进行知识推理，对知识推理的样本集进行置信度判断，筛选可靠的样本集进入子集迭代；
6) 根据子集和样本进行更新；
7) 未满足迭代循环
$ {\rm{max}}G $ 次，否则跳转到9)；8) 未满足学习率的下降阈值，跳转到2)，满足跳转到9)；
9) 得到优化的解集。
3. 机床仿真研究
为了验证本文所提方法的实际效果，以制造机床生产过程为对象。机床加工制造过程中的机床能耗对产品效益和环境的影响很大，如何通过优化工艺参数进而优化工艺能耗是智能制造领域一直以来的一个重要研究课题。机床制造过程中的工艺参数主要有4个辅助变量：切削速度
$ N $ 、进给量$ f $ 、轴向切削深度${a_{\rm{p}}}$ 、径向切削深度${a_{\rm{e}}}$ 。该实验过程数据通过截选共有500组数据，为了详细展现本文算法性能，纵向比较了几点创新对模型的影响，具体比较如下：1) SOM (self-organizing feature map)方法[25]，仅利用SOM方法当中的映射策略，将原始的特征信息映射到了新的特征空间中，没有考虑到优化中历史信息的有效利用。
2) DGSOM (dynamic growing self-organizing f-eature map)方法[26]，直接利用带有神经元方向和特征的SOM网络模型，在优化过程中考虑了系统的复杂度，但是没有设计到优化中的历史特征信息的复用和推理。
3) MOPSO (multi-objective particle swarm opti-mization)方法[27]，针对多目标优化问题考虑了解的优化水平和帕累托边界的分布，但是在最小约束去除问题过程中知识将历史信息作为每次过程中的一个无关解，没有将其合理利用在下一步迭代当中。
4) ABC (artificial bee colony algorithm)方法[28]，其根据优化目标生成多维度的初始化种群，引入了交叉和变异的机制来解决算法优化中的搜索效率，避免了陷入局部最优的局面。但是没有使用有效的优化推理策略，判断优化中的信息置信度。
5) CF-SOM (collaborative filtering-self-organ-izing feature map)[29]，其结合提出模型中的所有得分数，将模型中的受益点结合起来，在自组织映射的基础上通过过滤和内容的寻优提升了系统的精度但是降低了系统当中的速度。
6) 本文方法，综合了以上方法中的迭代、变异、以及特征信息中的神经元方向等，在本文知识推理策略下进行算法的优化，对历史特征中的信息采取了进一步的利用，提升算法的效率。
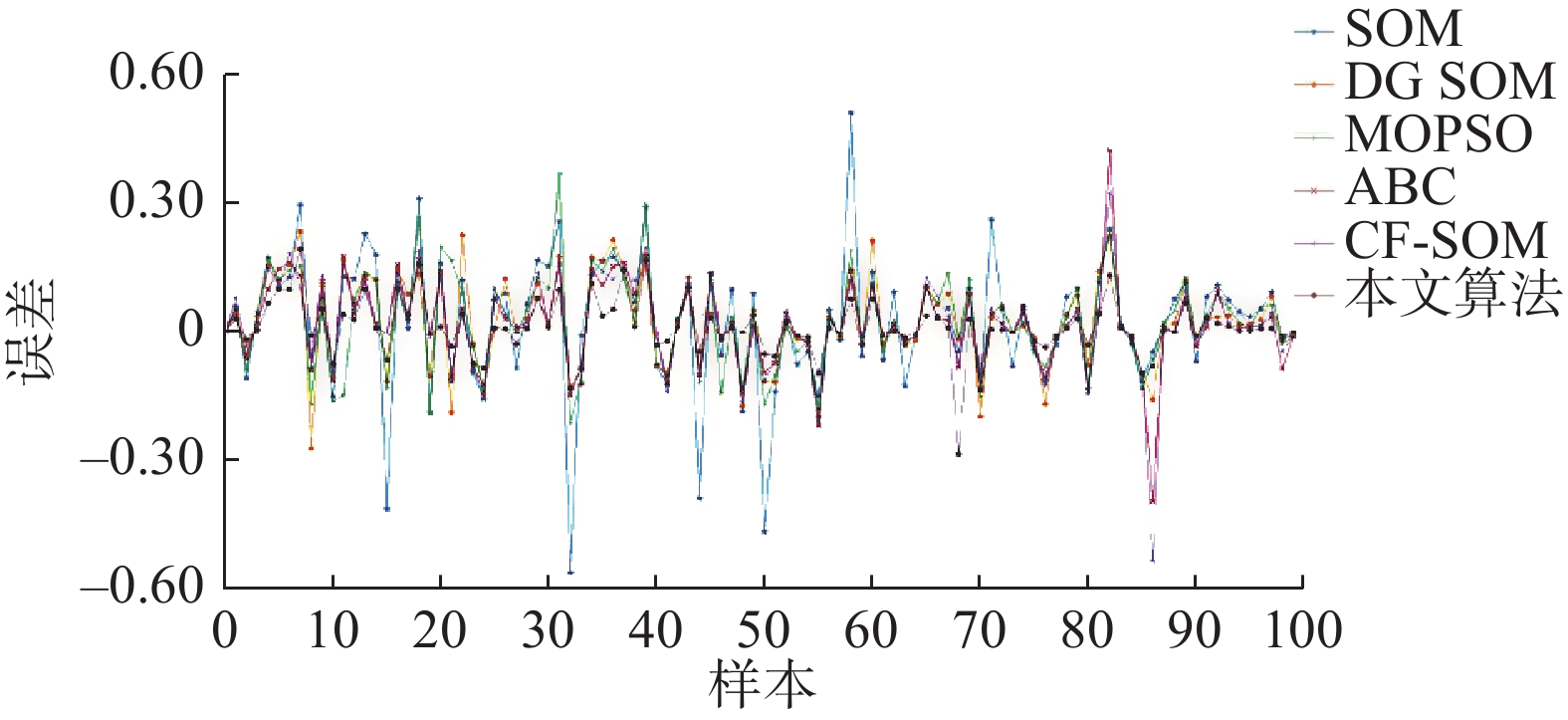
图7给出算法对真实值的跟踪误差，从图7可以看出来，SOM算法表现的效果为最差的，因为其在初始化网络之后需要进行复杂的运算，对于局部最优值的效果表现不好；而DGSOM算法虽然通过引入方向参数减少了学习次数，对整体系统的复杂度进行了化简，在特征参数的表现下避免了整体的网络激活特性，但是在个别样本处的表现效果仍然不理想，因为其没有对SOM网络运行过程中产生的优解进行进一步地操作；MOPSO算法当中在考虑了最小约束集、路径长度和成本等因素的条件下，构建个人最优和全局最优的迭代公式进行更新粒子的速度和位置，但是在迭代优化当中没有对最优的粒子进行进一步地推理和利用，整体效果是比较良好的，但仍有待改进；ABC算法中在雇佣蜂和观察蜂的构造阶段引入了遗传算法中的交叉和变异操作，从而对邻域的搜索策略进行更新，在保证多样性的同时，确保了子代种群当中的多样性，提升了全局搜索最优解的能力，但是由于多样的变异操作，在部分样本中出现了误差增大的现象，降低了预测的效果；CF-SOM算法中采用了将内容和过滤作为一种策略，利用自组织映射神经网络对模型当中的优胜点进行了筛选，提升了一定的精度和准确度，但是牺牲了其在运行中时间方面的运行速度，并且在一定的局部表现出比较差的效果；本文算法在考虑迭代过程中优胜单元的同时，将每个优胜单元进行存储，对于以往的优胜单元采取知识推理策略，将历史信息进行最大化的开发，增强算法中的每代种群中的多样性，并且引入置信度判断，进一步提升了每次知识推理的准确性，引入知识推理框架提高了历史特征信息的利用率，综合考虑其迭代过程中的准确性和充分性，获得了良好的效果。
图 7 预测误差Fig. 7 Prediction error下载:
全尺寸图片
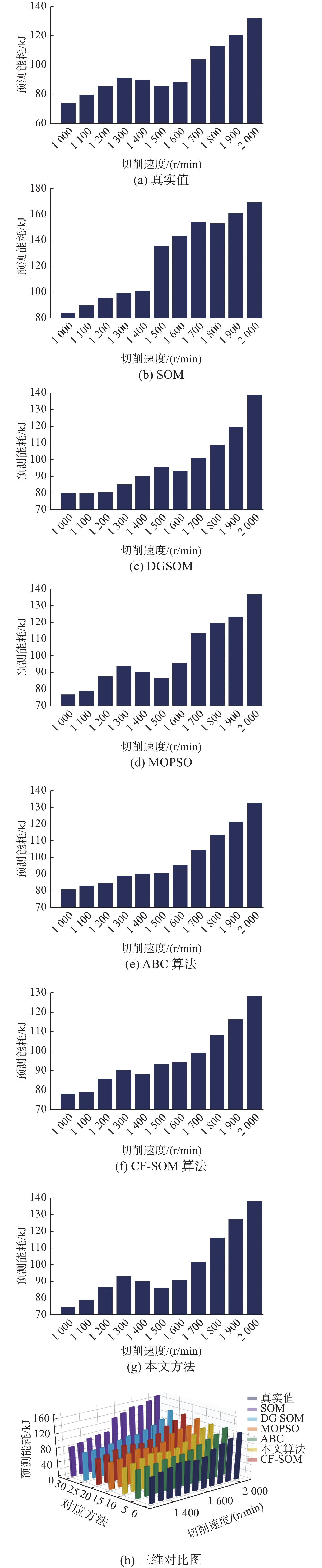
由图7可知，本文方法的整体效果更好。为了更加直观地对比各方法的预测优化效果，图8给出了工艺能耗真实值和各方法下的预测效果值。通过分析不同算法在不同切削速度区域的效果发现，在切削速度比较低的时候，SOM算法出现了比较大的误差，因为工艺过程中能耗不仅和切削速度有关系，还和多种工艺参数之间具有联系，所以在真实值分布下，SOM算法和ABC算法在切削速度比较低的时候具有一定的预测误差，而DGSOM算法在切削速度中间部分的时候具有比较差的预测结果，MOPSO算法和本文算法整体上在切削速度的低、中、高区域都具有相对较小的误差。而CF-SOM在切削速度比较低时表现得具有一定误差，但是其在高区域表现得比较稳定；如三维柱状图中显示的一样，可以看出SOM算法在没有优化措施的情况下表现效果比较差。而其他算法在不同的部分的表现效果是有优劣的。表1为几种方法之间的性能指标比较。由表1可知本文方法在运行速度和准确性方面具有良好的表现。
图 8 多种方法预测值和真实值统计Fig. 8 Predictive value and true value statistics by multiple methods下载:
全尺寸图片
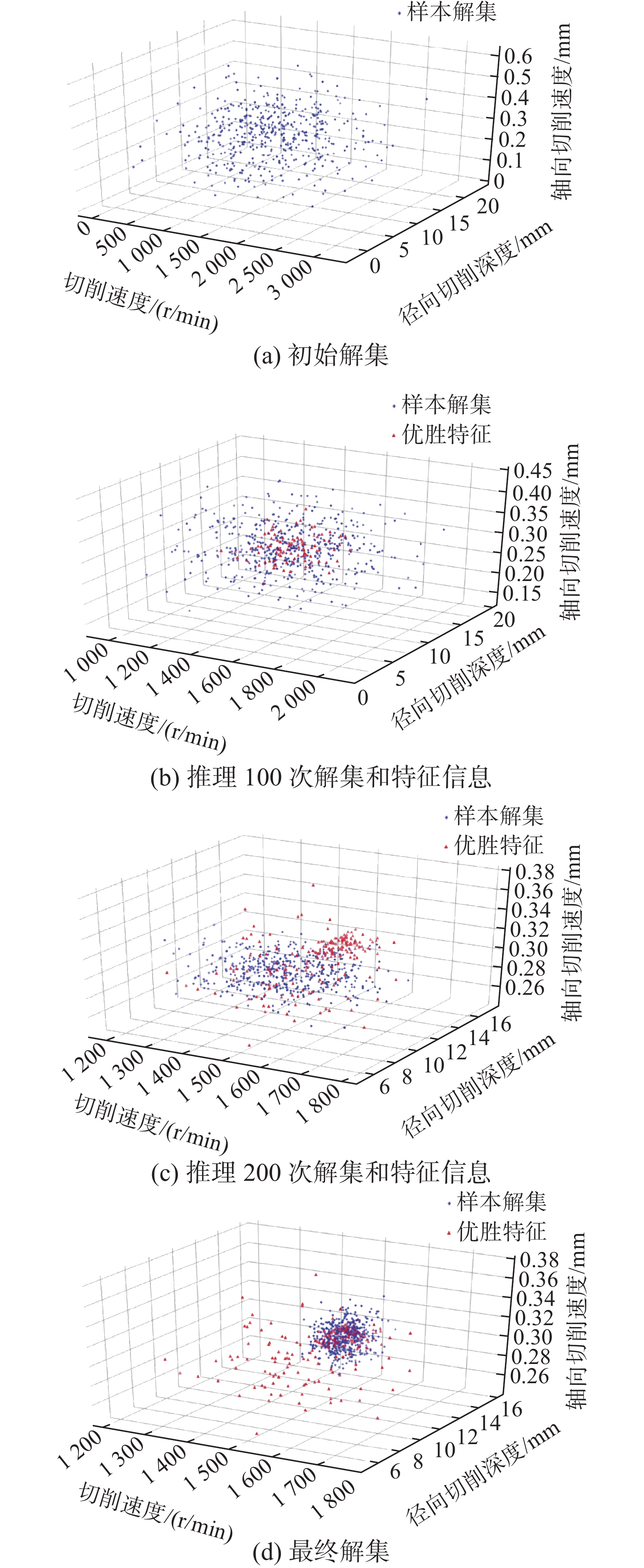
表 1 不同方法性能比较Table 1 Performance comparison of different methods方法 骨干网络 RMSE 时长/ms 自组织映射 SOM 0.1589 96 动态自组织映射 DGSOM 0.1361 118 协同过滤自组织 CF-SOM 0.1286 238 多目标粒子群 MOPSO 0.1186 135 改进人工蜂 ABC 0.1214 128 本文所提方法 KGSOM 0.1131 123 由表1的对比证明了本文方法的优越性，为了更加直观地体现出本文算法在迭代过程中对于历史特征信息的操作过程，选取了样本中的切削速度、轴向切削深度和径向切削深度，利用三维图表现了在迭代过程中的解集变化，如图9所示。
图 9 本文方法迭代信息变化Fig. 9 Iterative information changes of the method in this paper下载:
全尺寸图片
在初次解集生成时可以看到生成的解集是具有多样性的，但是没有明显的特征中心；在多次迭代过程中，通过知识推理过程将生成的特征信息进行利用，逐渐生成聚拢的特征信息，在多次迭代之后，发现特征样本集的相似度得到了显著的提升，通过知识推理实现了特征样本的有效更新；在最终阶段可以发现，已经完成了对过往历史特征信息的充分利用，并且还保留着先前每次迭代过程中的存储特征信息，通过对迭代过程中的信息充分利用，实现了比较良好的预测优化。上述分析对比验证了本文方法的实际效果，发现在对特征信息样本充分利用之后，可以在初始信息多样性的情况下取得比较良好的预测优化效果。
4. 结束语
本文所提出的方法，通过定义知识推理准则和知识推理框架，从协同训练、多样性的样本、置信度判断等多角度出发，实现了对于特征信息的有效利用，在充分利用特征信息样本的情况下，结合知识推理框架大幅度提升了推理网络的预测效果。用智能机床制造数据验证本文算法的实际效果，实验表明在多变量的具有多样性样本下，具有良好的预测优化效果，并且为特征信息的利用提供了一种新的思路。
-
图 1 图节点信息匹配
Fig. 1 Map information matching
下载:
全尺寸图片
图 2 算法的基本思想
Fig. 2 Basic concept of the algorithm
下载:
全尺寸图片
图 3 自组织映射网络结构层
Fig. 3 Self-organizing mapping network architecture layer
下载:
全尺寸图片
图 4 改进自组织映射算法流程
Fig. 4 Flow of improve self-organizing mapping algorithm
下载:
全尺寸图片
图 5 SOM协同训练
Fig. 5 SOM combined training
下载:
全尺寸图片
图 6 知识推理的过程
Fig. 6 Knowledge reasoning process
下载:
全尺寸图片
图 7 预测误差
Fig. 7 Prediction error
下载:
全尺寸图片
图 8 多种方法预测值和真实值统计
Fig. 8 Predictive value and true value statistics by multiple methods
下载:
全尺寸图片
图 9 本文方法迭代信息变化
Fig. 9 Iterative information changes of the method in this paper
下载:
全尺寸图片
表 1 不同方法性能比较
Table 1 Performance comparison of different methods
方法 骨干网络 RMSE 时长/ms 自组织映射 SOM 0.1589 96 动态自组织映射 DGSOM 0.1361 118 协同过滤自组织 CF-SOM 0.1286 238 多目标粒子群 MOPSO 0.1186 135 改进人工蜂 ABC 0.1214 128 本文所提方法 KGSOM 0.1131 123 -
[1] JIA Yanjie, CHEN Xi, YU Jieqiong, et al. Speaker recognition based on characteristic spectrograms and an improved self-organizing feature map neural network[J]. Complex & intelligent systems, 2021, 7(4): 1749–1757. [2] QIU Dongwei, XU Hao, LUO Dean, et al. A rainwater control optimization design approach for airports based on a self-organizing feature map neural network model[J]. PLoS one, 2020, 15(1): e0227901. doi: 10.1371/journal.pone.0227901 [3] NG R W, BEGAM K M, RAJKUMAR R K, et al. An improved self-organizing incremental neural network model for short-term time-series load prediction[J]. Applied energy, 2021, 292: 116912. doi: 10.1016/j.apenergy.2021.116912 [4] 王华鲜, 华容, 刘华平, 等. 无人机群多目标协同主动感知的自组织映射方法[J]. 智能系统学报, 2020, 15(3): 609–614. doi: 10.11992/tis.201908022 WANG Huaxian, HUA Rong, LIU Huaping, et al. Self-organizing feature map method for multi-target active perception of unmanned aerial vehicle systems[J]. CAAI transactions on intelligent systems, 2020, 15(3): 609–614. doi: 10.11992/tis.201908022 [5] 李昌华, 董鑫, 李智杰. 改进的半监督协同SOM图匹配算法[J]. 计算机工程与设计, 2019, 40(5): 1355–1359. doi: 10.16208/j.issn1000-7024.2019.05.029 LI Changhua, DONG Xin, LI Zhijie. Improved semi-supervised collaborative SOM graph matching algorithm[J]. Computer engineering and design, 2019, 40(5): 1355–1359. doi: 10.16208/j.issn1000-7024.2019.05.029 [6] UNDERWOOD K L, RIZZO D M, DEWOOLKAR M M, et al. Analysis of reach-scale sediment process domains in glacially-conditioned catchments using self-organizing maps[J]. Geomorphology, 2021, 382: 107684. doi: 10.1016/j.geomorph.2021.107684 [7] SPASSIANI A C, MASON M S. Application of self-organizing maps to classify the meteorological origin of wind gusts in Australia[J]. Journal of wind engineering and industrial aerodynamics, 2021, 210: 104529. doi: 10.1016/j.jweia.2021.104529 [8] CHEN Yang, ASHIZAWA N, YEO C K, et al. Multi-scale self-organizing map assisted deep autoencoding Gaussian mixture model for unsupervised intrusion detection[J]. Knowledge-based systems, 2021, 224: 107086. doi: 10.1016/j.knosys.2021.107086 [9] JAYARATNE M, ALAHAKOON D, DE SILVA D. Unsupervised skill transfer learning for autonomous robots using distributed growing self organizing maps[J]. Robotics and autonomous systems, 2021, 144: 103835. doi: 10.1016/j.robot.2021.103835 [10] DONG Bin, WENG Guirong, JIN Ri. Active contour model driven by self organizing maps for image segmentation[J]. Expert systems with applications, 2021, 177: 114948. doi: 10.1016/j.eswa.2021.114948 [11] 翟永杰, 杨旭, 赵振兵, 等. 融合共现推理的Faster R-CNN输电线路金具检测[J]. 智能系统学报, 2021, 16(2): 237–246. doi: 10.11992/tis.202012023 ZHAI Yongjie, YANG Xu, ZHAO Zhenbing, et al. Integrating co-occurrence reasoning for faster R-CNN transmission line fitting detection[J]. CAAI transactions on intelligent systems, 2021, 16(2): 237–246. doi: 10.11992/tis.202012023 [12] 饶子昀, 张毅, 刘俊涛, 等. 应用知识图谱的推荐方法与系统[J]. 自动化学报, 2021, 47(9): 2061–2077. doi: 10.16383/j.aas.c200128 RAO Ziyun, ZHANG Yi, LIU Juntao, et al. Recommendation methods and systems using knowledge graph[J]. Acta automatica sinica, 2021, 47(9): 2061–2077. doi: 10.16383/j.aas.c200128 [13] LIU Chenguang, YU Yongli, LI Xingxin, et al. Application of entity relation extraction method under CRF and syntax analysis tree in the construction of military equipment knowledge graph[J]. IEEE access, 2005, 8: 81–88. [14] YAN Hehua, YANG Jun, WAN Jiafu. KnowIME: a system to construct a knowledge graph for intelligent manufacturing equipment[J]. IEEE access, 2020, 8: 41805–41813. [15] YU Fang, ZHOU Qing, LU Xiaoshan, et al. A first-order logic framework of major choosing decision making with an uncertain reasoning function[J]. IEEE transactions on systems, man, and cybernetics:systems, 2018, 48(1): 89–98. doi: 10.1109/TSMC.2016.2578459 [16] XIONG Wenhan, HOANG T, WANG W Y. DeepPath: a reinforcement learning method for knowledge graph reasoning[C]//Proceedings of the 2017 Conference on Empirical Methods in Natural Language Processing. Stroudsburg: Association for Computational Linguistics, 2017: 564−573. [17] WANG Xiang, WANG Dingxian, XU Canran, et al. Explainable reasoning over knowledge graphs for recommendation[EB/OL]. (2018−11−12)[2020−01−01]. https://arxiv.org/abs/1811.04540. [18] BELLOMARINI L, BENEDETTO D, GOTTLOB G, et al. Vadalog: a modern architecture for automated reasoning with large knowledge graphs[J]. Information systems, 2022, 105: 101528. doi: 10.1016/j.is.2020.101528 [19] ZHANG Rui, HRISTOVSKI D, SCHUTTE D, et al. Drug repurposing for COVID-19 via knowledge graph completion[J]. Journal of biomedical informatics, 2021, 115: 103696. doi: 10.1016/j.jbi.2021.103696 [20] WANG Qi, JI Yuede, HAO Yongsheng, et al. GRL: Knowledge graph completion with GAN-based reinforcement learning[J]. Knowledge-based systems, 2020, 209: 106421. doi: 10.1016/j.knosys.2020.106421 [21] 刘烨宸, 李华昱. 领域知识图谱研究综述[J]. 计算机系统应用, 2020, 29(6): 1–12. doi: 10.15888/j.cnki.csa.007431 LIU Yechen, LI Huayu. Survey on domain knowledge graph research[J]. Computer systems & applications, 2020, 29(6): 1–12. doi: 10.15888/j.cnki.csa.007431 [22] 杜会芳, 王昊奋, 史英慧, 等. 知识图谱多跳问答推理研究进展、挑战与展望[J]. 大数据, 2021, 7(3): 60–79. DU Huifang, WANG Haofen, SHI Yinghui, et al. Progress, challenges and research trends of reasoning in multi-hop knowledge graph based question answering[J]. Big data research, 2021, 7(3): 60–79. [23] MELIN P, MONICA J C, SANCHEZ D, et al. Analysis of spatial spread relationships of coronavirus (COVID-19) pandemic in the world using self organizing maps[J]. Chaos, solitons & fractals, 2020, 138: 109917. [24] 王文广. 知识图谱推理: 现代的方法与应用[J]. 大数据, 2021, 7(3): 42–59. WANG Wenguang. Knowledge graph reasoning: modern methods and applications[J]. Big data research, 2021, 7(3): 42–59. [25] SHEN Fei, LANGARI R, YAN Ruqiang. Transfer between multiple machine plants: a modified fast self-organizing feature map and two-order selective ensemble based fault diagnosis strategy[J]. Measurement, 2020, 151: 107155. doi: 10.1016/j.measurement.2019.107155 [26] 许曈, 凌有铸, 陈孟元. 一种融合DGSOM神经网络的仿生算法研究[J]. 智能系统学报, 2017, 12(3): 405–412. doi: 10.11992/tis.201704038 XU Tong, LING Youzhu, CHEN Mengyuan. A bio-inspired algorithm integrated with DGSOM neural network[J]. CAAI transactions on intelligent systems, 2017, 12(3): 405–412. doi: 10.11992/tis.201704038 [27] XU Bo, ZHOU Feng, GATES A M. Multi-objective particle swarm optimization algorithm for the minimum constraint removal problem[J]. International journal of computational intelligence systems, 2020, 13(1): 291–299. doi: 10.2991/ijcis.d.200310.005 [28] 曹知奥, 汪晋宽, 韩英华, 等. 基于交叉−变异人工蜂群算法的微网优化调度[J]. 控制与决策, 2020, 35(9): 2059–2069. doi: 10.13195/j.kzyjc.2019.0506 CAO Zhiao, WANG Jinkuan, HAN Yinghua, et al. Crossover-mutation based artificial bee colony algorithm for optimal scheduling of microgrid[J]. Control and decision, 2020, 35(9): 2059–2069. doi: 10.13195/j.kzyjc.2019.0506 [29] AFOUDI Y, LAZAAR M, AL ACHHAB M. Hybrid recommendation system combined content-based filtering and collaborative prediction using artificial neural network[J]. Simulation modelling practice and theory, 2021, 113: 102375. doi: 10.1016/j.simpat.2021.102375
