Zero-shot image classification method combining VAE and StackGAN
-
摘要: 零样本分类算法旨在解决样本极少甚至缺失类别情况下的分类问题。随着深度学习的发展，生成模型在零样本分类中的应用取得了一定的突破，通过生成缺失类别的图像，将零样本图像分类转化为传统的基于监督学习的图像分类问题，但生成图像的质量不稳定，如细节缺失、颜色失真等，影响图像分类准确性。为此，提出一种融合变分自编码(variational auto-encoder, VAE)和分阶段生成对抗网络(stack generative adversarial networks, StackGAN)的零样本图像分类方法，基于VAE/GAN模型引入StackGAN，用于生成缺失类别的数据，同时使用深度学习方法训练并获取各类别的句向量作为辅助信息，构建新的生成模型stc-CLS-VAEStackGAN，提高生成图像的质量，进而提高零样本图像分类准确性。在公用数据集上进行对比实验，实验结果验证了本文方法的有效性与优越性。Abstract: The zero-shot classification algorithm is designed to solve the classification problem in case of a few samples or even missing categories. With the development of deep learning, the application of the generation model in zero-shot classification has made a breakthrough. By generating images of missing categories, the zero-shot image classification is transformed into a traditional image classification problem based on supervised learning. However, the generated samples are unstable in quality, including missing details and color distortion, thus affecting the accuracy of image classification. To this end, the zero-shot image classification method combining variational auto-encoding (VAE) and stack generative adversarial networks (StackGAN) is proposed. Based on the VAE/GAN model, StackGAN is introduced to generate the data of missing categories. Meanwhile, the deep learning method is used to train and obtain the sentence vectors of each category as auxiliary information and build a new generation model stc–CLS–VAEStackGAN to improve the quality of generated images and subsequently improve the classification accuracy of the zero-shot images. A comparative experiment was conducted on the public dataset, and the experimental results verified the effectiveness and superiority of the method proposed herein.
-
近年来，深度学习算法在机器学习领域取得了高速发展，尤其在图像识别领域，计算机的识别精度已经达到甚至超过人类识别精度，但需要消耗大量的人力物力以获得足够数量的人工标注数据[1-2]。在很多实际应用中，大量有标签的数据难以获取，物体种类也处于不断增长的趋势，这就要求计算机训练过程不断增加新样本及新物体种类[3]。如何在样本标签数据不足甚至完全缺失的情况下利用计算机和已有知识对其进行分类识别，成为深度学习应用研究中亟须解决的问题。为此，零样本学习应运而生。
零样本学习(zero-shot learning, ZSL)也称作零样本分类，是指根据一些已有类别标签(seen classes)的样本数据，辅以相关常识信息或先验知识(辅助信息)，用于训练某种学习模型，对训练数据或标注完全缺失的类别(unseen classes)进行预测和识别的一类技术[4-7]。零样本分类中训练集和测试集的类别是不相交的，这明显区别于传统的基于监督学习的分类任务。该类方法可以看作视觉数据与文本等其他模态数据间的一种跨模态学习。零样本分类方法的发展主要包括3个阶段[8-9]：
1）早期的零样本分类方法大多为基于直接语义预测的方法，其中直接属性预测模型(direct attribute prediction，DAP)是零样本分类的先驱工作，通过建立视觉数据与属性特征之间的关系，对无标签数据进行分类[10-12]。此类模型虽然在零样本分类领域取得了一定的成果，但依赖于类别的属性特征，极易受到人工属性标注的影响。
2）为更好地解决基于直接语义预测方法存在的问题，出现了基于嵌入模型的方法，其核心思想是将不同模态的数据映射到某一个公共空间中，再根据相似性度量进行零样本分类。Du等[13]提出基于类内类间约束的语义映射模型，实现类别间知识的有效迀移。陈祥凤等[14]提出基于度量学习改善SAE的零样本分类算法，以缓解跨领域漂移。吴晨等[15]提出将融合的语义词向量线性映射到图像特征空间完成分类。谢于中等[16]利用典型相关分析将跨模态特征映射至公共特征空间实现图像的零样本分类。但在训练类与测试类之间建立联系较为困难，且存在领域漂移问题[17]。
3）为解决上述问题，基于深度网络进行视觉样本生成的零样本分类方法涌现出来。Xian等[18]通过构建生成模型，以类别属性作为辅助信息生成未见类别对应的视觉特征。Sariyildiz等[19]提出新的损失函数来提高生成样本质量。Mandal等[20]引入非条件判别器来判别图像属于可见类还是未见类，提高分类准确率。Xian等[21]提出一个结合VAE和生成对抗网络(generative adversarvial networks, GAN)优势的条件生成模型来进行数据生成。Kim等[22]提出零样本生成模型ZSGAN，通过学习可见类和未见类图像与属性之间的关系生成未见类图像。Verma等[23]提出一种基于类属性条件设置的元学习方法ZSML（zero-shot meta-learning），将生成器模块和带有分类器的判别器模块分别同元学习代理相关联，利用少量可见类样本训练模型。Ma等[24]提出一种相似度保持损失，使GAN的生成器减小生成样本与真实样本之间的距离，利用相似度消除异常的生成样本。Liu等[25]提出一种双流生成式对抗网络合成具有语义一致性和明显类间差异的视觉样本，同时保留用于零样本学习的类内多样性。Liu等[26]提出一种包含两个端到端模型的跨类生成对抗网络用于提高生成的未见类样本的质量。Tang等[27]提出一种结构对齐的生成对抗网络，以缓解语义差距和领域漂移等问题。Li等[28]通过构建基于增强语义特征的生成网络来合成未见类别的可分离视觉表示。Gao等[29]提出一种VAE与GAN相结合的生成模型(Zero-VAE-GAN)，以缓解领域漂移问题。但已有模型生成图像的质量仍然不稳定，图像细节的效果较差，影响零样本图像分类的效果。
为此，本文使用VAE/GAN变体模型作为生成模型主体，同时将StackGAN模型引入其中，得到生成模型stc-CLS-VAEStackGAN，利用StackGAN分阶段生成图像的特点提高图像质量，同时使用深度学习方法对各类别文本信息进行句向量的提取，将其作为辅助信息约束变分自编码器和生成对抗网络的生成工作。
1. 相关工作
1.1 VAE/GAN模型
变分自编码器(variational auto-encoder, VAE)[30]的作用是求解给定输入空间和特征空间之间的映射，使得输入特征的重建误差达到最小。但VAE只能得到一个平均的结果，这也是导致其生成图像质量较低，图像较模糊的原因。研究人员提出VAE/GAN模型[31]，将VAE与GAN进行融合，判别器的加入使得VAE产生的图像变得清晰。然而，常规VAE/GAN中编码器得到的隐变量并不完全符合期望样式。于是，出现了VAE/GAN的变体模型，其结构如图1所示，它改变了判别器结构，使其能更精细地鉴别输入图像的种类。
图 1 VAE/GAN模型结构Fig. 1 Structure of VAE/GAN model
下载:
全尺寸图片
真实图像作为编码器输入，通过编码得到隐变量作为解码器的输入以生成图像，此时VAE希望真实图像和生成图像之间的差异越小越好。判别器则需判别输入的图像属于真实数据分布
$ \mathop p\nolimits_{{\text{data}}} $ 还是生成数据分布$ \mathop p\nolimits_{\text{G}} $ 。在VAE和GAN的共同作用下，生成更加相似且清晰的图像。1.2 StackGAN模型
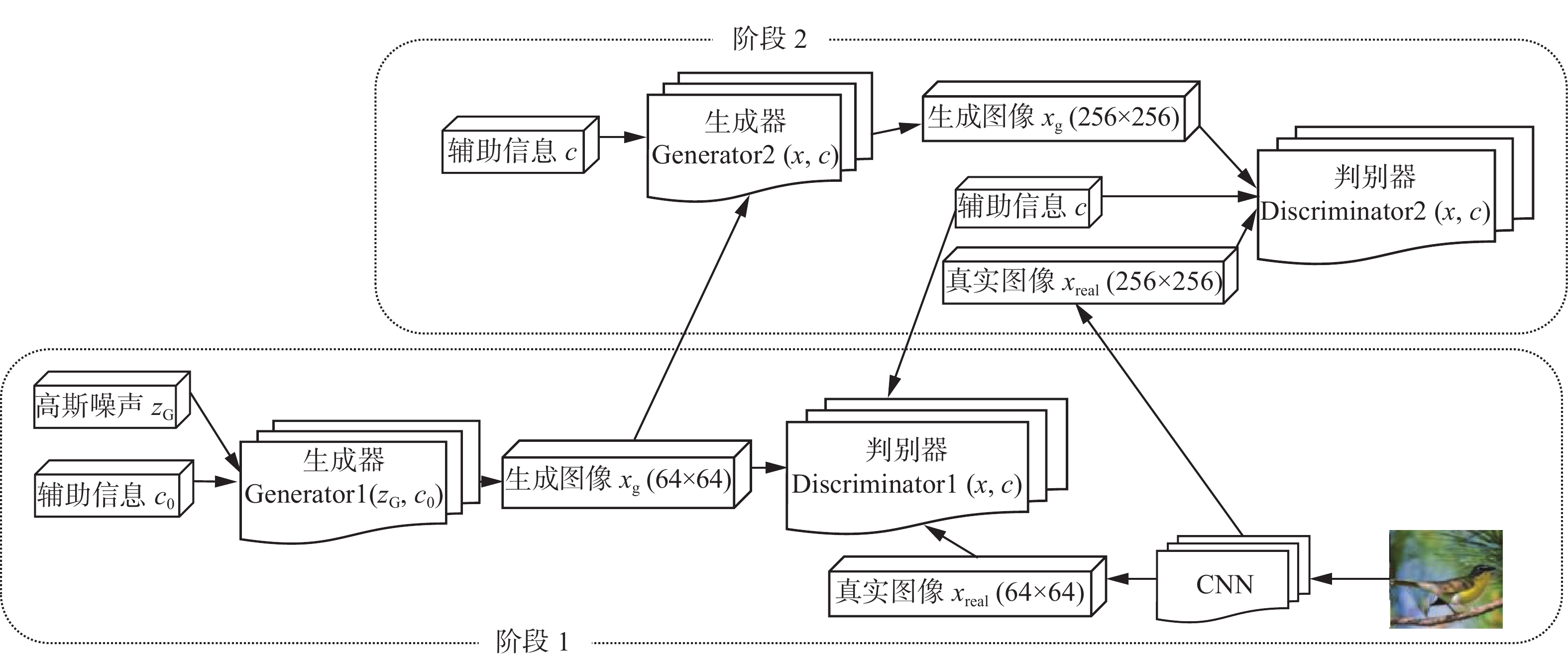
根据文字描述生成高质量图像的任务是计算机视觉领域的一个挑战。条件生成对抗网络(conditional GAN, CGAN)可以生成和文本比较相关的图像，但是分辨率不够，细节部分缺失严重，不够生动具体。如果简单地增加更多的采样层来提高分辨率，会导致模型不稳定或者生成一些奇形怪状的图像，这种现象在分辨率提高时会更加严重。分阶段生成对抗网络StackGAN本质上是2个CGAN的堆叠[32]，其结构如图2所示，采用分阶段的方式(两个阶段)生成高分辨率且置信度高的图像。
图 2 StackGAN模型结构Fig. 2 Structure of StackGAN model下载:
全尺寸图片
阶段1：主要用于生成粗略的形状和颜色，通过文本嵌入从中采样出服从
$ N(\mathop \mu \nolimits_0 (\mathop \varphi \nolimits_{\text{t}} ),\sum\nolimits_0 {(\mathop \varphi \nolimits_{\text{t}} )} ) $ 分布的辅助信息$ \mathop c\nolimits_{\text{0}} $ ，并随机采样高斯噪声$\mathop {\boldsymbol{z}}\nolimits_{\text{G}}$ ，二者作为阶段1的输入，用来训练生成器Generator1 和判别器Discriminator1，分别对应如下目标函数：$$ \begin{gathered} \max \mathop L\nolimits_{\mathop {\text{D}}\nolimits_{\text{1}} } = \mathop E\nolimits_{(x_{\text{real,}}t)\sim \mathop p\nolimits_{{\text{data}}} } [\log (\mathop D\nolimits_1 (\mathop x\nolimits_{{\text{real}}} ,\mathop \varphi \nolimits_{\text{t}} ))] +\\ \mathop E\nolimits_{\mathop {\boldsymbol{z}}\nolimits_{\text{G}} \sim \mathop p\nolimits_{\mathop {\boldsymbol{z}}\nolimits_{\text{G}} } ,t \sim \mathop p\nolimits_{{\text{data}}} } [\log (1 - \mathop D\nolimits_{\text{1}} (\mathop G\nolimits_{\text{1}} (\mathop {\boldsymbol{z}}\nolimits_{\text{G}} ,\mathop c\nolimits_{\text{0}} ),\mathop \varphi \nolimits_{\text{t}} ))] \\ \end{gathered} $$ $$ \begin{gathered} \min \mathop L\nolimits_{\mathop {\text{G}}\nolimits_{\text{1}} } = \mathop E\nolimits_{\mathop {\boldsymbol{z}}\nolimits_{\text{G}} \sim \mathop p\nolimits_{\mathop {\boldsymbol{z}}\nolimits_{\text{G}} } ,t \sim \mathop p\nolimits_{{\text{data}}} } [\log (1 - \mathop D\nolimits_{\text{1}} (\mathop G\nolimits_{\text{1}} ({\boldsymbol{z}}_{\text{G}},\mathop c\nolimits_{\text{0}} ),\mathop \varphi \nolimits_{\text{t}} ))] + \\ \lambda \mathop D\nolimits_{{\text{KL}}} (N(\mathop \mu \nolimits_0 (\mathop \varphi \nolimits_{\text{t}} ),\sum\nolimits_0 {(\mathop \varphi \nolimits_{\text{t}} )} )\left\| {N(0,I)} \right.) \\ \end{gathered} $$ 式中：
$ \mathop G\nolimits_{\text{1}} $ 和$ \mathop D\nolimits_{\text{1}} $ 分别表示Generator1和Discriminator1的函数; 真实图像$ \mathop x\nolimits_{{\text{real}}} $ 和文本描述t源自于$ \mathop p\nolimits_{{\text{data}}} $ ；$ \mathop {\boldsymbol{z}}\nolimits_{\text{G}} $ 表示服从高斯分布的噪声向量；$ \lambda $ 为正则化参数。阶段2：在 阶段1的基础上，修正低分辨率图像的缺陷，完善被忽略的文本信息细节，生成高分辨率图像。以辅助语义向量以及阶段1的输出
$\mathop s\nolimits_{\text{0}} = \mathop G\nolimits_1 (\mathop {\boldsymbol{z}}\nolimits_{\text{G}} ,\mathop c\nolimits_0 )$ 作为输入来训练生成器Generator2和判别器Discriminator2，其目标函数分别为$$ \begin{gathered} \max \mathop L\nolimits_{\mathop {\text{D}}\nolimits_{\text{2}} } = \mathop E\nolimits_{(x_{\text{real}},t) \sim \mathop p\nolimits_{{\text{data}}} } [\log (\mathop D\nolimits_2 (\mathop x\nolimits_{{\text{real}}} ,\mathop \varphi \nolimits_{{t}} ))] + \\ \mathop E\nolimits_{\mathop s\nolimits_{\text{0}} \sim \mathop p\nolimits_{\mathop G\nolimits_{\text{1}} } ,t \sim \mathop p\nolimits_{{\text{data}}} } [\log (1 - \mathop D\nolimits_{\text{2}} (\mathop G\nolimits_{\text{2}} (\mathop s\nolimits_{\text{0}} ,c),\mathop \varphi \nolimits_{{t}} ))] \\ \end{gathered} $$ $$ \begin{gathered} \min \mathop L\nolimits_{\mathop {\text{G}}\nolimits_{\text{2}} } = \mathop E\nolimits_{\mathop s\nolimits_0 \sim \mathop p\nolimits_{\mathop G\nolimits_1 } ,t \sim \mathop p\nolimits_{{\text{data}}} } [\log (1 - \mathop D\nolimits_2 (\mathop G\nolimits_2 (\mathop s\nolimits_{\text{0}} ,c),\mathop \varphi \nolimits_{{t}} ))] + \\ \lambda \mathop D\nolimits_{{\text{KL}}} (N(\mu (\mathop \varphi \nolimits_{{t}} ),\sum {(\mathop \varphi \nolimits_{{t}} )} )\left\| {N(0,I)} \right.) \\ \end{gathered} $$ 式中：
$ \mathop G\nolimits_{\text{2}} $ 和$ \mathop D\nolimits_{\text{2}} $ 分别表示Generator2和Discriminator2的函数；$ \mathop s\nolimits_{\text{0}} $ 源自于阶段1的生成数据分布$ \mathop p\nolimits_{\mathop {\text{G}}\nolimits_{\text{1}} } $ 。同时，本模型引入条件增强来从独立高斯分布
$ N(\mu (\mathop \varphi \nolimits_{\text{t}} ),\sum {(\mathop \varphi \nolimits_{\text{t}} )} ) $ 中随机采样产生额外的条件变量$ \lambda $ ，使得在给定较少文本–图像数据对时，能够产生更多的训练样本，增加生成样本的随机性。1.3 零样本生成模型f-CLSWGAN
基于生成对抗网络的零样本生成模型f-CLSWGAN由生成网络、判别网络和分类网络3部分构成。生成网络部分采用WGAN模型，以各类别的属性信息
$ c(y) $ 和噪声$ \mathop {\boldsymbol{z}}\nolimits_{\text{G}} $ 共同作为输入，生成未知类图像$ \mathop x\nolimits_{\text{g}} $ 。属性信息$ c(y) $ 、未知类图像$ \mathop x\nolimits_{\text{g}} $ 以及真实图像$ \mathop x\nolimits_{{\text{real}}} $ 作为判别网络的输入，判别真伪后产生一个损失值用以优化生成网络。生成网络和判别网络二者相互对抗学习。同时，生成的图像作为分类网络的输入进行分类，同样产生一个损失值，两部分共同指导生成网络进行优化，最终生成足够接近真实图像的未知类图像。2. 模型改进
基于生成模型的零样本图像分类任务流程如图3所示。本文主要针对生成模型部分进行改进，以进一步提高生成的未见类图像质量。
图 3 基于生成模型的零样本图像分类流程图Fig. 3 Flow chart of zero-shot image classification based on generative model下载:
全尺寸图片
2.1 VAE-StackGAN模型
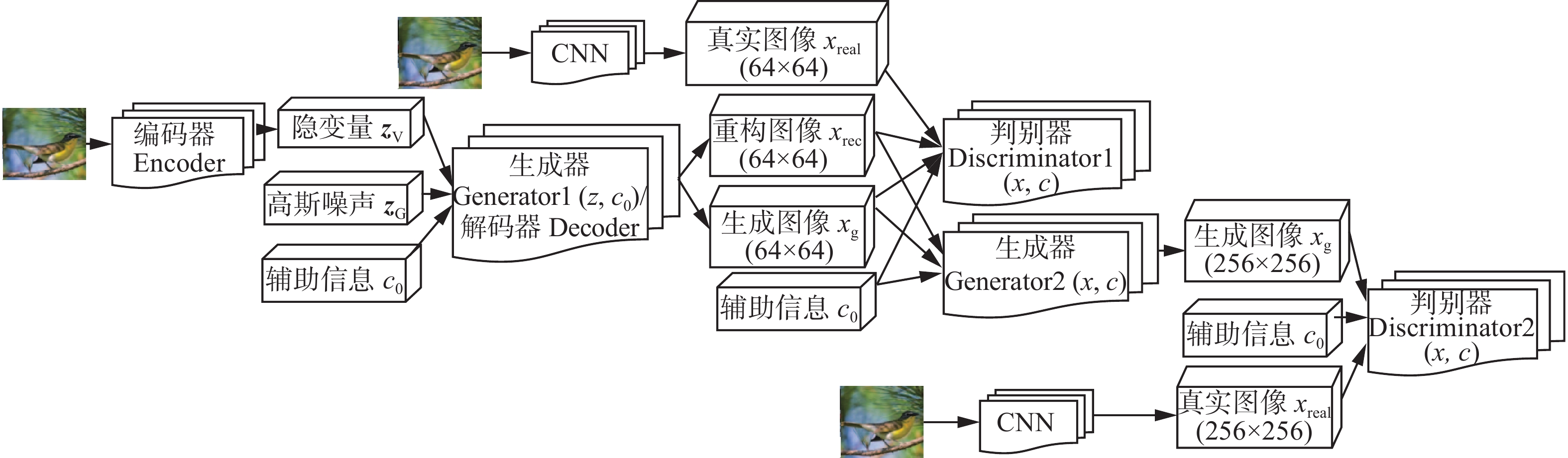
针对现有VAE/GAN模型训练不稳定，生成图像质量低的问题，本文基于VAE/GAN变体模型引入StackGAN，得到VAE-StackGAN模型，如图4所示。VAE-StackGAN模型中真实图像作为VAE编码器Encoder的输入，通过编码得到隐变量
$\mathop {\boldsymbol{z}}\nolimits_{\text{V}}$ 。$\mathop {\boldsymbol{z}}\nolimits_{\text{V}}$ 作为VAE解码器Decoder的输入，得到重构图像$ \mathop x\nolimits_{{\text{rec}}} $ 。随机噪声$\mathop {\boldsymbol{z}}\nolimits_{\text{G}}$ 和辅助信息$ \mathop c\nolimits_{\text{0}} $ 作为StackGAN 模型阶段1生成器Generator1的输入，得到生成图像$ \mathop x\nolimits_{\text{g}} $ 。VAE和StackGAN两生成模型通过解码器和生成器共享参数进行连接。对于阶段1的判别器Discriminator1，将真实图像$ \mathop x\nolimits_{{\text{real}}} $ 、$ \mathop x\nolimits_{{\text{rec}}} $ 、$ \mathop x\nolimits_{\text{g}} $ 和$ c_0 $ 作为输入，通过更精细地学习$ \mathop x\nolimits_{{\text{rec}}} $ 和$ \mathop x\nolimits_{\text{g}} $ 之间的细微差别，使得编码器得到更接近$\mathop {\boldsymbol{z}}\nolimits_{\text{G}}$ 的隐变量$\mathop {\boldsymbol{z}}\nolimits_{\text{V}}$ 。则StackGAN中阶段1的目标函数为$$ \begin{gathered} \min \mathop L\nolimits_{\mathop {\text{G}}\nolimits_{\text{1}} } = \mathop E\nolimits_{{\boldsymbol{z}}_{\text{G}} \sim \mathop p\nolimits_{{\boldsymbol{z}}_{\text{G}}} ,t \sim \mathop p\nolimits_{{\text{data}}} } [\log (1 - {D_1}({G_1}({z_{\text{G}}},{c_{\text{0}}}),{\varphi _{{t}}}))] +\\ \mathop E\nolimits_{{\boldsymbol{z}}_{\text{V}} \sim \mathop p\nolimits_{(\left. {{\boldsymbol{z}}_{\text{V}}} \right|x_{\text{real}})} ,t \sim \mathop p\nolimits_{{\text{data}}} } [\log (1 - \mathop D\nolimits_1 (\mathop G\nolimits_1 ({\text{Enc}}(x_{\text{real}}),\mathop c\nolimits_0 ),\mathop \varphi \nolimits_{{t}} ))] + \\ \lambda \mathop D\nolimits_{{\text{KL}}} (N(\mathop \mu \nolimits_0 (\mathop \varphi \nolimits_{{t}} ),\sum\nolimits_{\text{0}} {(\mathop \varphi \nolimits_{{t}} )} )\left\| {N(0,I)} \right.) \\ \end{gathered} $$ $$\begin{array}{l} \max \mathop L\nolimits_{\mathop {\rm{D}}\nolimits_{\rm{2}} } = \mathop E\nolimits_{(x_{\rm{real}},t)\sim \mathop p\nolimits_{{\rm{data}}} } [\log (\mathop D\nolimits_{\rm{2}} (\mathop x\nolimits_{{\rm{real}}} ,\mathop \varphi \nolimits_{\rm{t}} ))]+\\ \mathop E\nolimits_{\mathop s\nolimits_{\rm{G}} \sim\mathop p\nolimits_{\mathop G\nolimits_{\rm{1}} } ,t\sim\mathop p\nolimits_{{\rm{data}}} } [\log (1 - \mathop D\nolimits_{\rm{2}} (\mathop G\nolimits_{\rm{2}} (\mathop s\nolimits_{\rm{G}} ,c),\mathop \varphi \nolimits_{\rm{t}} ))]+\\ \mathop E\nolimits_{\mathop s\nolimits_{\rm{V}} \sim\mathop p\nolimits_{\mathop G\nolimits_{\rm{1}} } ,t\sim\mathop p\nolimits_{{\rm{data}}} } [\log (1 - \mathop D\nolimits_{\rm{2}} (\mathop G\nolimits_{\rm{2}} (\mathop s\nolimits_{\rm{V}} ,c),\mathop \varphi \nolimits_{\rm{t}} ))] \end{array}$$ 式中
$ {\text{Enc}}( \cdot ) $ 表示VAE编码器Encoder。
图 4 VAE-StackGAN网络结构Fig. 4 Network structure of VAE-StackGAN下载:
全尺寸图片
VAE和StackGAN中的阶段1为VAE-StackGAN模型的主要部分，生成包含基本轮廓和颜色的图像，而StackGAN中阶段2的生成器Generator2以阶段1生成的
$ \mathop x\nolimits_{{\text{rec}}} $ 和$ \mathop x\nolimits_{\text{g}} $ 以及阶段2辅助语义信息$ c $ 作为输入，在此基础上根据$ c $ 对阶段1产生图像的细节部分进行细化，以生成更真实的图像$ \mathop x\nolimits_{\text{g}} $ 。将$ \mathop x\nolimits_{\text{g}} $ 和$ \mathop x\nolimits_{{\text{real}}} $ 以及$ c $ 一同作为阶段2判别器Discriminator2的输入，经过判别得到一个分类结果，产生的损失值用来指导生成器优化。阶段2的目标函数为$$ \begin{gathered} \min \mathop L\nolimits_{\mathop {\text{G}}\nolimits_{\text{2}} } = \mathop E\nolimits_{\mathop s\nolimits_{\text{G}} \sim \mathop p\nolimits_{\mathop {\text{G}}\nolimits_{\text{1}} } ,t \sim \mathop p\nolimits_{{\text{data}}} } [\log (1 - \mathop D\nolimits_{\text{2}} (\mathop G\nolimits_{\text{2}} (\mathop s\nolimits_{\text{G}} ,c),\mathop \varphi \nolimits_{\text{t}} ))] + \\ \mathop E\nolimits_{\mathop s\nolimits_{\text{V}} \sim \mathop p\nolimits_{\mathop {\text{G}}\nolimits_{\text{1}} } ,t \sim \mathop p\nolimits_{{\text{data}}} } [\log (1 - \mathop D\nolimits_{\text{2}} (\mathop G\nolimits_{\text{2}} (\mathop s\nolimits_{\text{V}} ,c),\mathop \varphi \nolimits_{\text{t}} ))] + \\ \lambda \mathop D\nolimits_{{\text{KL}}} (N(\mu (\mathop \varphi \nolimits_{\text{t}} ),\sum {(\mathop \varphi \nolimits_{\text{t}} )} )\left\| {N(0,I)} \right.) \\ \end{gathered} $$ $$ \begin{gathered} \max \mathop L\nolimits_{\mathop {\text{D}}\nolimits_{\text{2}} } = \mathop E\nolimits_{(x_{\text{real}},t) \sim \mathop p\nolimits_{{\text{data}}} } [\log (\mathop D\nolimits_{\text{2}} (\mathop x\nolimits_{{\text{real}}} ,\mathop \varphi \nolimits_{\text{t}} ))] + \\ \mathop E\nolimits_{\mathop s\nolimits_{\text{G}} \sim \mathop p\nolimits_{\mathop G\nolimits_{\text{1}} } ,t \sim \mathop p\nolimits_{{\text{data}}} } [\log (1 - \mathop D\nolimits_{\text{2}} (\mathop G\nolimits_{\text{2}} (\mathop s\nolimits_{\text{G}} ,c),\mathop \varphi \nolimits_{\text{t}} ))] + \\ \mathop E\nolimits_{\mathop s\nolimits_{\text{V}} \sim \mathop p\nolimits_{\mathop G\nolimits_{\text{1}} } ,t \sim \mathop p\nolimits_{{\text{data}}} } [\log (1 - \mathop D\nolimits_{\text{2}} (\mathop G\nolimits_{\text{2}} (\mathop s\nolimits_{\text{V}} ,c),\mathop \varphi \nolimits_{\text{t}} ))] \\ \end{gathered} $$ 式中：
$\mathop s\nolimits_{\text{G}} = \mathop G\nolimits_1 (\mathop {\boldsymbol{z}}\nolimits_{\text{G}} ,\mathop c\nolimits_0 )$ 表示随机噪声通过生成器生成的图像；$\mathop s\nolimits_{\text{V}} = \mathop G\nolimits_1 ({\rm{En}}c(\mathop x\nolimits_{{\text{real}}} ),\mathop c\nolimits_0 )$ 表示通过解码器重构得到的图像。VAE-StackGAN模型的目标函数为
$$ \mathop {\min }\limits_{G_1,G_2} \mathop {\max }\limits_{D_1,D_2} \mathop L\nolimits_{{\text{VAE - StackGAN}}} = \mathop {\min }\limits_{G_1,G_2} \mathop {\max }\limits_{D_1,D_2} \mathop L\nolimits_{{\text{StackGAN}}} + \mathop L\nolimits_{{\text{VAE}}} $$ VAE-StackGAN模型改变了判别器结构，使其可以更精细地判别出生成图像的类别，学习重构图像
$ \mathop x\nolimits_{{\text{rec}}} $ 与生成图像$ \mathop x\nolimits_{\text{g}} $ 之间的差异，以优化生成器的参数，但编码器产生的隐变量$\mathop {\boldsymbol{z}}\nolimits_{\text{V}}$ 和生成器输入的随机噪声$\mathop {\boldsymbol{z}}\nolimits_{\text{G}}$ 仍存在差异。为此，本文在目标函数中增加正则项，使用KL散度帮助优化$\mathop {\boldsymbol{z}}\nolimits_{\text{V}}$ 和$\mathop {\boldsymbol{z}}\nolimits_{\text{G}}$ 之间的距离。此时，VAE-StackGAN模型的目标函数为$$ \begin{aligned} &\mathop {\min }\limits_{G_1,G_2} \mathop {\max }\limits_{D_1,D_2} \mathop L\nolimits_{{\rm{VAE - StackGAN}}} = \mathop {\min }\limits_{G_1,G_2} \mathop {\max }\limits_{D_1,D_2} \mathop L\nolimits_{{\rm{StackGAN}}} + \mathop L\nolimits_{{\rm{VAE}}}+ \\ & \quad\quad\quad\quad\quad \mathop D\nolimits_{{\rm{KL}}} (p(\mathop {\boldsymbol{z}}\nolimits_{\rm{V}} \left| {\mathop x\nolimits_{{\rm{real}}} } \right.)\left\| {p(\mathop {\boldsymbol{z}}\nolimits_{\rm{G}} )} \right.) \end{aligned} $$ 式中：
$ \mathop L\nolimits_{{\text{VAE}}} $ 为VAE模型的目标函数；$ \mathop L\nolimits_{{\text{StackGAN}}} $ 为StackGAN模型的目标函数；$ p(\mathop z\nolimits_G ) $ 为StackGAN的噪声分布。假设$ p(\mathop z\nolimits_G ) $ 为服从高斯分布的随机噪声，采用KL散度计算两分布之间的距离，目的是使$\mathop {\boldsymbol{z}}\nolimits_{\text{V}}$ 不断向期望的形式更新。2.2 零样本图像分类方法
在VAE-StackGAN模型的基础上构建本文零样本图像分类方法，包括句向量的提取、图像的生成以及分类器的训练3部分。
首先是句向量的提取。本文采用循环卷积神经网络对各类别的文本信息进行无监督学习，提取各类别的语义句向量，并作为辅助信息输入到生成模型中。每轮训练选取文本中不同的句向量以保证后续生成图像的多样性。
其次是图像的生成。零样本生成模型f-CLSWGAN采用条件生成对抗网络，使用基于属性的语义辅助信息结合Wasserstein距离计算方法作为生成模型，生成未见类数据特征。但仅采用生成对抗网络得到的效果并不理想，因此本文采用VAE-StackGAN作为零样本生成模型的主体网络。并与语义句向量进行结合，得到零样本生成模型stc-CLS-VAEStackGAN。
将语义句向量代替属性信息。编码器对可见类图像进行编码，生成器根据语义信息生成未见类图像，判别器根据相应类别的句向量对输入图像进行判别。同时保留f-CLSWGAN中的分类器部分，生成的图像也作为分类器的输入，进行类别的判断，此处分类器设置的目的是约束生成器生成具有分类特征的图像，辅助生成模型进行优化。此时基于语义句向量的零样本生成模型的目标函数为
$$ \mathop {\min }\limits_{G_1,G_2} ,\mathop {\max }\limits_{D_1,D_2} \mathop L\nolimits_{{\text{VAE - StackGAN}}} + \beta \mathop L\nolimits_{{\text{CLS}}} $$ 最后是分类器的训练。随着对分类精度要求的不断提高，模型深度越来越深，模型复杂度也越来越高。但模型过于庞大会导致响应速度慢、内存不足等问题，因此本文使用深度可分离卷积MobileNet网络，结合SoftMax回归模型进行分类。
在生成模型部分生成了未见类图像，填充了数据集，因此现有数据集包括可见类与未见类图像。生成模型的加入将零样本图像分类任务转变成传统图像分类任务，使用多类别分类器进行训练，训练好的分类器即可对测试集图像进行分类。
3. 实验结果与讨论
3.1 数据集与实验配置
本文采用零样本学习领域常用的CUB (caltech-uCSD-Birds-200-2011)[33]和AwA (animals with attributes)[34]数据集进行模型训练及测试，并采用两个数据集默认的可见类与未见类划分方式。CUB数据集共包含200个鸟类类别，共11788张图片，类别间差异较小，属于精细分类，可见类包含150个类别，其中的100个类别为训练集，50个类别为验证集；未见类包含50个类别，为测试集。AwA数据集中共包含50个动物类别，共30475张图片，可见类包含40个类别，其中的27个类别为训练集，13个类别为验证集；未见类包含10个类别，为测试集。可见类与未见类样本不重叠。
3.2 评价指标
GAN网络生成图像的任务中，评价模型表现的一项重要指标是初始评分(inception score, IS)[35]，可以用来评价模型生成图像的清晰度和多样性。对于一个清晰的图像，它属于某一类的概率应该非常大，而属于其他类的概率应该很小，同时如果一个模型能生成足够多样的图像，那么它生成的图像在各个类别中的分布应该是平均的。IS计算公式为
$$ {\text{IS}}(G) = \exp (\mathop E\nolimits_{{\text{x}}\sim\mathop p\nolimits_{\text{G}} } \mathop D\nolimits_{{\text{KL}}} (p(\left. y \right|x)\left\| {p(y)} \right.)) $$ $$ \mathop D\nolimits_{{\text{KL}}} (P\left\| Q \right.) = \sum\limits_i {P(i)\log \frac{{P(i)}}{{Q(i)}}} $$ 式中：
$x \sim \mathop p\nolimits_G$ 表示生成器生成图像；$ p(y|x) $ 表示该图像属于各个类别的概率分布；$ p(y) $ 表示生成器生成的全部图像在所有类别上的边缘分布。对于本文方法及对比方法的零样本图像分类结果，采用类别的平均分类准确率进行评价。该指标是评价模型有效性的较好指标，能更好地反映数据集类内数据量不均衡时分类模型的识别效果，削弱实验的随机性。平均分类准确率公式为
$$ f(acc) = \dfrac{1}{{\left| Y \right|}}\sum\limits_{i = 0}^{\left| y \right|} {\left(\dfrac{{\mathop N\nolimits_{\rm{C}}^{Y - i} }}{{\mathop N\nolimits_{\rm{T}}^{Y - i} }}\right)} $$ 式中：
$ Y $ 为总体类别个数；$ \mathop N\nolimits_{\text{T}} $ 为当前类别样本数量；$ \mathop N\nolimits_{\text{C}} $ 为当前类别分类正确样本数量。3.3 本文生成模型定性与定量分析
本文通过在VAE/GAN变体模型中引入StackGAN网络，得到VAE-StackGAN生成模型，用于生成未见类图像。
基于CUB数据集，对比VAE-StackGAN、VAE/GAN和StackGAN模型的生成图像效果，并计算IS指标，计算结果如表1所示。从表1中可见，VAE-StackGAN模型的IS值较StackGAN和VAE/GAN分别提升0.26和0.33。该指标值在图像质量方面与人类的感知高度相关，更高的分数意味着更好的图像质量。因此，VAE-StackGAN模型明显优于StackGAN和VAE/GAN模型。
表 1 不同方法在CUB数据集上的IS 指标Table 1 Inception score of different methods on CUB dataset方法 IS指标 VAE/GAN 3.63 ± 0.06 StackGAN 3.70 ± 0.04 VAE-StackGAN 3.96 ± 0.03 图5为不同方法的生成图像对比，可以更直观地看出，本文生成模型VAE-StackGAN具有更好的性能，相比于原始模型更加注重目标颜色的细节，从而使得生成的目标图像更加逼真，更加符合其相应类别特征。因此，整体来看，本文模型生成图像的效果优于StackGAN模型。
图 5 生成图像效果对比Fig. 5 Comparison of generate figures下载:
全尺寸图片
3.4 实验结果评估
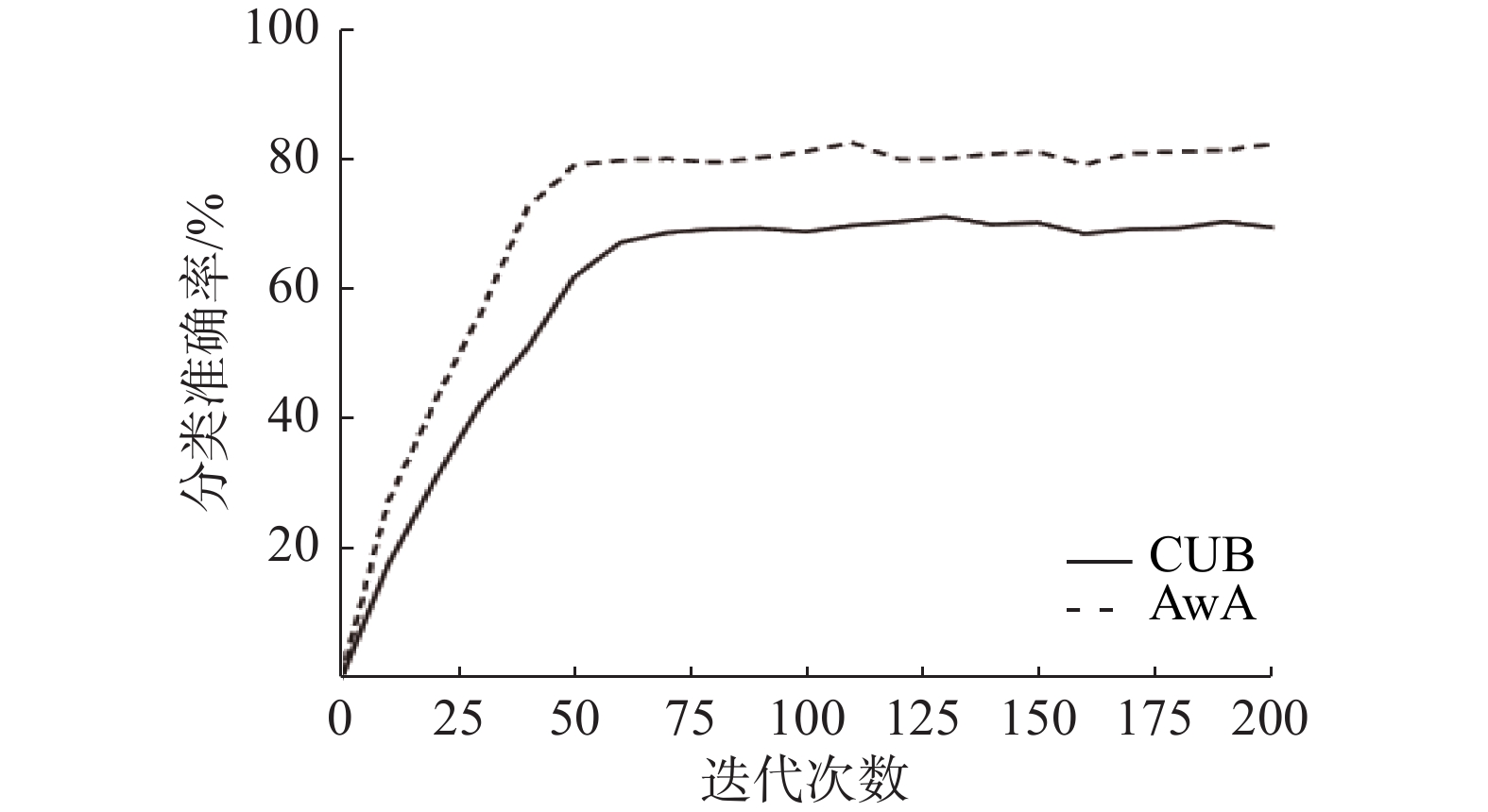
基于CUB和AwA1数据集，将本文方法stc-CLS-VAEStackGAN用于零样本图像分类，平均分类准确率随迭代次数变化的曲线如图6所示。随着迭代次数的增加，平均分类准确率逐渐提升并且趋于稳定，尽管个别值在小范围内有所波动，但处于正常波动范围内，证明了本模型具有较好的收敛性。
将stc-CLS-VAEStackGAN与现有其他生成模型进行零样本图像分类对比，使用类别平均分类准确率作为评价指标。stc-CLS-VAEStackGAN为基于生成模型的方法，因此同样选取基于生成模型且具有代表性、较新提出的模型作为对比方法，包括f-CLSWGAN[18]、FD-fGAN-Attention[36]、Zero-VAE-GAN[29]、ZSML[23]、SPGAN[24]和SAGAN[27]。需说明的是，以上对比方法的相应文献中所采用的数据集以及训练集、测试集的划分均与本文相同，因此这些方法的平均分类准确率指标值采用相应文献所提供的数值。
图 6 平均分类准确率随迭代次数的变化Fig. 6 Variation of the average classification accuracy with the number of iterations下载:
全尺寸图片
表2为不同方法在CUB和AwA两个数据集上的平均分类准确率指标值。从表中可以看出，本文生成模型stc-CLS-VAEStackGAN在AwA数据集上的平均分类准确率明显高于所有对比算法，在CUB数据集上的平均分类准确率虽略低于ZSML，但均明显高于其他对比算法。stc-CLS-VAEStackGAN基于VAE/GAN的变体模型，通过两种互补的生成模型VAE和GAN分别捕获不同的数据分布，弥补了各自的缺点，其中变体判别器可以更加精细地学习重构图像与生成图像之间差异，提高生成图像效果。将StackGAN引入其中，采用分阶段方法细化图像生成过程，进一步提高了图像生成质量。同时采用句向量代替属性信息，使得语义描述更加准确，生成图像更加多样化。对比实验结果验证了本文方法的有效性。
表 2 不同方法的平均分类准确率对比Table 2 Comparison of the average classification accuracy of different methods% 方法 CUB AwA f-CLSWGAN 57.3 68.2 FD-fGAN-Attention 58.5 71.6 Zero-VAE-GAN 54.8 71.4 SPGAN 58.6 71.5 ZSML 69.6 73.5 SAGAN 58.1 71.6 stc-CLS-VAEStackGAN 68.8 79.2 3.5 算法鲁棒性测试
为测试本文图像生成模型VAE-StackGAN的鲁棒性，将数据集中各类别的文本信息进行加噪处理，包括标签关键字删除、替换、交换顺序等，并根据处理后的文本信息提取类别句向量作为辅助信息，分别采用VAE-StackGAN模型和原始模型StackGAN进行图像生成。表3显示了两种模型生成相应类别图像的IS评价指标值。对文本信息进行上述加噪处理后，可能造成一些关键信息的缺失或异常，因此从表3中可以看出，文本信息加噪后，两种模型生成图像的IS评价指标均有所下降，但VAE-StackGAN模型的IS指标下降幅度小于原始模型StackGAN，验证了VAE-StackGAN模型的鲁棒性有所提高。
表 3 生成模型鲁棒性测试Table 3 Robustness test of generative models方法 文本信息 IS指标 VAE-StackGAN 不加噪 3.96 ± 0.03 加噪 3.87 ± 0.05 StackGAN 不加噪 3.70 ± 0.04 加噪 3.59 ± 0.03 图7为文本信息加噪前后，VAE-StackGAN模型的生成图像。整体来看，加入噪声后生成的图像在细节方面可能会有缺失或者存在多余的噪声背景，但仍具有相应类别的特征，整体效果并没有发生巨大的差距。
图 7 生成模型鲁棒性测试Fig. 7 Robustness test of generative models下载:
全尺寸图片
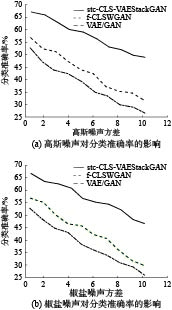
为测试本文零样本图像分类方法stc-CLS-VAEStackGAN的鲁棒性，对实验中扩充后的图像数据集样本进行加噪声处理，加入高斯噪声用于模拟实际应用中较为常见的由不良照明引起的图像模糊问题；加入椒盐噪声，随机改变一些像素值以产生黑白相间的亮暗点，用于模拟实际应用中较常见的由图像切割引起的噪点问题，然后进行图像分类，评价分类方法的准确率。stc-CLS-VAEStackGAN是在f-CLSWGAN和VAE/GAN的基础上改进得到的，因此图8对比了这3种方法在图像加噪后的分类准确率。由图8可见，在任意噪声强度处，stc-CLS-VAEStackGAN的分类准确率均明显高于其他两种方法；随着加入高斯噪声的方差逐渐增大，以及椒盐噪声的增强，3种方法的图像分类准确率均有所下降，但CLS-VAEStackGAN的准确率下降程度较为平缓。上述结果验证了，本文stc-CLS-VAEStackGAN方法不仅提高了零样本图像分类准确率，而且具有较好的鲁棒性。
图 8 零样本图像分类方法鲁棒性的测试Fig. 8 Robustness test of zero-shot image classification methods下载:
全尺寸图片
4. 结束语
本文提出一种融合VAE与StackGAN的零样本图像分类方法，通过生成未见类的图像填充图像数据集，将零样本图像分类任务转变为传统的基于监督学习的图像分类任务。基于VAE/GAN的变体模型引入StackGAN，采用分阶段方法细化图像生成过程，提高图像生成质量；并通过提取类别的句向量信息代替其属性信息，增加语义描述的准确性，使生成图像更加多样化，进而提高零样本图像分类的准确性。在现有公用数据集上进行对比实验，实验结果验证了本文方法的有效性。
-
图 1 VAE/GAN模型结构
Fig. 1 Structure of VAE/GAN model
下载:
全尺寸图片
图 2 StackGAN模型结构
Fig. 2 Structure of StackGAN model
下载:
全尺寸图片
图 3 基于生成模型的零样本图像分类流程图
Fig. 3 Flow chart of zero-shot image classification based on generative model
下载:
全尺寸图片
图 4 VAE-StackGAN网络结构
Fig. 4 Network structure of VAE-StackGAN
下载:
全尺寸图片
图 5 生成图像效果对比
Fig. 5 Comparison of generate figures
下载:
全尺寸图片
图 6 平均分类准确率随迭代次数的变化
Fig. 6 Variation of the average classification accuracy with the number of iterations
下载:
全尺寸图片
图 7 生成模型鲁棒性测试
Fig. 7 Robustness test of generative models
下载:
全尺寸图片
图 8 零样本图像分类方法鲁棒性的测试
Fig. 8 Robustness test of zero-shot image classification methods
下载:
全尺寸图片
表 1 不同方法在CUB数据集上的IS 指标
Table 1 Inception score of different methods on CUB dataset
方法 IS指标 VAE/GAN 3.63 ± 0.06 StackGAN 3.70 ± 0.04 VAE-StackGAN 3.96 ± 0.03 表 2 不同方法的平均分类准确率对比
Table 2 Comparison of the average classification accuracy of different methods
% 方法 CUB AwA f-CLSWGAN 57.3 68.2 FD-fGAN-Attention 58.5 71.6 Zero-VAE-GAN 54.8 71.4 SPGAN 58.6 71.5 ZSML 69.6 73.5 SAGAN 58.1 71.6 stc-CLS-VAEStackGAN 68.8 79.2 表 3 生成模型鲁棒性测试
Table 3 Robustness test of generative models
方法 文本信息 IS指标 VAE-StackGAN 不加噪 3.96 ± 0.03 加噪 3.87 ± 0.05 StackGAN 不加噪 3.70 ± 0.04 加噪 3.59 ± 0.03 -
[1] KRIZHEVSKY A, SUTSKEVER I, HINTON G E. ImageNet classification with deep convolutional neural networks[J]. Communications of the ACM, 2017, 60: 84–90. doi: 10.1145/3065386 [2] LECUN Y, BENGIO Y, HINTON G. Deep learning[J]. Nature, 2015, 521(7553): 436–444. doi: 10.1038/nature14539 [3] BIEDERMAN I. Recognition-by-components: a theory of human image understanding[J]. Psychological review, 1987, 94(2): 115–147. doi: 10.1037/0033-295X.94.2.115 [4] PALATUCCI M, POMERLEAU D, HINTON G E, et al. Zero-shot Learning with semantic output codes[C]// Advances in Neural Information Processing Systems 22: 23rd Annual Conference on Neural Information Processing Systems 2009. Vancouver: NIPS, 2009: 1410−1418. [5] LAMPERT C H, NICKISCH H, HARMELING S. Learning to detect unseen object classes by between-class attribute transfer[C]//2009 IEEE Conference on Computer Vision and Pattern Recognition. Miami: IEEE, 2009: 951−958. [6] ROHRBACH M, STARK M, SCHIELE B. Evaluating knowledge transfer and zero-shot learning in a large-scale setting[C]// Computer Vision and Pattern Recognition (CVPR), 2011 IEEE Conference on. IEEE, 2011: 1641−1648. [7] HABIBIAN A, MENSINK T, SNOEK C G M. Video2vec embeddings recognize events when examples are scarce[J]. IEEE transactions on pattern analysis and machine intelligence, 2017, 39(10): 2089–2103. doi: 10.1109/TPAMI.2016.2627563 [8] 冀中, 汪浩然, 于云龙, 等. 零样本图像分类综述: 十年进展[J]. 中国科学:信息科学, 2019, 49(10): 1299–1320. doi: 10.1360/N112018-00312 JI Zhong, WANG Haoran, YU Yunlong, et al. A decadal survey of zero-shot image classification[J]. Scientia sinica (informationis), 2019, 49(10): 1299–1320. doi: 10.1360/N112018-00312 [9] 张鲁宁, 左信, 刘建伟. 零样本学习研究进展[J]. 自动化学报, 2020, 46(1): 1–23. ZHANG Luning, ZUO Xin, LIU Jianwei. Research and development on zero-shot learning[J]. Acta automatica sinica, 2020, 46(1): 1–23. [10] 冀中, 孙涛, 于云龙. 一种基于直推判别字典学习的零样本分类方法[J]. 软件学报, 2017, 28(11): 2961–2970. JI Zhong, SUN Tao, YU Yunlong. Transductive discriminative dictionary learning approach for zero-shot classification[J]. Journal of software, 2017, 28(11): 2961–2970. [11] WANG Xuesong, CHEN Chen, CHENG Yuhu. Zero-shot learning by exploiting class-related and attribute-related prior knowledge[J]. IET computer vision, 2016, 10(6): 483–492. doi: 10.1049/iet-cvi.2015.0131 [12] 赵鹏, 汪纯燕, 张思颖, 等. 一种基于融合重构的子空间学习的零样本图像分类方法[J]. 计算机学报, 2021, 44(2): 409–421. doi: 10.11897/SP.J.1016.2021.00409 ZHAO Peng, WANG Chunyan, ZHANG Siying, et al. A zero-shot image classification method based on subspace learning with the fusion of reconstruction[J]. Chinese journal of computers, 2021, 44(2): 409–421. doi: 10.11897/SP.J.1016.2021.00409 [13] DU Yujiao, XIAO Bo, XU Wenchao, et al. Destination prediction for sharing-bikes’ trips[C]//2018 International Conference on Network Infrastructure and Digital Content (IC-NIDC). Guiyang: IEEE, 2018: 198−202. [14] 陈祥凤, 陈雯柏. 度量学习改进语义自编码零样本分类算法[J]. 北京邮电大学学报, 2018, 41(4): 69–75. CHEN Xiangfeng, CHEN Wenbai. Improving semantic autoencoder zero-shot classification algorithm by metric learning[J]. Journal of Beijing university of posts and telecommunications, 2018, 41(4): 69–75. [15] 吴晨, 袁昱纬, 王宏伟, 等. 基于词向量融合的遥感场景零样本分类算法[J]. 计算机科学, 2019, 46(12): 286–291. doi: 10.11896/jsjkx.181202257 WU Chen, YUAN Yuwei, WANG Hongwei, et al. Word vectors fusion based remote sensing scenes zero-shot classification algorithm[J]. Computer science, 2019, 46(12): 286–291. doi: 10.11896/jsjkx.181202257 [16] 冀中, 谢于中, 庞彦伟. 基于典型相关分析和距离度量学习的零样本学习[J]. 天津大学学报(自然科学与工程技术版), 2017, 50(8): 813–820. JI Zhong, XIE Yuzhong, PANG Yanwei. Zero-shot learning based on canonical correlation analysis and distance metric learning[J]. Journal of Tianjin University (science and technology edition), 2017, 50(8): 813–820. [17] XIAN Yongqin, LAMPERT C H, SCHIELE B, et al. Zero-shot learning-A comprehensive evaluation of the good, the bad and the ugly[J]. IEEE transactions on pattern analysis and machine intelligence, 2019, 41(9): 2251–2265. doi: 10.1109/TPAMI.2018.2857768 [18] XIAN Yongqin, LORENZ T, SCHIELE B, et al. Feature generating networks for zero-shot learning[C]//2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Salt Lake City: IEEE, 2018: 5542−5551. [19] SARIYILDIZ M B, CINBIS R G. Gradient matching generative networks for zero-shot learning[C]//2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR). Long Beach: IEEE, 2019: 2163−2173. [20] MANDAL D, NARAYAN S, DWIVEDI S K, et al. Out-of-distribution detection for generalized zero-shot action recognition[C]//2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR). Long Beach : IEEE, 2019: 9977−9985. [21] XIAN Yongqin, SHARMA S, SCHIELE B, et al. F-VAEGAN-D2: a feature generating framework for any-shot learning[C]//2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR). Long Beach : IEEE, 2019: 10267−10276. [22] KIM H, LEE J, BYUN H. Unseen image generating domain-free networks for generalized zero-shot learning[J]. Neurocomputing, 2020, 411: 67–77. doi: 10.1016/j.neucom.2020.05.043 [23] VERMA V K, BRAHMA D, RAI P. Meta-learning for generalized zero-shot learning[J]. Proceedings of the AAAI conference on artificial intelligence, 2020, 34(4): 6062–6069. doi: 10.1609/aaai.v34i04.6069 [24] MA Yuanbo, XU Xing, SHEN Fumin, et al. Similarity preserving feature generating networks for zero-shot learning[J]. Neurocomputing, 2020, 406: 333–342. doi: 10.1016/j.neucom.2019.08.111 [25] LIU Huan, YAO Lina, ZHENG Qinghua, et al. Dual-stream generative adversarial networks for distributionally robust zero-shot learning[J]. Information sciences, 2020, 519: 407–422. doi: 10.1016/j.ins.2020.01.025 [26] LIU Jinlu, ZHANG Zhaocheng, YANG Gang. Cross-class generative network for zero-shot learning[J]. Information sciences, 2021, 555: 147–163. doi: 10.1016/j.ins.2020.12.063 [27] TANG C, HE Z, LI Y, ET Al. Zero-shot learning via structure-aligned generative adversarial network[J]. IEEE transactions on neural networks and learning systems, 2021(99): 1–14. [28] LI Zhiqun, CHEN Qiong, LIU Qingfa. Augmented semantic feature based generative network for generalized zero-shot learning[J]. Neural networks:the official journal of the international neural network society, 2021, 143: 1–11. doi: 10.1016/j.neunet.2021.04.014 [29] GAO RUI, HOU XINGSONG, QIN JIE, et al. Zero-VAE-GAN: generating unseen features for generalized and transductive zero-shot learning[J]. IEEE transactions on image processing, 2020, 29: 3665–3680. doi: 10.1109/TIP.2020.2964429 [30] KINGMA D P, WELLING M. Auto-Encoding Variational Bayes[EB/OL]. (2014−05−01)[2022−03−10]https://arxiv.org/abs/1312.6114v2. [31] LARSEN A B L, SØNDERBY S K, LAROCHELLE H, et al. Autoencoding beyond pixels using a learned similarity metric[EB/OL]. (2016−02−10)[2022−03−10]https://arxiv.org/abs/1512.09300. [32] ZHANG Han, XU Tao, LI Hongsheng, et al. StackGAN: text to photo-realistic image synthesis with stacked generative adversarial networks[EB/OL]. (2017−08−05)[2022−03−10]https://arxiv.org/abs/1612.03242v2. [33] Wah C, Branson S, Welinder P, et al. The Caltech-UCSD Birds-200-2011 Dataset[J]. California institute of technology, 2011. [34] LAMPERT C H, NICKISCH H, HARMELING S. Attribute-based classification for zero-shot visual object categorization[J]. IEEE transactions on pattern analysis and machine intelligence, 2014, 36(3): 453–465. doi: 10.1109/TPAMI.2013.140 [35] CHE TONG, LI YANRAN, JACOB A P, et al. Mode regularized generative adversarial networks[EB/OL]. (2017−03−02)[2022−03−10]https://arxiv.org/abs/1612.02136 . [36] 魏宏喜, 张越. 基于生成对抗网络的零样本图像分类[J]. 北京航空航天大学学报, 2019, 45(12): 2345–2350. WEI Hongxi, ZHANG Yue. Zero-shot image classification based on generative adversarial network[J]. Journal of Beijing University of Aeronautics and Astronautics, 2019, 45(12): 2345–2350.
