Research on security risk assessment of SCADA system based on the cloud model and combination weighting
-
摘要: 当前数据采集与监控系统(supervisory control and data acquisition, SCADA)系统面临着巨大的安全威胁，对其风险状况进行监测和评估是一项有效的应对措施。为有效处理评估过程中存在的模糊性和随机性问题，将云模型理论引入SCADA系统安全风险评估中，提出了一种基于云模型和组合权重的安全风险评估模型。该模型从SCADA系统的资产、威胁、脆弱性、安全措施4方面构建安全风险评估指标体系，采用最小二乘法求出评估指标的最优组合权重，借助云发生器得到评估指标的云模型数字特征和SCADA系统的综合评估云，然后基于黄金分割率构建标准评估云，同时结合改进的云相似度计算方法得出最终评估结果，最后通过实验验证了模型的有效性和可行性。研究结果表明，该模型能够得到准确的评估结果，与模糊综合评价等方法相比，该评估方法具备更高的可信性，评价效果更好。该方法不仅有助识别SCADA系统的安全风险威胁，而且为其他领域的安全风险评估提供了一定的参考。Abstract: The current (supervisory control and data acquisition, SCADA) system faces a huge security threat, and monitoring and evaluating its risk status is an effective countermeasure. In this paper, a cloud model theory is introduced to the security risk assessment of the SCADA system, and a security risk assessment model is proposed based on the cloud model and combination weighting to effectively deal with the problem of ambiguity and randomness in the assessment process. Firstly, a security risk assessment index system is constructed from assets, threats, vulnerabilities, and security measures of a SCADA system, Then the least squares estimate is used to obtain optimal combination weighting, and the cloud digital characteristics are calculated with the help of cloud generator, to get comprehensive security risk assessment cloud. Next, according to the golden ratio, the standard evaluation cloud is constructed and combined with the improved cloud similarity calculation method to obtain the final evaluation result. Finally, the effectiveness and feasibility of the model are verified through experiments. The research results show that the model can obtain accurate evaluation results, and compared with the fuzzy comprehensive evaluation method, it shows that this method has higher credibility and better evaluation effect. This method not only helps in identifying security risk threats in the SCADA system but also provides a certain reference for security risk assessment in other fields.
-
数据采集与监控系统(supervisory control and data acquisition, SCADA)系统是一个综合利用计算机技术、控制技术和通信网络技术的数据采集与监视控制系统[1]，包含了上位机、下位机和数据通信网络3个部分，主要负责完成各种设备过程的自动控制、实时监控和数据采集，为安全生产、调度、管理、优化和故障诊断提供了必要和完整的数据及技术手段，在电力、冶金、石油、化工、铁路等领域应用十分广泛。
近年来，随着全球信息化和工业化融合进程的不断加深，通用的软件、硬件、协议和技术越来越多地应用到工业生产领域[2]中，也将更多的漏洞和威胁带入到SCADA系统中，使SCADA系统面临着巨大的安全挑战。因此如何保障SCADA系统的安全已经成为当前国内外研究的热点问题，其中的一个重点就是如何对SCADA系统进行安全评估，分析其安全现状。
目前，国内外研究人员通常从定性、定量、定性与定量相结合三方面来对SCADA系统的安全状况进行评估。定性评估方法具有较大的主观性，无法给出量化的结论，系统安全状况之间的差异很难区分。定量评估方法无法将所有的数据信息完全量化，简化其过程又可能会导致评估结果产生误差[3]。因此融合了二者优点的定性与定量相结合的评估方法得到了更加广泛的应用，也取得了一定的成果，相关的研究方法包括了层次分析法、模糊综合评估法、灰色评估等。例如姜莹莹等[4]通过层次分析法(AHP)，结合模糊综合评估法对油气SCADA系统进行综合评估，得到了系统的整体安全状况。Bian等[5]通过改进的层次分析法和模糊综合评估法，从风险、公共、服务三方面进行网络安全态势的评估。Markovic-Petrovic等[6]提出了一种新的综合考虑了主客观因素的模糊层次分析法，减少了主观性。Li等[7]提出了一种基于熵权和灰色预测的SCADA系统通信网络风险预测模型。万书亭等[8]将变权模糊综合评估和灰色理论相结合构建出评估模型，实现了风电机组的性能评估。杨力等[9]在综合分析油气SCADA系统的结构和安全威胁的基础上，提出了一种基于因素状态空间和模糊综合评估的新型风险评估方法，以及将因素空间理论与MATLAB模糊逻辑工具结合得到Mamdani推理模型，实现了SCADA系统的风险评估[10]。
上述方法在评估过程中，大多采用单一权重和隶属函数，主观因素较强，且隶属函数在处理模糊现象时将模糊问题精确化，无法完整体现出评估过程中的不确定性，导致结果不够科学准确。云模型能够将定性概念的模糊性和随机性有效集成，实现定性概念与其定量表示之间的转换，比隶属函数具备更强的普适性和描述不确定性的能力[11]。因此，本文提出了一种基于云模型和组合权重的SCADA系统安全风险评估模型，通过最小二乘法求出组合权重，使权重的确定更加科学合理，再通过云模型的云发生器和相似度计算得出综合风险评估结果，为SCADA系统的安全风险评估研究提供一个新的途径。
1. 组合权重
评估指标的权重确定方法主要分为主观赋权和客观赋权两种。主观赋权依靠专家经验确定权重，方法简单，在一定的程度上可以反映出实际情况，但人为主观性太强；客观赋权根据样本数据来确定权重，忽视了不同指标的重要程度，从而可能导致权重结果与实际指标重要性相反。因此本文采用主客观组合赋权方法来克服单一赋权方法的局限性，消除主客观偏差，降低信息损失，使权重结果更加接近于实际结果。
1.1 主观权重
采用层次分析法确定主观权重。层次分析法是将与决策相关的元素分解为目标、准则、指标等层次，在此基础上进行定量和定性分析的方法。
层次分析法的具体运算步骤如下[4]：
1) 确定评估目标，建立层次分析模型。仔细分析问题，逐层分解，确定问题的评估目标，建立起目标、准则、指标三层评估模型。
2) 构造判断矩阵。在指定上层某一元素的条件下，根据比较标度对本层的各元素进行两两比较，建立起相应的判断矩阵。
3) 单层次计算并进行安全性判断，即层次单排序。
4) 对判断矩阵进行一致性检验，计算出目标总排序。若一致性指标CR<0.1，则判断矩阵的一致性可以接受，否则修正判断矩阵。
1.2 客观权重
采用熵权法确定客观权重。熵权法主要是根据指标信息熵的大小计算出相应指标的权重，某个指标的信息熵越小，表示其所含的信息量越大，在评估中所起到的作用也就越大，所占权重也越大；反之，指标信息熵越大，所占权重越小。具体运算步骤如下[7]：
1) 确定评估矩阵
${\boldsymbol{X}}$ 。假设SCADA系统的评估指标有$m$ 个，每个指标有$n$ 个专家评估,${x_{ij}}$ 表示第$i$ 个专家第$j$ 个指标的评估值。2) 对评估矩阵
${\boldsymbol{X}}$ 进行标准化处理，得到矩阵${\boldsymbol{Y}}$ 。$$ {y_{ij}} = \frac{{{x_{ij}} - \min ({x_j})}}{{\max ({x_j}) - \min ({x_j})}} $$ (1) 3) 计算指标的信息熵。
$$\begin{aligned} {p_{ij}} = \dfrac{{{y_{ij}}}}{{\displaystyle\sum\limits_{i = 1}^n {{y_{ij}}} }} \end{aligned}$$ (2) $$ {e_j} = - \dfrac{1}{{\ln n}}\displaystyle\sum\limits_{i = 1}^n {{p_{ij}}\ln ({p_{ij}})} $$ (3) 4) 计算出指标客观权重。
$$ {{\rm ws}_j} = \dfrac{{1 - {e_j}}}{{\displaystyle\sum\limits_{j = 1}^m {(1 - {e_j})} }} $$ (4) 1.3 组合权重优化模型
利用一定的数学优化模型对主客观权重进行有机组合得到的最优权重值，就是组合权重。本文充分考虑影响SCADA系统风险大小的多种因素，选择最小二乘法优化模型计算出最优组合权重值。
假设主观权重值为
${\rm{wc}} = {[{{\rm wc}_1}\;\;{{\rm wc}_2}\;\; \cdots\;\;{{\rm wc}_m}]^{\rm{T}}}$ ，客观权重值为${\rm{ws}} = {[{{\rm ws}_1}\;\;{{\rm ws}_2}\;\;\cdots \;\;{{\rm ws}_m}]^{\rm{T}}}$ ,组合权重值为${\boldsymbol{w}} = {[{w_1}\;\;{w_2}\;\; \cdots \;\;{w_m}]^{\rm{T}}}$ ，评估矩阵${\boldsymbol{X}}$ 标准化处理之后得到的矩阵${\boldsymbol{Y}} = {[{y_{ij}}]_{n \times m}}$ ，其中$n$ 表示评估数据条数，$m$ 表示评估指标个数，根据最小二乘法构造出最优组合权重的目标函数和约束条件如下：$$\begin{gathered} \min f(w) = \sum\limits_{i = 1}^n \sum\limits_{j = 1}^m \left\{ {{[({{\rm wc}_j} - {w_j}){y_{ij}}]}^2} + {[({{\rm ws}_j} - {w_j}){y_{ij}}]^2}\right\} \\ {\rm{s.t.}}\quad \sum\limits_{j = 1}^m {{w_j} = 1} ,{w_j} \geqslant 0 \end{gathered}$$ (5) 利用拉格朗日乘子法求解上述目标函数，偏导方程组转化为矩阵形式如下：
$$ \left[ {\begin{array}{*{20}{c}} {\boldsymbol{A}}&{\boldsymbol{E}} \\ {{{\boldsymbol{E}}^{\rm T}}}&0 \end{array}} \right] \times \left[ {\begin{array}{*{20}{c}} {\boldsymbol{w}} \\ \lambda \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\boldsymbol{B}} \\ 1 \end{array}} \right] $$ (6) 其中：
$$\begin{gathered} {\boldsymbol{E}} = {\left[ {1\;\;1\;\; \cdots \;\;1} \right]^{\text{T}}} \\ {\boldsymbol{A}} = {\rm diag} \left[ {\sum\limits_{i = 1}^n {y_{i1}^2}\;\;\sum\limits_{i = 1}^n {y_{i2}^2\;\;\cdots \;\;\sum\limits_{i = 1}^n {y_{im}^2} } } \right] \\ {\boldsymbol{B}} = \left[ \begin{gathered} \sum\limits_{i = 1}^n {\frac{{(w{c_1} + w{s_1})y_{i1}^2}}{2}} \\ \sum\limits_{i = 1}^n {\frac{{(w{c_2} + w{s_2})y_{i2}^2}}{2}} \\ \quad\quad\quad \vdots \\ \sum\limits_{i = 1}^n {\frac{{(w{c_m} + w{s_m})y_{im}^2}}{2}} \\ \end{gathered} \right] \\ {\boldsymbol{w}} = {[{w_1}\;\;{w_2}\;\; \cdots \;\;{w_m}]^{\text{T}}} \end{gathered}$$ (7) 对式(6)、(7)进行推导，得到最优组合权重为
$$ {\boldsymbol{w}} = {{\boldsymbol{A}}^{ - 1}}\left[ {{\boldsymbol{B}} + \frac{{1 - {{\boldsymbol{E}}^{\text{T}}}{{\boldsymbol{A}}^{ - 1}}{\boldsymbol{B}}}}{{{{\boldsymbol{E}}^{\text{T}}}{{\boldsymbol{A}}^{ - 1}}{\boldsymbol{E}}}}{\boldsymbol{E}}} \right] $$ (8) 2. 云模型
云模型是由李德毅等[11]在概率论和模糊数学理论的基础上提出的用于处理某个定性概念与其定量表示的不确定性转换模型。它利用3个数字特征来描述定性概念，主要反映出概念的模糊性和随机性，并将二者完全集成在一起，构成概念内涵和概念外延之间的转换。目前云模型已经广泛应用于众多领域行业中，例如陈圆超等[12]将云模型与级差最大化组合赋权相结合用以综合评估矿井通风系统。张仕斌等[13]针对复杂网络交易环境中的信任问题，引入云模型进行可信度评估。受此启发，将云模型应用于SCADA系统的安全风险评估中，能够有效克服过程中的不确定性，使评估结果更加科学可信。
2.1 云模型数字特征
云模型用期望
${\text{Ex}}$ 、熵${\text{En}}$ 和超熵${\text{He}}$ 3个数字特征来整体表征一个概念[11]。期望
${\text{Ex}}$ 是云滴在论域空间中分布的数学期望，是最能代表定性概念的点。距离期望越近，云滴就越集中，对概念的认知就越统一。熵
${\text{En}}$ 是对定性概念不确定性的度量，定性概念的随机性和模糊性共同决定，既反映了云滴的离散程度，也反映了云滴的取值范围。超熵
$ {\text{He}} $ 是熵的不确定性度量，是熵的熵，表示为云的厚度。2.2 云发生器
云发生器是用来实现不确定性概念中定性与定量之间转换的算法，是云模型中最关键的部分，主要分为正向云发生器和逆向云发生器，本文主要利用二阶正态云发生器。
正向云发生器是由云的数字特征
${\text{Ex}}$ 、${\text{En}}$ 、${\text{He}}$ 产生定量的数值，即云滴，其算法过程如算法1所示。算法1 正向云发生器算法
输入
$({\text{Ex,En,He)}}$ 和要生成的云滴个数$N$ 输出
$({x_i},{u_i})$ ,$i = 1,2, \cdots ,N$ 1) 生成以
${\text{En}}$ 为期望，$ {\text{H}}{{\text{e}}^2} $ 为方差的一个正态随机数${y_i} = {R_N}({\text{En,He}})$ ；2) 生成以
${\text{Ex}}$ 为期望，$ y_i^2 $ 为方差的一个正态随机数${x_i} = {R_N}({\text{Ex, }}{y_i})$ ；3) 计算确定度
$ {u_i} $ ：$$ {u_i} = \exp \left( { - \frac{{{{\left( {{x_i} - {\text{Ex}}} \right)}^2}}}{{2y_i^2}}} \right) $$ (9) 4) 具有确定度
$ {u_i} $ 的${x_i}$ 成为云的一个云滴；5) 重复步骤1)到4)，直到生成
$N$ 个云滴组成云。逆向云发生器是将一定数量的精确数据转换为以数字特征表示的定性概念。现有的逆向云发生器算法可分为有确定度和无确定度两种。刘常昱等[14]于2004年根据一阶样本绝对中心距和样本方差提出了一种经典的无确定度逆向云算法，然而该方法在SCADA系统安全风险评估计算过程中可能会出现样本方差过小或者熵的估计值过大的情况，导致计算出的超熵估计值会出现虚数。
因此引入文献[15]改进的算法，具体过程如算法2所示。
算法2 逆向云发生器算法
输入 样本点
${x_i}$ ,$i = 1,2, \cdots ,n$ 输出 数字特征
$({\text{Ex,En,He)}}$ 估计值1) 根据样本点
${x_i}$ 计算出相应的样本均值$\bar X$ ：$$ \bar X = \frac{1}{n}\sum\limits_{i = 1}^n {{x_i}} $$ (10) 2) 计算期望
${\text{Ex}} = \bar X$ ；3) 计算熵
${\text{En}}$ ：$$ {\text{En}} = \sqrt {\frac{{\text{π}} }{2}} \times \frac{1}{n}\sum\limits_{i = 1}^n {\left| {{x_i} - {\text{Ex}}} \right|} $$ (11) 4) 计算样本方差
${S^2}$ ，如果${S^2} - {\text{E}}{{\text{n}}^2} < 0$ ，转步骤5)，反之转步骤6)；$$ {S^2} = \frac{1}{{n - 1}}\sum\limits_{i = 1}^n {({x_i} - {{\bar X}^2})} $$ (12) 5) 删除当前样本中距离期望
${\text{Ex}}$ 最近的一个云滴样本后转步骤4)；6) 计算超熵
${\text{He}} = \sqrt {{S^2} - {\text{E}}{{\text{n}}^2}} $ 。3. SCADA系统安全风险评估模型
3.1 SCADA系统安全风险评估指标体系
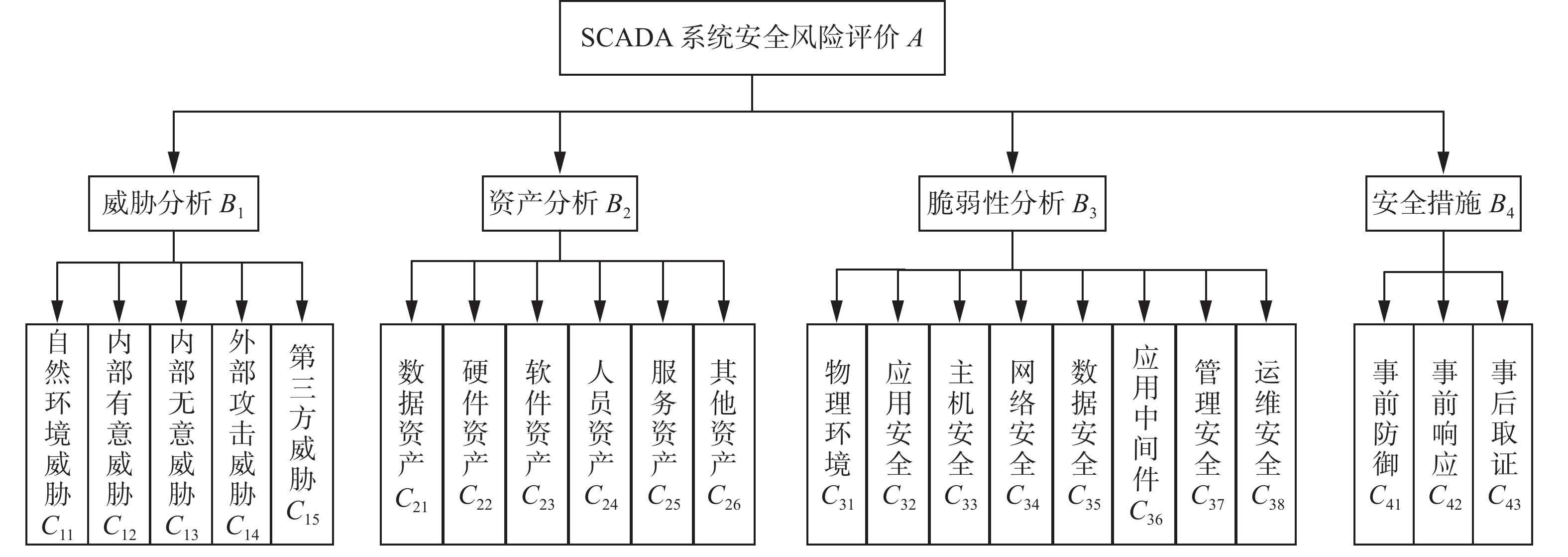
对SCADA系统进行安全风险评估，首先要分析建立起科学全面的评估指标体系。本文依据GB/T 29084–2007等标准规范、相关单位风险评估报告和前人的研究，详细分析了SCADA系统的基本结构以及系统所存在的薄弱点和问题，初步构建出评估指标体系，再采用delphi法和实地调研对指标进行合理性验证，最终从可能受影响的资产、威胁、脆弱性、安全措施4个方面构建出包含4个一级评估指标(准则层)和22个二级指标(指标层)的SCADA系统安全风险指标体系，如图1所示。与现有的指标体系相比，本文所构建的指标体系更加全面和客观，综合考虑了SCADA系统中影响安全的各种重要因素，安全事件发生的不同阶段下保护措施配置情况，通用性更强。
图 1 SCADA系统安全风险评估指标体系Fig. 1 SCADA system safety risk assessment index system
下载:
全尺寸图片
自然环境威胁包括断电、静电、灰尘、潮湿、温度、鼠蚁虫害、电磁干扰、洪灾、 火灾、地震、意外事故等环境危害或自然灾害。内部有意威胁包括不满的或有预谋的内部人员对系统重要信息进行恶意窃取、泄露和破坏。内部无意威胁包括内部人员由于不注意或不遵循规章制度和操作流程而导致故障、信息泄露和权限滥用等，以及内部人员由于缺乏培训、专业技能不足、规章制度和职责不明确等问题而导致的失误和系统被攻击。外部攻击包括黑客、恐怖分子、敌对势力和敌对国家等外部人员利用系统的脆弱性对系统进行破坏以获取利益。第三方威胁包括承包商或第三方平台存在的漏洞或后门被恶意利用等。
数据资产包括源代码、控制台实时数据、应用程序数据、数据库数据、操作/产品/用户手册等电子文档、生产运行计划和报告、各类纸质文档等。硬件资产包括PLC、DCS、RTU等现场控制设备，路由器、网关、交换机等网络设备，防火墙、入侵检测系统等安全设备，服务器、工作站、小型机等计算机设备，磁盘阵列、移动硬盘、光盘等存储设备，光纤、双绞线等传输线路，空调、文件柜、门禁等保障设备，以及打印机、传真等其他设备。软件资产包括数据库系统、上位组态和监控软件、操作系统等系统软件，远程控制软件、数据库软件、工具软件、OPC等应用软件，各种源程序。人员资产包括运维人员、系统调试人员、安全管理人员等。服务资产包括对外开展的各类信息服务、各种网络设备等提供的网络服务、各类管理信息系统提供的办公服务。其他资产包括客户关系、企业公众形象等。
脆弱性分析中物理环境主要从防盗、防火、防静电、电磁防护等方面进行识别；应用、主机、网络和数据安全除了从安全审计、访问控制、身份鉴别等方面进行识别，还需要分别从应用健壮性、通信的完整性和保密性、入侵防范、恶意代码防范、数据传输完整性和保密性、网络边界隔离等方面进行识别。应用中间件需要识别交易完整性、协议安全、数据完整性等。管理安全需要从安全策略、资产分类与控制、人员安全、系统开发与维护等方面进行识别，运维安全需要从配置管理、密码管理、变更管理、外包运维管理等方面进行识别。
3.2 标准评估云
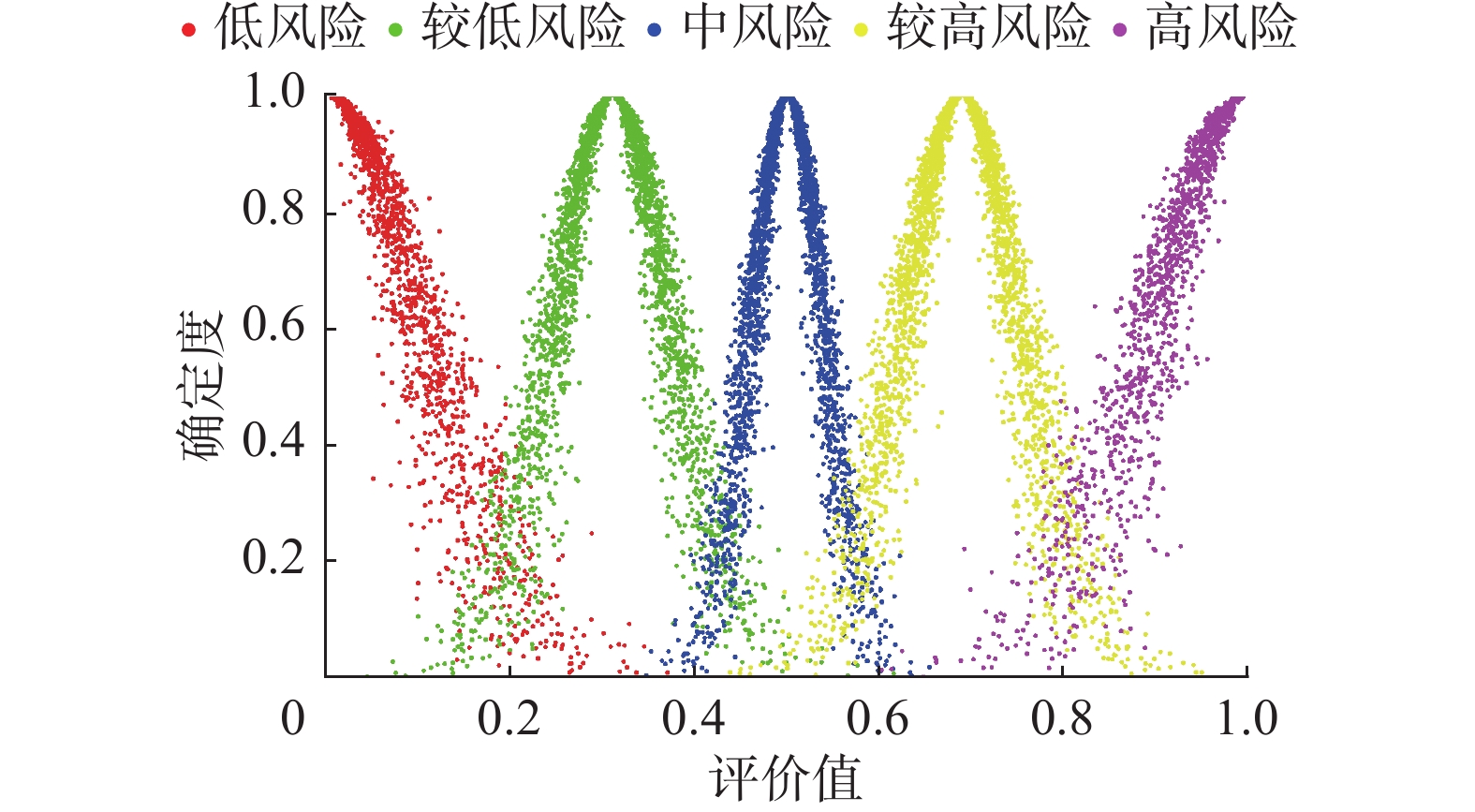
安全风险评估结果的确定与评语的划分等级密切相关。根据实际情况，首先将SCADA系统的安全风险评估结果划分为低风险、较低风险、中风险、较高风险、高风险5个等级，对应的评分值取值范围设定为[0, 1]，数值越高，说明风险越高，安全性就越差，然后基于黄金分割率的定性变量云化方法[16]和算法1计算不同等级的云滴群的确定度，构建出标准评估云。
基于黄金分割率的变量云化方法的计算规则如表1所示，其中
${B_{\min }}$ 和${B_{\max }}$ 对应于评分取值范围，${\text{H}}{{\text{e}}_3}$ 为常数，视具体情况取值，本文中${\text{H}}{{\text{e}}_3} = 0.008$ ，根据此计算规则计算得出具体各等级的数字特征值如表2所示，同时根据表2构建出相应的标准评估云，如图2所示。表 1 标准评估云计算规则Table 1 Standard Evaluation Cloud Computing Rules${\text{Ex}}$值 ${\text{En}}$值 ${\text{He}}$值 ${\text{E}}{{\text{x}}_{\text{1}}} = {B_{\min }}$ ${\text{E} }{ {\text{n} }_1} = \dfrac{ { {\text{E} }{ {\text{n} }_2} } }{ {0.618} }$ ${\text{H} }{ {\text{e} }_1}{\text{ = } }\dfrac{ { {\text{H} }{ {\text{e} }_2} } }{ {0.618} }$ ${\text{E} }{ {\text{x} }_2} = {\text{E} }{ {\text{x} }_3} - \dfrac{ {0.382({B_{\max } } - {B_{\min } })} }{2}$ ${\text{E} }{ {\text{n} }_2} = \dfrac{ {0.382({B_{\max } } - {B_{\min } })} }{6}$ ${\text{H} }{ {\text{e} }_2}{\text{ = } }\dfrac{ { {\text{H} }{ {\text{e} }_3} } }{ {0.618} }$ ${\text{E} }{ {\text{x} }_3} = \dfrac{ { {B_{\max } } + {B_{\min } } } }{2}$ ${\text{E}}{{\text{n}}_3} = 0.618{\text{E}}{{\text{n}}_{\text{4}}}$ ${\text{H}}{{\text{e}}_3}$ ${\text{E} }{ {\text{x} }_{\text{4} } } = {\text{E} }{ {\text{x} }_3}{\text{ + } }\dfrac{ {0.382({B_{\max } } - {B_{\min } })} }{2}$ ${\text{E} }{ {\text{n} }_4} = \dfrac{ {0.382({B_{\max } } - {B_{\min } })} }{6}$ ${\text{H} }{ {\text{e} }_4}{\text{ = } }\dfrac{ { {\text{H} }{ {\text{e} }_3} } }{ {0.618} }$ ${\text{E}}{{\text{x}}_5} = {B_{\max }}$ ${\text{E} }{ {\text{n} }_5}{\text{ = } } \dfrac{ { {\text{E} }{ {\text{n} }_4} } }{ { {\text{0} }{\text{.618} } } }$ ${\text{H} }{ {\text{e} }_5}{\text{ = } }\dfrac{ { {\text{H} }{ {\text{e} }_4} } }{ {0.618} }$ 表 2 各风险评估等级云数字特征Table 2 Cloud digital characteristics at different risk assessment levels风险等级 云模型数字特征 低风险 (0,0.104,0.021) 较低风险 (0.31,0.064,0.013) 中风险 (0.5,0.04,0.008) 较高风险 (0.69,0.064,0.013) 高风险 (1,0.104,0.021) 
图 2 标准评估云Fig. 2 Standard evaluation cloud下载:
全尺寸图片
3.3 云相似度计算及其改进
在对比综合评估云和标准评估云时，传统的方法是以期望值
${\text{Ex}}$ 为基准，但当${\text{Ex}}$ 处于两个等级之间时，这种界定方法有很强的主观随意性。因此受相关文献[17]的启发，本文采用正态云之间的相似度来比较云图，进而提出了一种基于修正期望曲线和KL散度的云相似度计算方法(impoved Kullback Leibler divergence based on cloud model，IKLCM)。正态云是最基本的云模型，其期望曲线反映了正态云的重要几何特征，是贯穿于云滴群的骨架，所有的云滴都是在其周围波动，波动的程度由超熵控制。龚艳冰等[18]在此基础上定义了正态云的修正期望曲线：
若云滴
$x$ 满足$x \sim N({\text{Ex}},{\text{E}}{{\text{n}'}^2})$ ，${\text{En}} \ne 0$ ，${\text{En}'} \sim N{\text{(En,}} {{\text{He}}^2})$ ，则$$ y(x) = \exp \left( { - \frac{{{{(x - {\text{Ex}})}^2}}}{{2({\text{E}}{{\text{n}}^2} + {\text{H}}{{\text{e}}^2})}}} \right) $$ (13) 称为正态云的修正期望曲线。
KL散度是两个概率分布之间差异的非对称性度量，常用来度量两个概率分布之间的差异性，KL散度越大，两个概率分布的差异性越大[19-20]，因此本文通过KL散度来度量两个正态云的修正期望曲线的差异性，从而度量两个正态云的相似度。对于连续型随机变量
$P$ 和$Q$ ，其概率密度函数分别为$p(x)$ 和$q(x)$ ，KL散度的定义为$$ {D_{\rm KL}}(P\parallel Q) = \int {p(x)\log \frac{{p(x)}}{{q(x)}}{\rm{d}}x} $$ (14) 由此，许昌林等[21]提出了KL散度的一种对称形式，即
$D(P\parallel Q) = {D_{\rm KL}}(P\parallel Q) + {D_{\rm KL}}(Q\parallel P)$ ，结合修正期望曲线，可以推导出两个正态云的差异度计算公式为$$ \begin{aligned} &D({S_i},{S_j}) = \frac{1}{2} \times \left[ {{{({{\rm{Ex}}_i} - {{\rm{Ex}}_j})}^2} + (\sigma _i^2 + \sigma _j^2)} \right] \times \left(\frac{1}{{\sigma _i^2 + \sigma _j^2}}\right) - 2 \\ &\quad\quad\quad\quad{\sigma _i}^2 = {\rm{En}}_i^2 + {\rm{He}}_i^2,{\sigma _j}^2 = {\rm{En}}_j^2 + {\rm{He}}_j^2 \\ \end{aligned} $$ (15) 因为两个正态云的差异度越大，其相似度却越小，为了更加方便地与其他相似度计算方法进行对比，引入了指数函数将两个正态云的差异性与相似度进行融合，即相似度
${\rm{sim}}({S_i},{S_j})$ 为$$ {\rm{sim}}({S_i},{S_j}) = \exp ( - D({S_i},{S_j})) $$ (16) 由指数函数和KL散度的性质可知，式(16)是单调递减函数，且KL散度为非负值，因此相似度的计算结果必然在[0, 1]之间。
3.4 综合评估
首先由算法2计算出指标层各指标的云数字特征，然后根据式(17)~(19)计算出相应准则层和目标层各指标的云模型数字特征，代入算法1得到了SCADA系统的安全风险综合评估云，最后通过文中的IKLCM云相似度计算方法，比较综合评估云与标准评估云的相似度，得出整个SCADA系统的安全风险评估结果。
$$ {\text{Ex}} = \dfrac{{\displaystyle\sum\limits_{i = 1}^n {{w_i}} \times {\text{E}}{{\text{x}}_i}}}{{\displaystyle\sum\limits_{i = 1}^n {{w_i}} }} $$ (17) $$ {\text{En}} = \dfrac{{\displaystyle\sum\limits_{i = 1}^n {w_i^2 \times {\text{E}}{{\text{n}}_i}} }}{{\displaystyle\sum\limits_{i = 1}^n {w_i^2} }} $$ (18) $$ {\text{He}} = \dfrac{{\displaystyle\sum\limits_{i = 1}^n {w_i^2 \times {\text{H}}{{\text{e}}_i}} }}{{\displaystyle\sum\limits_{i = 1}^n {w_i^2} }} $$ (19) 式中：
${w_i}$ 为相应指标层或准则层各指标的组合权重；${\text{(E}}{{\text{x}}_i}{\text{, E}}{{\text{n}}_i}{\text{, H}}{{\text{e}}_i})$ 为相应指标层或准则层的云数字特征；$n$ 为相应层次的指标个数。4. 实例分析
4.1 SCADA系统安全风险综合评估
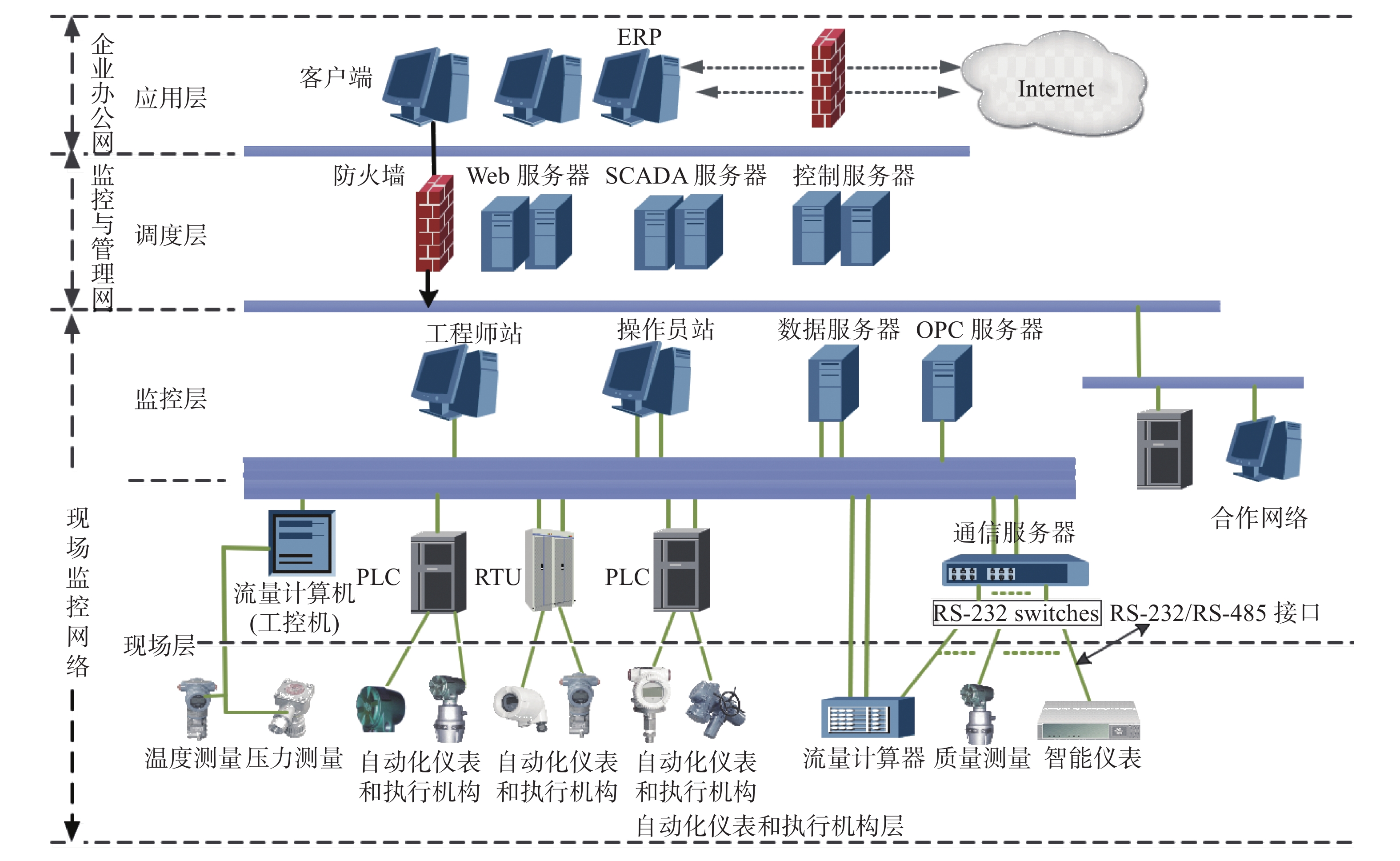
本文采用某西南油气SCADA系统作为研究对象进行可行性验证，该研究对象是典型的工控网络结构，如图3所示。整个系统中通信网络使用工业以太网，核心部件分上位机和下位机，上位机主要包含Web服务器、工程师站、操作员站、历史数据服务器等设备，下位机主要包含远程终端单元和可编辑逻辑控制器等设备。其中，现场测控点与下位机通过现场总线和平行接线两种方式进行通信，实现数据采集和设备过程的直接控制，下位机通过卫星、有限光缆、无线数传电台和GPRS等方式与上位机通信，实现控制信号和各种数据信息的传递，在上位机各计算机和服务器之间采用工业以太网进行数据交互和资源共享，从而实现数据的分析和处理，各设备状态、生产参数、环境参数等的显示，远程监控，故障预警处理等功能。
图 3 SCADA网络结构图Fig. 3 SCADA network structure figure下载:
全尺寸图片
依据前文构建的SCADA系统安全风险评估模型，邀请相关领域的专家组成评估小组，分别对指标层的所有指标进行打分和重要性判断，根据层次分析法，分别构造出准则层指标之间的判断矩阵和每个准则层指标下所有的二级指标之间的判断矩阵，计算出各判断矩阵的特征值和特征向量，一致性检验通过后对特征向量归一化后即可得到SCADA系统各层评估指标的主观权重。根据打分结果，利用熵权法得到指标层各评估指标的客观权重，再对每个准则层指标下所有二级指标的客观权重求和即可得到准则层各指标的客观权重。结合上述所得结果，根据式(7)和式(8)，计算得到各层指标的组合权重，结果如表3和表4所示。
表 3 指标层各指标权重Table 3 Each index weight in index layer指标 主观权重 客观权重 组合权重 ${C_{11}}$ 0.005 0.088 0.046 ${C_{12}}$ 0.018 0.055 0.036 ${C_{13}}$ 0.024 0.028 0.026 ${C_{14}}$ 0.034 0.030 0.032 $ {C_{15}} $ 0.008 0.052 0.030 ${C_{21}}$ 0.031 0.078 0.054 ${C_{22}}$ 0.186 0.019 0.102 ${C_{23}}$ 0.042 0.020 0.031 ${C_{24}}$ 0.094 0.032 0.063 $ {C_{25}} $ 0.107 0.031 0.069 $ {C_{26}} $ 0.023 0.048 0.035 $ {C_{31}} $ 0.011 0.021 0.016 ${C_{32}}$ 0.026 0.018 0.022 ${C_{33}}$ 0.086 0.019 0.052 ${C_{34}}$ 0.058 0.033 0.045 $ {C_{35}} $ 0.039 0.156 0.097 续表 3 指标 主观权重 客观权重 组合权重 $ {C_{36}} $ 0.012 0.030 0.021 $ {C_{37}} $ 0.026 0.049 0.037 ${C_{38}}$ 0.016 0.055 0.035 ${C_{41}}$ 0.031 0.029 0.030 ${C_{42}}$ 0.113 0.047 0.080 ${C_{43}}$ 0.014 0.060 0.037 表 4 准则层各指标权重Table 4 Each index weight in criterion layer指标 主观权重 客观权重 组合权重 ${B_1}$ 0.089 0.253 0.170 ${B_2}$ 0.483 0.228 0.354 ${B_3}$ 0.274 0.381 0.325 ${B_4}$ 0.158 0.136 0.147 将专家对22个指标的打分结果转化为定量数据作为算法2的输入，计算出指标层各指标的云模型数字特征，然后将指标层各指标的组合权重与云数字特征值相结合，利用式(17)~(19)计算出准则层的云模型数字特征，结果如表5所示。再结合准则层的指标权重经式(17)~(19)计算得到目标层云数字特征为(0.410, 0.230, 0.055)。
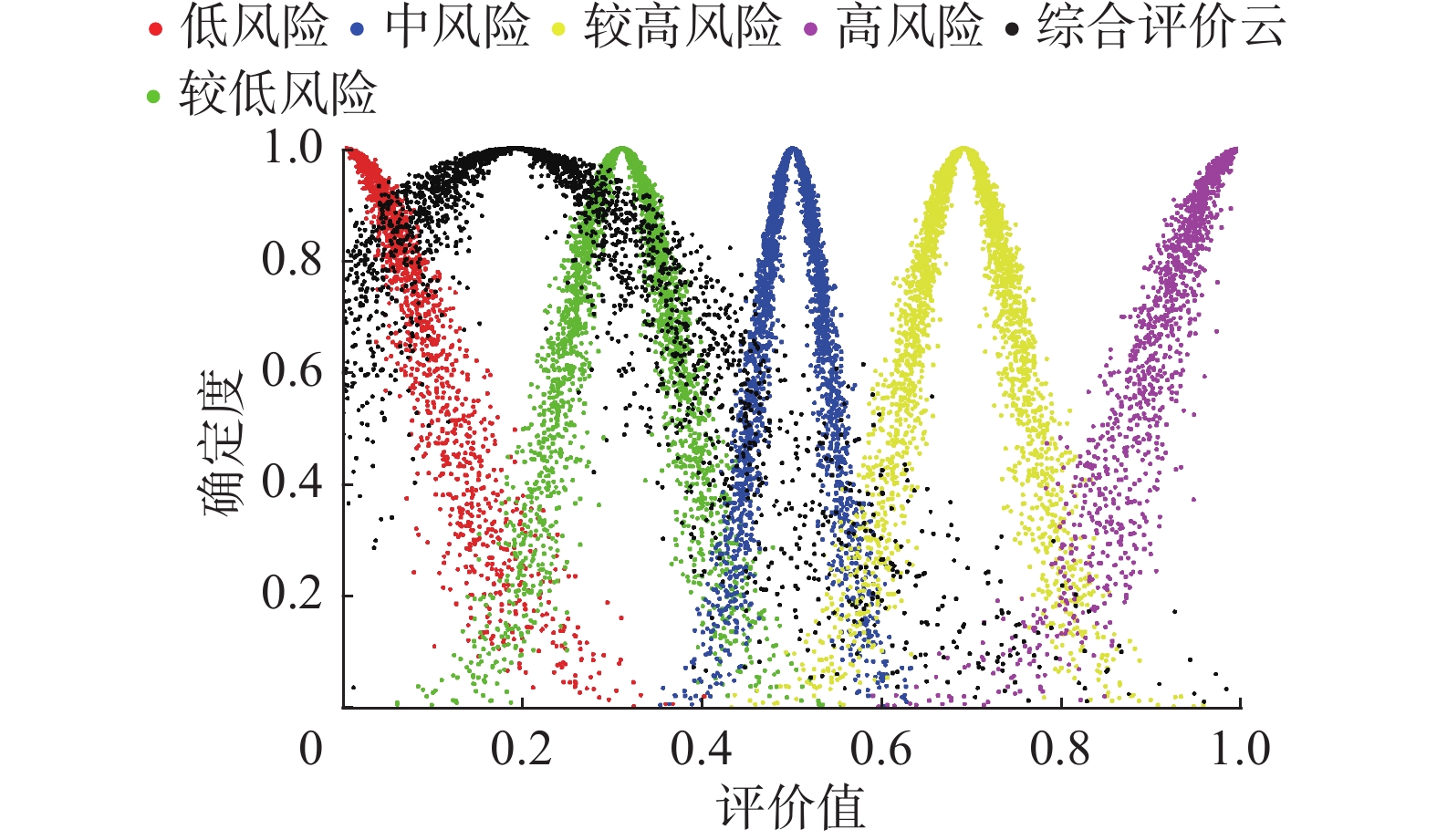
表 5 准则层和指标层各指标云数字特征Table 5 Each index cloud digital characteristics in the criterion and index layer准则层 云数字特征 指标层 云数字特征 ${B_1}$ (0.320,0.228,0.075) ${C_{11}}$ (0.191,0.223,0.062) ${C_{12}}$ (0.349,0.266,0.097) ${C_{13}}$ (0.395,0.203,0.025) ${C_{14}}$ (0.441,0.235,0.100) $ {C_{15}} $ (0.291,0.194,0.086) ${B_2}$ (0.429,0.220,0.051) ${C_{21}}$ (0.275,0.275,0.059) ${C_{22}}$ (0.441,0.183,0.034) ${C_{23}}$ (0.454,0.196,0.018) ${C_{24}}$ (0.554,0.344,0.087) $ {C_{25}} $ (0.370,0.194,0.057) $ {C_{26}} $ (0.500,0.127,0.067) ${B_3}$ (0.370,0.252,0.057) $ {C_{31}} $ (0.567,0.279,0.065) ${C_{32}}$ (0.429,0.171,0.036) ${C_{33}}$ (0.592,0.270,0.070) ${C_{34}}$ (0.383,0.213,0.038) $ {C_{35}} $ (0.141,0.236,0.049) $ {C_{36}} $ (0.441,0.235,0.100) $ {C_{37}} $ (0.403,0.296,0.099) ${C_{38}}$ (0.454,0.376,0.069) ${B_4}$ (0.560,0.181,0.045) ${C_{41}}$ (0.559,0.162,0.060) ${C_{42}}$ (0.513,0.148,0.033) ${C_{43}}$ (0.662,0.348,0.093) 根据目标层的云数字特征值生成相应的综合评估云，与标准评估云对比，结果如图4所示，由IKLCM得出综合评估云与较低风险云的相似度最高，可知该系统的综合风险评估结果为较低风险。同理可以得出指标体系中所有指标的评估云图和风险状况，以指标
${C_{11}}$ 为例，其结果如图5所示，可知该部分为低风险，由表6可知，该系统中风险最大的部分是安全措施，结合实际工控环境，可以发现SCADA系统中主机、服务器等设备缺乏入侵检测、恶意代码防范、安全审计等安全措施，从而导致安全措施部分存在较高的安全风险，需要及时处理。
图 4 综合评估云Fig. 4 Comprehensive evaluation cloud下载:
全尺寸图片
图 5 指标${C_{11}}$ 评估云Fig. 5 Index${C_{11}}$ evaluation cloud下载:
全尺寸图片
表 6 准则层各指标风险状况Table 6 Each index risk status in the criterion layer指标 风险状况 ${B_1}$ 较低风险 ${B_2}$ 较低风险 ${B_3}$ 较低风险 ${B_4}$ 较高风险 4.2 对比实验分析
4.2.1 不同相似度方法比较
目前，云模型的相似度计算方法主要有基于云模型数字特征和基于云模型的几何形态两种度量方法。张光卫等[22]提出的夹角余弦法(likeness comparing method based on cloud mode, LICM)，将云模型的数字特征作为向量，通过计算向量的夹角余弦来度量两个云模型的相似度，在协同过滤中取得了较好的效果，然而在云模型的期望远大于熵和超熵时，这种度量方法容易忽视熵和超熵，导致相似度整体偏大，区分性差；李海林等[23]提出了通过计算两个正态云模型的期望曲线(expectation based on cloud model, ECM)和最大边界曲线(maximum boundary based on cloud model, MCM)重合部分的面积来度量云模型的相似度，克服了基于特征向量和随机选取云滴的相似度计算方法带来的云模型期望过于显著、时间复杂度过高和结果不稳定等问题，然而ECM法完全忽视了超熵的作用，而MCM法考虑了超熵的作用，但超熵很大时，相似度结果误差较大；许昌林等[21]通过KL散度结合最大边界曲线(kullback leibler divergence based on cloud model, KLDCM)来度量云模型的相似度，KL散度能很好地刻画两个概率分布的差异，且具有较高的普适性，然而超熵很大时，相似度结果误差较大。本文提出的IKLCM法通过修正期望曲线和KL散度相结合，克服了上述方法的不足，较为全面地考虑到了期望、熵和超熵的作用。
为了更好地验证上述结论，说明本文提出的IKLCM法与其他4种方法的差异性，采用文献[24]和文献[22]的示例数据进行实验，并分析比较它们的实验结果。文献[24]中给出了3个正态云
${S_1}$ (3, 3.123, 2.05)、${S_2}$ (2, 3, 1)和${S_3}$ (1.585, 3.556, 1.358)，分别利用LICM、ECM、MCM、KLDCM和本文提出的IKLCM对其进行相似度计算，结果如表7所示。由表7可知，IKLCM方法的结果表明，
${S_2}$ 和${S_3}$ 的相似度最大为0.9193，该结果与实际直观结果一致。可以看出，LICM方法的计算结果几乎都接近为1，区分性差；ECM方法完全忽视了超熵的作用，导致计算结果不准确；MCM方法和KLDCM方法采用最大边界曲线扩大了超熵的作用，导致结果与实际直观结果不一致。然后再对文献[22]给出的4个正态云进行对比，
${S_1}$ (1.5, 0.62666, 0. 3390)、${S_2}$ (4.6, 0.60159, 0.30862)、${S_3}$ (4.4,0.75199,0.27676)、${S_4}$ (1.6,0.60159,0.30862)，结果如表8所示。由表8可知，IKLCM法的结果表明，${S_1}$ 和${S_4}$ 的相似度最大为0.97，${S_2}$ 和${S_3}$ 的相似次之为0.88，其余相似度都为0，该结果与实际直观结果一致。5种方法的计算结果相同，但LICM方法的相似度几乎都接近为1，区分度差，MCM方法和KLDCM方法中(${S_1},{S_4}$ )和$ ({S_2},{S_3}) $ 的相似度差0.01，ECM方法中(${S_1},{S_4}$ )和$ ({S_2},{S_3}) $ 的相似度差0.08，而IKLCM方法中(${S_1},{S_4}$ )和$ ({S_2},{S_3}) $ 的相似度差0.09，因此IKLCM方法能更好地区分正态云的相似度。4.2.2 不同评估方法结果比较
选取AHP-模糊综合评价[25]、灰色评估[26]、熵权–云模型[27]3种评估方法与本文基于组合权重和云模型的评估方法对SCADA系统的风险状况评估结果进行比较，结果如表9所示。
表 9 不同评估方法结果的比较Table 9 Comparison of different evaluation methods result评估方法 对各风险等级隶属度或相似度 评估结果 低 较低 中 较高 高 AHP–模糊综合评价 0.12 0.30 0.33 0.19 0.06 中风险 灰色评估 0.21 0.27 0.24 0.20 0.08 较低风险 熵权–云模型 0.51 0.95 0.89 0.00 0.00 较低风险 组合权重–云模型 0.00 0.11 0.00 0.00 0.00 较低风险 由表9可知，4种评估方法评价结果基本一致，表明基于云模型和组合权重的评估方法是合理有效的。结合实例进行分析，与模糊综合评估和灰色评估方法相比，本文方法区分性更大，不仅考虑了过程中存在的随机性，解决了隶属度函数、白化函数精确化等问题，还将评价结果制成云图，实现了评价结果的可视化，使结果更加直观清晰，也能得到每一项指标的风险状况，深入分析SCADA系统风险产生原因。
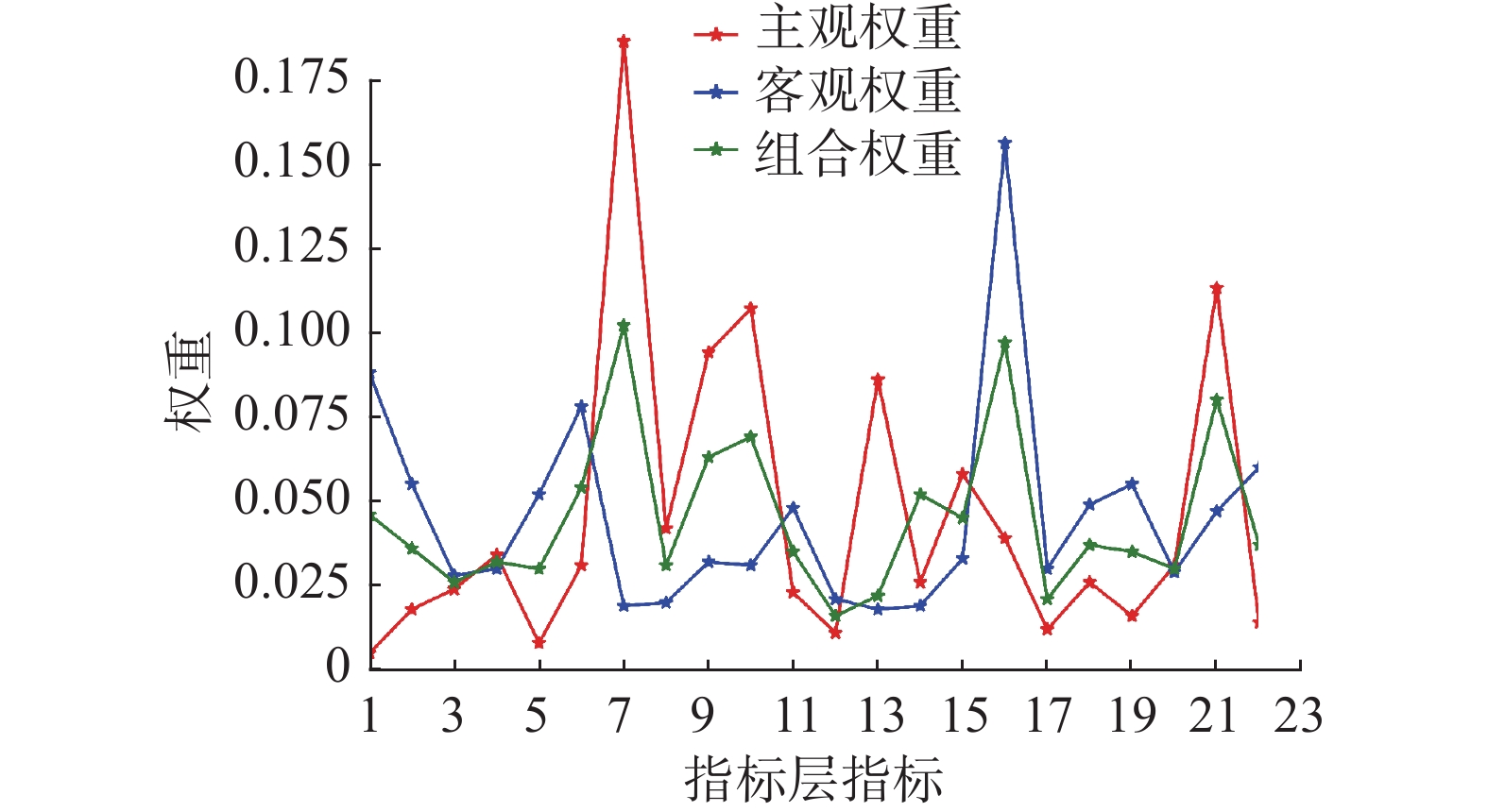
图6给出了熵权、AHP和组合赋权3种情况下所得的指标层指标的权重对比，可以看出组合赋权有效地减少了评估过程中的主观随意性，中和了熵权法的不足，在一定程度上提高了评估的准确性。
图 6 不同赋权方法的结果对比Fig. 6 Comparison of the results of different weighting methods下载:
全尺寸图片
5. 结束语
本文首先从资产、威胁、脆弱性等方面构建出SCADA系统风险评估指标体系，接着通过组合权重优化模型确定了指标权重，云模型相关理论构建出风险评估模型，并通过实验验证了该模型。本文将主客观权重相结合，克服了单一权重的信息损失问题，引入云模型理论，比传统的隶属度函数、白化函数在处理不确定性问题上考虑更加全面客观，改进了云相似度计算方法，更准确地反映了标准评估云与综合评估云之间的相似度，提高了评估结果的可靠性。本文的研究不仅有助于识别和预测SCADA系统的安全威胁，保障SCADA系统的安全，而且对风险评估的进一步研究具有重要意义，但是文中的逆向云算法在样本量小的情况下，超熵估计值误差较大，因此，今后的研究工作会对逆向云算法进行改进，提高评价结果的精度。
-
图 1 SCADA系统安全风险评估指标体系
Fig. 1 SCADA system safety risk assessment index system
下载:
全尺寸图片
图 2 标准评估云
Fig. 2 Standard evaluation cloud
下载:
全尺寸图片
图 3 SCADA网络结构图
Fig. 3 SCADA network structure figure
下载:
全尺寸图片
图 4 综合评估云
Fig. 4 Comprehensive evaluation cloud
下载:
全尺寸图片
图 5 指标
${C_{11}}$ 评估云Fig. 5 Index
${C_{11}}$ evaluation cloud下载:
全尺寸图片
图 6 不同赋权方法的结果对比
Fig. 6 Comparison of the results of different weighting methods
下载:
全尺寸图片
表 1 标准评估云计算规则
Table 1 Standard Evaluation Cloud Computing Rules
${\text{Ex}}$值 ${\text{En}}$值 ${\text{He}}$值 ${\text{E}}{{\text{x}}_{\text{1}}} = {B_{\min }}$ ${\text{E} }{ {\text{n} }_1} = \dfrac{ { {\text{E} }{ {\text{n} }_2} } }{ {0.618} }$ ${\text{H} }{ {\text{e} }_1}{\text{ = } }\dfrac{ { {\text{H} }{ {\text{e} }_2} } }{ {0.618} }$ ${\text{E} }{ {\text{x} }_2} = {\text{E} }{ {\text{x} }_3} - \dfrac{ {0.382({B_{\max } } - {B_{\min } })} }{2}$ ${\text{E} }{ {\text{n} }_2} = \dfrac{ {0.382({B_{\max } } - {B_{\min } })} }{6}$ ${\text{H} }{ {\text{e} }_2}{\text{ = } }\dfrac{ { {\text{H} }{ {\text{e} }_3} } }{ {0.618} }$ ${\text{E} }{ {\text{x} }_3} = \dfrac{ { {B_{\max } } + {B_{\min } } } }{2}$ ${\text{E}}{{\text{n}}_3} = 0.618{\text{E}}{{\text{n}}_{\text{4}}}$ ${\text{H}}{{\text{e}}_3}$ ${\text{E} }{ {\text{x} }_{\text{4} } } = {\text{E} }{ {\text{x} }_3}{\text{ + } }\dfrac{ {0.382({B_{\max } } - {B_{\min } })} }{2}$ ${\text{E} }{ {\text{n} }_4} = \dfrac{ {0.382({B_{\max } } - {B_{\min } })} }{6}$ ${\text{H} }{ {\text{e} }_4}{\text{ = } }\dfrac{ { {\text{H} }{ {\text{e} }_3} } }{ {0.618} }$ ${\text{E}}{{\text{x}}_5} = {B_{\max }}$ ${\text{E} }{ {\text{n} }_5}{\text{ = } } \dfrac{ { {\text{E} }{ {\text{n} }_4} } }{ { {\text{0} }{\text{.618} } } }$ ${\text{H} }{ {\text{e} }_5}{\text{ = } }\dfrac{ { {\text{H} }{ {\text{e} }_4} } }{ {0.618} }$ 表 2 各风险评估等级云数字特征
Table 2 Cloud digital characteristics at different risk assessment levels
风险等级 云模型数字特征 低风险 (0,0.104,0.021) 较低风险 (0.31,0.064,0.013) 中风险 (0.5,0.04,0.008) 较高风险 (0.69,0.064,0.013) 高风险 (1,0.104,0.021) 表 3 指标层各指标权重
Table 3 Each index weight in index layer
指标 主观权重 客观权重 组合权重 ${C_{11}}$ 0.005 0.088 0.046 ${C_{12}}$ 0.018 0.055 0.036 ${C_{13}}$ 0.024 0.028 0.026 ${C_{14}}$ 0.034 0.030 0.032 $ {C_{15}} $ 0.008 0.052 0.030 ${C_{21}}$ 0.031 0.078 0.054 ${C_{22}}$ 0.186 0.019 0.102 ${C_{23}}$ 0.042 0.020 0.031 ${C_{24}}$ 0.094 0.032 0.063 $ {C_{25}} $ 0.107 0.031 0.069 $ {C_{26}} $ 0.023 0.048 0.035 $ {C_{31}} $ 0.011 0.021 0.016 ${C_{32}}$ 0.026 0.018 0.022 ${C_{33}}$ 0.086 0.019 0.052 ${C_{34}}$ 0.058 0.033 0.045 $ {C_{35}} $ 0.039 0.156 0.097 续表 3 指标 主观权重 客观权重 组合权重 $ {C_{36}} $ 0.012 0.030 0.021 $ {C_{37}} $ 0.026 0.049 0.037 ${C_{38}}$ 0.016 0.055 0.035 ${C_{41}}$ 0.031 0.029 0.030 ${C_{42}}$ 0.113 0.047 0.080 ${C_{43}}$ 0.014 0.060 0.037 表 4 准则层各指标权重
Table 4 Each index weight in criterion layer
指标 主观权重 客观权重 组合权重 ${B_1}$ 0.089 0.253 0.170 ${B_2}$ 0.483 0.228 0.354 ${B_3}$ 0.274 0.381 0.325 ${B_4}$ 0.158 0.136 0.147 表 5 准则层和指标层各指标云数字特征
Table 5 Each index cloud digital characteristics in the criterion and index layer
准则层 云数字特征 指标层 云数字特征 ${B_1}$ (0.320,0.228,0.075) ${C_{11}}$ (0.191,0.223,0.062) ${C_{12}}$ (0.349,0.266,0.097) ${C_{13}}$ (0.395,0.203,0.025) ${C_{14}}$ (0.441,0.235,0.100) $ {C_{15}} $ (0.291,0.194,0.086) ${B_2}$ (0.429,0.220,0.051) ${C_{21}}$ (0.275,0.275,0.059) ${C_{22}}$ (0.441,0.183,0.034) ${C_{23}}$ (0.454,0.196,0.018) ${C_{24}}$ (0.554,0.344,0.087) $ {C_{25}} $ (0.370,0.194,0.057) $ {C_{26}} $ (0.500,0.127,0.067) ${B_3}$ (0.370,0.252,0.057) $ {C_{31}} $ (0.567,0.279,0.065) ${C_{32}}$ (0.429,0.171,0.036) ${C_{33}}$ (0.592,0.270,0.070) ${C_{34}}$ (0.383,0.213,0.038) $ {C_{35}} $ (0.141,0.236,0.049) $ {C_{36}} $ (0.441,0.235,0.100) $ {C_{37}} $ (0.403,0.296,0.099) ${C_{38}}$ (0.454,0.376,0.069) ${B_4}$ (0.560,0.181,0.045) ${C_{41}}$ (0.559,0.162,0.060) ${C_{42}}$ (0.513,0.148,0.033) ${C_{43}}$ (0.662,0.348,0.093) 表 6 准则层各指标风险状况
Table 6 Each index risk status in the criterion layer
指标 风险状况 ${B_1}$ 较低风险 ${B_2}$ 较低风险 ${B_3}$ 较低风险 ${B_4}$ 较高风险 表 9 不同评估方法结果的比较
Table 9 Comparison of different evaluation methods result
评估方法 对各风险等级隶属度或相似度 评估结果 低 较低 中 较高 高 AHP–模糊综合评价 0.12 0.30 0.33 0.19 0.06 中风险 灰色评估 0.21 0.27 0.24 0.20 0.08 较低风险 熵权–云模型 0.51 0.95 0.89 0.00 0.00 较低风险 组合权重–云模型 0.00 0.11 0.00 0.00 0.00 较低风险 -
[1] 王华忠. 监控与数据采集(SCADA)系统及其应用[M]. 北京: 电子工业出版社, 2010. [2] 陶耀东, 李宁, 曾广圣. 工业控制系统安全综述[J]. 计算机工程与应用, 2016, 52(13): 8–18. doi: 10.3778/j.issn.1002-8331.1602-0207 TAO Yaodong, LI Ning, ZENG Guangsheng. Review of industrial control systems security[J]. Computer engineering and applications, 2016, 52(13): 8–18. doi: 10.3778/j.issn.1002-8331.1602-0207 [3] 王增光, 卢昱, 陈立云. 网络安全风险评估方法综述[J]. 飞航导弹, 2018(4): 62–66,73. WANG Zengguang, LU Yu, CHEN Liyun. Review of cyber security risk assessment method[J]. Aerodynamic missile journal, 2018(4): 62–66,73. [4] 姜莹莹, 曹谢东, 白琳, 等. 基于层次分析法的SCADA系统安全评价[J]. 物联网技术, 2013, 3(12): 71–73,75. doi: 10.3969/j.issn.2095-1302.2013.12.025 JIANG Yingying, CAO Xiedong, BAI Lin, et al. Safety evaluation of SCADA system based on AHP[J]. Internet of Things technologies, 2013, 3(12): 71–73,75. doi: 10.3969/j.issn.2095-1302.2013.12.025 [5] BIAN Nayun, WANG Xiaofeng, MAO Li. Network security situational assessment model based on improved AHP_FCE[C]//2013 Sixth International Conference on Advanced Computational Intelligence (ICACI). Hangzhou: IEEE, 2013: 200−205. [6] MARKOVIC-PETROVIC J D, STOJANOVIC M D, BOSTJANCIC RAKAS S V. A fuzzy AHP approach for security risk assessment in SCADA networks[J]. Advances in electrical and computer engineering, 2019, 19(3): 69–74. doi: 10.4316/AECE.2019.03008 [7] LI Meng, LI Wenjing, YU Peng, et al. Risk prediction of the SCADA communication network based on entropy-gray model[C]//2017 13th International Conference on Network and Service Management (CNSM). Tokyo. IEEE, 2017: 256−261. [8] 万书亭, 万杰, 张成杰. 基于灰色理论和变权模糊综合评判的风电机组性能评估[J]. 太阳能学报, 2015, 36(9): 2285–2291. doi: 10.3969/j.issn.0254-0096.2015.09.037 WAN Shuting, WAN Jie, ZHANG Chengjie. Comprehensive evaluation of wind power unit performance evaluation based on grey theory and variable weight fuzzy mathematics[J]. Acta energiae solaris sinica, 2015, 36(9): 2285–2291. doi: 10.3969/j.issn.0254-0096.2015.09.037 [9] YANG Li, CAO Xiedong, LI Jie. A new cyber security risk evaluation method for oil and gas SCADA based on factor state space[J]. Chaos, solitons & fractals, 2016, 89: 203–209. [10] YANG Li, CAO Xiedong, GENG Xinyu. A novel intelligent assessment method for SCADA information security risk based on causality analysis[J]. Cluster computing, 2019, 22(3): 5491–5503. [11] 李德毅, 杜鹢. 不确定性人工智能[M]. 北京: 国防工业出版社, 2005. [12] 陈圆超, 戴剑勇, 谢东. 矿井通风系统的组合赋权云模型综合评价[J]. 系统工程, 2020, 38(6): 35–42. CHEN Yuanchao, DAI Jianyong, XIE Dong. Comprehensive evaluation of mine ventilation system based on combination weighting cloud model[J]. Systems engineering, 2020, 38(6): 35–42. [13] 张仕斌, 许春香. 基于云模型的信任评估方法研究[J]. 计算机学报, 2013, 36(2): 422–431. ZHANG Shibin, XU Chunxiang. Study on the trust evaluation approach based on cloud model[J]. Chinese journal of computers, 2013, 36(2): 422–431. [14] 刘常昱, 冯芒, 戴晓军, 等. 基于云X信息的逆向云新算法[J]. 系统仿真学报, 2004, 16(11): 2417–2420. doi: 10.3969/j.issn.1004-731X.2004.11.013 LIU Changyu, FENG Mang, DAI Xiaojun, et al. A new algorithm of backward cloud[J]. Acta simulata systematica sinica, 2004, 16(11): 2417–2420. doi: 10.3969/j.issn.1004-731X.2004.11.013 [15] 陈昊, 李兵, 刘常昱. 一种无确定度的逆向云算法[J]. 小型微型计算机系统, 2015, 36(3): 544–549. doi: 10.3969/j.issn.1000-1220.2015.03.027 CHEN Hao, LI Bing, LIU Changyu. An algorithm of backward cloud without certainty degree[J]. Journal of Chinese computer systems, 2015, 36(3): 544–549. doi: 10.3969/j.issn.1000-1220.2015.03.027 [16] 邸凯昌. 空间数据发掘与知识发现[M]. 武汉: 武汉大学出版社, 2000. [17] GENG Xinyu, YE Jinchi, XIA Zhen, et al. An improved algorithm of nearness degree of incidence based on grey neural network[J]. IEEE access, 2020, 8: 207044–207053. doi: 10.1109/ACCESS.2020.3038162 [18] 龚艳冰, 蒋亚东, 梁雪春. 基于模糊贴近度的正态云模型相似度度量[J]. 系统工程, 2015, 33(9): 133–137. GONG Yanbing, JIANG Yadong, LIANG Xuechun. Similarity measurement for normal cloud models based on fuzzy similarity measure[J]. Systems engineering, 2015, 33(9): 133–137. [19] KULLBACK S, LEIBLER R A. On information and sufficiency[J]. The annals of mathematical statistics, 1951, 22(1): 79–86. doi: 10.1214/aoms/1177729694 [20] BUDKA M, GABRYS B, MUSIAL K. On accuracy of PDF divergence estimators and their applicability to representative data sampling[J]. Entropy, 2011, 13(7): 1229–1266. doi: 10.3390/e13071229 [21] 许昌林, 王国胤. 正态云概念的漂移性度量及分析[J]. 计算机科学, 2014, 41(7): 9–14,51. doi: 10.11896/j.issn.1002-137X.2014.07.002 XU Changlin, WANG Guoyin. Excursive measurement and analysis of normal cloud concept[J]. Computer science, 2014, 41(7): 9–14,51. doi: 10.11896/j.issn.1002-137X.2014.07.002 [22] 张光卫, 李德毅, 李鹏, 等. 基于云模型的协同过滤推荐算法[J]. 软件学报, 2007, 18(10): 2403–2411. doi: 10.1360/jos182403 ZHANG Guangwei, LI Deyi, LI Peng, et al. A collaborative filtering recommendation algorithm based on cloud model[J]. Journal of software, 2007, 18(10): 2403–2411. doi: 10.1360/jos182403 [23] 李海林, 郭崇慧, 邱望仁. 正态云模型相似度计算方法[J]. 电子学报, 2011, 39(11): 2561–2567. LI Hailin, GUO Chonghui, QIU Wangren. Similarity measurement between normal cloud models[J]. Acta electronica sinica, 2011, 39(11): 2561–2567. [24] 张勇, 赵东宁, 李德毅. 相似云及其度量分析方法[J]. 信息与控制, 2004, 33(2): 129–132. doi: 10.3969/j.issn.1002-0411.2004.02.001 ZHANG Yong, ZHAO Dongning, LI Deyi. The similar cloud and the measurement method[J]. Information and control, 2004, 33(2): 129–132. doi: 10.3969/j.issn.1002-0411.2004.02.001 [25] 贾驰千, 冯冬芹. 基于模糊层次分析法的工控系统安全评估[J]. 浙江大学学报(工学版), 2016, 50(4): 759–765. doi: 10.3785/j.issn.1008-973X.2016.04.022 JIA Chiqian, FENG Dongqin. Security assessment for industrial control systems based on fuzzy analytic hierarchy process[J]. Journal of Zhejiang university (engineering science edition), 2016, 50(4): 759–765. doi: 10.3785/j.issn.1008-973X.2016.04.022 [26] 谷倩倩, 丁松滨. 基于综合集成赋权法的航空公司飞行安全风险灰色评估[J]. 交通信息与安全, 2017, 35(6): 38–45. doi: 10.3963/j.issn.1674-4861.2017.06.006 GU Qianqian, DING Songbin. A gray evaluation method of flight safety risk based on comprehensive integration weight method[J]. Journal of transport information and safety, 2017, 35(6): 38–45. doi: 10.3963/j.issn.1674-4861.2017.06.006 [27] 赵辉, 王玥, 张旭东, 等. 基于云模型的特色小镇PPP项目融资风险评价[J]. 土木工程与管理学报, 2019, 36(4): 81–88. doi: 10.3969/j.issn.2095-0985.2019.04.013 ZHAO Hui, WANG Yue, ZHANG Xudong, et al. Financing risk evaluation of featured town PPP project based on cloud model[J]. Journal of civil engineering and management, 2019, 36(4): 81–88. doi: 10.3969/j.issn.2095-0985.2019.04.013
