Emotional EEG signal recognition method using multi-path graph attention network
-
摘要: 情绪是一种大脑产生的主观认知的概括。脑信号解码技术可以以一种较客观的方式来有效地研究人的情绪及其相关认知行为。本文提出了一种基于图注意力网络的脑电情绪识别方法(multi-path graph attention networks, MPGAT)，该方法通过对脑电信号通道建图，利用卷积层提取脑电信号的时域特征以及各频带的特征，使用图注意力网络进一步捕捉情绪脑电信号的局部特征以及各脑区之间的内在功能关系，进而构建出更好的脑电信号表征。MPGAT在SEED和SEED-IV数据集的跨被试情绪识别平均准确率分别为86.03%、72.71%，在DREAMER数据集的效价(valence)和唤醒(arousal)维度的跨被试平均准确率分别为76.35%和75.46%，达到并部分超过了目前最先进脑电情绪识别方法的性能。本文所提出的脑电信号处理方法有望为情绪认知科学研究与情绪脑机接口系统提供新的技术手段。Abstract: Emotion is a generalization of subjective cognition produced by the brain. Brain signal decoding technology can effectively study human emotions and related cognitive behaviors more objectively. This paper proposes a multi-path graph attention networks (MPGAT) method for electroencephalogram (EEG) emotion recognition based on graph attention networks. This method uses convolutional layers to extract the time domain features of EEG signals and the features of each frequency band by mapping EEG signal channels; moreover, it uses the graph attention network to further capture the local features of emotional EEG signals and the internal functional relationships among the brain regions; constructing a better representation of EEG signals later. The average accuracy of MPGAT’s cross-subject emotion recognition in the SEED and SEED-IV datasets were 86.03% and 72.71%, respectively, and the average cross-subject accuracy rates of the valence and arousal dimensions in the DREAMER dataset were 76.35% and 75.46%, respectively, meeting and partially exceeding the performance of the most advanced EEG emotion recognition methods. The EEG signal processing method proposed in this paper can provide novel technical means for the scientific research of emotional cognition and emotional brain-computer interface system.
-
人对客观世界事物的感情态度和相应的行为反应被称为情绪[1]。近年来，基于生理信号的情绪识别研究受到了广泛关注。人在情绪体验中即时反应所产生的生理信号具有实时性、客观性、难以伪装等特点，因此使用生理信号进行情绪识别能够得到相对客观真实的结果[2]。常用于情绪分析的生理信号有脑电(electroencephalogram, EEG)、心电(electrocardiogram, ECG)、肌电(electromyography, EMG) 和皮肤温度(skin temperature, SKT) 等[3]。大量神经元同步发生的电位之和称为脑电信号，脑电信号是大量脑神经细胞的电生理活动在头皮上的汇总，常使用非侵入式电极对头皮脑电信号进行采集[4]。脑电信号包含了大量的生理信息，可以准确地表征大脑的神经活动，利用脑电信号研究情绪特征能够获得更多神经活动信息，提高情绪识别的准确率[5]。
以往的研究表明，大脑皮层有两个区域与情感活动密切相关，即杏仁核（位置靠近海马体，在颞叶的前部）和额叶前皮层（覆盖额叶的一部分）。在情绪体验期间，大脑皮层的某个特定部位通常会被激活，同时整个脑区也会呈现出全局特征，例如杏仁核的激活与消极情绪有关，右额叶的激活与负面情绪有关[6]。不同脑区的神经活动在情绪体验期间具有内在的联系，而脑电极测得的脑电信号也能体现出不同脑区的某种内在联系。
情绪脑电的分类过程包括特征提取和分类两个阶段。脑电信号是一种高动态、非线性的数据，原始的脑电数据量大且具有冗余性，因此提取脑电数据的特征是至关重要的。脑电信号的特征分析方法主要分为时域方法、频域方法、时频分析、非线性动力学分析等[7]。其中，被广泛使用的脑电信号的频域特征分析方法之一是将EEG信号分解为几个频带如delta频带(1~3 Hz)、theta频带(4~7 Hz)、alpha频带(8~13 Hz)、beta频带(14~30 Hz)和gamma频带(>31 Hz)。Li等[8]发现使用gamma频带上的特征进行情绪脑电分类时有更高的准确率。另外，脑电信号的非线性特征分析也是一种主流的研究方法。常用的脑电信号非线性特征有转移熵(symbolic transfer entropy)、排列熵(permutation entropy)、微分熵(differential entropy，DE)等。熵是描述信号不确定性的参数，值越大信号的不确定性越高。Duan等[9]发现在情绪脑电分类任务中使用微分熵特征的分类效果比使用其他特征的分类效果更加好，相较于传统特征如能量谱 (energy spectrum，ES)，使用微分熵的效果准确性更高，稳定性更好。
情绪脑电信号很微弱容易受到外界干扰，为了有效分析脑电信号，提出了许多基于机器学习的脑电信号分析方法[4]。深度学习是机器学习的一个分支，因为其具有强大的数据表征学习能力，研究人员开始把它应用到了脑电情绪分类任务中，用来解码复杂的情绪脑电。Alhagry等[10]利用长短期记忆网络(long short-term memory, LSTM)对情绪脑电信号进行分类，在DEAP数据集上取得87.99%的准确率。为了消除脑电信号的个体差异，Li等[11]使用了一种深度自适应网络(domain adaptation networks, DAN)，通过调整深度网络结构提高迁移特征的能力，并将其应用于SEED和SEED-IV数据集上的情绪识别任务，能够很好地处理跨被试情绪识别任务。Li等[12]提出一种BiHDM (bi-hemispheric discrepancy)模型，这个模型将脑电通道分为左半脑和右半脑，分别训练网络，结果证明了将非对称差分信息纳入脑电情绪识别的有效性。Liu等[13]将眼动信号和EEG脑电信号特征融合在一起，提出了一种多模态的情绪脑电识别网络(bimodal deep autoencoder, BDAE)，在SEED数据集上达到91.01%的准确率。
深度学习方法中的卷积神经网络(convolutional neural network，CNN)具有强大的建模能力，成功应用于自然语言处理、图像识别、时间序列预测等领域。卷积神经网络适合处理欧氏数据(Euclidean structure data)，不能有效地处理非欧氏数据(non-Euclidean structure data)，数据见文献[14]。脑电信号通道分布排列不均匀，不满足平移不变性，即每个通道节点都具有不相同的局部结构，适合使用图数据表示。同时，因为情绪脑电通道之间具有一定的联系，而卷积神经网络无法捕捉脑电通道之间的依赖关系，因此在脑电信号情绪识别任务中表现不佳。图神经网络在处理图数据方面取得了令人瞩目的成果，越来越多研究人员投入到图神经网络的研究中。近期的研究表明，图神经网络适用于脑电情绪识别任务，其性能达到或超过了其他类型的方法[15]。为了探索脑电数据的图结构中更深层信息，Zhang等[16]提出了一种名为GCB-net (graph convolutional broad network)的网络模型，并在SEED和DREAMER数据集上取得了较高准确率。Zhong等[17]为了捕获本地和全局通道间关系，提出了正则化图神经网络(regularized graph neural network, RGNN)，该网络可以捕获通道间的局部和全局联系，同时减少噪音的干扰，从而提高了情绪脑信号识别的鲁棒性。Song等[18]提出了一种用于情感识别的动态图卷积神经网络(dynamical graph convolutional neural network, DGCNN)，对EEG信号通道建图，网络可以动态地改变图的拓扑结构，挖掘出EEG电极通道间的功能联系。目前，大多数情绪识别研究利用卷积神经网络提取脑电信号的特征，使用图神经网络的研究较少。同时，以往的研究一般利用神经科学的结论选择特定的通道进行分析，而对情绪脑电通道间的联系性还没有深入研究，这导致无法更好地识别脑电通道的信号模式，因此分析脑电通道之间的联系是必要的。
针对以上研究现状及挑战，本文提出一种基于图注意力网络的脑电情绪识别方法，此方法将脑电信号建模为图数据并结合到图神经网络中，能够学习各脑电通道之间的相关性[19]。本文在3个数据集（SEED、SEED-IV和DREAMER）中进行本方法的验证实验，结果显示本方法的识别准确率较高、稳定性较好。本文的主要工作和贡献有：
1）所提出的MPGAT在跨被试情绪脑电信号分类任务上表现优秀，在SEED、SEEDIV和DREAMER数据集上测试结果表明，MPGAT达到当前最先进模型的性能水平；
2）MPGAT利用多通路结构来提取脑电信号的多尺度时频特征，进而实现多通路多尺度脑电信号特征融合[20]；
3）同时运用了图注意力机制来捕捉不同对象的情绪脑电信号的时空域特征，实现跨被试情绪识别。
1. 图注意力网络方法
1.1 脑电特征图构建方法
目前，脑电采集方法通常是将若干个脑电极固定在人头部或大脑皮层的相应位置，由脑电极测量大脑皮层神经活动引起的电压变化。脑电极的分布位置是由一些标准规定的，比如国际10/20系统[6]。脑电极的分布位置是固定的且有一定的规律，所以脑电信号可以被视为一种经典的非欧氏结构化数据，非常适合用图数据来表示：
$$ \begin{aligned} &\quad\quad\quad \mathcal{G} = (\mathcal{V},\varepsilon ) \hfill \\ &\mathcal{V} = \left\{ {{v_i}\mid i = 1,2, \cdots ,N} \right\} \hfill \\ &\quad\mathcal{E} = \left\{ {{e_{ij}}\mid {v_i},{v_j} \in \mathcal{V}} \right\} \hfill \\ \end{aligned} $$ 式中：
$\mathcal{V}$ 代表图$\mathcal{G}$ 的节点（总共有N个节点）；$\mathcal{E}$ 是图$\mathcal{G}$ 的无向边边集。脑电信号的图表示方法中，往往用一个节点代表一个EEG电极，根据脑电节点的位置由K-近邻算法(KNN)生成边集$\mathcal{E}$ ，从而可以将脑电信号表示为一个无向图。1.2 图注意力网络方法
根据以往的研究，图卷积神经网络分为谱方法和空间方法。谱方法利用卷积定理，使信号映射到谱空间,克服了非欧氏数据缺失平移不变性特点；空间方法是直接在图数据上进行操作，通过聚合邻居节点的信息达到卷积效果。
图注意力网络（graph attention networks, GAT）是一种基于注意力机制来进行图结构数据分类的网络，属于图卷积神经网络的空间方法，其基本思想是利用自注意力策略，通过聚合邻居点的信息来计算每个图节点在图数据的隐藏表征，并利用注意力机制定义信息融合函数[21]。与其他图网络不同的是，图注意力网络是通过节点的特征表达来计算关联权重，而不是根据边的信息计算权重。
图注意力网络的输入是一系列节点的特征向量，可表示为
${\boldsymbol{H}} = \left\{ {{{\boldsymbol h}_1},{\boldsymbol h_2}, \cdots ,{\boldsymbol h_N}} \right\},{\boldsymbol h_i} \in {{\bf{R}}^{N \times F}}$ ，其中$N$ 是节点数量，F是特征维数。图注意力网络使用了一种自注意力机制$a$ 来计算输入特征向量的注意力系数，并进行归一化，具体如式(1)、(2)。$$ {e_{ij}} = a\left( {{\boldsymbol{Wh}}_{i},{\boldsymbol{Wh}}_{j}} \right) $$ (1) $$ {\alpha _{ij}} = {{\rm{softmax}} _j}\left( {{e_{ij}}} \right) = \dfrac{{\exp \left( {{e_{ij}}} \right)}}{{\displaystyle\sum\limits_{k \in {\mathcal{N}_i}} {\exp } \left( {{e_{ik}}} \right)}} $$ (2) 式中：
${e_{ij}}$ 是节点$i$ 与节点$j$ 之间的注意力权重；${\alpha _{ij}}$ 是归一化后的注意力权重，表示$ 节点j $ 对$ 节点i $ 的重要程度；$\boldsymbol h$ 是特征向量；$\boldsymbol W$ 是权重矩阵。由式(1)、(2)可得，图注意力网络计算节点
$i$ 的一阶邻居节点的注意力系数，注意力权重和表达式为$$ {\alpha }_{ij}=\dfrac{{\rm{exp}}\left({{L}}\left({\boldsymbol{a}}^{{\rm T}}\left[{\boldsymbol{Wh}}_{{i}}\Vert {\boldsymbol{Wh}}_{{j}}\right]\right)\right)}{{\displaystyle\sum _{k\in {\mathcal{N}}_{i}}{\rm{exp}}}\left({{L}}\left({\boldsymbol{h}}^{\rm T}\left[{\boldsymbol{Wh}}_{{i}}\Vert {\boldsymbol{Wh}}_{{k}}\right]\right)\right)} $$ (3) 式中：
${{\boldsymbol a}^{\rm{T}}}$ 代表注意力权重向量的转置；${ L} \left( \cdot \right)$ 表示LeakyReLU激活函数。为了使网络获得更多信息，图注意力网络使用了一种多头机制，使得每个头捕获不同的信息，最后将多头的信息通过一个线性层融合在一起，注意力系数与对应的特征向量组合起来，计算每个节点的最终输出特征：$$ {\boldsymbol h}_i^\prime = \sigma \left( {\dfrac{1}{K}\displaystyle\sum\limits_{k = 1}^K {\displaystyle\sum\limits_{j \in {\mathcal{N}_i}} {\alpha _{ij}^k} } {{\boldsymbol W}^{k}}{{\boldsymbol h}_{j}}} \right) $$ (4) 式中：
$\boldsymbol W$ 是线性层的权重矩阵；$\sigma $ 是非线性激活函数；${\boldsymbol{h}}_i'$ 是图注意力网络最终输出网络。图注意力网络通过注意力机制，分配不同权重给节点，有效地提高了网络的表征能力。同时，图注意力网络运行非常高效，计算复杂度为
$O\left( {\left| V \right|FF' + \left| E \right|F'} \right)$ 。$F$ 是输入向量的维度，$\left| V \right|$ 是节点数量，$\left| E \right|$ 是边数量。在情绪体验期间，大脑的特定部位被激活，呈现出局部特征。研究表明，不同大脑脑区具有联系性。图网络能够发掘出不同脑电通道之间的联系性，注意力机制给予节点不同的权重，赋予了网络更好的表征性能。图注意力网络应用到脑电信号上，能够得到更能表现情感特征的脑电信号表征，从而得到更好的分类效果。
1.3 MPGAT情绪识别模型
本文提出了一种基于图注意力网络的跨被试情绪脑电识别模型。本文的模型MPGAT具有多个通路，目的是运用多通路来提取多个尺度的时频特征和通道联系。每个通路首先对EEG信号进行卷积池化，这是为了提取单个EEG通道内特征信号的时频域特征。而不同的通路由拥有不同的卷积核的卷积层和池化层提取EEG信号的全局或局部的时频特征，这样可以挖掘出EEG信号在不同尺度的特征数据。通路对EEG信号进行卷积池化后，再利用图网络去提取通道间的联系信息，即情绪体验期间多个EEG脑电极之间采集到信号之间的全局或局部联系信息，获取不同脑区之间相干程度信息，从而得到更精细、更准确的情绪脑电识别模型。MPGAT网络的总体结构分为3个路径，每个路径的组成为卷积池化模块、图注意力网络层、全连接层和输出层，如图1所示。每个卷积池化模块包括不同大小卷积核的二维卷积和最大值池化。该模型首先使用二维卷积和最大值池化对脑电特征数据进行降采样和特征提取，将卷积池化的输出矩阵进行形状重塑成一个一维特征向量，再将这个特征向量与EEG电极图相结合，输入图注意力网络。将3个图注意力网络的输出拼接在一起输入一个全连接层，得到情绪预测结果。
图 1 MPGAT模型框架图Fig. 1 Framework of MPGAT model
下载:
全尺寸图片
1.3.1 卷积池化模块
MPGAT第一层由3个卷积池化模块组成，卷积池化模块只针对单一EEG通道，其目的是取单个脑电信号通道内5个频带之间的时频特征，形式是一个形状为5×T的二维矩阵，T为EEG特征信号长度。具体而言，就是将EEG特征图数据复制为3份，同时输入到3个卷积池化模块中。其中，模块主要由二维卷积和最大值池化组成。1×1卷积核的作用是增加脑电信号的维度。不同的通路使用了不同大小的卷积核和下采样层，小卷积核能提取邻接频带的关联信息，即提取频带间的局部时频特征。而大卷积核对全部5个频带卷积获取全局特征，通过不同通路的卷积池化操作，使得不同通路具有不同的感受野。卷积池化操作后使用非线性激活函数为网络增加非线性特性，可以概括为
$${\boldsymbol{z}} = \sigma \left( {{{\boldsymbol{w}}_k}*{\boldsymbol{x}} + {{\boldsymbol{b}}_k}} \right) $$ (5) 式中：
${\boldsymbol{x}}$ 和$\boldsymbol z$ 分别是输入和输出特征矩阵；${\text{*}}$ 代表卷积运算；${{\boldsymbol{w}}_k}$ 是某个卷积层的权重矩阵；${{\boldsymbol{b}}_k}$ 是偏置参数；$\sigma $ 表示非线性激活函数。在卷积池化模块中，激活函数主要使用ReLU函数：
$$ {R} (x) = \left\{ {\begin{aligned} &{x,\quad x > 0} \\ &{0,\quad x \leqslant 0} \end{aligned}} \right. $$ (6) 式中：R(·)代表ReLU函数。
由于每个被试的脑电数据分布相差较大，网络需要适应不同的数据分布，导致网络训练速度下降和出现过拟合现象。为了解决这个问题，在卷积之后和使用ReLU激活函数之前增加一个批量归一化层(batch normalization, BN)。在使用ReLU激活函数之后，增加dropout层，目的是进一步防止过拟合现象以及提高网络的泛化能力。
1.3.2 图注意力层
图注意力网络可以学习多通道间的依赖关系，且不改变脑电特征图的结构。本模型的图网络层包括3个平行的模块，每个模块有两层图注意力网络。图网络的输入是一维特征向量，因此需要把卷积池化模块的二维矩阵输出重塑为一维特征向量。为了尽可能地学习脑电通道间的依赖关系，需要把卷积池化模块的二维矩阵输出重塑为一维特征向量。
1.3.3 全连接线性层
将图注意力网络的输出特征
${h_k}$ 拼接在一起，就得到了全连接层的输入向量$\boldsymbol z$ ：$$ {\boldsymbol{z}} = C\left( {{{\boldsymbol h}_{1}},{{\boldsymbol h}_{2}},{{\boldsymbol h}_3}} \right) $$ (7) 式中：C表示向量拼接函数。
全连接层后使用LogSoftMax函数得出最后的情绪脑电预测结果，
$\boldsymbol w$ 和$\boldsymbol b$ 表示权重矩阵和偏置项：$$ P = L({\boldsymbol{wz}} + {\boldsymbol{b}}) $$ (8) $$ L\left( {{x_i}} \right) = \log \left( {\dfrac{{\exp \left( {{x_i}} \right)}}{{\displaystyle\sum\limits_j {\exp } \left( {{x_j}} \right)}}} \right) $$ (9) 式中：
$ P $ 代表预测结果；$ L( \cdot ) $ 代表LogSoftmax函数。2. 实验设计
2.1 数据集
SEED数据集是上海交通大学BCMI实验室采集的情绪脑电数据集，全称为“SJTU Emotion EEG Dataset”。数据集中总共包含15位受试者针对15个实验的62通道脑电信号。研究人员准备了15个时长为4 min左右的电影片段，这些电影片段被分为3个类别，分别是消极、中性和积极。积极类型的影片是喜剧，观看时会激发被试者的快乐等积极情绪；而消极类型的影片是天灾人祸类型的悲剧电影，会令被试者激发悲伤等消极情绪；中性电影是世界遗产纪录片，不会激发被试的积极或者消极情感。受试者被要求观看这些电影片段，在每个片段播放完毕后，受试者有45 s的时间进行自我评价和心情平复。
SEED数据集所提供的脑电数据为62通道的脑电数据，每个被试者都会进行3轮试验，每次试验相隔1~2周时间，整个数据集共包括45次试验的数据。每个试验的数据都进行了预处理，原始数据被降采样为200 Hz，且经带通滤波器处理后保留0~75 Hz的数据。
SEED-IV数据集同样是BCMI实验室采集的情绪脑电数据集。与SEED数据集不同的是，研究人员准备了72个电影片段，分为4个类别，分别是开心、伤心、恐惧和中性。每个被试者接受了3次实验，每次观看24个电影片段。试验期间，被试者的脑电信号和眼动信号分别被62通道的ESI NeuroScan系统和SMI记录仪记录。
DREAMER数据集是一个常用的情绪识别数据集。研究人员让被试者观看剪辑过的电影片段，以诱发被试者的情绪，并使用14通道的脑电采集设备记录EEG数据。每段影片播放完毕后，研究人员根据被试者的评价使用效价、唤醒、支配3个维度对情绪进行分类。数据集包含了快乐、兴奋、幸福、平静、愤怒、厌恶、恐惧、悲伤和惊讶9种情绪诱发影片各2段，一共18个电影片段。
对于SEED和SEED-IV数据集，脑电数据的微分熵特征通过短时傅里叶变换和不重叠的汉明窗口（为1 s）计算得出，并在5个频段中求平均值。微分熵的公式为
$$ h(X) = - \int_\mathcal{S} f (x)\log f(x){\text{d}}x $$ (10) 为了简化计算，假设脑电信号遵循高斯分布为
$x \sim N\left( {\mu ,{\sigma ^2}} \right)$ ，微分熵的计算可以简化为$$ h(X) = \frac{1}{2}\ln 2{\text{π e}}{\sigma ^2} $$ (11) 在DREAMER数据集中，本文使用1~75 Hz带通滤波器来减少EEG信号的噪具体地。具体地，通过使用短期傅里叶变换（short-time Fourier transform, STFT）从EEG信号中获得theta频带(4~7 Hz)、alpha频带(8~13 Hz)、beta频带(14~30 Hz)和gamma频带(>31 Hz)。特征提取方面，本文假设脑电信号遵循高斯分布，根据式(11)、(12)可以得到DREAMER数据集的微分熵特征。
2.2 实验环境和参数设置
本文实验的软硬件环境为：Ubuntu 18.04操作系统，模型搭建框架为Pytorch 1.7.0和Pytorch-geometric 1.7.0，使用一张2080TI显卡加速训练任务，CUDA版本为11.2，内存64 GB，显存11 GB。
本文使用交叉验证方法评估本文提出的方法，具体方法是使用其中一个被试者的脑电数据作为测试集，其他被试者的脑电数据作为训练集。因为SEED和SEED-IV的被试数量同样是15，模型训练分别在SEED和SEED-IV上进行15次，每一次的测试集数据为其中一个被试者的脑电数据，保证每个被试者的数据都参与了测试集，而在DREAMER数据集上被试者数量为23，同样使用留一法进行交叉验证实验。本文实验利用了SEED和SEED-IV数据集中的预处理特征数据进行情绪识别实验，而在DREAMER数据集上使用微分熵特征进行实验。本文的实验采用了Adam优化器加速模型的训练过程[22]，batch size为16，学习率为0.00001。同时，使用Dropout算法抑制模型的过拟合现象。在训练过程中，训练集的评价指标为AUC参数达到0.999以上时停止训练。
3. 实验结果与讨论
3.1 实验结果对比
表1给出了在SEED数据集和SEED-IV数据集中，本文使用的MPGAT和其他论文模型的平均准确率和标准差。其中，传统机器学习方法可以被运用在情绪分类任务上，Collobert等[23]提出了支持向量机(supported vector machine, SVM)和转导支持向量机T-SVM；Pan等[24]提出迁移成分分析(transfer component analysis, TCA)。深度学习方法也被运用在情绪分类中，类似的研究有：Song等[18]使用动态图卷积神经网络，能够动态改变图信号，获得更佳的表征；Li等[11]使用深度适应网络进行跨被试情绪识别；Li等[12]为了模拟两个半球脑电信号之间的不对称差异，提出了一种新颖的双半球差异模型（BiHDM）用于脑电情绪识别。
表 1 不同模型在SEED和SEED-IV数据集上的平均准确率和标准差Table 1 Average accuracy and standard deviation of different models on the SEED and SEED-IV datasets% 作为对比，本文使用GCN[24]、GAT[21]与MPGAT在SEED和SEED-IV数据集上进行了实验。从表1中可得，本文提出的MPGAT在SEED数据集上平均准确率为86.03%，方差为7.40，在SEED-IV数据集上平均准确率为72.71%，方差为4.38。同时，在SEED数据集中，GCN的平均准确率比MPGAT低1.08%，GAT的平均准确率比MPGAT低0.45%。在SEEDIV数据集中，MPGAT的平均准确率比GAT和GCN分别高2.38%和0.38%。MPGAT在SEED和SEEDIV数据集上的标准差在所有模型中较低，说明MPGAT在执行情绪识别任务上具有良好的稳定性。
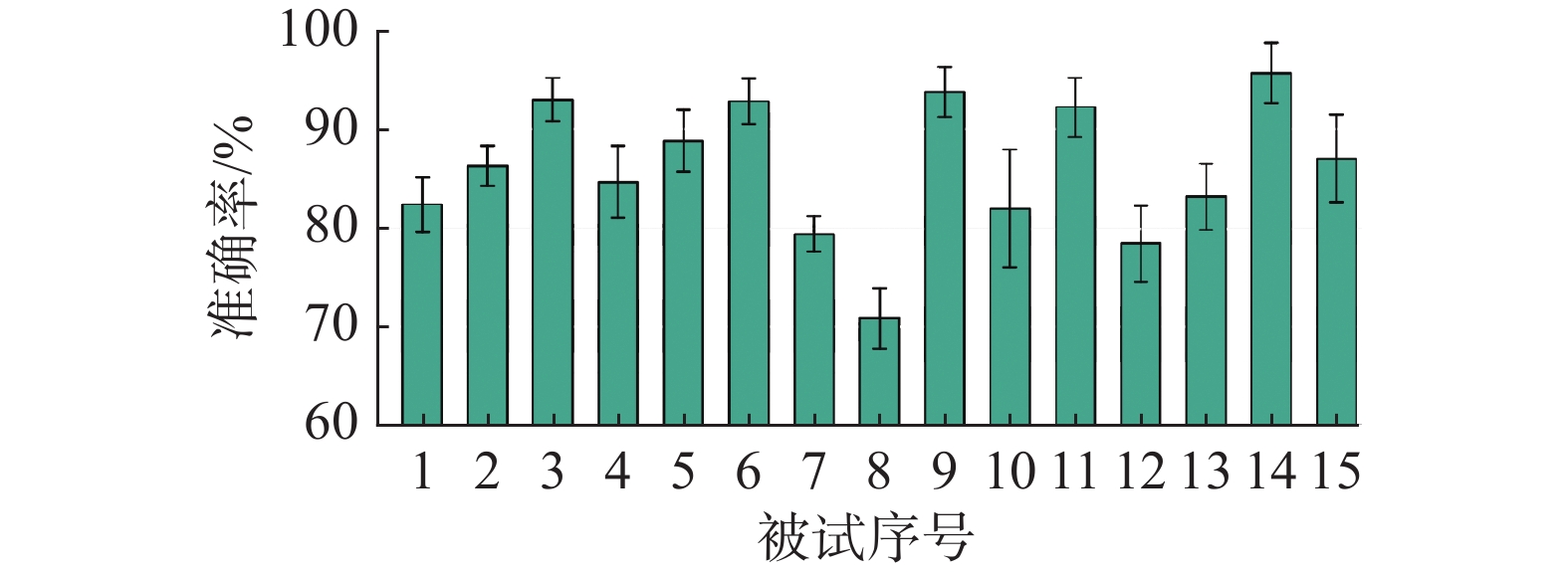
为了验证MPGAT的稳定性，本文利用交叉验证法进行了30次跨被试者情绪分类实验。如图2所示，由于不同被试者个体之间的情绪脑电差异较大，导致跨被试情绪识别结果准确率波动较大。从图2可以得出，被试序号3、6、9、11、14的平均准确率显著高于总平均准确率，而被试序号7、8、12的平均准确率低于80%。总体来说，MPGAT的情绪识别平均准确率达到了最先进模型的准确率，由此证明本文提出的基于图注意力网络的情绪识别方法是有效的。
图 2 MPGAT模型对于SEED数据集每个被试的实验结果Fig. 2 Experimental results of the MPGAT model for each subject in the SEED dataset下载:
全尺寸图片
表2给出了在DREAMER数据集上MPG
AT和其他论文模型的平均准确率和标准差。其中，Zheng等[26]使用SVM和深度信念网络（deep belief networks，DBN）进行情绪分类任务。SVM和DBN模型的效价与唤醒的平均准确率分别为56.57%和58.91%，56.43%和58.94%。实验结果表明，MPGAT在DREAMER数据集上的效价与唤醒的平均准确率分别为76.35%、75.46%，在唤醒维度上是所有模型最高的。因此，MPGAT在DREAMER数据集上具有良好的识别表现，同时也进一步验证了MPGAT的先进性和可行性。 表 2 不同模型在DREAMER数据集上的平均准确率和标准差Table 2 Average accuracy and standard of different models on the DREAMER datasets% 3.2 MPGAT各通路对实验结果的影响
MPGAT的特点是具有多条通路提取EEG特征信号的信息，不同通路的卷积池化模块具有不同的卷积核。为了验证通路对实验结果的影响，本文在SEED数据集进行了消融实验。3个通路中缺失通路一时准确率为85.42%，缺失通路二时准确率为85.36%，缺失通路三时准确率为85.67%，分别低于具有3个通路的MPGAT模型0.61%、0.67%、0.36%。这就表明，3个通路能够多尺度地获取信息，把3个通路的输出拼接起来，再通过线性层，能够对情绪识别任务的准确率产生增益。
3.3 不同特征对实验结果的影响
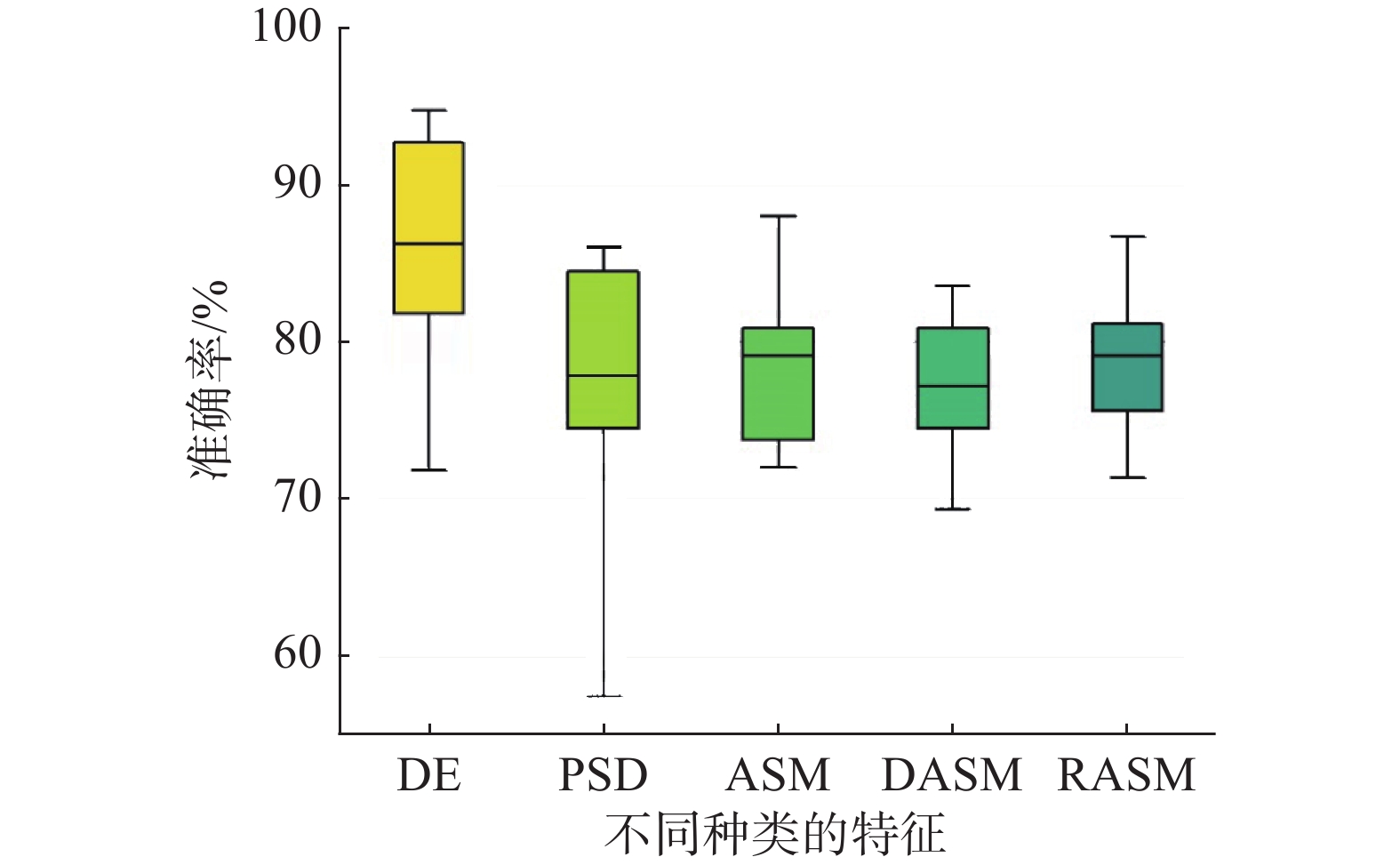
原始情绪脑电是非平稳、非线性的随机信号，数据量冗余较大，且信噪比较低，而脑电信号特征参数如功率谱密度(power spectral density, PSD)、微分熵等更能代表脑电信号在某些方面的突出特征，因此情绪分类任务一般使用脑电信号的特征进行分类。以往的研究表明，使用不同特征会对情绪识别结果产生显著影响。如图3所示，RASM(rational asymmetry)和DASM(differential asymmetry)是由DE特征计算得出的，旨在表达不对称性[9]：
$$ D = h\left( {{\boldsymbol{X}}_i^l} \right) - h\left( {{\boldsymbol{X}}_i^{\text{r}}} \right) $$ (12) $$ R = \frac{{h\left( {{\boldsymbol{X}}_i^l} \right)}}{{h\left( {{\boldsymbol{X}}_i^{\text{r}}} \right)}} $$ (13) 式中：D代表DASM；R代表RASM。
图 3 MPGAT在SEED数据集不同特征的实验结果Fig. 3 Experimental results of different features of the MPGAT in the SEED dataset下载:
全尺寸图片
本文在SEED数据集上分别使用DE、PSD、ASM、DASM以及RASM特征进行跨被试情绪识别任务，结果显示DE的分类结果显著优于其他特征，与以往的研究基本一致。另外，PSD、ASM、DASM、RASM特征的平均准确率分别为77.56%、8.43%、77.33%、78.49%，均低于微分熵DE特征。
3.4 图连通性对结果的影响与脑电地形图分析
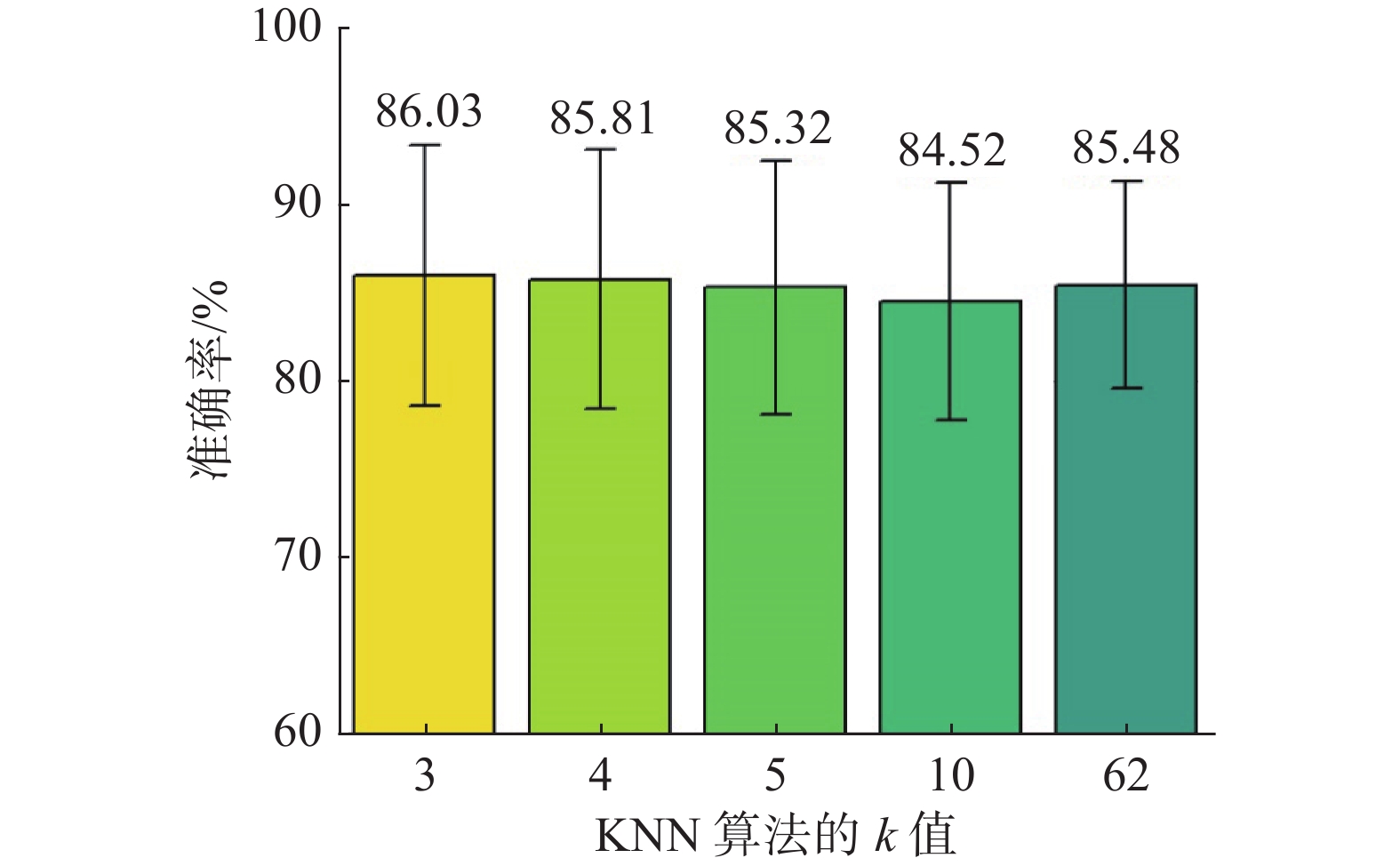
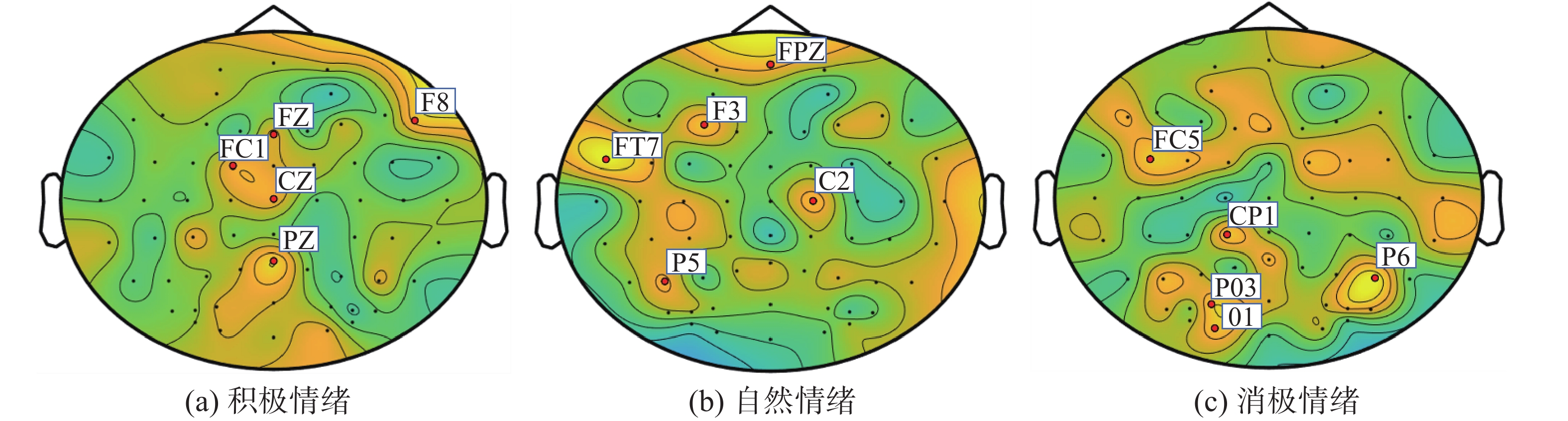
本文提出的EEG建图算法能够利用不同EEG电极的情绪脑电数据的联系。EEG图的连通性也会对模型准确率产生一定的影响，而本文利用k近邻算法作为对EEG电极建模的算法。如图4所示，针对k近邻算法的不同k值对模型的影响进行了实验。其中，k值为3时模型准确率达到最高为86.03%，k值为4、5、10的准确率分别为85.81%、85.32%、84.52%，平均准确率随着k值的增大而减小。由此可知，图连通性越大，准确率并不会相应提高，反而图注意网络的情绪脑电表征能力会得到削弱。当k=62时，因为电极数为62，此时EEG图为全连接图，每个节点都可以获取其他所有节点的信息，但是此时准确率比k值为3时的准确率低0.55%。图5是模型训练结束后特征可视化得到的脑电地形图。从图5中可得，积极情绪中权重较大的电极分别是P8、FZ、FC1、CZ、PZ。激活电极主要分布在脑部顶叶所在的位置，同时额叶也有一定程度的激活。自然情绪中权重较大的电极分别是FPZ、F3、FT7、C2、P5，激活电极的分布较为分散，额叶有较为明显的激活。消极情绪权重较大的电极分别是FC5、CP1、PO3、O1、P6，激活电极分布在脑部枕叶所在的位置。
图 4 不同k值的KNN算法建图在SEED数据集实验结果Fig. 4 KNN algorithm mapping experiment results using different k values in the SEED dataset下载:
全尺寸图片
图 5 MPGAT模型的特征向量可视化图Fig. 5 Feature vector visualization diagram of MPGAT model下载:
全尺寸图片
4. 结束语
本文提出了一种基于图注意力网络的跨被试脑电情绪识别方法。本研究根据脑电极位置将脑电信号建模为图数据，输入图注意力网络模型进行训练并得出结果。本文提出的MPGAT通过融合多个平行的图注意力模块的输出特征向量，以捕捉不同脑区之间的局部和全局特征。与其他模型准确率相比，MPGAT具有较高的准确率和较好的稳定性，达到了最先进模型的水平。未来，我们将改进MPGAT，使其计算复杂度降低同时准确率得到提升。本文的模型有望为情绪认知科学研究与情绪脑机接口系统提供新的技术手段。
-
图 1 MPGAT模型框架图
Fig. 1 Framework of MPGAT model
下载:
全尺寸图片
图 2 MPGAT模型对于SEED数据集每个被试的实验结果
Fig. 2 Experimental results of the MPGAT model for each subject in the SEED dataset
下载:
全尺寸图片
图 3 MPGAT在SEED数据集不同特征的实验结果
Fig. 3 Experimental results of different features of the MPGAT in the SEED dataset
下载:
全尺寸图片
图 4 不同k值的KNN算法建图在SEED数据集实验结果
Fig. 4 KNN algorithm mapping experiment results using different k values in the SEED dataset
下载:
全尺寸图片
图 5 MPGAT模型的特征向量可视化图
Fig. 5 Feature vector visualization diagram of MPGAT model
下载:
全尺寸图片
表 1 不同模型在SEED和SEED-IV数据集上的平均准确率和标准差
Table 1 Average accuracy and standard deviation of different models on the SEED and SEED-IV datasets
% 表 2 不同模型在DREAMER数据集上的平均准确率和标准差
Table 2 Average accuracy and standard of different models on the DREAMER datasets
% -
[1] 张冠华, 余旻婧, 陈果, 等. 面向情绪识别的脑电特征研究综述[J]. 中国科学(信息科学), 2019, 49(9): 1097–1118. doi: 10.1360/N112018-00337 ZHANG Guanhua, YU Minjing, CHEN Guo, et al. A review of research on EEG features for emotion recognition[J]. Scientia sinica informationis, 2019, 49(9): 1097–1118. doi: 10.1360/N112018-00337 [2] ZHENG Weilong, ZHU Jiayi, PENG Yong, et al. EEG-based emotion classification using deep belief networks[C]//2014 IEEE International Conference on Multimedia and Expo (ICME). Shanghai: IEEE, 2014: 1−6. [3] BABLANI A, EDLA D R, TRIPATHI D, et al. Survey on brain-computer interface: an emerging computational intelligence paradigm[J]. ACM computing surveys, 2019, 52(1): 1–32. [4] WU C H, HUANG Y M, HWANG J P. Review of affective computing in education/learning: Trends and challenges[J]. British journal of educational technology, 2016, 47(6): 1304–1323. doi: 10.1111/bjet.12324 [5] 潘家辉, 何志鹏, 李自娜, 等. 多模态情绪识别研究综述[J]. 智能系统学报, 2020, 15(4): 633–645. PAN Jiahui, HE Zhipeng, LI Zina, et al. A survey of multi-modal emotion recognition research[J]. Journal of intelligent systems, 2020, 15(4): 633–645. [6] ALARCÃO S M, FONSECA M J. Emotions recognition using EEG signals: a survey[J]. IEEE transactions on affective computing, 2017, 10(3): 374–393. [7] HE Zhipeng, LI Zina, YANG Fuzhou, et al. Advances in multimodal emotion recognition based on brain–computer interfaces[J]. Brain sciences, 2020, 10(10): 687. doi: 10.3390/brainsci10100687 [8] LI Mu, LU Baoliang. Emotion classification based on gamma-band EEG[C]//2009 Annual International Conference of the IEEE Engineering in Medicine and Biology Society. Minneapolis: IEEE, 2009: 1223−1226. [9] DUAN Ruonan, ZHU Jiayi, LU Baoliang. Differential entropy feature for EEG-based emotion classification[C]//2013 6th International IEEE/EMBS Conference on Neural Engineering (NER). San Diego: IEEE, 2013: 81−84. [10] ALHAGRY S, FAHMY A A, EL-KHORIBI R A. Emotion recognition based on EEG using LSTM recurrent neural network[J]. (IJACSA) international journal of advanced computer science and applications, 2017, 8(10): 355–358. [11] LI He, JIN Yiming, ZHENG Weilong, et al. Cross-subject emotion recognition using deep adaptation networks[C]//25th International Conference on Neural Information Processing. Siem Reap: Springer, 2018: 403−413. [12] LI Yang, WANG Lei, ZHENG Wenming, et al. A novel bi-hemispheric discrepancy model for EEG emotion recognition[J]. IEEE transactions on cognitive and developmental systems, 2020, 13(2): 354–367. [13] LIU Wei, ZHENG Weilong, LU Baoliang. Emotion recognition using multimodal deep learning[C]//23rd International Conference on Neural Information Processing. Kyoto: Springer, 2016: 521−529. [14] 徐冰冰, 岑科廷, 黄俊杰, 等. 图卷积神经网络综述[J]. 计算机学报, 2020, 43(5): 755–780. doi: 10.11897/SP.J.1016.2020.00755 XU Bingbing, CEN Keting, HUANG Junjie, et al. A survey on graph convolutional neural network[J]. Chinese journal of computers, 2020, 43(5): 755–780. doi: 10.11897/SP.J.1016.2020.00755 [15] WU Zonghan, PAN Shirui, CHEN Fengwen, et al. A comprehensive survey on graph neural networks[J]. IEEE transactions on neural networks and learning systems, 2021, 32(1): 4–24. doi: 10.1109/TNNLS.2020.2978386 [16] ZHANG Tong, WANG Xuehan, XU Xiangmin, et al. GCB-Net: Graph convolutional broad network and its application in emotion recognition[J]. IEEE transactions on affective computing, 2022, 13(1): 379–388. doi: 10.1109/TAFFC.2019.2937768 [17] ZHONG Peixiang, WANG Di, MIAO Chunyan. EEG-based emotion recognition using regularized graph neural networks[J]. IEEE transactions on affective computing, 2020(99): 1. [18] SONG Tengfei, ZHENG Wenming, SONG Peng, et al. EEG emotion recognition using dynamical graph convolutional neural networks[J]. IEEE transactions on affective computing, 2020, 11(3): 532–541. doi: 10.1109/TAFFC.2018.2817622 [19] WAN Sheng, PAN Shirui, YANG Jian, et al. Contrastive and generative graph convolutional networks for graph-based semi-supervised learning[EB/OL]. (2020−09−19)[ 2021−07−02].https://arxiv.org/abs/2009.07111v2. [20] WAN Sheng, GONG Chen, ZHONG Ping, et al. Multiscale dynamic graph convolutional network for hyperspectral image classification[J]. IEEE transactions on geoscience and remote sensing, 2020, 58(5): 3162–3177. doi: 10.1109/TGRS.2019.2949180 [21] VELIČKOVIĆ P, CUCURULL G, CASANOVA A, et al. Graph attention networks[EB/OL]. (2018−02−04)[ 2021−07−02].https://arxiv.org/abs/1710.10903. [22] KINGMA D, BA J. Adam: a method for stochastic optimization[EB/OL]. (2017−01−30)[ 2021−07−02].https://arxiv.org/abs/1412.6980. [23] COLLOBERT R, SINZ F, WESTON J, et al. Large scale transductive SVMs[J]. The journal of machine learning research, 2006, 7(8): 1687–1712. [24] KIPF T N, WELLING M. Semi-supervised classification with graph convolutional networks[EB/OL]. (2017−02−22)[ 2021−07−02].https://arxiv.org/abs/1609.02907. [25] PAN S J, TSANG I W, KWOK J T, et al. Domain adaptation via transfer component analysis[J]. IEEE transactions on neural networks, 2011, 22(2): 199–210. doi: 10.1109/TNN.2010.2091281 [26] ZHENG Weilong, LU Baoliang. Investigating critical frequency bands and channels for EEG-based emotion recognition with deep neural networks[J]. IEEE transactions on autonomous mental development, 2015, 7(3): 162–175. doi: 10.1109/TAMD.2015.2431497
