Active learning algorithm and its application based on a two-tier optimization strategy
-
摘要: 针对工业生产过程中有标签样本少而人工标记代价高的问题，提出一种基于双层优选策略的主动学习算法。首先，建立不同预测模型对无标签样本的信息量进行评估；其次，充分考虑样本的分布信息，从样本的不确定性、差异性和代表性3个角度出发，提出新的评价指标，优选无标签样本，并去除冗余信息；最后，对双层优选的样本进行人工标记，重构有标签样本集后进行建模应用。通过脱丁烷塔的工业过程数据进行算法的应用仿真，验证了所提算法的有效性与性能。Abstract: Aiming at the problem that the number of label samples is small and the cost of manual labeling is high in the industrial production process, an active learning algorithm based on a two-tier optimization strategy is proposed. First, establish different prediction models to evaluate the amount of information contained in unlabeled samples; secondly, fully consider the distribution information of the samples and, from the three perspectives of sample uncertainty, difference, and representativeness, propose new evaluation indicators, preferably unlabeled samples, and remove redundant information; finally, the double-layered preferred samples are manually labeled, and the labeled sample set is reconstructed for modeling application. The application simulation of the algorithm through the industrial process data of the debutanizer verifies the effectiveness and performance of the proposed algorithm.
-
在传统机器学习建模方法中，由于环境条件的限制，采集到的样本中通常无标签样本占比大，有标签样本占比少。为充分利用这些样本信息，半监督学习和主动学习算法相继提出并应用于图像分类[1-2]、故障检测[3-4]、工业过程建模[5-6]等领域。
传统的半监督学习算法通过对无标签样本进行标记以扩大有标签样本集，以此达到提升模型精度的目的[7-10]。区别于半监督学习算法仅利用无标签样本来提升模型性能，主动学习借助专家知识，对优选出的无标签样本进行人工标记[11-12]，获取其真实标签，并将标记后的样本加入有标签样本集中重新训练模型。因此，主动学习算法的关键在于如何实现以最小的标记代价最大程度地提升模型的预测性能。
主动学习可划分为基于流和基于池[13-15]两类。基于流的主动学习通常需根据不同情况设置不同阈值实行较为困难。基于池的主动学习根据信息度量指标对无标签样本进行排序，挑选最具信息量的样本进行标记。通过设置合适的评价指标可有效完成对整个无标签样本集的筛选。因此，许多学者围绕基于池的主动学习进行研究，并提出多种行之有效的评价指标。如Ge等[16]提出将主动学习与高斯过程回归相结合，根据高斯过程回归的预测方差衡量样本的不确定性。Tang等[17]则利用核主成分分析进行特征提取并根据不同学习器的预测输出挑选无标签样本，但该类算法通常未能兼顾到其余无标签样本的分布信息。Douak等[18]则根据欧氏距离定义无标签样本与有标签样本集的差异，但该算法仅从无标签样本与有标签样本差异性角度进行选取，容易选出离群样本。离群无标签样本虽与有标签样本差异性较大但标记后甚至会降低模型性能。为避免选出离群无标签样本，Rodrigue等[19]将整个样本集划分为多个簇，选取聚类簇的中心样本作为待标记样本，Demir等[20]则将支持向量回归机与核k均值聚类相结合进行无标样本的挑选，但聚类算法选出的无标签样本可能存在冗余且缺乏信息量。
此外，根据评价指标进行无标签样本的挑选，经常存在一小块区域内多个样本被同时选中的问题，而相似样本一般会提供相同的信息，进行标记后造成人力物力的浪费。因此，需降低所选无标签样本间的冗余。综上所述，本文提出一种带双层优选策略的主动学习算法，一方面根据不同模型对无标签样本预测输出的差值衡量样本的不确定性，同时引入样本的分布信息，设计出一种新的评价指标用于无标签样本的挑选。另一方面，对于优选出的无标签样本进一步衡量样本间的差异性并去除冗余信息。基于脱丁烷塔工业过程数据仿真，验证了所提算法选取的样本具有更高的信息量，可以有效地降低人工标记代价。
1. 主动学习算法及建模
基于主动学习算法的机器学习建模主要包括两个步骤：无标签样本的质量评估和对优选出的高质量样本进行人工标记后建立预测模型。因此，无标签样本的选择策略和有标签样本的建模方法是提升模型预测性能的关键。
1.1 无标签样本选择策略
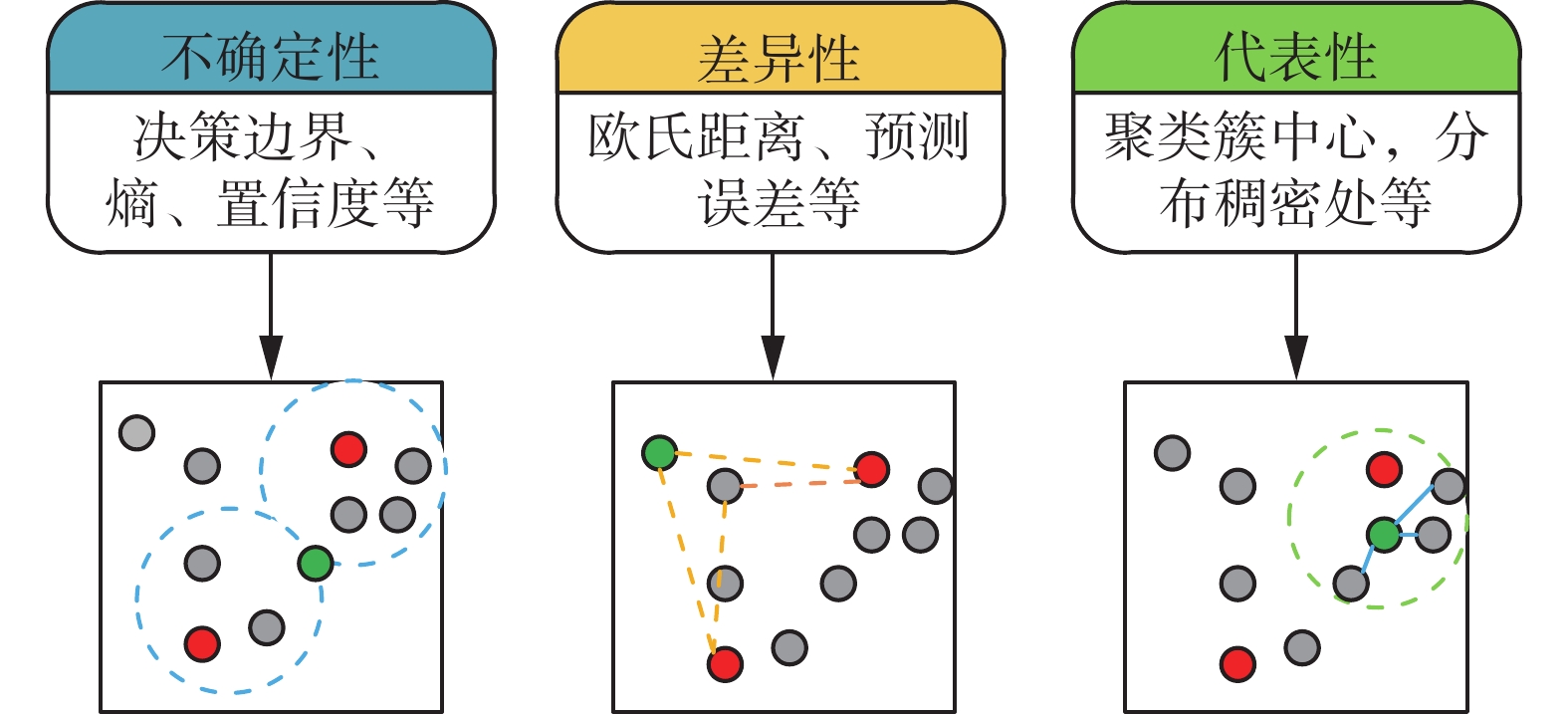
无标签样本选择策略大致分为基于不确定性、差异性和代表性3种[21-23]。不同策略的选取结果如图1所示，红色样本点为有标签样本，灰色为无标签样本，绿色样本点为选中无标签样本。
图 1 主动学习样本选择策略Fig. 1 Active learning sample selection strategy
下载:
全尺寸图片
基于不确定性的选择策略侧重于选取易被机器误判的样本交由人工标记；基于差异性的选取策略则侧重于选取与有标签样本差异较大的无标签样本来扩大模型的预测空间；而基于代表性的选取策略核心思想为与该样本相似的样本越多，则该样本的代表性越强，一般选取聚类簇中心或分布稠密处的样本作为待标记样本。基于不确定性和差异性的选择策略选出的样本都侧重于扩大模型的预测空间，但容易选出离群样本。而基于代表性的选择策略考虑到样本间的相似性，但选出的样本经常彼此间存在冗余。为了克服上述问题，本文构建了一种新的评价指标，该项指标在确保样本自身具有较高信息量的同时，还考虑到其余样本间的分布信息，避免挑选出离群样本。
1.2 高斯过程回归
高斯过程回归[24-25](Gaussian process regression, GPR)算法适用于非线性数据的建模，且模型涉及的参数少优化更加便捷。在GPR建模中，通过选取合适的高斯核函数构建协方差矩阵，完成对样本的预测。本文均采用平方指数函数来构建协方差函数：
$$ k({x_i},{x_j}) = \delta _f^2\exp \left[ - \frac{{{{({{\boldsymbol{x}}_i} - {{\boldsymbol{x}}_j})}^{\rm T}}({{\boldsymbol{x}}_i} - {{\boldsymbol{x}}_j})}}{{2{l^2}}}\right] + {\delta _{ij}}\delta _n^2 $$ (1) 式中：
${\delta _f}$ 为信号标准差；$l$ 为尺度参数；当$i = j$ 时，${\delta _{ij}} = 1$ ，否则等于0；${\delta _n}$ 为噪声标准差。设${\boldsymbol{\theta}} = [\delta _f^2\;{l^2}\;\delta _n^2]$ 为模型的超参数，利用极大似然估计求得超参数最优值。$$ L({\boldsymbol{\theta}} ) = - \frac{n}{2}\ln (2{\text{π}} ) - \frac{1}{2}\ln (\det ({\boldsymbol{K}})) - \frac{1}{2}{y^{\rm T}}{{\boldsymbol{K}}^{ - 1}}y $$ (2) 式中
${\boldsymbol{K}}$ 为协方差矩阵，其元素${K_{ij}} = k({{\boldsymbol{x}}_i},{{\boldsymbol{x}}_j})$ 。在获得最优超参数后，对于1个新的测试样本${{\boldsymbol{x}}_q}$ ，可根据式(3)求其预测值，根据式(4)求取方差。$$ {y_q} = {\boldsymbol{k}}_q^{\rm{T}}{{\boldsymbol{K}}^{ - 1}}y $$ (3) $$ {\delta ^2} = k({{\boldsymbol{x}}_q},{{\boldsymbol{x}}_q}) - {\boldsymbol{k}}_q^{\rm{T}}{{\boldsymbol{K}}^{ - 1}}{{\boldsymbol{k}}_q} $$ (4) 式中：
${y_q}$ 为预测值，${\delta ^2}$ 为方差，${{\boldsymbol{k}}_q} = [k({{\boldsymbol{x}}_q},{{\boldsymbol{x}}_1})\; k({{\boldsymbol{x}}_q}, {{\boldsymbol{x}}_2})\;\cdots\; k({{\boldsymbol{x}}_q},{{\boldsymbol{x}}_q})]^{\rm T}$ 为${x_q}$ 与标记样本的协方差矩阵，式(4)中$k({{\boldsymbol{x}}_q},{{\boldsymbol{x}}_q})$ 为待预测样本构建的协方差矩阵。2. 双层优选策略下的主动学习算法
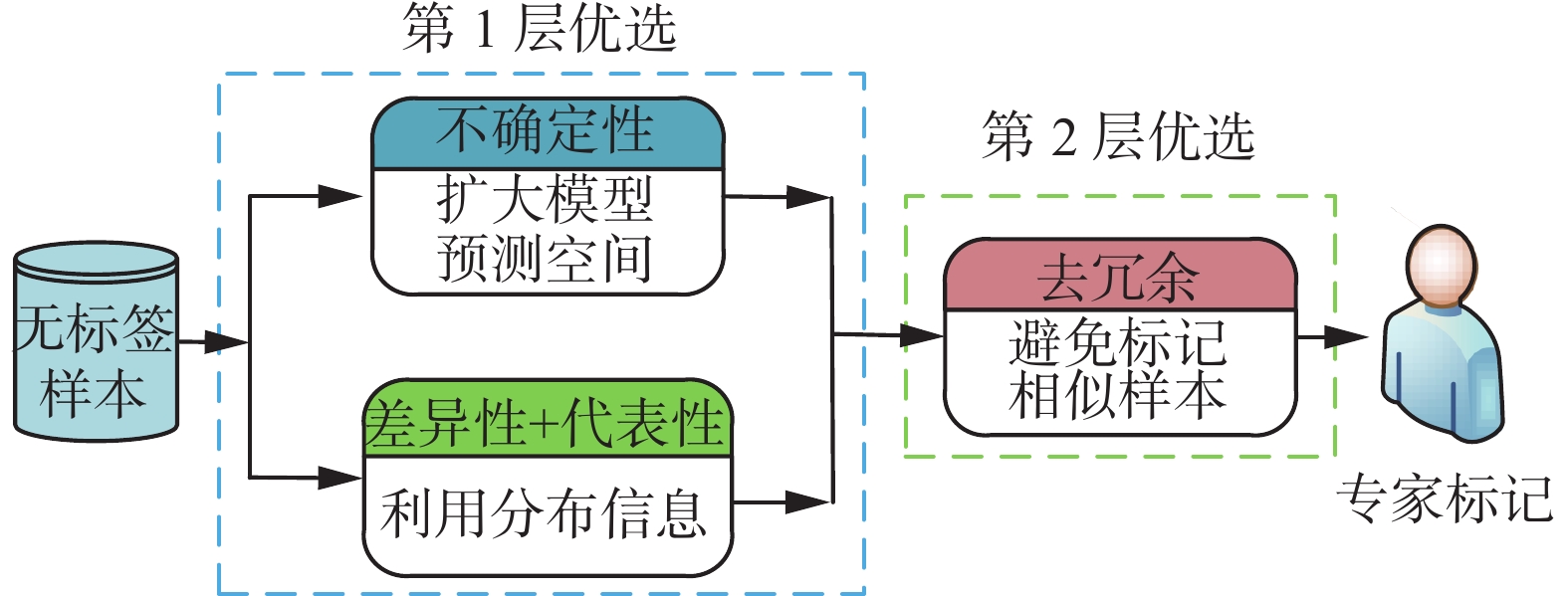
本文所提的基于双层优选的主动学习算法，第1层通过衡量无标签样本的不确定性、差异性和代表性进行优选；第2层对优选出的无标签样本去除冗余信息，从而达到以较小的标记代价最大程度提升模型性能的目的。算法基本原理如图2所示。
图 2 双层优选的主动学习算法Fig. 2 Active learning algorithm with double-layer optimization下载:
全尺寸图片
2.1 第1层优选策略
在首先将有标签样本集均分后分别建立GPR模型
$\theta = {\rm{abs}}({y_1} - {y_2})$ 和$\theta = {\rm{ abs}}({y_1} - {y_2})$ ，并利用这两个模型完成对无标签样本的预测，分别得到预测值$\theta = {\rm{abs}}({y_1} - {y_2})$ 和$\theta = {\rm{abs}}({y_1} - {y_2})$ 。根据差值衡量不确定性的公式为$$ \theta = {\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{abs}}({y_1} - {y_2}) $$ (5) 式中：abs为对预测值的差值取绝对值，
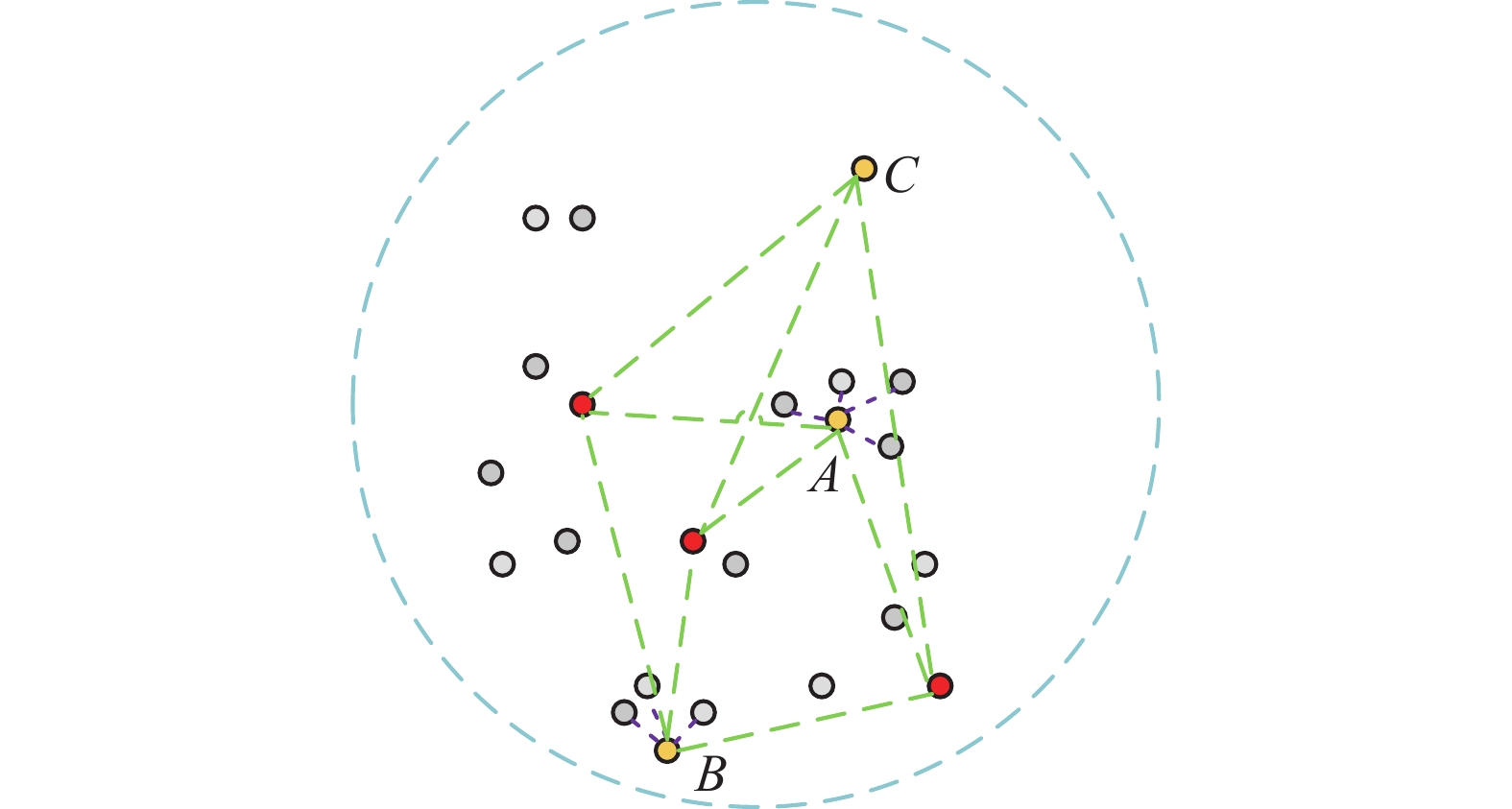
$\theta $ 为样本不确定性度量值。$\theta $ 值越大，说明不同模型对该无标签样本的预测分歧越大，挑选该类样本进行标记，可有效降低预测误差较大的样本数目。但仅根据$\theta $ 值进行样本的选取，未能有效利用其余无标签样本的信息，造成资源的浪费。在根据不确定性进行优选的基础上，进一步利用样本的分布信息，判断目标样本与有标签样本的差异性和自身是否具有代表性。通常无标签样本的差异性和代表性会有一定的冲突，如图3所示。红色样本点表示有标签样本，灰色样本点表示无标签样本，现需选出1个样本进行标记后加入有标签样本集。显然样本C与有标签样本的差异性大于样本A和B，但样本点C严重偏离其他无标签样本，若选中C进行标记，甚至会降低模型预测精度。样本A与样本B则较为相似，对两者信息量进行衡量，选取对模型提升最为有利的样本。
图 3 样本的代表性与差异性Fig. 3 Sample representativeness and differences下载:
全尺寸图片
从差异性角度出发，首先根据有标签样本建立模型并获取无标签样本预测值
${y_p}$ ；其次计算${y_p}$ 与有标签样本真值${y_L}$ 的差值并取绝对值，得到${N_{\rm u}}$ 个无标签样本预测值与${y_L}$ 的最小差值${d_n}$ ；最后挑选数值较大的${d_n}$ 所对应的样本，如式(6)和式(7)所示：$$ {{\boldsymbol{d}}_{nm}} = {\text{abs}}({{\boldsymbol{y}}_P} - {{\boldsymbol{y}}_L}),\; {{m = 1,2,}}\cdots{{,}}{{{N}}_{\text{L}}},\;{{n = 1,2,}}\cdots{{,}}{{{N}}_{\text{u}}} $$ (6) $$ {d_n} = \mathop {\min }\limits_m {{\boldsymbol{d}}_{nm}},\;{{n = 1,2,}}\cdots{{,}}{{{N}}_{\text{u}}} $$ (7) 式中：
${{{N}}_{\text{L}}}$ 和${{{N}}_{\text{u}}}$ 分别为有标签样本和无标签样本数目。在上述迭代过程中，通过选取与${y_L}$ 差值较大的无标签样本来扩大模型的预测空间，但通常会出现部分所选样本在分布上严重偏离其余无标签样本，进行标记后将降低模型的预测性能。为避免选出离群样本，求取每个无标签样本到其余无标签样本的平均欧氏距离，如式(8)和式(9)所示：$$ d_n^x = \frac{1}{{{N_{\rm{u}}}}}\sum\limits_{i = 1}^{{N_{\rm{u}}}} {\left\| {{{\boldsymbol{x}}_i} - {{\boldsymbol{x}}_U}} \right\|} $$ (8) $$ \delta = \frac{{{d_n}}}{{d_n^x}} $$ (9) 式中
$\delta $ 为样本差异性与代表性度量值。若某样本与其余无标签样本的欧氏距离过大则$d_n^x$ 的数值增大，即使该样本与有标签样本差异显著，也将不被选入待标记样本。综上分析，利用有标签样本的建模信息，同时将样本的分布信息考虑其中得到第一层优选的评价指标，如公式(10)所示：$$ \alpha = \theta \delta $$ (10) 式中
$\alpha $ 为评价指标度量值。由于$\theta $ 与$\delta $ 两者数量级不同，因此采用乘积形式。第一层优选过程中，在根据样本不确定性选取的基础上，进一步度量样本的分布信息，判断其对模型性能的提升是否有利。若某样本因误判导致预测分歧较大，而根据$\delta $ 值进行判别后发现在分布信息上不利于提升模型的预测精度，也将无法通过第一轮优选。因此，根据$\alpha $ 值衡量每个无标签样本信息量，对其进行排序后挑选出固定数目的信息量最高的样本作为候选样本。2.2 第2层优选策略
在主动学习迭代过程中，通常无标签样本数量大，彼此间存在信息重复，即使按照
$\alpha $ 值挑选出信息量丰富的无标签样本彼此间仍会存在信息冗余，而标记相似样本将造成人力的浪费。为此从信息冗余角度对第1层优选出的固定数目的候选样本进行第2层优选。在第1层优选中，若设置候选样本数过多，经过第2层优选后虽然样本间冗余性较低，但样本所含信息量也随之减少。通过设置合适的候选样本数，使样本整体具备较高的信息量的同时，有效扩大模型的预测空间，在去冗余后对模型性能的提升更为有利。经过多次实验，最终确定候选样本数为每次迭代过程中人工标记样本数的两倍。如图4所示为候选无标签样本分布图，假设黄色点为通过评价指标挑选的无标签样本集，红色点为有标签样本，绿色虚线区域则表示无标签样本进行标记后所拓展的模型空间。
由图4可以看出，选出的样本点虽然扩大了模型空间，但部分无标签样本如
${D_1}$ 、${D_2}$ 、${D_3}$ 之间相似程度较高，考虑到标记代价昂贵，若标记相似的无标签样本，则会造成人力物力的浪费。为避免样本的冗余添加，使用最远优先遍历算法[26]进行第2层优选，该算法的核心思想为：对于2个样本，它们之间距离越大则冗余性越低。算法定义如式(11)和式(12)所示：$$ d({\boldsymbol{x}},{{\boldsymbol{x}}_l}) = \mathop {\min }\limits_{{{{x}}_l} \in {S_1}} \left\| {{\boldsymbol{x}} - {{\boldsymbol{x}}_l}} \right\| $$ (11) $$ {x_i} = \mathop {\arg {\kern 1pt} {\kern 1pt} \max }\limits_{x \in {S_2}} {\kern 1pt} {\kern 1pt} d({\boldsymbol{x}},{{\boldsymbol{x}}_l}) $$ (12) 式中：
${S_1}$ 表示从集合${S_2}$ 中挑选出的待标记样本集，${S_2}$ 表示候选样本集$S$ 中剩余样本组成的集合。该算法首先从候选样本集$S$ 中，选择综合评价指标$\alpha $ 值最大的无标签样本$\boldsymbol x$ 加入待标记样本集${S_1}$ 。根据式(11)和式(12)挑选下一个样本${{\boldsymbol{x}}_i}$ 加入${S_1}$ ，候选样本集$S$ 则除去${{\boldsymbol{x}}_i}$ 。经过二层优选得到的待标记样本在具备信息量的同时，彼此之间差异性较大，标记后对模型的提升更为有利。
图 4 候选样本分布图Fig. 4 Candidate sample distribution map下载:
全尺寸图片
2.3 主动学习建模流程
本文提出具有双层优选策略的主动学习算法，从不确定性、差异性、代表性3个角度出发进行无标签样本的优选，并考虑样本间的冗余信息，以全面地提升主动学习算法性能。算法流程如图5所示，具体建模步骤如下。
图 5 主动学习算法流程Fig. 5 Active learning algorithm下载:
全尺寸图片
1) 采集的数据集中，根据有标签样本建立GPR模型，并对无标签样本进行预测；
2) 将有标签样本集均分并建立不同的GPR模型，分别对样本进行预测，通过不同模型预测值间的差值 衡量不确定性；
3) 通过式(9)得到无标签样本差异性与代表性度量值 ，并与不确定性度量值 相乘得到评价指标。通过指标完成对无标签样本的第1次优选，符合条件的样本加入候选样本集 ；
4) 通过最远优先遍历算法完成第2次优选，选出的无标签样本进行人工标记后加入有标签样本集；
5) 更新GPR模型，检验模型精度，若未达到迭代次数则返回2)，达到则停止。
3. 仿真实验
3.1 数值仿真及分析
为验证本文所提算法的性能，与传统的基于欧式距离的主动学习算法进行对比。为分析两种选择策略对于无标签样本选取上的区别，对函数
$Z = \sin 3X + \cos 3Y$ 做回归分析，其中$X$ 、$Y$ 均服从正态分布。数据集划分4组有标签样本集，56组无标签样本集，10组测试集。每次迭代分别选取5个无标签样本进行标记。为了更好地展现2种算法所选样本差异，选取的无标签样本及样本标记后预测误差分布如图6所示。
图 6 无标签样本选取散点及预测误差分布图Fig. 6 Unlabeled sample selection scatter points and prediction error distribution map下载:
全尺寸图片
图6中，基于欧氏距离的主动学习(distance active learning, DAL)[18]算法所选出的样本仅考虑与有标签样本的差异性，选择了部分离群点并且样本之间存在冗余。本文算法选取的样本则分散在模型空间中且彼此间冗余性低。进一步分析选中的无标签样本进行标记后，对模型预测效果的提升明显。无标签样本预测误差分布如图(c)，(d)所示，其中红色实心点为已标记样本点，绿色和紫色实心点分别为根据DAL算法和本文所提算法选择出的样本。黄色实心点则为无标签样本，色标值表示样本的预测误差。可以看出在已标记样本点周围的无标签样本的预测误差都较低，而无标签样本附近缺少已标记样本点则误差会相对较高。图(c)中在根据DAL算法挑选部分无标签样本进行标记后，其余大部分无标签样本的预测误差都在1到2之间，图(d)中根据本文算法挑选无标签样本进行标记后，样本预测误差则在0.5~1.5。以均方根误差[27](root mean squared error, RMSE)衡量模型预测精度，计算公式为
$$ {\text{RMSE}} = \sqrt {\frac{1}{n}\sum\limits_{i = 1}^n {{{({y_i} - {{\hat y}_i})}^2}} } $$ 式中：
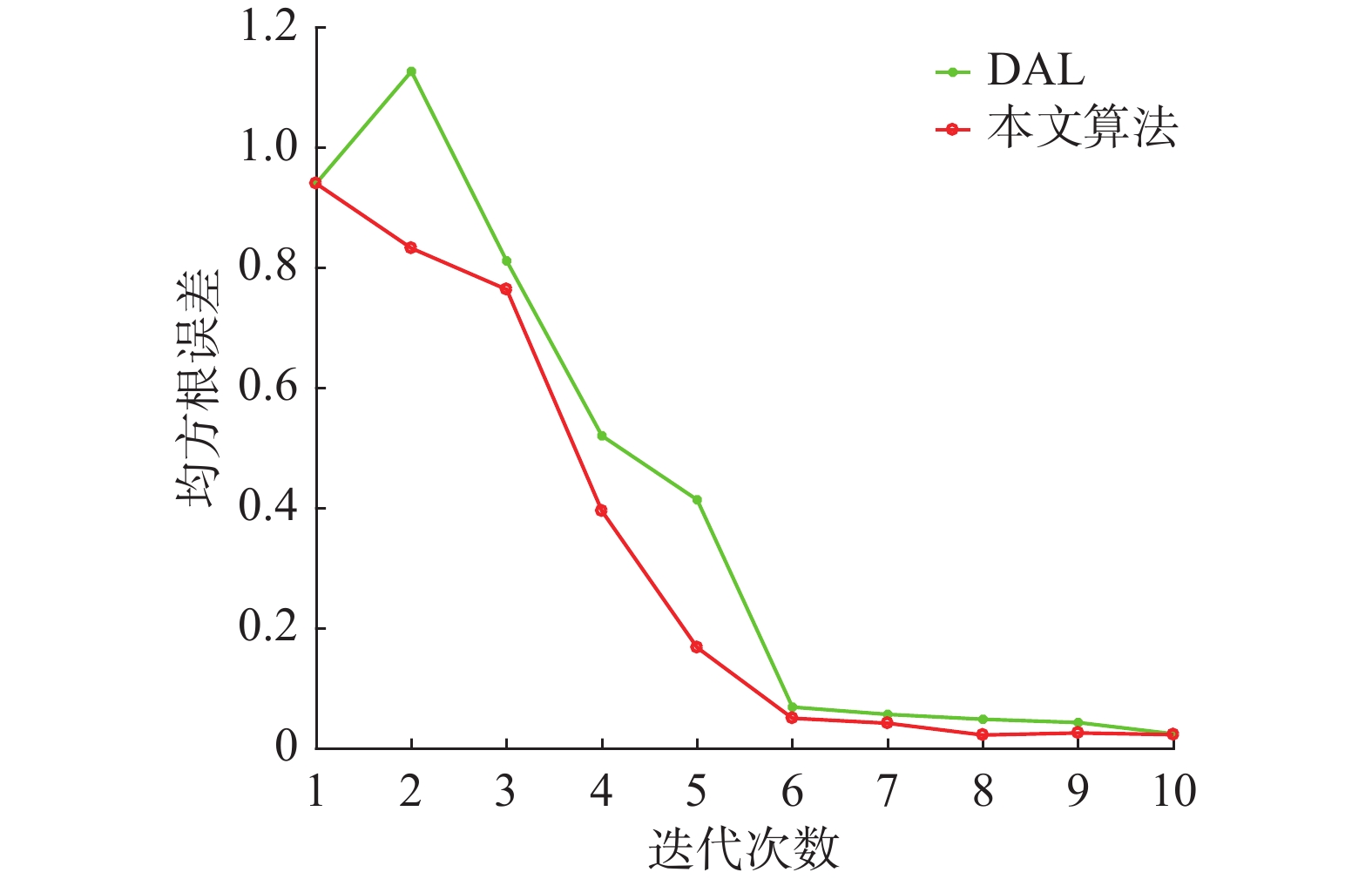
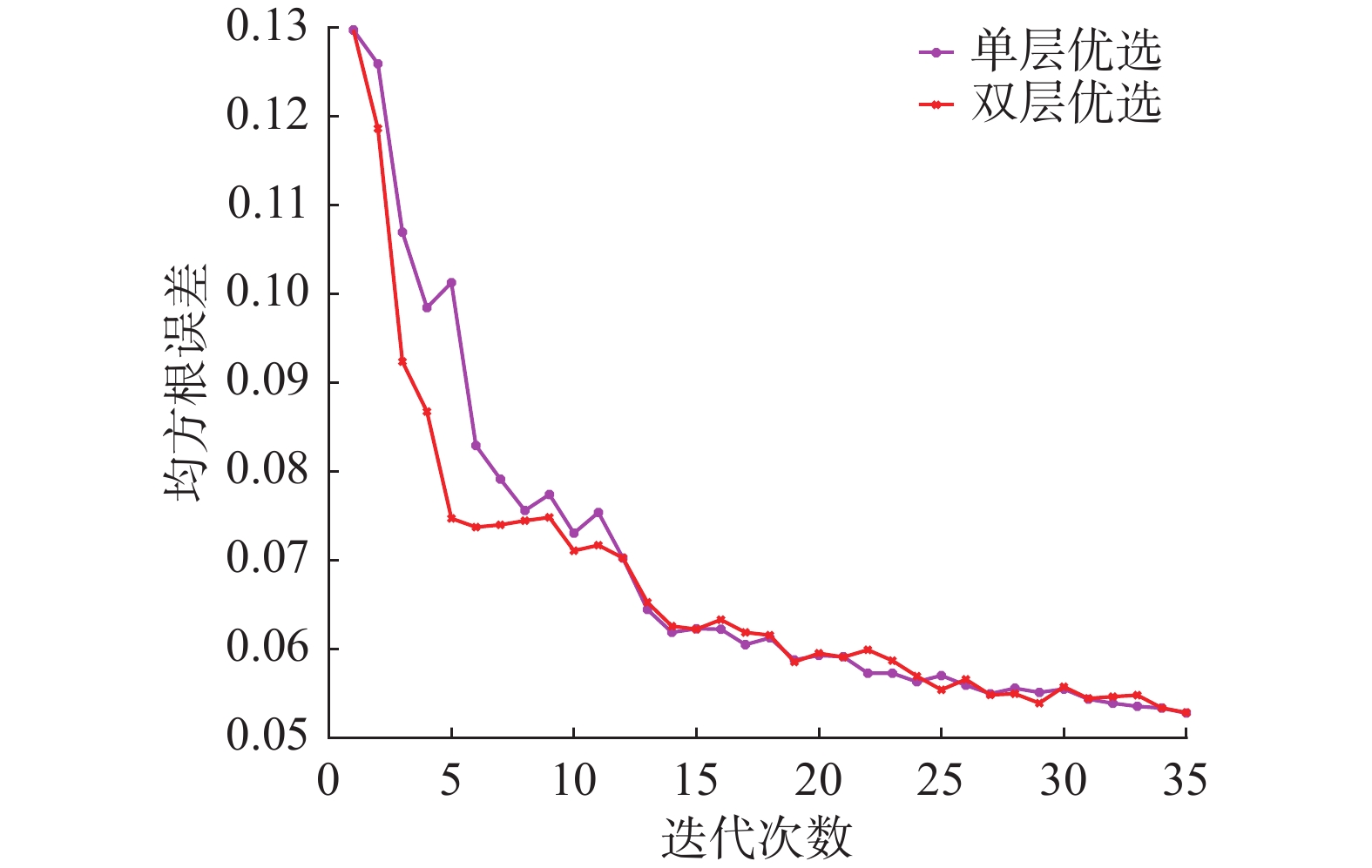
$n$ 为样本数，${y_i}$ 为真值，${\hat y_i}$ 为预测值。进行10次迭代，每次选取5个无标签样本进行标记，模型性能随迭代次数的变化如图7所示。
图 7 算法性能对比Fig. 7 Algorithm performance contrast下载:
全尺寸图片
从图7中可以看出，DAL算法由于仅考虑样本间的差异性，在前期迭代过程中容易选出离群样本，而根据本文所提算法选取的无标签样本在扩大模型预测空间的同时自身仍具备代表性并且在经过第2层优选后去除了样本间的冗余信息，使所选样本较为均匀地分散在模型空间，有效地提升了模型预测精度。
3.2 实验仿真
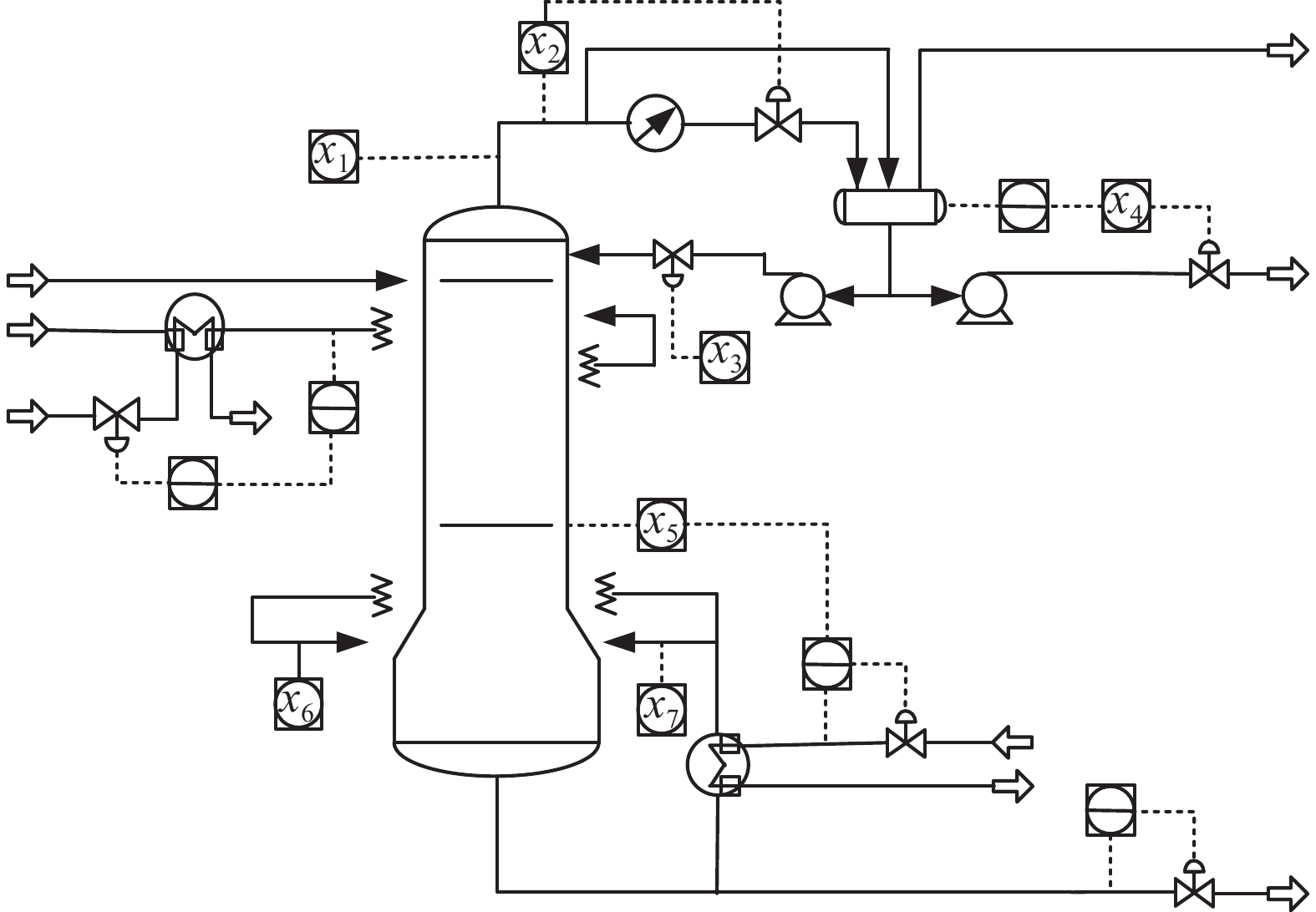
以脱丁烷塔工业过程数据为对象进一步验证算法性能。脱丁烷塔装置如图8所示，脱丁烷塔在分离石油过程中是不可或缺的装置[28]。丁烷浓度是检测石油分离程度的一项重要指标，然而塔底的丁烷浓度难以检测，需根据其他可监测变量建立预测模型，塔中可监测变量如表1所示。
图 8 脱丁烷塔工艺流程Fig. 8 Debutanizer process下载:
全尺寸图片
实时采样获得2 000组脱丁烷塔过程数据。随机选出30个有标签样本，1 800个无标签样本。每次挑选50个无标签样本标记后加入有标签样本集，另选出200组样本作为测试样本。
表 1 脱丁烷塔过程变量Table 1 Process variables of the debutanizer输入变量 变量描述 输入变量 变量描述 $u_1$ 塔顶温度 $u_5$ 塔板温度 $u_2$ 塔底温度 $u_6$ 塔底温度1 $u_3$ 回流量 $u_7$ 塔底温度2 $u_4$ 下一级流量 — — 首先，分析不同学习步长对模型性能的影响。从图9中可以看出较小的学习步长前期取得较好的效果，但随着标记数目的增加，差别便不再显著。学习步长减小意味着标记相同数目，人工标记次数增加，因此需结合实际情况进行考虑。本文重点考虑减少人工标记次数，经多次仿真实验，最终每次选取50个无标签样本进行标记。
图 9 不同学习步长下模型性能变化Fig. 9 Model performance changes under different learning steps下载:
全尺寸图片
此外，对迭代过程中的评价指标变化情况进行分析。根据评价指标优选得到的无标签样本作为候选样本。本文所选取的候选样本数目为目标选取的样本数的2倍即选取100个候选样本，对候选样本的评价指标度量值进行加和取平均，则每次迭代过程中，候选样本的评价指标均值如图10所示。
图 10 迭代过程中的评价指标Fig. 10 Evaluation index in iterative process下载:
全尺寸图片
由图10可以看出，随着迭代过程的进行，候选无标签样本的评价指标度量值越来越小，这主要是因为前期选择的都为信息量较为丰富的无标签样本使剩余样本所含的额外信息越来越少，后期因剩余无标签样本信息量过少，使得评价指标均值趋于停滞。这也验证了根据评价指标进行无标签样本选取的可行性。
其次，分析第一层优选中各模块对模型性能的影响，分别对不确定性指标
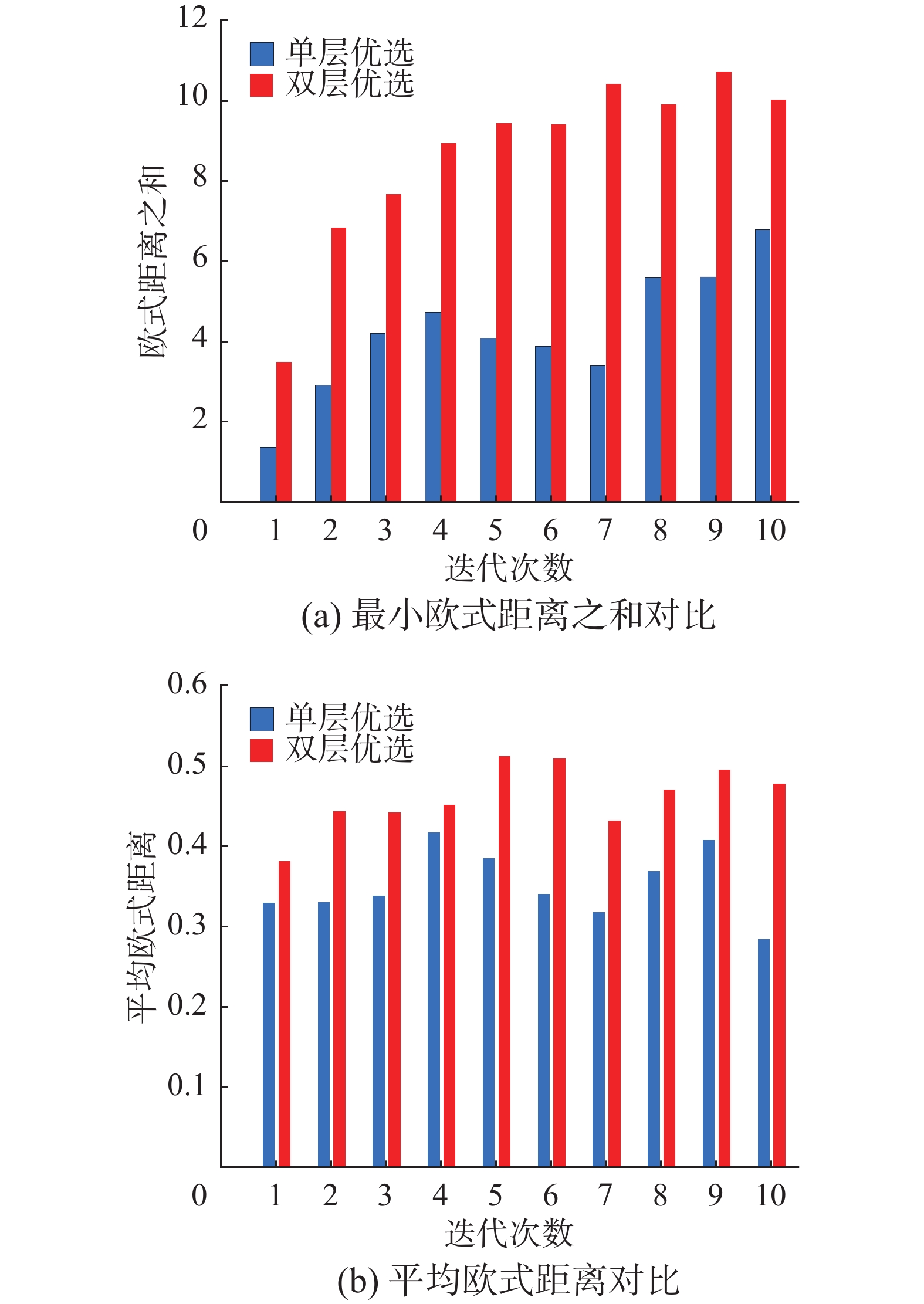
$\theta $ 和利用样本分布信息所获得的差异性与代表性度量值$\delta $ 以及第一层优选中的评价指标$\alpha $ 进行分析。不同指标对模型的提升效果如图11所示。相比于指标$\theta $ 和$\delta $ ，根据评价指标$\alpha $ 选取的无标签样本，在具备较高不确定的同时，扩大了模型的预测空间，同时避免了单一角度选取的所带来的误判和离群点问题，因此所含信息量更为丰富。
图 11 不同指标对模型性能影响Fig. 11 Impact of different indicators on model performance下载:
全尺寸图片
最后，对候选样本去冗余后对模型性能的提升效果进行研究。通过计算样本彼此间欧氏距离，加和后求取平均值和取其最小值相加这2种方法来衡量经过第二层优选后样本间的差异性。第一层优选得到100个候选无标签样本虽然信息量较高，但部分样本间存在冗余。若根据综合评价指标选取度量值最大的前50个样本作为待标记样本而不考虑彼此间的冗余，则每次迭代过程中，最小欧式距离之和如图12(a)中蓝色柱形所示，经过第二层优选后的最小欧式距离之和如图12(a)中红色柱形图所示。而经过第一层优选后样本间的平均欧氏距离如图12(b)中蓝色柱形所示，经过第二层优选后的样本间平均欧式距离则如图12(b)中红色柱形图所示。单层与双层优选后模型性能对比如图13所示。
图 12 单层与双层优选策略下样本间差异性对比Fig. 12 Comparison of differences between samples under single-layer and double-layer optimization strategies下载:
全尺寸图片
图 13 单层与双层优选策略对比Fig. 13 Contrast of single-layer and double-layer optimization strategies下载:
全尺寸图片
从图12和图13中可以看出，第1层优选仅根据样本的信息量进行选取容易造成候选样本集内部存在冗余信息，不利于模型性能提升。第2层的优选在保证样本具备高信息量的同时，排除少部分具有相似信息的高质量样本，有效地降低了样本间的冗余，在模型迭代初期，进行人工标记后对模型效果的提升更为有利。为验证本文所提算法有效性，与基于欧氏距离、预测值(prediction active learning, PAL)和期望变更(excepted change active learning, ECAL )3种主动学习算法进行对比。
1) DAL[18]：以无标签样本与有标签样本间的欧氏距离作为评价指标来挑选样本。
2) PAL[29]：有标签样本建模后获取无标签样本预测值，预测值与有标签样本真值作差并以差值作为评价指标来挑选信息量较大的无标签样本。
3) ECAL[30]：有标签样本建立模型并获取无标签样本的预测值，在设计损失函数后将无标签样本依次加入有标签样本集，根据损失的梯度估计样本的不确定性。
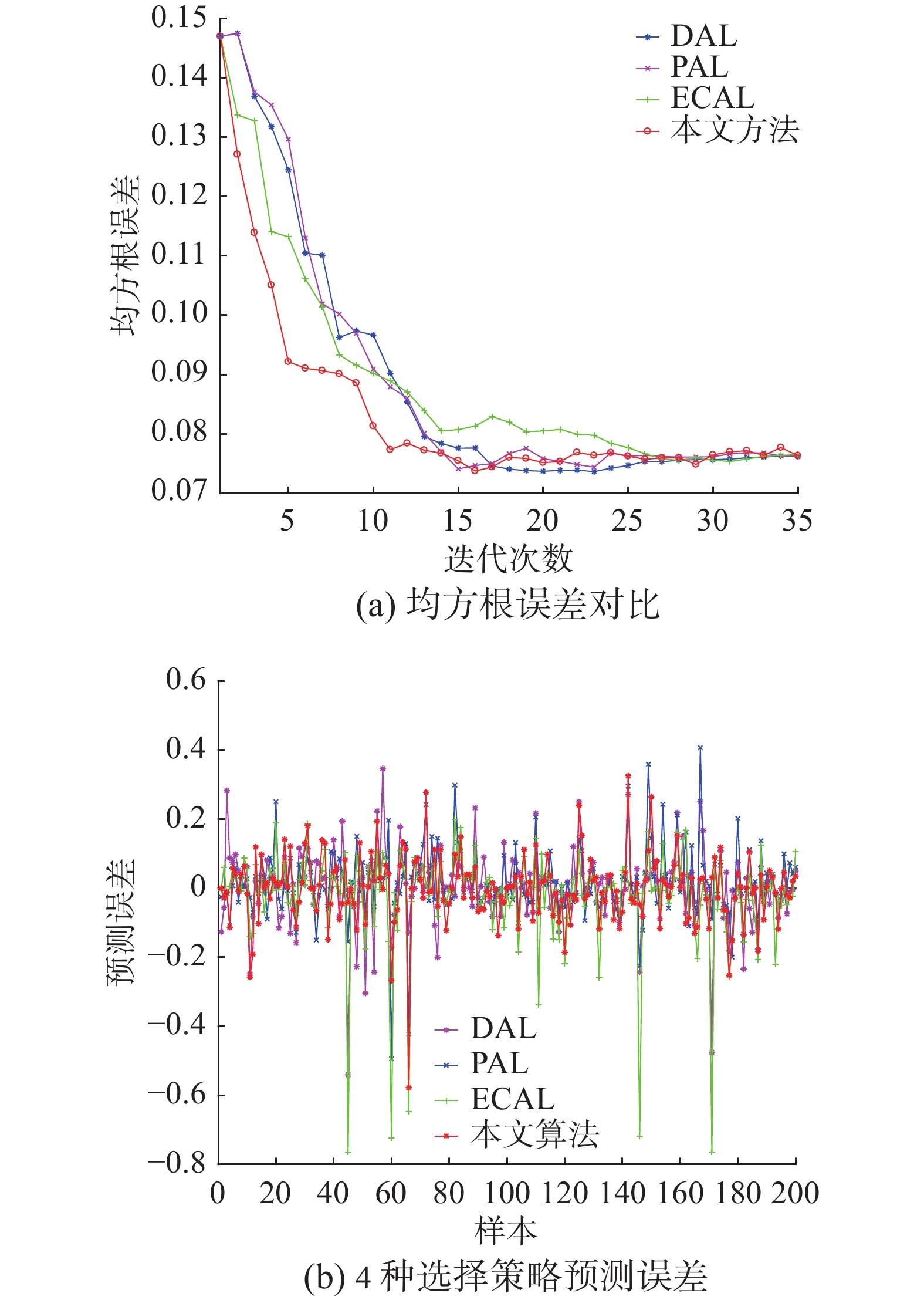
4) 本文所提算法：每次选取50个无标签样本进行标记，标记后加入有标签样本集，达到设置的迭代次数则停止迭代。随机选择初始有标签样本，均方根误差如图14(a)所示。图14(b)则展示了随机选择第6次迭代即标记250个无标签样本后，4种选择策略的预测误差。
图 14 4种主动学习算法对比Fig. 14 Contrast of four active learning algorithms下载:
全尺寸图片
从图14(a)中可以看出，在迭代初期根据本文所提算法挑选的无标签样本质量要优于其他3种算法。在后期4种算法的下降趋势都趋于停滞，出现这样的现象的原因是，在前期4种算法选择的都为质量较高的无标签样本，使得后续迭代过程中剩余无标签样本所包含的信息量减少，对模型的提升效果不再显著。同时本文所提算法在第11次迭代后，再继续添加无标签样本，对模型的提升效果较为有限。而要达到同样的效果，DAL，PAL，ECAL则要进行更多次的迭代。因此，在相同标记代价下，本文所提算法对模型提升效果更为有利。4种主动学习算法预测丁烷浓度的指标如表2所示，其中，ARE为平均相对误差，定义为
$$ {\text{ARE}} = \frac{1}{n}\sum\limits_{i = 1}^n {\left| {\frac{{{{\hat y}_i} - {y_i}}}{{{y_i}}}} \right|} $$ 式中：
$n$ 为样本数，$ {\hat y_i} $ 为预测值，${y_i}$ 为真值。从表2可以看出，本文所提算法的2个误差评价指标都要低于其他3种方法，表明所建立的模型具有更好的预测性能与泛化能力。表 2 4种主动学习方法性能指标Table 2 Performance indicators of four active learning methods编号 性能指标 DAL ECAL PAL 本文算法 3 RMSE 0.136 9 0.132 7 0.137 6 0.1139 ARE 0.348 9 0.321 7 0.331 5 0.3118 5 RMSE 0.124 5 0.113 2 0.129 7 0.0921 ARE 0.324 6 0.303 3 0.304 6 0.2868 7 RMSE 0.110 1 0.101 4 0.101 9 0.0906 ARE 0.290 1 0.269 4 0.260 9 0.2298 10 RMSE 0.096 6 0.090 2 0.090 9 0.0813 ARE 0.236 8 0.232 9 0.231 4 0.2163 4. 结束语
本文提出了一种双层优选的主动学习建模算法。该算法的第一层利用不同模型对无标签样本的信息量进行初步评估，并引入样本的分布信息，构建评价指标后完成对无标签样本的第一次优选。在第二层对优选后的样本去冗余，得到彼此差异性较大的无标签样本作为待标记样本。通过数值仿真分析和脱丁烷塔过程的应用仿真，验证了该选择策略的有效性。并与现有的几种选择策略进行对比，实验证明本文选择策略更具备优越性，即在相同的人工标记消耗下获得更高质量的无标签样本。
-
图 1 主动学习样本选择策略
Fig. 1 Active learning sample selection strategy
下载:
全尺寸图片
图 2 双层优选的主动学习算法
Fig. 2 Active learning algorithm with double-layer optimization
下载:
全尺寸图片
图 3 样本的代表性与差异性
Fig. 3 Sample representativeness and differences
下载:
全尺寸图片
图 4 候选样本分布图
Fig. 4 Candidate sample distribution map
下载:
全尺寸图片
图 5 主动学习算法流程
Fig. 5 Active learning algorithm
下载:
全尺寸图片
图 6 无标签样本选取散点及预测误差分布图
Fig. 6 Unlabeled sample selection scatter points and prediction error distribution map
下载:
全尺寸图片
图 7 算法性能对比
Fig. 7 Algorithm performance contrast
下载:
全尺寸图片
图 8 脱丁烷塔工艺流程
Fig. 8 Debutanizer process
下载:
全尺寸图片
图 9 不同学习步长下模型性能变化
Fig. 9 Model performance changes under different learning steps
下载:
全尺寸图片
图 10 迭代过程中的评价指标
Fig. 10 Evaluation index in iterative process
下载:
全尺寸图片
图 11 不同指标对模型性能影响
Fig. 11 Impact of different indicators on model performance
下载:
全尺寸图片
图 12 单层与双层优选策略下样本间差异性对比
Fig. 12 Comparison of differences between samples under single-layer and double-layer optimization strategies
下载:
全尺寸图片
图 13 单层与双层优选策略对比
Fig. 13 Contrast of single-layer and double-layer optimization strategies
下载:
全尺寸图片
图 14 4种主动学习算法对比
Fig. 14 Contrast of four active learning algorithms
下载:
全尺寸图片
表 1 脱丁烷塔过程变量
Table 1 Process variables of the debutanizer
输入变量 变量描述 输入变量 变量描述 $u_1$ 塔顶温度 $u_5$ 塔板温度 $u_2$ 塔底温度 $u_6$ 塔底温度1 $u_3$ 回流量 $u_7$ 塔底温度2 $u_4$ 下一级流量 — — 表 2 4种主动学习方法性能指标
Table 2 Performance indicators of four active learning methods
编号 性能指标 DAL ECAL PAL 本文算法 3 RMSE 0.136 9 0.132 7 0.137 6 0.1139 ARE 0.348 9 0.321 7 0.331 5 0.3118 5 RMSE 0.124 5 0.113 2 0.129 7 0.0921 ARE 0.324 6 0.303 3 0.304 6 0.2868 7 RMSE 0.110 1 0.101 4 0.101 9 0.0906 ARE 0.290 1 0.269 4 0.260 9 0.2298 10 RMSE 0.096 6 0.090 2 0.090 9 0.0813 ARE 0.236 8 0.232 9 0.231 4 0.2163 -
[1] MA Lei, FU Tengyu, LI Manchun. Active learning for object-based image classification using predefined training objects[J]. International journal of remote sensing, 2018, 39(9): 2746–2765. doi: 10.1080/01431161.2018.1430398 [2] GU Yingjie, JIN Zhong, CHIU S C. Active learning combining uncertainty and diversity for multi-class image classification[J]. IET computer vision, 2015, 9(3): 400–407. doi: 10.1049/iet-cvi.2014.0140 [3] 唐明珠, 阳春华, 桂卫华, 等. 基于代价敏感主动学习的氧化铝蒸发过程故障检测[J]. 化工学报, 2011, 62(8): 2108–2115. doi: 10.3969/j.issn.0438-1157.2011.08.004 TANG Mingzhu, YANG Chunhua, GUI Weihua, et al. Fault detection using modified cost-sensitive active learning for alumina evaporation process[J]. CIESC journal, 2011, 62(8): 2108–2115. doi: 10.3969/j.issn.0438-1157.2011.08.004 [4] YIN Lili, WANG Huangang, FAN Wenhui. Active learning based support vector data description method for robust novelty detection[J]. Knowledge-based systems, 2018, 153: 40–52. doi: 10.1016/j.knosys.2018.04.020 [5] FU Yifan, ZHU Xingquan, LI Bin. A survey on instance selection for active learning[J]. Knowledge and information systems, 2013, 35(2): 249–283. [6] SHI Xudong, XIONG Weili. Approximate linear dependence criteria with active learning for smart soft sensor design[J]. Chemometrics and intelligent laboratory systems, 2018, 180: 88–95. doi: 10.1016/j.chemolab.2018.07.009 [7] HUANG Gao, SONG Shiji, GUPTA J N D, et al. Semi-supervised and unsupervised extreme learning machines[J]. IEEE transactions on cybernetics, 2014, 44(12): 2405–2417. doi: 10.1109/TCYB.2014.2307349 [8] 周志华. 基于分歧的半监督学习[J]. 自动化学报, 2013, 39(11): 1871–1878. doi: 10.3724/SP.J.1004.2013.01871 ZHOU Zhihua. Disagreement-based semi-supervised learning[J]. Acta automatica sinica, 2013, 39(11): 1871–1878. doi: 10.3724/SP.J.1004.2013.01871 [9] 侯杰, 茅耀斌, 孙金生. 一种最大化样本可分性半监督Boosting算法[J]. 南京理工大学学报, 2014, 38(5): 675–681. doi: 10.14177/j.cnki.32-1397n.2014.05.038 HOU Jie, MAO Yaobin, SUN Jinsheng. Semi-supervised separability-maximum boosting[J]. Journal of Nanjing University of Science and Technology, 2014, 38(5): 675–681. doi: 10.14177/j.cnki.32-1397n.2014.05.038 [10] 曲昭伟, 吴春叶, 王晓茹. 半监督自训练的方面提取[J]. 智能系统学报, 2019, 14(4): 635–641. doi: 10.11992/tis.201806006 QU Zhaowei, WU Chunye, WANG Xiaoru. Aspects extraction based on semi-supervised self-training[J]. CAAI transactions on intelligent systems, 2019, 14(4): 635–641. doi: 10.11992/tis.201806006 [11] ZHANG Lijun, CHEN Chun, BU Jiajun, et al. Active learning based on locally linear reconstruction[J]. IEEE transactions on pattern analysis and machine intelligence, 2011, 33(10): 2026–2038. doi: 10.1109/TPAMI.2011.20 [12] TONG S, KOLLER D. Support vector machine active learning with applications to text classification[J]. Journal of machine learning research, 2002, 2: 45–66. [13] COHN D, ATLAS L, LADNER R. Improving generalization with active learning[J]. Machine learning, 1994, 15(2): 201–221. [14] CAI Wenbin, ZHANG Muhan, ZHANG Ya. Batch mode active learning for regression with expected model change[J]. IEEE transactions on neural networks and learning systems, 2017, 28(7): 1668–1681. doi: 10.1109/TNNLS.2016.2542184 [15] SUGIYAMA M, NAKAJIMA S. Pool-based active learning in approximate linear regression[J]. Machine learning, 2009, 75(3): 249–274. doi: 10.1007/s10994-009-5100-3 [16] GE Zhiqiang. Active probabilistic sample selection for intelligent soft sensing of industrial processes[J]. Chemometrics and intelligent laboratory systems, 2016, 151: 181–189. doi: 10.1016/j.chemolab.2016.01.003 [17] TANG Qifeng, LI Dewei, XI Yugeng. A new active learning strategy for soft sensor modeling based on feature reconstruction and uncertainty evaluation[J]. Chemometrics and intelligent laboratory systems, 2018, 172: 43–51. doi: 10.1016/j.chemolab.2017.11.001 [18] DOUAK F, MELGANI F, ALAJLAN N, et al. Active learning for spectroscopic data regression[J]. Journal of chemometrics, 2012, 26(7): 374–383. doi: 10.1002/cem.2443 [19] RODRIGUEZ A, LAIO A. Clustering by fast search and find of density peaks[J]. Science, 2014, 344(6191): 1492–1496. doi: 10.1126/science.1242072 [20] DEMIR B, BRUZZONE L. A multiple criteria active learning method for support vector regression[J]. Pattern recognition, 2014, 47(7): 2558–2567. doi: 10.1016/j.patcog.2014.02.001 [21] SUGIYAMA M. Active learning in approximately linear regression based on conditional expectation of generalization error[J]. Journal of machine learning research, 2006, 7: 141–166. [22] 胡峰, 张苗, 于洪. 基于三支决策的主动学习方法[J]. 控制与决策, 2019, 34(4): 718–726. doi: 10.13195/j.kzyjc.2017.1342 HU Feng, ZHANG Miao, YU Hong. An active learning method based on three-way decision model[J]. Control and decision, 2019, 34(4): 718–726. doi: 10.13195/j.kzyjc.2017.1342 [23] WU Dongrui. Pool-based sequential active learning for regression[J]. IEEE transactions on neural networks and learning systems, 2019, 30(5): 1348–1359. doi: 10.1109/TNNLS.2018.2868649 [24] RANJAN R, HUANG Biao, FATEHI A. Robust Gaussian process modeling using EM algorithm[J]. Journal of process control, 2016, 42: 125–136. doi: 10.1016/j.jprocont.2016.04.003 [25] 何志昆, 刘光斌, 赵曦晶, 等. 高斯过程回归方法综述[J]. 控制与决策, 2013, 28(8): 1121–1129,1137. doi: 10.13195/j.cd.2013.08.3.hezhk.013 HE Zhikun, LIU Guangbin, ZHAO Xijing, et al. Overview of Gaussian process regression[J]. Control and decision, 2013, 28(8): 1121–1129,1137. doi: 10.13195/j.cd.2013.08.3.hezhk.013 [26] 李兴亮, 毛睿. 基于近期最远遍历的支撑点选择[J]. 南京大学学报(自然科学版), 2017, 53(3): 483–496. doi: 10.13232/j.cnki.jnju.2017.03.013 LI Xingliang, MAO Rui. Pivot selection on recent farthest traversal[J]. Journal of Nanjing University (natural sciences edition), 2017, 53(3): 483–496. doi: 10.13232/j.cnki.jnju.2017.03.013 [27] 曹鹏飞, 罗雄麟. 化工过程软测量建模方法研究进展[J]. 化工学报, 2013, 64(3): 788–800. doi: 10.3969/j.issn.0438-1157.2013.03.003 CAO Pengfei, LUO Xionglin. Modeling of soft sensor for chemical process[J]. CIESC journal, 2013, 64(3): 788–800. doi: 10.3969/j.issn.0438-1157.2013.03.003 [28] FORTUNA L, GRAZIANI S, XIBILIA M G. Soft sensors for product quality monitoring in debutanizer distillation columns[J]. Control engineering practice, 2005, 13(4): 499–508. doi: 10.1016/j.conengprac.2004.04.013 [29] WU Dongrui, LIN C T, HUANG Jian. Active learning for regression using greedy sampling[J]. Information sciences, 2019, 474: 90–105. doi: 10.1016/j.ins.2018.09.060 [30] YANG Jian, ZHAO Xin, WEI Haikun, et al. Sample selection based on active learning for short-term wind speed prediction[J]. Energies, 2019, 12(3): 337. doi: 10.3390/en12030337
