基于扩张鸽群优化的舰载无人机横侧向着舰自主控制

何杭轩; 段海滨; 张秀林; 邓亦敏

doi:10.11992/tis.202106035

基于扩张鸽群优化的舰载无人机横侧向着舰自主控制

doi: 10.11992/tis.202106035

何杭轩¹,
段海滨^{1, 2, ,},
张秀林³,
邓亦敏¹

1.
北京航空航天大学自动化科学与电气工程学院, 北京 100083;
2.
鹏城实验室, 广东深圳 518000;
3.
中国航空工业集团公司沈阳飞机设计研究所, 辽宁沈阳 110035

基金项目: 国家自然科学基金项目(91948204, U20B2071, T2121003, U1913602, U19B2033)；科技创新2030–“新一代人工智能”重大项目(2018AAA0102403).

详细信息

作者简介:
何杭轩，硕士研究生，主要研究方向为群体智能、无人机自主控制;

段海滨，教授，博士生导师，主要研究方向为无人机集群自主控制、计算机仿生视觉与智能感知、仿生智能计算理论及应用。主持国家自然基金重大研究计划重点项目、重点项目、面上项目等7 项，出版专著 4部;

张秀林，研究员，型号副总设计师，主要研究方向为飞行控制律设计、飞机操纵性与稳定性分析.

通讯作者:
段海滨. E-mail： hbduan@buaa.edu.cn.

中图分类号: TP391; V249.122
出版历程
- 收稿日期: 2021-06-21
- 修回日期: 2020-11-01
- 网络出版日期: 2021-12-27

Lateral automatic carrier landing control based on expanded pigeon inspired optimization

1.
School of Automation Science and Electrical Engineering, Beihang University, Beijing 100083, China;
2.
Peng Cheng Laboratory, Shenzhen 518000, China;
3.
Shenyang Aircraft Design and Research Institute, Aviation Industry Corporation of China, Shenyang 110035, China

摘要

摘要: 舰载无人机着舰会受到舰尾流、航母甲板运动的干扰。为加快无人机在着舰时横侧向响应以及提高舰载机着舰对干扰的鲁棒性，本文提出了一种基于扩张鸽群优化算法的显式模型预测控制方法，并将其应用于舰载机姿态控制器设计，用于解决所设计控制器的参数优化问题。与基本鸽群优化算法、粒子群算法的仿真对比实验表明，相比传统智能优化算法，本文所提出的扩张鸽群优化算法收敛更快，普适性和稳定性也更强，采用显式模型预测控制的舰载无人机着舰系统相比比例-积分-微分控制下的系统响应更快，鲁棒性更强。
- 自动着舰 /
- 鸽群优化 /
- 姿态控制 /
- 舰尾流 /
- 甲板运动 /
- 显式模型预测 /
- 着舰 /
- 扩张鸽群优化
Abstract: Carrier landing of unmanned aerial vehicles (UAV) can be disturbed by carrier air wake and deck motion. To improve the response speed and disturbance rejection ability of UAV carrier landing, this paper proposes an explicit model predictive control method based on expanded pigeon inspired optimization (EPIO), and apply it in the design of carrier attitude controler to solve parameter optimization problem of the designed controler. Simulations and comparative experiments are conducted on the proposed basic pigeon inspired optimization algorithm and the particle swarm optimization algorithm, which show quicker rate of convergence, stronger universality and stability of EPIO. The designed control method is verified to be faster and more robust after compared with the proportional-integral-derivative control method.
- automatic carrier landing /
- pigeon inspired optimization /
- attitude control /
- carrier air wake /
- deck motion /
- explicit model predictive control /
- carrier landing /
- expanded pigeon inspired optimization

HTML全文

舰载无人机自动着舰技术是当前提高舰载机作战能力的关键技术之一。在着舰时，无人机会受到各种不利环境因素，如舰尾流扰动、航母甲板运动等干扰，这使得着舰难度大大增加，同时也对自动着舰控制提出了更高、更严峻的要求。

着舰控制不仅要求保证舰载机精准跟踪给定的下滑道，还要能够对环境干扰具有足够的鲁棒性。对复杂环境下舰载机着舰问题，不少学者利用传统以及先进控制方法进行了研究。在着舰的纵向控制方面，Zhu等^[1]提出采用自适应反步滑模型控制方法来抑制舰尾流对着舰高度的影响。Koo等^[2]针对航母的升沉问题，分别对无人机和航母进行建模，根据相对运动利用模型预测控制设计着舰轨迹，并对无人机本体采用线性二次调节器。也有学者对舰载机进行了纵向和横侧向全量控制律设计。马坤^[3]分析了舰尾流和甲板运动的影响，提出采用预见控制设计舰载无人机的控制和导引律。Zhen等^[4]设计了采用预见控制的舰载机控制律和引导律，并与比例–积分–微分(proportional-integral-derivative, PID)、线性二次控制进行对比。Guan等^[5]针对着舰情况下的舰尾流和甲板运动干扰，设计了基于反步法的有限时间控制方法，并给出了稳定性证明。赵东宏^[6]提出相对角运动、相对线运动模型，设计了纵向和横侧向PID控制律，实现了无侧滑、无侧偏控制，但系统响应较慢。此外，大部分文献仍然集中于研究舰载机着舰的纵向控制，且较多采用线性化数学模型，导致问题研究具有局限性。显式模型预测控制既拥有传统模型预测控制方法的优点，同时又具备了不需要耗时的在线优化特点，在飞行器控制等领域取得了很成功的应用^[7-9]。本文采用论文显示模型预测控制方法，针对舰载无人机横侧向非线性模型设计控制器，并对控制器中的参数进行优化。

鸽群优化(pigeon inspired optimization, PIO)算法是一种新型的模拟鸽群归巢时不同阶段下不同导航机制的群体智能算法^[10]。鸽群优化算法由于具有收敛速度快，搜索效率高的特点，在不同领域中都得到了广泛应用^[11-14]。Qiu等^[15]通过引入鸽群的层次网络特点改进鸽群优化，解决了无人机分布式集群控制问题。霍梦真等^[16]利用鸽群优化算法提高了无人机目标搜索效率。

为进一步提高基本鸽群优化算法的搜索能力和收敛速度，本文提出一种扩张鸽群优化(expanded pigeon inspired optimization, EPIO)方法，通过改变地图与指南针算子中速度更新方法以及位置更新策略，提高鸽群跳出局部最优解的概率，并结合舰载机着舰模型，对其控制器参数进行优化。

针对复杂环境下舰载无人机着舰横侧向控制问题，本文提出了采用显式模型预测控制(explicit nonlinear model predictive control, ENMPC)方法，在对无人机进行数学建模的基础上，设计了无人机横侧向控制器。为提高控制器效能，本文设计了一种扩张鸽群优化模型，对所设计的控制器进行参数优化，并与其他启发优化算法进行实验对比分析，最后将显式模型预测控制器与传统的PID控制器进行了对比验证。

1. 舰载无人机横侧向数学模型

本文所采用的舰载机模型为六自由度运动模型。假设地面坐标系为惯性坐标系，舰载无人机为刚体，其质量 $m$ 以及重心不随时间变化。本文采用美式坐标系，设无人机空间位置为 $\left( {x,y,z} \right)$ ，绕机体轴转动的角速度为 $\left( {p,q,r} \right)$ ，沿机体轴运动的线速度为 $\left( {u,v,w} \right)$ ，机体的滚转角、俯仰角和偏航角分别为 $\left( {\phi ,\theta ,\psi } \right)$ ，绕机体轴的转动惯量为 $\left( {{I_x},{I_y},{I_z}} \right)$ 。则横侧向数学模型为^[17]

$\left\{ \begin{split} &mV\dot \beta = Y - mV( - p\sin \alpha + r\cos \alpha ) \\ &\dot \phi = p + (r\cos \phi + q\sin \phi )\tan \theta \\ &\dot \psi = \dfrac{1}{{\cos \theta }}(r\cos \phi + q\sin \phi ) &\\ &\dot p = \left( {{c_1}r + {c_2}p} \right)q + {c_3}\bar L + {c_4}N \\ &\dot r = \left( {{c_8}p - {c_2}r} \right)q + {c_4}\bar L + {c_9}N \\ \end{split} \right.$

(1)

式中： ${c_1} = \dfrac{{\left( {{I_y} - {I_z}} \right){I_z} - I_{xz}^2}}{\displaystyle\sum }$ ； ${c_2} = \dfrac{{\left( {{I_x} - {I_y} + {I_z}} \right){I_{xz}}}}{\displaystyle\sum }$ ； ${c_3} = \dfrac{{{I_z}}}{\displaystyle\sum }$ ； ${c_4} = \dfrac{{{I_{xz}}}}{\displaystyle\sum }$ ； ${c_8} = \dfrac{{{I_x}\left( {{I_x} - {I_y}} \right) + I_{xz}^2}}{\displaystyle\sum }$ ； ${c_9} = \dfrac{{{I_x}}}{\displaystyle\sum }$ ； $\displaystyle\sum = {I_x}{I_z} - I_{xz}^2$ ； $V$ 为舰载无人机速度； $\beta$ 为侧滑角； $\alpha$ 为迎角； $Y$ 为侧向力； ${\bar L、N}$ 分别为滚转、偏航力矩。

2. 舰载无人机横侧向控制器设计

本文着舰策略采用侧航法，即自动着舰过程中保持 $\beta = 0$ ，无人机地速矢量与航空母舰保持一致，在着舰瞬间改平机头，从而使飞机与航母着舰中心线保持一致。因此，在横侧向控制中选择侧滑角 $\beta$ 和滚转角 $\phi$ 为控制对象，控制输入为副翼 ${\delta _a}$ 和方向舵 ${\delta _r}$ 。横侧向运动不同于纵向运动，滚转与侧滑相互影响，因此两个控制量 ${{\delta _a}、{\delta _r}}$ 在侧滑和滚转通道中均有作用。

首先推导滚转角通道控制器。令 ${y_1} = \phi$ ，且 ${{\delta _a}、{\delta _r}}$ 同时出现在 ${y_1}$ 的二阶导数中，因此 ${y_1}$ 的相对阶数 ${\rho _1} = 2$ ， ${y_1}$ 及其一阶导与二阶导分别如下：

$\left\{ \begin{split} &{y_1} = \phi \\ &{{\dot y}_1} = \dot \phi = p + q\sin \phi \tan \theta + r\cos \phi \tan \theta \\ & {{\ddot y}_1} = \dot p + \dot r\cos \phi \tan \theta + \dot q\sin \phi \tan \theta + \\ & \quad \dfrac{q\theta \sin \phi} {{\cos ^2}\theta} + q\dot \phi \cos \phi \tan \theta + \\ & \quad \dfrac{r\dot \theta \cos \phi }{{\cos ^2}\theta} - r\dot \phi \sin \phi \tan \theta \\ \end{split} \right.$

(2)

其中控制量 ${{\delta _a}、{\delta _r}}$ 分别出现在滚转加速度 $\dot p$ 和偏航角加速度 $\dot r$ 中。可得式(3)：

${\ddot y_1} = \left[ {\begin{array}{*{20}{l}} {{k_1}}&{{k_2}} \end{array}} \right]\left[ {\begin{array}{*{20}{l}} {{y_{1D}} - \phi } \\ {{{\dot y}_{1D}} - \dot \phi } \end{array}} \right] + {\ddot y_{1D}}$

(3)

其中， $y_{1D}$ 为 $y_1$ 的期望值，将式(2)代入式(3)得到一个包含 ${{\delta _a}、{\delta _r}}$ 的二元方程。由于一个方程中包含两个未知数，因此还需要构建另一个方程，从而求解控制量 ${{\delta _a}、{\delta _r}}$ 。

设 ${y_2} = \beta$ ，可得控制量 ${{\delta _a}、{\delta _r}}$ 同样出现在 ${y_2}$ 的二阶导数中， ${y_2}$ 及其一阶导与二阶导分别如下：

$\left\{ \begin{aligned} &{y_2} = \beta \\ &{{\dot y}_2} = \dot \beta = \left[ - T\cos \alpha \sin \beta + Y -\right.\\ &\quad\left. mV\left( { - p\sin \alpha + r\cos \alpha } \right) + {G_{ya}} \right]/\left( {mV} \right)\\ &{{\ddot y}_2} = \ddot \beta = \left( - \dot T\cos \alpha \sin \beta + T\dot \alpha \sin \alpha \sin \beta \right.-\\ &\quad\left. T\dot \beta \cos \alpha \cos \beta + \dot Y + {{\dot G}_{ya}} \right)/\left( {mV} \right) - \\ &\quad\left( { - \dot p\sin \alpha - pcos\alpha \dot \alpha + \dot r\cos \alpha \sin \alpha \dot \alpha } \right) \end{aligned} \right.$

(4)

式中，T为推力，G_ya为气流坐标系中重力沿y轴方向分量。

同理可得式(5)：

${\ddot y_2} = \left[ {\begin{array}{*{20}{l}} {{k_3}}&{{k_4}} \end{array}} \right]\left[ {\begin{array}{*{20}{l}} {{y_{2D}} - \beta } \\ {{{\dot y}_{2D}} - \dot \beta } \end{array}} \right] + {\ddot y_{2D}}$

(5)

其中 $y_{2D}$ 为y₂的期望值，联立式(3)、(5)可得方程组：

$\left[ {\begin{array}{*{20}{l}} {{{\ddot y}_1}} \\ {{{\ddot y}_2}} \end{array}} \right] = \left[ {\begin{array}{*{20}{l}} {{k_1}\left( {{y_{1D}} - \phi } \right) + {k_2}\left( {{{\dot y}_{1D}} - \dot \phi } \right)} \\ {{k_3}\left( {{y_{2D}} - \beta } \right) + {k_4}\left( {{{\dot y}_{2D}} - \dot \beta } \right)} \end{array}} \right] + \left[ {\begin{array}{*{20}{l}} {{{\ddot y}_{1D}}} \\ {{{\ddot y}_{2D}}} \end{array}} \right]$

(6)

即可解得控制量为

$\left[ {\begin{array}{*{20}{c}} {{\delta _a}} \\ {{\delta _r}} \end{array}} \right] = {B^{ - 1}}\left[ {K\left( {Y_D^U - {Y^U}} \right) + Y_D^{L1} - A} \right]$

(7)

舰载无人机位置控制采用PI控制。整体结构框图如图1所示。

图 1 横侧向着舰自动控制框图

Fig. 1 Diagram of lateral-directional automatic control

下载: 全尺寸图片

3. 扩张鸽群优化算法

3.1 基本鸽群优化算法

基本鸽群优化算法由两个算子组成^[10]，分别为地图与指南针算子和地标算子。在地图与指南针算子中，鸽子主要依赖自己前一次位置和当前全局最优位置来达到更新自己位置的目的。在地标算子中，鸽群通过群体适应度平均值以及每次迭代减半群体数量来加快收敛速度。

1) 地图与指南针算子

设有D维搜索空间，第i只鸽子的位置为X_i=[x_i1 x_i2 … x_iD]，速度为V_i=[v_i1 v_i2 … v_iD]。更新公式为

${{\boldsymbol{V}}_i}(t) = {{\boldsymbol{V}}_i}(t - 1) \times {{\rm{e}}^{ - Rt}} + {\rm rand} \times \left( {{{\boldsymbol{X}}_{{\rm{gbest }}}} - {{\boldsymbol{X}}_i}(t - 1)} \right)$

(8)

${{\boldsymbol{X}}_i}(t) = {{\boldsymbol{X}}_i}(t - 1) + {{\boldsymbol{V}}_i}(t)$

(9)

式中：R为地图与指南针算子，X_gbest为全局最优位置。

2) 地标算子

在地标算子中，由于鸽群中部分个体对地标不熟悉，因此在每次迭代中减半个体数目。剩下的个体通过群体的中心更新位置，如式(10)、(11)：

${N_p}(t) = \frac{{{N_p}(t - 1)}}{2}$

(10)

${{\boldsymbol{X}}_{{\text{center}}}}(t) = \frac{{\displaystyle\sum {{{\boldsymbol{X}}_i}} (t) \cdot F\left( {{{\boldsymbol{X}}_i}(t)} \right)}}{{\displaystyle\sum F \left( {{{\boldsymbol{X}}_i}(t)} \right)}}$

(11)

${{\boldsymbol{X}}_i}(t) = {{\boldsymbol{X}}_i}(t - 1) + {\rm rand} \times \left( {{{\boldsymbol{X}}_{{\text{center}}}}(t - 1) - {{\boldsymbol{X}}_i}(t - 1)} \right)$

(12)

式中：N_p为个体数目；X_center为鸽群中心位置； $F({\boldsymbol{X}}_i\left( t \right))$ 为每只鸽子的适应度函数值。

3.2 扩张鸽群优化算法

为进一步提高基本鸽群优化算法的搜索能力，同时加快收敛速度，本文提出了两项改进方法。

首先在地图与指南针算子中，引入随机因子 $\alpha$ ^[18]，如式(13)和(14)：

$\alpha = \left( {1 + {\text{rand}}} \right){\text{rand}}$

(13)

${{\boldsymbol{V}}_i}(t) = \alpha {{\boldsymbol{V}}_i}(t - 1) \times {{\rm{e}}^{ - Rt}} + {\rm rand} \times \left( {{{\boldsymbol{X}}_{{\text{gbest }}}} - {{\boldsymbol{X}}_i}(t - 1)} \right)$

(14)

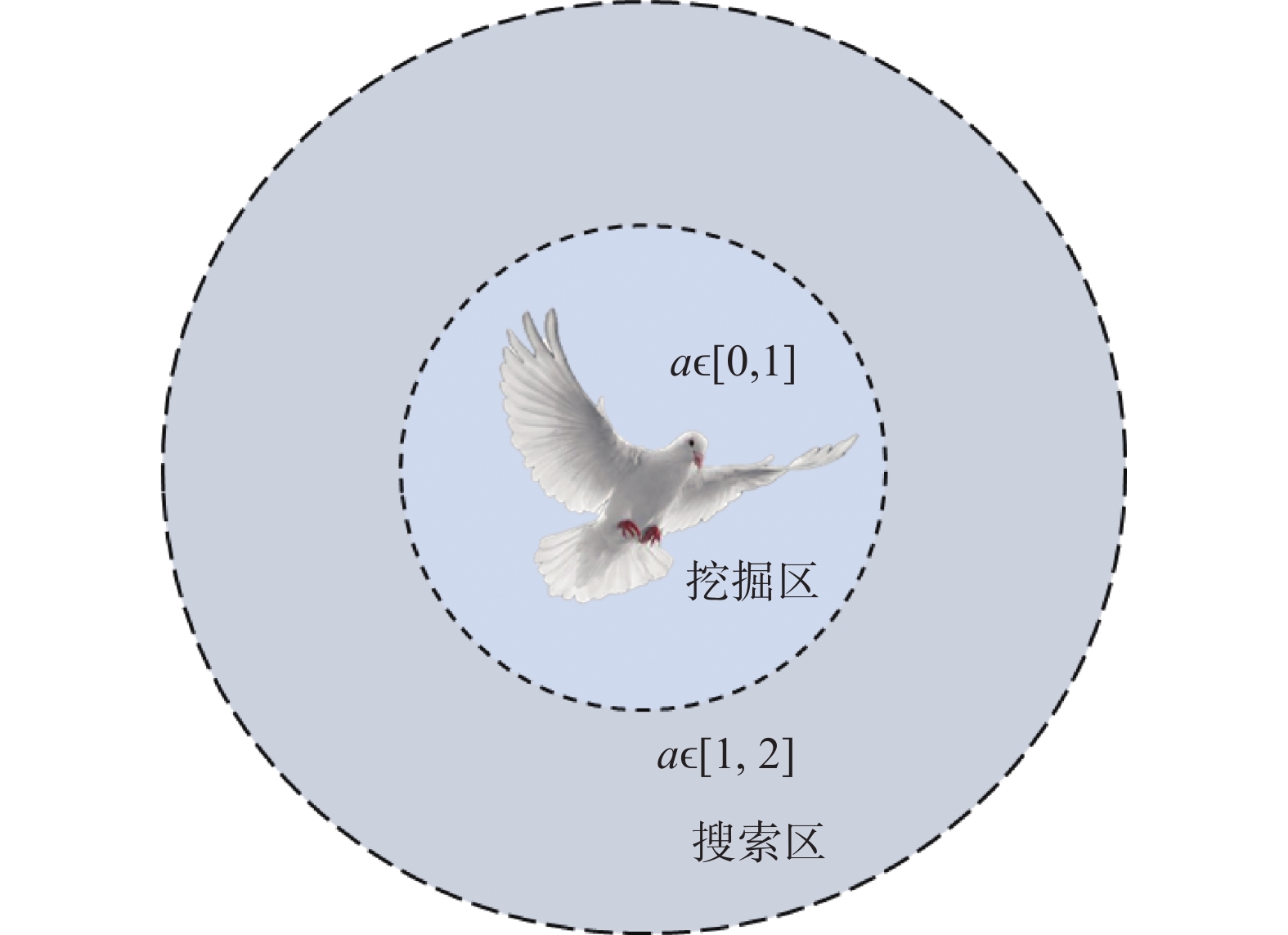
在基本地图与指南针算子中，每只鸽子的速度随着迭代次数的增加逐渐减小，这意味着鸽群总体搜索速度下降，搜索能力减弱，但此时可能并没有靠近全局最优，容易导致“早熟”现象发生。在改进的地图与指南针算子中，随机因子 $\alpha \in \left[ {0,2} \right]$ ，因此在 $\alpha \in \left[ {0,1} \right]$ 时，鸽子速度减小，进行小范围最优解的挖掘，加快收敛速度，而当 $\alpha \in \left[ {1,2} \right]$ 时，鸽子速度增大，进行大范围搜索，增强跳出局部最优的可能性。二维空间鸽群寻优说明图如图2所示。

图 2 二维空间速度更新区域

Fig. 2 2D velocity update area

下载: 全尺寸图片

其次，在地图与指南针算子迭代的中后期，受文献[19]的启发，将鸽群的位置更新策略调整为

${{\boldsymbol{X}}_i}\left( t \right) = {{\boldsymbol{X}}_{{\text{gbest}}}} - n P$

(15)

式中： ${\rm{fa}} = 2\left( {1 - {{\left( {\dfrac{t}{{{{Nc}}_1}}} \right)}^2}} \right)$ ； $n = {\rm{fa}} \times \left( {2{\text{rand}} - 1} \right)$ ； $P = \left| 2{\text{rand}} \times\right. \left.{{\boldsymbol{X}}_{{\text{gbest}}}} - {{\boldsymbol{X}}_i}\left( {t - 1} \right) \right|$ ； ${{Nc}}_1$ 为地图与指南针算子的最大迭代次数。

式(15)表明此时鸽群迭代以当前最优位置为中心，距离0~2的范围内进行搜索，在加快收敛速度的同时保留搜索能力。同时fa以二次函数形式递减，目的是为了在初期削弱当前最优位置对个体的影响。本文所提扩张鸽群优化算法的具体实现流程如图3所示， $Nc_2$ 表示地表算子最大迭代次数。

图 3 扩张鸽群优化算法流程

Fig. 3 Flowchart of Expanded pigeon inspired optimization

下载: 全尺寸图片

4. 仿真及分析

4.1 基准函数测试

为了验证本文所提扩张鸽群优化算法的有效性，首先利用6个基准函数分别对扩张鸽群优化算法、基本鸽群优化算法和粒子群优化算法(particle swarm optimization, PSO)进行对比。基准函数如表1所示。对每种优化算法，6个基准函数分别运行30次，取30次的平均值、最大值、最小值和标准差得到表2。

表 1 基准函数

Table 1 Benchmark functions

函数名	公式	类型
Sphere	${f_1}(x) = \displaystyle\sum\limits_{i = 1}^d {x_i^2}$	单峰
Schwefel_P221	${f_2} = \max \left\{ {\left\| {{x_i}} \right\|} \right\}$	单峰
Schwefel_P222	${f_3} = \displaystyle\sum\limits_{i = 1}^d {\left\| { {x_i} } \right\|} + \prod\limits_{i = 1}^d {\left\| { {x_i} } \right\|}$	单峰
Ackley	$\begin{gathered} {f_4} = - 20\exp \left( { - 0.2\sqrt {\dfrac{1}{d}\displaystyle\sum\limits_{i = 1}^d {x_i^2} } } \right)-\\ \exp \left( {\dfrac{1}{d}\displaystyle\sum\limits_{i = 1}^d {\cos } \left( {2{\text{π} } {x_i} } \right)} \right) + 20 + {\rm{e}} \end{gathered}$	多模态
Rastrigin	$\begin{gathered} {f_5} = \displaystyle\sum\limits_{i = 1}^d {\left( {x_i^2 - 10\cos \left( {2{\text{π} } {x_i} } \right)} \right)} + 10d \\ \end{gathered}$	多模态
Griewank	${f_6} = \dfrac{1}{ {4\;000} }\displaystyle\sum\limits_{i = 1}^d {x_i^2} - \prod\limits_{i = 1}^d {\cos } \left( {\dfrac{ { {x_i} } }{ {\sqrt i } } } \right) + 1\quad$	多模态

表 2 基准函数测试结果

Table 2 Test results of benchmark functions

函数名	优化算法	平均值	最小值	最大值	标准值
Sphere	EPIO	1.07E-56	4.41E-81	3.19E-55	5.73E-56
	PIO	8.74E-28	2.28E-67	2.62E-26	4.71E-27
	PSO	1.68E-07	8.22E-09	7.33E-07	1.82E-07
Schwefel_P221	EPIO	0.0151	5.61E-39	0.2098	0.0468
	PIO	0.0977	6.80E-23	0.7386	0.1422
	PSO	0.0418	5.61E-39	0.4826	0.1172
Schwefel_P222	EPIO	1.45E-32	4.01E-47	4.12E-31	7.39E-32
	PIO	0.0267	1.22E-27	0.1520	0.0429
	PSO	0.0017	4.01E-47	0.0105	0.0026
Ackley	EPIO	8.88E-16	8.88E-16	8.88E-16	0.00E+00
	PIO	1.2323	2.41E-07	3.5854426	0.9943
	PSO	0.7925	5.34E-05	2.1200547	0.8057

续表 2
函数名	优化算法	平均值	最小值	最大值	标准值
Rastrigin	EPIO	0.2428	0.00E+0	7.2834901	1.3074
	PIO	26.2030	3.32E+0	55.725074	10.3730
	PSO	17.6874	3.9799	38.803556	9.2541
Griewangk	EPIO	0.0872	0.0000	0.3383	0.1034
	PIO	0.2476	0.0690	0.5468	0.1201
	PSO	0.1799	0.3383	0.4582	0.1102

由表2可得，本文所提算法在不同类型基准函数测试中表现均为最优，说明其普适性较好。本文同时给出平均值和标准差两种统计方法，其中平均值表明优化结果的中间值，而标准差表明了平均值的可靠性。从标准差来看，扩张鸽群优化算法也均表现最优，说明该算法具备良好的稳定性。

4.2 舰载无人机着舰横侧向控制器参数优化

采用MATLAB/Simulink作为仿真软件，搭建无人机着舰控制模型。将扩张鸽群优化方法用于优化无人机着舰横侧向控制器的参数，并与基本鸽群优化算法，粒子群优化算法进行对比。优化的参数包括位置控制中的K_p、K_i，以及显示模型预测控制器中的4个参数，即k₁、k₂、k₃、k₄。在这4个控制器参数中，k₁和k₃用于控制角度变量，k₂ 和k₄用于控制角速度变量，通过调节这两种参数可以实现快速响应并且减少震荡。适应度函数选择平方误差积分准则(integral of squared error criterion, ISE)，如式(16)：

${\rm{ISE}} = \int_0^\infty | e(t){|^2}{\rm{d}}t$

(16)

优化迭代曲线如图4所示，迭代最终适应度函数值如表3。由扩张鸽群优化算法优化后的变量如表4所示。由图表可得，扩张鸽群优化算法在迭代次数不到一半时已经收敛，且最终收敛的位置相比另外两种算法更加优越。粒子群算法虽然在早期收敛速度较快，但也因此陷入局部最优。

图 4 参数优化迭代曲线

Fig. 4 Parameter optimization iteration curve

下载: 全尺寸图片

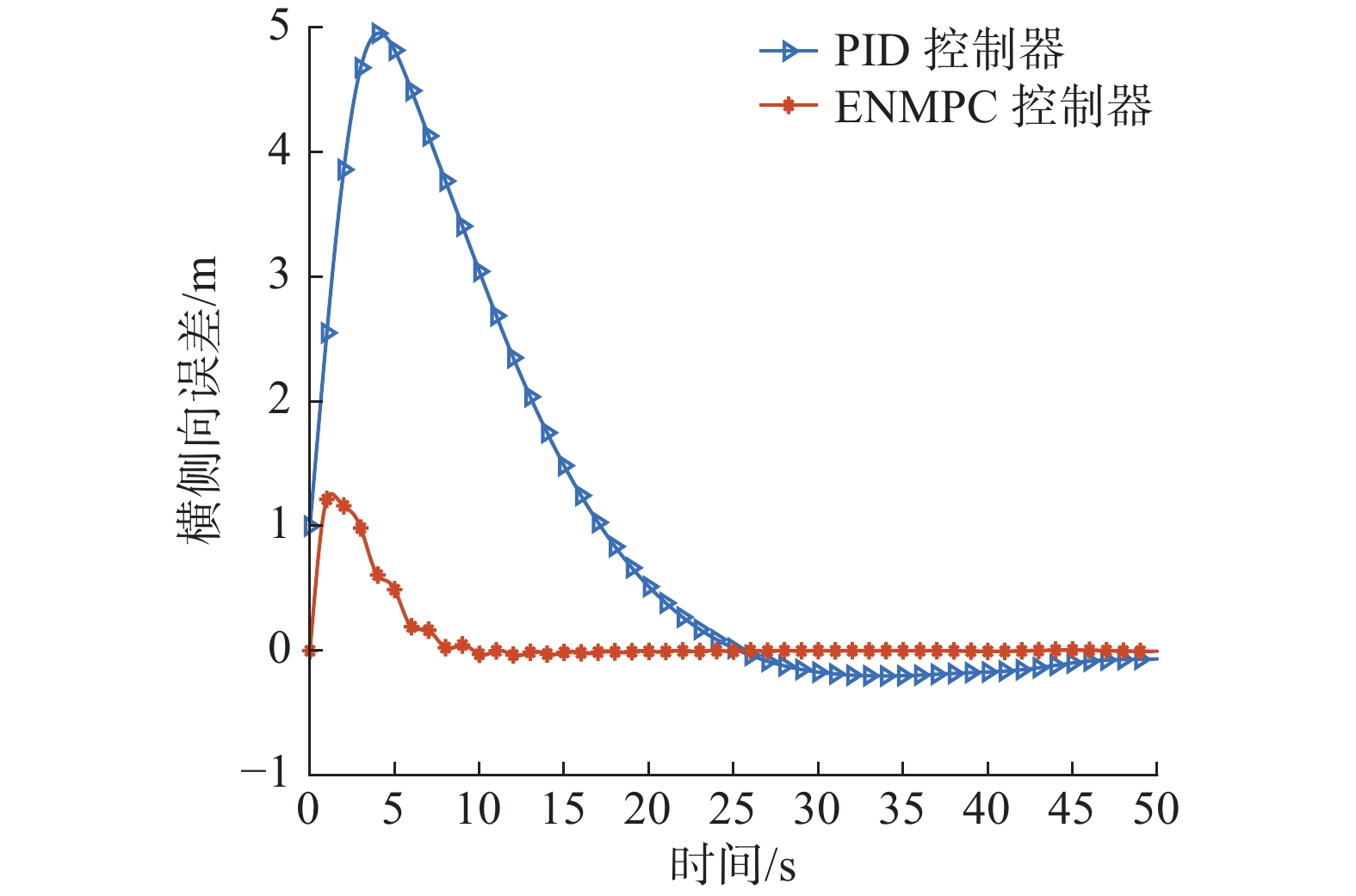
表 3 迭代结果最终值

Table 3 Results of the iteration

优化算法	最终适应度值
EPIO	1.3083E+03
PIO	1.3203E+03
PSO	1.3348E+03

首先给出无环境干扰时，舰载无人机跟踪航母甲板中心线的情况。将参数优化后的显式模型预测控制器与未优化显式模型预测控制器以及PID控制进行对比，如图5。可以看出，PID控制下的舰载机响应最慢，超调最大，最大误差达到4.99 m，且在着舰最后依然有一定的横侧向位置误差，收敛较慢；相比PID控制器，显式模型预测控制的系统响应较快，约在15 s后进入稳态。经过参数优化后，响应超调最小，且振荡相比未优化时更平缓。

表 4 优化后变量

Table 4 Optimized parameters

变量	数值
K_p	0.03
K_i	0.12
k₁	10
k₂	1.7788
k₃	1.7788
k₄	5.3923

图 5 着舰横侧向误差

Fig. 5 Lateral-directional error of carrier landing

下载: 全尺寸图片

考虑舰载无人机在着舰时会有舰尾流以及甲板运动的干扰，而这两类干扰是影响舰载机着舰精度的主要因素，因此加入横侧向舰尾流和甲板运动模型。横侧向舰尾流主要考虑海面大气紊流 ${V_1}$ 和随机性航母尾流扰动 ${V_4}$ ，其中大气紊流与机–船相对距离没有关系，随机尾流的起因是航母运动。甲板运动考虑偏航运动 ${\psi _s}$ (度)，分别如式(17)~(19)：

${V_1} = \frac{{26.59\left( {1 + {{(121.92\varOmega )}^2}} \right)}}{{\left[ {1 + {{(30.48\varOmega )}^2}} \right]\left[ {1 + {{(40.64\varOmega )}^2}} \right]}}$

(17)

${V_4} = \left[ {\rm rand} \right] \times \left[ {\frac{s}{{s + 0.1}}} \right]\sin (10{\text{π}} t)\frac{{0.035{V_{{\text{wod }}}}\sqrt {6.66} }}{{3.33s + 1}}$

(18)

${\psi }_{s}=0.25\mathrm{sin}\left(0.7t\right)+0.5\mathrm{sin}\left(0.1t\right)$

(19)

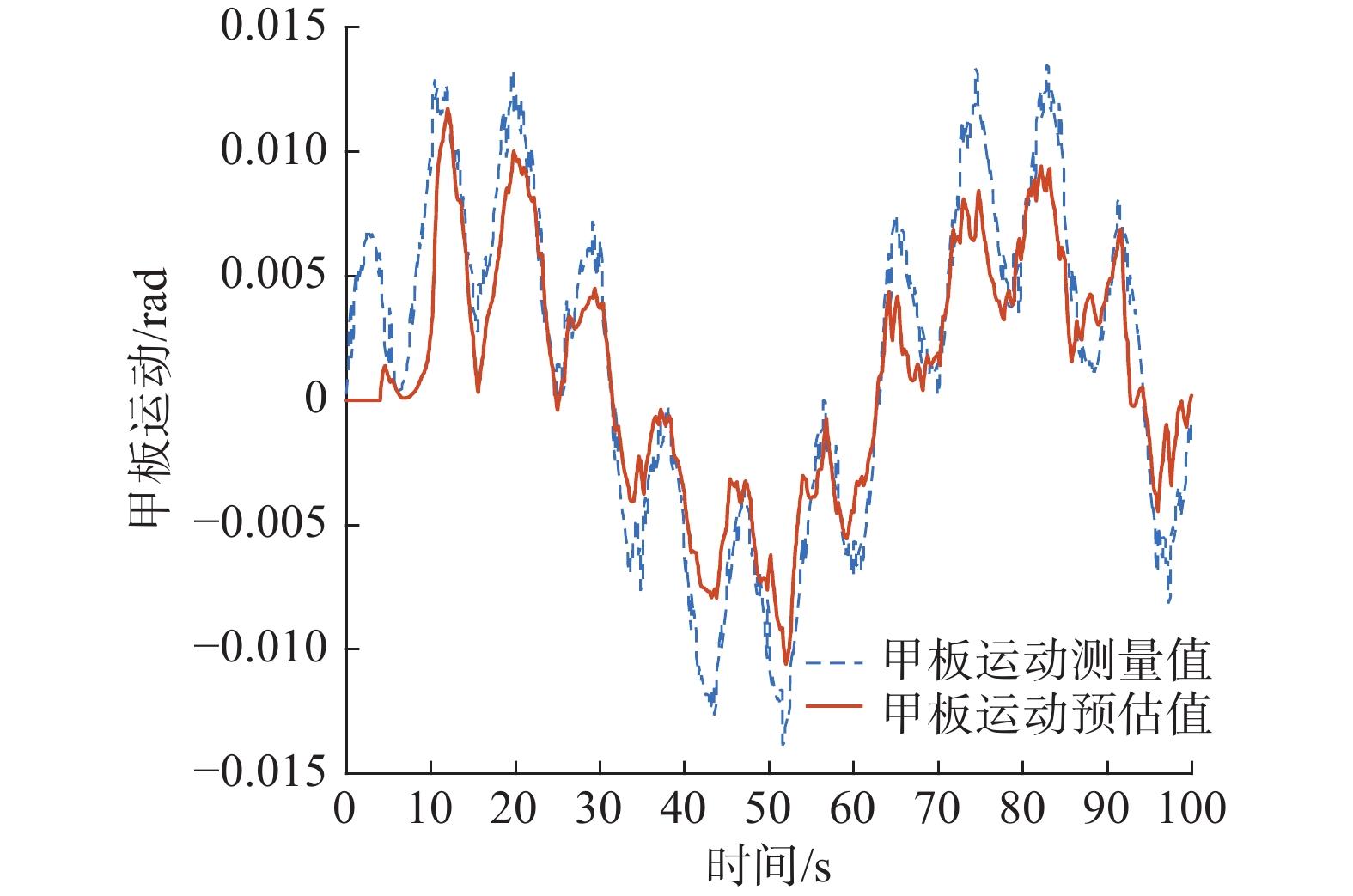
式中： $\varOmega$ 为空间频率； ${V_{{\text{wod }}}}$ 为甲板风。甲板运动采用AR模型进行预测^[20]，图6为取阶数n=20，预测前2 s运动状态下曲线图。

图 6 甲板偏航运动预测

Fig. 6 Deck yaw motion prediction

下载: 全尺寸图片

图7为只加入甲板运动情况下显式模型预测控制与PID控制比较，图8为加入两类干扰时的横侧向跟踪比较。从图7中可以看出，由于已经对甲板运动进行了预估和补偿，甲板运动的干扰在横侧向跟踪中并不明显。

图 7 加入甲板运动时两种控制器横侧向跟踪对比

Fig. 7 Comparison lateral-directional tracking of the two controllers when the deck motion is considered

下载: 全尺寸图片

图 8 加入两类干扰时两种控制器横侧向跟踪对比

Fig. 8 Comparison of lateral-directional tracking of the two controllers when two kinds of disturbances are considered

下载: 全尺寸图片

对比图7与图8可以发现，横侧向舰尾流对舰载无人机着舰时控制影响较大，主要体现在原来的稳态阶段。显示模型预测控制由于具备了在线优化过程，鲁棒性更强，而PID控制对干扰更加敏感，导致出现的偏差更大。

5. 结束语

1）本文设计了一种基于显式模型预测的舰载无人机横侧向姿态控制器，对无人机横侧向着舰进行仿真并与PID控制器进行对比，结果表明显式模型预测控制方法下的系统响应更快，对干扰的鲁棒性更强。

2）本文所提出的扩张鸽群优化算法与基本鸽群优化算法、粒子群优化算法相比具有更好的收敛性，且由基准函数的测试结果表明，扩张鸽群优化算法具有一定的普适性和稳定性。

图 1 横侧向着舰自动控制框图

Fig. 1 Diagram of lateral-directional automatic control

下载: 全尺寸图片

图 2 二维空间速度更新区域

Fig. 2 2D velocity update area

下载: 全尺寸图片

图 3 扩张鸽群优化算法流程

Fig. 3 Flowchart of Expanded pigeon inspired optimization

下载: 全尺寸图片

图 4 参数优化迭代曲线

Fig. 4 Parameter optimization iteration curve

下载: 全尺寸图片

图 5 着舰横侧向误差

Fig. 5 Lateral-directional error of carrier landing

下载: 全尺寸图片

图 6 甲板偏航运动预测

Fig. 6 Deck yaw motion prediction

下载: 全尺寸图片

图 7 加入甲板运动时两种控制器横侧向跟踪对比

Fig. 7 Comparison lateral-directional tracking of the two controllers when the deck motion is considered

下载: 全尺寸图片

图 8 加入两类干扰时两种控制器横侧向跟踪对比

Fig. 8 Comparison of lateral-directional tracking of the two controllers when two kinds of disturbances are considered

下载: 全尺寸图片

表 1 基准函数

Table 1 Benchmark functions

函数名	公式	类型
Sphere	${f_1}(x) = \displaystyle\sum\limits_{i = 1}^d {x_i^2}$	单峰
Schwefel_P221	${f_2} = \max \left\{ {\left\| {{x_i}} \right\|} \right\}$	单峰
Schwefel_P222	${f_3} = \displaystyle\sum\limits_{i = 1}^d {\left\| { {x_i} } \right\|} + \prod\limits_{i = 1}^d {\left\| { {x_i} } \right\|}$	单峰
Ackley	$\begin{gathered} {f_4} = - 20\exp \left( { - 0.2\sqrt {\dfrac{1}{d}\displaystyle\sum\limits_{i = 1}^d {x_i^2} } } \right)-\\ \exp \left( {\dfrac{1}{d}\displaystyle\sum\limits_{i = 1}^d {\cos } \left( {2{\text{π} } {x_i} } \right)} \right) + 20 + {\rm{e}} \end{gathered}$	多模态
Rastrigin	$\begin{gathered} {f_5} = \displaystyle\sum\limits_{i = 1}^d {\left( {x_i^2 - 10\cos \left( {2{\text{π} } {x_i} } \right)} \right)} + 10d \\ \end{gathered}$	多模态
Griewank	${f_6} = \dfrac{1}{ {4\;000} }\displaystyle\sum\limits_{i = 1}^d {x_i^2} - \prod\limits_{i = 1}^d {\cos } \left( {\dfrac{ { {x_i} } }{ {\sqrt i } } } \right) + 1\quad$	多模态

表 2 基准函数测试结果

Table 2 Test results of benchmark functions

函数名	优化算法	平均值	最小值	最大值	标准值
Sphere	EPIO	1.07E-56	4.41E-81	3.19E-55	5.73E-56
	PIO	8.74E-28	2.28E-67	2.62E-26	4.71E-27
	PSO	1.68E-07	8.22E-09	7.33E-07	1.82E-07
Schwefel_P221	EPIO	0.0151	5.61E-39	0.2098	0.0468
	PIO	0.0977	6.80E-23	0.7386	0.1422
	PSO	0.0418	5.61E-39	0.4826	0.1172
Schwefel_P222	EPIO	1.45E-32	4.01E-47	4.12E-31	7.39E-32
	PIO	0.0267	1.22E-27	0.1520	0.0429
	PSO	0.0017	4.01E-47	0.0105	0.0026
Ackley	EPIO	8.88E-16	8.88E-16	8.88E-16	0.00E+00
	PIO	1.2323	2.41E-07	3.5854426	0.9943
	PSO	0.7925	5.34E-05	2.1200547	0.8057

续表 2
函数名	优化算法	平均值	最小值	最大值	标准值
Rastrigin	EPIO	0.2428	0.00E+0	7.2834901	1.3074
	PIO	26.2030	3.32E+0	55.725074	10.3730
	PSO	17.6874	3.9799	38.803556	9.2541
Griewangk	EPIO	0.0872	0.0000	0.3383	0.1034
	PIO	0.2476	0.0690	0.5468	0.1201
	PSO	0.1799	0.3383	0.4582	0.1102

表 3 迭代结果最终值

Table 3 Results of the iteration

优化算法	最终适应度值
EPIO	1.3083E+03
PIO	1.3203E+03
PSO	1.3348E+03

表 4 优化后变量

Table 4 Optimized parameters

变量	数值
K_p	0.03
K_i	0.12
k₁	10
k₂	1.7788
k₃	1.7788
k₄	5.3923

参考文献(20)

[1]	ZHU Qidan, YANG Zhibo. Design of air-wake rejection control for longitudinal automatic carrier landing cyber-physical system[J]. Computers & electrical engineering, 2020, 84: 106637.
[2]	KOO S, KIM S, SUK J. Model predictive control for UAV automatic landing on moving carrier deck with heave motion[J]. IFAC-PapersOnLine, 2015, 48(5): 59–64. doi: 10.1016/j.ifacol.2015.06.464
[3]	马坤. 基于预见控制的无人机着舰控制研究[D]. 南京: 南京航空航天大学, 2017. MA Kun. Research on preview control based carrier landing control for unmanned aerial vehicle[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2017.
[4]	ZHEN Ziyang, JIANG Shuoying, MA Kun. Automatic carrier landing control for unmanned aerial vehicles based on preview control and particle filtering[J]. Aerospace science and technology, 2018, 81: 99–107. doi: 10.1016/j.ast.2018.07.039
[5]	GUAN Zhiyuan, LIU Hu, ZHENG Zewei, et al. Fixed-time control for automatic carrier landing with disturbance[J]. Aerospace science and technology, 2021, 108: 106403. doi: 10.1016/j.ast.2020.106403
[6]	赵东宏. 大展弦比无人机自动着舰技术研究[D]. 南京: 南京航空航天大学, 2018. ZHAO Donghong. The research of carrier landing control of the high-aspect-ratio UAV[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2018.
[7]	LIU Cunjia, CHEN Wenhua, ANDREWS J. Explicit non-linear model predictive control for autonomous helicopters[J]. Proceedings of the institution of mechanical engineers, part G:journal of aerospace engineering, 2012, 226(9): 1171–1182. doi: 10.1177/0954410011418585
[8]	HU Xioabing, CHEN CHEN Wenhua. Model predictive control for non-linear missiles[J]. Proceedings of the institution of mechanical engineers, part I:journal of systems and control engineering, 2007, 221(8): 1077–1089. doi: 10.1243/09596518JSCE394
[9]	SLEGERS N, KYLE J, COSTELLO M. Nonlinear model predictive control technique for unmanned air vehicles[J]. Journal of guidance, control, and dynamics, 2006, 29(5): 1179–1188. doi: 10.2514/1.21531
[10]	DUAN Haibin, QIAO Peixin. Pigeon-inspired optimization: a new swarm intelligence optimizer for air robot path planning[J]. International journal of intelligent computing and cybernetics, 2014, 7(1): 24–37. doi: 10.1108/IJICC-02-2014-0005
[11]	DUAN Haibin, QIU Huaxin. Advancements in pigeon-inspired optimization and its variants[J]. Science China information sciences, 2019, 62(7): 1–10.
[12]	DUAN Haibin, WANG Xiaohua. Echo state networks with orthogonal pigeon-inspired optimization for image restoration[J]. IEEE transactions on neural networks and learning systems, 2016, 27(11): 2413–2425. doi: 10.1109/TNNLS.2015.2479117
[13]	XU Xiaobin, DENG Yimin. UAV power component—DC brushless motor design with merging adjacent-disturbances and integrated-dispatching pigeon-inspired optimization[J]. IEEE transactions on magnetics, 2018, 54(8): 1–7.
[14]	SUN Yongbin, DUAN Haibin, XIAN Ning. Fractional-order controllers optimized via heterogeneous comprehensive learning pigeon-inspired optimization for autonomous aerial refueling hose-drogue system[J]. Aerospace science and technology, 2018, 81: 1–13. doi: 10.1016/j.ast.2018.07.034
[15]	QIU Huaxin, DUAN Haibin. A multi-objective pigeon-inspired optimization approach to UAV distributed flocking among obstacles[J]. Information sciences, 2020, 509: 515–529. doi: 10.1016/j.ins.2018.06.061
[16]	HUO Mengzhen, DUAN Haibin. An adaptive mutant multi-objective pigeon-inspired optimization for unmanned aerial vehicle target search problem[J]. Control theory & applications, 2020, 37(3): 584-591.
[17]	江驹, 王新华, 甄子洋. 舰载机起飞着舰引导与控制[M]. 北京: 科学出版社, 2019.
[18]	徐博, 张大龙. 基于量子行为鸽群优化的无人机紧密编队控制[J]. 航空学报, 2020, 41(8): 323722. XU Bo, ZHANG Dalong. Tight formation flight control of UAVs based on pigeon inspired algorithm optimization by quantum behavior[J]. Acta aeronautica et astronautica sinica, 2020, 41(8): 323722.
[19]	MIRJALILI S, MIRJALILI S M, LEWIS A. Grey wolf optimizer[J]. Advances in engineering software, 2014, 69: 46–61. doi: 10.1016/j.advengsoft.2013.12.007
[20]	於家鹏, 苏本如, 余滋红. 船舶运动极短期预报研究[J]. 舰船科学技术, 1995, 17(1): 10–15. YU Jiapeng, SU Benru, YU Zihong. Research on extremely short-term prediction of ship motion[J]. Ship science and technology, 1995, 17(1): 10–15.

点击查看大图

图(8) / 表(5)

摘要

1. 舰载无人机横侧向数学模型
2. 舰载无人机横侧向控制器设计
3. 扩张鸽群优化算法
3.1 基本鸽群优化算法
3.2 扩张鸽群优化算法
4. 仿真及分析
4.1 基准函数测试
4.2 舰载无人机着舰横侧向控制器参数优化
5. 结束语

基于扩张鸽群优化的舰载无人机横侧向着舰自主控制

doi: 10.11992/tis.202106035

通讯作者: 段海滨. E-mail： hbduan@buaa.edu.cn.

出版历程

Lateral automatic carrier landing control based on expanded pigeon inspired optimization

1. 舰载无人机横侧向数学模型

2. 舰载无人机横侧向控制器设计

3. 扩张鸽群优化算法

3.1 基本鸽群优化算法

3.2 扩张鸽群优化算法

4. 仿真及分析

4.1 基准函数测试

4.2 舰载无人机着舰横侧向控制器参数优化

5. 结束语

出版历程

目录

1. 舰载无人机横侧向数学模型

2. 舰载无人机横侧向控制器设计

3. 扩张鸽群优化算法

3.1 基本鸽群优化算法

3.2 扩张鸽群优化算法

4. 仿真及分析

4.1 基准函数测试

4.2 舰载无人机着舰横侧向控制器参数优化

5. 结束语

通讯作者:
段海滨. E-mail： hbduan@buaa.edu.cn.