近些年来，随着深度学习的兴起，人们看到了人工智能的巨大潜力，同时希望人工智能技术应用到更复杂和尖端的领域。而现实状况是数据分散在各个用户或行业中，用户数据存在隐私上的敏感性和安全性。如何在保护数据隐私前提下进行机器学习模型训练，让人工智能技术发挥出更强大的作用成为一种挑战。

为了让这些隐私数据流动起来，同时应对非独立同分布数据的影响，Google科学家Mcmahan等^[1]提出联邦学习(federated learning)，通过协调大量远程分布式设备在保护用户数据隐私的前提下训练一个高质量的全局模型。

目前的联邦学习算法还存在诸多问题。首先，每个设备CPU、GPU、ISP、电池以及网络连接（3G、4G、5G、WIFI）^[2]等硬件差异导致设备间存在很大的系统异构性。传统的联邦学习方法FedAvg^[1]在规定时间内将没有训练结束的设备简单丢弃，这在现实情况中是不可取的，浪费了大量的计算资源。其次，每个设备的数据分布和类型存在很大的差异^[3]，跨设备的数据是非独立同分布的（non-IID），这是数据的异构性。不同的异构环境中模型的收敛效果差别很大，甚至无法收敛。这些系统级别的异构性给联邦学习带来了极大的挑战。

现有针对异构性问题的分布式优化算法中，大部分都是针对特定异构环境设定的。例如:文献[4-6]提出让所有设备都参与每一轮的训练，虽然在异构数据环境中的收敛性得到了保证，但是这在现实的联邦环境^[1]中是不可行的。这不仅增加了服务器的通信负担，而且参与联邦训练的设备也应随机抽取。也有方法通过共享本地数据来解决数据异构性的问题^[7-8]，但这违背了联邦学习保护用户数据隐私的前提。在联邦设置中，文献[9]通过在服务器端设计基于动量优化器FEDYOGI来加快异构数据环境中全局模型收敛速度，这虽然提高了模型的收敛速度，但却增加了服务器的计算量，在有限的计算资源下不是好的选择。此外，也有研究者利用二阶拟牛顿法优化模型^[10]，在相同的异构环境中，与FedAvg相比达到相同精度下减少了通信轮数，提高了通信效率，但这潜在增加了客户端本地的计算量。

除了数据异构性，每个参与联邦训练的客户端的硬件存在差异，这导致设备间存在很大的系统异构性^[11]。例如：在文献[12-15]中，介绍了在异构环境中目前最新的联邦学习研究进展，在全局模型聚合阶段的更新方式同FedAvg^[1]一样，在指定的时间窗口内，服务器将未完成训练的设备直接丢弃，不允许上传本轮训练的模型参数。各参与训练的设备不能根据自己硬件性能在本地执行可变数量的本地工作，缺乏自主调节能力。

在解决联邦学习异构性的问题上，近邻优化的更新方式广泛地用于研究，包括高效通信分布式机器学习^[16]、联邦学习中公平性和鲁棒性的权衡^[17]。近邻优化在原理上与有偏正则化相同，其中文献[18]中考虑有偏正则化的方法对FedAvg进行重新参数化，提出FedProx，通过有偏正则化约束每个设备学习的本地模型更加接近于全局模型，并允许各参与训练的设备在本地执行可变数量的工作，在异构环境中提供了收敛的保证。由于FedProx在优化全局模型参数 $w$ 时和FedAvg方式相同，通过简单平均本地上传的模型参数来更新全局模型参数，导致全局模型收敛速度慢，缺乏直接对全局模型参数的优化。

受小批量近似更新的元学习机制^[19]的启发，本文提出了基于隐式随机梯度下降优化的联邦学习算法，在本地模型更新阶段通过近邻优化约束本地模型更新更加接近于全局模型，在全局模型聚合阶段通过求解近似全局梯度，利用梯度下降来更新全局模型参数。最终实现全局模型能够在较少的通信轮数下达到更快更稳定的收敛结果。

本文的贡献主要体现在以下3个方面：

1） 区别于已有的方法，不在对全局模型参数进行简单平均。在全局模型聚合阶段，通过利用本地上传的模型参数近似求出平均全局梯度，同时也避免求解一阶导数。

2） 针对异构性导致的全局模型收敛慢甚至无法收敛的问题，区别于现有的联邦学习算法，本文提出基于隐式随机梯度下降优化的联邦学习算法，通过隐式随机梯度下降来更新全局模型参数，能够使全局模型参数实现更加高效的更新，从而可以在有限的计算资源下加快模型的收敛速度。

3） 和现有的工作相比，本文的算法在高度异构的合成数据集上，30轮左右就可以达到FedAvg的收敛效果，40轮左右可以达到FedProx的收敛效果。在相同收敛效果的前提下，本文的算法比FedProx减少了近50%的通信轮数。

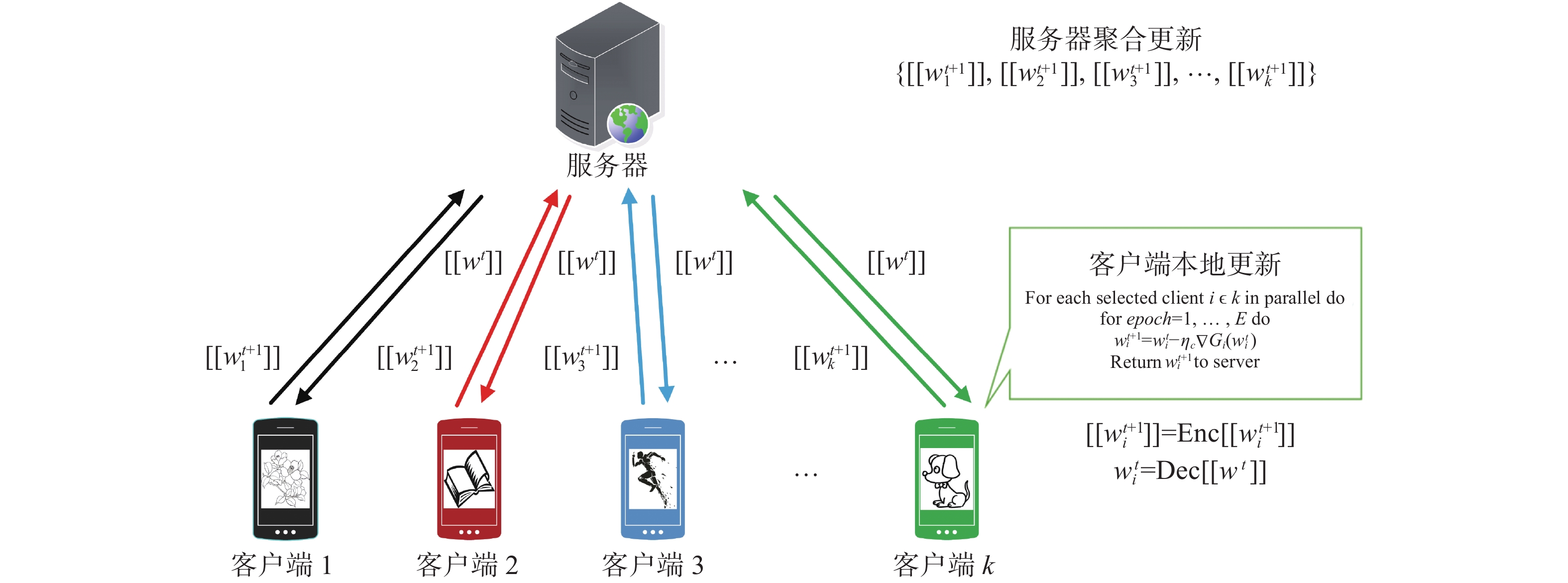
1.   客户端–服务器的联邦学习更新架构

联邦学习更新架构主要有客户端–服务器和去中心化对等计算架构。其中最常用的是客户端–服务器的联邦学习更新架构。训练过程主要分为两个阶段：本地模型更新阶段和全局模型聚合阶段。具体更新过程如图1所示。

图  1  客户端-服务器联邦学习架构

Fig.  1  Federated learning architecture of client and server

下载: 全尺寸图片

1）本地模型更新

在本地模型更新阶段，服务器首先随机选取 $K$ 个客户端，然后服务器发送全局模型参数 $[[{w^t}]]$ 给被选客户端，客户端利用本地数据并行执行 $E$ 个epoch的随机梯度下降，然后将更新后的模型参数经过同态加密算法^[20]加密 $[[w_i^{t + 1}]] = {\text{Enc}}[w_i^{t + 1}]$ ，之后再上传至服务器。

2）全局模型聚合

服务器聚合来自各个客户端加密后的模型参数 $\{ [[w_1^{t + 1}]],[[w_2^{t + 1}]],[[w_3^{t + 1}]], \cdots ,[[w_k^{t + 1}]]\}$ ，对模型参数进行加权平均计算，最后服务器将更新后的全局模型参数 $[[{w^t}]]$ 发送给下一轮被选客户端。客户端接收全局模型参数并将其解密 $w_i^t = {\text{Dec }}[[{w^t}]]$ ，进行下一轮模型参数更新。重复上述过程，直至损失收敛。

2.   隐式随机梯度下降优化的联邦学习算法设计

在本节中，主要介绍联邦近邻优化算法和隐式随机梯度下降优化算法的关键要素。由于联邦学习是通过大量设备与中央服务器协同学习一个最优的全局模型，因此我们的最终目标是最小化：

式中： ${w_k}$ 是设备 $k$ 在本地迭代过程中所得的近似最优解； $w$ 是需要求解全局模型的最优解； ${F_k}\left( {{w_k}} \right): = $ $ {{\bf{E}}_{{x_k} \sim {\mathcal{D}_k}}}\left[ {\mathcal{L}\left( {f\left( {{w_k},{x_i}} \right),{y_i}} \right)} \right]$ ,每个设备本地数据 ${x_k}$ 服从不同的分布 ${\mathcal{D}_k}$ ,损失函数是预测值与真实值之间的差。式(1)包含两方面的优化过程：1）在本地模型训练阶段，每个设备通过全局模型参数 $w$ 学习一个本地近似最优 ${w_k}$ ；2）在全局模型聚合阶段，服务器通过各设备上传的 ${w_k}$ 利用隐式随机梯度下降来调整全局模型参数 $w$ ，使 $w$ 与所有 ${w_k}$ 的平均距离较小。具体的算法流程为：

输入　 ${w^0}$ 随机初始化参数， $N$ 总设备;

输出　最终的全局模型参数 ${w^{t + 1}}$ 。

1) FOR 全局轮数 $t = 0,1, \cdots ,T - 1$ ;

2) Server以概率 ${p_k}$ 随机选取 $K$ 个设备并指定固定学习率 ${\eta _c}$ ;

3) Server发送当前全局模型 ${w^t}$ 给所选设备;

4) 每个设备 $k = 1,2, \cdots ,K$ 并行计算： $ {F_k}\left( {{w_k}} \right) = $ $ \dfrac{1}{{{n_k}}}\sum\limits_{i \in {n_k}} {\mathcal{L}\left( {f\left( {{w_k},{x_i}} \right),{y_i}} \right)} $ ；

5) $w_k^{t + 1} = {\text{arg}}\mathop {{\text{min}}}\limits_{{{{w}}_{{k}}}} \left[ {{F_k}\left( {{w_k}} \right) + } {\dfrac{\lambda }{2}\left\| {{w_k} - {w^t}} \right\|_2^2} \right]$ ;

6) 重复4)~ 5)，结束并行计算，每个设备将计算结果 $ w_k^{t + 1} $ 传至Server；

7) Server以固定轮数衰减的学习率 ${\eta _g}$ 对 $\lambda \left( {{w^t} - w_k^ * } \right)$ 做梯度下降更新全局模型参数：

8) Server将更新后的模型参数 ${w^{t + 1}}$ 发送给Clients;

9) 重复2)~8) $t$ 次；

10) END

在算法1中，步骤4)~6)为本地模型训练阶段，7)~9)为Server全局模型更新阶段，然后将更新后的模型参数发送给下一轮参与训练的设备。不断重复以上过程，直至模型损失收敛。

2.1   联邦近邻优化

在本地模型训练阶段，主要在本地模型更新时引入带参数的近邻算子约束本地模型更新更加接近于全局模型，这种本地优化算法被称为FedProx算法^[18]，每个设备 $k$ 的本地目标函数被重新定义为

式中： $\lambda $ 是一个约束本地模型和全局模型差异的超参数； ${w^t}$ 表示在第 $t$ 轮服务器聚合更新之后的全局模型参数。

2.2   基于隐式随机梯度下降的全局模型更新优化

本地训练结束后，每个设备将更新后的模型参数 $w_k^{t + 1}$ 上传至服务器，服务器通过聚合本地模型参数更新全局模型参数。从加快全局模型收敛速度的目标出发，在服务器全局模型聚合阶段利用隐式随机梯度下降算法对全局模型参数进一步优化，使其能够在有限的资源下以更少的通信轮数达到更快更稳定的收敛效果。

由于客户端本地目标函数为 $\mathop {{\text{min}}}\limits_{{w_k}} {\text{ }}{G_k}\left( {{w_k}} \right) = $ $ {F_k}\left( {{w_k}} \right) + \dfrac{\lambda }{2}\left\| {{w_k} - {w^t}} \right\|_2^2$ ，假设 $w_k^ * $ 是目标函数 ${G_k}\left( {{w_k}} \right)$ 的最优解，且函数 ${F_k}\left( {{w_k}} \right)$ 可微。由一阶最优条件可以得到：

由链式法则可以得到：

所以 $\nabla {G_k}\left( {{{\boldsymbol{w}}^t}} \right) = \lambda \left( {{{\boldsymbol{w}}^t} - {\boldsymbol{w}}_k^ * } \right)$ ，式（4）展现了全局模型的梯度估计可以通过求解当前任务的近似更新来计算。在第 $t$ 轮，所选设备在本地数据集上利用随机梯度下降更新E轮后，求出近似最优解 $w_k^{t + 1}$ 。服务器通过式(4)可以计算出平均的全局梯度:

由于精确的本地最优解 $ w_{k}^{*} $ 很难去估计，本文用次优解 $w_k^{t + 1}$ 来代替 $w_k^ * $ ，因此全局模型参数更新为

式中： ${S_t}$ 为K个设备的子集； $t$ 为当前训练轮数； ${\eta _g} = \dfrac{1}{t}{\eta _{gi}}$ 为按固定轮数衰减的学习率； $ {\eta _{gi}} $ 为初始化学习率，在训练模型初期用较大的学习率对全局模型进行优化，随着通信轮数的不断增加学习率逐步减小，有效保证了全局模型在训练过程中能以较快的速度逐步趋于稳定。更新后的 ${w^{t + 1}}$ 作为下一轮训练的全局模型参数。

从式(3)~(6)推导过程很容易看出，本文提出基于隐式随机梯度下降优化的联邦学习算法是直接对全局模型参数进行优化，而不是简单平均所有设备上传的本地模型参数作为更新后的全局模型参数。因为 $\nabla {G_k}\left( {{w^t}} \right) = \lambda \left( {{w^t} - w_k^ * } \right)$ ，所以在服务器端只需通过 $\lambda \left( {{w^t} - \dfrac{1}{K}\displaystyle\sum\limits_{k \in {S_t}} {w_k^ * } } \right)$ 就可以得到平均全局模型梯度，因此避免了求解一阶导数，然后利用随机梯度下降对全局模型参数进行更新。相比于FedProx，本算法在信息比较冗余的情况下能更高效地利用有效信息。其次，在迭代的过程中也会很快收敛到最小值附近，加快模型的收敛速度。

3.   实验与结果

为了验证本文提出的隐式随机梯度下降优化算法的有效性，本文在3个真实数据集和3个合成数据集上进行实验，在分类和回归任务上进行评估，并与当前具有代表性的解决异构性问题的方法FedProx^[18]以及经典的FedAvg^[1]算法进行比较。

3.1   实验设置

在Linux系统下，包括2块GeForce GTX 1080 Ti和1块GeForce GTX TITAN X的服务器上进行仿真实验，代码使用Tensorflow框架实现，基于Python3来实现基于隐式随机梯度下降优化的联邦学习算法。其中，训练轮数、每轮迭代次数、选择设备数量、学习率等超参数设置如表1所示。

为了保证评估方法与结果的公平性，本文提出的方法与FedProx、FedAvg使用了相同的本地求解器，在模拟系统异构设置时，掉队的设备数量分别设置为0%、50%、90%。生成合成数据集本文使用了和FedProx类似的方法，通过式（7）生成本地数据：

式中： $ W\in {ℝ}{10\times 60}；x\in {ℝ}{60}；b\in {ℝ}{10}。 $ 通过式（7）生成30个设备的数据集，同样每轮随机抽取10个参与训练。

3.2   3个真实数据集和模型

Sent140^[21]是一个Twitter带有表情的文本信息情感分类数据集，该任务使用的是一个两层LSTM，包含256个隐藏层单元，每个Twitter帐户对应一个设备。该模型以25个字符序列作为输入，通过两个LSTM层和一个全连接层，每个训练样本输出一个字符。

MNIST^[22]是一个0~9手写体数字识别数据集，在这个任务上利用逻辑回归的方法研究手写数字图像分类问题。为了生成非独立同分布数据，本文将数据随机分布在1000个设备中，每个设备只有2种数字。模型的输入是28 $ \times $ 28维的图像，输出是0~9这10个数字的标签。

EMNIST^[23]是MNIST数据集的扩展，包含0~9数字和26个英文字母的大小写，构成了更大难度的62类手写字符图像分类任务，但在实验中只随机抽取10个小写字母，每个设备分配5个类，在这个任务上利用逻辑回归的方法研究图像分类问题。模型的输入是28 $ \times $ 28维的图像，输出是a~j这10个类的标签。

对于以上所有数据集，客户端的本地数据分配遵循幂律分布^[24]。本文在本地分配80%为训练集，20%为测试集。各设备数据集组成如表2所示。

3.3   合成数据集实验结果分析

首先在第1个实验中，为了验证本文的算法在异构数据集上有更快的收敛速度，本文在3组合成数据集上进行实验，分别是Synthetic_0_0、Synthetic_0.5_0.5、Synthetic_1_1，从左到右数据异构性逐渐增强，异构性越强，对模型收敛影响越大。本文通过损失的减小速度和梯度方差^[25]的变化来衡量模型的收敛速度，结果如图2所示。为了证明本文方法的公平性和有效性，约束项 $\lambda $ 统一设置成相同的值。由图2训练损失和梯度方差可以看出，本文的方法在第30轮左右达到了FedAvg的收敛效果，在第40轮左右达到了FedProx的收敛效果，并且40轮以后还在继续收敛。梯度方差（variance of local gradient, VLG）越小表示越稳定，收敛性越好。VLG可表示为

图  2  合成数据集实验结果分析

Fig.  2  Analysis of experimental results of synthetic datasets

下载: 全尺寸图片

实验中，通过使所有设备执行相同的工作量来模拟不存在系统异构性的情况，随着数据异构性增强，全局模型收敛结果最终会趋于某个区间，因此本文取最后一半通信轮数的平均测试精度作为模型好坏的评判标准，在合成数据集上平均测试精度如表3所示，可以看出本文提出的算法平均测试精度普遍高于FedProx和FedAvg。

3.4   真实数据集实验结果分析

在本实验中，为了验证本文提出的算法在高度系统异构性和数据异构性环境下的整体效果，本节在3个联邦学习常用真实数据集和一个合成数据集上比较不同算法的稳定性和收敛效果，其中Synthetic_1_1客户端本地类别设置为5，实现在数据异构性基础上模拟不同系统异构性的联邦设置。

本文通过约束设备的本地工作量，使每个设备训练指定的Ｅ来模拟系统的异构性，对于不同的异构设置，随机选择不同的E(E<20)分配给0%、50%和90%当前参与训练的设备。当掉队者为0%时，代表所有设备执行相同的工作量(E=20)。在指定的全局时间周期内，当E<20时，FedAvg会丢掉这些掉队者，本文的算法和FedProx会合并这些掉队者，不同的是本文在全局模型聚合阶段会有效地使用合并掉队者的模型参数，利用隐式随机梯度下降对全局模型进一步优化。真实数据集上的训练损失如图3所示，从上到下3行图片分别代表0%、50%和90%的掉队者。随着迭代轮数的不断增加，平均损失逐渐趋于稳定，从图3中可以看出本文提出的算法的收敛速度明显优于Fedavg和FedProx。

图  3  真实联邦数据集实验结果分析

Fig.  3  Analysis of experimental results of realistic federated datasets

下载: 全尺寸图片

表4给出了在高度异构环境下模型的平均测试精度，从表中可以看出掉队者为90%时，本文提出的算法的平均测试精度最高，其次是FedProx。本文算法在MNIST数据集上比FedProx高5%。实验中，在Sent140数据集上通过设置相同超参数进行比较不同算法运行时间，在通信轮数为200的情况下，FedAvg、FedProx和本文所提算法运行时间分别为67 min、108 min、108 min。

4.   结束语

本文提出了一种基于隐式随机梯度下降优化的联邦学习算法。全局模型聚合阶段不再是简单的平均各设备上传的模型参数，而是利用本地上传的模型参数近似求出全局梯度，同时避免求解一阶导数。 利用随机梯度下降对全局模型参数进行更新，在信息冗余的情况下能更准确地利用有效信息，随着通信轮数不断增加，全局模型会很快收敛到最小值附近。在3个合成数据集和3个真实数据集上的实验结果充分表明：该算法能够在不同异构环境中均表现出更快更稳健的收敛结果，显著提高了联邦学习在实际应用系统中的稳定性和鲁棒性。