Image super-resolution reconstruction based on widely activated deep residual networks
-
摘要: 为了得到更好的图像评价指标，均方误差损失是大多数现有的与深度学习方法结合的图像超分辨率技术都在使用的目标优化函数，但大多数算法构建出来的图像因严重丢失高频信息和模糊的纹理边缘而不能达到视觉感受的需求。针对上述问题，本文提出融合感知损失的广泛激活的非常深的残差网络的超分辨率模型，通过引入感知损失、对抗损失，并结合平均绝对误差组成新的损失函数，通过调整不同损失项的权重对损失函数进行优化，提高了对低分率图像的特征重构能力，高度还原图像缺失的高频信息。本文选取峰值信噪比(peak signal-to-noise ratio, PSNR)和结构相似度(structural similarity, SSIM)两个国际公认的评判指标作为客观评判标准，更换数据集进行实验分析、结果对比，在主观视觉上直观观察效果，结果从不同角度证明本文方法性能较对比模型有所提升，证明了引入感知损失后，模型更好地构建了低分辨率图的纹理细节，可以获得更好的视觉体验。Abstract: To obtain good image evaluation indexes, the mean squared error loss is used as an objective optimization function in image super-resolution technologies combined with the deep learning method. However, most constructed images cannot meet the visual experience requirement due to the serious loss of high-frequency signals and fuzzy texture edges. In response to the above problems, in this paper, we propose a super-resolution model for a widely activated deep residual network combining perceptual loss. A new loss function is formed by introducing perceptual and adversarial losses and is optimized by adjusting the weight of different losses. The loss function is optimized to improve the feature reconstruction ability of low-resolution images and highly restore the high-frequency information missing from the images. Two internationally recognized evaluation indicators, namely, peak signal-to-noise ratio and structural similarity, are selected as objective evaluation criteria. A comparative analysis is performed on different datasets, and the images produced are subjected to direct and subjective observations. The results show that the performance of the proposed method is improved in different aspects in comparison with the compared models. Hence, after the introduction of perceptual loss, the model can effectively reconstruct the texture details of low-resolution images and offer an outstanding visual experience.
-
如今，图像处理技术和信息交互快速发展，图像作为极其重要的信息载体，在公共安防、医学诊疗、卫星遥感等应用领域中愈发重要，但环境和噪声等因素的干扰，导致图像出现质量低或者细节的纹理信息缺乏等问题[1]。图像超分辨率(super resolution, SR)，特别单图像超分辨率(single image super-resolution, SISR)，几十年来受到广泛关注。单图像超分辨率为了通过技术手段将低分辨率(low-resolution, LR)图像重新构建为高分辨率(high-resolution, HR)图像，使其具有良好的高频、纹理和边缘信息。经过几十年发展，图像超分辨率逐渐被分为基于插值[2-3]、基于重建[4]和基于学习[5]三大类。
基于插值和重建超分辨率算法属于传统算法，都运用经典的数学模型算法，但随着放大因子的增大，这两种算法提供的用于重新构建高分辨率图像的细节信息资源不足的弊端逐渐显露，使得这些传统算法很难达到重建高频信息的目的。
深度学习高速发展以来，图像重建领域也开始使用深度学习模型来完成特定任务。2014年，Dong等[6]最先将卷积神经网络应用到图像超分辨率任务上，提出了超分辨率卷积神经网络(super-resolution convolutional neural network，SRCNN)模型，该模型进行端到端的图像对训练，在当时大大提高了重建效果，同时也开辟了超分辨率技术的新时代。2016年，Kim等[7]将超分辨率任务与残差思想进行结合，提出了使用非常深的卷积网络超分辨率(super-resolution using very deep convolution network, VDSR)模型，同时将网络的深度增加到了20层，证明了深层网络能提取出更多的特征，取得更好的重建效果。Lim等[8]通过对残差结构的改进，提出增强型深度超分辨率网络 (enhanced deep super-resolution network, EDSR)模型，通过移除批规范化处理[9](batch normalization, BN)操作，增加层数，提取更多特征，从而获得更满意的结果。
针对上述模型中存在的对不同层的图像信息使用率不足等问题，本文提出了融合感知损失的广泛激活的深度残差网络的超分辨率模型(widely-activated deep residual network for super-resolution combining perceptual loss, PWDSR)，通过已训练的VGG模型[10]提取激活前的特征，使用激活前的特征会克服两个缺点：第一，深层网络中，激活后得到的稀疏特征能够提供的监督效果非常弱，影响性能；第二，激活后的特征会使得重建后的图像与真实图像在亮度上有所差异。融合感知损失更着眼于纹理而不是目标物体。
本文的主要贡献包括以下方面：
1) 使用权重归一化代替批量归一化，提高了学习率和训练、测试准确率;
2) 使用预训练的深度模型提取激活前的特征得到感知损失，通过构建的图像与真实图像计算对抗损失，并结合图像的像素损失，构建了新损失函数;
3) 使用全局跳跃连接避免梯度消失的问题，促进梯度的反向传播，从而加快训练过程；
4) 实验证明了本文提出的损失函数改进在不同数据集上可以取得更好的评价指标，在主观视觉效果也有所提高；
5) 本文提供了高倍重建任务中优化损失函数、调整残差块等新的研究方向。
1. 相关工作
1.1 超分辨率网络
从超分辨率卷积神经网络[6](SRCNN)首次提出端到端卷积神经网络作为新的映射方式开始，超分辨率与卷积神经网络模型越来越密切。
1.1.1 上采样
超分辨率卷积神经网络[6](SRCNN)对图像进行上采样，在高分辨率特征空间上计算卷积导致其效率是低分辨率空间的S2倍(S为放大因子)，因此效率低下。另一个有效的替代方案是子像素卷积[11](sub-pixel convolution)，该卷积比反卷积层引入更少的伪像误差。
1.1.2 标准化
从3层的超分辨率卷积神经网络[6](SRCNN)到160层的多尺度超分辨率网络[8](multi-scale deep super-resolution, MDSR)，图像超分辨率网络越来越深入，训练变得更加困难。批量归一化[9](batch normalization, BN)在许多任务中能解决训练困难的问题，例如SRResNet[12](super-resolution residual network)中使用了批量归一化。
BN通过再次校准中间特征的均值和方差来解决训练深度神经网络时内部协变量偏移的问题。简单来说，如果忽略BN中可学习参数的重新缩放，那么训练期间可用训练小批量的均值和方差对每一层的特征进行归一化：
$$ \hat x = \frac{{{x_B} - {{\rm{E}}_B}\left[ {{x_B}} \right]}}{{\sqrt {{{\rm{Var}}_B}\left[ {{x_B}} \right] + \varepsilon } }} $$ (1) 式中：xB是当前训练批次的特征，它是一个较小的值用来避免零除。然后将一阶和二阶统计信息更新为全局统计信息：
$$ {\rm{E}}\left[ x \right] \leftarrow {{\rm{E}}_B}\left[ {{x_B}} \right] $$ (2) $$ {\rm{Var}}\left[ x \right] \leftarrow {{\rm{Var}}_B}\left[ {{x_B}} \right] $$ (3) 其中←表示分配移动线。这些全局统计信息将用于标准化：
$$ {\hat x_{\rm{test}}} = \frac{{{x_{\rm{test}}} - {\rm{E}}\left[ x \right]}}{{\sqrt {{\rm{Var}}\left[ x \right] + \varepsilon } }} $$ (4) 但BN用于超分辨率任务时存在以下问题：1)图像SR通常仅使用较小的图像块(48×48)来加快训练速度，小图像块的均值和方差相差很大，影响统计数据；2)图像SR网络中没有使用正则化器会过度拟合训练数据集；3)图像SR网络的训练和测试时使用不同公式会降低密集像素值预测的准确性。
1.1.3 跳跃连接
跳跃连接在深层神经网络中具有优良表现，其可以兼顾低级特征和高级特征。非常深的卷积网络超分辨率[7](super-resolution using very deep convolution network, VDSR)模型使用全局跳跃连接。残差密集网络[13](RDN)使用所有卷积层的分层特征。
1.1.4 分组卷积和深度可分离卷积
分组卷积将特征按通道划分为多个组，并分别在组内执行卷积，然后进行串联以形成最终输出。在组卷积中，参数的数量可以减少g倍，其中g是组数。
深度可分离卷积是深度非线性卷积(即在输入的每个通道上独立执行的空间卷积)，然后是点卷积(即1×1卷积)。也可以将其视为特定类型的组卷积，其中组数g是通道数。
1.2 广泛激活的深度残差网络
广泛激活的深度残差网络[14](widely-activated deep residual network for super-resolution, WDSR)在ReLU激活层之前扩展特征，同时追求不会额外增加运算量。该模型压缩残差等价映射路径的特征，同时扩展激活前的特征，如图1所示，并与增强型深度超分辨率网络[8](EDSR)中的基础残差块(图1(a))进行对比。WDSR-A中的(图1(b))具有细长的映射路径，在每个残差块中激活之前都具有较宽的(2~4倍)通道。WDSR-B(图1(c))具有线性低秩卷积堆栈，同时在不额外增加运算量的情况下加宽激活范围(6~9倍)。首先使用1×1卷积核增加通道数，在ReLU激活层之后使用有效的线性低秩卷积，用两个低秩的卷积核替换一个大的卷积核(1×1卷积核降低通道数，3×3卷积核执行空间特征提取)。在WDSR-A和WDSR-B中，所有ReLU激活层仅应用于两个较宽的功能部件(具有较大通道的功能部件)之间。
图 1 广泛激活的残差块与基础残差块的对比Fig. 1 Comparison of the residual block with wide activation and the original residual block
下载:
全尺寸图片
2. 本文模型
受增强型超分辨率生成对抗网络[15](enhanced super-resolution generative adversarial networks, ESRGAN)中使用感知域损失的启发，本文针对广泛激活的深度残差网络存在对不同层级图像信息使用不足的问题，引入感知域损失，通过调整损失权重进行优化。本文网络模型如图2所示。
图 2 融合感知损失的广泛激活的深度残差网络的超分辨率模型Fig. 2 Widely-activated deep residual network for super-resolution combining perceptual loss下载:
全尺寸图片
本文调用已训练的VGG19模型作为特征提取器。VGG网络模型[10]如图3所示。
图 3 VGG结构模型Fig. 3 VGG structure model下载:
全尺寸图片
2.1 权重归一化
由于批量归一化干扰图像超分辨率的准确性，故本文使用权重归一化(weigh normalization, WN)来代替批量归一化。权重归一化是神经网络中权重向量的重新参数化，将这些权重向量的长度与其方向解耦，使其不会在小批量中引入示例之间的依赖关系，并且在训练和测试中具有相同的表示形式。输出y的形式为
$$ {\boldsymbol{y}} = {\boldsymbol{w}} \cdot {\boldsymbol{x}} + b $$ (5) 式中：w是k维权重向量；b是标量偏差项；x是输入的k维向量。WN使用以下参数重新参数化权重向量：
$$ {\boldsymbol{w}} = \frac{g}{{\left\| {\boldsymbol{v}} \right\|}}{\boldsymbol{v}}$$ (6) 其中，v是一个k维矢量，g是一个标量，||v||表示v的欧几里得范数。通过这种形式化，得到||w||=g，而与参数v无关。对于图像超分辨率，WN只是一种重新参数化技术，并且具有完全相同的表示能力，因此不会影响准确性。同时，WN可以提高学习率，并提高训练和测试准确性。
2.2 损失函数改进
模型重新构建图像的结果很大程度上取决于损失函数的选择，一般超分辨率模型选择平均绝对误差(mean absolute error, MAE)或者均方误差(mean-square error, MSE)作为优化的目标，原因是在测试时可以获得较高的评价指标，但是在进行8倍等大尺度的超分辨率重建任务中，重新构建的图像缺失大量高频信息，导致构建的图像不能达到视觉要求。本文模型使用感知损失函数lp，像素损失函数l1和对抗损失函数lg，通过配置3种损失函数不同权重使其更好地对高频信息进行重新构建，总损失函数可表示为
$$ l = {\lambda _1}{l_{\text{p}}} + {\lambda _2}{l_1} + {\lambda _3}{l_{\rm{g}}} $$ (7) 其中，λi代表调节各个损失项权重的正则因子，i = 1, 2, 3。
为了在重建时保证重建图像与对应低分辨率图像在低频部分保持图像结构的一致性，像素损失使用平均绝对误差，公式为
$$ {l_1} = \frac{1}{n}\sum {\left| {S - H} \right|} $$ (8) 式中：S代表生成图像；H代表真实高分辨率图像；n代表网络超参数batch的大小。
根据生成对抗网络的思想，在网络重建出一幅高分辨率图像之后，与其对应真实高分辨率图像进行比较计算，假设N个batch，生成n个标签，公式为
$$ {l_{\rm{g}}} = \left\{ {{r_1},{r_2}, \cdots ,{r_N}} \right\} $$ (9) $$ {r_n} = - \left[ {{y_n} \cdot \log \left( {\sigma \left( {{x_n}} \right)} \right) + \left( {1 - {y_n}} \right) \cdot \log \left( {1 - \sigma \left( {{x_n}} \right)} \right)} \right] $$ (10) 其中，σ(xn)为sigmoid函数，可以把x映射到(0, 1)之间：
$$ \sigma \left( x \right) = \frac{1}{{1 + {{\rm{e}}^{ - x}}}} $$ (11) 本文使用的特征是预训练的深度网络激活层前的特征。公式为
$$ {l_{{p}}} = \sum\limits_{i = 1}^N {\frac{1}{{{C_j}{H_j}{W_j}}}\left[ {{{\left\| {{\phi _j}\left( p \right) - {\phi _j}\left( q \right)} \right\|}_1}} \right]} $$ (12) 式中：p、q分别代表真实高分辨率图像和生成图像；φ表示预训练的神经网络；j表示该网络的第j层；Cj×Hj×Wj为第j层特征图的形状，使用的是每个卷积模块的激活值。
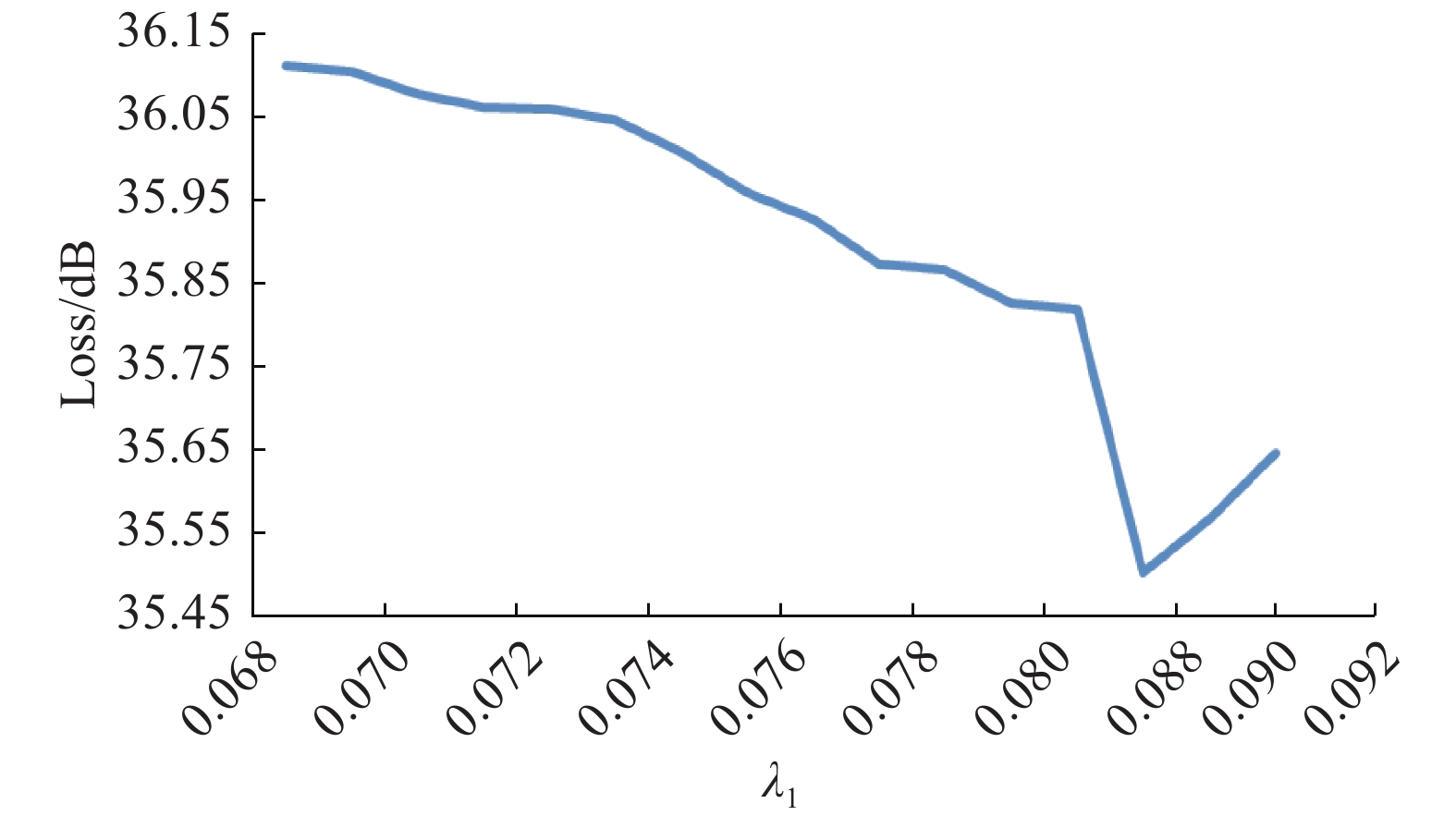
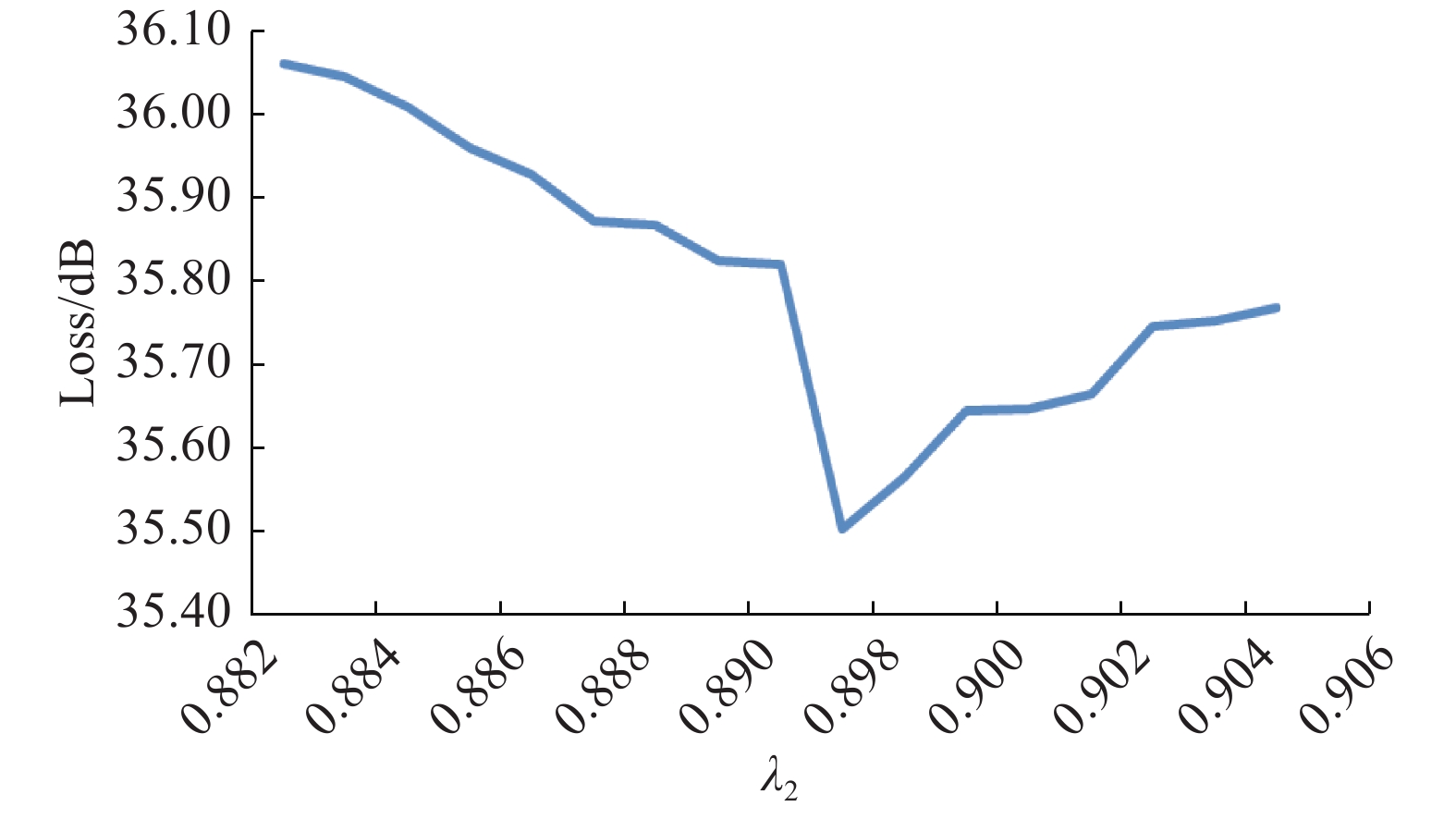
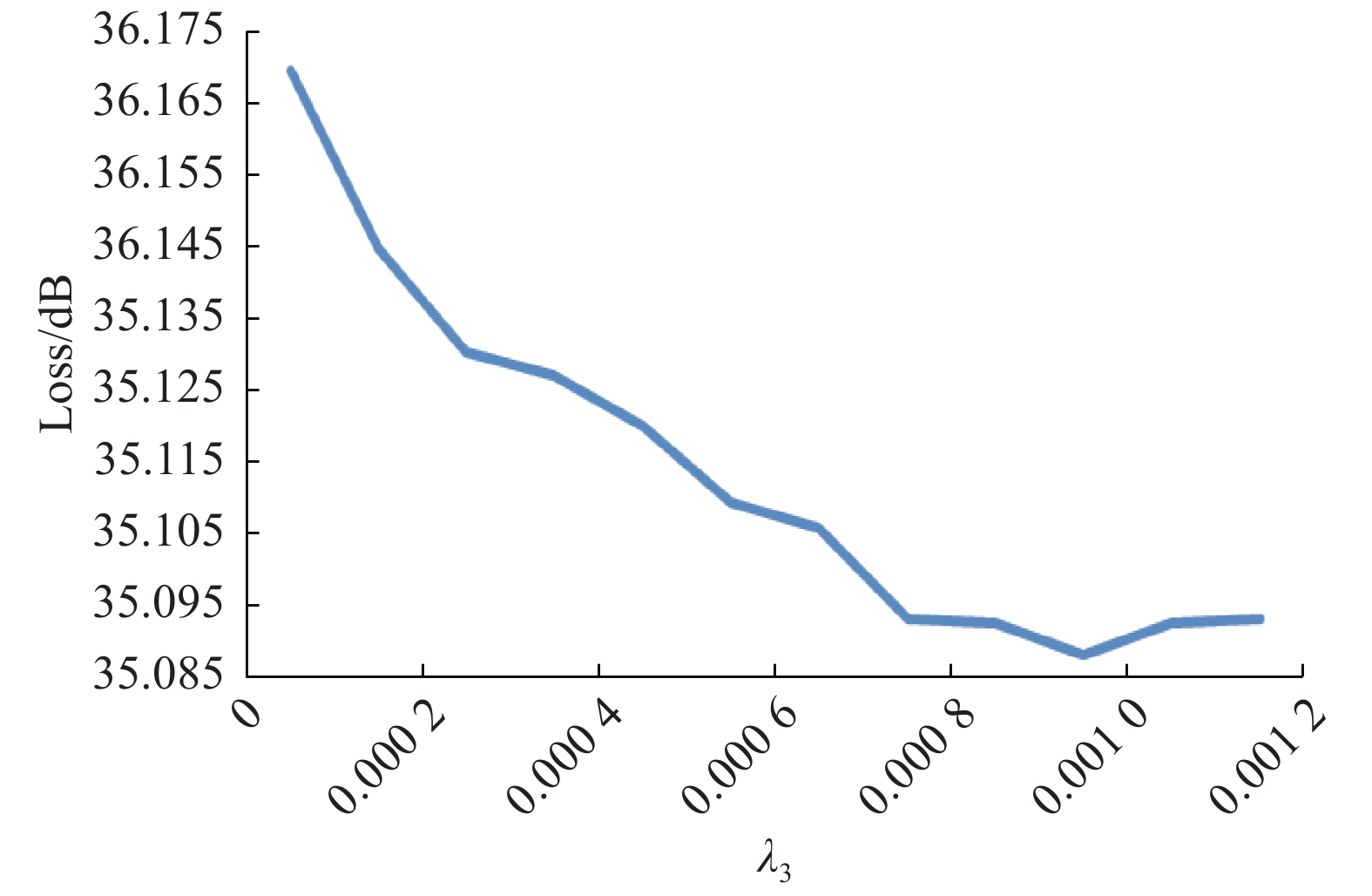
为确定损失函数中不同分量的权重值，本文进行了参数实验，根据收敛情况确定权重值，图4~6分别为感知损失、像素损失、对抗损失随权重的变化曲线，损失函数收敛到最小值时对应值即为正则因子λi权重值，i = 1, 2, 3。
PWDSR算法描述如下：
输入 低分辨率图像，真实高分辨率图像；
输出 生成的高辨率图像。
1)低分辨率图像 → GPU
$ \Rightarrow $ 低分辨率图像对应张量，真实高分辨率图像 → GPU$\Rightarrow $ 高分辨率图像对应张量；2)低分辨率图像对应张量→ PWDSR
$\Rightarrow $ 超分辨率生成图像对应张量；3)不同层feature map → VGG
$\Rightarrow $ lp；4) [高分辨率图像对应张量−低分辨率图像对应张量]
$\Rightarrow $ l1，lg；5)通过公式
$l = {\lambda _1}{l_{\rm{p}}} + {\lambda _2}{l_1} + {\lambda _3}{l_{\rm{g}}}$ 计算损失；7)是否达到epoch最大值，是则输出超分辨率图像对应张量；否则继续训练；
6) PWDSR ← l；
8)超分辨率图像对应张量→ CPU
$\Rightarrow $ 生成的高分辨率图像。
图 4 感知损失收敛曲线Fig. 4 Perceptual loss convergence curve下载:
全尺寸图片
图 5 像素损失收敛曲线Fig. 5 Pixel loss convergence curve下载:
全尺寸图片
图 6 对抗损失收敛曲线Fig. 6 Adversarial loss convergence curve下载:
全尺寸图片
3. 实验设置
本实验在Windows 10操作系统中使用PyTorch深度学习框架，Python版本为3.7.6，硬件配置为Intel(R) Core(TM) i5-7300HQ CPU @ 2.50 GHz, 24 GB内存，显卡为NIDIA GeForce GTX 1050 Ti，使用CUDA 10.2 + cudnn 7.4.1进行GPU加速，在训练过程中，采用Adam梯度下降算法，设置初始学习率为0.001，模型的epoch设置为200，每10次保存一次网络模型。
3.1 数据集
DIV2K数据集是用于NTIRE大赛的标准数据集，该数据集包含1000张2K分辨率的高清图像，其中800张作为训练数据集，100张用于验证，100张用于测试。该数据集还包含高清分辨率图像对应的低分辨率图像(使用插值法获得)便于训练。本文中，将DIV2K数据集中编号1~800的图像作为训练集，编号801~900的图像作为验证集，编号901~1000的图像作为测试集，另选Set5、Set14为测试集进行对比。Set5为5张动植物的图像，Set14数据集包含14张自然景象的图像。
3.2 评价指标
图像超分辨率效果的客观评价指标为峰值信噪比(peak signal-to-noise ratio, PSNR)和结构相似性(structural similarity, SSIM)。
3.2.1 峰值信噪比
峰值信噪比是图像超分辨率评价指标中使用最多的一种标准，其使用均方误差来对图片质量作判断。对于单色m×n的高清原图I与超分辨率得到的图片K，两者之间的均方误差公式为
$$ {\rm{MSE}} = \frac{1}{{mn}}\sum\limits_{i = 1}^{m - 1} {\sum\limits_{j = 1}^{n - 1} {{{\left[ {I\left( {x,y} \right) - K\left( {x,y} \right)} \right]}^2}} } $$ (13) 峰值信噪比的公式为
$$ {\rm{PSNR}} = 10 \cdot {\rm{lg}}\left( {\frac{{{\rm{MAX}}_I^2}}{\rm{MSE}}} \right) = 20 \cdot {\rm{lg}}\left( {\frac{{{{\rm{MAX}}_I}}}{{\sqrt {\rm{MSE}} }}} \right) $$ (14) 式中：MAXI表示像素最大值，如果采样点用8位表示，则为255。可见，MSE与PSNR成反比，PSNR越大代表重新构建的图像效果越好。
3.2.2 结构相似度
结构相似度是图像超分辨率重建的另一个应用较为广泛的测量指标，其输入是两张图像，其中一张是未经压缩的无失真图像y，另一张是重新构建出的图像x，那么SSIM公式为
$$ {\rm{SSIM}}\left( {x,y} \right) = {\left[ {l\left( {x,y} \right)} \right]^\alpha } \cdot {\left[ {c\left( {x,y} \right)} \right]^\beta } \cdot {\left[ {s\left( {x,y} \right)} \right]^\gamma } $$ (15) 式中：α>0，β>0，γ>0，l是亮度(luminance)比较，c是对比度(contrast)比较，s是结构(structure)比较：
$$ l\left( {x,y} \right) = \frac{{2{\mu _x}{\mu _y} + {c_1}}}{{\mu _x^2 + \mu _y^2 + {c_1}}} $$ $$ c\left( {x,y} \right) = \frac{{2{\sigma _{xy}} + {c_2}}}{{\sigma _x^2 + \sigma _y^2 + {c_2}}} $$ $$ s\left( {x,y} \right) = \frac{{{\sigma _{xy}} + {c_3}}}{{{\sigma _x}{\sigma _y} + {c_3}}} $$ 一般c3=c2/2，其中µx、µy表示均值。σx2、σy2表示方差，σxy表示x与y的协方差。在实际应用中通常设α=β=γ=1，故可将式(15)简化为
$$ {\rm{SSIM}}\left( {x,y} \right) = \frac{{\left( {2{\mu _x}{\mu _y} + {c_1}} \right)\left( {{\sigma _{xy}} + {c_2}} \right)}}{{\left( {\mu _x^2 + \mu _y^2 + {c_1}} \right)\left( {\sigma _x^2 + \sigma _y^2 + {c_2}} \right)}} $$ 可以看出，SSIM具有对称性，即SSIM(x, y)=SSIM(y, x)，SSIM∈[0, 1]，SSIM与输出图像和无失真图像的差距成反比，SSIM越大图像质量越好。当两幅图像一模一样时，SSIM=1。
3.3 实验结果及分析
本实验从客观评价结果和主观评价结果两方面来表现改进模型的超分辨率能力，通过不同方式证明了本文提出的模型改进能优于其他模型。
3.3.1 客观评价结果
本文在3个公开数据集上测试了WDSR-A、WDSR-B以及本文模型，分别计算在不同数据集上采用不同算法进行上采样2、3、4倍时的PSNR和SSIM，对比结果如表1所示。
表 1 在不同数据集上对比放大倍数为2、3、4的重构图像的PSNR和SSIMTable 1 Comparison of PSNR and SSIM of 2, 3, and 4 times reconstructed images on different datasets数据集 放大倍数 WDSR-A WDSR-B PWDSR PSNR/dB SSIM t/min PSNR/dB SSIM t/min PSNR/dB SSIM t/min DIV2K 2 33.8613 0.8040 1054.0 34.8217 0.8357 1055.0 35.0280 0.8521 1056.5 3 31.0211 0.7084 1332.8 31.0644 0.7145 1335.0 31.1129 0.7202 1337.5 4 28.7837 0.6321 1695.5 28.9369 0.6367 1697.5 29.0079 0.6524 1702.5 Set5 2 35.0688 0.9002 89.4 35.1157 0.9020 89.5 35.3112 0.9084 89.6 3 31.0657 0.7165 107.9 31.3806 0.7345 108.0 31.7262 0.7465 109.1 4 29.3180 0.6730 144.2 29.3658 0.6851 144.7 29.5172 0.6964 145.6 Set14 2 31.0615 0.7131 262.5 31.1140 0.7252 264.6 31.1448 0.7308 266.0 3 27.8946 0.6180 328.1 28.0032 0.6225 329.7 28.9950 0.6434 331.9 4 26.2087 0.6043 420.8 26.3112 0.6087 422.1 27.2699 0.6176 424.4 注：粗体字代表最好结果 从实验结果不难发现，更换不同数据集，本文提出的方法在2、3、4倍重建任务中，都能够取得较好的PSNR和SSIM值，相较于其他模型，在客观指标上有所提升。
3.3.2 主观评价结果
本文分别选取了DIV2K、Set5、Set14数据集中的3张高分辨率图像进行放大倍数为2、3、4的重构对比，为了更好地体现对比结果，本文将选取不同图片的不同细节进行放大对比：图7选取DIV2K数据集中图像绿叶的右端枝叶部分进行4倍重建对比，图8选取Set5数据集中图像婴儿的左眼及上方部分进行3倍重建对比，图9选取Set14数据集中图像女孩的左眼及下方部分进行4倍重建对比。
图 7 编号0803(DIV2K) 4倍重建视觉比较Fig. 7 Visual comparison of SR results of “0803” (DIV2K) with scale factor 4下载:
全尺寸图片
图 8 baby(Set5) 3倍重建视觉比较Fig. 8 Visual comparison of SR results of “baby” (Set5) with scale factor 3下载:
全尺寸图片
图 9 comic(Set14) 4倍重建视觉比较Fig. 9 Visual comparison of SR results of “comic” (Set14) with scale factor 4下载:
全尺寸图片
从视觉对比结果可以看出，3种模型在2、3、4倍的重建任务中都可以完成重建高分辨率图像，但本文提出模型在不同倍数重建任务中，能够重建出更好的纹理细节，达到更好的视觉效果，说明重新构建出的图像更接近原始高分辨率图像。
4. 结束语
本文在广泛激活的深度残差网络的基础上，融合感知损失、对抗损失、像素损失，对整体损失函数进行优化，使用已训练好的VGG19模型提取激活前的特征得到感知损失，避免了使用激活后的稀疏特征导致的性能不良等问题。本文使用权重归一化代替批量归一化，提高了学习率和训练、测试准确率。使用全局跳跃连接，避免梯度消失的问题，同时有助于梯度的反向传播，加快训练过程。从实验结果可以看出，本文提出的损失函数改进在不同数据集上可以取得更好的评价指标，在主观视觉效果也有所提高。在高倍重建任务上还有提升空间，后续工作以调整残差块和优化损失函数等方向进行展开。
-
图 1 广泛激活的残差块与基础残差块的对比
Fig. 1 Comparison of the residual block with wide activation and the original residual block
下载:
全尺寸图片
图 2 融合感知损失的广泛激活的深度残差网络的超分辨率模型
Fig. 2 Widely-activated deep residual network for super-resolution combining perceptual loss
下载:
全尺寸图片
图 3 VGG结构模型
Fig. 3 VGG structure model
下载:
全尺寸图片
图 4 感知损失收敛曲线
Fig. 4 Perceptual loss convergence curve
下载:
全尺寸图片
图 5 像素损失收敛曲线
Fig. 5 Pixel loss convergence curve
下载:
全尺寸图片
图 6 对抗损失收敛曲线
Fig. 6 Adversarial loss convergence curve
下载:
全尺寸图片
图 7 编号0803(DIV2K) 4倍重建视觉比较
Fig. 7 Visual comparison of SR results of “0803” (DIV2K) with scale factor 4
下载:
全尺寸图片
图 8 baby(Set5) 3倍重建视觉比较
Fig. 8 Visual comparison of SR results of “baby” (Set5) with scale factor 3
下载:
全尺寸图片
图 9 comic(Set14) 4倍重建视觉比较
Fig. 9 Visual comparison of SR results of “comic” (Set14) with scale factor 4
下载:
全尺寸图片
表 1 在不同数据集上对比放大倍数为2、3、4的重构图像的PSNR和SSIM
Table 1 Comparison of PSNR and SSIM of 2, 3, and 4 times reconstructed images on different datasets
数据集 放大倍数 WDSR-A WDSR-B PWDSR PSNR/dB SSIM t/min PSNR/dB SSIM t/min PSNR/dB SSIM t/min DIV2K 2 33.8613 0.8040 1054.0 34.8217 0.8357 1055.0 35.0280 0.8521 1056.5 3 31.0211 0.7084 1332.8 31.0644 0.7145 1335.0 31.1129 0.7202 1337.5 4 28.7837 0.6321 1695.5 28.9369 0.6367 1697.5 29.0079 0.6524 1702.5 Set5 2 35.0688 0.9002 89.4 35.1157 0.9020 89.5 35.3112 0.9084 89.6 3 31.0657 0.7165 107.9 31.3806 0.7345 108.0 31.7262 0.7465 109.1 4 29.3180 0.6730 144.2 29.3658 0.6851 144.7 29.5172 0.6964 145.6 Set14 2 31.0615 0.7131 262.5 31.1140 0.7252 264.6 31.1448 0.7308 266.0 3 27.8946 0.6180 328.1 28.0032 0.6225 329.7 28.9950 0.6434 331.9 4 26.2087 0.6043 420.8 26.3112 0.6087 422.1 27.2699 0.6176 424.4 注：粗体字代表最好结果 -
[1] 雷鹏程, 刘丛, 唐坚刚, 等. 分层特征融合注意力网络图像超分辨率重建[J]. 中国图象图形学报, 2020, 25(9): 1773–1786. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGTB202009004.htm LEI Pengcheng, LIU Cong, TANG Jiangang, et al. Hierarchical feature fusion attention network for image super-resolution reconstruction[J]. Journal of image and graphics, 2020, 25(9): 1773–1786. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGTB202009004.htm [2] HUANG Zhengzhong, CAO Liangcai. Bicubic interpolation and extrapolation iteration method for high resolution digital holographic reconstruction[J]. Optics and lasers in engineering, 2020, 130: 106090. doi: 10.1016/j.optlaseng.2020.106090 [3] HAO Sai, DONG Xianghuai. Interpolation-based plane stress anisotropic yield models[J]. International journal of mechanical sciences, 2020, 178: 105612. doi: 10.1016/j.ijmecsci.2020.105612 [4] 贺璟, 郝晓丽, 吕进来. 梯度插值与可变阈值改进的POCS算法[J]. 中国科技论文, 2017, 12(14): 1655–1658,1684. doi: 10.3969/j.issn.2095-2783.2017.14.016 HE Jing, HAO Xiaoli, LÜ Jinlai. POCS algorithm based on gradient interpolation and variable threshold[J]. China sciencepaper, 2017, 12(14): 1655–1658,1684. doi: 10.3969/j.issn.2095-2783.2017.14.016 [5] 白蔚, 杨撒博雅, 刘家瑛, 等. 基于显著性稀疏表示的图像超分辨率算法[J]. 中国科技论文, 2014, 9(1): 103–107. doi: 10.3969/j.issn.2095-2783.2014.01.020 BAI Wei, YANG Saboya, LIU Jiaying, et al. Image super resolution based on salient sparse coding[J]. China sciencepaper, 2014, 9(1): 103–107. doi: 10.3969/j.issn.2095-2783.2014.01.020 [6] DONG Chao, LOY C C, HE Kaiming, et al. Learning a deep convolutional network for image super-resolution[C]//Proceedings of the 13th European Conference on Computer Vision. Zurich, Switzerland, 2014: 184−199. [7] KIM J, LEE J K, LEE K M. Accurate image super-resolution using very deep convolutional networks[C]//Proceedings of 2016 IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas, USA, 2016: 1646−1654. [8] LIM B, SON S, KIM H, et al. Enhanced deep residual networks for single image super-resolution[C]//Proceedings of 2017 IEEE Conference on Computer Vision and Pattern Recognition Workshops. Honolulu, USA, 2017: 136−144. [9] IOFFE S, SZEGEDY C. Batch normalization: accelerating deep network training by reducing internal covariate shift[C]//Proceedings of the 32nd International Conference on Machine Learning. Lille, France, 2015: 448−456. [10] SIMONYAN K, ZISSERMAN A. Very deep convolutional networks for large-scale image recognition[EB/OL]. (2015-04-10)[2021-01-01].https://arxiv.org/abs/1409.1556. [11] SHI Wenzhe, CABALLERO J, HUSZÁR F, et al. Real-time single image and video super-resolution using an efficient sub-pixel convolutional neural network[C]//Proceedings of 2016 IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas, USA, 2016: 1874−1883. [12] LEDIG C, THEIS L, HUSZÁR F, et al. Photo-realistic single image super-resolution using a generative adversarial network[C]//Proceedings of 2017 IEEE Conference on Computer Vision and Pattern Recognition. Honolulu, USA, 2017: 4681−4690. [13] ZHANG Yulun, TIAN Yapeng, KONG Yu, et al. Residual dense network for image super-resolution[C]//Proceedings of 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Salt Lake City, USA, 2018: 2472−2481. [14] YU Jiahui, FAN Yuchen, YANG Jianchao, et al. Wide activation for efficient and accurate image super-resolution[EB/OL]. (2018-12-21)[2021-01-01]. https://arxiv.org/abs/1808.08718v1. [15] WANG Xintao, YU Ke, WU Shixiang, et al. ESRGAN: enhanced super-resolution generative adversarial networks[C]//Proceedings of the European Conference on Computer Vision. Munich, Germany, 2018: 63−79.
