A heterogeneous variation firefly algorithm with maximin strategy
-
摘要: 针对多目标萤火虫算法勘探能力弱、求解精度差的问题,本文提出了一种基于最大最小策略和非均匀变异的萤火虫算法(HVFA-M)。该算法首先引入Maximin策略,实现对外部档案的动态调整和对精英解的随机选择;其次,精英解结合当前最好解共同引导萤火虫进行全局搜索以扩大算法的搜索范围,提高算法的勘探能力,从而增加找寻全局最优解的概率;最后,在算法全面勘探的基础上,添加非均匀变异算子使得算法融合局部搜索的思想引导种群进行局部开采,进一步增强算法的寻优能力。将HVFA-M 与经典及新近多目标进化算法进行比较,实验结果表明:HVFA-M 能有效提升算法的勘探能力,在解的收敛性和多样性也表现出良好的性能。Abstract: Aiming at weak exploration ability and poor solving accuracy of multi-objective firefly algorithms, a heterogeneous variation firefly algorithm with maximin strategy (HVFA-M) is proposed in this paper. Firstly, the Maximin strategy is introduced to realize dynamic adjustment of external archive and random selection of elite solutions; Secondly, the elite solutions guide the firefly global search together with the current best solution to expand the search range and improve the exploration ability of the algorithm, so as to increase the probability of finding the global optimal solution; Finally, on the basis of comprehensive exploration of the algorithm, the heterogeneous variation operator is added to make the algorithm integrate the idea of local search to guide the population to carry out local mining, so as to further enhance the optimization ability of the algorithm. By comparing HVFA-M with the classical and recent multi-objective evolutionary algorithms, the experimental results show that HVFA-M can effectively improve the exploration ability of the algorithm, and also shows good performance in the convergence and diversity of solutions.
-
现实生活中许多优化问题涉及多个相互制约且相互冲突的目标,这类问题称为多目标优化问题(multi-objective optimization problem, MOP)[1]。解决MOP的难点在于改进其中一个目标必然会导致另一个或多个剩余目标的退化,因此针对MOP求解并不能同单目标优化问题一样找到一个唯一的最优解使得各个目标同时取得最优值,而是通过各个目标函数的相互协调,得到一组权衡最优解,即Pareto最优解集[2]。为尽可能的趋近于真实的Pareto最优解集,通常采用多目标进化算法(multi-objective evolutionary algorithms, MOEA)[3]求解MOP。
近30年来,MOEA研究成果丰富,种类繁多,主要包括基于Pareto支配关系的MOEA、基于精英保留机制的MOEA、基于分解的MOEA、基于指标的MOEA、混合机制的MOEA以及新型进化机制的MOEA,不同种类的MOEA表现出不同的优劣势与差异性。基于Pareto支配关系的MOEA原理简单,参数少,易于理解,代表算法有非支配排序遗传算法(nondominated sorting genetic algorithm, NSGA)[4]及其改进版本NSGA-II[5]、NSGA-III[6]和多目标遗传算法(multi-objective genetic algorithm, MOGA)[7]等。基于精英保留机制的MOEA通过建立外部档案(external archive, EA)[8]来存储精英解以增加解群的多样性从而获得优良的Pareto前沿,代表算法有强度Pareto进化算法(strength pareto evolutionary algorithm, SPEA)[9]及其改进版本SPEA2[10]、Pareto存档进化策略算法(pareto archived evolution strategy, PAES)[8]及其改进版本PESA和PESA-II[11]等。基于分解的MOEA将MOP转化为一组单目标优化问题,在此基础上进行子问题邻域信息协同求解,代表算法有基于分解的多目标进化算法(multi-objective evolutionary algorithm based on decomposition, MOEA/D)[12]以及在此基础上改进的基于多层交互偏好的多目标分解进化算法(multi-layer interaction preference based multi-objective evolutionary algorithm through decomposition, MLIP-MOEA/D)[13]等。基于指标的MOEA运用性能评价指标来引导搜索及对解进行选择,使算法能够找到针对评价指标好的解,代表算法有多目标搜索中基于指标的选择算法(indicator-based selection in multi-objective search, IBEA)[14]和基于超体积的多目标快速优化算法(algorithm for fast hypervolume-based many-objective optimization, HypE)[15]等。混合机制的MOEA通过结合每个MOEA和元启发式算法的优点以克服单个MOEA或元启发式算法的固有局限性,从而进一步提高解空间搜索的有效性,代表算法有超多目标进化算法(hyper multi-objective evolutionary algorithm, HMOEA)[16]和自适应多种群混合进化算法(hybrid evolutionary algorithm with adaptive multi-population strategy, HMOEA-AMP)[17]等。近年来,基于新型进化机制的MOEA在多目标优化领域崭露头角,如多目标粒子群算法(multi-objective particle swarm optimization, MOPSO)[18],多目标灰狼算法(multi-objective grey wolf optimizer, MOGWO)[19]等,这类算法通过引入元启发式算法和新型进化机制来求解多目标优化问题,提供了研究MOP的新思路,在多目标优化领域广受关注。
Yang[20]通过对萤火虫种群行为的模拟和简化,提出了萤火虫算法(firefly algorithm, FA)。FA与其他进化算法相比,前者在概念、过程、涉及的参数和适用性方面具有优势[21-22],鉴于FA的种群搜索特性以及良好的优化性能,Yang[23]将其应用于求解多目标优化问题,提出了多目标萤火虫算法(multi-objective firefly algorithm, MOFA)。MOFA改进了FA中的移动公式,使公式的随机项随迭代次数呈非线性递减,并采用权重比策略确定当前最好解,但萤火虫的移动仅受制于支配解或者当前最好解,算法的搜索范围具有局限性,勘探能力有待增强,导致MOFA易早熟且收敛性能差。
为了提升MOFA的勘探能力,增强算法的优化性能,Tsai等[24]提出了一种基于非支配排序的多目标萤火虫算法(non-dominated sorting firefly algorithm for multi-objective optimization, MONSFA),MONSFA中提供了两种随机搜索策略供萤火虫选择移动,通过随机改变萤火虫的搜索方向来提高算法的勘探能力,同时运用NSGA-II的非支配排序和拥挤距离策略实现种群再生和档案维护以提高算法的全局搜索能力。谢承旺等[25]提出了一种多策略协同的多目标萤火虫算法(multi-objective firefly algorithm based on multiply cooperative strategies, MOFA-MCS),该算法改进了MOFA的学习公式,通过随机选取档案精英解作为引导者指引粒子学习来间接阻止种群向局部区域靠拢,拓宽种群的搜索范围以达到提升算法勘探能力的目的。LYU等[26]提出了一种基于补偿因子与精英学习的多目标萤火虫算法(multi-objective firefly algorithm based on compensation factor and elite learning, CFMOFA),CFMOFA中通过精英学习来扩大萤火虫的探测范围,以此来提高Pareto最优解集的多样性和准确性。
上述提到的各改进算法在一定程度上均提升了算法的勘探能力,但大都是对算法的局部进行改进,算法的整体性能并未取得大的突破,且学习策略单一,具有一定的局限性,一方面,萤火虫移动的方向过于片面,种群的勘探能力有待进一步提高,解集覆盖域不够广泛;另一方面,算法的寻优性能差,难以收敛到真实的Pareto最优解。基于此,为提升算法的勘探能力,增强算法的全局搜索能力,本文提出了一种基于最大最小策略和非均匀变异的萤火虫算法(heterogeneous variation firefly algorithm with maximin strategy, HVFA-M)。HVFA-M具有如下特点:1)引入Maximin策略[27],一方面用于维护档案群体的多样性,以获得分布性较好的解集,另一方面用于从外部档案中随机挑选精英解,参与种群进化;2)精英解[19]配合当前最好解引导萤火虫移动,以扩大种群的搜索范围,增大Pareto最优解所在区域被探测到的可能性,使得解集覆盖域更广,有利于提高解集分布的广泛性;3)萤火虫位置更新后进行非均匀变异[28],促使算法进行局部搜索,在提高算法全局探索能力的同时兼顾算法的局部开采能力,有利于收敛到真实的Pareto最优解。以上3种策略分工明确,协同实施,作用于HVFA-M的不同阶段,显著增强了算法的勘探能力和寻优能力,提高了多目标萤火虫算法的收敛性及多样性。
1. 基础知识
1.1 多目标优化问题
以最小化问题为例,MOP的数学模型通常可以描述为以下形式:
$$ \left\{ \begin{gathered} \min {\boldsymbol{y}} = F\left( {\boldsymbol{x}} \right) = \left[ {{f_1}\left( x \right),{f_2}\left( x \right), \cdots ,{f_m}\left( x \right)} \right] \hfill \\ {\boldsymbol{x}} = \left[ {{x_1},{x_2}, \cdots ,{x_n}} \right] \in {\boldsymbol{X}} \subset {{\bf{R}}^n} \hfill \\ {\boldsymbol{y}} = \left[ {{y_1},{y_2}, \cdots ,{y_m}} \right] \in {\boldsymbol{Y}} \subset {{\bf{R}}^m} \hfill \\ \end{gathered} \right. $$ (1) 式中:
${\boldsymbol{x}}$ 表示决策向量;$ n $ 为决策向量的维数;${\boldsymbol{X}}$ 是$ n $ 维决策空间;${\boldsymbol{y}}$ 表示目标向量;$ m $ 为目标函数的个数;${\boldsymbol{Y }}$ 是$ m $ 维目标空间。对于任意两个决策向量${{\boldsymbol{x}}_i},{{\boldsymbol{x}}_j} \in {\boldsymbol{X}}$ ,当且仅当$\left\{ \begin{gathered} \forall l \in \left\{ {1,2, \cdots ,m} \right\}:{f_l}\left( {{{\boldsymbol{x}}_i}} \right) \leqslant {f_l}\left( {{{\boldsymbol{x}}_j}} \right) \hfill \\ \exists h \in \left\{ {1,2, \cdots ,m} \right\}:{f_h}\left( {{{\boldsymbol{x}}_i}} \right) < {f_h}\left( {{{\boldsymbol{x}}_j}} \right) \hfill \\ \end{gathered} \right.$ 成立时,称${{\boldsymbol{x}}_i}$ Pareto支配${{\boldsymbol{x}}_j}$ ,记为${{\boldsymbol{x}}_i} \prec {{\boldsymbol{x}}_j}$ 。若$\neg \exists {\boldsymbol{x}} \in{\boldsymbol{ X}}$ ,使得${\boldsymbol{x}} \prec {{\boldsymbol{x}}^*}$ 成立,则称${{\boldsymbol{x}}^*}$ 为非支配解个体,种群中所有非支配解个体组成的集合称为Pareto最优解集(pareto-optimal set, PS),其在目标空间的投影称为Pareto最优前沿(pareto-optimal front, PF)。1.2 多目标萤火虫算法
萤火虫算法中,亮度和吸引力是两个关键要素。亮度表征了萤火虫所处位置的优劣,吸引力决定了萤火虫移动的方向,所有萤火虫根据位置更新公式移动到新的位置后,更新自身亮度,并根据吸引规则进行下一次移动。通常将萤火虫
${{\boldsymbol{x}}_i}$ 的绝对亮度$I\left( {{{\boldsymbol{x}}_i}} \right)$ 表示为$I\left( {{{\boldsymbol{x}}_i}} \right) \Leftrightarrow f\left( {{{\boldsymbol{x}}_i}} \right)$ ,即用萤火虫$ {{\boldsymbol{x}}_i} $ 所在位置解的目标函数值表征$ {{\boldsymbol{x}}_i} $ 的绝对亮度。吸引力$ \beta $ 是一个相对参数,取决于每一只萤火虫所处的相对位置,根据萤火虫之间的吸引力与它们的亮度成正比,而与它们的距离成反比的特性[22],萤火虫$ j $ 对萤火虫$ i $ 的吸引力可定义为$$ {\beta _{ij}} = {\beta _0}{{\rm{e}}^{ - \gamma {r_{ij}}^2}} $$ (2) 式中:
$ {\beta _0} $ 为最大吸引力,即在光源处$ {r_{ij}} = 0 $ 萤火虫的吸引力(通常取值为1);$ \gamma $ 为光吸收系数,用来体现光强随距离增加和传播媒质的吸收而逐渐减弱的特性,从而描述出吸引力的变化,一般取$ \gamma \in \left[ {0.01,100} \right] $ ;$ {r_{ij}} $ 为萤火虫$ i $ 到萤火虫$ j $ 之间的空间距离,一般采用欧氏距离计算,但不仅仅局限于欧氏距离。对于任意给定的两只萤火虫,萤火虫
$ i $ 被萤火虫$ j $ 吸引并朝着$ j $ 所在的方向移动,其位置更新公式为$$ {x_i}\left( {t + 1} \right) = {x_i}\left( t \right){\text{ + }}{\beta _{ij}}\left( {{x_j}\left( t \right) - {x_i}\left( t \right)} \right) + \alpha \cdot{\varepsilon _i} $$ (3) 式中:第2部分是学习部分,取决于吸引力的大小;第3部分是随机部分,是带有特定系数的随机项。其中
$ t $ 为算法的迭代次数,$ {x_i}\left( t \right) $ 和$ {x_j}\left( t \right) $ 分别为算法在第$ t $ 次迭代时,萤火虫$ i $ 和萤火虫$ j $ 的空间位置;$ \alpha $ 为步长因子,取值为$ \left[ {0,1} \right] $ 内均匀分布的随机数,$ {\varepsilon _i} $ 为服从均匀分布、高斯分布或者其他分布得到的随机数向量。多目标萤火虫算法中,根据Pareto 支配的定义确定任意两只萤火虫之间是否存在吸引关系,以萤火虫
$ i $ 作为研究对象,若萤火虫$ j \prec i $ ,$ i $ 被$ j $ 吸引,并按照式(3)朝着萤火虫$ j $ 所在的位置和方向移动。若萤火虫$ i $ 不被其他任何萤火虫支配,则根据式(4)进行位置更新[21]:$$ {x_i}\left( {t + 1} \right) = {g^*} + \alpha \cdot{\varepsilon _i} $$ (4) 其中,
$ {g^*} $ 表示当前最好解,$ \alpha $ 和$ {\varepsilon _i} $ 的含义同式(3),其取值可参考文献[23]。$ {g^*} $ 是由式(5)将多目标函数以随机加权和的方式转换成一个组合的单目标函数而取得的最优值,若求取的是最小化问题,则$ {g^*} $ 是令单目标函数最小化得到的针对给定的多目标优化问题的当前最小解。$$ \left\{ \begin{gathered} \psi \left( x \right) = \sum\limits_{k = 1}^K {{w_k}{f_k}} \hfill \\ \sum\limits_{k = 1}^K {{w_k} = 1} \hfill \\ \end{gathered} \right. $$ (5) 式中:
$ K $ 表示目标函数的个数;$ {w_k} \in \left( {0,1} \right) $ ,权重$ {w_k} $ 应该在每次迭代中随机选择,以便非支配解沿着帕累托前沿进行不同的采样。1.3 Maximin 策略
Maximin策略起源于游戏理论,由Balling[29]首次将其应用于求解多目标优化问题,并得出其在不使用其他多样性维护机制的条件下可以实现非劣解前沿均匀分布的目标。Maximin策略中,运用Maximin适应值函数计算出每只萤火虫的Maximin适应值,借助Maximin适应值的大小区分每只萤火虫的优劣,萤火虫 的Maximin适应值函数定义为
$$\begin{aligned} {f_{\rm Maximin }}\left( {{{\boldsymbol{x}}_i}} \right) = {\max_j}= 1,2, \cdots ,n_{\rm pop};j \ne i\\ \left\{ {{{\min }_l}{{_ = }_{1, \cdots ,m}}\left\{ {{f_l}\left( {{{\boldsymbol{x}}_i}} \right) - {f_l}\left( {{{\boldsymbol{x}}_j}} \right)} \right\}} \right\} \;\; \end{aligned}$$ (6) 式中:
$l = 1,2, \cdots ,m$ ,$ m $ 为目标函数的个数;$n_{\rm pop }$ 为种群大小。首先计算出萤火虫$ i $ 与其他萤火虫对应不同目标函数上的差值,从中选取最小值$\min \left( {{{\boldsymbol{x}}_i}} \right)$ ,再从$ i $ 与其他所有萤火虫计算所得的所有$\min \left( {{{\boldsymbol{x}}_i}} \right)$ 中选取最大值$\max \left( {\min \left( {{{\boldsymbol{x}}_i}} \right)} \right)$ 作为$ i $ 的Maximin适应值。显然,非劣解的Maximin适应值均小于零,即在解群中根据Maximin适应值的正负便可辨别非劣解,同时,Maximin策略可用于“奖励”分散的非劣解和“惩罚”聚集的非劣解[27],即分散解的Maximin适应值更小,聚集解的Maximin适应值较大。Maximin策略凭借这两个独特的性质成为求解MOP的一个有效工具,一方面,区分了非劣解的优劣;另一方面,根据这一区分可以保留种群中Maximin适应值小且分散的解,保证了解集之间分布的均匀性。标准的Maximin策略计算不在同一数量级的目标值时,得到的Maximin适应值具有偏向性,其次,支配解的存在会影响非支配解的Maximin适应值。针对Maximin策略存在的缺陷,徐鸣等[30]提出应先对所有目标值进行规范化处理,Gong等[31]提出应仅计算非劣解的Maximin适应值,此外,贾树晋等[27]提出为了获得广泛的Pareto最优端,应令边界解的Maximin适应值最小以避免其丢失。因此在本文算法中运用改进的Maximin策略[27],定义为
$$ \left\{ \begin{gathered} {f_l}\left( {{{\boldsymbol{x}}_i}} \right) = \frac{{{f_l}\left( {{{\boldsymbol{x}}_i}} \right) - \mathop {\min }\limits_l \left( {{f_l}\left( {{{\boldsymbol{x}}_i}} \right)} \right)}}{{\mathop {\max }\limits_l \left( {{f_l}\left( {{{\boldsymbol{x}}_i}} \right)} \right) - \mathop {\min }\limits_l \left( {{f_l}\left( {{{\boldsymbol{x}}_i}} \right)} \right)}} \hfill \\ {f_{\rm Maximin }}\left( {{{\boldsymbol{x}}_i}} \right) = \mathop {\max }\limits_{\mathop {{{{x}}_i},{{{x}}_j} \in EA}\limits_{i \ne j} } \left\{ {\mathop {\min }\limits_l \left\{ {{f_l}\left( {{{\boldsymbol{x}}_i}} \right) - {f_l}\left( {{{\boldsymbol{x}}_j}} \right)} \right\}} \right\} \hfill \\ {f_{\rm Maximin }}\left( {{{\boldsymbol{x}}_{bs}}} \right) = \mathop {\min }\limits_{{{{x}}_i} \in {\rm{EA}}} {f_{\rm Maximin }}\left( {{{\boldsymbol{x}}_i}} \right) \hfill \\ \end{gathered} \right. $$ (7) 式中:
$l = 1, 2,\cdots ,m$ ;${f_l}\left( {{{\boldsymbol{x}}_i}} \right)$ 指萤火虫$ i $ 进行规范化后第$ l $ 维目标值;${{\boldsymbol{x}}_{bs}}$ 表示非支配解集的边界解。2. HVFA-M算法
2.1 Maximin策略维护种群多样性和选取精英解
MOEA 通常采用设置一定大小的外部档案来储存算法在迭代过程中产生的非劣解,为避免资源赘余,引入Maximin 策略[27]。Maximin 策略作为一种多样性维护策略,常用于多目标优化算法中维护种群的多样性,本文算法中,Maximin策略不仅作为外部档案更新策略,还作为精英选择策略,一方面用以维持解群的多样性,另一方面用以区分精英解之间的优劣信息,便于选择较优的精英解参与种群进化。当外部档案EA 中非劣解的数量超过算法限制的最大容量时,运用Maximin策略删除多余的非劣解。具体步骤为:
1) 根据式(7) 计算EA 中每个非劣解的Maximin 适应值;
2) 将EA 中所有的非劣解按照Maximin 适应值进行升序排序;
3) 删除Maximin 适应值最大的解,重复此步骤,直到档案中的容量达到其限定值。
2.2 学习策略的改进
从式(3)、(4) 可以看出,标准MOFA中被支配的萤火虫仅仅受到支配它的萤火虫和随机项的影响,不受任何支配的萤火虫仅仅受到当前最好解和随机项的影响,而存储在外部档案中的非劣解,也就是精英解,也没有得到充分的利用,这导致种群进化缓慢,使得算法的勘探能力弱,不利于解集逼近并广泛完整的表达真实的Pareto前沿。基于外部档案中的精英解携带了优良的种群信息,可以指导种群进化,本文对学习公式进行了改进,引入精英解结合当前最好解共同引导萤火虫移动,合理的继承了解群中的优良基因,扩大了算法的搜索范围,有利于算法获得位置更为优异,分布更为均匀,覆盖范围更为广泛的Pareto 最优解集。改进如下:
1) 当萤火虫
$ i $ 被$ j $ 支配时,萤火虫$ i $ 的位置更新公式为$$ \begin{gathered} {x_i}\left( {t + 1} \right) = {x_i}\left( t \right) + {w_1}{\beta _{ij}}\left( {{x_j}\left( t \right) - {x_i}\left( t \right)} \right) + \hfill \\ {w_2}{\beta _{i{g^*}}}\left( {{g^*} - {x_i}\left( t \right)} \right) +{w_3}{\beta _{i{d_1}^*}}\left( {{d_1}^* - {x_i}\left( t \right)} \right) + \alpha .{\varepsilon _i} \hfill \\ \end{gathered} $$ (8) 2) 当萤火虫
$ i $ 不被其他任何萤火虫支配时,萤火虫$ i $ 的位置更新公式为$$ {x_i}\left( {t + 1} \right) = {w_4}{x_i}\left( t \right) + {w_5}{g^*} + {w_6}{d_2}^* + \alpha .{\varepsilon _i} $$ (9) 式中:
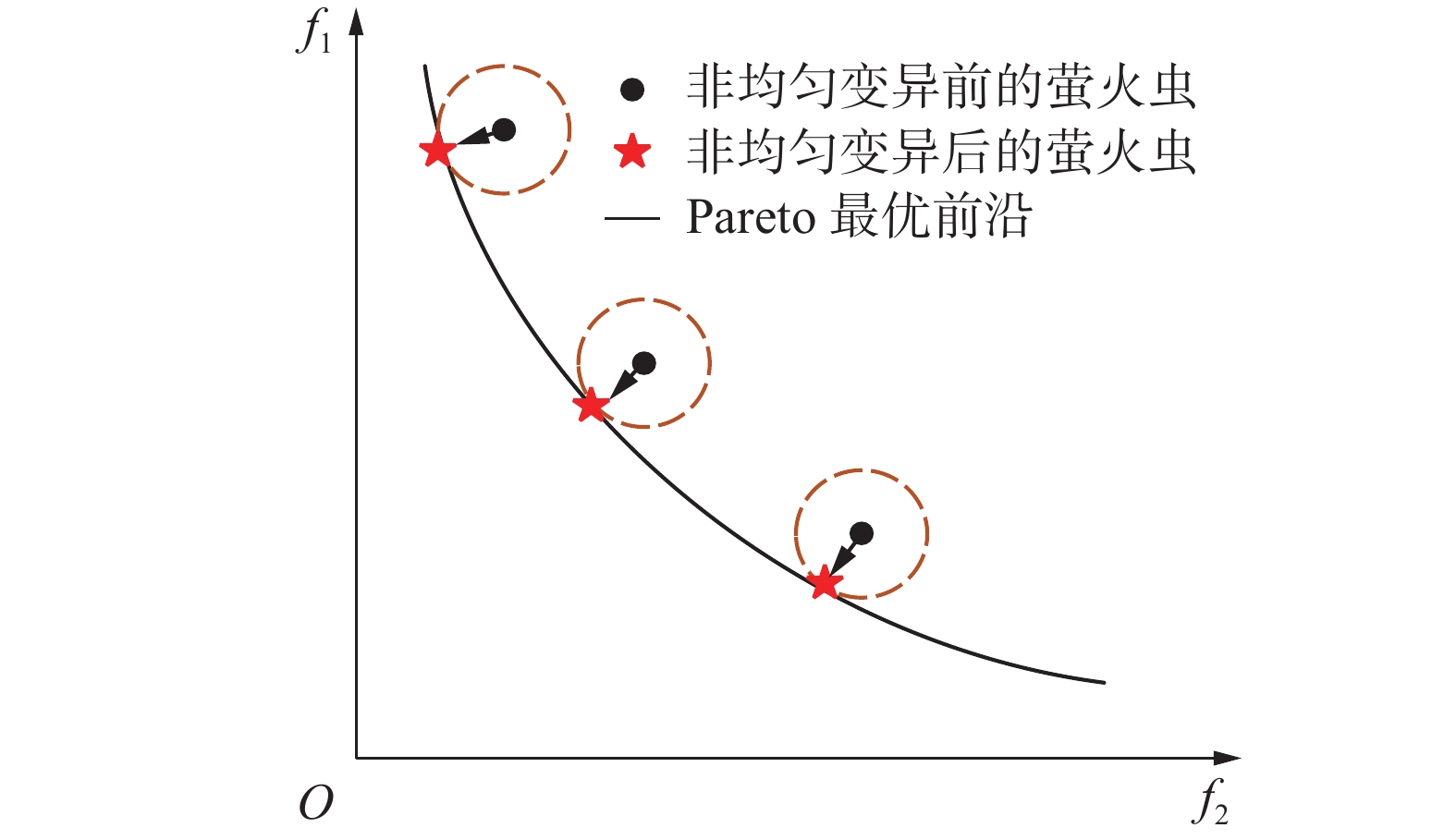
$ {w_1}、{w_2}、{w_3}、{w_4}、{w_5}、{w_6} \in \left[ {0,1} \right] $ ;$\displaystyle\sum\limits_{i = 1}^3 {{w_i} = 1}$ ;$\displaystyle\sum\limits_{i = 4}^6 {{w_i} = 1}$ ;$ {d_1}^*、{d_2}^* $ 为从外部档案中随机选择的两个精英解。以存在支配关系的萤火虫的位置更新公式为例,求解二目标最小化问题,给出MOFA和HVFA-M两种算法搜索范围的简化模型,如图1所示。图1中,黑色曲线为Pareto最优前沿,红色五角星代表外部档案中的精英解,红色圆点代表当前最好解
$ {g^*} $ ,黑色圆点表示萤火虫,橙色圆圈为萤火虫的搜索范围。MOFA中,若萤火虫$ j < i $ ,萤火虫$ i $ 朝着萤火虫$ j $ 所在的位置移动,根据式(3),结合式(2)知$ {\beta _{ij}} \in \left[ {0,1} \right] $ ,则萤火虫$ i $ 在学习部分的作用下初始移动到A点,再随机扰动到橙色圆圈区域内的某一点上,如图1(a)中B点所在位置。HVFA-M运用了新的学习公式,在学习部分添加当前最好解$ {g^*} $ 和档案精英解$ {d_1}^* $ ,结合支配$ i $ 的解$ j $ ,三者共同引导并制约萤火虫$ i $ 的移动,同时令$ {w_1} $ ,$ {w_2} $ ,$ {w_3} $ 作为约束参数,防止移动发生偏置,使得萤火虫$ i $ 初始移动的位置落在一段曲线所在的区域上,如图1(b)中红色曲线区域,再在扰动项的作用下萤火虫$ i $ 的位置最终落在由多个橙色圆圈组成的区域内的某一点上。将这一思想同样运用于种群中不存在支配关系的萤火虫中,可以得出,在MOFA中,萤火虫仅仅进行小规模的探测,算法的勘探能力有限,难以获得较好的Pareto最优解集;而HVFA-M运用改进的学习策略,充分发挥精英解和当前最好解的优势,使得萤火虫的移动突破了以往的小范围束缚,拓宽了萤火虫的运动方向,扩大了萤火虫的搜索范围,有效提高了算法发现Pareto最优解的几率,增强了解集分布的广泛性,为算法收敛到真实的Pareto最优解奠定了良好的基础。2.3 非均匀变异机制
萤火虫算法收敛速度较快,导致多目标萤火虫算法后期在寻优过程中易陷入早熟收敛,很难收敛于真实的Pareto 前沿,通常通过引入变异算子解决这一问题。非均匀变异算子[28]作为一种动态变异算子,在初始阶段能够均匀的搜索空间,具备一定的全局搜索能力;在后期则具备一定的局部搜索能力,有利于寻找到更好的非支配解,进一步提高解的质量。基于此,引入非均匀变异算子,每一代萤火虫
$ i $ 进行位置更新后,按照一种随迭代次数动态递减的变异概率$ {p_m} $ 随机对$ i $ 的向量进行扰动,这里${p_m}= 1 - \dfrac{t}{{G_{\rm{max}} }}$ ,若选中的是第$ k $ 维分量($ 1 \leqslant k \leqslant n $ ,$ n $ 为向量的维数),变异操作可定义为[26]$$x_{i}^{k'} = \left\{ \begin{array}{l} x_i^k + \Delta \left( {t,{u_k} - x_i^k} \right),\begin{array}{*{20}{c}} \quad{\gamma = 0} \end{array}\\ x_i^k - \Delta \left( {t,x_i^k - {l_k}} \right),\begin{array}{*{20}{c}} \quad{\gamma = 1} \end{array} \end{array} \right.$$ (10) $$ \Delta \left(t\text{,}y\right)=y\ast \left(1-{r}^{{\left(1-\frac{t}{G_{\rm{max}}}\right)}^{b}}\right) $$ (11) 式中:
$ {u_k} $ 和$ {l_k} $ 分别为向量取值范围的最大值与最小值;$ \gamma $ 随机的取0或1;$ t $ 为当前迭代次数;$G_{\rm{max}}$ 为最大迭代次数;$ r $ 为$ \left[ {0,1} \right] $ 内的随机数;$ b $ 为系统参数,决定了随机数扰动对迭代次数$ t $ 的依赖程度,取值一般为2到5,本文中取$ b = 3 $ 。算法前期,$ t $ 较小,该算子均匀的搜索空间,充分发挥萤火虫算法的全局搜索能力;算法后期,随着$ t $ 增大,该算子的搜索变得局部化,使得变异后产生的新解以更大的概率逼近真实的Pareto 最优解,如图2所示。非均匀变异算子的引入平衡了算法全局搜索和局部开采的能力,进一步提高了算法的寻优能力,有效增强了算法的收敛性。2.4 算法流程
结合Maximin 策略、学习公式改进及非均匀变异机制3种策略,给出HVFA-M 的算法流程,如算法1所示。
算法1 基于最大最小策略和非均匀变异的萤火虫算法
输入 决策向量的维数
$n$ ,决策变量的区间范围$\left[ {a,b} \right]$ ,种群规模$n_{\rm pop}$ ,外部档案容量$n_{\rm rep}$ ,最大迭代次数$G_{\rm{max}}$ ,光吸收系数$\gamma $ ,最大吸引度${\beta _0}$ ,以及初始步长$\alpha $ 。输出 Pareto最优解集
1)萤火虫种群初始化。产生规模为
$n_{\rm pop}$ 的初始群体,$n_{\rm rep} =0$ ,迭代次数$t = 0$ 。2)计算萤火虫在每一个目标函数上的适应值,并根据Pareto关系进行评价,将非支配解复制到
$n_{\rm rep}$ 中。3)根据式(7)计算所有非支配萤火虫的Maximin适应值。
4) 当
$t < G_{\rm{max}}$ 时,重复5)~11)。5) 对萤火虫进行遍历,重复6)~8)。
6) 萤火虫i与萤火虫j进行比较,重复7)~8)。
7)萤火虫之间进行相互学习。若萤火虫
$j < i$ ,按照式(8)进行位置更新;若萤火虫$ i $ 不受支配,则按照式(9)进行位置更新。8)非均匀变异。对位置更新后的萤火虫进行变异,若变异后的萤火虫优于变异前的萤火虫,则将该位置替换为变异后的萤火虫,否则不做任何操作。
9)更新所有非支配萤火虫的Maximin适应值。
10)外部档案更新与维护。若外部档案中非支配解的数量超出其最大容量
$n_{\rm rep}$ ,按照Maximin适应值的大小对档案中的所有非支配解进行排序,通过删去Maximin适应值最大的解来实现外部档案动态调整的目的,直到满足条件为止11)
$t = t + 1$ 2.5 算法时间复杂度分析
由于萤火虫算法采用全吸引模型,MOFA算法采用两层循环遍历所有萤火虫,故其时间复杂度为
$O({N^2})$ 。HVFA-M算法在MOFA的基础上,添加了Maximin策略,在求解Maximin适应值时,新增两个循环,第一个循环遍历所有目标$m$ ,第二个循环遍历了所有萤火虫,故其时间复杂度为$O({N^2}) + $ $ O(mN)$ 。由于求解的目标个数较种群规模少($m < N$ ),比较可得,HVFA-M与MOFA的时间复杂度在同一数量级。3. 实验与结果
3.1 测试函数
为评估HVFA-M的性能,本文使用9个经典的MOP对HVFA-M进行性能测试[32-34],这9个多目标测试函数由5个2-目标函数和4个3-目标函数组成。其定义及特征如表1、2所示。
表 1 2-目标测试函数集Table 1 2-objective test function函数 定义 变量范围 Pareto 前沿特征 ZDT1 $\begin{gathered} {f_1}(x) = {x_1},{f_2}(x) = g(x)[1 - \sqrt { {x_1}/g(x)} ] \\ g(x) = 1 + 9\sum\limits_{i = 2}^n { {x_i} } /(n - 1) \\ \end{gathered}$ $n = 30,0 \leqslant {x_i} \leqslant 1,i = 1,2, \cdots ,n$ 凸型 ZDT2 $\begin{gathered} {f_1}(x) = {x_1},{f_2}(x) = g(x)[1 - {({x_1}/g(x))^2}] \\ g(x) = 1 + 9\sum\limits_{i = 2}^n { {x_i} } /(n - 1) \\ \end{gathered}$ $n = 30,0 \leqslant {x_i} \leqslant 1,i = 1, 2, \cdots ,n$ 凹型 ZDT3 $\begin{gathered} {f_1}(x) = {x_1} \\ {f_2}(x) = g(x)[1 - \sqrt { {x_1}/g(x)} - {x_1}\sin (10{\text{π} } {x_1})/g(x)] \\ g(x) = 1 + 9\sum\limits_{i = 2}^n { {x_i} } /(n - 1) \\ \end{gathered}$ $n = 30,0 \leqslant {x_i} \leqslant 1,i = 1, 2, \cdots,n$ 非连续型 ZDT4 $\begin{gathered} {f_1}(x) = {x_1},{f_2}(x) = g(x)[1 - \sqrt { {x_1}/g(x)} ] \\ g(x) = 1 + 10(n - 1) + \sum\limits_{i = 2}^n {[{x_i}^2 - 10\cos (4{\text{π} } {x_1})]} \\ \end{gathered}$ $n = 10,0 \leqslant {x_i} \leqslant 1,i = 1, 2, \cdots ,n$ 凸型+多模态 ZDT6 $\begin{gathered} {f_1}(x) = 1 - \exp ( - 4{x_1}){\sin ^6}(6{\text{π} } {x_1}) \\ {f_2}(x) = g(x)[1 - {({f_1}(x)/g(x))^2}] \\ g(x) = 1 + 9{[\sum\limits_{i = 2}^n { {x_i} } /(n - 1)]^{0.25} } \\ \end{gathered}$ $n = 10,0 \leqslant {x_i} \leqslant 1,i = 1, 2, \cdots ,n$ 凹型+多模态+有偏 表 2 3-目标测试函数集Table 2 3-objective test function函数 定义 变量范围 Pareto 前沿特征 Viennet1 $\begin{gathered} {f_1}(x,y) = {x^2} + {(y - 1)^2} \\ {f_2}(x,y) = {x^2} + {(y + 1)^2} + 1 \\ {f_3}(x,y) = {(x - 1)^2} + {y^2} + 2 \\ \end{gathered}$ $ - 2 \leqslant x,y \leqslant 2 $ 凸型 Viennet3 $\begin{gathered} {f_1}(x,y) = 0.5({x^2} + {y^2}) + \sin ({x^2} + {y^2}) \\ {f_2}(x,y) = {(3x - 2y + 4)^2}/8 + {(x - y + 1)^2}/27 + 15\\ {f_3}(x,y) = 1/({x^2} + {y^2} + 1) - 1.1{{\rm{e}}^{( - {x^2} - {y^2})} } \\ \end{gathered}$ $ - 3 \leqslant x,y \leqslant 3 $ 混合型+退化型 DTLZ4 $\begin{gathered} {f_1}\left( x \right) = \left( {1 + g\left( x \right)} \right)\cos \left( { {x_1}^\alpha {\text{π} } /2} \right)\cos \left( { {x_2}^\alpha {\text{π} } /2} \right) \\ {f_2}\left( x \right) = \left( {1 + g\left( x \right)} \right)\cos \left( { {x_1}^\alpha {\text{π} } /2} \right)\sin \left( { {x_2}^\alpha {\text{π} } /2} \right) \\ {f_3}\left( x \right) = \left( {1 + g\left( x \right)} \right)\cos \left( { {x_1}^\alpha {\text{π} } /2} \right)\sin \left( { {x_1}^\alpha {\text{π} } /2} \right)\\ g\left( x \right) = \sum\limits_{i = 3}^n { { {\left( { {x_i} - 0.5} \right)}^2} } \\ \end{gathered}$ $n = 12,0 \leqslant {x_i} \leqslant 1,i = 1, 2, \cdots ,n$ 凹型+有偏 DTLZ7 $\begin{gathered} {f_1}\left( x \right) = {x_1} \\ {f_2}\left( x \right) = {x_2} \\ {f_3}\left( x \right) = \left( {1 + g\left( x \right)} \right)h\left( x \right) \\ h\left( x \right) = 3 - \left( { { { {x_1}\left( {1 + \sin \left( {3{\text{π} } {x_1} } \right)} \right) + {x_2}\left( {1 + \sin \left( {3{\text{π} } {x_2} } \right)} \right)} \mathord{ {\vphantom { { {x_1}\left( {1 + \sin \left( {3{\text{π} } {x_1} } \right)} \right) + {x_2}\left( {1 + \sin \left( {3{\text{π} } {x_2} } \right)} \right)} {1 + g\left( x \right)} } } } {1 + g\left( x \right)} } } \right) \\ g\left( x \right) = 1 + \dfrac{9}{22}\sum\limits_{i = 3}^n { {x_i} } \\ \end{gathered}$ $n = 12,0 \leqslant {x_i} \leqslant 1,i = 1, 2, \cdots ,n$ 不连续+混
合+多模态3.2 与经典多目标优化算法进行比较
为验证HVFA-M的性能,将HVFA-M 与MOPSO[18],NSGA-III[6],MOEA/D[12],PESA-II[11]及MOFA[23] 5种经典多目标优化算法进行比较,所有对比算法的参数设置均取自于相应文献,如表3所示。为分别验证HVFA-M 的收敛性和Pareto 最优解集的广泛性,采用generation distance(GD)[35]、maximum spread(MS)[36] 性能评价指标量化算法获得的Pareto 最优前沿的收敛性和广泛性,其中GD 反映了算法所得的近似Pareto 前沿对真实Pareto前沿的逼近程度,GD值越小,表示算法收敛性越好;MS 反映出算法所得的Pareto 最优前沿在目标空间中分布的广泛程度,MS值越大,表示解集的广泛性越好。为评价HVFA-M的综合性能,即避免算法收敛性差而导致的更广泛的分布的影响,采用inverted generation distance(IGD)[37]评价指标来判断算法的优劣,IGD指标可同时评价算法的收敛性和多样性,IGD值越小,算法的综合性能越好。为保证所有算法比较的公平性,所有算法的最大迭代次数
$G_{\max} $ 设置为300,种群大小$ n_{\rm pop} $ 设置为50,外部档案EA 的大小$ n_{\rm rep} $ 设置为200;$p_{\rm crossover}=0.5 $ ,$n_{\rm crossover}=2 {\rm{rand}} \left[\dfrac{1}{2}p_{\rm crossover}\times n_{\rm pop}\right]$ 为减少随机因素的干扰,所有算法在每个测试函数上均独立运行30次,评价指标数据为算法独立运行30次的平均值。表4~6给出了HVFA-M 与其他5种经典算法在9个测试函数上的GD 、MS、IGD 的均值和标准差,表格中加粗数据表示不同算法在同一测试函数上取得的最优值。
表 4 HVFA-M与5种经典算法在GD上的实验结果Table 4 Experimental results of HVFA-M and five classical algorithms on GD函数 结果 MOPSO NSGA-III MOEA/D PESA-II MOFA HVFA-M ZDT1 均值 1.2977E-03 1.3871E-03 2.2896E-02 7.8901E-03 2.5460E-03 6.4501E-05 标准差 2.8147E-03 1.2612E-04 1.4276E-02 2.5693E-03 3.9532E-03 1.1522E-05 续表 4 函数 结果 MOPSO NSGA-III MOEA/D PESA-II MOFA HVFA-M ZDT2 均值 9.9875E-02 1.2441E-03 1.1472E-01 1.7782E-02 5.5263E-03 4.6663E-05 标准差 2.2884E-01 1.7162E-04 9.7900E-02 8.6836E-03 3.0860E-03 1.4150E-05 ZDT3 均值 5.1072E-03 1.0554E-03 2.4292E-02 8.7494E-03 5.7601E-03 1.5972E-04 标准差 6.5526E-03 1.6489E-04 6.9302E-03 6.1008E-03 9.3471E-03 3.1267E-05 ZDT4 均值 2.5060E-01 1.2326E-01 8.0502E-01 1.9292E-01 6.8391E-04 1.7833E-04 标准差 2.1668E-01 1.1286E-02 7.2731E-01 2.4313E-01 1.2067E-04 2.6718E-05 ZDT6 均值 7.4952E-02 1.9384E-05 2.8674E-01 1.3117E-02 2.2315E-01 6.5920E-05 标准差 1.7363E-01 6.1940E-06 1.3486E-01 1.6442E-02 7.0215E-02 2.3485E-05 Viennet1 均值 8.1619E-03 5.2861E-03 1.6919E-03 6.0808E-03 7.2847E-03 7.7879E-03 标准差 9.0303E-04 8.4433E-04 5.7563E-04 7.4795E-04 1.0309E-03 7.6160E-04 Viennet3 均值 4.2190E-04 4.3547E-04 1.9124E-03 2.7074E-04 2.8235E-04 2.3738E-04 标准差 4.9400E-04 2.3034E-04 4.2731E-03 1.3696E-04 1.3960E-04 8.7578E-05 DTLZ4 均值 1.0121E-02 1.3455E-03 4.8552E-03 9.2903E-03 4.8590E-02 6.4492E-03 标准差 1.4976E-02 2.1031E-04 8.5008E-03 2.7186E-03 9.9670E-02 6.8052E-03 DTLZ7 均值 1.9468E-03 1.4038E-03 2.8358E-02 6.1249E-03 7.5825E-03 5.6839E-03 标准差 3.3627E-04 5.4064E-04 3.2902E-02 3.2818E-03 8.5173E-03 9.2137E-03 表 5 HVFA-M与5种经典算法在MS上的实验结果Table 5 Experimental results of HVFA-M and five classical algorithms on MS函数 结果 MOPSO NSGA-III MOEA/D PESA-II MOFA HVFA-M ZDT1 均值 9.9532E-01 9.7650E-01 8.2378E-01 9.3922E-01 9.6855E-01 9.8304E-01 标准差 1.4780E-02 2.0823E-02 9.7648E-02 1.8436E-02 1.7669E-02 2.2414E-02 ZDT2 均值 7.9907E-01 8.0148E-01 9.8565E-01 8.2032E-01 9.5006E-01 9.9583E-01 标准差 4.5177E-01 1.3166E-01 2.7933E-01 4.2053E-02 2.8259E-02 6.1360E-03 ZDT3 均值 9.7723E-01 9.4376E-01 7.3036E-01 9.4677E-01 9.9077E-01 9.9310E-01 标准差 2.2748E-02 8.0080E-02 1.0102E-01 1.0685E-02 4.2752E-03 7.1158E-03 ZDT4 均值 1.1070E+00 7.8171E-01 5.7929E+00 1.1167E+00 9.6326E-01 9.8619E-01 标准差 4.0091E-01 8.6406E-02 5.1800E+00 7.1394E-01 2.2307E-02 2.3020E-02 ZDT6 均值 1.0611E+00 9.4826E-01 2.5313E+00 9.9472E-01 3.1585E-01 9.3313E-01 标准差 3.2987E-01 1.9002E-01 1.0706E+00 1.7429E-02 3.8652E-01 8.4860E-02 Viennet1 均值 8.6285E-01 7.9327E-01 6.5751E-01 8.3395E-01 8.5044E-01 8.5953E-01 标准差 4.0523E-03 4.8758E-02 6.6312E-02 3.0382E-02 1.3831E-02 6.7998E-03 Viennet3 均值 9.9357E-01 8.0888E-01 4.0857E-01 9.7154E-01 8.6247E-01 9.7631E-01 标准差 5.2464E-03 1.1254E-02 2.1803E-01 1.4494E-02 6.8271E-02 3.0879E-02 DTLZ4 均值 1.0000E+00 9.3232E-01 7.2184E-01 1.0000E+00 3.8661E-01 1.0000E+00 标准差 0.0000E+00 8.8136E-02 3.0791E-01 0.0000E+00 3.0780E-01 0.0000E+00 DTLZ7 均值 9.9419E-01 9.8131E-01 7.6360E-01 9.7643E-01 9.9119E-01 9.9528E-01 标准差 2.9812E-03 1.8577E-02 1.3043E-01 8.7316E-03 3.8632E-03 2.6912E-03 表 6 HVFA-M与5种经典算法在IGD上的实验结果Table 6 Experimental results of HVFA-M and five classical algorithms on IGD函数 结果 MOPSO NSGA-III MOEA/D PESA-II MOFA HVFA-M ZDT1 均值 1.7622E-02 2.0314E-02 3.3407E-01 1.1912E-01 2.0675E-02 4.7067E-03 标准差 3.8599E-02 1.5463E-03 1.9274E-01 2.9386E-02 2.5839E-03 1.0060E-03 ZDT2 均值 5.8606E-01 4.2013E-02 1.6083E+00 1.7840E-01 4.0414E-02 5.5019E-03 标准差 6.9047E-01 2.2793E-02 5.6079E-01 6.7750E-02 1.1922E-02 1.1734E-03 ZDT3 均值 3.5534E-02 2.3518E-02 5.6371E-01 1.1090E-01 2.0014E-02 4.8115E-03 标准差 4.8917E-02 8.8535E-03 4.0581E-01 2.7488E-02 4.2937E-03 8.9670E-04 ZDT4 均值 2.3022E+00 1.5256E+00 4.9223E+00 2.0751E+00 3.1044E-02 4.9915E-03 标准差 1.2885E+00 2.1740E-01 4.0798E+00 1.3397E+00 4.9771E-02 6.6118E-04 ZDT6 均值 9.2151E-02 1.5124E-01 3.7339E+00 1.1819E-02 3.9865E-01 2.6650E-02 标准差 4.6295E-01 2.0674E-01 1.3125E+00 1.7120E-02 1.1804E-01 3.2112E-02 Viennet1 均值 1.1211E-01 1.1922E-01 4.1273E-01 1.0497E-01 1.3883E-01 1.1735E-01 标准差 3.1571E-04 8.8636E-03 6.6881E-02 4.4940E-03 8.8571E-03 6.4486E-03 Viennet3 均值 5.6165E-02 2.3134E+00 2.2724E+00 4.6818E-02 1.6815E+00 4.1028E-01 标准差 1.3429E-02 8.3183E-02 4.5867E-01 5.7189E-03 7.0318E-01 2.7305E-01 DTLZ4 均值 1.5414E-01 2.9362E-01 3.7357E-01 7.3128E-02 8.3614E-01 2.9010E-01 标准差 1.6638E-01 3.2877E-01 2.9153E-01 7.7684E-03 1.1724E-01 1.0492E-01 DTLZ7 均值 5.4109E-02 5.3313E-02 6.4660E-01 6.8882E-02 7.4329E-02 2.1629E-01 标准差 3.1230E-03 2.8313E-03 2.8774E-01 5.9113E-03 6.6499E-03 6.3615E-02 根据表4,单方面考虑算法的收敛性看,HVFA-M 在9个测试函数上有5次取得最优,相对于其他5种对比算法获得的最优值的次数最多,尤其对于测试函数ZDT1—ZDT4,在收敛性上的优势更为突出,充分体现出其勘探能力强,收敛性能好的优点。根据表5,从算法求取的Pareto 最优解集的广泛性角度分析,HVFA-M 在9个测试函数上有4次取得最优值,且在剩余的5个测试函数上的取值与最优值相差不大,充分凸显出其搜索范围广、覆盖面积大的特点。根据表6,综合来看,HVFA-M 在9个测试函数上有4次取得最优,且在ZDT6、Viennet1问题上,HVFA-M 与最优值之间具有相同的数量级,表明二者之间差异性小,充分说明HVFA-M 在收敛性和多样性方面具有较强的优势。
表7给出了各种算法在3种评价指标上分别取得最优值的数目。表8采用Friedman检验给出6种对比算法在3种性能评价指标上的平均排名。
从表7给出的各算法优势解的总数统计来看,HVFA-M 在3种评价指标上共有13次取得了最优值,排名第一,远胜于其他5种对比算法,PESA-II次之,共取得5次最优,最差的是MOFA,无一次取得最优。综合来看,HVFA-M相对于其他5种对等比较算法表现出显著的性能优势。
表 7 HVFA-M与5种经典算法的优势解统计Table 7 Statistics of dominant solutions of HVFA-M and five classical algorithms评价指标 HVFA-M MOPSO NSGA-III MOEA/D PESA-II MOFA GD 5 0 3 1 0 0 MS 4 4 0 2 1 0 IGD 4 0 1 0 4 0 Total 13 4 4 3 5 0 表 8 各算法在GD、MS、IGD上基于Friedman检验的平均排名Table 8 Average ranking of each algorithm based on Friedman test on GD, MS and IGDGD MS IGD 算法 秩 算法 秩 算法 秩 MOPSO 4.00 MOPSO 4.67 MOPSO 3.00 NSGA-III 2.22 NSGA-III 2.44 NSGA-III 3.44 MOEA/D 5.00 MOEA/D 2.67 MOEA/D 5.78 PESA-II 3.78 PESA-II 3.44 PESA-II 2.78 MOFA 4.00 MOFA 3.00 MOFA 3.78 HVFA-M 2.00 HVFA-M 4.78 HVFA-M 2.22 从表8可以看出,HVFA-M 在GD、MS、IGD上的名次均是最好的,在GD上随后依次是NSGA-III、PESA-II 、MOFA、和MOPSO,最差的是MOEA/D;在MS上随后依次是MOPSO、PESA-II 、MOFA和MOEA/D,最差的是NSGA-III;在IGD上随后依次是PESA-II、MOPSO、NSGA-III和MOFA,最差的是MOEA/D。Friedman检验结果表明HVFA-M较其他5种对比算法求解的精确度更高、覆盖率更广、综合性能显著。
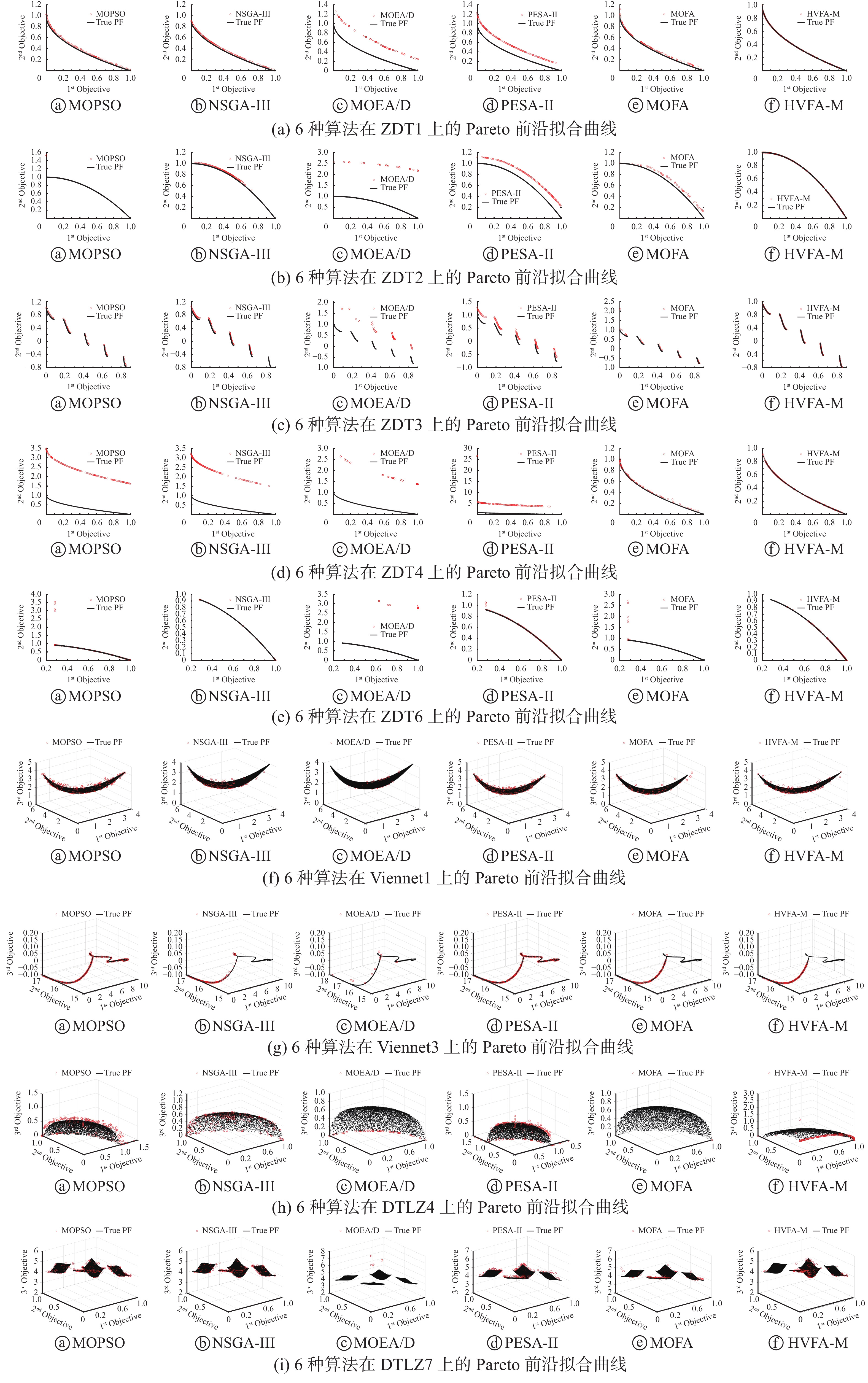
为更加直观的展现HVFA-M 的优势,图3列出了HVFA-M 与5种经典算法在9种测试函数上的Pareto前沿拟合曲线图,其中黑线表示真实的Pareto前沿,红色圆圈表示算法所得的Pareto前沿。该曲线图清晰的呈现出各个算法在各个测试问题上求取的Pareto 前沿与真实Pareto 前沿的拟合情况,与表4~8给出的实验结果保持一致,均表明HVFA-M 较其他5种算法具有最优的GD、 MS 和IGD 性能,即具有较好的收敛性和多样性。
3.3 与新近的多目标优化算法比较
为进一步验证HVFA-M 的有效性,本部分将HVFA-M 与6种新近的多目标优化算法 SMSEMOA[38]、TVMOPSO[39]、DMSPSO[40]、NSLS[41]、MOEA/IGD-NS[42]以及CFMOFA[26] 进行比较,所有对比算法的参数设置均取自于相应文献,如表9所示。这里选取6个基准MOP 测试问题组成的测试集合,包括5个2-目标的ZDT 系列函数ZDT1、ZDT2、ZDT3、ZDT4和ZDT6,以及1个3-目标的DTLZ 系列函数DTLZ4,并利用IGD评价指标来判断算法的优劣。实验中,为了确保公平性,EA最大设为100,除SMSEMOA、TVMOPSO 以及DMSPSO 算法的评估次数维持其实验原始设计外,其他所有算法的2-目标测试问题的最大迭代次数设置为250,3-目标测试问题的最大迭代次数设置为500;为平衡随机性,算法独立运行30次,结果取其平均值,实验结果由表10 给出,其中加粗数据表示不同算法在同一测试函数上获得的最优值。
表 9 各算法参数设置Table 9 Parameter setting of each algorithm算法 参数设置 参考文献 SMSEMOA $ \mu = 0.5,\sigma = 0.8 $ [38] TVMOPSO $\begin{gathered} {c_{1i} } = 2.5,{c_{1f} } = 0.5,{c_{2i} } = 0.5,{c_{2f} } = 2.5 \\{w_1} = 0.7,{w_2} = 0.4 \\b = 5 \\ \end{gathered}$ [39] DMSPSO $ P{c_i} = 1,Pc\_mean = 0.1 $ [40] NSLS $ \mu = 0.5,\sigma = 0.1 $ [41] MOEA/IGD-NS $ \begin{gathered} {p_c} = 1,{p_m} = 1/n, \hfill \\ {\eta _c} = 20,{\eta _m} = 20 \hfill \\ \end{gathered} $ [42] CFMOFA $ \alpha = 0.2,{\beta _0} = 1,\gamma = 1 $ [26] HVFA-M $ \alpha = 0.2,{\beta _0} = 1,\gamma = 1 $ — 根据表10, HVFA-M在6个测试函数上取得了3次最优的IGD均值,TVMOPSO、MOEA/IGD-NS、CFMOFA仅仅各取得一次最优,SMSEMOA、DMSPSO、NSLS在6个测试函数上均无一次能获得最优的IGD均值。表11采用Friedman检验给出了HVFA-M与6种新近算法基于IGD指标的平均排名,可以看出,HVFA-M排名第一,MOEA/IGD-NS 次之,随后依次是CFMOFA、TVMOPO、SMSEMOA、NSLS,最差的是DMSPSO,Friedman检验的结果与表10中的IGD均值结果保持一致。综合来看,HVFA-M较其他6种对比算法具有更强IGD性能,即表现出更强的收敛性与多样性。
表 10 HVFA-M与6种新近算法的IGD实验结果Table 10 Experimental results of HVFA-M and six recent algorithms on IGD函数 HVFA-M SMSEMOA TVMOPSO DMSPSO NSLS MOEA/IGD-NS CFMOFA ZDT1 9.2072E-03 1.2130E-01 1.4500E-02 1.6990E-01 6.9510E+00 1.6180E-02 9.3163E-03 ZDT2 1.0394E-02 5.6200E-01 5.0000E-02 2.2090E-01 8.7910E+00 3.0260E-02 1.0637E-02 ZDT3 9.8143E-03 1.0240E-01 5.7300E-02 1.9800E-01 7.3500E+00 6.6420E-02 1.2421E-02 ZDT4 1.0186E-02 1.2240E+00 4.2990E-01 1.4066E+00 1.3870E+00 1.6500E-02 9.3726E-03 ZDT6 7.4405E-02 8.9630E-01 3.6000E-03 5.7500E-02 8.0810E-03 4.4610E-03 1.0674E-02 DTLZ4 3.8892E-01 3.3100E-01 4.1570E-01 4.5360E-01 2.1160E-01 1.0060E-01 8.5813E-01 表 11 各算法在IGD上基于Friedman检验的平均排名Table 11 Average ranking of each algorithm based on Friedman test on IGD平均排名 算法 秩 1 HVFA-M 2.50 2 MOEA/IGD-NS 2.83 3 CFMOFA 3.00 4 TVMOPO 3.33 5 SMSEMOA 5.17 6 NSLS 5.33 7 DMSPSO 5.83 经过两次实验比较可知,HVFA-M 是一种可行且有效的多目标优化算法,表现出很强的收敛性及多样性。究其原因:首先,运用Maximin策略一方面有效维护了解群的多样性,另一方面用于选择精英解参与种群进化;其次,档案精英解结合当前最好解指导萤火虫移动,有利于提升算法的勘探能力,扩大种群搜索范围,增强算法的收敛性和广泛性;最后,引入非均匀变异算子平衡算法全局与局部搜索的能力,促进种群全局勘探的同时兼顾种群局部开发,进一步提高种群的寻优能力,促进算法收敛。以上3种策略分工合作,相互结合,共同提高了HVFA-M收敛性、多样性的综合性能。
3.4 3种改进策略的有效性分析
本文提出的HVFA-M是MOFA与多种策略的融合,它将MOFA与3种策略融合在一起:Maximin多样性维护策略(K1)、改进学习策略(K2)和非均匀变异机制(K3)。为了分析3种改进策略对算法性能产生的影响,将MOFA与每种策略融合进行测试。选取表1、2中的9个典型的多目标测试函数进行数值实验,所涉及的算法描述如下。
MOFA:标准MOFA不添加任何策略。
MOFA+K1:添加Maximin多样性维护策略的MOFA。
MOFA+K1+K2: 添加Maximin多样性维护策略和改进学习策略的MOFA。
MOFA+K3:添加非均匀变异机制的MOFA。
MOFA+K1+K3:添加Maximin多样性维护策略和非均匀变异机制的MOFA.
HVFA-M: K1、K2、K3的3种策略融合的MOFA。
需要指出的是,由于策略K2是在添加策略K1的基础上实现,因此无法单独给出MOFA添加策略K2的实验结果。表12给出了添加不同策略的MOFA9个测试问题上获得的IGD均值和方差,算法的参数设置与3.2节相同,其中加粗数据为最好的测试结果。
表 12 算法策略分析的IGD实验结果Table 12 Experimental results of algorithm strategy analysis on IGD函数 结果 MOFA MOFA+K1 MOFA+K1+K2 MOFA+K3 MOFA+K1+K3 HVFA-M ZDT1 均值 2.0675E-02 2.0432E-02 5.1013E-03 1.4158E-02 7.9827E-03 4.7067E-03 标准差 2.5839E-03 1.9979E-03 8.3910E-04 5.4982E-03 1.7564E-03 1.0060E-03 ZDT2 均值 4.0414E-02 4.2695E-02 6.0413E-03 2.3624E-02 2.0898E-02 5.5019E-03 标准差 1.1922E-02 1.0503E-02 1.7518E-03 8.0941E-03 1.0236E-02 1.1734E-03 ZDT3 均值 2.0014E-02 3.1858E-02 5.1938E-03 2.9100E-02 2.7860E-02 4.8115E-03 标准差 4.2937E-03 1.3235E-02 1.4863E-03 9.7382E-03 1.6728E-02 8.9670E-04 续表 12 函数 结果 MOFA MOFA+K1 MOFA+K1+K2 MOFA+K3 MOFA+K1+K3 HVFA-M ZDT4 均值 3.1044E-02 1.9330E-02 5.0936E-03 2.1491E-02 1.4433E-02 4.9915E-03 标准差 4.9771E-02 5.9326E-03 8.6590E-04 4.6590E-03 4.7103E-03 6.6118E-04 ZDT6 均值 3.9865E-01 3.3093E-01 3.5287E-02 1.6228E-01 1.6434E-01 2.6650E-02 标准差 1.1804E-01 1.8959E-01 3.4129E-02 5.1589E-02 4.8816E-02 3.2112E-02 Viennet1 均值 1.3883E-01 1.2980E-01 1.1894E-01 1.4921E-01 1.3454E-01 1.1735E-01 标准差 8.8571E-03 6.8442E-03 5.4589E-03 1.0091E-02 8.1772E-03 6.4486E-03 Viennet3 均值 1.6815E+00 1.1077E+00 9.3716E-01 1.5519E+00 4.8214E-01 4.1028E-01 标准差 7.0318E-01 7.3381E-01 6.7591E-01 7.5224E-01 2.3678E-01 2.7305E-01 DTLZ4 均值 8.3614E-01 8.4014E-01 3.2316E-01 4.3098E-01 6.2593E-01 2.9010E-01 标准差 1.1724E-01 1.3204E-01 1.3806E-01 6.9890E-02 1.6231E-01 1.0492E-01 DTLZ7 均值 7.4329E-02 8.0647E-02 2.2526E-01 7.7829E-02 8.5866E-02 2.1629E-01 标准差 6.6499E-03 9.5865E-03 5.0379E-02 1.1365E-02 1.2180E-02 6.3615E-02 根据表12可以看出,仅添加Maximin多样性维护策略和仅添加非均匀变异机制对改进MOFA的帮助有限,而在Maximin策略的基础上添加改进学习策略或非均匀变异机制均能有效改善算法的性能,特别是MOFA在Maximin多样性维护策略的基础上,添加通过Maximin适应值筛选出精英解来引导学习的改进学习公式策略,对算法的帮助更大。对于DTLZ7测试函数,由于其具有离散、混合和多模态的组合特征,使得3种策略均不适用于求解此类问题。从算法获得的最优值的数目上看,MOFA融合3种策略改进的HVFA-M,能够显著提高Pareto最优解集的质量。表13给出了 HVFA-M与对比算法基于IGD指标的Friedman检验结果,可以看出,HVFA-M排名第一,其次是MOFA+K1+K2、MOFA+K1+K3、MOFA+K3、MOFA+K1,最差的是MOFA。综合来看,MOFA通过结合3种策略,获得了更好的优化性能。
表 13 算法策略分析的IGD平均排名Table 13 Average ranking of algorithm strategy analysis on IGD平均排名 算法 秩 1 HVFA-M 1.44 2 MOFA+K1+K2 2.56 3 MOFA+K1+K3 3.44 4 MOFA+K3 4.11 5 MOFA+K1 4.67 6 MOFA 4.78 4. 结论
多目标萤火虫算法的勘探能力弱,求解精度差,本文针对这一问题,提出了一种新的多目标优化方法——基于最大最小策略和非均匀变异的萤火虫算法(HVFA-M)。首先,Maximin策略用作外部档案的动态调整以保证目标空间中非劣解的良好覆盖从而确保精英解参与种群进化;其次,档案精英解配合当前最好解引导萤火虫移动,使得萤火虫移动的方向更全面,以提高算法的勘探能力从而增大解群寻找最优解的概率;最后非均匀变异算子的引入使得算法融入了一定的局部搜索思想,以提高解的寻优能力从而进一步加快算法收敛。在多目标领域广泛使用的几个基准测试函数上,将HVFA-M 与几种经典及新近算法进行比较研究,数值结果和图形结果清晰地表明,本文所提出的HVFA-M 具有很强的竞争力,是解决多目标优化问题的一种可行且有效的选择。本文的研究重点是小规模多目标优化问题,下一步,将验证HVFA-M 在大规模多目标测试问题上的性能,并运用HVFA-M 求解工程实践中的多目标优化问题。
-
表 1 2-目标测试函数集
Table 1 2-objective test function
函数 定义 变量范围 Pareto 前沿特征 ZDT1 $\begin{gathered} {f_1}(x) = {x_1},{f_2}(x) = g(x)[1 - \sqrt { {x_1}/g(x)} ] \\ g(x) = 1 + 9\sum\limits_{i = 2}^n { {x_i} } /(n - 1) \\ \end{gathered}$ $n = 30,0 \leqslant {x_i} \leqslant 1,i = 1,2, \cdots ,n$ 凸型 ZDT2 $\begin{gathered} {f_1}(x) = {x_1},{f_2}(x) = g(x)[1 - {({x_1}/g(x))^2}] \\ g(x) = 1 + 9\sum\limits_{i = 2}^n { {x_i} } /(n - 1) \\ \end{gathered}$ $n = 30,0 \leqslant {x_i} \leqslant 1,i = 1, 2, \cdots ,n$ 凹型 ZDT3 $\begin{gathered} {f_1}(x) = {x_1} \\ {f_2}(x) = g(x)[1 - \sqrt { {x_1}/g(x)} - {x_1}\sin (10{\text{π} } {x_1})/g(x)] \\ g(x) = 1 + 9\sum\limits_{i = 2}^n { {x_i} } /(n - 1) \\ \end{gathered}$ $n = 30,0 \leqslant {x_i} \leqslant 1,i = 1, 2, \cdots,n$ 非连续型 ZDT4 $\begin{gathered} {f_1}(x) = {x_1},{f_2}(x) = g(x)[1 - \sqrt { {x_1}/g(x)} ] \\ g(x) = 1 + 10(n - 1) + \sum\limits_{i = 2}^n {[{x_i}^2 - 10\cos (4{\text{π} } {x_1})]} \\ \end{gathered}$ $n = 10,0 \leqslant {x_i} \leqslant 1,i = 1, 2, \cdots ,n$ 凸型+多模态 ZDT6 $\begin{gathered} {f_1}(x) = 1 - \exp ( - 4{x_1}){\sin ^6}(6{\text{π} } {x_1}) \\ {f_2}(x) = g(x)[1 - {({f_1}(x)/g(x))^2}] \\ g(x) = 1 + 9{[\sum\limits_{i = 2}^n { {x_i} } /(n - 1)]^{0.25} } \\ \end{gathered}$ $n = 10,0 \leqslant {x_i} \leqslant 1,i = 1, 2, \cdots ,n$ 凹型+多模态+有偏 表 2 3-目标测试函数集
Table 2 3-objective test function
函数 定义 变量范围 Pareto 前沿特征 Viennet1 $\begin{gathered} {f_1}(x,y) = {x^2} + {(y - 1)^2} \\ {f_2}(x,y) = {x^2} + {(y + 1)^2} + 1 \\ {f_3}(x,y) = {(x - 1)^2} + {y^2} + 2 \\ \end{gathered}$ $ - 2 \leqslant x,y \leqslant 2 $ 凸型 Viennet3 $\begin{gathered} {f_1}(x,y) = 0.5({x^2} + {y^2}) + \sin ({x^2} + {y^2}) \\ {f_2}(x,y) = {(3x - 2y + 4)^2}/8 + {(x - y + 1)^2}/27 + 15\\ {f_3}(x,y) = 1/({x^2} + {y^2} + 1) - 1.1{{\rm{e}}^{( - {x^2} - {y^2})} } \\ \end{gathered}$ $ - 3 \leqslant x,y \leqslant 3 $ 混合型+退化型 DTLZ4 $\begin{gathered} {f_1}\left( x \right) = \left( {1 + g\left( x \right)} \right)\cos \left( { {x_1}^\alpha {\text{π} } /2} \right)\cos \left( { {x_2}^\alpha {\text{π} } /2} \right) \\ {f_2}\left( x \right) = \left( {1 + g\left( x \right)} \right)\cos \left( { {x_1}^\alpha {\text{π} } /2} \right)\sin \left( { {x_2}^\alpha {\text{π} } /2} \right) \\ {f_3}\left( x \right) = \left( {1 + g\left( x \right)} \right)\cos \left( { {x_1}^\alpha {\text{π} } /2} \right)\sin \left( { {x_1}^\alpha {\text{π} } /2} \right)\\ g\left( x \right) = \sum\limits_{i = 3}^n { { {\left( { {x_i} - 0.5} \right)}^2} } \\ \end{gathered}$ $n = 12,0 \leqslant {x_i} \leqslant 1,i = 1, 2, \cdots ,n$ 凹型+有偏 DTLZ7 $\begin{gathered} {f_1}\left( x \right) = {x_1} \\ {f_2}\left( x \right) = {x_2} \\ {f_3}\left( x \right) = \left( {1 + g\left( x \right)} \right)h\left( x \right) \\ h\left( x \right) = 3 - \left( { { { {x_1}\left( {1 + \sin \left( {3{\text{π} } {x_1} } \right)} \right) + {x_2}\left( {1 + \sin \left( {3{\text{π} } {x_2} } \right)} \right)} \mathord{ {\vphantom { { {x_1}\left( {1 + \sin \left( {3{\text{π} } {x_1} } \right)} \right) + {x_2}\left( {1 + \sin \left( {3{\text{π} } {x_2} } \right)} \right)} {1 + g\left( x \right)} } } } {1 + g\left( x \right)} } } \right) \\ g\left( x \right) = 1 + \dfrac{9}{22}\sum\limits_{i = 3}^n { {x_i} } \\ \end{gathered}$ $n = 12,0 \leqslant {x_i} \leqslant 1,i = 1, 2, \cdots ,n$ 不连续+混
合+多模态表 3 各算法参数设置
Table 3 Parameter setting of each algorithm
表 4 HVFA-M与5种经典算法在GD上的实验结果
Table 4 Experimental results of HVFA-M and five classical algorithms on GD
函数 结果 MOPSO NSGA-III MOEA/D PESA-II MOFA HVFA-M ZDT1 均值 1.2977E-03 1.3871E-03 2.2896E-02 7.8901E-03 2.5460E-03 6.4501E-05 标准差 2.8147E-03 1.2612E-04 1.4276E-02 2.5693E-03 3.9532E-03 1.1522E-05 续表 4 函数 结果 MOPSO NSGA-III MOEA/D PESA-II MOFA HVFA-M ZDT2 均值 9.9875E-02 1.2441E-03 1.1472E-01 1.7782E-02 5.5263E-03 4.6663E-05 标准差 2.2884E-01 1.7162E-04 9.7900E-02 8.6836E-03 3.0860E-03 1.4150E-05 ZDT3 均值 5.1072E-03 1.0554E-03 2.4292E-02 8.7494E-03 5.7601E-03 1.5972E-04 标准差 6.5526E-03 1.6489E-04 6.9302E-03 6.1008E-03 9.3471E-03 3.1267E-05 ZDT4 均值 2.5060E-01 1.2326E-01 8.0502E-01 1.9292E-01 6.8391E-04 1.7833E-04 标准差 2.1668E-01 1.1286E-02 7.2731E-01 2.4313E-01 1.2067E-04 2.6718E-05 ZDT6 均值 7.4952E-02 1.9384E-05 2.8674E-01 1.3117E-02 2.2315E-01 6.5920E-05 标准差 1.7363E-01 6.1940E-06 1.3486E-01 1.6442E-02 7.0215E-02 2.3485E-05 Viennet1 均值 8.1619E-03 5.2861E-03 1.6919E-03 6.0808E-03 7.2847E-03 7.7879E-03 标准差 9.0303E-04 8.4433E-04 5.7563E-04 7.4795E-04 1.0309E-03 7.6160E-04 Viennet3 均值 4.2190E-04 4.3547E-04 1.9124E-03 2.7074E-04 2.8235E-04 2.3738E-04 标准差 4.9400E-04 2.3034E-04 4.2731E-03 1.3696E-04 1.3960E-04 8.7578E-05 DTLZ4 均值 1.0121E-02 1.3455E-03 4.8552E-03 9.2903E-03 4.8590E-02 6.4492E-03 标准差 1.4976E-02 2.1031E-04 8.5008E-03 2.7186E-03 9.9670E-02 6.8052E-03 DTLZ7 均值 1.9468E-03 1.4038E-03 2.8358E-02 6.1249E-03 7.5825E-03 5.6839E-03 标准差 3.3627E-04 5.4064E-04 3.2902E-02 3.2818E-03 8.5173E-03 9.2137E-03 表 5 HVFA-M与5种经典算法在MS上的实验结果
Table 5 Experimental results of HVFA-M and five classical algorithms on MS
函数 结果 MOPSO NSGA-III MOEA/D PESA-II MOFA HVFA-M ZDT1 均值 9.9532E-01 9.7650E-01 8.2378E-01 9.3922E-01 9.6855E-01 9.8304E-01 标准差 1.4780E-02 2.0823E-02 9.7648E-02 1.8436E-02 1.7669E-02 2.2414E-02 ZDT2 均值 7.9907E-01 8.0148E-01 9.8565E-01 8.2032E-01 9.5006E-01 9.9583E-01 标准差 4.5177E-01 1.3166E-01 2.7933E-01 4.2053E-02 2.8259E-02 6.1360E-03 ZDT3 均值 9.7723E-01 9.4376E-01 7.3036E-01 9.4677E-01 9.9077E-01 9.9310E-01 标准差 2.2748E-02 8.0080E-02 1.0102E-01 1.0685E-02 4.2752E-03 7.1158E-03 ZDT4 均值 1.1070E+00 7.8171E-01 5.7929E+00 1.1167E+00 9.6326E-01 9.8619E-01 标准差 4.0091E-01 8.6406E-02 5.1800E+00 7.1394E-01 2.2307E-02 2.3020E-02 ZDT6 均值 1.0611E+00 9.4826E-01 2.5313E+00 9.9472E-01 3.1585E-01 9.3313E-01 标准差 3.2987E-01 1.9002E-01 1.0706E+00 1.7429E-02 3.8652E-01 8.4860E-02 Viennet1 均值 8.6285E-01 7.9327E-01 6.5751E-01 8.3395E-01 8.5044E-01 8.5953E-01 标准差 4.0523E-03 4.8758E-02 6.6312E-02 3.0382E-02 1.3831E-02 6.7998E-03 Viennet3 均值 9.9357E-01 8.0888E-01 4.0857E-01 9.7154E-01 8.6247E-01 9.7631E-01 标准差 5.2464E-03 1.1254E-02 2.1803E-01 1.4494E-02 6.8271E-02 3.0879E-02 DTLZ4 均值 1.0000E+00 9.3232E-01 7.2184E-01 1.0000E+00 3.8661E-01 1.0000E+00 标准差 0.0000E+00 8.8136E-02 3.0791E-01 0.0000E+00 3.0780E-01 0.0000E+00 DTLZ7 均值 9.9419E-01 9.8131E-01 7.6360E-01 9.7643E-01 9.9119E-01 9.9528E-01 标准差 2.9812E-03 1.8577E-02 1.3043E-01 8.7316E-03 3.8632E-03 2.6912E-03 表 6 HVFA-M与5种经典算法在IGD上的实验结果
Table 6 Experimental results of HVFA-M and five classical algorithms on IGD
函数 结果 MOPSO NSGA-III MOEA/D PESA-II MOFA HVFA-M ZDT1 均值 1.7622E-02 2.0314E-02 3.3407E-01 1.1912E-01 2.0675E-02 4.7067E-03 标准差 3.8599E-02 1.5463E-03 1.9274E-01 2.9386E-02 2.5839E-03 1.0060E-03 ZDT2 均值 5.8606E-01 4.2013E-02 1.6083E+00 1.7840E-01 4.0414E-02 5.5019E-03 标准差 6.9047E-01 2.2793E-02 5.6079E-01 6.7750E-02 1.1922E-02 1.1734E-03 ZDT3 均值 3.5534E-02 2.3518E-02 5.6371E-01 1.1090E-01 2.0014E-02 4.8115E-03 标准差 4.8917E-02 8.8535E-03 4.0581E-01 2.7488E-02 4.2937E-03 8.9670E-04 ZDT4 均值 2.3022E+00 1.5256E+00 4.9223E+00 2.0751E+00 3.1044E-02 4.9915E-03 标准差 1.2885E+00 2.1740E-01 4.0798E+00 1.3397E+00 4.9771E-02 6.6118E-04 ZDT6 均值 9.2151E-02 1.5124E-01 3.7339E+00 1.1819E-02 3.9865E-01 2.6650E-02 标准差 4.6295E-01 2.0674E-01 1.3125E+00 1.7120E-02 1.1804E-01 3.2112E-02 Viennet1 均值 1.1211E-01 1.1922E-01 4.1273E-01 1.0497E-01 1.3883E-01 1.1735E-01 标准差 3.1571E-04 8.8636E-03 6.6881E-02 4.4940E-03 8.8571E-03 6.4486E-03 Viennet3 均值 5.6165E-02 2.3134E+00 2.2724E+00 4.6818E-02 1.6815E+00 4.1028E-01 标准差 1.3429E-02 8.3183E-02 4.5867E-01 5.7189E-03 7.0318E-01 2.7305E-01 DTLZ4 均值 1.5414E-01 2.9362E-01 3.7357E-01 7.3128E-02 8.3614E-01 2.9010E-01 标准差 1.6638E-01 3.2877E-01 2.9153E-01 7.7684E-03 1.1724E-01 1.0492E-01 DTLZ7 均值 5.4109E-02 5.3313E-02 6.4660E-01 6.8882E-02 7.4329E-02 2.1629E-01 标准差 3.1230E-03 2.8313E-03 2.8774E-01 5.9113E-03 6.6499E-03 6.3615E-02 表 7 HVFA-M与5种经典算法的优势解统计
Table 7 Statistics of dominant solutions of HVFA-M and five classical algorithms
评价指标 HVFA-M MOPSO NSGA-III MOEA/D PESA-II MOFA GD 5 0 3 1 0 0 MS 4 4 0 2 1 0 IGD 4 0 1 0 4 0 Total 13 4 4 3 5 0 表 8 各算法在GD、MS、IGD上基于Friedman检验的平均排名
Table 8 Average ranking of each algorithm based on Friedman test on GD, MS and IGD
GD MS IGD 算法 秩 算法 秩 算法 秩 MOPSO 4.00 MOPSO 4.67 MOPSO 3.00 NSGA-III 2.22 NSGA-III 2.44 NSGA-III 3.44 MOEA/D 5.00 MOEA/D 2.67 MOEA/D 5.78 PESA-II 3.78 PESA-II 3.44 PESA-II 2.78 MOFA 4.00 MOFA 3.00 MOFA 3.78 HVFA-M 2.00 HVFA-M 4.78 HVFA-M 2.22 表 9 各算法参数设置
Table 9 Parameter setting of each algorithm
算法 参数设置 参考文献 SMSEMOA $ \mu = 0.5,\sigma = 0.8 $ [38] TVMOPSO $\begin{gathered} {c_{1i} } = 2.5,{c_{1f} } = 0.5,{c_{2i} } = 0.5,{c_{2f} } = 2.5 \\{w_1} = 0.7,{w_2} = 0.4 \\b = 5 \\ \end{gathered}$ [39] DMSPSO $ P{c_i} = 1,Pc\_mean = 0.1 $ [40] NSLS $ \mu = 0.5,\sigma = 0.1 $ [41] MOEA/IGD-NS $ \begin{gathered} {p_c} = 1,{p_m} = 1/n, \hfill \\ {\eta _c} = 20,{\eta _m} = 20 \hfill \\ \end{gathered} $ [42] CFMOFA $ \alpha = 0.2,{\beta _0} = 1,\gamma = 1 $ [26] HVFA-M $ \alpha = 0.2,{\beta _0} = 1,\gamma = 1 $ — 表 10 HVFA-M与6种新近算法的IGD实验结果
Table 10 Experimental results of HVFA-M and six recent algorithms on IGD
函数 HVFA-M SMSEMOA TVMOPSO DMSPSO NSLS MOEA/IGD-NS CFMOFA ZDT1 9.2072E-03 1.2130E-01 1.4500E-02 1.6990E-01 6.9510E+00 1.6180E-02 9.3163E-03 ZDT2 1.0394E-02 5.6200E-01 5.0000E-02 2.2090E-01 8.7910E+00 3.0260E-02 1.0637E-02 ZDT3 9.8143E-03 1.0240E-01 5.7300E-02 1.9800E-01 7.3500E+00 6.6420E-02 1.2421E-02 ZDT4 1.0186E-02 1.2240E+00 4.2990E-01 1.4066E+00 1.3870E+00 1.6500E-02 9.3726E-03 ZDT6 7.4405E-02 8.9630E-01 3.6000E-03 5.7500E-02 8.0810E-03 4.4610E-03 1.0674E-02 DTLZ4 3.8892E-01 3.3100E-01 4.1570E-01 4.5360E-01 2.1160E-01 1.0060E-01 8.5813E-01 表 11 各算法在IGD上基于Friedman检验的平均排名
Table 11 Average ranking of each algorithm based on Friedman test on IGD
平均排名 算法 秩 1 HVFA-M 2.50 2 MOEA/IGD-NS 2.83 3 CFMOFA 3.00 4 TVMOPO 3.33 5 SMSEMOA 5.17 6 NSLS 5.33 7 DMSPSO 5.83 表 12 算法策略分析的IGD实验结果
Table 12 Experimental results of algorithm strategy analysis on IGD
函数 结果 MOFA MOFA+K1 MOFA+K1+K2 MOFA+K3 MOFA+K1+K3 HVFA-M ZDT1 均值 2.0675E-02 2.0432E-02 5.1013E-03 1.4158E-02 7.9827E-03 4.7067E-03 标准差 2.5839E-03 1.9979E-03 8.3910E-04 5.4982E-03 1.7564E-03 1.0060E-03 ZDT2 均值 4.0414E-02 4.2695E-02 6.0413E-03 2.3624E-02 2.0898E-02 5.5019E-03 标准差 1.1922E-02 1.0503E-02 1.7518E-03 8.0941E-03 1.0236E-02 1.1734E-03 ZDT3 均值 2.0014E-02 3.1858E-02 5.1938E-03 2.9100E-02 2.7860E-02 4.8115E-03 标准差 4.2937E-03 1.3235E-02 1.4863E-03 9.7382E-03 1.6728E-02 8.9670E-04 续表 12 函数 结果 MOFA MOFA+K1 MOFA+K1+K2 MOFA+K3 MOFA+K1+K3 HVFA-M ZDT4 均值 3.1044E-02 1.9330E-02 5.0936E-03 2.1491E-02 1.4433E-02 4.9915E-03 标准差 4.9771E-02 5.9326E-03 8.6590E-04 4.6590E-03 4.7103E-03 6.6118E-04 ZDT6 均值 3.9865E-01 3.3093E-01 3.5287E-02 1.6228E-01 1.6434E-01 2.6650E-02 标准差 1.1804E-01 1.8959E-01 3.4129E-02 5.1589E-02 4.8816E-02 3.2112E-02 Viennet1 均值 1.3883E-01 1.2980E-01 1.1894E-01 1.4921E-01 1.3454E-01 1.1735E-01 标准差 8.8571E-03 6.8442E-03 5.4589E-03 1.0091E-02 8.1772E-03 6.4486E-03 Viennet3 均值 1.6815E+00 1.1077E+00 9.3716E-01 1.5519E+00 4.8214E-01 4.1028E-01 标准差 7.0318E-01 7.3381E-01 6.7591E-01 7.5224E-01 2.3678E-01 2.7305E-01 DTLZ4 均值 8.3614E-01 8.4014E-01 3.2316E-01 4.3098E-01 6.2593E-01 2.9010E-01 标准差 1.1724E-01 1.3204E-01 1.3806E-01 6.9890E-02 1.6231E-01 1.0492E-01 DTLZ7 均值 7.4329E-02 8.0647E-02 2.2526E-01 7.7829E-02 8.5866E-02 2.1629E-01 标准差 6.6499E-03 9.5865E-03 5.0379E-02 1.1365E-02 1.2180E-02 6.3615E-02 表 13 算法策略分析的IGD平均排名
Table 13 Average ranking of algorithm strategy analysis on IGD
平均排名 算法 秩 1 HVFA-M 1.44 2 MOFA+K1+K2 2.56 3 MOFA+K1+K3 3.44 4 MOFA+K3 4.11 5 MOFA+K1 4.67 6 MOFA 4.78 -
[1] FARAG M A, MOUSA A A, EL-SHORBAGY M A, et al. A new hybrid metaheuristic algorithm for multiobjective optimization problems[J]. International journal of computational intelligence systems, 2020, 13(1): 920–940. doi: 10.2991/ijcis.d.200618.001 [2] BAROCIO E, REGALADO J, CUEVAS E, et al. Modified bio-inspired optimisation algorithm with a centroid decision making approach for solving a multi-objective optimal power flow problem[J]. IET generation, transmission & distribution, 2017, 11(4): 1012–1022. [3] LIAGKOURAS K, METAXIOTIS K. Enhancing the performance of MOEAs: an experimental presentation of a new fitness guided mutation operator[J]. Journal of experimental & theoretical artificial intelligence, 2017, 29(1): 91–131. [4] KHAN A, BAIG A R. Multi-objective feature subset selection using non-dominated sorting genetic algorithm[J]. Journal of applied research and technology, 2015, 13(1): 145–159. doi: 10.1016/S1665-6423(15)30013-4 [5] DEB K, PRATAP A, AGARWAL S, et al. A fast and elitist multiobjective genetic algorithm: NSGA-II[J]. IEEE transactions on evolutionary computation, 2002, 6(2): 182–197. doi: 10.1109/4235.996017 [6] DEB K, JAIN H. An evolutionary many-objective optimization algorithm using reference-point-based nondominated sorting approach, part I: solving problems with box constraints[J]. IEEE transactions on evolutionary computation, 2014, 18(4): 577–601. doi: 10.1109/TEVC.2013.2281535 [7] LÜCKEN C, BARÁN B, BRIZUELA C. A survey on multi-objective evolutionary algorithms for many-objective problems[J]. Computational optimization and applications, 2014, 58(3): 707–756. [8] KNOWLES J D, CORNE D W. Approximating the nondominated front using the Pareto archived evolution strategy[J]. Evolutionary computation, 2000, 8(2): 149–172. doi: 10.1162/106365600568167 [9] ZITZLER E, THIELE L. Multiobjective evolutionary algorithms: a comparative case study and the strength Pareto approach[J]. IEEE transactions on evolutionary computation, 1999, 3(4): 257–271. doi: 10.1109/4235.797969 [10] ADHAM A M, MOHD-GHAZALI N, AHMAD R. Performance optimization of a microchannel heat sink using the improved strength pareto evolutionary algorithm (SPEA2)[J]. Journal of engineering thermophysics, 2015, 24(1): 86–100. doi: 10.1134/S1810232815010087 [11] GADHVI B, SAVSANI V, PATEL V. Multi-objective optimization of vehicle passive suspension system using NSGA-II, SPEA2 and PESA-II[J]. Procedia technology, 2016, 23: 361–368. doi: 10.1016/j.protcy.2016.03.038 [12] QI Yutao, MA Xiaoliang, LIU Fang, et al. MOEA/D with adaptive weight adjustment[J]. Evolutionary computation, 2014, 22(2): 231–264. doi: 10.1162/EVCO_a_00109 [13] LIU Ruochen, ZHOU Runan, REN Rui, et al. Multi-layer interaction preference based multi-objective evolutionary algorithm through decomposition[J]. Information sciences, 2020, 509: 420–436. doi: 10.1016/j.ins.2018.09.069 [14] BASSEUR M, LIEFOOGHE A, LE K, et al. The efficiency of indicator-based local search for multi-objective combinatorial optimisation problems[J]. Journal of heuristics, 2012, 18(2): 263–296. doi: 10.1007/s10732-011-9178-y [15] BADER J, ZITZLER E. HypE: an algorithm for fast hypervolume-based many-objective optimization[J]. Evolutionary computation, 2011, 19(1): 45–76. doi: 10.1162/EVCO_a_00009 [16] GUO Weian, CHEN Ming, WANG Lei, et al. Hyper multi-objective evolutionary algorithm for multi-objective optimization problems[J]. Soft computing, 2017, 21(20): 5883–5891. doi: 10.1007/s00500-016-2163-5 [17] WANG Hongfeng, FU Yaping, HUANG Min, et al. A hybrid evolutionary algorithm with adaptive multi-population strategy for multi-objective optimization problems[J]. Soft computing, 2017, 21(20): 5975–5987. doi: 10.1007/s00500-016-2414-5 [18] COELLO C A C, PULIDO G T, LECHUGA M S. Handling multiple objectives with particle swarm optimization[J]. IEEE transactions on evolutionary computation, 2004, 8(3): 256–279. doi: 10.1109/TEVC.2004.826067 [19] MIRJALILI S, SAREMI S, MIRJALILI S M, et al. Multi-objective grey wolf optimizer: a novel algorithm for multi-criterion optimization[J]. Expert systems with applications, 2016, 47: 106–119. doi: 10.1016/j.eswa.2015.10.039 [20] YANG Shexin. Nature—Inspired metaheuristic algorithm[M]. Frome: Luniver Press, 2008. [21] 赵嘉, 谢智峰, 吕莉, 等. 深度学习萤火虫算法[J]. 电子学报, 2018, 46(11): 2633–2641. doi: 10.3969/j.issn.0372-2112.2018.11.010 ZHAO Jia, XIE Zhifeng, LYU Li, et al. Firefly algorithm with deep Learning[J]. Acta electronica sinica, 2018, 46(11): 2633–2641. doi: 10.3969/j.issn.0372-2112.2018.11.010 [22] ZHAO Jia, CHEN Wenping, XIAO Renbin, et al. Firefly algorithm with division of roles for complex optimal scheduling[J]. Frontiers of information technology & electronic engineering, 2021, 22(10): 1311–1333. [23] YANG Xinshe. Multiobjective firefly algorithm for continuous optimization[J]. Engineering with computers, 2013, 29(2): 175–184. doi: 10.1007/s00366-012-0254-1 [24] TSAI C W, HUANG Yaoting, CHIANG Mingchao. A non-dominated sorting firefly algorithm for multi-objective optimization[C]//2014 14th International Conference on Intelligent Systems Design and Applications. New York, USA: 2014: 62-67. [25] 谢承旺, 张飞龙, 陆建波, 等. 一种多策略协同的多目标萤火虫算法[J]. 电子学报, 2019, 47(11): 2359–2367. doi: 10.3969/j.issn.0372-2112.2019.11.018 XIE Chengwang, ZHANG Feilong, LU Jianbo, et al. Multi-objective firefly algorithm based on multiply cooperative strategies[J]. Acta electronica sinica, 2019, 47(11): 2359–2367. doi: 10.3969/j.issn.0372-2112.2019.11.018 [26] LYU L, ZHAO Jia, WANG Jiayuan, et al. Multi-objective firefly algorithm based on compensation factor and elite learning[J]. Future generation computer systems, 2019, 91: 37–47. doi: 10.1016/j.future.2018.07.047 [27] 贾树晋, 杜斌, 岳恒. 基于局部搜索与混合多样性策略的多目标粒子群算法[J]. 控制与决策, 2012, 27(6): 813–818,826. https://www.cnki.com.cn/Article/CJFDTOTAL-KZYC201206001.htm JIA Shujin, DU Bin, YUE Heng. Local search and hybrid diversity strategy based multi-objective particle swarm optimization algorithm[J]. Control and decision, 2012, 27(6): 813–818,826. https://www.cnki.com.cn/Article/CJFDTOTAL-KZYC201206001.htm [28] ZHAO Xinchao, GAO Xiaoshan, HU Zechun. Evolutionary programming based on non-uniform mutation[J]. Applied mathematics and computation, 2007, 192(1): 1–11. doi: 10.1016/j.amc.2006.06.107 [29] BALLING R. The maximin fitness function; multi-objective city and regional planning[C]. International Conference on Evolutionary Multi-criterion Optimization, 2003: 1−15. [30] 徐鸣, 沈希, 马龙华, 等. 一种多目标粒子群改进算法的研究[J]. 控制与决策, 2009, 24(11): 1713–1718,1728. doi: 10.3321/j.issn:1001-0920.2009.11.022 XU Ming, SHEN Xi, MA Longhua, et al. Research on modified multi-objective particle swarm optimization[J]. Control and decision, 2009, 24(11): 1713–1718,1728. doi: 10.3321/j.issn:1001-0920.2009.11.022 [31] GONG Maoguo, JIAO Licheng, ZHANG Xiangrong. A population-based artificial immune system for numerical optimization[J]. Neurocomputing, 2008, 72(1-3): 149–161. doi: 10.1016/j.neucom.2007.12.041 [32] ZITZLER E, DEB K, THIELE L. Comparison of multiobjective evolutionary algorithms: empirical results[J]. Evolutionary computation, 2000, 8(2): 173–195. doi: 10.1162/106365600568202 [33] DEB K, THIELE L, LAUMANNS M, et al. Scalable multi-objective optimization test problems[C]. Proceedings of the 2002 Congress on Evolutionary Computation. Honolulu, US: IEEE, 2002, 1: 825−830. [34] TANG Lixin, WANG Xianpeng. A hybrid multiobjective evolutionary algorithm for multiobjective optimization problems[J]. IEEE transactions on evolutionary computation, 2013, 17(1): 20–45. doi: 10.1109/TEVC.2012.2185702 [35] ZHENG Li ming, WANG Qiang, ZHANG Sheng xin, et al. Population recombination strategies for multi-objective particle swarm optimization[J]. Soft computing, 2017, 21(16): 4693–4705. doi: 10.1007/s00500-016-2078-1 [36] XING Huanlai, WANG Zhaoyuan, LI Tianrui, et al. An improved MOEA/D algorithm for multi-objective multicast routing with network coding[J]. Applied soft computing, 2017, 59: 88–103. doi: 10.1016/j.asoc.2017.05.033 [37] WANG Wan liang, LI Wei kun, WANG Zheng, et al. Opposition-based multi-objective whale optimization algorithm with global grid ranking[J]. Neurocomputing, 2019, 341: 41–59. doi: 10.1016/j.neucom.2019.02.054 [38] ZITZLER E, KÜNZLI S. Indicator-based selection in multiobjective search[C]//Parallel problem solving from nature-PPSN VIII. Birmingham, UK: Springer, 2004: 832−842. [39] TRIPATHI P K, BANDYOPADHYAY S, PAL S K. Multi-objective particle swarm optimization with time variant inertia and acceleration coefficients[J]. Information sciences, 2007, 177(22): 5033–5049. doi: 10.1016/j.ins.2007.06.018 [40] LIANG J J, QU B Y, SUGANTHAN P N, et al. Dynamic multi-swarm particle swarm optimization for multi-objective optimization problems[J]. 2012 IEEE congress on evolutionary computation, 2012: 1−8. [41] CHEN Bili, ZENG Wenhua, LIN Yangbin, et al. A new local search-based multiobjective optimization algorithm[J]. IEEE transactions on evolutionary computation, 2015, 19(1): 50–73. doi: 10.1109/TEVC.2014.2301794 [42] TIAN Ye, ZHANG Xingyi, CHENG Ran, et al. A multi-objective evolutionary algorithm based on an enhanced inverted generational distance metric[C]//2016 IEEE Congress on Evolutionary Computation. Vancouver, Canada. IEEE, 2016: 5222−5229.











































































































 下载:
下载: