实际应用中，实例通常与多个标记相关联，例如一首歌曲可能与多种情感相关，一张图片可能与多种事物相关，一个网页可能与多个主题相关。近年来，多标记学习引起了人们关注。

多标记学习旨在从一系列候选标记集中选出与实例相关的标记，探索标记关联关系对多标记学习有很大帮助。例如，图像标注中，标记红绿灯和马路同时出现，那么很大概率也会出现汽车标记，而出现轮船这一标记的概率会很小。已有多种多标记学习算法通过考虑标记关联关系来提高分类效果，典型的是将原始标记向量投影到一个低维标记空间中^[1],分类时基于低维标记向量，通过标记关联关系恢复原始标记向量，文献[2]利用标记关联矩阵的低秩性刻画标记关联关系，文献[3]考虑全局和局部标记关联关系。

尽管许多多标记学习方法已被提出，但是仍然存在以下问题。1)大部分现有多标记学习方法仅考虑单视图特征数据，而实际应用中，一个实例可能有多种不同的视图特征表示，例如，一张图像可以用纹理、形状、颜色等不同类别特征来描述。2)训练样本标记不完整时，难以定义合理的标记关联关系，例如网页分类中，存在人工难以确定某些主题是否与网页相关的情况。3)多种基于单视图或多视图的弱标记学习方法已被提出，但很少有考虑数据特征不完整情况。数据特征不完整时，多标记学习模型性能会受到不好的影响，多视图数据中视图特征不完整时，问题会更加复杂，例如一个网页可以由视频、音频、评论等多种方式描述，但某些网页，仅包含以上一种或两种描述。

近期，大量关于图的流形正则化方法被嵌入到分类任务，通过有效表征节点之间关联关系，提高分类性能。因此，针对以上问题，本文提出自适应标记关联与实例关联诱导的缺失多视图弱标记学习算法，可以同时解决多视图多标记学习领域里视图特征不完整、标记不完整问题。算法目标是基于不完整多视图特征数据，学习一个潜在共享表示，并联合弱标记数据，学习一个鲁棒的分类器，在其中融合实例关联关系、标记关联关系使学到的共享表示及分类器更加合理。最后用交替方向法(alternating direction method，ADM)求解，在4个多视图多标记数据集上实验，结果表明所提方法能够有效解决不完整多视图弱标记学习问题。

1.   相关工作

多标记学习具有一定挑战性，因为基于一个未标记实例预测出的标记集合数量与标记候选集标记个数成指数关系，为解决以上问题，现有方法主要通过融合标记关联关系，来促进多标记学习。根据考虑标记相关性的策略可以将多标记学习分为3大类，即一阶策略、二阶策略、高阶策略^[4]。

其中，一阶策略是指逐个处理每个标记，典型算法BR(binary relevance)^[5]，将多标记学习问题分解为许多独立的二元分类问题。一阶策略优点在于其概念简单，另一方面，由于忽略了标记之间相关性，结果可能欠佳。二阶策略是指算法考虑标记两两之间关系来解决多标记学习问题，典型算法CLR (calibrated label ranking)^[6]，由于二阶策略利用了标记相关性，从而此类方法可以实现良好的泛化性能，但一些真实应用中，标记相关性超出了二阶假设，因此该策略会受到影响。高阶策略是指算法考虑标记之间高阶关系来解决多标记学习任务，考察所有标记之间相互关联关系，典型算法有random k-labelsets^[7]，该算法基本思想是将多标记学习问题转化为多个类别的分类任务。近期，文献[8]基于样本标记数据，通过k近邻描述标记之间相似性，促进多标记学习，文献[9]利用结构性稀疏刻画样本特征和标记噪声，解决数据特征和标记同时存在噪声的问题，文献[10]提出一种弱标记学习方法，利用实例关联关系和标记关联关系，集多个模型于一体，有效解决了标记不完整场景，文献[11]结合神经网络，选择可预测的地标，通过标记关联关系恢复整个标签集合，能够有效处理多标记学习问题中标签数量大的情况。与一阶策略和二阶策略相比，高阶策略具有更强的相关性建模能力，更好的泛化性能。

为了有效处理多标记学习任务，一些自适应算法被提出，该类方法通过嵌入经典流行的学习技术解决多标记学习问题。典型的算法有一阶策略ML-KNN (multi-label k-nearest neighbor)^[12]和ML-DT (multi-label decision tree) ^[13]，分别利用惰性学习和决策树技术来处理多标记学习任务，二阶策略CML (collective multi-label classifier)^[14]利用信息论技术处理多标记学习任务。

多标记学习算法一般考虑实例特征是单视图特征，然而，实际应用中，实例通常有不同类别的视图特征，因此，多视图多标记学习引起了人们的兴趣。文献[15]基于多视图特征数据，利用矩阵分解得到潜在共享表示进行多标记学习，文献[16]假设共享表示矩阵低秩，进而使用矩阵补全算法进行多标记学习，文献[17]联合多视图特征数据，通过特征选择得到一组低维有效的特征进行多标记学习，文献[18]提出一种不完整多视图弱标记学习算法，用标记关联矩阵低秩性刻画标记关联关系，同时学习共享表示、局部标记关联关系和一个分类器，性能良好，文献[19]提出多视图网络模型框架，针对不完整多视图异构数据具有强适应性，文献[20]采用矩阵分解，从具有特定约束的多视图数据中获得分层表示，文献[21]利用生成对抗网络处理缺失视图问题。

2.   模型框架

多视图多标记学习中，训练集表示为 $\chi = \{ {{\boldsymbol{X}}^{{v}}}\} _{v = 1}^m$ ，包含 $n$ 个样本、每个样本有 $m$ 个视图，其中 ${{\boldsymbol{X}}^{{v}}} = [{{x}}_{{1}}^{{v}}\;{{x}}_{{2}}^{{v}}\;\cdots\;{{x}}_{{n}}^{{v}}] \in {{\bf{R}}^{{{{d}}_{{v}}} \times {{n}}}}$ 表示第 $v$ 个视图的特征空间。 ${\boldsymbol{Y}} = [{{{y}}_{{1}}}\;{{{y}}_{{2}}}\;\cdots\;{{{y}}_{{n}}}] \in {\{ - 1,1\} ^{c \times n}}$ ， ${y_{ij}} = - 1$ 时，第 $i$ 个标记与第 $j$ 个样本不相关， ${y_{ij}} = 1$ 时，第 $i$ 个标记与第 $j$ 个样本相关。本文研究不完整多视图弱标记学习，即多视图多标记学习中，存在视图不完整、标记不完整情形。

对于视图不完整，具体表现为一个实例并不是在所有视图中的特征都存在，即对于第 $v$ 个视图的特征矩阵 ${{\boldsymbol{X}}^{{v}}}$ ，存在成列缺失，解决该问题的一种简单方法就是删除在任何视图中存在缺失特征的样本，但是这会大量减少能使用的训练样本数量。对于标记不完整，具体表现为标记矩阵 ${\boldsymbol{Y}} = [{{{y}}_{{1}}}\;{{{y}}_{{2}}}\;\cdots\;{{{y}}_{{n}}}] \in {\{ - 1,0,1\} ^{c \times n}}$ ，当 ${y_{ij}} = - 1$ 时，第 $i$ 个标记与第 $j$ 个样本不相关，当 ${y_{ij}} = 1$ 时，第 $i$ 个标记与第 $j$ 个样本相关，当 ${y_{ij}} = 0$ 时，不确定第 $i$ 个标记是否与第 $j$ 个样本相关，即第 $i$ 个标记关于第 $j$ 个样本，可能是正标记，也可能是负标记。本文目标就是基于以上描述的不完整多视图弱标记数据，学习一个分类器来预测未标记的不完整多视图实例的相关标记。ACMVML模型框架如图1所示。

图  1  ACMVWL的模型框架

Fig.  1  Model framework of ACMVWL

下载: 全尺寸图片

2.1   基本模型

对于多视图多标记学习，如何得到一个具有判别性的共享表示和如何基于共享表示、标记信息训练一个有效鲁棒的分类器是两个需要解决的问题。首先，假设样本不同视图特征来源于一个共享表示， ${{\boldsymbol{X}}^{{v}}} = {{\boldsymbol{P}}^{{v}}}{\boldsymbol{V}}$ ，其中 ${{\boldsymbol{X}}^{{v}}} \in {{\bf{R}}^{{{{d}}_{{v}}} \times {{n}}}}$ 表示第 $v$ 个视图的特征矩阵， ${\boldsymbol{V}} \in {{\bf{R}}^{{{k}} \times {{n}}}}$ 表示共享表示矩阵， ${{\boldsymbol{P}}^{{v}}} \in {{\bf{R}}^{{{{d}}_{{v}}} \times k}}$ 表示与第 $v$ 个视图相关的投影矩阵，可以理解为 ${{\boldsymbol{X}}^{{v}}}$ 是基于共享表示 ${\boldsymbol{V}}$ ，通过投影矩阵 ${{{P}}^{{v}}}$ 投影而得。利用矩阵分解框架，可以将以上描述刻画为

其中，约束项 ${({{\boldsymbol{P}}^{{v}}})^{\rm{T}}}{{\boldsymbol{P}}^{{v}}} = {\boldsymbol{I}}$ 可以避免有无穷多组解，通过(1)学习到的共享表示 ${\boldsymbol{V}}$ 可以捕获多视图特征的互补信息^[22]。

多视图特征数据成列缺失时，一种简单方法即通过已有数据特征均值来填充，但这种方法会带来较大误差，当缺失很多时对模型影响尤为明显，因此不是处理不完整多视图数据的有效方法。本模型采用一种监督方法，充分利用已有的多视图数据学习一个潜在共享表示，即

式中： $ \circ $ 是哈达玛积，符号两边矩阵对应元素相乘； ${{\boldsymbol{O}}^{{v}}} \in {\{ 1,0\} ^{{{{d}}_{{v}}} \times n}}$ 是指示矩阵，当 ${{\boldsymbol{X}}^{{v}}}$ 中某些列缺失时， ${{\boldsymbol{O}}^{{v}}}$ 对应列元素为0，否则为1。

但是(2)学到的共享表示 ${\boldsymbol V}$ ，没有考虑标记信息，因此判别能力不强，为增强其判别能力，通常可以联系标记信息，将其融合到统一框架。考虑到弱标记情形，标记信息不完整，与利用不完整特征数据相仿,充分利用已确定的那部分标记信息，提出基本模型：

式中： ${\boldsymbol{M}} \in {\{ 1,0\} ^{{{c}} \times {{n}}}}$ ，当 $ {Y_{ij}} = 0 $ 时， $ {M_{ij}} = 0 $ ，否则 $ {M_{ij}} = 1 $ ； ${\boldsymbol{W}} \in {{\bf{R}}^{c{{ \times }}k}}$ 表示线性分类器，可以理解为将共享表示 ${\boldsymbol{V}}$ 投影到标记空间的映射；变量 $ {\lambda _1} $ 为超参数。将学习共享表示和分类器融合到统一框架，可以使学到的共享表示 ${\boldsymbol{V}}$ 更具判别性，减小共享表示与标记空间之间的鸿沟^[23]。

2.2   标记流形正则化

考虑标记关联关系在弱标记学习中非常重要，通常可以提高多标记学习性能^[24]。近年来，流形正则化思想被广泛利用到分类任务中，其中可以利用图的拉普拉斯矩阵刻画节点之间关联关系。

基于标记关联关系的流形正则化思想可以理解为若两个标记之间相似性越高，则分类器输出的关于两个标记的预测结果也越相近，否则相反。换句话说，正相关的两个标记引导分类器关于其输出尽可能相似，负相关的两个标记引导分类器关于其输出尽可能有差异。设 ${\boldsymbol{F}} = {\boldsymbol{WV}} \in {{\bf{R}}^{{{c}} \times {{n}}}}$ ， ${\boldsymbol{F}}$ 表示基于 $ n $ 个样本特征的预测结果， ${{{f}}_{{{i,:}}}}$ 指 ${\boldsymbol{F}}$ 的第 $ i $ 行，如果第 $ i $ 个标记与第 $ j $ 个标记越相似，则 ${{{f}}_{{{i,:}}}}$ 和 ${{{f}}_{{{j,:}}}}$ 也应该越相似，基于标记流形正则化可以定义为

式中： ${{\boldsymbol{S}}_{{c}}}$ 是 $ c \times c $ 维标记关联矩阵，如果标记 $ i $ 和 $ j $ 越相关，则 ${[{{\boldsymbol{S}}_{{c}}}]_{i,j}}$ 越大，通过最小化(4)， $\left\| {{{{f}}_{{{i,:}}}} - {{{f}}_{{{j,:}}}}} \right\|_2^2$ 将会越小。设 ${{\boldsymbol{D}}_{{c}}}$ 为对角矩阵，其对角线元素为 ${{\boldsymbol{S}}_{{c}}}{\boldsymbol A}$ ，其中 ${\boldsymbol A}$ 是全1向量，(4)中流形正则化项等价于 ${\rm Tr}\; ({{\boldsymbol{F}}^{\rm{T}}}{\boldsymbol{L}_{{c}}}{\boldsymbol{F}})$ ^[25], ${{\boldsymbol{L}}_{{c}}} = {{\boldsymbol{D}}_{{c}}} - {{\boldsymbol{S}}_{{c}}}$ 为标记关联矩阵 ${{\boldsymbol{S}}_{{c}}}$ 的 $ c \times c $ 维拉普拉斯矩阵。问题(3)基础上增加基于标记关联关系的流形正则化,变量 $ {\lambda _2} $ 为超参数，模型可以表达为

2.3   自适应标记关联

标记流形正则化的成功取决于有一个好的标记关联矩阵（或者一个好的标记拉普拉斯矩阵）。一种简单方法是基于距离度量标记关联关系，比如高斯距离、余弦距离等来直接计算两个标记之间关联关系^[26]，但是因为训练集中一些标记有很少的正例，关联关系的估算会不太理想，部分标记缺失时，这种估算方法得出的关联关系会更没有说服力，因为估算出的标记分布与真实标记分布差异很大。为了有效描述标记关联关系，本文直接学习一个关于标记的拉普拉斯矩阵间接刻画标记关联关系。拉普拉斯矩阵具有对称半正定性，若直接学习 ${{\boldsymbol{L}}_{{c}}}$ ，无法得到一个对称半正定的拉普拉斯矩阵，且可能会产生平凡解 ${{\boldsymbol{L}}_{{c}}} = {{0}}$ 。因此，可以将 ${{\boldsymbol{L}}_{{c}}}$ 分解为 ${{\boldsymbol{Z}}_{{c}}}{\boldsymbol{Z}}_{{c}}^{\rm T}$ ，其中 ${{\boldsymbol{Z}}_{{c}}} \in {{\bf{R}}^{{{c}} \times {{l}}}}$ ,将学习拉普拉斯矩阵问题转化为学习 ${{\boldsymbol{Z}}_{{c}}}$ ，在优化时，会产生平凡解 ${{\boldsymbol{Z}}_{{c}}} = {0}$ ；为了避免平凡解，可以增加约束 ${\text{diag}}({{\boldsymbol{Z}}_{{c}}}{\boldsymbol{Z}}_{{c}}^{\rm T} ) = 1$ ，这一约束也可以使模型得到一个标准拉普拉斯矩阵^[27]，该标准拉普拉斯矩阵可以有效表征节点之间关联关系，文献[3]利用此方法取得了有效结果。基于以上讨论，融合分解拉普拉斯矩阵及增加约束 ${\text{diag}}({{\boldsymbol{Z}}_{{c}}}{\boldsymbol{Z}}_{{c}}^{\rm T} ) = 1$ ，可以得到下面的优化问题：

2.4   自适应实例关联

多视图多标记学习性能与学到的共享表示 ${\boldsymbol{V}}$ 密切相关，与多标记学习领域考虑标记关联关系的重要作用类似，如果能够获取实例之间关联关系，就可以利用实例分布辅助学习共享表示 ${\boldsymbol{V}}$ 。设 ${{\boldsymbol{S}}_{{n}}}$ 是 $ n \times n $ 维实例关联矩阵， ${{{v}}_{{{:,i}}}}$ 指 ${\boldsymbol{V}}$ 的第 $ i $ 列， ${{{v}}_{{{:,}}j}}$ 指 ${\boldsymbol{V}}$ 的第 $ j $ 列，分别代表在完整共享表示空间里的第 $ i $ 和第 $ j $ 个实例。若第 $ i $ 个实例与第 $ j $ 个实例越相似，则 ${{{v}}_{{{:,i}}}}$ 和 ${{{v}}_{{{:,}}j}}$ 也应该越相似，基于实例流形正则化可以定义为

设 ${{\boldsymbol{D}}_{{n}}}$ 为对角矩阵，对角线元素为 ${{\boldsymbol{S}}_{{n}}}{\boldsymbol A}$ ，(7)中流形正则化项等价于 ${\rm tr} ({\boldsymbol{V}}{{\boldsymbol{L}}_{{n}}}{{\boldsymbol{V}}^{\rm T} })$ ， ${{\boldsymbol{L}}_{{n}}} = {{\boldsymbol{D}}_{{n}}} - {{\boldsymbol{S}}_{{n}}}$ 为实例关联矩阵 ${{\boldsymbol{S}}_{{n}}}$ 的 $ n \times n $ 维拉普拉斯矩阵。利用流行正则化技术时，通常可以基于距离度量计算实例关联关系，当多视图特征数据成列缺失，一种简单方法即将缺失部分特征取值为未缺失部分特征的均值，将填充后的多视图数据连接成单视图，基于距离计算实例关联关系。但这种方法会带来较大误差，缺失很多时对模型影响尤为明显，因此不可行。与学习标记拉普拉斯矩阵相仿，本文学习一个刻画实例关联关系的标准拉普拉斯矩阵，将 ${{\boldsymbol{L}}_{{n}}}$ 分解为 ${{\boldsymbol{Z}}_{{n}}}{\boldsymbol{Z}}_{{n}}^{\rm T}$ ，其中 ${{\boldsymbol{Z}}_{{n}}} \in {{\bf{R}}^{{{n}} \times {{r}}}}$ ,将学习拉普拉斯矩阵问题转化为学习 ${{\boldsymbol{Z}}_{{n}}}$ ，在问题(6)的基础上增加基于实例关联关系的流形正则化，并且将F范数的平方作用于 ${\boldsymbol{W}}$ 、 ${\boldsymbol{V}}$ 来增强模型稳定性，变量 $ {\lambda _3} $ 、 $ {\lambda _4} $ 为超参数，模型可以表达为

3.   优化求解

问题(8)可以用交替方向法(alternating direction method, ADM)求解，该方法能够迭代地调整变量以找到有效结果。每次迭代中，用梯度下降法^[28]分别更新 $\{ {{\boldsymbol{Z}}_{{n}}}{{,}}{{\boldsymbol{Z}}_{{c}}}{{,{\boldsymbol{V}},{\boldsymbol{W}},}}{{\boldsymbol{P}}^{{v}}}\}$ 中的一个变量，同时固定其他变量，整个优化问题可以简化为5个子问题，借助工具包MANOPT^[29]实现求解，详细的更新过程将在下面进行讨论。

1) 更新 ${{\boldsymbol{Z}}_{{n}}}$ ，问题(8)简化为

因为约束 ${\text{diag}}({{\boldsymbol{Z}}_{{n}}}{\boldsymbol{Z}}_{{n}}^{\rm T} ) = 1$ ，所以该问题没有闭式解，这里用梯度下降法求解，目标函数关于 ${{\boldsymbol{Z}}_{{n}}}$ 的梯度如下

为了满足约束 ${\text{diag}}({{\boldsymbol{Z}}_{{n}}}{\boldsymbol{Z}}_{{n}}^{\rm T} ) = 1$ ，可以在每一轮更新后，将 ${{\boldsymbol{Z}}_{{n}}}$ 的每一行单位标准化：

其中 ${{\boldsymbol{Z}}_{{{n,i,:}}}}$ 指矩阵 ${{\boldsymbol{Z}}_{{n}}}$ 的第 $i$ 行。

2) 更新 ${{\boldsymbol{Z}}_{{c}}}$ ，问题(8)简化为

与问题(9)目标函数同理，问题(10)关于 ${{\boldsymbol{Z}}_{{c}}}$ 的梯度为

为了满足约束 ${\text{diag}}({{\boldsymbol{Z}}_{{c}}}{\boldsymbol{Z}}_{{c}}^{\rm T} ) = 1$ ，使

3) 更新 ${\boldsymbol{V}}$ ，问题(8)简化为

目标函数关于 ${\boldsymbol{V}}$ 的梯度为

4) 更新 ${\boldsymbol{W}}$ ，问题(8)简化为

关于 ${\boldsymbol{W}}$ 的梯度为

5) 更新 ${{\boldsymbol{P}}^{{v}}}$ ， $v \in \{ 1,2,\cdots,m\}$ ，问题(8)简化为

因为 ${({{\boldsymbol{P}}^{{v}}})^{\rm T} }{{\boldsymbol{P}}^{{v}}} = {\boldsymbol{I}}$ ，所以该问题没有闭式解，用梯度下降法进行求解，目标函数关于 ${{\boldsymbol{P}}^{{v}}}$ 的梯度如下：

对于约束 ${({{\boldsymbol{P}}^{{v}}})^{\rm T} }{{\boldsymbol{P}}^{{v}}} = {\boldsymbol{I}}$ ，调用工具包MANOPT，利用梯度下降法，在球形空间 ${({{\boldsymbol{P}}^{{v}}})^{\rm T} }{{\boldsymbol{P}}^{{v}}} = {\boldsymbol{I}}$ 里，搜索最优解。优化算法重复上述更新过程，直至收敛。其中初始化 ${\boldsymbol{W}} = {\rm rand} (c,k)$ ， ${\boldsymbol{V}} = {\rm rand} (k,n)$ ， ${{\boldsymbol{Z}}_{{c}}} = {\rm rand} (c,l)$ ， ${{\boldsymbol{Z}}_n} = {\rm rand} (n,r)$ 。

4.   实验

4.1   数据集

本文在4个多视图多标记数据集上进行实验：C-orel5k，ESPGame，IAPRTC12，Mirflickr。数据集来源于网站(http://lear.inrialpes.fr/people/guillaumin/data.php)。详细信息如表1所示。

4.2   实验设置

本文将所提模型同几个相关算法比较，包括文献[3]提出的基于全局和局部标记关联关系的多标记学习算法(Glocal)，捕获全局和局部标记关联关系，促进多标记学习，HNOML^[9] 利用结构性稀疏刻画样本特征和标记噪声，解决数据特征和标记同时存在噪声的问题，LrMMC^[16]假设多视图特征数据来源于一个共享表示且共享表示矩阵低秩，进而使用矩阵补全算法进行多标记学习，MVLIV^[20]提出了一种多视图学习方法，考虑了视图不完整情形，IMVWL^[18]提出一种不完整多视图弱标记学习算法，用矩阵低秩性来刻画标记关联关系，同时学习潜在共享表示、局部标记关联关系和一个分类器。其中，方法ML-KNN、Glocal、LrMMC不能直接处理不完整多视图弱标记学习问题，对于算法ML-KNN、Glocal、LrMMC，将缺失部分特征取值为未缺失部分特征的均值，对于算法ML-KNN、MVLIV将缺失标记视为负标记，对于单视图多标记学习算法ML-KNN、Glocal，将处理后的多视图特征数据叠加成一个向量。

对于本文模型ACMVWL的超参数 ${\lambda _1},{\lambda _2},{\lambda _3},{\lambda _4}$ ，从集合 $\{ {10^{ - 4}},{10^{ - 3}},\cdots,{10^2}\}$ 通过网格搜索、三折交叉验证策略确定每个参数的最佳值，推荐分别设为100，10，1，1。维度 $k$ 、 $l$ 、 $r$ 分别以视图特征最低维度 ${d_{\min }}$ 、候选标记数量 $c$ 、训练样本数量 $n$ 为基准，按比例 $\{ 0.1,0.2,\cdots,1\}$ 测试，选取各自的值，推荐 $k = 0.5{d_{\min }}$ ， $l = 0.3c$ ， $r = 0.1n$ 。其余算法尽力调参，以达到最好效果。并且进行一组消融实验，验证本文提出模型关键项的有效作用。

4.3   对比实验

对比实验特征缺失率取50%，标记缺失率取50%，实验结果（平均值 $ \pm $ 标准差）如表2，最优值标记为粗体，次优值标记为下划线，其中最后一行统计了各个算法分别取得最优值和次优值的次数。可以观察到，模型ACMVWL在4个真实数据集的5个评价指标上，90%（18/20）情况下取得最优值或次优值,

相比于其他算法有一定的优势。作为多视图多标记学习算法MVLIV，由于没有考虑标记不完整，并且学习共享表示时未考虑标记信息所以结果欠佳，最优值和次优值为0%。算法LrMMC由于没有考虑特征和标记不完整，所以它的结果是很一般的，20%的情况下取得最优或次优。IMVWL算法学习标记关联关系，同时考虑到了特征缺失和标记缺失，在35%的情况下取得最优或次优值，并且在评价指标上明显优于LrMMC和MVLIV。HNOML算法同时考虑特征噪声和标记噪声，20%的情况下取得最优或次优结果。Glocal考虑了标记之间的全局关联关系与局部关联关系并且同时考虑到标记不完整情况，实验结果最优或次优的情况占80%，性能良好。

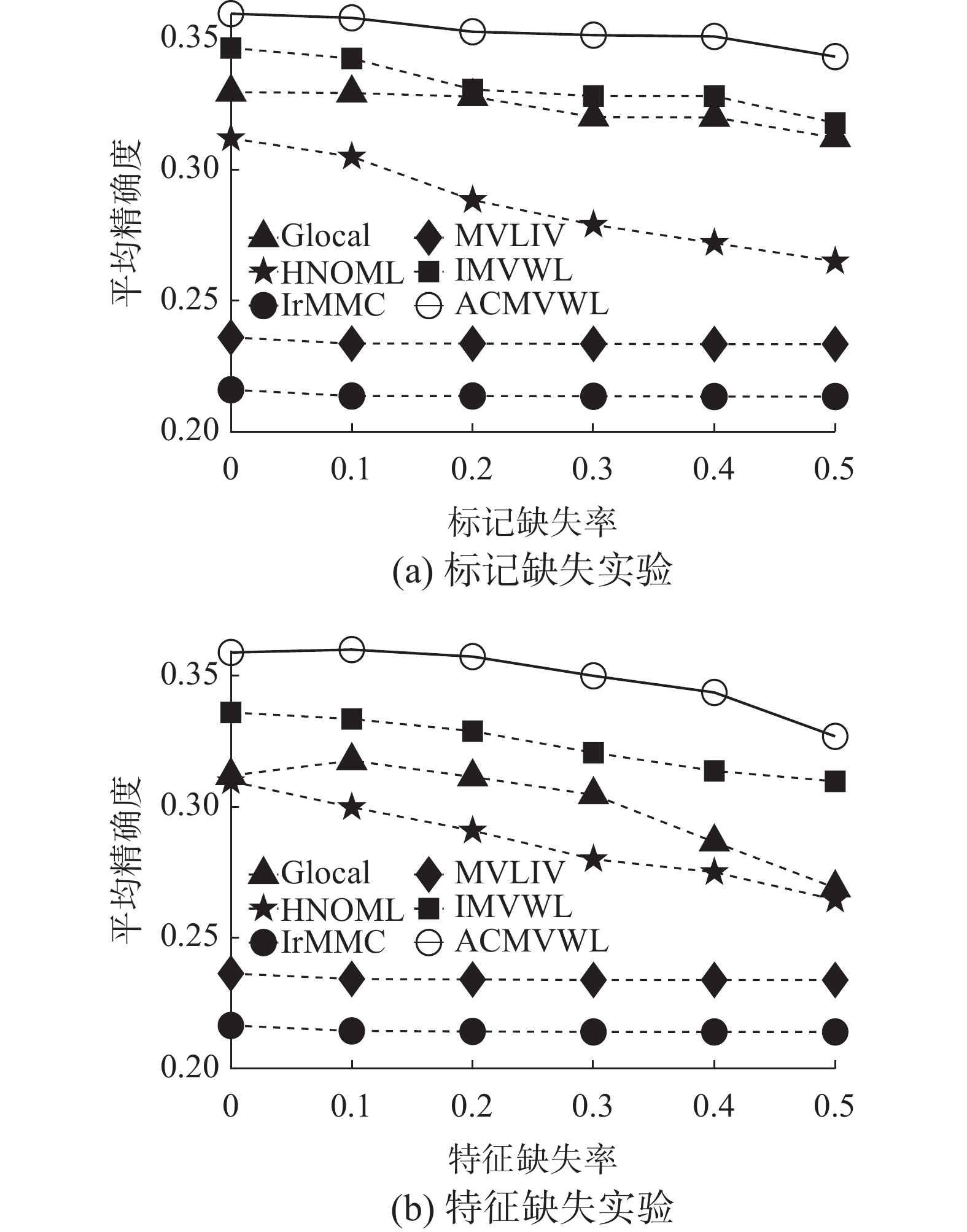
为验证所提模型分别在特征和标记不同缺失率下的表现，本文在Corel5k数据集上进行实验，图2(a)为特征完整，标记缺失率变化对比结果，图2(b)为标记完整，特征缺失率变化对比结果。6种算法里，本文模型排名居前，在不同的标记缺失率和特征缺失率下取得了有效表现,并且随着缺失率越大，优势越明显，且随着标记不完整和视图特征不完整程度变大，算法结果整体小幅度下降。

图  2  在数据集Corel5k上不同标记缺失率和特征缺失率对比

Fig.  2  Comparison of different missing rates of label and feature on Corel5k

下载: 全尺寸图片

4.4   消融实验

模型通过学习标记关联关系、实例关联关系，并且嵌入流形正则化思想，使学到的潜在共享表示以及分类器更加合理。为验证学习标记关联关系与实例关联关系对模型预测的有效作用，进行一组消融实验。结果（平均值 $ \pm $ 标准差）如表3，最优值标记为粗体，次优值标记为下划线。ACMVWL即为本文模型，ACMVWL-NI为消除学习实例关联关系项的模型( ${\lambda _3} = 0$ ),ACMVWL-NIL为消除学习标记关联关系和实例关联关系项的基本模型( ${\lambda _2} = 0,{\lambda _3} = 0$ )，根据表3可以发现，模型ACMVWL表现排名第一，ACMVWL-NI排名第二，ACMVWL-NIL排名第三，效果最差。可以得出结论学习标记关联关系和实例关联关系有助于提高模型预测表现。

4.5   参数分析

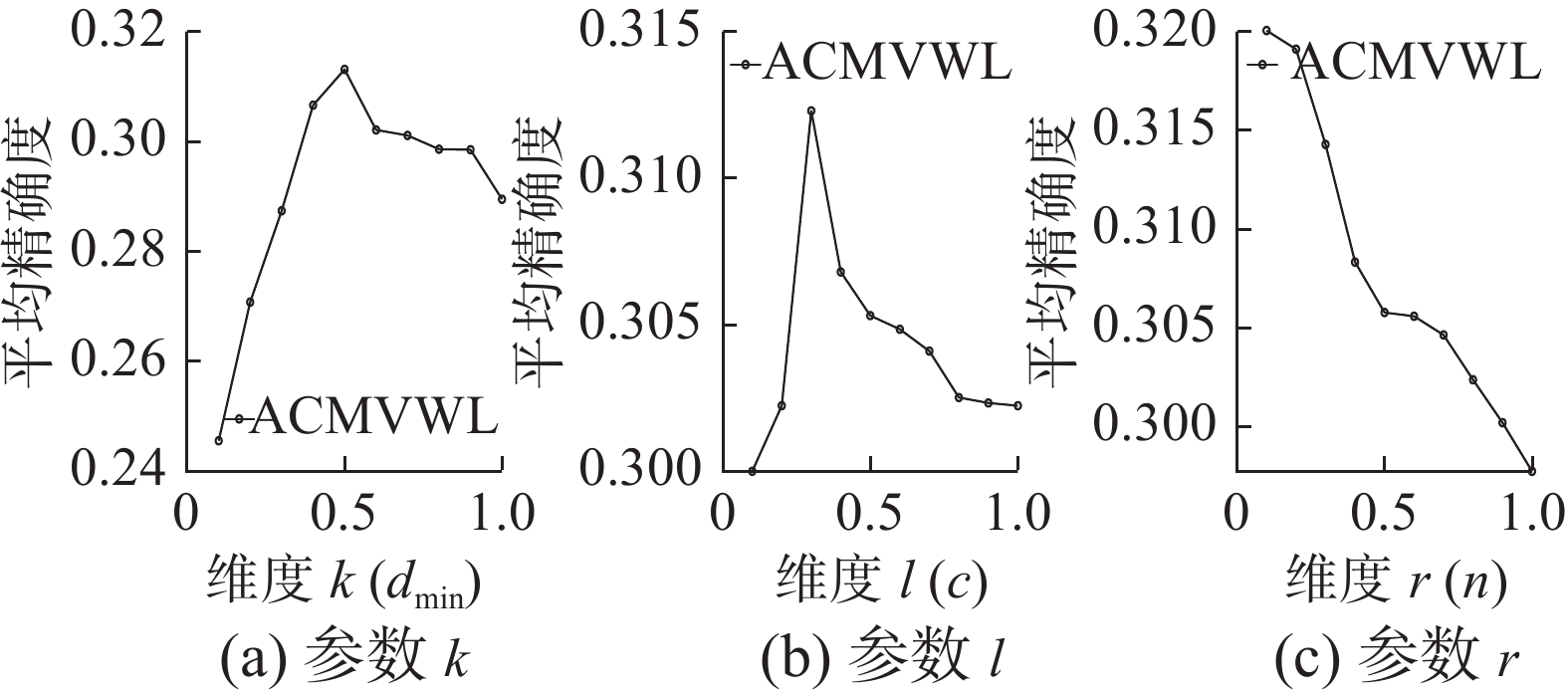
这组实验主要研究共享表示 ${\boldsymbol{V}}$ 的维度 $k$ ，学习标记关联关系、实例关联关系用到的 ${{\boldsymbol{Z}}_{{c}}}$ 和 ${{\boldsymbol{Z}}_{{n}}}$ ，其中 ${{\boldsymbol{Z}}_{{c}}}$ 的维度 $ l $ ， ${{\boldsymbol{Z}}_{{n}}}$ 的维度 $ r $ ，对上述3个维度参数进行实验，实验固定其他参数，分别探索其中一个参数的变化对模型的影响，结果如图3可以发现，当 $ k = 0.5{d_{\min }} $ ， $ l = 0.3c $ ， $ r = 0.1n $ 时，模型性能较好。

图  3  数据集Corel5k上维度k、l、r的变化对Average precision影响

Fig.  3  The influence of different dimension of k, l, r on Average precision of Corel5k

下载: 全尺寸图片

4.6   收敛性分析

本文模型ACMVWL用交替方向法求解，图4为算法在数据集Corel5k和IAPRTC12上收敛情况，可以明显看出迭代次数很少的情况下即可收敛，符合预期。

图  4  Corel5k和IAPRTC12上的收敛曲线

Fig.  4  Coverage curves on Corel5k and IAPRTC12

下载: 全尺寸图片

4.7   复杂度分析

模型求解过程可以简化为5个子问题，分别求解 $\{ {{\boldsymbol{Z}}_{{n}}}{{,}}{{\boldsymbol{Z}}_{{c}}}{{,{\boldsymbol{V}},{\boldsymbol{W}},}}{{\boldsymbol{P}}^{{v}}}\}$ ，总体时间复杂度表示为

5.   结束语

本文提出一种自适应标记关联与实例关联诱导的缺失多视图弱标记学习算法，可以同时解决多视图多标记学习领域里视图特征不完整、标记不完整问题。算法核心思想是基于不完整多视图特征数据，学习一个潜在共享表示，并联合弱标记数据，学习一个鲁棒的分类器，最后融合自适应标记关联关系以及实例关联关系，使学到的共享表示以及分类器更加合理。在4个代表性多视图多标记学习相关数据集上的实验也证明了所提模型有效性。后续工作，计划将模型推广到深度学习，结合深度神经网络增强模型性能。