随着知识与信息数量的快速增长以及信息获取便利性的增加，企事业组织所面临的内外部环境更加复杂，业务问题呈现非线性、不确定性、多维化和实时交互性等特点。业务环境的高度不确定性和面临问题的开放性，人工智能与问题处理的深入研究迫切需要有一种自觉地为信息科学与智能科学服务的定性定量相结合的智能数学模型。经典数学适于描述物质世界的数量与空间关系，智能数学必须能描述信息拓展与智能机理。整体观强调功能与结构二者之间的统一，机制主义人工智能理论强调：智能活动的目的决定效用，效用选择形式，形式信息与效用信息相结合产生全面的语义信息^[1]。全面兼顾形式、效用、语义实现信息向知识的转换以至智能生成机制的研究需要新的数学理论支撑。1982年，直接以认知为描述对象的三个数学理论诞生：形式概念分析(formal concept analysis)^[2]、粗糙集(rough sets)^[3]和因素空间(factor space)^[4]。1983年，蔡文提出可拓集合^[5]，后来发展成为可拓学(Extenics)^[6-7]。因素空间和可拓学所研究的主要内容都与模糊数学和问题处理有关。

在大数据与人工智能环境下，因素空间与可拓学迎来了新的发展机遇，在数据科学领域取得了一系列进展^[8-11]。但两者的交叉研究还比较缺乏，本文拟通过两者的互补性分析，讨论其在问题处理方面交叉研究的可行性，并尝试构建因素空间与可拓学融合的问题处理模型，促使开放性问题求解从模糊性、不确定性向数量化、必然性转化，以进一步提升问题处理的智能化水平，推动智能数学研究方向的发展。

1.   因素空间与可拓学理论方法体系

1.1   因素空间的理论与方法体系

因素空间是在概率论和模糊数学基础上发展起来的研究因素相关性的数学，是笛卡尔空间的推广和模糊数学的深化^[12-13]，模糊性是由于认知因素不充分而导致的概念划分的不确定性。通过因素探索随机性与模糊性这两种不确定性之间的联系，指明了随机性是由于测量因素的不充分而造成事件发生的不确定性，随机性是因果律的破缺，概率是在不充分条件与结果之间所存在着的广义因果律。以因素显隐等实现确定性与不确定性的相互转化，在知识表示、模糊控制、模糊推理机的研制等方面形成了模糊落影等理论及其应用体系。

因素是因果分析的要素和问题分析的表达要素，在单因素分析基础上，把所有与问题有关的单因素综合起来，得到一个以多因素为轴的坐标空间，称为因素空间。因素空间的定义如下^[9]：

设 $F = \left\{ {{f_1} ,{f_2} ,\cdots ,{f_n}} \right\}$ 是定义在U上的因素集，即 ${f_j}:U \to X\left( {{f_j}} \right)\left( {j = 1,2, \cdots ,n} \right)$ 。

定义1^[13] 　设 $F' = P\left( F \right) = \left( {F', \vee , \wedge ,\neg ,0,1} \right) $ 是一个布尔代数，记 $X\left( F \right) = {\left\{ {X\left( f \right)} \right\}_{\left( {f \in F'} \right)}} $ ，称 $\psi = \left( {U,X\left( F \right)} \right) $ 为U上的一个因素空间，如果满足条件：

1） $X\left( 0 \right) = \left\{ \text{Ø} \right\}$ ；

2）对任意 $ T \subseteq F $ 及 $s,t \in T $ ，若 $s \wedge t = 0 $ (s与t称为不可约)，则

$X\left( { \vee \left\{ {f|f \in T} \right\}} \right) = {\Pi _{f \in T}}X\left( f \right) $ ( $\Pi $ 是笛卡尔乘积)

其中， $F = \left\{ {{f_1}, {f_2} ,\cdots ,{f_n}} \right\} = \left\{ {{f_1} \vee {f_2} \vee \cdots \vee {f_n}} \right\} = 1$ 称为全因素，0称为空因素。记号∨和∧分别叫做因素的合成和分解运算。

对任意 $f = \left\{ {{f_{\left( 1 \right)}},{f_{\left( 2 \right)}}, \cdots ,{f_{\left( k \right)}}} \right\} \subseteq F$ ，用同一符号来记 $f = {f_{\left( 1 \right)}} \vee {f_{\left(2 \right)}} \vee \cdots \vee {f_{\left( k \right)}},{f_1},{f_2}, \cdots ,{f_k}$ 称为元因素。如和人有关的因素F={性别，年龄，身高，体重，文化程度，职称，组织能力，亲和力，…}，因素集可以视为集中各因素的合成因素。

在属性层次上盲目寻找原因很难，在因素层次上找到关键因素才能更快识别原因^[14]。因素通常有4种情况：1）传统数学中所有的变量，如时间、距离和质量等，可以用实数值来描述；2）指标体系中所使用的指标，如产量、价格、成本、收益、能耗等；3）感知过程中所观测的变量，如身高、体重、性别、相貌、装束、性格等，既可以取实数值，也可以取高、常、矮等定性的自然语言词。定量与定性这两种描述可以通过模糊数学的方法互相转换；4）主观度量或带有目的或效用性的度量，如满意度、生活压力、社会冲突、和谐度、生产效益等都是因素。因素空间所描述的可能是自然界与社会生活中的任何事物。

因素空间的假设是，随机性是由于某些具有影响力的因素尚未被考虑到或测量到，如果所有因素的状态都确定，则结果便唯一确定。因素的增加会降低认识的模糊性，仅以年龄为因素，则“年轻”这一概念的隶属曲线比较模糊，但若加上“面容”和“精力”等因素，年轻的隶属曲线就比原来清晰。从因素层面寻找对结果最有影响的变量，因素空间为事物描述和认知提供了普适性的描述框架^[15]。在综合现有文献基础上，绘制因素空间理论与方法体系示意图如图1所示。

图  1  因素空间理论与方法体系示意图

Fig.  1  Schematic diagram of theory and methods of factor space

下载: 全尺寸图片

背景关系是因素空间的核心概念之一，它决定了概念生成和因素之间的推理知识，概念和推理等高级智能活动可由背景关系简洁地刻画出来^[16-17]；因素库以因素空间为母体，由一个主表及若干衍生表所组成，每张表就是某个因素空间的一组样本点。所有同表头样本在去掉对象列以后的叠加就是背景关系，背景关系具有凸性，可以用背景基来取代，背景基形成的因素库数据生态在大数据处理方面具有一些优越的特性^[8,14]。

模糊落影理论构造了随机与模糊这两种不确定性之间的对偶模型，指出模糊试验等价于幂上的随机试验，隶属度的客观度量可以用随机集的覆盖频率来实现^[11]。这一理论使模糊集合论变为集合论往幂上的提升,建立了论域与其幂对应的存在唯一性定理。

1.2   可拓学的理论与方法体系

可拓学把矛盾问题作为研究对象，以形式化模型研究事物拓展的可能性及策略生成的基本规律与方法^[6-7]。可拓学是一门横跨哲学、数学和工程学的新学科^[18]，可拓学理论包括基元理论、可拓集合理论和可拓逻辑^[6-7]，其理论框架图可参考文献[7]。

基元理论以（对象，特征，量值）描述万事万物及其联系，分别建立了物元、事元和关系元（统称为基元）模型；研究了基元的拓展性和变换、运算的规律，建立了定量与定性相结合的可拓模型作为处理矛盾问题的形式化工具。研究了基元的拓展分析理论和物的共轭分析理论，提出了可拓变换理论^[19]。

可拓集合提出了表述事物性质动态变化的集合概念，把辩证法关于矛盾转化和变换的思想引入集合论。以基元为元素的基元可拓集合把质与量综合考虑，从动态转化角度对论域做了5类划分，研究了关联函数以及定量化的计算公式，以关联函数值表征事物具有某种性质及性质的量变和质变程度，为解决矛盾问题和决策提供了集合论的理论与方法基础^[20-21]。可拓集合定义如下

定义2 ^[7] 　设U为论域，u为U中的任一元素，k是U到实域R的一个映射， $ T = ({T_U},{T_k},{T_u}) $ 是给定的变换，称

为论域U上的一个可拓集， $ y = k(u) $ 为 $ \mathop E\limits^ \sim (T) $ 的关联函数， $ {y'} = {T_k}k({T_u}u) $ 为 $ \mathop E\limits^ \sim (T) $ 的可拓函数。其中T_U、T_k、T_u分别为对论域U、关联准则k和元素u的变换。

以可拓模型表达物、事、关系和特征的变换以及变换所引起的其他物、事、关系和特征的传导变换，研究了基元和复合元的可拓推理规则及解决矛盾问题的推理形式，把形式逻辑和辩证逻辑相结合，初步构建了以解决矛盾问题的变换和推理为核心的可拓逻辑^[9]。在理论研究基础上，可拓学研究者提出了一套可拓创新方法，并提出了矛盾问题转化的基本方法，包括化不相容问题为相容问题的可拓策略生成方法、处理对立问题的转换桥方法，为形式化、流程化解决矛盾问题提供了理论依据与方法体系。

2.   因素空间与可拓学的互补性分析

从研究内容、研究方法等方面对因素空间与可拓学进行互补性分析，初步结论如下。

2.1   数学基础和主要研究对象高度相关

两者具有共同的数学基础，都与模糊集与模糊逻辑的研究有内在联系，但各自拓展了模糊数学的研究范围。两者都以问题处理为主要研究对象。可拓学以矛盾问题为研究对象，提出了一套通过基元建模、拓展、变换和评价处理矛盾问题的理论与方法；因素空间研究不确定性结果产生的原因，通过背景关系、因素显隐实现不确定性的问题的转化与求解。

模糊集合无法描述在一定条件下非与是的转化，可拓集合把辩证法关于矛盾转化和变换的思想引入集合论，从动态转化的角度研究集合内元素、准则和论域的变化。因素空间从动态角度研究因素的变化如何影响模糊性和不确定性，提出了一套理论与算法，两者均把非定量变量纳入研究内容，从研究内容的动态性、系统性和非数量化等方面拓展了集合论与模糊数学的研究范围。两者的模型与研究对象对照表如表1所示。

2.2   因素与基元有紧密的内在联系

因素空间中的因素是可拓学基元理论中的特征，特征包括事物的属性。所有指标体系中的指标、参数和人工智能所用的属性、状态、特征都是因素。因素是变量，因素的相或每个因素的状态在可拓学基元理论中表述为特征的量值。例如降雨量这个因素的相如“雨量充沛”“中等雨量”“雨量极少”等在基元理论中表述为（对象A，降雨量，充沛）。可增加参变量如地点、时间等进行更准确描述。如M₁(t) =（地点A(t)，降雨量，v₁(t)），其中，v₁(t)=中等；M₂(t) =（铁块M(t)，温度，v₂(t)），其中，v₂(t)>=(800℃,+∞)等。因素空间特别强调：属性被动地描述事物，因素更具有启发性和牵引性。因果分析不要在属性层次上求索，一定要在因素和变量层次上。因素是属性的纲领，是广义的基因，是信息提取的视角，是概念划分的依据，是因果分析的要素。一个因素的属性分解为其他几个因素属性的逻辑组合，可以使知识的表达更加细腻，降低对知识理解的随机性、增强可操作性。

尽管每一事物都有多种属性，但是，我们不可能也无必要去穷尽一个事物的所有属性。这些属性在认识事物的本质特征的过程中的地位与作用是不同的。在不同的任务、场合或目的下，我们关注事物的属性也不尽相同。其重要任务是寻找与问题处理有关的主要因素。基元理论为系统性地识别因素准备了信息基础，而因素理论则为基元拓展处理矛盾问题指明了方向。大数据时代，因素库和基元库的构建都需要从多源异构的数据中抽取信息，因素抽取与基元抽取更将是相辅相成的。

2.3   解决问题的思路在显隐方面具有一致性

因素空间理论认为，一切困难都是解决问题的关键因素还没有显露出来。人工智能的问题就是找隐含的因素/特征的问题，隐因素一旦找到，问题便迎刃而解了。事物只有在变化中才能显示因素之间的相互影响。因素空间的基本任务就是要化隐为显。通过显因分析寻找关键因素或凸显隐藏的关键因素^[22-24]。

可拓学基元理论的核心观念是基元的可拓性和物的共轭性，现实世界是一个物元集合或物元系统，它们的相互作用构成事元集合或事元系统；它们的相互影响构成关系元系统。问题的不相容往往是对象的特征和量值不足，通过物的实部虚部、硬部软部、正部负部和显部潜部等共轭性分析及对象、特征和量值的拓展，往往可以化解矛盾。可拓学是把事物状态的“此”与“彼”置于变化之中，考察事物“此”与“彼”在一定条件下的相互转化。转化可以通过适当的可拓变换来实现^[19]。

与共轭分析类似，目标因素具有对称性。企业以追求利润的最大化为目标，与之对称的，企业还必须努力使风险最小化。目标都要成双地出现，对称的一对因素互称为对偶。收益与成本、经济增长与环境保护、物质财富与精神文明、民主与集中、数量与质量、创新与传承、深度与广度等都是对偶因素的例子。目标因素的对称性使目标因素成对地出现，目标与限制是对称的，可以互相转换。

不充分的条件虽不能决定结果但却能制约结果的发生频率，体现这种内在必然性联系的就是概率，概率是广义的因果律。将基本空间的因素分为两个部分，可观察、可控的因素算一部分，这部分因素所导引的变量是非随机变量，余下的因素算是第二部分，统归为一个余因素。它所导引的变量是随机性的。从中挑选出少数几个特别的因素作为精细处理的对象，剩下那些影响微弱且相互独立的众多因素，都归顺于中心极限定理。这样一来，随机变量的一般分解式是：

这里，f(x)是一个以向量x为自变量的普通函数，f^(x)是由样本经过最小二乘或其他方法所拟合出的函数，它是对少数几个特别的因素所作的精细处理，δ是高斯分布，被看成是噪音。要减少随机性，就是要加深对第二项的因素分析和掌控^[25-26]。可拓学的潜部分析与拓展分析可以逐步实现余因素向第一类因素的转化。

2.4   解决问题的方法与算法具有互补性

因素空间强调不要孤立静止地从属性和状态层面上去找问题产生的原因，要从变化中寻找主导的影响因素。在因素空间中寻找关键因素称做因素显隐，显隐问题主要有3种途径，解方程、回归与优化，都可归结为一个求投影的问题，如解投影方程。显隐的代数原理中，隐因素可以通过显因素作线性变换而显现出来，有时隐因素是显因素的加权合成。隐因素显隐算法可以为拓展与变换提供更多数学算法，而可拓学挖掘变换知识的可拓数据挖掘算法与关联函数则可以为因素显隐提供转化思路与更精准的优化。

因素空间的因果分析理论认为，关联不是相关，因果可以逆转。关联是指两个属性或事件在一个实体中同时存在或发生；相关是指一个因素的变化会引起另一个因素的变化。因素空间承认广义的因果性，万事万物具有普遍的因果联系，好稻米是因为有好种子，好种子也是因为有好稻米。背景关系和背景分布是相关性的化身，相关决定因果。因果分析都有条件因素和结果因素两个方面，前一方是因，后一方是果（广义）。在每个时刻，都暂时锁定目标，只是多对一地考虑因果。而多个条件总可以先简化为二。所以，因果三角就是两因一果的思考模式。

可拓学的基元库构建与拓展为因素分析打下信息基础。拓展分析中的蕴含分析包括因果蕴含和存在蕴含，并建立了形式化表述模型。因果分析法可以在算法层面与可拓学的相关分析、蕴含分析相交叉，在多指标因素分析法及多标准因素分析推理模型的基础上开发新的算法模型，得到更系统的备选条件与因果联系，进一步拓展因果分析的应用。

基于因素空间理论解决问题的基本流程为：面对一个问题，先由因素谱找到对应的因素空间，再从因素空间约简^[27]、推理^[24]给出问题的局部解答，并向更深层次的因素空间转移。在因素空间中生成概念、因果归纳、推理，众多因素空间联结成因素藤，形成一种双层结构。如此往复，直到问题解决。

基于可拓学方法解决矛盾问题的一般流程^[7,21]为：1）根据矛盾问题P，分析目标G是什么，条件L是什么；2）若是条件与目标之间的矛盾，则根据不相容问题的目标事元和条件事元的与运算模型建立矛盾问题的可拓模型P=G×L，并找出其核问题P₀=g₀×l₀，从而建立核问题的相容度函数k(x)，判断相容函数是否小于零k(x)<0；若是目标间的矛盾，则根据对立问题目标事元间的与运算关系建立矛盾问题的可拓模型P=(G₁ $ \wedge $ G₂)×L，根据转换桥法对对立目标进行转换；3）然后依据创意生成的“4种拓展分析方法”和“共轭分析方法”对所需解决矛盾的基元进行可拓变换，从而生成多种解决方案；4）最后根据优度评价方法对所有的解决方案进行优度评价并选出最优的解决方案。

可拓学的基元分析与可拓模型及其运算^[28]可以为因素空间构建提供更系统的数据和信息，关键因素的显隐算法可以为可拓学核问题的分析扩充新的算法。因素藤为拓展变换提供更多特征和方向，共轭分析和拓展变换又为因素藤扩充因素提供了新的方法。面向问题处理的基元–因素模型为进一步研究复杂问题的智能化处理打下了一定的信息基础^[29]。

3.   因素空间与可拓学融合的问题处理模型

3.1   模型的原理

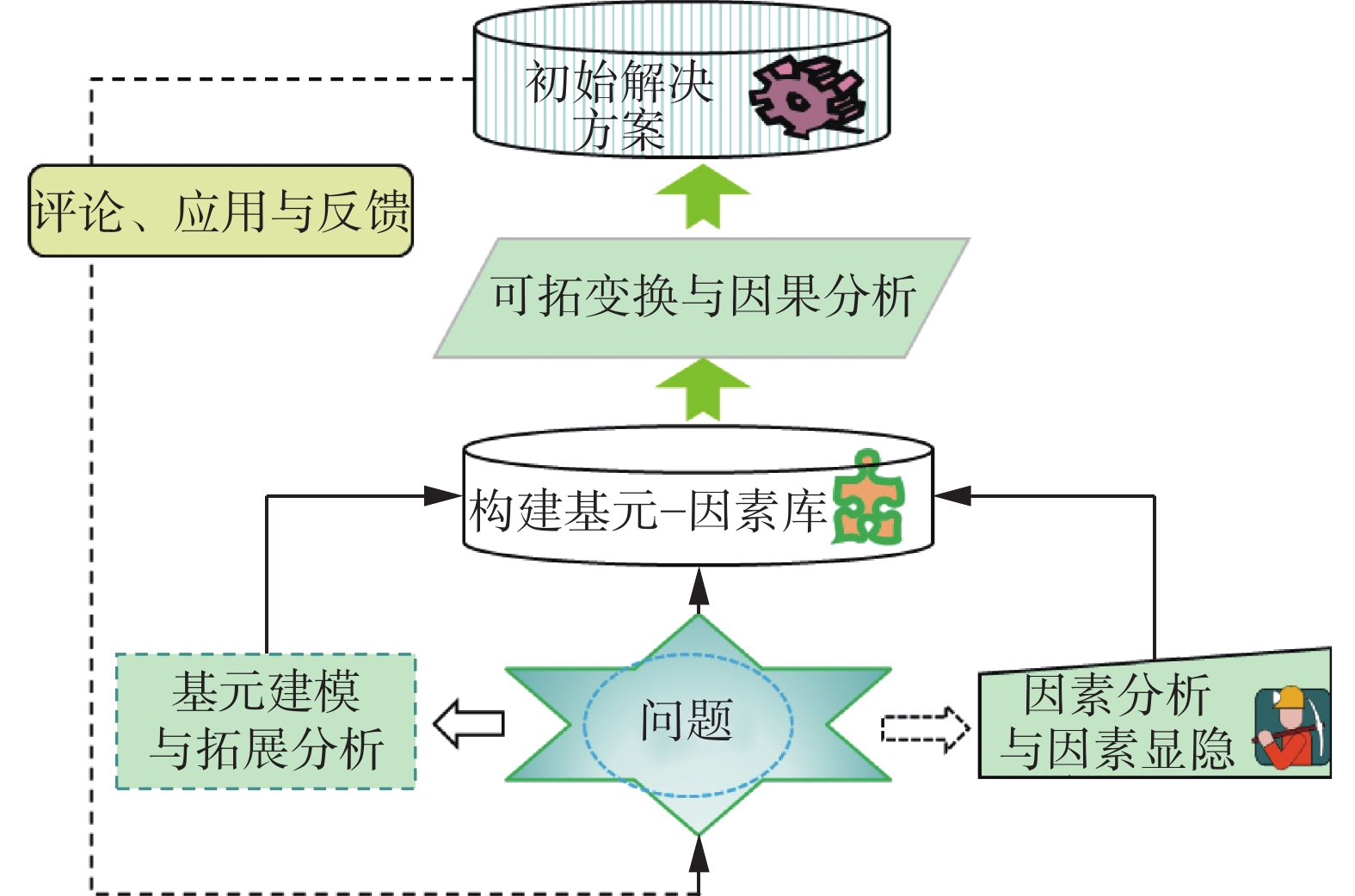
可拓学为问题处理建立了一套基本的理论方法体系，包括基元建模、拓展、变换与优度评价等方法工具，利用可拓学进行问题建模和拓展，侧重形式化、流程化的信息发散与知识拓展，以问题求解的程序性知识与专家的隐性知识对接。因素空间理论则为问题处理提供必要的因素知识表达与计算的数学方法，侧重信息与知识的约简和收敛，以问题求解的描述性知识与知识图谱与Web数据中的显性知识对接。因素通过变换显示其影响，变化中的因素对应不同的基元特征。融合可拓学与因素空间理论的问题求解模型如图2所示。

图  2  融合可拓学与因素空间理论的问题求解模型

Fig.  2  problem solving model integrating Extenics and factor space

下载: 全尺寸图片

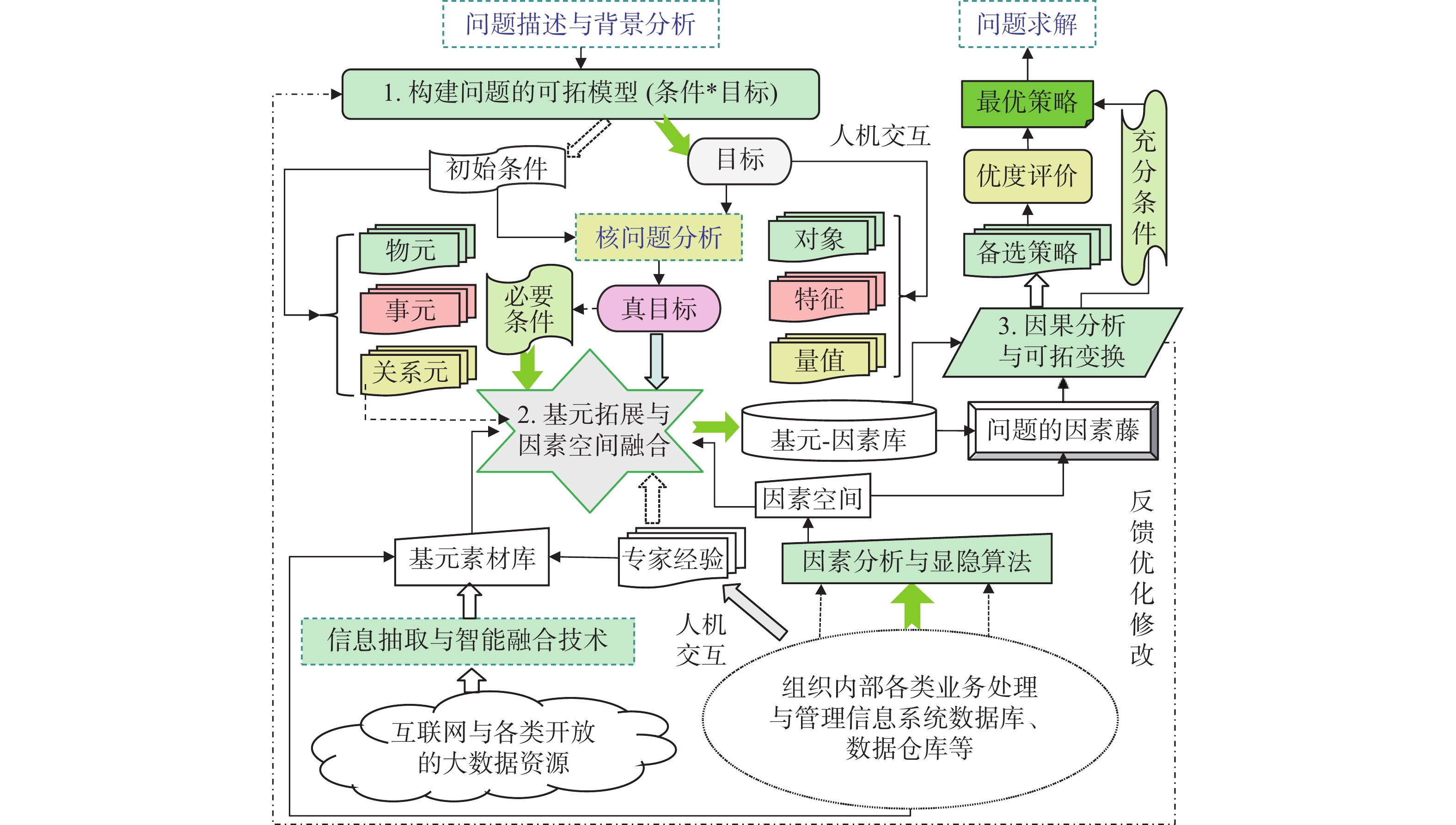
根据问题描述进行问题条件和目标的基元建模与拓展分析，分别得到条件、目标相关的系统性的基元信息。对问题进行条件与目标的相关因素分析与因素显隐，得到问题处理的初始因素空间。基元与因素空间融合构建基元–因素库作为素材输入实施可拓变换与因果分析，得到解决问题的初始方案。对方案进行评价、试用并反馈，得到可行性方案，成功验证后再存入或更新补充基元–因素库。其详细实施步骤如图3所示。

图  3  融合可拓学与因素空间理论的问题求解模型实施过程示意

Fig.  3  Schematic diagram of implementation process of problem solving model integrating Extenics and factor space

下载: 全尺寸图片

3.2   模型的构建与实施

第1步建立问题的可拓模型，问题P=G×L,G为目标，L为条件。目标和条件均以（对象，特征，量值）的三元组表示，多个特征和量值形成矩阵结构：

式中：O表示对象（物、动作或关系词）；c₁,c₂,…,c_n表示对象O的n个特征；v₁,v₂,…,v_n表示对象O关于上述特征的相应量值。在基元表达基础上分析核问题，确认真正的目标及目标实现的必要条件。

第2步分别从真目标和条件出发做基元拓展并与因素空间融合。分别拓展条件和目标的基元对象、特征与量值，基元拓展的信息基础基元素材库来自于Web信息抽取、数据库和数据仓库及专家经验等。与之融合的因素空间来源于因素分析与显隐的结果，其主要数据源还包括数据库和数据仓库及专家的经验。融合后得到基元–因素库，基元的某个特征被识别为解决问题的关键因素，因素空间则提供更细致的数量化的因素支撑。多个因素空间组合形成问题处理相关的因素藤。因素藤实现信息与知识的融合，形成更大的认知描述网络。

第3步是因果分析与可拓变换。将基元–因素库和因素藤作为输入信息，在目标与条件的蕴含分析和相关分析基础上做因果分析和可拓变换，在因素空间中进行从条件到目标结果的因果分析，提取能够体现条件因素对结果因素所产生的影响，进而做因果推理，然后选取基元的对象、特征或量值做可拓变换，得到系统性的解决问题的备选策略。对备选策略做优度评价，得到最优策略用于问题求解。如果求解结果不够理想，则进一步做问题分析，重复上述步骤。因果出理性，因果生逻辑。若A则B，A就是因，B就是果。概率都是相对于一定条件而言的。p(B|A)=t(A->B)^[13]。抽象随机变量在因素空间中最终会变成一个必然的映射。对结果有影响的因素考虑的越全面，结果就越确定。以因果分析算法等抽取跟待解决问题紧密相关的特征，对选取的特征（因素）做可拓变换，评估问题的解决程度。通过类似列方程、解方程的系统方式实现问题处理从不确定性和随机性向必然性的转化。

3.3   应用验证与适用范围分析

模型的初步应用验证有多个案例，模型与案例详细的分析篇幅过大，本文仅选其一简要描述。提升集团公司的利润是一个边界较为开放的复杂问题，涉及众多因素，比如产品定位、原料供货方及其价格、加工方式、物流、销售方式、退货方式、集团的考核指标、奖金的分配比例、广告、研发费用支出与电子商务运营模式等。以集团公司的管理信息系统数据为基础，构建问题的初始模型及较为系统全面的基元库，分别从对象、特征和量值入手分析基元之间的关联，再利用主成分分析、分类、聚类等数据挖掘方法，得到月末特征指标相关的主要因素，标识构建基元–因素库，识别各基元–因素表之间的关联与相关关系，确定因果关系链，最终找到提升利润的关键因素支点，即对生产厂设置的利润指标不合理。改变集团对生产厂的考核指标及其设定后，集团整体利润有显著提升。

随着管理信息系统的广泛应用及物联网的普及推广，数据获取的便利性、快捷性及云处理能力有了很大提高。在智能制造大数据环境下，环境的动态性不确定性及交互性，使原有的很多边界条件相对确定的封闭性问题的范围越来越小，而大量的问题呈现出不确定性、动态性和边界的开放性。因此本模型的研究应用有较为广泛的应用空间。其实际应用的潜在优势在于定性定量相结合、因素与基元点面相结合，从较为系统全面的基元库构建入手，再利用因素空间的因果分析、因素显隐等算法抽取对问题处理有决定作用的关键因素，实现发散与收敛的结合。该模型的适用范围主要是需要有一定的真实客观的标签数据，同时问题的条件和目标具有一定的可拓展性，事物的特征具有一定的可转化性。比如所加工的精度可以在一定范围内调节，客户服务的时间可以在一定范围内浮动等。通过从现有条件出发，拓展出一定的隐含条件空间，或通过蕴含分析拓展出隐含的目标基元信息，实现关键因素识别和问题求解的转化。

4.   结束语

因素空间是概率论和模糊数学发展必然产生的更深层次的数学概念。因素是事物描述和因果分析思维过程的更深层次的特征。模糊落影理论、因素凸显算法等将为大数据浪潮驱动的范式转变做好必需的数学准备，因素空间理论可以有效地剖析不确定性产生的机理及彼此之间的关系，把非结构化大数据转化为小数据，为信息和智能科学提供统一的数学语言和普适的描述框架。

可拓集合的建立，使数学的静态分类拓展为可拓学中基于变换的动态分类；关联函数的建立，使从康托集合只描述量变拓展为可拓集合描述量变和质变；基元概念的建立，使数学模型拓展为把定性与定量结合起来研究的可拓模型；可拓论将使数学和逻辑产生较大的变革，而产生可拓数学成为智能数学的重要组成部分。

可拓学与因素空间有很多交集，但和而不同。两者的融合交叉研究将进一步提高问题处理的系统性和智能化水平。几个主要的未来交叉研究方向包括：1）基于基元模型的因素的动态性抽取与因素的可拓性、转化性研究；2）定性定量相结合的问题导向的基元、因素合取、析取与分解等运算；3）大数据环境下的基元智能构建与因素因果强度识别算法；4）模糊、不确定边界条件问题的拓展与求解等。

在上述研究基础上，将进一步研究基元–因素化融合生成解决问题策略的动态结构，特别是基元库与因素库互补的耦合重构方法；解决互联网海量信息与领域大数据集成应用中问题求解因素的智能抽取等基础性问题，为互联网海量信息在问题处理方面的深度利用提供基础理论与新的方法。