Early warning model for abnormal workingconditions of CBiA-PSL pumping wells
-
摘要: 油田生产过程中，油井受各种因素的影响容易发生泵漏、管漏等异常工况，会降低油井产出甚至导致躺井，对异常工况预警是油田智能化管理的重要任务。基于CNN-BiGRU联合网络，提出一种改进的网络结构CBiA-PSL模型（CNN BiGRU attention-positive sharing loss），用于油井异常工况预警。模型利用CNN学习工况样本灰度图像的深度特征，BiGRU有效避免信息损失并加强CNN池化层特征的联系，注意力机制对隐藏状态加权计算以完成有效特征筛选。针对工况数据集不平衡的问题，提出正共享损失函数PSL，将异常数据（正类）划分为子类，每个子类都共享整个正类的损失，且给样本少的正类更高的权重。实验结果表明，CBiA-PSL模型预测效果更佳，对于异常类和整体的预测都有较高的精度。Abstract: In the process of oilfield production, which is affected by various factors, oil wells are prone to abnormal working conditions, such as pump and pipe leakages, which will reduce the output of oil wells and even lead to lying in wells. Early warning of abnormal working conditions is an important task of intelligent oilfield management. Based on the convolutional neural network–bidirectional gated recurrent unit (CNN–BiGRU) joint network, an improved network structure CNN–BiGRU attention-positive sharing loss (CBiA-PSL) model is proposed for early warning of abnormal oil well conditions. The model uses the CNN to learn the depth features of the gray image of the sample, BiGRU to effectively prevent information loss and strengthen the connection between the features of the CNN pool layer, and attention mechanism to weigh the hidden state to complete effective feature screening. To address the imbalance of the working condition dataset, a PSL function, which divides the abnormal data (positive class) into subclasses, is proposed. Each subclass shares the loss of the entire positive class and provides a high weight to the positive class with only a few samples. The experimental results show that the CBiA-PSL model has a better prediction effect and a higher accuracy for anomaly and overall prediction than other models.
-
油田生产信息化建设，基本实现了油水井、站库数据的实时采集，油井的智能化管理需求日益突出。在油田生产过程中，油井受各种因素的影响出故障的概率很高，经常造成油井产量降低甚至躺井。目前，识别异常工况主要依靠简单的参数超阈值报警，导致报警频繁且有效率不高，问题原因仍主要采取人工分析，数据变化趋势难以自动跟踪、问题隐患难以超前发现、预防性治理和优化措施难以精准实施，难以满足信息化条件下“预警式管理”的要求。所以，预警油井异常工况，指导技术人员超前采取治理与优化措施，对于提高油井开采效率，降低躺井率与维护成本，实现智能化精细化管理具有重要意义[1]。
为了提高油井异常工况的识别精度，世界各地的学者进行了大量的研究。考虑到油井生产数据的特征，即异常工况样本少、维数大等特点，近年来识别异常工况的方法可分为两类：基于统计[2]和传统机器学习的方法[3]以及基于深度学习的方法[4-6]。对于第一类，Zhang等[7]将支持向量机与遗传算法相结合，提出基于GA-SVM与频域光谱法的变压器油浸绝缘体的湿度预测；周斌等[8]提出一种基于Hessian正则化支持向量机（Hessian正则化SVM）的多视角协同识别抽油机井工况方法。这些研究提高了异常工况检测的准确性，但它们都忽略了工况数据类别不平衡的问题。王利君等[9]使用集成SMOTE、CLUSTER与随机森林的集成学习方法SCRF进行结蜡预测，考虑了类别不平衡，但忽略了高维数据的问题且目标数据集相对较小，模型的泛化性能和自学习能力不足。
近年来，由于深度学习模型具有强大的特征提取能力及拟合海量数据的能力，因此被广泛应用于故障检测领域[10]。例如，Wei等[11]提出基于电机数据的深度学习的抽油杆泵故障诊断，利用CNN作特征提取器弥补了专家经验的不足；Chen等[12]提出基于多尺度CNN和LSTM的轴承故障诊断，使用两个不同内核大小的CNN从原始数据中提取不同的频率信号特征，然后利用LSTM识别故障类型；Cabrera等[13]提出基于LSTM的往复式压缩机故障诊断模型，其中超参数搜索由在每次迭代中限制搜索空间的贝叶斯方法完成；魏晓良等[14]提出了一种基于长短时记忆（LSTM）和一维卷积神经网络（1D-CNN）相结合的空化故障诊断方法，用于高速柱塞泵故障诊断；Liang等[15]提出一种使用自适应矩估计最大值（adamax）优化算法的双向门控递归神经网络（adamax-BiGRU）的瓦斯浓度预测模型，预警煤矿瓦斯事故。这些研究初步证明了深度学习模型在故障检测领域的有效性。但是，LSTM具有许多参数和复杂的结构，容易出现过拟合的问题。作为LSTM的变体，GRU具有简单的结构、较少的参数和较短的训练时间，这比LSTM更具优势。但是，GRU仅按顺序考虑前向信息，不考虑反向信息。由两个GRU组成的双向GRU（BiGRU）可以利用附加的后向生产数据，从而进一步提高模型预警异常的准确性。
在上述方法中，存在一个主要问题：实际生产数据中抽油井异常记录远小于正常生产记录，即抽油井异常工况数据集往往存在类别不平衡的问题。上述方法仅考虑总体准确率，而忽略了类不平衡问题，导致少数类分类出错率较高，实际上的异常工况检测效果不理想。因此，本文提出了一种正共享损失函数[16]，以增强少数类，即异常工况的检出效率。
本文的主要工作如下：
1）针对工况样本的灰度图像，在CNN-BiGRU联合网络模型上引入注意力机制，从而提高模型对特征的学习能力，进一步提高识别异常工况的准确率。
2）除了将CNN-BiGRU-Attention网络用作特征提取器外，提出了正共享损失函数PSL。PSL引入一个额外的正则化项，以强调正负类的损失，且给样本少的正类更高的权重，旨在减弱不平衡，有助于更好地识别异常工况。
1. CNN-BiGRU联合网络特征学习
CNN网络主要有两个算子[17]，一个是卷积层，另一个是池化层。卷积层作为特征提取器将数据集的工况样本的灰度特征矩阵分割成若干子矩阵，每个卷积层中所有的特征子矩阵与同一个权值矩阵（卷积核）做卷积运算，通过卷积核刻画图片的局部模式来提取图像的局部特征[18]。卷积运算可以提取数据集中人类无法理解的异常工况的局部抽象特征，起到过滤作用。池化层在卷积层之后，对卷积得来的特征进行筛查，减少特征数量来降低计算量，同时可以起到保留异常工况特征以及防止过拟合的作用。
门控循环单元(gate recurrent unit, GRU)是一种特殊的循环神经网络(recurrent neural network, RNN)，其与长短期记忆网络(long-short term memory, LSTM)相似，是为了解决长期记忆和反向传播中的梯度爆炸、梯度消失和长距离依赖等问题而提出的。
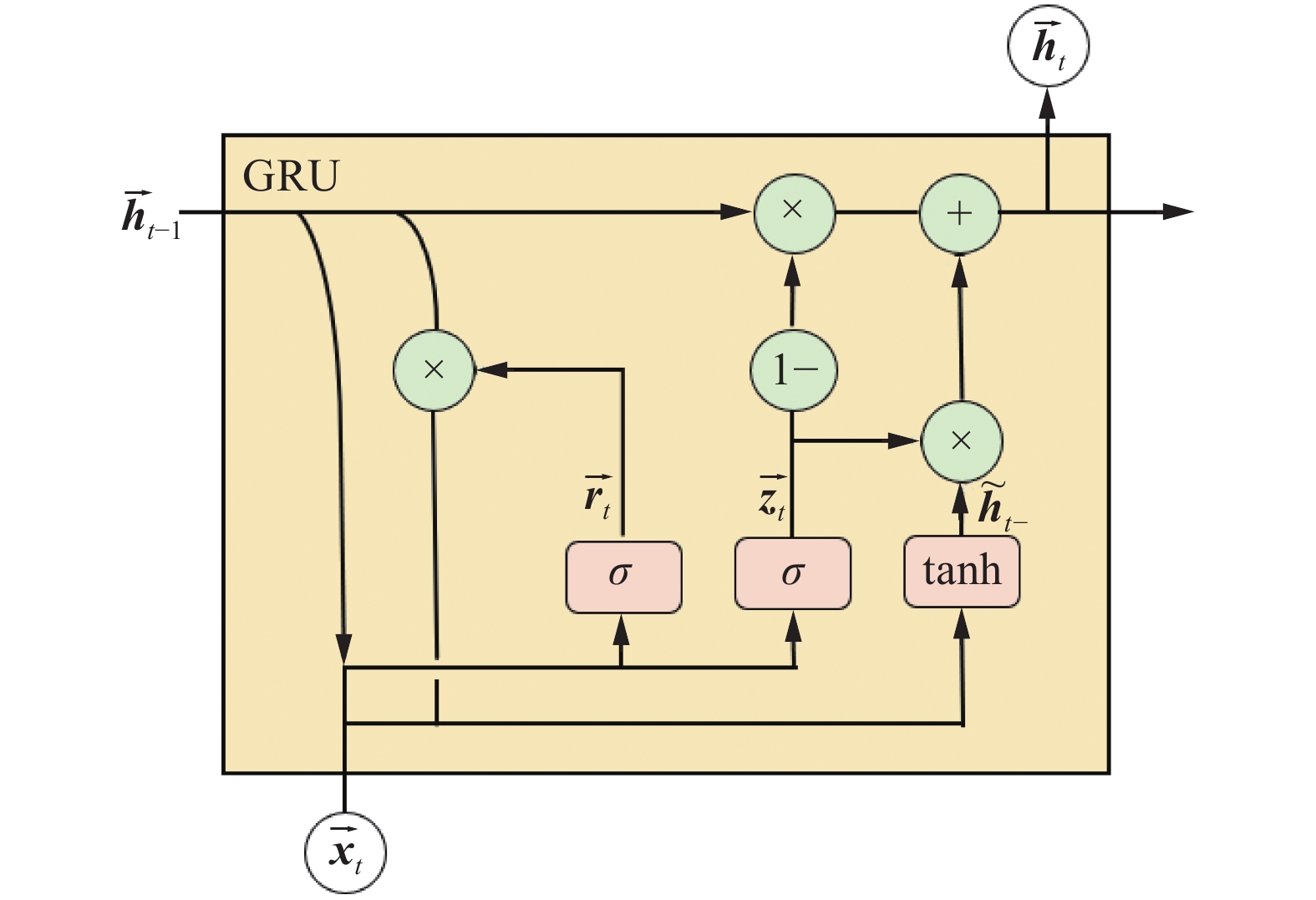
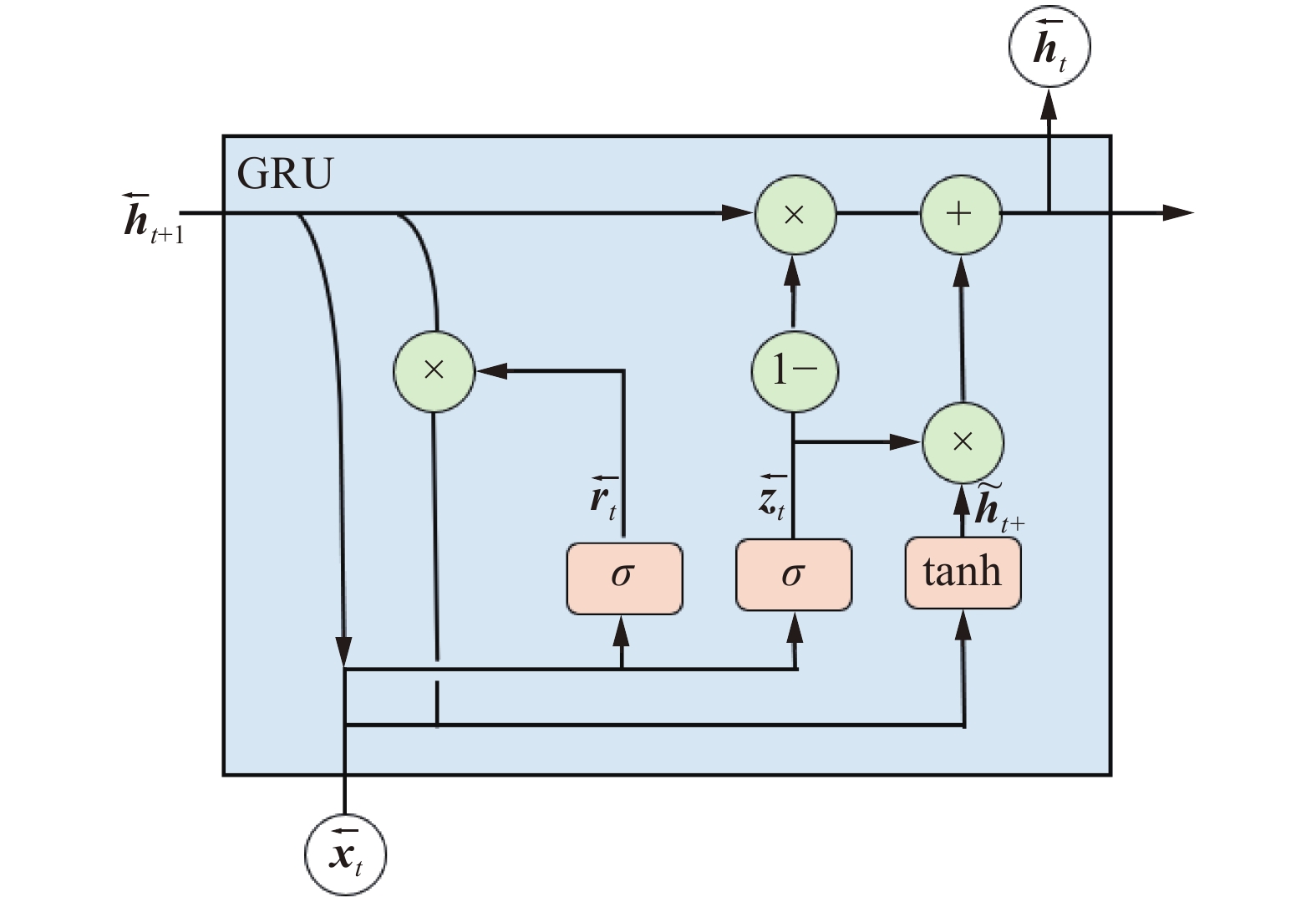
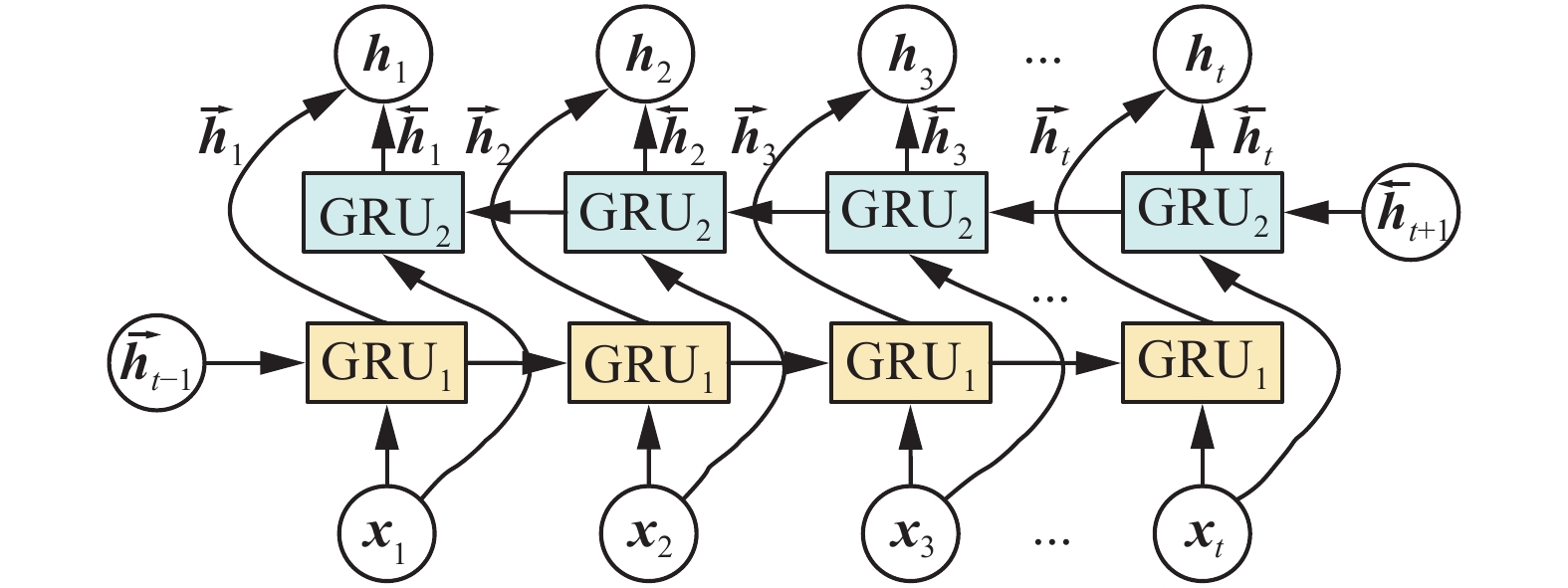
GRU适宜于处理时间序列数据，对比LSTM，GRU在性能相当的同时参数量更少，结构简单，更易收敛，且计算速度比LSTM更快。双向GRU[19]在输入序列上有两个GRU互相连接，每一个输入的异常工况特征图都会从正向和反向经过GRU，为神经网络提供上下文的全局特征。在图1中，每个GRU单元都在两个方向上进行处理：GRU1是正向GRU，其内部结构如图2所示；GRU2是反向GRU，其内部结构如图3所示。
图 1 BiGRU的网络结构Fig. 1 Network structure of BiGRU
下载:
全尺寸图片
图 2 正向GRU单元的内部结构Fig. 2 Internal structure of forward GRU unit下载:
全尺寸图片
图 3 反向GRU单元的内部结构Fig. 3 Internal structure of reverse GRU unit下载:
全尺寸图片
图2中的正向计算过程如下：
定义
${\boldsymbol{r}}_{{t}}$ 是正向GRU在t时刻的重置门。公式如下：$$ {\overrightarrow{{\boldsymbol{r}}}}_{t}=\sigma ({\overrightarrow{{\boldsymbol{W}}}}_{r}{\overrightarrow{{\boldsymbol{x}}}}_{t}+{\overrightarrow{{\boldsymbol{U}}}}_{r}{\overrightarrow{{\boldsymbol{h}}}}_{t-1}) $$ 式中：
$ \sigma $ 为sigmoid函数；${{{\boldsymbol{x}}}}_{{t}}$ 和${{{\boldsymbol{h}}}}_{{t}-1}$ 分别是当前输入值和上一个激活值；${\boldsymbol{W}}_{{r}}$ 是输入权重矩阵；${\boldsymbol{U}}_{{r}}$ 是循环连接的权重矩阵。类似地，定义
${\boldsymbol{z}}_{{t}}$ 是正向GRU在t时刻的更新门。公式如下：$$ {\overrightarrow{{\boldsymbol{z}}}}_{t}=\sigma ({\overrightarrow{{\boldsymbol{W}}}}_{z}{\overrightarrow{{\boldsymbol{x}}}}_{t}+{\overrightarrow{{\boldsymbol{U}}}}_{z}{\overrightarrow{{\boldsymbol{h}}}}_{t-1}) $$ 定义
${\boldsymbol{h}}_{{t}}$ 是正向GRU在t时刻的激活值，即上一个激活值${\boldsymbol{h}}_{{t}-1}$ 和候选激活值${\stackrel{~}{\boldsymbol{h}}}_{{t}-}$ 之间的折中。$$ {\overrightarrow{{\boldsymbol{h}}}}_{t}=\left(1-{\overrightarrow{{\boldsymbol{z}}}}_{t}\right)\cdot {\overrightarrow{{\boldsymbol{h}}}}_{t-1}+{\overrightarrow{{\boldsymbol{z}}}}_{t}\cdot {\stackrel{~}{{\boldsymbol{h}}}}_{t-} $$ ${\stackrel{~}{\boldsymbol{h}}}_{{t}-}$ 公式如下：$$ {\stackrel{~}{{\boldsymbol{h}}}}_{t-}={\rm{tanh}}({\overrightarrow{{\boldsymbol{W}}}}_{\stackrel{~}{{{h}}}}{\overrightarrow{{\boldsymbol{x}}}}_{t}+{\overrightarrow{{\boldsymbol{r}}}}_{t}\cdot {\overrightarrow{{\boldsymbol{U}}}}_{\stackrel{~}{{{h}}}}{\overrightarrow{{\boldsymbol{h}}}}_{t-1}) $$ 式中：“·”代表哈达玛乘积（Hadamard）。
当重置门
${\boldsymbol{r}}_{{t}}$ 关闭时，即其值接近于0，GRU忽略先前的激活值${\boldsymbol{h}}_{{t}-1}$ ，仅由当前输入${\boldsymbol{x}}_{{t}}$ 决定。这允许${\stackrel{~}{\boldsymbol{h}}}_{{t}}$ 丢弃不相关的信息，从而更有效地表达有用的信息。另一方面，更新门
${\boldsymbol{z}}_{{t}}$ 控制将${\boldsymbol{h}}_{{t}-1}$ 中的多少信息传递给当前${\boldsymbol{h}}_{{t}}$ 。同样，图3中的反向计算过程如下：
$$ {\overleftarrow{{\boldsymbol{r}}}}_{t}=\sigma ({\overleftarrow{{\boldsymbol{W}}}}_{r}{\overleftarrow{{\boldsymbol{x}}}}_{t}+{\overleftarrow{{\boldsymbol{U}}}}_{r}{\overleftarrow{{\boldsymbol{h}}}}_{t+1}) $$ $$ {\overleftarrow{{\boldsymbol{z}}}}_{t}=\sigma ({\overleftarrow{{\boldsymbol{W}}}}_{z}{\overleftarrow{{\boldsymbol{x}}}}_{t}+{\overleftarrow{{\boldsymbol{U}}}}_{z}{\overleftarrow{{\boldsymbol{h}}}}_{t+1}) $$ $$ {\overleftarrow{{\boldsymbol{h}}}}_{t}=\left(1-{\overleftarrow{{\boldsymbol{z}}}}_{t}\right)\cdot {\overleftarrow{{\boldsymbol{h}}}}_{t+1}+{\overleftarrow{{\boldsymbol{z}}}}_{t}\cdot {\stackrel{~}{{\boldsymbol{h}}}}_{t+} $$ $$ {\stackrel{~}{{\boldsymbol{h}}}}_{t+}={\rm{tanh}}({\overleftarrow{{\boldsymbol{W}}}}_{\stackrel{~}{h}}{\overleftarrow{{\boldsymbol{x}}}}_{t}+{\overleftarrow{{\boldsymbol{r}}}}_{t}\cdot {\overleftarrow{{\boldsymbol{U}}}}_{\stackrel{~}{h}}{\overleftarrow{{\boldsymbol{h}}}}_{t+1}) $$ 将两个方向的结果求平均，以获得最终输出
${\boldsymbol{h}}_{{t}}$ 。$$ {\boldsymbol{h}}_{{t}}=({\overrightarrow{\boldsymbol{h}}}_{{t}}+{\overleftarrow{\boldsymbol{h}}}_{{t}})/2 $$ 2. CBiA-PSL工况预警模型
为了更好地解决深度学习预测模型中工况属性的选择问题，且所提出的方法对图像处理更有效，将油井数据转化为灰度图像。数据集中共有41维特征，为了保留数据集中每个样本的所有特征，用8个0填充，将其转化为7×7灰度图像。转化后的灰度图像如图4所示，从左到右依次为无异常、泵漏、管漏，同一类别的图片几乎相同，但是不同类别的图片之间存在很大差异。
图 4 样本灰度图像Fig. 4 Sample gray image下载:
全尺寸图片
2.1 CNN-BiGRU-Attention特征筛选
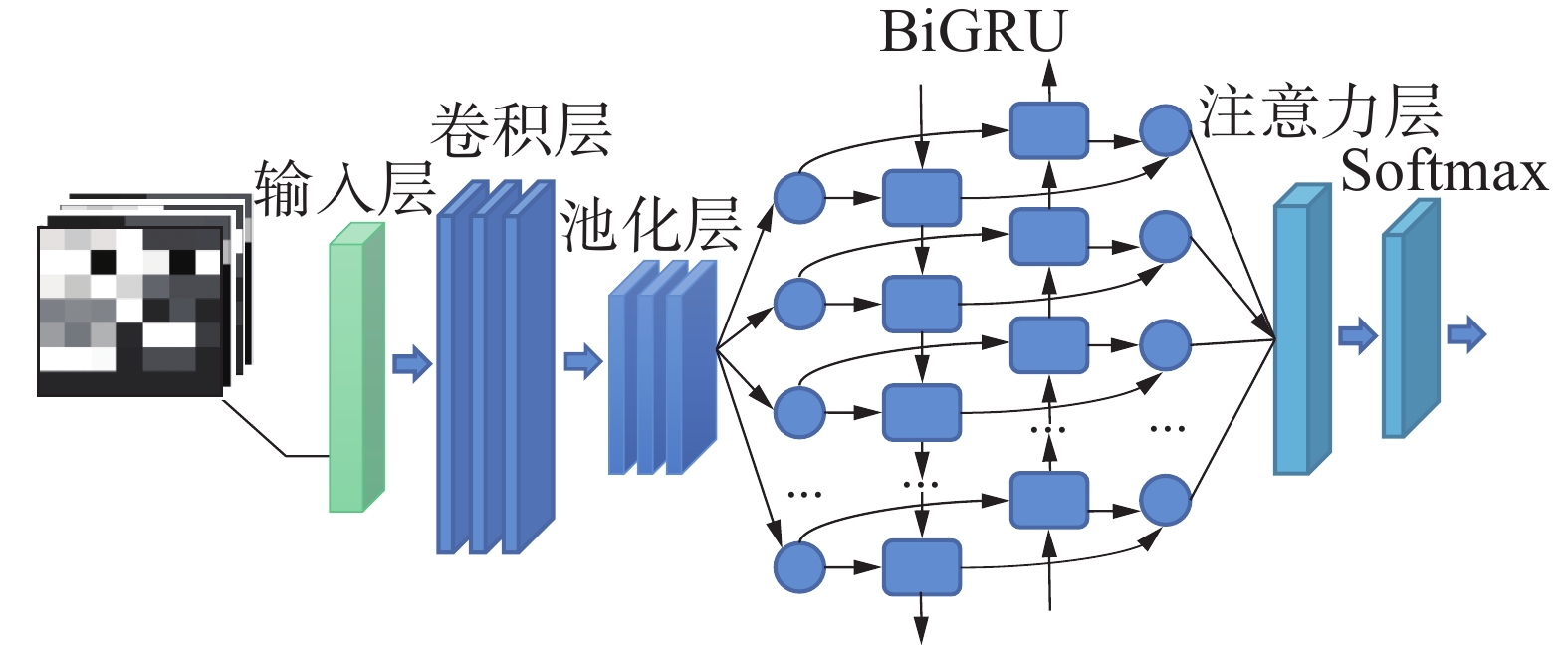
本文提出的CBiA-PSL模型是基于CNN-BiGRU-Attention网络和正共享损失函数PSL。CNN-BiGRU-Attention在CNN-BiGRU联合网络的基础上引入注意力机制，其结构如图5所示。首先，7×7工况样本灰度图像作为CNN的输入，利用CNN、BiGRU提取前后向相关特征，克服了CNN缺乏对上下文的全局关注与BiGRU缺乏对局部关注的不足，结合两者的优点从全局和局部对异常工况特征学习训练，并通过Attention层增强相关特征表示[20-21]，最后，通过softmax层输出分类结果。
图 5 CNN-BiGRU-Attention模型结构Fig. 5 Model structure of CNN-BiGRU-Attention下载:
全尺寸图片
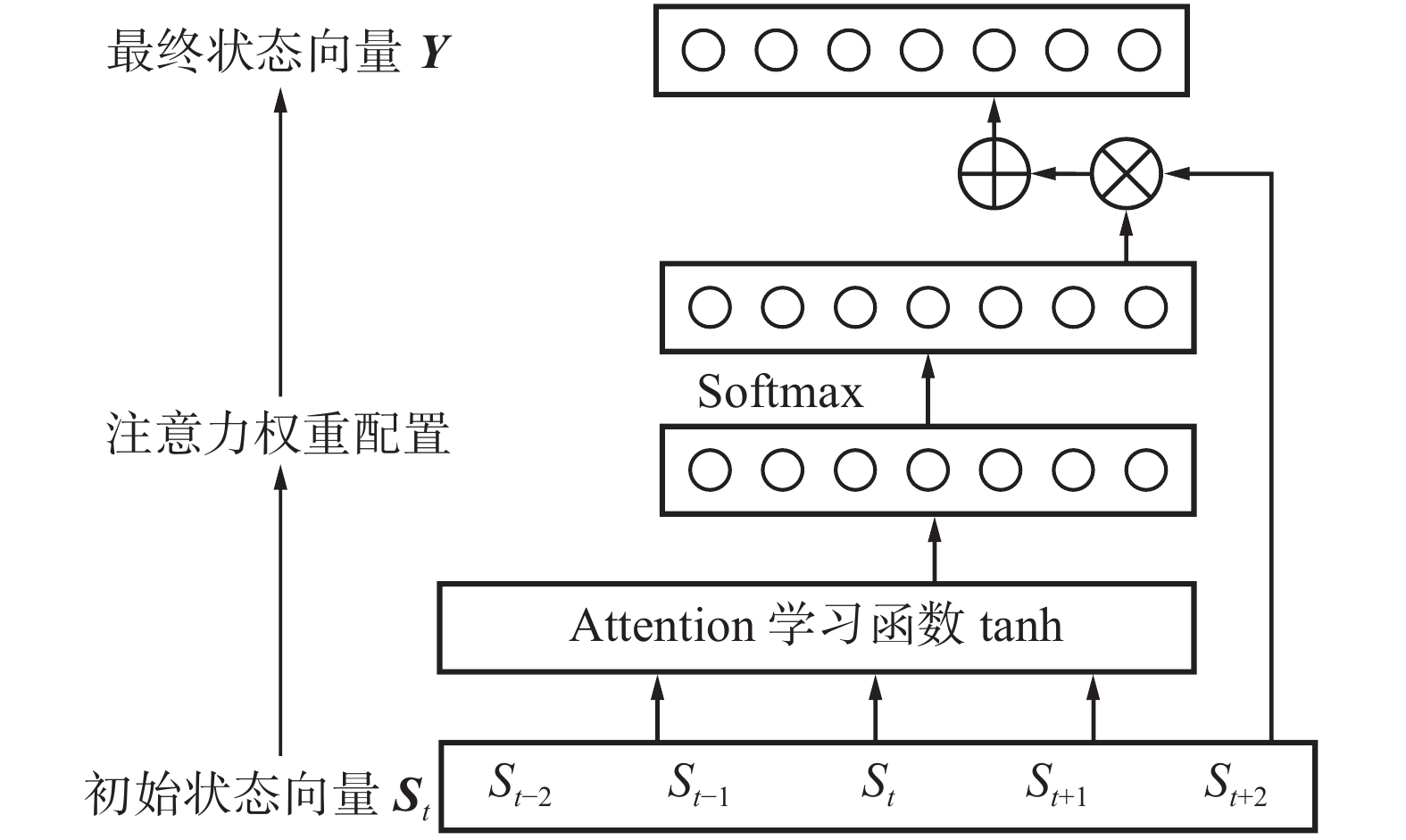
在CNN-BiGRU联合网络架构的基础上增加注意力机制对隐藏状态加权计算以完成有效特征筛选。其核心是权重系数，首先学习每个特征的重要程度，而后根据重要程度为每个特征分配相应的权重，以区分各特征的重要性大小，提高工况识别的准确率。本文使用前馈注意力机制，其结构如图6所示。
图 6 注意力机制结构Fig. 6 Structure of attention mechanism下载:
全尺寸图片
首先生成目标注意力权重
${{\boldsymbol{e}}}_{t}$ ，公式如下：$$ {\boldsymbol{e}}_{t}=\sigma ({\boldsymbol{w}}_{t}{\boldsymbol{S}}_{t}+{\boldsymbol{b}}_{t}) $$ 式中：
$ \sigma $ 是注意力学习函数tanh；${\boldsymbol{S}}_{{t}}$ 是第t个特征向量的初始状态向量；${\boldsymbol{w}}_{{t}}$ 表示第t个特征向量的权重系数矩阵；${\boldsymbol{b}}_{{t}}$ 表示第t个特征向量相对应的偏移量。然后将注意力权重概率化，通过softmax函数生成概率向量
${\boldsymbol{\alpha }}_{{t}}$ ，公式如下：$$ {{\boldsymbol{\alpha}} }_{t}=\frac{{\rm{exp}}\left({\boldsymbol{e}}_{t}\right)}{\displaystyle\sum _{i=1}^{t}{\rm{exp}}\left({\boldsymbol{e}}_{i}\right)} $$ 最后，注意力权重配置。将生成的注意力权重配置给对应的隐层状态
${\boldsymbol{S}}_{{t}}$ ，使模型生成的注意力权重发挥作用，Y是最终输出的状态向量，为${\boldsymbol{S}}_{{t}}$ 的加权平均值，权值是${\boldsymbol{\alpha }}_{{t}}$ ，公式如下：$$ {\boldsymbol{Y}}=\sum _{t=1}^{n}{\boldsymbol{\alpha} }_{t}\cdot {\boldsymbol{S}}_{t} $$ 2.2 正共享损失函数
在交叉熵损失函数中通过引入一个额外的正则化因子强调正类、负类的区别，构造正共享损失函数PSL，且给样本数少的正类更高的权重，以减弱不平衡，更好地区分各类异常与正常的生产状态，提高识别异常工况的准确率。
训练CNN-BiGRU-Attention网络的目标是对异常工况特征进行提取，最大化识别异常工况的概率，这是通过最小化交叉熵损失函数实现的。给定一个包含m个样本的训练集：
$ {\left\{{x}^{\left(i\right)},{y}^{\left(i\right)}\right\}}_{i=1}^{m} $ ，$ {x}^{\left(i\right)} $ 是第i个样本，${y}^{\left(i\right)}\in \left\{{0,1},2,\cdots ,K\right\}$ 是它的标签。$ {y}^{\left(i\right)}=0 $ 表示$ {x}^{\left(i\right)} $ 是负样本，$ {y}^{\left(i\right)}=k > 0 $ 表示$ {x}^{\left(i\right)} $ 是正样本且$ {x}^{\left(i\right)} $ 属于第k种工况。$({\alpha }_{j}^{\left(i\right)};j={1,2},\cdots,K)$ 表示Softmax层的输出，$ {x}^{\left(i\right)} $ 分类为j的概率为$$ {p}_{j}^{\left(i\right)}=\frac{{\rm{exp}}\left({\alpha }_{j}^{\left(i\right)}\right)}{\displaystyle\sum_{l=0}^{K}{\rm{exp}}\left({\alpha }_{l}^{\left(i\right)}\right)} $$ 损失函数如下：
$$ {\rm{Loss}}_{0}=-\frac{1}{m}\left[\sum _{i=1}^{m}\sum _{j=0}^{K}1\left({y}^{\left(i\right)}=j\right){\rm{log}}{p}_{j}^{\left(i\right)}\right] $$ 标准交叉熵损失函数会平均惩罚每个类的错分类误差。但在实际情况下，将正样本分类为错误的非零标签并不是重大错误，因为仍将其识别为异常。也就是说，异常类间的分类出错一般可以忽略，但异常和无异常间分类出错是不可容忍的，即应更关注零标签和非零标签之间的错误分类导致的损失。为此，引入了额外的正则化因子，增加了异常工况错分类到正常和正常错分类到异常类的损失。改进后的损失函数如下：
$$\begin{aligned} {\rm{Loss}}={{\rm{Loss}}}_{0}-\frac{1}{m}\cdot \quad\quad\quad\quad\quad\quad\quad\quad\\ \left\{\sum _{i=1}^{m}\lambda \left[\left(1\left({y}^{\left(i\right)}=0\right)\right){\rm{log}}{p}_{0}^{\left(i\right)}+\omega \sum _{j=1}^{K}\left(1({y}^{\left(i\right)}=j)\right){\rm{log}}(1-{p}_{0}^{\left(i\right)})\right]\right\} \end{aligned}$$ (1) 式中：
$ \lambda $ 为控制参数。当$ \lambda $ 趋向于0时，式（1）为标准交叉熵损失函数；当$ \lambda $ 足够大时，区分不同异常工况的效果变弱，式（1）变为解决二分类问题的损失函数，旨在识别异常工况和正常生产数据。实验中，默认设置$ \lambda $ =1。在实际情况下，我们更关注能不能识别出异常工况，而不是异常工况间被错分类的概率，因此引入的正则化项中各正类别的损失在其他正类间共享，称式（1）为正共享损失函数。异常工况样本数少，数据集中正样本数远小于负样本数，数据不平衡，因此为正类项引入参数
$ \omega $ ，$ \omega $ 为负样本数与正样本数的比值，旨在减弱不平衡，公式如下：$$ \omega =\frac{\displaystyle\sum _{i=1}^{m}1({y}^{\left(i\right)}=0)}{\displaystyle\sum _{i=1}^{m}\displaystyle\sum _{j=1}^{K}1({y}^{\left(i\right)}=j)} $$ 通过以上这两个措施，从而让CNN-BiGRU-Attention模型学习到更加具有辨别力的特征。通过标准反向传播来更新网络参数，
${{\rm{Loss}}}_{0}$ 为标准交叉熵损失函数，其导数已在文献[16]中提供，损失函数中第二部分$ {\alpha }_{0}^{\left(i\right)} $ 和${\alpha }_{l(l=1,2,\cdots ,K)}^{\left(i\right)}$ 的偏导数计算如下：$$ \frac{\partial {\rm{log}}{p}_{0}^{\left(i\right)}}{\partial {a}_{0}^{\left(i\right)}}=1-{p}_{0}^{\left(i\right)} $$ $$ \frac{\partial {\rm{log}}(1-{p}_{0}^{\left(i\right)})}{\partial {a}_{0}^{\left(i\right)}}=-{p}_{0}^{\left(i\right)} $$ $$ \frac{\partial {\rm{log}}{p}_{0}^{\left(i\right)}}{\partial {a}_{l}^{\left(i\right)}}=-{p}_{l}^{\left(i\right)} $$ $$ \frac{\partial {\rm{log}}(1-{p}_{0}^{\left(i\right)})}{\partial {a}_{l}^{\left(i\right)}}=\frac{{p}_{l}^{\left(i\right)}{p}_{0}^{\left(i\right)}}{1-{p}_{0}^{\left(i\right)}} $$ 正共享损失函数的偏导数计算如下：
$$ \frac{\partial {\rm{Loss}}}{\partial {a}_{0}^{\left(i\right)}}=\frac{1}{m}\left\{\begin{array}{c}\left(\lambda +1\right)\left[1\left({y}^{\left(i\right)}=0\right)\right]\left({p}_{0}^{\left(i\right)}-1\right)+ (\lambda +1)\displaystyle\sum _{j=1}^{K}\left[1({y}^{\left(i\right)}=j)\right]{p}_{0}^{\left(i\right)}\end{array}\right\} $$ $$ \frac{\partial {\rm{Loss}}}{\partial {a}_{l}^{\left(i\right)}}=\frac{1}{m}\left\{\begin{array}{c}\left(\lambda \left[1\left({y}^{\left(i\right)}=0\right)\right]+1\right){p}_{l}^{\left(i\right)}- \left[1\left({y}^{\left(i\right)}=l\right)\right]-\lambda \displaystyle\sum _{j=1}^{K}\left[1\left({y}^{\left(i\right)}=j\right)\right]\left(\frac{{p}_{0}^{\left(i\right)}{p}_{l}^{\left(i\right)}}{1-{p}_{0}^{\left(i\right)}}\right)\end{array}\right\} $$ 3. 实验与结果分析
3.1 数据集描述
本文使用的数据集来源于胜利油田若干采油厂上百万条抽油井生产数据。原始的数据包括井组相关资料、日常管理资料、实时生产数据、示功图采集数据、功图分析数据、工况日志数据和管柱等资料，时间范围是2019~2020年。井组相关资料主要存储单井基础信息，包括井号、井别、地质储量、对应的注水井配注量等数据资料；日常管理资料、实时生产数据、示功图采集数据和功图分析数据主要存储动态示功图及动态参数，如上下行电流、热洗周期、日产液量、日产油量、含水等；工况日志数据主要存储异常发生的井号、时间、工况类型、治理措施等；管柱资料主要存储管柱图、泵效、泵挂深等资料。以上数据在实际使用时往往存在问题：1）数据存在缺失、无效波动、重复值；2）数据时间段不连续；3）工况标签缺失等。因此，为提高工况预警的准确性和精度，在建立异常预测模型前需进行预处理，得到数据质量较高的数据集。
3.2 数据预处理
初始油井实时数据通过缺失值填写、光滑噪声数据、删除重复数据、去除无效波动、数值规约、切片等手段预处理，共保留135个特征字段。在数百个工况属性中，由于许多工况属性具有相似的公式和表达式，这些属性之间相关性很高，去冗余后保留38个特征字段。考虑到油井异常会导致示功图载荷和面积有较大变化，对示功图进行特征量分解，获取功图面积、载荷差、载荷比3个新的特征，同时构造工况标识字段，泵漏标记为1，管漏标记为2，正常标记为0。原始数据经过预处理后，得到样本数据集，共包含41个特征参数和1个目标参数。将异常工况类（含泵漏、管漏）统称为正类，无异常统称为负类。预处理后的样本情况如表1所示，正负类样本极不平衡。划分数据集中70%作为训练集，30%作为测试集。
表 1 预处理后的样本情况Table 1 Sample condition after pretreatment工况 样本数量 占总样本比例 正常 2 288 074 0.93 泵漏 60 158 0.02 管漏 114 720 0.05 3.3 实验设置
本文实验在服务器下进行，硬件设备CPU型号为Intel(R) Xeon(R) CPU E5-2630L v3 @ 1.80 GHz，内存大小48 GB。实验环境为Python3.8，借助Keras2.4.3搭建神经网络，后端使用TensorFlow2.4.0。
实验参数设置如下：卷积核大小设置为5×5，步长为1，隐藏层的数量为1，隐藏层单元数为128，隐藏层丢包率为0.5。学习率为0.01，BiGRU的时间步长为8，隐层单元数为64，批次大小为128，迭代次数为50。
3.4 评价指标
3.4.1 对比度得分
可以通过测试集上每个样本的分类准确率来验证模型的有效性，但是对于检测问题，正样本和负样本之间的对比度更能反映模型性能。因此，定义对比度得分作为度量，
$ {\left\{{x}_{v}^{\left(i\right)},{y}_{v}^{\left(i\right)}\right\}}_{i=1}^{m} $ 为测试集，$ {p}_{0}^{\left(i\right)} $ 是模型把$ {x}_{v}^{\left(i\right)} $ 分为负类的概率。对比度得分定义如下：$$ \gamma =\frac{1}{m}\sum _{i=1}^{m}\left[\begin{array}{c}\left(1\left({y}_{v}^{\left(i\right)}=0\right)-1\left({y}_{v}^{\left(i\right)} > 0\right)\right) \left({p}_{0}^{\left(i\right)}-(1-{p}_{0}^{\left(i\right)})\right)\end{array}\right] $$ γ的取值范围是−1~1，表示模型识别正样本、负样本的能力。
3.4.2 混淆矩阵
混淆矩阵如表2所示。
${\rm{TP}}_m$ 表示正确预测的m类阳性样本数，$E_{mn}$ 表示m被归类为n的错误分类样本数。${\rm{FN}}_m$ 表示m被归类为其他类的错分类样本数，${\rm{FN}}_{\rm{A}}=E_{{\rm{AB}}}+E_{{\rm{AC}}}$ ，${\rm{FN_{BC}}}$ 可同样计算得到；${\rm{FP}}_m$ 表示其他类被归类为m的错分类样本数，${\rm{FP}}_A=E_{{\rm{BA}}}+E_{{\rm{CA}}}$ ；${\rm{TN_m}}$ 表示正确预测的m类负样本数，${\rm{TN}}_A=S-{\rm{FN}}_A-{\rm{FP}}_A-{\rm{TP}}_A$ 。真阳性率${\rm{TPR}}_m$ 表示所有实际为m类的样本被正确判断为m类的比率，公式如式（1）所示；假阳性率${\rm{FPR}}_m$ 表示所有实际为其他类的样本被错误判断为m类的比率，公式如式（2）所示。$$ {{\rm{TPR}}}_{m}=\frac{{{\rm{TP}}}_{m}}{{{\rm{TP}}}_{m}+{{\rm{FN}}}_{m}} $$ (1) $$ {{\rm{FPR}}}_{m}=\frac{{{\rm{FP}}}_{m}}{{{\rm{FP}}}_{m}+{{\rm{TN}}}_{m}} $$ (2) 表 2 多分类的混淆矩阵Table 2 Confusion matrix of multi classification真实标签 预测标签 A B C A TPA EAB EAC B EBA TPB EBC C ECA ECB TPC 为了评估CBiA-PSL模型，本文选择了3个指标：AC（准确率）、DR（检出率）和FR（错误报警率）：
$$ {\rm{AC}}=\sum _{m}\frac{{{\rm{TP}}}_{m}}{S} $$ (3) $$ {{\rm{DR}}}_{m}={{\rm{TPR}}}_{m} $$ (4) $$ {{\rm{FR}}}_{m}={{\rm{FPR}}}_{m} $$ (5) 3.5 结果分析
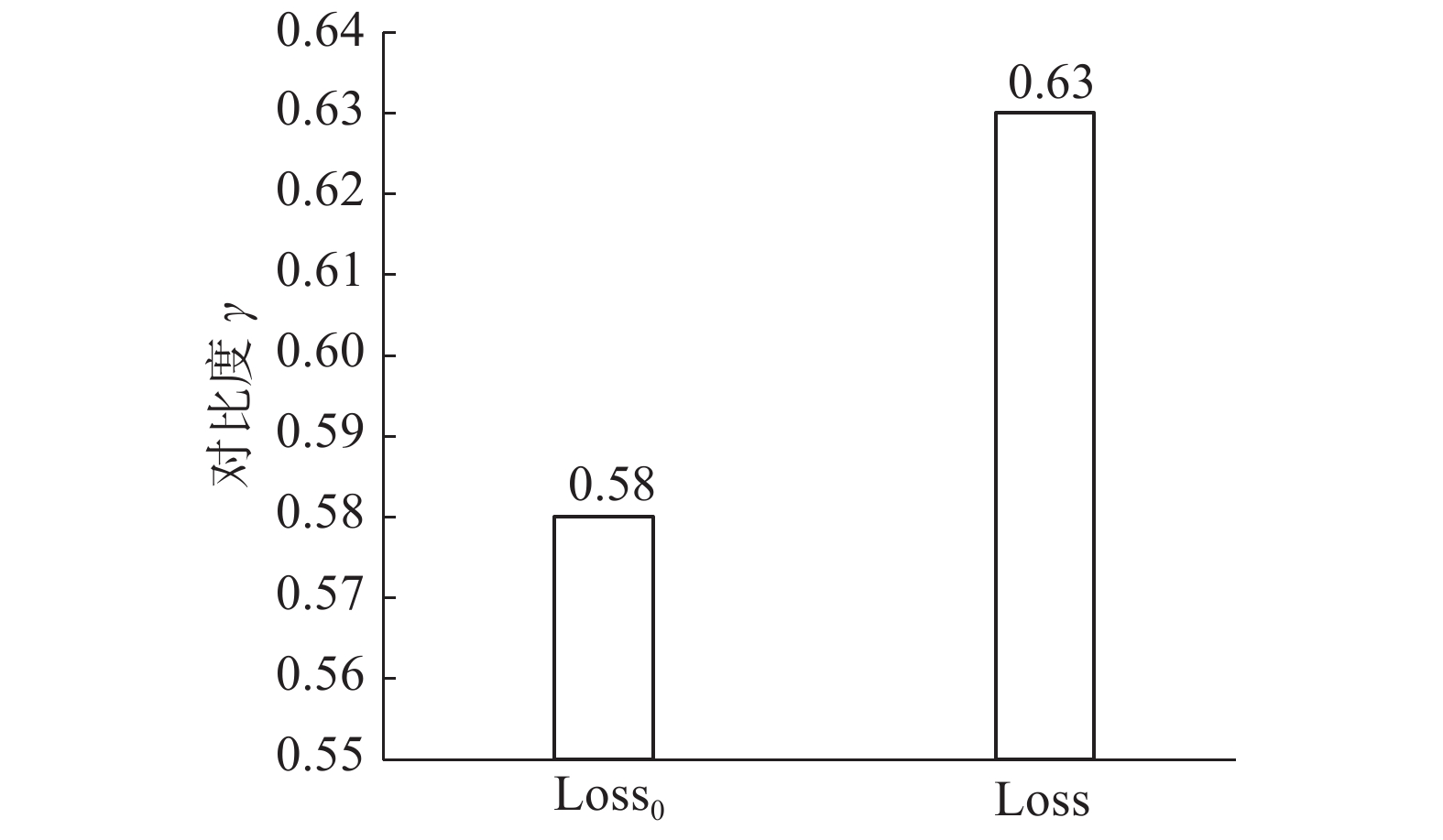
将学习速率设置为0.01，对损失函数执行随机梯度下降（SGD），50次迭代后，采用标准交叉熵损失函数（
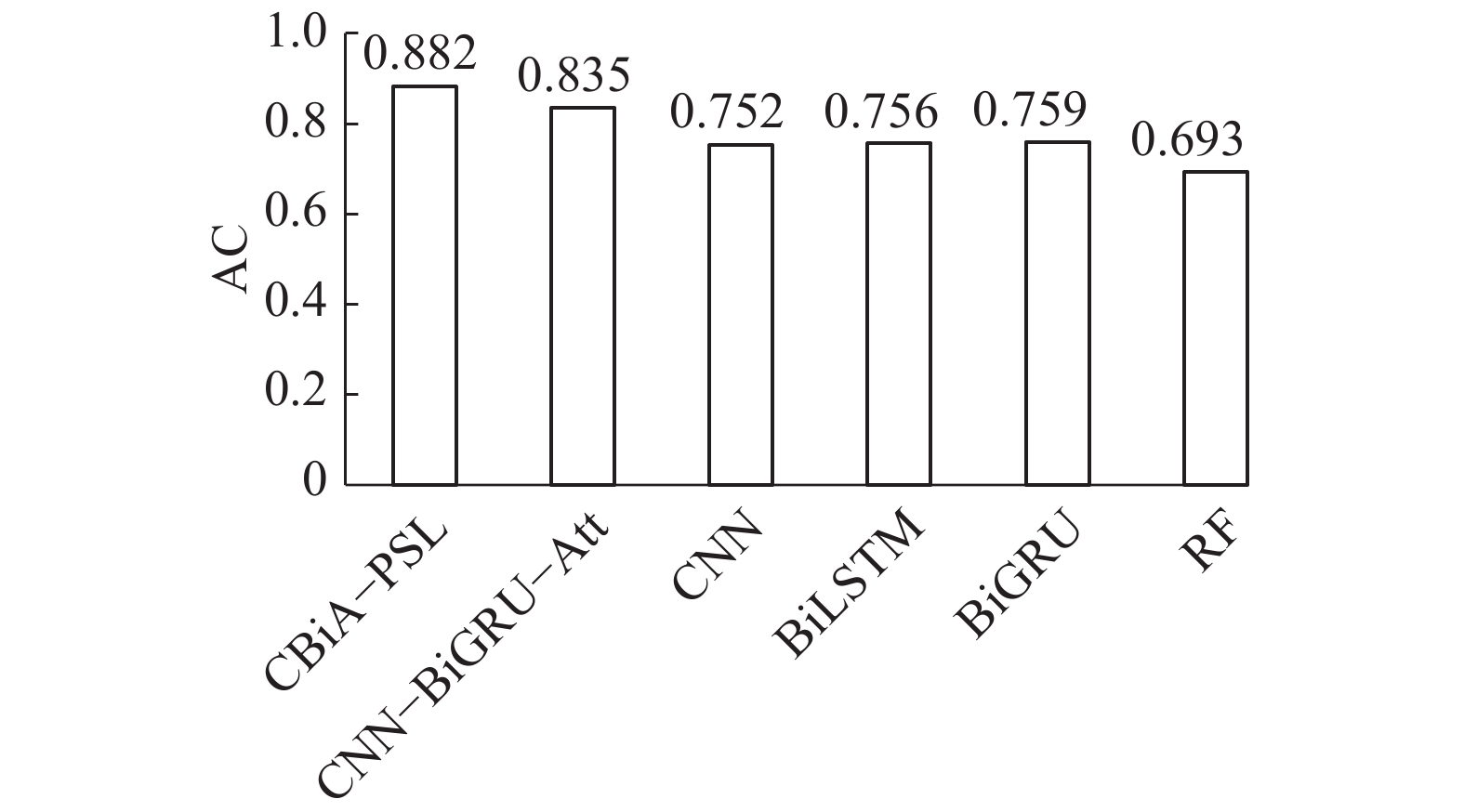
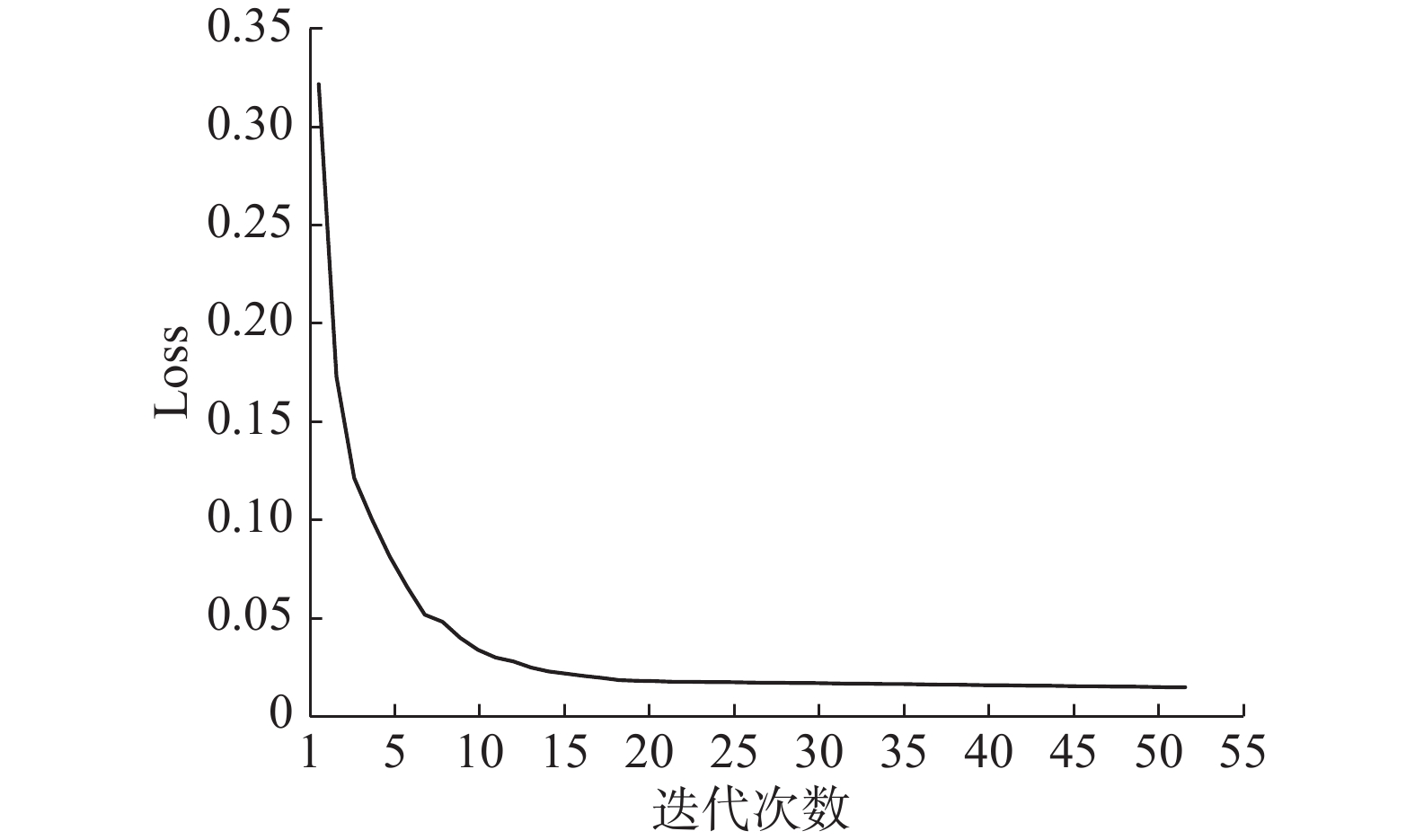
${{\rm{Loss}}}_{0}$ ）的CNN-BiGRU-Attention模型的对比度得分为0.58，采用正共享损失函数PSL（${\rm{Loss}}$ ）的CNN-BiGRU-Attention模型的对比度得分为0.63，有0.05的提高，如图7所示。这表明引入正共享损失函数可以提高异常类的检出效率。第2个实验将CBiA-PSL与其他5种用于异常工况检测的机器学习/深度学习方法进行比较，包括：CNN-BiGRU-Attention、卷积神经网络CNN、双向长短时记忆网络BiLSTM、双向门控循环单元BiGRU、随机森林RF。各模型的AC值、DR值、FR值如图8、表3、表4所示，CBiA-PSL模型训练过程的损失如图9所示。从图8可以看到，CBiA-PSL的AC值为88.2%，高于其他5种方法。此外，分析表3可以得出结论，CBiA-PSL可以提高少数类（泵漏、管漏）的DR值，且正常类的DR值保持不变，即提高了异常类的检出率。分析表4，少数类的FR值有时为0，式（1）~（5）表明该方法未检测到异常类别时，DR和FR均为0。表4表明本文提出的方法可以将异常类的错误报警率维持在较低水平。因此，本文所提出的方法CBiA-PSL可以在总体准确率较高的情况下，提高异常类的检出率，并降低错误报警率。
图 7 对比度得分Fig. 7 Contrast score下载:
全尺寸图片
图 8 各模型的AC值Fig. 8 AC value of each model下载:
全尺寸图片
表 3 各模型的DR值Table 3 DR value of each model算法 工况 正常 泵漏 管漏 CBiA-PSL 0.921 0.712 0.781 CNN-BiGRU-Att 0.921 0.601 0.710 CNN 0.921 0.499 0.645 BiLSTM 0.921 0.531 0.653 BiGRU 0.920 0.529 0.657 RF 0.921 0.503 0.594 表 4 各模型的FR值Table 4 FR value of each model算法 工况 正常 泵漏 管漏 CBiA-PSL 0.045 0.003 0.011 CNN-BiGRU-Att 0.113 0.006 0.011 CNN 0.120 0.003 0.010 BiLSTM 0.127 0.007 0.010 BiGRU 0.129 0.007 0.010 RF 0.097 0 0.013 
图 9 模型训练集的损失图Fig. 9 Loss graph of model training set下载:
全尺寸图片
4. 结束语
本文基于CNN-BiGRU联合网络特征学习模型，使用改进的CBiA-PSL网络进行抽油井异常工况预警，利用CNN局部特征的强学习能力提取工况样本灰度图像的局部特征，BiGRU提取全局前后向特征并加强CNN池化层特征的联系，加入注意力机制获取样本中的重点特征，降低噪声特征的干扰，从而完成有效特征筛选，提高模型对异常工况特征的学习能力。除了将CNN-BiGRU-Attention网络用作特征提取器外，针对工况样本数据集不平衡的问题，本文提出正共享损失函数PSL，该函数强调异常类和非异常的损失，而不是每个子类的损失，有助于学习比Softmax损失函数更多的判别特征，且给样本少的正类更高的权重，以学习参数，减弱了不平衡，有助于更好地识别异常工况。
实验结果表明，用本文提出的CBiA-PSL网络模型进行异常工况预警，可以取得较高的AC值、DR值，较低的FR值，即本文提出的CBiA-PSL方法能有效处理不平衡数据集，并且对于异常类和整体的预测都有较高的精度。未来的工作如下，由于预警时间也是异常预警的关键，因此在保证准确率的同时必须确保模型能满足异常预警的时间要求，同时优化网络模型参数，进一步提升模型对异常工况预警的精度。
-
图 1 BiGRU的网络结构
Fig. 1 Network structure of BiGRU
下载:
全尺寸图片
图 2 正向GRU单元的内部结构
Fig. 2 Internal structure of forward GRU unit
下载:
全尺寸图片
图 3 反向GRU单元的内部结构
Fig. 3 Internal structure of reverse GRU unit
下载:
全尺寸图片
图 4 样本灰度图像
Fig. 4 Sample gray image
下载:
全尺寸图片
图 5 CNN-BiGRU-Attention模型结构
Fig. 5 Model structure of CNN-BiGRU-Attention
下载:
全尺寸图片
图 6 注意力机制结构
Fig. 6 Structure of attention mechanism
下载:
全尺寸图片
图 7 对比度得分
Fig. 7 Contrast score
下载:
全尺寸图片
图 8 各模型的AC值
Fig. 8 AC value of each model
下载:
全尺寸图片
图 9 模型训练集的损失图
Fig. 9 Loss graph of model training set
下载:
全尺寸图片
表 1 预处理后的样本情况
Table 1 Sample condition after pretreatment
工况 样本数量 占总样本比例 正常 2 288 074 0.93 泵漏 60 158 0.02 管漏 114 720 0.05 表 2 多分类的混淆矩阵
Table 2 Confusion matrix of multi classification
真实标签 预测标签 A B C A TPA EAB EAC B EBA TPB EBC C ECA ECB TPC 表 3 各模型的DR值
Table 3 DR value of each model
算法 工况 正常 泵漏 管漏 CBiA-PSL 0.921 0.712 0.781 CNN-BiGRU-Att 0.921 0.601 0.710 CNN 0.921 0.499 0.645 BiLSTM 0.921 0.531 0.653 BiGRU 0.920 0.529 0.657 RF 0.921 0.503 0.594 表 4 各模型的FR值
Table 4 FR value of each model
算法 工况 正常 泵漏 管漏 CBiA-PSL 0.045 0.003 0.011 CNN-BiGRU-Att 0.113 0.006 0.011 CNN 0.120 0.003 0.010 BiLSTM 0.127 0.007 0.010 BiGRU 0.129 0.007 0.010 RF 0.097 0 0.013 -
[1] ZHANG Bin, GAO Xianwen, LI Xiangyu. Complete simulation and fault diagnosis of sucker-rod pumping (includes associated comment)[J]. SPE production & operations, 2021, 36(2): 277–290. [2] DUAN Jimiao, LIU Huishu, JIANG Junzhe, et al. Numerical prediction of wax deposition in oil-gas stratified pipe flow[J]. International journal of heat and mass transfer, 2017, 105: 279–289. doi: 10.1016/j.ijheatmasstransfer.2016.09.082 [3] ALSAIHATI A, ELKATATNY S, MAHMOUD A A, et al. Use of machine learning and data analytics to detect downhole abnormalities while drilling horizontal wells, with real case study[J]. Journal of energy resources technology, 2021, 143(4): 043201. doi: 10.1115/1.4048070 [4] ÖZMEN Ö, SINANOĞLU C, CALISKAN A, et al. Prediction of leakage from an axial piston pump slipper with circular dimples using deep neural networks[J]. Chinese journal of mechanical engineering, 2020, 33(1): 28. doi: 10.1186/s10033-020-00443-5 [5] RAHMANIFARD H, PLAKSINA T. Application of artificial intelligence techniques in the petroleum industry: a review[J]. Artificial intelligence review, 2019, 52(4): 2295–2318. doi: 10.1007/s10462-018-9612-8 [6] ZHAO Minghang, KANG M, TANG Baoping, et al. Deep residual networks with dynamically weighted wavelet coefficients for fault diagnosis of planetary gearboxes[J]. IEEE transactions on industrial electronics, 2018, 65(5): 4290–4300. doi: 10.1109/TIE.2017.2762639 [7] ZHANG Yiyi, LI Jiaxi, FAN Xianhao, et al. Moisture prediction of transformer oil-immersed polymer insulation by applying a support vector machine combined with a genetic algorithm[J]. Polymers, 2020, 12(7): 1579. doi: 10.3390/polym12071579 [8] 周斌, 王延江, 刘伟锋, 等. 基于Hessian正则化支持向量机的多视角协同识别抽油机井工况方法[J]. 石油学报, 2018, 39(12): 1429–1436. doi: 10.7623/syxb201812011 ZHOU Bin, WANG Yanjiang, LIU Weifeng, et al. A working condition recognition method of sucker-rod pumping wells based on Hessian-regularized SVM and multi-view co-training algorithm[J]. Acta petrolei sinica, 2018, 39(12): 1429–1436. doi: 10.7623/syxb201812011 [9] 王利君, 支志英, 贾鹿, 等. 基于SCRF的抽油井结蜡预测方法优化研究[J]. 计算机科学, 2019, 46(S2): 599–603. https://www.cnki.com.cn/Article/CJFDTOTAL-JSJA2019S2122.htm WANG Lijun, ZHI Zhiying, JIA Lu, et al. Study on optimized method for predicting paraffin deposition of pumping wells based on SCRF[J]. Computer science, 2019, 46(S2): 599–603. https://www.cnki.com.cn/Article/CJFDTOTAL-JSJA2019S2122.htm [10] LEI Yaguo, YANG Bin, JIANG Xinwei, et al. Applications of machine learning to machine fault diagnosis: a review and roadmap[J]. Mechanical systems and signal processing, 2020, 138: 106587. doi: 10.1016/j.ymssp.2019.106587 [11] WEI Jingliang, GAO Xianwen. Fault diagnosis of sucker rod pump based on deep-broad learning using motor data[J]. IEEE access, 2020, 8: 222562–222571. doi: 10.1109/ACCESS.2020.3036078 [12] CHEN Xiaohan, ZHANG Beike, GAO Dong. Bearing fault diagnosis base on multi-scale CNN and LSTM model[J]. Journal of intelligent manufacturing, 2021, 32(4): 971–987. doi: 10.1007/s10845-020-01600-2 [13] CABRERA D, GUAMÁN A, ZHANG Shaohui, et al. Bayesian approach and time series dimensionality reduction to LSTM-based model-building for fault diagnosis of a reciprocating compressor[J]. Neurocomputing, 2020, 380: 51–66. doi: 10.1016/j.neucom.2019.11.006 [14] 魏晓良, 潮群, 陶建峰, 等. 基于LSTM和CNN的高速柱塞泵故障诊断[J]. 航空学报, 2021, 42(3): 423876. https://www.cnki.com.cn/Article/CJFDTOTAL-HKXB202103037.htm WEI Xiaoliang, CHAO Qun, TAO Jianfeng, et al. Cavitation fault diagnosis method for high-speed plunger pumps based on LSTM and CNN[J]. Acta aeronautica et astronautica sinica, 2021, 42(3): 423876. https://www.cnki.com.cn/Article/CJFDTOTAL-HKXB202103037.htm [15] LIANG Rong, CHANG Xintan, JIA Pengtao, et al. Mine gas concentration forecasting model based on an optimized BiGRU network[J]. ACS omega, 2020, 5(44): 28579–28586. doi: 10.1021/acsomega.0c03417 [16] SHEN Wei, WANG Xinggang, WANG Yan, et al. DeepContour: a deep convolutional feature learned by positive-sharing loss for contour detection[C]//2015 IEEE Conference on Computer Vision and Pattern Recognition. Boston, USA, 2015: 3982-3991. [17] CHEN Yushi, JIANG Hanlu, LI Chunyang, et al. Deep feature extraction and classification of hyperspectral images based on convolutional neural networks[J]. IEEE transactions on geoscience and remote sensing, 2016, 54(10): 6232–6251. doi: 10.1109/TGRS.2016.2584107 [18] LU Wenjie, LI Jiazheng, WANG Jingyang, et al. A CNN-BiLSTM-AM method for stock price prediction[J]. Neural computing and applications, 2021, 33(10): 4741–4753. doi: 10.1007/s00521-020-05532-z [19] DIAZ M, MOETESUM M, SIDDIQI I, et al. Sequence-based dynamic handwriting analysis for Parkinson's disease detection with one-dimensional convolutions and BiGRUs[J]. Expert systems with applications, 2021, 168: 114405. doi: 10.1016/j.eswa.2020.114405 [20] VASWANI A, SHAZEER N, PARMAR N, et al. Attention is all you need[EB/OL]. (2017-05-12)[2021-05-01].https://arxiv.org/abs/1706.03762. [21] JAGVARAL B, LEE W K, ROH J S, et al. Path-based reasoning approach for knowledge graph completion using CNN-BiLSTM with attention mechanism[J]. Expert systems with applications, 2020, 142: 112960. doi: 10.1016/j.eswa.2019.112960
