A divide-and-conquer and integration algorithm for pairwise alignment of PPI networks
-
摘要: 生物网络比对是分析不同生物间进化关系的重要手段，它可以揭示不同物种间的保守功能并为物种间的注释转移提供重要信息。网络比对与子图同构类似，是一个NP-hard问题。本文提出了一种新的分治与整合策略的生物网络比对算法。首先进行模块划分，并根据已有的比对信息计算模块相似性；然后根据模块间结点的子比对获取候选结果集，最终通过超图匹配获得比对结果。使用已有的比对信息的集体行为预估模块间的相似性，大大提高了模块匹配的效率。基于路径和结点的得分函数保证了模块内结点的相似性。对于不同网络间结点的相似性，分别从结点自身和结点间的差异进行相似性判断。与现有算法相比，本文算法在生物和拓扑指标上均表现最佳。Abstract: Biological network alignment is an important means of analyzing the evolutionary relationships between different species. It can reveal the conservative function between different species and provide important information for cross-species annotation transfer. Network alignment, like subgraph isomorphism, is an NP-hard problem. In this paper, a new biological network alignment algorithm is proposed, which adopts the divide-and-conquer strategy as a whole. Firstly, module division is executed, and module similarity is calculated according to existing alignment information. The candidate result set is then obtained according to the subalignment of nodes between modules, and the alignment results are finally obtained through hypergraph matching. The collective behavior of the existing alignment information is used to estimate the similarity between modules, greatly improving module matching efficiency. The score function based on paths and nodes ensures the similarity of nodes in the same module. The similarity of nodes between different networks is judged by the nodes themselves and the difference between nodes. The algorithm in this paper performs best in both biological and topological evaluations when compared with the other existing algorithms.
-
近年来，随着酵母双杂交筛选，质谱法等高通量实验的发展，产生了大量的生物网络数据，其中包括PPI(protein-protein interaction)网络数据。PPI网络中包含着蛋白质间相互协作完成细胞内分子功能的信息，通过分析PPI网络可以发现这些信息，从而在分子层面上理解基因调控过程和疾病[1]。
网络比对是对PPI网络进行分析的一种手段，因为蛋白质之间的相互作用是跨物种保守的[2-3]，通过将已经研究充分的网络与研究不充分的网络进行比对，帮助发现保守的功能成分以及实现功能预测，可以更好地理解物种间的进化关系，进而为不同物种间的注释转移提供指导性的信息[4-5]。相关领域的研究者已经提出了很多关于成对网络的全局比对算法，使用拓扑序列信息构建相似性矩阵，搜索相似性矩阵从而构建比对的算法，如：CLMNA[6]、GRAAL[7]为首的GRAAL系列算法、GoT-WAVE[8]、ILP[9]。此外，一些学者也尝试将启发式算法运用到网络比对中，如SAlign[10]、SANA[11]、ImAlign[12]、MAGNA[13]及MAGNA++[14]。近几年模块化思想也被引用到了生物网络比对算法中来，如Proper[15]、ModuleAlign[16]、NAIGO[17]、AligNet[18]等。
文献[19]对现有的成对网络全局比对算法作比较后发现，不同算法的比对结果有较大的差异，不能同时达到拓扑指标以及生物指标得分均高。并且网络比对问题在计算上是NP-hard问题，现有的许多比对算法运行时间较长。本文提出了一种新的全局网络比对算法DIANA(divide-and-conquer and integration algorithm for network alignment)，能够在较短的时间内同时产生较高的拓扑与生物得分。其主要贡献如下：
1） 使用已有比对信息匹配关系来检测模块间的相似性，简化了模块匹配的时间复杂度。
2） 结合结点自身和结点间的路径来设计目标函数，保证了模块内结点的高相似性。
3） 对于不同网络中结点间的中心性差异，不仅考虑了结点间的差异值，同时考虑了结点自身的中心性大小，从而更充分挖掘结点的相似性特征。
1. 基于分治–整合策略的网络比对
1.1 PPI网络构建与算法
PPI网络可以被建模为一个无向图，其中结点表示网络中的蛋白质，网络的边表示蛋白质之间的相互作用。用G1=(V1,E1)，G2=(V2,E2)分别表示参与比对的两个PPI网络，且
$ \left|V_1\right| \leqslant \left|V_2\right| $ ，G1为源网络，G2为目标网络。网络比对的目的就是寻找G1到G2的映射关系，在网络之间传递功能知识，为确定跨物种具有相似功能的蛋白质提供基础[20]。本文算法DIANA是一种基于分治整合策略的生物网络比对算法， 主要可以分为模块划分、生成候选集、超图匹配3个阶段。首先根据结点相似性，分别将源网络和目标网络划分成若干个模块，同一模块内的结点，功能相似。然后，根据模块间的相似性将来自不同网络中的模块进行一对一匹配，将每对匹配上的模块进行模块内子比对，构成最终的候选结果集。最后，将候选结果集中的模块匹配关系及结点匹配关系抽象为超图，并进一步得到一对一的结点匹配关系。
1.2 模块划分
模块化是PPI网络的一个重要特性，具有相似功能的蛋白质往往会形成紧密连接的子网。为了更充分挖掘同一网络中结点的相似性信息，本文采用了基于结点和路径相结合的方法计算结点间的相似性，即采用度和最短路径长度衡量两个结点间的相似性，结点相似性计算如式(1)：
$$ {{\varOmega }}_{G}(u,v)=\frac{{\rm{deg}}_{u}\times {\rm deg}_{v}}{({\rm{deg}}_{G}{)}^{2}}+\frac{{\rm{Dim}}\left(G\right)+1-{\rm{dis}}(u,v)}{{\rm{Dim}}\left(G\right)+1} $$ (1) 式中：G为网络；u、v为G中的结点；degu指结点u的度；degG指图G中的最大度；
$ {\rm{Dim}}\left(G\right) $ 指图G的直径；${\rm{dis}}(u,v)$ 指结点u、v的最短路径长度。对于网络G=(V,E)，对网络中的所有结点均使用式(1)进行相似性计算，得到相似性矩阵
$\boldsymbol{\varOmega }$ 。依次以G中的结点为模块中心初始化|V|个模块。根据矩阵$\boldsymbol{\varOmega }$ 选取模块成员，对于每一个模块，将与模块中心存在相似性的结点按$\boldsymbol{\varOmega }$ 矩阵中的相似性值降序排列，选取前1/4的结点加入到该模块中，结点的选取比例为经验值。最终得到|V|个模块，且不同模块之间可能会存在重叠结点。1.3 产生候选结果集
1.3.1 模块比对
本文提出了一种新的模块相似性计算方法，模块间的相似性是模块间结点相似性的集体行为的总和。设一对相似性蛋白质分属于两个模块A、B，出现在模块A、B中的蛋白质数目越多，则模块A、B相似的概率越大。因此，本文采用相似蛋白质对在一对模块中的集体行为来衡量一对模块间的相似性并进行模块比对。
首先使用PrimAlign[21]生成了相似蛋白质对，然后根据相似蛋白质对在模块中的集体行为计算模块的相似性。生成相似蛋白质对也可以使用现有的任意网络比对工具，本文使用PrimAlign的理由如下：
1) 模块划分阶段产生的模块为重叠模块，一个结点可能存在于多个模块中，不同模块中的相同结点可能会存在多种匹配关系，而PrimAlign可以在两个网络间产生多对多的结点匹配关系，与模块的重叠特性相契合，因此可以很好地捕捉模块间的相似性。
2) PrimAlign产生的蛋白质对经GO术语[22]检测，生物功能相似性较高，约为现有算法的2倍，可以保证结点对间的相似性。
3) PrimAlign时间复杂度低，可在几秒内得到结果，保证了计算效率。
使用式(2)将得到的相似蛋白质对文件转换为模块相似性矩阵
${\boldsymbol{\pi }}_{{ij}}$ ，其中i，j分别为来自两个网络的蛋白质。$$ {\pi }_{ij}=\left\{\begin{aligned} &1,\quad {如果i和j是相似蛋白}\\ &0,\quad {其他}\end{aligned}\right. $$ (2) 根据矩阵
$\boldsymbol{\pi}$ 计算模块m1，m2的同源相似性得分HS，如式(3)：$$ {\rm{HS}}=\displaystyle\sum_{i\in m_1}\displaystyle\sum_{j\in m_2}{\pi}_{ij} $$ (3) 最后，模块间相似性得分计算如式(4)：
$$ {\boldsymbol {\mathcal{M}}}\left(m_1,m_2\right)={\rm{HS}}\left(m_1,m_2\right)+{\rm{BLAST}}\left(c_1,c_2\right) $$ (4) 式中：c1、c2分别为模块m1、m2的模块中心。BLAST为序列相似性。
根据式(4)得到模块间相似性矩阵
${\boldsymbol{\mathcal{M}}}$ ，构建加权完全二部图，将每个模块抽象为一个结点，结点之间的权重为对应的${\boldsymbol{\mathcal{M}}}$ 矩阵中的相似性值。使用最大加权二部匹配算法对二部图[23]求解，即可得到一对一的模块匹配关系。1.3.2 模块内子比对
模块比对阶段已经形成了一对一的模块匹配关系，本阶段主要是针对两个形成匹配关系的模块内部结点进行比对。它是整个网络比对问题的一个分治与简化，本文称来自源网络中的模块为源模块，来自目标网络中的模块为目标模块。因此在本阶段中，源网络与目标网络的比对问题被分解为若干组源模块与目标模块的比对问题。本阶段整体思想为：首先计算两个模块内结点间的相似性矩阵，接着根据相似性矩阵对两个模块内的结点进行比对。
根据特征向量中心性[24]和序列相似性计算不同模块中两个结点间的相似性
$ {\boldsymbol{\mathcal{W}}} $ ：$$ \begin{array}{c}{\boldsymbol{{\mathcal{W}}}}_{u\in {m}_{1}\wedge v\in {m}_{2}}\left(u,v\right)=\mathcal{P}\left(u,v\right)+{\rm{BLAST}}\left(u,v\right)\end{array} $$ (5) 式中：
$ \mathcal{P}(u,v) $ 表示结点u,v的特征向量中心性相似得分，其计算方法如式(6)：$$ \begin{array}{c}{\mathcal{P}}_{u\in {m}_{1}\wedge v\in {m}_{2}}\left(u,v\right)=\dfrac{{c}_{u}+{c}_{v}}{2}{\rm e}^{-\left|{c}_{u}-{c}_{v}\right|}\end{array} $$ (6) 其中cu指结点u的特征向量中心性。式(6)不仅考虑结点u，v的特征向量中心性之差，同时考虑了结点自身的中心性值，有助于把模块中具有较强的中心性地位且中心性相近的蛋白质对优先比对上。
根据式(5)形成的相似性矩阵
${\boldsymbol{\mathcal{W}}}$ 进行模块内比对步骤如下：1） 首先将模块m1、m2的模块中心c1、c2比对上；
2） 分别获取c1、c2的邻居，deg(c1)、deg(c2)；
3） 从
${\boldsymbol{\mathcal{W}}}$ 中获取包含deg(c1)和deg(c2)相似性值的子矩阵并使用匈牙利算法将deg(c1)、deg(c2)结点进行比对； 4） 将已扩展结点(c1,c2)移除，并对剩余已比对结点对依次重复步骤2)、3)。
将所有配对模块生成的子比对合并为候选集，此时的候选集中一个结点可能会和来自另一个网络中的多个结点形成比对关系，因此候选集为多对多匹配集合。
1.4 超图匹配
为从候选集中得到最终的一对一结点匹配，本文将候选集抽象为超图，其中源网络中的结点为超图的源结点，目标网络中的结点为超图的目标结点，每个子比对对应超图的一条超弧。使用加权二部超图匹配[25]算法将超图提取为仅包含一对一比对关系的二部图，即得到最终的结点匹配关系。
为减少时间复杂度，本文提出式(7)，根据
${\varGamma } $ 值选取部分子比对映射为超弧。式(7)综合考虑了子比对的保守性，序列相似性和比对上的结点对数：$$ \begin{array}{c}\varGamma \left(m_1,m_2\right)={\rm{CE}}\left(m_1,m_2\right)+B\left(m_1,m_2\right)+\dfrac{L\left({A}_{m_1,m_2}\right)}{{\rm{max}}\left({L}_{G_1,G_2}\right)}\end{array} $$ (7) 其中
${A}_{m_1,m_2}$ 表示模块$m_1$ 、$m_2$ 形成的子比对，见式(8)。${\rm{CE}}\left(m_1,m_2\right)$ 衡量了子比对${A}_{m_1,m_2}$ 的保守性,见式(9)、(10)。$B(m_1,m_2)$ 衡量了子比对的序列相似性，表示所有子比对中已比对结点的平均序列相似性得分，计算过程见式(11)。$L\left({A}_{m_1,m_2}\right)$ 表示子比对${A}_{m_1,m_2}$ 中所包含的已比对蛋白质对数。$\dfrac{L\left({a}_{m_1,m_2}\right)}{{\rm{max}}\left({L}_{G_1,G_2}\right)}$ 为归一化的子比对对数，$\mathrm{m}\mathrm{a}\mathrm{x}\left({L}_{G_1,G_2}\right)$ 为形成的子比对中，子比对结点数目的最大值。$$ \begin{aligned}{A}_{m_1,m_2}\left(i,j\right)= \left\{\begin{aligned} &1,\quad {{i}}\in |{{m_1}},{{j}}\in m_2,{i和j比对}\\ &0,\quad{其他} \end{aligned}\right.\end{aligned} $$ (8) $$ \begin{array}{c}{\rm{CE}}\left(m_1,m_2\right)=\displaystyle \sum_{i,k\in m_1}\displaystyle \sum_{j,l\in m_2}{C}_{ijkl}{A}_{m_1,m_2}\left(i,j\right){A}_{m_1,m_2}\left(k,l\right)\end{array} $$ (9) $$ \begin{aligned}{C}_{ijkl}= \left\{\begin{aligned} &1,\quad (i,k)\in {E}_{m_1},\;(j,l)\in {E}_{m_2}\\ &0,\quad {其他}\end{aligned}\right.\end{aligned} $$ (10) $$ \begin{array}{c}B\left(m_1,m_2\right)=\dfrac{\displaystyle\sum_{u,v\in {A}_{m_1,m_2}}{\rm{BLAST}}\left(u,v\right)}{L\left({A}_{m_1,m_2}\right)}\end{array} $$ (11) 获取最终一对一比对结果的过程为：首先将所有模块子比对按
${\varGamma }$ 值进行降序排列，并选取$\varGamma$ 值最大的子比对加入集合$Y$ 中；随后依次检查每个模块子比对的模块中心是否已在集合$Y$ 中，若存在，跳过，否则将当前模块子比对加入集合$Y$ 中；最终将$Y$ 映射为超图，并进行超图匹配即可得到最终一对一比对结果。2. 实验结果与分析
2.1 实验准备
比对算法：本文分别将DIANA与现有的7种网络比对算法进行比较，算法的详细信息及实验过程中所使用的参数信息见表1。
表 1 现有算法Table 1 T he state-of-the-art algorithms算法 年份 运行环境 SPINAL II 2013 JAVA MAGNA++ 2015 C++ ModuleAlign 2016 C++ INDEX 2017 C++ AligNet 2020 R ECAlign 2021 Python 数据集：DIANA分别在两种数据集上进行实验，分别为真实生物网络和合成网络，网络的详细信息见表2，其中ISOBASE[26]为真实PPI网络数据集，DMC、DMR为合成网络数据集，由NAPAbench[27]基准算法生成。
表 2 数据集Table 2 Dataset数据集 物种 节点数 边数 平均度 平均聚类系数 ISOBASE MUS 623 559 1.79 0.08 CEL 2995 4827 3.20 0.025 SCE 5524 82656 29.00 0.2 DME 7396 24937 6.70 0.024 HSA 10403 54654 10.50 0.12 DMC A 3000 6090 4.06 0.089 B 4000 8112 4.05 0.087 DMR A 3000 6017 4.01 0.006 B 4000 8238 4.11 0.005 2.2 实验结果
2.2.1 合成网络与真实网络
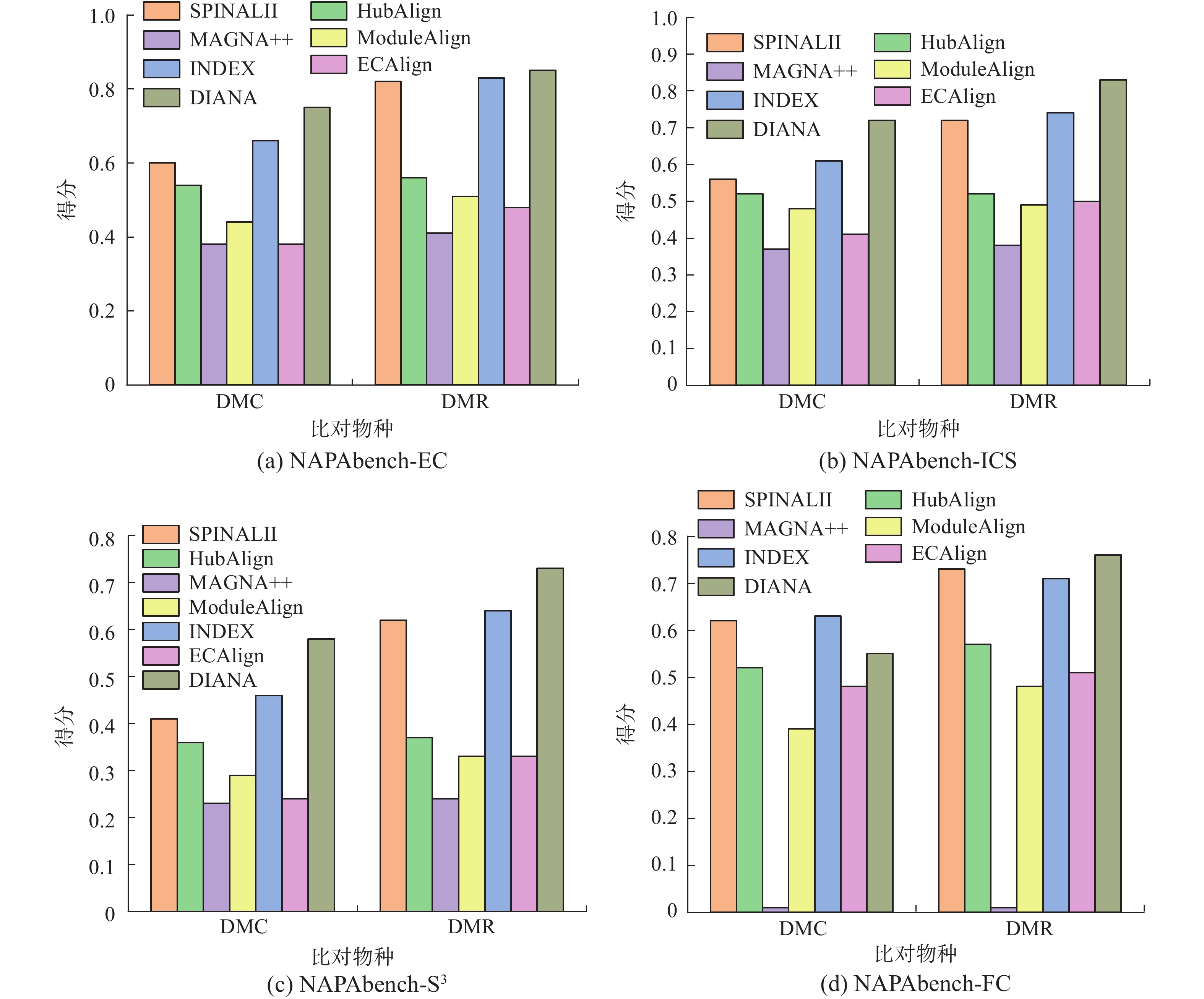
合成网络实验：由于AligNet需要同一个网络中结点间的BLAST相似性文件，而合成网络没有此相似性文件，因此，本阶段实验在除AligNet之外的其余算法间展开。其中EC[1]、ICS[1]、S3[7]是拓扑评价指标，FC[7]是生物指标。由图1可知，在DMC数据集上，DIANA在EC、ICS、S3上均表现最佳。在FC上，DIANA表现稍差于SPINAL II和INDEX，但差距较小。在DMR数据集上，DIANA在所有4个指标上均表现最佳，且其拓扑和生物得分均是MAGNA++的两倍多。在表2中可以看到，DMC、DMR中比对的两个网络的平均度和平均聚类系数接近，并且两个网络都是用NAPAbench[27]合成网络算法生成的，同源性相近，所以DIANA在几种算法中均取得最好的拓扑得分。
图 1 合成网络实验结果Fig. 1 Experiment results of synthetic networks
下载:
全尺寸图片
合成网络是由人工构造的PPI网络，根据实验表明，DIANA在两种合成数据集上均有较好的表现，证明在理论上DIANA可以产生优于现有其他算法的比对结果。
真实网络实验：根据物种特性，实验在ISOBASE数据集中选取了7对物种对用于真实网络实验，分别为：MUS-CEL、MUS-SCE、MUS-DME、CEL-SCE、CEL-DME、SCE-DME、SCE-HSA，实验结果见图2。同时SCE和HSA网络的平均度和平均聚类系数较大（见表2），而MUS、DME、CEL 3个网络的拓扑特征稍差，可以发现这与比对结果的拓扑得分是相关的。就EC而言，本文算法DIANA在大部分物种对上比对得分均为最佳，在MUS-DME上低于HubAlign和MAGNA++，在CEL-DME上低于HubAlign和INDEX，在CEL-SCE上略低于HubAlign，但整体差别都较小。就ICS和S3而言，DIANA算法在MUS-CEL物种对中，得分低于INDEX， MUS-DME物种对上低于算法INDEX和ECAlign外，在其余5个物种对上本文算法均表现最佳。在生物指标上，DIANA在SCE-DME上低于HubAlign、INDEX和ECAlign，在SCE-HSA上低于HubAlign外，而在其余5个物种对上仍表现最佳。综合来看，该组实验中共有28组数据，其中19组数据DIANA均表现最佳。
图 2 真实网络实验结果Fig. 2 Experiment results of real networks下载:
全尺寸图片
真实网络是根据真实生物中蛋白质间的相互作用构建的，通过在真实生物网络中的实验表明，与现有比对算法相比，DIANA算法能够更准确地匹配不同物种间的相似蛋白，在实际应用中是可行的。
2.2.2 DIANA的普适性与PrimAlign的有效性
1.3.1节已经说明了DIANA可以使用现有的任意网络比对算法进行模块相似性计算，且给出了使用PrimAlign进行模块相似性计算的原因，因此本阶段实验对DIANA的普适性和使用PrimAlign的有效性进行验证。图3给出了现有的6种网络比对算法在SCE-HAS上的初始结果以及不同版本的DIANA算法得出的比对结果。其中DIANA+*，表示DIANA使用了算法*产生的相似蛋白质对进行实验，DIANA表示使用PrimAlign生成的相似蛋白质对进行实验。
图 3 DIANA与优化算法Fig. 3 DIANA and improved algorithm下载:
全尺寸图片
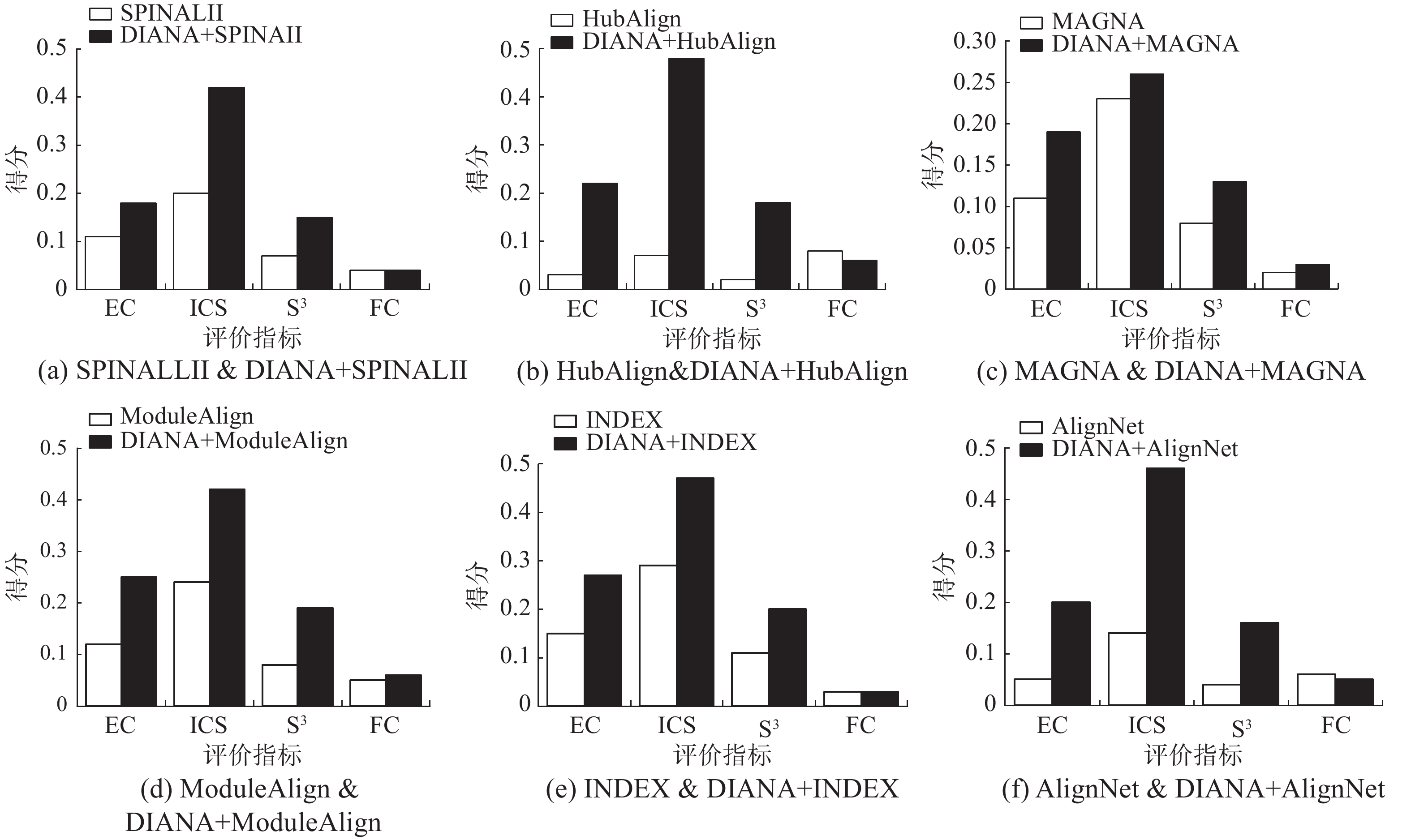
由图4可知，各种版本的DIANA算法在EC，S3上均优于现有的比对算法；在ICS上，除DIANA+MAGNA++低于INDEX外，其余版本的DIANA算法均优于现有的比对算法；在FC上，HubAlign最好，DIANA、DIANA + HubAlign、DIANA + ModuleAlign、DIANA + AligNet均优于除HubAlign之外的其他现有算法。因此，综合来看，本文算法无论与哪一种算法融合其比对结果均优于现有的比对算法，且DIANA表明在融合现有方法方面具有一定的普适性。
图 4 运行时间Fig. 4 Running time下载:
全尺寸图片
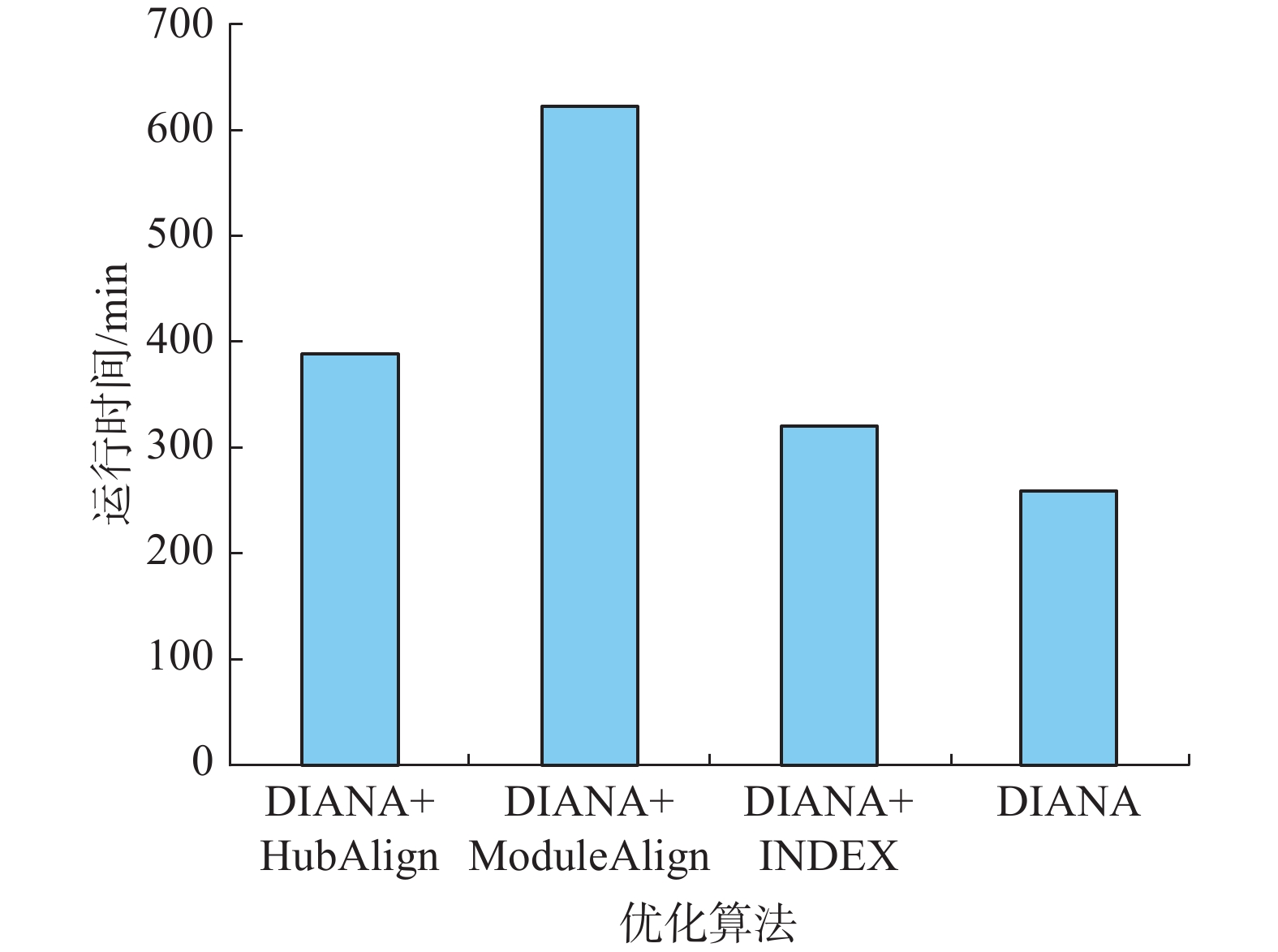
对于不同版本的DIANA算法之间，在EC上，DIANA+ModuleAlign，DIANA+INDEX得分略高于DIANA，在ICS上，DIANA+HubAlign得分最高，其次为DIANA，与DIANA+HubAlign差距很小。在S3上，DIANA+INDEX得分最高，DIANA紧随其后。在FC上，DIANA、DIANA+HubAlign DIANA+ModuleAlign得分最高。综上，DIANA、DIANA+HubAlign、DIANA+ModuleAlign、DIANA+INDEX都在某一指标上表现最佳，但综合来看，在各指标上的差距较小，均能得到较好的比对结果，而其余算法表现相对较差。图4给出的4种方法的运行时间，从图4可知，本文算法DIANA运行时间最短，DIANA+INDEX运行时间稍大于DIANA、DIANA+ModuleAlign运行时间最长，约为DIANA的2.4倍。因此综合在单个指标上的表现及运行时间， DIANA表现最佳，也进一步说明了使用PrimAlign的有效性。
2.2.3 DIANA对其他算法的优化
DIANA也可以作为一个优化工具，来提高当前网络比对算法获得网络比对的质量。在实验中，采用DIANA来提升SPINALII、HubAlign、MAGNA++、ModuleAlign、INDEX和AligNet所获得的初始比对质量。图5给出了经过DIANA优化的SPINAL II、HubAlign、MAGNA++、ModuleAlign、INDEX和AligNet 之前和之后的网络比对的质量对比。除在使用HubAlign和AligNet作为相似蛋白质对时，生物指标FC略低于原有算法，在其余实验中，经DIANA优化后的各项指标均远大于原有算法，尤其是ModuleAilgn，各项指标提升最大。虽然HubAlign和AligNet的 FC上有所下降，但在EC、ICS和S3上，优化之后的效果分别提升了7倍和4倍，可见DIANA在优化现有方法方面也具有很大优势。
图 5 DIANA优化实验Fig. 5 Improved experiments of DIANA下载:
全尺寸图片
2.2.4 复杂度分析
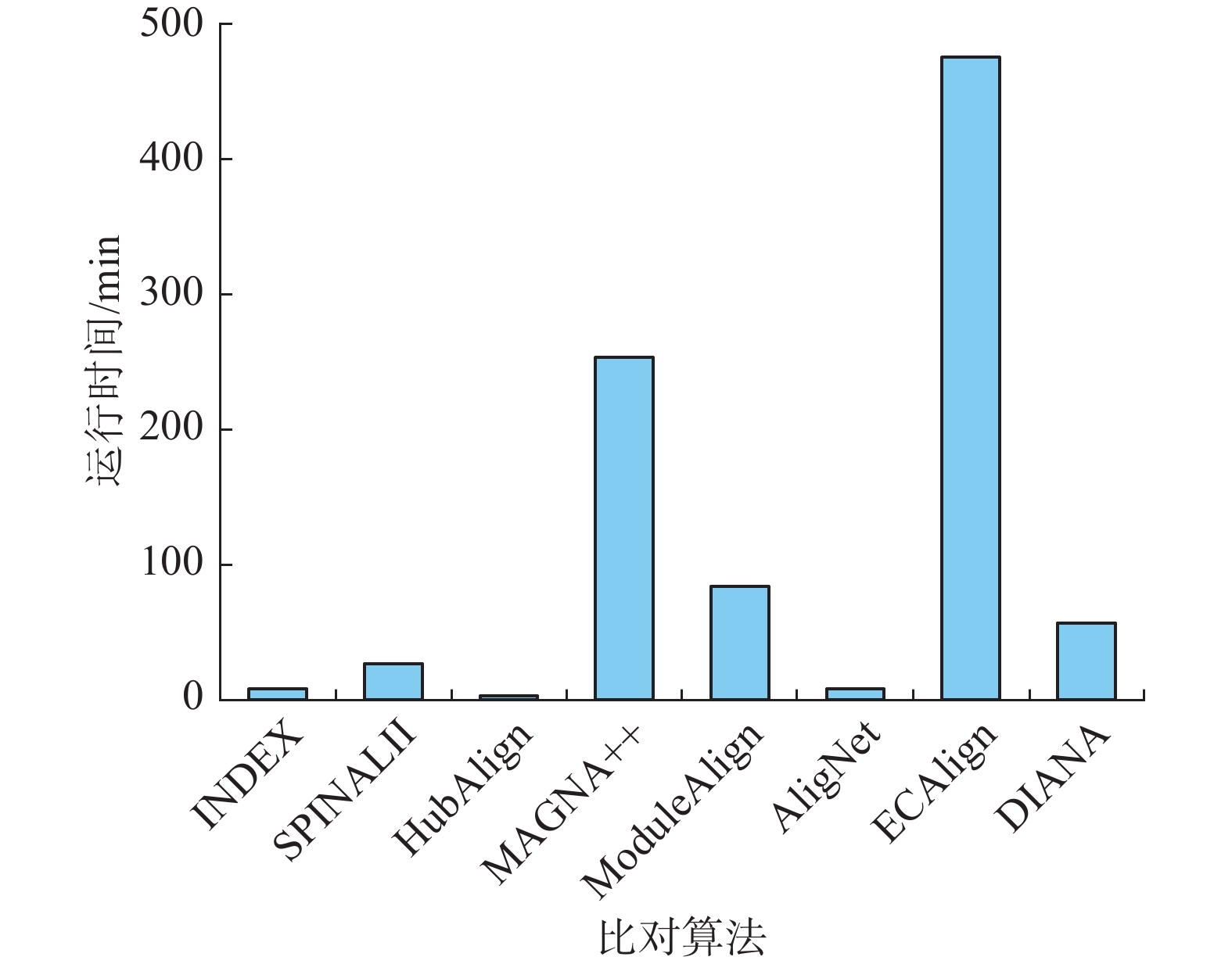
本文所有算法的硬件环境为：处理器为Intel core i5-7200 CPU @ 2.50 GHz，内存大小32 GB。空间上，相较于传统的二步式算法，本文算法采用模块化的思想，网络被分割为模块，然后进行模块间以及模块内的比对，且不同模块间节点有重叠，因此本算法对内存要求更高。时间上，DIANA算法第1)步中，对每一个节点进行模块划分，设n为G1网络的节点数，m为G2网络的节点数，其时间复杂度为
$ O(n+m) $ 。算法第2)步中，进行了子模块比对，对G1、G2网络中模块使用匈牙利算法进行比对，时间复杂度约为$ O(n\cdot m) $ 。最后，对候选结果集进行超图匹配，使用算法的时间复杂度为$ O(n\cdot m) $ 。最后，将本文使用的所有算法的运行时间进行比较，如图6所示，给出了算法的平均运行时间。ECAlign运行时间最长，该算法受网络规模影响较大，在MUS-CEL上大约运行3 min，而在SCE-HAS上则需要37 h。MAGNA++次之，该算法是一种群智能算法，每一对物种都需要进行上千次迭代才可以得到较好的比对结果，因此运行时间较长。DIANA运行速度适中，快于MAGNA++、ModuleAlign和ECAlign等算法。
图 6 不同算法运行时间Fig. 6 Running time of different algorithms下载:
全尺寸图片
3. 结束语
本文提出的算法DIANA使用一种基于分治–整合的策略进行生物网络比对。利用模块化思想，将网络比对问题分解为若干个模块间的比对问题，并利用超图匹配算法将模块间的子比对结果合并为最终一对一比对结果。分别将DIANA在合成网络和真实网络上进行实验，从理论和实际层面证明了本文算法在网络比对中的可行性与精准性。同时DIANA可以灵活地接收来自不同现有算法的比对结果，并作为模块比对阶段模块相似性计算的输入文件，本文算法具有较好的灵活性，且所得结果与原有比对相比具有较大提高，表明DIANA可以优化现有比对结果。
DIANA能获得高质量的比对结果，同时算法具有一定的普适性，但仍有提升空间，因此下一步的工作重点是继续探索更优化的模块相似性计算方法，弥补现有算法的不足，从而设计一种高精准度且普适性更高的生物网络。
-
图 1 合成网络实验结果
Fig. 1 Experiment results of synthetic networks
下载:
全尺寸图片
图 2 真实网络实验结果
Fig. 2 Experiment results of real networks
下载:
全尺寸图片
图 3 DIANA与优化算法
Fig. 3 DIANA and improved algorithm
下载:
全尺寸图片
图 4 运行时间
Fig. 4 Running time
下载:
全尺寸图片
图 5 DIANA优化实验
Fig. 5 Improved experiments of DIANA
下载:
全尺寸图片
图 6 不同算法运行时间
Fig. 6 Running time of different algorithms
下载:
全尺寸图片
表 1 现有算法
Table 1 T he state-of-the-art algorithms
算法 年份 运行环境 SPINAL II 2013 JAVA MAGNA++ 2015 C++ ModuleAlign 2016 C++ INDEX 2017 C++ AligNet 2020 R ECAlign 2021 Python 表 2 数据集
Table 2 Dataset
数据集 物种 节点数 边数 平均度 平均聚类系数 ISOBASE MUS 623 559 1.79 0.08 CEL 2995 4827 3.20 0.025 SCE 5524 82656 29.00 0.2 DME 7396 24937 6.70 0.024 HSA 10403 54654 10.50 0.12 DMC A 3000 6090 4.06 0.089 B 4000 8112 4.05 0.087 DMR A 3000 6017 4.01 0.006 B 4000 8238 4.11 0.005 -
[1] HASHEMIFAR S, XU Jinbo. HubAlign: an accurate and efficient method for global alignment of protein-protein interaction networks[J]. Bioinformatics (Oxford, England), 2014, 30(17): i438–i444. doi: 10.1093/bioinformatics/btu450 [2] MASKEY S, CHO Y R. LePrimAlign: local entropy-based alignment of PPI networks to predict conserved modules[J]. BMC genomics, 2019, 20(Suppl 9): 964. [3] 苗孟君, 丁彦蕊. PPI网络比对用于植物乳杆菌的糖代谢研究[J]. 计算机工程与应用, 2018, 54(6): 49–54. doi: 10.3778/j.issn.1002-8331.1611-0279 MIAO mengjun, DING yanrui. PPI network alignment for study on carbohydrate metabolism of Lactobacillus Plantarum[J]. Computer engineering and applications, 2018, 54(6): 49–54. doi: 10.3778/j.issn.1002-8331.1611-0279 [4] GAO Jianliang, TIAN Ling, LYU Tengfei, et al. Protein2Vec: aligning multiple PPI networks with representation learning[J]. IEEE/ACM transactions on computational biology and bioinformatics, 2021, 18(1): 240–249. doi: 10.1109/TCBB.2019.2937771 [5] WOO H M, YOON B J. MONACO: accurate biological network alignment through optimal neighborhood matching between focal nodes[J]. Bioinformatics, 2020, 37(10): 1401–1410. [6] MA Lijia, WANG Shiqiang, LIN Qiuzhen, et al. Multi-neighborhood learning for global alignment in biological networks[J]. IEEE/ACM transactions on computational biology and bioinformatics, 2021, 18(6): 2598–2611. doi: 10.1109/TCBB.2020.2985838 [7] KUCHAIEV O, MILENKOVIC T, MEMISEVIC V, et al. Topological network alignment uncovers biological function and phylogeny[J]. Journal of the royal society, interface, 2010, 7(50): 1341–1354. doi: 10.1098/rsif.2010.0063 [8] APARÍCIO D, RIBEIRO P, MILENKOVIĆ T, et al. Temporal network alignment via GoT-WAVE[J]. Bioinformatics (Oxford, England), 2019, 35(18): 3527–3529. doi: 10.1093/bioinformatics/btz119 [9] LLABRÉS M, RIERA G, ROSSELLÓ F, et al. Alignment of biological networks by integer linear programming: virus-host protein-protein interaction networks[J]. BMC bioinformatics, 2020, 21(Suppl 6): 434. [10] AYUB U, HAIDER I, NAVEED H. SAlign-a structure aware method for global PPI network alignment[J]. BMC bioinformatics, 2020, 21(1): 500. doi: 10.1186/s12859-020-03827-5 [11] MAMANO N, HAYES W B. SANA: simulated annealing far outperforms many other search algorithms for biological network alignment[J]. Bioinformatics, 2017, 33(14): 2156–2164. doi: 10.1093/bioinformatics/btx090 [12] WANG Shiqiang, MA Lijia, ZHANG Xiao. Adaptive artificial immune system for biological network alignment[M]//Intelligent Computing Theories and Application. Cham: Springer International Publishing, 2020: 560−570. [13] VIJAYAN V, SARAPH V, MILENKOVIĆ T. MAGNA++: Maximizing Accuracy in Global Network Alignment via both node and edge conservation[J]. Bioinformatics, 2015, 31(14): 2409–2411. doi: 10.1093/bioinformatics/btv161 [14] 陶斯涵, 丁彦蕊. 引入序列信息的残基相互作用网络比对算法[J]. 软件学报, 2019, 30(11): 3413–3426. DING yanrui, TAO sihan. Algorithm introduced sequence information for residue interaction network alignment[J]. Journal of software, 2019, 30(11): 3413–3426. [15] KAZEMI E, HASSANI H, GROSSGLAUSER M, et al. PROPER: global protein interaction network alignment through percolation matching[J]. BMC bioinformatics, 2016, 17(1): 1–16. [16] HASHEMIFAR S, MA Jianzhu, NAVEED H, et al. ModuleAlign: module-based global alignment of protein-protein interaction networks[J]. Bioinformatics, 2016, 32(17): i658–i664. doi: 10.1093/bioinformatics/btw447 [17] ZHU Lijuan, ZHANG Ju, ZHANG Yi, et al. NAIGO: an improved method to align PPI networks based on gene ontology and graphlets[J]. Frontiers in bioengineering and biotechnology, 2020, 8: 547. doi: 10.3389/fbioe.2020.00547 [18] ALCALÁ A, ALBERICH R, LLABRÉS M, et al. AligNet: alignment of protein-protein interaction networks[J]. BMC bioinformatics, 2020, 21(6): 1–22. [19] GUZZI P H, MILENKOVIC T. Survey of local and global biological network alignment: the need to reconcile the two sides of the same coin[J]. Briefings in bioinformatics, 2018, 19(3): 472–481. [20] ERTEN C. Global alignment of PPI networks[M]//Recent Advances in Biological Network Analysis. Cham: Springer International Publishing, 2020: 3-25. [21] KALECKY K, CHO Y R. PrimAlign: PageRank-inspired Markovian alignment for large biological networks[J]. Bioinformatics (Oxford, England), 2018, 34(13): i537–i546. doi: 10.1093/bioinformatics/bty288 [22] ASHBURNER M, BALL C A, BLAKE J A, et al. Gene ontology: tool for the unification of biology. The gene ontology consortium[J]. Nature genetics, 2000, 25(1): 25–29. doi: 10.1038/75556 [23] KUHN H W. The Hungarian method for the assignment problem[J]. Naval research logistics quarterly, 1955, 2(1-2): 83–97. doi: 10.1002/nav.3800020109 [24] LEI Xiujuan, YANG Xiaoqin, FUJITA H. Random walk based method to identify essential proteins by integrating network topology and biological characteristics[J]. Knowledge-based systems, 2019, 167: 53–67. doi: 10.1016/j.knosys.2019.01.012 [25] BORNDÖRFER R, HEISMANN O. The hypergraph assignment problem[J]. Discrete optimization, 2015, 15: 15–25. doi: 10.1016/j.disopt.2014.11.002 [26] PARK D, SINGH R, BAYM M, et al. IsoBase: a database of functionally related proteins across PPI networks[J]. Nucleic acids research, 2011, 39: D295-D300. [27] SAHRAEIAN S M E, YOON B J. A network synthesis model for generating protein interaction network families[J]. PLoS one, 2012, 7(8): e41474. doi: 10.1371/journal.pone.0041474
