Fine-grained image classification algorithm based on multi-granularity regions shuffle
-
摘要: 细粒度图像分类是计算机视觉领域一个具有挑战性的任务，在实际场景中具有很高的应用价值。其中不同子类别的物体整体轮廓差异较小，微小的判别性局部区域是分类的关键。然而，这些重要的局部区域的尺度可能不同, 不能用单一的标准去衡量它们。为了解决这个问题，本文提出了多粒度空间混乱模块来帮助神经网络学习如何寻找到不同尺度的判别性细节。该模块首先将图片划分为不同粒度的局部区域，然后随机打乱并重组构成新的输入图片。经过处理的图片具有区域无关性，从而迫使网络更好地在不同粒度层次下寻找有判别力的局部区域并从中学习特征。在3个广泛使用的细粒度图像分类数据集上的实验证明本文提出的模块可以有效地帮助网络寻找判别性局部区域从而提升了准确率并且网络不需要图片的任何部位标注信息。Abstract: Fine-grained image classification is a challenging task of computer vision due to the high application value in many reality scenes, having high value in actual application scenarios. The differences in the overall outline of objects from different sub-categories are slight, and the delicate, discriminative local regions are the key to improve the classification accuracy. However, these essential local areas may have different scales, which cannot be measured by a single criterion. Therefore, a multi-granularity regions shuffle module is proposed to help the neural network learn how to find discriminative details for different scales. The module would first divide the image into local areas with different granularity, and then these regions will be shuffled and reorganized to form a new image, which will also be inputted to the network. The irrelevance among regions of the new image forces the network to find discriminative local regions under different granularity and learn from regions. Experimental results of three datasets widely used as benchmarks in fine-grained image classification show that the proposed module can effectively help the network find discriminative local regions and achieve excellent performance with no additional information required to be marked on any part of the image.
-
细粒度图像分类是计算机视觉领域中一项非常具有挑战性的任务，它的目标是对图像中的物体在同一大类下的许多子类中进行正确分类[1] ，因此细粒度图像分类也被称作子类别图像分类[2]。细粒度图像分类存在类内相似度小且类间相似度大的分类难点[3]。在细粒度图像分类的数据中，具有区分度的重要信息往往包含在一些局部区域，并且多数情况下同一子类别物体也仅有局部微小区域不同，如何寻找到有判别力的局部区域，并借助于极其细微的局部差异较好地完成分类是细粒度图像分类任务的难点。
近年来深度学习技术[4-6]在人工智能领域已成为主流的方法，对基于卷积神经网络(convolutional neural networks, CNN)的细粒度图像分类按照监督信息，可以分为基于强监督信息和基于弱监督信息两类。基于强监督信息的细粒度图像分类方法为了获取更好的分类准确度，除了使用图像的类别标签以外，还使用了物体标注框(object bounding box)和部位标注点(part annotation)等额外的强监督信息，而基于弱监督信息的细粒度分类模型只使用图像级别的标注信息来提取有判别性的局部特征完成分类。为了更好地寻找判别性局部区域，本文提出了一种基于弱监督信息的细粒度图像分类方法，在骨干网络中加入多粒度空间混乱模块。空间混乱模块对图像进行碎片化后重组，打破图像整体关联性，迫使网络去寻找对分类更有帮助的局部区域，细粒度图像分类的重要判别点往往都在这些局部区域。在此基础上引入多粒度思想[7-9]，从多个粒度层面[10]更加全面地寻找不同粒度[11]的局部区域并提取特征，来提高分类准确率。
本文的主要贡献如下:
1) 提出了一种基于弱监督信息的细粒度图像分类方法，无需部位级别的标签，仅需类别标签即可达到不错的分类精度，而且模型的空间成本和时间成本低；
2) 提出空间混乱模块，对输入图像进行切分并打乱重组的操作，破坏图像局部区域之间的关联性，使网络更好地寻找有判别力的局部区域，方法简单但非常有效；
3) 在单一尺度的空间混乱模块基础上引入多粒度思想，迫使网络学习到如何捕捉不同粒度层次的判别性区域，使网络分类性能更鲁棒。
1. 相关工作
细粒度图像分类任务的研究方向主要分为两种：基于强监督信息和基于弱监督信息的细粒度图像分类。区别在于，基于强监督信息的方法在模型训练阶段，为了获得更好的分类精度，除了图像的类别标签外，还使用局部区域位置和标注框等额外的人工标注信息，用于定位图像局部关键区域。而基于弱监督信息的细粒度图像分类的方法仅仅依靠图像级别的标签，在不借助部位标注的情况下对细粒度图像进行分类。
1.1 基于强监督信息的方法
最早的具有代表性的方法是2014年被提出的基于部位的区域卷积神经网络[12]，该方法使用自底向上的区域选择算法[13]来产生候选区域，用区域卷积神经网络(regions with convolutional neural networks, R-CNN)算法给出评价分值，选出分值高的区域，进行特征级联作为总体特征送进支持向量机(support vector machines, SVM)分类器进行分类。Branson等[14]提出了姿态归一化网络，该研究工作采用对不同级别的图像块进行姿态对齐[15]的操作。来自悉尼科技大学Huang等 [16]在2016 年提出了部位堆叠网络(part-stacked CNN)，在部位级别的定位过程中采用了全卷积网络[17]，引入全卷积网络的好处在于特征图可以直接作为部件的定位结果应用于分类网络。Lin[18]提出的 深度定位对齐分类网络(deep localization alignment and classification, Deep LAC)使用同一个网络进行部件定位、对齐和分类，并且提出了阀门连接函数(valve linkage function, VLF)用来优化定位和分类子网络之间的连接。南京大学的魏秀参[19]在 2017 年提出了 掩码卷积神经网络(mask CNN)，该网络利用全卷积网络生成掩码，用于局部定位和选择深度描述符[20] 构建图像、头部、躯干和对象的四流网络，该网络是第一个端到端的用于细粒度图像分类网络模型。尽管基于强监督信息的分类模型获得了不错的分类精度，但使用的部位级标注信息获取困难且代价昂贵，使得这类算法的实际应用被局限了。
1.2 基于弱监督信息的方法
目前细粒度图像分类的一个明显趋势是在模型训练时仅使用图像级别标注信息，而不再使用额外的部位级别标注信息。 2015年两级注意力模型被提出，作者发现注意力机制对于细粒度图像的局部特征有很好的提取效果。同年文献[21]提出了多粒度卷积神经网络，该模型包含多个独立的CNN， 每个CNN内部有不同粒度的兴趣域。2016年Liu Xiao提出了一种基于强化学习的全卷积注意力局部网络[22]提出了一种基于强化学习的全卷积注意力局部网络，这个网络模拟人类视觉系统的识别过程，将相关区域放大处理进行进一步判断。 Lin等[23]设计了 双线性卷积神经网络(bilinear CNN)，该模型非常高效而且数学基础扎实，其中的双线性池化(bilinear pooling)[24]提供了比线性模型更精确的特征表示，并且可以端到端的进行优化，但是双线性模型的维度太高，很难泛化使用。
1.3 DCL
破坏和重建学习网络[25] (destruction and construction learning, DCL)是一种新颖的细粒度图像分类模型，该模型引入一个DCL流来自动从判别性区域中进行学习。 首先作者借鉴了自然语言处理中常用的打乱方法，提出区域混淆机制来划分输入图像并随机打乱它们，同时引入对抗性损失降低噪声的影响，使网络进行破坏学习，然后提出区域对齐网络恢复原始区域布局，通过重建对局部区域间的相关性进行建模。文献[25]的RCM部分将图像分为N
$ \text{×} $ N的局部区域，其中N被固定为7，这种情况下模型只能划分固定尺度大小的局部区域 无法获取到多种尺度的局部区域特征。本文将结合多粒度思想并参考DCL的RCM部分，将图像分为不同粒度大小的局部区域，从而使模型关注到不同尺寸大小的判别性局部区域用于分类。2. 空间混乱模块
在细粒度图像分类任务中，局部细节往往比全局结构信息更加重要。多数情况下不同的细粒度类别具有相同的全局结构而只在具体的局部细节上不同。将图像中的局部区域打乱，对细粒度识别不重要的一些不相关的区域就会被忽略，并且将迫使网络学习到具有辨别性的局部细节，从而更好地对图像进行分类。
在自然语言处理中，打乱句子中单词的顺序会迫使神经网络聚焦有判别性的词语，忽视无关词语。同样，将图像分为多个局部区域，把局部区域看作自然语言处理中的单词，然后进行随机的打乱重组，神经网络将更专注于从有判别性的局部区域学习分类的细节。为此，本文提出空间混乱模块，对输入图像进行碎片化打乱重组。
如图1所示，本文定义的局部区域随机重组模块将会对输入图像的局部区域进行打乱重组，得到新的局部区域无关联性的图像。这个模块的输入是一张图片I，图片的边长n(输入图片应该为经过大小归一化处理的正方形，故只需要边长即可)和划分粒度G，其中I是图片的三维向量，n代表图片的边长，即图片的尺寸是n×n像素，G代表将图片划分为G×G个子区域。首先，每个区域标记为R(k) ，k是将子区域划分后的一维排序的序号，
${1} \leqslant k \leqslant G^2$ ，子区域也可以用R(i，j)表示，i和j分别表示行索引和列索引，$1 \leqslant i,j \leqslant G$ 。可以通过i，j来表示k，具体为$$ k=i \times G+j,l \leqslant i,j \leqslant G $$ (1) 
图 1 空间混乱模块的流程Fig. 1 Process of regions shuffle
下载:
全尺寸图片
图片大小和粒度相除可得到子区域的边长s，即子区域的尺寸是s×s。利用边长s可以计算第i行第j列的子区域的图片的三维向量，用d来表示向量的维度，具体为
$$ {\boldsymbol{R}}(k)={\boldsymbol{R}}(i,j)-I[is:(i+1)s][js:(j+1)s]$$ (2) 将划分好的有序子区域进行随机化，生成一个长度为
${{G}}^{{2}}$ 的随机向量q，第m个元素的值为r，其中$1 \leqslant {m} \leqslant {{G}}^{{2}}$ 。向量q的元素取值r，服从U(1，G2)的均匀分布，即r的值在(1，G2)的区间内等概率随机选取一个值，概率公式如式(3)所示，向量q的表示如式(4)所示。$$p(x,n)=\frac{1}{n},x=1,2,\cdots,n$$ (3) $$ {\boldsymbol{q}}[m]=r,r \sim U(1,G^2),1 \leqslant m \leqslant G^2$$ (4) 原来的子区域列表按照随机向量q进行重新排列，得到新的子区域列表，然后按照对应位置进行拼接，得到重组后的完整图像
$\overline{{\boldsymbol{I}}}$ ：$${\bar {\boldsymbol{I}}}_{i,j}={\boldsymbol{R}}({\boldsymbol{q}}[k])={\boldsymbol{R}}({\boldsymbol{q}}[i \times G+j]), 1 \leqslant i,j \leqslant G$$ (5) 空间混乱模块的流程如算法1所示：
算法 1 空间混乱算法
输入 I,G,n,q
输出
$\bar {\boldsymbol{I}}$ 1) s ← n/G
2) for i= 1,2,···,G do
3) for j = 1,2,···,G for j = 1,2,···,G do
4) R(i,j) ← I[is : (i+1)s][js : (j+1)s]
5) k ←i×G+j
6) R(k) ← R(i,j)
7) end for
8) end for
9) fori= 1,2,···,G do
10) for j = 1,2, ···,G do
11) k ← i×G+j
12)
${\bar {\boldsymbol{I}}}_{i,j}$ ← Rq(k)13) end for
14) end for
该模块需要被添加在神经网络的训练初始阶段，从而引导网络去学习细粒度图像的重要细节。经过该模块处理后的局部区域混乱的图片能迫使网络寻找那些对分类有帮助的局部区域，并从这些局部区域中学习到相应的特征。
本模块的粒度参数的设置和添加轮次的选择将会在第4节实验部分给予详细说明。
3. 融入多粒度思想
粒计算是一种粒化的思维方式及方法论，粒计算中的多粒度思想可以看作是用一种基于多层次与多视角的问题求解方法。 给神经网络输入的数据集中的原始图片就可以看成最粗粒度的信息，本文第2节所述的空间混乱模块从粒计算角度来看，是将图像的粒度细化，得到更细粒度的信息的过程。
细粒度图像分类数据集中的物体外形都是相似的，可能只有很小的部位不同。比如CUB200数据集中，不同鸟类可能只是眼睛颜色不同或者翅膀的形状不同，能正确决定分类结果的就是一些有判别力的局部区域，但这些局部区域有大有小，比如翅膀相对眼睛是较大的，那么翅膀的形状在粒度较大的局部区域容易被神经网络所捕捉到，而眼睛在粒度较小的局部区域才会被网络发现是具有判别力的特征。
前文所述的空间混乱模块，是希望网络忽视图像的整体关联性，专注于学习如何寻找具有判别力的局部区域，但是，具有判别力的局部区域可能并不都在一个粒度层次上。本文引入空间混乱模块的作用其一就是希望网络不会仅仅学习到原始图像的最粗粒度的特征，也能学习到如何去寻找小的局部区域的有用特征。
由于图像分辨率不同以及待分类物体在图像中的占比大小不同，导致即使进行空间混乱模块后，同一类别的图像得到的局部区域代表的特征意义依然不同。如图2所示，同一类别下的图像中的物体由于大小和占比不同，经过空间混乱模块后得到的局部区域代表的部位意义也是有所区别的，上面的图片网络明显可以学习到头部级别的信息，下面的图片网络更关注的会在眼睛和喙。如果能在此基础上将图片通过其他粒度的空间混乱模块后，每个粒度做独立的引导，那么模型可以在不同的粒度学习到更多信息，做决策时将更加鲁棒。
图 2 同一类别下的不同图片经过空间混乱模块后的结果Fig. 2 Results of two images from the same category after regions shuffle下载:
全尺寸图片
综上所述，对第2节中提出的空间混乱模块融入多粒度思想进行改进。原始图像是粒度最大的，网络最容易从中学到整体轮廓这种物体级别的特征，但细粒度图像分类的模型只学习到大体轮廓是难以获取到较好的分类结果的。将空间混乱模块的粒度参数设置为不同的值，随着划分粒度的增加，模型将能关注到越来越微小的局部区域信息。
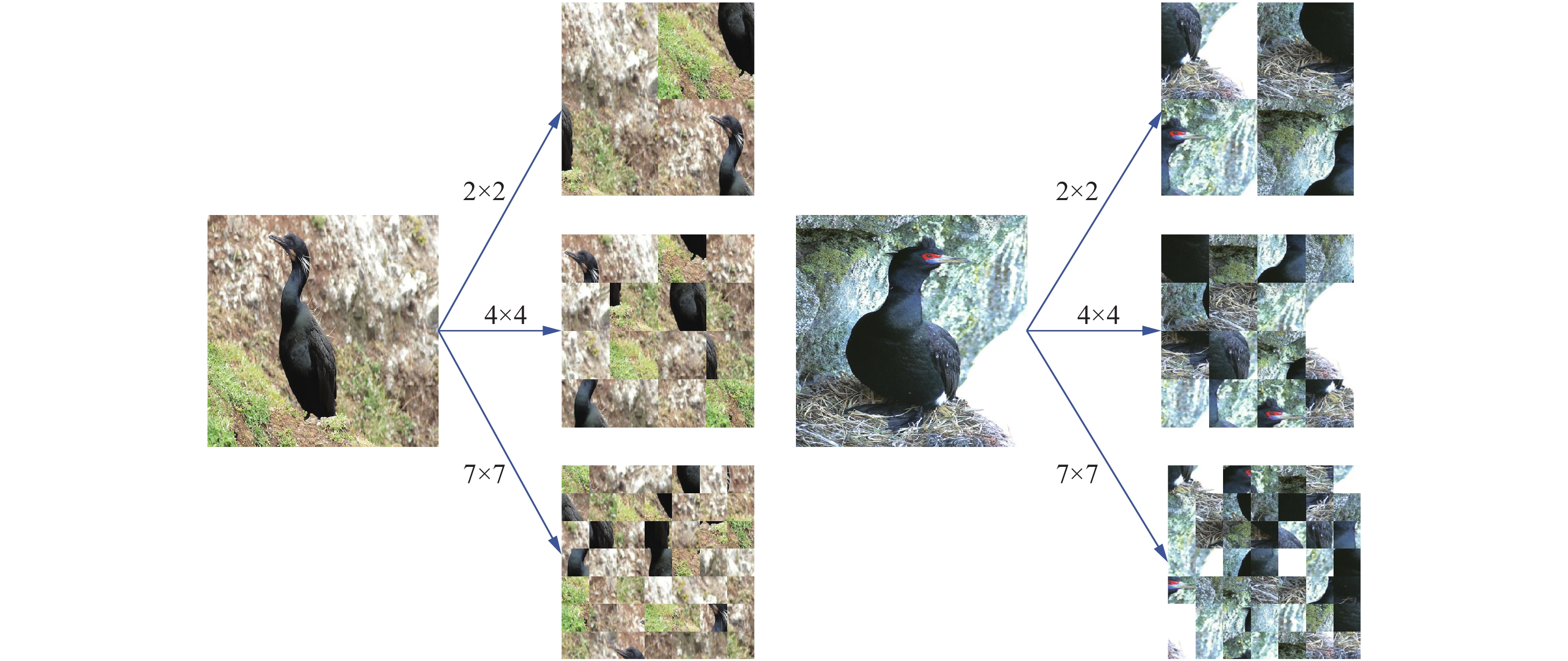
图3演示了当把空间混乱模块的粒度参数分别设为2、4、7的时候，同一输入的图像所能获得的不同粒度下的结果。图3中的两个原始图像属于两个不同的子类别，两个子类别细致的差异在于其中一个类别的鸟类面部是红色的，而另一个是黑色的且颈部有不同，除此之外的体型轮廓、大致颜色都是相近的。通过不同粒度的划分，可以明显观察到，经过粒度为2的空间混乱模块的结果可以从头部进行一定程度的区分，但差异性并不大，因为头部形状是相近的。但在经过粒度为4的空间混乱模块后，左图的第1行、第1列和右图的第3行、第4列有明显不同，可以区分，网络学习到如何在这个粒度下找到这两个判别性的区域将会对分类有非常大的帮助。这是单一粒度的空间模块所不能实现的效果。
图 3 图片经过不同粒度的空间混乱模块得到的结果Fig. 3 Results of the image after regions shuffle of different granularity下载:
全尺寸图片
4. 实验与结果
本节将通过实验阐述本文提出的技术的可行性和效果。具体包括使用本文提出的技术构建了一个模型，并且在3个标准细粒度图像分类数据集上评估了模型的性能，与其他主流算法的效果进行对比，并添加消融实验验证各模块的效果，实验过程中没有使用任何部位标注信息。
4.1 实验数据集
本次实验在3个细粒度图像分类数据集进行。3个数据集分别是CUB-200-2011鸟类数据集[26]、FGVC Aircraft飞机数据集[27]和Stanford Cars车类数据集[28]。表1展示了3个数据集的详细信息。
表 1 细粒度图像分类数据集Table 1 Fine-grained visual classification datasets数据集 类别数 训练数 测试数 CUB-200-2011 200 5 994 5 794 Stanford Cars 196 8 144 8 041 FGVC-Aircraft 100 6 667 3 333 4.2 实验细节
实验环境：本文实验所使用的深度学习框架是PyTorch，使用的显卡是Tesla V100。
实验参数细节：模型分别采用两种骨干网络，即 ResNet-50[29]和VGG-16[30]，这两个骨干网络均采用ImageNet数据集进行预训练。训练所使用的唯一标注信息是图像的类别标注信息。输入图片将被调整为512×512的固定大小，然后随机裁剪成448×448。 图像的数据增强操作包括随机水平翻转和随机旋转。 模型采用的优化器是随机梯度下降法(stochastic gradient descent, SGD)，其中动量参数设置为0.9，学习衰减率为0.000 1。训练的最大迭代轮次(Epoch)设为180，小批量样本数(mini-batch size)设为6，初始学习率设为0.001，并且每60轮衰减一次，衰减权重0.1。
多粒度空间混乱模块参数设置：粒度层次为3，具体粒度分别为2、4、7。多粒度空间混乱模块在第90轮开始加入到网络中，前90轮不使用多粒度空间混乱模块。测试阶段不使用该模块。
4.3 实验结果
首先对于多粒度空间混乱模块的参数设置都是经过实验得出的，主要包括使用轮次选择和多粒度空间混乱模块的粒度选择。多粒度空间混乱模块不适用于所有轮次，会增加噪声，不利于模型分类精度的提高，根据先整体后局部的思想和先局部后整体的思想分别进行了实验，先整体后局部的思想的具体实施是前90轮次禁用该模块， 90~180轮次采用该模块；先局部后整体的思想是前90轮次采用该模块 ，90~180轮次禁用该模块，最后得出最佳的方案是前90轮次禁用该模块，90~180轮次采用该模块。这说明模型先学习整体特征再学习局部区域特征是一种更有效的学习顺序。进行粒度选择分为粒度层次的选择和粒度组合的选择。粒度层次过多则模型复杂度会过大，并且随着粒度层次的增加并不会带来明显的准确度提升，通过尝试2层、3层和4层3种粒度层次，发现3层时效果最好。确定粒度层次后，还要选择具体的粒度组合，实验使用2、4、7、14这4种粒度进行组合，最大的粒度为14 ，因为更大的粒度将使图片完全混乱，对网络没有帮助反而降低网络的分类准确率。具体实验结果如表2所示，采用数据集为CUB-200-2011。
表 2 不同粒度的结果Table 2 Results of different granularity combination粒度组合 加入轮次 准确率/% (2, 7) 90~180 87.9 (2, 4) 90~180 87.8 (4, 7) 90~180 87.7 (4, 14) 90~180 87.6 (4, 7, 14) 0~90 88.0 (2, 4, 14) 0~90 88.1 (2, 7, 14) 0~90 88.1 (2, 4, 7) 0~90 88.3 (4, 7, 14) 90~180 88.1 (2, 4, 14) 90~180 88.4 (2, 7, 14) 90~180 88.4 (2, 4, 7) 90~180 88.6 进行消融实验，来体现多粒度空间混乱模块对于模型分类准确度的贡献，在加了粒度为4的空间混乱模块后，网络分类的准确率提高了2.0%，引入多粒度思想后，网络分类的准确率提高了3.1% ，采用数据集为CUB-200-2011，如表3所展示。
表 3 消融实验Table 3 Ablation experiment方法 准确率/% ResNet-50 85.5
87.5
88.6+Regions Shuffle +Multi-granularity 实验采用的模型无需任何部位级别标注，相对于其他需要对物体或部位进行定位或者采用多级网络的方法，空间复杂度和时间复杂度都有一定程度的降低，并且依然可以有较好的分类准确度。其中使用ResNet-50作为骨干网络时的准确率优于其他算法，对比其他算法的准确率如表4所示。
表 4 对比结果Table 4 Comparison results模型 鸟类数据集/% 飞机数据集/% 车类数据集/% Bilinear-CNN 84.1 84.1 91.3 KP 86.2 86.9 92.4 MA-CNN 86.5 89.9 92.8 PC 86.9 89.2 92.9 DFL-CNN 87.4 92.0 93.8 NTS-Net 87.5 91.4 93.9 DCL 87.8 92.2 94.5 Ours 88.6 92.8 94.7 5. 结束语
本文提出了多粒度空间混乱模块。 多粒度空间混乱模块是一个轻量级的模块，不会引入过多开销，但是可以通过引导网络学习寻找不同粒度下的判别性区域，来提高网络分类的准确率，是简单且实用的。未来会考虑不只在原始图像上进行随机打乱重组的操作，也在网络中的某一层的特征表示上进行一些混淆操作。.
-
图 1 空间混乱模块的流程
Fig. 1 Process of regions shuffle
下载:
全尺寸图片
图 2 同一类别下的不同图片经过空间混乱模块后的结果
Fig. 2 Results of two images from the same category after regions shuffle
下载:
全尺寸图片
图 3 图片经过不同粒度的空间混乱模块得到的结果
Fig. 3 Results of the image after regions shuffle of different granularity
下载:
全尺寸图片
表 1 细粒度图像分类数据集
Table 1 Fine-grained visual classification datasets
数据集 类别数 训练数 测试数 CUB-200-2011 200 5 994 5 794 Stanford Cars 196 8 144 8 041 FGVC-Aircraft 100 6 667 3 333 表 2 不同粒度的结果
Table 2 Results of different granularity combination
粒度组合 加入轮次 准确率/% (2, 7) 90~180 87.9 (2, 4) 90~180 87.8 (4, 7) 90~180 87.7 (4, 14) 90~180 87.6 (4, 7, 14) 0~90 88.0 (2, 4, 14) 0~90 88.1 (2, 7, 14) 0~90 88.1 (2, 4, 7) 0~90 88.3 (4, 7, 14) 90~180 88.1 (2, 4, 14) 90~180 88.4 (2, 7, 14) 90~180 88.4 (2, 4, 7) 90~180 88.6 表 3 消融实验
Table 3 Ablation experiment
方法 准确率/% ResNet-50 85.5
87.5
88.6+Regions Shuffle +Multi-granularity 表 4 对比结果
Table 4 Comparison results
模型 鸟类数据集/% 飞机数据集/% 车类数据集/% Bilinear-CNN 84.1 84.1 91.3 KP 86.2 86.9 92.4 MA-CNN 86.5 89.9 92.8 PC 86.9 89.2 92.9 DFL-CNN 87.4 92.0 93.8 NTS-Net 87.5 91.4 93.9 DCL 87.8 92.2 94.5 Ours 88.6 92.8 94.7 -
[1] 罗建豪, 吴建鑫. 基于深度卷积特征的细粒度图像分类研究综述[J]. 自动化学报, 2017, 43(8): 1306–1318.LUO Jianhao, WU Jianxin. A survey on fine-grained image categorization using deep convolutional features[J]. Acta automatica sinica, 2017, 43(8): 1306–1318. [2] ZHAO Bo, FENG Jiashi, WU Xiao, et al. A survey on deep learning-based fine-grained object classification and semantic segmentation[J]. International journal of automation and computing, 2017, 14(2): 119–135. [3] WEI Xiushen, WU Jianxin, CUI Quan. Deep learning for fine-grained image analysis: a survey[EB/OL]. (2019-07-06)[2021-05-26].https://arxiv.org/abs/1907.03069v1. [4] LECUN Y, BENGIO Y, HINTON G. Deep learning[J]. Nature, 2015, 521: 436–444. [5] BENGIO Y, SIMARD P, FRASCONI P. Learning long-term dependencies with gradient descent is difficult[J]. IEEE transactions on neural networks, 1994, 5(2): 157–166. [6] BENGIO Y, COURVILLE A, VINCENT P. Representation learning: a review and new perspectives[J]. IEEE transactions on pattern analysis and machine intelligence, 2013, 35(8): 1798–1828. [7] LANG Guangming, MIAO Duoqian, FUJITA H. Three-way group conflict analysis based on pythagorean fuzzy set theory[J]. IEEE transactions on fuzzy systems, 2020, 28(3): 447–461. [8] YUE X D, CHEN Y F, MIAO D Q, et al. Fuzzy neighborhood covering for three-way classification[J]. Information sciences, 2020, 507: 795–808. [9] CHEN Yumin, MIAO Duoqian. Granular regression with a gradient descent method[J]. Information sciences, 2020, 537: 247–260. [10] QIAN Jin, LIU Caihui, MIAO Duoqian, et al. Sequential three-way decisions via multi-granularity[J]. Information sciences, 2020, 507: 606–629. [11] 王子晔, 苗夺谦, 赵才荣, 等. 基于多粒度特征的行人跟踪检测结合算法[J]. 计算机研究与发展, 2020, 57(5): 996–1002.WANG Ziye, MIAO Duoqian, ZHAO Cairong, et al. A pedestrian tracking algorithm based on multi-granularity feature[J]. Journal of computer research and development, 2020, 57(5): 996–1002. [12] ZHANG Ning, DONAHUE J, GIRSHICK R, et al. Part-based R-CNNs for fine-grained category detection[C]//Proceedings of the 13th European Conference on Computer Vision. Zurich, Switzerland, 2014: 834–849. [13] UIJLINGS J R R, VAN DE SANDE K E A, GEVERS T, et al. Selective search for object recognition[J]. International journal of computer vision, 2013, 104(2): 154–171. [14] BRANSON S, HORN G V, BELONGIE S, et al. Bird species categorization using pose normalized deep convolutional nets[EB/OL]. (2014-06-11)[2021-05-26].https://arxiv.org/abs/1406.2952. [15] FELZENSZWALB P F, GIRSHICK R B, MCALLESTER D, et al. Object detection with discriminatively trained part-based models[J]. IEEE transactions on pattern analysis and machine intelligence, 2010, 32(9): 1627–1645. [16] HUANG Shaoli, XU Zhe, TAO Dacheng, et al. Part-Stacked CNN for Fine-Grained Visual Categorization[C]//Proceedings of 2016 IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas, America, 2016: 1173–1182. [17] LONG J, SHELHAMER E, DARRELL T. Fully convolutional networks for semantic segmentation[C]//Proceedings of 2015 IEEE Conference on Computer Vision and Pattern Recognition. Boston, America, 2015: 3431–3440. [18] LIN Di, SHEN Xiaoyong, LU Cewu, et al. Deep LAC: Deep localization, alignment and classification for fine-grained recognition[C]//Proceedings of 2015 IEEE Conference on Computer Vision and Pattern Recognition. Boston, America, 2015: 1666–1674. [19] WEI Xiushen, XIE Chenwei, WU Jianxin, et al. Mask-CNN: Localizing parts and selecting descriptors for fine-grained bird species categorization[J]. Pattern recognition, 2018, 76: 704–714. [20] WEI Xiushen, LUO Jianhao, WU Jianxin, et al. Selective convolutional descriptor aggregation for fine-grained image retrieval[J]. IEEE transactions on image processing, 2017, 26(6): 2868–2881. [21] WANG Dequan, SHEN Zhiqiang, SHAO Jie, et al. Multiple granularity descriptors for fine-grained categorization[C]//Proceedings of 2015 IEEE International Conference on Computer Vision. Santiago, Chile, 2015: 2399–2406. [22] XIAO L, XIA T, WANG J, et al. Fully convolutional attention localization networks: efficient attention localization for fine-grained recognition[EB/OL]. (2016-03-22)[2021-05-26]. https://arxiv.org/abs/1603.06765v1. [23] LIN T Y, ROYCHOWDHURY A, MAJI S. Bilinear CNN models for fine-grained visual recognition[C]//Proceedings of 2015 IEEE International Conference on Computer Vision. Santiago, Chile, 2015: 1449–1457. [24] LIN T Y, MAJI S. Improved bilinear pooling with CNNs[C]//Proceedings of the British Machine Vision Conference. London, UK, 2017. [25] CHEN Yue, BAI Yalong, ZHANG Wei, et al. Destruction and construction learning for fine-grained image recognition[C]//Proceedings of 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Long Beach, America, 2019: 5157–5166. [26] WAH C, BRANSON S, WELINDER P, et al. The caltech-ucsd birds-200-2011 dataset[R]. Pasadena: California Institute of Technology, 2011. [27] MAJI S, RAHTU E, KANNALA J, et al. Fine-grained visual classification of aircraft[EB/OL]. (2013-06-21)[2021-05-26].https://arxiv.org/abs/1306.5151. [28] KRAUSE J, STARK M, DENG Jia, et al. 3D object representations for fine-grained categorization[C]//Proceedings of 2013 IEEE International Conference on Computer Vision. Sydney, Australia, 2013: 554–561. [29] HE Kaiming, ZHANG Xiangyu, REN Shaoqing, et al. Deep residual learning for image recognition[C]//Proceedings of 2016 IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas, America, 2016: 770–778. [30] SIMONYAN K, ZISSERMAN A. Very deep convolutional networks for large-scale image recognition[EB/OL]. (2014-09-04)[2021-05-26]. https://arxiv.org/abs/1409.1556.
