Autonomous remotely operated vehicle return control in a narrow underwater environment
-
摘要: 为满足缆控水下机器人（remotely operated vehicle，ROV）在水下狭窄环境中作业完毕后的顺利回收需求，研究仿真ROV的路径跟踪以及动力定位系统。基于非对称ROV构建数学模型，利用李雅普诺夫函数，采用反向递推和反馈线性化，设计了基于反步法的自适应控制器。该控制器通过反馈线性化，将已知非线性参数转化成线性参数，不确定的非线性参数应用自适应控制律进行放宽。通过仿真对该控制器应用于ROV的可行性进行验证表明：基于反步自适应控制以及视线导引的算法，ROV在水下狭窄环境中路径跟踪效果良好，动力定位稳定，鲁棒性良好，能够很好地解决ROV模型的不确定性与非线性问题。该控制器为ROV在水下狭窄环境中的回收作业提供了很好的解决方案。Abstract: The path following and dynamic positioning systems of the simulated remotely operated vehicle (ROV) were studied to meet the successful recovery requirements of the ROV after the completion of the operation in the narrow underwater environment. On the basis of a mathematical model built by asymmetric ROV, an adaptive controller based on the backstepping method was designed using the Lyapunov function, reverse recursion, and feedback linearization. Feedback linearization converts known nonlinear parameters into linear parameters, while adaptive control laws relax uncertain nonlinear parameters. The feasibility of applying the controller to the ROV was verified by simulation. Based on the backstepping adaptive control and line-of-sight guidance algorithm, the ROV has a good path following effect in the narrow underwater environment, good robustness, and stable dynamic positioning, which can well solve the uncertainty and nonlinear problems of the ROV’s model. This controller provides an excellent solution for ROV recovery in a narrow underwater environment.
-
缆控水下机器人是海洋勘探与开发以及协助海洋大型工程等领域不可或缺的重大海洋装备之一[1]。现如今随着海洋事业的高速发展以及考虑潜水员的安全工作深度等，水下机器人需要在更深、更复杂、甚至更狭窄的环境中工作，所需要的工程装备愈发复杂，对其作业精度以及机动性的要求也越来越高，良好的控制系统是达到这些要求的基础[2]。由于自治水下机器人（autonomous underwater vehicle, AUV）对于信号处理的弱势以及需要提前路径规划的原因不适合在复杂、狭窄、未知的环境下工作[3]。因此在这类空间下的工作只有缆控水下机器人（remotely operated vehicle，ROV）才能胜任，为了安全顺利地完成任务，ROV需要具有抗干扰的控制系统以及路径跟踪算法。
ROV模型具有不确定性与非线性的特点，这需要自适应控制来加强ROV的鲁棒性，如宋大雷等[4]将无模型自适应控制方法应用于ROV定深控制当中，仿真结果表明，在定深控制当中，自适应比PID控制具有更强的抗干扰能力。但无模型仿真仅可验证控制器性能，对实际作业提供的帮助有限。霍星星等[5]针对参数变化、流以及其他未知干扰对深海作业级ROV位姿控制的影响，设计了基于模糊补偿的ROV自适应位姿控制器。结果表明该控制器具有良好的跟踪性能、抗干扰能力和鲁棒性。但该论文应用的理想对称数学模型会降低仿真精度。相较于小型观察级ROV，作业级ROV受到外界的扰动会产生较大的影响，视线导引算法（line of sight, LOS）设计简便，抗干扰能力强，控制效果出色，且在自治水下机器人方面已发展成熟，如郭亦平等[6]采用视线导引法，利用空间几何原理，将空间视线导引法的三维航迹跟踪控制转换为航向角跟踪控制与纵倾角跟踪控制，设计了纵倾模型预测控制算法。陈霄等[7]为提高风浪流等外界环境干扰下，无人水面艇路径跟踪控制的准确性和鲁棒性，提出了两种改进积分视线导引策略，并基于改进导引策略和反馈控制思想实现了无人水面艇水平面的路径跟踪。理论分析和仿真实验证明了算法的有效性和先进性。
本文针对ROV的非线性以及不确定性，采用反步自适应设计控制器，实现路径跟踪的自主返回，以及动力定位，为ROV的安全顺利回收提供了方案。本文将反步自适应控制与视线导引法结合，消除位姿、速度、航向的误差，精准跟踪原始路径，达到ROV的自主返回目的，以及运用ROV的非对称数学模型来提高仿真精度。通过仿真来验证控制器以及路径跟踪算法的可行性。
1. 数学模型
1.1 坐标系建立
如图1所示，为使描述ROV状态明了与简洁，用两个坐标系对其描述，固定坐标系{n}={N, E, D}，其中N与E构成的平面与地球表面相切。另一个坐标系则为随体坐标系{b}={xb, yb, zb}，也称为动系[8]。
图 1 坐标系与ROV运动参数Fig. 1 Coordinate system and ROV motion parameters
下载:
全尺寸图片
1.2 运动学模型
ROV随体坐标系通过绕坐标轴的3次旋转可以与固定坐标系重合[9]。因此，ROV随体坐标系下的速度与ROV相对于固定坐标系的空间位置之间的转换关系为
$$ \dot {\boldsymbol{\eta}} = {{\boldsymbol{J}}_{\boldsymbol{\Theta}} }({\boldsymbol{\eta}} ){\boldsymbol{V}} $$ 式中：
${\boldsymbol{V}} = {[ {\boldsymbol{v}}\;{\boldsymbol{\omega}} ]^{\rm{T}}}$ ，v为线速度矩阵，ω为角速度矩阵，${\boldsymbol{v}} = {[ {{u}}\;{{v}}\;{{w}} ]^{\rm{T}}}$ ，${\boldsymbol{\omega}} = {[ p\;q\;r ]^{\rm{T}}}$ ，${\boldsymbol{\Theta}} = {[ \phi \;\theta \;\psi ]^{\rm{T}}}$ 为姿态向量，$\boldsymbol {J_\Theta }({\boldsymbol{\eta}} )$ 为转换矩阵，即$$ {\boldsymbol{J_\Theta} }({\boldsymbol{\eta}} ) = \left[ {\begin{array}{*{20}{c}} {{\boldsymbol{R}}_b^n({{\boldsymbol{\Theta}} _{nb}})}&{{{\boldsymbol{O}}_{3 \times 3}}} \\ {{{\boldsymbol{O}}_{3 \times 3}}}&{{{\boldsymbol{T_\Theta}} }({{\boldsymbol{\Theta }}_{nb}})} \end{array}} \right] $$ 式中：
${\boldsymbol{R}}_b^n({{\boldsymbol{\Theta}} _{nb}})$ 为线速度转换矩阵，${\boldsymbol{T_\Theta} }({{\boldsymbol{\Theta }}_{nb}})$ 为角速度转换矩阵，ROV工作时的横摇和纵摇一般很小，因此可假设$ \phi {\text{ = }}\theta \approx 0 $ ，则${\boldsymbol{J_\Theta} }({\boldsymbol{\eta}} )$ 简化为$$ {\boldsymbol{P}}(\psi ) = \left[ {\begin{array}{*{20}{c}} {{\boldsymbol{R}}_b^n(\psi )}&{{{\boldsymbol{O}}_{3 \times 3}}} \\ {{{\boldsymbol{O}}_{3 \times 3}}}&{{{\boldsymbol{I}}_{3 \times 3}}} \end{array}} \right] $$ 1.3 动力学模型
动力学方程可以写为
$$ {\boldsymbol{M}}\dot {\boldsymbol{V}} + {\boldsymbol{C}}({\boldsymbol{V}}){\boldsymbol{V}}{{ + }}{\boldsymbol{D}}({\boldsymbol{V}}){\boldsymbol{V}} + {\boldsymbol{g}}({\boldsymbol{\eta}} ) = {\boldsymbol{\tau }} + {{\boldsymbol{\tau}} _c} $$ (1) 式中：
${\boldsymbol{M}} = {{\boldsymbol{M}}_{\rm{RB}}} + {{\boldsymbol{M}}_A}$ 为ROV的质量矩阵，${{\boldsymbol{M}}_{\rm{RB}}}$ 为ROV的刚体质量矩阵，${{\boldsymbol{M}}_A}$ 为附加质量矩阵；C(V)为科里奥利矩阵；D(V)为阻尼矩阵；${{\boldsymbol{M}}_A}$ 与D(V)将在1.5节展开；${\boldsymbol{\tau}}$ 为推进器推力（力矩）；${{\boldsymbol{\tau }}_c}$ 为流引起的外部干扰；g(η)为静力（力矩），其中W、B分别为重力与浮力的数值，xg、yg、zg为ROV的重心相对于动系的坐标，xb、yb、zb为ROV的浮心相对于动系的坐标。$$ {\boldsymbol{g}}\left( {\boldsymbol{\eta}} \right) = \left[ {\begin{array}{*{20}{c}} {(W - B)\sin (\theta )} \\ { - (W - B)\cos (\theta )\sin (\phi )} \\ { - (W - B)\cos (\theta )\cos (\phi )} \\ { - ({y_g}W - {y_b}B)\cos (\theta )\cos (\phi ) + ({z_g}W - {z_b}B)\cos (\theta )\sin (\phi )} \\ {({z_g}W - {z_b}B)\sin (\theta ) + ({x_g}W - {x_b}B)\cos (\theta )\cos (\phi )} \\ { - ({x_g}W - {x_b}B)\cos (\theta )\sin (\phi ) + ({y_g}W - {y_b}B)\sin (\phi )} \end{array}} \right] $$ 1.4 推进器模型
图 2 水平面推进器布置Fig. 2 Arrangement of horizontal thrusters下载:
全尺寸图片
下面引入推进器推力（力矩）公式
$$ {\boldsymbol{\tau }} = {\boldsymbol{TKu }}$$ 式中：T为推进器布置矩阵，K为推力系数矩阵[10]。
$$ \left\{\begin{aligned} &{\boldsymbol{K}}={\rm{diag}}\{{K}_{1},{K}_{2},\cdots ,{K}_{{r}}\}\\ &{\boldsymbol{K}}^{-1}={\rm{diag}}\left\{\frac{1}{{K}_{1}},\frac{1}{{K}_{2}},\cdots ,\frac{1}{{K}_{\text{r}}}\right\}\end{aligned} \right.$$ u为推进器的输入
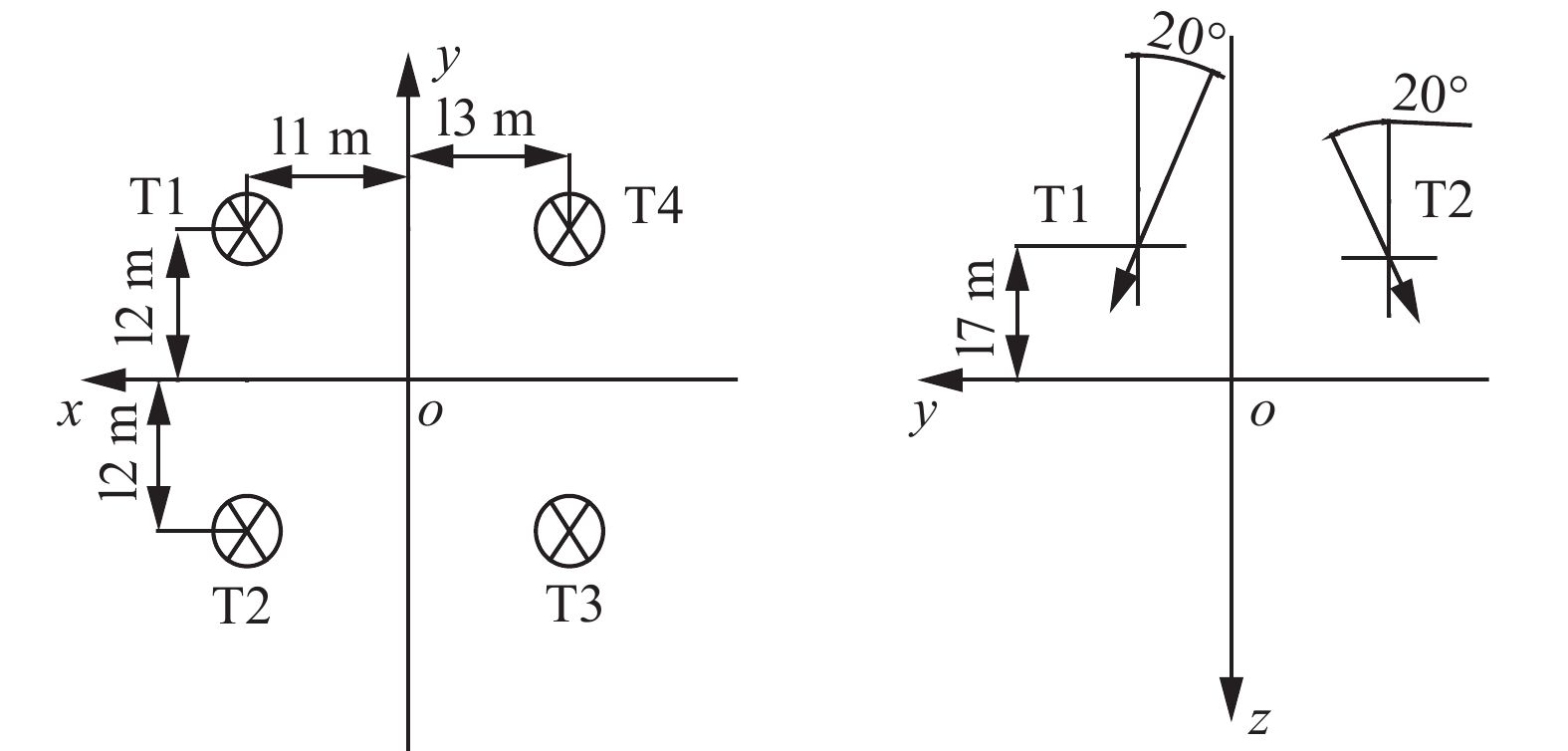
$$ {\boldsymbol{u}} = {[ {{u_1}}\;{{u_2}}\;{{u_3}}\;{{u_4}}\;{{u_5}}\;{{u_6}}\;{{u_7}}\;{{u_8}} ]^{\rm{T}}} $$ 将图2、3中推进器各位置以及角度参数代入推进器布置矩阵T，可在仿真中输出各方向推力（力矩）。
图 3 垂直面推进器布置Fig. 3 Arrangement of vertical thrusters下载:
全尺寸图片
1.5 水动力模型
1.5.1 黏性水动力
考虑到ROV的一般工作状态（大漂角以及原地回转可以忽略），忽略与角速度有关的二阶项粘性水动力，攻角与漂角的耦合在操作中很少出现，因此也进行忽略，最后通过拘束实验得出阻尼矩阵，即
$$ {\boldsymbol{D}}\left( {\boldsymbol{V}} \right){\text{ = }}\left[ {\begin{array}{*{20}{c}} {{X_{u\left| u \right|}}\left| u \right|}&0&{{X_{w\left| w \right|}}\left| w \right| + {X_{ww}}w}&0&0&0 \\ 0&{{Y_{v\left| v \right|}}\left| v \right| + {Y_{uv}}u}&0&{{Y_p}}&0&{{Y_r}} \\ {{Z_{u\left| u \right|}}\left| u \right| + {Z_{uu}}u + {Z_{u\left| w \right|}}\left| w \right| + {Z_{uw}}w}&{{Z_{v\left| v \right|}}\left| v \right| + {Z_{vv}}v}&{{Z_{w\left| w \right|}}\left| w \right|}&0&{{Z_q}}&0 \\ 0&{{K_{v\left| v \right|}}\left| v \right| + {K_{uv}}u}&0&{{K_p}}&0&0 \\ {{M_{u\left| u \right|}}\left| u \right| + {M_{uu}}u + {M_{u\left| w \right|}}\left| w \right|}&{{M_{v\left| v \right|}}\left| v \right| + {M_{vv}}v + {M_{uv}}u}&{{M_{w\left| w \right|}}\left| w \right| + {M_{ww}}w + {M_{uw}}u}&0&{{M_q}}&0 \\ 0&{{N_{v\left| v \right|}}\left| v \right| + {N_{uv}}u}&0&{{N_p}}&0&{{N_r}} \end{array}} \right] $$ 1.5.2 惯性水动力
若ROV上下、左右、前后都对称的话，附加质量矩阵除对角线之外所有项均为零。本文引用的ROV左右对称，前后上下不对称。因此只有附加质量系数λ12、λ14、λ16、λ23、λ25、λ34、λ36、λ45、λ56为零。描述惯性水动力（力矩）时，可用惯性水动力系数来代替附加质量。在水池经过纵荡、垂荡、横荡等实验，得出如下式所示的惯性水动力模型[11]：
$$ {{\boldsymbol{R}}_{\rm OV}}{{ = }}\left[ {\begin{array}{*{20}{c}} {{{{X}}_{\dot u}}}&0&0&0&0&0 \\ 0&{{{{Y}}_{\dot v}}}&0&{{{{Y}}_{\dot p}}}&0&{{{{X}}_{\dot r}}} \\ 0&0&{{{{Z}}_{\dot w}}}&0&{{{{Z}}_{\dot q}}}&0 \\ 0&{{{{K}}_{\dot v}}}&0&{{{{K}}_{\dot p}}}&0&0 \\ 0&0&{{{{M}}_{\dot w}}}&0&{{{{M}}_{\dot q}}}&0 \\ 0&{{{{N}}_{\dot v}}}&0&0&0&{{{{N}}_{\dot r}}} \end{array}} \right] $$ 本文采用的数学模型水动力参数是基于S.J [12-13]研制的作业级ROV推导出的。其外形特点为左右对称，前后以及上下均不对称。该ROV长3.5 m，宽和高均为2 m。由表1看出，ROV耦合水动力系数在关于对角线对称的项的大小是不同的，甚至有2倍的差异。因此对于一般的ROV建立数学模型时，应用非对称理论是有必要的，不可忽略。
表 1 ROV参数Table 1 ROV parameters参数 值 参数 值 m/kg 4992 $ {Y_{\dot r} } $/kg·m −2413 W/N 48972 $ {K_{\dot v} } $/kg·m −1690 B/N 49504 ${M_{\dot w} }$/kg·m −2151 Ixx/kg·m−2 6779 $ {N_{\dot v} } $/kg·m −1921 Iyy/kg·m−2 7913 $ {K_{\dot p} } $/kg·m2 −2142 Izz/kg·m−2 8624 $ {M_{\dot q} } $/kg·m2 −5486 ${X_{\dot u}} $/kg −6212 $ {N_{\dot r} } $/kg·m2 −5862 ${Y_{\dot v} } $/kg −2876 ${X_{u\left| u \right|}} $/kg·m−1 −1952 $ {Z_{\dot w} } $/kg −5883 ${Y_{v\left| v \right|}} $/kg·m−1 −2427 $ {Y_{\dot p} } $/kg·m −8525 ${Z_{w\left| w \right|} } $/kg·m−1 −3537 $ {Z_{\dot q} } $/kg·m −4533 ${N_{r\left| r \right|} } $/kg·m2 221 2. 控制系统
2.1 控制器设计
针对ROV模型不确定性和非线性的问题，通过反向递推和反馈线性化，将系统的状态向量转化为误差变量并将其线性化，设计了基于反步法的自适应控制器。通过建立子系统的李雅普诺夫函数递推出整个系统的李雅普诺夫函数，使每个子系统收敛从而保证整个系统的收敛[14]。
控制器的目标是求解出自适应更新率，使位姿误差、速度误差、以及航向误差趋于零，达到路径跟踪以及动力定位的目的。应用全局微分同胚[15]，定义ηp为6×1向量矩阵，即
$$ {{\boldsymbol{\eta}} _p} = {{\boldsymbol{P}}^{\rm{T}}}(\psi )\left[ {\begin{array}{*{20}{c}} {\boldsymbol{p}} \\ {\boldsymbol{\Theta}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{R}}^{\rm{T}}}(\psi )}&{{{\boldsymbol{O}}_{3 \times 3}}} \\ {{{\boldsymbol{O}}_{3 \times 3}}}&{{{\boldsymbol{I}}_{3 \times 3}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\boldsymbol{p}} \\ {\boldsymbol{\Theta}} \end{array}} \right] = {\boldsymbol{T}}({\boldsymbol{\eta}} ) $$ 式中：ηp为坐标系{b}上的位置和姿态信息，
${\boldsymbol{p}} = {[{{N}},{{E}},{{D}}]^{\rm{T}}}$ 。对ηp求导再应用${\bar {\boldsymbol{R}}^{\rm{T}}} = - {\boldsymbol{S}}({\boldsymbol{\omega }}){{\boldsymbol{R}}^{\rm{T}}}$ [16]和p=Rpp得到$$ {\dot {\boldsymbol{\eta }}_p} = {\boldsymbol{V}} - \left[ {\begin{array}{*{20}{c}} {{\boldsymbol{S}}({\boldsymbol{\omega}} ){{\boldsymbol{p}}_p}} \\ {{{\boldsymbol{O}}_{3 \times 1}}} \end{array}} \right] $$ 式中：S(ω)为差积算子。位姿误差以及速度误差的表达式为
$$ \left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{e}}_1}(t)} \\ {{{\boldsymbol{e}}_2}(t)} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{P}}^{\rm{T}}}(\psi )({\boldsymbol{\eta}} (t) - {{\boldsymbol{\eta}} _d}(t))} \\ {{\boldsymbol{V}}(t) - {{\boldsymbol{V}}_d}(t)} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{{\tilde {\boldsymbol{\eta}} }_p}(t)} \\ {\tilde {\boldsymbol{V}}(t)} \end{array}} \right] $$ (2) 式中：
${{\boldsymbol{e}}_1}$ 为位姿误差，${{\boldsymbol{e}}_2}$ 为速度误差，${{\boldsymbol{\eta}} _d}(t)$ 为期望位置，${{\boldsymbol{V}}_d}(t)$ 为期望速度，带有波浪线的参数指的是实际与期望的差值。2.1.1 位置与姿态的稳定性
对式（2）提出
${{\boldsymbol{e}}_1}$ 得$$ {{\boldsymbol{e}}_1} = \left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{R}}^{\rm{T}}}({\boldsymbol{p}} - {{\boldsymbol{p}}_d})} \\ {{\boldsymbol{\Theta}} - {{\boldsymbol{\Theta}} _d}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{{\tilde {\boldsymbol{p}}}_p}} \\ {\tilde {\boldsymbol{\Theta}} } \end{array}} \right] $$ 对
${{\boldsymbol{e}}_1}$ 求导得$$ {\dot {\boldsymbol{e}}_1} = \left[ {\begin{array}{*{20}{c}} {\tilde {\boldsymbol{v}} - {\boldsymbol{S}}(\tilde {\boldsymbol{\omega}} ){{\tilde {\boldsymbol{p}}}_p}} \\ {\tilde {\boldsymbol{\omega}} } \end{array}} \right] $$ (3) 定义第一个李雅普诺夫函数V1
$$ {{\boldsymbol{V}}_1}({{\boldsymbol{e}}_1},t) = \frac{1}{2}{\boldsymbol{e}}_1^{\rm{T}}{{\boldsymbol{e}}_1},{{\boldsymbol{V}}_1} \geqslant 0, \forall {{\boldsymbol{e}}_1} $$ 对时间求导，将式（3）代入得
$$ {\dot {\boldsymbol{V}}_1}({{\boldsymbol{e}}_1},t) = \left[ {\begin{array}{*{20}{c}} {\tilde {\boldsymbol{p}}_p^{\rm{T}}\tilde {\boldsymbol{v}} - \tilde {\boldsymbol{p}}_p^{\rm{T}}{\boldsymbol{S}}(\tilde {\boldsymbol{\omega}} ){{\tilde {\boldsymbol{p}}}_p}} \\ {{{\tilde {\boldsymbol{\theta}} }^{\rm{T}}}\tilde {\boldsymbol{\omega}} } \end{array}} \right] $$ 因为
$\tilde {\boldsymbol{p}}_p^{\rm{T}}{\boldsymbol{S}}(\tilde {\boldsymbol{\omega}} ){\tilde {\boldsymbol{p}}_p} = 0$ ，所以上式简化为$$ {\dot {\boldsymbol{V}}_1}({{\boldsymbol{e}}_1},t) = {\boldsymbol{e}}_1^{\rm{T}}{{\boldsymbol{e}}_2} $$ 式中：
${{\boldsymbol{e}}_2} = {\left[ {\tilde {\boldsymbol{v}}}\;{\tilde {\boldsymbol{\omega}} } \right]^{\rm{T}}}$ 通过选择${\boldsymbol e}_{2}\text{=}－{\boldsymbol{K}}_{1}{\boldsymbol e}_{1}$ 作为虚拟输入，其中K1=KT>0为6×6正定矩阵，上式变成$$ {\dot {\boldsymbol{V}}_1}({{\boldsymbol{e}}_1},t) = - {\boldsymbol{e}}_1^{\rm{T}}{{\boldsymbol{K}}_1}{{\boldsymbol{e}}_1} \leqslant - {\lambda _{\rm min}}({{\boldsymbol{K}}_1}){\boldsymbol{e}}_1^{\rm{T}}{{\boldsymbol{e}}_1} $$ 2.1.2 速度稳定性
对式（2）提出
${{\boldsymbol{e}}_2}$ 得$$ {{\boldsymbol{e}}_2} = \left[ {\begin{array}{*{20}{c}} {\tilde {\boldsymbol{v}}} \\ {\tilde {\boldsymbol{\omega}} } \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{\boldsymbol{v}} - {{\boldsymbol{v}}_d}} \\ {{\boldsymbol{\omega}} - {{\boldsymbol{\omega}} _d}} \end{array}} \right] = {\boldsymbol{V}} - {{\boldsymbol{V}}_d} = \tilde {\boldsymbol{V}} $$ 由2.2.1节可知
${\boldsymbol e}_{2}\text{=}-{\boldsymbol{K}}_{1}{\boldsymbol e}_{1}$ 所以Vd为$$ {{\boldsymbol{V}}_d} = {{\boldsymbol{V}}_v} + {{\boldsymbol{K}}_1}{{\boldsymbol{e}}_1} $$ 式中：Vv为虚拟速度，如果V→Vv，则可满足
${\boldsymbol e}_{2}{=}-{\boldsymbol{K}}_{1}{\boldsymbol e}_{1}$ ，定义新变量${\bar {\boldsymbol{e}}_2} = {\boldsymbol{V}} - {{\boldsymbol{V}}_v}$ ，构造第2个李雅普诺夫函数：$$ {{\boldsymbol{V}}_2}({{\boldsymbol{e}}_1},{\bar {\boldsymbol{e}}_2},t) = {{\boldsymbol{V}}_1}({{\boldsymbol{e}}_1}) + \frac{1}{2}\bar {\boldsymbol{e}}_2^{\rm{T}}{\boldsymbol{M}}{\bar {\boldsymbol{e}}_2},{{\boldsymbol{V}}_2} \geqslant {{0}}, \forall {\bar {\boldsymbol{e}}_2} $$ 求导得：
$$ {\dot {\boldsymbol{V}}_2}({{\boldsymbol{e}}_1},{\bar {\boldsymbol{e}}_2},t) = - {\boldsymbol{e}}_1^{\rm{T}}{{\boldsymbol{K}}_1}{{\boldsymbol{e}}_1} + \bar {\boldsymbol{e}}_2^{\rm{T}}{\boldsymbol{M}}(\dot {\boldsymbol{V}} - {\dot {\boldsymbol{V}}_v}) $$ (4) 将式（1）代入式（4）线性化可得
$$ \begin{gathered} {\boldsymbol{M}}{{\dot {\boldsymbol{V}}}_v} + {\boldsymbol{D}}({\boldsymbol{V}}){\boldsymbol{V}} + {\boldsymbol{C}}({\boldsymbol{V}}){\boldsymbol{V}} + {\boldsymbol{g}}({\boldsymbol{\eta}} ) - {{\boldsymbol{\tau}} _c} = {{\boldsymbol{\phi}} ^{\rm{T}}}({{\dot {\boldsymbol{V}}}_v},{\boldsymbol{V}},{\boldsymbol{\eta}} ){\boldsymbol{\theta}} \end{gathered} $$ 式中：
${\boldsymbol{\phi }}$ 为已知6×11矩阵；${\boldsymbol{\theta}}$ 为体现了ROV模型的不确定性，包含未知参数、重力浮力以及流引起的外部干扰的矢量。式（4）简化为$$ {\dot {\boldsymbol{V}}_2}({{\boldsymbol{e}}_1},{\bar {\boldsymbol{e}}_2},t) = - {\boldsymbol{e}}_1^{\rm{T}}{{\boldsymbol{K}}_1}{{\boldsymbol{e}}_1} + \bar {\boldsymbol{e}}_2^{\rm{T}}({\boldsymbol{\tau }} - {{\boldsymbol{\phi}} ^{\rm{T}}}{\boldsymbol{\theta }}) $$ 因此τ为
$$ {\boldsymbol{\tau}} = - {{\boldsymbol{K}}_2}{\bar {\boldsymbol{e}}_2} + {{\boldsymbol{\phi}} ^{\rm{T}}}\hat {\boldsymbol{\theta}} $$ 式中：
$\hat {\boldsymbol{\theta}}$ 为${\boldsymbol{\theta}}$ 估计值，为自适应参数；同样K2=K2T>0为6×6正定矩阵，因此$$ {\dot {\boldsymbol{V}}_2}({{\boldsymbol{e}}_1},{\bar {\boldsymbol{e}}_2},t) = - {\boldsymbol{e}}_1^{\rm{T}}{{\boldsymbol{K}}_1}{{\boldsymbol{e}}_1} - \bar {\boldsymbol{e}}_2^{\rm{T}}{{\boldsymbol{K}}_2}{\bar {\boldsymbol{e}}_2} + \bar {\boldsymbol{e}}_2^{\rm{T}}{{\boldsymbol{\phi}} ^{\rm{T}}}\tilde {\boldsymbol{\theta}} $$ 2.1.3 整个系统的李雅普诺夫函数
定义
$\tilde {\boldsymbol{\theta}} = \hat {\boldsymbol{\theta}} - {\boldsymbol{\theta}}$ ，构造整个系统的李雅普诺夫函数$$ {{\boldsymbol{V}}_3}({{\boldsymbol{e}}_1},{\bar {\boldsymbol{e}}_2},\tilde {\boldsymbol{\theta}} ,t) = {{\boldsymbol{V}}_2} + \frac{1}{2}{\tilde {\boldsymbol{\theta}} ^{\rm{T}}}{\Gamma ^{ - 1}}\tilde {\boldsymbol{\theta}} ,{{\boldsymbol{V}}_3} \geqslant {{0}} $$ 式中：Γ=ΓT>0，为6×6正定矩阵。对时间求导得：
$$ \begin{gathered} {{\dot {\boldsymbol{V}}}_3}({{\boldsymbol{e}}_1},{{\bar {\boldsymbol{e}}}_2},\tilde {\boldsymbol{\theta}} ,t) = - {{\boldsymbol{e}}_1^{\rm{T}}}{{\boldsymbol{K}}_1}{{\boldsymbol{e}}_1} - {\bar {\boldsymbol{e}}_2}^{\rm{T}}{{\boldsymbol{K}}_2}{{\bar {\boldsymbol{e}}}_2} + {{\tilde {\boldsymbol{\theta}} }^{\rm{T}}}({\boldsymbol{\phi}} {{\bar {\boldsymbol{e}}}_2} + {\Gamma ^{ - 1}}{\dot {\tilde {\boldsymbol{\theta}}} }) \end{gathered} $$ (5) 设定M、D、g(η)、洋流Vc为常量，即以上参数的导数为零，通过构造自适应更新率
$$ {\dot {\hat {\boldsymbol{\theta}}}} = - {\boldsymbol{\Gamma}} {\boldsymbol{\phi}} {\bar {\boldsymbol{e}}_2} $$ 式（5）变为
$$ {\dot {\boldsymbol{V}}_3}({{\boldsymbol{e}}_1},{\bar {\boldsymbol{e}}_2},\tilde {\boldsymbol{\theta}} ,t) = - {\boldsymbol{e}}_1^{\rm{T}}{{\boldsymbol{K}}_1}{{\boldsymbol{e}}_1} - \bar {\boldsymbol{e}}_2^{\rm{T}}{{\boldsymbol{K}}_2}{\bar {\boldsymbol{e}}_2} $$ 应用Petros [17]中的Lemma定理，在状态空间
$\left\{ {{{\boldsymbol{e}}_1},{{\bar {\boldsymbol{e}}}_2}} \right\}$ 证明整个系统的李雅普诺夫函数的稳定性，由于初始误差有界，因此${{\boldsymbol{e}}_1},{ {\dot{\boldsymbol e}_1}},{{\bar {\boldsymbol e}}_2},{ {\dot {\bar {\boldsymbol e}}}_1} \in {{\boldsymbol{L}}_\infty }$ ，显然${\dot {\boldsymbol{V}}_3} \in {{\boldsymbol{L}}_\infty }$ ，对${\dot {\boldsymbol{V}}_3}$ 积分得$$ \int_0^\infty {{{\dot {\boldsymbol{V}}}_3}{\rm{dt}} = {{\boldsymbol{V}}_3}(\infty ) - } {{\boldsymbol{V}}_3}(0) < \infty $$ (6) 由于
${{\boldsymbol{V}}_3} \geqslant 0$ 且${\dot {\boldsymbol{V}}_3} \leqslant 0$ ，所以${{\boldsymbol{V}}_3}(\infty ) < \infty$ 。当$ t \to \infty $ 时${{\boldsymbol{V}}_3}$ 在在状态空间$\left\{ {{{\boldsymbol{e}}_1},{{\bar {\boldsymbol{e}}}_2}} \right\}$ 收敛于一个有限值，将${\dot {\boldsymbol{V}}_3}$ 代入式（6）得$$ - {{\boldsymbol{K}}_1}\int_0^\infty {{\boldsymbol{e}}_1^{\rm{T}}{{\boldsymbol{e}}_1}{\rm{d}}t - {{\boldsymbol{K}}_2}\int_0^\infty {\bar {\boldsymbol{e}}_2^{\rm{T}}{{\bar {\boldsymbol{e}}}_2}{\rm{d}}t < \infty } } $$ 由于被积项大于等于0，所以
$$ \left\{ \begin{gathered} \sqrt {\int_0^\infty {{\boldsymbol{e}}_1^{\rm{T}}{{\boldsymbol{e}}_1}} \;{\rm{d}}t }< \infty \\ \sqrt {\int_0^\infty {\bar {\boldsymbol{e}}_2^{\rm{T}}{{\bar {\boldsymbol{e}}}_2}} \;{\rm{d}}t } < \infty \\ \end{gathered} \right. $$ 由Lemma2.1可知，
${{\boldsymbol{e}}_1},{\bar {\boldsymbol{e}}_2} \in {{\boldsymbol{L}}_2}$ ，因此当$ t \to \infty $ 时，${{\boldsymbol{e}}_1},{\bar {\boldsymbol{e}}_2} \to 0$ 。航向控制推导与上述方法同理。2.2 路径跟踪
2.2.1 视线导引算法
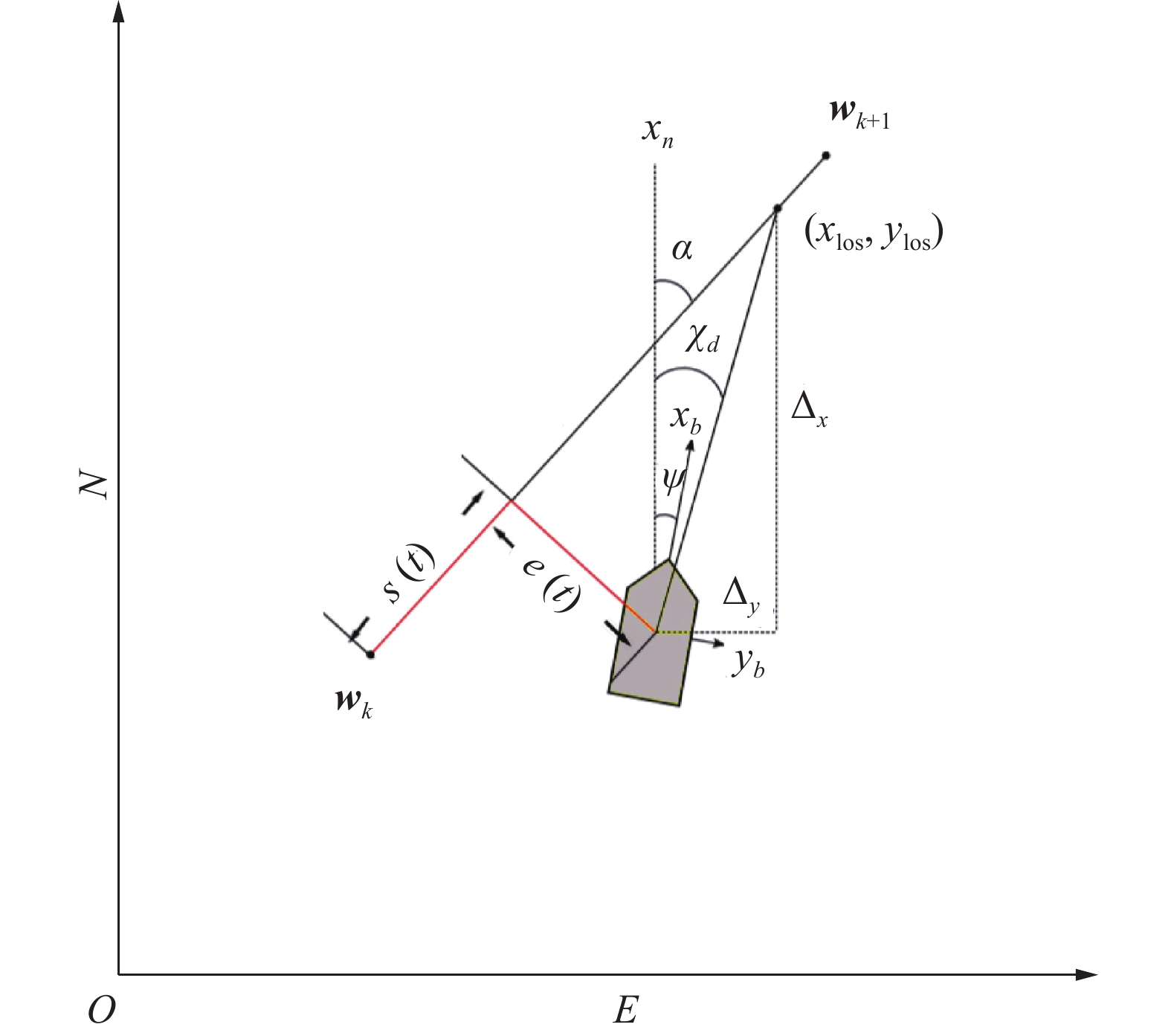
如图4所示，视线导引算法引入两个航路点wk=[xkyk]T和wk+1=[xk+1 yk+1]T。 s(t)和e(t)可从图中看出来，s(t)为以wk为原点沿着路径到e(t)与路径交点的距离，e(t)为路径与ROV的垂直距离，也就是偏航距[18]。
图 4 LOS制导示意图Fig. 4 Guidance system of the LOS下载:
全尺寸图片
要实现路径跟踪的目标为
$$ \begin{gathered} \mathop {\lim }\limits_{t \to \infty } e(t) = 0 \\ {\chi _d} = {\alpha _k} \\ \end{gathered} $$ 其中
$$ {\chi _d}(e) = {\alpha _k} + \arctan \left(\frac{{ - e}}{\varDelta }\right) $$ 式中：Δ为超前距离，即e(t)与路径的交点沿着路径向下一个航路点前进的距离。终点为(xlos, ylos)。
判定切换到下一个航路点的方法为：以ROV为圆心画一个半径一定的圆，行驶过程中航路点进入圆的范围，那么跟踪就切换到下一个航路点上，即：
$$ {\left[ {{x_{k + 1}} - x(t)} \right]^2} + {[{y_{k + 1}} - y(t)]^2} \leqslant {R^2} $$ 当跟踪到最后一个航路点时，ROV需要缓慢减速直至为零，解决方案如下式
$$ \left[ {\begin{aligned} {{u_d}} \\ {{v_d}} \end{aligned}} \right] = \left[ {\begin{aligned} { - {u_{\max }}\dfrac{s}{{\sqrt {{s^2} + \varDelta _s^2} }}} \\ { - {v_{\max }}\dfrac{e}{{\sqrt {{e^2} + \varDelta _e^2} }}} \end{aligned}} \right] $$ (7) 式中：Δs>0和Δe>0为速度调优参数。可令ROV在驶向最后一个航路点时速度平滑地下降为零。本文通过手柄操纵ROV获得轨迹上的航路点，并通过航路点进行路径跟踪实现ROV的自主返回。
2.2.2 全驱动路径跟踪模式
如图5所示，在较为狭窄的环境中，全驱动的ROV相较于欠驱动潜器[19]进行回收作业时，即无法“掉头”的环境中，可以采用“倒车”来解决，且“倒车”对于拥有中继器的ROV更容易实现回收。
图 5 狭窄路径示意图Fig. 5 Case of the narrow path下载:
全尺寸图片
3. 仿真模拟
仿真采用“手动操作+路径跟踪倒车返回+动力定位”的形式。依据水下机器人操作安全规范[20]，设定流速为0.5 m/s，与ROV初始动系纵轴夹角45°。
3.1 仿真结果与分析
本文ROV的仿真流程为：初始位置设为（0, 0, −10），通过手柄操纵ROV，再启动路径跟踪系统使ROV自动返回，当ROV返回到原点之后静置一段时间来验证动力定位系统，之后结束仿真。其中，手动操纵、路径跟踪倒车返回以及动力定位的切换时刻分别为：16 s、397 s、1137 s。控制参数、以及路径跟踪相关参数如 表2、3所示。
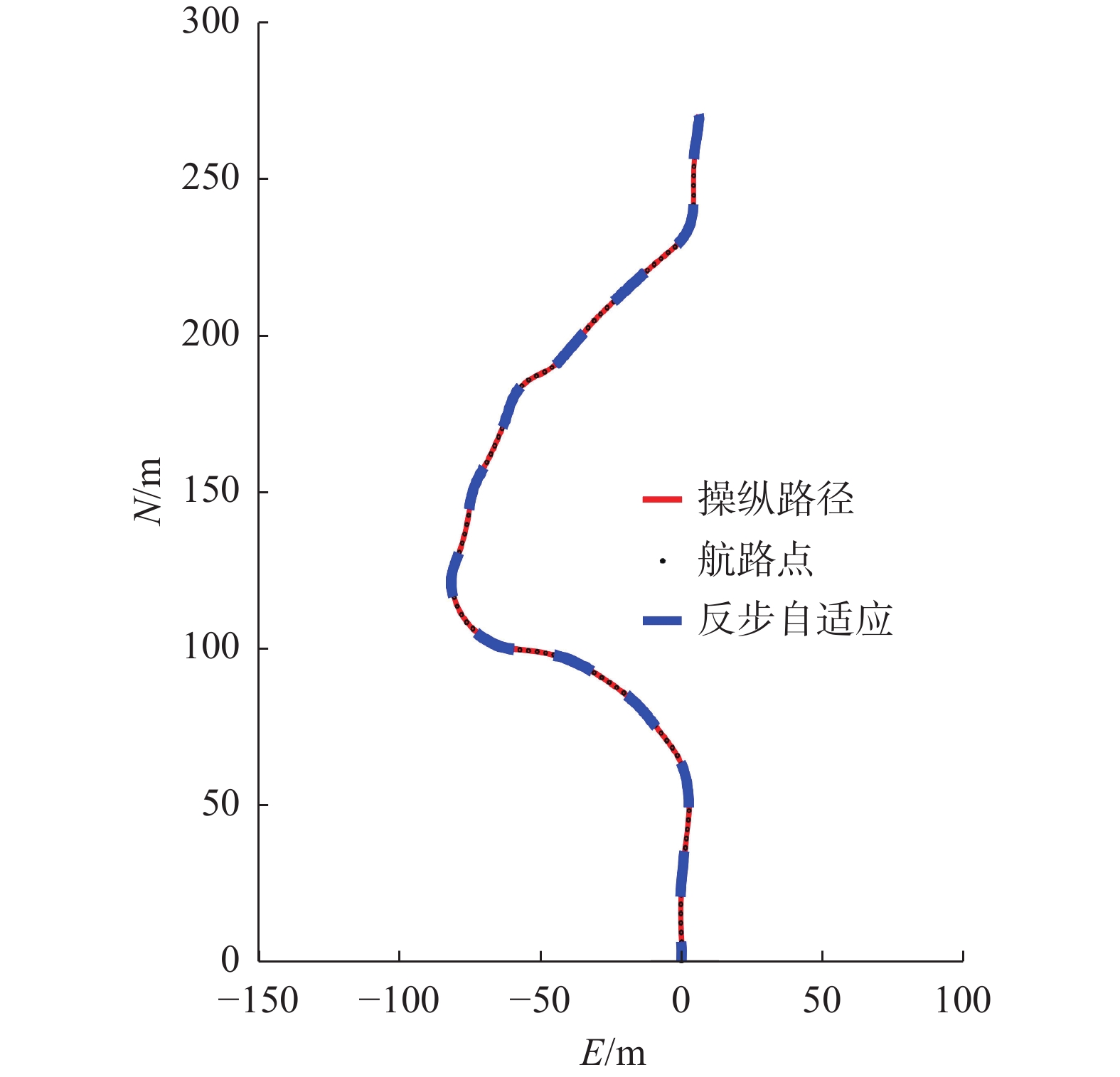
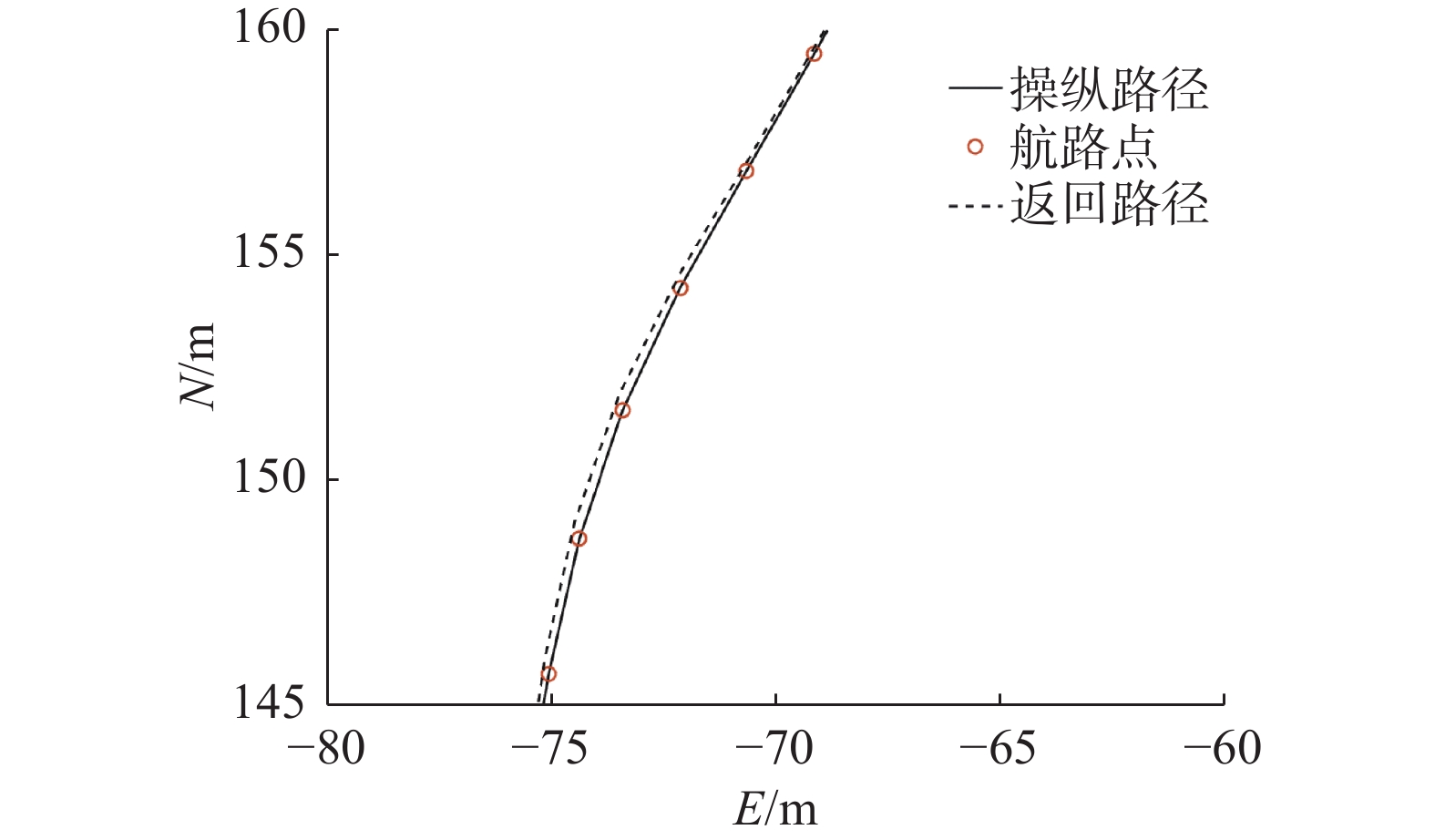
表 2 控制参数Table 2 Control parametersK1 diag{0.8949,0.9325,0.5458,0.4937,1.0239,1.0016} K2 diag{19156,10608,16065,−138323,24532,28484} Γ(0) diag{1,1,1,1} 表 3 路径跟踪的各仿真参数Table 3 Simulation parameters for path tracing参数 描述 值 R 切换半径/m 0.4 Δ 超前距离/m 20 Δs 速度调节参数 15 Δe 速度调节参数 15 图6示踪图为ROV通过手柄操纵的操纵路径、路径跟踪的返回路径，以及航路点的集合，流场方向如左下角所示。图7为示踪图的部分放大，可以清晰地看到操纵路径与返回路径仅有些许误差。
图 6 示踪图Fig. 6 Tracer figure下载:
全尺寸图片
图 7 示踪图局部放大Fig. 7 Local magnification of the tracer figure下载:
全尺寸图片
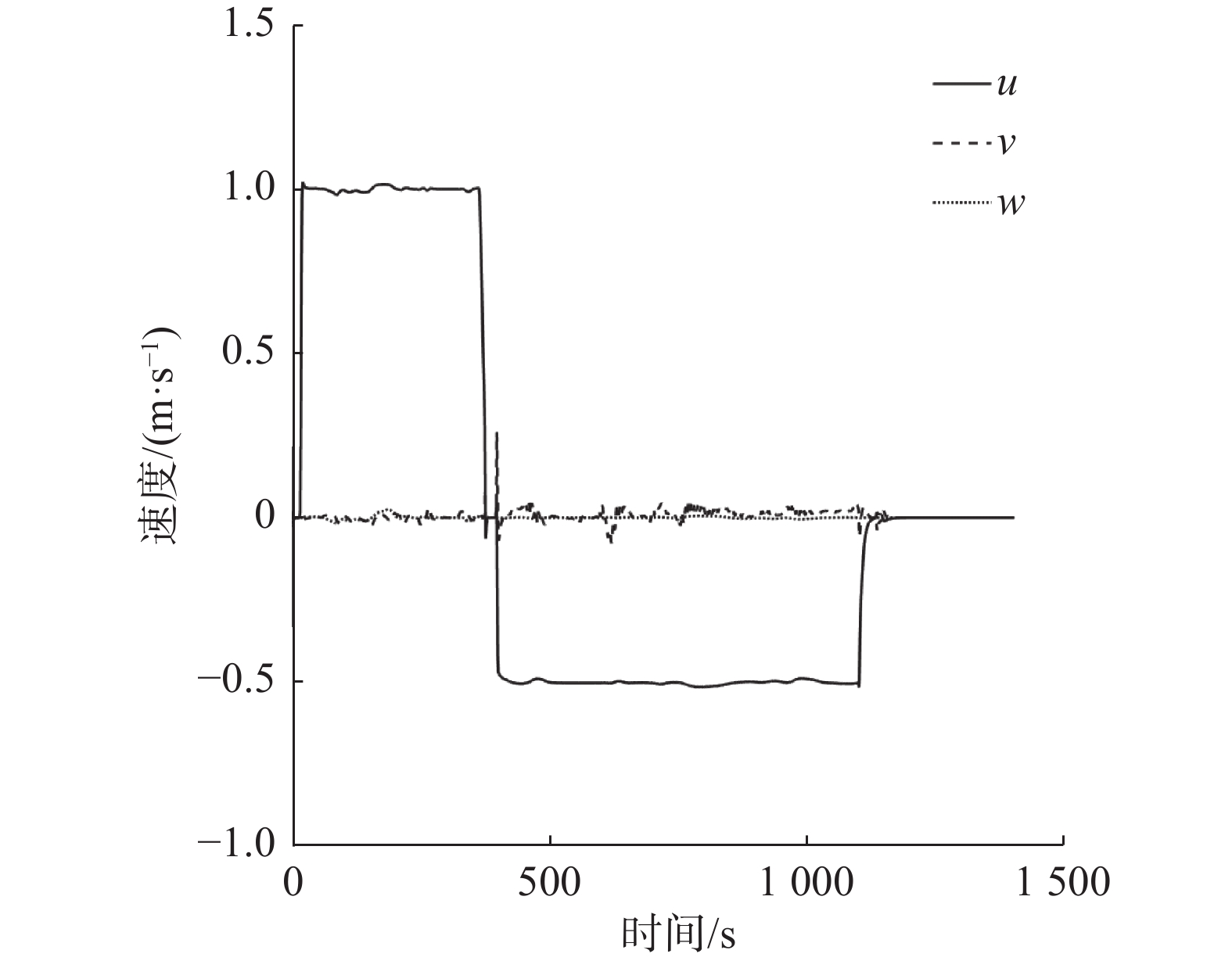
图8为ROV在仿真过程中的线速度。可以看到ROV纵向最大操纵速度为1 m/s，之后以0.5 m/s的恒定速度自主返回，在1 102 s时利用式（7）使ROV的速度平滑地减小为零。
图 8 线速度Fig. 8 Linear velocity下载:
全尺寸图片
图9展示的是ROV在仿真过程中的推力。如图9所示，在仿真过程中根据设计要求，推进器所能提供的最大推力为8 000 N，图9中的ROV推力在整个仿真过程中都在最大值以下，因此该推进器满足要求。其中3处突变是因为手柄操纵、路径跟踪、以及动力定位这3种模式进行切换造成的。
图 9 推进器推力Fig. 9 Propeller thrust下载:
全尺寸图片
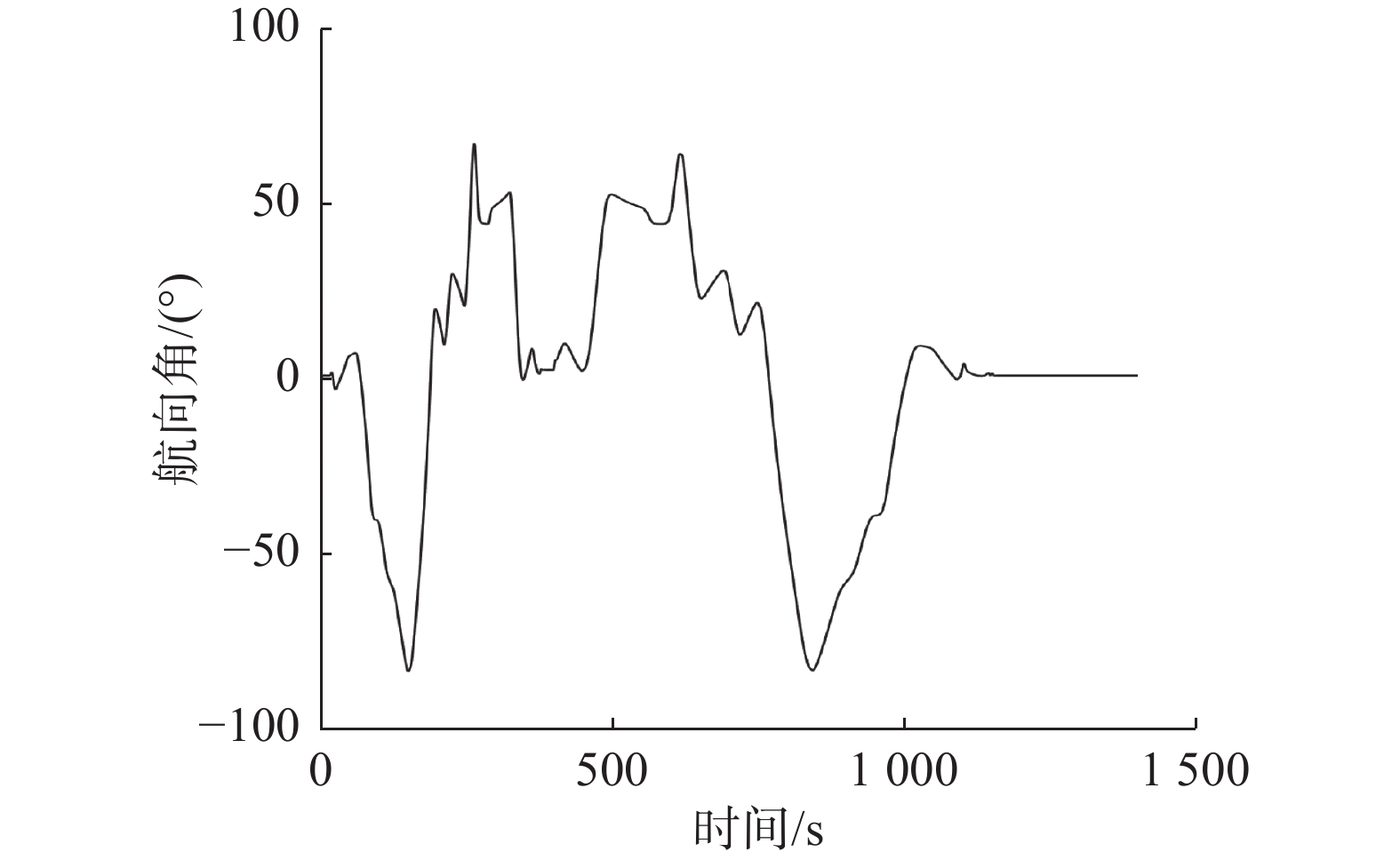
图10为操纵路径与自主返回路径之间的误差，其最大没有超过0.8 m，误差没有达到ROV宽度的一半，且这与该ROV的主尺度相比已在合理范围之内，因此该控制器与路径跟踪算法可应用到狭窄环境中，与图11结合可看出，较大误差出现在斜率较大处，即航向角变化过快处。
图 10 偏航距Fig. 10 Crosstrack error下载:
全尺寸图片
动力定位的误差可以从1 137 s之后看出，误差几乎为零，由图11的航向角看出，动力定位时航向角也几乎没有误差，说明在有海流的情况下，该控制器抗干扰能力强。
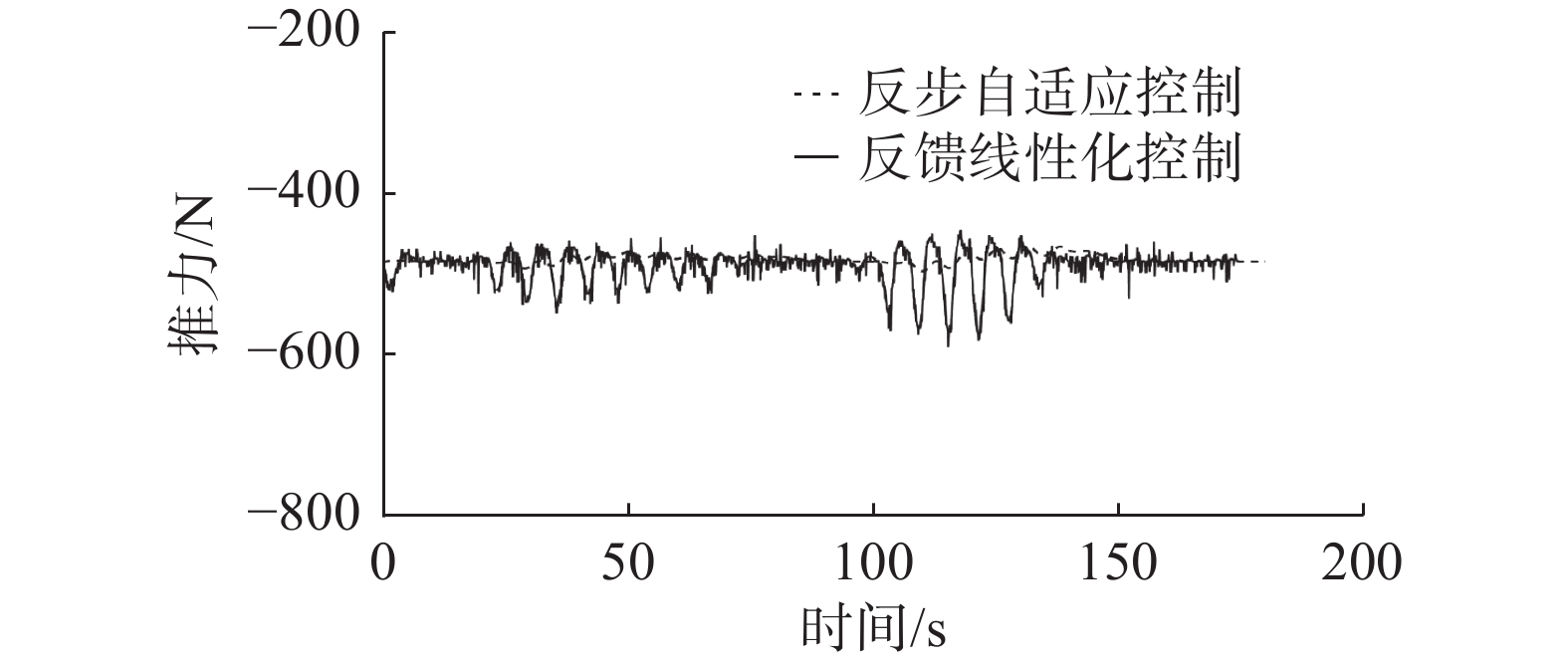
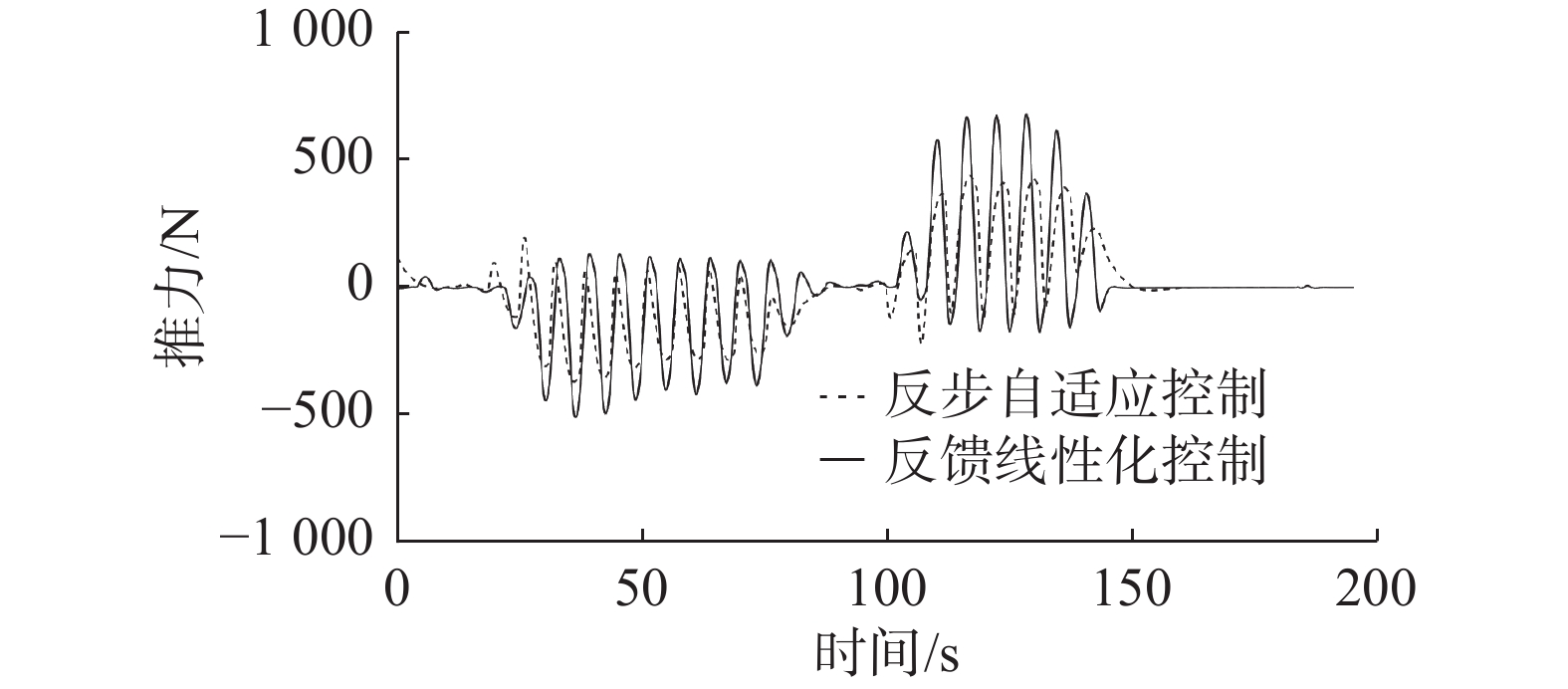
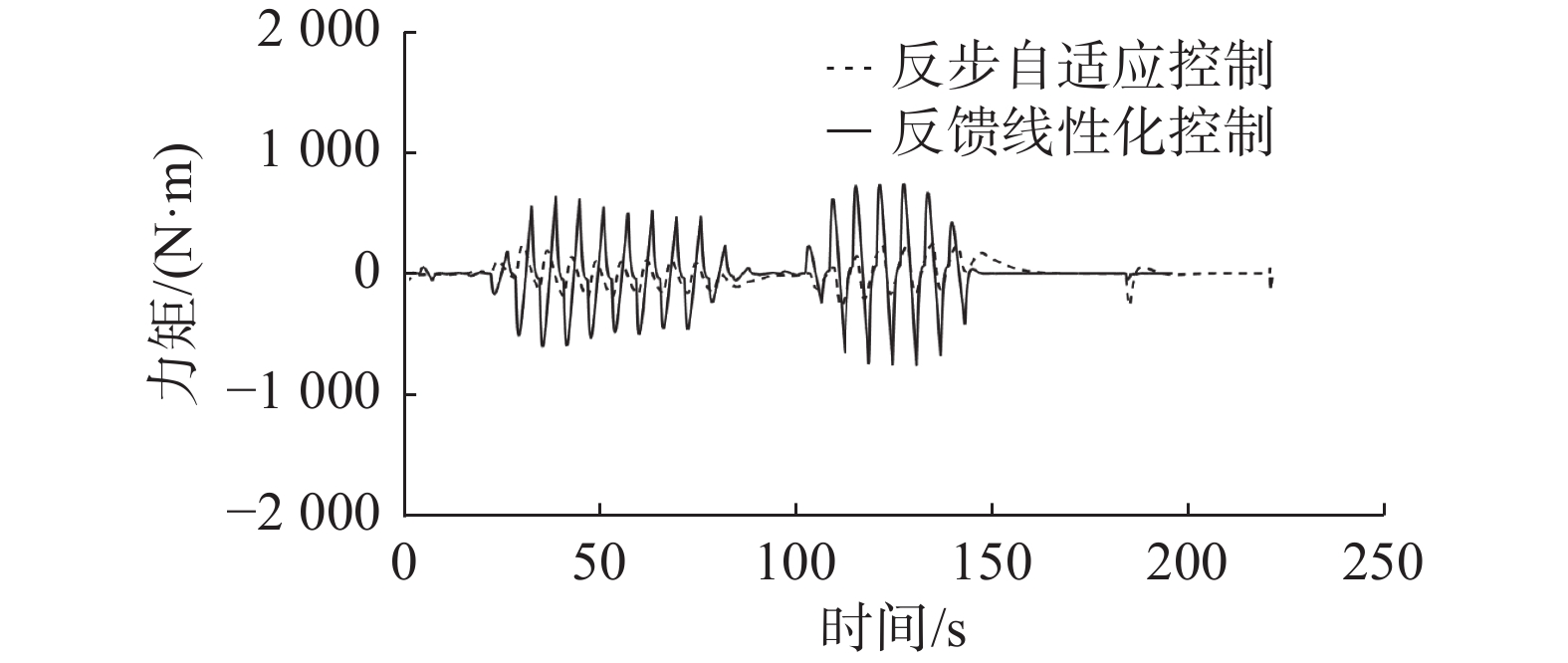
选出路径跟踪中的其中一段特征路径与未加自适应的反馈线性化控制器进行推力（力矩）的对比，如图12、13、14所示，X方向反步自适应推力变化更加平稳，在力与力矩的周期性变化区间上，反步自适应有着更小的超调量。
图 11 航向角Fig. 11 heading angle下载:
全尺寸图片
图 12 X方向推力Fig. 12 Thrust in the X direction下载:
全尺寸图片
图 13 Y方向推力Fig. 13 Thrust in the Y direction下载:
全尺寸图片
图 14 N方向力矩Fig. 14 Torque in the N direction下载:
全尺寸图片
4. 结束语
本文针对ROV的非线性以及不确定性，将反步自适应控制器与视线导引法结合，消除位姿、速度、航向的误差，精准跟踪原始路径，达到ROV的自主返回目的。通过分析路径跟踪误差与ROV本身尺度的关系，得出该控制器可在狭窄环境中完成对大型作业级ROV的自主返回控制的结论，同时在研究航向角变化中可知，为尽量减小路径跟踪误差，ROV在实际操作中的航向变化要尽量平缓一些；通过分析动力定位时的位置以及航向误差，得出在有海流的情况下，该控制器具有较强的抗干扰能力；通过推力（力矩）方面的对比得出相较于反馈线性化控制，反步自适应具有更强的稳定性。综上所述，将反步自适应控制器与视线导引法结合，可安全顺利地完成ROV在狭窄环境下的回收作业。
-
图 1 坐标系与ROV运动参数
Fig. 1 Coordinate system and ROV motion parameters
下载:
全尺寸图片
图 2 水平面推进器布置
Fig. 2 Arrangement of horizontal thrusters
下载:
全尺寸图片
图 3 垂直面推进器布置
Fig. 3 Arrangement of vertical thrusters
下载:
全尺寸图片
图 4 LOS制导示意图
Fig. 4 Guidance system of the LOS
下载:
全尺寸图片
图 5 狭窄路径示意图
Fig. 5 Case of the narrow path
下载:
全尺寸图片
图 6 示踪图
Fig. 6 Tracer figure
下载:
全尺寸图片
图 7 示踪图局部放大
Fig. 7 Local magnification of the tracer figure
下载:
全尺寸图片
图 8 线速度
Fig. 8 Linear velocity
下载:
全尺寸图片
图 9 推进器推力
Fig. 9 Propeller thrust
下载:
全尺寸图片
图 10 偏航距
Fig. 10 Crosstrack error
下载:
全尺寸图片
图 11 航向角
Fig. 11 heading angle
下载:
全尺寸图片
图 12 X方向推力
Fig. 12 Thrust in the X direction
下载:
全尺寸图片
图 13 Y方向推力
Fig. 13 Thrust in the Y direction
下载:
全尺寸图片
图 14 N方向力矩
Fig. 14 Torque in the N direction
下载:
全尺寸图片
表 1 ROV参数
Table 1 ROV parameters
参数 值 参数 值 m/kg 4992 $ {Y_{\dot r} } $/kg·m −2413 W/N 48972 $ {K_{\dot v} } $/kg·m −1690 B/N 49504 ${M_{\dot w} }$/kg·m −2151 Ixx/kg·m−2 6779 $ {N_{\dot v} } $/kg·m −1921 Iyy/kg·m−2 7913 $ {K_{\dot p} } $/kg·m2 −2142 Izz/kg·m−2 8624 $ {M_{\dot q} } $/kg·m2 −5486 ${X_{\dot u}} $/kg −6212 $ {N_{\dot r} } $/kg·m2 −5862 ${Y_{\dot v} } $/kg −2876 ${X_{u\left| u \right|}} $/kg·m−1 −1952 $ {Z_{\dot w} } $/kg −5883 ${Y_{v\left| v \right|}} $/kg·m−1 −2427 $ {Y_{\dot p} } $/kg·m −8525 ${Z_{w\left| w \right|} } $/kg·m−1 −3537 $ {Z_{\dot q} } $/kg·m −4533 ${N_{r\left| r \right|} } $/kg·m2 221 表 2 控制参数
Table 2 Control parameters
K1 diag{0.8949,0.9325,0.5458,0.4937,1.0239,1.0016} K2 diag{19156,10608,16065,−138323,24532,28484} Γ(0) diag{1,1,1,1} 表 3 路径跟踪的各仿真参数
Table 3 Simulation parameters for path tracing
参数 描述 值 R 切换半径/m 0.4 Δ 超前距离/m 20 Δs 速度调节参数 15 Δe 速度调节参数 15 -
[1] 宋宪仓, 杜君峰, 王树青, 等. 海洋科学装备研究进展与发展建议[J]. 中国工程科学, 2020, 22(6): 76–83. SONG Xiancang, DU Junfeng, WANG Shuqing, et al. Research progress of marine scientific equipment and development recommendations in China[J]. Strategic study of CAE, 2020, 22(6): 76–83. [2] 曹宏涛, 张奇峰, 唐实. 国际援潜救生及深海打捞ROV现状与关键技术[J]. 舰船科学技术, 2021, 43(23): 16–20. CAO Hongtao, ZHANG Qifeng, TANG Shi. Current status and key technologies of remotely operated vehicles in international submarine rescue and deep-sea salvage[J]. Ship science and technology, 2021, 43(23): 16–20. [3] 赵留平, 李环, 王鹏. 水下无人系统智能化关键技术发展现状[J]. 无人系统技术, 2020, 3(6): 12–24. ZHAO Liuping, LI Huan, WANG Peng. Development of key technologies for intelligent unmanned underwater system[J]. Unmanned systems technology, 2020, 3(6): 12–24. [4] 宋大雷, 路宁, 周丽芹, 等. 无模型自适应控制算法在ROV定深控制中的仿真[J]. 船舶工程, 2019, 41(9): 87–92,103. SONG Dalei, LU Ning, ZHOU Liqin, et al. Simulation of model-free adaptive control algorithm in ROV depth control[J]. Ship engineering, 2019, 41(9): 87–92,103. [5] 霍星星, 葛彤, 王旭阳. 基于模糊补偿的深海作业级远程操控潜水器自适应位姿控制[J]. 上海交通大学学报, 2017, 51(4): 403–409. doi: 10.16183/j.cnki.jsjtu.2017.04.004 HUO Xingxing, GE Tong, WANG Xuyang. Adaptive position and attitude control for deep sea work-class remotely operated underwater vehicle based on fuzzy compensation[J]. Journal of Shanghai Jiaotong university, 2017, 51(4): 403–409. doi: 10.16183/j.cnki.jsjtu.2017.04.004 [6] 郭亦平, 王益民, 林莉, 等. 基于空间视线导引法的AUV三维航迹控制技术研究[J]. 声学与电子工程, 2019(4): 28–32. GUO Yiping, WANG Yimin, LIN Li, et al. Research on AUV 3D track control technology based on spatial line of sight guidance[J]. Acoustics and electronics engineering, 2019(4): 28–32. [7] 陈霄, 刘忠, 张建强, 等. 基于改进积分视线导引策略的欠驱动无人水面艇路径跟踪[J]. 北京航空航天大学学报, 2018, 44(3): 489–499. doi: 10.13700/j.bh.1001-5965.2017.0192 CHEN Xiao, LIU Zhong, ZHANG Jianqiang, et al. Path following of underactuated USV based on modified integral line-of-sight guidance strategies[J]. Journal of Beijing university of aeronautics and astronautics, 2018, 44(3): 489–499. doi: 10.13700/j.bh.1001-5965.2017.0192 [8] FOSSEN T I. Handbook of marine craft hydrodynamics and motion control[M]. Chichester: John Wiley & Sons, Ltd, 2011. [9] 唐东生, 谷海涛, 冯萌萌, 等. 面向AUV自主回收的拖曳装置水动力特性研究[J]. 舰船科学技术, 2021, 43(5): 107–114. doi: 10.3404/j.issn.1672-7649.2021.03.021 TANG Dongsheng, GU Haitao, FENG Mengmeng, et al. Research on hydrodynamic characteristics of towing device for autonomous recovery of AUV[J]. Ship science and technology, 2021, 43(5): 107–114. doi: 10.3404/j.issn.1672-7649.2021.03.021 [10] 赵言锋, 林明星, 代成刚, 等. ROV水动力性能及推力控制分配研究与仿真[J]. 中国科学:技术科学, 2020, 50(3): 287–298. doi: 10.1360/SST-2019-0251 ZHAO Yanfeng, LIN Mingxing, DAI Chenggang, et al. Research and simulation of ROV hydrodynamic performance and thrust control distribution[J]. Scientia sinica (technologica), 2020, 50(3): 287–298. doi: 10.1360/SST-2019-0251 [11] 徐诗婧. 开架式ROV水动力特性与运动仿真研究[D]. 哈尔滨: 哈尔滨工程大学, 2018: 57−60. XU Shijing. Research on hydrodynamic performance and motion simulation for open-frame ROV[D]. Harbin: Harbin Engineering University, 2018: 57−60. [12] XU S J, MA Q W, HAN D F. Experimental study on inertial hydrodynamic behaviors of a complex remotely operated vehicle[J]. European journal of mechanics - B/fluids, 2017, 65: 1–9. doi: 10.1016/j.euromechflu.2017.01.013 [13] XU S J, HAN D F, MA Q W. Hydrodynamic forces and moments acting on a remotely operate vehicle with an asymmetric shape moving in a vertical plane[J]. European journal of mechanics - B/fluids, 2015, 54: 1–9. doi: 10.1016/j.euromechflu.2015.05.007 [14] 安顺, 何燕, 王龙金. 基于反步自适应控制算法的船舶航向控制方法[J]. 机电设备, 2020, 37(6): 65–69. doi: 10.16443/j.cnki.31-1420.2020.06.014 AN Shun, HE Yan, WANG Longjin. A ship course control approach based on backstepping adaptive algorithm[J]. Mechanical and electrical equipment, 2020, 37(6): 65–69. doi: 10.16443/j.cnki.31-1420.2020.06.014 [15] HOLDEN C, PETTERSEN K Y. Robust globally exponentially stabilizing control law for fully actuated 6-dof auvs[J]. IFAC proceedings volumes, 2007, 40(17): 343–348. doi: 10.3182/20070919-3-HR-3904.00060 [16] EGELAND O, GRAVDAHL J T. Modeling and simulation for automatic control[M]. Trondheim: Marine Cybernetics, 2002: 240−241. [17] IOANNOU P, SUN Jing. Robust adaptive control [M]. New York: Dover Publications, 2012 [18] YU Caoyang, LIU Chunhu, XIANG Xianbo, et al. Line-of-sight guided time delay control for three-dimensional coupled path following of underactuated underwater vehicles with roll dynamics[J]. Ocean engineering, 2020, 207: 107410. doi: 10.1016/j.oceaneng.2020.107410 [19] 姚金艺, 曾庆军, 赵强, 等. 全驱动型AUV三维路径跟踪控制系统设计及分析[J]. 中国舰船研究, 2019, 14(6): 22–29. doi: 10.19693/j.issn.1673-3185.01520 YAO Jinyi, ZENG Qingjun, ZHAO Qiang, et al. Design and analysis of fully-actuated AUV’s three-dimensional path tracking control system[J]. Chinese journal of ship research, 2019, 14(6): 22–29. doi: 10.19693/j.issn.1673-3185.01520 [20] 吕骥, 张洪星, 陈浩. 水下机器人(ROV)在水库大坝检测作业的安全分析[J]. 水利规划与设计, 2017(10): 112–114. doi: 10.3969/j.issn.1672-2469.2017.10.031 LYU Ji, ZHANG Hongxing, CHEN Hao. ROV safety analysis of reservoir dam inspection operation[J]. Water resources planning and design, 2017(10): 112–114. doi: 10.3969/j.issn.1672-2469.2017.10.031
