Application of improved EMD-GRU hybrid model in runoff forecasting
-
摘要: 为解决径流预测模型存在的预测精确度低、稳定性差、延时高等问题，结合门控制循环单元神经网络（gated recurrent unit, GRU）,集合经验模态分解（ensemble empirical mode decomposition, EEMD）的各自优点，提出一种基于改进EEMD方法的深度学习模型（EEMD-GRU）。该模型首先以智能算法对径流信号进行边界拓延，以解决EEMD边界效应。然后利用改进EEMD方法将径流信号分解为若干稳态分量，将各分量作为GRU模型的输入并对其进行预测。实验结果表明，与结合了经验模态分解的支持向量回归模型相比，并行EEMD-GRU径流预测模型的预测精准度、可信度和效率分别提高82.50%、144.67%和95.49%。基于EEMD-GRU的最优运算结果表明，该方法可进一步减少区域防洪的经济损失，提高灾害监管的工作效率。Abstract: Runoff prediction models suffer from low prediction accuracy, poor stability, and high delay. Combined with the advantages of gate control recurrent unit (GRU) neural network and ensemble empirical mode decomposition (EEMD), we propose a deep learning model based on the improved EEMD method (EEMD-GRU) to solve the aforementioned problems of runoff models. Our model initially uses an intelligent algorithm to extend the boundary of the runoff signal to solve the EEMD boundary effect. Subsequently, the improved EEMD method is used to decompose the runoff signals into numerous steady-state components. Each component is then used as the input in the GRU model and is predicted. The experimental results show that the prediction accuracy, credibility, and efficiency of the parallel EEMD-GRU runoff prediction model improve by 82.50%, 144.67%, and 95.49%, respectively, in comparison to the support vector regression model combined with empirical mode decomposition. The optimal calculation results based on EEMD-GRU show that this method can further reduce the economic loss of regional flood control and improve the efficiency of disaster supervision.
-
河川径流作为水循环的关键节点，对其进行精确预报具有重要意义。变化环境下径流的波动系数不断加大，极端气候背景下的径流趋势呈现更大的波动性，给径流的准确预报提出了更高的要求。如何根据不同流域，提出更加稳定、高效的预报模型，具有重要的理论意义和应用价值。
目前，以物理认识为基础的机理驱动模型和以统计科学为基础的数据驱动模型在径流预报领域取得了一定的进展。以气象数据作为输入，利用半分布式水文模型对径流进行预测，并以异常相关系数作为评估指标，实验结果表明，确定性预测精度较高[1]。将分布式水文模型和气象遥相关分析相结合，采用水文模型提供初始条件，利用遥相关指数确定气象输入，开展流域水库入库径流的长期预测[2]。然而，机理驱动模型往往存在可解释性差，主观干扰因素众多等问题。数据驱动模型可以有效缓解机理模型带来的不足[3-6]。例如，以支持向量回归 (support vector regression, SVR ) 模型预测集水区洪水发生概率，结果表明，SVR模型对于提前1~3 h的预测具有令人满意的预测性能[7]。利用自适应神经模糊推理系统（adaptive neuro-fuzzy inference system, ANFIS）对区域径流进行预测。结果表明，ANFIS模型的平均绝对误差优于其他模型[8]。然而，以统计科学为基础的数据模型往往存在预测精度低，可解释性差等问题。混合模型可有效缓解数据模型的不足。结合人工神经网络（artificial neural network, ANN）模型和Muskingum-Cunge方法，进而构建一种基于BR-ANN的洪水预报模型。研究区的验证对比结果表明，BR-ANN模型具有优越的综合预测能力[9]。将 SWAT模型与ANN模型结合并用于区域径流预测，结果表明SWAT-ANN的预测精度优于SWAT 模型[10]。结合经验模式分解（empirical mode decompostion, EMD）算法与长短时记忆神经网络（long short-term memory networks, LSTM），进而构建EMD-LSTM模型。并使用均方根误差 （root mean square error, RMSE）、决定系数、Willmott一致性指数（Willmott index, WI）和Legates-McCabe指数（legates McCabe index, LMI）作为评估标准，结果表明该方法在特大洪水年预测可靠性较高[11]。然而，EMD方法在分解过程中往往存在模态混叠和端点效应[12-14]。
针对以上问题，本文结合改进集合经验模态分解（ensemble empirical mode decomposition, EEMD）与门控制循环单元神经网络（goted recurrent unit, GRU）构建一种基于改进EEMD的神经网络模型（EEMD-GRU）。该模型将改进EEMD方法和GRU模型进行融合，同时引入并行计算思想，实现对径流的精确、高效、稳定预测。经验证，相比于结合了EMD的SVR模型，并行EEMD-GRU模型表现出更加高效、可靠的性能。
1. 相关理论
1.1 GRU深度学习
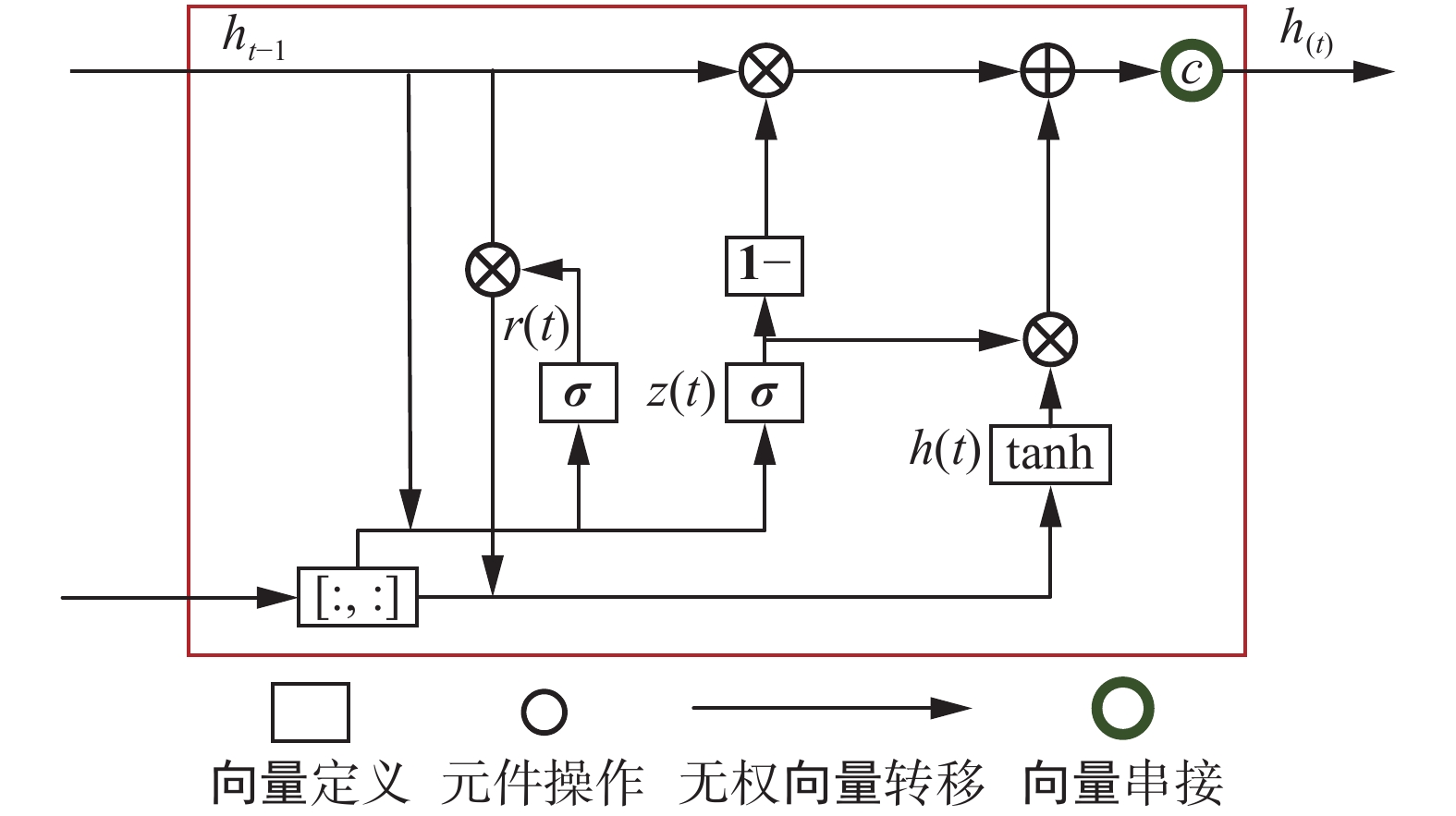
GRU基于循环神经网络。同循环神经网络相比，GRU具有计算效率高，逻辑简单等优势[15]。其基本结构如图1所示。
图 1 GRU神经元结构Fig. 1 GRU neuron structure
下载:
全尺寸图片
GRU的提出是为了克服RNN无法很好地处理远距离依赖的问题，在保持了LSTM效果的同时使结构更加简单。GRU仅保留了重置门和更新门，即图中
$ r(t) $ 和$ z(t) $ ，其中重置门输出矩阵${{\boldsymbol{r}}_{{t}}}$ 可定义为$$ {{\boldsymbol{r}}_{{t}}} = \sigma \left( {{{\boldsymbol{w}}_r} \cdot [{h_{(t - 1)}},{x_{(t)}}]} \right) $$ 式中：
${{\boldsymbol{w}}_{{r}}}$ 为重置门的权重矩阵；$ {\boldsymbol{\sigma }}$ 为sigmoid函数；$ {h_{(t - 1)}} $ 为t−1时刻的隐含状态；$ {x_{(t)}} $ 为t时刻输入数据。更新门输出矩阵${{\boldsymbol{z}}_{{t}}}$ 可定义为$$ {{\boldsymbol{z}}_{{t}}} = \sigma \left( {{{\boldsymbol{w}}_{{z}}} \cdot [{h_{(t - 1)}},{x_t}]} \right) $$ 式中：
${{\boldsymbol{w}}_{{z}}}$ 为更新门的权重矩阵；则GRU网络的输出可定义为$$ {{\hat y}_{(t)}} = \sigma ({{\boldsymbol{w}}_{{o}}}{h_{(t)}} + c) $$ 式中：
${{\boldsymbol{W}}_o}$ 为输出权重矩阵；$ c $ 为输出偏置[16-18]。1.2 集合经验模态分解
EEMD在经验模态分解的基础上，通过引入白噪声，有效消除了模态混叠现象，使得EEMD的分解结果更加具有物理意义[19-24]，集合经验模态分解的基本原理可以描述如下：
1）将正态分布的白噪声信号
$ {n_i}(t) $ 加到原始信号$ x(t) $ 得到信号$ {x_i}(t) $ ，定义为$$ {x_i}(t) = x(t) + {n_i}(t) $$ 2）将加入白噪声的信号作为一个整体，然后进行经验模态分解（EMD），得到各IMF分量，定义为
$$ {x_i}(t) = \sum\limits_{j = 1}^n {{c_{ij}}(t) + {r_i}(t)} $$ 式中：
$ {c_{ij}}(t) $ 为第i次加入白噪声后分解得到的第j个IMF分量；$ {r_i}(t) $ 是分解后的剩余分量；$ n $ 为IMF分量的个数。3）重复1）~2），对各阶分量取平均，得到最终IMF分量
$ {c_j}(t) $ 为$$ {c_j}(t) = \frac{1}{w}\sum\limits_{i = 1}^w {{x_{ij}}(t)} $$ 式中
$ w $ 为添加白噪声的次数，即总体平均数。EEMD的提出是解决EMD分解过程中出现的模态混叠现象，使得在模态分解过程中可以很好地避免IMF分量不精确等问题[25-26]。
2. 径流预报方法构建
2.1 基于智能算法的端点效应改进方案
解决集合经验模态分解边界效应的方法一般是对信号进行边界拖延。本文利用极限学习算法作为模态分解端点效应的解决方案，具体步骤如下：
1）以右边界为例，选取合适的拓延步长，作为原始信号的拓延信号序列长度；
2）将原始信号划分为测试集、训练集，进而构建极限学习预测模型；
3）将原始信号右端点利用预测模型进行预测，预测信号与原始信号合并；
4）利用相同的原理拓延原始信号的左边界。
2.2 并行EEMD-GRU径流预测方法
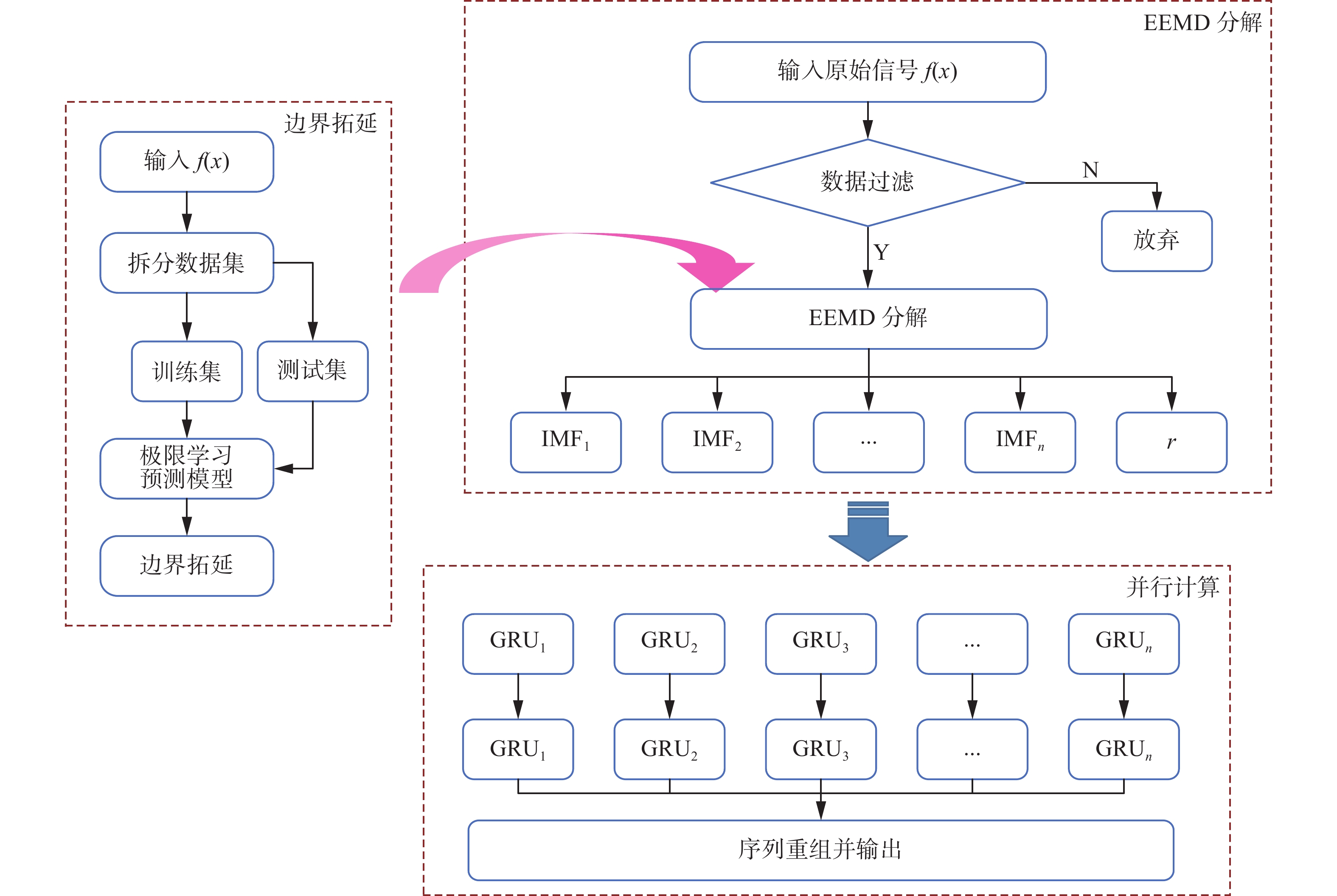
综合实时采集技术，以黄河流域部分干流共32个水文站的实际水文数据作为数据支撑，进行数据清洗、分解、预测、重构等一系列操作，最终获得高精度径流预测值，进而为水库的安全运行和区域防洪减灾提供决策支持。图2给出了并行EEMD-GRU的数据流程图，其基本实现如下。
图 2 并行EEMD-GRU流程Fig. 2 Parallel EEMD-GRU flow下载:
全尺寸图片
1) 以黄河流域部分干流为实验对象，实时采集水文站径流数据
$ f(t) $ ，通过数据清洗技术，对空数据、非数值型数据等非法数据进行过滤，然后对其进行归一化，其中归一化方程可定义为$$ {{\boldsymbol{x}}^*} = \frac{{x - \min (x)}}{{\max (x) - \min (x)}} $$ 式中：
$ \max (x) $ 为样本数据的最大值；$ \min (x) $ 为样本数据的最小值。2) 基于带外误差理论，以目标站点为基准，将目标预测站上下游水文站径流数据作为特征
${{\boldsymbol{x}}^*}$ ,对目标预测站进行特征选择。首先，将径流样本通过重复抽样的方式构建样本，训练模型，然后利用剩余样本对模型进行评估，并计算样本误差，记作$ {E_1} $ ，最后将剩余样本加入噪声，计算剩余样本的误差，记作$ {E_2} $ ，特征$f_i ({{\boldsymbol{x}}^*} )$ 的重要性可定义为$$ {f_i}({{{\boldsymbol{x}}^*}}) = \sum\limits_{i = 1}^N {\frac{{{E_2}_i - {E_1}_i}}{N}} $$ $f_i ({{\boldsymbol{x}}^*} )$ 值越大，表明特征${{{\boldsymbol{x}}^*}}$ 的重要程度越高。3) 将归一化并经过特征选择的数据首先进行边界拓延，然后进行EEMD分解，分解为若干本征模态分量，并将各分量分别拆分为训练集和测试集；
4) 对训练集与测试集进行数据划分，将过去5 d（通过实验分析，将预测集序列长度设置为5模型效果最优）设置为输入变量，分别对未来1、4、6、16、21、31 d进行预测；
5) 对预测分量进行重组，由此得到输出序列。
3. 结果和分析
本文选取黄河流域2002—2019年径流观测数据作为数据支撑，以EMD-SVR[27]和GRU[28]作为对比模型，以纳什指数(Ens)、平均绝对误差、相关误差、运行时间（run time）作为评估标准，实现对算法的可信度、稳定度、精准度和执行效率的全面评估。其中Ens纳什效率系数用于评估预测模型的可信度与稳定度。Ens取值为负无穷至1，Ens接近1，表示模式质量好，模型可信度高。相对误差和平均绝对误差分别评估实时误差与整体误差。
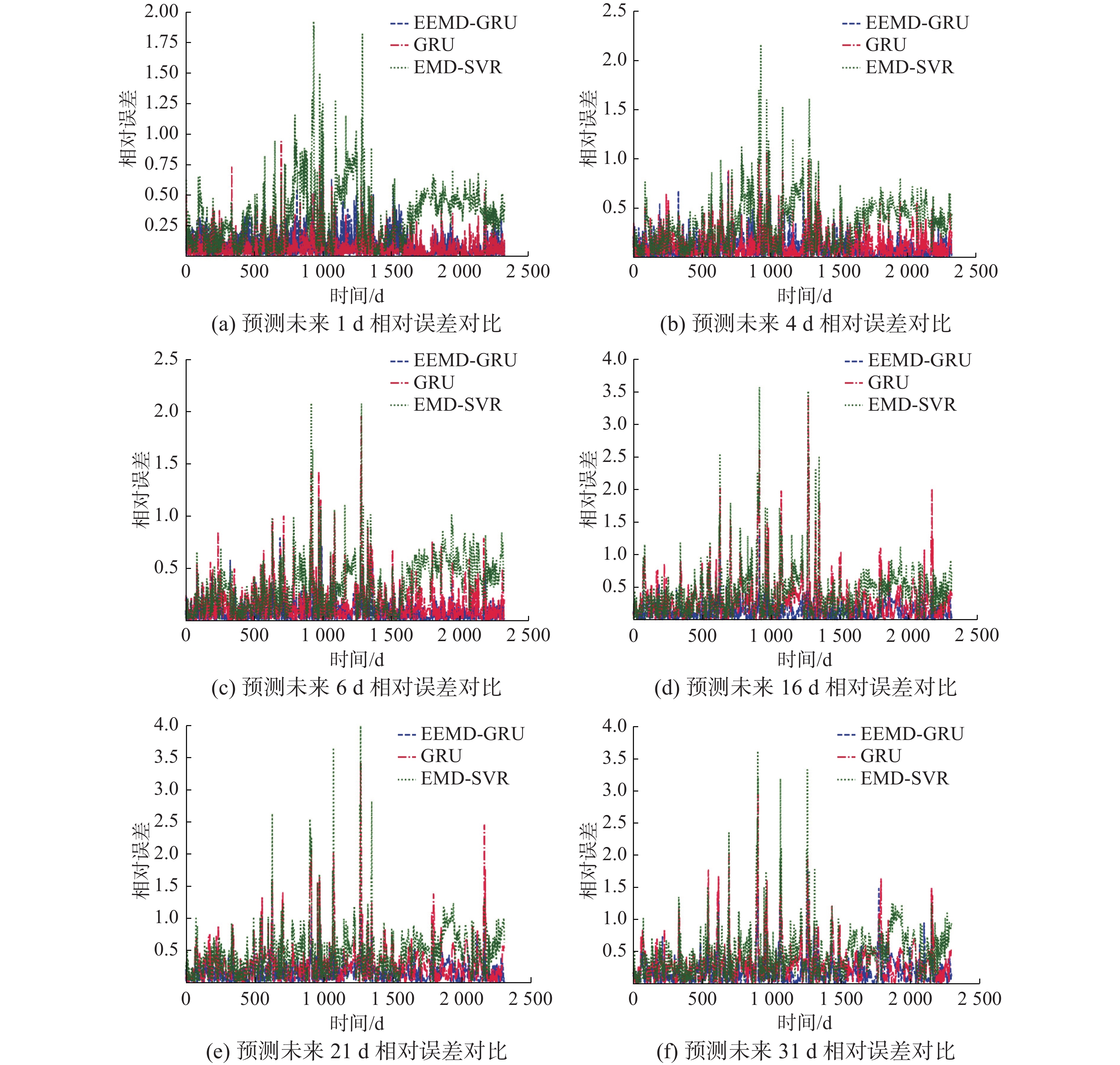
并行EEMD-GRU方法及EMD-SVR方法分别对未来1、4、6、16、21、31 d径流深度进行预测，结果如图3所示。
图 3 不同模型不同时间尺度下的预测曲线对比Fig. 3 Comparison of prediction curves under different models and different time scales下载:
全尺寸图片
根据图3可知，在低延时的未来预测中，EEMD-GRU与GRU表现能力相似，但是随着预测天数的增加，EEMD-GRU相对于GRU和EMD-SVR具有较高的精确度。由于EEMD可有效提高GRU模型的鲁棒性。使得固定未来天数，调整预测序列的特征和序列长度，EEMD-GRU相比GRU模型稳定性高。
根据图4可以了解到，EEMD-GRU相对于GRU模型和EMD-SVR模型，预测误差更小，精度更高，且相对于其他模型更加稳定。由于EMD方法存在模态混叠和端点效应，EMD-SVR模型预测精度最差。
图 4 不同模型不同时间尺度下的相对误差对比Fig. 4 Comparison of relative errors of different models and different time scales下载:
全尺寸图片
综合表1与图5，由于EEMD-GRU引入了分解合成策略，有效提高了模型的非稳态信号处理能力，模型的预测精度提高，可信度增强。算法的运行时间可以作为算法运行效率的一个衡量标准，EEMD-GRU模型相对于EMD-SVR模型由于加入了并行计算的概念，使得模型的整体预测效率提高。
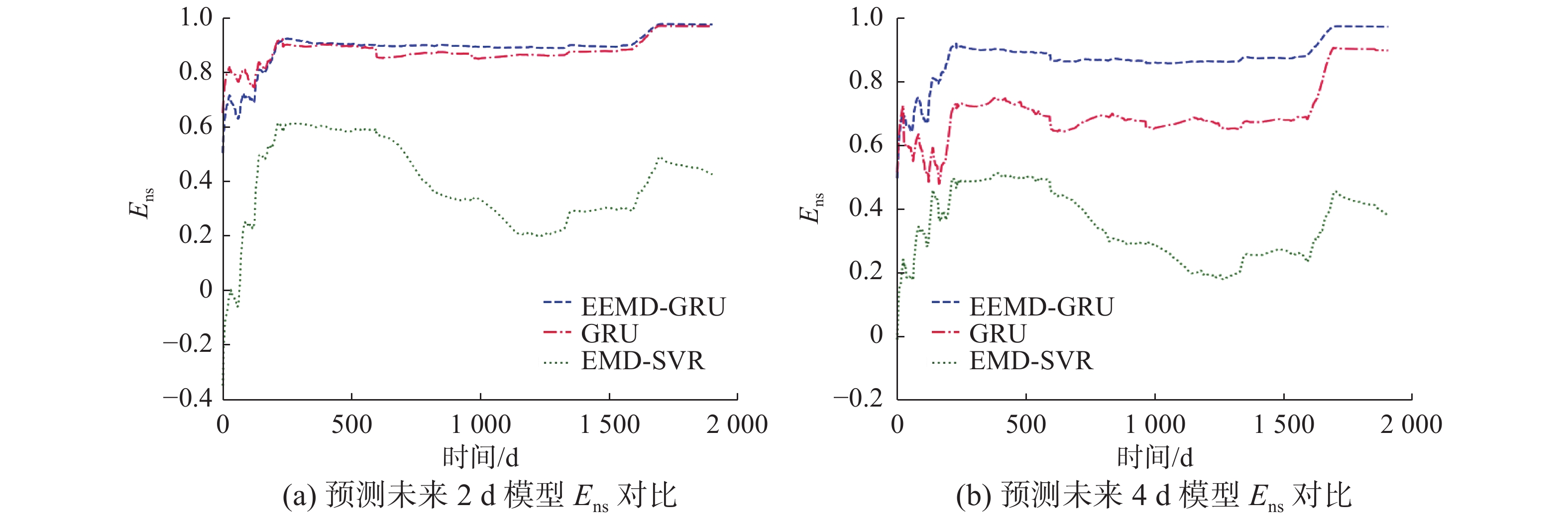
图6反应了各个算法在预测过程中的实时可信度表现。在中长期径流预测中，预见期的增加，序列的非稳态性增强，对模型的鲁棒性要求更高。预见期为未来16 d、31 d时，EMD-SVR和GRU模型相对于EEMD-GRU模型，可信度较差。
表 1 不同模型不同时间尺度下指标数值对比Table 1 Comparison of index values under different models and different time scales预见期（未来）/d 模型 Ens 平均绝对误差 运行时间/s 1 EEMD-GRU 0.986 53.275 0.062 GRU 0.953 92.375 0.781 EMD-SVR 0.403 304.371 1.374 续表 1 预见期（未来）/d 模型 Ens 平均绝对误差 运行时间/s 4 EEMD-GRU 0.963 84.841 0.046 GRU 0.882 138.948 1.062 EMD-SVR 0.348 314.534 1.687 6 EEMD-GRU 0.961 85.480 0.046 GRU 0.847 158.460 0.890 EMD-SVR 0.230 336.510 1.453 16 EEMD-GRU 0.909 126.920 0.047 GRU 0.651 242.192 0.828 EMD-SVR 0.186 360.657 1.593 21 EEMD-GRU 0.895 137.606 0.047 GRU 0.564 253.497 0.797 EMD-SVR 0.082 389.773 1.671 31 EEMD-GRU 0.824 168.525 0.062 GRU 0.419 287.513 0.797 EMD-SVR 0.047 395.967 1.656 
图 5 智能计算模型指标评估图Fig. 5 Intelligent calculation model index evaluation chart下载:
全尺寸图片
6下载:
全尺寸图片
图 6 智能计算模型${\boldsymbol{E}}_{{\boldsymbol{ns}}} $ 评估图Fig. 6 Intelligent calculation model${\boldsymbol{E}}_{{\boldsymbol{ns}}} $ evaluation chart下载:
全尺寸图片
4. 结束语
本文在模态分解方法与深度学习方法的思想上，构造了并行EEMD-GRU径流预测方法，主要结论有：
1）本文所提出的并行EEMD-GRU模型对于不同预测步长，预测时间均有有较高的精度、可信度和预测效率，预测模型具有一定的泛化性和鲁棒性，通过与原生GRU模型和EMD-SVR模型的对比中发现，所构建的混合模型精准度、可信度和效率高于其他模型。
2) 由于引入了EEMD分解算法，使得混合模型整体计算性能有所下降，虽然所引入的并行计算思想可以有效解决模型计算消耗，但随之而来的的确是内存消耗问题，希望在今后的研究中更加关注模型的高性能计算，使得模型综合能力可以进一步提升。
-
图 1 GRU神经元结构
Fig. 1 GRU neuron structure
下载:
全尺寸图片
图 2 并行EEMD-GRU流程
Fig. 2 Parallel EEMD-GRU flow
下载:
全尺寸图片
图 3 不同模型不同时间尺度下的预测曲线对比
Fig. 3 Comparison of prediction curves under different models and different time scales
下载:
全尺寸图片
图 4 不同模型不同时间尺度下的相对误差对比
Fig. 4 Comparison of relative errors of different models and different time scales
下载:
全尺寸图片
图 5 智能计算模型指标评估图
Fig. 5 Intelligent calculation model index evaluation chart
下载:
全尺寸图片
6
下载:
全尺寸图片
图 6 智能计算模型
${\boldsymbol{E}}_{{\boldsymbol{ns}}} $ 评估图Fig. 6 Intelligent calculation model
${\boldsymbol{E}}_{{\boldsymbol{ns}}} $ evaluation chart下载:
全尺寸图片
表 1 不同模型不同时间尺度下指标数值对比
Table 1 Comparison of index values under different models and different time scales
预见期（未来）/d 模型 Ens 平均绝对误差 运行时间/s 1 EEMD-GRU 0.986 53.275 0.062 GRU 0.953 92.375 0.781 EMD-SVR 0.403 304.371 1.374 续表 1 预见期（未来）/d 模型 Ens 平均绝对误差 运行时间/s 4 EEMD-GRU 0.963 84.841 0.046 GRU 0.882 138.948 1.062 EMD-SVR 0.348 314.534 1.687 6 EEMD-GRU 0.961 85.480 0.046 GRU 0.847 158.460 0.890 EMD-SVR 0.230 336.510 1.453 16 EEMD-GRU 0.909 126.920 0.047 GRU 0.651 242.192 0.828 EMD-SVR 0.186 360.657 1.593 21 EEMD-GRU 0.895 137.606 0.047 GRU 0.564 253.497 0.797 EMD-SVR 0.082 389.773 1.671 31 EEMD-GRU 0.824 168.525 0.062 GRU 0.419 287.513 0.797 EMD-SVR 0.047 395.967 1.656 -
[1] LIU Lüliu, XIAO Chan, DU Liangmin, et al. Extended-range runoff forecasting using a one-way coupled climate–hydrological model: case studies of the Yiluo and Beijiang Rivers in China[J]. Water, 2019, 11(6): 1150. doi: 10.3390/w11061150 [2] WANG Jida, SHENG Yongwei, TONG T S D. Monitoring decadal lake dynamics across the Yangtze Basin downstream of Three Gorges Dam[J]. Remote sensing of environment, 2014, 152: 251–269. [3] LIANG Zhongmin, LI Yujie, HU Yiming, et al. A data-driven SVR model for long-term runoff prediction and uncertainty analysis based on the Bayesian framework[J]. Theoretical and applied climatology, 2018, 133(1/2): 137–149. [4] SONG Peibing, LIU Weifeng, SUN Jiahui, et al. Annual runoff forecasting based on multi-model information fusion and residual error correction in the Ganjiang river basin[J]. Water, 2020, 12(8): 2086. doi: 10.3390/w12082086 [5] CHU Haibo, WEI Jiahua, LI Jiaye, et al. Improved medium-and long-term runoff forecasting using a multimodel approach in the Yellow River headwaters region based on large-scale and local-scale climate information[J]. Water, 2017, 9(8): 608. doi: 10.3390/w9080608 [6] 梁浩, 黄生志, 孟二浩, 等. 基于多种混合模型的径流预测研究[J]. 水利学报, 2020, 51(1): 112–125. LIANG Hao, HUANG Shengzhi, MENG Erhao, et al. Runoff prediction based on multiple hybrid models[J]. Journal of hydraulic engineering, 2020, 51(1): 112–125. [7] WU Jian, LIU Haixing, WEI Guozhen, et al. Flash flood forecasting using support vector regression model in a small mountainous catchment[J]. Water, 2019, 11(7): 1327. doi: 10.3390/w11071327 [8] KOVAČEVIĆ M, IVANIŠEVIĆ N, DAŠIĆ T, et al. Application of artificial neural networks for hydrological modelling in karst[J]. Građevinar, 2018, 70(1): 1–10. [9] YUAN Ximin, ZHANG Xingyuan, TIAN Fuchang. Research and application of an intelligent networking model for flood forecasting in the arid mountainous basins[J]. Journal of flood risk management, 2020, 13(3): e12638. [10] LV Zhihua, ZUO Junjie, RODRIGUEZ D. Predicting of runoff using an optimized SWAT-ANN: a case study[J]. Journal of hydrology:regional studies, 2020, 29: 100688. doi: 10.1016/j.ejrh.2020.100688 [11] LIU Darong, JIANG Wenchao, MU Lin, et al. Streamflow prediction using deep learning neural network: case study of Yangtze River[J]. IEEE access, 2020, 8: 90069–90086. doi: 10.1109/ACCESS.2020.2993874 [12] TAO Xiong, BAO Yukun, HU Zhongyi. Does restraining end effect matter in EMD-based modeling framework for time series prediction? Some experimental evidences[J]. Neurocomputing, 2014, 123: 174–184. doi: 10.1016/j.neucom.2013.07.004 [13] 舒忠平, 杨智春. 抑制经验模分解边缘效应的极值点对称延拓法[J]. 西北工业大学学报, 2006, 24(5): 639–643. doi: 10.3969/j.issn.1000-2758.2006.05.023 SHU Zhongping, YANG Zhichun. A better method for effectively suppressing end effect of empirical mode decomposition (EMD)[J]. Journal of Northwestern Polytechnical University, 2006, 24(5): 639–643. doi: 10.3969/j.issn.1000-2758.2006.05.023 [14] WU Fangji, QU Liangsheng. An improved method for restraining the end effect in empirical mode decomposition and its applications to the fault diagnosis of large rotating machinery[J]. Journal of sound and vibration, 2008, 314(3/4/5): 586–602. [15] JIN Xuebo, YANG Nianxiang, WANG Xiaoyi, et al. Hybrid deep learning predictor for smart agriculture sensing based on empirical mode decomposition and gated recurrent unit group model[J]. Sensors, 2020, 20(5): 1334. doi: 10.3390/s20051334 [16] GAO Wei, WAI R J. A novel fault identification method for photovoltaic array via convolutional neural network and residual gated recurrent unit[J]. IEEE access, 2020, 8: 159493–159510. doi: 10.1109/ACCESS.2020.3020296 [17] RADOJIČIĆ D, KREDATUS S. The impact of stock market price Fourier transform analysis on the Gated Recurrent Unit classifier model[J]. Expert systems with applications, 2020, 159: 113565. doi: 10.1016/j.eswa.2020.113565 [18] XIAO Yi, LI Keying, HU Yi, et al. Combining STRIPAT model and gated recurrent unit for forecasting nature gas consumption of China[J]. Mitigation and adaptation strategies for global change, 2020, 25(7): 1325–1343. doi: 10.1007/s11027-020-09918-1 [19] XIE Ruimin, HAO Kuangrong, HUANG Biao, et al. Data-driven modeling based on two-stream λ gated recurrent unit network with soft sensor application[J]. IEEE transactions on industrial electronics, 2020, 67(8): 7034–7043. doi: 10.1109/TIE.2019.2927197 [20] YAN Ruiqing, LIU Wei, ZHU Meng, et al. Real-time abnormal light curve detection based on a gated recurrent unit network[J]. Research in astronomy and astrophysics, 2020, 20(1): 7. doi: 10.1088/1674-4527/20/1/7 [21] DEVI A S, MARAGATHAM G, BOOPATHI K, et al. Hourly day-ahead wind power forecasting with the EEMD-CSO-LSTM-EFG deep learning technique[J]. Soft computing, 2020, 24(16): 12391–12411. doi: 10.1007/s00500-020-04680-7 [22] HASAN N. A methodological approach for predicting COVID-19 epidemic using EEMD-ANN hybrid model[J]. Internet of things, 2020, 11: 100228. doi: 10.1016/j.iot.2020.100228 [23] LIU Guancong, XIAO Xia, SONG Hang, et al. Precise detection of early breast tumor using a novel EEMD-based feature extraction approach by UWB microwave[J]. Medical and biological engineering and computing, 2021, 59(3): 721–731. [24] LIU Wei, LI Peiyao, WANG Keyu, et al. Coal-gangue interface detection based on ensemble empirical mode decomposition energy entropy[J]. IEEE access, 2021, 9: 54639–54648. doi: 10.1109/ACCESS.2021.3070447 [25] HABEN S, ARORA S, GIASEMIDIS G, et al. Review of low voltage load forecasting: methods, applications, and recommendations[J]. Applied energy, 2021, 304: 117798. doi: 10.1016/j.apenergy.2021.117798 [26] VALERO M, LI Fangyu, ZHAO Liang, et al. Vibration sensing-based human and infrastructure safety/health monitoring: a survey[J]. Digital signal processing, 2021, 114: 103037. doi: 10.1016/j.dsp.2021.103037 [27] DUAN W Y, HAN Y, HUANG L M, et al. A hybrid EMD-SVR model for the short-term prediction of significant wave height[J]. Ocean engineering, 2016, 124: 54–73. doi: 10.1016/j.oceaneng.2016.05.049 [28] GAO Shuai, HUANG Yuefei, ZHANG Shuo, et al. Short-term runoff prediction with GRU and LSTM networks without requiring time step optimization during sample generation[J]. Journal of hydrology, 2020, 589: 125188. doi: 10.1016/j.jhydrol.2020.125188
