A multi-view clustering algorithm based on deep matrix factorization with graph regularization
-
摘要: 针对现实社会中由多种表示或视图组成的多视图数据广泛存在的问题，深度矩阵分解模型因其能够挖掘数据的层次信息而备受关注,但该模型忽略了数据的几何结构信息。为解决以上问题，本文提出基于深度图正则化矩阵分解的多视图聚类算法，通过获取每个视图的局部结构信息和全局结构信息在逐层分解中加入两个图正则化限制，保护多视图数据的几何结构信息，同时将视图的权重与特征表示矩阵进行结合获得共识表示矩阵，最大化视角间的互补性，保证数据的一致性和差异性。除此之外，本文使用迭代更新变量的方法最小化目标函数，不断优化模型并进行收敛性分析。将本文算法和多个算法在三个人脸数据集和两个图像数据集上运行，通过多项指标的对比可以看出本文提出的算法具备良好的性能表现。Abstract: In view of the extensive multi-view data composed of multiple representations or views in real world, the deep matrix factorization (DMF) model has attracted much attention because of its ability to explore the hierarchical information of data. However, it ignores geometric structure of data. In order to solve the above problem, this paper proposes a multi-view clustering algorithm based on deep matrix factorization with graph regularization, which can protect geometric structure information of data by acquiring the local and global structure information of each view and adding two graph regularization limits in the layer-by-layer decomposition. It combines the weight of views with feature representation matrix to acquire consensus representation matrix to maximize complementarity of data and ensure consistency and difference among data. In addition, this paper uses the iterative updating variables method to minimize the objective function, continuously optimize model and conduct convergence analysis. This algorithm and other multiple algorithms are run on three face benchmark datasets and two image data sets. Through the comparison of multiple indicators, it can be seen that the algorithm proposed in this paper has good performance.
-
随着多元化数据的产生与积累，传统聚类算法只针对于单一视角进行数据的相似性聚类对于现实中的很多数据不再适用。现实社会中，数据集往往从多个数据源收集，或存在不同的表示形式和特征信息构成多视图数据[1-3]。例如，同一事件通过不同的内容形式播报出来；同一文档可以翻译成多种语言；网页数据可以通过文本或网页链接获取。相较于单一视角的数据，多视图数据从多个视角呈现对象，使之特征信息更加完整。那么，如何利用多个视图的完整信息发现不同视图间存在的一致的潜在信息成为多视图聚类算法的目标[4-5]。
近年来，多视图聚类算法获得了越来越多的关注和发展。根据多视图聚类算法的根本机制和原则，多视图聚类算法主要包括基于K-means的算法、基于矩阵分解的算法、基于图的算法以及基于子空间的算法[6]。例如，伍国鑫等[7]结合co-training的思想提出了一个改进的多视图K-means聚类算法。Xu等[8]提出了一种基于K-means处理高维数据的算法，将多视图聚类和特征选择集成到一个联合框架中，选择合适的视图和重要的特征聚类。最近提出的FRMVK算法提出使用较小权重消除不相关特征，实现简化有效特征信息的目的[9]。Nie等[10]开发了一种基于图的聚类算法，能够同时学习多视图聚类和局部结构。之后，Nie等[11]又提出了一种基于图的多视图聚类算法，其基础思想是从一系列低质量的特定视图中生成一个具备鲁棒性的共有图。Gao等[12]在早期考虑尝试扩展传统的基于子空间的多视图聚类算法，称为多视图子空间聚类算法(multi-view subspace clustering, MVSC) 。Zhang等[6]提出可以在隐藏公共空间中进行子空间聚类。针对多个视图在聚类性能上贡献度的差异问题，黄静对每个视图进行了加权[13]；范瑞东等[14]则采用了更具鲁棒性的自加权方式。Zheng等[15]提出使用
${l_{2,1}}$ 范式解决融合的多视图数据中特定样本与特定簇之间的关联性问题，从而获得多视图数据的共有信息。在众多研究中，非负矩阵分解算法及其扩展算法因其良好的聚类可解释性而受到越来越多的关注[16]，如何通过非负矩阵分解获取多视图数据潜在的数据信息成为热点研究方向之一[17]。半非负矩阵分解算法(semi-nonnegative matrix factorization, Semi-NMF)是为扩展非负矩阵分解算法(nonnegative matrix factorization, NMF)的应用范围而提出的算法[18]。考虑到特征表示矩阵与原始数据矩阵之间的映射矩阵存在隐藏的层次结构信息，Trigeorgis等[19]提出一种深度半非负矩阵分解模型，通过逐层分解自动学习数据点的层次属性。从数据的几何结构出发，数据点往往是从嵌入在高维环境空间中的低维流形空间中采样而得[20]，数据的固有几何结构在矩阵分解中并没有得到充分的运用。而现有的很多算法证明了图正则化从样本的相似性上保护了数据的几何结构[21]，例如，Zhao等[20]将深度矩阵分解模型应用于多视图，并在最后一层分解中加入图正则化，有效提高模型性能。算法MMNMF将共识系数矩阵与多流形正则化相结合，在对数据进行矩阵分解的同时保护数据的局部几何结构[22]。Zhang等[23]通过图嵌入增强了有用的信息，并在每个视图中使用正交约束进行聚类，从而删除多余信息。
考虑到深度半非负矩阵分解模型和图正则化各自对于数据的层次属性和固有几何结构的作用，同时从保护数据的局部结构和全局结构两个方面出发，在深度分解模型中，对每一层的特征表示矩阵加入两个图正则化限制，从而充分挖掘出数据的层次属性信息的同时保护数据的固有几何结构。换言之相较于现有的基于矩阵分解的多视图聚类算法，本文提出的算法不仅使用了局部结构的相似性而且加入了全局结构的不相似性共同构成图正则化器，从而更全面的保护和使用数据的几何结构关系。与此同时，图正则化器不只作为共识表示矩阵的调节器，同时将其加入每一层分解中，使得多视角的几何结构关系扩展至每个视角的每一层的表示矩阵中，保持几何关系的稳定性，最大化视角间关系。除此之外，考虑到多视图数据的差异性，对每个视图加入一个权重值，调节每个视图在共识表示矩阵中所占比重。本文针对所提出的模型采用相应的迭代优化算法，从理论上证明算法的收敛性。在多个数据集上的实验结果与分析证实了算法的性能优越性。
1. 相关工作
1.1 半非负矩阵分解算法
非负矩阵分解(nonnegative matrix factorization, NMF)算法对基础矩阵Z和特征矩阵H的非负限制使得算法本身更具备聚类易解释性, 但与此同时数据矩阵X的适用性也受到了限制。为了扩展矩阵分解的应用范围，Ding等[18]提出了一种半非负矩阵分解算法(semi-nonnegative matrix factorization, Semi-NMF)，改变了对数据矩阵X和基础矩阵Z的限制条件，其优化问题为
$$ \begin{gathered} \mathop {\min }\limits_{{\boldsymbol{Z}},{\boldsymbol{H}}} \left\| {{\boldsymbol{X}} - {\boldsymbol{ZH}}} \right\|_F^2 \hfill \\ {\rm{s.t.}}\;{\boldsymbol{H}} \geqslant 0 \hfill \\ \end{gathered} $$ (1) 式中：
$\left\| \cdot \right\|$ 代表Frobenius范数；${\boldsymbol{X}}\in {\bf{R}}^{d\times n}$ 是输入的数据矩阵，包括n个样本；${\boldsymbol{Z}}\in {\bf{R}}^{d\times k}$ 是分解后的基础矩阵；${\boldsymbol{H}}\in {\bf{R}}^{k\times n}$ 是分解后的特征表示矩阵，它是非负的；k是数据矩阵经过矩阵分解之后的维度。使用迭代的优化算法，文献[18]给出式(1)中基础矩阵Z和特征表示矩阵H的更新策略为$$\begin{aligned} &\quad\quad\quad\quad\quad\quad {\boldsymbol{Z}} = {\boldsymbol{X}}{{\boldsymbol{H}}^\dagger } \\ &{\boldsymbol{H}} = {\boldsymbol{H}}\cdot \sqrt {\frac{{{{\left[ {{{\boldsymbol{H}}^{\rm{T}}}{\boldsymbol{X}}} \right]}^{\rm pos}} + {{\left[ {{{\boldsymbol{H}}^{\rm{T}}}{\boldsymbol{H}}} \right]}^{\rm neg}}{\boldsymbol{Z}}}}{{{{\left[ {{{\boldsymbol{H}}^{\rm{T}}}{\boldsymbol{X}}} \right]}^{\rm neg}} + {{\left[ {{{\boldsymbol{H}}^{\rm{T}}}{\boldsymbol{H}}} \right]}^{\rm pos}}{\boldsymbol{Z}}}}} \end{aligned}$$ 式中：
${{\boldsymbol{H}}^\dagger }$ 是指矩阵H的Moore-Penrose伪逆矩阵；矩阵M的${\left[ {\boldsymbol{M}} \right]^{\rm pos}}$ 表示矩阵的负数均用0代替，相似的${\left[ {\boldsymbol{M}} \right]^{\rm neg}}$ 表示矩阵中的正数均用0代替，两者的计算公式如下：$$ \forall i,j.{\left[{\boldsymbol{M}}\right]}_{i,j}^{\rm pos}=\frac{\left|{\boldsymbol M}_{i,j}\right|+{\boldsymbol M}_{i,j}}{2}，{\left[{\boldsymbol{M}}\right]}_{i,j}^{\rm neg}=\frac{\left|{\boldsymbol M}_{i,j}\right|-{\boldsymbol M}_{i,j}}{2} $$ 1.2 深度矩阵分解算法
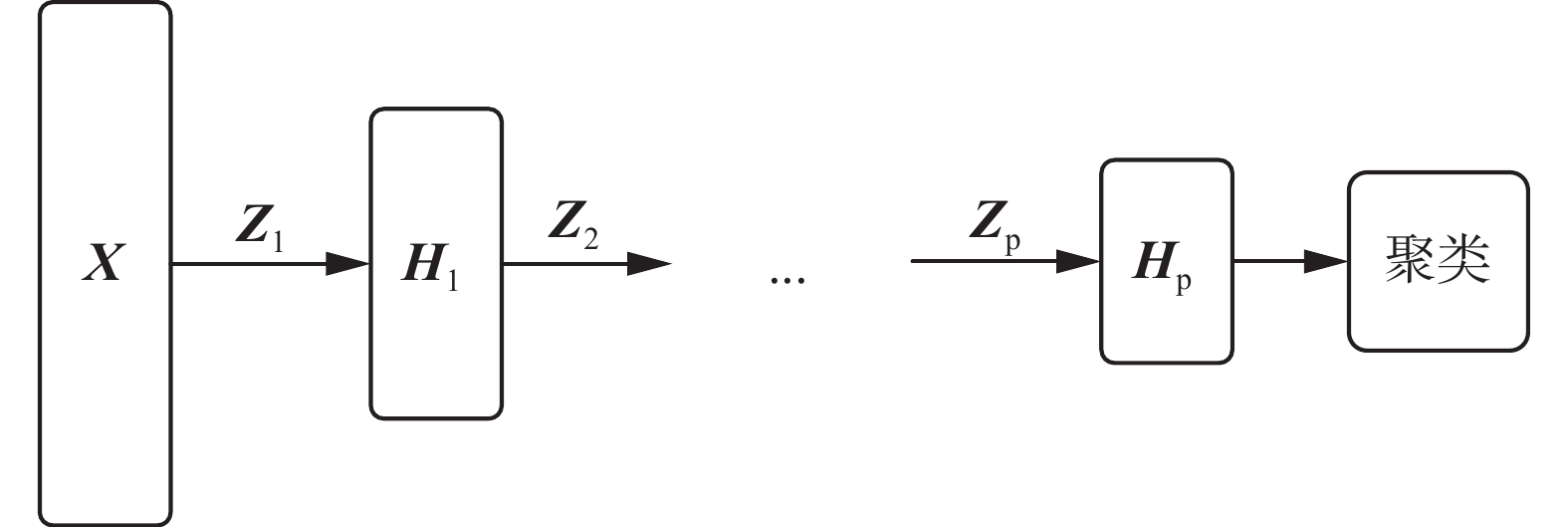
Semi-NMF是NMF算法的扩展算法，从聚类的角度出发，分解之后产生的基础矩阵Z可以看作是聚类质心矩阵，特征矩阵H可以看作数据点聚类之后的成员关系矩阵[18,24]。那么，半非负矩阵分解产生的低维表示矩阵H与原始特征矩阵X之间的映射矩阵Z中很有可能包含更为复杂的层次结构信息。因此，Trigeorgis等[19]提出一种深度矩阵分解模型(deep Semi-nonnegative matrix factorization, Deep Semi-NMF)。其算法结构如图1所示。
图 1 深度半非负矩阵分解Fig. 1 Deep semi-nonnegative matrix factorization
下载:
全尺寸图片
从图1中可以看出，深度矩阵分解算法使用多层分解的方式，将i层的分解矩阵
${{\boldsymbol{Z}}_i}$ 作为下一层分解的输入矩阵，最后一层的特征表示矩阵将用于聚类获得数据的类别信息。多层次分解的具体过程和优化问题如下列公式所示：$$ \begin{gathered} \left\{ \begin{array}{l} {\boldsymbol{X}} \approx {{\boldsymbol{Z}}_1}{{\boldsymbol{H}}_1}\\ {\boldsymbol{X}} \approx {{\boldsymbol{Z}}_1}{{\boldsymbol{Z}}_2}{{\boldsymbol{H}}_2}\\ \quad\vdots \\ {\boldsymbol{X}} \approx {{\boldsymbol{Z}}_1}{{\boldsymbol{Z}}_2} \cdots {{\boldsymbol{Z}}_p}{{\boldsymbol{H}}_p} \end{array} \right. \end{gathered} $$ $$ \begin{gathered} \mathop {\min }\limits_{{\boldsymbol{Z}},{\boldsymbol{H}}} \left\| {{\boldsymbol{X}} - {{\boldsymbol{Z}}_1}{{\boldsymbol{Z}}_2}\cdots{{\boldsymbol{Z}}_p}{{\boldsymbol{H}}_p}} \right\|_F^2 \\ {\rm{s.t.}}\;{\boldsymbol{H}}_i^v \geqslant 0,\quad i = 1,2,\cdots, P \\ \end{gathered} $$ 式中：
${{\boldsymbol{Z}}_i}$ 是第i层的映射矩阵；${{\boldsymbol{H}}_i}$ 是第i层的特征表示矩阵。2. 多视图深度图正则化矩阵分解聚类算法
深度半非负矩阵分解算法通过逐层分解的方式证实了原始数据与特征表示矩阵之间隐藏着低维特征属性的层次属性，但是在应用于多视图聚类时忽略了数据的固有几何结构。本文提出多视图深度图正则化矩阵分解聚类算法，通过对深度矩阵分解的各层加入两个图正则化的限制，保护数据的几何结构信息。
2.1 图正则化
假如两个数据点
${X_i}$ 和${X_j}$ 在数据分布中有相近的内部几何关系，那么在新的基础空间中对应的表示矩阵${Z_i}$ 和${Z_j}$ 应该拥有类似的关系，这就是流形假设[25-26]。这种几何结构信息可以通过构建数据点的最近邻图进行有效的建模[27]。Mikhail通过最近邻图对数据局部几何结构的保护提出降维算法——拉普拉斯特征映射(laplacian eigenmaps, LE)[28]。在此基础上，SNE(stochastic neighbor embedding)算法加入数据几何结构的全局关系，认为高维空间数据点之间的不相似性关系在低维空间中保持不变[29]。EE(elastic embedding)算法[30]沿用SNE的思想，改变全局结构的计算方式，使得算法更简单，更易实现。EE算法的目标函数为$$ E({\boldsymbol{X}};\lambda ) = \sum\limits_{n,m = 1}^N {w_{nm}^ + {{\left\| {{x_n} - {x_m}} \right\|}^2} + \lambda \sum\limits_{n,m = 1}^N {w_{nm}^ - \exp ( - {{\left\| {{x_n} - {x_m}} \right\|}^2})} } $$ 其中：第1部分的
$w_{nm}^ + $ 为相似性权重，保护数据的局部几何结构，使用数据的全连接图进行计算$w_{nm}^ + = \exp \left( {{{ - {{\left\| {{x_n} - {x_m}} \right\|}^2}} \mathord{\left/ {\vphantom {{ - {{\left\| {{x_n} - {x_m}} \right\|}^2}} {2{\sigma ^2}}}} \right. } {2{\sigma ^2}}}} \right)$ ；第2部分的$w_{nm}^ - $ 为排斥性权重，说明数据的不相似性，保护数据的全局几何结构，$w_{nm}^ - = {\left\| {{x_n} - {x_m}} \right\|^2}$ ，且$w_{nm}^ + = w_{nm}^ - = 0$ ，$\forall n = m$ ，将全连接图与局部几何结构相结合构建全局结构关系$\widetilde {w_{nm}^ - } = w_{nm}^ - \exp ( - {\left\| {{x_n} - {x_m}} \right\|^2})$ 。2.2 多视图深度图正则化矩阵分解聚类算法的目标函数
受到EE算法[30]对数据几何结构的保护以及数据隐藏的层次属性的启发，在深度矩阵分解的各层中加入局部几何结构和全局几何结构信息，将两个图正则化嵌入深度分解的各层，使得数据的几何结构对数据新的表示矩阵进行微调。算法的目标就是为了最小化下列问题：
$$ \begin{array}{l} \quad\quad \mathop {\min }\limits_{{\boldsymbol{Z}}_l^v,{\boldsymbol{H}}_l^v\atop \scriptstyle{{\boldsymbol{H}}_p},{\alpha ^v}} \displaystyle\sum\limits_{v = 1}^V {{{({\alpha ^v})}^\gamma }}\left( \left\| {{{\boldsymbol{X}}^v} - {\boldsymbol{Z}}_1^v \cdots {\boldsymbol{Z}}_p^v{{\boldsymbol{H}}_p}} \right\|_F^2 + \right.\\ \dfrac{\eta }{2}{\displaystyle\sum\limits_{l = 1}^P} {\displaystyle\sum\limits_{i = 1}^m} {\displaystyle\sum\limits_{j = 1}^n} {w_{{l_{ij}}}^{v + }{{\left\| {{\boldsymbol{H}}_{{l_i}}^v - {\boldsymbol{H}}_{{l_j}}^v} \right\|}^2}} + \dfrac{\beta }{2}{\displaystyle\sum\limits_{l = 1}^P} {\displaystyle\sum\limits_{i = 1}^m} {\displaystyle\sum\limits_{j = 1}^n} {w_{{l_{ij}}}^{v - }}\\ \quad\quad\quad\quad\left. \exp \left( - {{\left\| {{\boldsymbol{H}}_{{l_i}}^v - {\boldsymbol{H}}_{{l_j}}^v} \right\|}^2}\right) \right)\\ \quad\quad\quad{\rm{s.t.}}\;{{\boldsymbol{H}}_l^v} \geqslant 0,{\displaystyle\sum\limits_{v = 1}^V }{{\alpha ^v} = 1,{\alpha ^v} \geqslant 0} \end{array} $$ (2) 其中优化问题(式(2))中对数据的局部几何结构的计算可进一步简化：
$$ \begin{gathered} \frac{1}{2}\sum\limits_{i = 1}^m {\sum\limits_{j = 1}^n {w_{ij}^{v + }} } {\left\| {{\boldsymbol{H}}_i^v - {\boldsymbol{H}}_j^v} \right\|^2} = \sum\limits_{i = 1}^m {{\boldsymbol{H}}_i^{{v^{\rm{T}}}}{\boldsymbol{H}}_i^vd_{ii}^{v + } - } \sum\limits_{i = 1}^n {{\boldsymbol{H}}_i^{{v^{\rm{T}}}}{\boldsymbol{H}}_j^vw_{ij}^{v + }} = \\ {\rm{tr}}({{\boldsymbol{H}}^{{v^{\rm{T}}}}}{D^{v + }}{{\boldsymbol{H}}^v}) - {\rm{tr}}({{\boldsymbol{H}}^{{v^{\rm{T}}}}}{W^{v + }}{{\rm{H}}^v}) = {\rm{tr}}({{\boldsymbol{H}}^{{v^{\rm{T}}}}}{L^{v + }}{{\boldsymbol{H}}^v}) \hfill \\ \end{gathered} $$ 那么优化问题(2)可以改写为：
$$ \begin{array}{l} \mathop {\min }\limits_{{\boldsymbol{Z}}_l^v,{{\boldsymbol{H}}_l^p}\atop \scriptstyle{{\boldsymbol{H}}_p},{\alpha ^v}} {\displaystyle\sum\limits_{v = 1}^V} {{{\left( {{\alpha ^v}} \right)}^\gamma }\left(\left\| {{{\boldsymbol{X}}^v} - {{\boldsymbol{Z}}_1^v} \cdots {{\boldsymbol{Z}}_P^v}{{\boldsymbol{H}}_P}} \right\|_F^2 + \eta \displaystyle\sum\limits_{l = 1}^P {{\rm{tr}}({\boldsymbol{H}}_l^{{v^{\rm{T}}}}L_l^v{\boldsymbol{H}}_l^v)} \right.}+ \\ \quad\quad\quad\quad\quad \left.\dfrac{\beta }{2}\displaystyle\sum\limits_{l = 1}^P {\displaystyle\sum\limits_{i = 1}^m {\displaystyle\sum\limits_{j = 1}^n {w_{{l_{ij}}}^{v - }\exp \left( - {{\left\| {{\boldsymbol{H}}_{{l_i}}^v - {\boldsymbol{H}}_{{l_j}}^v} \right\|}^2}\right)} } } \right) \end{array} $$ (3) 根据对数据全局几何结构的计算方式，优化问题(3)可进一步简化为
$$ \begin{array}{l} \mathop {\min }\limits_{{\boldsymbol{Z}}_l^v,{\boldsymbol{H}}_l^p\hfill\atop \scriptstyle{{\boldsymbol{H}}_p},{\alpha ^v}\hfill} \displaystyle\sum\limits_{v = 1}^V {{{\left( {{\alpha ^v}} \right)}^\gamma }\left(\left\| {{{\boldsymbol{X}}^v} - {\boldsymbol{Z}}_1^v \cdots {\boldsymbol{Z}}_P^v{{\boldsymbol{H}}_P}} \right\|_F^2 + \lambda \displaystyle\sum\limits_{l = 1}^P {{\rm{tr}}({\boldsymbol{H}}_l^{{v^{\rm{T}}}}L_l^v{\boldsymbol{H}}_l^v)}\right )} \\ \quad\quad\quad\quad{\rm{s.t.}}\;{\boldsymbol{H}}_l^v \geqslant 0,{{\boldsymbol{H}}_P} \geqslant 0,\displaystyle\sum\limits_{v = 1}^V {{\alpha ^v} = 1,{\alpha ^v} \geqslant 0} \end{array} $$ (4) 式中：
$L_l^v = D_l^v - W_l^v$ ；$W_l^v = W_l^{v + } - \eta \tilde W_l^{v - }$ ；$\lambda = {\eta \mathord{\left/ {\vphantom {\eta \beta }} \right. } \beta }$ 。$W_l^{v + }$ 和$\tilde W_l^{v - }$ 的计算方式沿用EE算法对局部矩阵和全局矩阵的计算方式。3. 算法优化
为优化模型的性能，在对数据进行深度图正则化矩阵分解之前，需要对每个视角各层的基础矩阵和特征表示矩阵进行初始化。这里使用加入了图正则化的半非负矩阵分解算法进行各层的初始化。之后，使用迭代更新的方式优化函数变量。算法的成本函数为
$$ \begin{gathered} C = \sum\limits_{v = 1}^V {{{({\alpha ^v})}^\gamma }(\left\| {{{\boldsymbol{X}}^v} - {\boldsymbol{Z}}_1^v \cdots {\boldsymbol{Z}}_P^v{{\boldsymbol{H}}_P}} \right\|_F^2 + \lambda \sum\limits_{l = 1}^P {{\rm{tr}}({\boldsymbol{H}}_l^{{v^{\rm{T}}}}L_l^v{\boldsymbol{H}}_l^v)} )} = \\ \sum\limits_{v = 1}^V {{\left( {{\alpha ^v}} \right)}^\gamma }\left[ {\rm{tr}}\left( { \begin{gathered} \left\|{{\boldsymbol{X}}^{{v^{\rm{T}}}}}{{\boldsymbol{X}}^v} - 2{{\boldsymbol{X}}^{\rm{T}}}{\boldsymbol{Z}}_1^v \cdots {\boldsymbol{Z}}_p^v{{\boldsymbol{H}}_p} +\right.\\ \left. {\boldsymbol{H}}_p^{\rm{T}}{\boldsymbol{Z}}_p^{{v^{\rm{T}}}} \cdots {\boldsymbol{Z}}_1^{{v^{\rm{T}}}}{\boldsymbol{Z}}_1^v \cdots {\boldsymbol{Z}}_p^v{{\boldsymbol{H}}_p} \right\|\\ \end{gathered} } \right) + \right.\\ \left.\lambda \sum\limits_{l = 1}^P{\rm{tr}}\left( {{\boldsymbol{H}}_l^{{v^{\rm{T}}}}L_l^v{\boldsymbol{H}}_l^v} \right) \right] \\ \end{gathered} $$ (5) 根据拉格朗日乘子法，对每个变量进行求导更新计算。
1) 固定变量
${\boldsymbol{H}}_l^v$ 、${{\boldsymbol{H}}_P}$ 、${\alpha ^v}$ ，优化更新${\boldsymbol{Z}}_l^v$ ，成本函数C对其求偏导，并设为0，即$\dfrac{{\delta C}}{{\delta {\boldsymbol{Z}}_i^v}} = 0$ 。$$ \begin{gathered} {\boldsymbol{Z}}_l^v = {\left( {{{\boldsymbol{\varPsi}} ^{\rm{T}}}{\boldsymbol{\varPsi}} } \right)^{ - 1}}{{\boldsymbol{\varPsi}}^{\rm{T}}}{{\boldsymbol{X}}^v}{\boldsymbol{H}}_l^v{({\boldsymbol{H}}_l^v{\boldsymbol{H}}_l^{{v^{\rm{T}}}})^{ - 1}} \hfill \\ {\boldsymbol{Z}}_l^v = {{\boldsymbol{\varPsi}} ^\dagger }{{\boldsymbol{X}}^v}{\boldsymbol{H}}_l^{{v^\dagger }} \hfill \\ \end{gathered} $$ 式中：
${\boldsymbol{\varPsi}}= \left[ {{\boldsymbol{Z}}_1^v \cdots {\boldsymbol{Z}}_{l - 1}^v} \right]$ ，符号$\dagger $ 代表矩阵的Moore-Penrose伪逆形式。2) 固定变量
${\boldsymbol{Z}}_l^v$ 、${\alpha ^v}$ ，优化更新${\boldsymbol{H}}_l^v$ ，${{\boldsymbol{H}}_P}$ 。当
$l < P$ 时，更新${\boldsymbol{H}}_l^v$ 。根据拉格朗日乘子法得到有关该变量有约束条件的拉格朗日函数，对其进行求导并使之为0，由此可得到${\boldsymbol{H}}_l^v$ 的更新公式，定理1可以证实其收敛性。$$ {\boldsymbol{H}}_l^v = {\boldsymbol{H}}_l^v \cdot \sqrt {\frac{{{{\left[ {{{\boldsymbol{\varPsi}} ^{\rm{T}}}{{\boldsymbol{X}}^v}} \right]}^{\rm pos}} + {{\left[ {{{\boldsymbol{\varPsi}} ^{\rm{T}}}{\boldsymbol{\varPsi}} {\boldsymbol{H}}_l^v} \right]}^{\rm neg}} + \lambda G({\boldsymbol{H}})}}{{{{\left[ {{{\boldsymbol{\varPsi}} ^{\rm{T}}}{{\boldsymbol{X}}^v}} \right]}^{\rm neg}} + {{\left[ {{{\boldsymbol{\varPsi}} ^{\rm{T}}}{\boldsymbol{\varPsi}}{\boldsymbol{H}}_l^v} \right]}^{\rm pos}} + \lambda F({\boldsymbol{H}})}}} $$ (6) 其中：
$G({\boldsymbol{H}}) = {[{\boldsymbol{H}}_l^v{\boldsymbol{W}}_l^v]^{\rm pos}} + {[{\boldsymbol{H}}_l^v{\boldsymbol{D}}_l^v]^{\rm neg}}$ ，$F({\boldsymbol{H}}) = {[{\boldsymbol{H}}_l^v{\boldsymbol{W}}_l^v]^{\rm neg}} + $ $ {[{\boldsymbol{H}}_l^v{\boldsymbol{D}}_l^v]^{\rm pos}}$ 。定理1 更新公式(6)的有限解满足KKT条件。
证明 有关
${\boldsymbol{H}}_l^v$ 的优化问题是含有不等式约束条件的拉格朗日函数：$$\begin{aligned} &L\left( {{\boldsymbol{H}}_l^v} \right) = \sum\limits_{v = 1}^V {{\left( {{\alpha ^v}} \right)}^\gamma }\left( \left\| {{{\boldsymbol{X}}^v} - {\boldsymbol{Z}}_1^v \cdots {\boldsymbol{Z}}_l^v{\boldsymbol{H}}_l^v} \right\|_F^2 + \right.\\ &\quad\quad\quad\left.\lambda {\rm{tr}}\left( {{\boldsymbol{H}}_l^{{v^{\rm{T}}}}L_l^v{\boldsymbol{H}}_l^v} \right) - \xi {\boldsymbol{H}}_l^v \right) \end{aligned}$$ (7) 其中参数
$\xi $ 是为了满足不等式约束条件${\boldsymbol{H}}_l^v \geqslant 0$ 而产生的乘子。对式(7)进行求导并使之为0，即$\dfrac{{\delta L}}{{\delta {\boldsymbol{H}}_l^v}} = 2{{\boldsymbol{\varPsi}} ^{\rm{T}}}\left( {{\boldsymbol{\varPsi}} {\boldsymbol{H}}_l^v - {{\boldsymbol{X}}^v}} \right) + 2{\boldsymbol{H}}_l^v\left( {{\boldsymbol{D}}_l^v - {\boldsymbol{W}}_l^v} \right) - \xi = 0$ ，根据对偶性定理，可以得到：$$ {\left( {2{{\boldsymbol{\varPsi}} ^{\rm{T}}}\left( {{\boldsymbol{\varPsi}} {\boldsymbol{H}}_l^v - {{\boldsymbol{X}}^v}} \right) + 2{\boldsymbol{H}}_l^v({\boldsymbol{D}}_l^v - {\boldsymbol{W}}_l^v)} \right)_{ab}}{\left( {{\boldsymbol{H}}_l^v} \right)_{ab}} = \xi {\left( {{\boldsymbol{H}}_l^v} \right)_{ab}} = 0 $$ (8) 该等式在固定点上需要满足收敛性，即
${\left( {{\boldsymbol{H}}_l^v} \right)^\infty } = {\left( {{\boldsymbol{H}}_l^v} \right)^{t + 1}} = {\left( {{\boldsymbol{H}}_l^v} \right)^t} = {\boldsymbol{H}}_l^v$ 。$$ {\left( {{\boldsymbol{H}}_l^v} \right)_{ab}} = {\left( {{\boldsymbol{H}}_l^v} \right)_{ab}} \cdot \sqrt {\frac{{\left[ {{{\boldsymbol{\varPsi}} ^{\rm{T}}}{{\boldsymbol{X}}^v}} \right]_{ab}^{\rm pos} + \left[ {{{\boldsymbol{\varPsi}} ^{\rm{T}}}{\boldsymbol{\varPsi}} {\boldsymbol{H}}_l^v} \right]_{ab}^{\rm neg} + \lambda {{\left( {G({\boldsymbol{H}})} \right)}_{ab}}}}{{{{\left[ {{{\boldsymbol{\varPsi}} ^{\rm{T}}}{{\boldsymbol{X}}^v}} \right]}^{\rm neg}} + {{\left[ {{{\boldsymbol{\varPsi}} ^{\rm{T}}}{\boldsymbol{\varPsi}} {\boldsymbol{H}}_l^v} \right]}^{\rm pos}} + \lambda {{\left( {F({\boldsymbol{H}})} \right)}_{ab}}}}} $$ 其中：
$G({\boldsymbol{H}}) = {[{\boldsymbol{H}}_l^v{\boldsymbol{W}}_l^v]^{{\text{pos}}}} + {[{\boldsymbol{H}}_l^v{\boldsymbol{D}}_l^v]^{{\text{neg}}}}$ ，$F({\boldsymbol{H}}) = {[{\boldsymbol{H}}_l^v{\boldsymbol{W}}_l^v]^{{\text{neg}}}} + $ $ {[{\boldsymbol{H}}_l^v{\boldsymbol{D}}_l^v]^{{\text{pos}}}}$ 。根据
${\boldsymbol{M}} = {\left[ {\boldsymbol{M}} \right]^{{\text{pos}}}} - {\left[ {\boldsymbol{M}} \right]^{{\text{neg}}}}$ ，式(8)可以简化为$$ {\left( {2{{\boldsymbol{\varPsi}} ^{\rm{T}}}\left( {{\boldsymbol{\varPsi}} {\boldsymbol{H}}_l^v - {{\boldsymbol{X}}^v}} \right) + 2{\boldsymbol{H}}_l^v({\boldsymbol{D}}_l^v - {\boldsymbol{W}}_l^v)} \right)_{ab}}\left( {{\boldsymbol{H}}_l^v} \right)_{ab}^2 = 0 $$ 根据等式的收敛性，式(7)与式(8)等价。当其中一个等式满足时另一个等式也是满足的，且具有可逆性。
当
$l = P$ 时，更新变量${{\boldsymbol{H}}_P}$ 。${{\boldsymbol{H}}_P}$ 是通过逐层分解获得的视角间共有的特征表示矩阵，优化问题同样满足KKT条件，同时考虑到视角的互补性和差异性，在更新每个视角的最后一层时在式(5)的基础上加入视角权重获得共识表示矩阵。$$ {{\boldsymbol{H}}_P} = {\boldsymbol{H}}_P^v \cdot \sqrt {\sum\limits_{v = 1}^V {{{\left( {{\alpha ^v}} \right)}^\gamma }} \frac{{{{\left[ {{{\boldsymbol{\varPsi}} ^{\rm{T}}}{{\boldsymbol{X}}^v}} \right]}^{\rm pos}} + {{\left[ {{{\boldsymbol{\varPsi}} ^{\rm{T}}}{\boldsymbol{\varPsi}} {\boldsymbol{H}}_l^v} \right]}^{\rm neg}} + \lambda G({\boldsymbol{H}})}}{{{{\left[ {{{\boldsymbol{\varPsi}} ^{\rm{T}}}{{\boldsymbol{X}}^v}} \right]}^{\rm neg}} + {{\left[ {{{\boldsymbol{\varPsi }}^{\rm{T}}}{\boldsymbol{\varPsi}} {\boldsymbol{H}}_l^v} \right]}^{\rm pos}} + \lambda F({\boldsymbol{H}})}}} $$ (9) 式中：
$G({\boldsymbol{H}}) = {[{\boldsymbol{H}}_l^v{\boldsymbol{W}}_l^v]^{\rm pos}} + {[{\boldsymbol{H}}_l^v{\boldsymbol{D}}_l^v]^{\rm neg}}$ ；$F({\boldsymbol{H}}) = {[{\boldsymbol{H}}_l^v{\boldsymbol{W}}_l^v]^{\rm neg}} + $ $ {[{\boldsymbol{H}}_l^v{\boldsymbol{D}}_l^v]^{\rm pos}}$ 。3) 固定变量
$Z_l^v$ 、${\boldsymbol{H}}_l^v$ 、${{\boldsymbol{H}}_P}$ 优化更新视角权重${\alpha ^v}$ 。根据文献[15]可以得到视角权重的更新公式。$$ {\alpha ^v} = \dfrac{{{{\left( {\gamma F(v)} \right)}^{\frac{1}{{1 - \gamma }}}}}}{{\displaystyle\sum\limits_{v = 1}^V {{{\left( {\gamma F(v)} \right)}^{\frac{1}{{1 - \gamma }}}}} }} $$ (10) 式中
$F\left( v \right) = \left\| {{{\boldsymbol{X}}^v} - {\boldsymbol{Z}}_1^v \cdots {\boldsymbol{Z}}_l^v{\boldsymbol{H}}_l^v} \right\|_F^2 + \lambda \displaystyle\sum\limits_{l = 1}^P{\rm{tr}}\left( {{\boldsymbol{H}}_l^{{v^{\rm{T}}}}L_l^v{\boldsymbol{H}}_l^v} \right)$ 。多视图深度图正则化矩阵分解聚类算法的整体优化过程如下：
输入 多视图数据
${\boldsymbol{X}} = \left\{ {{X^1},{X^2},\cdots,{X^v}} \right\}$ ，参数λ，γ，各层维度$= \left[ {{l_1},{l_2},\cdots,{l_P}} \right]$ ，最近邻居数k；输出 各层基础矩阵
${\boldsymbol{Z}}_l^v$ 和特征矩阵${\boldsymbol{H}}_l^v$ 以及视角间的共识表示矩阵${{\boldsymbol{H}}_P}$ 。1) 使用加入图正则化的Semi-NMF算法初始化每个视角各层的基础矩阵
${\boldsymbol{Z}}_l^v$ 和特征矩阵${\boldsymbol{H}}_l^v$ ;视角权重${\alpha ^v} = {1 \mathord{\left/ {\vphantom {1 V}} \right. } V}$ ;构建每个视角的全局图和局部图。2)当v = 1:V 时
3) 当l = P−1:1时，根据逐层分解的方式更新各层特征矩阵：
$${\boldsymbol{H}}_l^v = {\boldsymbol{Z}}_{l + 1}^v{\boldsymbol{H}}_{l + 1}^v $$ 4)当l=1:P时
$${\boldsymbol{\varPsi}} = \prod\limits_{i = 1}^{l-1} {{\boldsymbol{Z}}_i^v} $$ $$ {\boldsymbol{Z}}_l^v = \left\{ \begin{gathered} {\boldsymbol{XH}}_l^{{v^\dagger }},l = 1 \hfill \\ {\boldsymbol{\varPsi}} {{\boldsymbol{X}}^v}{\boldsymbol{H}}_l^\dagger ,l \ne 1 \hfill \\ \end{gathered} \right. $$ 5) 当l<P时，使用式(6)更新
${\boldsymbol{H}}_l^v$ 。6) 当l=P时，使用式(9)更新
${{\boldsymbol{H}}_P}$ 。7) 使用式(10)更新视角权重
${\alpha ^v}$ 。8) 重复2)~7)直至收敛。
4. 实验
4.1 实验设置
本实验中选择了5个数据集，包括3个面部基准数据集和2个图像数据集，面部数据集和图像数据集均具备良好的结构信息，能更显著的表现逐层分解中加入图正则化的效果。
Yale面部数据集由15个人在面部表情和配置信息不同的情况下产生的共165张GIF格式的灰度图像。每个人有11张图片，面部表情和配置信息包括表情、光照方向、情绪(快乐/悲伤)、有无眼镜等[3]。
Extend Yale B面部数据集由38个人在将近64个不同光照条件下所得的面部图像组成。在实验中，选择了640张，10个子集的面部图像进行测试。
UMIST面部数据集包括20个人的564张图像(混合种族、性别、外观)。每个人都以一系列的姿势显示，从侧面到正面，均已PGM的格式存在，大约220像素×220像素，256灰度，像素值用作特征表示[31]。
COIL-20(columbia university image library)图像数据集包含了20个对象物体，每个物体在水平上旋转360°，每隔5°拍摄一张照片，因此每个对象共72幅图，图片大小为64像素×64像素，总共1440张图像。
Caltech101数据集是图像数据集，共包括了101种分类，每个分类包含了40张到800张不等的图片，大多数类别有50张图片。每一张图片的大小为300像素 × 200像素。我们选择了20个类别，共2386张图像。
本实验中选择了9对比算法。
BestSC：在多视图数据的每个视角数据采用标准的谱聚类算法[32]，记录最好的实验结果。
ConcateFea：将所有视角的特征结合起来，使用谱聚类算法获得实验结果。
ConcatePCA：将所有视角的特征结合起来，使用PCA将特征矩阵映射到低维子空间，使用谱聚类算法获得聚类结果。
Co-Reg SPC：通过共正则化聚类假设的方式使得数据点在不同视角中拥有相同的聚类成员关系[33]。
Co-Train SPC：基于潜在聚类为同一类别分配一个数据点，无关视角的假设，通过协同训练的方式获得视角之间一致的聚类[34]。
Min-Disagreement SPC：该算法以最小化不一致性为标准构建二分图，使用谱聚类算法进行聚类[35]。
DiMSC：在子空间聚类的背景下，使用希尔伯特施密特独立标准(HSIC)探索多视图数据的完整性信息[36]。
GMVNMF：将PVC算法[37]从双视图扩展到多视图聚类，同时加入视角图拉普拉斯规则化探索每个视角中数据分布的内部几何结构[38]。
DMF_MVC：将deep semi-nmf model[19]应用于多视图数据，同时对最终获得的特征表示矩阵加入视角的图拉普拉斯矩阵进行微调[20]。
为更加全面的比较算法性能，本文中选择了6种不同的度量指标，包括标准化互信息(normalized mutual information, NMI)，准确率(accuracy, ACC)，调整兰德指数(adjusted rand index, AR)，综合评价指标(f-score)，精确率(precision)，召回率(recall)。这些指标都是数值越大，性能越好。在实验中，每个算法都采用其原算法中最佳的参数设置并运行10次以上，最终结果以均值和标准差的方式呈现。
4.2 实验结果与分析
表1是本文算法与其他对比算法在Yale面部数据集上的实验结果。从实验结果可以看出，本文提出的算法相较于其他对比算法性能均良好，其中NMI和ACC两个指标提高了10%以上，其余指标均在15%以上。表2是算法在Extend Yale B面部数据集上的实验结果。在该数据集上，本文提出的算法在各项指标上均有所提高。将其与各项指标的最佳数值对比，在NMI上提高了4.4%，在ACC上提高了3.4%，在AR上提高了4.9%，在F-Measure上提高了5.2%，在精确率和召回率上各提高了2.1%和1.3%，均值保持在3.5%。表3是算法在面部数据集UMIST上的实验结果。从实验结果上看，本文提出的算法比其他算法拥有5个指标的提高，且均在2%~5%以上。在召回率上，本文算法性能并没有达到最好，但是总体来看，本文的算法性能更加稳定。表4是算法在图像数据集COIL-20上的实验结果。从表中可以看出，本文提出的算法较之其他算法表现良好。同时，各项指标的提高均值来看，本文算法与基于谱聚类的算法性能相近，尤其是BestSC算法，这就说明本文算法能够捕捉最佳视角信息并使用图规则化改善聚类性能。表5是各算法在Caltech101-20图像数据集上的性能表现。从数据中可以看出，Co-Train SPC算法因其协同训练的方式能够最大化视角间的标准化互信息。虽然在某些指标上，本文提出的算法并未达到最优，但是在其他指标上表现良好，且比协同训练的两种算法提高了10%以上。
表 1 不同算法在Yale面部数据集上的实验结果(均值±标准差)Table 1 Experimental results of different algorithms on the Yale face dataset (mean ± standard deviation)算法 NMI ACC AR F-score Precision Recall BestSC 0.670±0.010 0.642±0.010 0.453±0.110 0.489±0.103 0.466±0.107 0.514±0.010 ConcateFea 0.585±0.004 0.556±0.005 0.341±0.006 0.383±0.005 0.369±0.006 0.398±0.005 ConcatePCA 0.464±0.017 0.372±0.018 0.165±0.014 0.217±0.013 0.210±0.013 0.226±0.014 Co-Reg SPC 0.645±0.002 0.078±0.017 0.429±0.034 0.466±0.032 0.439±0.029 0.497±0.037 Co-Train SPC 0.669±0.028 0.084±0.065 0.457±0.038 0.491±0.035 0.469±0.033 0.516±0.028 Min-D SPC 0.655±0.001 0.642±0.000 0.444±0.000 0.476±0.001 0.463±0.000 0.498±0.000 DiMSC 0.635±0.001 0.569±0.001 0.408±0.001 0.447±0.001 0.412±0.001 0.489±0.001 GMVNMF 0.529±0.003 0.407±0.003 0.243±0.010 0.308±0.008 0.219±0.008 0.524±0.006 DMF_MVC 0.716±0.040 0.721±0.050 0.519±0.007 0.549±0.002 0.534±0.002 0.565±0.004 DGRMF_MVC 0.851±0.001 0.872±0.001 0.737±0.001 0.753±0.001 0.740±0.001 0.766±0.001 表 2 不同算法在Extend Yale B面部数据集上的实验结果(均值±标准差)Table 2 Experimental results of different algorithms on the Extend Yale B face dataset (mean ± standard deviation)算法 NMI ACC AR F-score Precision Recall BestSC 0.469±0.156 0.468±0.144 0.287±0.140 0.361±0.123 0.336±0.122 0.391±0.123 ConcateFea 0.401±0.001 0.342±0.001 0.164±0.000 0.262±0.000 0.221±0.000 0.322±0.001 ConcatePCA 0.507±0.002 0.556±0.002 0.342±0.001 0.410±0.001 0.391±0.001 0.431±0.003 Co-Reg SPC 0.182±0.015 0.101±0.005 0.087±0.009 0.179±0.007 0.175±0.008 0.183±0.007 Co-Train SPC 0.336±0.018 0.117±0.035 0.184±0.012 0.267±0.012 0.261±0.016 0.277±0.018 Min-D SPC 0.496±0.001 0.492±0.000 0.233±0.001 0.324±0.000 0.271±0.001 0.401±0.000 DiMSC 0.238±0.001 0.287±0.001 0.139±0.000 0.228±0.000 0.217±0.001 0.239±0.001 GMVNMF 0.263±0.005 0.316±0.004 0.124±0.004 0.215±0.003 0.204±0.003 0.228±0.003 DMF_MVC 0.580±0.014 0.645±0.005 0.288±0.011 0.379±0.009 0.293±0.010 0.537±0.018 DGRMF_MVC 0.624±0.005 0.679±0.010 0. 393±0.002 0.462±0.003 0.412±0.005 0.550±0.010 表 3 不同算法在UMIST面部数据集上的实验结果(均值±标准差)Table 3 Experimental results of different algorithms on the UMIST face dataset (mean ± standard deviation)算法 NMI ACC AR F-score Precision Recall BestSC 0.768±0.010 0.562±0.021 0.502±0.024 0.529±0.022 0.498±0.022 0.564±0.024 ConcateFea 0.764±0.007 0.549±0.019 0.491±0.018 0.518±0.017 0.488±0.018 0.554±0.017 ConcatePCA 0.534±0.008 0.459±0.011 0.251±0.010 0.291±0.009 0.277±0.012 0.310±0.008 Co-Reg SPC 0.676±0.007 0.047±0.011 0.391±0.009 0.423±0.008 0.414±0.008 0.432±0.009 Co-Train SPC 0.684±0.022 0.039±0.045 0.400±0.029 0.431±0.027 0.418±0.026 0.447±0.031 Min-D SPC 0.805±0.001 0.647±0.000 0.604±0.001 0.625±0.001 0.604±0.000 0.649±0.000 DiMSC 0.619±0.001 0.453±0.001 0.320±0.001 0.355±0.001 0.560±0.001 0.354±0.001 GMVNMF 0.758±0.002 0.506±0.005 0.436±0.002 0.478±0.002 0.330±0.001 0.864±0.004 DMF_MVC 0.769±0.030 0.595±0.009 0.507±0.008 0.534±0.004 0.495±0.060 0.581±0.009 DGRMF_MVC 0.851±0.001 0.713±0.001 0.644±0.001 0.663±0.010 0.630±0.001 0.744±0.002 表 4 不同算法在COIL-20数据集上的实验结果(均值±标准差)Table 4 Experimental results of different algorithms on the COIL-20 dataset (mean ± standard deviation)算法 NMI ACC AR F-score Precision Recall BestSC 0.943±0.021 0.853±0.024 0.826±0.026 0.836±0.024 0.771±0.029 0.913±0.037 ConcateFea 0.932±0.001 0.780±0.001 0.770±0.001 0.782±0.001 0.688±0.001 0.907±0.001 ConcatePCA 0.554±0.004 0.514±0.005 0.321±0.003 0.374±0.003 0.329±0.007 0.435±0.010 Co-Reg SPC 0.812±0.015 0.044±0.036 0.655±0.032 0.672±0.030 0.651±0.038 0.696±0.023 Co-Train SPC 0.824±0.014 0.081±0.031 0.669±0.050 0.686±0.047 0.665±0.037 0.714±0.023 Min-D SPC 0.897±0.001 0.836±0.000 0.789±0.001 0.800±0.001 0.773±0.000 0.828±0.000 DiMSC 0.843±0.013 0.771±0.018 0.724±0.020 0.737±0.019 0.730±0.018 0.745±0.020 GMVNMF 0.788±0.012 0.500±0.001 0.424±0.036 0.466±0.032 0.314±0.029 0.911±0.017 DMF_MVC 0.923±0.014 0.770±0.018 0.759±0.021 0.773±0.020 0.683±0.024 0.891±0.030 DGRMF_MVC 0.948±0.001 0.876±0.008 0.846±0.005 0.854±0.005 0.802±0.007 0.913±0.002 表 5 不同算法在Caltech101-20数据集上的实验结果(均值±标准差)Table 5 Experimental results of different algorithms on the Caltech101-20 dataset (mean ± standard deviation)算法 NMI ACC AR F-score Precision Recall BestSC 0.510±0.011 0.392±0.050 0.251±0.058 0.328±0.056 0.522±0.090 0.239±0.038 ConcateFea 0.385±0.003 0.340±0.017 0.190±0.011 0.267±0.012 0.457±0.014 0.188±0.010 ConcatePCA — — — — — — Co-Reg SPC 0.536±0.013 0.051±0.038 0.268±0.021 0.328±0.021 0.651±0.030 0.220±0.015 Co-Train SPC 0.610±0.020 0.103±0.060 0.321±0.035 0.379±0.035 0.727±0.030 0.256±0.010 Min-D SPC 0.400±0.001 0.328±0.002 0.196±0.001 0.270±0.001 0.475±0.005 0.189±0.001 DiMSC 0.304±0.007 0.261±0.009 0.130±0.009 0.199±0.008 0.405±0.018 0.132±0.006 GMVNMF 0.417±0.005 0.382±0.011 0.280±0.009 0.382±0.006 0.440±0.015 0.338±0.007 DMF_MVC 0.468±0.030 0.465±0.026 0.268±0.043 0.373±0.030 0.431±0.064 0.332±0.024 DGRMF_MVC 0.583±0.006 0.526±0.006 0.404±0.007 0.476±0.006 0.646±0.016 0.377±0.004 值得注意的是，本文的算法是基于矩阵分解的。在对比算法中，算法GMVNMF和DMF_MVC也是建立在矩阵分解之上的，且均加入了图正则化。从实验结果中可以看出，本文提出的算法在4个数据集上的表现比两种算法都好。其中，在Yale面部数据集上，本文算法相较于两种算法在各项指标上平均提高了43.1%和18.7%；在Extend Yale B面部数据集上分别平均提高了27.8%和6.6%；在UMIST面部数据集上，本文提出的算法在与算法GMVNMF进行比较时虽然在召回率上表现略低，但是在NMI上提高了9.3%，在ACC上提高了20.7%，在AR上提高了20.8%，在F-Measure上提高了18.5%，在精确率上提高了30%，均值仍能保持在14.5%，并且本文提出的算法在各项指标上表现更加稳定；在与算法DMF_MVC进行比较时，本文的算法在各项指标上分别提高了8.2%、11.8%、13.7%、12.9%、13.5%和16.3%，均值达在12.7%。在COIL-20图像数据集上则平均提高了30.6%和7.3%；在Caltech101-20图像数据集上平均提高了12.9%和11.2%。由此可见，本文算法使用的图正则化计算方式和逐层加入视角图正则化对于聚类有显著的改善效果。
4.3 算法分析
4.3.1 参数分析
算法中包括了视角权重和图正则化使用的平衡参数γ、λ，深度矩阵分解的各层维度以及计算局部图和全局图使用的最近邻值k，两者结合计算图矩阵的平衡参数η，其中λ与η有计算关联性。考虑到数据中局部关系和全局关系的等价值性，实验中固定设置
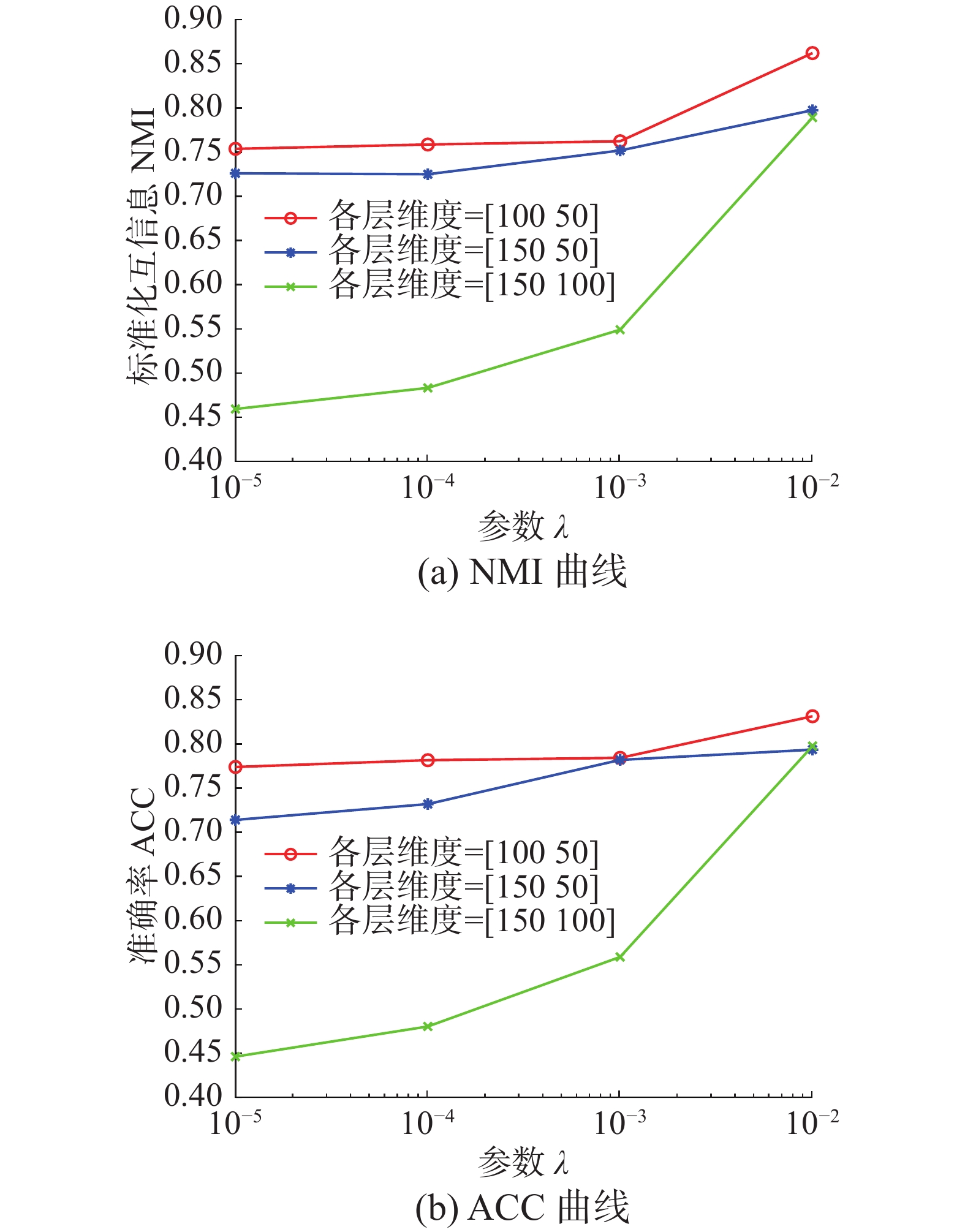
$\eta {\text{ = 1}}$ 。参数$\gamma =\left\{{10}^{-4}，{10}^{-3}， $ $ {10}^{-2},{{10}}^{{-1}},{{10}}^{{0}},{{10}}^{{1}},{{10}}^{{2}}\right\}$ ，参数$\lambda {=}\left\{{{10}}^{{-5}},{{10}}^{{-4}},{{10}}^{{-3}}, {{10}}^{{-2}}\right\}$ ，最近邻值k的选择在KNN算法中是一个开放性的问题，这里选择$\left\{\text{5},\text{10},\text{15}\right\}$ 3个值进行测试。图2和图3是在参数γ、λ和各层维度{[100 50],[150 50],[150 100]}影响下，算法生成的NMI和ACC的变化曲线。首先，从图2中可以看出，当γ变化时，NMI和ACC的各3条曲线变化幅度并不大，均控制在0.03以下，这就说明γ的变化对算法的性能影响不大。其次，从图3中NMI和ACC的变化曲线中可以看出，只有在分解维度为[150 100]时，参数λ的变化对于性能的影响才是最大的，同时，当λ=0.01时两项指标均达到最大且变化明显。最后从图2和图3中可以看出算法在分解维度为[100 50]时效果最好，且最为稳定；在分解维度为[150 100]时效果最差，同时曲线波动也最大。
图 2 不同参数γ和各层维度下算法在Yale面部数据集上的性能变化（k=5，λ=0.01）Fig. 2 Performance changes of the algorithm on the Yale face dataset under different parameters γ and each layer dimension (k=5，λ=0.01)下载:
全尺寸图片
图 3 不同参数λ和各层维度下算法在Yale面部数据集上的性能变化（k=5，γ=0.1）Fig. 3 Performance changes of the algorithm on the Yale face dataset under different parameters λ and each layer dimension (k=5，γ=0.1)下载:
全尺寸图片
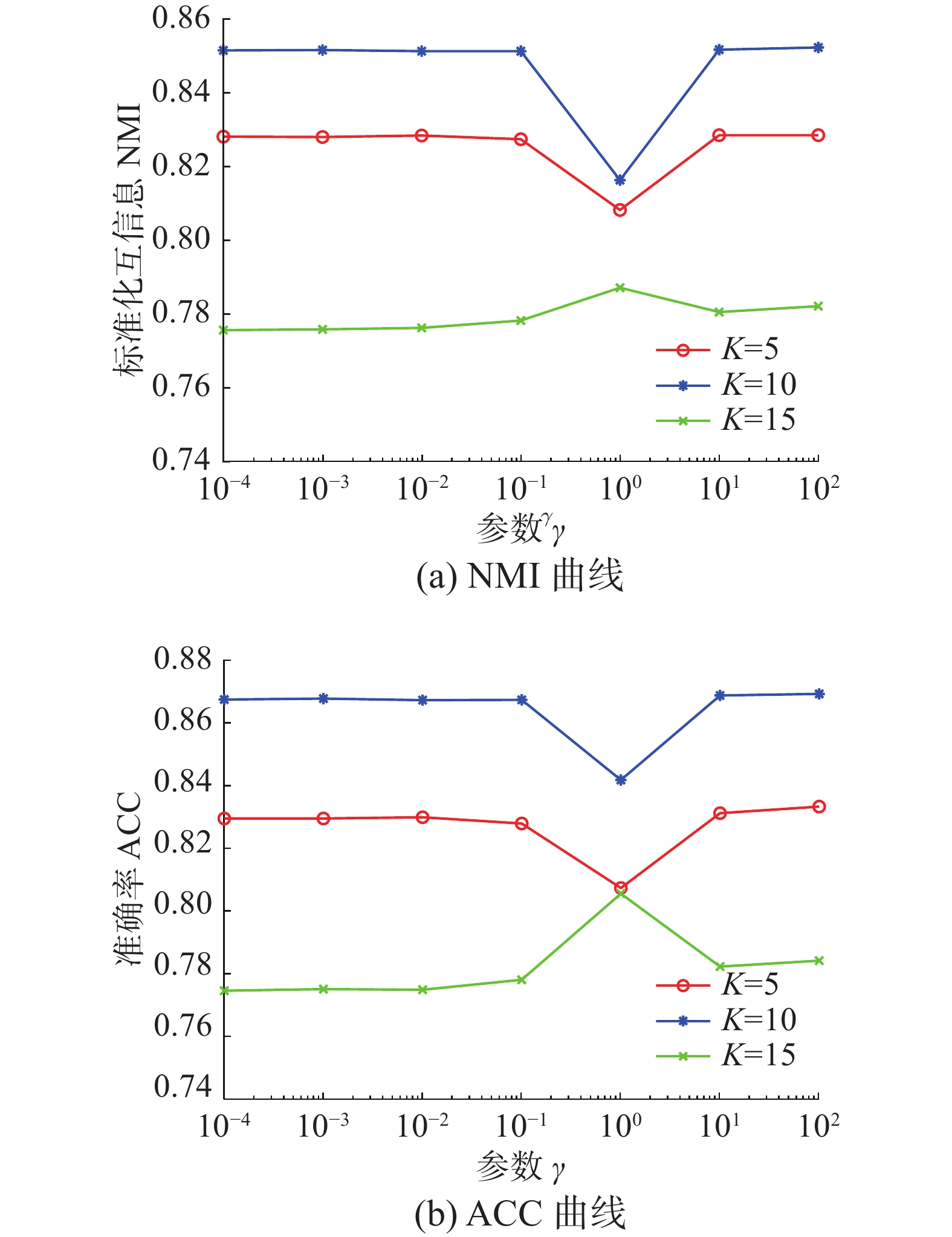
图4是算法在参数γ和最近邻k两者影响下生成的NMI和ACC数值折线图。从图中可以看出，NMI和ACC在k=10时达到最大值，在k=15时值最小，同时k=10与k=5对算法的影响控制在0.03之内；再结合图2可以进一步看出，参数γ在取
$\gamma =\left\{{10}^{-4},{10}^{-3},{{10}}^{{-1}},{{10}}^{{1}}\right\}$ 中的值时，效果能够达到最优。
图 4 不同参数γ和最近邻k下算法在Yale面部数据集上的性能变化（λ=0.01，各层维度=[100 50]）Fig. 4 Performance changes of the algorithm on the Yale face dataset under different parameters γ and the nearest neighbors k (λ=0.01，各层维度=[100 50])下载:
全尺寸图片
4.3.2 收敛性分析
关于算法的收敛性问题，从理论上来说，定理1说明了算法模型在每个视角的特征表示矩阵和共识表示矩阵优化问题上均落在一个固定点上。如图5是在实验中，设定参数值γ=10，λ=0.01，k=10，各层维度=[100 50]，优化问题(4)与NMI随着迭代次数不断增加而产生的变化曲线。从图5中可以明确看出，随着迭代次数的增加，目标函数值逐渐降低，NMI增加并逐渐保持稳定。当迭代次数在1~15时，目标函数值下降迅速；当达到20次或保持在50~67次时，NMI一直稳定在最高值，之后逐渐保持稳定，且目标函数值下降缓慢。为保证实验数据的稳定性，实验中迭代次数设定为100次。
图 5 迭代更新时算法的目标函数值和性能变化(γ=10, λ=0.01, k=10,各层维度=[100 50])Fig. 5 The objective function value and performance change of the algorithm during iterative update (γ=10, λ=0.01, k=10, layer dimension=[100 50])下载:
全尺寸图片
4.3.3 聚类可视化分析
为更形象的展示本文算法聚类过程，我们可视化了聚类结果，如图6所示。我们选择了每个数据集中的3个类别，每个类中包含随机的10张图片。从图中可以看出每个类中均包含非本类别中的图片对象。从图6(a)中可以看出，每个类中包含少量的错误对象，证明了算法的高准确率，同样的效果也可以从图6(d)中看到。在Extend YaleB数据集的3个类别中，算法的准确率并没有达到最优，如图6(c)中所示，算法在第3个类别中存在一定的错误。在图像数据集中，算法在COIL-20数据集上的表现良好(图6(b))，每个类别从上到下的准确率可以达到90%，90%，80%。对于图像构成更为复杂的Caltech101-20数据集，算法的准确度还有一定的进步空间(图6(e))。
4.3.4 复杂度分析
图7展示了所有算法在5个数据集上的运行时间变化。本文所使用的实验环境是Inter Core i7 8500 8 GB内存，Matlab R2018a版本。为保证数据的稳定性，大多数算法均运行了10次以上。结合运行时间和实验数据集两个内容可以看出大多数算法的时间复杂度与数据点的量级有直接联系。数据点越多，算法中涉及的计算和处理所消耗的时间越多。在时间复杂度上，基于矩阵分解的算法所需要的时间复杂度为
$ O\left({n}^{3}\right) $ 。同时，通过上述对算法收敛性的内容可以看出，基于矩阵分解的算法需要100次以上的迭代才能保持性能稳定，因此，基于矩阵分解的算法比其他大多数算法都需要消耗更长的时间。值得注意的是，相较于相近的DMF_MVC算法，本文提出的算法在时间复杂度上并没有明显的提高。这就说明本文的算法在保证性能提高的同时并没有增加时间消耗。
图 6 算法在各数据集上的聚类可视化Fig. 6 Cluster visualization of the algorithm on each dataset下载:
全尺寸图片
图 7 各算法在数据集上的运行时间Fig. 7 Running time of each algorithm on the dataset下载:
全尺寸图片
5. 结束语
本文中提出一种基于深度图正则化矩阵分解的多视图聚类算法，该算法使用深度非负矩阵分解模型并逐层加入图正则化限制，获取数据层次信息的同时保护数据的几何结构。权重的使用和共识表示矩阵的生成确保数据的一致性和差异性。实验数据表明，该算法在含有丰富几何结构的数据集上能够达到较高的准确率和稳定性。今后，需要加强对数据几何结构信息以及多视图数据表示学习的研究，提高多视图聚类的性能。
-
图 1 深度半非负矩阵分解
Fig. 1 Deep semi-nonnegative matrix factorization
下载:
全尺寸图片
图 2 不同参数γ和各层维度下算法在Yale面部数据集上的性能变化（k=5，λ=0.01）
Fig. 2 Performance changes of the algorithm on the Yale face dataset under different parameters γ and each layer dimension (k=5，λ=0.01)
下载:
全尺寸图片
图 3 不同参数λ和各层维度下算法在Yale面部数据集上的性能变化（k=5，γ=0.1）
Fig. 3 Performance changes of the algorithm on the Yale face dataset under different parameters λ and each layer dimension (k=5，γ=0.1)
下载:
全尺寸图片
图 4 不同参数γ和最近邻k下算法在Yale面部数据集上的性能变化（λ=0.01，各层维度=[100 50]）
Fig. 4 Performance changes of the algorithm on the Yale face dataset under different parameters γ and the nearest neighbors k (λ=0.01，各层维度=[100 50])
下载:
全尺寸图片
图 5 迭代更新时算法的目标函数值和性能变化(γ=10, λ=0.01, k=10,各层维度=[100 50])
Fig. 5 The objective function value and performance change of the algorithm during iterative update (γ=10, λ=0.01, k=10, layer dimension=[100 50])
下载:
全尺寸图片
图 6 算法在各数据集上的聚类可视化
Fig. 6 Cluster visualization of the algorithm on each dataset
下载:
全尺寸图片
图 7 各算法在数据集上的运行时间
Fig. 7 Running time of each algorithm on the dataset
下载:
全尺寸图片
表 1 不同算法在Yale面部数据集上的实验结果(均值±标准差)
Table 1 Experimental results of different algorithms on the Yale face dataset (mean ± standard deviation)
算法 NMI ACC AR F-score Precision Recall BestSC 0.670±0.010 0.642±0.010 0.453±0.110 0.489±0.103 0.466±0.107 0.514±0.010 ConcateFea 0.585±0.004 0.556±0.005 0.341±0.006 0.383±0.005 0.369±0.006 0.398±0.005 ConcatePCA 0.464±0.017 0.372±0.018 0.165±0.014 0.217±0.013 0.210±0.013 0.226±0.014 Co-Reg SPC 0.645±0.002 0.078±0.017 0.429±0.034 0.466±0.032 0.439±0.029 0.497±0.037 Co-Train SPC 0.669±0.028 0.084±0.065 0.457±0.038 0.491±0.035 0.469±0.033 0.516±0.028 Min-D SPC 0.655±0.001 0.642±0.000 0.444±0.000 0.476±0.001 0.463±0.000 0.498±0.000 DiMSC 0.635±0.001 0.569±0.001 0.408±0.001 0.447±0.001 0.412±0.001 0.489±0.001 GMVNMF 0.529±0.003 0.407±0.003 0.243±0.010 0.308±0.008 0.219±0.008 0.524±0.006 DMF_MVC 0.716±0.040 0.721±0.050 0.519±0.007 0.549±0.002 0.534±0.002 0.565±0.004 DGRMF_MVC 0.851±0.001 0.872±0.001 0.737±0.001 0.753±0.001 0.740±0.001 0.766±0.001 表 2 不同算法在Extend Yale B面部数据集上的实验结果(均值±标准差)
Table 2 Experimental results of different algorithms on the Extend Yale B face dataset (mean ± standard deviation)
算法 NMI ACC AR F-score Precision Recall BestSC 0.469±0.156 0.468±0.144 0.287±0.140 0.361±0.123 0.336±0.122 0.391±0.123 ConcateFea 0.401±0.001 0.342±0.001 0.164±0.000 0.262±0.000 0.221±0.000 0.322±0.001 ConcatePCA 0.507±0.002 0.556±0.002 0.342±0.001 0.410±0.001 0.391±0.001 0.431±0.003 Co-Reg SPC 0.182±0.015 0.101±0.005 0.087±0.009 0.179±0.007 0.175±0.008 0.183±0.007 Co-Train SPC 0.336±0.018 0.117±0.035 0.184±0.012 0.267±0.012 0.261±0.016 0.277±0.018 Min-D SPC 0.496±0.001 0.492±0.000 0.233±0.001 0.324±0.000 0.271±0.001 0.401±0.000 DiMSC 0.238±0.001 0.287±0.001 0.139±0.000 0.228±0.000 0.217±0.001 0.239±0.001 GMVNMF 0.263±0.005 0.316±0.004 0.124±0.004 0.215±0.003 0.204±0.003 0.228±0.003 DMF_MVC 0.580±0.014 0.645±0.005 0.288±0.011 0.379±0.009 0.293±0.010 0.537±0.018 DGRMF_MVC 0.624±0.005 0.679±0.010 0. 393±0.002 0.462±0.003 0.412±0.005 0.550±0.010 表 3 不同算法在UMIST面部数据集上的实验结果(均值±标准差)
Table 3 Experimental results of different algorithms on the UMIST face dataset (mean ± standard deviation)
算法 NMI ACC AR F-score Precision Recall BestSC 0.768±0.010 0.562±0.021 0.502±0.024 0.529±0.022 0.498±0.022 0.564±0.024 ConcateFea 0.764±0.007 0.549±0.019 0.491±0.018 0.518±0.017 0.488±0.018 0.554±0.017 ConcatePCA 0.534±0.008 0.459±0.011 0.251±0.010 0.291±0.009 0.277±0.012 0.310±0.008 Co-Reg SPC 0.676±0.007 0.047±0.011 0.391±0.009 0.423±0.008 0.414±0.008 0.432±0.009 Co-Train SPC 0.684±0.022 0.039±0.045 0.400±0.029 0.431±0.027 0.418±0.026 0.447±0.031 Min-D SPC 0.805±0.001 0.647±0.000 0.604±0.001 0.625±0.001 0.604±0.000 0.649±0.000 DiMSC 0.619±0.001 0.453±0.001 0.320±0.001 0.355±0.001 0.560±0.001 0.354±0.001 GMVNMF 0.758±0.002 0.506±0.005 0.436±0.002 0.478±0.002 0.330±0.001 0.864±0.004 DMF_MVC 0.769±0.030 0.595±0.009 0.507±0.008 0.534±0.004 0.495±0.060 0.581±0.009 DGRMF_MVC 0.851±0.001 0.713±0.001 0.644±0.001 0.663±0.010 0.630±0.001 0.744±0.002 表 4 不同算法在COIL-20数据集上的实验结果(均值±标准差)
Table 4 Experimental results of different algorithms on the COIL-20 dataset (mean ± standard deviation)
算法 NMI ACC AR F-score Precision Recall BestSC 0.943±0.021 0.853±0.024 0.826±0.026 0.836±0.024 0.771±0.029 0.913±0.037 ConcateFea 0.932±0.001 0.780±0.001 0.770±0.001 0.782±0.001 0.688±0.001 0.907±0.001 ConcatePCA 0.554±0.004 0.514±0.005 0.321±0.003 0.374±0.003 0.329±0.007 0.435±0.010 Co-Reg SPC 0.812±0.015 0.044±0.036 0.655±0.032 0.672±0.030 0.651±0.038 0.696±0.023 Co-Train SPC 0.824±0.014 0.081±0.031 0.669±0.050 0.686±0.047 0.665±0.037 0.714±0.023 Min-D SPC 0.897±0.001 0.836±0.000 0.789±0.001 0.800±0.001 0.773±0.000 0.828±0.000 DiMSC 0.843±0.013 0.771±0.018 0.724±0.020 0.737±0.019 0.730±0.018 0.745±0.020 GMVNMF 0.788±0.012 0.500±0.001 0.424±0.036 0.466±0.032 0.314±0.029 0.911±0.017 DMF_MVC 0.923±0.014 0.770±0.018 0.759±0.021 0.773±0.020 0.683±0.024 0.891±0.030 DGRMF_MVC 0.948±0.001 0.876±0.008 0.846±0.005 0.854±0.005 0.802±0.007 0.913±0.002 表 5 不同算法在Caltech101-20数据集上的实验结果(均值±标准差)
Table 5 Experimental results of different algorithms on the Caltech101-20 dataset (mean ± standard deviation)
算法 NMI ACC AR F-score Precision Recall BestSC 0.510±0.011 0.392±0.050 0.251±0.058 0.328±0.056 0.522±0.090 0.239±0.038 ConcateFea 0.385±0.003 0.340±0.017 0.190±0.011 0.267±0.012 0.457±0.014 0.188±0.010 ConcatePCA — — — — — — Co-Reg SPC 0.536±0.013 0.051±0.038 0.268±0.021 0.328±0.021 0.651±0.030 0.220±0.015 Co-Train SPC 0.610±0.020 0.103±0.060 0.321±0.035 0.379±0.035 0.727±0.030 0.256±0.010 Min-D SPC 0.400±0.001 0.328±0.002 0.196±0.001 0.270±0.001 0.475±0.005 0.189±0.001 DiMSC 0.304±0.007 0.261±0.009 0.130±0.009 0.199±0.008 0.405±0.018 0.132±0.006 GMVNMF 0.417±0.005 0.382±0.011 0.280±0.009 0.382±0.006 0.440±0.015 0.338±0.007 DMF_MVC 0.468±0.030 0.465±0.026 0.268±0.043 0.373±0.030 0.431±0.064 0.332±0.024 DGRMF_MVC 0.583±0.006 0.526±0.006 0.404±0.007 0.476±0.006 0.646±0.016 0.377±0.004 -
[1] 唐静静, 田英杰. 多视角学习综述[J]. 数学建模及其应用, 2017, 6(3): 1–15,25. doi: 10.3969/j.issn.2095-3070.2017.03.001 TANG Jingjing, TIAN Yingjie. A survey on multi-view learning[J]. Mathematical modeling and its applications, 2017, 6(3): 1–15,25. doi: 10.3969/j.issn.2095-3070.2017.03.001 [2] 何雪梅. 多视图聚类算法综述[J]. 软件导刊, 2019, 18(4): 79–81,86. https://www.cnki.com.cn/Article/CJFDTOTAL-RJDK201904019.htm HE Xuemei. A survey of multi-view clustering AlgorithmsChinese full text[J]. Software guide, 2019, 18(4): 79–81,86. https://www.cnki.com.cn/Article/CJFDTOTAL-RJDK201904019.htm [3] WANG Qianqian, DING Zhengming, TAO Zhiqiang, et al. Partial multi-view clustering via consistent GAN[C]//2018 IEEE International Conference on Data Mining. New York, USA: IEEE, 2018: 1290−1295. [4] CHAO Guoqing, SUN Shiliang, BI Jinbo. A survey on multiview clustering[J]. IEEE transactions on artificial intelligence, 2021, 2(2): 146–168. doi: 10.1109/TAI.2021.3065894 [5] YANG Yan, WANG Hao. Multi-view clustering: a survey[J]. Big data mining and analytics, 2018, 1(2): 83–107. doi: 10.26599/BDMA.2018.9020003 [6] ZHANG Guangyu, ZHOU Yuren, WANG Changdong, et al. Joint representation learning for multi-view subspace clustering[J]. Expert systems with applications, 2021, 166: 113913. doi: 10.1016/j.eswa.2020.113913 [7] 伍国鑫, 刘秉权, 刘铭. 一种改进的多视图K-均值聚类算法[J]. 智能计算机与应用, 2014, 4(3): 11–14,18. doi: 10.3969/j.issn.2095-2163.2014.03.003 WU Guoxin, LIU Bingquan, LIU Ming. An improved multi-view K-means clustering algorithm[J]. Intelligent computer and applications, 2014, 4(3): 11–14,18. doi: 10.3969/j.issn.2095-2163.2014.03.003 [8] XU Jinglin, HAN Junwei, NIE Feiping. Discriminatively embedded K-means for multi-view clustering[C]//2016 IEEE Conference on Computer Vision and Pattern Recognition. New York, USA: IEEE, 2016: 5356−5364. [9] YANG M S, SINAGA K P. A feature-reduction multi-view k-means clustering algorithm[J]. IEEE access, 2019, 7: 114472–114486. doi: 10.1109/ACCESS.2019.2934179 [10] NIE Feiping, CAI G, LI Xuelong. Multi-view clustering and semi-supervised classification with adaptive neighbours[C]//31th AAAI Conference on Artificial Intelligence. San Francisco, California. AAAI, 2017: 2408−2414. [11] NIE Feiping, LI Jing, LI Xuelong. Self-weighted multiview clustering with multiple graphs[C]//Proceedings of the Twenty-Sixth International Joint Conference on Artificial Intelligence. Melbourne, Australia: International Joint Conferences on Artificial Intelligence Organization, 2017: 2564−2570. [12] GAO Hongchang, NIE Feiping, LI Xuelong, et al. Multi-view subspace clustering[C]//2015 IEEE International Conference on Computer Vision. New York, USA: IEEE, 2015: 4238−4246. [13] 黄静. 加权多视图子空间聚类算法研究[D]. 广州: 广东工业大学, 2019: 1−65. HUANG Jing. Research on weighted multi-view subspace clustering algorithm[D]. Guangzhou: Guangdong University of Technology, 2019: 1−65. [14] 范瑞东, 侯臣平. 鲁棒自加权的多视图子空间聚类[J]. 计算机科学与探索, 2021, 15(6): 1062–1073. doi: 10.3778/j.issn.1673-9418.2007003 FAN Ruidong, HOU Chenping. Robust auto-weighted multi-view subspace clustering[J]. Journal of frontiers of computer science and technology, 2021, 15(6): 1062–1073. doi: 10.3778/j.issn.1673-9418.2007003 [15] ZHENG Qinghai, ZHU Jihua, LI Zhongyu, et al. Feature concatenation multi-view subspace clustering[J]. Neurocomputing, 2020, 379: 89–102. doi: 10.1016/j.neucom.2019.10.074 [16] 张祎. 多视图矩阵分解的聚类分析[D]. 大连: 大连理工大学, 2018: 1−69. ZHANG Yi. Clustering analysis on multi-view matrix factorization[D]. Dalian: Dalian University of Technology, 2018: 1−69. [17] 张祎, 孔祥维, 王振帆, 等. 基于多视图矩阵分解的聚类分析[J]. 自动化学报, 2018, 44(12): 2160–2169. https://www.cnki.com.cn/Article/CJFDTOTAL-MOTO201812003.htm ZHANG Yi, KONG Xiangwei, WANG Zhenfan, et al. Matrix factorization for multi-view clustering[J]. Acta automatica sinica, 2018, 44(12): 2160–2169. https://www.cnki.com.cn/Article/CJFDTOTAL-MOTO201812003.htm [18] DING C, LI Tao, JORDAN M I. Convex and semi-nonnegative matrix factorizations[J]. IEEE transactions on pattern analysis and machine intelligence, 2010, 32(1): 45–55. doi: 10.1109/TPAMI.2008.277 [19] TRIGEORGIS G, BOUSMALIS K, ZAFEIRIOU S, et al. A deep semi-nmf model for learning hidden representations[C]//International Conference on Machine Learning. Beijing, China. PMLR, 2014: 1692−1700. [20] ZHAO Handong, DING Zhengming, FU Yun. Multi-view clustering via deep matrix factorization[C]// 31th AAAI Conference on Artificial Intelligence. San Francisco, California. AAAI, 2017: 2921−2927. [21] HU Juncheng, LI Yonghao, GAO Wanfu, et al. Robust multi-label feature selection with dual-graph regularization[J]. Knowledge-based systems, 2020, 203: 106126. doi: 10.1016/j.knosys.2020.106126 [22] ZONG Linlin, ZHANG Xianchao, ZHAO Long, et al. Multi-view clustering via multi-manifold regularized non-negative matrix factorization[J]. Neural networks, 2017, 88: 74–89. doi: 10.1016/j.neunet.2017.02.003 [23] ZHANG Xinyu, GAO Hongbo, LI Guopeng, et al. Multi-view clustering based on graph-regularized nonnegative matrix factorization for object recognition[J]. Information sciences, 2018, 432: 463–478. doi: 10.1016/j.ins.2017.11.038 [24] ZHAO Handong, DING Zhengming, SHAO Ming, et al. Part-level regularized semi-nonnegative coding for semi-supervised learning[C]//2015 IEEE International Conference on Data Mining. New York, USA: IEEE, 2015: 1123−1128. [25] BELKINZ M, NIYOGI P. Laplacian eigenmaps and spectral techniques for embedding and clustering[J]Advances in neural information processing systems. 2001, 14: 585−591. [26] ISCEN A, TOLIAS G, AVRITHIS Y, et al. Label propagation for deep semi-supervised learning[C]//2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition. New York, USA: IEEE, 2019: 5065−5074. [27] HU Hongwei, MA Bo, SHEN Jianbing, et al. Manifold regularized correlation object tracking[J]. IEEE transactions on neural networks and learning systems, 2018, 29(5): 1786–1795. doi: 10.1109/TNNLS.2017.2688448 [28] BELKIN M, NIYOGI P. Laplacian eigenmaps for dimensionality reduction and data representation[J]. Neural computation, 2003, 15(6): 1373–1396. doi: 10.1162/089976603321780317 [29] HINTON G, ROWEIS S T. Stochastic neighbor embedding[C]//2002 Neural Information Processing Systems. New York, USA: ACM, 2002, 15: 833−840. [30] CARREIRA-PERPINAN M A. The elastic embedding algorithm for dimensionality reduction[C]//2010 International Conference on Machine Learning. New York, USA: ACM, 2010, 10: 167−174. [31] LI Zhihui, NIE Feiping, CHANG Xiaojun, et al. Balanced clustering via exclusive lasso: a pragmatic approach[C]//2018 AAAI Conference on Artificial Intelligence. Menlo Park, CA: AAAI, 2018, 32(1): 3596−3603. [32] NG A, JORDAN M, WEISS Y. On spectral clustering: analysis and an algorithm[J]. Advances in Neural Information Processing Systems, 2001, 14: 849–856. [33] KUMAR A, RAI P, DAUME H. Co-regularized multi-view spectral clustering[J]. Advances in Neural Information Processing Systems, 2011, 24: 1413–1421. [34] KUMAR A, DAUME H. A co-training approach for multi-view spectral clustering[C]//28th International Conference on Machine Learning. New York, USA: ACM, 2011: 393–400. [35] DE Sa V R. Spectral clustering with two views[C]//2005 ICML workshop on learning with multiple views. New York, USA: ACM, 2005: 20−27. [36] CAO Xiaochun, ZHANG Changqing, FU Huazhu, et al. Diversity-induced Multi-view subspace clustering[C]//2015 IEEE Conference on Computer Vision and Pattern Recognition. New York, USA: IEEE, 2015: 586−594. [37] LI Shaoyuan, JIANG Yuan, ZHOU Zhihua. Partial multi-view clustering[C]//2014 AAAI Conference on Artificial Intelligence. Menlo Park, CA: AAAI, 2014: 1968−1974. [38] RAI N, NEGI S, CHAUDHURY S, et al. Partial multi-view clustering using graph regularized NMF[C]//2016 23rd International Conference on Pattern Recognition. New York, USA: IEEE, 2016: 2192−2197.
