在大数据时代的背景下，数据呈现大量(数据量大)、多样(数据样式多)、高速(数据产生迅速)、低价值密度(数据有用性低)等特点，数据维度也出现井喷式剧增，同时也带来了一些隐私安全问题。2020年4月，Cyble安全公司报道称有约2.67亿Facebook用户信息被黑客盗取，并公开在暗网销售，造成大量用的敏感信息泄露，同年6月，我国郑州某民办高校约2万名学生身份信息泄露，多名学生及家长接到大量骚扰和威胁电话。2021年1月8日，某国外论坛公开贩卖国内某银行1679万条数据，并公开大量敏感数据样本。同年3月，安全研究人员发现某印度政府网站上存在安全问题导致孟加拉邦百万人次核酸检测结果泄露。报告中含有姓名、年龄、居住地址、检测时间、婚姻状况等大量敏感信息。大量的例子都说明大数据时代的背景下，数据安全问题变得尤为突出。

隐私数据泄露的同时也加剧了隐私保护的发展，相对于传统的数据匿名化保护方法(如k-匿名^[1]，l-多样性^[2]，t-紧密性^[3]， $ \left( {\alpha ,k} \right) $ -匿名^[4])存在不能抵御全部背景知识攻击^[5]的缺点，差分隐私因具有严格的数学定义和逻辑证明更加受到人们的广泛关注。差分隐私在隐私保护数据发布(privacy-preserving data publishing，PPDP)应用广泛，可以对隐私进行量化分析，在降低数据泄露风险的同时能更好地保障数据的效用性。

大数据呈现数据量大、数据样式多、数据产生迅速、数据有用性低特点，数据规模越来越大，数据相比于以往更加复杂多变，高维数据存在“维度灾难”，导致传统的分析手段失效，对于高维数据的挖掘变得更加困难。为了解决上述问题，常利用数据降维的思想，使高维数据映射到低维空间，在低维空间进行数据分析。本文综述了常见的对于高维数据的研究和差分隐私的结合方法，保证了在挖掘高维数据的同时可以降低数据泄露的风险。最后对未来的研究方向进行展望。

1 特征降维和差分隐私

特征降维^[6-7]是处理高维数据最常用的手段，如图1所示，一般特征降维分为特征抽取与特征选择两方面。前者是将原始数据的特征重新组合，生成包含原始信息的更精炼更具有代表性的特征；后者则是对数据进行筛选，筛选出原始数据的部分特征，生成特征子集，特征子集反映出原始数据的绝大部分规律，子集的数据结构更加清晰，便于分析。

而差分隐私是通过对输出的结果添加适当的噪声(多数为拉普拉斯机制、高斯机制和指数机制)实现对原始数据集的扰动，从而实现数据的隐私保护。差分隐私严格的数学定义如定义1。

定义1　 $ \varepsilon $ -差分隐私( $ \varepsilon $ -differentail prvac)：对兄弟数据集D₁和D₂(相差一条记录)，及其所有子集S，满足随机算法A：

$ \Pr \left[ {A\left( {{D_1}} \right) \in S} \right] \leqslant {{\rm{e}}^\varepsilon }\Pr \left[ {A\left( {{D_2}} \right) \in S} \right] $

则算法A满足 $ \varepsilon $ -差分隐私，其中e为自然对数， $ \varepsilon $ 为隐私预算(衡量隐私保护程度)。一般情况下，实现差分隐私可以通过拉普拉斯机制(数值型)和指数机制(离散型)。因为两种机制都依靠全局敏感度，故先定义全局敏感度。

定义2　全局敏感度(global sensitivity)：给定查询函数 $ f:D \to {R^d} $ ，D为输入数据集， $ {R^d} $ 为输出数据集。在任意一对D₁和D₂上，函数 $ f $ 的全局敏感度为

$ \Delta f = \mathop {\max }\limits_{{D_1},{D_2}} {\left\| {f\left( {{D_1}} \right) - f\left( {{D_2}} \right)} \right\|_1} $

其中 $ {\left\| {f\left( {{D_1}} \right) - f\left( {{D_2}} \right)} \right\|_1} $ 是 $ f\left( {{D_1}} \right) $ 和 $ f\left( {{D_2}} \right) $ 间的一阶距离。全局敏感度度量了当输入数据集变化时，对相应输出结果的影响。有了全局敏感度的概念后，给出Laplace机制和指数机制定义。

定义3　拉普拉斯机制(Laplace mechanism)：给定数据集D和隐私预算 $ \varepsilon $ ，函数 $ f $ 的全局敏感度为 $ \Delta f $ ，当 $ f $ 的输出满足：

$ A\left( D \right){\rm{ = }}f\left( D \right){\rm{ + Lap}}\left( {\Delta f/\varepsilon } \right) $

则称算法A满足 $ \varepsilon $ -差分隐私，其中 $ {\rm{Lap}}\left( {\Delta f/\varepsilon } \right) $ 为满足Laplace分布的随机噪声，如图2所示。

定义4　指数机制(index mechanism)：给定数据集D，输出为一个实体对象 $ \gamma \in R,\mu \left( {D,R} \right) $ 为可用性函数， $ \Delta \mu $ 为函数 $ \mu \left( {x,R} \right) $ 的敏感度，若以正比于 $ \exp \left( {\dfrac{{\varepsilon \cdot u\left( {x,r} \right)}}{{2\vartriangle u}}} \right) $ 的概率从输入中选择并输出r，则算法A满足 $ \varepsilon $ -差分隐私。其中 $\Delta u=\underset{r\in R，{\Vert {x-y}\Vert }_{1}\leqslant 1}{{\displaystyle {\rm{max}}}}|u\left({x},r\right)- $ $ u\left(y,r\right)|$ 。

经过特征降维后的数据，仍具有原始数据的绝大部分信息，再经过差分隐私处理后用于数据发布，在保证数据分析有效性的同时，可以大大提高数据的隐私保护程度。

1.1 基于线性特征抽取的差分隐私

特征抽取^[8]一般分为线性特征抽取和非线性特征抽取两类。由于线性特征抽取应用较多，这里则着重介绍。它是根据数据之间的线性关系进行数据的特征转换，产生的新特征复杂度更小，维数更低。

代表的方法是主成分分析方法^[9]，由于差分隐私直到2006年才由Dwork首次提出^[10-12]，所以主成分分析差分隐私算法近几年才慢慢成为研究的热点，它采用高维数据的主成分降维与加噪机制融合的方式，有效对高维数据进行隐私保护的同时还可以保证数据的高可用性。2012年，Chaudhuri等^[13]首次提出可用于数据发布的隐私保护算法，该算法采用指数机制来添加噪音实现了PCA满足差分隐私的要求，相较于子线性查询(SULQ)框架，采用此种方式可以得到数据的更多方差。但该算法缺乏收敛时间保证。针对这个问题，2013年，Kapralov等^[14]在此基础上提出一种用于低秩近似矩阵的混合规划算法，解决了因收敛时间保证从而造成隐私泄露的问题，但该算法时间复杂度较高，在用于高维数据发布时执行效率较低。

而Jiang等^[15]则是采用拉普拉斯机制来实现主成分分析差分隐私保护，它将一部分隐私预算去构建噪声协方差矩阵，剩余的隐私预算用于对投影矩阵的加噪。戚名钰等^[16]和徐亚红等^[17]分别在2017年和2018年对此方法进行改进，两者同样采用拉普拉斯机制，直接分解原始数据的协方差矩阵，然后在投影矩阵上加噪音，相比原来更为简便。但前者针对数据发布后面临的数据挖掘工作，又提出了一种基于线性判别分析的差分隐私数据发布算法，该算法是针对分类问题的优化，提高了发布数据分类精度和高可用性。后者通过设计的3种不同的加噪方式，得出了均分加噪效果更好的结论。

2020年，彭长根等^[18]根据传统的主成分分析差分隐私算法大多只能用于捕获线性关系，提出最大信息系数(MIC)实现主成分分析的差分隐私算法(MIC-PCA-DP)，该算法利用MIC构建主成分分析，在捕获线性关系的同时也可以捕获非线性关系和多函数关系，利用特征值占比加噪的方式对降维后的数据进行合理加噪，优化了噪声的分配方式，使算法执行效率进一步提升。2021年，顾贞等^[19]提出概率主成分分析的差分隐私数据发布方法，即由概率主成分分析的生成模型生成数据集发布，使得发布的数据集满足差分隐私。该方法在SVM分类准确率方面可以保持良好的数据效用。

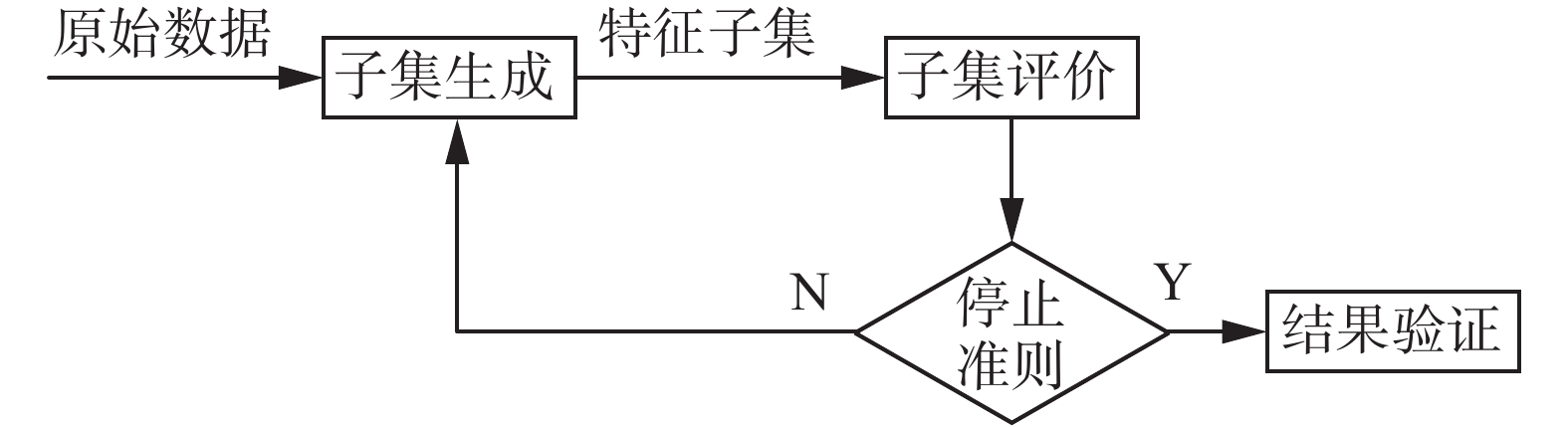
1.2 基于特征选择的差分隐私

特征选择^[20]是数据预处理的一种常用手段，它能有效降低高维数据的特征维数，过滤重复数据和噪声数据，输出满足要求的特征子集。特征选择通常包含特征子集生成、特征子集评价、停止准则和验证过程4个过程，如图3所示。

2013年，万文强^[21]首次将差分隐私机制融入到特征选择之中，将差分隐私与基于统计理论(基尼指数和误分类增益)的特征选择相结合，并采用分布式计算框架(Map-Reduce)实现分布式环境下的差分隐私特征选择方法。DPDFS算法能在选取重要特征的同时，有效保护用户数据隐私性不被泄露。

但上述算法并未考虑进行差分隐私的先后顺序对数据安全性的影响，且对于隐私预算 $ \varepsilon $ 的选取比较随机，效率较低。DPDFS算法只适用于数据的预处理阶段，对后续的数据挖掘(分类和聚类等)并不适用。下述方法是针对上述问题的解决方案。

2014年，Yang等^[22]，首先验证了基于差分隐私的集成特征选择算法的性能，得出在相同的环境下，先加入差分隐私保护的效果优于先进行特征选择的效果，并利用Objective Perturbation策略增加了特征选择算法的隐私保护强度。

2018年，高原秀男^[23]针对概率攻击问题，提出来基于特征选择和离群点检测的差分隐私算法，并针对医疗数据进行分析实验，在满足安全性要求的前提下，提高数据发布的可用性。DPFSOD是一种聚类算法，可以用于数据分析阶段，且对于隐私预算 $ \varepsilon $ 的选择，采用了数据集分簇后最小簇中元组数目相结合的方式，得到隐私预算 $ \varepsilon $ 值的取值范围。2018年，刘中锋^[24]，针对多值的特征选择，提出了基于局部学习的带有输出干扰策略的差分隐私集成特征选择算法，该算法采用了基于输出干扰的策略(向输出结果添加噪声)来保护隐私。并证明了局部差分隐私特征选择算法性能优于全局差分隐私特征选择算法。

以上提出的3种方法，均从不同角度改进了DPDFS算法的不足，在同一数据集上，均能达到更优的隐私保护效果。

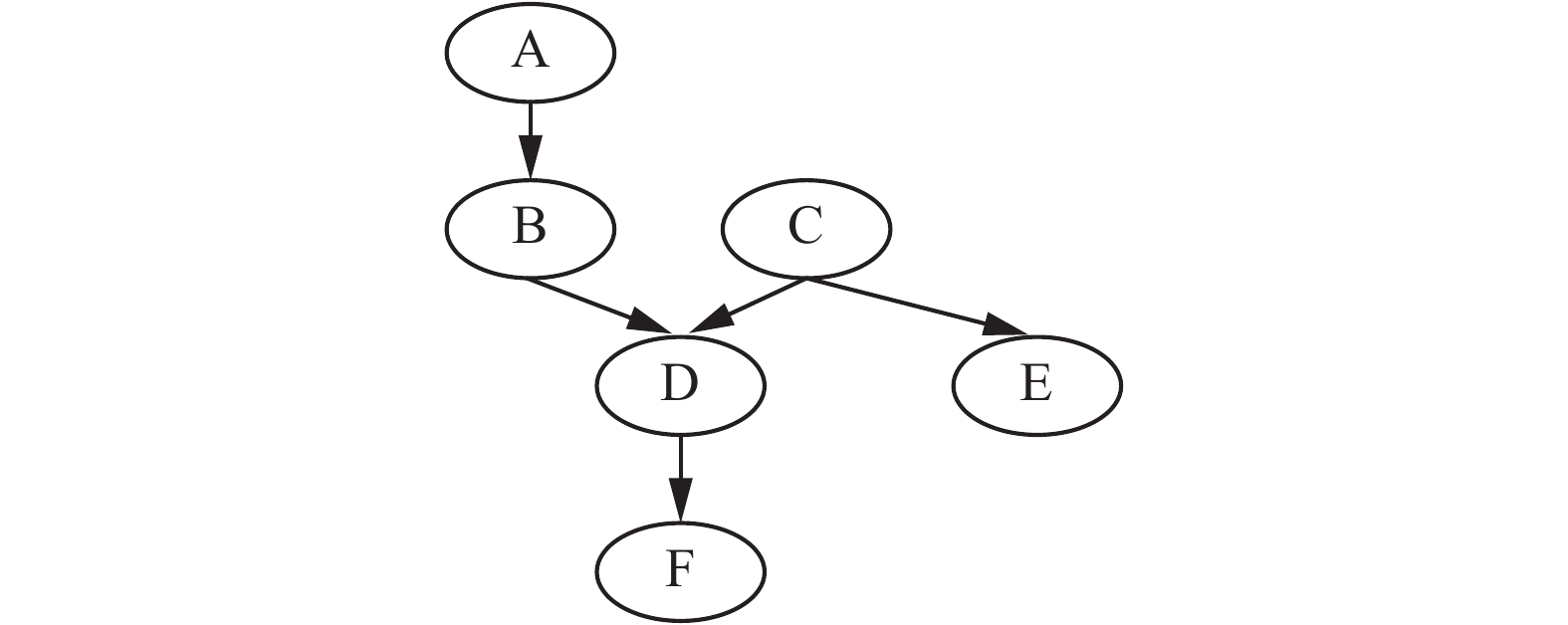
2 贝叶斯网络和差分隐私 2.1 贝叶斯网络模型

1988年，慕春棣等^[25]首次提出贝叶斯网络(Bayesian network)的概念，其本质是一种概率图模型，即通过先验知识，建立随机变量间的依赖关系，进而求取条件概率。贝叶斯网络是由结点(代表变量)和连接结点的边(代表依赖关系)组成，本质为一个有向无环图(directed acyclic graph，DAG)，可以有效处理变量间的依赖关系。图4是一个简单的贝叶斯网络模型，其中包含6个属性结点和5条有向边。

相比于特征降维方法，贝叶斯网络用图模型来表示数据间的依赖关系，更加直观且更容易被理解。高维数据因具有“维度灾难”和数据稀疏性等特点，使得数据的效用性很低，使得一般的隐私保护方法失去原有的保护效果。但贝叶斯网络能更容易确保数据属性间的一致性和完备性，因此在高维数据中有更广泛的应用空间，同时贝叶斯网络采用属性节点间的互信息大小来表示属性间的依赖程度，它将先验知识和样本知识结合，更加适用于稀疏性的高维数据。

2.2 基于贝叶斯网络的差分隐私

对高维数据的隐私保护方法研究中，很多没有考虑“维度灾难”问题直接加噪；也有一部分研究是对高维数据降维再对降维后的数据集注入噪声，但是这些方法仍然存在一些问题。为解决这些问题，2014 年，Zhang等^[26]提出了一种基于贝叶斯网络的差分隐私保护发布方法(PrivBayes)。该方法利用构建的贝叶斯网络实现对高维数据的降维，然后采用拉普拉斯机制对构建好的贝叶斯网络进行加噪，实现了差分隐私保护。但在构建贝叶斯网络时，首个属性字段节点选择方式随机，这种构造方式导致构造出来的贝叶斯网络具有不确定性，容易遭到攻击者模拟攻击，造成隐私的泄露。由于指数机制对属性对进行选择，随着属性对的增多，选择精度会明显下降。针对属性对选择随机的问题，2016年王良等^[27]提出了一种基于加权贝叶斯网络的隐私数据发布方法(加权PrivBayes)，该方法通过属性字段结点在发布数据集中的重要程度，为每一个属性字段结点增加一个权重值。并将K₂评分函数和互信息相结合，所构建的贝叶斯网络模型的分类精度更高。进一步优化属性字段结点加入噪声的顺序，相比于PrivBayes模型在发布数据集精确性和算法效率性上有明显提升。

上述方法同样存在构建的贝叶斯网络不唯一，精度不够高的问题，如果对原始数据集多次构建，可能会泄露隐私。同时该方法的隐私预算需要手动分配，有可能导致噪声的加入不合理，对数据的效用性和隐私性有影响。下面的研究就上面出现的问题给出了较合理的解决方案。

2017年汤诗一^[28]提出利用小波变换的方式实现差分隐私下的数据发布，同时用改良的F函数(捕获更多的互信息量)替换互信息，得到更准确的依赖关系，从而使构建的贝叶斯网络的精度更高。算法的核心思想是使用低维边缘分布去刻画贝叶斯网络，随后对低维边缘分布中的每一项均添加相同的拉普拉斯噪声，抽样形成带噪声的合成数据集D*。虽然小波变换实现了范围查询精度的提升，但该算法只能在单机环境下运行，且未将敏感字段作为第一考虑对象，导致算法普适性不足。

针对PriveBayes算法中加入噪声不合理，影响数据效用性的问题，2019年Li等^[29]提出SSPrivBayes(smooth sensitivity privacy Bayes)算法，该算法引入了平滑敏感度的概念，即在分析实际的数据集的同时考虑局部数据集变化，从而得到不同属性敏感度，有利于在进行差分隐私时减少噪声的摄入，来提高数据发布的效用性。并针对PriveBayes算法在构建贝叶斯网络搜索空间效率低的问题，提出了一种高效的贝叶斯网络搜索空间算法PBCPC(privacy Bayesian candidate parents and children)，该算法通过启发式方法得到目标变量的候选父子集，在属性数量过多时，算法运行效率明显高于PriveBayes。2018年，Wei等^[30]针对高维数据差分隐私发布中存在的数据稀疏性问题，提出基于马尔可夫网的高维数据差分隐私发布的方法(PrivMN)，即采用马尔可夫模型度量属性间的依赖性，然后结合图形近似推理算法计算高维数据差分隐私的分布，该算法能有效降低噪声摄入量，同时还解决了在精确推理中存在的计算复杂性高的问题。

针对现有的在基于构建贝叶斯网络差分隐私模型中，存在的贝叶斯网络不唯一和隐私预算分配不合理的情况，2019年唐雨薇^[31]提出了一种优化的贝叶斯差分隐私(OBDP)模型。该模型通过互信息构建网络、评分函数和组合优化算法得到候选稀疏节点集，采用爬山算法计算两个节点的净增益，确保构建的网络是唯一的。同时划分敏感属性和非敏感属性及不同的属性簇，对不同的属性簇添加不同程度的噪声，从而确保隐私运算分配更合理。

上述方法从不同角度优化了贝叶斯网络，但都不适用于群智感知系统的高维数据发布，因此，任雪斌等^[32]针对群智感知系统采用本地差分隐私保护方法，即用感知服务器接收用户的隐私信息，然后计算其联合概率分布和互信息值从而构建出贝叶斯网络模型，最后按不同属性信息降维，合成新的数据集，经过大量仿真实验对比，验证了该合成数据的有效性。2020年，肖彪等^[33]利用属性段首选机制并利用聚类的方法取代等宽法对数据进行离散化处理，该算法避免了对首个属性段属性的随机化选择，提高了数据的可用性。

3 树模型和差分隐私

树模型^[34]，即通过构建特征子树实现高维数据的降维。最早，在PrivBayes的基础上Chen等^[35]在2015年提出一种基于抽样推理的差分隐私发布方法(JTree算法)，该方法采用基于抽样的框架和阈值机制相融合的方式构建属性依赖图，然后利用联合树最小化误差，在依赖图中识别出一组边缘表逼近联合分布，最终实现高维数据发布。

但上述方法中构建的团图容易出现局部最优。针对这些问题，2018年张啸剑等^[36]提出了一种基于联合树的差分隐私高维数据发布算法(PrivHD算法)，该算法利用马尔可夫网络对高维数据进行降维并结合高通滤波的方式对生成的属性对进行过滤，最后采用联合树生成完全团图，该过程符合差分隐私要求，在数据查询和分类上均高于JTree算法。同年，苏炜航等^[37]采用隐树模型对高维数据的关联属性对进行过滤，该算法(LTMDP算法)在生成隐变量过程中通过互信息值提前分组，在分组过程中引入指数机制使该过程满足差分隐私，在隐树结构学习中引入拉普拉斯机制并采用自顶向下的采样方式生成高维数据集，该算法采用隐树模型在执行效率和分析精度上高于PrivBayes算法。2019年，郝志峰等^[38]引入格雷码和语义树对PrivBayes算法改进，提出了基于语义树和贝叶斯网络的发布算法(PrivBayes-Hierarchical算法)，该算法用格雷码使插入的噪声鲁棒性更好，提高数据的高可用性，同时采用语义层次树减少数据误差，提高分类精度。

上述3种方法均采用不同的树模型，对从不同角度对PrivBayes算法进行改进，因此在执行效率上均优于传统的PrivBayes算法。

针对在高维数据中搜索日志泄露的问题，陆叶等^[39]利用前缀树的思想，提出一种满足差分隐私的前缀树方法，该算法通过前缀树把项集中小于k的剪枝，然后关联频繁项，对用户的ID进行差分隐私保护，保证了用户的敏感信息不被泄露，但该算法执行效率较低。同样采用前缀树的实例，2017年王晓男^[40]针对多维顺序数据，采用改良的前缀树对数据集采用分层加噪，减少了隐私预算的消耗，在降低相对误差的同时使模型的执行效率和安全性得到提升。2020年，邓蔚等^[41]采用指数机制和Laplace机制分别处理连续型特征和离散型特征并准确找到最佳分裂特征和分裂点,采用等差预算分配加噪策略。该算法充分利用了隐私预算，提高了分类准确度。

4 粗糙集及随机投影的差分隐私 4.1 基于粗糙集的差分隐私

随着数据维度的增加，数据之间关联程度也会提高，而差分隐私对于关联数据的保护水平往往很低，原因是维数的增加导致噪声的增多，如果采用传统的加噪方式，可能会破坏属性间的关联性，从而降低数据的效用性。虽然很多方法针对这个问题，采用互信息去计算属性间的相关性，然后对不同数据采用分别加噪的方式去降低噪声的添加量，但对敏感数据和非敏感数据的区分往往存在较大误差。

粗糙集理论是由Pawlak教授^[42]提出的，它是用于处理不确定关系的一种数学工具。

定义5　决策系统(decision system)：在粗糙集理论中，知识的表达是用决策系统表示的，一个决策系统由一个四元组表示：

$ S=(U,A,V,f) $

式中：U为非空有限集，称为论域；A为非空有限属性集，由条件属性集C和决策属性集D组成；V=U_α∈AV_α，V_α是属性α的值域；f : U×A→V是信息函数(样本空间到属性空间)数据属性间的关联性，可以用粗糙集中属性依赖度k进行衡量(k为1表示D完全依赖C)，然后再针对不同的属性添加合理的噪声。属性集D在C上的依赖度公式为

$ k=\frac{{\mathop a\limits^ \circ}_{X \in U / D}\;|\underline{C}(X)|}{|U|} $

Pawlak属性约简算法^[43]可以有效把高维数据中不相关的冗余信息剔除，得到分类规则。该算法的主要思想是求出核属性并启发式扩展，最后得到一个约简。但该方法计算核属性过程较繁琐，因此王一斌^[44]利用差别矩阵来构成差分函数，通过析取和合取运算去简化区分函数，从而可以快速得到所有的约简。2017年孙志鹏^[45]针对高维数据的属性约简利用粗糙集理论去改进K均值算法，提出自适应的粗糙集K均值算法，该算法有效提高了聚类的精度。2019年Li等^[46]针对医疗数据，首次将差分隐私和粗糙集提取规则相结合，提出了一种挖掘医疗数据中隐藏模式、保障患者隐私的新方法(DPRers)。该算法利用拉普拉斯机制在数据挖掘过程中增加噪声，同时使数据的效用最大化。2019年Luo等^[47]利用粗糙集对高维数据的降维的同时，引入信息熵衡量数据的敏感度达到更合理的加噪方式，提高了数据的效用性。

粗糙集具有的优势和高维数据的特点十分契合，比普通的降维方法有着天然的优势，因此两者的结合往往能够起到很好的隐私保护效果。

4.2 基于随机投影的差分隐私

随机投影^[48]能有效解决高维数据“维度灾难”问题。它的理论依据是Johnson-Lindenstrauss引理。

定义6　Johnson-Lindenstrauss引理：任意给定一个整数d>0，存在 $ \varepsilon \in \left( {0,1} \right) $ 和 $ \delta < 1/2 $ ， $k = $ $ O \left( {\dfrac{1}{{{\varepsilon ^2}}}\log \left( {\dfrac{1}{d}} \right)} \right)$ ，存在一个映射 $f:{\bf{R}}^d \to {\bf{R}}^k$ ， $x \in {\bf{R}}^d$ ，

$ {P_r}\left[ {\left| {\left\| {f(x)} \right\|_2^2 - \left\| x \right\|_2^2} \right| \geqslant \varepsilon \left\| x \right\|_2^2} \right] \leqslant \delta $

Johnson-Lindenstrauss引理^[49]表明将d维空间的n个点映射到k维(k<d)，可以保证原空间中任意两点间的距离是近似不变的。因此通过随机投影技术能够实现高维数据的有效降维，同时经过数据扰动后也能有效保留数据的可用性。

当投影矩阵构建完成后，投影矩阵泄露可能也会导致数据的泄露。针对这个问题，2013年杨静等^[50]利用哈希函数产生随机投影矩阵并引入安全子空间去保障构建投影矩阵的安全性。同年，针对高维数据的稀疏性问题，Hardt等^[51]利用随机投影方法使输入矩阵满足差分隐私的低秩近似逼近，同时给出误差边界，并针对误差边界为空的情况，通过幂迭代法替换原来生成的特征向量，增强扰动可靠性的同时，该方法还能减少由于添加噪声所引起的误差边界，消除了数据矩阵秩具有的依赖关系。2014年赵家石^[52]就高维稀疏数据易遭到攻击者通过重建原始数据，导致隐私泄露的问题，采用噪声投影扰动和差分隐私结合，即先进行投影转换，在此基础上添加噪声(相互独立的随机数)，可有效确保扰动数据的可用性。

两者都是针对高维数据的稀疏性问题，但从不同角度给出了不同的处理方案，共同点都是采用投影转换的思考方式。

近年，在保护数据据隐私的前提下去发布高维数据集引起了数据库界越来越多的关注。2017年Xu等^[53]针对现有的差分隐私无法解决由于干扰误差和计算复杂度增加对高维数据发布失效的问题，提出了一种基于随机投影的数发布算法(DPPro)，主要思想采用随机投影将数据集从高维空间投影到随机选择的低维空间中，以保持欧式距离不变，从而使用户根据距离进行分割。然后对每个矢量添加高斯噪声，这样，可以在最小化添加噪声量的同时最大化提高效用性，确保发布数据的隐私性。针对高维数值型数据(多个数值型属性)，在处理较大属性个数时误差较大的问题，2020年孙慧中等^[54]满足本地差分隐私的高维数值型数据收集算法(Multi-RPHM),与DPPro算法不同之处的，用户自己通过随机投影对原始高维数据降维，然后发送给数据收集者，数据收集者再进行维度还原，生成高维扰动数据集用于数据发布。

5 方法对比

本节将以上提到的技术及算法进行汇总比较，列举出了各种方法代表算法的优缺点，如表1所示，基于特征抽取、贝叶斯网络、树模型、粗糙集、投影和差分隐私结合的方法比较。

为了更直观比较各个技术的内在联系和主要区别，给出各个算法的针对不同场景的对比表格，包括PPCA和DPPro、PrivBayes和DPRers、PrivMN和PrivHD在不同场景下的优缺点和数据可用性分析，如表2所示。

6 结束语

大数据时代下，对高维数据的挖掘比以往任何时候都更加迫切，采用非常规手段往往会导致用户隐私的泄露。差分隐私是一种被严格证明的隐私保护模型，可有效抵制各种安全攻击。因此把差分隐私应用到高维数据上可以有效实现数据的隐私安全保障。本文就高维数据的差分隐私模型作出详细归纳总结，包括将特征降维、贝叶斯网络、树模型等方法与其结合应用，分析了不同方法的优缺点和应用场景。

未来，数据将会更加复杂多变，因此必定会产生更多问题。

1)属性关联性强。数据属性之间往往存在关联性，随着数据维度的增加，属性间的关联性更加复杂。近期提出一些研究方法，如通过粗糙集的属性依赖度去度量属性的关系程度，然后针对不同属性添加不同的噪声。但相关研究的文章仍然较少，未来有较大的空间亟待研究。

2)算法复杂度高。目前，差分隐私在高维数据的应用大多停留在实验阶段，往往伴随着较高的时间复杂度，导致算法的效率较低，无法高效地应用到生产实践中。因此，亟需对算法进行优化，以满足实际应用的需要。