Finite-time trajectory tracking control based on an adaptive neural network for a quadrotor UAV
-
摘要: 针对带有模型不确定性和未知外部干扰的四旋翼无人机轨迹跟踪控制问题，提出一种基于径向基(radial basis function, RBF)神经网络的自适应全局快速终端滑模控制方法，确保系统对期望轨迹的有限时间跟踪。该方法考虑到全局快速终端滑模控制在实际应用中的适应性和抖振问题，利用RBF神经网络替代等效控制量，以神经网络的在线学习能力补偿系统内部的不确定性和未知的外部干扰，有效地降低了系统的抖振；根据Lyapunov方法导出的自适应律在线调整神经网络权值，以保证闭环系统的稳定性。通过一系列仿真算例和飞行实验验证了该方法的有效性与可行性，结果表明：该控制方法相对于滑模控制的抖振更小，具有更好的收敛性和抗干扰能力，同时对模型的参数摄动具有更强的鲁棒性。Abstract: Aimed at the trajectory tracking control problem of a quadrotor UAV with model uncertainties and unknown external disturbances, an adaptive global fast terminal sliding mode control method based on the RBF neural network has been proposed herein. The proposed method assists the system in tracking the desired trajectory in finite time. Considering the adaptability of global fast terminal sliding mode control in practical applications and chattering problems, the equivalent control quantity has been replaced by RBF neural networks. The chattering of the system has been reduced effectively by compensating for model uncertainty and unknown external disturbances with online learning of neural networks. According to the adaptive law derived from the Lyapunov method, the weights of neural networks are adjusted online to ensure the stability of the closed-loop system. Through a series of simulation examples and flight experiments, the effectiveness and feasibility of the proposed method have been validated. Results show that the proposed method has less chattering, better convergence, and anti-interference ability. It is also more robust toward model parameter perturbation compared to the sliding mode control.
-
四旋翼无人机因其结构简单、操控方便、灵活机动等优点，被广泛应用于军事和民用领域，如农林植保、电力巡检、军事侦查、空运物流等[1-2]。四旋翼飞行器是高度非线性、欠驱动、强耦合的时变系统[3-4]，对外部干扰极为敏感。飞行环境复杂多变，因此要求飞行控制系统具有较强的适应性、鲁棒性、抗干扰性和快速收敛能力[5-6]。针对四旋翼无人机的控制难点，目前常采用非线性控制策略或智能控制方法设计飞行控制器，如滑模控制[7-8]、反步法[9-10]、模糊控制[11]、模型预测控制[12]、自抗扰控制[13-14]、强化学习控制[15]、神经网络[16]等。然而，上述方法较为依赖精确的数学模型或者大量的飞行数据，对未建模动态特性和未知干扰的适应性较差。另外，常见的控制算法大都无法保证系统状态变量能在有限时间内收敛，导致响应速度较慢。
跟踪误差收敛速度是四旋翼无人机这一类实时控制系统的重要性能指标[17-18]，研究发现全局快速终端滑模控制(global fast terminal sliding mode control, GFTSM)能有效处理有限时间收敛问题。GFTSM引入了快速终端（fast terminal）吸引子使得任意系统状态在有限时间收敛，又保证了线性滑动模态在接近平衡态时的快速性，使得系统状态在有限时间内始终以最快速度收敛到平衡状态。文献[19-20]研究了基于GFTSM的旋翼飞行器姿态控制系统，取得了不错的效果。文献[21]将递归控制方法与鲁棒控制算法相结合，针对四旋翼飞行器的位置跟踪和姿态控制，设计了一种有限时间自适应积分反步快速终端滑模控制。文献[22]采用自适应模糊全局快速终端滑模控制(adaptive fuzzy global fast terminal sliding mode control, AF-GFTSMC)方法，在存在外部扰动和参数不确定性的情况下，研究过驱动无人飞行器的跟踪控制问题。然而，上述针对GFTSM算法的研究工作也存在一些固有缺陷，如固定的扰动上界、依赖部分模型信息、抖振现象明显等，这些不足极大地限制了GFTSM方法在实际应用中的表现。
利用神经网络的万能逼近能力描述复杂系统的非线性动态特性，是处理模型不确定性和未知扰动的一种有效途径[23]。神经网络与GFTSM的结合不仅可以减轻GFTSM对部分模型信息和扰动上界的依赖，还可以有效削弱系统抖振现象[24-25]。目前，结合GFTSM与RBF神经网络技术的四旋翼轨迹跟踪控制研究鲜有报道，本文旨在利用这一技术提高四旋翼飞行器在模型不确定性和外界干扰下的控制性能，即利用自适应RBF神经网络在线估计GFTSM控制律中含有模型信息和扰动上界的等效控制量，在无需模型信息的情况下实现跟踪误差的有限时间快速收敛。另外，在Lyapunov理论框架下分析了控制系统的稳定性和快速收敛性。最后，通过仿真算例和飞行实验对本文方法的快速收敛性、鲁棒性和抗干扰能力进行验证。
1. 四旋翼动力学模型
四旋翼主要由两组旋转方向相反的旋翼组成，每个旋翼产生升力
${F_i}$ 和力矩${M_i}(i = 1,2,3,4)$ ，如图1所示。
图 1 四旋翼的结构Fig. 1 Quadrotor Structure
下载:
全尺寸图片
系统通过改变每个旋翼的转速控制机体的旋转力矩和水平分力，进而驱动四旋翼完成飞行动作。为了简化建模过程，假设四旋翼质心、几何中心与坐标系原点重合。整个系统的动力学模型可根据牛顿欧拉法获得，其中位置动力学模型为
$$ m\ddot {\boldsymbol{P}} = {\boldsymbol{FRe}}_3 - mg{{\boldsymbol{e}}_3} + {{\boldsymbol{d}}_F} $$ (1) 式中：
${\boldsymbol{P}} = {\left[ x\;y\;z \right]^{\text{T}}}$ 表示四旋翼质心在惯性坐标系$OXYZ$ 下的位置向量；$m$ 为机身质量；${{\boldsymbol{e}}_3} = {\left[ 0\;0\;1 \right]^{\text{T}}}$ 表示垂直方向的单位向量；$\boldsymbol F$ 为四个旋翼的总升力；${{\boldsymbol{d}}_F}$ 表示集成了气流产生的扰动力和系统参数不确定性的总扰动项；${\boldsymbol{R}}$ 表示体坐标系${O_1}{X_1}{Y_1}{Z_1}$ 到惯性坐标系$OXYZ$ 的转换矩阵，即$$ {\boldsymbol{R}} = \left[ {\begin{array}{*{20}{c}} {{c_\theta }{c_\psi }}&{{s_\theta }{c_\psi }{s_\phi } - {s_\psi }{c_\phi }}&{{s_\theta }{c_\psi }{s_\phi } + {s_\psi }{s_\phi }} \\ {{c_\theta }{s_\psi }}&{{s_\theta }{s_\psi }{s_\phi } + {c_\psi }{c_\phi }}&{{s_\theta }{s_\psi }{c_\phi } - {c_\psi }{s_\phi }} \\ { - {s_\theta }}&{{c_\theta }{s_\phi }}&{{c_\theta }{c_\phi }} \end{array}} \right] $$ (2) 接着，四旋翼的姿态子动力学方程为
$$ {\boldsymbol{J}}\dot {\boldsymbol{\omega }} = - {\boldsymbol{\omega }} \times {\boldsymbol{J\omega}} + {\boldsymbol{\varGamma}} + {{\boldsymbol{d}}_\varGamma } $$ (3) 式中：
${\boldsymbol{\omega}} = {[ {{\omega _x}}\;{{\omega _y}}\;{{\omega _z}} ]^{\text{T}}}$ 表示无人机在体坐标系上的角速度向量；${\boldsymbol{J}}$ 为飞行器转动惯量；${\boldsymbol{\varGamma}} = {[ {{\varGamma _\phi }}\;{{\varGamma _\theta }}\;{{\varGamma _\psi }} ]^{\text{T}}}$ 表示机体的旋转力矩；${{\boldsymbol{d}}_\varGamma }$ 表示包含了气流产生的扰动力矩和姿态子系统参数不确定性的总扰动项。$$ \dot {\boldsymbol{\varTheta}} = {\boldsymbol{T}}({\boldsymbol{\varTheta}} ){\boldsymbol{\omega}} $$ (4) 式中：
${\boldsymbol{\varTheta}} = {\left[ \phi \;\;\theta \;\;\psi \right]^{\text{T}}}$ 表示无人机的姿态角向量，$ \phi $ 是横滚角，$\theta $ 是俯仰角，$\psi $ 是偏航角；${\boldsymbol{T}}({\boldsymbol{\varTheta}} )$ 为映射矩阵，即$$ {\boldsymbol{T}}({\boldsymbol{\varTheta}} ){\text{ = }}\left[ {\begin{array}{*{20}{c}} 1&{\sin \phi \tan \theta }&{\cos \phi \tan \theta } \\ 0&{\cos \phi }&{ - \sin \phi } \\ 0&{\sin \phi \sec \theta }&{\cos \phi \sec \theta } \end{array}} \right] $$ (5) 2. 四旋翼轨迹跟踪控制器设计
考虑到四旋翼是欠驱动系统，本文采用双层控制结构设计轨迹跟踪控制器：外层根据位置参考信号
${{\boldsymbol{P}}_r} = {\left[ {{x_r}}\;{{y_r}}\;{{z_r}} \right]^{\text{T}}}$ 计算平移运动所需的俯仰角$ {\theta _r} $ 、横滚角$ {\phi _r} $ 以及总升力$ F $ ，内环姿态控制器跟踪外环提供的参考姿态角计算旋转力矩${\boldsymbol{\varGamma}}$ 。控制系统的结构如图2所示。
图 2 四旋翼轨迹跟踪控制器结构Fig. 2 Structure of quadrotor trajectory tracking controller下载:
全尺寸图片
2.1 位置控制器设计
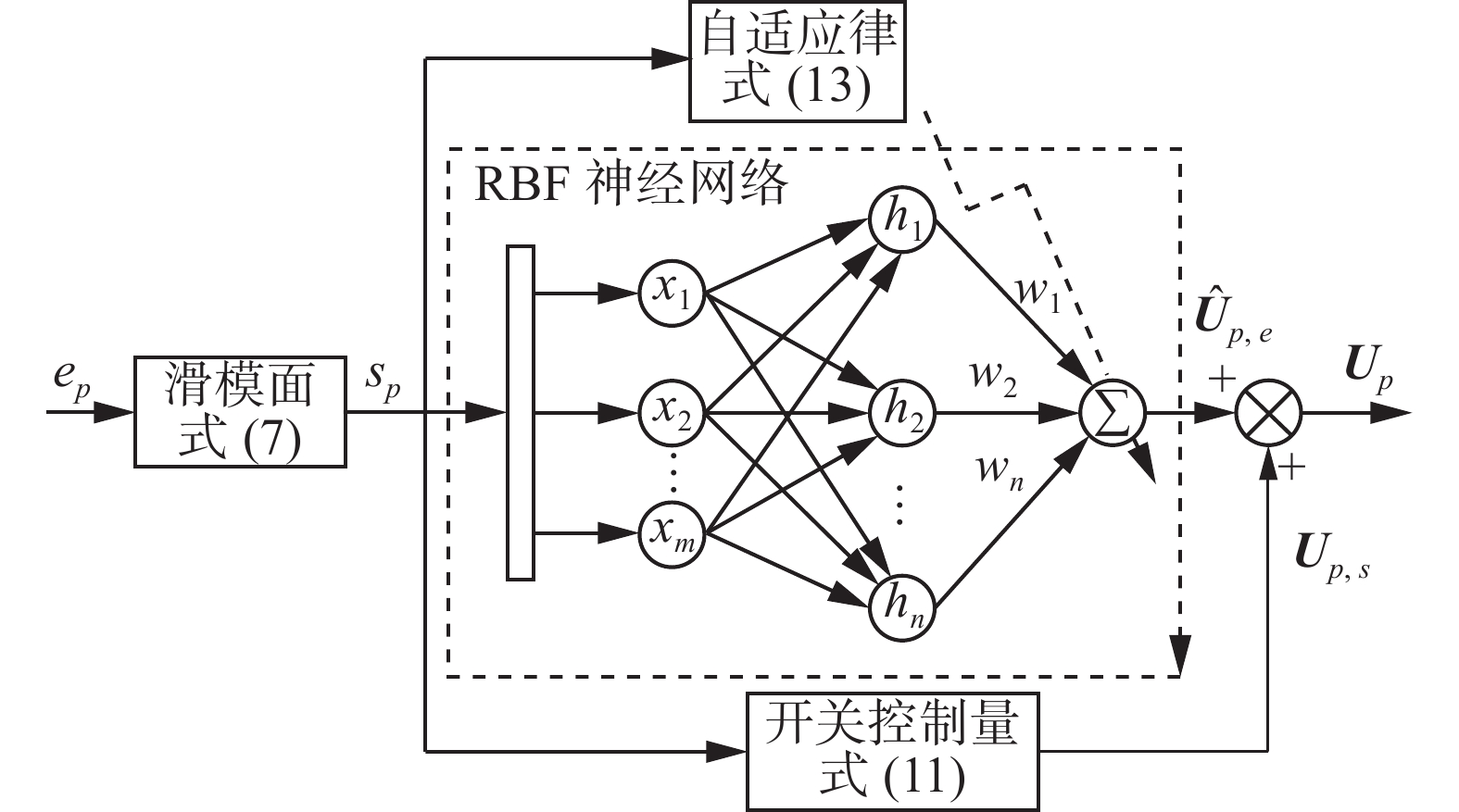
基于RBF神经网络的位置控制器结构如图3所示。假设参考位置向量
${{\boldsymbol{P}}_r}$ 光滑且具有二阶导数，则位置跟踪误差为${{\boldsymbol{e}}_p} = {\boldsymbol{P}} - {{\boldsymbol{P}}_r}$ ，由式（1）可得位置系统误差方程为$$ {\ddot {\boldsymbol{e}}_p} = \frac{{{{\boldsymbol{U}}_p} + {{\boldsymbol{d}}_{\boldsymbol{F}}}}}{m} - g{{\boldsymbol{e}}_3} - {\ddot {\boldsymbol{P}}_d} $$ (6) 式中
${{\boldsymbol{U}}_p} = {\boldsymbol{FR}}{{\boldsymbol{e}}_3}$ 为待设计的位置系统虚拟控制量。
图 3 基于RBF神经网络的GFTSM控制器结构Fig. 3 Structure of GFTSM controller based on RBF neural network下载:
全尺寸图片
根据GFTSMC理论取滑模面为
$$ {{\boldsymbol{s}}_p} = {\dot {\boldsymbol{e}}_p} + {\alpha _1}{{\boldsymbol{e}}_p} + {\beta _1}{\boldsymbol{e}}_p^{{q_1}/{r_1}} $$ (7) 式中：
$ {\alpha _1} > 0 $ ，$ {\beta _1} > 0 $ ；${q_1}$ 和${r_1}$ $({q_1} < {r_1})$ 均为正奇数。通过对
${{\boldsymbol{s}}_p}$ 求导，并代入式（6）得$$ \begin{aligned} &\quad \quad{{\dot {\boldsymbol{s}}}_p} = {{\ddot {\boldsymbol{e}}}_p} + {\alpha _1}{{\dot {\boldsymbol{e}}}_p} + {\beta _1}\dfrac{{{q_1}}}{{{r_1}}}{\boldsymbol{e}}_{p^{({q_1} - {r_1})/{r_1}}}{{\dot {\boldsymbol{e}}}_p} =\\ & \dfrac{{{{\boldsymbol{U}}_p} + {{\boldsymbol{d}}_F}}}{m} - g{{\boldsymbol{e}}_3} - {{\ddot {\boldsymbol{P}}}_d} + {\alpha _1}{{\dot {\boldsymbol{e}}}_p} + {\beta _1}\dfrac{{{q_1}}}{{{r_1}}}{\boldsymbol{e}}_{p^{({q_1} - {r_1})/{r_1}}}{{\dot {\boldsymbol{e}}}_p} \hfill \\ \end{aligned} $$ (8) 根据滑模控制原理，控制律
${\boldsymbol{U}}_p$ 可以设计为等效控制量${\boldsymbol{U}}_{p,e}^ *$ 与开关控制量${{\boldsymbol{U}}_{p,s}}$ 之和：$$ {\boldsymbol{U}}_p^{} = {\boldsymbol{U}}_{p,e}^ * + {{\boldsymbol{U}}_{p,s}} $$ 式中：
${{\boldsymbol{U}}}_{p,e} ^* \;=\; m(g{{\boldsymbol{e}}_3} \;+\; {\ddot {\boldsymbol{P}}_d}\; -\; {\alpha _1}{\dot {\boldsymbol{e}}_p} \;- \;{\beta _1}\dfrac{{{q_1}}}{{{r_1}}}{\boldsymbol{e}}_{p^{({q_1} - {r_1})/{r_1}}}{\dot {\boldsymbol{e}}_p}) - {{\boldsymbol{d}}_F}$ ；${{\boldsymbol{U}}_{p,s}} = - {\lambda _1}{{\boldsymbol{s}}_p} - {\delta _1}{\boldsymbol{s}}_p^{q/r}$ ；${\lambda _1}$ 和$ {\delta _1} $ 为待定控制参数。在实际工程中，干扰力和模型不确定性是未知的，为此本文设计RBF神经网络在线逼近
${\boldsymbol{U}}_{p,e}^ *$ 。根据${\boldsymbol{U}}_{p,e}^ *$ 的计算公式，网络输入取${{\boldsymbol{x}}_1} = [ {{\boldsymbol{s}}_p^{\text{T}}}\;{\ddot {\boldsymbol{P}}_r^{\text{T}}} ]$ ，则RBF神经网络输出$\hat {\boldsymbol{U}}_{p,e}^{}$ 为$$ \hat {\boldsymbol{U}}_{p,e}^{} = {\boldsymbol{Wh}}({x_1}) $$ (9) 式中：
${\boldsymbol{W}}$ 为神经网络权值；${\boldsymbol{h}}({{\boldsymbol{x}}_1}) = {[ {h_{1}(x)}\; {h_{2}(x)} \cdots \;{{h_{n}(x)}} ]^{\text{T}}}$ 为网络的隐含层输出，其中${h_j}(x) = \exp \left({\left\| {{{\boldsymbol{x}}_1} - {{\boldsymbol{c}}_j}} \right\|^2}/{\boldsymbol{b}}_j^2\right), $ $ (j = 1,2, \cdots ,n)$ 为高斯基函数；${{\boldsymbol{c}}_j}$ 和${\boldsymbol{b}}_j$ 为高斯基函数的参数。设计权值自适应律为
$$ \dot {\boldsymbol{W}} = - \frac{{{\eta _1}}}{m}{{\boldsymbol{s}}_p}{\boldsymbol{h}}({{\boldsymbol{x}}_1}) $$ (10) 则位置子系统实际控制律为
$$ {{\boldsymbol{U}}_p} = \hat {\boldsymbol{U}}_{p,e}^{} + {{\boldsymbol{U}}_{p,s}} $$ (11) 在得到控制律
${{\boldsymbol{U}}_p}$ 之后还需推导升力$F$ 和姿态子系统参考信号${{\boldsymbol{\varTheta}} _r} = {\left[ {{\phi _r}}\;{{\theta _r}}\;{{\psi _r}} \right]^{\text{T}}}$ 。根据${{\boldsymbol{U}}_p}= {{F}}{{\boldsymbol{Re}}_3}$ ，以及式（1）、（2）将$ {U_p} $ 展开可以得到：$$ {{\boldsymbol{U}}_p} = \left[ {\begin{array}{*{20}{c}} {{u_x}} \\ {{u_y}} \\ {{u_z}} \end{array}} \right]{\text{ = }}\left[ {\begin{array}{*{20}{c}} {{{F}}\left( {\sin \theta \cos \psi \cos \phi + \sin \psi \sin \phi } \right)} \\ {{{F}}\left( {\sin \theta \sin \psi \cos \phi - \cos \psi \sin \phi } \right)} \\ {{{F}}\cos \theta \cos \phi } \end{array}} \right] $$ (12) 将偏航角
$ {\psi _r} $ 作为自定义参考信号，${{\boldsymbol{U}}_p} = {[{{u_x}}\;{{u_y}}\;{{u_z}} ]^{\text{T}}}$ 由式（12）计算，进一步推导系统需要的中间控制信号为$$ \left\{ \begin{aligned} &{\phi _r} = \arctan \left( {\cos {\theta _r}\frac{{{u_x}\sin {\psi _r} + {u_y}\cos {\psi _r}}}{{{u_z}}}} \right) \hfill \\ &{\theta _r} = \arctan \left( {\frac{{{u_x}\cos {\psi _r} + {u_y}\sin {\psi _r}}}{{u_z^{}}}} \right) \hfill \\ &F = \frac{{{u_z}}}{{\cos {\theta _r}\cos {\phi _r}}} \hfill \\ \end{aligned} \right. $$ 定理 如果采用控制律式（11）、神经网络输出式（9）以及权值自适应律式（10），则闭环系统稳定且跟踪误差
$ {{\boldsymbol{e}}_p} $ 在有限时间内收敛于零。证明 假设存在最优权值
${{\boldsymbol{W}}^ * }$ ，使得神经网络可以以极小的误差$\varepsilon $ 逼近${\boldsymbol{U}}_{p,e}^ *$ ，即$$ {\boldsymbol{U}}_{p,e}^ * = {{\boldsymbol{W}}^ * }{\boldsymbol{h}}({\boldsymbol{x}}) + \varepsilon $$ 取实际权值与最优权值之差为
$\tilde {\boldsymbol{W}} = {\boldsymbol{W}} - {{\boldsymbol{W}}^ * }$ ，则$$ \hat {\boldsymbol{U}}_{p,e} - {\boldsymbol{U}}_{p,e}^ * = \tilde {\boldsymbol{Wh}}({\boldsymbol{x}}) + \varepsilon $$ (13) 将式（11）和式（13）代入式（8）得
$$ \begin{aligned} {{\dot {\boldsymbol{s}}}_p} &= \dfrac{1}{m}\left( - \lambda {{\boldsymbol{s}}_p} - {\delta _1}{\boldsymbol{s}}_p^{q/r} + {{\hat {\boldsymbol{U}}}_p} - {\boldsymbol{U}}_p^ * \right) =\\ & \frac{1}{m}\left( - \lambda {{\boldsymbol{s}}_p} - {\delta _1}{\boldsymbol{s}}_p^{q/r} + \tilde {\boldsymbol{Wh}}({\boldsymbol{x}}) + \varepsilon \right) \hfill \\ \end{aligned} $$ (14) 取Lyapunov函数
${V_1}$ 为$$ {V_1} = \frac{1}{2}s_p^2 + \frac{1}{{2\eta }}{\tilde {\boldsymbol{W}}^{\rm{T}}}\tilde {\boldsymbol{W}} $$ 对
${V_1}$ 取导数得$$ \begin{aligned} &\quad\quad\quad\quad\quad\quad\quad{{\dot V}_1}= {\boldsymbol{s}}_p\dot {\boldsymbol{s}}_p + \dfrac{1}{\eta }{{\tilde {\boldsymbol{W}}}^{\rm{T}}}\dot {\boldsymbol{W}} = \\ & \quad - \dfrac{\lambda }{m}{\boldsymbol{s}}_p^2 - \dfrac{{{\delta _1}}}{m}{\boldsymbol{s}}_p^{(r + q)/r} + \frac{1}{m}{{\boldsymbol{s}}_p}\left(\tilde {\boldsymbol{Wh}}({\boldsymbol{x}}) + \varepsilon \right) + \frac{1}{\eta }{{\tilde {\boldsymbol{W}}}^{\rm{T}}}\dot {\boldsymbol{W}} = \\ & - \dfrac{\lambda }{m}{\boldsymbol{s}}_p^2 - \dfrac{1}{m}{\boldsymbol{s}}_p^{(r + q)/r}\left({\delta _1} + \dfrac{\varepsilon }{{{\boldsymbol{s}}_p^{q/r}}}\right) + {{\tilde {\boldsymbol{W}}}^{\rm{T}}}\left(\dfrac{1}{m}{{\boldsymbol{s}}_p}{\boldsymbol{h}}({\boldsymbol{x}}) + \dfrac{1}{\eta }\dot {\boldsymbol{W}}\right)= \\ & \quad\quad\quad\quad\quad - \dfrac{\lambda }{m}{\boldsymbol{s}}_p^2 - \dfrac{1}{m}{\boldsymbol{s}}_p^{(r + q)/r}\left({\delta _1} + \dfrac{\varepsilon }{{{\boldsymbol{s}}_p^{q/r}}}\right) \\ \end{aligned} $$ (15) 由式（15）可以证明，当参数
${\delta _1} > \dfrac{\varepsilon }{{\left| {{\boldsymbol{s}}_p^{q/r}} \right|}}$ 时，$\dot V_1\leqslant 0$ ，滑模函数${\boldsymbol{s}}_p$ 和$\tilde {\boldsymbol{W}}$ 收敛于零，闭环系统稳定。因此，参数${\delta _1}$ 可以设计为$$ {\delta _1} = \dfrac{\varepsilon }{{\left| {{\boldsymbol{s}}_p^{q/r}} \right|}} + {\sigma _1} $$ 式中
${\sigma _1}$ 是正数。当滑模函数
${\boldsymbol{s}}_p = 0$ 时，由式（7）得$$ {\dot {\boldsymbol{e}}_p}{\text{ = }} - {\alpha _1}{{\boldsymbol{e}}_p} - {\beta _1}{\boldsymbol{e}}_p^{{q_1}/{r_1}} $$ 取Lyapunov函数
${V_2}$ 为$$ {V_2} = \dfrac{1}{2}{\boldsymbol{e}}_p^2 $$ 对
${V_2}$ 求导数得$$ {\dot V_2} = {\boldsymbol{e}}_p^{}\dot {\boldsymbol{e}}_p= - {\alpha _1}{\boldsymbol{e}}_p^2 - {\beta _1}{\boldsymbol{e}}_p^{({r_1} + {q_1})/{r_1}} \leqslant 0 $$ (16) 由式（16）可知，当
${\boldsymbol{s}}_p^{}$ 收敛于0时，${\boldsymbol{e}}_p^{}$ 也收敛于0。将式（14）改写为
$$ {\dot {\boldsymbol{s}}_p} = - \lambda '{{\boldsymbol{s}}_p} - \delta '{\boldsymbol{s}}_p^{{q_1}/{r_1}} $$ (17) 式中：
$\lambda ' = \dfrac{\lambda }{m}$ ；$\delta '=\dfrac{\delta }{m} - \dfrac{{\tilde {\boldsymbol{Wh}}({\boldsymbol{x}}) + \varepsilon }}{{m{\boldsymbol{s}}_p^{q/r}}}$ 。通过求解式（17）可以得到从任意非零初始状态
${{\boldsymbol{s}}_p}(0) \ne 0$ 收敛到${{\boldsymbol{s}}_p}({t_s}) \ne 0$ 所经历的时间$ {t_s} $ 为$$ \begin{aligned} {t_s} &= \dfrac{{{r_1}}}{{\lambda '({r_1} - {q_1})}}\ln \dfrac{{\lambda '{{\boldsymbol{s}}_p}{{(0)}^{({r_1} - {q_1})/{q_1}}} + \delta '}}{{\delta '}} \leqslant \\ &\quad \dfrac{{{r_1}}}{{\lambda '({r_1} - {q_1})}}\ln \dfrac{{\lambda '{{\boldsymbol{s}}_p}{{(0)}^{({r_1} - {q_1})/{q_1}}} + \sigma }}{\sigma } \hfill \\ \end{aligned} $$ 补充1 在自适应律式（13）的作用下，权值
${\boldsymbol{W}}$ 无限接近最优权值，逼近误差$\varepsilon $ 趋于0。因此$\delta $ 的切换幅值极小，开关控制量${{\boldsymbol{U}}_{p,s}}$ 的切换幅值也极小，可以消除抖振现象。补充2 只要合理设置控制参数，系统的跟踪误差
${{\boldsymbol{e}}_p}$ 将会在有限时间内随${{\boldsymbol{s}}_p}$ 快速收敛到0。2.2 姿态控制器设计
为了跟踪位置子系统给出的参考姿态角
${{\boldsymbol{\varTheta}} _r}$ ，需要设计姿态控制律计算控制力矩${\boldsymbol{\varGamma}}$ 。根据式（3）、（4），四旋翼的旋转动力学方程可以改写为$$ {\boldsymbol{J}}\ddot {\boldsymbol{\varTheta}} = f(\cdot)\dot {\boldsymbol{\varTheta}} + {\boldsymbol{\varGamma}} + {{\boldsymbol{d}}_\varGamma } $$ 式中
$f(\cdot)=f(\dot {\boldsymbol{\varTheta}} ,{\boldsymbol{\varTheta}} ,{\boldsymbol{J}})$ ，表示姿态子系统部分动态。定义姿态子系统的跟踪误差为
${{\boldsymbol{e}}_a} = {\boldsymbol{\varTheta}} - {{\boldsymbol{\varTheta}} _r}$ ，则姿态误差系统为$$ {\ddot {\boldsymbol{e}}_a} = \dfrac{1}{\boldsymbol J}(f( \cdot )\dot {\boldsymbol{\varTheta}} + {\boldsymbol{\varGamma}} + {{\boldsymbol{d}}_\varGamma }) - {\ddot {\boldsymbol{\varTheta}}_r} $$ 根据GFTSMC理论引入滑模函数为
$$ {{\boldsymbol{s}}_a} = {\dot {\boldsymbol{e}}_a} + {\alpha _2}{{\boldsymbol{e}}_a} + {\beta _2}{\boldsymbol{e}}_a^{{q_2}/{r_2}} $$ 式中：
${\alpha _2} > 0；{\beta _2} > 0$ ；${q_2}$ 、${r_2}$ $({q_2} < {r_2})$ 均为正奇数。通过对
${{\boldsymbol{s}}_a}$ 求导可得：$$ \begin{aligned} & \quad\quad\quad{{\dot {\boldsymbol{s}}}_a}= {{\ddot {\boldsymbol{e}}}_a} + {\alpha _2}{{\dot {\boldsymbol{e}}}_a} + {\beta _2}\dfrac{{{q_2}}}{{{r_2}}}{\boldsymbol{e}}_a^{({q_2} - {r_2})/{r_2}}{{\dot {\boldsymbol{e}}}_a} = \\ & \dfrac{1}{\boldsymbol J}(f( \cdot )\dot {\boldsymbol{\varTheta}} + {\boldsymbol{\varGamma}} + {{\boldsymbol{d}}_\varGamma }) - {{\ddot {\boldsymbol{\varTheta}} }_r} + {\alpha _2}{{\dot {\boldsymbol{e}}}_a} + {\beta _2}\dfrac{{{q_2}}}{{{r_2}}}{\boldsymbol{e}}_a^{({q_2} - {r_2})/{r_2}}{{\dot {\boldsymbol{e}}}_a} \\ \end{aligned} $$ 根据滑模控制原理，可以将姿态环控制律
${\boldsymbol{U}}_a^ *$ 设计为等效控制量${\boldsymbol{U}}_{a,e}^ *$ 与开关控制量${{\boldsymbol{U}}_{a,s}}$ 之和，即$$ {\boldsymbol{U}}_a^ * = {\boldsymbol{U}}_{a,e}^ * + {{\boldsymbol{U}}_{a,s}} $$ 其中：
$$ {\boldsymbol{U}}_{a,e}^ * = - {\boldsymbol{J}}( - {\ddot {\boldsymbol{\varTheta}} _r} + \alpha {\dot {\boldsymbol{e}}_a} + \beta \dfrac{{{q_2}}}{{{r_2}}}{\boldsymbol{e}}_a^{({q_2} - {r_2})/{r_2}}{\dot {\boldsymbol{e}}_a}) - f( \cdot )\dot {\boldsymbol{\varTheta}} - {{\boldsymbol{d}}_\varGamma } $$ (18) $$ {{\boldsymbol{U}}_{a,s}} = - {\lambda _2}{{\boldsymbol{s}}_a} - {\delta _2}{\boldsymbol{s}}_a^{{q_2}/{r_2}} $$ 式中
${\lambda _2}$ 和$ {\delta _2} $ 为待定控制参数。$$ {\delta _2} = \dfrac{\varepsilon }{{\left| {{\boldsymbol{s}}_p^{{q_2}/{r_2}}} \right|}} + {\sigma _2} $$ 式中
${\sigma _2}$ 是正数。根据式（18），网络输入可取
${{\boldsymbol{x}}_2} = [{{\boldsymbol{s}}_a^{\text{T}}}\;\;{\ddot {\boldsymbol{\varTheta}} _r^{\text{T}}} ]$ ，则RBF神经网络输出$\hat {\boldsymbol{U}}_{a,e}^{}$ 为$$ \hat {\boldsymbol{U}}_{a,e} = {{\boldsymbol{W}}_2}{\boldsymbol{h}}({{\boldsymbol{x}}_2}) $$ 式中
${{\boldsymbol{W}}_2}$ 为姿态子系统的神经网络权值。设计权值自适应律为
$$ {\dot {\boldsymbol{W}}_2} = - \dfrac{{{\eta _2}}}{{{m_2}}}{{\boldsymbol{s}}_a}{\boldsymbol{h}}({{\boldsymbol{x}}_2}) $$ 则姿态子系统实际控制律为
$$ {\boldsymbol{\varGamma}} = \hat {\boldsymbol{U}}_{a,e}^{} + {{\boldsymbol{U}}_{a,s}} $$ 姿态控制子系统的稳定性分析和快速收敛性分析类似于位置控制子系统，不再赘述。
3. 仿真及实验验证
本节开展四旋翼的轨迹跟踪仿真实验及飞行实验，通过与传统滑模控制方法的对比验证本文方法的快速收敛性、鲁棒性和抗干扰能力。仿真在Matlab环境中进行，控制对象的数学模型根据式（6）建立，模型参数如表1所示。
表 1 仿真参数Table 1 simulation parameter物理参数 数值 质量m/ kg 2.1 重力加速度g/m·s−2 9.8 旋翼中心到飞行器质心距离 $l$/ m 0.275 x轴转动惯量 ${J_x}$/ kg∙m2 0.039 y轴转动惯量 ${J_y}$/ kg∙m2 0.039 z轴转动惯量 ${J_z}$/ kg∙m2 0.046 控制律参数设置为：
$ {\alpha _1} = 4.5 $ ，$ {\beta _1} = 1.4 $ ，${q_1} = 3$ ，${r_1} = 7$ ，${\sigma _1} = 0.2$ ，${\lambda _1} = 10$ ，$ {\alpha _2} = 8.2 $ ，$ {\beta _2} = 2.5 $ ，${q_2} = 3.5$ ，${r_2} = 7.5$ ，${\sigma _2} = 0.2$ ，${\lambda _2} = 20$ 。自适应律参数设置为：${\eta _1} = 10.5$ ，${\eta _2} = 14.5$ 。BRF神经网络参数设置为：$n = 5$ ，$c = [{ - 2.6}\;\;{ - 1.2}\;\;0\;\;{ - 1.2}\;\;{ - 2.6} ]$ ，$b = 2$ 。3.1 收敛快速性对比
四旋翼初始位置取
$[{0.6}\;\;{ - 0.5}\;\;{0.4} ]$ ，初值姿态角取$[0\;0\;0 ]$ ，参考位置设为$[0\;0\;0 ]$ ，参考偏航角设为$ {30^{\text{o}}} $ 。仿真得到两种控制方法达到稳态的时间，结果如表2所示。本文方法具有更快的收敛速度，其位置和偏航角的收敛速度比传统滑模控制算法分别快了23.5%、23.3%、18.2%和27.8%。表 2 收敛时间Table 2 Convergence time控制
通道本文控制
方法/s常规滑模
控制/s加快百
分比/%x 1.83 2.26 23.5
y 1.72 2.12 23.3
z 1.65 1.95 18.2 $\psi $ 0.72 0.92 27.8 3.2 鲁棒性对比
四旋翼初始位置取
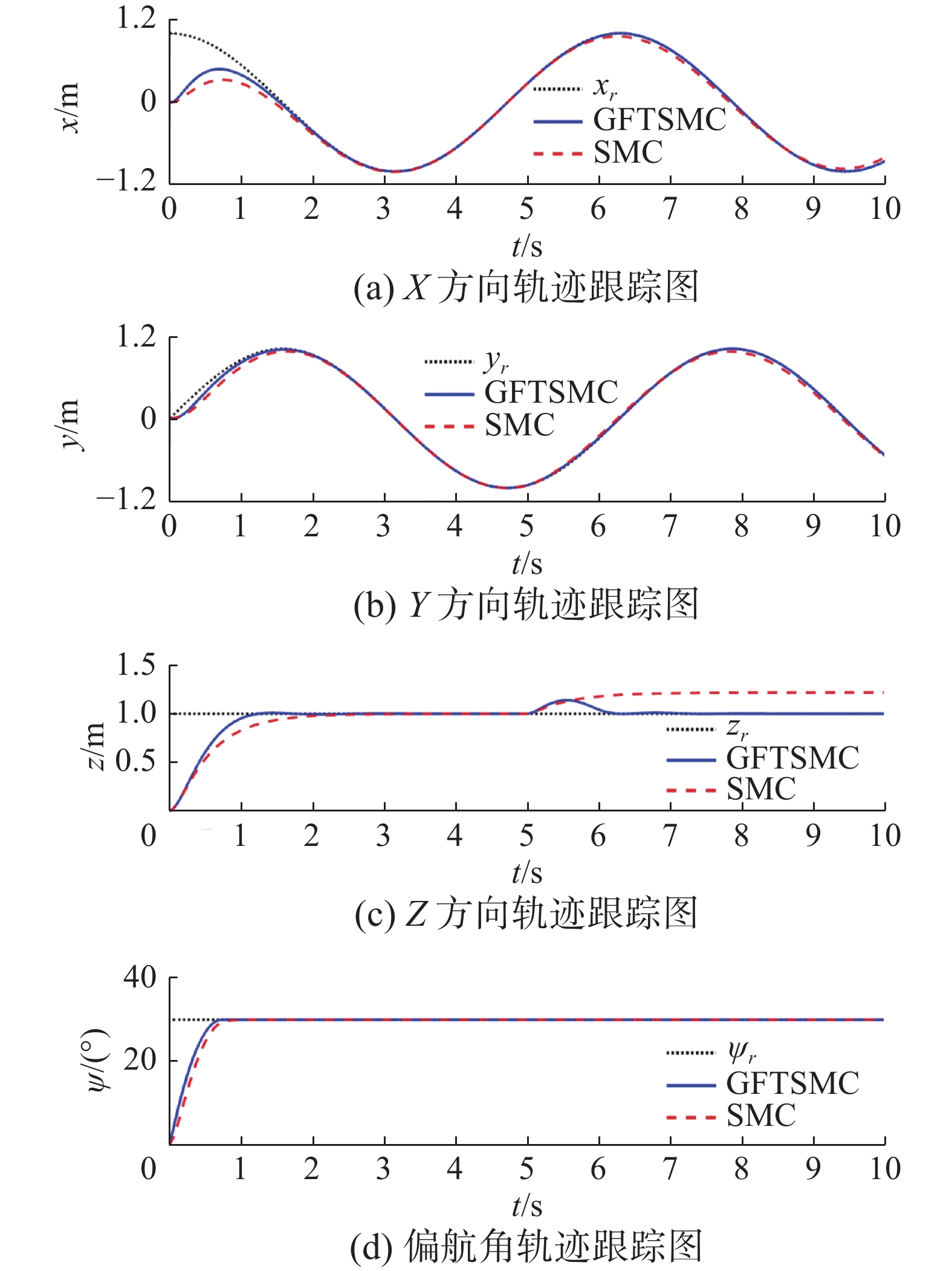
$[ 0\;0\;0 ]$ ，初值姿态角取$[ 0\;0\;0 ]$ ，参考位置设为$[ {\cos (t)}\;\;{\sin (t)}\;\;1 ]$ ，参考偏航角设为$ {30^{\text{o}}} $ 。在仿真时间$t = 5\;{\rm{s}}$ 时将飞行器质量减少40%。两种控制方法的跟踪曲线对比如图4所示，从图中可以看出，当飞行器质量大幅减小时，本文控制算法的飞行高度上升约0.128 m，调整时间约为1.15 s，而传统滑模控制的飞行高度上升约为0.22 m，且难以消除稳态误差。仿真结果说明本文算法的鲁棒性要强于传统滑模控制。3.3 抗干扰性能对比
为了比较两种方法的抗干扰能力，设置位置子系统和姿态子系统的干扰分别为
$$\begin{aligned} &{d_F} = [ {0.8\sin (4t)}\;\;{0.8\cos (4t)}\;\;{0.8\sin (4t)} ] \\ &{d_\varGamma } = [ {2\sin (4t)}\;\;{2\cos (4t)}\;\;{2\sin (4t)} ] \end{aligned}$$ 四旋翼模型初始位置取
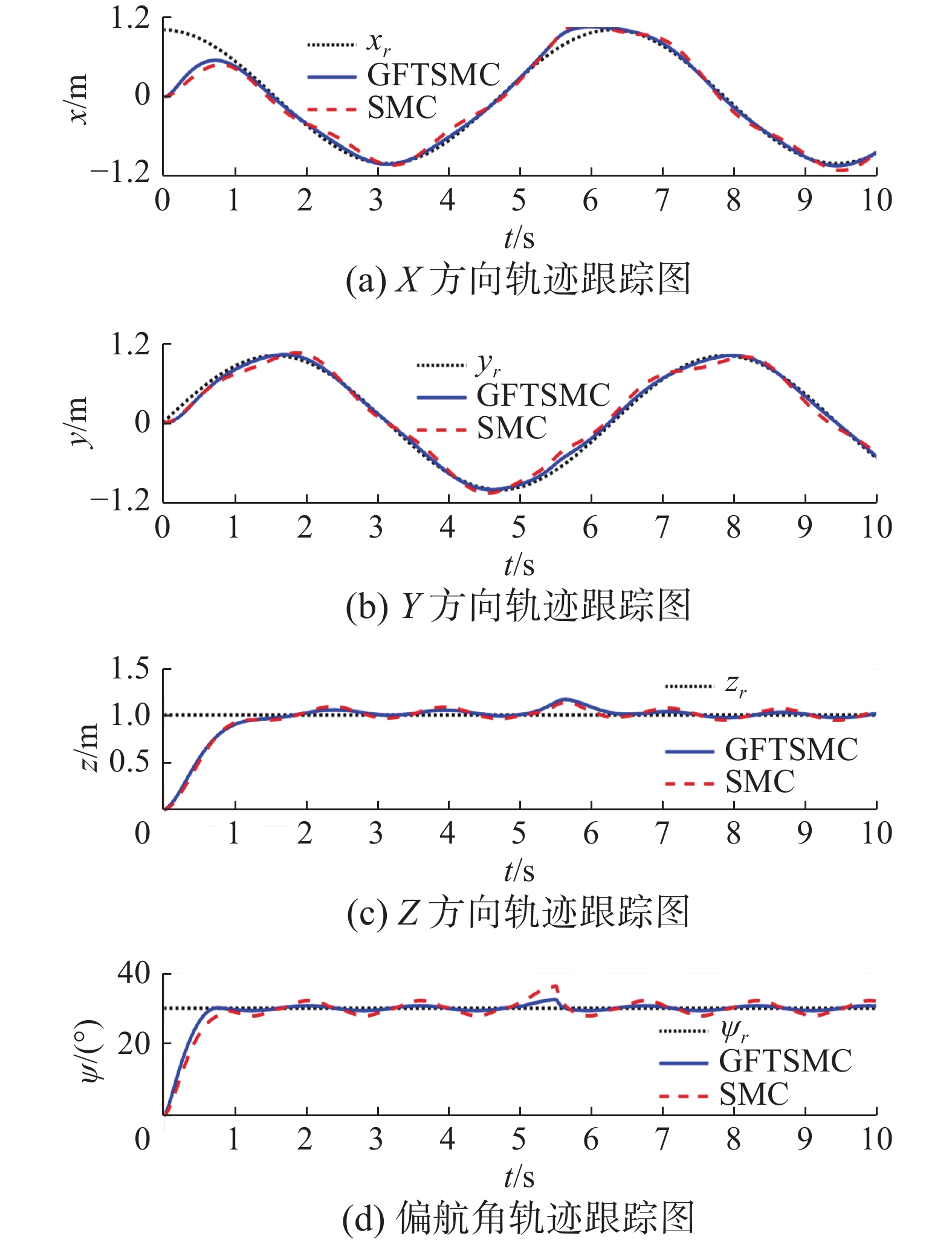
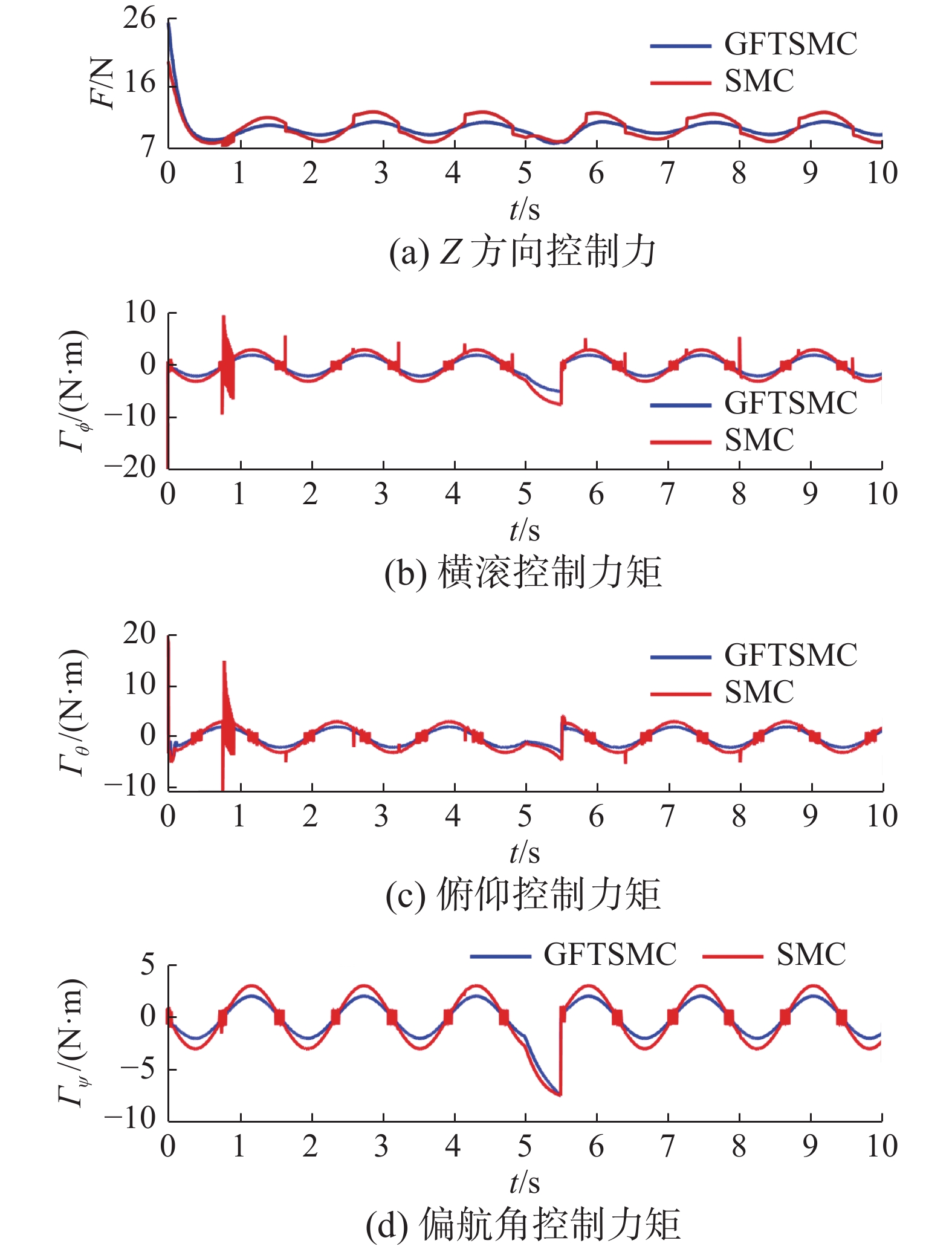
$[ 0\;0\;0 ]$ ，初始姿态角取$[ 0\;0\;0 ]$ ，参考位置设为$[ {\cos (t)}\;{\sin (t)}\;1 ]$ ，参考偏航角设为$ {30^{\text{o}}} $ 。当t = 5~5.5 s时加入幅值为10的脉冲干扰信号。图5为无人机4个通道的轨迹跟踪曲线，本文算法展现出更强的抗扰动能力。表3为4个通道的跟踪误差均方差。从表3可知，本文算法与常规滑模控制算法相比，位置和偏航角的跟踪误差均方差分别降低了14.1%、17.1%、22.4%和26.7%。数据表明本文方法的抗干扰性能优于常规滑模控制。图6为4个通道的控制量对比，可以看出传统滑模控制算法有明显的抖振现象，而本文控制方法有效消除了抖振。
图 4 鲁棒性对比结果Fig. 4 Comparison results of robustness下载:
全尺寸图片
图 5 抗干扰能力对比结果Fig. 5 Comparison results of anti-interference下载:
全尺寸图片
表 3 跟踪误差均方差Table 3 Mean square error of the tracking error控制
通道本文控
制方法常规滑
模控制均方差降幅
百分比/%x 1.98 m 2.26 m 14.1 y 1.81 m 2.12 m 17.1 z 1.92 m 2.35 m 22.4 $\psi $ 4.5° 5.7° 26.7 
图 6 控制量对比结果Fig. 6 Comparison results of control output下载:
全尺寸图片
3.4 实验验证
本文的控制算法在自制样机上进行了实验验证，实现了阵风干扰下对指定空间位置的精准跟踪，如图7所示。
图 7 飞行实验Fig. 7 Flight experiment下载:
全尺寸图片
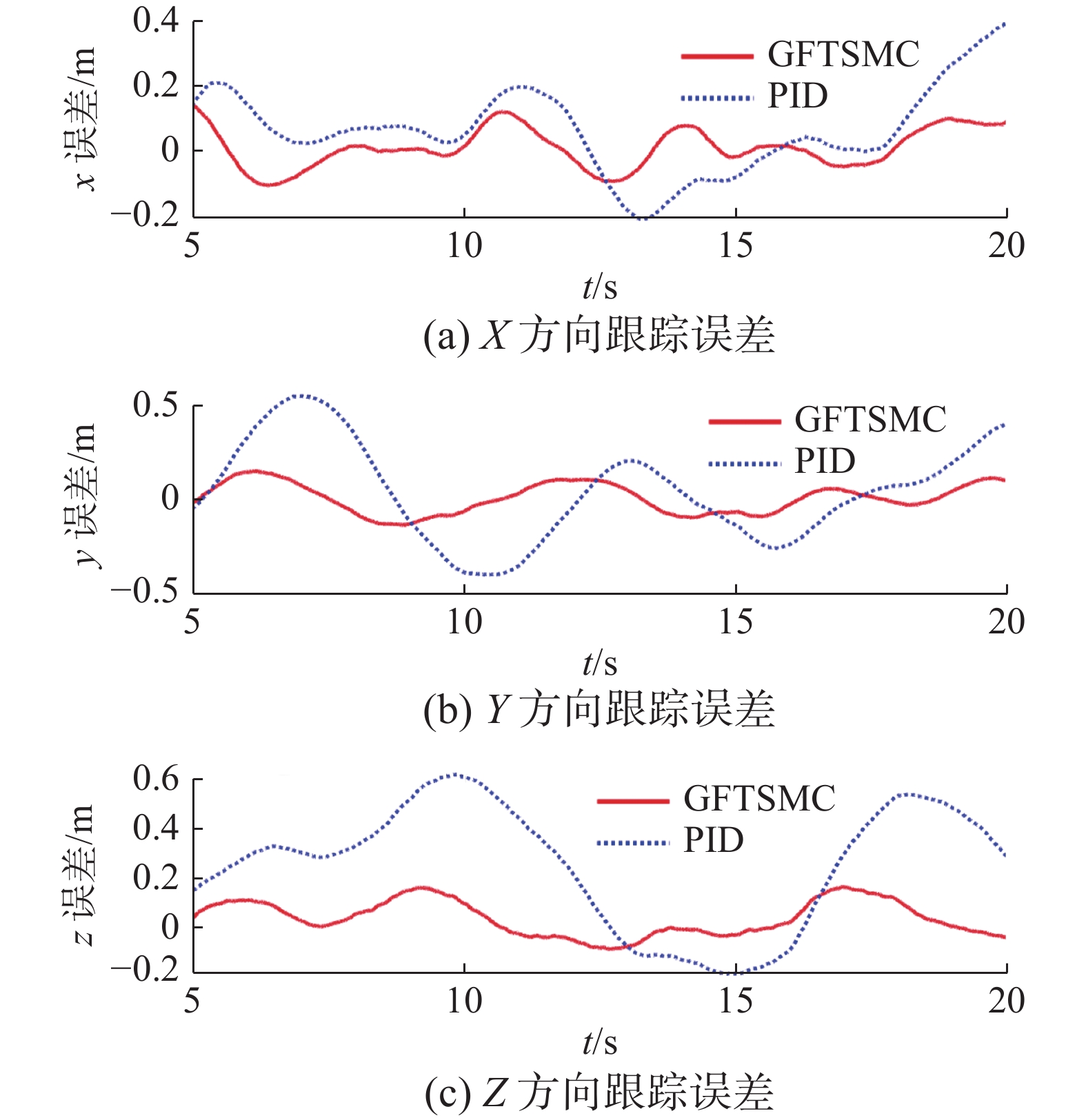
实验样机采用了轴距为550 mm的十字机架、15寸桨叶、PIXHAWK4飞控和双GPS模块，机身总重2.1 kg。实验中分别采用PID控制器和本文设计的控制器在相同环境下对指定的经纬度及高度进行定点悬停，两种控制方法的位置跟踪误差如图8所示。从图中可以看出，本文设计的控制器的位置跟踪误差约为
$ \pm 0.18\;{\text{m}}$ ，优于PID控制器的$ \pm 0.6\;{\text{m}}$ 。
图 8 位置跟踪误差对比Fig. 8 Comparison of position tracking errors下载:
全尺寸图片
4. 结束语
本文针对复杂集总干扰下的四旋翼飞行器系统，结合全局快速终端滑模控制的有限时间快速收敛能力和自适应BRF神经网络的学习能力设计了一种高性能轨迹跟踪控制器。仿真结果和飞行实验表明，相对于滑模控制和PID控制，本文控制方法具有收敛速度快、抗干扰能力强、鲁棒性能强、抖振小等优点。未来将进一步研究如何利用该方法的鲁棒性和学习能力处理四旋翼系统的控制输入饱和、部分执行器故障等复杂控制问题。
-
图 1 四旋翼的结构
Fig. 1 Quadrotor Structure
下载:
全尺寸图片
图 2 四旋翼轨迹跟踪控制器结构
Fig. 2 Structure of quadrotor trajectory tracking controller
下载:
全尺寸图片
图 3 基于RBF神经网络的GFTSM控制器结构
Fig. 3 Structure of GFTSM controller based on RBF neural network
下载:
全尺寸图片
图 4 鲁棒性对比结果
Fig. 4 Comparison results of robustness
下载:
全尺寸图片
图 5 抗干扰能力对比结果
Fig. 5 Comparison results of anti-interference
下载:
全尺寸图片
图 6 控制量对比结果
Fig. 6 Comparison results of control output
下载:
全尺寸图片
图 7 飞行实验
Fig. 7 Flight experiment
下载:
全尺寸图片
图 8 位置跟踪误差对比
Fig. 8 Comparison of position tracking errors
下载:
全尺寸图片
表 1 仿真参数
Table 1 simulation parameter
物理参数 数值 质量m/ kg 2.1 重力加速度g/m·s−2 9.8 旋翼中心到飞行器质心距离 $l$/ m 0.275 x轴转动惯量 ${J_x}$/ kg∙m2 0.039 y轴转动惯量 ${J_y}$/ kg∙m2 0.039 z轴转动惯量 ${J_z}$/ kg∙m2 0.046 表 2 收敛时间
Table 2 Convergence time
控制
通道本文控制
方法/s常规滑模
控制/s加快百
分比/%x 1.83 2.26 23.5
y 1.72 2.12 23.3
z 1.65 1.95 18.2 $\psi $ 0.72 0.92 27.8 表 3 跟踪误差均方差
Table 3 Mean square error of the tracking error
控制
通道本文控
制方法常规滑
模控制均方差降幅
百分比/%x 1.98 m 2.26 m 14.1 y 1.81 m 2.12 m 17.1 z 1.92 m 2.35 m 22.4 $\psi $ 4.5° 5.7° 26.7 -
[1] 蒋林, 冷雪峰, 罗小华, 夏旭洪. 基于模糊单神经元PID的四旋翼控制研究[J]. 计算机仿真, 2019, 36(10): 39–43. doi: 10.3969/j.issn.1006-9348.2019.10.009 JIANG LIN, LENG XUEFENG, LUO XIAOHUA, XIA XUHONG. Quadrotor control based on fuzzy-single neuron PID controller[J]. Computer simulation, 2019, 36(10): 39–43. doi: 10.3969/j.issn.1006-9348.2019.10.009 [2] FOEHN P, ROMERO A, SCARAMUZZA D. Time-optimal planning for quadrotor waypoint flight[J]. Science robotics, 2021, 6(56): 1221–1240. doi: 10.1126/scirobotics.abh1221 [3] MU C, ZHANG Y. Learning-based robust tracking control of quadrotor with time-varying and coupling uncertainties[J]. IEEE transactions on neural networks and learning systems, 2019, 31(1): 259–273. [4] HOU Z, LU P, TU Z. Nonsingular terminal sliding mode control for a quadrotor UAV with a total rotor failure[J]. Aerospace science and technology, 2020, 98: 105716. doi: 10.1016/j.ast.2020.105716 [5] ZHANG X, WANG Y, ZHU G, et al. Compound adaptive fuzzy quantized control for quadrotor and its experimental verification[J]. IEEE transactions on cybernetics, 2020, 51(3): 1121–1133. [6] GUO K, JIA J, YU X, et al. Multiple observers based anti-disturbance control for a quadrotor UAV against payload and wind disturbances[J]. Control engineering practice, 2020, 102: 0967–0661. [7] XIONG J J, ZHANG G. Discrete-time sliding mode control for a quadrotor UAV[J]. Optik, 2016, 127(8): 3718–3722. doi: 10.1016/j.ijleo.2016.01.010 [8] MOFID O, MOBAYEN S, WONG W K. Adaptive terminal sliding mode control for attitude and position tracking control of quadrotor UAVs in the existence of external disturbance[J]. IEEE access, 2020, 9: 3428–3440. [9] YU Y, GUO Y, PAN X, et al. Robust backstepping tracking control of uncertain MIMO nonlinear systems with application to quadrotor UAVs[C]//2015 IEEE International Conference on Information and Automation. Lijiang, China, 2015: 2868−2873. [10] GLIDA H E, ABDOU L, CHELIHI A, et al. Optimal model-free backstepping control for a quadrotor helicopter[J]. Nonlinear dynamics, 2020, 100(4): 3449–3468. doi: 10.1007/s11071-020-05671-x [11] BHATKHANDE P, HAVENS T C. Real time fuzzy controller for quadrotor stability control[C]//2014 IEEE International Conference on Fuzzy Systems. Beijing, China, 2014: 913−919. [12] ALEXIS K, PAPACHRISTOS C, Siegwart R, et al. Robust model predictive flight control of unmanned rotorcrafts[J]. Journal of intelligent and robotic systems, 2016, 81(3-4): 443–469. [13] 唐堂, 罗晓曙. 四旋翼无人机姿态非线性控制研究[J]. 计算机仿真, 2019, 36(1): 71–76. doi: 10.3969/j.issn.1006-9348.2019.01.015 TANG TANG, LUO XIAOSHU. The research on nonlinear control of quadrotor UAV attitude[J]. Computer simulation, 2019, 36(1): 71–76. doi: 10.3969/j.issn.1006-9348.2019.01.015 [14] AHMED N, CHEN M, SHAO S. Disturbance observer based tracking control of quadrotor with high-order disturbances[J]. IEEE access, 2020, 8: 8300–8313. doi: 10.1109/ACCESS.2020.2964013 [15] HWANGBO J, SA I, Siegwart R, et al. Control of a quadrotor with reinforcement learning[J]. IEEE robotics and automation letters, 2017, 2(4): 2096–2103. doi: 10.1109/LRA.2017.2720851 [16] SHARMA M, KAR I. Control of a quadrotor with network induced time delay[J]. ISA transactions, 2021, 111: 132–143. doi: 10.1016/j.isatra.2020.11.008 [17] WANG N, DENG Q, XIE G, et al. Hybrid finite-time trajectory tracking control of a quadrotor[J]. ISA transactions, 2019, 90: 278–286. doi: 10.1016/j.isatra.2018.12.042 [18] 刘凯悦, 冷建伟. 关于四旋翼无人机目标轨迹跟踪控制的研究[J]. 计算机仿真, 2017, 34(5): 103–107. doi: 10.3969/j.issn.1006-9348.2017.05.022 LIU KAIYUE, LENG JIANWEI. The study on the desired trajectory tracking control of quadrotor UAV[J]. Computer simulation, 2017, 34(5): 103–107. doi: 10.3969/j.issn.1006-9348.2017.05.022 [19] XIONG J J, ZHANG G B. Global fast dynamic terminal sliding mode control for a quadrotor UAV[J]. ISA transactions, 2017, 66: 233–240. doi: 10.1016/j.isatra.2016.09.019 [20] HUA C C, WANG K, CHEN J N, et al. Tracking differentiator and extended state observer-based nonsingular fast terminal sliding mode attitude control for a quadrotor[J]. Nonlinear dynamics, 2018, 94(1): 343–354. doi: 10.1007/s11071-018-4362-3 [21] ELIKER K, ZHANG W. Finite-time adaptive integral backstepping fast terminal sliding mode control application on quadrotor UAV[J]. International journal of control, automation and systems, 2020, 18(2): 415–430. doi: 10.1007/s12555-019-0116-3 [22] JOKAR H, VATANKHAH R. Adaptive fuzzy global fast terminal sliding mode control of an over-actuated flying robot[J]. Journal of the brazilian society of mechanical sciences and engineering, 2020, 42(4): 1–18. [23] CUI R, YANG C, LI Y, et al. Adaptive neural network control of AUVs with control input nonlinearities using reinforcement learning[J]. IEEE transactions on systems, man, and cybernetics:Systems, 2017, 47(6): 1019–1029. doi: 10.1109/TSMC.2016.2645699 [24] ZHU Y, FEI J. Adaptive global fast terminal sliding mode control of grid-connected photovoltaic system using fuzzy neural network approach[J]. IEEE access, 2017, 5: 9476–9484. doi: 10.1109/ACCESS.2017.2707668 [25] LABBADI M, CHERKAOUI M. Robust adaptive nonsingular fast terminal sliding-mode tracking control for an uncertain quadrotor UAV subjected to disturbances[J]. ISA transactions, 2020, 99: 290–304. doi: 10.1016/j.isatra.2019.10.012
