近年来，许多研究者致力于使用表示学习的手段来学习用户表征，刻画用户的历史行为，并将其用于各种各样的在线服务中，比如商品推荐、优惠券投放、在线广告等。但现有的方法大多聚焦于对用户历史的点击/购买商品序列建模，无法直接应用于具有强时空语义的实际场景中(如美团、饿了么等本地生活平台)。在这样的场景中，要同时解决“When”、“Where”和“What”的问题，即在特定的时间、特定的地点为用户推荐合适的商品。为此，需要学习一个好的用户表征，它不仅仅能捕获用户在点击/购买序列上表现的兴趣偏好，更要刻画这些兴趣偏好随着时间和位置的演化特征。本文的核心研究任务是如何在时间和空间的维度上学习用户的统一表征，刻画用户行为的时空语义。

在时间建模上，考虑到行为稀疏性和用户关联性，本文主要在用户−商品交互(如购买)的时序图上进行用户表示学习。国外针对时序比较成熟的表示学习方法主要有3类：1) 基于随机游走的方法^[1-2]直接将时序信息融合到随机游走序列中，并通过经典的skip-gram方法学习动态表征。但这类方法忽略了节点和边上的丰富信息，并无法进行归纳学习。2) 基于时间切片的方法^[3-4]先在不同的时间切片上进行表示学习，然后通过神经网络将不同切片上的表示融合为最终的节点表示。这类方法忽略了每个时间切片内的动态性，一定程度上损害了节点关系随时间演化的特性；3) 基于连续时间的方法^[5-6]尝试在连续时间上进行时间序列或时序图的表示学习。但是此类方法大多仍然无法进行归纳学习。更重要的是，它们在进行时间编码的时候忽略了时序图上节点间的交互和时间维度上的上下文信息及其影响。

在空间建模上，如何对地理位置进行编码至关重要。当前的表征方法包括使用geohash网格信息、兴趣点(point of interest,POI)或兴趣面(area of interest,AOI)的one-hot编码，以及使用经纬度信息等。但是这些方式都有自己的缺点：1) geohash网格信息或者POI信息虽然可以精确区分不同的地点，但是由于数量太大，做one-hot编码特征会导致模型参数爆炸。另外geohash网格或POI忽视了地理位置的远近关系信息，不利于模型使用。2) AOI/POI的数量在几百万左右，规模不算很大，但是很多AOI/POI覆盖的面积很大，这样就不能区分其中包含的不同位置实体，另外目前AOI/POI的覆盖率也不是很高；3) 直接经纬度信息虽然避免了one-hot编码特征维度过大的问题，也保持了地理位置的远近关系，但是由于经度和纬度值的微小变化，实际位置就会偏离很远，模型很难使用这类特征。

针对以上不足，本文的目标是开发一个统一的用户表示框架——GTRL (geography and time aware representation learning)，可以同时在时间和空间维度上对用户的历史行为轨迹进行联合建模。

在时间信息建模上，首先，GTRL通过Mercer理论^[7]来实现函数式的时间编码，将时间戳(时间差)映射到高维空间中，并保存节点的时序性。其次，设计了连续时间和上下文感知的图注意力网络(C²GAT)，一个既可以利用图上高阶结构信息也可以在连续时间上刻画节点局部上下文的、全新的、归纳式的图表示学习模型。

在空间信息建模上，为GTRL设计了一种新颖的地理位置编码器——GeoEncoder，以更高效简洁的方式将每个地理位置映射为固定长度的字符串。基于经典的n-gram技术，GTRL可以在更加细粒度的视角上对位置信息进行刻画。最后，依赖新兴的注意力机制对用户的历史位置轨迹进行了深度建模，最终生成了用户的地理偏好表征。

在模型优化方面，GTRL致力于同时解决上述的“When”、“Where”和“What”3个问题，因此为GTRL设计了统一的联合优化方案。值得注意的是，在优化时间上，该方案引入了用户行为中的时间间隔信息，用以刻画行为的周期性、偏好的衰减性等一系列细粒度特征。

最后，本文在公开数据集和工业数据集上设计了大量的实验，一方面验证了GTRL的性能可以超过当前学术界最优的基线模型，另一方面证明了GTRL在实际业务场景中的优势。

1 整体框架

本文提出的GTRL整体算法框架如图1所示，框架会利用用户的历史行为进行建模，包括历史交互的商品(如用户购买过的商品)，交互时间以及交互发生的地理位置(购买的商铺所在的地理位置)。框架的两个核心模块共同支持时空表示学习：1) 时序信息表示模块包含函数式的时间编码及连续时间和上下文感知的图注意力网络，主要用于学习时序图上的用户表示；2) 空间信息表示模块包含层次化的地理位置编码和深度用户轨迹建模子模块，主要对用户历史位置偏好表征的生成。为了统一解决时空语义场景的通用问题(即“When”、“Where”和“What”3个问题)，设计了统一的且可解耦的目标函数来同时优化交互预测、时间间隔预测以及地理位置预测。

2 时序信息建模

为了更好地克服行为稀疏性和捕获用户行为的高阶关联性，本文从图的角度出发进行时序信息的建模，并设计了连续时间和上下文感知的时序图学习方法，主要分为两个部分：1) 为了避免离散时间建模带来的信息损失，GTRL尝试用函数式的时间编码技术将时间戳映射到连续可微的向量空间上更好地保存时序图上的动态性；2) 在最近新兴的图神经网络结构上，融合时间编码，设计了连续时间和上下文感知的注意力机制，可在图上按时间顺序选取重要的邻居，并同时考虑不同邻居在时间上的相互影响。

2.1 函数式的时间编码

函数式时间编码的目的是找到一个从时间域到d 维向量空间的映射 $ {\boldsymbol {\varPhi} }( \cdot ) $ 。具体地，考虑任意两个时间戳 $ {t}_{1},{t}_{2}\in \mathcal{T} $ ，需要关心的是如何学习这两个时间间隔之间的关系模式，可以表示成它们对应的时间编码的内积，即 $ \left\langle {\boldsymbol {\varPhi} }\left({t}_{1}\right), {\boldsymbol {\varPhi} }\left({t}_{2}\right)\right\rangle $ 。由此，可以将上述的时序模式进一步形式化成具有平移不变性的核函数 $ \mathcal{K} $ ，且其映射函数为 $ {\boldsymbol {\varPhi} }( \cdot ) $ 。

为了学习上述的时序核函数及其映射函数，在Mercer理论的启发下，可以将该映射函数定义为

$ t\mapsto {\boldsymbol {\varPhi }}^{\mathcal{M}}\left(t\right): = \left[\sqrt{{c}_{1}}{\phi }_{1}\left(t\right),\sqrt{{c}_{2}}{\phi }_{2}\left(t\right), \cdots \right] $

经验上来说，时序模式可以被一系列周期核函数刻画，参照文献[8]介绍的定理，以 $ \omega $ 为频率的映射函数 ${\boldsymbol {\varPhi } }( \cdot )$ 可以进一步被形式化为

$ t\mapsto {{ \boldsymbol {\varPhi }}}_{\omega }^{\mathcal{M}}\left(t\right): = \left[\sqrt{{c}_{1}}, \cdots ,\sqrt{{c}_{2j}}{\rm{cos}}\left(\frac{j\text{π} t}{\omega }\right),\sqrt{{c}_{2j+1}}{\rm{sin}}\left(\frac{j\text{π} t}{\omega }\right), \cdots \right] $

这样一个傅里叶级数形式的表示有比较好的截断特性，因为可以用截断的d维的映射函数 ${{\boldsymbol {\varPhi }}}_{\omega ,d}^{\mathcal{M}}\left(t\right)$ 来近似原始的无穷维的映射。随后，将 $ k $ 个周期(即 $ \{{\omega }_{1},{\omega }_{2},\cdots ,{\omega }_{k}\} $ )的映射函数拼接，形成最终的时间编码为

$ t\mapsto {\boldsymbol{\varPhi }}_{d}^{\mathcal{M}}(t): = \left[{{\boldsymbol{\varPhi } }}_{{\omega }_{1},d}^{\mathcal{M}}\left(t\right)||\cdots ||{{\boldsymbol{\varPhi } }}_{{\omega }_{k},d}^{\mathcal{M}}\left(t\right)\right] $

值得注意的是，这样的时间编码是节点无关的。换句话说，由于时间编码和节点不相关，会导致相同时间间隔下的任意两个节点的时间编码都是一样的。但在具体的应用场景中，如个性化推荐，用户在过去同一时间上购买的两个不同的商品，对当下用户兴趣的影响是不同的。如一天前喝过咖啡今天很可能会继续喝，但一天前吃过火锅今天再吃的可能性就比较低了。因此，这样的节点无关的时间编码不适合用于后续图神经网络来进行时序图表示。给定一个特定的节点 $ v $ ，可以进一步将该节点的时间编码定义为

$ \begin{array}{c} v,t\mapsto {\boldsymbol{\varPhi }}_{\omega }^{\mathcal{M}}(v,t): = \\ \left[\sqrt{{c}_{1}\left(v\right)}, \cdots ,\sqrt{{c}_{2j}\left(v\right)}{\rm{cos}}\left(\dfrac{j\text{π} t}{\omega }\right), \sqrt{{c}_{2j+1}\left(v\right)}{\rm{sin}}\left(\dfrac{j\text{π} t}{\omega }\right), \cdots \right] \end{array} $

$ v,t\mapsto {\boldsymbol{\varPhi }}_{d}^{\mathcal{M}}\left(v,t\right): = \left[{\boldsymbol{\varPhi }}_{{\omega }_{1},d}^{\mathcal{M}}\left(v,t\right)||\cdots ||{\boldsymbol{\varPhi }}_{{\omega }_{k},d}^{\mathcal{M}}\left(v,t\right)\right] $

式中 ${c}_{i}\left(u\right):{\bf{R}}^{d}\to {\bf{R}},{i}=1, 2, \cdots$ 是一系列节点相关的映射函数，用来计算傅里叶系数。由于多层感知机对复杂交互的优秀建模能力，在实验中将其用于实现 $ {c}_{i}\left(u\right) $ ，并强制感知机的最后一层输出为正数，以此来满足Mercer理论的内在特性。

2.2 连续时间和上下文感知的图注意力网络

在Mercer理论的帮助下，可以对时序图上的每个节点相关的时间间隔进行时间编码，以此在连续时间上建模节点的时序模式。在此基础上，本文设计了连续时间和上下文感知的图注意力网络(C²GAT)来自适应地学习图上的时序信息，一方面在时间上衡量不同邻居节点的重要性/相关性，另一方面考虑邻居节点间在时间维度上的相互影响。具体地，在C²GAT的第l层，给定一个t时刻的目标节点 $ {v}_{t} $ ，需要对该节点的邻居节点集合 $ {\mathcal{N}}_{{v}_{t}}\left(t\right)=\left\{v\right|{t}_{v}<t\} $ 产生一个注意力分布用来融合每个邻居节点的表示。由于之前定义的时间核函数具有平移不变性，可以使用时间差 $ {\left\{t-{t}_{v}\right\}}_{v\in {\mathcal{N}}_{{v}_{t}}\left(t\right)} $ 来替代绝对时间。在t时刻，对于目标节点 $ {v}_{t} $ 及其任意一个邻居 $ v\in {\mathcal{N}}_{{v}_{t}}\left(t\right) $ ，该节点对之间的连续时间和上下文感知的注意力值可以计算为

$ {\alpha }_{{v}_{t},v}\left(t\right)=\frac{{\boldsymbol Q}_{{v}_{t}}\left(t\right){\boldsymbol K}_{v}^{{\rm{T}}}\left(t\right)}{\sqrt{d}} $

$ {\boldsymbol Q}_{{v}_{t}}\left(t\right)=\left[{h}_{{v}_{t}}^{(l-1)}\left(t\right)\left|\right| 0 \left|\right|{\boldsymbol{\varPhi }}_{d}^{\mathcal{M}}\left(0\right)\right]{\boldsymbol W}_{Q} $

$ {\boldsymbol K}_{v}\left(t\right)=\left[{\mathcal{F}}^{\left(l-1\right)}\left(v,t,{t}_{v}\right)\left|\right|{e}_{{v}_{t},v}\left(t\right)\left|\right|{\boldsymbol{\varPhi }}_{d}^{\mathcal{M}}\left(t-{t}_{v}\right)\right]{\boldsymbol W}_{K} $

式中： $ {\boldsymbol W}_{Q} $ 和 $ {\boldsymbol W}_{K} $ 是两个映射矩阵，分别用来获取“Query”和“Key”矩阵； $ {\boldsymbol e}_{{v}_{t},v}\left(t\right) $ 为t时刻节点 $ { v}_{t} $ 和节点v的边特征向量； $ {h}_{*}^{(l-1)} $ 为节点在C²GAT第l-1层的输出。显然，这里设计的注意力机制可以灵活地扩展为多头注意力机制，以此保证更加稳定的训练。如上所述，节点邻居间在时间上的上下文信息及其相互影响是刻画目标节点和邻居节点注意力值的一个很重要的因素。为此，设计了一个上下文聚合函数 $ {\mathcal{F}}^{\left(l-1\right)}\left(v,t,{t}_{v}\right) $ 来显式地刻画这样的影响。给定目标节点 $ {v}_{t} $ ，对任意一个邻居节点v及其对于的时间 $ {t}_{v} $ ，可以定义如下的上文邻居集合 ${S}_{{v}_{t},v}\left({t}_{v}\right)=\{{v'}\in {\mathcal{N}}_{{v}_{t}}(t\left)\right|{t}'_{{v}}\leqslant {t}_{v}\}$ ，进一步地，这里可以使用两种聚合函数来实现 $ \mathcal{F}\left(\cdot \right) $ 。

循环聚合器在序列上下文上应用复杂的LSTM(long short-term memory)结构来赋予C²GAT强大的表达能力。

$ {\mathcal{F}}_{R}={\rm{LSTM}}\left({h'}_{v}^{\left(l-1\right)}(t);{v'}\in {S}_{u,v}({t}_{v})\right) $

卷积聚合器使用了卷积操作来保证C²GAT可以扩展到大规模数据集上。

$ {\mathcal{F}}_{C}=\sum\limits_{i=1}^{d-1}\sum\limits_{j=0}^{\left|{S}_{u,v}\left({t}_{v}\right)\right|}{h}_{j}^{\left(l-1\right)}\left(t\right){W}_{j,i} $

式中 $W\in {\bf{R}}^{\left|{S}_{u,v}\left({t}_{v}\right)\right|\times d\times d}$ 是卷积核。

通过叠加L层上述的C²GAT层，该方法可以从更广更深的维度在时序图中利用高阶的结构信息。由此，可以将每个节点在t时刻的节点表示记为 $ {\left\{{h}_{v}^{\mathcal{T}}\left(t\right)={h}_{v}^{\left(L\right)}\left(t\right)\right\}}_{v\in \mathcal{V}} $ 。本文更关心用户的表示，因此，对于每个用户u，将其在t时刻的表示重写为 $ {h}_{u}^{\mathcal{T}}\left(t\right) $ 。

3 空间信息建模

空间信息建模，即建模用户在空间上的轨迹信息，是对用户时空行为刻画的另外一个主要模块。具体来说，空间轨迹一方面可以在空间上区别人与人之间关系，刻画用户的空间迁移性，从而实现更好的用户表示；另一方面，它也可以描述人与物(服务、权益和店铺等)的关系，增强模型的预测能力。为此，本文设计了层级化的地理编码和深度的历史轨迹建模来实现这一目标，如图2所示。

3.1 层级化的地理编码

为了避免传统地理位置编码(geohash网格、POI或者AOI的one-hot编码以及经纬度编码等)的不足，设计的地理位置编码器(GeoEncoder)参考了谷歌地图和必应地图中广泛使用的Tile Map System，将全地图等分为4块，分别标为0、1、2、3。然后将标号为“0”的地块(Tile)继续等分为4小块，分别标为00、01、02、03，这4小块有共同的前缀：“0”，也就是它们上层那个地块的编号。其他标号为“1”、“2”、“3”的地块进行同样的划分操作。这样递归地将地图不断划分下去，直到最小地块满足要求的进度为止。采样这种地理编码方式，中国地图，考虑最小地块长度为10米，只需要长度为19的序列编码就可以覆盖全国所有位置。这样产出的编码具有很好的性质：给定任意两个地块，它们的共同前缀越短，它们距离越远；反之则越近。图3具体展示了对位置“杭州市−西湖区−天目里”的层级化地理编码。

但是并不能直接使用这个编码作为ID特征。进一步地，参考2020 KDD的工作^[8]，可以对这个编码做n-gram处理(一般取n=6)转换成序列的形式。具体来说，给定编码“120220011012000332”做6-gram处理之后会变为[‘120220’, ‘202200’, ‘022001’, ‘220011’, ‘200110’, ‘001101’, ‘011012’, ‘110120’, ‘101200’, ‘012000', ‘120003’, ‘200033’, ‘000332’]的序列，其中单词量为4 096(4⁶)。

一个地理位置基于GeoEncoder + n-gram做序列编码之后，该序列从左到右逐步刻画了更细粒度的位置信息。可以类比于从国家粒度，逐步精细到地区、省、市、县等。不同的是，GeoEncoder + n-gram的序列编码方式还可以描述相对位置信息。考虑n=1的最简单情况，当一个序列编码的第k个位置为0、1、2和3时，表示它在当前区域的西北、东北、西南和东南区域。当n取值变大，序列编码则可以表示更复杂的相对位置信息。为刻画上述序列编码层级递进的性质，GTRL的地理编码模块使用LSTM模型来建模序列编码得到每个地理位置的低维表征。

3.2 深度的历史轨迹建模

对每个用户u，将其历史的轨迹(即地理位置)集合表示为 $ {\mathcal{H}}_{u}^{G} $ 。通过层次化的地理编码，每个位置g都被表示为低维向量 $ {h}_{g} $ 。显然，对于一个目标位置 $ {g}_{t} $ 来说，用户历史地理位置对其有着不同的影响。因此，本文设计了一个注意力层来刻画这些信息。具体地，该注意力层为每个历史位置学习一个自适应的注意力值：

$ {\alpha }_{g_{t},g}=\frac{{\rm{exp}}\left({\boldsymbol v}^{\rm T}f({\boldsymbol W}_{1}^{G}\left[{h}_{g_t}\right|\left|{h}_{g}\right]\right)}{\displaystyle\sum\nolimits_{g{'}\in {\mathcal{H}}_{u}^{G}}{\boldsymbol v}^{\rm T}f{\boldsymbol W}_{1}^{G}\left[{h}_{{g}_{t}}\left|\right|{h}_{g{'}}\right]} $

式中： ${\boldsymbol W}_{1}^{G}$ 和 ${\boldsymbol v}$ 分别为映射矩阵和映射向量； $ f(\cdot ) $ 为激活函数，一般定义为 ${\rm{tanh}}(\cdot )$ 。紧接着，利用学到的自适应注意力值，通过加权的方式整合历史地理位置信息，从而生成最终的用户地理位置偏好表示。

$ {h}_{u}^{G}=\sum\nolimits_{g\in {\mathcal{H}}_{u}^{G}}{\alpha }_{{g}_{t},g}{h}_{g} $

4 模型学习

如上，GTRL已经从空间和时序的角度来充分刻画用户的行为偏好，分别为 $ {\mathrm{ }h}_{u}^{G} $ 和 $ {h}_{u}^{\mathcal{T}}\left(t\right) $ 。现在，本文将讨论如何将学习到的用户时空表示用于实际的场景中。以具有强时空语义的推荐场景为例，该场景主要关心用户在当前时刻和当前地点是否会点击/购买一件商品。其中， $ {\mathrm{ }h}_{u}^{G} $ 和 $ {h}_{u}^{\mathcal{T}}\left(t\right) $ 分别刻画了用户在时间和空间上的历史交互行为，另一方面，用户行为中的时间间隔也往往蕴涵着丰富的信息。比如在O2O业务的优惠券核销率预估场景中，用户从拿到优惠券到核销的时间间隔越短则说明用户有较强的使用券的心智，反之则说明用户对券的使用心智较弱。

为此，GTRL使用时序点过程的方式来建模用户行为的时间间隔，该方法的核心为定义强度函数，在本文中可以表示为 $ {\lambda }_{{v}_{t}}\left(\tau \right|{h}_{u}\left(t\right)) $ ，其中 $ {v}_{t} $ 为目标商品， $ \tau =t-{t}_{i} $ 为当前时刻距上一时刻的时间间隔， $ {h}_{u}\left(t\right)={h}_{u}^{G}\left|\right|{h}_{u}^{\mathcal{T}}\left(t\right) $ 表示融合用户历史时空语义的最终表示。参照FullyNet的思想^[9]，GTRL直接建模累计强度函数为

$ {\psi }_{{v}_{t}}\left(\tau |{h}_{u}\left(t\right)\right)={\int }_{0}^{\tau }{\lambda }_{{v}_{t}}\left(s|{h}_{u}\left(t\right)\right){\rm d}s $

相比于传统的时序点过程，GTRL使用了一种强度自由的形式来建模用户的时间间隔，可以更好地适应复杂的真实应用场景。由于神经网络强大的拟合能力，GTRL将其作为累积强度函数是实现基础，整体的公式为

$ {\psi }_{{v}_{t}}\left(\tau |{h}_{u}\left(t\right)\right)=f({\boldsymbol W}_{L}\cdots f({\boldsymbol W}\left[{h}_{u}\left(t\right)|\left|\tau \right]+{{\boldsymbol{b}}}_{1}\right)+{{\boldsymbol{b}}}_{L}) $

$ {\rm{s.t.}}\;\;\;\;{\boldsymbol W}_{1},{\boldsymbol W}_{2},\cdots ,{\boldsymbol W}_{L}\geqslant 0,{{\boldsymbol{b}}}_{1},{{\boldsymbol{b}}}_{2},\cdots ,{{\boldsymbol{b}}}_{L}\geqslant 0 $

式中： ${\boldsymbol W}_{*}$ 和 ${{\boldsymbol{b}}}_{*}$ 分别为权重矩阵和偏置向量； $ f(\cdot ) $ 为激活函数，在这里被定义为 $ \mathrm{R}\mathrm{e}\mathrm{L}\mathrm{U}(\cdot ) $ 。最终，强度函数可以通过微分得到，即 ${\lambda }_{{v}_{t}}\left(\tau |{h}_{u}\left(t\right)\right)=\dfrac{\partial {\psi }_{{v}_{t}}\left(\tau |{h}_{u}\left(t\right)\right)}{\partial \tau }。$

为了解决时间 $ t $ 、位置 $ g $ 、商品 $ v $ 的联合预测，GTRL通过如下的联合分布来估计：

$ p\left(v,g,t|u\right)=p\left(v|u\right)\cdot p\left(g|u\right)\cdot p\left(t,|u,v\right) $

式中：下一次交互预测 $ p\left(v|u\right) $ 与下一次位置预测 $ p\left(g|u\right) $ 分别由以 $ {h}_{u}\left(t\right) $ 为输入的多层感知机器得到；而下一次交互间隔预测 $ p\left(t,|u,v\right) $ 由时序点过程支持。由于商品和位置量级很大，GTRL使用了随机负采样的方式来进行近似计算。最后，根据极大似然估计的策略，最终的损失函数为

$\begin{aligned} \mathcal{L}=\sum\limits_{\left(u,v,g,\tau ,y\right)\in {S}_{v}}\mathcal{C}\left(y,p\left(v|u\right)\right)+\sum\limits_{\left(u,v,g,\tau ,y\right)\in {S}_{g}}\mathcal{C}\left(y,p\left(g|u\right)\right)-\\ \sum\limits_{\left(u,v,g,t,\tau \right)\in {S}^+}\left(\mathrm{log}{\lambda }_{v}\left(\tau \right)+\sum\limits_{{v}^{'}\in {P}_{\rm {neg}}}{\int }_{0}^{\tau }{\lambda }_{{v}^{'}}\left(s\right){\rm d}s\right)\quad\quad \quad \end{aligned}$

式中： $ {S}_{v}={S}_{v}^{+}\cup {S}_{v}^{-} $ 表示对商品进行负采样后的所有训练样本集合；同理， $ {S}_{g}={S}_{g}^{+}\cup {S}_{g}^{-} $ 表示对地理位置进行负采样后的所有训练样本集合； $ {S}^{+}={S}_{v}^{+}\cup {S}_{v}^{-} $ 为训练集合中所有正样本集合； $ \mathcal{C}(\cdot ,\cdot ) $ 表示交叉熵损失函数。值得注意的是，GTRL框架与具体的任务是完全解耦的，使用者可以选取框架中的任意子模块进行任意预测任务(如下一个商品预测，下一个时间间隔预测或下一个地理位置预测)。

5 实验分析 5.1 公开数据集上的有效性实验

首先，本文分别在4个公开数据集(Reddit、Wikipedia、MOOC和LastFM)上进行(推导式/归纳式)链路预测和节点分类任务，来验证GTRL中的时序信息建模模块(即C²GAT)的有效性。4个数据集的详细统计信息如表1所示。

在实验中，选取了9个经典的基准方法，大致可以分为3类：1) 基于深度递归网络的方法：Time-LSTM^[10]和Jodie^[11]；2)静态的图神经网络方法：GraphSAGE^[12]和GAT^[13]；3) 时序图神经网络方法：CTDNE^[14]，M²DNE^[15]、GCRN^[16]、GraphSAGE-T和GAT-T和TGAT^[5]。

本文将C²GAT与上述的9个基准方法在(推导式/归纳式)链路预测和节点分类任务上的性能对比实验结果分别展示在表2和表3中。从表2、3中可以得出如下两点结论：

1) GTRL中集成的C²GAT模型同时在链路预测和节点分类任务上都一致且明显优于其余基准模型，验证了C²GAT的有效性。这得益于C²GAT使用了一种更加有效的方式来捕获图上的动态性，并同时利用高阶结构信息和局部序列式的上下信息。

2) 在这些对比方法中，多数情况下，时序图模型的性能优于静态图模型优于深度序列模型。这证明了动态性、高阶结构以及节点/边特征对于时序图表示学习的重要性。

5.2 工业数据集上的实验

首先在支付宝首页的本地生活场景进行了一系列关于时间维度的实验，选取了外卖(“饿了么”服务)、旅游(“飞猪”服务)和栏目排序这3个具有强时间语义的数据集，具体的数据集统计信息见表4。

考虑到数据规模的量级，本文针对性地选取了一系列代表性的基准方法，如基于特征的DeepFM^[17]模型、基于序列的GRU4Rec^[18]、DIN^[11]、SASRec^[20]，以及基于兴趣演化的DIEN^[21]和Time-LSTM^[10]模型。详细的性能比较如表5所示。可以发现：在3个实际的场景数据集上，本文提出的方法对比最优的基准方法可以带来0.12%～1.71%的提升，验证了该方法在实际场景中捕获时间语义的有效性。

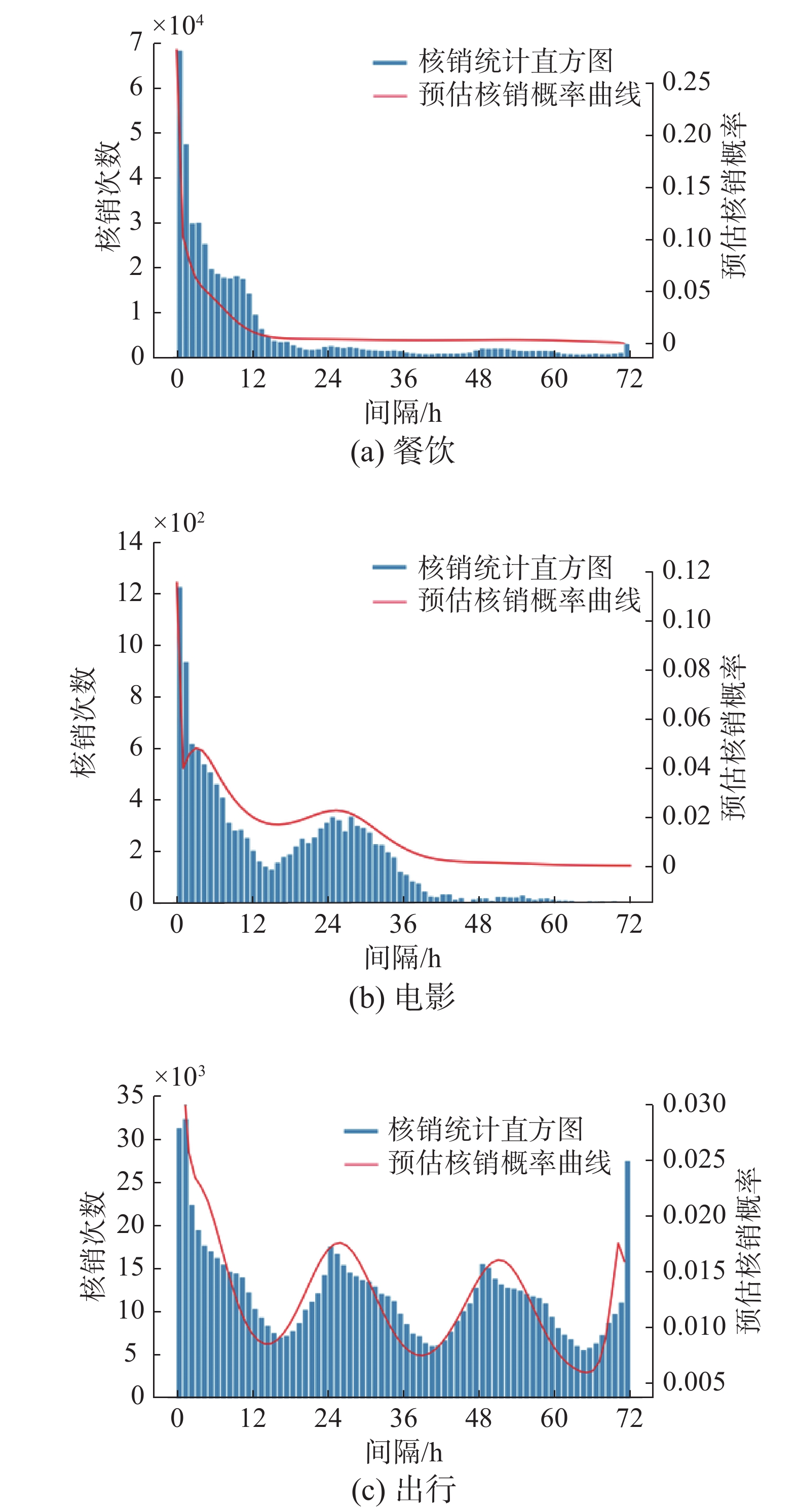
进一步，将更加显式地展示GTRL在时间间隔预测上的有效性。因此，本文在支付宝/本地生活的券核销预估中应用了GTRL。首先对比线上最优的基准方法(MMoE^[22])，GTRL在核销率上可以带来4.23%的提升。其次，展示了这个任务中三类券的真实核销量−时间分布(蓝色柱状图)以及GTRL对券核销时间分布的估计(红色实线)，如图4所示。可以发现，GTRL的预测与真实的核销分布基本吻合，也反映出了不同类型券核销的时间周期性：1) 餐饮券：领券后一般都是尽快核销，核销量随时间呈明显衰减趋势；2) 电影券：领券后尽快核销(现领现买)，领券第2天核销(1天后看电影)；3) 出行券：时间衰减不明显，根据实际出行需求进行核销，呈现天周期。

除了预测时间任务外，GTRL也可以进行空间地理信息的建模^[23-25]。将GTRL应用于建模用户历史线下交易的空间轨迹。首先，本文将学习到的用户空间表征进行可视化，如图5所示。

从图5中，可以发现：1) 每个城市聚簇明显，北京−天津、佛山−广州、苏州−上海、成都−重庆4组城市对也呈现聚簇状态，其中成都−重庆呈现较为明显的分离(可能是成都−重庆距离较远)。2) 图(b)中：上海与苏州昆山的聚簇overlap较大(住昆山，在上海工作)，苏州主城区和张家港则明显呈现独立聚簇。进一步地，在双十二的券抽奖场景上线了GTRL-G模型以帮助预测用户未来支付的位置，对比线上基线模型(MMoE)，GTRL-G在整体核销率上可以带来3.31%的提升，在非消费券核销率上可以带来13.94%的提升。

6 结束语

本文提出了一个统一的用户表示学习框架——GTRL，可以有效地捕获用户行为在时空维度的语义。具体地，GTRL在时间建模上使用了函数式的时间编码和连续时间和上下文感知的图注意力网络用于在图上灵活地捕获高阶的结构化时序信息。与此同时，GTRL在空间建模上引入了层级化的地理编码和深度历史轨迹建模模块高效地刻画了用户的地理位置偏好。最后GTRL给出了一个统一且可解耦的优化方案来联合预测下一次交互，及相应的时间和地理位置。大量的公开数据集和工业数据集上的实验分别验证了GTRL相较学术界基线模型的优势，以及在实际业务场景中的有效性。在未来的工作中，将进一步致力于研究用户行为的稀疏性问题，将更加复杂的结构信息(如用户侧的社交网络信息和商品侧的知识图谱信息)集成到GTRL框架中。