Improved slap swarm algorithm for scheduling of flexible job shop
-
摘要: 针对以最小化最大完工时间的柔性作业车间调度问题，在标准樽海鞘群算法(salp swarm slgorithm, SSA)的基础上，提出一种改进的樽海鞘群算法。采用基于工序和基于设备的二维向量进行编码，并考虑设备负载进行种群初始化。基于Lévy飞行对领导者位置更新方式进行离散化改进；在追随者位置更新公式中引入自适应惯性权重,使算法的全局搜索和局部搜索能力得到更好的平衡。为提高搜索效率，设计了交叉算子和基于关键路径的变异算子来保证种群的多样性，同时引入模拟退火(simulated annealing，SA)策略，改善算法的局部搜索能力。通过采用标准算例进行对比计算，结果验证了所提算法的有效性。Abstract: To deal with the scheduling of a flexible job shop and minimize the maximum completion time, an improved salp swarm algorithm (SSA), based on the standard SSA, is proposed in this paper. Two-dimensional vectors based on the process and equipment are encoded, and the population is initialized with the consideration of the machine workload. Based on a Lévy flight, the leader position update method is discretely improved. The adaptive inertial weight is introduced into the follower position update formula to balance the global search and local search performance of the algorithm. To improve the search efficiency, the proposed SSA adopts crossover and mutation operators based on the critical path to guarantee population diversity. Moreover, simulated annealing is applied to improve the local search capacity of the algorithm. Standard examples are compared and calculated, and the results verify the effectiveness of the proposed algorithm.
-
Keywords:
- flexible job shop /
- salp swarm algorithm /
- Lévy flight /
- discretization /
- inertia weight /
- critical path /
- simulated annealing /
- local search
-
先进的调度方法能够提高生产效率和经济效益，其主要任务是在时间和资源的双重约束下，合理、科学地对可用共享资源和生产任务进行分配与管理，尽可能使性能评价指标达到最优。柔性作业车间调度问题(flexible job shop scheduling problem，FJSP)作为车间作业调度的延伸，突破了一道工序只能在一台设备加工的局限，引入了设备指派决策，扩大了可行域的搜索范围，具有更高的理论计算复杂度。FJSP广泛应用于航空航天、交通运输、智能制造和运筹优化等领域，因此针对FJSP的研究具有重要理论价值和实际应用价值。
针对柔性作业车间调度优化问题，目前主要的求解算法可以分为两大类：精确算法和近似算法[1]。由于问题的高度复杂性，研究者大多采用智能优化算法求解，诸如模拟退火与禁忌搜索混合算法[2]、遗传–禁忌搜索混合算法[3]、改进迭代贪婪算法[4]等。近年来随着计算机科学技术的不断进步，许多新的群体智能算法不断涌现，如人工免疫算法[5]、混合灰狼优化算法[6]等。也有使用分派规则构建启发式算法的文献[7]。此外针对FJSP的扩展问题，先后有文献讨论顺序相关调整时间[8]、能耗约束[9]、动态事件[10-11]、多时间约束[12]等变种。尽管出现了大量启发式求解策略，但求解效率依然有进一步提升的空间和基于群集智能发展高效调度框架的必要。
樽海鞘群算法在2017年由澳大利亚学者Mirjalili等[13]提出，该算法通过模拟自然界中樽海鞘群在海洋中的觅食行为，实现对解空间的探索。该算法具有收敛速度快，鲁棒性强且易于实现等显著特点，已成功地应用于光伏系统优化[14]、特征提取[15]、图像处理[16]和生物医学信号处理[17]等问题求解。Jia等[18]提出了SSACL算法，使用交叉策略和Lévy飞行分别改进了樽海鞘群领导者和跟随者的运动方式，在基准函数测试中表现出良好的计算性能。然而，该算法在生产调度领域的研究并不多见，且现有的文献多集中于并行机调度问题的研究。Jouhari等[19]针对不相关的并行机调度问题，利用樽海鞘群算法进行局部搜索以增强优化器的性能并减少计算时间。Ewees等[20]提出了一种基于萤火虫算法的改进樽海鞘群算法来求解带调整时间不相关的并行机调度问题。Sun等[21]提出了将樽海鞘群算法应用于车间调度问题，结合樽海鞘群算法全局搜索框架，基于关键路径设计多个邻域算子进行局部搜索，对可重入作业车间调度问题进行了有效的求解。本文利用Lévy飞行和交叉变异算子对樽海鞘群算法进行改进，并结合局部邻域搜索策略来求解柔性作业车间调度问题。鉴于樽海鞘群算法的优越性，非常有必要研究其在生产调度领域的应用。
本文提出一种融合模拟退火策略的改进樽海鞘群算法求解FJSP。基于设备负载进行种群初始化，利用交叉和变异遗传算子对个体进行改进，采用Lévy飞行对领导者个体位置进行更新。为防止求解陷入局部最优，融合模拟退火进行邻域搜索，提升算法的全局搜索和局部搜索能力。同时，为验证模型的准确性并为所提算法提供参考依据，采用Gurobi数学求解器进行精确求解混合整数规划模型。运用改进的樽海鞘群算法求解FJSP，并和其他研究文献进行综合对比，进一步阐明所提算法的有效性。
1. 问题描述与模型构建
1.1 问题描述
FJSP描述如下：给出
$n$ 个工件的集合$J$ 和$m$ 台设备的集合$M$ 。每个工件$i$ 的加工工序都是确定的且不尽相同，其中工件$i$ 的第$j$ 道工序($ {O_{ij}} $ )可以在兼容设备子集${M_{ij}} \subseteq M$ 的任何设备上加工。每道工序的加工时间与所选择的加工设备有关，每个工件都必须严格按照预定好的顺序进行加工，且每台设备在同一时刻只能加工一个工件。调度的目标是让每道工序选择最合适的加工设备，并确定每台设备上的最佳处理顺序和加工开始结束时间。因此，该组合优化问题分为两个子问题：1)设备选择问题，即为工序选择合适的加工设备；2)工序排列问题，即确定每台操作设备的最佳加工工序序列，以此确定两个子问题的最优值来使得整个调度系统实现特定的优化目标。本文考虑最小化最大完工时间${C_{\max }}$ ，即makespan。此外，在建模过程中还需满足如下约束条件：
1)工件在到达时间之前不允许加工，所有工件在零时刻都可以被加工；
2)同一工件的工序有加工顺序约束，不同的工件没有加工顺序约束；
3)同一台设备在同一时刻只能加工一个工件；
4)同一工件的同一道工序在同一时刻只能被一台设备加工；
5)工件在某台设备上开始加工，不允许中断；
6)所有加工设备是连续可用的，设备的调试与设置时间可以忽略不计。
1.2 模型构建
针对柔性作业车间调度问题，以最小化最大完工时间
${C_{\max }}$ 为目标，基于文献[8]的模型构建本问题的整数规划(MIP)模型，各参数定义见表1。$$ 目标函数：{\rm{min}}\; {C_{\max }} $$ (1) s.t.
$$ \sum\limits_{k \in {M_{ij}}} {{z_{ijk}} = 1} ,\; \forall j \in {J_i},i \in J $$ (2) $$ {s_{ij}} \geqslant {s_{i(j - 1)}} + \sum\limits_{k \in {M_{i(j - 1)}}} {{p_{i(j - 1)k}}{z_{i(j - 1)k}}} ,\; \forall j \in {J_i}\backslash \{ 1\} ,i \in J $$ (3) $$ {s_{ij}} \geqslant {s_{{i'}{j'}}} + {p_{{i'}{j'}k}} - (2 - {z_{ijk}} - {z_{{i'}{j'}k}} + {y_{ij{i'}{j'}}})\varDelta $$ $$ \forall j \in {J_i},{j'} \in {J_{{i'}}},i,{i'} \in J(i \ne {i'}),k \in {M_{ij}} \cap {M_{{i'}{j'}}} $$ (4) $$ {s_{{i'}{j'}}} \geqslant {s_{ij}} + {p_{ijk}} - (3 - {z_{ijk}} - {z_{{i'}{j'}k}} + {y_{ij{i'}{j'}}})\varDelta $$ $$ \forall j \in {J_i},{j'} \in {J_{{i'}}},i,{i'} \in J(i \ne {i'}),k \in {M_{ij}} \cap {M_{{i'}{j'}}} $$ (5) $$ {C_{\max }} \geqslant {s_{i{n_i}}} + \sum\limits_{k \in {M_{i{n_i}}}} {{p_{i{n_i}k}}{z_{i{n_i}k}}} \forall i \in J $$ (6) $$ {z_{ijk}} \in \{ 0,1\} \forall j \in {J_i},i \in J,k \in {M_{ij}} $$ (7) $$ {y_{ij{i'}{j'}}} \in \{ 0,1\} \forall j \in {J_i},{j'} \in {J_{{i'}}},i,{i'} \in J $$ (8) 表 1 符号与参数Table 1 Symbols and parameters参数 说明 $J$ 工件集合， $J = \{ 1,2, \cdots ,n\} $ $M$ 加工设备集合， $M = \{ 1,2, \cdots ,m\} $ ${O_{ij}}$ 工件 $i$的第 $j$道工序 ${J_i}$ 工件 $i$的工序集合， ${J_i} = \{ 1,2, \cdots, {n_i}\} ,{n_i}$为其工序总数 ${M_{ij}}$ 工件 $i$的第 $j$道工序的可选加工设备集合 ${P_{ijk}}$ 工件 $i$的第 $j$道工序在设备 $k$上的加工时间 ${s_{ij}}$ 工件 $i$的第 $j$道工序的加工开始时间 $\varDelta$ 足够大的正数 ${z_{ijk}}$ 假设工序 ${O_{ij}}$选择设备 $k$，变量的值为1，否则为0 ${y_{ij{i'}{j'} } }$ 假设 ${O_{ij}}$先于 ${O_{ {i'}{j'} } }$加工，变量的值为1，否则为0 目标函数(1)最小化最大完工时间makespan。式(2)确保每道工序当且仅能指派给可用设备集中的一台进行加工。式(3)保证同一工件相邻工序间的先后关系。式(4)和式(5)防止在同一设备
$k$ 上进行处理的工序作业时间发生重叠，当且仅当工序${O_{ij}}$ 和工序${O_{{i'}{j'}}}$ 都分配给设备$k$ (即${z_{ijk}}$ =${z_{{i'}{j'}k}}$ = 1)时，两个约束方才起作用。式(4)确保当工序${O_{{i'}{j'}}}$ 完工后处理工序${O_{ij}}$ ，则${y_{ij{i'}{j'}}}$ =0。式(5)表示${y_{ij{i'}{j'}}}$ =1的情况。对于其他情况，式(4)和式(5)则自动满足。式(6)确定最大完工时间。式(7)和(8)决定两组0、1变量的取值。2. 樽海鞘群算法
樽海鞘群算法模拟樽海鞘的聚集行为，组成樽海鞘链在海底进行捕食和移动。在SSA中，樽海鞘链可以分为两类：领导者和追随者，链的头部是领导者，其余的都是跟随者。与其他群体优化算法类似，樽海鞘群的位置定义在多维搜索空间内，寻找多维空间中食物源
$F$ 的位置是樽海鞘群追随的重要指标。领导者根据$F$ 的位置修正自身的位置，追随者跟随领导者位置变化更新自身的位置。在樽海鞘群算法中，定义每个樽海鞘个体的位置向量
$\boldsymbol{X}$ 用于在$N$ 维空间中搜索，其中$N$ 为决策变量的数目。樽海鞘群算法中位置向量$\boldsymbol{X}$ 将由维度为$D$ 的$N$ 个樽海鞘个体组成，其中第$i$ 个樽海鞘个体位置表示为樽海鞘个体位置为$$ {{\boldsymbol{X}}_i} = [x_i^1\; x_i^2\; \cdots \; x_i^D],\quad i = 1,2, \cdots ,N $$ 因此，种群向量由
$N \times D$ 维矩阵构成，即：$$ {\boldsymbol{X}} = \left[ {\begin{array}{*{20}{c}} {x_1^1}&{x_2^1}& \cdots &{x_D^1} \\ {x_1^2}&{x_2^2}& \cdots &{x_D^2} \\ \vdots & \vdots & \quad & \vdots \\ {x_1^N}&{x_2^N}& \cdots &{x_D^N} \end{array}} \right] $$ 矩阵中的第一个向量为领导者，其余向量为追随者。食物源
$F$ 的位置是所有樽海鞘个体的目标位置。因此，领导者的位置更新公式为$$ x_j^1 = \left\{ {\begin{array}{*{20}{c}} {{F_j} + {c_1}(({{\rm{ub}}_j} - {{\rm{lb}}_j}){c_2} + {{\rm{lb}}_j}),\quad{c_3} \geqslant 0} \\ {{F_j} - {c_1}(({{\rm{ub}}_j} - {{\rm{lb}}_j}){c_2} + {{\rm{lb}}_j}),\quad{c_3} < 0} \end{array}} \right. $$ (9) 式中：
$ x_j^1 $ 表示领导者在第$j$ 维的位置；$ {F_j} $ 表示第$j$ 维食物源的位置；${{\rm{ub}}_j}$ 和${{\rm{lb}}_j}$ 分别表示在第$j$ 维搜索空间上、下界；$ {c_1} $ 、$ {c_2} $ 、$ {c_3} $ 是控制参数。由式(9)可知，领导者的位置更新与食物源的位置相关。系数
$ {c_1} $ 叫做收敛因子，其定义如下：$$ {c_1} = 2{{\rm{e}}^{ - {{(\frac{{4t}}{{{t_{\max }}}})}^2}}} $$ (10) 式中：
$t$ 为当前迭代次数；${t_{\max }}$ 为最大迭代次数。参数
$ {c_2} $ 和$ {c_3} $ 是 [0,1]区间内均匀生成的随机数，$ {c_2} $ 决定了在第$j$ 维空间领导者更新的移动步长，$ {c_3} $ 决定的是移动的方向的正反。根据牛顿运动定律，对跟随者的位置更新进行公式化：
$$ x_j^i = \frac{1}{2}at_0^2 + {v_0}{t_0} $$ (11) 式中：
$i \geqslant 2$ ，$x_j^i$ 表示第$j$ 维空间跟随者的位置；${v_0}$ 表示初始速度；${t_0}$ 表示时间；$a = ({v_{{\text{final}}}} - {v_0})/t$ ，${v_{{\text{final}}}} = $ $ (x_j^{i - 1} - x_j^x)/{t_0}$ ；$ x_j^{i - 1} $ 表示第$i - 1$ 个追随者在第$j$ 维空间跟随者的位置。由于时间在优化过程中表示为迭代，所以
${t_0} = 1$ 迭代差值为1，初始速度${v_0} = 0$ ，并且追随者的位置更新只与它前一个樽海鞘个体位置相关，所以位置更新公式进而可以表示为$$ x_j^i = \frac{1}{2}(x_j^i + x_j^{i - 1}) $$ (12) 式中：
$i \geqslant 2$ ，$x_j^i$ 表示第$i$ 个樽海鞘个体在第$j$ 维空间的位置。根据以上个体位置更新方式，可以模拟樽海鞘群的行为机制。3. 改进樽海鞘群算法
自提出以来，SSA算法在求解连续优化问题得到了广泛的应用，但在组合优化领域的应用较少。因此，针对FJSP的特点，提出一种基于离散思想的SSA，引入基于设备负载最小的选择方案来加快算法收敛；采用交叉变异算子调整工序与设备编码，以此扩大解的搜索空间从而加快算法的搜索效率；防止求解陷入局部最优或者无法完全收敛，融合模拟退火策略进行局部领域搜索，进而得到改进离散化樽海鞘群算法(improved discretized salp swarm algorithm，IDSSA)求解FJSP。
3.1 编码
针对FJSP的特性，IDSSA编码由设备选择部分(MS)和工序排序部分(OS)两个向量组成，每个向量的长度均等于总工序数之和。设备选择部分从第一个工件的第一道加工工序开始直到最后一个工件的最后一道加工工序依次分配加工设备，数字
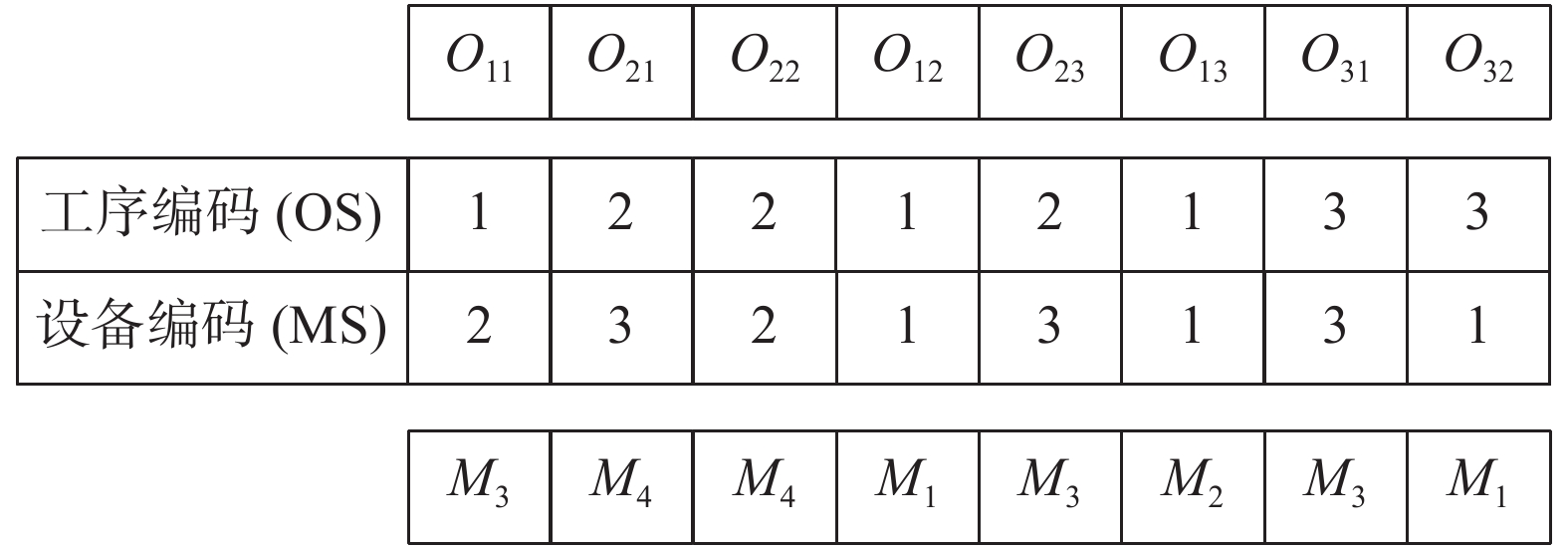
$k$ 为对应工序可选设备集内的第$k$ 台设备；工序排序部分中的每一维向量代表待加工工件序号，其出现的次数代表工件的第几道工序。$({O_{11}},{M_3}), ({O_{21}},{M_4}),({O_{22}},{M_4}),({O_{12}},{M_1}),({O_{23}},{M_3}), ({O_{13}},{M_2}),$ $({O_{31}},{M_3}),({O_{32}},{M_1}) $ 是利用二维向量编码的个体。个体的编码方式如图1所示。
图 1 IDSSA编码示意Fig. 1 IDSSA code representation
下载:
全尺寸图片
3.2 种群初始化
种群初始化是樽海鞘群算法的重要步骤，初始解的质量对SSA的收敛速度和寻优效率至关重要。在生成初始解时，不仅要保证解决方案的多样性而且还要保证解的质量。到目前为止，大多数文献采用随机初始化的方法初始化加工设备，无法保证最短时间的加工设备被选择。因此，最初未选择的设备将永远不会被选择，这使得算法仅赖于设备突变操作来选择这些设备，但突变操作只有很小的发生概率，初始解的多样性也就无法得到保证。FJSP设备选择的难点在于每一道工序选择加工设备时，对设备而言，设备的负载变化会对加工过程中设备选择的结果产生影响，因此需要考虑加工该工序后的设备负载变化。使用SSA进行初始化时，由于没有任何先验知识可以参考，本文参考Kacem等[22]提出的初始种群定位法，该方法在考虑设备的负载前提下为工序分配设备，为每一道工序的可选设备集中寻找时间表中具有最短加工时间的设备，利用该设备处理工序。然后对设备负载进行更新操作，即将前一道工序的加工时间加到同一列的其他项。
3.3 位置更新方式
SSA中领导者的位置更新方式适用于求解连续函数优化问题，无法直接用于离散问题，因此需要对更新策略进行离散化改进：
$$ x_j^1 = \left\{ {\begin{array}{*{20}{c}} {{F_j} + {{\boldsymbol{c}}_1}L,\quad r < 0.5} \\ {{F_j} - {{\boldsymbol{c}}_1}L,\quad r \geqslant 0.5} \end{array}} \right. $$ (13) 式中：
${F_j}$ 表示第$j$ 维食物源的位置；系数向量$ {c_1} $ 是SSA中最重要的参数，用于平衡算法的局部搜索和全局探索，随着迭代次数的增加逐渐变化，最后趋近于0；$r$ 为区间[0，1]的随机数，当$ r < 0.5 $ ，樽海鞘群个体$x_j^i$ 向食物源${F_j}$ 趋近，相反则远离。$L$ 为Lévy飞行步长，可有效避免陷入局部最优，更加快速找到全局最优解，Lévy飞行步长定义为$$ L{\text{ = }}\mu {\text{/}}{\left| \upsilon \right|^{\frac{1}{\beta }}} $$ (14) $$ \left\{ {\begin{array}{*{20}{c}} {\mu \sim N(0,\sigma _\mu ^2)} \\ {\upsilon \sim N(0,\sigma _\upsilon ^2)} \end{array}} \right. $$ (15) 式中：
$\mu $ 和$\upsilon $ 服从正态分布，其中的${\sigma _\mu }$ 和${\sigma _\upsilon }$ 由式(16)计算可得：$$ \left\{ {\begin{aligned} &{{\sigma _\mu }=\sqrt[\beta ]{{\dfrac{{\Gamma (1 + \beta )\sin ({\text{π}} \beta /2)}}{{\Gamma [(1 + \beta )/2]\beta \cdot {2^{\frac{{\beta - 1}}{2}}}}}}}} \\ &{{\sigma _\upsilon }=1} \end{aligned}} \right. $$ (16) 式中，
$\Gamma $ 是gamma函数，参数$\beta $ 是区间[0，2]的随机数，一般$\beta $ =1.5。追随者的位置更新策略是让其有针对性的移动，找到更好的适应度位置，从而加快最优解的搜索。追随者的移动是由自身位置和前一个个体的位置综合决定，对前一个个体位置有较强的依赖性。若追随者位置陷入局部最优，容易造成算法搜索停滞。为了更好地平衡算法的开发能力和搜索能力，引入线性递减的惯性权重，平衡先前个体对当前个体的影响。因此，引入惯性权重的跟随者位置更新公式为$$ x_j^i = \frac{1}{2}(x_j^i + \omega (t)x_j^{i - 1}) $$ (17) $$ {\omega _{(t)}} = \frac{{{\omega _{(s)}}({\omega _{(s)}} - {\omega _{(e)}})({t_{\max }} - t)}}{{{t_{\max }}}} $$ (18) 式中：
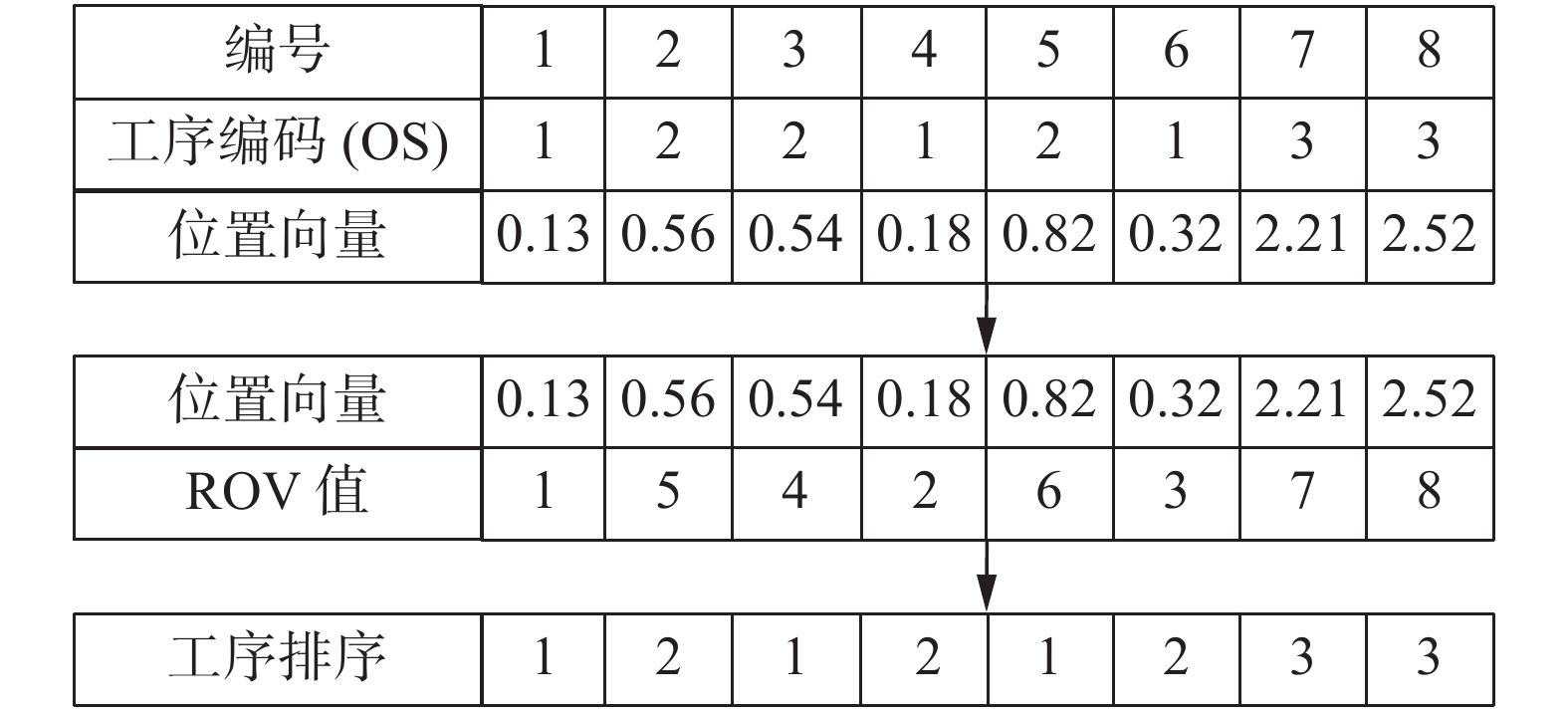
${\omega _{(s)}}$ 为初始惯性权重；${\omega _{(e)}}$ 为最大迭代次数时的惯性权重。初始迭代时较大的惯性权重有助于提升算法的搜索能力，迭代后期惯性权重较小时，有助于提升算法的开发能力。SSA算法中每个个体经过离散化处理后，利用ROV(ranked order value)规则，分别对每个个体的工序位置向量赋予唯一的ROV值，然后根据ROV值即可构造工序编码。个体位置转换为工序排序过程如图2所示，其中相同的工序编号表示同工件的不同工序，出现的次数代表工件的第几道工序。
图 2 个体位置转换为工序排序过程Fig. 2 Process of converting individual positions into process sequencing下载:
全尺寸图片
设备编码个体的位置向量限制在[1，
$m$ ]内，其中$m$ 为加工设备数，若计算得到的向量里元素值超过此区间，则取边界值。经过位置更新后，设备位置向量为小数，对其进行向上取整。位置更新后产生的设备编码可能为非可行解，需要对非可行解进行修正：1)设备向量对应的工序的可选加工设备集中仅有一台设备(即该工序仅能在一台设备上加工)，则选择该工序对应的设备序号更新设备位置向量；2)位置更新后的某道工序选择的设备不能加工该工序，则在该工序的可选加工集中随机选择一台设备替换该设备。3.4 交叉操作
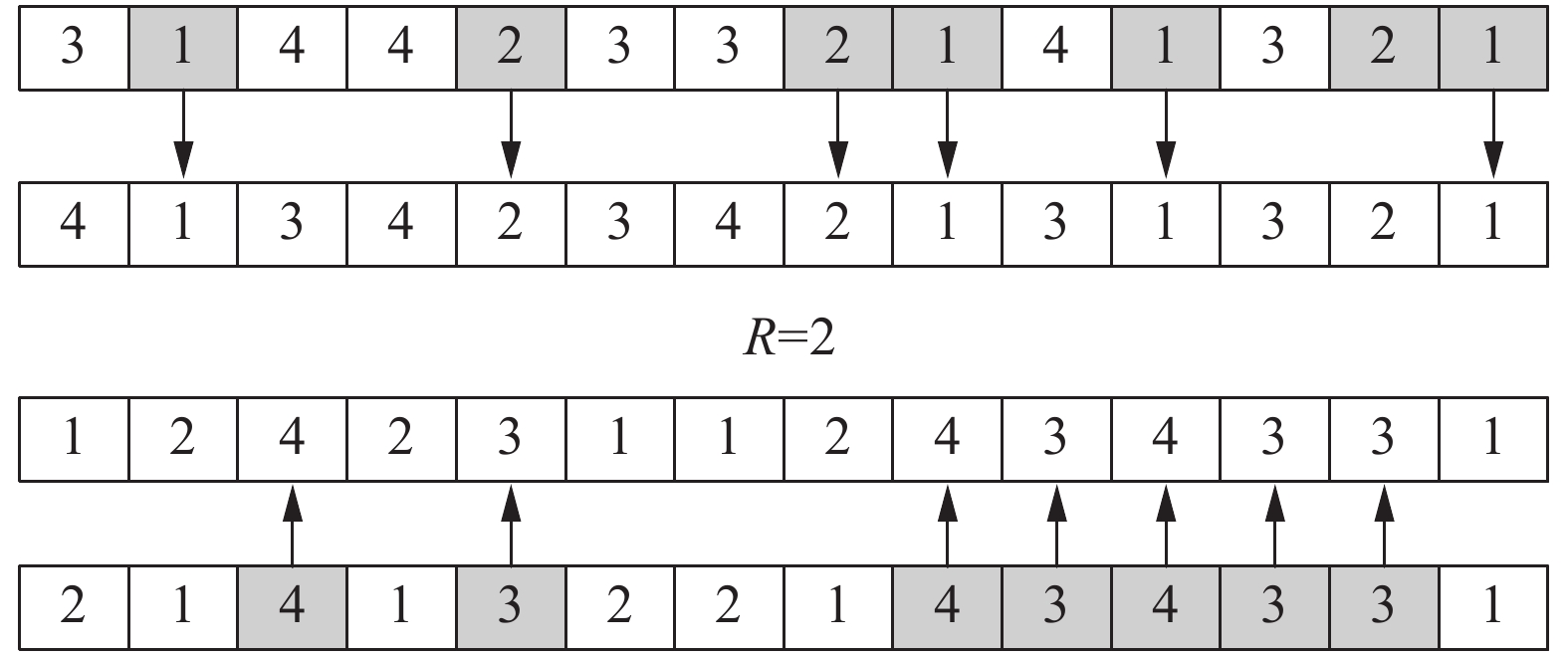
考虑到遗传算法有比较强的全局搜索能力[23]，融合交叉和变异算子对标准SSA算法进行改进，以增加种群的多样性并加快收敛速度。SSA算法不依赖遗传算子进化而是通过个体的位置移动来寻找问题最优个体。引入POX交叉算子(如图3所示)在OS部分操作方式如下：
1) 生成一个从1到工件数的随机整数R；
2)父代个体P1将工件序号小于或等于R的工件复制给子代个体C1；父代个体P2将工件序号大于R的工件复制给子代个体C2，保留其位置，并将对应的设备号复制到相应位置；
3)复制父代P1未出现在子代C2的工件序号到C2，复制父代P2未出现在C1的工件序号到子代C1，并保留其顺序，同时复制设备号到对应位置。
图 3 工序编码的交叉操作Fig. 3 Cross operation of process code下载:
全尺寸图片
位置更新过程中从子代C1和子代C2中随机选择一个作为后代，POX交叉过程使子代保留父代在每台设备的加工次序，并保留部分工件的位置。
交叉算子在MS部分操作如下：针对设备选择部分，采用两点交叉的方法，对于选定的两个父代个体，随机设置两个交叉点，交换所设定的两个交叉点之间的父代个体都有的工序所对应的设备序号。
3.5 变异操作
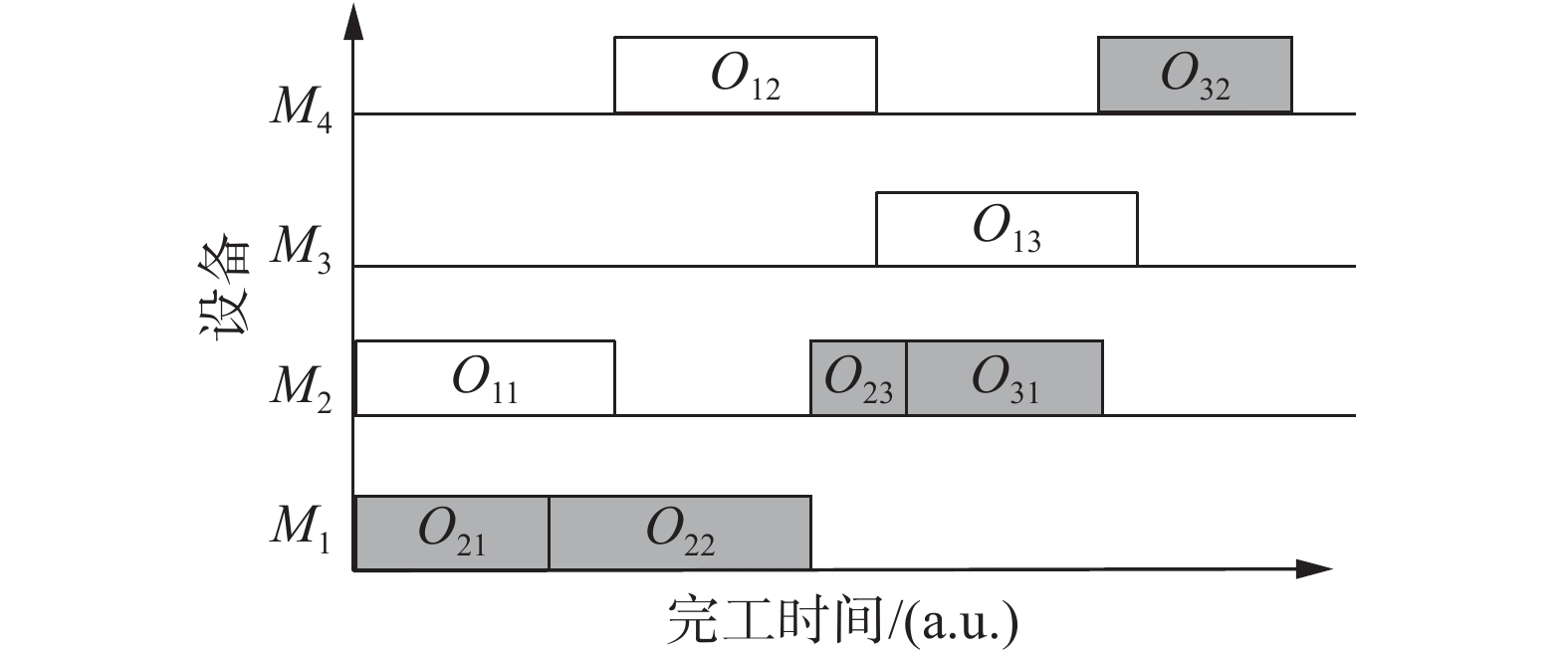
变异操作目的是为了增加种群多样性，改善算法的寻优能力。FJSP的变异操作后需要保证变异后解的可行性。和交叉操作一样，分别基于OS和MS进行变异操作。设计变异算子时，引入关键路径的思想。FJSP的一个可行解可用有向图来表示，其中从有向图起点到终点的最长路径称为关键路径。关键路径直接影响调度方案的最大完工时间。关键路径上的关键工序也称作关键工序，通过对关键工序进行扰动，有可能会减少最大完工时间。图4为图1对应的甘特图，其中阴影部分为关键工序。
图 4 基于关键路径甘特图Fig. 4 Gantt chart based on the critical path下载:
全尺寸图片
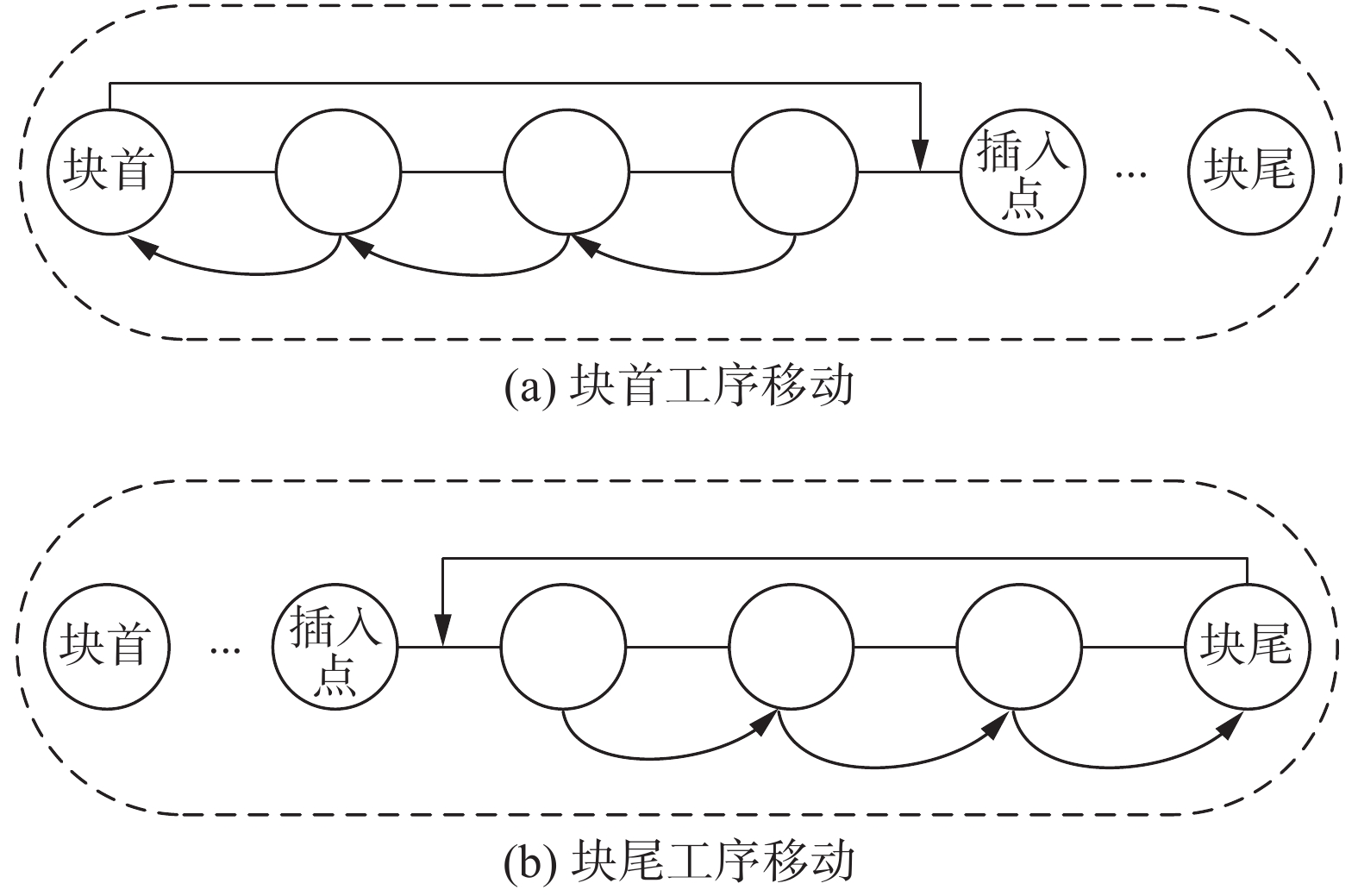
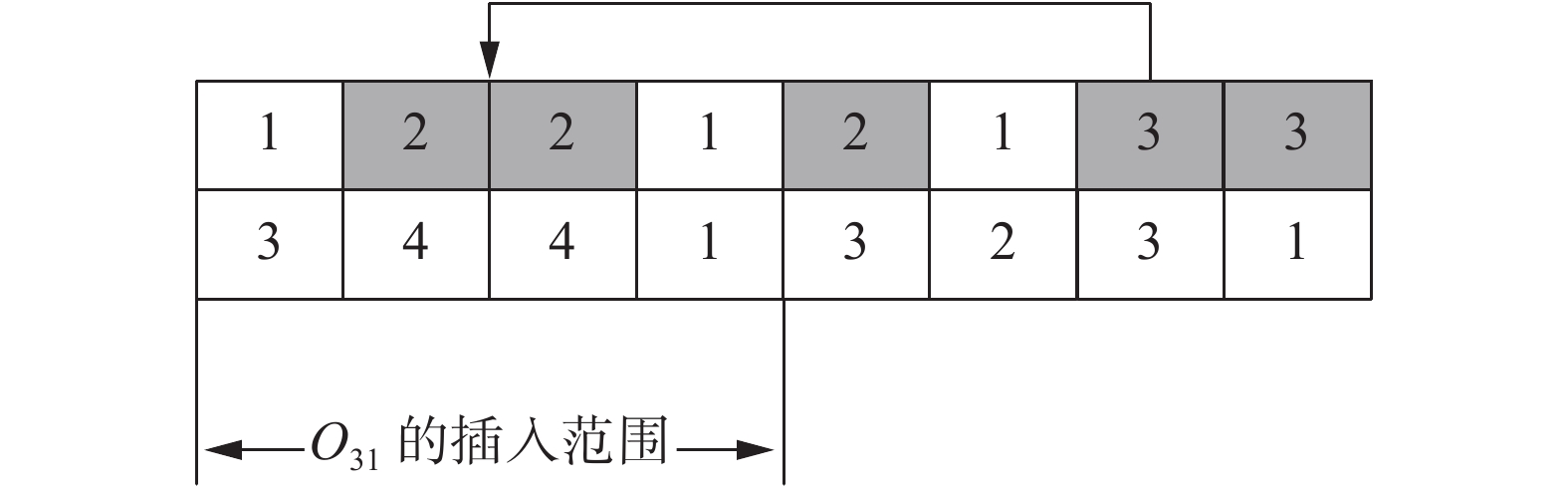
在满足加工优先级约束前提下，寻找关键路径上的所有关键块，随机选择关键块为移动源，选择不相邻的工序为移动点，向前或向后插入移动源，其余工序依次向前或向后改变位置，如图5所示。
图 5 关键工序邻域结构示意Fig. 5 Diagram of neighborhood structure of key processes下载:
全尺寸图片
对OS部分的变异操作引入基于关键路径的变异算子，将变异位置的选择缩短到关键路径上。具体操作过程为随机选择一道关键工序，满足工序加工优先级约束的前提下，将它插入到紧邻的前一道关键工序的某个位置，同时将相应的设备分配同步前移或者后移。图6为选中关键工序
${O_{31}}$ 的情况，并将其插入在另外一道关键工序${O_{22}}$ 之前。
图 6 工序编码的关键工序变异操作Fig. 6 Key process mutation operation for process coding下载:
全尺寸图片
对MS部分的变异操作为随机选择一道关键工序，在选择的关键工序可行加工设备集中选择加工时间最少的设备替换当前加工设备。这种选择方式增加种群的多样性，扩大解的搜索范围。
3.6 局部邻域搜索策略
采用上述编码和位置更新方式，有效地提高算法求解效率和收敛速度，但同时容易陷入局部最优解或无法完全收敛。SA算法具有较强的邻域搜索能力，将SA算法与IDSSA算法相结合可以有效提升算法的全局搜索和局部搜索能力，进而提升算法性能。本文基于设备负载的变异方式产生邻域解，具体流程如下：寻找所有加工设备中工作负载最大的设备，并在设备对应加工工序中随机选择一道工序，在考虑工序的优先级约束前提下将其分配到可选设备集中负载最小的设备。融合SA算法只对MS向量进行调整，让OS向量匹配到更合适的设备，从而平衡了设备工作负载。但同时会增加搜索时间，因此本文在初始种群中随机选择部分个体进行局部邻域搜索，增加种群的多样性。
3.7 IDSSA流程
IDSSA算法流程具体步骤如下：
1)初始化参数，根据3.2节的初始定位法生成初始解，并随机化食物源F的位置。
2)计算个体的目标函数值，将算法最优适应值为迭代过程中最佳的计算结果。
3)根据改进的位置更新公式分别对樽海鞘领导者和跟随者的位置进行更新。引入惯性权重对追随者个体位置进行优化，并记录当前种群中最优食物源的位置。
4)利用交叉、变异算子分别对个体的工序向量和设备向量进行交叉操作，增加可行解的搜索范围。
5)更新算法相关参数。
6)判断是否达到最优目标值，若新解的目标函数值优于当前解，则更新最优解并将其输出，否则采用SA算法，随机选择部分个体进行局部邻域搜索。
7)判断是否满足终止条件，即是否达到最大迭代次数。若满足，则跳转到8)，反之，执行2)。
8)算法结束。
4. 计算结果与分析
为了测试IDSSA算法在解决全局优化问题中的效果，将IDSSA算法和Jia等[18]提出的SSACL算法、标准SSA算法进行计算对比。IDSSA算法利用Lévy飞行改进领导者更新方式，在追随者更新公式上引入自适应惯性权重，利用交叉、变异策略增加种群多样性，并加入邻域搜索进一步改善算法的局部寻优能力。
采用CEC2005的10个基准测试函数，选取的测试函数包含单峰和多峰两种类型函数，其中单峰函数在定义上下限区间内只有一个全局最优，因此可以测试算法的开拓能力；多峰函数在定义区间含有多个全局最优和局部最优解，可以测试算法的全局搜索能力。函数的维度、定义域、理论最优解和类型如表2所示。
为了对比的公平性，将算法的参数和SSACL算法设置一致：种群大小为30，迭代次数为500。为了避免随机误差的影响，每个测试函数独立运行30次。计算对比数据如表3所示，表中每个测试函数的适应度均值和标准差分别反映了不同算法的收敛精度和稳定性。
对于表3中的测试函数，SSACL算法和IDSSA算法比标准SSA算法寻优结果都要好。在求解精度上，IDSSA算法有4个基准函数计算结果表现最好；就算法测试函数的平均值和标准差而言，IDSSA算法也表现出良好的计算优势，表明对标准SSA算法进行改进有效地提升了算法性能。
在验证IDSSA求解FJSP的改进效果和有效性方面，本文采用国际通用的10个Brandimarte基准算例、Fattahi提出的20个基准算例进行对比分析。Brandimarte算例中，工件数量
$n$ 从10到20，设备数量$m$ 从4到15进行组合选取，每组算例中的工序数从5到15；Fattahi算例中，工件数量$n$ 从2到12，设备数量$m$ 从2到8进行组合选取，每组算例中的工序数从2到4。使用Python3.6实现算法。计算机硬件配置为英特尔i56400 CPU(2.70 GHz)、8 GB RAM，在Windows 10的操作系统下运行程序。表 2 基准函数Table 2 Benchmark functions函数 维度 定义域 理论最优解 类型 ${F_1}(x) = \displaystyle\sum_{i = 1}^n {x_i^2}$ 30 [−100,100] 0 单峰 ${F_2}(x) = \displaystyle\sum_{i = 1}^n {|{x_i}|} - \prod\limits_{i = 1}^n {|{x_i}|}$ 30 [−10,10] 0 单峰 $F{}_3(x) = {\displaystyle\sum_{i = 1}^n {\left(\displaystyle\sum_{j = 1}^i { {x_j} } \right)} ^2}$ 30 [−100,100] 0 单峰 ${F_4}(x) = {\max _i}\{ |{x_i}|,1 \leqslant i \leqslant n\} $ 30 [−100,100] 0 单峰 ${F_5}(x) = \displaystyle\sum_{i = 1}^n {[100{ {({x_{i + 1} } - x_i^2)}^2} + { {({x_i} - 1)}^2}]}$ 30 [−30,30] 0 单峰 ${F_6}(x) = \displaystyle\sum_{i = 1}^n { { {(|{x_i} + 0.5|)}^2} }$ 30 [−100,100] 0 单峰 ${F_7}(x) = \displaystyle\sum_{i = 1}^n {ix_i^4} + {\rm{random}}[0,1)$ 30 [−1.28,1.28] 0 单峰 ${F_8}(x) = \displaystyle\sum_{i = 1}^n { - {x_i} } \sin \left(\sqrt {|{x_i}|} \right)$ 30 [−500,500] −418.982 $ \times D$ 单峰 ${F_9}(x) = \displaystyle\sum_{i = 1}^n {\left[x_i^2 - 10\cos (2{\text{π} } {x_i}) + 10\right]}$ 30 [−5.12,5.12] 0 多峰 $\begin{gathered} {F_{10} }(x) = - 20\exp \left( - 0.2\sqrt {\dfrac{1}{n}\displaystyle\sum_{i = 1}^n {x_i^2} } \right) - \exp \left(\dfrac{1}{n}\displaystyle\sum_{i = 1}^n {\cos (2{\text{π}} {x_i})} \right) \hfill + 20 + e \hfill \end{gathered}$ 30 [−32,32] 0 多峰 表 3 基准函数优化结果对比Table 3 Comparison of optimization results of benchmark functions函数 指标 SSA SSACL IDSSA 函数 指标 SSA SSACL IDSSA F1 最优值 4.40×10−10 1.48×10−205 0.00×100 F6 最优值 3.86×10−10 1.63×10−17 1.47×10−15 平均值 9.53×10−10 2.33×10−79 3.83×10−135 平均值 1.01×10−9 8.28×10−17 6.73×10−11 标准差 3.71×10−10 1.27×10−18 2.06×10−135 标准差 4.27×10−10 3.15×10−19 1.99×10−10 F2 最优值 5.13×10−6 2.20×10−126 0.00×100 F7 最优值 2.62×10−3 2.23×10−6 2.23×10−5 平均值 2.49×10−3 1.36×10−118 1.42×10−41 平均值 1.28×10−2 7.13×10−5 4.11×10−5 标准差 1.04×10−2 5.63×10−118 6.37×10−41 标准差 9.60×10−3 7.78×10−5 1.88×10−5 F3 最优值 5.21×10−9 1.02×10−201 0.00×100 F8 最优值 −3.38×103 −4.19×103 −1.04×104 平均值 2.37×10−6 1.68×10−184 1.14×10−78 平均值 −2.81×103 −4.11×103 −8.58×103 标准差 6.75×10−6 0.00×100 6.17×10−78 标准差 3.69×102 3.41×102 1.19×103 F4 最优值 9.78×10−6 7.42×10−13 1.01×10−158 F9 最优值 5.97×100 0.00×100 3.07×10−4 平均值 1.89×10−5 3.96×10−12 1.49×10−27 平均值 1.79×101 9.47×10−16 6.78×10−4 标准差 8.30×10−6 2.87×10−8 8.01×10−27 标准差 7.11×100 5.19×10−15 6.38×10−4 F5 最优值 4.30×100 0.00×100 0.00×100 F10 最优值 9.14×10−6 8.88×10−16 8.88×10−16 平均值 3.69×102 8.87×100 9.40×10−2 平均值 9.43×10−1 3.97×10−15 8.88×10−16 标准差 6.56×102 4.01×100 7.60×10−2 标准差 1.03×100 1.23×10−15 0.00×100 4.1 算法参数选取
参数设置对算法性能有很大的影响，参数选取标准是通过解的质量和算法运行时间来衡量，文中利用Brandimate提出的算例Mk01结果来确定算法参数。以解的平均偏差和平均运行时间为基准，经过多次计算从而确定相关参数。本文所提的IDSSA主要包括
$\beta $ 、${T_0}$ 、$\mu $ 、${\omega _{(s)}}$ 、${\omega _{(e)}}$ 和${T_{\lim }}$ 等6个参数。基于计算结果，参数$\beta $ 设置为1.5；初始温度${T_0}$ 和冷却系数$\mu $ 分别被设置为100和0.95；利用Gurobi求解限制时间为${T_{\lim }}$ =1 200 s；经过正交实验后确定${\omega _{(s)}}$ =0.9，${\omega _{(e)}}$ =0.4时算法具有最佳性能。4.2 结果分析
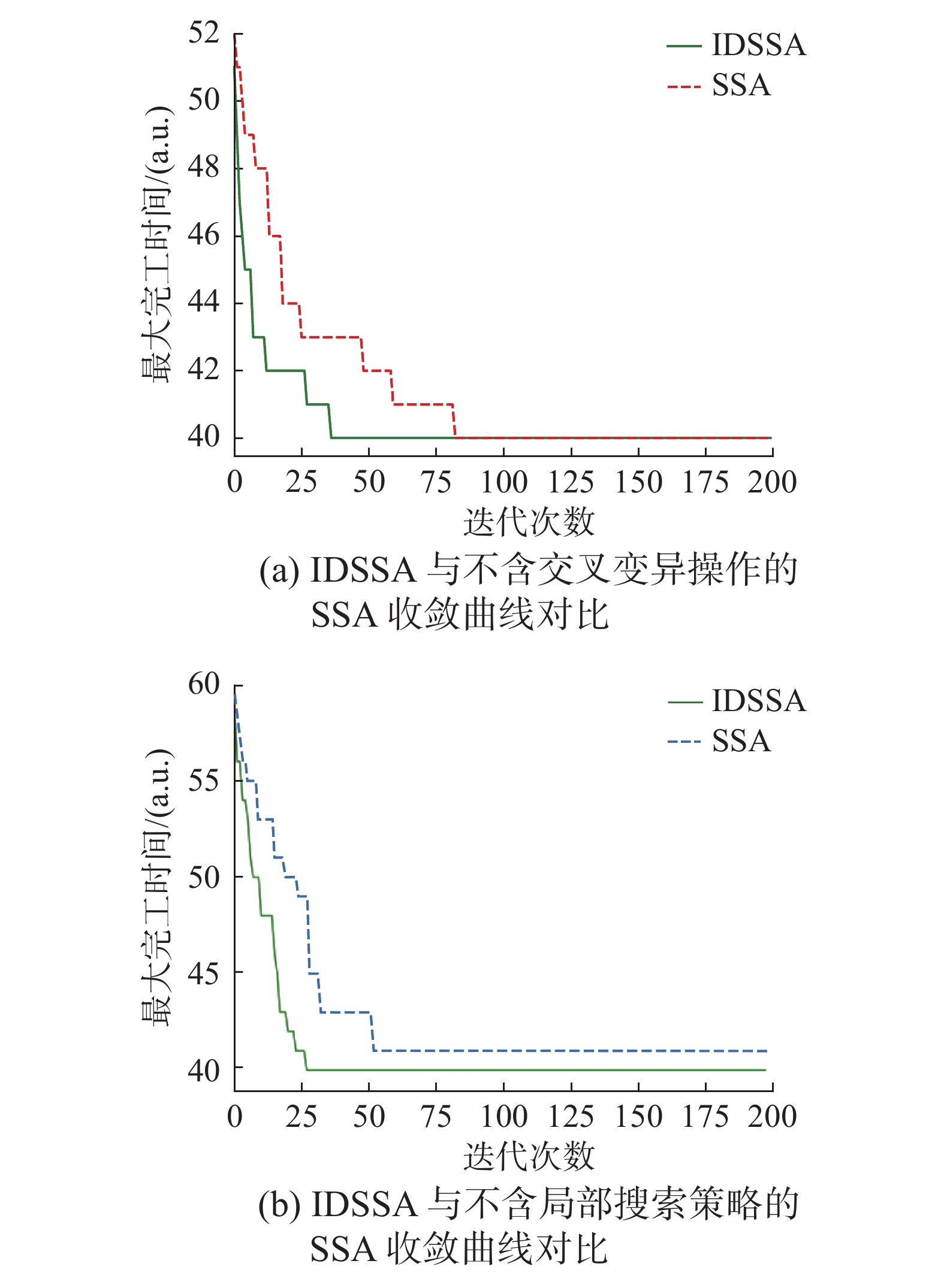
为了更好评估融合交叉与变异算子的IDSSA算法的有效性和稳定性，选取Brandimate提出的算例Mk01进行测算。收敛曲线如图7(a)所示，通过观察IDSSA算法与不含交叉变异操作的改进SSA算法的收敛曲线，发现引入交叉与变异算子的IDSSA算法收敛曲线下降更快。较之SSA算法，IDSSA算法收敛速度和稳定性得到进一步改善。同时，为验证局部邻域搜索策略的有效性，同样选取算例Mk01进行测算。收敛曲线如图7(b)所示，将IDSSA算法与不含局部搜索策略的改进SSA算法进行对比发现，IDSSA算法表现出了更高的搜索精度。
为验证所提MIP模型的正确性并给所提算法运算结果提供对比参考，采用Brandimarte基准算例[24]进行测试，运用Gurobi 8.1.1进行精确求解。为了达到性能评价的目的，在本文所提算法和HGWO算法[6]、Heuristic算法[7]以及后续对比算法的参数设置上选择了最佳的、相同的参数配置以保证了算法的可比性。由于问题的难求解性，处理MIP模型时将Gurobi时间限定为1 200 s，若求解时间未超过1 200 s，则输出解为最优解。除此之外，还采用Fattahi基准算例进行对比，并与文献中的算法进行对比，包括HTS/SA算法[2]、MIG算法[4]、AIA算法[5]。
比较本文提出算法与其他文献算法相较当前最优解的相对百分偏差RPD(relative percent deviation)，计算公式为
$$ {\rm{RPD}} = [({C_{\max }} - {\rm{UB}})/{\rm{UB}}] \times 100{\text{%}} $$ (19) 其中对于每个算例，
${\rm{UB}}$ 表示当前算例目前最佳目标函数值，${C_{\max }}$ 表示当前算例求解的最大完工时间。表4为Brandimarte基准算例测试结果。表4中
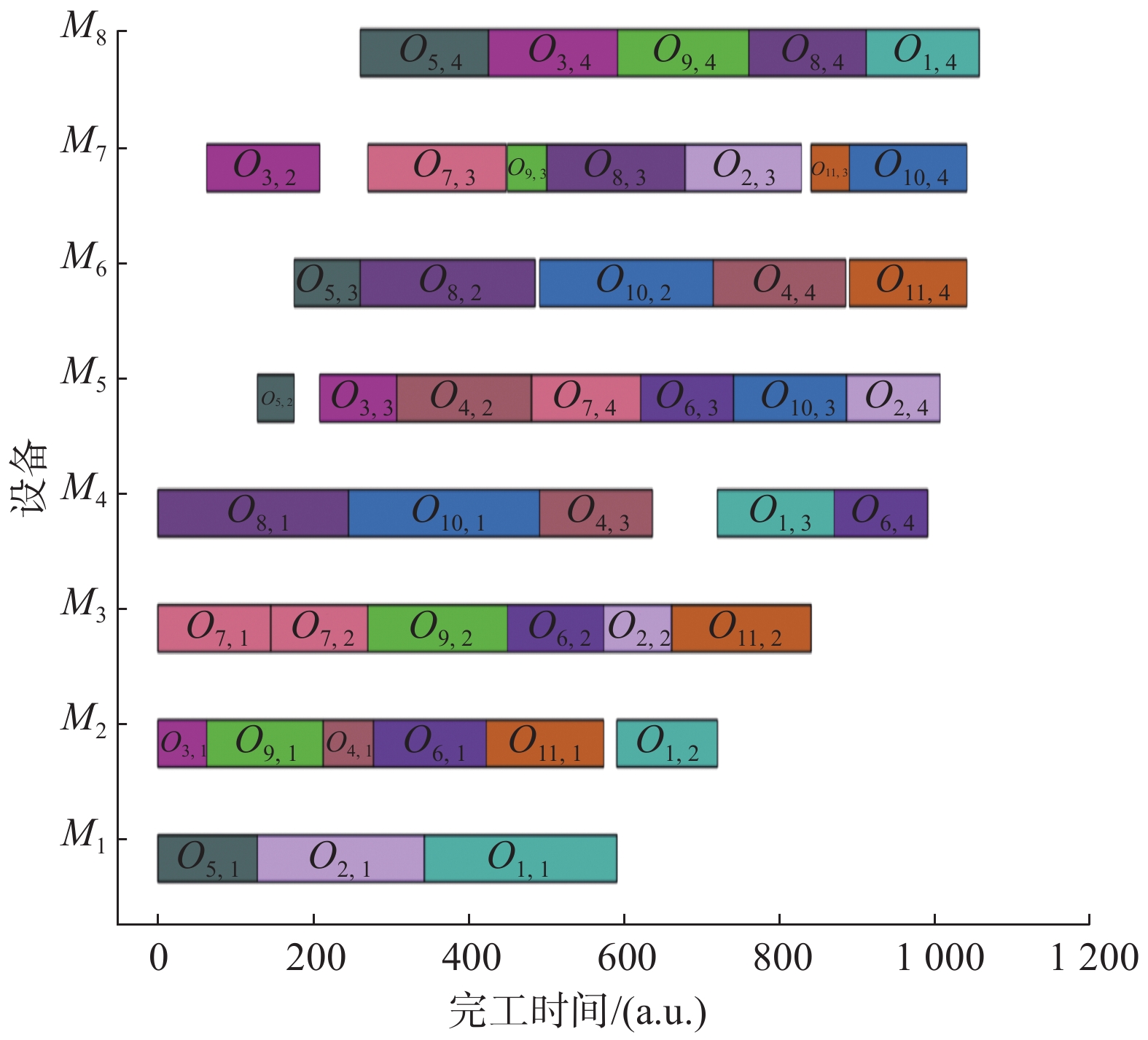
$n \times m$ 表示对应算例的工件数和设备数。ARPD表示当前算法的相对百分偏差平均值(%)。CPU表示算法运行时间，s。为了排除误差的影响，更加准确地对比所提算法的可行性和有效性，将每个算例运行10次。可以看出所提出的MIP在求解较小规模算例得到了令人满意的解，在求解较大规模算例陷入局部最优，不能在有效的时间内得到较优解。本文所提出的IDSSA和其他参考文献提出的算法相比，计算结果中9个算例优于Heuristic，相比HGWO存在较大的优势。相较当前最优解的平均偏差来看，IDSSA和其他算法相比偏差值最小，即从整体上来看，所提出的IDSSA优于MIP和参考文献[6-7]所提出的其他两种算法。表 4 Brandimate算例计算结果对比Table 4 Comparison of calculation results of Brandimate instances算例 n×m UB MIP HGWO[6] Heuristic[7] IDSSA Cmax RPD/% CPU/s Cmax RPD/% CPU/s Cmax RPD/% CPU/s Cmax RPD/% CPU/s Mk01 10×6 40 40 0 6.0 40 0 36.3 42 5.00 0.09 40 0 14.2 Mk02 10×6 26 27 3.84 4.2 29 11.53 38.7 28 7.69 0.17 26 0 12.5 Mk03 15×8 204 204 0 42.4 204 0 165.8 204 0 0.52 204 0 1.2 Mk04 15×8 60 62 3.33 462.8 65 8.33 75.9 75 25.00 0.20 65 8.33 18.6 
图 7 IDSSA与SSA的收敛曲线比较Fig. 7 Comparison of IDSSA and SSA convergence curves下载:
全尺寸图片
续表 4 算例 n×m UB MIP HGWO[6] Heuristic[7] IDSSA Cmax RPD/% CPU/s Cmax RPD/% CPU/s Cmax RPD/% CPU/s Cmax RPD/% CPU/s Mk05 15×4 173 182 5.20 485.3 175 1.15 96.7 179 3.46 0.20 175 1.15 24.9 Mk06 10×15 58 67 15.51 672.2 79 36.20 168.6 69 18.96 0.45 67 15.51 13.6 Mk07 20×5 139 154 10.79 533.0 149 7.19 92.1 149 7.19 0.39 145 4.31 100.2 Mk08 20×10 523 523 0 359.6 523 0 340.8 555 6.11 0.66 523 0 33.8 Mk09 20×10 307 325 5.86 945.5 325 5.86 378.9 342 11.40 0.94 325 5.86 28.5 Mk10 20×15 198 265 33.83 105.8 253 27.77 388.5 242 22.22 1.20 232 17.17 45.6 ARPD/% 7.83 9.80 10.70 5.23* 表5给出了本文算法在Fattahi测试集上的性能，对比方法有HTS/SA[2]、AIA[4]、MIG[5]等。在较小规模算例上，表中列举算法求解性能差异不大，而在较大规模算例(即MFJS9和MFJS10)上，本文算法显示出良好的求解性能。图8为IDSSA算法求解问题MFJS9输出结果的甘特图。
表 5 Fattahi算例计算结果对比Table 5 Comparison of calculation results of Fattahi instances算例 n×m UB HTS/SA[2] AIA[4] MIG[5] IDSSA Cmax RPD/% CPU/s Cmax RPD/% CPU/s Cmax RPD/% CPU/s Cmax RPD/% CPU/s SFJS1 2×2 66 66 0 2 66 0 0.03 66 0 0.00 66 0 0.02 SFJS2 2×2 107 107 0 3 107 0 0.03 107 0 0.00 107 0 0.02 SFJS3 3×2 221 221 0 5 221 0 0.04 221 0 0.00 221 0 0.04 SFJS4 3×2 355 355 0 7 355 0 0.04 355 0 0.00 355 0 0.04 SFJS5 3×2 119 119 0 9 119 0 0.04 119 0 0.00 119 0 0.04 SFJS6 3×3 320 320 0 7 320 0 0.04 320 0 0.00 320 0 0.05 SFJS7 3×5 397 397 0 9 397 0 0.04 397 0 0.00 397 0 0.05 SFJS8 3×4 253 256 0 10 253 0 0.05 253 0 0.00 253 0 0.06 SFJS9 3×3 210 210 0 11 210 0 0.05 210 0 0.00 210 0 0.05 SFJS10 4×5 516 516 0 10 516 0 0.05 516 0 0.00 516 0 0.07 MFJS1 5×7 396 469 18.43 30 468 18.18 9.23 462 16.67 0.00 468 18.18 0.29 MFJS2 5×7 396 468 18.18 30 448 13.13 9.35 446 12.63 0.00 446 12.63 0.47 MFJS3 6×7 396 538 35.85 50 468 18.18 10.06 450 13.64 0.002 458 15.65 2.24 MFJS4 7×7 496 618 24.59 80 554 11.69 10.54 554 11.69 0.00 554 11.69 8.69 MFJS5 7×7 414 625 50.96 64 527 27.29 10.61 514 24.15 0.00 514 24.15 1.95 MFJS6 8×7 469 730 55.65 102 635 35.39 22.18 634 35.18 0.00 634 35.18 12.67 MFJS7 8×7 619 947 52.98 190 879 42.00 24.82 881 42.33 0.00 877 41.68 22.68 MFJS8 9×8 619 922 48.94 182 884 42.81 26.94 889 43.62 0.00 884 42.81 58.32 MFJS9 11×8 764 1105 44.63 330 1088 42.41 30.76 1059 38.61 0.005 1055 38.08 136.35 MFJS10 12×8 944 1384 46.61 430 1267 34.22 90.94 1214 28.60 0.005 1196 26.69 162.65 ARPD/% 19.90 14.27 13.35 13.33* 
图 8 MFJS9调度甘特图Fig. 8 MFJS9 scheduling Gantt chart下载:
全尺寸图片
5. 结束语
本文在标准樽海鞘群算法的基础上，提出了一种融合模拟退火算法的改进樽海鞘群算法。基于Lévy飞行对领导者的位置更新方式进行离散化改进，引入自适应惯性权重对追随者的位置进行移动，平衡算法的开发能力和搜索能力。建立问题的混合整数规划模型并利用标准算例检验算法的性能，结果表明：改进的樽海鞘群算法在求解单目标柔性业车间问题取得了比较好的结果，算法的鲁棒性和有效性得到了验证。同时，本文为连续化SSA算法进行离散化求解工程实际问题提供了一种可行的改进方式。
下一步还将开展算法的计算时间复杂度理论分析及算法的收敛特性理论证明相关工作。同时，深入分析FJSP的问题特征，在实际的生产作业中，存在着物料组成、工人技能、设备资源受限等诸多约束条件，考虑将改进的樽海鞘群算法应用到更加复杂的工程实践问题当中，进一步验证算法的性能。
-
图 1 IDSSA编码示意
Fig. 1 IDSSA code representation
下载:
全尺寸图片
图 2 个体位置转换为工序排序过程
Fig. 2 Process of converting individual positions into process sequencing
下载:
全尺寸图片
图 3 工序编码的交叉操作
Fig. 3 Cross operation of process code
下载:
全尺寸图片
图 4 基于关键路径甘特图
Fig. 4 Gantt chart based on the critical path
下载:
全尺寸图片
图 5 关键工序邻域结构示意
Fig. 5 Diagram of neighborhood structure of key processes
下载:
全尺寸图片
图 6 工序编码的关键工序变异操作
Fig. 6 Key process mutation operation for process coding
下载:
全尺寸图片
图 7 IDSSA与SSA的收敛曲线比较
Fig. 7 Comparison of IDSSA and SSA convergence curves
下载:
全尺寸图片
图 8 MFJS9调度甘特图
Fig. 8 MFJS9 scheduling Gantt chart
下载:
全尺寸图片
表 1 符号与参数
Table 1 Symbols and parameters
参数 说明 $J$ 工件集合， $J = \{ 1,2, \cdots ,n\} $ $M$ 加工设备集合， $M = \{ 1,2, \cdots ,m\} $ ${O_{ij}}$ 工件 $i$的第 $j$道工序 ${J_i}$ 工件 $i$的工序集合， ${J_i} = \{ 1,2, \cdots, {n_i}\} ,{n_i}$为其工序总数 ${M_{ij}}$ 工件 $i$的第 $j$道工序的可选加工设备集合 ${P_{ijk}}$ 工件 $i$的第 $j$道工序在设备 $k$上的加工时间 ${s_{ij}}$ 工件 $i$的第 $j$道工序的加工开始时间 $\varDelta$ 足够大的正数 ${z_{ijk}}$ 假设工序 ${O_{ij}}$选择设备 $k$，变量的值为1，否则为0 ${y_{ij{i'}{j'} } }$ 假设 ${O_{ij}}$先于 ${O_{ {i'}{j'} } }$加工，变量的值为1，否则为0 表 2 基准函数
Table 2 Benchmark functions
函数 维度 定义域 理论最优解 类型 ${F_1}(x) = \displaystyle\sum_{i = 1}^n {x_i^2}$ 30 [−100,100] 0 单峰 ${F_2}(x) = \displaystyle\sum_{i = 1}^n {|{x_i}|} - \prod\limits_{i = 1}^n {|{x_i}|}$ 30 [−10,10] 0 单峰 $F{}_3(x) = {\displaystyle\sum_{i = 1}^n {\left(\displaystyle\sum_{j = 1}^i { {x_j} } \right)} ^2}$ 30 [−100,100] 0 单峰 ${F_4}(x) = {\max _i}\{ |{x_i}|,1 \leqslant i \leqslant n\} $ 30 [−100,100] 0 单峰 ${F_5}(x) = \displaystyle\sum_{i = 1}^n {[100{ {({x_{i + 1} } - x_i^2)}^2} + { {({x_i} - 1)}^2}]}$ 30 [−30,30] 0 单峰 ${F_6}(x) = \displaystyle\sum_{i = 1}^n { { {(|{x_i} + 0.5|)}^2} }$ 30 [−100,100] 0 单峰 ${F_7}(x) = \displaystyle\sum_{i = 1}^n {ix_i^4} + {\rm{random}}[0,1)$ 30 [−1.28,1.28] 0 单峰 ${F_8}(x) = \displaystyle\sum_{i = 1}^n { - {x_i} } \sin \left(\sqrt {|{x_i}|} \right)$ 30 [−500,500] −418.982 $ \times D$ 单峰 ${F_9}(x) = \displaystyle\sum_{i = 1}^n {\left[x_i^2 - 10\cos (2{\text{π} } {x_i}) + 10\right]}$ 30 [−5.12,5.12] 0 多峰 $\begin{gathered} {F_{10} }(x) = - 20\exp \left( - 0.2\sqrt {\dfrac{1}{n}\displaystyle\sum_{i = 1}^n {x_i^2} } \right) - \exp \left(\dfrac{1}{n}\displaystyle\sum_{i = 1}^n {\cos (2{\text{π}} {x_i})} \right) \hfill + 20 + e \hfill \end{gathered}$ 30 [−32,32] 0 多峰 表 3 基准函数优化结果对比
Table 3 Comparison of optimization results of benchmark functions
函数 指标 SSA SSACL IDSSA 函数 指标 SSA SSACL IDSSA F1 最优值 4.40×10−10 1.48×10−205 0.00×100 F6 最优值 3.86×10−10 1.63×10−17 1.47×10−15 平均值 9.53×10−10 2.33×10−79 3.83×10−135 平均值 1.01×10−9 8.28×10−17 6.73×10−11 标准差 3.71×10−10 1.27×10−18 2.06×10−135 标准差 4.27×10−10 3.15×10−19 1.99×10−10 F2 最优值 5.13×10−6 2.20×10−126 0.00×100 F7 最优值 2.62×10−3 2.23×10−6 2.23×10−5 平均值 2.49×10−3 1.36×10−118 1.42×10−41 平均值 1.28×10−2 7.13×10−5 4.11×10−5 标准差 1.04×10−2 5.63×10−118 6.37×10−41 标准差 9.60×10−3 7.78×10−5 1.88×10−5 F3 最优值 5.21×10−9 1.02×10−201 0.00×100 F8 最优值 −3.38×103 −4.19×103 −1.04×104 平均值 2.37×10−6 1.68×10−184 1.14×10−78 平均值 −2.81×103 −4.11×103 −8.58×103 标准差 6.75×10−6 0.00×100 6.17×10−78 标准差 3.69×102 3.41×102 1.19×103 F4 最优值 9.78×10−6 7.42×10−13 1.01×10−158 F9 最优值 5.97×100 0.00×100 3.07×10−4 平均值 1.89×10−5 3.96×10−12 1.49×10−27 平均值 1.79×101 9.47×10−16 6.78×10−4 标准差 8.30×10−6 2.87×10−8 8.01×10−27 标准差 7.11×100 5.19×10−15 6.38×10−4 F5 最优值 4.30×100 0.00×100 0.00×100 F10 最优值 9.14×10−6 8.88×10−16 8.88×10−16 平均值 3.69×102 8.87×100 9.40×10−2 平均值 9.43×10−1 3.97×10−15 8.88×10−16 标准差 6.56×102 4.01×100 7.60×10−2 标准差 1.03×100 1.23×10−15 0.00×100 表 4 Brandimate算例计算结果对比
Table 4 Comparison of calculation results of Brandimate instances
算例 n×m UB MIP HGWO[6] Heuristic[7] IDSSA Cmax RPD/% CPU/s Cmax RPD/% CPU/s Cmax RPD/% CPU/s Cmax RPD/% CPU/s Mk01 10×6 40 40 0 6.0 40 0 36.3 42 5.00 0.09 40 0 14.2 Mk02 10×6 26 27 3.84 4.2 29 11.53 38.7 28 7.69 0.17 26 0 12.5 Mk03 15×8 204 204 0 42.4 204 0 165.8 204 0 0.52 204 0 1.2 Mk04 15×8 60 62 3.33 462.8 65 8.33 75.9 75 25.00 0.20 65 8.33 18.6 续表 4 算例 n×m UB MIP HGWO[6] Heuristic[7] IDSSA Cmax RPD/% CPU/s Cmax RPD/% CPU/s Cmax RPD/% CPU/s Cmax RPD/% CPU/s Mk05 15×4 173 182 5.20 485.3 175 1.15 96.7 179 3.46 0.20 175 1.15 24.9 Mk06 10×15 58 67 15.51 672.2 79 36.20 168.6 69 18.96 0.45 67 15.51 13.6 Mk07 20×5 139 154 10.79 533.0 149 7.19 92.1 149 7.19 0.39 145 4.31 100.2 Mk08 20×10 523 523 0 359.6 523 0 340.8 555 6.11 0.66 523 0 33.8 Mk09 20×10 307 325 5.86 945.5 325 5.86 378.9 342 11.40 0.94 325 5.86 28.5 Mk10 20×15 198 265 33.83 105.8 253 27.77 388.5 242 22.22 1.20 232 17.17 45.6 ARPD/% 7.83 9.80 10.70 5.23* 表 5 Fattahi算例计算结果对比
Table 5 Comparison of calculation results of Fattahi instances
算例 n×m UB HTS/SA[2] AIA[4] MIG[5] IDSSA Cmax RPD/% CPU/s Cmax RPD/% CPU/s Cmax RPD/% CPU/s Cmax RPD/% CPU/s SFJS1 2×2 66 66 0 2 66 0 0.03 66 0 0.00 66 0 0.02 SFJS2 2×2 107 107 0 3 107 0 0.03 107 0 0.00 107 0 0.02 SFJS3 3×2 221 221 0 5 221 0 0.04 221 0 0.00 221 0 0.04 SFJS4 3×2 355 355 0 7 355 0 0.04 355 0 0.00 355 0 0.04 SFJS5 3×2 119 119 0 9 119 0 0.04 119 0 0.00 119 0 0.04 SFJS6 3×3 320 320 0 7 320 0 0.04 320 0 0.00 320 0 0.05 SFJS7 3×5 397 397 0 9 397 0 0.04 397 0 0.00 397 0 0.05 SFJS8 3×4 253 256 0 10 253 0 0.05 253 0 0.00 253 0 0.06 SFJS9 3×3 210 210 0 11 210 0 0.05 210 0 0.00 210 0 0.05 SFJS10 4×5 516 516 0 10 516 0 0.05 516 0 0.00 516 0 0.07 MFJS1 5×7 396 469 18.43 30 468 18.18 9.23 462 16.67 0.00 468 18.18 0.29 MFJS2 5×7 396 468 18.18 30 448 13.13 9.35 446 12.63 0.00 446 12.63 0.47 MFJS3 6×7 396 538 35.85 50 468 18.18 10.06 450 13.64 0.002 458 15.65 2.24 MFJS4 7×7 496 618 24.59 80 554 11.69 10.54 554 11.69 0.00 554 11.69 8.69 MFJS5 7×7 414 625 50.96 64 527 27.29 10.61 514 24.15 0.00 514 24.15 1.95 MFJS6 8×7 469 730 55.65 102 635 35.39 22.18 634 35.18 0.00 634 35.18 12.67 MFJS7 8×7 619 947 52.98 190 879 42.00 24.82 881 42.33 0.00 877 41.68 22.68 MFJS8 9×8 619 922 48.94 182 884 42.81 26.94 889 43.62 0.00 884 42.81 58.32 MFJS9 11×8 764 1105 44.63 330 1088 42.41 30.76 1059 38.61 0.005 1055 38.08 136.35 MFJS10 12×8 944 1384 46.61 430 1267 34.22 90.94 1214 28.60 0.005 1196 26.69 162.65 ARPD/% 19.90 14.27 13.35 13.33* -
[1] 裴小兵, 于秀燕. 改进猫群算法求解置换流水车间调度问题[J]. 智能系统学报, 2019, 14(4): 769–778. https://www.cnki.com.cn/Article/CJFDTOTAL-ZNXT201904023.htm PEI Xiaobing, YU Xiuyan. Improved cat swarm optimization for permutation flow shop scheduling problem[J]. CAAI transactions on intelligent systems, 2019, 14(4): 769–778. https://www.cnki.com.cn/Article/CJFDTOTAL-ZNXT201904023.htm [2] FATTAHI P, MEHRABAD M S, JOLAI F. Mathematical modeling and heuristic approaches to flexible job shop scheduling problems[J]. Journal of intelligent manufacturing, 2007, 18(3): 331–342. doi: 10.1007/s10845-007-0026-8 [3] LI Xinyu, GAO Liang. An effective hybrid genetic algorithm and tabu search for flexible job shop scheduling problem[J]. International journal of production economics, 2016, 174: 93–110. doi: 10.1016/j.ijpe.2016.01.016 [4] AL AQEL G, LI Xinyu, GAO Liang. A modified iterated greedy algorithm for flexible job shop scheduling problem[J]. Chinese journal of mechanical engineering, 2019, 32(1): 21. doi: 10.1186/s10033-019-0337-7 [5] BAGHERI A, ZANDIEH M, MAHDAVI I, et al. An artificial immune algorithm for the flexible job-shop scheduling problem[J]. Future generation computer systems, 2010, 26(4): 533–541. doi: 10.1016/j.future.2009.10.004 [6] 姜天华. 混合灰狼优化算法求解柔性作业车间调度问题[J]. 控制与决策, 2018, 33(3): 503–508. https://www.cnki.com.cn/Article/CJFDTOTAL-KZYC201803016.htm JIANG Tianhua. Flexible job shop scheduling problem with hybrid grey wolf optimization algorithm[J]. Control and decision, 2018, 33(3): 503–508. https://www.cnki.com.cn/Article/CJFDTOTAL-KZYC201803016.htm [7] ZIAEE M. A heuristic algorithm for solving flexible job shop scheduling problem[J]. The international journal of advanced manufacturing technology, 2014, 71(1): 519–528. [8] SHEN Liji, DAUZÈRE-PÉRÈS S, NEUFELD J S. Solving the flexible job shop scheduling problem with sequence-dependent setup times[J]. European journal of operational research, 2018, 265(2): 503–516. doi: 10.1016/j.ejor.2017.08.021 [9] 杨冬婧, 雷德明. 新型蛙跳算法求解总能耗约束FJSP[J]. 中国机械工程, 2018, 29(22): 2682–2689. doi: 10.3969/j.issn.1004-132X.2018.22.005 YANG Dongjing, LEI Deming. A novel shuffled frog-leaping algorithm for FJSP with total energy consumption constraints[J]. China mechanical engineering, 2018, 29(22): 2682–2689. doi: 10.3969/j.issn.1004-132X.2018.22.005 [10] ZHOU Yong, YANG Jianjun. Automatic design of scheduling policies for dynamic flexible job shop scheduling by multi-objective genetic programming based hyper-heuristic[J]. Procedia CIRP, 2019, 79: 439–444. doi: 10.1016/j.procir.2019.02.118 [11] BAYKASOĞLU A, MADENOĞLU F S, HAMZADAYI A. Greedy randomized adaptive search for dynamic flexible job-shop scheduling[J]. Journal of manufacturing systems, 2020, 56: 425–451. doi: 10.1016/j.jmsy.2020.06.005 [12] ZHANG Guohui, HU Yifan, SUN Jinghe, et al. An improved genetic algorithm for the flexible job shop scheduling problem with multiple time constraints[J]. Swarm and evolutionary computation, 2020, 54: 100664. doi: 10.1016/j.swevo.2020.100664 [13] MIRJALILI S, GANDOMI A H, MIRJALILI S Z, et al. Salp Swarm Algorithm: a bio-inspired optimizer for engineering design problems[J]. Advances in engineering software, 2017, 114: 163–191. doi: 10.1016/j.advengsoft.2017.07.002 [14] 杨博, 钟林恩, 朱德娜, 等. 部分遮蔽下改进樽海鞘群算法的光伏系统最大功率跟踪[J]. 控制理论与应用, 2019, 36(3): 339–352. doi: 10.7641/CTA.2019.80899 YANG Bo, ZHONG Linen, ZHU Dena, et al. Modified salp swarm algorithm based maximum power point tracking of power-voltage system under partial shading condition[J]. Control theory & applications, 2019, 36(3): 339–352. doi: 10.7641/CTA.2019.80899 [15] IBRAHIM R A, EWEES A A, OLIVE D, et al. Improved salp swarm algorithm based on particle swarm optimization for feature selection[J]. Journal of ambient intelligence and humanized computing, 2019, 10(8): 3155–3169. doi: 10.1007/s12652-018-1031-9 [16] BHANDARI A K, KANDHWAY P, MAURYA S. Salp swarm algorithm-based optimally weighted histogram framework for image enhancement[J]. IEEE transactions on instrumentation and measurement, 2020, 69(9): 6807–6815. doi: 10.1109/TIM.2020.2976279 [17] RACHAPUDI V, DEVI G L. Optimal bag-of-features using random salp swarm algorithm for histopathological image analysis[J]. International journal of intelligent information and database systems, 2020, 13(2/3/4): 339–355. doi: 10.1504/IJIIDS.2020.109450 [18] JIA Heming, LANG Chunbo. Salp swarm algorithm with crossover scheme and Lévy flight for global optimization[J]. Journal of intelligent & fuzzy systems, 2021, 40(5): 9277–9288. [19] JOUHARI H, LEI Deming, AL-QANESS M A A, et al. Modified Harris hawks optimizer for solving machine scheduling problems[J]. Symmetry, 2020, 12(9): 1460. doi: 10.3390/sym12091460 [20] EWEES A A, AL-QANESS M A A, ELAZIZ M A. Enhanced salp swarm algorithm based on firefly algorithm for unrelated parallel machine scheduling with setup times[J]. Applied mathematical modelling, 2021, 94: 285–305. doi: 10.1016/j.apm.2021.01.017 [21] SUN Zaixing, HU Rong, QIAN Bin, et al. Salp swarm algorithm based on blocks on critical path for reentrant job shop scheduling problems[C]//Proceedings of the 14th International Conference on Intelligent Computing. Wuhan, China, 2018. [22] KACEM I, HAMMADI S, BORNE P. Approach by localization and multiobjective evolutionary optimization for flexible job-shop scheduling problems[J]. IEEE transactions on systems, man, and cybernetics, part C (applications and reviews), 2002, 32(1): 1–13. doi: 10.1109/TSMCC.2002.1009117 [23] LIU Zhengchao, GUO Shunsheng, WANG Lei. Integrated green scheduling optimization of flexible job shop and crane transportation considering comprehensive energy consumption[J]. Journal of cleaner production, 2019, 211: 765–786. doi: 10.1016/j.jclepro.2018.11.231 [24] BRANDIMARTE P. Routing and scheduling in a flexible job shop by tabu search[J]. Annals of operations research, 1993, 41(3): 157–183. doi: 10.1007/BF02023073
