融合振幅随机补偿与步长演变机制的改进原子搜索优化算法

刘威; 郭直清; 刘光伟; 靳宝; 王东

doi:10.11992/tis.202103033

融合振幅随机补偿与步长演变机制的改进原子搜索优化算法

doi: 10.11992/tis.202103033

刘威^{1, 2, 3, ,},
郭直清^{1, 2, 3},
刘光伟⁴,
靳宝^{1, 2, 3},
王东⁴

1.
辽宁工程技术大学理学院，辽宁阜新 123000;
2.
辽宁工程技术大学智能工程与数学研究院，辽宁阜新 123000;
3.
辽宁工程技术大学数学与系统科学研究所，辽宁阜新 123000;
4.
辽宁工程技术大学矿业学院，辽宁阜新 123000

基金项目: 国家自然科学基金项目(51974144, 51874160)；辽宁省教育厅项目(LJKZ0340)；辽宁工程技术大学学科创新团队资助项目(LNTU20TD-01, LNTU20TD-07).

详细信息

作者简介:
刘威，副教授，博士，中国人工智能学会会员，中国计算机学会会员，主要研究方向为深度神经网络、机器学习、矿业系统工程;

郭直清，硕士研究生，主要研究方向为机器学习与优化算法、数学建模与数据分析;

刘光伟，教授，博士生导师，博士，主要研究方向为露天矿开采设计理论、矿业系统工程.

通讯作者:
刘威. E-mail： lv8218218@126.com.

中图分类号: TP18
出版历程
- 收稿日期: 2021-03-24
- 网络出版日期: 2022-04-19

Improved atom search optimization by combining amplitude random compensation and step size evolution mechanism

LIU Wei^{1, 2, 3, ,},
GUO Zhiqing^{1, 2, 3},
LIU Guangwei⁴,
JIN Bao^{1, 2, 3},
WANG Dong⁴

1.
College of Science, Liaoning Technical University, Fuxin 123000, China;
2.
Institute of Intelligent Engineering and Mathematics, Liao ning Technical University, Fuxin 123000, China;
3.
Institute of Intelligent Engineering and Methematics, Liaoning Technical University, Fuxin 123000, China;
4.
College of Mines, Liaoning Technical University, Fuxin 123000, China

摘要

摘要: 针对原子优化算法寻优精度弱且易陷入局部极值的问题，本文从种群多样性、参数适应性和位置动态性角度提出一种融合混沌优化、振幅随机补偿和步长演变机制改进的原子搜索优化算法(improved atom search optimization, IASO)，并将其成功应用于分类任务。首先，引入帐篷映射(Tent混沌)增强原子种群在搜索空间中的分布均匀性；其次，通过构建振幅函数对算法参数进行随机扰动并加入步长演变因子更新原子位置，以增强算法全局性和收敛性；最后，再将改进算法应用于误差反馈神经网络(BP神经网络)参数优化。通过与6种元启发式算法在20个基准测试函数下的数值实验对比表明：IASO不仅在求解多维基准函数上具有好的寻优性能，且在对BP神经网络参数进行优化时相较于2种对比算法具有更高的分类精度。
- 元启发式算法 /
- 原子搜索优化算法 /
- Tent混沌优化 /
- 振幅随机补偿 /
- 步长演变机制 /
- BP神经网络参数优化 /
- 分类 /
- 机器学习
Abstract: The weak optimization accuracy of the atom search optimization algorithm can easily fall into a local extremum owing to population diversity, parameter adaptability, and position dynamics. To overcome this challenge, we propose an improved ASO algorithm (IASO) by integrating chaos optimization, amplitude random compensation, and step size evolution mechanism and successfully apply it to classification tasks. First, tent chaos is introduced to enhance the distribution uniformity of atomic population in the search space. Then, an amplitude function is constructed to randomly perturb the algorithm parameters, and the step evolution factor is added to update the atomic position to enhance the globality and convergence of the algorithm. Finally, the improved algorithm is applied to the parameter optimization of the error feedback BP neural network. Compared with the numerical calculations of six metaheuristic algorithms under 20 benchmark functions, the experimental results indicate that IASO not only shows a good optimization performance in solving multidimensional benchmark functions but also a higher classification accuracy than two comparison algorithms in optimizing the BP neural network parameters.
- meta-heuristics algorithms /
- atom search optimization /
- tent chaos optimization /
- amplitude random compensation /
- step size evolution mechanism /
- parameter optimization of BP neural network /
- classification /
- machine learning

HTML全文

元启发式算法是指研究者受仿生学启发，从自然界中的随机现象获取灵感，将随机算法与局部算法相结合来求解复杂优化问题的一类算法^[1]。此类算法相对于启发式算法的最大改进在于引入了随机因素的影响，从而使算法存在一定概率跳出局部最优，更有可能得到问题全局最优解，同时由于其对目标函数、初始值等无任何特殊要求，因此成为了最优化问题研究的热点问题之一。根据算法启发机制不同，元启发式算法可归结于两类：模仿生物学过程的算法和基于物理学原理的算法。其中模仿生物学过程的算法又可分为两类：基于生物进化的演化算法和基于动物社会性行为的群智能算法。基于生物进化的演化算法主要以遗传算法 (genetic algorithm, GA)^[2]为代表，同时还有进化策略(evolutionary strategies, ES)^[3]、文化基因算法 (memetic algorithm, MA)^[4]等；基于动物社会性行为的群智能算法是近年来元启发式算法研究的热点，有模拟鸟群捕食的粒子群算法 (particle swarm optimization, PSO)^[5]、基于乌鸦智能行为的乌鸦搜索算法 (crow search algorithm, CSA)^[6]、模拟樽海鞘聚集行为的樽海鞘群算法 (Salp swarm algorithm, SSA)^[7]、模拟蝴蝶觅食和求偶行为的蝴蝶优化算法(butterfly optimization algorithm, BOA)^[8]、模拟飞蛾飞行行为的飞蛾扑火优化算法 (moth-flame optimization, MFO)^[9]等；基于物理学原理的算法有模仿固体退火的模拟退火算法 (simulated annealing, SA)^[10]、模仿万有引力原理的引力搜索算法 (gravitational search algorithm, GSA)^[11]、模仿多元宇宙理论中黑洞、白洞及虫洞概念的多元宇宙优化算法 (multi-verse optimizer, MVO)^[12]等。

原子搜索优化算法(atom search optimization，ASO)是Zhao等^[13-14]受分子动力学启发提出的一种以物理学为灵感的基于原子运动的新型智能元启发式优化算法。该算法模仿由相互作用和约束力控制的原子运动，通过Lennard-Jones(L-J)势产生的相互作用力和原子共价键产生的约束力共同作用于原子，使不同质量的原子具有不同的速度和加速度，从而不断地更新原子所在位置，直到原子处于最优位置时，算法迭代完成。由于其启发机制简单、参数少、探索(exploration)和挖掘(exploitation)性强等特点已被应用于地下水中的弥散系数估计^[13]、水文地质参数估计^[14]、自动聚类^[15]、燃料电池模型参数估计^[16]等多个领域。

为提高ASO算法的收敛速度、求解精度及跳出局部最优能力，本文从原子群多样性、模型参数设置和原子位置更新角度提出了一种融合混沌优化、振幅随机补偿和步长演变机制的模拟原子位置更新过程的改进ASO算法(improved atom search optimization, IASO)，并将其应用于BP神经网络参数优化。通过对10个可变维基准测试函数在不同维度下以及10个固定多维度基准测试函数与5种元启发算法进行仿真实验对比，数值实验结果不仅验证了IASO相对于传统ASO算法和对比算法具有更好的寻优精度和全局性能，而且在对BP神经网络参数优化时表现出更高的分类性能。

1. 原子搜索优化算法(ASO)

对于ASO算法，其基本理论主要包含3个部分^[13-14]：原子运动约束方程、L-J势产生的相互作用力以及键长势引起的约束力。假设一个分子系统是由 $N$ 个原子构成的D维空间， $x_i^d(t)$ 为第 $i$ 个原子在第d个维度下第 $t$ 次迭代时的位置， $a_i^d(t)$ 为第 $i$ 个原子在第d个维度下第 $t$ 次迭代时的加速度， $v_i^d(t)$ 为第 $i$ 个原子在第d个维度下第 $t$ 次迭代时的速度， $F_i^d(t)$ 为第 $i$ 个原子在第d个维度下第 $t$ 次迭代时由L-J势产生的相互作用力， $G_i^d(t)$ 为第 $i$ 个原子在第d个维度下第 $t$ 次迭代时由原子共价键产生的约束力。

1.1 原子运动约束方程

ASO算法中假设原子运动满足牛顿第二定律，由于原子受L-J势产生的相互作用力和原子共价键产生的约束力共同作用，故带约束的原子运动方程表示为

$$ F_{i}^d (t)+ G_{i}^d(t) = m_{i}^d(t)a_{i}^d(t) $$

(1)

式中： $F_i^d(t)$ 为第 $i$ 个原子在第d个维度下第 $t$ 次迭代时由L-J势产生的相互作用力； $G_i^d(t)$ 为第 $i$ 个原子在第d个维度下第 $t$ 次迭代时由原子共价键产生的约束力。第 $i$ 个原子第 $t$ 次迭代时的加速度为

$$ a_i^d(t) = \frac{{F_i^d(t) + G_i^d(t)}}{{m_i^d(t)}} $$

(2)

式中： $m_i^d(t)$ 是第 $t$ 次迭代时第 $i$ 个原子在第d个维度下的质量，可通过第 $i$ 个原子的函数适应度值来计算，即

$$ m_i^d(t) = \dfrac{{M_i^d(t)}}{{\displaystyle\sum_{j = 1}^N {M_j^d(t)} }} $$

(3)

式中 $M_i^d(t) = {{\text{e}}^{ - \tfrac{{{\text{Fi}}{{\text{t}}_i}(t) - {\text{Fi}}{{\text{t}}_{{\text{best}}}}(t)}}{{{\text{Fi}}{{\text{t}}_{{\text{worst}}}}(t) - {\text{Fi}}{{\text{t}}_{{\text{best}}}}(t)}}}}$ 。

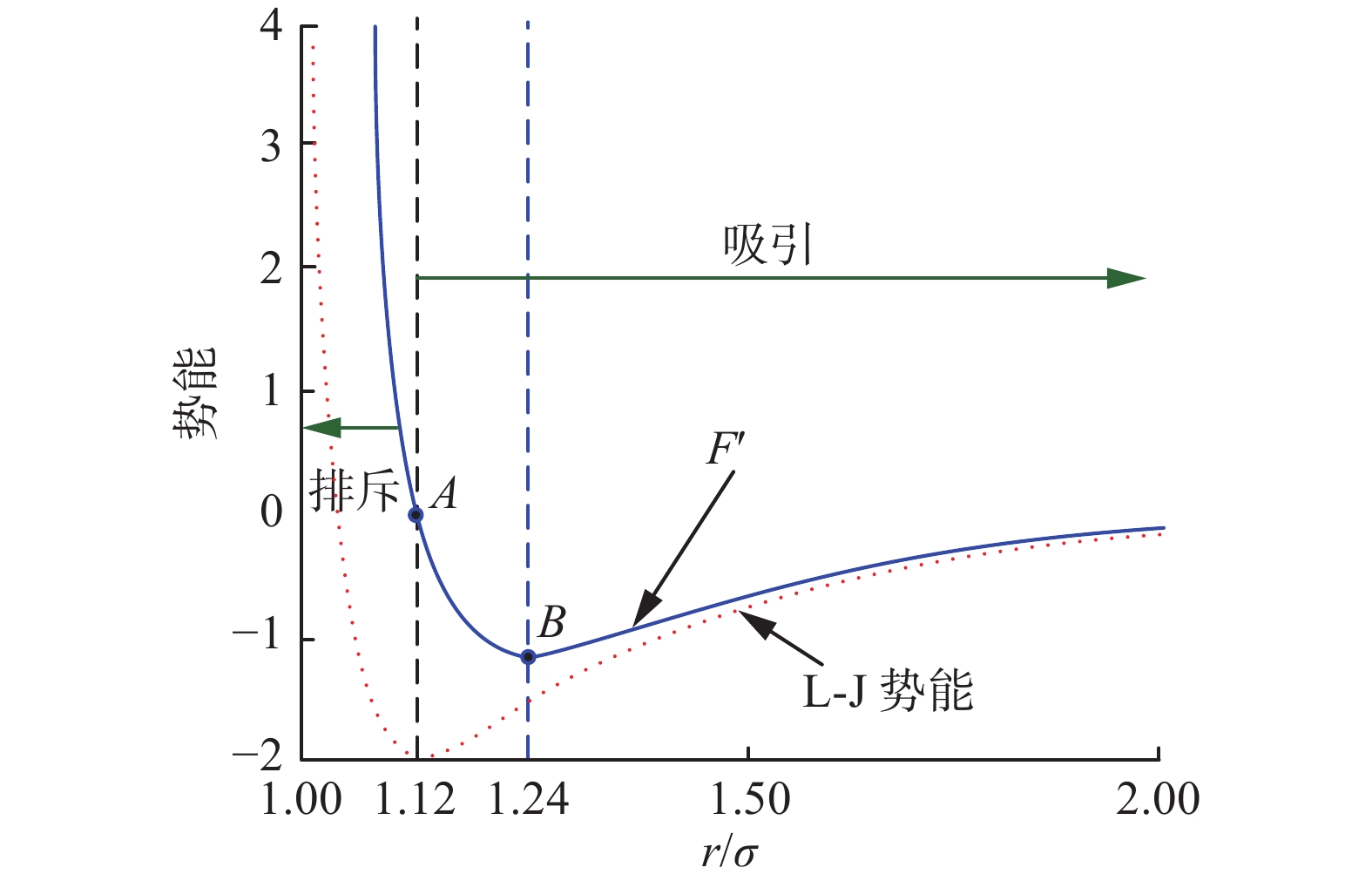
对于最小化问题， ${\text{Fi}}{{\text{t}}_i}(t)$ 是第 $i$ 个原子在第 $t$ 次迭代时的函数适应度值， ${\text{Fi}}{{\text{t}}_{{\text{best}}}}(t) = \mathop {\min }\limits_{i \in \{ 1,2, \cdots ,N\} } {\text{Fi}}{{\text{t}}_i}(t)$ 与 ${\text{Fi}}{{\text{t}}_{{\text{worst}}}}(t) = \mathop {\max }\limits_{i \in \{ 1,2, \cdots ,N\} } {\text{Fi}}{{\text{t}}_i}(t)$ 分别表示在第 $t$ 次迭代时最差原子和最佳原子的目标函数适应值。

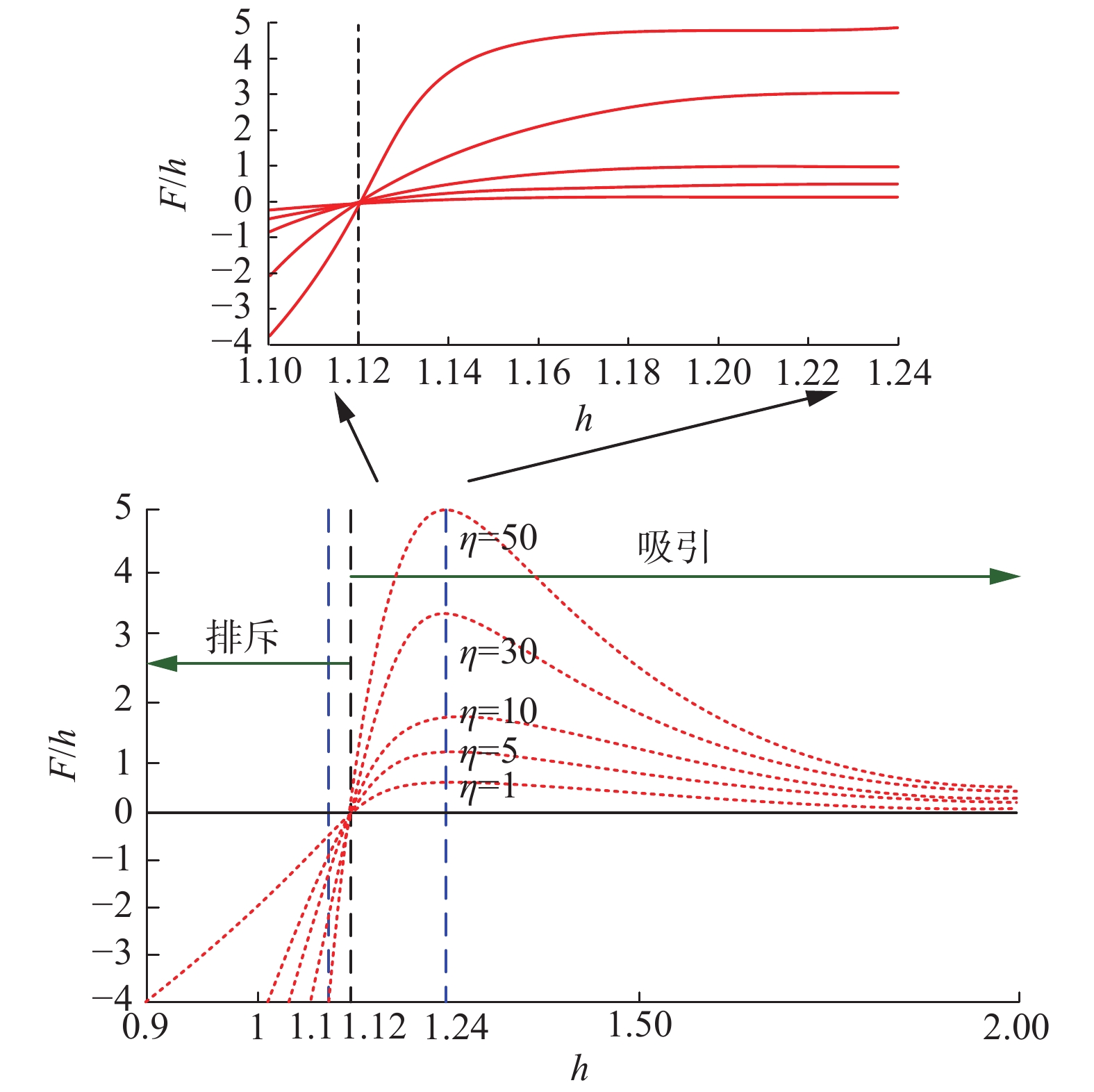
在ASO算法的整个寻优过程中，原子的加速度决定了原子所处位置和速度，其主要来源于两个部分：由L-J势引起的相互作用力和由键长势引起的约束力。但在分子动力学理论框架下，原子间的相互排斥相对于平衡距离的变化幅度( $r = 1.12$ )远大于相互吸引的变化幅度(见图1)，这表明了算法随着迭代次数的增加，ASO并没有获得更多的正吸引和更少的负排斥，这就导致不能直接使用L-J势引起的相互作用力和键长势引起的约束力来处理优化问题，因此Zhao等^[13-14]在分子动力学的原有模型基础上重新定义了原子系统的相互作用力和约束力。

图 1 原子力曲线

Fig. 1 Force curve of atoms

下载: 全尺寸图片

1.2 L-J势产生的相互作用力

$$ F_{ij}'(t) = - \eta (t)[2{({h_{ij}}(t))^{13}} - {({h_{ij}}(t))^7}] $$

(4)

式中 $\eta (t)$ 是调整排斥和吸引区的深度函数，即

$$ \eta (t) = \alpha {\left(1 - \dfrac{{t - 1}}{T}\right)^3}{{\text{e}}^{ - \tfrac{{20t}}{T}}} $$

(5)

式中： $\alpha $ 为深度权重； $T$ 为最大迭代次数。 $h$ 与 $F'$ 的关系由图2显示，从图2中可以看出：对于不同 $\eta $ 值，当 $h$ 介于0.9~1.12时发生排斥，当 $h$ 在1.12~2时发生吸引，而当 $h = 1.12$ 时发生平衡。从平衡( $h = 1.12$ )开始，吸引力随着 $h$ 的增加先逐渐增加并达到最大值( $h = 1.24$ )，然后再逐渐减小，直到 $h=2$ 时，吸引力约等于零。

因此，为保证ASO算法的全局有效性将函数值较小的排斥力下限设置为 $h = 1.1$ ，函数值较大的吸引力上限设置为 $h = 1.24$ ，即

$$ {h}_{ij}(t)=\left\{\begin{aligned} &{h}_{\mathrm{min}}\text{，}\quad \frac{{r}_{ij}(t)}{\sigma (t)} < {h}_{\mathrm{min}}\\ &\frac{{r}_{ij}(t)}{\sigma (t)}\text{，}\quad {h}_{\mathrm{min}}\leqslant \frac{{r}_{ij}(t)}{\sigma (t)}\leqslant {h}_{\mathrm{max}}\\ &{h}_{\mathrm{max}}\text{，}\quad\frac{{r}_{ij}(t)}{\sigma (t)} > {h}_{\mathrm{max}}\end{aligned}\right. $$

(6)

式中： ${h_{{\text{min}}}}$ 和 ${h_{{\text{max}}}}$ 分别是 $h$ 的下限和上限；长度标度 $\sigma (t)=\left|\left| {x}_{ij}(t),\dfrac{{\displaystyle \sum _{j\in {K}_{\text{best}}}{x}_{ij}(t)}}{K(t)}\right|\right|_{2}$ ， $ {K_{{\text{best}}}} $ 是原子总体的一个子集，由具有最佳函数适应值的前 $k$ 个原子组成。

$$ K(t) = N - (N - 2) \times \sqrt {\frac{t}{T}} $$

(7)

$$ {h_{ij}}(t) = \left\{ \begin{gathered} {h_{\min }} = {g_0} + g(t) \hfill \\ {h_{\max }} = u \hfill \\ \end{gathered} \right. $$

(8)

式中 $g(t)$ 是使算法保证全局性的漂移算子，表示为

$$ g(t) = 0.1 \times {\text{sin}}\left(\frac{{\text{π }}}{2} \times \frac{t}{T}\right) $$

(9)

因此，由L-J势产生的相互作用力为

$$ F_i^d(t) = \mathop \sum \limits_{j \in {K_{{\text{best}}}}} {\text{ran}}{{\text{d}}_j}F_{ij}^d(t) $$

(10)

式中：d代表当前搜索空间维度， $d=1,\;2,\;\cdots ,\;D$ ； ${\text{ran}}{{\text{d}}_{ij}}$ 是 $[0,1]$ 中的一个随机数。

图 2 ${F'}$ 、 $h$ 和 $\eta $ 函数关系

Fig. 2 ${F'}$ ， $h$ and $\eta $ functional relation

下载: 全尺寸图片

1.3 键长势引起的约束力

只依靠L-J势引起的相互作用力只能描述简单分子的运动，对于更复杂的分子或原子系统，需引入一种几何约束的分子动力学方法并结合原子内部运动来模拟原子寻优过程。在ASO算法中，假设每个原子都与最佳原子有共价键且每个原子都受到来自最佳原子的约束力，则第 $i$ 个原子约束为

$$ {\theta _i}(t) = \left[|{x_i}(t) - {x_{{\text{best}}}}(t){|^2} - b_{i,{\text{best}}}^2\right] $$

(11)

式中： ${x_{{\text{best}}}}(t)$ 是第 $t$ 次迭代时最佳原子的位置； ${b_{i,{\text{best}}}}$ 是第 $i$ 个原子与最佳原子之间的固定键长。故第 $i$ 个原子的约束力为

$$ \begin{gathered} G_i^d(t) = - \lambda (t)\nabla \theta _i^d(t) = - 2\lambda (t)(x_i^d(t) - x_{{\text{best}}}^d(t)) \\ \end{gathered} $$

(12)

式中：d代表当前搜索空间维度，且 $d=1,2,\cdots ,D$ ； $\lambda (t)$ 为拉格朗日乘子，令 $2\lambda \to \lambda $ ，则共价键引起的约束力可重新定义为

$$ G_i^d(t) = - \lambda (t)(x_i^d(t) - x_{{\text{best}}}^d(t)) $$

(13)

式中：d代表当前搜索空间维度，且 $d = 1,2, \cdots ,D$ ； $\lambda (t) = \beta {{\text{e}}^{ - \frac{{20t}}{T}}}$ ， $\beta $ 是乘数权重。故在相互作用力和几何约束下，第 $i$ 个原子在 $t$ 时刻的加速度为

$$ \begin{aligned} &\quad\quad\quad a_i^d(t) = \dfrac{{F_i^d(t) + G_i^d(t)}}{{m_i^d(t)}}=\\ & \;\;- \alpha {\left(1 - \dfrac{{t - 1}}{T}\right)^3}{{\rm{e}}^{ - \tfrac{{20t}}{T}}}\dfrac{{(x_i^d(t) - x_j^d(t))}}{||{{x_i}(t),{x_j}(t){||_2}}}\times\\ &\quad\displaystyle\sum\limits_{j \in {K_{{\rm{best}}}}} {\dfrac{{{\rm{ran}}{{\rm{d}}_j}[2{{({h_{ij}}(t))}^{13}} - {{({h_{ij}}(t))}^7}]}}{{m_i^d(t)}}} +\\ & \quad\quad\quad\quad \beta {{\rm{e}}^{ - \tfrac{{20t}}{T}}}\dfrac{{(x_{{\rm{best}}}^d(t) - x_i^d(t))}}{{m_i^d(t)}} \end{aligned}$$

(14)

为简化ASO算法，在算法的全局寻优过程中，第 $t + 1$ 次迭代时第 $i$ 个原子在第d维的位置和速度分别表示为

$$ v_i^d(t + 1) = {\text{rand}}_i^dv_i^d(t) + a_i^d(t) $$

(15)

$$ x_i^d(t + 1) = x_i^d(t) + v_i^d(t + 1) $$

(16)

式中：d代表当前搜索空间维度，且 $d = 1, 2,\cdots ,D$ ； $x_i^d(t)$ 为第 $i$ 个原子在第d个维度下第 $t$ 次迭代时的位置； $a_i^d(t)$ 为第 $i$ 个原子在第d个维度下第 $t$ 次迭代时的加速度； $v_i^d(t + 1)$ 为第 $i$ 个原子在第d个维度下第 $t + 1$ 次迭代时的速度。

2. 改进的原子搜索优化算法(IASO)

2.1 初始原子种群的混沌优化

最优化问题的解集大多都存在于多参数表示的多维空间中，没有任何先验知识能够表明全局最优解所处位置，因此对于元启发式智能优化算法来说，最优化问题求解结果的好坏往往与初始种群存在较大关系，初始种群多样性越丰富得到的结果越有可能接近于全局最优解甚至会使得收敛速度加快^[17-18]。故初始化种群在整个空间的均匀覆盖性显得极为重要，ASO算法在设计初就尽量保证种群覆盖整个优化问题的解空间，但在其种群实际初始化时仍采用随机初始化方法，这导致初始种群对整个解空间覆盖能力不够强进而影响ASO算法性能。

混沌序列随机性和遍历性等特点使得生成的初始解在整个解空间中分布更加均匀，有利于求解最优问题的全局最优解，现已被广泛应用于元启发式优化算法的种群初始化中，故本文也将混沌序列引入ASO算法用于初始化原子种群。目前常用的混沌序列生成方法主要有Logstic映射和Tent映射，赵欣^[19]的研究已指出Tent映射生成的混沌序列具有更好的均匀分布性，更符合元启发智能算法的初始种群生成，其序列生成函数为

$$ {x}_{N+1}=\left\{\begin{array}{l} 2{x}_{N},\quad {x}_{N}\in [0,0.5]\\ 2(1-{x}_{N}),\quad {x}_{N}\in (0.5,1]\end{array}\right. $$

(17)

对式（17）进行伯努利位移变化后，得

$$ {x_{N + 1}} = (2{x_N}) {\rm{mod}} 1 $$

(18)

式中 $N$ 为原子个数，初始种群的大小由原子个数 $N$ 和搜索空间维度D决定。利用式（18）生成初始种群用以代替ASO算法中随机生成的初始种群从而丰富初始种群的多样性，促使算法寻优结果更接近于全局最优解。

2.2 振幅函数随机参数优化

ASO在寻觅最优解的过程中，深度函数 $\eta (t)$ 与拉格朗日乘子 $\lambda (t)$ 作为其中重要的两个参数被用于调整原子自身和原子之间的力相互作用以增强或加快算法全局搜索和局部开发能力，更有利于求解全局最优解。但ASO算法在实际寻优过程中， $\eta (t)$ 与 $\lambda (t)$ 均仅使用非线性递减函数来加快算法收敛速度，而对算法的全局性探索没有相应策略。

为提高算法的全局探索能力，本文受简谐振动启发影响引入振幅函数对算法参数 $\eta (t)$ 与 $\lambda (t)$ 进行修正，利用振幅函数波动跳跃的性质增强算法跳出局部最优的可能。引入的振幅函数 $s(t)$ 定义为

$$ s(t) = {\text{rand}}\left( {\left| {\cos (d t + N)} \right|} \right) $$

(19)

式中： $N$ 为原子个数； $t$ 为迭代次数； $d$ 为原子搜索空间维度； ${\text{rand}}()$ 为随机函数，表示在振幅函数生成的数中随机选择一个作为最终作用于参数 $\eta (t)$ 与 $\lambda (t)$ 的波动因子。

根据振幅函数波动性质易知：当算法中引入振幅因子修正参数时，参数继承其跳跃波动性，加强了算法跳出局部最优的可能。但由于引入的振幅因子属于 $[0,1]$ ，导致搜索步长仅在原有解邻域内进行探索开发，对整个全局解空间的探索性不够强，故对式(19)进行修正，得到修正后振幅函数为

$$ s(t) = {\text{rand}}\left( {\left| {\cos (d t + N)} \right|} \right) + 1 $$

(20)

式(20)是由式(19)经过平移后得到的，其不仅保留了振幅函数本身波动性质促使算法跳出局部最优，而且还加大了算法对解空间的搜索半径，增强了算法对全局的寻优能力。

经过振幅函数作用后的深度函数 $\eta (t)$ 与拉格朗日乘子 $\lambda (t)$ 可重新定义为

$$ \eta (t) = \alpha {\left(1 - \dfrac{{t - 1}}{T}\right)^3}{{\text{e}}^{ - \tfrac{{20t s}}{T}}} $$

(21)

$$ \lambda (t) = \beta {{\text{e}}^{ - \tfrac{{20t s}}{T}}} $$

(22)

式中 $s$ 称为振幅因子，由式(20)计算得出。故第 $i$ 个原子在 $t$ 时刻加速度可被重新定义为

$$\begin{aligned} &a_i^d(t) = - \alpha {\left(1 - \dfrac{{t - 1}}{T}\right)^3}{{\rm{e}}^{ - \tfrac{{20t s}}{T}}}\dfrac{{(x_i^d(t) - x_j^d(t))}}{{{{\left\| {{x_i}(t),{x_j}(t)} \right\|}_2}}}\eta (t)=\\ &\quad \beta {{\rm{e}}^{ - \tfrac{{20t s}}{T}}}\dfrac{{(x_{{\rm{best}}}^d(t) - x_i^d(t))}}{{m_i^d(t)}} + \alpha {(1 - \dfrac{{t - 1}}{T})^3}\times\\ &\quad\quad{{\rm{e}}^{ - \tfrac{{20t s}}{T}}}\sum\limits_{j \in {K_{{\rm{best}}}}} {\dfrac{{{\rm{ran}}{{\rm{d}}_j}[2{{({h_{ij}}(t))}^{13}} - {{({h_{ij}}(t))}^7}]}}{{m_i^d(t)}}} \end{aligned} $$

(23)

2.3 步长演变搜索机制

在ASO算法中，原子群在解空间中所探索开发得到的最优解为最优原子个体所处的位置，这表明了原子所处位置对ASO算法寻优的重要性。在原子质量一定的情况下，原子间相互作用力及原子与最优原子个体间的约束力影响原子运动速度和加速度进而影响原子更新后的位置，最终作用于ASO算法本身，致使算法迭代寻优过程变慢，故想加快算法收敛速度需对原子搜索步长也即位置更新公式进行修正。

根据式(16)可知，ASO算法中原子个体位置的更新等于上一次原子自身位置和本次原子运动后的速度之和。而原子运动的一般过程表明：当原子个体逐渐接近于最优原子个体时，由于原子做变速运动，原子位置也随其速度的变化而不断变化。根据原子间相互作用力和约束力作用可知，若想使原子位置快速趋近于最佳原子位置，原子速度应逐渐降低直至为0，也即是说，原子位置变化应逐渐变慢直至不再发生改变。

因此，为解决ASO算法收敛速度慢的问题，本文从原子位置更新过程出发，引入步长演变因子 $\omega (t)$ 对原子位置更新公式进行修正，使原子位置更新过程随算法迭代次数增加而逐渐变慢直至不再变化。 $\omega (t)$ 定义为

$$ \omega (t) = {{\text{e}}^{ - \tfrac{{d \times t}}{T}}} $$

(24)

式中： $t$ 为迭代次数； $d$ 为原子搜索空间维度； $T$ 为最大迭代次数。由式(24)可知， $\omega (t) \in [0,1]$ 且是一个随着解空间维度和算法迭代次数增加而快速演变的因子。

综上所述，得出新原子位置更新策略为

$$ x_i^d(t + 1) = \left( {x_i^d(t) + v_i^d(t + 1)} \right)\omega (t) $$

(25)

式中： $x_i^d(t)$ 为第 $i$ 个原子第 $t$ 次迭代时位置； $v_i^d(t + 1)$ 为第 $i$ 个原子第 $t + 1$ 次迭代时的速度； $\omega (t)$ 为模拟原子位置更新过程的步长演变因子。

由于 $\omega (t) \in [0,1]$ ，故式(25)的含义为：随着原子个体不断运动逐渐接近于原子最优个体时，其位置动态更新过程随着算法寻优过程逐渐变慢直至其位置与最优原子个体重合，此时得到的原子个体的位置分布即为原子群的最优解。

2.4 IASO算法的实现

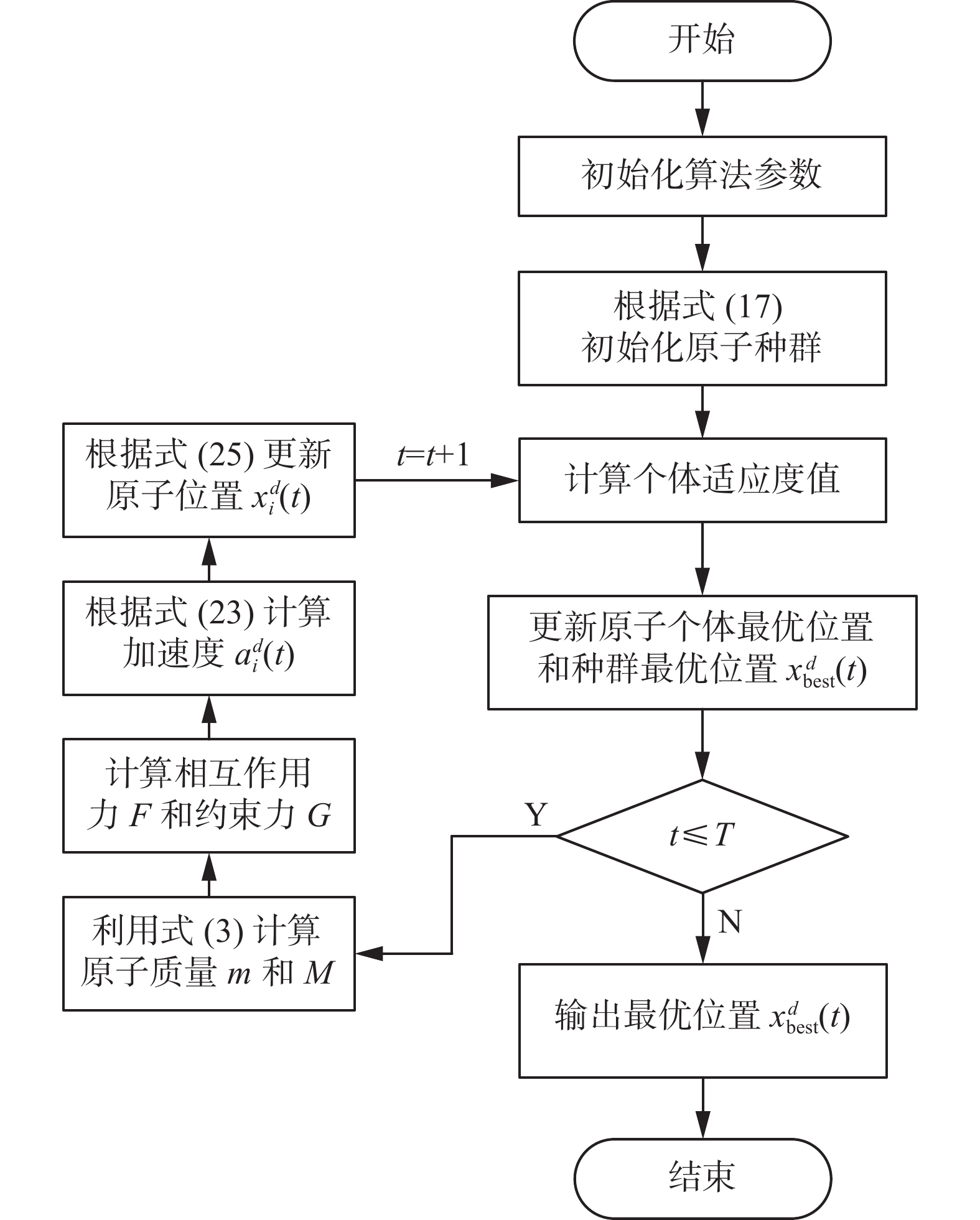
综上所述，IASO算法求解最优化问题的寻优过程如图3所示。

图 3 IASO算法流程

Fig. 3 Flow chart of the IASO algorithm

下载: 全尺寸图片

3. 数值实验与结果分析

为探究和验证IASO算法的寻优性能，本文选取20个经典基准测试函数，其中设计了3组实验，主要包括以下3个部分：

1) 30维度和100维度下IASO与4种元启发式算法的数值实验对比，即选择10个经典基准测试函数与4种元启发式算法在两个维度下分别进行对比实验并以其数值实验结果对比验证改进算法拥有较好的优化性能。

2) 混合多维度基准测试函数下IASO与4种元启发式算法的数值实验结果对比，即选择10个混合多维度的经典基准测试函数与4种元启发式算法进行对比实验并以其数值实验结果对比验证改进算法拥有较好的优化性能。

3) Wilcoxon秩和检验与算法时间对比，即计算Wilcoxon秩和检验p值以及统计各对比算法运行时间，通过数值实验结果验证IASO比其他算法具有更好的稳定性和优化性。

3.1 实验环境及初始参数设置

1) 实验环境

操作系统Windows 10，CPU为Intel(R) Core(TM) i7-5557U，主频3.10 GHz，内存为8 GB，实验平台为MATLAB2016a。

2) 实验初始参数设置

为保证实验的客观和公平性,本文将所有对比算法的种群规模统一设置为50，最大迭代次数统一设置为1000，其中ASO算法和IASO算法的参数 $\alpha = 50$ ， $\beta = 0.2$ ；各实验组均独立进行100次数值实验，并计算100次实验结果的均值(Mean)、标准差(Std)及100次实验中的最优值(Best)作为算法评价指标。

3) 经典基准函数

为验证改进算法具有更高的收敛性和全局性，本文选取20个经典基准函数进行数值实验，其中 ${f_1}\~{f_{10}}$ 为可变维度基准函数(每组基准函数的最优值均为0，详细描述见表1)； ${f_{11}}$ ~ ${f_{20}} $ 为混合多维度的经典基准函数，具体函数名如下： ${f_{11}}$ 为Shekel Foxholes1， ${f_{12}}$ 为Kowalik, ${f_{13}}$ 为Six-Hump, ${f_{14}}$ 为Branin, ${f_{15}}$ 为Goldstin- Price, ${f_{16}}$ 为Hartman1, ${f_{17}}$ 为Hartman 2, ${f_{18}}$ 为shekel Foxholes2, ${f_{19}}$ 为shekel Foxholes3, ${f_{20}}$ 为shekel Foxholes4。

表 1 基准测试函数

Table 1 Benchmark function

函数名	表达式	区间	单/多峰	最优值
Sphere	${f_1}(x) = \displaystyle\sum\limits_{i = 1}^D {x_i^2}$	[−100,100]	单峰	0
Schwefel 2.22	${f_2}(x) = \displaystyle\sum\limits_{i = 1}^D {\left\| { {x_i} } \right\|} + \prod\limits_{i = 1}^D {\left\| { {x_i} } \right\|}$	[−10,10]	单峰	0
Schwefel 1.2	${f_3}(x) = \displaystyle\sum\limits_{i = 1}^D { { {\left(\displaystyle\sum\limits_{j = 1}^i { {x_j} } \right)}^2} }$	[−100,100]	单峰	0
Step	${f_4}(x) = \displaystyle\sum\limits_{i = 1}^D { { {({x_i} + 0.5)}^2} }$	[−100,100]	单峰	0
Quartic	${f_5}(x) = \displaystyle\sum\limits_{i = 1}^D {ix_i^4} + {\text{rand} }\left[ {0,1} \right)$	[−1.28,1.28]	单峰	0
Rastrigin	${f_6}(x) = \displaystyle\sum\limits_{i = 1}^D { { {\left[ {x_i^2 - 10\cos (2{\text{π } }{x_i}) + 10} \right]}^2} }$	[−5.12,5.12]	多峰	0
Ackley	${f_7}(x) = - 20\exp \left( - 0.2\sqrt {\dfrac{1}{n}\displaystyle\sum\limits_{i = 1}^D {x_i^2} } \right) - \exp \left[ {\dfrac{1}{n}\displaystyle\sum\limits_{i = 1}^D {\cos (2{\text{π } }{x_i})} } \right] + 20 + {\rm{e}}$	[−32,32]	多峰	0
Griewank	${f_8}(x) = \dfrac{1}{ {4000} }\displaystyle\sum\limits_{i = 1}^D { { {({x_i} - 100)}^2} } + \prod\limits_{i = 1}^D {\cos \left(\dfrac{ { {x_i} - 100} }{ {\sqrt i } }\right) + 1}$	[−600,600]	多峰	0
Levy	$f_{8}(x)=\frac{1}{4000} \sum_{i=1}^{D}\left(x_{i}-100\right)^{2}+\prod_{i=1}^{D} \cos \left(\frac{x_{i}-100}{\sqrt{i}}\right)+1$ $f_{9}(x)=\sin ^{2}\left(\pi \omega_{i}\right)+\sum_{i=1}^{D}\left(\omega_{i}-1\right)^{2}\left[1+10 \sin ^{2}\left(\pi \omega_{i}+1\right)\right]+$	[−10,10]	多峰	0
Weierstrass	${f_{10} }(x) = \displaystyle\sum\limits_{i = 1}^D {\left[ { { {0.5}^i}\cos \left( {2{\text{π } }{3^i}\left( { {x_i} + 0.5} \right)} \right)} \right]} - D\displaystyle\sum\limits_{i = 1}^D { { {0.5}^i}\cos \left( {2{\text{π } }{3^i} \times 0.5} \right)}$	[−0.5,0.5]	多峰	0

3.2 不同算法在30维和100维下的对比实验

为验证IASO算法寻优性能，以BOA、MFO、MVO、SSA和传统ASO作为实验对比算法，分别对D=30维和D=100维下的10个基准测试函数进行仿真对比实验。对比算法参数设置及评价指标以3.1节为准，得到具体实验统计结果见表2和表3。

表 2 6种算法对10个基准函数的统计指标对比结果(D=30)

Table 2 Comparison of the statistical indexes of ten benchmark functions via six algorithms (D=30)

基准函数	评价指标	BOA	MFO	MVO	SSA	ASO	IASO
f₁	Mean	1.70×10⁻¹⁴	1.60×10³	1.76×10⁻¹	9.46×10⁻⁹	2.05×10⁻²³	0.00×10⁰
f₁	Std	8.04×10⁻¹⁶	3.69×10³	4.90×10⁻²	1.90×10⁻⁹	2.27×10⁻²³	0.00×10⁰

续表 2
基准函数	评价指标	BOA	MFO	MVO	SSA	ASO	IASO
	Best	1.52×10⁻¹⁴	2.32×10⁻⁶	8.34×10⁻²	4.94×10⁻⁹	7.91×10⁻²⁵	0.00×10⁰
f₂	Mean	9.72×10⁻¹²	3.21×10¹	2.87×10⁻¹	4.89×10⁻¹	5.30×10⁻¹¹	1.54×10⁻¹⁸⁴
	Std	2.13×10⁻¹²	1.94×10¹	8.36×10⁻²	6.06×10⁻¹	6.86×10⁻¹¹	0.00×10⁰
	Best	3.20×10⁻¹²	5.98×10⁻⁵	1.67×10⁻¹	6.71×10⁻⁵	7.91×10⁻²⁵	4.88×10⁻¹⁸⁸
f₃	Mean	1.71×10⁻¹⁴	1.48×10⁴	2.15×10¹	4.23×10¹	2.02×10²	0.00×10⁰
	Std	9.37×10⁻¹⁶	1.22×10⁴	1.01×10¹	3.10×10¹	1.29×10²	0.00×10⁰
	Best	1.39×10⁻¹⁴	3.14×10²	6.47×10⁰	3.93×10⁰	1.96×10¹	0.00×10⁰
f₄	Mean	0.00×10⁰	1.20×10³	6.30×10⁰	9.35×10⁰	0.00×10⁰	0.00×10⁰
	Std	0.00×10⁰	3.27×10³	3.26×10⁰	5.48×10⁰	0.00×10⁰	0.00×10⁰
	Best	0.00×10⁰	0.00×10⁰	1.00×10⁰	1.00×10⁰	0.00×10⁰	0.00×10⁰
f₅	Mean	6.12×10⁻⁴	2.54×10⁰	1.45×10⁻²	5.44×10⁻²	2.57×10⁻²	2.34×10⁻⁵
	Std	2.55×10⁻⁴	5.93×10⁰	7.14×10⁻³	2.26×10⁻²	9.47×10⁻³	2.17×10⁻⁵
	Best	1.38×10⁻⁴	2.18×10⁻²	5.98×10⁻³	1.41×10⁻²	8.23×10⁻³	2.23×10⁻⁷
f₆	Mean	3.92×10⁰	1.45×10²	1.12×10²	4.95×10¹	2.86×10¹	0.00×10⁰
	Std	2.76×10¹	3.54×10¹	2.82×10¹	1.50×10¹	7.60×10⁰	0.00×10⁰
	Best	0.00×10⁰	7.16×10¹	5.48×10¹	1.99×10¹	1.19×10¹	0.00×10⁰
f₇	Mean	1.13×10¹	1.30×10¹	6.05×10⁻¹	1.69×10⁰	3.21×10⁻¹²	2.24×10⁻¹⁵
	Std	4.51×10¹	8.53×10⁰	5.73×10⁻¹	9.65×10⁻¹	3.27×10⁻¹²	1.73×10⁻¹⁵
	Best	0.00×10⁰	5.70×10⁻⁴	8.47×10⁻²	2.06×10⁻⁵	9.21×10⁻¹³	8.88×10⁻¹⁶
f₈	Mean	1.27×10⁻¹⁵	1.27×10¹	4.47×10⁻¹	1.10×10⁻²	1.05×10⁻²	0.00×10⁰
	Std	1.39×10⁻¹⁵	3.40×10¹	9.99×10⁻²	1.10×10⁻²	1.52×10⁻²	0.00×10⁰
	Best	0.00×10⁰	8.06×10⁻⁶	1.84×10⁻¹	1.91×10⁻⁸	0.00×10⁰	0.00×10⁰
f₉	Mean	2.01×10⁰	2.65×10¹	1.60×10¹	5.23×10⁰	2.73×10⁻²	2.54×10⁰
	Std	2.42×10⁻¹	9.74×10⁰	9.61×10⁰	3.28×10⁰	1.08×10⁻¹	2.11×10⁻¹
	Best	1.54×10⁰	3.27×10⁰	5.52×10⁻¹	8.95×10⁻²	6.43×10⁻²⁵	2.04×10⁰
f₁₀	Mean	1.42×10⁻¹⁶	4.98×10⁰	9.53×10⁰	1.12×10¹	3.48×10⁻³	0.00×10⁰
	Std	1.42×10⁻¹⁵	3.00×10⁰	2.83×10⁰	3.28×10⁰	1.49×10⁻²	0.00×10⁰
	Best	0.00×10⁰	1.25×10⁻²	4.88×10⁰	5.54×10⁰	1.09×10⁻⁹	0.00×10⁰

表 3 6种算法对10个基准函数的统计指标对比结果(D=100)

Table 3 Comparison of statistical indexes of 10 benchmark functions by six algorithms(D=100)

测试函数	评价指标	BOA	MFO	MVO	SSA	ASO	IASO
f₁	Mean	1.77×10⁻¹⁴	2.72×10⁴	2.37×10¹	8.12×10⁻³	1.63×10⁻⁴	0.00×10⁰
	Std	9.07×10⁻¹⁶	1.56×10⁴	3.59×10⁰	8.85×10⁻³	7.41×10⁻⁴	0.00×10⁰
	Best	1.55×10⁻¹⁴	1.93×10³	1.69×10¹	4.68×10⁻⁴	4.26×10⁻¹⁷	0.00×10⁰
f₂	Mean	6.02×10⁺⁴⁸	1.70×10²	9.21×10⁺²²	1.31×10¹	2.79×10⁰	0.00×10⁰
	Std	2.87×10⁺⁴⁹	4.52×10¹	9.00×10⁺²³	3.52×10⁰	2.22×10⁰	0.00×10⁰
	Best	4.90×10⁺³⁷	7.18×10¹	2.42×10²	6.60×10⁰	4.52×10⁻²	0.00×10⁰

续表 3
测试函数	评价指标	BOA	MFO	MVO	SSA	ASO	IASO
f₃	Mean	1.77×10^-14	1.75×10⁵	3.14×10⁴	2.01×10⁴	3.16×10⁴	0.00×10⁰
	Std	1.17×10⁻¹⁵	5.90×10⁴	4.30×10³	1.03×10⁴	6.11×10³	0.00×10⁰
	Best	1.42×10⁻¹⁴	8.40×10⁴	2.07×10⁴	6.97×10³	2.08×10⁴	0.00×10⁰
f₄	Mean	0.00×10⁰	2.76×10⁴	1.46×10²	2.37×10²	3.76×10¹	0.00×10⁰
	Std	0.00×10⁰	1.28×10⁴	3.94×10¹	7.99×10¹	3.44×10¹	0.00×10⁰
	Best	0.00×10⁰	3.73×10³	6.30×10¹	1.11×10²	4.00×10⁰	0.00×10⁰
f₅	Mean	5.84×10⁻⁴	1.30×10²	2.37×10⁻¹	7.55×10⁻¹	3.53×10⁻¹	2.39×10⁻⁵
	Std	2.27×10⁻⁴	1.01×10²	5.17×10⁻²	1.75×10⁻¹	9.39×10⁻²	2.17×10⁻⁵
	Best	1.23×10⁻⁴	6.41×10⁰	1.30×10⁻¹	4.86×10⁻¹	1.80×10⁻¹	5.07×10⁻⁷
f₆	Mean	0.00×10⁰	7.14×10²	6.08×10²	1.35×10²	1.24×10²	0.00×10⁰
	Std	0.00×10⁰	7.22×10¹	7.21×10¹	3.87×10¹	1.73×10¹	0.00×10⁰
	Best	0.00×10⁰	5.86×10²	3.99×10²	5.47×10¹	8.86×10¹	0.00×10⁰
f₇	Mean	8.21×10⁻¹¹	1.99×10¹	5.57×10⁰	5.21×10⁰	1.33×10⁰	3.77×10⁻¹⁵
	Std	8.13×10⁻¹⁰	2.28×10⁻¹	5.55×10⁰	1.02×10⁰	5.28×10⁻¹	1.40×10⁻¹⁵
	Best	0.00×10⁰	1.89×10¹	2.47×10⁰	3.20×10⁰	5.08×10⁻⁹	8.88×10⁻¹⁶
f₈	Mean	1.10×10⁻¹⁴	2.68×10²	1.21×10⁰	1.13×10⁻¹	4.09×10⁻²	0.00×10⁰
	Std	5.27×10⁻¹⁵	1.34×10²	3.03×10⁻²	3.44×10⁻²	6.21×10⁻²	0.00×10⁰
	Best	8.88×10⁻¹⁶	3.97×10¹	1.15×10⁰	5.27×10⁻²	4.88×10⁻¹⁵	0.00×10⁰
f₉	Mean	9.10×10⁰	1.81×10²	1.18×10²	1.70×10¹	6.03×10⁰	9.12×10⁰
	Std	2.04×10⁻¹	4.71×10¹	2.26×10¹	6.15×10⁰	2.93×10⁰	1.53×10⁻¹
	Best	8.44×10⁰	1.10×10²	7.10×10¹	3.52×10⁰	9.02×10⁻¹	8.79×10⁰
f₁₀	Mean	1.14×10⁻¹⁵	5.93×10¹	8.22×10¹	6.22×10¹	1.28×10¹	0.00×10⁰
	Std	5.60×10⁻¹⁵	6.96×10⁰	7.64×10⁰	5.48×10⁰	2.91×10⁰	0.00×10⁰
	Best	0.00×10⁰	4.38×10¹	6.54×10¹	4.50×10¹	6.10×10⁰	0.00×10⁰

由表2和表3可以看出：与其他元启发算法相比，本文改进的ASO算法(IASO)具有较好的寻优性能。

1) 在同等种群规模、迭代次数和相同维度下，除 ${f_7}$ 和 ${f_9}$ 函数外，IASO在其余基准测试函数上的计算精度相较于对比算法均高出数个、数百个数量级甚至达到了最优值，数值实验结果体现了IASO具有更好的计算效果和寻优能力；虽然在 ${f_7}$ 函数上IASO的Best指标比BOA算法差，但通过对比Mean和Std两个指标可以发现，IASO算法的稳定性高于BOA，进一步验证了IASO算法的可靠性和稳健性；同时IASO无论是在单峰函数( ${f_1}$ 、 ${f_3}$ 和 ${f_4}$ )还是多峰函数( ${f_6}$ 、 ${f_8}$ 和 ${f_{10}}$ )上都寻得了3个指标的最优计算精度，显示了IASO不仅具有更强的局部开发能力和收敛精度，而且还拥有更好的全局探索能力。

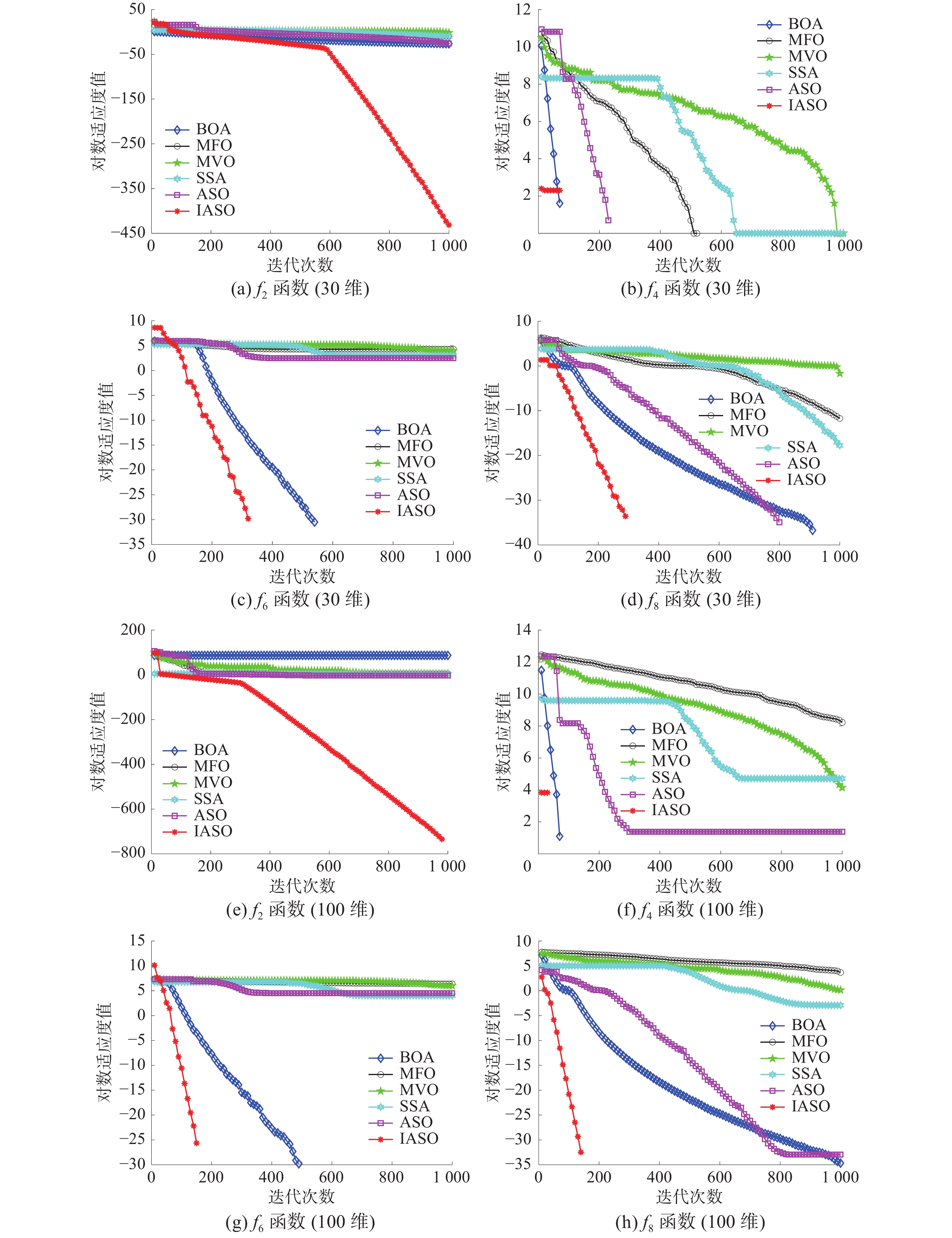
2) 在相同种群规模、迭代次数，但不同的维度下，由表2和表3对比可知：IASO在30维和100维下对10个测试函数的寻优结果并无显著差异甚至效果更佳( ${f_2}$ )，而其余5个对比算法在100维度时的寻优能力明显弱于30维时的寻优能力，这表明改进算法在高维度时表现出更好的稳定性和适用性，说明IASO在解决高维度函数时的优越搜索性能。

3) 通过图4迭代曲线可知：无论是在30维还是100维下，IASO都显现出更好的寻优能力和稳定性。由迭代曲线图可知，IASO算法不仅在迭代前期就表现出好的搜索性能，而且还能让这种优势一直保持到算法迭代终止直到逼近函数的理论最优值。综上所述，在对可变维度的10个基准测试函数上进行仿真实验时，IASO在100次独立重复实验中表现出更好的收敛精度和局部开发能力且具有更好的全局探索能力和算法稳健性。

图 4 IASO与5种算法的最佳适应度对数对比曲线

Fig. 4 Logarithmic comparison curve of optimal fitness between IASO and five algorithms

下载: 全尺寸图片

3.3 不同算法在混合多维度函数下的对比实验

为更近一步评估IASO有效性和稳定性，以BOA、MFO、MVO、SSA和ASO作为实验对比算法，对经典的10个混合多维度基准测试函数进行仿真对比实验，对比算法参数设置及评价指标以3.1节为准，得到具体实验统计结果见表4。

表 4 6种算法对10个混合多维度基准函数的统计指标对比结果

Table 4 Comparison of statistical indexes of ten mixed multi-dimensional benchmark functions by six algorithms

基准函数	评价指标	BOA	MFO	MVO	SSA	ASO	IASO
f₁₁	Mean	1.00×10⁰	1.33×10⁰	9.98×10⁻¹	9.98×10⁻¹	1.03×10⁰	1.37×10⁰
	Std	8.01×10⁻³	1.05×10⁰	5.79×10⁻¹²	1.82×10⁻¹⁶	1.81×10⁻¹	5.11×10⁻¹
	Best	9.98×10⁻¹	9.98×10⁻¹	9.98×10⁻¹	9.98×10⁻¹	9.98×10⁻¹	9.98×10⁻¹
f₁₂	Mean	3.36×10⁻⁴	1.09×10⁻³	4.64×10⁻³	9.11×10⁻⁴	8.42×10⁻⁴	4.54×10⁻⁴
	Std	2.78×10⁻⁵	4.29×10⁻⁴	8.00×10⁻³	2.99×10⁻⁴	2.37×10⁻⁴	5.83×10⁻⁵
	Best	3.09×10⁻⁴	5.78×10⁻⁴	3.08×10⁻⁴	3.58×10⁻⁴	6.33×10⁻⁴	3.07×10⁻⁴
f₁₃	Mean	−1.37×10⁴	−1.03×10⁰	−1.03×10⁰	−1.03×10⁰	−1.03×10⁰	−1.03×10⁰
	Std	1.35×10⁴	6.78×10⁻¹⁶	4.47×10⁻⁸	9.67×10⁻¹⁵	6.65×10⁻¹⁶	1.86×10⁻⁴
	Best	−1.28×10⁰	−1.03×10⁰	−1.03×10⁰	−1.03×10⁰	−1.03×10⁰	−1.03×10⁰
f₁₄	Mean	3.99×10⁻¹	3.98×10⁻¹	3.98×10⁻¹	3.98×10⁻¹	3.98×10⁻¹	4.01×10⁻¹
	Std	1.17×10⁻³	0.00×10⁰	1.19×10⁻⁷	1.63×10⁻¹⁴	0.00×10⁰	3.59×10⁻³
	Best	3.98×10⁻¹	3.98×10⁻¹	3.98×10⁻¹	3.98×10⁻¹	3.98×10⁻¹	3.98×10⁻¹
f₁₅	Mean	3.02×10⁰	3.00×10⁰	3.00×10⁰	3.00×10⁰	3.00×10⁰	3.02×10⁰
	Std	2.99×10⁻²	8.77×10⁻¹⁶	4.72×10⁻⁷	4.33×10⁻¹⁴	7.69×10⁻¹⁶	1.92×10⁻²
	Best	3.00×10⁰	3.00×10⁰	3.00×10⁰	3.00×10⁰	3.00×10⁰	3.00×10⁰
f₁₆	Mean	−6.89×10⁰	−3.86×10⁰	−3.86×10⁰	−3.86×10⁰	−3.86×10⁰	−3.86×10⁰
	Std	6.65×10⁰	2.71×10⁻¹⁵	1.33×10⁻⁷	1.43×10⁻¹⁴	2.71×10⁻¹⁵	4.17×10⁻³
	Best	−4.00×10⁰	−3.86×10⁰	−3.86×10⁰	−3.86×10⁰	−3.86×10⁰	−3.86×10⁰
f₁₇	Mean	−2.76×10⁰	−3.22×10⁰	−3.26×10⁰	−3.24×10⁰	−3.32×10⁰	−3.32×10⁰
	Std	3.26×10⁻²	4.99×10⁻²	6.06×10⁻²	5.73×10⁻²	1.34×10⁻¹⁵	8.60×10⁻²
	Best	−2.56×10⁰	−3.32×10⁰	−3.32×10⁰	−3.32×10⁰	−3.86×10⁰	−3.32×10⁰
f₁₈	Mean	−4.96×10⁰	−6.73×10⁰	−8.46×10⁰	−8.81×10⁰	−8.89×10⁰	−4.77×10⁰
	Std	5.88×10⁻¹	3.38×10⁰	2.43×10⁰	2.77×10⁰	2.36×10⁰	1.09×10⁰
	Best	−6.96×10⁰	−1.02×10¹	−1.02×10¹	−1.02×10¹	−1.02×10¹	−9.92×10⁰
f₁₉	Mean	−5.16×10⁰	−7.82×10⁰	−8.58×10⁰	−9.62×10⁰	−9.07×10⁰	−4.62×10⁰
	Std	1.01×10⁰	3.50×10⁰	2.90×10⁰	2.07×10⁰	2.48×10⁰	3.79×10⁻¹
	Best	−8.97×10⁰	−1.04×10¹	−1.04×10¹	−1.04×10¹	−1.04×10¹	−5.92×10⁰
f₂₀	Mean	−5.18×10⁰	−9.61×10⁰	−9.46×10⁰	−9.21×10⁰	−9.39×10⁰	−4.74×10⁰
	Std	9.63×10⁻¹	2.44×10⁰	2.19×10⁰	2.75×10⁰	2.37×10⁰	4.53×10⁻¹
	Best	−7.96×10⁰	−1.05×10¹	−1.05×10¹	−1.05×10¹	−1.05×10¹	−6.23×10⁰

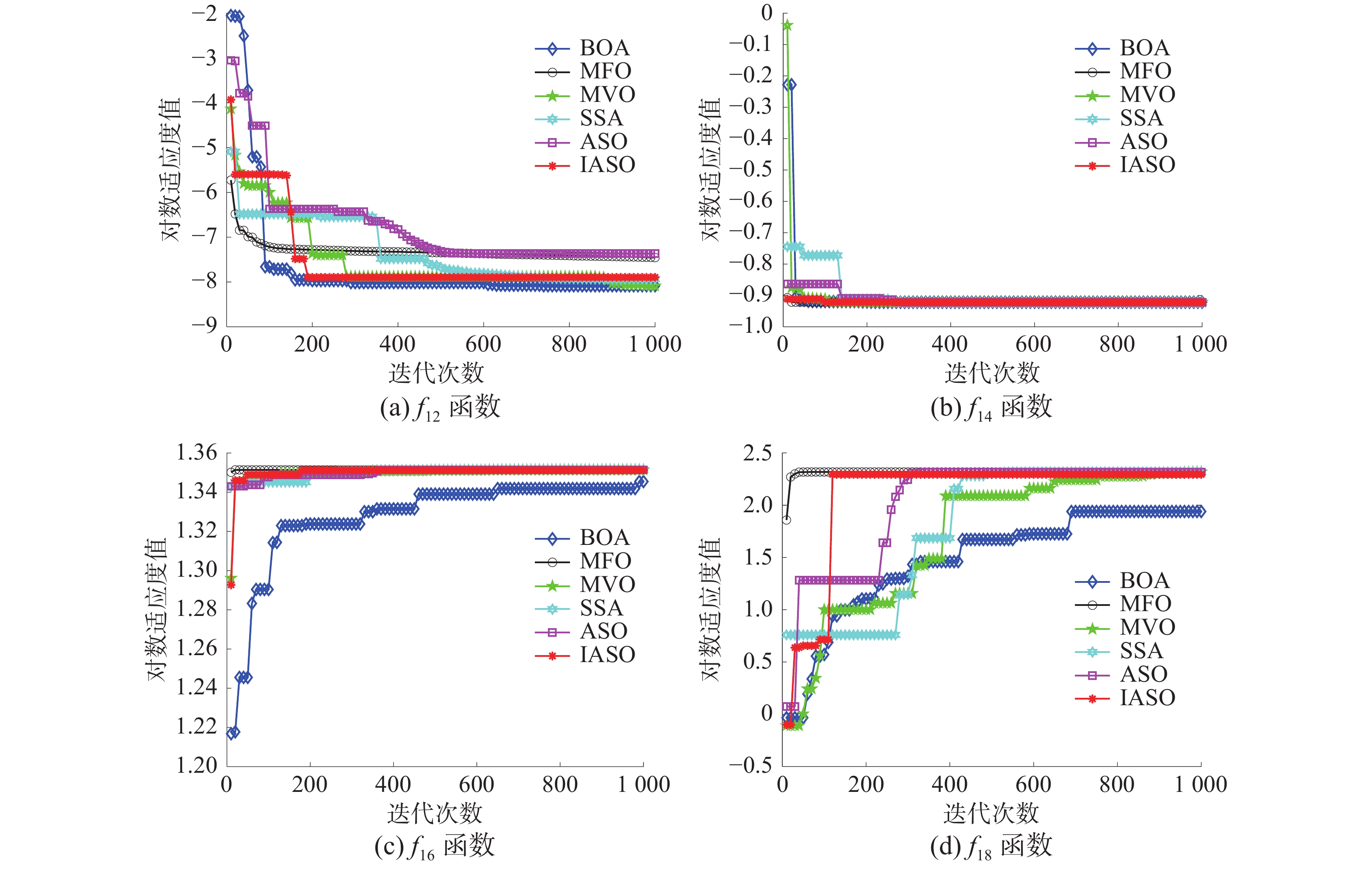
由表4可知，IASO在 ${f_{11}}$ ~ ${f_{17}}$ 上寻优效果显著且在Best指标上已经寻得了函数的最优值，但在 ${f_{18}}$ 、 ${f_{19}}$ 和 ${f_{20}}$ 上的寻优效果弱于对比算法，这是由于IASO利用非线性快速收敛因子加快原子位置更新方程，而 ${f_{18}}$ 、 ${f_{19}}$ 和 ${f_{20}}$ 函数最优值在小范围内波动，故导致其不能跳出局部最优。

若想增加IASO在 ${f_{18}}$ 、 ${f_{19}}$ 和 ${f_{20}}$ 函数上的寻优精度，可将快速收敛因子函数值在1附近波动，但此时IASO在其余所有测试函数上的寻优精度都会降低，同时从图5的迭代收敛曲线可知：IASO在求解混合多维函数的迭代过程中显现出更好的寻优能力和更快的迭代速度。因此，从整体上来说，IASO相较于其余算法表现出更好的寻优性能。

图 5 IASO与5种算法的最佳适应度对数对比曲线

Fig. 5 Logarithmic comparison curve of optimal fitness between IASO and five algorithms

下载: 全尺寸图片

3.4 Wilcoxon秩和检验

100次独立重复实验计算所得均值和标准差在整体上衡量了算法优越性，但并不能反馈算法每次运行结果。为更好地评估改进算法的有效性和稳定性，Derrac等^[20]提出算法应该进行统计检验。本文采用Wilcoxon秩和检验在5%的显著性水平下进行并给出30维和100维下的 ${f_2}$ 、 ${f_4}$ 、 ${f_6}$ 、 ${f_8}$ 、 ${f_{10}}$ 以及混合多维度 ${f_{12}}$ 、 ${f_{14}}$ 、 ${f_{16}}$ 、 ${f_{18}}$ 、 ${f_{20}}$ 的IASO和其他算法的Wilcoxon秩和检验中计算的p值。例如，若最佳算法是IASO，则在IASO vs. ASO、IASO vs. BOA等之间进行比较。表5中N/A为“不适用”，表示相应算法可以在秩和检验中无统计数据与自身进行比较；符号“+”、“−”和“=”分别表示IASO性能优于、劣于和相当于对比算法；当统计检验值p<0.05时被认为是拒绝零假设的有力验证^[21]，表5中标粗部分表示p>0.05。

表 5 基准函数的威尔科克森秩和检验p值

Table 5 p-value of the Wilcoxon rank-sum test of benchmark functions

测试函数	IASO vs. ASO p-value win	IASO vs. BOA p-value win	IASO vs. MFO p-value win	IASO vs. MVO p-value win	IASO vs. SSA p-value win
f₂(30维)	5.22×10⁻¹³⁸ +	2.94×10⁻⁵⁵ +	3.02×10⁻²⁰¹ +	6.61×10⁻²⁴⁴ +	1.22×10⁻²¹² +
f₄(30维)	1.71×10⁻²⁵ +	9.55×10⁻¹−	5.70×10⁻¹¹³ +	N/A =	N/A =
f₆(30维)	3.86×10⁻²³¹ +	7.23×10⁻¹⁹ +	4.09×10⁻²⁴² +	3.39×10⁻²⁵⁰	9.11×10⁻²⁴⁰ +
f₈(30维)	9.71×10⁻¹⁰⁴ +	7.98×10⁻¹⁰⁸ +	1.51×10⁻²⁷⁵ +	N/A =	1.22×10⁻²⁸⁴ +
f₁₀(30维)	6.59×10⁻¹³⁵ +	9.06×10⁻¹¹ +	8.68×10⁻¹⁶⁸ +	5.19×10⁻²⁰⁹	1.09×10⁻²⁰¹ +
f₂(100维)	3.82×10⁻²⁵⁸ +	N/A =	5.62×10⁻²⁹² +	3.26×10⁻²⁹⁴	2.22×10⁻²⁸⁵ +
f₄(100维)	N/A =	8.42×10⁻⁴ +	N/A =	N/A =	N/A =
f₆(100维)	4.26×10⁻³⁰⁴ +	5.44×10⁻⁴⁹ +	3.94×10⁻³¹¹ +	2.18×10⁻³¹⁵	3.02×10⁻³⁰⁷ +
f₈(100维)	6.84×10⁻²⁵⁴ +	5.75×10⁻²³⁶ +	N/A =	N/A =	N/A =
f₁₀(100维)	2.57×10⁻²⁶⁷ +	4.80×10⁻¹²⁶ +	2.61×10⁻²⁸⁶ +	1.04×10⁻²⁸⁷ +	1.36×10⁻²⁸⁵ +
f₁₂	4.46×10⁻¹⁸⁶ +	2.47×10⁻¹⁸² +	5.80×10⁻¹⁷¹ +	1.25×10⁻⁷⁰ +	5.68×10⁻¹⁸ +

续表 5
测试函数	IASO vs. ASO p-value win	IASO vs. BOA p-value win	IASO vs. MFO p-value win	IASO vs. MVO p-value win	IASO vs. SSA p-value win
f₁₄	9.33×10⁻¹⁸ +	1.37×10⁻²⁶¹ +	N/A =	6.06×10⁻⁹⁰ +	1.27×10⁻⁴ +
f₁₆	2.42×10⁻³⁶ +	1.25×10⁻²²⁷ +	N/A =	2.61×10⁻¹¹ +	6.91×10⁻⁴² +
f₁₈	2.22×10⁻⁷⁴ +	2.17×10⁻²²⁶ +	N/A =	8.63×10⁻¹²² +	3.39×10⁻⁹ +
f₂₀	1.05×10⁻²⁰⁸ +	2.77×10⁻⁷¹ +	N/A =	2.79×10⁻¹⁰¹ +	N/A =
+/=/−	14/1/0	13/1/1	9/6/0	11/4/0	11/4/0

由表5可知，IASO仅在30维与 ${f_4}$ 的IASO vs. BOA时p值大于0.05，而在其余所有对比算法的测试函数上的秩和检验结果p值都小于0.05。从整体上来说，IASO在统计上是显著的，也即IASO相对于对比算法具有更高收敛精度。

3.5 时间对比分析

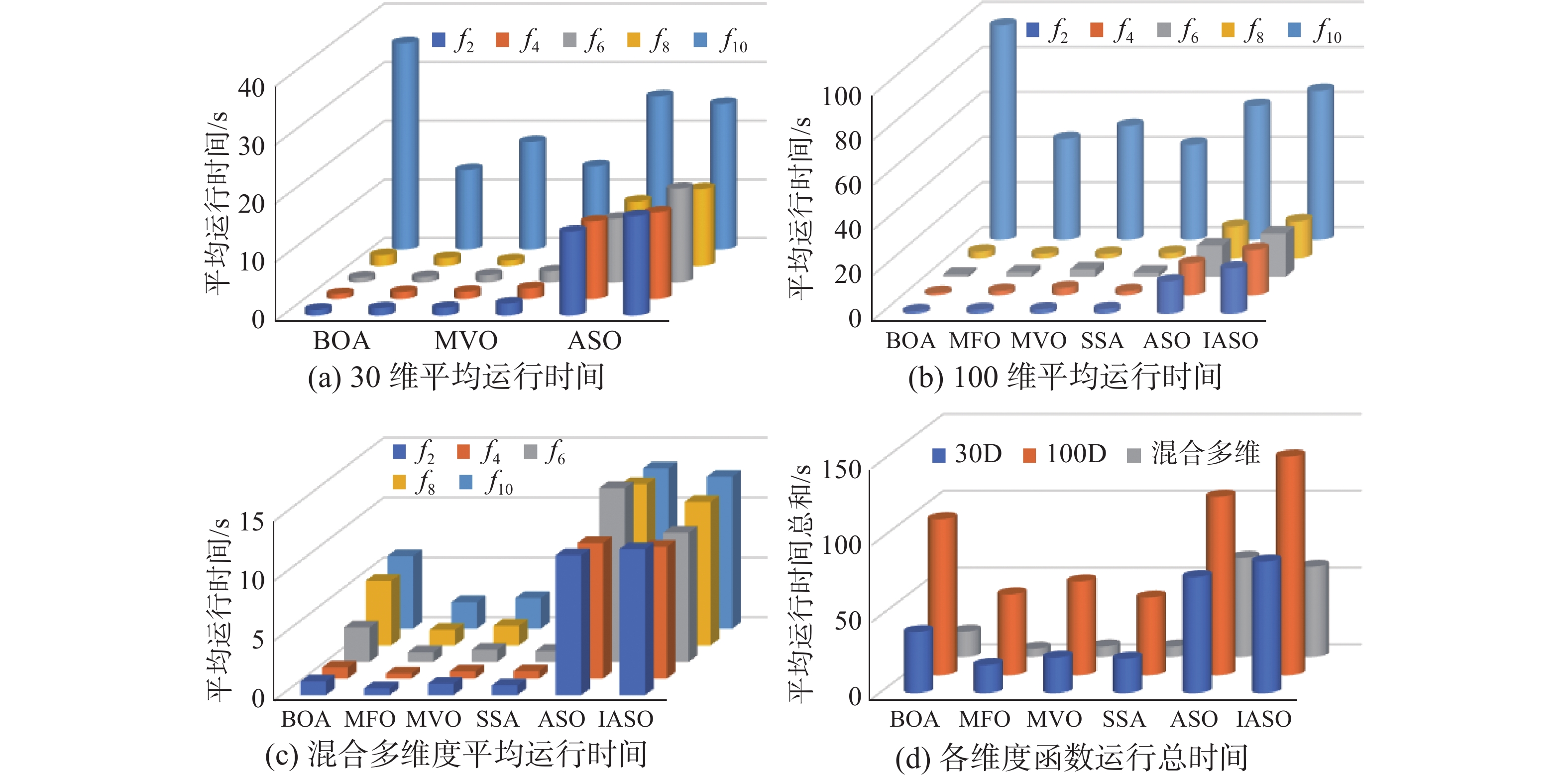
算法运行时间一定程度上反应了算法时间复杂度大小，故本文对6种不同算法在20个基准测试函数上进行了100次独立重复实验，分别记录了 ${f_1}$ ~ ${f_{10}} $ 在30维和100维下各算法平均运行时间以及 ${f_{11}}$ ~ ${f_{20}} $ 在各算法下的平均运行时间，图6表示6个算法在部分基准测试函数上的运行时间柱状图。

图6(a)、(b)分别表示6种算法在 ${f_2}$ 、 ${f_4}$ 、 ${f_6}$ 、 ${f_8}$ 、 ${f_{10}}$ 在30和100维下的平均运行时间，图6(c)表示6种算法在 ${f_{12}}$ 、 ${f_{14}}$ 、 ${f_{16}}$ 、 ${f_{18}}$ 及 ${f_{20}}$ 上的平均运行时间，图6(d)表示6种算法在30和100维下20个基准测试函数的平均运行时间之和。由图6(a)、6(b)、6(c)、6(d)可知，在给出的5个基准函数中，IASO在100次独立重复实验下的平均运行时间远高于BOA、MFO、MVO和SSA算法，这是由于ASO自身导致，而IASO平均运行时间略高于ASO(因为改进算法过程中引入了非线性因子，导致算法复杂度升高)，但当维度增加时，相较于其余对比算法IASO平均运行时间的增加幅度更小，这表明IASO更适用于求解高维测试函数；同时，虽然IASO算法平均运行时间略高于ASO算法，但综合其寻优能力IASO具有更好寻优性能。

图 6 不同智能优化算法运行时间对比

Fig. 6 Running time comparison of different intelligent optimization algorithms

下载: 全尺寸图片

4. 基于IASO的BP神经网络参数优化方法

通过上述对比实验可知：IASO在不同基准测试函数和不同维度下的寻优结果相较于其余对比算法具有更好的优越性和更快的收敛性，故本文将IASO求解复杂优化问题时具有的性能优势引入到BP神经网络参数优化中，提出了一种基于IASO方法的BP神经网络参数优化方法(IASO-BP)，并将其用于UCI数据集分类。

4.1 算法设计步骤

针对分类问题，本文以BP神经网络的分类准确率最大化为优化原则，将BP神经网络的训练过程转化为优化问题寻优过程，利用IASO对优化目标进行求解^[22]。其基本思想是：通过IASO算法优化BP神经网络初始权值和阈值，并将BP神经网络的训练误差作为个体的适应度值，最后选择最优初始权值和阈值构建BP神经网络分类模型。其对应的神经网络分类数学模型为^[23-25]

$$ \begin{gathered} Z= \max F(\omega ,b) \hfill \\ {\text{s}}{\text{.t}}{\text{.}}\left\{ \begin{gathered} \omega \in [{\omega _{\min }},{\omega _{\max }}] \hfill \\ b \in [{b_{\min }},{b_{\max }}] \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered} $$

(26)

式中：Z为分类精度值； $\omega $ 为BP神经网络权值； $b$ 为阈值； $F$ 表示选择BP神经网络权值和阈值时的分类精度。

设数据集为Dataset，神经网络输入层节点为a，隐含层节点为b，输出层节点为c，个体维度为Dim，IASO-BP具体实现步骤如下：

1）数据预处理及参数初始化。

2）权值与阈值参数编码。利用BP神经网络进行初始网络训练得到网络权值和阈值，进行实值编码，得到初始原子种群。

3）计算初始原子种群适应度。将BP神经网络的训练误差作为个体适应度值，则适应度函数 ${f_i}(x)$ 可表示为

$$ {f_i}(x) = \sum\limits_{i = 1}^{{\text{Dim}}} {{{({{\hat y}_i} - {y_i})}^2}} $$

(27)

式中：Dim代表个体维度； ${\hat y_i}$ 为网络期望输出值； ${y_i}$ 为实际输出值。

4）原子种群寻优更新。根据IASO算法更新原子种群并采用式(27)计算适应度值。

5）判定是否满足终止条件。若满足则输出最优个体 ${x_i}$ 及最优权值 $\omega $ 和阈值 $b$ ；反之跳转到4）继续执行优化。

6）更新BP神经网络的权值 $\omega $ 和阈值 $b$ 并利用更新后的网络对数据集进行分类。

4.2 仿真实验

为验证IASO-BP在进行分类时具有更高的精度，本文采用UCI数据集中的8个数据集进行数值实验，并将IASO-BP与一般BP神经网络和ASO-BP进行仿真实验，具体实验过程如下。

1) 数据集说明

为验证IASO-BP的有效性，本文从UCI数据集中选取8个数据集进行数值对比实验，包括皮肤科数据集(Dermatology)、糖尿病数据集(Diabetes)、肝脏疾病数据集(Bupa)、玻璃数据集(Glass)、印度人数据集(Indian)、植物叶片数据集(Leaf)、帕金森数据集(Parkinsons)及手写数字数据集(Pendigits)，数据集信息详见表6。

表 6 UCI中8个数据集物理属性

Table 6 Physical attributes of eight datasets in UCI

数据集	类别数/类	特征数/个	样本数/个	训练集/个	测试集/个
Dermatology	6	33	366	256	110
Diabetes	2	8	768	537	231
Bupa	2	6	345	241	104
Glass	6	9	214	149	65
Indian	2	8	583	408	175
Leaf	12	36	340	237	103
Parkinsons	5	22	529	136	59
Pendigits	10	17	461	7694	3298

2) 实验环境及初始化参数

为保证实验的公平性，本文所采用的仿真环境为：操作系统Windows 10，CPU为Intel(R) Core(TM) i7-5557U，主频3.10 GHz，内存为8 GB，实验平台为MATLAB2016a。针对同一数据集，本文初始参数为：最大迭代次数统一为20次，种群数量为20，权值和阈值边界范围为[−10,10]，ASO与IASO参数为 $\alpha = 50$ ， $\beta = 0.2$ 。分别对8个数据集进行100次实验并计算100次实验结果的均值(Mean)、标准差(Std)及最大值(Max)和最小值(Min)作为实验最终评价指标，得到实验结果如表7所示。

表 7 不同算法分类准确率

Table 7 Classification accuracy of different algorithms %

数据集	算法	评价指标(分类准确率)
数据集	算法	Mean	Std	Max	Min
Dermatology	BP	27.46	23.22	78.91	2.73
	ASO-BP	95.51	1.52	98.83	93.75
	IASO-BP	98.95	0.64	99.61	97.66
Diabetes	BP	65.61	26.91	97.02	12.10
	ASO-BP	98.31	0.94	99.63	96.83
	IASO-BP	98.86	0.45	99.63	98.14
Bupa	BP	86.06	17.10	100	45.64
	ASO-BP	98.80	0.50	99.59	97.53
	IASO-BP	99.25	0.61	100	98.34
Glass	BP	57.18	31.15	91.28	10.07
	ASO-BP	91.95	2.07	94.63	87.92
	IASO-BP	96.64	1.05	98.66	95.30
Indian	BP	73.70	31.02	100	8.82
	ASO-BP	97.08	1.04	98.53	95.34
	IASO-BP	99.75	0.26	100	99.26
Leaf	BP	9.87	15.48	41.77	0
	ASO-BP	96.33	1.59	98.73	94.51
	IASO-BP	99.16	0.40	99.58	98.31

续表 7
数据集	算法	评价指标(分类准确率)
数据集	算法	Mean	Std	Max	Min
Parkinsons	BP	92.57	6.76	100	79.41
	ASO-BP	97.87	1.12	100	96.32
	IASO-BP	98.75	1.10	100	97.06
Pendigits	BP	18.19	18.92	49.55	0.42
	ASO-BP	99.34	0.40	99.83	98.66
	IASO-BP	99.97	0.03	100	99.91

5. 结束语

本文针对原子优化算法收敛速度慢、求解精度低和易陷入局部最优等问题，围绕算法的改进与应用进行了研究，通过不同数值实验结果对比分析得到以下结论：

1) 提出了一种融合混沌优化并基于振幅随机补偿和步长演变策略模拟原子位置动态演变更新过程的改进ASO算法(IASO)，数值实验结果表明：IASO相较于5种对比算法在求解精度、收敛速度、局部极值逃逸能力和算法稳定性方面均有显著性提高，通过Wilcoxon秩和检验p值结果进一步验证了IASO的可行性和有效性。

2) 将IASO引入BP神经网络优化过程中，设计出一种融合IASO和BP神经网络的分类模型(IASO-BP)，并将其用于分类任务，数值实验结果表明：IASO-BP能对BP神经网络权值和阈值进行有效优化，优化后网络模型与BP神经网络和ASO-BP相比显示出更高的分类准确性。

本文所研究工作是对元启发式算法优化神经网络结构参数的一次有益尝试，数值实验结果充分表明了IASO算法和IASO算法的可行性和有效性。后续研究将围绕基于IASO(或其他元启发式算法)优化其他浅层神经网络参数，以及搜索最优深度神经网络架构等方面来开展工作。

图 1 原子力曲线

Fig. 1 Force curve of atoms

下载: 全尺寸图片

图 2 ${F'}$ 、 $h$ 和 $\eta $ 函数关系

Fig. 2 ${F'}$ ， $h$ and $\eta $ functional relation

下载: 全尺寸图片

图 3 IASO算法流程

Fig. 3 Flow chart of the IASO algorithm

下载: 全尺寸图片

图 4 IASO与5种算法的最佳适应度对数对比曲线

Fig. 4 Logarithmic comparison curve of optimal fitness between IASO and five algorithms

下载: 全尺寸图片

图 5 IASO与5种算法的最佳适应度对数对比曲线

Fig. 5 Logarithmic comparison curve of optimal fitness between IASO and five algorithms

下载: 全尺寸图片

图 6 不同智能优化算法运行时间对比

Fig. 6 Running time comparison of different intelligent optimization algorithms

下载: 全尺寸图片

表 1 基准测试函数

Table 1 Benchmark function

函数名	表达式	区间	单/多峰	最优值
Sphere	${f_1}(x) = \displaystyle\sum\limits_{i = 1}^D {x_i^2}$	[−100,100]	单峰	0
Schwefel 2.22	${f_2}(x) = \displaystyle\sum\limits_{i = 1}^D {\left\| { {x_i} } \right\|} + \prod\limits_{i = 1}^D {\left\| { {x_i} } \right\|}$	[−10,10]	单峰	0
Schwefel 1.2	${f_3}(x) = \displaystyle\sum\limits_{i = 1}^D { { {\left(\displaystyle\sum\limits_{j = 1}^i { {x_j} } \right)}^2} }$	[−100,100]	单峰	0
Step	${f_4}(x) = \displaystyle\sum\limits_{i = 1}^D { { {({x_i} + 0.5)}^2} }$	[−100,100]	单峰	0
Quartic	${f_5}(x) = \displaystyle\sum\limits_{i = 1}^D {ix_i^4} + {\text{rand} }\left[ {0,1} \right)$	[−1.28,1.28]	单峰	0
Rastrigin	${f_6}(x) = \displaystyle\sum\limits_{i = 1}^D { { {\left[ {x_i^2 - 10\cos (2{\text{π } }{x_i}) + 10} \right]}^2} }$	[−5.12,5.12]	多峰	0
Ackley	${f_7}(x) = - 20\exp \left( - 0.2\sqrt {\dfrac{1}{n}\displaystyle\sum\limits_{i = 1}^D {x_i^2} } \right) - \exp \left[ {\dfrac{1}{n}\displaystyle\sum\limits_{i = 1}^D {\cos (2{\text{π } }{x_i})} } \right] + 20 + {\rm{e}}$	[−32,32]	多峰	0
Griewank	${f_8}(x) = \dfrac{1}{ {4000} }\displaystyle\sum\limits_{i = 1}^D { { {({x_i} - 100)}^2} } + \prod\limits_{i = 1}^D {\cos \left(\dfrac{ { {x_i} - 100} }{ {\sqrt i } }\right) + 1}$	[−600,600]	多峰	0
Levy	$\begin{gathered} {f_9}(x) = {\sin ^2}({\text{π } }{\omega _i}) + \displaystyle\sum\limits_{i = 1}^D { { {({\omega _i} - 1)}^2} } \left[ {1 + 10{ {\sin }^2}({\text{π } }{\omega _i} + 1)} \right] \hfill +\\ \;\;\;\;\;\;\;\; {({\omega _D} - 1)^2}\left[ {1 + { {\sin }^2}(2{\text{π } }{\omega _d})} \right],{\text{ } }\;\;{\omega _i} = 1 + \frac{ { {x_i} - 1} }{4} \hfill \\ \end{gathered}$	[−10,10]	多峰	0
Weierstrass	${f_{10} }(x) = \displaystyle\sum\limits_{i = 1}^D {\left[ { { {0.5}^i}\cos \left( {2{\text{π } }{3^i}\left( { {x_i} + 0.5} \right)} \right)} \right]} - D\displaystyle\sum\limits_{i = 1}^D { { {0.5}^i}\cos \left( {2{\text{π } }{3^i} \times 0.5} \right)}$	[−0.5,0.5]	多峰	0

表 2 6种算法对10个基准函数的统计指标对比结果(D=30)

Table 2 Comparison of the statistical indexes of ten benchmark functions via six algorithms (D=30)

基准函数	评价指标	BOA	MFO	MVO	SSA	ASO	IASO
f₁	Mean	1.70×10⁻¹⁴	1.60×10³	1.76×10⁻¹	9.46×10⁻⁹	2.05×10⁻²³	0.00×10⁰
f₁	Std	8.04×10⁻¹⁶	3.69×10³	4.90×10⁻²	1.90×10⁻⁹	2.27×10⁻²³	0.00×10⁰

续表 2
基准函数	评价指标	BOA	MFO	MVO	SSA	ASO	IASO
	Best	1.52×10⁻¹⁴	2.32×10⁻⁶	8.34×10⁻²	4.94×10⁻⁹	7.91×10⁻²⁵	0.00×10⁰
f₂	Mean	9.72×10⁻¹²	3.21×10¹	2.87×10⁻¹	4.89×10⁻¹	5.30×10⁻¹¹	1.54×10⁻¹⁸⁴
	Std	2.13×10⁻¹²	1.94×10¹	8.36×10⁻²	6.06×10⁻¹	6.86×10⁻¹¹	0.00×10⁰
	Best	3.20×10⁻¹²	5.98×10⁻⁵	1.67×10⁻¹	6.71×10⁻⁵	7.91×10⁻²⁵	4.88×10⁻¹⁸⁸
f₃	Mean	1.71×10⁻¹⁴	1.48×10⁴	2.15×10¹	4.23×10¹	2.02×10²	0.00×10⁰
	Std	9.37×10⁻¹⁶	1.22×10⁴	1.01×10¹	3.10×10¹	1.29×10²	0.00×10⁰
	Best	1.39×10⁻¹⁴	3.14×10²	6.47×10⁰	3.93×10⁰	1.96×10¹	0.00×10⁰
f₄	Mean	0.00×10⁰	1.20×10³	6.30×10⁰	9.35×10⁰	0.00×10⁰	0.00×10⁰
	Std	0.00×10⁰	3.27×10³	3.26×10⁰	5.48×10⁰	0.00×10⁰	0.00×10⁰
	Best	0.00×10⁰	0.00×10⁰	1.00×10⁰	1.00×10⁰	0.00×10⁰	0.00×10⁰
f₅	Mean	6.12×10⁻⁴	2.54×10⁰	1.45×10⁻²	5.44×10⁻²	2.57×10⁻²	2.34×10⁻⁵
	Std	2.55×10⁻⁴	5.93×10⁰	7.14×10⁻³	2.26×10⁻²	9.47×10⁻³	2.17×10⁻⁵
	Best	1.38×10⁻⁴	2.18×10⁻²	5.98×10⁻³	1.41×10⁻²	8.23×10⁻³	2.23×10⁻⁷
f₆	Mean	3.92×10⁰	1.45×10²	1.12×10²	4.95×10¹	2.86×10¹	0.00×10⁰
	Std	2.76×10¹	3.54×10¹	2.82×10¹	1.50×10¹	7.60×10⁰	0.00×10⁰
	Best	0.00×10⁰	7.16×10¹	5.48×10¹	1.99×10¹	1.19×10¹	0.00×10⁰
f₇	Mean	1.13×10¹	1.30×10¹	6.05×10⁻¹	1.69×10⁰	3.21×10⁻¹²	2.24×10⁻¹⁵
	Std	4.51×10¹	8.53×10⁰	5.73×10⁻¹	9.65×10⁻¹	3.27×10⁻¹²	1.73×10⁻¹⁵
	Best	0.00×10⁰	5.70×10⁻⁴	8.47×10⁻²	2.06×10⁻⁵	9.21×10⁻¹³	8.88×10⁻¹⁶
f₈	Mean	1.27×10⁻¹⁵	1.27×10¹	4.47×10⁻¹	1.10×10⁻²	1.05×10⁻²	0.00×10⁰
	Std	1.39×10⁻¹⁵	3.40×10¹	9.99×10⁻²	1.10×10⁻²	1.52×10⁻²	0.00×10⁰
	Best	0.00×10⁰	8.06×10⁻⁶	1.84×10⁻¹	1.91×10⁻⁸	0.00×10⁰	0.00×10⁰
f₉	Mean	2.01×10⁰	2.65×10¹	1.60×10¹	5.23×10⁰	2.73×10⁻²	2.54×10⁰
	Std	2.42×10⁻¹	9.74×10⁰	9.61×10⁰	3.28×10⁰	1.08×10⁻¹	2.11×10⁻¹
	Best	1.54×10⁰	3.27×10⁰	5.52×10⁻¹	8.95×10⁻²	6.43×10⁻²⁵	2.04×10⁰
f₁₀	Mean	1.42×10⁻¹⁶	4.98×10⁰	9.53×10⁰	1.12×10¹	3.48×10⁻³	0.00×10⁰
	Std	1.42×10⁻¹⁵	3.00×10⁰	2.83×10⁰	3.28×10⁰	1.49×10⁻²	0.00×10⁰
	Best	0.00×10⁰	1.25×10⁻²	4.88×10⁰	5.54×10⁰	1.09×10⁻⁹	0.00×10⁰

表 3 6种算法对10个基准函数的统计指标对比结果(D=100)

Table 3 Comparison of statistical indexes of 10 benchmark functions by six algorithms(D=100)

测试函数	评价指标	BOA	MFO	MVO	SSA	ASO	IASO
f₁	Mean	1.77×10⁻¹⁴	2.72×10⁴	2.37×10¹	8.12×10⁻³	1.63×10⁻⁴	0.00×10⁰
	Std	9.07×10⁻¹⁶	1.56×10⁴	3.59×10⁰	8.85×10⁻³	7.41×10⁻⁴	0.00×10⁰
	Best	1.55×10⁻¹⁴	1.93×10³	1.69×10¹	4.68×10⁻⁴	4.26×10⁻¹⁷	0.00×10⁰
f₂	Mean	6.02×10⁺⁴⁸	1.70×10²	9.21×10⁺²²	1.31×10¹	2.79×10⁰	0.00×10⁰
	Std	2.87×10⁺⁴⁹	4.52×10¹	9.00×10⁺²³	3.52×10⁰	2.22×10⁰	0.00×10⁰
	Best	4.90×10⁺³⁷	7.18×10¹	2.42×10²	6.60×10⁰	4.52×10⁻²	0.00×10⁰

续表 3
测试函数	评价指标	BOA	MFO	MVO	SSA	ASO	IASO
f₃	Mean	1.77×10^-14	1.75×10⁵	3.14×10⁴	2.01×10⁴	3.16×10⁴	0.00×10⁰
	Std	1.17×10⁻¹⁵	5.90×10⁴	4.30×10³	1.03×10⁴	6.11×10³	0.00×10⁰
	Best	1.42×10⁻¹⁴	8.40×10⁴	2.07×10⁴	6.97×10³	2.08×10⁴	0.00×10⁰
f₄	Mean	0.00×10⁰	2.76×10⁴	1.46×10²	2.37×10²	3.76×10¹	0.00×10⁰
	Std	0.00×10⁰	1.28×10⁴	3.94×10¹	7.99×10¹	3.44×10¹	0.00×10⁰
	Best	0.00×10⁰	3.73×10³	6.30×10¹	1.11×10²	4.00×10⁰	0.00×10⁰
f₅	Mean	5.84×10⁻⁴	1.30×10²	2.37×10⁻¹	7.55×10⁻¹	3.53×10⁻¹	2.39×10⁻⁵
	Std	2.27×10⁻⁴	1.01×10²	5.17×10⁻²	1.75×10⁻¹	9.39×10⁻²	2.17×10⁻⁵
	Best	1.23×10⁻⁴	6.41×10⁰	1.30×10⁻¹	4.86×10⁻¹	1.80×10⁻¹	5.07×10⁻⁷
f₆	Mean	0.00×10⁰	7.14×10²	6.08×10²	1.35×10²	1.24×10²	0.00×10⁰
	Std	0.00×10⁰	7.22×10¹	7.21×10¹	3.87×10¹	1.73×10¹	0.00×10⁰
	Best	0.00×10⁰	5.86×10²	3.99×10²	5.47×10¹	8.86×10¹	0.00×10⁰
f₇	Mean	8.21×10⁻¹¹	1.99×10¹	5.57×10⁰	5.21×10⁰	1.33×10⁰	3.77×10⁻¹⁵
	Std	8.13×10⁻¹⁰	2.28×10⁻¹	5.55×10⁰	1.02×10⁰	5.28×10⁻¹	1.40×10⁻¹⁵
	Best	0.00×10⁰	1.89×10¹	2.47×10⁰	3.20×10⁰	5.08×10⁻⁹	8.88×10⁻¹⁶
f₈	Mean	1.10×10⁻¹⁴	2.68×10²	1.21×10⁰	1.13×10⁻¹	4.09×10⁻²	0.00×10⁰
	Std	5.27×10⁻¹⁵	1.34×10²	3.03×10⁻²	3.44×10⁻²	6.21×10⁻²	0.00×10⁰
	Best	8.88×10⁻¹⁶	3.97×10¹	1.15×10⁰	5.27×10⁻²	4.88×10⁻¹⁵	0.00×10⁰
f₉	Mean	9.10×10⁰	1.81×10²	1.18×10²	1.70×10¹	6.03×10⁰	9.12×10⁰
	Std	2.04×10⁻¹	4.71×10¹	2.26×10¹	6.15×10⁰	2.93×10⁰	1.53×10⁻¹
	Best	8.44×10⁰	1.10×10²	7.10×10¹	3.52×10⁰	9.02×10⁻¹	8.79×10⁰
f₁₀	Mean	1.14×10⁻¹⁵	5.93×10¹	8.22×10¹	6.22×10¹	1.28×10¹	0.00×10⁰
	Std	5.60×10⁻¹⁵	6.96×10⁰	7.64×10⁰	5.48×10⁰	2.91×10⁰	0.00×10⁰
	Best	0.00×10⁰	4.38×10¹	6.54×10¹	4.50×10¹	6.10×10⁰	0.00×10⁰

表 4 6种算法对10个混合多维度基准函数的统计指标对比结果

Table 4 Comparison of statistical indexes of ten mixed multi-dimensional benchmark functions by six algorithms

基准函数	评价指标	BOA	MFO	MVO	SSA	ASO	IASO
f₁₁	Mean	1.00×10⁰	1.33×10⁰	9.98×10⁻¹	9.98×10⁻¹	1.03×10⁰	1.37×10⁰
	Std	8.01×10⁻³	1.05×10⁰	5.79×10⁻¹²	1.82×10⁻¹⁶	1.81×10⁻¹	5.11×10⁻¹
	Best	9.98×10⁻¹	9.98×10⁻¹	9.98×10⁻¹	9.98×10⁻¹	9.98×10⁻¹	9.98×10⁻¹
f₁₂	Mean	3.36×10⁻⁴	1.09×10⁻³	4.64×10⁻³	9.11×10⁻⁴	8.42×10⁻⁴	4.54×10⁻⁴
	Std	2.78×10⁻⁵	4.29×10⁻⁴	8.00×10⁻³	2.99×10⁻⁴	2.37×10⁻⁴	5.83×10⁻⁵
	Best	3.09×10⁻⁴	5.78×10⁻⁴	3.08×10⁻⁴	3.58×10⁻⁴	6.33×10⁻⁴	3.07×10⁻⁴
f₁₃	Mean	−1.37×10⁴	−1.03×10⁰	−1.03×10⁰	−1.03×10⁰	−1.03×10⁰	−1.03×10⁰
	Std	1.35×10⁴	6.78×10⁻¹⁶	4.47×10⁻⁸	9.67×10⁻¹⁵	6.65×10⁻¹⁶	1.86×10⁻⁴
	Best	−1.28×10⁰	−1.03×10⁰	−1.03×10⁰	−1.03×10⁰	−1.03×10⁰	−1.03×10⁰
f₁₄	Mean	3.99×10⁻¹	3.98×10⁻¹	3.98×10⁻¹	3.98×10⁻¹	3.98×10⁻¹	4.01×10⁻¹
	Std	1.17×10⁻³	0.00×10⁰	1.19×10⁻⁷	1.63×10⁻¹⁴	0.00×10⁰	3.59×10⁻³
	Best	3.98×10⁻¹	3.98×10⁻¹	3.98×10⁻¹	3.98×10⁻¹	3.98×10⁻¹	3.98×10⁻¹
f₁₅	Mean	3.02×10⁰	3.00×10⁰	3.00×10⁰	3.00×10⁰	3.00×10⁰	3.02×10⁰
	Std	2.99×10⁻²	8.77×10⁻¹⁶	4.72×10⁻⁷	4.33×10⁻¹⁴	7.69×10⁻¹⁶	1.92×10⁻²
	Best	3.00×10⁰	3.00×10⁰	3.00×10⁰	3.00×10⁰	3.00×10⁰	3.00×10⁰
f₁₆	Mean	−6.89×10⁰	−3.86×10⁰	−3.86×10⁰	−3.86×10⁰	−3.86×10⁰	−3.86×10⁰
	Std	6.65×10⁰	2.71×10⁻¹⁵	1.33×10⁻⁷	1.43×10⁻¹⁴	2.71×10⁻¹⁵	4.17×10⁻³
	Best	−4.00×10⁰	−3.86×10⁰	−3.86×10⁰	−3.86×10⁰	−3.86×10⁰	−3.86×10⁰
f₁₇	Mean	−2.76×10⁰	−3.22×10⁰	−3.26×10⁰	−3.24×10⁰	−3.32×10⁰	−3.32×10⁰
	Std	3.26×10⁻²	4.99×10⁻²	6.06×10⁻²	5.73×10⁻²	1.34×10⁻¹⁵	8.60×10⁻²
	Best	−2.56×10⁰	−3.32×10⁰	−3.32×10⁰	−3.32×10⁰	−3.86×10⁰	−3.32×10⁰
f₁₈	Mean	−4.96×10⁰	−6.73×10⁰	−8.46×10⁰	−8.81×10⁰	−8.89×10⁰	−4.77×10⁰
	Std	5.88×10⁻¹	3.38×10⁰	2.43×10⁰	2.77×10⁰	2.36×10⁰	1.09×10⁰
	Best	−6.96×10⁰	−1.02×10¹	−1.02×10¹	−1.02×10¹	−1.02×10¹	−9.92×10⁰
f₁₉	Mean	−5.16×10⁰	−7.82×10⁰	−8.58×10⁰	−9.62×10⁰	−9.07×10⁰	−4.62×10⁰
	Std	1.01×10⁰	3.50×10⁰	2.90×10⁰	2.07×10⁰	2.48×10⁰	3.79×10⁻¹
	Best	−8.97×10⁰	−1.04×10¹	−1.04×10¹	−1.04×10¹	−1.04×10¹	−5.92×10⁰
f₂₀	Mean	−5.18×10⁰	−9.61×10⁰	−9.46×10⁰	−9.21×10⁰	−9.39×10⁰	−4.74×10⁰
	Std	9.63×10⁻¹	2.44×10⁰	2.19×10⁰	2.75×10⁰	2.37×10⁰	4.53×10⁻¹
	Best	−7.96×10⁰	−1.05×10¹	−1.05×10¹	−1.05×10¹	−1.05×10¹	−6.23×10⁰

表 5 基准函数的威尔科克森秩和检验p值

Table 5 p-value of the Wilcoxon rank-sum test of benchmark functions

测试函数	IASO vs. ASO p-value win	IASO vs. BOA p-value win	IASO vs. MFO p-value win	IASO vs. MVO p-value win	IASO vs. SSA p-value win
f₂(30维)	5.22×10⁻¹³⁸ +	2.94×10⁻⁵⁵ +	3.02×10⁻²⁰¹ +	6.61×10⁻²⁴⁴ +	1.22×10⁻²¹² +
f₄(30维)	1.71×10⁻²⁵ +	9.55×10⁻¹−	5.70×10⁻¹¹³ +	N/A =	N/A =
f₆(30维)	3.86×10⁻²³¹ +	7.23×10⁻¹⁹ +	4.09×10⁻²⁴² +	3.39×10⁻²⁵⁰	9.11×10⁻²⁴⁰ +
f₈(30维)	9.71×10⁻¹⁰⁴ +	7.98×10⁻¹⁰⁸ +	1.51×10⁻²⁷⁵ +	N/A =	1.22×10⁻²⁸⁴ +
f₁₀(30维)	6.59×10⁻¹³⁵ +	9.06×10⁻¹¹ +	8.68×10⁻¹⁶⁸ +	5.19×10⁻²⁰⁹	1.09×10⁻²⁰¹ +
f₂(100维)	3.82×10⁻²⁵⁸ +	N/A =	5.62×10⁻²⁹² +	3.26×10⁻²⁹⁴	2.22×10⁻²⁸⁵ +
f₄(100维)	N/A =	8.42×10⁻⁴ +	N/A =	N/A =	N/A =
f₆(100维)	4.26×10⁻³⁰⁴ +	5.44×10⁻⁴⁹ +	3.94×10⁻³¹¹ +	2.18×10⁻³¹⁵	3.02×10⁻³⁰⁷ +
f₈(100维)	6.84×10⁻²⁵⁴ +	5.75×10⁻²³⁶ +	N/A =	N/A =	N/A =
f₁₀(100维)	2.57×10⁻²⁶⁷ +	4.80×10⁻¹²⁶ +	2.61×10⁻²⁸⁶ +	1.04×10⁻²⁸⁷ +	1.36×10⁻²⁸⁵ +
f₁₂	4.46×10⁻¹⁸⁶ +	2.47×10⁻¹⁸² +	5.80×10⁻¹⁷¹ +	1.25×10⁻⁷⁰ +	5.68×10⁻¹⁸ +

续表 5
测试函数	IASO vs. ASO p-value win	IASO vs. BOA p-value win	IASO vs. MFO p-value win	IASO vs. MVO p-value win	IASO vs. SSA p-value win
f₁₄	9.33×10⁻¹⁸ +	1.37×10⁻²⁶¹ +	N/A =	6.06×10⁻⁹⁰ +	1.27×10⁻⁴ +
f₁₆	2.42×10⁻³⁶ +	1.25×10⁻²²⁷ +	N/A =	2.61×10⁻¹¹ +	6.91×10⁻⁴² +
f₁₈	2.22×10⁻⁷⁴ +	2.17×10⁻²²⁶ +	N/A =	8.63×10⁻¹²² +	3.39×10⁻⁹ +
f₂₀	1.05×10⁻²⁰⁸ +	2.77×10⁻⁷¹ +	N/A =	2.79×10⁻¹⁰¹ +	N/A =
+/=/−	14/1/0	13/1/1	9/6/0	11/4/0	11/4/0

表 6 UCI中8个数据集物理属性

Table 6 Physical attributes of eight datasets in UCI

数据集	类别数/类	特征数/个	样本数/个	训练集/个	测试集/个
Dermatology	6	33	366	256	110
Diabetes	2	8	768	537	231
Bupa	2	6	345	241	104
Glass	6	9	214	149	65
Indian	2	8	583	408	175
Leaf	12	36	340	237	103
Parkinsons	5	22	529	136	59
Pendigits	10	17	461	7694	3298

表 7 不同算法分类准确率

Table 7 Classification accuracy of different algorithms %

数据集	算法	评价指标(分类准确率)
数据集	算法	Mean	Std	Max	Min
Dermatology	BP	27.46	23.22	78.91	2.73
	ASO-BP	95.51	1.52	98.83	93.75
	IASO-BP	98.95	0.64	99.61	97.66
Diabetes	BP	65.61	26.91	97.02	12.10
	ASO-BP	98.31	0.94	99.63	96.83
	IASO-BP	98.86	0.45	99.63	98.14
Bupa	BP	86.06	17.10	100	45.64
	ASO-BP	98.80	0.50	99.59	97.53
	IASO-BP	99.25	0.61	100	98.34
Glass	BP	57.18	31.15	91.28	10.07
	ASO-BP	91.95	2.07	94.63	87.92
	IASO-BP	96.64	1.05	98.66	95.30
Indian	BP	73.70	31.02	100	8.82
	ASO-BP	97.08	1.04	98.53	95.34
	IASO-BP	99.75	0.26	100	99.26
Leaf	BP	9.87	15.48	41.77	0
	ASO-BP	96.33	1.59	98.73	94.51
	IASO-BP	99.16	0.40	99.58	98.31

续表 7
数据集	算法	评价指标(分类准确率)
数据集	算法	Mean	Std	Max	Min
Parkinsons	BP	92.57	6.76	100	79.41
	ASO-BP	97.87	1.12	100	96.32
	IASO-BP	98.75	1.10	100	97.06
Pendigits	BP	18.19	18.92	49.55	0.42
	ASO-BP	99.34	0.40	99.83	98.66
	IASO-BP	99.97	0.03	100	99.91

参考文献(25)

[1]	董如意. 元启发式优化算法研究与应用[D]. 长春: 吉林大学, 2019: 1−3. DONG Ruyi. Research and application of meta-heuristic optimization algorithms[D]. Changchun: Jilin University, 2019: 1−3.
[2]	HOLLAND J H. Genetic algorithms[J]. Scientific American, 1992, 267(1): 66–72. doi: 10.1038/scientificamerican0792-66
[3]	EIBEN A E, BÄCK T. Empirical investigation of multiparent recombination operators in evolution strategies[J]. Evolutionary computation, 1997, 5(3): 347–365. doi: 10.1162/evco.1997.5.3.347
[4]	MOSCATO P. On evolution, search, optimization, genetic algorithms and martial arts-towards memetic algorithms [J]. Caltech Concurrent Computation Program, 1989.
[5]	KENNEDY J, EBERHART R. Particle swarm optimization [C]// Proceedings of ICNN'95-International Conference on Neural Networks. IEEE, 1995: 1942−1948.
[6]	ASKARZADEH A. A novel metaheuristic method for solving constrained engineering optimization problems: Crow search algorithm[J]. Computers and structures, 2016, 169: 1–12. doi: 10.1016/j.compstruc.2016.03.001
[7]	MIRJALILI S, GANDOMI A H, MIRJALILI S Z, et al. Salp swarm algorithm: a bio-inspired optimizer for engineering design problems[J]. Advances in engineering software, 2017, 114: 163–191. doi: 10.1016/j.advengsoft.2017.07.002
[8]	ARORA S, SINGH S. Butterfly optimization algorithm: a novel approach for global optimization[J]. Soft computing, 2019, 23(3): 715–734. doi: 10.1007/s00500-018-3102-4
[9]	MIRJALILI S. Moth-flame optimization algorithm: a novel nature-inspired heuristic paradigm[J]. Knowledge-based systems, 2015, 89: 228–249. doi: 10.1016/j.knosys.2015.07.006
[10]	KIRKPATRICK S, GELATT C D Jr, VECCHI M P. Optimization by simulated annealing[J]. Science, 1983, 220(4598): 671–680. doi: 10.1126/science.220.4598.671
[11]	GONÇALVES M S, LOPEZ R H, MIGUEL L F F. Search group algorithm: a new metaheuristic method for the optimization of truss structures[J]. Computers and structures, 2015, 153: 165–184. doi: 10.1016/j.compstruc.2015.03.003
[12]	MIRJALILI S, MIRJALILI S M, HATAMLOU A. Multi-verse optimizer: a nature-inspired algorithm for global optimization[J]. Neural computing and applications, 2016, 27(2): 495–513. doi: 10.1007/s00521-015-1870-7
[13]	ZHAO Weiguo, WANG Liying, ZHANG Zhenxing. A novel atom search optimization for dispersion coefficient estimation in groundwater[J]. Future generation computer systems, 2019, 91: 601–610. doi: 10.1016/j.future.2018.05.037
[14]	ZHAO Weiguo, WANG Liying, ZHANG Zhenxing. Atom search optimization and its application to solve a hydrogeologic parameter estimation problem[J]. Knowledge-based systems, 2019, 163: 283–304. doi: 10.1016/j.knosys.2018.08.030
[15]	ELAZIZ M A, NABIL N, EWEES A A, et al. Automatic data clustering based on hybrid atom search optimization and sine-cosine algorithm[C]//2019 IEEE Congress on Evolutionary Computation. Wellington: IEEE, 2019: 2315−2322.
[16]	AGWA A M, EL-FERGANY A A, SARHAN G M. Steady-state modeling of fuel cells based on atom search optimizer[J]. Energies, 2019, 12(10): 1884. doi: 10.3390/en12101884
[17]	柳缔西子, 范勤勤, 胡志华. 基于混沌搜索和权重学习的教与学优化算法及其应用[J]. 智能系统学报, 2018, 13(5): 818–828. LIU D, FAN Qinqin, HU Zhihua. Teaching-learning-based optimization algorithm based on chaotic search and weighted learning and its application[J]. CAAI transactions on intelligent systems, 2018, 13(5): 818–828.
[18]	贾鹤鸣, 彭晓旭, 邢致恺, 等. 改进萤火虫优化算法的Renyi熵污油图像分割[J]. 智能系统学报, 2020, 15(2): 367–373. JIA Heming, PENG Xiaoxu, XING Zhikai, et al. Renyi entropy based on improved firefly optimization algorithm for image segmentation of waste oil[J]. CAAI transactions on intelligent systems, 2020, 15(2): 367–373.
[19]	赵欣. 不同一维混沌映射的优化性能比较研究[J]. 计算机应用研究, 2012, 29(3): 913–915. doi: 10.3969/j.issn.1001-3695.2012.03.031 ZHAO Xin. Research on optimization performance comparison of different one-dimensional chaotic maps[J]. Application research of computers, 2012, 29(3): 913–915. doi: 10.3969/j.issn.1001-3695.2012.03.031
[20]	DERRAC J, GARCÍA S, MOLINA D, et al. A practical tutorial on the use of nonparametric statistical tests as a methodology for comparing evolutionary and swarm intelligence algorithms[J]. Swarm and evolutionary computation, 2011, 1(1): 3–18. doi: 10.1016/j.swevo.2011.02.002
[21]	NABIL E. A modified flower pollination algorithm for global optimization[J]. Expert systems with applications, 2016, 57: 192–203. doi: 10.1016/j.eswa.2016.03.047
[22]	刘威, 付杰, 周定宁, 等. 基于改进郊狼优化算法的浅层神经进化方法研究[J]. 计算机学报, 2021, 44(6): 1200–1213. doi: 10.11897/SP.J.1016.2021.01200 LIU Wei, FU Jie, ZHOU Dingning, et al. Research on shallow neural network evolution method based on improved coyote optimization algorithm[J]. Chinese journal of computers, 2021, 44(6): 1200–1213. doi: 10.11897/SP.J.1016.2021.01200
[23]	马创, 周代棋, 张业. 基于改进鲸鱼算法的BP神经网络水资源需求预测方法[J]. 计算机科学, 2020, 47(S2): 486–490. MA Chuang, ZHOU Daiqi, ZHANG Ye. BP neural network water resource demand prediction method based on improved whale algorithm[J]. Computer science, 2020, 47(S2): 486–490.
[24]	马创涛, 邵景峰. 烟花算法改进BP神经网络预测模型及其应用[J]. 控制工程, 2020, 27(8): 1324–1331. MA Chuangtao, SHAO Jingfeng. Prediction model based on improved BP neural network with fireworks algorithm and its application[J]. Control engineering of China, 2020, 27(8): 1324–1331.
[25]	王振东, 刘尧迪, 胡中栋, 等. 利用改进灰狼算法优化BP神经网络的入侵检测[J]. 小型微型计算机系统, 2021, 42(4): 875–884. doi: 10.3969/j.issn.1000-1220.2021.04.034 WANG Zhendong, LIU Yaodi, HU Zhongdong, et al. Use improved grey wolf algorithm to optimize BP neural network intrusion detection[J]. Journal of Chinese computer systems, 2021, 42(4): 875–884. doi: 10.3969/j.issn.1000-1220.2021.04.034

点击查看大图

图(6) / 表(11)

摘要

融合振幅随机补偿与步长演变机制的改进原子搜索优化算法

doi: 10.11992/tis.202103033

通讯作者: 刘威. E-mail： lv8218218@126.com.

出版历程

Improved atom search optimization by combining amplitude random compensation and step size evolution mechanism

1. 原子搜索优化算法(ASO)

1.1 原子运动约束方程

1.2 L-J势产生的相互作用力

1.3 键长势引起的约束力

2. 改进的原子搜索优化算法(IASO)

2.1 初始原子种群的混沌优化

2.2 振幅函数随机参数优化

2.3 步长演变搜索机制

2.4 IASO算法的实现

3. 数值实验与结果分析

3.1 实验环境及初始参数设置

3.2 不同算法在30维和100维下的对比实验

3.3 不同算法在混合多维度函数下的对比实验

3.4 Wilcoxon秩和检验

3.5 时间对比分析

4. 基于IASO的BP神经网络参数优化方法

4.1 算法设计步骤

4.2 仿真实验

5. 结束语

出版历程

目录

通讯作者:
刘威. E-mail： lv8218218@126.com.