凡事预则立,不预则废。但事物的预测通常受多种不确定性干扰。鉴于作者于1989年提出的集对分析（set pair analysis theory, SPA）理论对系统不确定性采取“客观承认，系统描述，定量刻画、具体分析”的处置方针，把系统的确定性关系与不确定关系作为一个不确定性子系统做数学处理^[1-3],吸引了不同领域的众多科技工作者把SPA应用于系统预测研究,通过对已有预测模型的集对分析，不同程度地提高了预测精度，取得满意或较为满意的预测效果。在中国知网上，采用“高级检索”“主题：集对分析”，“篇关摘：预测”，检索到250多篇文献。本文综述其中一部分有代表性的文献，指出基于集对分析的系统智能预测原理是通过系统已有数据做合理的结构化聚类和合适的联系数表达与不确定性分析进行预测建模,每次预测前,让预测模型通过回顾性学习使预测值与系统历史数据最大程度拟合，从而改善模型的预测功能，保证和提高预测精度。

1.   集对分析在天气预报中的应用

1.1   集对分析在天气降水预报中的应用

例1　天气系统同时具有确定性和随机不确定性。基于概率的多元回归模型REEP是世界各国进行天气预报的基本模式。由文献[4]可知，王国强在1998年就把集对分析用于天气降水预报研究，通过对进入预报模型的预报因子及其数值按集对分析理论进行预处理，提高了天气降水预报的准确率，在对93 次个例的降水预报作回顾性检验时，81次预报结论不变，有12 次修改了预报结论，其中11次修改成功，1次修改失败,成功率0.917，见表1，其中Y表示降水，1指降水发生，0指没有降水发生。

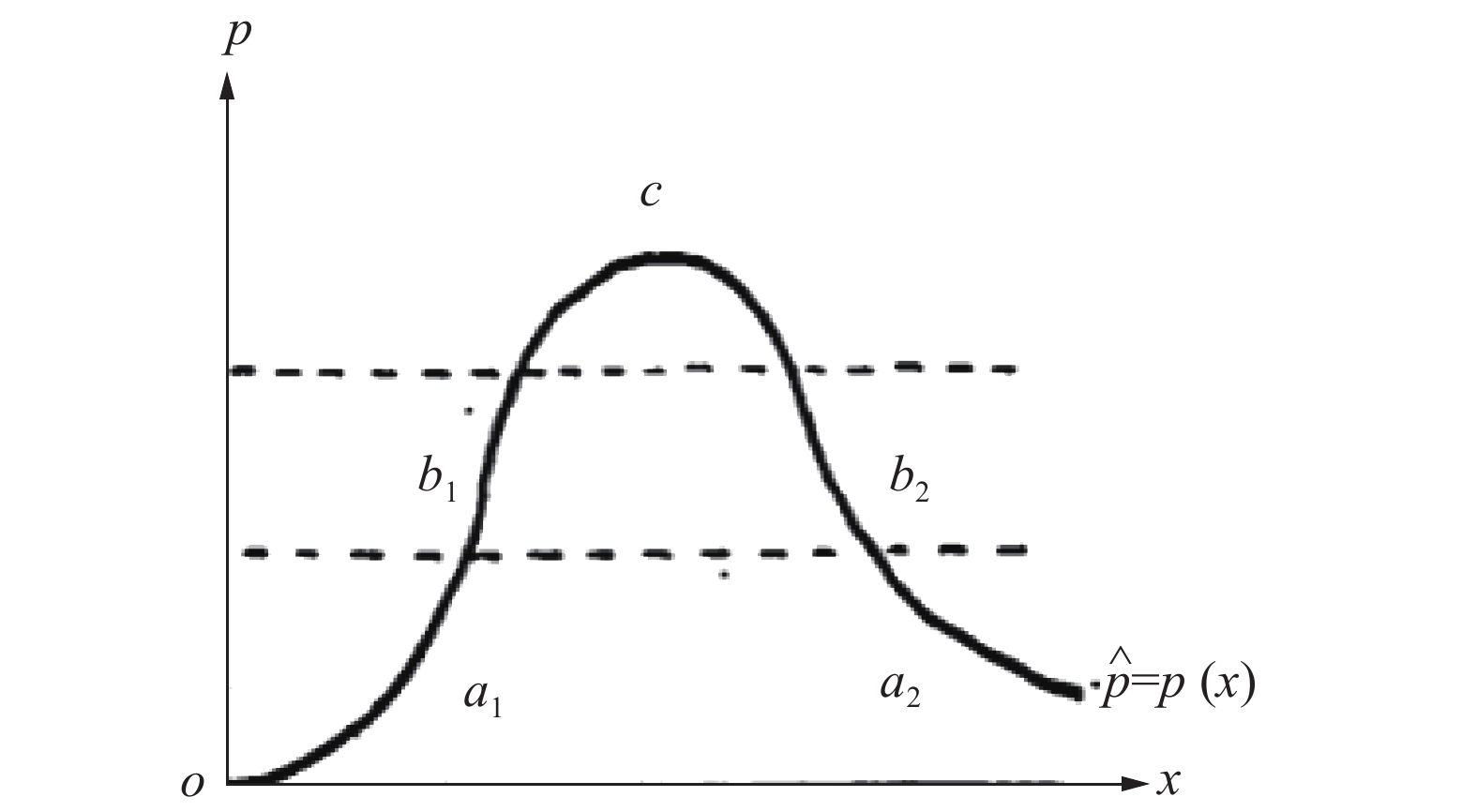
预处理的基本步骤是：首先，在众多的气象要素中确定预报降水事件W的n个“最佳因子”集合（做中长期降水预报涉及的因素多达10多个，短期和近期降水预报涉及的因素较少，如文献[4]中取n＝5），但这n个“最佳因子”在每一次降水预报中对指示W所起的“作用”有强(处于高概率区)有弱(处于低概率区)见图1和图2, 是一个动态变化着的组合；因此第2步，计算这n个因子的变异系数，变异系数最大的因子被认为是指示降水事件W的弱势因子(变异系数的计算公式为 $ cv = s/\overline x $ ，原理见文献[4-6])，该弱势因子会干扰其他强势因子指示降水事件W的出现，因此第3 步，把弱势因子的数值按集对分析中的“i比例取值原理”(见文献[4])分解给强势因子，加强预报模型做出降水事件W出现的概率，i比例取值公式如下：

图  1  事件W出现的高（c）中（b）低（a）概率

Fig.  1  High (c) medium (b) low (a) probability of occurrence of event W

下载: 全尺寸图片

图  2  单峰曲线时的高（c）中（b）低（a）概率

Fig.  2  Probability of high (c) medium (b) low (a) at unimodal curve

下载: 全尺寸图片

从而把 $ \mu = a + bi + cj $ 转换成：

以上3个基本步骤中的关键是对不确定性的合理处置。如第一步，要在众多的气象要素中确定预报降水事件W的n个“最佳因子”集合，既需要统计数据，也需要有预报经验；既需要有大范围的历史和即时气象信息，也需要给定降水区域附近小范围的历史和即时气象信息；即样本大小要合理；等等；第2步中把最大变异系数对应的因子确定为弱势因子(文献[4-5])，但次大变异系数对应的因子也可以视情况确定为次弱势因子，也就是按变异系数的由小到大把“最佳因子”分成“强势”“中间势”“弱势”三类；第3步中对“弱势”因子数值的“比例分解”，其中的“比例”可以利用式(1)也可以有理由地“加权”；而要把上述诸多不确定性转化为确定性(式(2))，每次预报降水事件W前作回顾性预报是不可或缺的重要一环。多年的预报实践证明了上述基于集对分析理论的天气降水预报多元回归模型，精度较高。例如，文献[5]中报告了2002年绍兴市全年共出现13 个大–暴雨，报对了10个，漏报的3个都是雨量相对较小的降水，雨量较大的降水一个未漏。

例2　冯利华(2000，2014)先后把王国强等在文献[4-6]中应用SPA提高天气预报准确率的思路和方法用于浙江省台风降雨量回顾性预报，证实了通过反复调整预报模型中各预报因子同(强势因子)异(强弱之间)反(弱势因子)相关区的分界值和不确定性分析，可以使台风降水计算等级和实际等级的历史拟合率达到最大，结果比较理想^[7-8]。

1.2   集对分析在沙尘暴预报中的应用

例3　王繁强(2006)沿用王国强等在文献[4-6]中的思路，把集对分析用于沙尘暴预报^[9]，在以往对沙尘暴研究成果的基础上，以强风、热力和沙源三大影响因子为着眼点，结合2001—2003年的沙尘暴天气个例，对沙尘暴天气进行了分类，分别选取预报因子，建立基于SPA的沙尘暴预报模型，于2004年春季进行了短期(24 h)预报试用，结果表明，这一方法具有较好的预报效果。

2.   集对分析在水文水资源预测中的应用

2.1   集对分析在水资源预测中的应用

例4　王红芳等^[10]在2006年研究了基于集对分析的年径流预测法。通过长江寸滩站年径流集对预测实例分析并与模糊优选预测结果对比，表明基于集对分析的预测法计算简单、关系结构清晰、预测精度较高。

例5　金菊良等^[11]于2009年提出基于集对分析的水资源相似预测模型SPA-SF，并用于新疆伊犁河流域雅马渡站年平均流量预测，结果说明：用SPA-SF预测水资源的丰枯变化，物理概念清晰，计算直观，预测精度较高。

例6　刘银迪等^[12]提出一种基于序位的集对分析降雨量预测模型(ordinal-set pair analysis O-SPA)，并用于辽河流域1956–2006年水文雨量站年降雨量预测，预测精度全部满足《水文情报预报规范》对年降雨量预报的精度要求。

例7　Zhang等^[13]在采用集对分析方法同时引入协整理论，提出基于误差修正模型的径流预测模型并用于西北黑河径流序列预测，模型能够较好地模拟和预测河川径流。

例8　卢家海^[14]采用人工智能BP模型、小波BP模型及GA-BP模型对径流进行预测，然后将径流的实测值系列A和上述3种模型的预测值Bi建立集对H(A, Bi)，利用集对分析的同、异、反特性进行联系度计算，据此确定径流预测模型的相对隶属度，并对隶属度进行归一化处理，得到上述3种模型的权重，再依据此权重建立相应的径流组合预测模型。应用1950—1975年小浪底水库的资料，对径流组合预测模型进行模拟，结果显示其预测精度明显高于单个模型的预测精度。

例9　袁喆等^[15]分别采用熵权法和集对分析法构建基于熵权法的集合模型(EW-CM)和基于集对分析法的集合模型(SPA-CM)，分别应用于滦河流域径流过程的模拟和预测，对比结果表明：SPA-CM模型径流预测效果在一定程度上优于单一模型，综合分析表明SPA-CM模型最优。

例10　李深奇等^[16] (2016)提出了率定量化标准系数的SPA年径流预测模型，首先对量化标准系数进行率定，再用SPA模型对径流进行预测。将该模型应用于长江宜昌站，并与经验标准预测结果进行对比。结果表明，率定量化标准后的预测结果能更好、更准确地反映原序列的变化,精度更高。

例11　刘祖发等^[17]将小波消噪(wavelet de-noise, WD)与秩次集对分析(rank set pair analysis, RSPA)方法耦合，建立基于小波消噪的秩次集对分析水文预测模型(WD-RSPA)，并应用于马口站年总径流量以及深圳市年总降雨量预测。结果表明：当集合维数T=4时，coif3-RSPA模型预测马口站径流量的预测误差|e|=11.97%；T=6时，db5-RSPA模型预测深圳市降雨量的预测误差|e|=17.73%。相较于传统AR(1)模型和单一的RSPA模型，WD-RSPA模型更接近真实值，是一种切实可行的水文时间序列预测方法。

例12　侯泽宇等^[18]将有序样品聚类、集对分析和马尔可夫链3种方法相结合，对传统的加权马尔可夫链预测方法进行了多方面改进，建立了基于有序样品聚类的集对权马尔可夫链年降水量预测模型，并将其应用于吉林省白城地区白城站2008—2010年年降水量的预测。将预测结果与实测值对比发现：三结合法有效提高了预测精度。实测值均位于预测区间内。结果令人满意。

例13　万阳^[19]依据都江堰雨量站1961—2002年的年降雨量资料，基于集对分析方法构建了2种(秩次加权集对预报模型和量化加权集对预报模型)年降雨量预报模型，然后利用预报模型对2003—2006年的年降水量进行预测，并将预测结果对比。结果显示，2种年降雨量预报模型预报结果均满足水文预报精度要求。相比较而言，秩次加权集对分析方法预测结果更加接近实际值，推荐采用秩次加权集对分析方法预测年降雨量。

例14　莫崇勋等^[20]根据中国西南典型岩溶区澄碧河流域内平塘站1963—2007年的水文气象资料，利用集对分析方法（SPA）的相似预测模型，分析和预测该流域水资源情况。结果表明，1993—2007年径流预测的NSE为0.687，RSR为0.559，整体达到“良”等级，平均误差11.4%，预测精度符合要求；集对分析方法在岩溶区流域中长期水资源预测中有很好的适用性。

2.2   集对分析在地下水预测中的应用

例15　何思为等^[21]利用甘肃省白银市景泰县2处地下水位测站的长序列观测资料，研究了秩次集对方法预测地下水位动态变化的优势。

例16　徐源蔚等^[22]把集对分析与相似预测结合，从同、异、反三方面定量刻画地下水位的当前样本与历史样本之间的相似性，建立了基于集对分析的地下水位相似预测模型。实例表明：基于集对分析的地下水位相似预测模型的平均相对误差小于3%。

例17　Zhang等^[23]把秩次集对分析与小波分析结合，对北京水库日极端气温和天津水库月极端气温进行精确模拟和预报，获得较为满意的结果。

例18　史红波^[24]将丹东地区作为研究对象，结合地下水位的相关数据信息，在集对分析基础上选择相似预测模型构建地下水样本，进而对地下水位进行预测。实例检验结果显示，丹东地区运用集对分析对地下水位相似预测模型的评价相对误差小于4%。

例19　Su博士等^[25]采用集对分析(spa)-马尔可夫链模型对地下水水质评价和预测，以西安市为例，以1996—2015年的地下水水质监测数据为例，验证了spa-markov 模型的可行性。

3.   集对分析在城市需水供水预测中的应用

3.1   集对分析在城市需水预测中的应用

例20　张云云等^[26]从2000—2014年的《中国统计年鉴》中收集年居民生活用水量时间序列数据，利用聚类和集对分析，计算居民生活用水量与影响因子人口总数的联系度，预测人口总数在未来的增长率，预测未来居民生活用水量及其增长速度，其预测误差均在2%以内，表明集对分析聚类预测模型对于生活用水量预测具有较高精度。

例21　郭彦等^[27]提出基于集对分析的多元回归、神经网络和灰色系统预测模型(SPA-CF)预测区域需水量，结果表明，SPA-CF是一种直观、简便、通用的组合预测新模型，具有推广应用价值。

例22　和蕊等^[28]用集对分析聚类预测法建立了城市生活需水量聚类预测模型，利用我国北京市实际数据进行验证，证实模型计算简单且精度较高。

例23　汪明武等^[29]提出基于联系隶属度的城市需水量预测模型，实例应用表明模型有效。

例24　周戎星等^[30]把基于集对分析的相似预测模型应用于山东省2010—2014年的用水量预测。预测结果与实测值相对误差较小。

例25　王培等^[31]用集对分析相似预测法对克拉玛依市三坪地区需水量预测，发现集对分析相似预测法计算简单，精度优于传统ARIMA模型。

3.2   集对分析在城市供水预测与调度中的应用

例26　郭旭宁等^[32]提出了确定供水水库群联合调度规则的集对分析新方法。首先把离散微分动态规划(DDDP)和拟定供水调度图确定的相同时段同一蓄水状态下的水库供水决策构成一组集对，通过遗传算法优化调度图中各调度线的位置，使两种供水决策联系度最大，从而得到最优调度图。根据该原理，以水库群虚拟聚合水库为研究对象，采用多维DDDP与遗传算法确定聚合水库最优调度图，并以此作为水库群的供水规则。在多维DDDP确定的供水决策样本系列中，选取与当前时段蓄水、来水情况最相似(联系度最大)的若干样本作为参照样本，将参照样本下水库放水量的加权平均值作为该水库当前时段的放水量。以观音阁、葠窝水库群为例，验证了采用集对分析方法确定供水水库群联合调度规则的有效性和合理性。

例27　张明等^[33]从同、异、反三个方面度量漏损预测样本与历史样本的相似性，建立了基于集对分析的漏损预测(SPA-LF)模型。应用结果表明，SPA-LF对预测过程不确定性的描述较为详细，供水管网漏点数及漏损频率预测结果均显示出SPA-LF模型的有效性，减小了预测过程的不确定性，与灰色系统模型、指数平滑模型及神经网络模型预测结果相比，SPA-LF模型取得了满意的预测精度。且计算简单，使用方便，可为供水管网的维护及管道更新提供决策支持。

4.   集对分析在电力与能源预测中的应用

4.1   集对分析在风电功率预测中的应用

例28　郭钰锋等^[34]把集对分析原理引入风速的区间预测，利用风向、温度、气压、湿度等影响因素的训练数据，并考虑风速点预测的结果误差分布及风速变化率的影响，确定未来某时间段内风速的预测值所属的分类集合，以该分类集合的上下限作为风速预测区间的上下限，从而实现了风速的区间预测。以某风电场的数据进行训练和预测，验证了基于SPAT的风速区间预测方法的有效性。

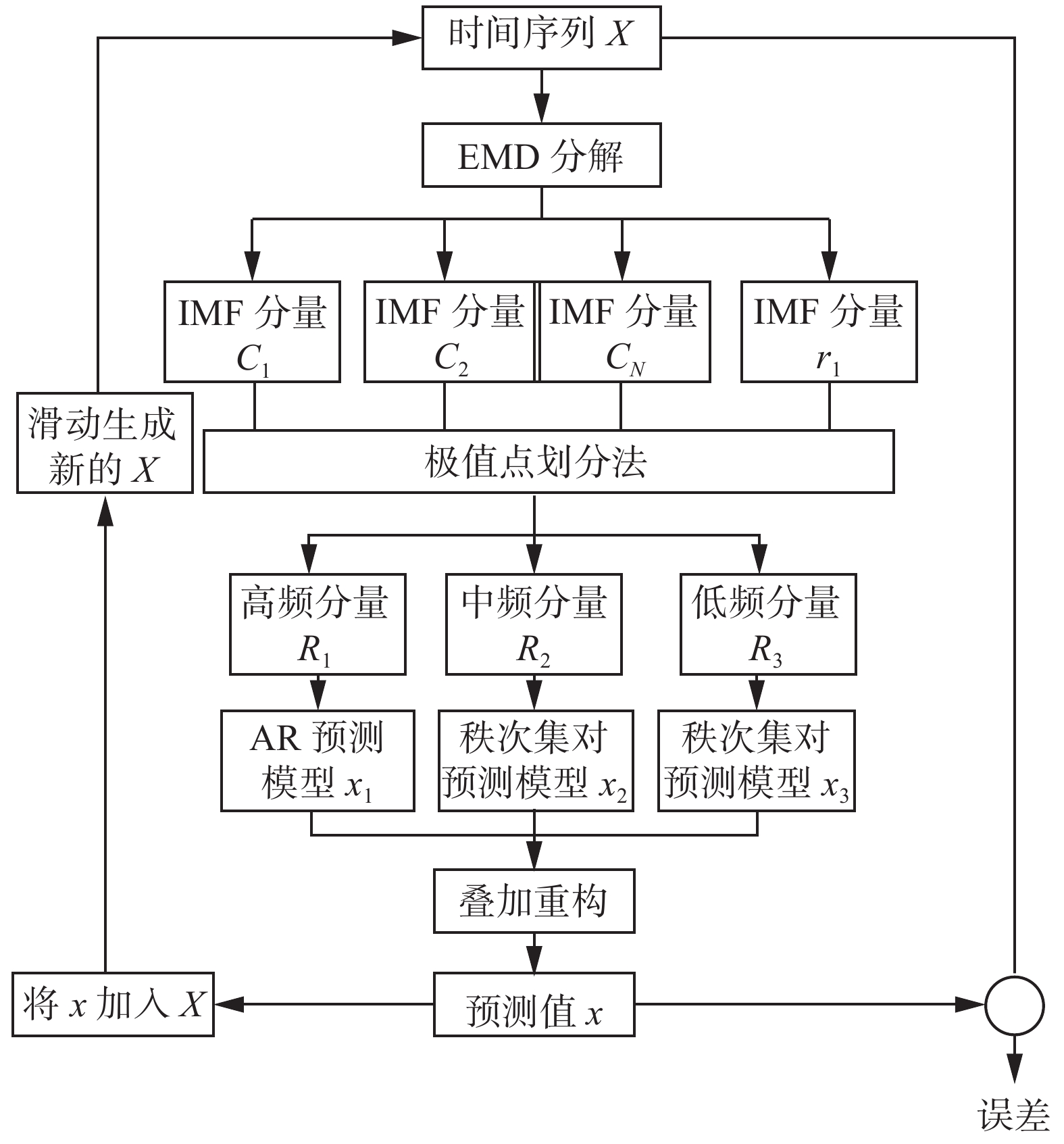
例29　风电功率时间序列的随机性和波动性使得风电功率多步预测难以达到理想的预测准确度，杨茂等^[35]提出一种基于经验模态分解(EMD)集对分析的风电功率实时预测模型。1)将风电功率时间序列经EMD分解，处理成有限个相对平稳的分量；2)利用极值点划分法，按波动程度相近的原则将分量重构为高频、中频和低频3个分量，再对3个分量各自的特点建立预测模型；3)把3个分量的预测结果叠加作为原始风电功率的预测值，并用滚动的方式实现多步预测。采用3个不同装机容量的风电场的实测风电功率数据进行仿真，结果表明该方法提高了多步预测的准确度，显示出了良好的预测性能，算法结构见图3。

图  3  滚动式多步预测算法结构

Fig.  3  Structure diagram of rolling multistep prediction algorithm

下载: 全尺寸图片

注意：本例中采用滚动方式实现多步预测的做法，本质上与例1在每次预报前对预测模型用因子组合进行调整的做法异曲同工，能有效地提高多步预测的准确度，例30也同此。

例30　杨茂等^[36]在传统ARIMA算法的基础上，引入集对分析理论对风电功率进行超短期区间滚动预测。首先采用改进的K-means算法，建立风电功率与风速、风向之间的集对关系；在点预测结果的基础上，估计区间上下限,经过误差调整，最后得到区间预测结果。算例表明，所提出的基于集对分析聚类算法的超短期风电功率区间预测能够得到更精确的预测区间。

例31　白静芬等^[37]针对电能量值传递过程中精度需求，提出基于标准电能表组的量值传递方法，在此基础上提出基于集对分析预测的电能量值校准方法，利用集对分析预测算法获得的预测值对标准电能表组的测量值进行修正，从而获得更为准确的电能量值。采用3个标准电能表1年的测量数据进行验证。结果表明：基于集对分析预测的电能量值校准方法能够有效提高电能测量精度。

4.2   集对分析在电力负荷预测中的应用

例32　彭明鸿等^[38]提出一种中长期电力负荷预测的集对分析聚类算法。该方法采用集对分析中的同异反模式进行模式识别，并根据聚类分析的基本思想进行分类预测。最后采用福建省年用电量数据进行了实例验证，结果表明该预测方法有效。

例33　赵高飞^[39]以某市为例，收集整理了2004—2014年用电量及其影响因素的数据，应用集对分析方法对用电量进行预测，并与实际值比对。结果表明该方法应用于用电量预测计算简单，思路清晰，精度较高。

例34　杨茂等^[40]把秩次集对分析应用到风电功率时间序列实时预测。

例35　叶郑庚^[41]用联系数预测电动汽车的充电负荷，为电网安全运行与优化调度提供参考。

例36　肖白等^[42]提出一种新的空间负荷预测方法。首先，在电力地理信息系统中，根据待预测区域内各10 kV馈线供电范围生成Ⅰ类元胞，将Ⅰ类元胞的历史负荷数据分别按不同的集合容量生成多个历史数据集合和1个目标数据集合；其次，对各历史数据集合进行秩次变换得到相应的秩次集合，并分别将其与目标数据秩次集合构成集对；然后，寻找与目标数据集合相似的历史数据集合，选取相对误差最小的集合容量对应的预测值作为各Ⅰ类元胞负荷预测值；最后，以等大小网格生成Ⅱ类元胞，根据Ⅰ类元胞负荷预测值结合用地信息求出各Ⅱ类元胞的负荷预测值，从而得到网格化后的空间负荷预测结果。工程实例验证了所提方法的实用性和有效性。

4.3   集对分析在太阳辐照度区间预测中的应用

例37　罗明武等^[43]提出一种基于集对分析的太阳辐照度区间预测方法。经过数据预处理后，分别建立相似日辐照度与主因素集对和相似日主因素与待预测日主集对，计算相似日主因素与待预测日主因素的同异反距离模型并进行计算，实例表明所提方法有效。

5.   集对分析在地质灾害预测中的应用

5.1   集对分析在岩爆预测中的应用

例38　陈红江等^[44]基于SPAT选取影响岩爆的主要因素最大切向应力 $ \sigma \theta $ 、单轴抗压强度 $ \sigma c $ 、单轴抗拉强度 $ \sigma t $ 、弹性能量指数Wst和岩石的脆性指数Is，并把 $ \sigma \theta /\sigma c $ 、 $ \sigma c/\sigma t $ 、Wet和Is作为岩爆预测的主控因子，建立了岩爆预测的集对分析模型，对各个工程岩爆烈度级别进行预测。结合国内外一些典型深埋长大隧道工程实例进行分析计算，通过实际预测分析对比表明，集对分析模型简便易行，评价结果准确，在隧道岩爆烈度级别的评判中具有广泛的实用价值。

例39　汪明武等^[45]应用SPAT建立了基于接近度概念的模糊差异度系数的改进计算模型，实例及同其他方法的对比应用表明：该模型预测岩爆有效可行，结果较好。

例40　汪明武等^[46]建立了岩爆烈度的联系数–证据预测模型，该模型基于联系数定量表达评价指标，通过联系云构建评价矩阵，用D-S证据理论得到基本概率赋值，基于距离函数组合权重与融合均值证据预测样本的岩爆等级。实例表明模型有效可行。

例41　Wang等^[47]把集对分析与云模型结合给出了一种不同等级岩爆的预测模型。

例42　赵浩杨等^[48]基于组合赋权SPA，建立岩爆倾向性预测模型。首先从岩性、应力、围岩3个方面确立预测指标，其次利用组合数有序加权平均算子赋权法（combination weighting averaging, C-OWA）、关联准则重要性赋权法（criteria importance though intercrieria correlation, CRITIC）、博弈论分别计算出主观权重、客观权重、组合权重；最后用集对分析理论中的四元联系度预测出岩爆等级。将该模型应用于西藏甲玛铜多金属矿等工程的岩爆倾向性预测中，得出该矿的综合联系度为u₁=−0.302 9，为弱岩爆，与实际相符。

5.2   集对分析在滑坡变形预测中的应用

例43　刘晓等^[49]把集对分析理论(SPAT)与模糊马尔可夫(fuzzy-Markov)理论结合，对滑坡SPA模型中的不确定系数进行二次预测，结果表明：复合模型能够进一步提高整体预测精度，在岩土监测分析领域中具有良好的实用价值。

例44　桂蕾等^[50]把集对分析法引用到滑坡空间预测，以MAPGIS为操作平台，在对巴东县新城区滑坡灾害发育的地质背景、分布规律和发育特征进行统计分析的基础上，根据统计结果确定预测危险性等级评价标准，然后根据各预测单元的属性信息判别各预测单元指标等级，最后利用集对分析理论对各预测单元进行危险性等级预测。将所得空间预测图与已知滑坡分布图进行比较，结果可靠、方法可行，得出联系度和集对势理论结合能够提高预测精度的结论。

例45　彭丽娟等^[51]把基于集对分析理论的预报模型用于湖北恩施地区的滑坡灾害易发性预测，并对预测结果进行分析，高易发区占总面积的15.89%，中易发区占12.96%，低易发区和不易区分别占45.15%和26%。滑坡易发因素组合主要是地层岩性(志留系和三叠系巴东组)和坡度(10°~30°)，与该区的实际情况较符合。

5.3   集对分析在岩溶塌陷和泥石流预测中的应用

例46　段先前等^[52]，选择岩性、岩溶发育程度、地形地貌、地质构造、土层厚度、土层岩性、地下水位距基岩面距离、地下水位变幅、地下水径流强度、地表水入渗、人工抽水强度和其他人类工程活动12个指标为岩溶塌陷主要影响因素，并将塌陷危险性划分为5个等级，用定量或定性的方法对指标进行赋值，构建其分级标准。运用集对分析方法，将影响因素实测值分别与5个危险性等级评价标准组成集对，计算其联系度，最后根据联系数的排序结果，判定岩溶塌陷危险性等级。利用该方法对贵州定扒地区岩溶塌陷危险性进行预测，结果表明，该模型评价结果与实际情况相符。

例47　任玉鹏等^[53]以白龙江流域21条典型泥石流沟为研究对象，将用集对分析法得出的评价结果作为泥石流当前活动性状态，与定量方法——地貌信息熵理论得出的评价结果进行比对，定性、定量相结合动态预测未来泥石流的活动趋势。

6.   集对分析在社会经济预测中的应用

6.1   集对分析在我国城镇居民消费预测中的应用

例48　郑丕谔等^[54]于2001年基于集对分析方法和近20年来的居民消费数据，建立了我国城镇居民的消费增量预测模型。通过和常规回归方法相比较，阐明了集对分析方法在研究居民消费增量的等级变化问题方面的优点。

6.2   集对分析在邮电业务量预测中的应用

例49　高洁等^[55]于2002年提出一种基于集对分析的聚类预测法。该方法融合了集对分析中的同异反模式识别的“择近原则”和聚类分析的基本思想进行分类预测。将该方法应用于我国邮电业务总量预测的研究，与其他预测方法比较，结果表明该预测方法有效。

6.3   集对分析在区域综合承载力预测中的应用

例50　魏超^[56]以集对分析理论为基础，根据空间集合欧式距离理论，构建区域承载力集对预测模型(SPA-RCC)。将八市1996—2013年区域承载力研究数据分为实验数据和检验数据，实验数据用于预测模型构建，检验数据用于模型的精确度分析。结果表明，基于集对分析的区域承载力预测模型的误差率处于−8.63%~−7.19%，精确度高于非线性预测模型，可用来预测区域承载力的变化。

例51　Wei等^[57]利用集对分析模型对跨国公司的成长趋势进行预测，建立了跨国公司的动态预测模型。该模型在长江8个沿海城市的案例中进行了测试，模型的平均误差率仅为0.38%，最低误差率为0.01%。

6.4   人力资源预测

例52　孙晋众等^[58]建立基于马尔可夫链的集对分析的动态模型，并将其应用于人力资源动态绩效的评价与预测，取得很好的效果。孙晋众等^[59]2009年还提出一种基于模糊集值统计的集对预测方法。

6.5   社会风险预测

例53　常志朋等^[60]基于高阶Markov链理论、变权方法和集对分析方法，构建重大决策社会风险预测模型。首先将重大决策前后的社会风险指标状态集组成集对；再利用指标变权计算不同时刻的集对联系度和状态转移概率矩阵，以克服传统常权无法反映指标值次序重要性的问题；最后，利用更接近客观实际的高阶Markov链预测集对联系度，进行社会风险态势分析，以某市PX项目决策为例进行方法验证和比较，结果表明所构建模型与传统模型相比，可以更有效、更准确地对重大决策社会风险进行预测 。

例54　亢永等^[61]提出集状态评价和预测分析于一体的城市埋地燃气系统动态危险性评价预测方法。该方法利用SPA的多元联系数对系统的危险等级进行划分，运用马尔可夫链的遍历性，并将结果与集对势相结合，预测城市埋地燃气管道系统最终的危险水平。

7.   集对分析在环境预测中的应用

7.1   城市空气污染预报

例55　城市空气质量与一定范围内污染源的分布和排放有关，与大气运动对空气中污染物的稀释、扩散、清除和聚集的强度有关。前者可用当地环境监测站的实测空气质量记录来反映，并认为污染源在短期内有相对稳定性，而空气污染预报主要从天气过程与污染物的关系出发进行研究。诸晓明等^[62]把集对分析用于城市空气污染预报研究，预报结果较为满意。他们认为：“在城市空气污染预报模型中，精心挑选的因子具有较好的预报性能，但是因子的优良性能并非始终不变，而有时个别因子的不良表现往往可能导致预报的失败。 根据集对分析(SPA)把不确定性和确定性作为一个动态的同异反系统处理的思想，动态地分析和处理每次预报中因子作用的变化，即每次预报前, 先对因子进行态势判别和同异反分析，让可能干扰预报的弱势因子的作用受到有效抑制，让有助于预报的强势因子的作用得到充分发挥，从而实现因子作用大小在各次预报中的动态变化，因而能得到较为满意的效果。”具体操作步骤与本文1.1节的例1中所述相同。这个例子也再一次说明了在传统的多元回归预报模型中增加基于集对分析的预报因子不确定性的动态处理有助于提高预报准确率。

7.2   降水酸度及水质预报

例56　徐源蔚等^[63]建立了基于集对分析的降水酸度及水质相似预测模型(SFM-SPA)，并运用该模型进行了降水酸度及水质预测的实例验证。结果表明，在限定条件下，利用模型进行环境预测可行，且直观和计算简便。

7.3   城市生态系统预测

例57　自然生态环境是城市社会经济健康发展的重要物质基础，生态足迹作为生态环境承载状态测度的指标，受到社会、经济、人口等多种因素影响，具有时空动态性和不确定性等特征。李湘梅等^[64]在对1988—2004年武汉市生态足迹及其社会经济影响因子时间序列分析的基础上，构建集对分析动态模型：1)建立分类模式系统与参照系统的集对及其联系度；2)利用历史数据样本检验联系度；3)计算模拟系统的预测值；调试满意后，对武汉市2005—2020年总生态足迹发展趋势进行了预测；结果表明，2005—2020年总生态足迹将由1810.925万hm²增长到2873.857万hm²，呈现出低于GDP和生态效率增长速率的趋势，生态环境将进一步恶化，据此就武汉市生态系统的发展提出对策与建议。

例58　周敬宣等^[65]以武汉市为研究对象，将城市总生态足迹与其相关影响因子联系起来考虑，融合集对分析中的同异反模式识别的“择近原则”和聚类分析思想构造集对分析动态模型，利用模型对武汉市2005—2020年总生态足迹发展趋势进行了预测，误差均小于0.3%。

例59　吴开亚等^[66]建立了用集对分析聚类预测方法进行区域生态足迹动态预测的(SPA-CP)具体实施方案。应用结果表明，这套建模方案的物理概念清晰，计算简便，精度较高，通用性较强，在不同区域生态足迹动态预测中有应用价值。

8.   集对分析在民航–铁路–公路运输预测中的应用

8.1   集对分析在民航风险预测中的应用

例60　刘玲莉等^[67]以集对分析中的同异反模式识别的“择近原则”和聚类分析理论为基础，利用相关性分析得出与民航运输事故征候量变化高度相关的因素，并利用事故征候量与其影响因素的历史数据，建立了民航运输事故征候集对分析聚类预测模型，通过对我国2011年民航运输事故征候量的预测，结果表明民航运输事故征候的集对分析聚类预测模型的精度要高于其他预测模型(表2)，并且所需样本少、运算简便，具有较高的实用价值。

例61　高扬等^[68]利用QAR数据作为支撑，结合集对分析和马尔可夫理论建立飞行安全态势评估模型。该模型以QAR超限事件为评估指标，采用集对分析中的联系度来描述安全风险等级；运用马尔可夫理论确定安全状态的转移概率矩阵，以预测飞行安全动态变化趋势。以某公司A320机队6个月发生频率最高的7类超限事件对模型进行验证。结果表明：该公司2月、6月和预测月份的安全状态为一般风险，其他月份为低风险；总体安全状态也为一般风险，并有增加趋势。

例62　张一瑫等^[69]把集对分析(SPA)理论和马尔可夫链(MC)结合，预测航空维修安全动态变化趋势。以某航空兵机务大队为例作了验证。

8.2   集对分析在铁路集装箱运量预测中的应用

例63　朱昌锋等^[70]提出了一种基于集对聚类预测和神经网络模型组合的铁路集装箱运量预测方法，该方法将集对聚类预测模型的预测值作为输入，相应的实际集装箱货运量作为输出，建立了神经网络模型结构，并提出了相应的算法，最后以实例分析了该模型的可行性和科学性。

8.3   集对分析在路基沉降预测中的应用

例64　Li等^[71]提出了一种基于改进集对分析的组合预测模型。该模型首先构造集对来表示预测值与实测值之间的关系。然后基于贝叶斯决策理论对集对关系辨识的风险进行表示，并利用自适应搜索算法得到集对关系的最优判据。然后分析预测模型与实测数据之间的关系，最后进行了单一预测模型的组合。通过案例分析和与其他方法的比较，验证了模型的可靠性和有效性。

例65　蒋红妍等^[72]在2008年基于对路面性能的分析，把集对聚类预测用于路面性能预测，实例验证了这种新方法的可操作性和良好效果。

9.   集对分析在矿山安全预测中的应用

例66　尹君等^[73]从尾矿库安全管理的决策需求出发，通过对尾矿库危险源进行分析，建立了尾矿库安全评价预测指标体系，详细探讨了差异度和集对势在尾矿库安全评价和预测中的应用。

例67　念其锋等^[74]构建了煤与瓦斯突出区域的联系熵预测方法。通过应用实例预测，计算结果与实际情况相吻合，对煤矿实现煤与瓦斯突出区域预测具有一定指导意义 。

例68　侯公羽等^[75]对煤矿长斜井盾构机(tunnel boring machine,TBM)施工的风险因素进行了识别，根据改进的集对势理论给出风险趋势的预测方法。利用该模型对台格庙矿区煤矿长斜井(1#、2#实验井)TBM施工风险进行了评估与趋势预测。

例69　谭翀等^[76]把集对分析用于武汉地区某露天采石场的安全状况评价和预测，结果表明，该方法计算简单，评价结果较可靠。

10.   集对分析在其他预测中的应用

例70　谢力等^[77]把集对分析用于舰船装备维修费单项预测。

例71　金英伟等^[78]把集对分析用于技术创新产品购买意愿的分析及预测。

例72　Lin Bu等^[79]提出了一种基于集对分析(SPA)和隧道地震预测(TSP)相结合的围岩分类预测方法。

例73　袁宏俊等^[80]利用区间数和二元联系数的相互转化关系,把区间数组合预测问题转换成二元联系数组合预测问题。在联系数贴近度的最优准则下，建立基于联系数贴近度的区间型组合预测模型，并对某省社会保障水平适度区间值进行预测，结果显示所建立的模型能有效提高预测的精度。

例74　上海中医药大学李斌教授团队蒯仂等^[81]把集对分析与马尔可夫链结合，用于中医药治疗糖尿病致皮肤溃疡有效性预测。

例75　作者与赵森烽还探讨了赵森烽–克勤概率在系统预测中的应用^[82-83]。

11.   讨论

1）由本文提到的75个应用实例看出，基于集对分析的系统智能预测已应用于“天”“地”“生”“人”“社”“经”不同领域的不同场景。预测结果总体上较为满意，究其原因，是上述文献的作者在有关系统预测问题的研究中灵活地应用集对分析的思想（把对事物的确定性联系（关系，信息）与不确定性联系（关系，信息）作为一个对立统一体研究的思想）、理论（基于集对分析的不确定性系统理论和同异反系统理论^[84-85]）、方法（把人们对事物的确定性联系（关系，信息）与不确定性的联系（关系，信息）的辩证认识转换成一个具体的系统数学模型——集对及其联系数，充分利用联系数的确定–不确定结构可以在不确定性分析基础上动态优化的功能进行系统的结构化动态预测建模，由此去发展和完善多元回归模型、相似预测模型、马尔可夫理论、经验模态分解等传统的预测模型和预测理论，从而使得基于集对分析的系统智能预测不仅适用性强，而且有较好的预测精度。

2）在75个应用实例中，最为突出的工作是例1中王国强的工作。据王国强介绍，他是1995年听过本文作者关于集对分析的一次学术报告后开始把集对分析试用于天气降水预报多元回归算法研究，取得确实成果并经反复验证后在中国气象局1998年5月长沙召开的重特大灾害性天气预报会商会上报告集对分析在优化传统多元回归预测算法中的作用，受到国家气象局等到会专家高度评价；这里简称其为“王方法”。从人工智能的角度看,“王方法”具有智能预测的特点：①在众多影响天气降水的气象因子中寻求“最优因子集合”；②每次预报前对“最优因子集合”中的每个因子做“相对确定的强势（指示事件W出现）”“相对不确定的弱势（干扰强势因子指示事件W出现）”的动态分析，实现“最优因子”的“最佳组合”，从而客观地刻画出影响天气降水气象因子的同异反关系结构；③对同异反关系结构的历史数据经统计处理后作同异反联系数表达和不确定性分析；④把经前3步处理后的数据进入预报模型做回顾性预报，以检验前3步工作的预报精度，精度不满意时需要调整前述的最优气象因子选择与强势弱势因子的判定，调整同异反的划界标准和不确定系数的分解比例，最终使模型的回顾性预报值与历史数据最大程度拟合，从而保证模型的当前预报精度。

3）从信息能的角度看，“王方法”的实质是把天气系统看作是含有能量的系统，因为天气系统是一个有自组织\自演化的非线性动力学系统，其中的能量来自多个方面，但气象工作者只是接收到天气系统所提供的信息，并要借助一定的数学模型处理这些信息去推导天气系统的未来行为，这个推导的过程就是把天气系统所具有的信息能转换成智能的过程；借助模型，保持天气系统中的信息能与人脑智能在能量意义上同构，是提高预测模型智能化，保证预报精度的基本要求。

4）本文把包括“王方法”在内的集对分析系统预测统称为一种智能预测，因为：①集对分析与一些成熟的统计预测模型具有良好的亲和性、耦合性和互补性，如例1、2、3、21、48、54，通过集对分析预处理进入多元回归预测模型的数据提高预报精度；如例12、19、43、51、52、58、59、73，则主要是把集对分析与马尔可夫链结合进行预测；②集对分析与相似预测结合，如例5、14、16、18、22、24、27，与聚类法结合有例20、22、30、32、49、57、60、62、68；与BP神经网络结合的如例8；③集对的概念与联系数及其伴随函数具有丰富的系统结构信息，目前已经知道联系数是一个大家族，如多元联系数(二元联系数、三元联系数、四元联系数、五元联系数···无穷多元联系数），多维联系数（二维联系数、三维联系数、四维联系数、五维联系数···无穷多维联系数），多重联系数（二重联系数、三重联系数、四重联系数、五重联系数···无穷多重联系数），多次联系数（二次联系数、三次联系数、四次联系数、五次联系数···无穷多次联系数，以及多元多维多重多次联系数，还有联系数的各种伴随函数，如偏联系数、邻联系数、复联系数、势函数、态势函数，等，这些联系数及其伴随函数可以根据不同的系统预测问题和不同的预测场景单一选用或组合选用，或直接用于预测建模，或用于已有预测模型的改进和优化，或利用联系数的某些系统结构信息开展系统预测，这方面有例4、6、13、15、23、26、28、31、33、34、35、36、38、38、39、40、44、45、46、47、50、53、56、61、63、64、65、66、68、69、70、71、72等30多个实例。需要指出的是，这些实例中用到的联系数及其算法可以借助一定的算法相互转换，如三元联系数 $\mu = 0.5 + $ $ 0.3i + 0.2j$ ，既可以“压缩”成二元联系数 ${\mu}' = 0.5 + 0.5i$ ，也可以扩展成四元联系数 $\mu ''=0.5+0.2i_{1}+ 0.1i_{2}+ 0.2$ 或五元联系数 $\mu'''=0.5+ $ $ 0.15i_{1}+ 0.1i_{2}+0.05i_{3}+ 0.2j$ ，或者把 $ 0.2j $ 也分成两部分得六元联系数 $\mu''''=0.5+0.15i_{1}+0.1i_{2}+0.05i_{3}+ $ $ 0.15j_{1}+ 0.05j_{2}$ 等，从而灵活地获得被预测对象更多的系统结构信息和不确定性信息。

5）不同领域不同场景应用集对分析进行系统预测的具体思路可以不同，但基本步骤可以归纳成：①构造集对并分析集对中两个集合的全部关系，包括确定的关系和不确定的关系，根据关系的结构选用合适的联系数作为集对的特征函数；②建立基于联系数的预测模型，包括利用联系数改进和完善已有的预测模型； ③利用模型的计算和围绕模型的不确定性分析做出预测或预报，包括回顾性预测和当前场景下的实时预测，其中围绕模型的不确定性分析是关键，这里说的不确定性包括了一般情况下的随机性、模糊性、突发性、不确知性，也包括了反常性和极端性以及模型本身的不完备性和适用性等。概言之，就是“以确定的数学建模计算应对被测系统的确定性规律，以围绕预测模型的不确定分析应对被测系统的不确定性，从而实现对不确定性系统的智能预测”，这里的归纳也是本文的主要创新点。

6）预测是决策的基础，但限于本文主题，对此不展开说明，有意者可参见文献[86-87]；预测也是控制的基础，待另文综述，敬请读者谅解。

12.   结束语

事物是确定性与不确定性的统一体，系统是事物的存在方式。系统的未来与系统的过去和现在既有确定的对应规律，也有不确定性关系；智能预测应当在充分计及系统不确定性的基础上做出与实际情况相吻合的预测；对此，基于集对分析的“以确定的数学建模计算应对系统确定的对应规律，以围绕预测模型的不确定分析应对系统的不确定关系”这种具有辩证思维特征的新颖预测思路为我们提供了一条有效的智能预测途径；但是，客观世界中的各种系统预测问题纷繁复杂，基于集对分析的智能预测仍有许多问题要深入系统研究。期待更多专家学者创造性地应用集对分析于各种系统的智能预测研究。