Nonnegative low-rank matrix factorization with adaptive graph neighbors
-
摘要: 图正则化(nonnegative matrix factorization, NMF)算法(graph regularization nonnegative matrix factorization, GNMF)仍存在一些不足之处:GNMF算法并没有考虑数据的低秩结构;在GNMF算法中,其拉普拉斯图是使用K近邻(K nearest neighbor,KNN)方法预先定义的,而KNN方法无法总是获得最优图解,从而使得GNMF算法的性能不能达到最优。为此,本文提出了一种自适应图正则化的非负矩阵分解算法(nonnegative low-rank matrix factorization with adaptive graph neighbors,NLMFAN)。一方面,通过引入低秩约束,使得NLMFAN可以获得原始数据集的有效低秩结构;另一方面,设计了一种通过自适应求解相似度矩阵的方法来进行图的构建,即图的构造和矩阵分解的结果被融入一个整体的框架中,使得图中节点的相似性是自动从数据中学习得到的。此外,本文还给出了一种求解NLMFAN的有效算法。在多种数据集上的实验验证了本文所提出的算法的有效性。Abstract: The exsting graph regularization nonnegative matrix factorization (GNMF) method still has some shortcomings: The GNMF algorithm does not consider the low-rank structure of data. In the GNMF algorithm, the Laplacian graph uses the K-nearest neighbor (KNN) method, and the KNN method cannot always obtain the optimal diagram, which makes the performance of the GNMF algorithm not optimal. For this reason, we propose an algorithm called nonnegative low-rank matrix factorization with adaptive graph neighbors (NLMFAN). On the one hand, by introducing low-rank constraints, NLMFAN can obtain the effective low-rank structure of the original dataset. On the other hand, a method for adaptively solving the similarity matrix is designed to construct the graph. This implies that the structure of the graph and the results of the matrix decomposition are integrated into an integrated framework so that the similarity of the nodes in the graph is automatically learned from the data. In addition, an effective algorithm for solving NLMFAN is given, and experiments on a variety of datasets verify the effectiveness of the algorithm.
-
聚类是计算机视觉中一项受到广泛关注且充满挑战的任务。近些年来,图聚类因为相较于其他方法表现出了更好的性能而被广泛应用于图像分类、图像检索等方面[1-2]。在信息检索、计算机视觉和模式识别的许多问题中,由于样本数据的维数很高,使得从样本直接学习并聚类的的方法是往往不可行的[3]。因此,人们希望找到两个或多个低维矩阵,使它们的乘积可以很好地近似于原始矩阵,越来越多的矩阵分解技术如LU分解、QR分解、矢量量化和奇异值分解(singular value decomposition, SVD)、非负矩阵分解(non-negative matrix factorization, NMF)等由此被提出[4-6]。在面部识别和文档聚类任务中,NMF已被证明优于SVD等其他矩阵分解技术[7]。NMF的目的是找到两个非负矩阵,它们的乘积可以很好地近似原始矩阵。由于NMF更新规则仅允许加法运算,矩阵分解的非负约束使得学习到的成分矩阵成为基于局部的表示,且是学习对象各部分的最佳选择。为了提高NMF的性能,学界已提出了许多NMF的拓展算法,例如L2.1范数非负矩阵分解[8]、结构不相干的低秩矩阵分解[9]等。
近年来,有些研究者提出了基于流形学习的算法,例如局部线性嵌入[10]、拉普拉斯特征图[11]等,这些研究表明,高维数据其本质分布于低维子空间。研究人员发现,在NMF算法中引入流形学习方法获得数据的流形结构,有助于提升NMF的性能[12]。Cai等[13-14]在NMF的基础上结合流形学习技术提出了图非负矩阵分解算法(graph nonnegative matrix factorization, GNMF)。Zhou等在GNMF的基础上为NMF添加了额外的约束[15],进一步提出了局部学习正则化NMF(local learning regularized NMF,LLNMF)[16]。Li等[17]提出图正则化非负矩阵分解(graph nonnegative low-rank matrix factorization, GNLMF),该方法使得图正则化时可以获得原始图像数据的低秩结构。Du等[18] 提出图嵌入正则化投影非负矩阵分解方法(graph embedding regularized projection nonnegative matrix factorization for face image feature extraction,GEPNMF),通过引入图嵌入正则化项,学习的子空间可以保留数据的局部几何结构,同时提升了算法判别力。Yin 等[19]提出一种拉普拉斯正则化低秩表示及其应用算法(Laplacian regularized low-rank representation and its applications,LLRR),该算法通过对图形的正则化,既能表示数据的全局低维结构,又能捕获数据中固有的非线性几何信息。Wang 等[20]提出一种降维局部约束图优化算法(locality constrained graph optimization for dimensionality reduction,LC-GODR),该算法将图优化和投影矩阵学习结合到了一个框架中。由于图不是预先构造并保持不变的,使得其在降维过程中的图形可以自适应更新。Meng 等[21]提出的具有稀疏和正交约束的对偶图正则化非负矩阵分解(dual-graph regularized non-negative matrix factorization with sparse and orthogonal constraints, SODNMF),此方法能同时考虑数据空间和特征空间的流形结构。受到Nie等[22]的启发,Huang等[23]提出了局部自适应结构的正则化非负矩阵分解算法(regularized nonnegative matrix factorization with adaptive local structure learning, NMFAN)。NMFAN算法使用自适应学习的方法来利用数据局部结构中流形信息,但是,NMFAN算法并没有利用数据的有效低秩结构信息。
以上这些算法通过构建拉普拉斯图来利用数据的局部流形结构信息,其所使用的图的极大地影响着算法的性能。研究人员往往利用K近邻(K nearest neighbor,KNN)来构建图。然而,一方面,KNN方法构造的图有可能会破坏部分原始数据的局部连通性;另一方面,其图的构造与矩阵分解的结果无关,从而使得相关算法的性能不能达到最优。此外,这些算法往往没有考虑数据的低秩结构,而数据的有效信息往往隐藏在其低秩结构中。为此,本文提出了一种自适应图正则化的非负矩阵分解算法(nonnegative low-rank matrix factorization with adaptive graph neighbors,NLMFAN)。一方面,NLMFAN通过引入低秩约束来获得原始数据集的潜藏的有效信息,以此提升现有算法性能;另一方面,NLMFAN将图的构造和矩阵分解的结果融入一个整体的框架中,自动从数据中学习得到图中节点的相似性,优化了算法精度。文中同时给出了一种求解NLMFAN的有效算法,并在多种数据集上进行了实验验证本文所提出的算法的有效性。
1. 相关工作
1.1 非负矩阵分解(NMF)
NMF是一种广泛使用的矩阵分解算法。它试图将一个非负矩阵分解为两个阶乘矩阵,其乘积是其自身的最佳近似值。给定一个数据矩阵
${\boldsymbol{ X}} = \left[ {{{\boldsymbol{x}}_1}\;{{\boldsymbol{x}}_2}\; \cdots \;{{\boldsymbol{x}}_n}} \right] \in {{\bf{R}}^{M \times N}}$ 的每一列都是样本矢量,NMF的目的是找到两个非负矩阵${\boldsymbol{U}} = \left[ {{{\boldsymbol{u}}_{ik}}} \right] \in {{\bf{R}}^{M \times K}}$ 和${\boldsymbol{V}} = \left[ {{{\boldsymbol{v}}_{ik}}} \right] \in {{\bf{R}}^{N \times K}}$ ,使得它们的乘积可以很好地近似于原始矩阵X:$$ {\boldsymbol{X}} \approx {\boldsymbol{UV}}^{\rm{T}} $$ (1) 即标准NMF的目标是搜索两个非负矩阵U和V以优化以下目标
$$ \left\{ \begin{array}{l} \mathop {\min }\limits_{{\boldsymbol{U}},{\boldsymbol{V}}} \left\| {{\boldsymbol{X - UV}}\left. {^{\rm{T}}} \right\|_{\rm{F}}^2} \right.\\ {\rm{s.t.}}\quad{\boldsymbol{U}} \geqslant 0,{\boldsymbol{V}} \geqslant 0 \end{array} \right.$$ (2) 其中||·||F表示矩阵的F范数,同时其存在以下更新规则的表示形式:
$$ {u_{ij}} \leftarrow {u_{ij}}\frac{{{{\left( {{\boldsymbol{UV}}} \right)}_{ij}}}}{{{{\left( {{{\boldsymbol{UV}}^{\rm{T}}}{\boldsymbol{V}}} \right)}_{ij}}}},{v_{ij}} \leftarrow {v_{ij}}\frac{{{{\left( {{{\boldsymbol{X}}^{\rm{T}}}{\boldsymbol{U}}} \right)}_{ij}}}}{{{{\left( {{{\boldsymbol{VU}}^{\rm{T}}}{\boldsymbol{U}}} \right)}_{ij}}}} $$ (3) 1.2 图正则化非负矩阵分解(GNMF)
为了能在NMF算法中保留其内在结构的同时探索数据的局部几何结构,近几年将流形学习与NMF相结合的算法研究成为热点。Cai等[13]通过将图正则化项融入到标准NMF算法框架中提出了图正则化非负矩阵分解(GNMF),其目标函数如下:
$$ \left\{ \begin{array}{l} \mathop {\min }\limits_{{\boldsymbol{U}},{\boldsymbol{V}}} \dfrac{1}{2}\left\| {\left. {{\boldsymbol{X - UV}}} \right\|_{\rm{F}}^2} \right. + \lambda \cdot {\rm{tr}}\left( {{{\boldsymbol{VL}}_{{\rm{ap}}}}{{\boldsymbol{V}}^{\rm{T}}}} \right)\\ {\rm{s.t.}}\quad{\boldsymbol{U}},{\boldsymbol{V}}\geqslant 0 \end{array} \right.$$ (4) 式中:
${\rm{tr}}\left( {{{\boldsymbol{VL}}_{{\rm{ap}}}}{{\boldsymbol{V}}^{\rm{T}}}} \right)$ 是图正则项;Lap是图拉普拉斯矩阵,$\lambda < 0$ 是图正则化参数。文献[13]中给出了GNMF算法的更新规则:$$\left\{\begin{aligned} &{u_{il}} \leftarrow {u_{il}}\frac{{\left( {{{\boldsymbol{XV}}^{\rm{T}}}} \right)}}{{\left( {{{\boldsymbol{UVV}}^{\rm{T}}}} \right)}}\\ &{v_{ij}} \leftarrow {v_{ij}}\frac{{{{\left( {{{\boldsymbol{U}}^{\rm{T}}}{\boldsymbol{X}} + \lambda {{\boldsymbol{VS}}_{\rm{ap}}}} \right)}_{lj}}}}{{{{\left( {{{\boldsymbol{U}}^{\rm{T}}}{\boldsymbol{UV}} + \lambda {\boldsymbol{VD}}} \right)}_{lj}}}}\end{aligned}\right.$$ (5) 其中,Dap是对角矩阵,
${{\boldsymbol{L}}_{{\rm{ap}}}}= {{\boldsymbol{D}}_{{\rm{ap}}}} - {{\boldsymbol{S}}_{\rm{ap}}}$ 。2. 自适应低秩非负矩阵分解算法
研究表明,原始图像数据通常嵌入位于高维欧式空间中的非线性低维流形上,且其有效信息通常隐藏在低秩结构中。另外,在图正则化相关算法中所使用的图一般是预先定义的,其图的构造与算法的其他部分往往互相独立。因此,这些算法使用的图并不一定是最优的。为此,在本小节提出一种自适应图正则化的非负矩阵分解算法NLMFAN,该算法同时兼顾了原始图像数据的有效低秩结构和自适应图构造。
2.1 NLMFAN的算法模型
设输入的原始数据集为X,先给出本文NLMFAN算法的求解形式如下:
$$ \left\{ \begin{split} &{\rm{min}} \left\| {\left. {{\boldsymbol{X}} - {\boldsymbol{L}} - {\boldsymbol{E}}} \right\|} \right._F^2 + \alpha \left( {\sum\limits_{j = 1}^n {\left( {\left. {\left\| {\left. {{{\boldsymbol{x}}_i} - {{\boldsymbol{x}}_j}} \right\|_2^2{s_{ij}} + \gamma s_{ij}^2} \right.} \right)} \right.} } \right) + \\ &\quad \lambda \cdot {\rm{tr}}\left( {{{\boldsymbol{V}}^{\rm{T}}}{{\boldsymbol{L}}_S}{\boldsymbol{V}}} \right)\\ &{\rm{s.t.}}{\boldsymbol{L}}={{\boldsymbol{UV}}^{\rm{T}}},{\boldsymbol{L}},{\boldsymbol{U}},{\boldsymbol{V}} \geqslant 0,{\rm{rank}}\left( {\boldsymbol{L}} \right) \leqslant r,{\rm{card}}\left( {\boldsymbol{E}} \right) \leqslant e,\\ &\quad {\boldsymbol{s}}_i^{\rm{T}} {\bf{{1}}}= 1,0 \leqslant {{\boldsymbol{s}}_i} \end{split} \right.$$ (6) 目标函数的第1项为在
${\rm{rank}}({\boldsymbol{L}}) \leqslant r, {\rm{cord}}({\boldsymbol{E}}) \leqslant e$ 条件的约束下通过原始数据集X求其低秩形式L,再对得出的结果使用NMF分解。其中矩阵X为原始数据集,L代表矩阵的低秩部分,E代表其稀疏部分,U、V由L非负矩阵分解得出。r为L的秩范围,e为E设置的稀疏范围,rank(L)表示矩阵L的秩,card(E)表示矩阵E的非零条目数,${\bf{{1}}}$ 表示一个所有元素都为1的列向量。目标函数的第2项为自适应正则项,使用其完成自适应相似矩阵的构造,其中α均为正则化参数。此处我们直接基于数据点间的欧几里得距离构造邻域矩阵,并设距离越小则成为最近邻的可能性越大。原数据集X中的任意一数据点xi,都有所有数据点
$\left\{{\boldsymbol{x}}_{1}, {\boldsymbol{x}}_{2}, \cdots, {\boldsymbol{x}}_{n}\right\}$ 可以作为近邻与xi连接,连接的概率为$ s_{i j} $ 。${\boldsymbol{s}}_{i} \in {\bf{R}}^{n \times 1}$ 表示向量,其第j个元素为${{s}}_{i j}$ 。在此基础上,可以得到相似度矩阵构建的求解函数为$$ \mathop {\min }\limits_{{\boldsymbol{s}}_i^{\rm{T}}{\bf{{1}}} = 1,0 \leqslant {{\boldsymbol{s}}_i} \leqslant 1} \sum\limits_{j = 1}^n {\left\| {\left. {{{\boldsymbol{x}}_i} - {{\boldsymbol{x}}_j}} \right\|_2^2} \right.} {s_{ij}} $$ (7) 上述相似度矩阵求解的问题存在简化的可能,即我们仅基于欧氏距离求解距离最近的点,并设其与
${\boldsymbol{x}}_{i}$ 的连通概率为1,其他的点概率都为0。此时,对于式(7)中所有的数据点xi,除其之外的所有同数据集的点都存在相同的连通概率即$\dfrac{1}{{n}}$ 。此时,式(7)可写作:$$ \min _{{{\boldsymbol{s}}_i^{\rm{T}}} {\bf{{1}}}=1,0 \leqslant {\boldsymbol{s}}_{i} \leqslant 1} \sum_{j=1}^{n} s_{i j}^{2} $$ (8) 结合式(7)和(8)可得目标函数中的第2项,即自适应正则项为
$$ \mathop {\min }\limits_{{\boldsymbol{s}}_i^{\rm{T}}{\bf{{1}}}= 1,0 \leqslant {{\boldsymbol{s}}_i} \leqslant 1} \sum\limits_{j = 1}^n {\left( {\left\| {\left. {{{\boldsymbol{x}}_i} - {{\boldsymbol{x}}_j}} \right\|_2^2{s_{ij}} + \gamma s_{ij}^2} \right.} \right)} $$ (9) 其中γ是正则化参数。通过求解式(9)获得的矩阵
$\boldsymbol{S} \in {\bf{R}}^{n \times n}$ ,可被视为相似度矩阵[22]。当我们假设每个点可以被表示为一个向量$ \boldsymbol{v}_{i} $ 时,则有:$$ \begin{array}{l} \dfrac{1}{2}\displaystyle\sum\limits_{i,j = 1}^n {\left\| {\left. {{{\boldsymbol{v}}_i} - {{\boldsymbol{v}}_j}} \right\|_2^2 = } \right.} \displaystyle\sum\limits_{i,j = 1}^n {{{\boldsymbol{v}}_i}{s_{ij}}{\boldsymbol{v}}_i^{\rm{T}}} - \displaystyle\sum\limits_{i,j = 1}^n {{{\boldsymbol{v}}_i}{s_{ij}}{\boldsymbol{v}}_i^{\rm{T}}}= \\ \quad\quad \displaystyle\sum\limits_{i,j = 1}^n {{{\boldsymbol{v}}_i}{{\left( {{{\boldsymbol{D}}_s}} \right)}_{ij}}{\boldsymbol{v}}_i^{\rm{T}}} - \displaystyle\sum\limits_{i,j = 1}^n {{{\boldsymbol{v}}_i}{s_{ij}}{\boldsymbol{v}}_i^{\rm{T}}} =\\ {\rm{tr}}\left( {{{\boldsymbol{V}}^{\rm{T}}}{{\boldsymbol{D}}_S}{\boldsymbol{V}}} \right) - {\rm{tr}}\left( {{{\boldsymbol{V}}^{\rm{T}}}{{\boldsymbol{W}}_S}{\boldsymbol{V}}} \right)= {\rm{tr}}\left( {{{\boldsymbol{V}}^{\rm{T}}}{{\boldsymbol{L}}_S}{\boldsymbol{V}}} \right) \end{array}$$ (10) 式中:
$ \boldsymbol{L}_{{s}} $ 是$ \boldsymbol{S} $ 的拉普拉斯矩阵,${\boldsymbol{L}}_{S}={\boldsymbol{D}}_{S}-{\boldsymbol{W}}_{S}$ ;${\boldsymbol{D}}_{5} \in {\bf{R}}^{k x h}$ 是$\displaystyle\sum_{j}\left(s_{i j}+s_{ji}\right) / 2$ 的对角阵。目标函数的第3项是局部图拉普拉斯约束函数,用其来衡量数据低维表示的平滑度,其中
$\rm{tr}(\cdot)$ 表示矩阵的秩。2.2 NLMFAN的算法求解
设计了一种有效的更新算法来求解NLMFAN,该算法通过固定其他变量迭代更新一个变量的值来优化目标,此过程重复直到收敛。
2.2.1 固定U、V更新S
观察式(6),不难发现在固定变量U、V的情况下更新S的最小化,式(6)可等价于解决式(11):
$$ \left\{\begin{array}{l} \mathop {\min }\limits_S\displaystyle\sum_{i, j}^{n}\left(\| {\boldsymbol{x}}_{i}-{\boldsymbol{x}}_{j}\|_{2} ^{2} s_{i j}+\gamma s_{ij}^{2}\right)+\beta \cdot {\rm{tr}}\left({\boldsymbol{V}}^{\rm{T}} {\boldsymbol{L}}_{S} {\boldsymbol{V}}\right) \\ \text { s.t. } {\boldsymbol{s}}_{i}^{\rm{T}} {\bf{1}}=1,0 \leqslant {\boldsymbol{s}}_{i} \leqslant 1 \end{array}\right. $$ (11) 其中
$\beta=\dfrac{\lambda}{\alpha}$ 。由式(6)结合式(11)有:$$ \left\{ \begin{array}{l} \mathop {\min }\limits_s \displaystyle\sum\limits_{i,j = 1}^n {\left( {\left\| {\left. {{{\boldsymbol{x}}_i} - {{\boldsymbol{x}}_j}} \right\|} \right._2^2{s_{ij}} + \gamma s_{ij}^2 + \frac{1}{2}\beta \left\| {\left. {{{\boldsymbol{v}}_i} - {{\boldsymbol{v}}_j}} \right\|} \right._2^2{s_{ij}}} \right)} \\ {\rm{s.t.}}\;{\boldsymbol{s}}_i^{\rm{T}}{\bf{1}} =1,0 \leqslant {{\boldsymbol{s}}_i} \leqslant 1 \end{array} \right. $$ (12) 本文可以对每个i解决式(12),此时式(12)可等价于:
$$ \left\{ \begin{array}{l} \mathop {\min }\limits_S \displaystyle\sum\limits_{i,j = 1}^n {\left( {\left\| {\left. {{{\boldsymbol{x}}_i} - {{\boldsymbol{x}}_j}} \right\|} \right._2^2 + \frac{1}{2}\beta \left\| {\left. {{{\boldsymbol{v}}_i} - {{\boldsymbol{v}}_j}} \right\|} \right._2^2{s_{ij}} + \gamma s_{ij}^2} \right)} \\ {\rm{s.t.}}\;{\boldsymbol{s}}_i^{\rm{T}}{\bf{1}}= 1,0 \leqslant {{\boldsymbol{s}}_i} \leqslant 1 \end{array} \right.$$ (13) 令
$d_{i j}^{x}=\| {\boldsymbol{x}}_{i}-{\boldsymbol{x}}_{j}\|_{2} ^{2}$ ,$d_{i j}^{V}=\dfrac{1}{2} \| {\boldsymbol{v}}_{i}-\left.{\boldsymbol{v}}_{j}\right|_{2} ^{2}$ ,且${\boldsymbol{d}}_{i} \in {\bf{R}}^{m \times 1}$ ,第j个元素为$d_{ij}=d_{fj}^{X}+\beta d_{i j}^{V}$ ,将其代入式(13)可得:$$ \mathop {\min }\limits_{{\boldsymbol{s}}_i^{\rm{T}}{{\textit{1}}} = 1,0 \leqslant {{\boldsymbol{s}}_i} \leqslant 1} \left\| {\left. {{{\boldsymbol{s}}_i} + \dfrac{1}{{2\gamma }}{{\boldsymbol{d}}_i}} \right\|} \right._2^2 $$ (14) 设ζ和η≥0为拉格朗日乘子,可以写出式(11)的拉格朗日函数:
$$ R\left({\boldsymbol{s}}_{i}, \eta, {\boldsymbol{\zeta}}_{i}\right)=\frac{1}{2}\left\|{\boldsymbol{s}}_{i}+\frac{1}{2 \gamma_{i}} {\boldsymbol{d}}_{i}^{x}\right\|_{2}^{2}-\eta\left({\boldsymbol{s}}_{i}^{\rm{T}} {\bf{1}}-1\right)-{\boldsymbol{\zeta}}_{i}^{\rm{T}}{\boldsymbol{s}}_{i} $$ (15) 根据KKT条件[23],满足
$s_{ij} \geqslant 0$ ,最优解可以定义为$$ s_{i j}=\left(-\frac{1}{2 \gamma_{i}} d_{i j}^{X}+\eta\right) $$ (16) 其中,
$\left\{d_{i 1}^{X}, d_{i 2}^{X}, \cdots, d_{\text {in }}^{X}\right\}$ 由小到大表示。如果最优si只有k个非零元素,则根据式(16)可知$s_{i k} > 0$ 且$s_{i, k+1}=0$ 。因此,有:$$ \left\{\begin{split} &-\dfrac{1}{2 \gamma_{i}} d_{{ik}}^{X}+\eta>0 \\ &-\dfrac{1}{2 \gamma_{i}} d_{4, k+1}^{X}+\eta \leqslant 0 \end{split}\right. $$ (17) 由式(17)和
${\boldsymbol{s}}_{t}^{\rm{T}}{\bf{1}}=1$ 的约束,有:$$ \sum_{j=1}^{k}\left(-\frac{1}{2 \gamma_{i}} d_{i j}^{X}+\eta\right)=1 \Rightarrow \eta=\frac{1}{k}+\frac{1}{2 k \gamma_{i}} \sum_{j=1}^{k} d_{i j}^{X} $$ (18) 结合式(17)和(18),可以得到:
$$ {\frac{k}{2}} {d_{ik}^{X}}-{\frac{1}{2}} {\sum_{j=1}^{k}} {d_{ij}^{X}}>{\gamma_{i}} \leqslant {\frac{k}{2}} {d_{i, k+1}^{X}}-{\frac{1}{2}} {\sum_{j=1}^{k}} {d_{ij}^{X}} $$ (19) 为了获得具有k个非零值的最优si,可以将γi设置为
$$ \gamma_{i}=\frac{k}{2} d_{i, k+1}^{X}-\frac{1}{2} \sum_{j=1}^{k} d_{i j}^{X} $$ (20) 为了便于计算,可以将整体γ设置为
$\gamma_{1}, \gamma_{2}, \cdots, \gamma_{n}$ 的均值,即$$ \gamma=\frac{1}{n} \sum_{i=1}^{n}\left(\frac{k}{2} d_{i, k+1}^{X}-\frac{1}{2} \sum_{j=1}^{k} d_{i j}^{X}\right) $$ (21) 通过取γi的平均值,所有si的平均非零元素应为k。我们不直接搜索正则化参数γ,而是搜索近邻数k。因为k是一个整数并且其值是有限的(即
$0\leqslant k\leqslant n $ ),所以参数搜索会更加容易。2.2.2 固定S、V更新U
观察式(6),不难发现在固定变量S、V的情况下更新U的最小化,式(6)可等价于解决下式:
$$ \begin{array}{l} \quad\quad\quad\quad\quad\quad \mathop {\min }\limits_{{\boldsymbol{L}},{\boldsymbol{E}}} \left\| {{\boldsymbol{X}} - {\boldsymbol{L}} - {\boldsymbol{E}}} \right\|_{{F}}^2\\ {\rm{s.t.}}{\boldsymbol{L}} = {\boldsymbol{U}}{{\boldsymbol{V}}^{\rm{T}}},{\boldsymbol{L}},{\boldsymbol{U}},{\boldsymbol{V}} \geqslant 0,{\rm{rank}}\left( {\boldsymbol{L}} \right)\leqslant r,{\rm{card}}\left( {\boldsymbol{E}} \right) \leqslant e \end{array}$$ (22) 在优先求解L时,求解式(22)可转换为先求解式(23)再求解U的过程:
$$\begin{array}{l} \quad\quad\quad\quad\mathop {\min }\limits_{{\boldsymbol{L}},{\boldsymbol{E}}} \left\| {{\boldsymbol{X}} - {\boldsymbol{L}} - {\boldsymbol{E}}} \right\|_F^2\\ {\rm{s.t.}}{\boldsymbol{L}} \geqslant 0,{\rm{rank}}({\boldsymbol{L}}) \leqslant r,{\rm{card}}({\boldsymbol{E}}) \leqslant e \end{array}$$ (23) 将式(23)可拆两个子问题来解决。当固定L或E时,有:
$$ \left\{ \begin{array}{l} {{\boldsymbol{L}}_{t}} = \arg {\min _{{\rm{rank}}\left( {\boldsymbol{L}} \right) \leqslant r}}\left\| {\left. {{\boldsymbol{X}} - {\boldsymbol{L}} - {{\boldsymbol{E}}_{t - 1}}} \right\|} \right._F^2\\ {{\boldsymbol{E}}_{t}} = \arg {\min _{{\rm{card}}\left( {\boldsymbol{E}} \right) \leqslant e}}\left\| {\left. {{\boldsymbol{X}} - {{\boldsymbol{L}}_t} - {\boldsymbol{E}}} \right\|} \right._F^2 \end{array} \right. $$ (24) 可见式(24)对于L或E都是凸的,因此可以固定一个变量并更新另一个,直到收敛。通过迭代X−Et−1将奇异值赋给Lt,在X−Lt上进行相同操作得到Et,由此得到两个子问题的解。
但是,在每次迭代中求X−Et−1的SVD都很耗时。 本文采用文献[24]中提出的双边随机投影(bilateral random projection , BRP)来解决式(24)。
对于给定的矩阵
${\boldsymbol{X}} \in {\bf{R}}^{\rm{mexh}}$ ,其r 个BRPs如下:$$ {\boldsymbol{Y}}_{1}={\boldsymbol{X A}}_{1} $$ (25) $$ {\boldsymbol{Y}}_{2}={\boldsymbol{X}}^{\rm{T}} {\boldsymbol{A}}_{2} $$ (26) 式中:
${\boldsymbol{A}}_{1} \in {\bf{R}}^{n \times r}, {\boldsymbol{A}}_{2} \in {\bf{R}}^{m \times r}$ 是随机矩阵,那么X的秩r逼近为$$ {\boldsymbol{L}}=(\tilde{{\boldsymbol{L}}})^{\frac{1}{2 q+1}}={\boldsymbol{Q}}_{1}\left[{\boldsymbol{R}}_{1}\left({\boldsymbol{A}}_{2}^{\rm{T}} {\boldsymbol{Y}}_{1}\right)^{-1} {\boldsymbol{R}}_{2}^{\rm{T}}\right]^{\frac{1}{2 q+1}} {\boldsymbol{Q}}_{2}^{\rm{T}} $$ (27) 由此可计算得出L。在此基础上,对式(28)求解:
$$ \left\{\begin{split} & \min _{t}\left\|{\boldsymbol{L}}-{\boldsymbol{U V}}^{\rm{T}}\right\|_{\rm F}^{2} \\ & \text { s.t. } {\boldsymbol{U}} \geqslant 0 \end{split}\right. $$ (28) 可以看出式(28)为式(1)中的标准NMF式。因此,对于等式中的U,我们有式(3)中完全相同的迭代更新规则:
$$ u_{ij} \leftarrow u_{ij} \frac{({\boldsymbol{X V}})_{ij}}{\left({\boldsymbol{U V}}^{\rm{T}} {\boldsymbol{V}}\right)_{ij}} $$ (29) 2.2.3 固定S、U更新V
观察式(6),不难发现在固定变量S、U的情况下更新V的最小化,式(6)可等价于解决下式:
$$\begin{array}{l} \quad\quad\quad\mathop {\min }\limits_{{\boldsymbol{L,E}}} \left\| {{\boldsymbol{X}} - {\boldsymbol{L}} - {\boldsymbol{E}}} \right\|_F^2 + \lambda \cdot {\rm{tr}}\left( {{{\boldsymbol{V}}^{\rm{T}}}{{\boldsymbol{L}}_S}{\boldsymbol{V}}} \right)\\ {\rm{s.t.}}{\boldsymbol{L}} = {\boldsymbol{UV}},{\boldsymbol{L}},{\boldsymbol{U}},{\boldsymbol{V}} \geqslant 0,{\rm{rank}}({\boldsymbol{L}}) \leqslant r,{\rm{card}}({\boldsymbol{E}}) \leqslant e \end{array} $$ (30) 参考2.2.2节中方法可得一确定L。由此,化式(30)为
$$ \begin{array}{l} \mathop {\min }\limits_{{\boldsymbol{L}},{\boldsymbol{E}}} \left\| {{\boldsymbol{L}} - {\boldsymbol{U}}{{\boldsymbol{V}}^{\rm{T}}}} \right\|_{\rm{F}}^2 + \lambda \cdot {\rm{tr}}\left( {{{\boldsymbol{V}}^{\rm{T}}}{{\boldsymbol{L}}_S}{\boldsymbol{V}}} \right)\\ \quad\quad\quad\quad{\rm{s.t.}}{\boldsymbol{V}} \geqslant 0 \end{array} $$ (31) 为了约束
${\boldsymbol{V}} \geqslant 0$ ,令$\xi \in {\bf{R}}^{n \times c}$ 表示对应的拉格朗日乘数,则可以将拉格朗日函数定义为$$ R({\boldsymbol{V}})=\left\|{\boldsymbol{L}}-{\boldsymbol{U V}}^{\rm{T}}\right\|_{\rm{F}}^{2}+\lambda \cdot{\rm{t r}}\left({\boldsymbol{V}}^{\rm{T}} {\boldsymbol{L}}_{S} {\boldsymbol{V}}\right)-{\rm{tr}}\left(\xi {\boldsymbol{V}}^{\rm{T}}\right) $$ (32) 设
$\dfrac{\partial R({\boldsymbol{V}})}{\partial {\boldsymbol{V}}}=0$ ,可得:$$ \xi=-2 {\boldsymbol{L}}^{\rm{T}} {\boldsymbol{U}}+2 {\boldsymbol{V U}}^{\rm{T}} {\boldsymbol{U}}+2 \lambda {\boldsymbol{L}}_{S} {\boldsymbol{V}} $$ (33) 根据KKT条件[23] 满足
$\xi_ {ij} v_{ij}=0$ ,有:$$ \left(-2 {\boldsymbol{L}}^{\rm{T}} {\boldsymbol{U}}+2 {\boldsymbol{V U}}^{\rm{T}} {\boldsymbol{U}}+2 \lambda {\boldsymbol{L}}_{S} {\boldsymbol{V}}\right)_{ij} {\boldsymbol{v}}_{ij}=0 $$ (34) 即
$$ \left(-{\boldsymbol{L}}^{\rm{T}} {\boldsymbol{U}}+{\boldsymbol{V}}{\boldsymbol{U}}^{\rm{T}} {\boldsymbol{U}}+\lambda {\boldsymbol{D}}_{S} {\boldsymbol{V}}-\lambda {\boldsymbol{W}}_{{S}} {V}\right)_{{ij}} {\boldsymbol{v}}_{{ij}}=0 $$ (35) 则式(35)遵从如下迭代规则:
$$ {\boldsymbol{v}}_{ij} \leftarrow {\boldsymbol{v}}_{ij} \frac{\left({\boldsymbol{L}}^{\rm{T}} {\boldsymbol{U}}+\lambda {\boldsymbol{W}}_{S} {\boldsymbol{V}}\right)_{ij}}{\left({\boldsymbol{V U}}^{\rm{T}} {\boldsymbol{U}}+\lambda {\boldsymbol{D}}_{S} {\boldsymbol{V}}\right)_{ij}} $$ (36) 至此,可以给出NLMFAN的算法求解步骤。
算法1 自适应图正则化的低秩非负矩阵分解算法
输入 数据矩阵
${\boldsymbol{X}} \in {\bf{R}}_{+}^{\operatorname{maxh}}$ 的初始值,簇号c,参数k、λ、β;输出 聚类指标矩阵
${\boldsymbol{V}} \in {\bf{R}}^{m+t}$ 。1)对X进行BRP操作,求出Y1和Y2;
2)对Y1和Y2进行QR分解,计算出矩阵X的低秩结构L;
3)通过对式(7)的最优解来初始化S;
4)重复更新
$$u_{i j} \leftarrow u_{i j} \dfrac{({\boldsymbol{XV}})_{i j}}{\left({\boldsymbol{U V}}^{\rm{T}} {\boldsymbol{V}}\right)_{ij}}, {\boldsymbol{v}}_{ij} \leftarrow {\boldsymbol{v}}_{ij} \dfrac{\left({\boldsymbol{L}}^{\rm{T}} {\boldsymbol{U}}+\lambda {\boldsymbol{W}}_{S} {\boldsymbol{V}}\right)_{ij}}{\left({\boldsymbol{V U}}^{\rm{T}} {\boldsymbol{U}}+\lambda {\boldsymbol{D}}_{S} {\boldsymbol{V}}\right)_{ij}} $$ 对于每个i,通过求解式(15)更新S的第i行。其中
${\boldsymbol{d}}_{i} \in {\bf{R}}^{n \times 1}$ ,第j个元素为$d_{ij}=\left\|{{\boldsymbol{x}}}_{i}-{{\boldsymbol{x}}}_{j}\right\|_{\rm{2}}^{2}+ \beta\left\|{{\boldsymbol{v}}}_{t}-{\boldsymbol{v}}_{j}\right\|_{2}^{2}$ ;直到收敛;5)求得聚类指标矩阵V。
2.3 NLMFAN算法收敛性分析
定理1 对于
${\boldsymbol{U}} \geqslant 0, {\boldsymbol{V}} \geqslant 0$ ,式(6)中的目标在式(14)、(21)、(36)中的更新规则下不增加,因此收敛。证明 显然,式(14)可以用第2.2节中描述的闭式解来解决。因此,我们只需要证明式(21)和式(36)在每次迭代中的更新规则下目标值是不增加的。 此外,因为式(6)中目标的第2项与U无关,第1项在计算L时不涉及U值的更新,且计算得出L后的操作符合标准NMF分解,所以NLMFAN中的U更新规则与原始NMF完全相同。 因此,可以使用NMF收敛的证明方式来证明在等式中更新规则下目标没有增加。有关详细信息,可参考文献[17]。
现在,只需要证明在式(36)中的更新规则下我们的目标不会增加即可,而式(32)中更新规则其实等价于文献[25]中式(26)、(36)的收敛性证明可参考文献[25]附录中证明过程,此处不列出。
3. 现实数据集实验评估
3.1 实验数据集
为了评估本文提出方法的性能,我们在实际基准数据集进行了实验。
本文实验用到的数据集包括CLUTO数据工具及UCI机器学习数据集。其中,CLUTO是一个软件包,用于对低维和高维数据集进行聚类,并分析各种聚类的特征。CLUTO的数据工具包中包含的信息检索、客户购买交易、网络、地理信息系统、科学和生物学等数据集非常适于聚类测试。UCI机器学习数据集是加州大学欧文分校提出的用于机器学习的数据库,该数据库目前共有559个数据集,其数目还在不断增加。UCI数据集是一个常用的标准测试数据集。
选取CLUTO数据工具中的4个数据集(Cacmcisi 、Hitech、K1a、K1b)与UCI机器学习数据集4个数据集(Abalone、Krvs、Wdbc、Vote)进行实验。表1给出了各数据集及其特征。
表 1 数据集及特征Table 1 Description of data sets数据集 样本量 特征量 类 数据集 样本量 特征量 类 Cacmcisi 4663 348 2 Abalone 2282 8 4 Hitech 2301 2216 6 Krvs 3196 36 2 K1a 2340 1326 6 Vote 435 16 2 K1b 2340 1326 6 Wdbc 569 30 2 3.2 实验步骤
为了进一步评估所提出方法的性能,将NLMFAN与一些经典算法和最新算法进行了对比实验。主成分分析(principal component analysis, PCA):经典的降维方法[26] 。NMF:标准NMF算法[6] 。LLNMF(2009):使用局部结构学习的NMF算法[16] 。GNMF(2011):图正则化的NMF[13-14]。NMFAN(2020):具有局部自适应结构的正则化NMF算法[25] 。
本文实验条件为Intel(R) Core(TM) i7-1065G7 1.50 GHz CPU,16 GB DDR3内存,Matlab2019b。在后续的性能评估中,以准确率(accurity, ACC)、标准互信息率(normalized mutual information, NMI)两个指标作为评价算法性能好坏的标准,在8个基准数据集上测试算法。实验中所用算法的参数已结合原论文根据需要调节至最优。
在每个数据集上都进行了算法精度与收敛速度测试,并从8个数据集中选取了4个用于测试λ参数对聚类性能的影响。
3.3 CLUTO数据集实验
CLUTO的4个文档数据集上进行了每组10次实验。实验结果均值如表2所示。
表 2 各算法在CLUTO数据集上聚类结果比较Table 2 ACC and NMI of clustering on CLUTO database% 数据集 PCA NMF LLNMF GNMF NMFAN NLMFAN ACC NMI ACC NMI ACC NMI ACC NMI ACC NMI ACC NMI Cacmcisi 68.67 68.69 90.46 90.46 74.20 74.20 92.09 92.09 92.22 92.22 92.44 92.44 Hitech 26.25 26.42 22.73 27.03 22.16 26.99 24.12 26.99 22.90 26.42 22.51 26.60 K1a 29.40 59.57 27.95 61.88 30.21 62.09 27.05 61.50 29.74 62.14 30.86 62.22 K1b 29.40 59.57 28.12 62.31 29.27 59.36 31.20 62.01 32.26 62.35 33.70 62.61 均值 38.43 53.56 43.32 60.42 38.96 55.66 43.62 60.65 44.28 60.78 44.88 60.97 从表2中可以看出: NMF相关算法的聚类结果还是优于传统聚类方法。同时,在NMF算法中,NLMFAN算法显示出了优于其他几种方法的聚类效果。尤其是与改进前的NMFAN算法相比,NLMFAN算法在每个数据集上的精度及平均精度均有所提高。
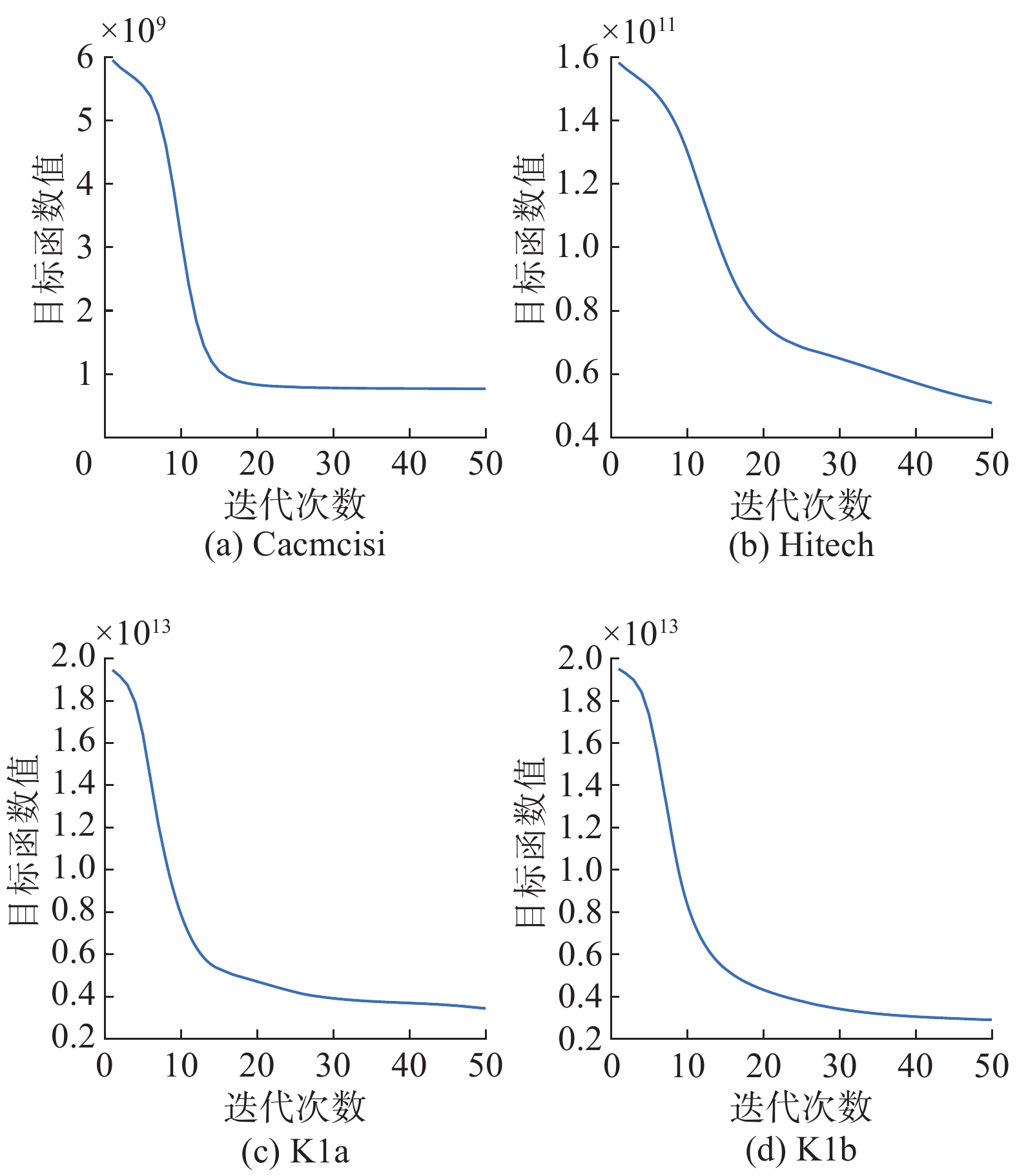
图1展现了在CLUTO的4个数据集上NLMFAN算法的收敛情况。图中目标函数值即最小误差值。可以看出,本文方法在数据集上均可快速收敛,迭代次数均在50次内。
3.4 UCI数据集实验
本节使用了与上节相同的几种算法在UCI的4个文档数据集上进行了每组十次实验。实验结果如表3所示。
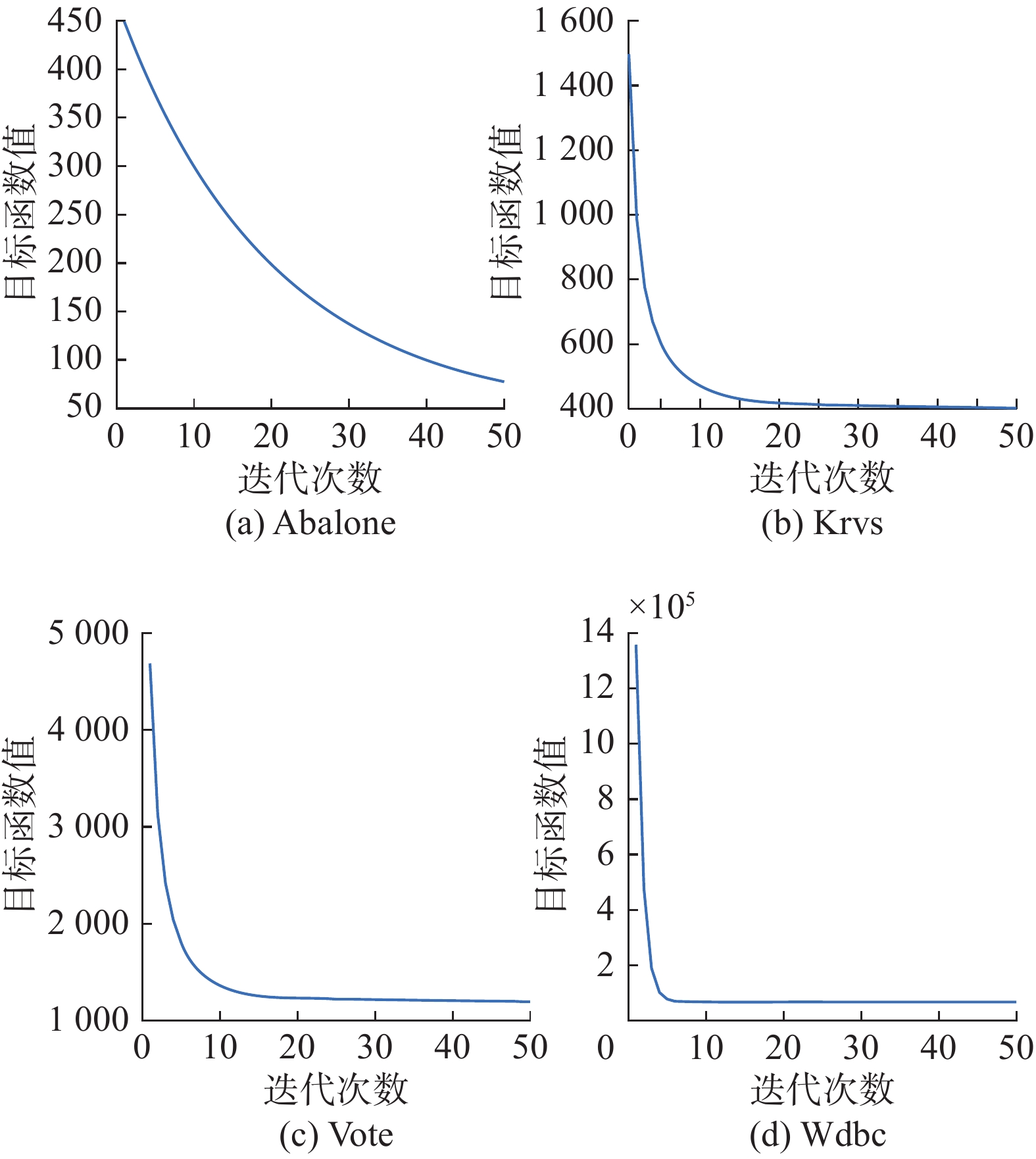
从表3中可以看出:在UCI数据集上,NLMFAN算法的聚类效果基本优于其他算法,同时其在Abalone数据集上的实验数据较原有的其他算法有5.89%~0.57%的提升。图2呈现了在UCI的4个数据集上NLMFAN算法的收敛情况。可以看出,NLMFAN算法在几个数据集上均有收敛,且速度较快。
3.5 参数选择实验
本节对算法中λ参数的选择进行讨论。本文从CLUTO中选取了Hitech、K1b,从UCI中选取了Abalone、Krvs,总计4个数据集进行实验。
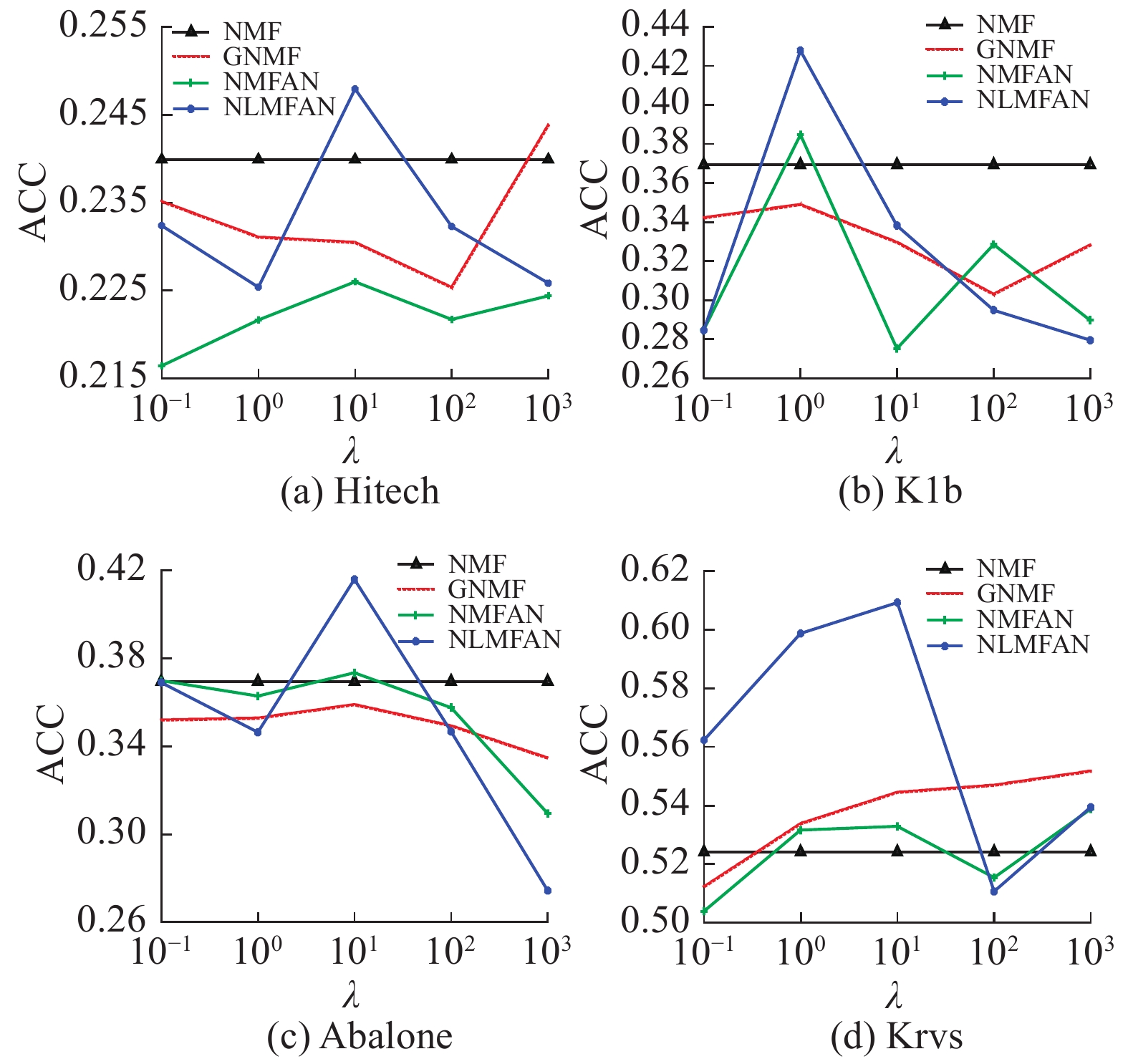
从图3可以看出:
1)除了NMF以外,GNMF、NMFAN、NLMFAN都受到λ值的影响。总体来说,当λ的值取在10以内时NLMFAN可以获得较好的聚类结果,当λ取到10时可以获得所有算法平均最优结果。
2)除了在Hitech数据集上有明显的波动外,GNMF在其他数据集上都没有明显波动变化,说明其受λ的影响不大。而根据提出GNMF的文献[13]中对其的实验结果表明,GNMF的结果会在固定λ值时,根据其选取的最近邻数k值的变化而变化。这是因为GNMF的精度主要依赖于其通过KNN方法构建的拉普拉斯图,且其图构造与NMF相互独立的计算模式使得该特征的表现尤为明显。而NMFAN与NLMFAN依赖的则是自适应选择最近邻后生成相似度矩阵的结果,即式(6)中包含基于相似度矩阵
${\boldsymbol{S}}$ 的拉普拉斯矩阵${\boldsymbol{L}}_{S}$ 的项,该项即为受到λ影响的图正则项。表 3 各算法在UCI数据集上聚类结果比较Table 3 ACC and NMI of clustering on UCI database% 数据集 PCA NMF LLNMF GNMF NMFAN NLMFAN ACC NMI ACC NMI ACC NMI ACC NMI ACC NMI ACC NMI Abalone 30.24 30.28 34.22 34.22 33.17 34.14 35.50 37.25 35.58 36.11 36.15 36.33 Krvs 52.19 52.22 52.22 52.22 57.48 57.48 54.82 54.82 52.47 52.47 52.57 52.57 Vote 61.61 61.61 85.98 85.98 64.60 64.60 86.44 86.44 87.36 87.36 87.59 87.59 Wdbc 62.92 62.92 84.53 84.53 51.14 62.74 85.41 85.41 85.41 85.41 85.46 85.46 均值 62.27 62.27 85.26 85.26 57.87 63.67 85.93 85.93 86.39 86.39 86.53 86.53 4. 结束语
在本文中,提出了一种自适应图正则化的非负矩阵分解算法(NLMFAN)。
1)提出了一种新的具有低秩特性的自适应邻域GNMF模型,同时也设计了一种求解NLMFAN的高效求解算法;
2)NLMFAN方法可以在低秩约束条件下同时执行局部结构学习和矩阵分解过程,即可以根据分解的结果自适应地学习局部流形结构,并重新构造合适的图以保留精炼的局部结构;
3)传统的基于图的方法通常基于固定的数据图对数据进行聚类,容易受到预先构造的不准确的图的影响。NLMFAN通过引入自适应邻居(adaptive neighbors,ANs)正则项对迭代中的相似度矩阵进行修正,从而减少分配ANs对数据点之间相似性带来的改变。
然而在许多聚类应用中,数据中的噪声是通过结构或组聚类来分布的,本文算法中并未考虑空间联系。在未来的工作中,我们将把结构化稀疏性作为约束来提升NLMFAN的性能。
-
表 1 数据集及特征
Table 1 Description of data sets
数据集 样本量 特征量 类 数据集 样本量 特征量 类 Cacmcisi 4663 348 2 Abalone 2282 8 4 Hitech 2301 2216 6 Krvs 3196 36 2 K1a 2340 1326 6 Vote 435 16 2 K1b 2340 1326 6 Wdbc 569 30 2 表 2 各算法在CLUTO数据集上聚类结果比较
Table 2 ACC and NMI of clustering on CLUTO database
% 数据集 PCA NMF LLNMF GNMF NMFAN NLMFAN ACC NMI ACC NMI ACC NMI ACC NMI ACC NMI ACC NMI Cacmcisi 68.67 68.69 90.46 90.46 74.20 74.20 92.09 92.09 92.22 92.22 92.44 92.44 Hitech 26.25 26.42 22.73 27.03 22.16 26.99 24.12 26.99 22.90 26.42 22.51 26.60 K1a 29.40 59.57 27.95 61.88 30.21 62.09 27.05 61.50 29.74 62.14 30.86 62.22 K1b 29.40 59.57 28.12 62.31 29.27 59.36 31.20 62.01 32.26 62.35 33.70 62.61 均值 38.43 53.56 43.32 60.42 38.96 55.66 43.62 60.65 44.28 60.78 44.88 60.97 表 3 各算法在UCI数据集上聚类结果比较
Table 3 ACC and NMI of clustering on UCI database
% 数据集 PCA NMF LLNMF GNMF NMFAN NLMFAN ACC NMI ACC NMI ACC NMI ACC NMI ACC NMI ACC NMI Abalone 30.24 30.28 34.22 34.22 33.17 34.14 35.50 37.25 35.58 36.11 36.15 36.33 Krvs 52.19 52.22 52.22 52.22 57.48 57.48 54.82 54.82 52.47 52.47 52.57 52.57 Vote 61.61 61.61 85.98 85.98 64.60 64.60 86.44 86.44 87.36 87.36 87.59 87.59 Wdbc 62.92 62.92 84.53 84.53 51.14 62.74 85.41 85.41 85.41 85.41 85.46 85.46 均值 62.27 62.27 85.26 85.26 57.87 63.67 85.93 85.93 86.39 86.39 86.53 86.53 -
[1] ZHAO K, HAIQI P, STEVEN C H H, et al. Robust graph learning from noisy data[J]. IEEE transactions on cybernetics, 2019, 50(5): 1833–1843. doi: 10.1109/TCYB.2018.2887094 [2] CHEN C F, WEI C P, WANG Y C F. Low-rank matrix recovery with structural incoherence for robust face recognition[C]//Proceedings of 2012 IEEE Conference on Computer Vision and Pattern Recognition. Providence, USA, 2012: 2618−2625. [3] DUDA R O, HART P E, STORK D G. Pattern classification[M]. 2nd ed. New York: Wiley-Interscience, 2000. [4] MAKHOUL J, ROUCOS S, GISH H. Vector quantization in speech coding[J]. Proceedings of the IEEE, 1985, 73(11): 1551–1588. doi: 10.1109/PROC.1985.13340 [5] TURK M, PENTLAND A. Eigenfaces for recognition[J]. Journal of cognitive neuroence, 1991, 13(6): 556–562. [6] LEE D D, SEUNG H S. Algorithms for non-negative matrix factorization[J]. Nips, 2000, 13(6): 556–562. [7] YANG C F, YE Mao, ZHAO Jing. Document clustering based on nonnegative sparse matrix factorization[C]//Proceedings of the First International Conference on Natural Computation. Changsha, China, 2005: 557−563. [8] LIU Guangcan, LIN Zhouchen, YAN Shuicheng, et al. Robust recovery of subspace structures by low-rank representation[J]. IEEE transactions on pattern analysis and machine intelligence, 2013, 35(1): 171–184. doi: 10.1109/TPAMI.2012.88 [9] LU Yuwu, YUAN Chun, ZHU Wenwu, et al. Structurally incoherent low-rank nonnegative matrix factorization for image classification[J]. IEEE transactions on image processing, 2018, 27(11): 5248–5260. doi: 10.1109/TIP.2018.2855433 [10] ROWEIS S T, SAUL L K. Nonlinear dimensionality reduction by locally linear embedding[J]. Science, 2000, 290(5500): 2323–2326. doi: 10.1126/science.290.5500.2323 [11] BELKIN M, NIYOGI P. Laplacian eigenmaps and spectral techniques for embedding and clustering[C]//Proceedings of the 14th International Conference on Neural Information Processing Systems: Natural and Synthetic. Vancouver, British Columbia, Canada, 2001: 585−2591. [12] BELKIN M, NIYOGI P, SINDHWANI V. Manifold regularization: a geometric framework for learning from labeled and unlabeled examples[J]. Journal of machine learning research, 2006, 7(11): 2399–2434. [13] CAI Deng, HE Xiaofei, HAN Jiawei, et al. Graph regularized nonnegative matrix factorization for data representation[J]. IEEE transactions on pattern analysis and machine intelligence, 2011, 33(8): 1548–1560. doi: 10.1109/TPAMI.2010.231 [14] CAI Deng, HE Xiaofei, WU Xiaoyun, et al. Non-negative matrix factorization on manifold[C]//Proceedings of 2008 Eighth IEEE International Conference on Data Mining. Pisa, Italy, 2008. [15] BOTTOU L, VAPNIK V. Local learning algorithm[J]. Neural computation, 1992, 4(6): 888–900. doi: 10.1162/neco.1992.4.6.888 [16] GU Quanquan, ZHOU Jie. Local learning regularized nonnegative matrix factorization[C]//Proceedings of the 21st International Joint Conference on Artificial Intelligence. Pasadena, USA, 2009: 1046−1051. [17] LI Xuelong, CUI Guosheng, DONG Yongsheng. Graph regularized non-negative low-rank matrix factorization for image clustering[J]. IEEE transactions on cybernetics, 2017, 47(11): 3840–3853. doi: 10.1109/TCYB.2016.2585355 [18] DU H, HU Q, ZHANG X, et al. Image feature extraction via graph embedding regularized projective non-negative matrix factorization[J]. Communications in computer & information ence, 2014, 483(1): 196–209. [19] YIN Ming, GAO Junbin, LIN Zhouchen. Laplacian regularized low-rank representation and its applications[J]. IEEE transactions on pattern analysis and machine intelligence, 2016, 38(3): 504–517. doi: 10.1109/TPAMI.2015.2462360 [20] WANG Jianzhong, ZHAO Rui, WANG Yang, et al. Locality constrained graph optimization for dimensionality reduction[J]. Neurocomputing, 2017, 245: 55–67. doi: 10.1016/j.neucom.2017.03.046 [21] MENG Yang, SHANG Ronghua, JIAO Licheng, et al. Dual-graph regularized non-negative matrix factorization with sparse and orthogonal constraints[J]. Engineering applications of artificial intelligence, 2018, 69: 24–35. doi: 10.1016/j.engappai.2017.11.008 [22] NIE Feiping, WANG Xiaoqian, HUANG Heng. Clustering and projected clustering with adaptive neighbors[C]//Proceedings of the 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York, USA, 2014. [23] LEMARÉCHAL C, BOYD S, VANDENBERGHE L. convex optimization, Cambridge university press, 2004 hardback, 65 US$, ISBN 0 521 83378 7[J]. European journal of operational research, 2006, 170(1): 326–327. doi: 10.1016/j.ejor.2005.02.002 [24] ZHOU Tianyi, TAO Dacheng. GoDec: randomized low-rank & sparse matrix decomposition in noisy case[C]//Proceedings of the 28th International Conference on Machine Learning. Bellevue, USA, 2011: 33−240. [25] HUANG Shudong, XU Zenglin, KANG Zhao, et al. Regularized nonnegative matrix factorization with adaptive local structure learning[J]. Neurocomputing, 2020, 382(11): 196–209. doi: 10.1016/j.neucom.2019.11.070 [26] WHITLARK D, DUNTEMAN G H. Principal components analysis[J]. Journal of marketing research, 1990, 27(2): 243.



















































































 下载:
下载: