Batch scheduling algorithm for flexible machining and assemblyjob shop when the machine breaks down
-
摘要: 针对传统的加工与装配分阶段独立调度中资源利用率不高的问题,将加工与装配联合同时进行调度。在考虑工件批量和批次的前提下提出一种改进遗传算法求解该问题,以最小化最大完工时间为优化目标建立数学模型,根据问题特性提出一种工件末工序前移的邻域结构,提升了算法的局部搜索能力进而改善整体求解质量。设计了一种基于装配设备负载均衡的混合贪婪解码方法,完成了装配设备选择。考虑到实际车间中机器故障的特点,提出了相应的响应策略和染色体更改规则,解决了动态调度问题。最后通过算例分析验证了所提算法和策略求解该问题的可行性和有效性。Abstract: To solve the problem of low resource utilization in traditional independent scheduling of machining and assembly by stages, the machining and assembly are simultaneously scheduled. An improved genetic algorithm is designed to solve the problem by considering the batch and sublots of the workpiece. First, a mathematical model is established to minimize the maximum completion time. According to the problem characteristics, a neighborhood structure with the workpiece’s last process is proposed, which enhances the local searching ability of the algorithm and improves the overall solution quality. Furthermore, a hybrid greed decoding method based on the load balancing of assembly equipment is designed to complete its selection. Considering the characteristics of machine breakdown in a real workshop, a corresponding response strategy and chromosome changing rule are introduced to solve the dynamic scheduling problem. Finally, the feasibility and effectiveness of the proposed algorithm and strategy for solving the problem are verified by example analysis.
-
作业车间调度问题(job-shop scheduling problem, JSP)最早由GAREY提出,并被证明是一个NP-Hard问题[1]。柔性作业车间调度问题(flexible job-shop scheduling problem, FJSP)是JSP的拓展问题,不同于JSP,FJSP中一道工序可在多台机器上加工,也已经被证明为NP-Hard问题[2]。因其复杂性、不确定性和多约束性等特点,学者一般会选用智能优化算法来求解车间调度问题,例如遗传算法[3]、灰狼算法[4]、蚁群算法[5]等。
近年来,大量学者对FJSP进行了深入的研究,比如石小秋等[6]以最小化完工时间为优化目标,提出一种自适应变级遗传杂草算法求解FJSP。李明等[7]针对具有顺序准备时间(sequence dependent setup time, SDST)和关键目标的低碳FJSP,给出了一种有效策略加强对关键目标优化的同时兼顾非关键目标的持续改进,提出了一种新型帝国竞争算法求解该问题。但是上述文献没有考虑到工件的批次和批量,引入批次和批量之后的FJSP更加贴近实际,有着重大研究价值。徐本柱等[8]提出了基于工序分批调度的概念,建立了以关键路径工序为中心的分批调度模型并证明了该模型的有效性。李聪波等[9]以车间总能耗最低和完工时间最小为优化目标建立了多工艺路线柔性作业车间分批优化调度模型,并采用多目标模拟退火算法对模型进行优化求解。
在实际生产中,工件的加工是制造过程的最底层,加工完成的工件需要组装为组件再由组件组装为成品,而无论是组件或者成品都有其物料清单(bill of material, BOM)需求。因此,把装配过程考虑到调度问题中是有必要的。柔性装配作业车间调度问题(flexible assembly job shop scheduling problem, FAJSP)是在FJSP的基础上考虑工件的装配关系约束的更为复杂和常见的问题。在FJSP中完工时间是指最后一个工件的最后一道工序的加工完成时间,而在FAJSP中完工时间是指最后一个成品的装配工序的完工时间。学者Nourali等[10-11]最早建立了FAJSP的混合整数规划数学模型,并在静态环境中以makespan为优化目标提出一种粒子群算法进行求解。但是其并没有考虑到动态环境因素,相比于静态车间调度问题,动态车间调度问题(dynamic job-shop scheduling problem, DJSP)与实际的生产环境更为相似。DJSP在静态调度的基础上需要考虑各种突发事件,比如机器损坏、紧急插单、工件交货期改变或者物料延迟等,其中机器损坏是动态事件中常见的事件之一,也是本文主要研究的动态事件。针对动态调度,Zhang等[12]提出了一种名为混合多智能体/蚁群算法(hybrid MAS/ACO, HMA)的结合了多智能体系统协商和蚁群优化的方法,并利用实验证明了该方法在求解DFJSP上的有效性和可行性;刘爱军等[13]对遗传算法进行改进并结合滚动窗口再调度技术,设计了基于事件和周期驱动的重调度策略用于解决DFJSP;Baykasoǧlu等[14]利用贪婪随机自适应搜索算法,给出了一种具有机器容量约束和建立次数依赖于序列的FJSP和DFJSP的求解算法并验证了其适用性。针对FAJSP的动态调度,杨小佳等[15]考虑现实生产中存在的随机扰动,采用了完全反应式与预测−反应式两类动态调度策略,并提出了相应的优先度规则算法和周期性滚动遗传算法用于求解该问题。
目前DFJSP已有大量研究,但是考虑到工件批量和装配因素的研究却十分匮乏。基于上述分析可知,综合考虑批量加工与装配联合调度的FAJSP具有重大的研究价值,本文将该问题描述为:柔性加工与装配作业车间分批联合调度问题。本文以最小化最大完工时间为优化目标,在考虑机器故障的基础上,建立了柔性加工与装配作业车间动态调度模型,并利用改进遗传算法进行求解。
1. 问题描述与数学模型
1.1 问题描述
本文研究的是柔性加工与装配作业车间分批联合调度问题,包括静态、动态调度问题,其中静态调度问题可以描述为:给定一组待生产的产品,其装配结构已知,同一车间中有
$m$ 台不同的加工机器用来加工工件,${a_m}$ 台不同的装配设备用来装配工件,$n$ 种工件在$m$ 台加工机器上加工,各工件包含多道工序且工序顺序固定不变,每道工序可在多台不同的机器上加工,各道工序在不同机器上的加工时间可能不同。完成加工的工件均由装配设备装配,这里本文提出装配柔性,类推工件加工柔性,即同一组件可选择不同的装配设备进行装配,在不同设备上的装配时间可能不同。调度的目标是为每一道加工工序和装配工序分配机器与设备,使成品的最终完工时间最小。动态调度在静态调度的基础上考虑到车间紧急事件的影响,系统对该事件做出应急反应。针对动态调度问题的研究来分类,可将其分为3类:周期性重调度、事件驱动重调度以及周期性和事件驱动混合重调度[16]。本文考虑机器故障,为了及时响应动态事件,采用基于事件的重调度策略。
1.2 数学模型
本文将在以下假设说明的前提下建立上述问题的数学模型:
1) 本文采用等量一致分批策略[17];
2) 一道装配工序同一时刻只能在一台装配设备上进行装配;
3) 在整个调度作业过程中最多只有一台机器发生故障;
4) 机器故障后可以经过维修时长
$ {L_t} $ 后继续投入使用;5) 机器故障时加工到一半的工件视为废品,应取出一个新的备用工件重新加工;
6) 各种工件、组件最终组装成同一种成品。
①相关符号定义
$i$ :工件号,$i = 1,2 \cdots ,n$ 。$k$ :加工机器号,$k = 1,2, \cdots ,m$ 。$ {B_i} $ :工件$i$ 的总批量。$b$ :加工批次号。$ {B_{ib}} $ :工件$i$ 的$b$ 批次的批量。${O_i}$ :工件$i$ 的工序数。$j$ :加工工序号,$j = 1,2, \cdots ,{O_i}$ 。${P_{ibj}}$ :工件$i$ 的$b$ 批次的第$j$ 道加工工序。$u$ :装配设备号,$u = 1,2, \cdots, {a_m}$ 。$z$ :组件号,$z = 1,2, \cdots ,d$ 。$c$ :成品号,$c = 1,2, \cdots,f$ 。${\text{R}}{{\text{Z}}_z}$ 、${\text{R}}{{\text{C}}_c}$ :当前预组装件$z$ 和成品$c$ 的数量。${A_{zu}}$ 、${A_{cu}}$ :组件$z$ 和成品$c$ 在装配设备$u$ 上的装配工序。②约束条件
式(1)为目标函数,即最小化成品的最大完工时间:
$$ \min \{ {C_{\max }}\} = \min \{ \max ({{T}}_{{\text{C}}_u})\} ,\quad u = 1,2, \cdot \cdot \cdot ,{a_m} $$ (1) 式中:
${C_{\max }}$ 为最大完工时间;${{T}}_{{\text{C}}_u}$ 为成品在装配设备$u$ 上的装配完工时间。式(2)为各工件各批次的加工工序之间的约束关系:
$$ {{t}}_{{\text{SP}}_{ib\left( {j + 1} \right)}} - {{t}}_{{\text{FP}}_{ibj}} \geqslant 0,\forall i,b,j = 1,2, \cdot \cdot \cdot ,{O_i} - 1 $$ (2) 式中:
${{t}}_{{\text{SP}}_{ibj}}$ 和${{t}}_{{\text{FP}}_{ibj}}$ 分别为${P_{ibj}}$ 的开工时间和完工时间。式(3)表示加工工序
$ {P_{ibj}} $ 在同一时刻只能在一台加工机器上加工:$$ \sum\limits_{k = 1}^{{m_{ij}}} {{X_{kibj}}} = 1,\quad \forall i,b,j $$ (3) 式中
${X_{kibj}}$ 取值为0或1,若$ {P_{ibj}} $ 在机器$k$ 上加工,$ {X_{kibj}} = 1 $ ,否则$ {X_{kibj}} = 0 $ 。式(4)为划分批次后的总工序数,
${p_i}$ 为共件$i$ 的批次数。$$ E={\displaystyle \sum _{i=1}^{n}{O}_{i}}{p}_{i} $$ (4) 式(5)表示同一时刻一台加工机器只能加工一道工序:
$$ {t_{\rm{SP}_{2}}}\geqslant {t_{\rm{SP}_{1}}}+{t_{\text{P}_{1}}}{B}_{{i}_{1}{b}_{1}}-C\left(1-{Y}_{k}{}_{{P}_{1}{P}_{2}}\right),\quad \forall k,i,b,j $$ (5) 式中
$ C $ 表示一个足够大的正整数,若机器$k$ 上的$ {P_1}({P_i}_{_1{b_1}{j_1}}) $ 先于$ {P_2}({P_i}_{_2{b_2}{j_2}}) $ 加工,$ {Y_{kP}}_{_1{P_2}} = 1 $ ,否则,${{t}}_{{\text{P}}_1}$ 为$ {P_1}({P_i}_{_1{b_1}{j_1}}) $ 的单件加工时间。式(6)表示同一时刻一台装配设备只能进行一道组件或成品的装配工序:
$$ {t_{\text{SA}_{2}}}\geqslant {t_{\text{SA}_{1}}}+{t_{\text{A}_{1}}}R-C\left(1-{Y}_{u}{}_{{A}_{1}{A}_{2}}\right),\quad \forall u $$ (6) 式中:
$ R $ 代表${\text{R}}{{\text{Z}}_z}$ 或者${\text{R}}{{\text{C}}_c}$ ;若装配设备$u$ 上的${A_1}$ (${A_{zu}}$ 或者${A_{cu}}$ )先于${A_2}$ 加工,$ {Y_{uA}}_{_1{A_2}} = 1 $ ,否则$ {Y_{uA}}_{_1{A_2}} = 0 $ ;${{t}}_{{\text{A}}_1}$ 为工序${A_1}$ 的单件装配时间。式(7)、(8) 、(9)为加工工序与装配工序的开始时间与结束时间的计算式。
$$ {t_{{\rm{FP}}_{ibj}}}={t_{{\text{SP}}_{ibj}}}+{t_{{\text{P}}_{ibj}}}{B}_{ib},\quad \forall i,b,j $$ (7) $$ {t_{{\text{FA}}_{zu}}}={t_{{\text{SA}}_{zu}}}+{t_{{\text{A}}_{zu}}}{R}_{zn},\quad \forall z,u $$ (8) $$ {t_{{\text{FA}}_{cu}}}={t_{{\text{SA}}_{cu}}}+{t_{{\text{A}}_{cu}}}{R}_{cu},\quad \forall c,u $$ (9) 2. 算法设计
遗传算法原理简单,通用性强,不受限制条件的约束,具有隐含并行性和全局解空间搜索能力[18],但其缺点是容易早熟收敛。本文选用改进过后的遗传算法解决上述NP-hard问题,辅以邻域搜索来增强局部搜索能力。针对本文问题特性设计出邻域结构N1,给出一种混合型解码方式进行求解,并在机器故障时提出相应调度策略。
2.1 编码与初始化
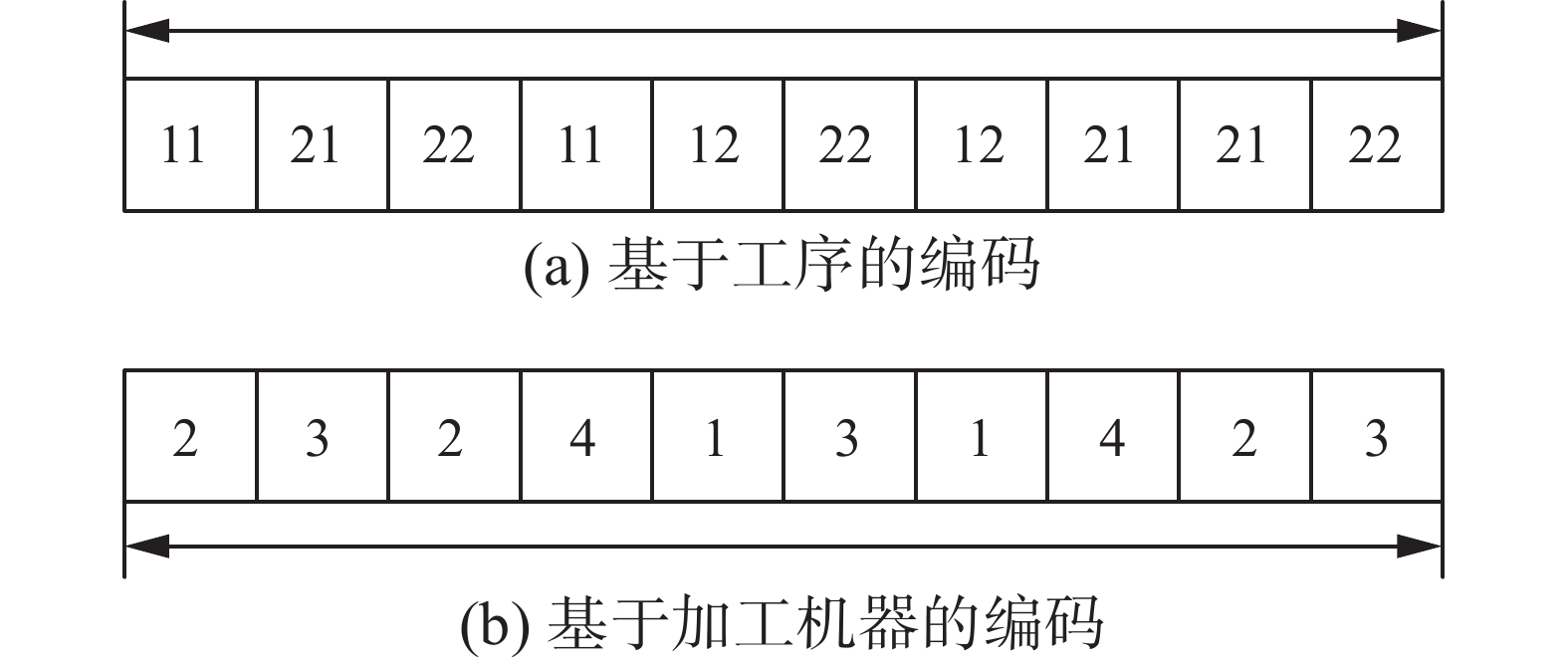
染色体的编码是遗传算法的关键,良好的编码方式会提高执行效率。本文采用MSOS编码方式[19]。染色体总长度为总工序数
$E$ ,如图1所示,由两部分组成,第一部分为基于工序的编码,用来确定各工件各批次各工序的加工顺序,从左往右第一个21表示工件2第1批次的第1道工序,以此类推;第二部分为基于加工机器的编码,用来确定加工各道工序的加工机器。由于装配阶段的独特性,编码中没有给出装配设备号。初始解的质量对算法的求解速度和质量极为重要,为提高初始解在机器选择部分中的质量和初始种群的多样性,使用GLR初始化方法[20]。设置全局选择、局部选择和随机选择的比例分别为0.6、0.3和0.1。
2.2 遗传算子设计
2.2.1 选择
选择是为了使质量高的个体能以更高的几率生存,避免有效基因的损失,从而加快全局收敛性,提高计算效率。本文使用锦标赛选择并辅以精英保留策略,锦标赛选择的操作方法为每次从种群中选出3个个体进行适应度的比较,将适应度高的个体插入到交叉池,如此循环,直到填满交叉池为止。
2.2.2 交叉
交叉是主要的遗传操作,利用父代个体产生适应度更高的新个体,有效增加种群多样性以保证算法的全局搜索能力。交叉的方式有很多,为避免产生非法解,工序部分采用基于工件优先顺序的交叉算子[21],基于加工机器的编码则采用两点交叉[22]。
2.2.3 变异
变异通过随机改变染色体的某些基因来生成新的个体,增加种群多样性,在一定程度上影响着遗传算法的局部搜索能力。本文采用两种变异算子,基于工序的编码采用交换变异算子,即从染色体中随机选择两个位置的基因,然后将它们进行位置交换;基于加工机器的编码则采用单点变异算子,随机选择一个基因位置,然后生成一个不大于该位置工序可选加工机器总数的随机整数,并将其填入所选的基因位置。
2.2.4 邻域搜索
遗传算法作为一种群优化算法,存在早熟和局部搜索能力差的问题。变邻域搜索算法通过不同邻域结构间的系统化切换,可以防止搜索陷入局部最优,增强局部搜索能力[23]。在柔性加工与装配作业车间分批联合调度问题中,最大完工时间为最终成品的组装完成时间,而组件和成品的组装开始时刻又受到零件最后一道工序完工时间的影响。基于此特点,本文设计了一种针对该问题的工件末工序前移的邻域结构N1和一种随机的邻域结构N2。
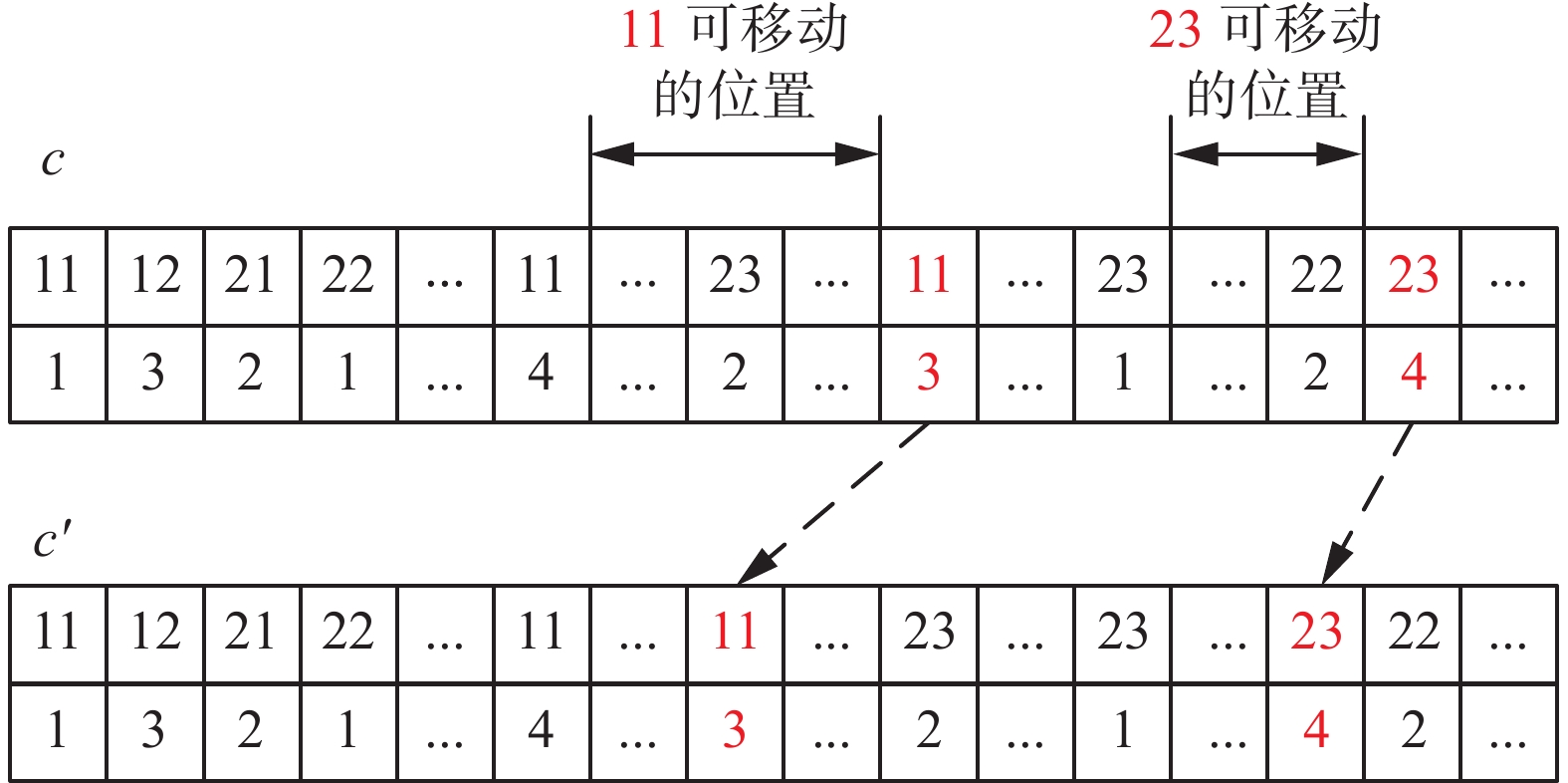
N1:在染色体中找到工件
$ i $ 的第$ b $ 批次的最后一道工序${P_{ib{O_i}}}$ ,并将其向前移动到${P_{ib({O_i} - 1)}}$ 与${P_{ib{O_i}}}$ 之间随机一个位置。对所有工件的所有批次的最后一道工序都执行上述操作,便可提前进行装配操作从而缩减最大完工时间。例如图2中,假设染色体c为某完整染色体片段,工件1和工件3的工序数均为3,将工序11和23的最后一道工序向前移动至其可移动范围,则c'为移动后的一种情况。N2:随机选择某个零件i总数基因10%的基因,为这些基因重新分配加工机器。
2.3 基于装配设备负载均衡的混合贪婪解码
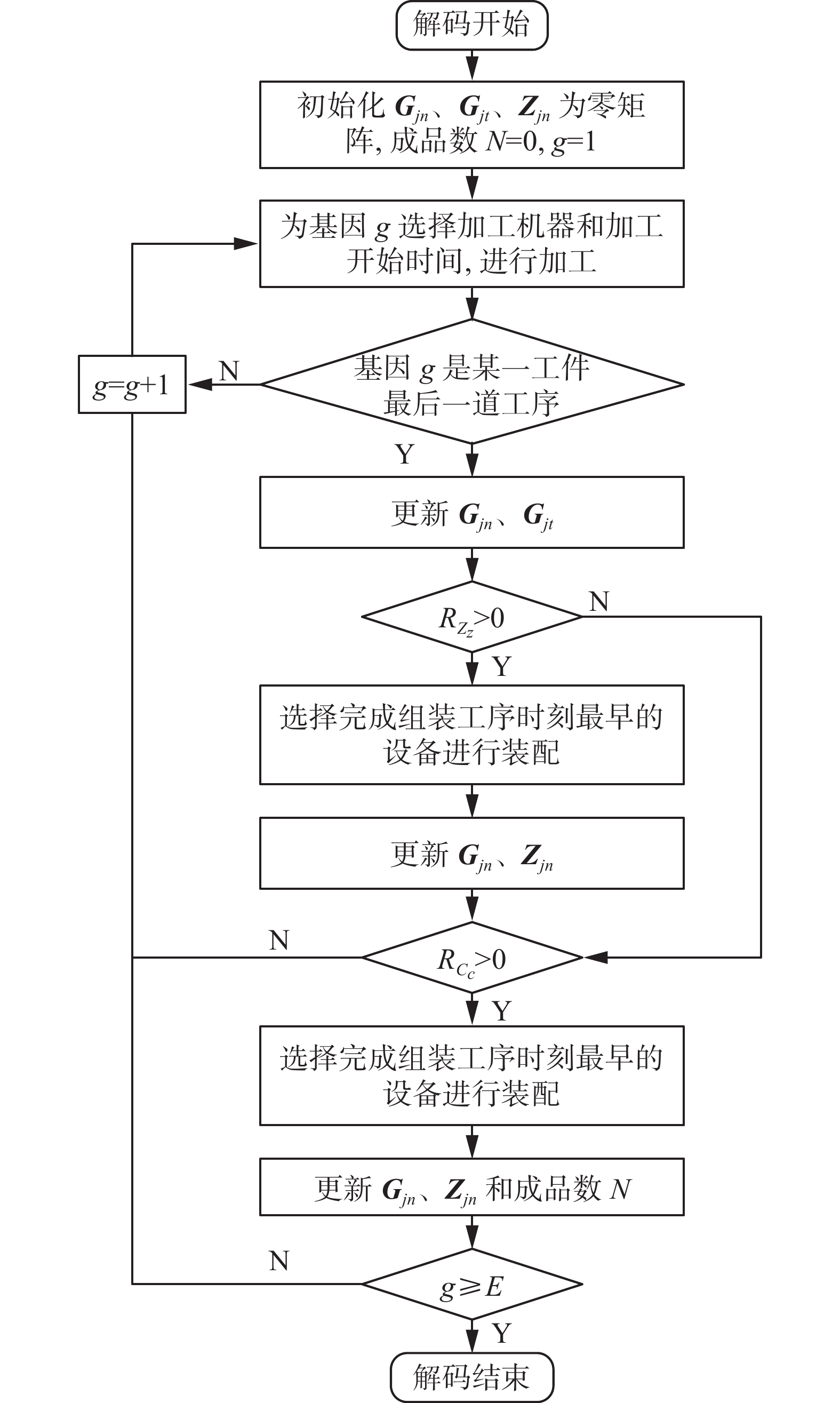
车间调度领域的解码方式可以分为三大类:半主动解码、主动解码和全主动解码[24],比如传统的贪婪解码属于主动解码。由于考虑到批量装配,而装配设备号未编入编码,所以单一的贪婪解码并不适用于此问题。考虑该问题的特性并希望快速和有效的完成解码,本文设计了一种基于装配设备负载均衡的混合贪婪解码,流程图如图3所示。
在工件加工的部分采用贪婪解码,在装配部分提出一种基于装配设备负载均衡的装配设备选择策略,该策略步骤如下:
1) 得到当前需要进行组装的工序
${A_{zu}}$ (或者${A_{cu}}$ )信息;2) 列出此工序所有可用装配设备
$u$ ;3) 选择可选设备中完成该装配工序时刻早的设备进行装配,即
$u$ 为使${t_{{\text{FA}}_{zu}}}$ (或者${t_{{\text{FA}}_{cu}} }$ )取得最小值的设备。融合上述策略后,基于装配设备负载均衡的混合贪婪解码具体步骤为:
1) 初始化参数,令基因位置
$g = 1$ ;2) 判断当前基因代表的工序是否为某一工件
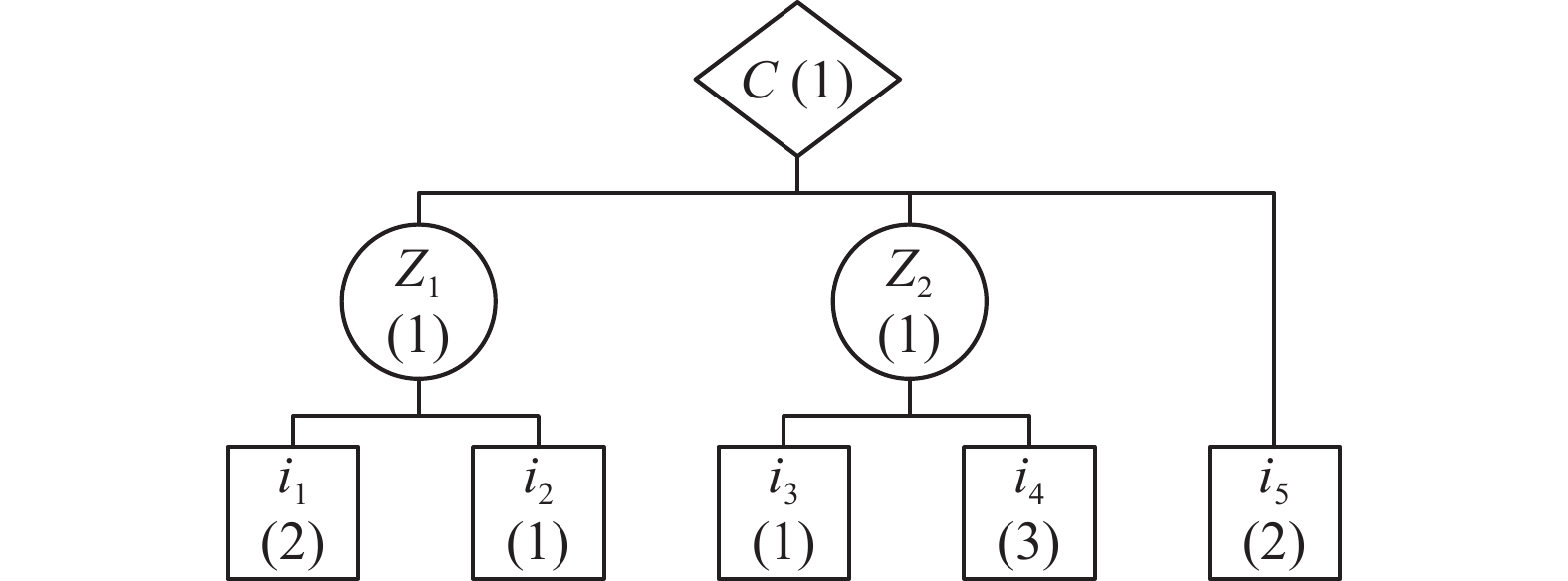
$i$ 的最后一步工序${P_{ib{O_i}}}$ ,若是则更新工件$i$ 的完工数,写入矩阵${{\boldsymbol{G}}_{jn}}(i,1)$ ,${{\boldsymbol{G}}_{jn}}(i,1) $ 为$n \times 1$ 矩阵,记录各个工件当前已完成加工而未参与组装的数目;更新记录完工时间,写入矩阵${{\boldsymbol{G}}_{jt}}(i,b)$ ,${{\boldsymbol{G}}_{jt}}(i,b) $ 为$n \times {p_i}$ 矩阵,记录各个工件各批次加工完成的时间;否则,令$g = g + 1$ 并重复步骤2);3) 根据BOM结构图判断更新完成的工件数量是否能组装成组件
$z$ ,若能则为此道装配工序分配机器进行组装并更新已完成的组件数,写入矩阵${{\boldsymbol{Z}}_{jn}}\left( {z,1} \right)$ ,${{\boldsymbol{Z}}_{jn}}\left( {z,1} \right) $ 为$d \times 1$ 矩阵,记录现有各个组件的数目,同时更新$ {{\boldsymbol{G}}_{jn}} $ ;否则直接转步骤4)。更新${{\boldsymbol{Z}}_{jn}}$ 和${{\boldsymbol{G}}_{jn}}$ 具体方法为:假设某BOM结构如图4,图中括号里的数字代表组成单件成品或组件需要的组件或者工件的数量,则式(10)、(11)为更新表达式,为方便描述,用M代表括号中的数字。$$ {{\boldsymbol{G}}_{jn}} = \left[{{{\boldsymbol{G}}_{Jn}}}\quad{\boldsymbol{R}}_Z\right] \times {\left[ 1\quad{ - {{M}}} \right]^{\rm{T}}} $$ (10) $$ {{\boldsymbol{Z}}_{jn}} = \left[{{{\boldsymbol{Z}}_{Jn}}}\quad{\boldsymbol{R}}_Z\right] \times {\left[1\quad{{{M}}}\right]^{\rm{T}}} $$ (11) 式中
${\boldsymbol{R}}_Z$ 矩阵为对应的预装组件数矩阵,比如在BOM结构的前提下,式(10)中${\boldsymbol{R}}_Z$ 与${{\boldsymbol{G}}_{jn}}$ 相对应,为${\left[{{\boldsymbol{R}}_{\rm{Z}_1}}\;\;{{\boldsymbol{R}}_{\rm{Z}_1}}\;\;{{\boldsymbol{R}}_{{\rm{Z}}_2}}\;\;{{\boldsymbol{R}}_{{\rm{Z}}_2}}\;\;0\right]^{\rm{T}}}$ 。4) 根据BOM结构判断更新完成后的工件数量和组件数量是否能组装成为成品,若能则为此道工序分配设备进行组装并更新已完成成品数量,同时按照式(10)、(12)更新
${{\boldsymbol{G}}_{jn}}$ 和${{\boldsymbol{Z}}_{jn}}$ ;否则令$ g = g + 1 $ 转步骤2)。$$ {{\boldsymbol{Z}}_{jn}} = [{{{\boldsymbol{Z}}_{jn}}}\quad{\boldsymbol{R}}]_C \times {[1\quad - {M}]^{\text{T}}} $$ (12) 式(10)、(11)、(12)中M表示一个可变参数,与参与计算的工件或者组件有关,比如
${\boldsymbol G}_{jn}\left(1,1\right)= $ $ {\boldsymbol G}_{jn}\left(1,1\right)-{\boldsymbol{R}}_{Z_{1}}M$ 中M与工件$ {i_1} $ 相关,则${M} = 2$ ,而${\boldsymbol Z}_{jn}\left(1,1\right)={\boldsymbol Z}_{jn}\left(1,1\right)+{{\boldsymbol{R}}_{\text{Z}_{1}}}M$ 中$M$ 与组件$ {z_1} $ 相关,则$M = 1$ 。2.4 机器故障发生后的调度策略
2.4.1 装配设备发生故障
与FJSP中的机器损坏不完全一样,在柔性加工与装配作业车间中除了工件加工机器可能会发生故障,用于装配的装配设备也存在着发生故障的可能性。由于本文引入了柔性装配,若装配设备发生故障,便不必停工等待设备修理,可以进行重调度,选择其他的装配设备进行装配作业,尽可能缩短最大完工时间。
2.4.2 加工机器发生故障
加工机器发生故障时会面临两种情况:
情况一:故障时此机器处于空闲状态;
情况二:故障时此机器正在加工某一批零件。
若为情况一,则根据静态调度的结果,记录当前还未完成加工的工序,在机器损坏时进行完全重调度。
若为情况二,机器损坏时正在被此机器加工的
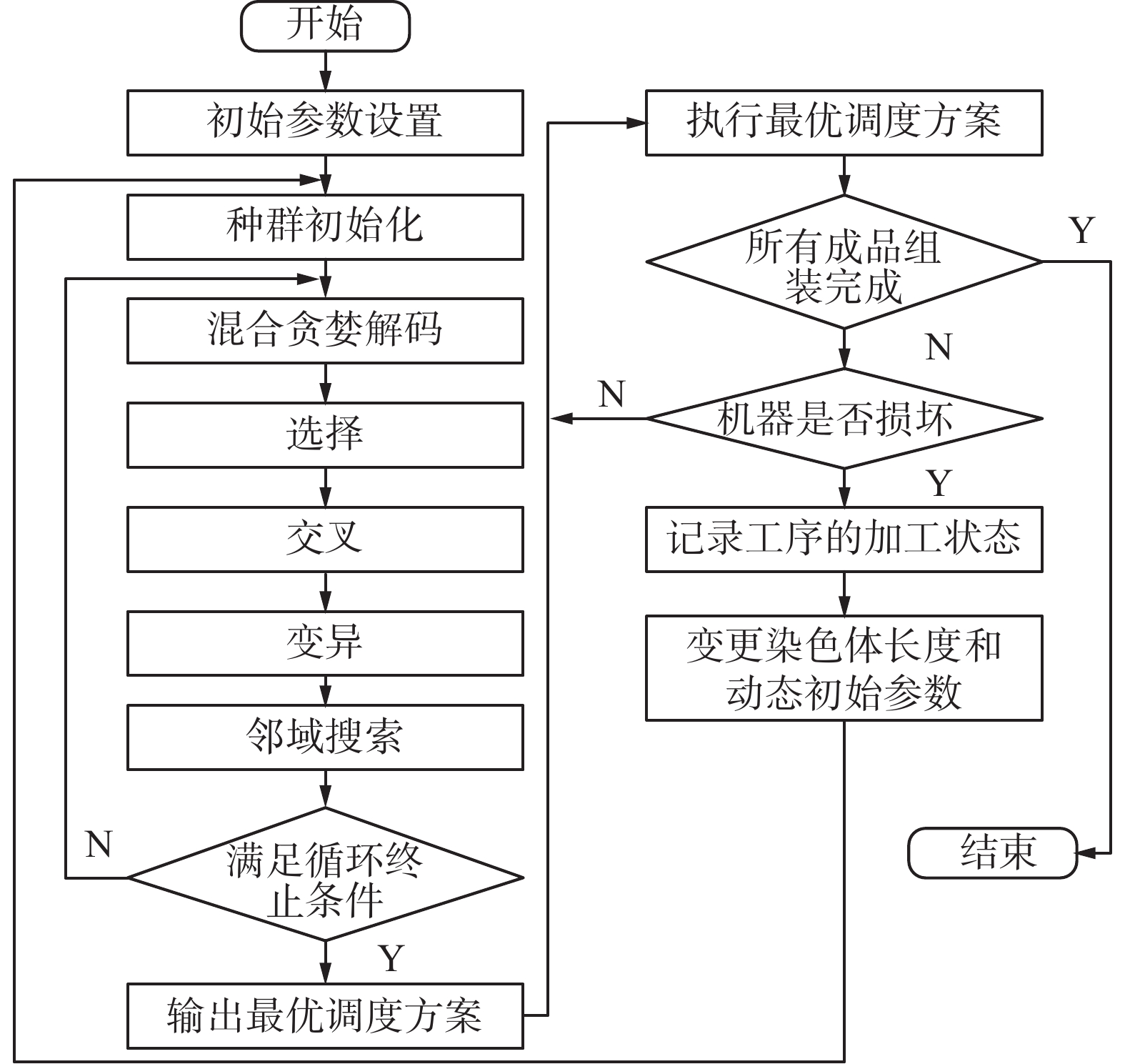
$ {P_{ibj}} $ 将会被分成两个批次,一批为已经完成了此道工序加工的工件,另外一批为还未来得及完成此道加工工序的工件。此时,由于工件$ i $ 的批次和批量都发生了改变,原来的染色体便不再合法,因此无法直接进行重调度。需要对染色体进行调整,加入新的基因,使重调度能够顺利进行,关于染色体的调整将结合算例1进行具体说明,算法总流程图如图5所示。综上,机器故障发生后的调度策略具体步骤为:
1) 判断在
$ {T_s} $ 时刻发生故障的机器类型,若是装配设备$ u $ 故障则转至步骤2);若是加工机器$ k $ 则转至步骤3);2) 判断设备
$ u $ 在故障时刻是否正在组装工件,若是则记录此工序完成组装的组件或者成品个数,转至步骤5);否则直接转至步骤5);3) 判断机器
$k$ 的当前情况,若是情况1则转至步骤5);若是情况2,即工序$ {P_{ibj}} $ 正在被此机器加工,则转至步骤4);4) 将
$ {B_{ib}} $ 个工件$ i $ 划分成已经完成此道工序加工的$ {B_{ib}}_1 $ 件和未完成加工的$ {B_{ib}}_2 $ 件两个批次,将新的基因考虑到动态染色体中;5) 记录现有的已完工工件数、组件数、成品数和所有机器的可开工时间;
6) 根据当前已完成加工的工序和最优静态甘特图得到还未加工的工序,将其考虑到动态染色体中;
7) 初始化动态染色体开始重调度,获得最优方案。
3. 算例分析
为了验证本文算法以及动态调度策略的有效性,以下设计了两个算例进行说明。在MATLAB 2016a上进行算例测试,运行环境为:Windows 10操作系统,3.00 GHz,8 GB RAM。设置算法相关参数:静态初始种群规模为400,动态初始种群规模为200,交叉率为0.8,变异率为0.2,迭代次数为120次。
3.1 算例1
算例1选用文献[25]中提出的问题并适当拓展修改。5种工件的批量分别为20、10、10、30、20,共有10台零件加工机器,3台装配设备。最后组装成一种成品,BOM结构如图4,装配工序信息如表1。
表 1 装配工序信息Table 1 Assembly process informationmin 装配设备 被组装的组件或成品 z1 z2 c u1 5 — — u2 — 6 — u3 — — 9 注:表中未填部分代表该设备无法组装对应的组件或成品。 为与文献[25]进行对比,在不同的分批原则上利用本文算法求解该问题,以最小化最大完工时间为优化目标得到的结果如表2。
表 2 算例1结果比较Table 2 Comparison of results of example 1min 分批原则 文献[25]中的最优值 本文的最优值 等分4批 162.6 145.2 等分3批 170.4 160.6 等分2批 196.5 196.5 从表2可以看出,除了在等分2批的情况下本文的最优值与文献[25]相同,在等分3批和等分4批的情况下本文的最优值均优于文献[25],验证了本文算法的整体有效性,等分4批时本文最优解甘特图如图6所示。
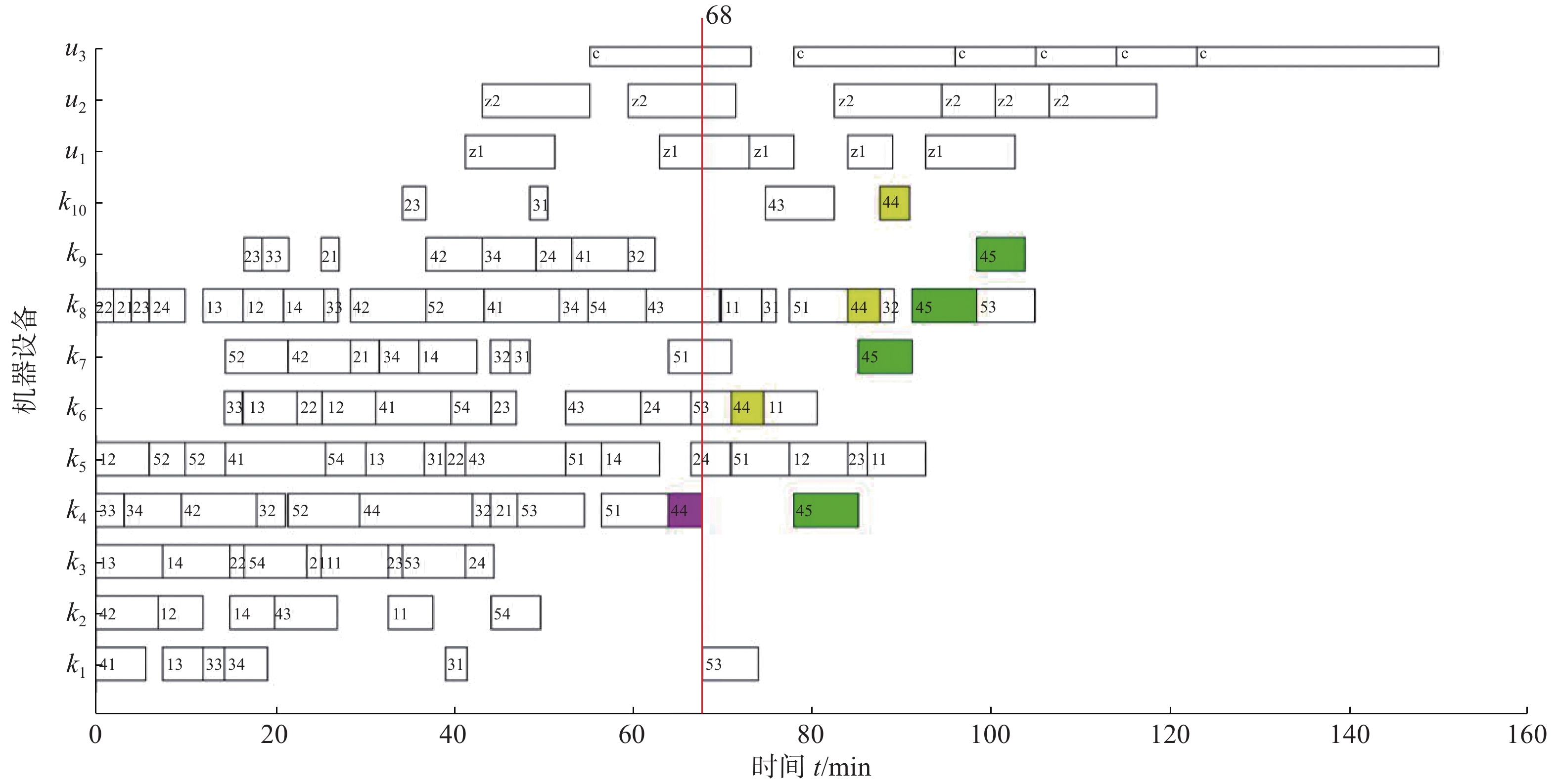
为了说明本文所提算法和解码在处理机器故障时的可行性,对该算例进行了适当拓展。不失一般性,在等分4批的情况下随机选择机器故障时间
$ {T_s} \in \left[ {55,75} \right] $ ,随机选择故障机器$ k \in \left[ {1,10} \right] $ 。假设损坏情况为4号机器在$ {T_s} = 68 $ min时发生故障,故障时长$ {L_t} = 10 $ min,即4号机器在78 min时可以正常运转。利用本文算法求解得动态调度后的最优解,给出机器4在$ {T_s} $ 时刻故障后的重调度甘特图(如图7),可见其在$ {T_s} $ 时刻之前(红色线条左边)的调度顺序与静态甘特图6一致。结合图例简单说明解码机器故障时染色体的更改原则:进行重调度之前首先判断在
${T_s}$ 时刻机器$ k $ 上工件的加工情况。例如:由图7可知,在68 min时机器4正在加工工件4的第4批次的第二道工序(图7中紫红色方块),此道工序中有3件工件完成了加工,有6件未完成加工,因此工件4在后续加工中由4个批次(批量分别为7、7、7、9)变成5个批次(批量分别为7、7、7、3、6)。进而重调度时需要将基因45也考虑进入染色体编码当中,由于45并未完成第二道工序加工,因此45剩4道工序(绿色方块)在重调度后进行,44则剩3道工序(黄色方块)在重调度后进行。3.2 算例2
在FAJSP的问题模型下引入批量和动态元素后的问题十分复杂而且本文提出了装配柔性,故而目前暂未寻得相关算例也没有基准测试算例集。在此生成一个参数随机的算例并完成静态与动态调度,用于说明本文所提算法和策略的有效性与可行性。算例2的BOM结构依旧采用图4,分批原则采用等分4批,其他模型参数设置如表3所示。加工工序信息和装配工序信息分别见表4和表5。
表 3 模型参数设置Table 3 Model parameter setting模型参数 参数设置 加工机器数量m 服从离散均匀分布U(5,11) 装配设备数量am 服从离散均匀分布U(2,6) 各工件的工序数Oi 服从离散均匀分布U(3,7) 每道加工工序的加工时间t/min 服从正态分布N(2,1) 单件组件组装时间 ${t_{{\rm{A}}_{zu}}} $/min 服从离散均匀分布U(5,10) 单件成品组装时间 ${t_{{\rm{A}}_{cu}}} $/min 服从离散均匀分布U(9,13) 表 4 加工工序信息Table 4 Process informationmin 工件 工序 可选加工机器 k1 k2 k3 k4 k5 k6 k7 k8 i1 O11 2.7 2.6 2.6 2.3 O12 1.8 1.5 1.9 O13 2.8 2.5 1.2 1.5 i2 O21 2.0 1.8 2.7 O22 2.5 2.1 O23 1.6 2.0 2.3 O24 2.2 2.2 2.6 O25 1.9 1.7 续表 4 工件 工序 可选加工机器 k1 k2 k3 k4 k5 k6 k7 k8 i3 O31 1.8 2.1 1.8 2.2 1.9 O32 1.4 1.3 O33 2.1 2.0 O34 1.9 1.8 1.7 O35 1.3 1.0 1.9 O36 2.1 2.6 2.7 2.9 2.5 i4 O41 2.8 2.6 O42 1.3 2.0 1.5 O43 2.5 2.6 O44 2.4 2.1 2.9 2.2 O45 3.0 2.7 O46 1.9 2.2 2.1 O47 2.8 2.8 2.8 i5 O51 1.5 1.7 1.2 O52 2.0 2.2 1.9 O53 2.5 2.4 2.3 1.9 2.6 2.2 注:表中未填部分代表该设备无法组装对应的组件或成品 表 5 装配工序信息Table 5 Assembly process information min装配设备 被组装的组件或成品 z1 z2 c u1 6 13 u2 7 8 u3 7 11 u4 8 9 12 静态调度情况:为验证邻域结构N1在柔性加工与装配作业车间分批联合调度问题中的有效性。分2种情况各独立运行程序20次得到的结果如表6。
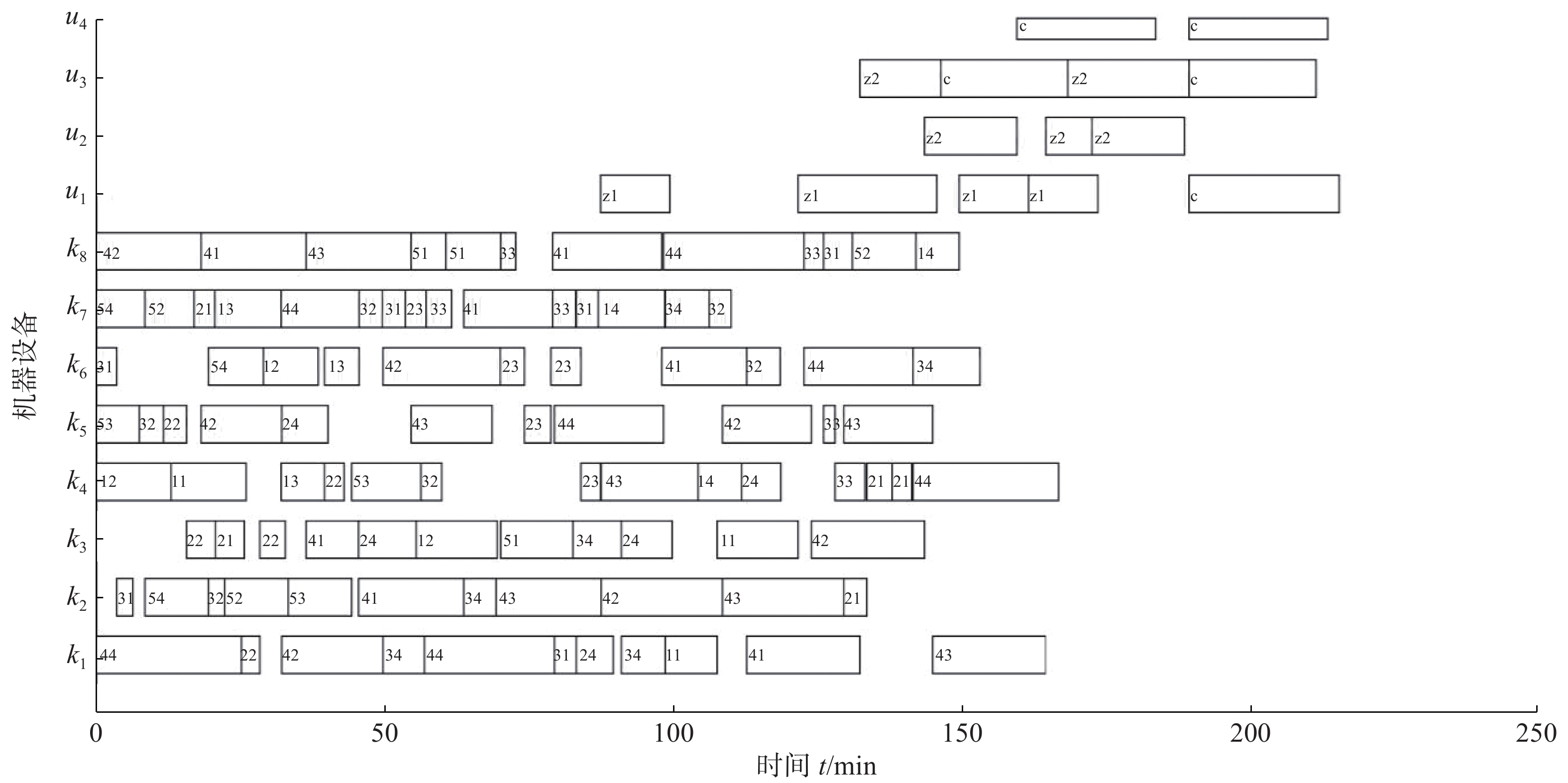
表 6 不同邻域情况下的结果比较Table 6 Comparison of results under different neighborhood structuresmin 同时采用N1和N2 单独采用N2 最优值 均值 最优值 均值 215.8 223.95 217.1 226.38 可见同时采用N1和N2时的最优值和均值均比单独采用N2时更好,验证了N1邻域结构在考虑批量装配问题上的有效性,在一定程度上提高了算法的局部搜索能力和整体性能。利用本文算法多次运行后得到的最优解甘特图如图8所示。
动态调度情况:
1) 工件加工机器发生故障:随机选择机器故障时间
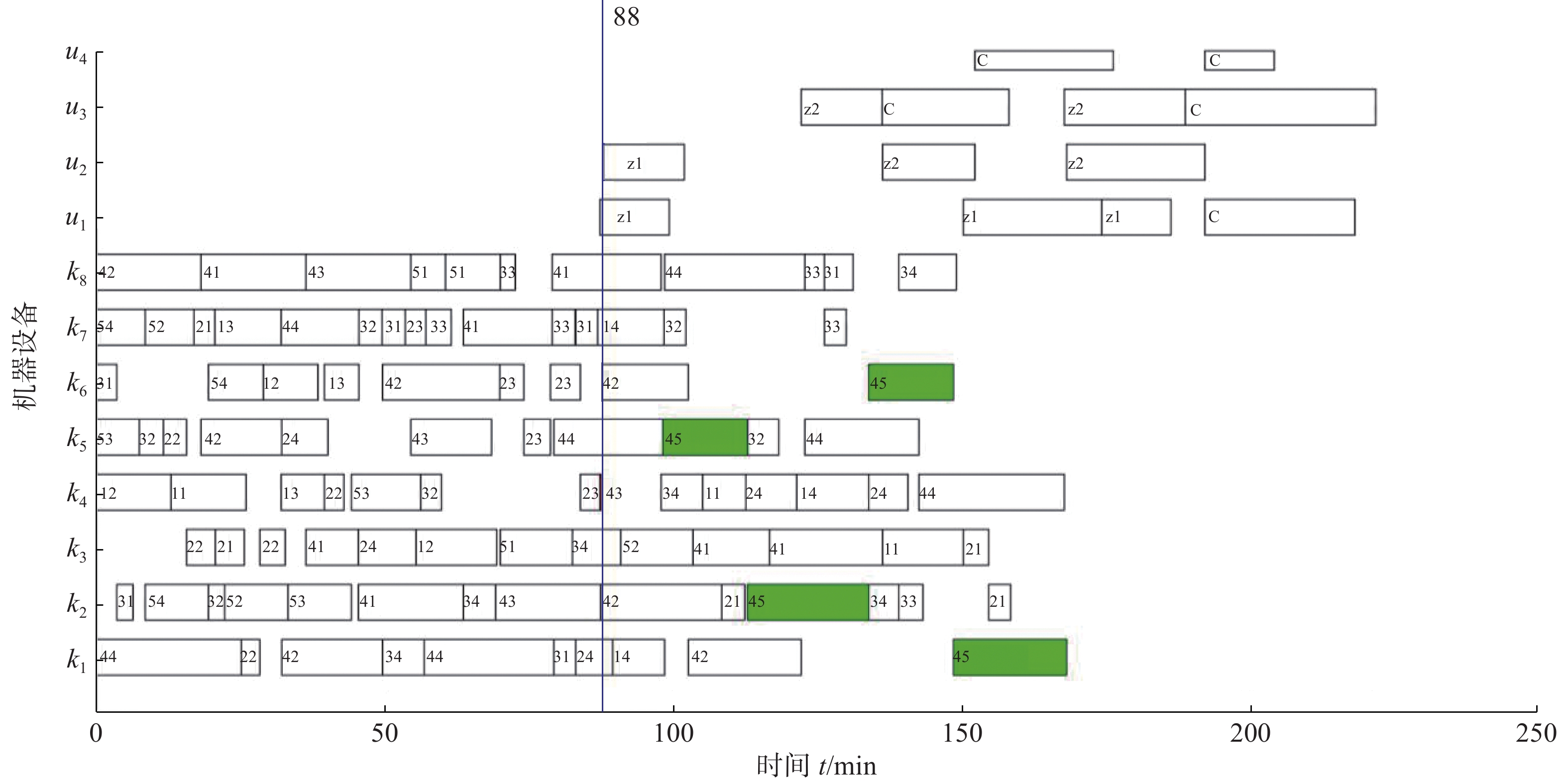
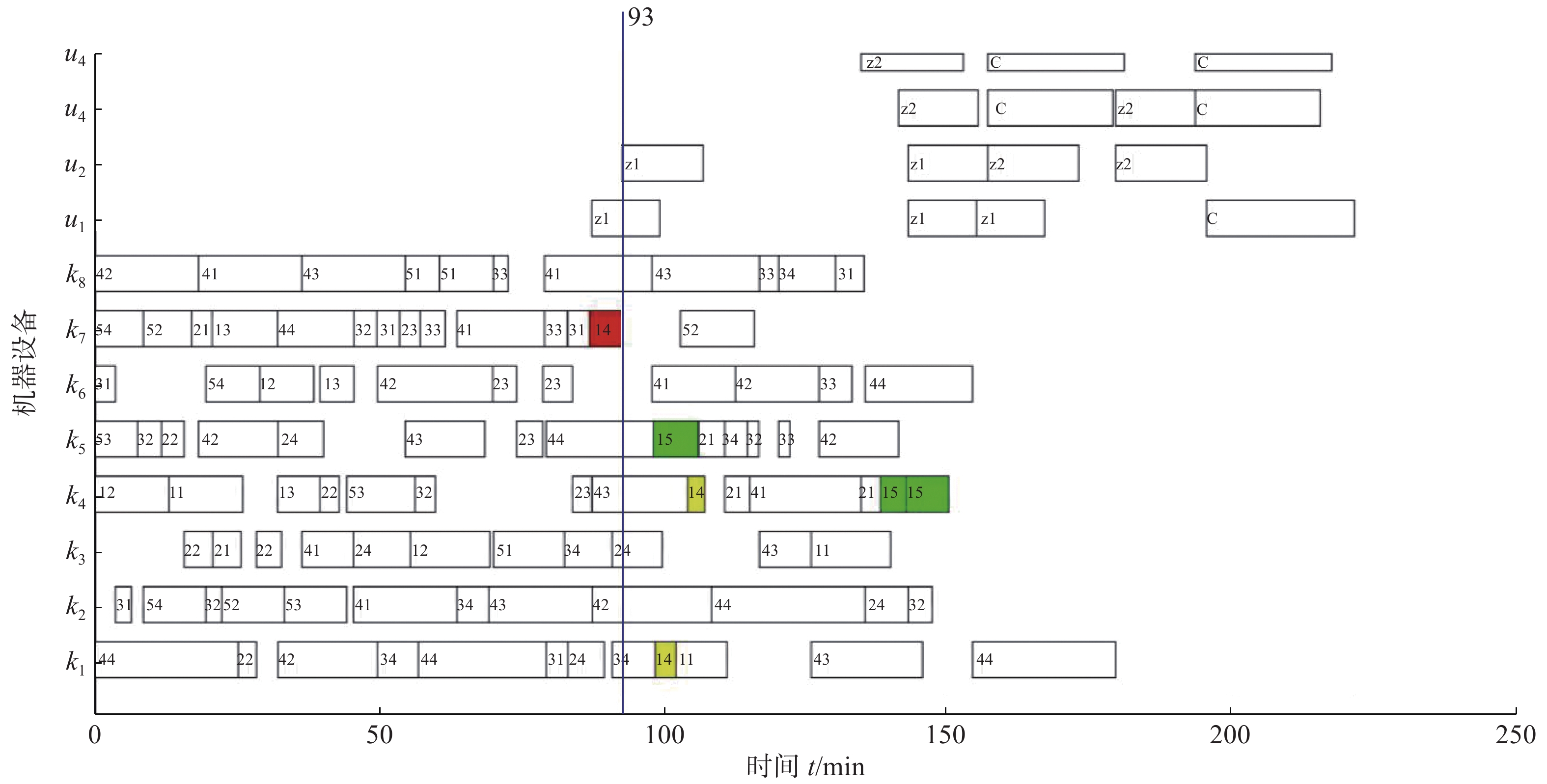
$ {T_s} \in \left[ {55,100} \right] $ ,随机选择故障机器$ k \in \left[ {1,8} \right] $ ,设置故障时长$ {L_t} = 10 $ min。随机抽取两种情况并利用本文算法解得对应静态调度最优解图8的动态调度甘特图如图9、图10所示。① 情况1:
${T_s} = 88,k = 4$ 。② 情况2:
$ {T_s} = 93,k = 7 $ 。图9和图10中的绿色方块均为重调度后产生的工件的第5批次,红色方块为机器故障时刻正在被加工的工序。由于在机器损坏时,工件4的第3批次还未完成一道工序的加工,因此图9中Ts时刻重调度后将没有43工序块。
2) 装配设备发生故障:随机选择机器故障时间
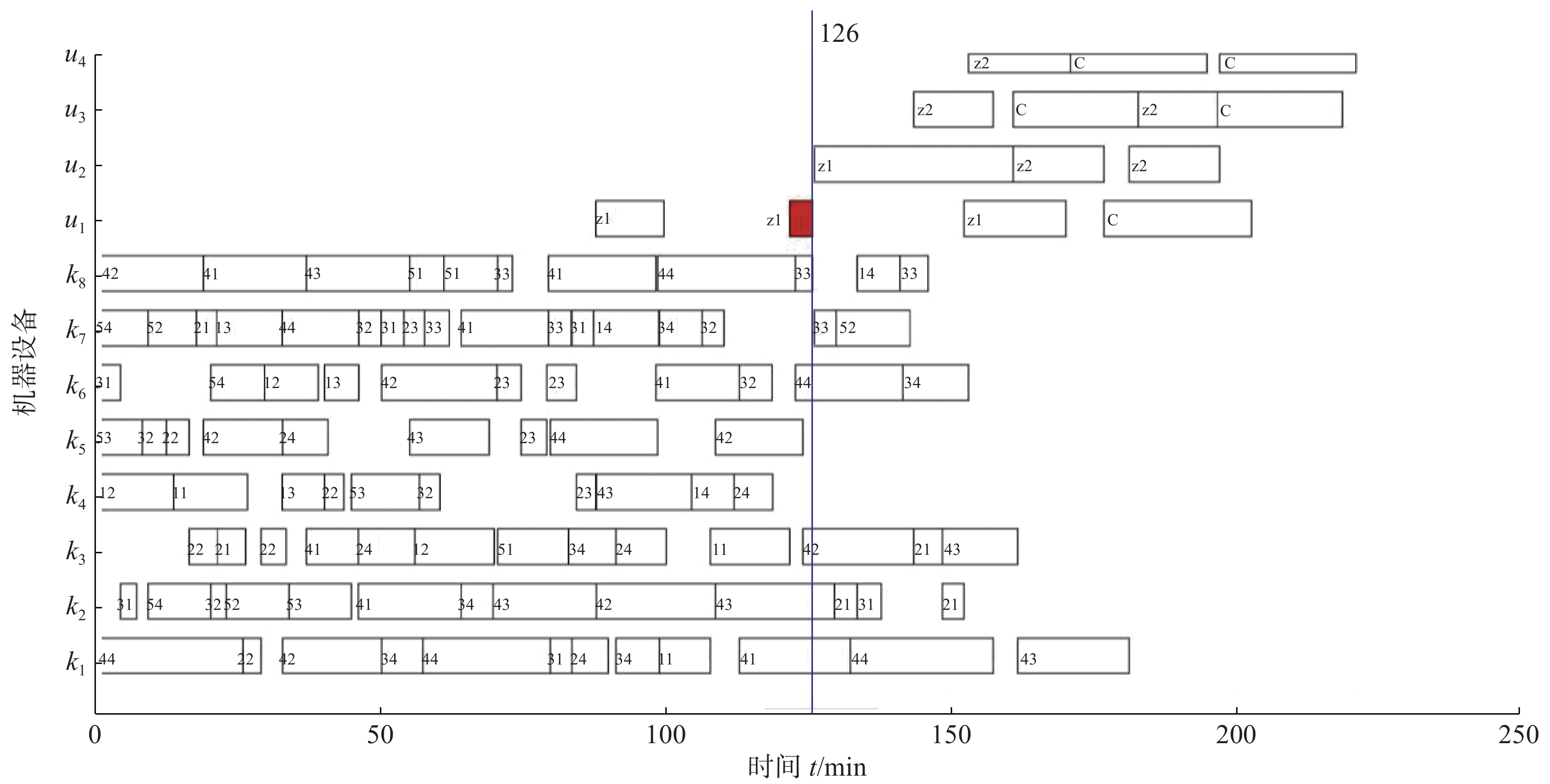
$ {T_s} \in \left[ {110,160} \right] $ ,随机选择故障机器$ u \in \left[ {1,4} \right] $ ,设置故障时长$ {L_t} = 10 $ min。随机抽取两种情况并利用本文算法解得对应静态调度最优解图8的动态调度甘特图,如图11、图12所示:① 情况1:
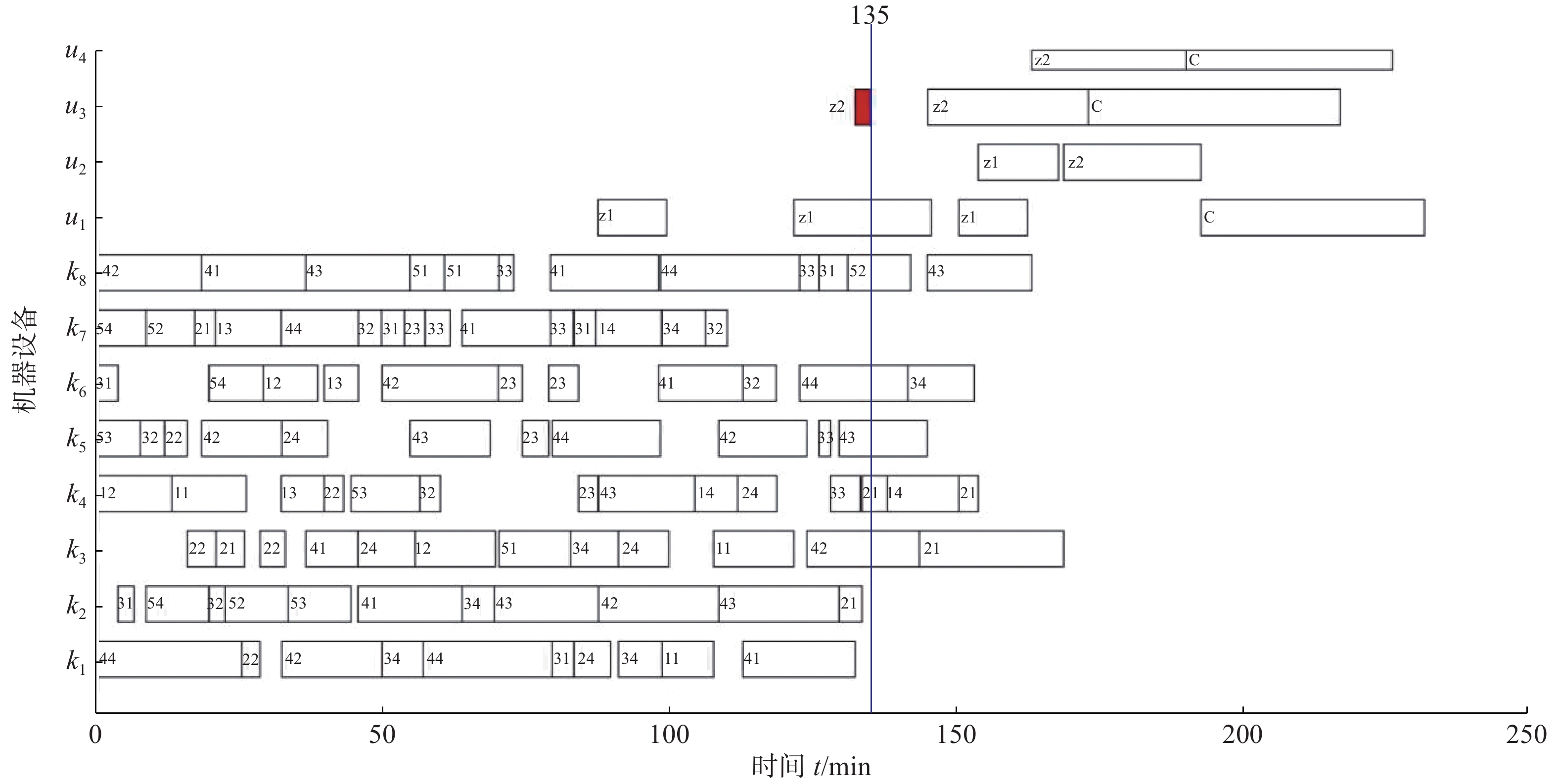
$ {T_s} = 126,u = 1 $ 。② 情况2:
$ {T_s} = 135,u = 3 $ 。4. 结束语
本文针对考虑机器故障的柔性加工与装配作业车间分批联合调度问题进行了研究,以成品的最终组装完成时间为优化目标,引入装配柔性,在遗传算法的基础上进行了改进后求解,并得出了以下结论:
1) 设计了一种针对该问题的工件末工序前移的邻域结构N1,通过算例结果分析可知N1邻域结构的采用使本文算法的局部搜索能力得到提高,求解质量得到改善。
2) 针对工件加工和组件装配两种不同类型的工序不能单一采用贪婪解码的问题,提出了一种基于装配设备负载均衡的混合贪婪解码,在装配解码部分融入一种基于装配设备负载均衡的装配设备选择策略,成功地解决了本文所研究的调度问题。
3) 针对工件加工机器和装配设备故障问题,提出了相应的调度策略和染色体更改规则用于处理机器故障动态事件。
4) 通过对已有算例和本文自编算例的测试,验证了本文所提算法在处理柔性加工与装配作业车间分批联合调度问题上的可行性和有效性。
针对柔性加工与装配作业车间分批联合调度问题,本文提出了相关解码和策略,但在分批原则上采用的是等量一致分批,动态事件只是考虑了一种。多样的分批原则和其他动态事件的考虑都是进一步研究的方向和要点。
-
表 1 装配工序信息
Table 1 Assembly process information
min 装配设备 被组装的组件或成品 z1 z2 c u1 5 — — u2 — 6 — u3 — — 9 注:表中未填部分代表该设备无法组装对应的组件或成品。 表 2 算例1结果比较
Table 2 Comparison of results of example 1
min 分批原则 文献[25]中的最优值 本文的最优值 等分4批 162.6 145.2 等分3批 170.4 160.6 等分2批 196.5 196.5 表 3 模型参数设置
Table 3 Model parameter setting
模型参数 参数设置 加工机器数量m 服从离散均匀分布U(5,11) 装配设备数量am 服从离散均匀分布U(2,6) 各工件的工序数Oi 服从离散均匀分布U(3,7) 每道加工工序的加工时间t/min 服从正态分布N(2,1) 单件组件组装时间 ${t_{{\rm{A}}_{zu}}} $/min 服从离散均匀分布U(5,10) 单件成品组装时间 ${t_{{\rm{A}}_{cu}}} $/min 服从离散均匀分布U(9,13) 表 4 加工工序信息
Table 4 Process information
min 工件 工序 可选加工机器 k1 k2 k3 k4 k5 k6 k7 k8 i1 O11 2.7 2.6 2.6 2.3 O12 1.8 1.5 1.9 O13 2.8 2.5 1.2 1.5 i2 O21 2.0 1.8 2.7 O22 2.5 2.1 O23 1.6 2.0 2.3 O24 2.2 2.2 2.6 O25 1.9 1.7 续表 4 工件 工序 可选加工机器 k1 k2 k3 k4 k5 k6 k7 k8 i3 O31 1.8 2.1 1.8 2.2 1.9 O32 1.4 1.3 O33 2.1 2.0 O34 1.9 1.8 1.7 O35 1.3 1.0 1.9 O36 2.1 2.6 2.7 2.9 2.5 i4 O41 2.8 2.6 O42 1.3 2.0 1.5 O43 2.5 2.6 O44 2.4 2.1 2.9 2.2 O45 3.0 2.7 O46 1.9 2.2 2.1 O47 2.8 2.8 2.8 i5 O51 1.5 1.7 1.2 O52 2.0 2.2 1.9 O53 2.5 2.4 2.3 1.9 2.6 2.2 注:表中未填部分代表该设备无法组装对应的组件或成品 表 5 装配工序信息
Table 5 Assembly process information min
装配设备 被组装的组件或成品 z1 z2 c u1 6 13 u2 7 8 u3 7 11 u4 8 9 12 表 6 不同邻域情况下的结果比较
Table 6 Comparison of results under different neighborhood structures
min 同时采用N1和N2 单独采用N2 最优值 均值 最优值 均值 215.8 223.95 217.1 226.38 -
[1] GAREY M R, JOHNSON D S, SETHI R. The complexity of flowshop and jobshop scheduling[J]. Mathematics of operations research, 1976, 1(2): 117–129. doi: 10.1287/moor.1.2.117 [2] HO N B, TAY J C, LAI E M K. An effective architecture for learning and evolving flexible job-shop schedules[J]. European journal of operational research, 2007, 179(2): 316–333. doi: 10.1016/j.ejor.2006.04.007 [3] 张超勇, 饶运清, 李培根, 等. 柔性作业车间调度问题的两级遗传算法[J]. 机械工程学报, 2007, 43(4): 119–124. doi: 10.3321/j.issn:0577-6686.2007.04.021 ZHANG Chaoyong, RAO Yunqing, LI Peigen, et al. Bilevel genetic algorithm for the flexible job-shop scheduling problem[J]. Chinese journal of mechanical engineering, 2007, 43(4): 119–124. doi: 10.3321/j.issn:0577-6686.2007.04.021 [4] 姜天华. 混合灰狼优化算法求解柔性作业车间调度问题[J]. 控制与决策, 2018, 33(3): 503–508. JIANG Tianhua. Flexible job shop scheduling problem with hybrid grey wolf optimization algorithm[J]. Control and decision, 2018, 33(3): 503–508. [5] ZHANG Sicheng, LI Xiang, ZHANG Bowen, et al. Multi-objective optimisation in flexible assembly job shop scheduling using a distributed ant colony system[J]. European journal of operational research, 2020, 283(2): 441–460. doi: 10.1016/j.ejor.2019.11.016 [6] 石小秋, 李炎炎, 邓丁山, 等. 基于自适应变级遗传杂草算法的FJSP研究[J]. 机械工程学报, 2019, 55(6): 223–232. doi: 10.3901/JME.2019.06.223 SHI Xiaoqiu, LI Yanyan, DENG Dingshan, et al. Self-adaptive multistage GA-IWO for solving flexible job shop scheduling problem[J]. Journal of mechanical engineering, 2019, 55(6): 223–232. doi: 10.3901/JME.2019.06.223 [7] 李明, 雷德明. 考虑准备时间和关键目标的柔性作业车间低碳调度研究[J]. 机械工程学报, 2019, 55(21): 139–149. LI Ming, LEI Deming. Research on flexible job shop low carbon scheduling with setup times and key objectives[J]. Journal of mechanical engineering, 2019, 55(21): 139–149. [8] 徐本柱, 吉靖, 费晓璐. 柔性作业车间中基于工序分批的调度问题与求解[J]. 中国机械工程, 2016, 27(23): 3221–3229. doi: 10.3969/j.issn.1004-132X.2016.23.016 XU Benzhu, JI Jing, FEI Xiaolu. Problems and solutions of flexible job-shop scheduling with operation lot-splitting[J]. China mechanical engineering, 2016, 27(23): 3221–3229. doi: 10.3969/j.issn.1004-132X.2016.23.016 [9] 李聪波, 沈欢, 李玲玲, 等. 面向能耗的多工艺路线柔性作业车间分批优化调度模型[J]. 机械工程学报, 2017, 53(5): 12–23. doi: 10.3901/JME.2017.05.012 LI Congbo, SHEN Huan, LI Lingling, et al. A batch splitting flexible job shop scheduling model for energy saving under alternative process plans[J]. Journal of mechanical engineering, 2017, 53(5): 12–23. doi: 10.3901/JME.2017.05.012 [10] NOURALI S, IMANIPOUR N, SHAHRIARI M R. A mathematical model for integrated process planning and scheduling in flexible assembly job shop environment with sequence dependent setup times[J]. International journal of mathematical analysis, 2012, 6(41): 2117–2132. [11] NOURALI S, IMANIPOUR N. A particle swarm optimization-based algorithm for flexible assemblyjob shop scheduling problem with sequence dependent setup times[J]. Scientia Iranica, 2014, 21(3): 1021–1033. [12] ZHANG Sicheng, WONG T N. Flexible job-shop scheduling/rescheduling in dynamic environment: a hybrid MAS/ACO approach[J]. International journal of production research, 2017, 55(11): 3173–3196. doi: 10.1080/00207543.2016.1267414 [13] 刘爱军, 杨育, 邢青松, 等. 柔性作业车间多目标动态调度[J]. 计算机集成制造系统, 2011, 17(12): 2629–2637. LIU Aijun, YANG Yu, XING Qingsong, et al. Dynamic scheduling on multi-objective flexible job shop[J]. Computer integrated manufacturing systems, 2011, 17(12): 2629–2637. [14] BAYKASOĞLU A, MADENOĞLU F S, HAMZADAYı A. Greedy randomized adaptive search for dynamic flexible job-shop scheduling[J]. Journal of manufacturing systems, 2020, 56: 425–451. doi: 10.1016/j.jmsy.2020.06.005 [15] 杨小佳, 刘建军, 陈庆新, 等. 变扰动强度下柔性装配作业车间调度性能分析[J]. 计算机集成制造系统, 2021, 27(3): 800–814. YANG Xiaojia, LIU Jianjun, CHEN Qingxin, et al. Performance analysis of flexible assembly job shop scheduling under variable disturbance intensity[J]. Computer integrated manufacturing systems, 2021, 27(3): 800–814. [16] 朱传军, 邱文, 张超勇, 等. 多目标柔性作业车间稳健性动态调度研究[J]. 中国机械工程, 2017, 28(2): 173–182. doi: 10.3969/j.issn.1004-132X.2017.02.009 ZHU Chuanjun, QIU Wen, ZHANG Chaoyong, et al. Multi-objective flexible job shop dynamic scheduling strategy aiming at scheduling stability and robustness[J]. China mechanical engineering, 2017, 28(2): 173–182. doi: 10.3969/j.issn.1004-132X.2017.02.009 [17] 张彪. 基于候鸟迁徙算法的批量流混合流水车间调度方法研究[D]. 武汉: 华中科技大学, 2019. ZHANG Biao. Research on lot streaming hybrid flowshop scheduling method based on migrating birds optimization algorithm[D]. Wuhan: Huazhong University of Science and Technology, 2019. [18] 王凌, 郑大钟. 基于遗传算法的Job Shop调度研究进展[J]. 控制与决策, 2001, 16(S1): 641–646. WANG Ling, ZHENG Dazhong. Advances in job shop scheduling based on genetic algorithm[J]. Control and decision, 2001, 16(S1): 641–646. [19] 张国辉. 柔性作业车间调度方法研究[D]. 武汉: 华中科技大学, 2009. ZHANG Guohui. Research on methods for flexible job shop scheduling problems[D]. Wuhan: Huazhong University of Science and Technology, 2009. [20] 张国辉, 高亮, 李培根, 等. 改进遗传算法求解柔性作业车间调度问题[J]. 机械工程学报, 2009, 45(7): 145–151. doi: 10.3901/JME.2009.07.145 ZHANG Guohui, GAO Liang, LI Peigen, et al. Improved genetic algorithm for the flexible job-shop scheduling problem[J]. Journal of mechanical engineering, 2009, 45(7): 145–151. doi: 10.3901/JME.2009.07.145 [21] 张超勇, 饶运清, 刘向军, 等. 基于POX交叉的遗传算法求解Job-Shop调度问题[J]. 中国机械工程, 2004, 15(23): 2149–2153. doi: 10.3321/j.issn:1004-132X.2004.23.020 ZHANG Chaoyong, RAO Yunqing, LIU Xiangjun, et al. An improved genetic algorithm for the job shop scheduling problem[J]. China mechanical engineering, 2004, 15(23): 2149–2153. doi: 10.3321/j.issn:1004-132X.2004.23.020 [22] 张超勇, 饶运清, 李培根, 等. 求解作业车间调度问题的一种改进遗传算法[J]. 计算机集成制造系统, 2004, 10(8): 966–970. doi: 10.3969/j.issn.1006-5911.2004.08.019 ZHANG Chaoyong, RAO Yunqing, LI Peigen, et al. An improved genetic algorithm for Job-Shop scheduling[J]. Computer integrated manufacturing systems, 2004, 10(8): 966–970. doi: 10.3969/j.issn.1006-5911.2004.08.019 [23] PONGCHAIRERKS P. An enhanced two-level metaheuristic algorithm with adaptive hybrid neighborhood structures for the job-shop scheduling problem[J]. Complexity, 2020, 2020: 3489209. [24] 张超勇, 管在林, 刘琼, 等. 一种新调度类型及其在作业车间调度中的应用[J]. 机械工程学报, 2008, 44(10): 24–31. doi: 10.3321/j.issn:0577-6686.2008.10.004 ZHANG Chaoyong, GUAN Zailin, LIU Qiong, et al. New scheduling type applied to solving job-shop scheduling problem[J]. Chinese journal of mechanical engineering, 2008, 44(10): 24–31. doi: 10.3321/j.issn:0577-6686.2008.10.004 [25] 巴黎, 李言, 曹源, 等. 考虑批量装配的柔性作业车间调度问题研究[J]. 中国机械工程, 2015, 26(23): 3200–3207. doi: 10.3969/j.issn.1004-132X.2015.23.014 BA Li, LI Yan, CAO Yuan, et al. Research on flexible job-shop scheduling problem with consideration of batch splitting and assembly[J]. China mechanical engineering, 2015, 26(23): 3200–3207. doi: 10.3969/j.issn.1004-132X.2015.23.014


















































































 下载:
下载: