Negative influence propagation suppression method based on a random walk under cost constraint
-
摘要: 在社交网络的信息传播机制中,不同用户之间信息扩散往往会受到用户之间影响力的影响,因此开展复杂网络分析研究显得格外必要。首先研究在代价约束下,社交网络的影响力传播模型,在未知网络传播原理的情况下,研究如何利用叠加的随机游走策略对网络的影响力传播进行度量,将影响力传播的范围控制在某一子图中,设计出抑制负影响力传播的有效方法。在此基础上,通过渗流来对抑制节点的范围进行控制。实验证明,本文的算法不仅可以有效地限制负影响力的传播,而且在代价约束下能够取得较好的性能。本文不仅对分析、理解和预测网络的拓扑结构、功能和动力学行为具有十分重要的理论意义,而且在舆情管控、虚假信息抑制等领域中也发挥着重要的作用。Abstract: The information diffusion mechanism of social networking among different users is often affected by the influence among users, so it is particularly necessary to carry out a complex network analysis. In this paper, we first study the influence propagation model of complex networks with cost constraints. In the case of the unknown network propagation principle, we use a superposed random walk strategy to measure the influence propagation of networks, control the scope of influence propagation in a certain sub-graph, and design an effective method to suppress negative influence propagation. On this basis, the idea of percolation is introduced to determine the set size of restraining nodes. Experimental results show that this algorithm can effectively limit the propagation of negative influence and achieve better performance under cost constraints. This paper is of great theoretical significance to analyzing, understanding, and predicting social network’s topological structure, function, and dynamic behavior. It plays an important role in public opinion control and false information suppression.
-
近年来,随着在线社交网络的蓬勃发展,成千上万的人通过形式多样的媒介产生前所未有的海量数据,并且数据呈现出多源化、异构化的趋势。其中,影响力最大化是社交网络分析中的一项重要的研究课题,主要是通过网络中的病毒式营销来驱动,目的是找到在特定传播模型下最大化影响力传播的关键用户子集[1-2]。
Morone和Makse在Nature上发表论文,对影响力最大化问题进行了深入探讨[3]。影响力最大化的目标就是在群体中寻找一些关键的种子节点集合用于去最大化其余节点。例如:在病毒式营销的情况下,公司希望依靠口碑推荐来增加其产品的销售,通过挖掘网络中的重要客户的影响力去最大化宣传效果[4]。2020年新型冠状病毒肺炎的爆发,牛津大学、哈佛大学医学院、波士顿儿童医院等团队在Science上发表论文,他们基于中国百度地图迁徙大数据平台的数据,分析了研究人员的迁徙与疫情之间的相关关系,为研究病毒传播提供了强有力的数据支撑[5]。另外,影响力最大化的研究对病毒传播、政府部门进行舆情管控、虚假信息控制以及这些信息的发布源追踪等提供了理论上的支撑,为社会的安全保障活动起到了应有的保障作用[6-7]。
影响力在传播的过程中,存在着正影响力,例如同意、支持、好评等,也存在着诸如差评、谣言等负影响力,很多负面消息都在网络中迅猛肆意地扩散,复杂网络中影响力最大化问题目标是希望能够最大程度地限制网络中负影响力的扩散,切断传播途径。新冠肺炎的爆发,网上出现了大量的谣言,这些谣言经过用户的转发大规模地扩散。例如,网络中曾传白岩松主持一场邀请钟南山院士介绍疫情的活动新闻。一时间,各微信群、朋友圈、论坛,甚至一些大V的博主都转发了该新闻,后来经证实这条新闻是谣言。可以看出负面影响力传播时间短,但是传播速度快,影响范围广。因此,如何对负影响力进行抑制,通过一些措施来制止谣言的传播显得格外重要[8]。
负影响力传播抑制最大化问题其实就是通过选择一些种子节点来尽可能地阻止其竞争实体的影响传播,He等[9]称此问题为影响阻塞最大化(influence blocking maximization,IBM)问题,同时证明了在竞争性线性阈值模型中IBM的目标函数是亚模的,贪婪算法可以达到最优解。当社交网络中出现负面信息并且部分用户已经受其影响时,Arazkhani等[10]提出了基于中心度测量的算法,以寻找适当的正影响种子节点进行扩散以最小化IBM问题。谭振华等[11]结合引力学思想,对负面信息的传播过程进行刻画,并充分考虑用户的个性化特征,对谣言的传播进行抑制。Tong等[12]发现经典的贪心算法与蒙特卡洛模拟相结合的算法运行时间过长,提出了一种随机近似算法,在保证性能的同时提升了运行效率。刘亚州等[13]考虑到不同节点在受到负影响力影响时的差异性以及影响力在网络上传播的特性,进行负影响力传播的研究。Lee等[14]通过分析在影响扩散过程中节点的潜在影响趋势,提出了影响分布重定向算法,通过重定向节点的影响分布,以最大化目标函数来定义影响扩散的初始种子节点。曹玖新等[15]通过K-核和节点的度,提出了基于核数层次特征和影响半径的核覆盖启发式算法。Peng等[16]通过引入社会关系图评估节点影响力,然后使用选举制查找最有影响力的节点,最后通过对前k个有影响力的节点采取免疫措施来阻止负影响力的传播。陈晋音等[17]对网络拓扑结构进行了修改,提出了基于信息级联预测模型的抑制虚假消息传播的算法。江成等[18]从负影响力传播的广度和深度两个维度,对负面信息传播影响力进行测度分析,从而设计出抑制负影响力传播的启发式策略。
目前还有一部分工作是基于网络的社区结构的。Arazkhani等[19]提出了一种使用模糊聚类和集中度度量来找到用于扩散正信息的节点的良好候选子集的方法。Lv等[20]根据影响力的种子节点在社区中的分布,首先确定种子节点的数量,然后,选择影响力最大的前k个节点,提出了一种网络社区结构的模型,从而解决社交网络中影响力扩散的局部性的问题。除此之外,Wang等[21]提出了一种具有用户体验的动态谣言影响最小化模型,该模型同时考虑了谣言的全球知名度和吸引力以及用户体验效用的约束,为每个节点分配一个容忍时间阈值,如果用户的阻止时间超过该阈值,则用户对该网络的满意度将会降低。Zhu等[22]发现位置信息可以在影响力传播中发挥重要作用,针对位置感知影响块最大化问题,通过寻找一个正种子集,以阻止负面影响在给定区域中的传播,提出了基于四叉树索引和最大影响树状结构的两种启发式算法。
从国内外研究现状可以看出,在负影响力抑制研究方面,传统的方法将正负影响力传播特征同等地看待,然而在真实环境中,相比于正影响力的传播,负影响力的传播速度更快,传播范围更广。因此在负影响力传播抑制的过程中,如何对负影响力的传播范围以及抑制节点的抑制范围进行合理的度量显得格外重要,本文利用叠加的随机游走策略对网络的影响力传播进行度量,将影响力传播的范围控制在某一子图中,设计出抑制负影响力传播的有效方法。
1. 问题的描述
本文将社交网络影响力传播问题用图的结构来进行模拟,首先用
$G = (V,E)$ 来定义该网络,其中$V$ 代表网络中节点的集合,节点可以被正影响力激活也可以被负影响力激活。$E$ 代表节点之间边的集合。如果社交网络G中存在两个节点$u$ 和$v$ ,且$u$ 和$v$ 不是同一个节点,那么$(u,v) \in E$ 表示$u$ 和$v$ 之间存在一条连边,它们之间可以进行影响力的直接传播,该传播概率用p来表示。其中,$n$ 表示网络G中节点的总个数,即$n = |V|$ ,用$m$ 表示网络G中的总边数,即$m = |E|$ 。那么影响力最大化问题即转化成在图G中寻找$k$ 个种子节点使其能够阻止节点的负影响力在网络中的传播。在网络G中,如果想要选择一些节点来抑制网络中节点负影响力的传播,则需要付出相应的代价。例如:某企业想通过明星代言来扩大自己的影响力,而每一位明星的出场费是不同的,并且企业的广告宣传费用是有限的,那么成本限制下影响力最大化就转化成如何在有限的成本下,邀请到的明星能够使得企业的影响力最大。因此,本文设
${\rm{cost}}(v)$ 为节点v的代价,成本的总代价为$Q$ 。设$I({S_N},{S_P})$ 为被负种子集合激活的顶点个数的期望值。 (${S_N}$ 为负种子集合,${S_P}$ 为正种子集合)因此,成本限制下的负影响力抑制问题的目的是在顶点集合$V\backslash {S_N}$ 中选择一个最优的正种子集合${S^*}$ ,使得$I({S_N},{S^*})$ 最小:$${S^*} = \arg \mathop {\min }\limits_{v \in (V\backslash {S_N})} I({S_N},{S_P}),\sum\limits_v {{\rm{cost}}(v)} \leqslant {{Q}}$$ (1) 2. 算法的主要思想与步骤
对网络中负节点影响力传播的范围进行模拟,使用抽样子图的方法对抑制节点的综合影响力进行精确地度量,设计出抑制负影响力传播的有效方法,算法步骤如下所示:
算法 基于随机游走的负影响力传播抑制方法(SRW-IBM)
输入 网络
$\rm G$ ,节点个数${\rm{|}}V{\rm{|}}$ ,负种子节点选择概率${N_p}$ 。输出 抑制节点集合
${S^*}$ 。1)设置节点被负影响力影响的阈值
${\theta _v}$ ;2)随机选择部分节点作为负种子集合
${S_N} = $ $ {N_p} \cdot |V|$ ;3)计算被负种子节点集合
${S_N}$ 激活的顶点集合$N({S_N},G)$ ;4)设最大的抑制节点集合为
$S = V - {S_N}$ ;5)针对抑制节点集合中的每一个节点u计算出节点u的传播半径r,并得出节点u的影响力传播子图
${G_u}(r)$ ;计算节点的综合抑制力
${I_u}$ ;End
6)根据渗流理论计算最优抑制节点个数
$k = \lambda {N_p} {\rm{|}}S{\rm{|}} {p_m}$ ,其中pm为相变值;7)选取综合影响力排名靠前的k个节点作为负影响力抑制节点集合
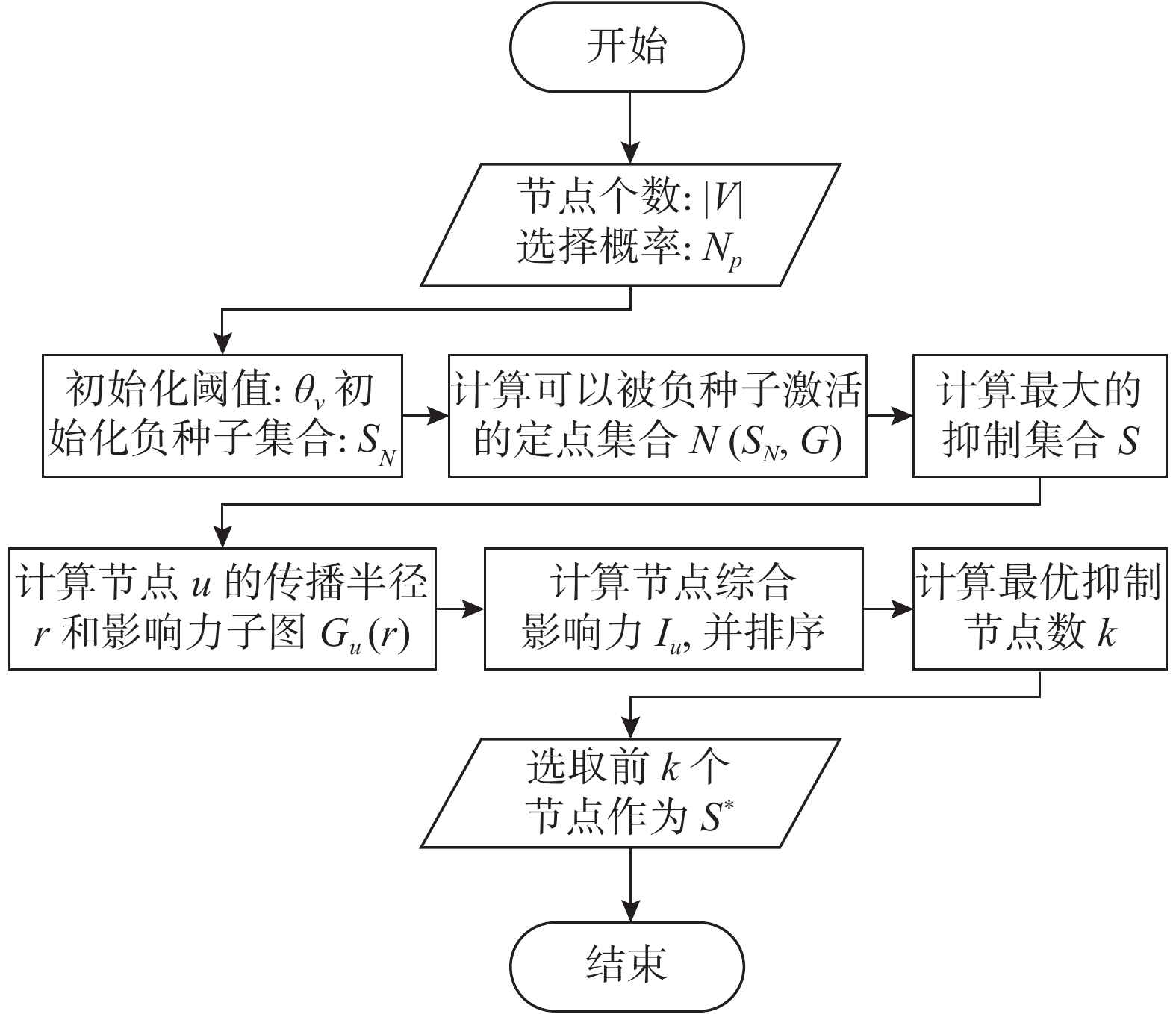
${S^*}$ 。算法的流程图如图1所示。
2.1 两点之间影响力权值计算
本文首先设置节点被负影响力影响的阈值
${\theta _v}$ ,如果两点之间的相似性大于该权值,那么该节点将被负激活。接下来对负节点的传播范围进行估计,设$N({S_N},G)$ 为在网络G中被负种子节点集合${S_N}$ 激活的顶点集合。我们将有叠加的局部随机游走(superposed random walk,SRW)的相关思想与影响力传播模型相结合,对负节点的传播范围进行度量。假设负影响力节点u从t时刻传播,定义${{\boldsymbol{\pi }}^t}(u,v)$ 为t+1时刻负影响力正好传播到节点v的概率,那么可以得到系统演化方程:$${{\boldsymbol{\pi }}^{t + 1}}(u) = {\boldsymbol{P}}{{\boldsymbol{\pi }}^t}(u),\quad t \geqslant 0$$ (2) 式中:
${{\boldsymbol{\pi }}^0}(u)$ 为一个$N\times 1 $ 的向量,只有第u个元素为1,其他元素为0。其中矩阵${\boldsymbol{P}} = [p(u,v)]$ 。$p(u,v) = $ $ a(u,v)/k(u)$ 。$a(u,v)$ 为邻接矩阵A中的元素,$k(u)$ 为节点u的度。设定各个节点的初始资源分布为$q(u)$ ,那么基于t步随机游走的两点之间影响力权值为$${{\boldsymbol{w}}^t}(u,v) = q(u) \cdot {{\boldsymbol{\pi }}^t}(u,v) + q(v) \cdot {{\boldsymbol{\pi }}^t}(v,u)$$ (3) 在这基础上,将t步及以前的结果加起来便得到SRW的影响力权值,即
$$ {{\boldsymbol{w}}^t}(u,v) = \sum\limits_{l = 1}^t {{{\boldsymbol{w}}^l}(u,v) = q(u)\sum\limits_{l = 1}^t {{{\boldsymbol{\pi }}^l}(u,v) + } } q(v)\sum\limits_{l = 1}^t {{{\boldsymbol{\pi }}^l}(v,u)} $$ (4) 对式(4)的计算,关键在于对
${{\boldsymbol{\pi }}^l}(u,v)$ 的计算。设${H^l}(x)$ 为由x出发所有长度不超过l的路径的集合。设路径$h \in {H^l}(x)$ ,定义$d(h)$ 为h中顶点u到v的距离。则${{\boldsymbol{\pi }}^l}(u,v)$ 可以写成:$${{\boldsymbol{\pi }}^l}(u,v) = \frac{1}{{|{H^l}(u)|}}\sum\limits_{h \in {H^l}(x)} {{I_d}} $$ (5) $${I_d} = \left\{ \begin{array}{l} 1,\begin{array}{*{20}{c}} {}&{d(h) = l} \end{array} \\ 0,\begin{array}{*{20}{c}} {}&{其他} \end{array} \end{array} \right.$$ (6) 在得出两个节点之间的影响力权值后,接下来可以求出每一个节点被负影响力节点激活的概率
${\lambda _v} = \displaystyle\sum\limits_{i = 1,i \ne v}^n {{{\boldsymbol{\pi }}^t}(u,v)} $ ,如果节点的激活概率大于负影响力影响的阈值${\theta _v}$ ,那么该节点将被负激活。2.2 抑制节点的影响力子图计算
确定了负激活顶点的集合后,接下来需要对网络中的每一个可能被负种子集合激活的节点v进行抑制,抑制其被负激活。如果v在被负激活之前能被正种子u激活,则称u为v的抑制顶点。其中顶点v的抑制顶点集合,称之为反向被抑制,用
${\rm{RI}}(v,G)$ 来表示。顶点u可以抑制被负激活的顶点集合,称之为节点u的正向抑制,用${\rm{PI}}(u,G)$ 来表示。为阻止节点v在被激活成负节点之前被正激活,需要设计抑制顶点被负激活的规则,即求每个顶点$v \in N({S_N},G)$ 的${\rm{RI}}(v,G)$ 的集合S。本文首先设最大的抑制节点集合$S = V - {S_N}$ ,在计算S中每个节点u的抑制集合${\rm{PI}}(u,G)$ 过程中,对每一节点在整个网络中进行遍历是一项巨大的耗时工程,因此本文拟对S中节点影响力的传播用抽样子图方法进行模拟,使得节点的正影响力在某一范围内进行传播,降低算法的搜索时间复杂度。首先,文中定义
${G_u}(r)$ 是以u为中心,r为半径的子图。给定一个$\varepsilon $ >0,即可以求出一个关于目标节点u的子图${G_u}(r)$ ,使得${G_u}(r)$ 中的顶点v与u的影响力不小于$\varepsilon $ ,而${G_u}(r)$ 外的顶点与u的影响力小于$\varepsilon $ 。这样,可不必考虑${G_u}(r)$ 以外的顶点,只需考虑${G_u}(r)$ 中的节点与u的影响力。接下来,在给定
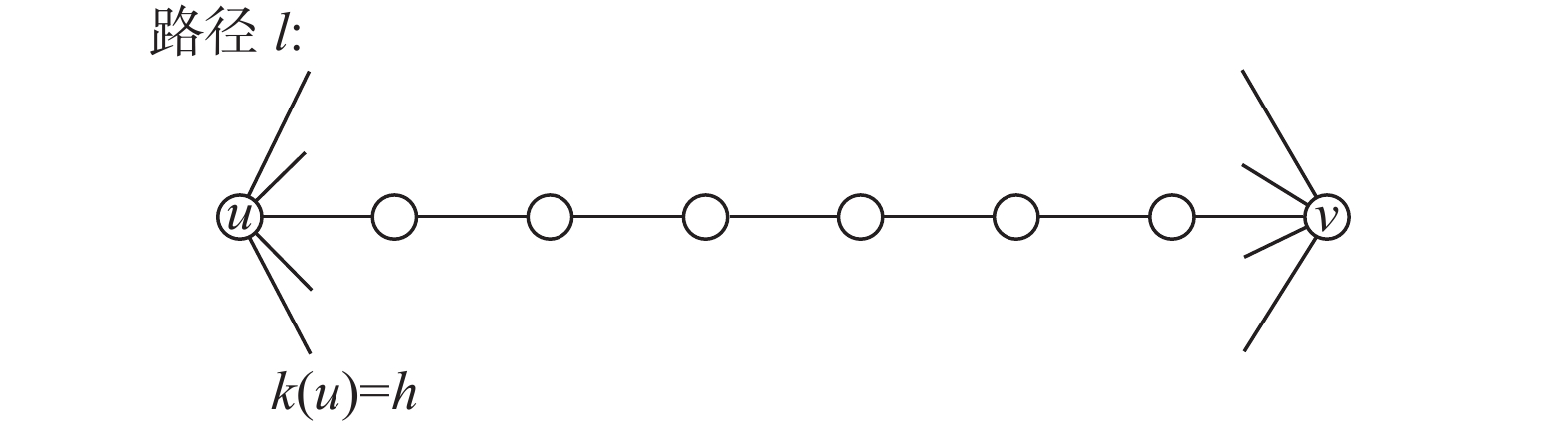
$\varepsilon $ 的情况下,关键是要计算节点u的子图半径r。记${{\boldsymbol{\pi }}^t}(u,v)$ 为${{\boldsymbol{\pi }}^t}(u)$ 的第v个分量,为影响力由顶点u出发,t时刻到达顶点v的概率。设$G$ 的子图${G_u}(r)$ 满足:对所有的节点$y \in G - {G_u}(r)$ ,有${{\boldsymbol{w}}^t}(u,v) \leqslant \varepsilon $ 。因为$y \in G - {G_u}(r)$ ,那么节点v到节点u的最短路径大于r,即影响力从u出发到v最快在r时间到达,即${{\boldsymbol{\pi }}^1}(u,v)$ ,${{\boldsymbol{\pi }}^2}(u,v)$ ,…,${{\boldsymbol{\pi }}^{r - 1}}(u,v)$ ,全为0。对于$t \geqslant r$ ,设$k(u) = h$ ,$k(u)$ 为节点u的度。则从u到v的路径最大可能的概率是由图2所示的路径l构成。路径l满足如下条件:起点u和终点v的度分别为$k(u)$ 和$k(v)$ ,路径l中其余节点的度皆为2。因此,粒子选择此路径的概率为
$$p(l) = \dfrac{1}{h}{\left(\dfrac{1}{2}\right)^{t - 1}}$$ 根据粒子选择路径的概率优化问题,本文使用牛顿法来进行求解。因此得出
${{\boldsymbol{\pi }}^t}(u,v)$ 和${{\boldsymbol{\pi }}^t}(v,u)$ 的取值范围是和搜索半径r相关的某一函数,记为$${{\boldsymbol{\pi }}^t}(u,v) = {{\boldsymbol{\pi }}^t}(v,u) = f(r)$$ 根据式(4)可知如果使得子图外的节点和目标节点的影响力权值满足
${\boldsymbol{w}}(u,v) \leqslant \varepsilon $ ,即要求其满足:$${{\boldsymbol{w}}^t}(u,v) = q(u)f(r) + {q_{\max }}f(r) = (q(u) + {q_{\max }})f(r) \leqslant \varepsilon $$ (7) 由此可得节点搜索半径的取值范围:
$$f(r) \leqslant \frac{\varepsilon }{{q(u) + {q_{\max }}}}$$ (8) 式中:
${q_{\max }} = \mathop {\max }\limits_{z \in G} q(z)$ ,$q(u) = k(u)/M$ ,$k(u)$ 为顶点u的度,M为网络中的总边数。这说明了,在对节点u进行影响力传播时,在给定$\varepsilon $ 时,搜素半径r只要满足式(8),即只需计算目标节点u的子图${G_u}(r)$ 中所有的节点对于节点u的影响力值,而不必计算节点u对图G中所有节点的影响力,因此可以有效降低算法的时间复杂度。抑制节点搜索子图的示意图如图3所示。2.3 抑制节点集合大小的计算
当完成节点影响力的模拟后,本文通过渗流来模拟网络传播影响力的固有能力,进行最优抑制节点个数的选取。在网络G中,本文通过改变传播概率
$p$ 的值,并在网络G上对节点进行随机选择,通过这种模拟方式模拟了影响力扩散的动态演化。其中被选中节点所形成的最大连通子图大小$s$ 与概率$p$ 之间就发生了幂律行为,在相变值${p_m}$ 处,$s$ 变化速率最快,意味着此时影响力传播速度最快,因此本文取${p_m}$ 作为影响力传播速度的上界,即当网络中传播概率$p > {p_m}$ 时,网络传播的能力变化已经不明显了,所以本文将${p_m}$ 作为网络G传播概率的临界概率,即渗流值,并作为网络传播影响力的固有能力的度量标准。因此本文抑制节点的个数定为$k = \lambda \times {N_p} \times {\rm{|}}S{\rm{|}} \times {p_m}$ ,此数值为抑制节点个数的上界,如果超过此数值,那么其余的抑制节点的抑制效果是不明显的。最后在确定完抑制种子节点的个数以后,需要从S集合中挑选出最优的抑制节点。算法首先计算每一个节点u的影响力子图,然后计算抑制集合中节点的个数
$|{\rm{PI}}(u,{G'})|$ ,然后,结合节点的度$k(u)$ 计算出每一个节点的综合抑制力:$${I_u} = |{\rm{PI}}(u,G'){|^\alpha } \cdot k{(u)^{1 - \alpha }}$$ 并对其进行排序,其中
$\alpha $ 为调节节点的影响力子图和节点度的参数。本文将其设置成0.5。最后根据综合抑制力选取前k个抑制节点作为负影响力抑制节点集合。3. 实验结果及分析
3.1 数据集介绍
在实验模拟中,本文通过4个真实数据集来对算法进行测试与分析,4个真实数据集分别是:email[23]、socfbBowdoin47[24]、hamsterster[25]和socfbSmith60[26]。其中,email由欧洲大型研究机构的电子邮件数据组成,数据由发送与接收的邮件信息组成,如果节点
$u$ 和$v$ 之间至少收发过一次邮件,那么$u$ 和$v$ 之间存在一条边。socfbBowdoin47和socfbSmith60是从FaceBook数据中提取出来的,代表着用户之间是否是好朋友。如果节点之间是好友关系,那么节点之间存在一条边。Hamsterster是从hamsterster.com网站上提取的朋友与亲人信息。所有数据集的拓扑属性如表1所示,其中n、m分别为网络中节点和边的总数,网络中最大节点的度用${d_{{\rm{max}}}}$ 表示,平均度用$\bar d$ 表示。网络的同配系数、聚集系数以及网络的密度分别用r、C、D来表示。4个不同的数据集具有不同的网络特性,例如email数据集的同配系数
$r < 0$ ,表示度大的节点倾向性和度小的节点相连接;而其余3个数据集的$r > 0$ ,表示度大的节点更倾向性和度大的节点相连接。hamsterster数据集聚集系数$C$ 更高,因此相比于其余3个数据集而言节点之间的连接更加紧密。表 1 4个不同数据集的拓扑属性Table 1 Topological properties of four different datasets数据集 $n$ $m$ $d_{{\rm{max}}}$ $\overline d $ $r$ $C$ $D$ email 986 16064 345 32.58 −0.03 0.41 0.03 socfbBowdoin47 2252 84387 670 74.94 0.06 0.29 0.03 hamsterster 2426 16630 273 13.70 0.05 0.54 0.01 socfbSmith60 2970 97133 349 65.40 0.04 0.28 0.02 3.2 最优种子节点数量的选取
为了计算网络G的相变值pm,首先需要计算函数F(x)的变化速率。图4中,p为传播概率,纵坐标为函数F(x)的变化速率rate,即函数dF(x)的值。图4中绿色的点用pm来表示,也是函数F(x)变化最快的时候。当网络的传播概率p小于相变值pm时,变化率r还处于较低水平,渗流后的网络由零散的小团块组成,当传播概率p大于pm时,渗流后的网络趋向由主团块组成,逐渐呈现出以最大连通子图为主的图结构。本文相变值pm反应了网络G传播影响力的固有能力,也就是相变值反应网络G中边被激活的能力,即在影响力传播模型下,被激活边占总边数的比例。
因此最终可以通过相变值计算出最优种子节点的个数。如图4所示,本文4个数据集的相变值pm分别为0.020、0.009、0.034、0.008。
3.3 影响力范围的比较与分析
本文将SRW算法和经典的度中心性(degree centrality,DC)[27]、网页排序(pagerank,PR)[28]、随机算法(random,RD)[29]的抑制影响力范围变化随着负种子集合大小变化的结果进行比较,实验结果如图5所示。
在图5中,横坐标为负种子节点占整个网络节点总数的百分比Np,纵轴上的IF表示k个种子节点的综合影响力之和。
计算公式为
$${\rm{IF}} = \sum\limits_{i = 1}^k {{I_{{u_i}}} = \sum\limits_{i = 1}^k {|{\rm{PI}}({u_i},G'){|^\alpha } \cdot k{{({u_i})}^{1 - \alpha }}} } $$ (9) 其中,
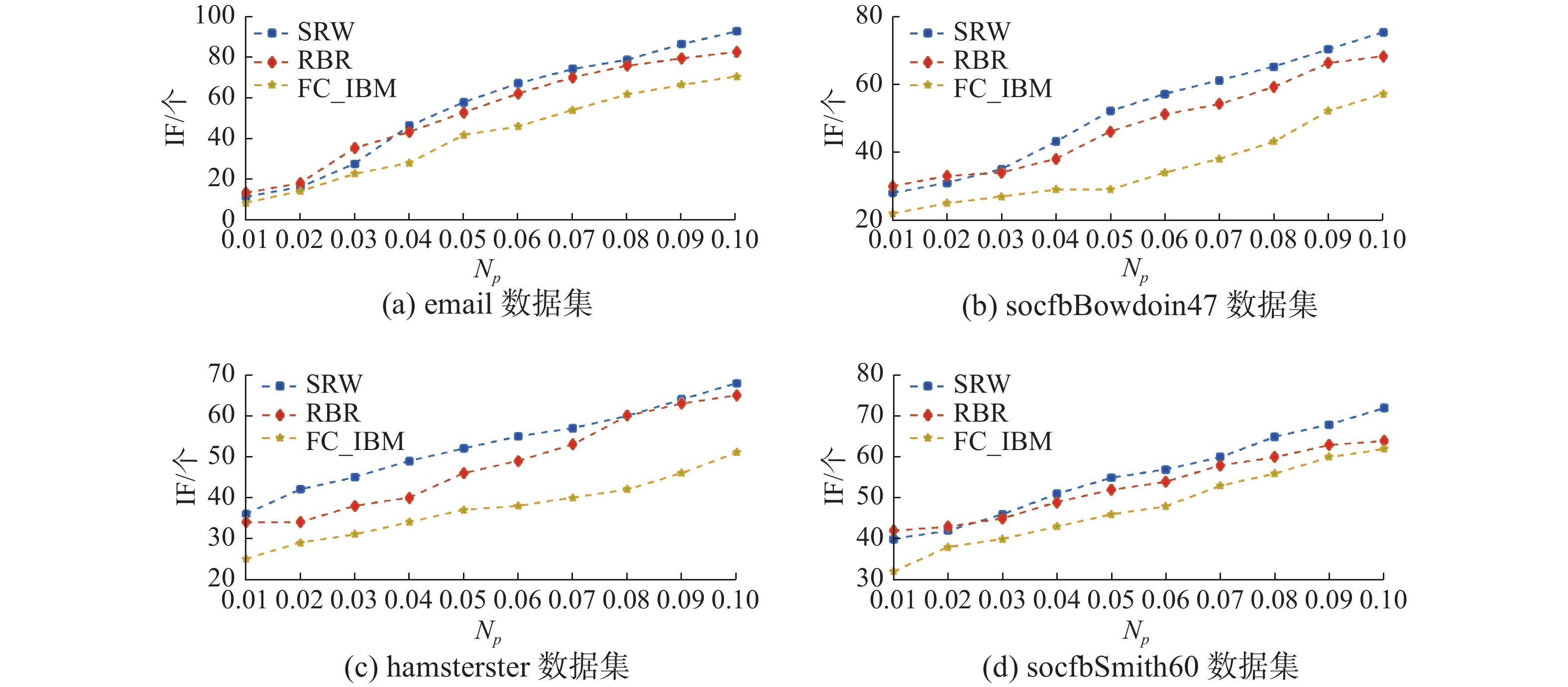
$\alpha \in (0,1)$ 为控制抑制节点个数和节点度影响力的参数。由实验结果可以发现,在不同数据集中,无论负种子集合大小如何变化,SRW算法在选取抑制节点集合所取得的效果几乎都是最优的。另外本文还将SRW算法和基于反向元组的随机化算法(reverse-tuple based randomized,RBR)[14]以及基于社区划分算法FC_IBM[19]的抑制影响力范围变化随着负种子集合大小变化的结果进行比较,如图6所示。
其中RBR算法在Np值较小的时候基于反向元组通过抽样的方法对负节点进行抑制,准确率较高。而FC_IBM算法首先通过模糊聚类对网络进行社区划分,虽然在社区结构比较明显的数据集上该算法的效果略优,但该方法在社区不明显的数据集中效果一般。因为在本文的4个数据集选取过程中,它们的社区结构不是太明显。并且真实数据集中存在着重叠社区的影响。因此本文提出的SRW算法效果的鲁棒性更强。
3.4 影响力成本的比较与分析
负影响力在传播的过程中,需要选取性价比较高的节点作为抑制节点集合,这样可以在有限的成本下最大化完成影响力的抑制。本文中,节点v的成本定义如下:
$${\rm{cost}}(v) = k(v)/{d_{{\rm{max}}}}$$ (10) 其值正比于节点的度,节点的度越大,表明需要选取该节点作为抑制该节点所需要的成本就越高。图7和图8分别为SRW算法与经典算法以及SRW算法与RBR、FC_IBM算法在选取抑制节点集合的成本代价总和随着负种子节点集合大小变化而变化的趋势。
从图7中可以看出,随着负种子节点的增加,抑制节点集合的种子节点成本也逐渐增加,因为需要有更多的种子节点来进行负影响力的抑制。但是其中SRW算法相对于Degree Centrality、PageRank、Random算法,选取的抑制节点集合所需要的成本是最低的。从图8中SRW算法与RBR算法的对比过程中发现,虽然在Np较小时候RBR算法的抑制影响力范围较优,但是他们选择的种子的成本也较大。综上所述,SRW算法在给定的抑制节点数量的前提下可以最大化地影响到其余节点,并且所取的代价也是较优的。
4. 结束语
在社交网络的信息传播机制中,不同用户之间信息扩散往往会受到用户之间影响力的影响。本文主要对负影响力的传播进行抑制研究,在未知影响力传播模型的基础上,通过有叠加的随机游走策略对负影响力传播进行模拟。在抑制节点的影响力度量中,提出了节点的影响力传播子图的概念,使得抑制节点的影响力传播局限在以该节点为源点的某一子图中,有效地降低了影响力计算模拟的复杂度。在此基础上,引入渗流的思想来进行抑制节点集合大小的选取,构建了代价约束下的抑制节点的最优选择方法。实验结果表明,该方法对负影响力抑制中,抑制节点的选取起着重要的指导性作用。
-
表 1 4个不同数据集的拓扑属性
Table 1 Topological properties of four different datasets
数据集 $n$ $m$ $d_{{\rm{max}}}$ $\overline d $ $r$ $C$ $D$ email 986 16064 345 32.58 −0.03 0.41 0.03 socfbBowdoin47 2252 84387 670 74.94 0.06 0.29 0.03 hamsterster 2426 16630 273 13.70 0.05 0.54 0.01 socfbSmith60 2970 97133 349 65.40 0.04 0.28 0.02 -
[1] HUANG Keke, WANG Sibo, BEVILACQUA G, et al. Revisiting the stop-and-stare algorithms for influence maximization[J]. Proceedings of the VLDB endowment, 2017, 10(9): 913–924. doi: 10.14778/3099622.3099623 [2] 吴信东, 李毅, 李磊. 在线社交网络影响力分析[J]. 计算机学报, 2014, 37(4): 735–752. https://www.cnki.com.cn/Article/CJFDTOTAL-JSJX201404002.htm WU Xindong, LI Yi, LI Lei. Influence analysis of online social networks[J]. Chinese journal of computers, 2014, 37(4): 735–752. https://www.cnki.com.cn/Article/CJFDTOTAL-JSJX201404002.htm [3] MORONE F, MAKSE H A. Influence maximization in complex networks through optimal percolation[J]. Nature, 2015, 524(7563): 65–68. doi: 10.1038/nature14604 [4] LYU Linyuan, CHEN Duanbing, REN Xiaolong, et al. Vital nodes identification in complex networks[J]. Physics reports, 2016, 650: 1–63. doi: 10.1016/j.physrep.2016.06.007 [5] TIAN Huaiyu, LIU Yonghonh, LI Yidan, et al. An investigation of transmission control measures during the first 50 days of the COVID-19 epidemic in China[J]. Science, 2020, 368(6491): 638–642. doi: 10.1126/science.abb6105 [6] CALIÒ A, INTERDONATO R, PULICE C, et al. Topology-driven diversity for targeted influence maximization with application to user engagement in social networks[J]. IEEE transactions on knowledge and data engineering, 2018, 30(12): 2421–2434. doi: 10.1109/TKDE.2018.2820010 [7] CHAKRABORTY S, STEIN S, BREDE M, et al. Competitive influence maximisation using voting dynamics[C]//Proceedings of 2019 IEEE/ACM International Conference on Advances in Social Networks Analysis and Mining. Vancouver, Canada, 2019: 978−985. [8] 刘雅辉, 靳小龙, 沈华伟, 等. 社交媒体中的谣言识别研究综述[J]. 计算机学报, 2018, 41(7): 1536–1558. doi: 10.11897/SP.J.1016.2018.01536� LIU Yahui, JIN Xiaolong, SHEN Huawei, et al. A survey on rumor identification over social media[J]. Chinese journal of computers, 2018, 41(7): 1536–1558. doi: 10.11897/SP.J.1016.2018.01536� [9] HE Xinran, SONG Guojie, CHEN Wei, et al. Influence blocking maximization in social networks under the competitive linear threshold model[C]//Proceedings of the 12th SIAM International Conference on Data Mining. Anaheim, USA, 2012: 463−474. [10] ARAZKHANI N, MEYBODI M R, REZVANIAN A. Influence blocking maximization in social network using centrality measures[C]//Proceedings of the 5th Conference on Knowledge Based Engineering and Innovation. Tehran, Iran, 2019: 492−497. [11] 谭振华, 时迎成, 石楠翔, 等. 基于引力学的在线社交网络空间谣言传播分析模型[J]. 计算机研究与发展, 2017, 54(11): 2586–2599. doi: 10.7544/issn1000-1239.2017.20160434 TAN Zhenhua, SHI Yingcheng, SHI Nanxiang, et al. Rumor propagation analysis model inspired by gravity theory for online social networks[J]. Journal of computer research and development, 2017, 54(11): 2586–2599. doi: 10.7544/issn1000-1239.2017.20160434 [12] TONG Guangmo, WU Weili, GUO Ling, et al. An efficient randomized algorithm for rumor blocking in online social networks[J]. IEEE transactions on network science and engineering, 2020, 7(2): 845–854. doi: 10.1109/TNSE.2017.2783190 [13] 刘亚州, 王静, 潘晓中, 等. 节点影响力下无标度网络谣言传播研究[J]. 小型微型计算机系统, 2018, 39(11): 2375–2379. doi: 10.3969/j.issn.1000-1220.2018.11.005 LIU Yazhou, WANG Jing, PAN Xiaozhong, et al. Research on scale-free network rumor spreading under node influence[J]. Journal of Chinese computer systems, 2018, 39(11): 2375–2379. doi: 10.3969/j.issn.1000-1220.2018.11.005 [14] LEE C L, SUNG C E, MA Haoshang, et al. IDR: positive influence maximization and negative influence minimization under competitive linear threshold model[C]//Proceedings of the 20th IEEE International Conference on Mobile Data Management (MDM). Hong Kong, China, 2019: 501−506. [15] 曹玖新, 董丹, 徐顺, 等. 一种基于k-核的社会网络影响最大化算法[J]. 计算机学报, 2015, 38(2): 238–248. https://www.cnki.com.cn/Article/CJFDTOTAL-JSJX201502002.htm CAO Jiuxin, DONG Dan, XU Shun, et al. A k-core based algorithm for influence maximization in social networks[J]. Chinese journal of computers, 2015, 38(2): 238–248. https://www.cnki.com.cn/Article/CJFDTOTAL-JSJX201502002.htm [16] PENG Sancheng, WU Min, WANG Guojun, et al. Containing smartphone worm propagation with an influence maximization algorithm[J]. Computer networks, 2014, 74: 103–113. doi: 10.1016/j.comnet.2014.09.004 [17] 陈晋音, 张敦杰, 林翔, 等. 基于影响力最大化策略的抑制虚假消息传播的方法[J]. 计算机科学, 2020, 47(S1): 17–23, 33. https://www.cnki.com.cn/Article/CJFDTOTAL-JSJA2020S1004.htm CHEN Jinyin, ZHANG Dunjie, LIN Xiang, et al. False message propagation suppression based on influence maximization[J]. Computer science, 2020, 47(S1): 17–23, 33. https://www.cnki.com.cn/Article/CJFDTOTAL-JSJA2020S1004.htm [18] 江成, 刘室辰. 谣言网络多级传播路径下关键引爆点识别模型和算法研究[J]. 情报杂志, 2020, 39(6): 152–158. doi: 10.3969/j.issn.1002-1965.2020.06.022 JIANG Cheng, LIU Shichen. Research on models and algorithms for identifying trigger points of rumor network under multi-level propagation paths[J]. Journal of intelligence, 2020, 39(6): 152–158. doi: 10.3969/j.issn.1002-1965.2020.06.022 [19] ARAZKHANI N, MEYBODI M R, REZVANIAN A. An efficient algorithm for influence blocking maximization based on community detection[C]//Proceedings of the 5th International Conference on Web Research. Tehran, Iran, 2019: 258−263. [20] LV Jiaguo, YANG Bin, YANG Zhen, et al. A community-based algorithm for influence blocking maximization in social networks[J]. Cluster computing, 2019, 22(3): 5587–5602. [21] WANG Biao, CHEN Ge, FU Luoyi, et al. DRIMUX: dynamic rumor influence minimization with user experience in social networks[J]. IEEE transactions on knowledge and data engineering, 2017, 29(10): 2168–2181. doi: 10.1109/TKDE.2017.2728064 [22] ZHU Wenlong, YANG Wu, XUAN Shichang, et al. Location-aware influence blocking maximization in social networks[J]. IEEE access, 2018, 6: 61462–61477. doi: 10.1109/ACCESS.2018.2876141 [23] YIN Hao, BENSON A R, LESKOVEC J, et al. Local higher-order graph clustering[C]//Proceedings of the 23rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. Halifax, Canada, 2017: 555−564. [24] TRAUD A L, MUCHA P J, PORTER M A. Social structure of Facebook networks[J]. Physica A: statistical mechanics and its applications, 2012, 391(16): 4165–4180. doi: 10.1016/j.physa.2011.12.021 [25] DÜNKER D, KUNEGIS J. Social networking by proxy: analysis of Dogster, Catster and Hamsterster[C]//Proceedings of the 24th International Conference on World Wide Web. Florence, Italy, 2015: 361−362. [26] TRAUD A L, KELSIC E D, MUCHA P J, et al. Comparing community Structure to characteristics in online collegiate social networks[J]. SIAM review, 2011, 53(3): 526–543. doi: 10.1137/080734315 [27] WANG Huijuan, HERNANDEZ J M, VAN MIEGHEM P. Betweenness centrality in a weighted network[J]. Physical review E, 2008, 77(4): 046105. doi: 10.1103/PhysRevE.77.046105 [28] BOLDI P, SANTINI M, VIGNA S. PageRank: functional dependencies[J]. ACM transactions on information systems, 2009, 27(4): 19. [29] MITZENMACHER M, UPFAL E. Probability and computing: Randomized algorithms and probabilistic analysis[J]. The bulletin of symbolic logic, 2006, 12(2): 304–307. doi: 10.1017/S107989860000278X







































 下载:
下载: