2. 江苏健康卫生职业学院 中西医结合学院,江苏 南京 210018
2. College of Integrated Chinese and Western Medicine, Jiangsu Health Vocational College, Nanjing 210018, China
选择性剪切事件是导致生物体多样性的重要原因之一。为了进一步揭示选择性剪切的内在机制,迫切需要计算剪切异构体的表达水平。与传统的基因芯片技术相比,高通量RNA测序(RNA sequencing,RNA-Seq)技术具有高通量、高灵敏度、可重复性好等优势,已成为转录组学分析的一个标准技术手段[1-5]。
RNA-Seq测序实验获得海量读段,将读段与参考注释序列进行匹配,之后便可估计剪切异构体的表达水平。但是在估计剪切异构体表达水平的过程中,面临着两个最大挑战,即读段的多源映射和数据偏差[6-7]。研究者提出了大量剪切异构体表达水平估计方法来解决上述的问题。rSeq方法把读段映射到外显子的过程当作一个泊松随机过程,其泊松分布的参数对应着基因所包含剪切异构体表达水平的线性加权[8]。但是rSeq 方法假设基因上读段分布是均匀的,这与真实数据分布特点不一致。在真实数据中,读段分布呈现明显的非均匀特征。读段的非均匀分布主要是由测序数据中的各种偏差造成的,比如GC碱基序列偏差,5端和3端的位置偏差以及实验技术性偏差等。针对偏差所导致问题,NURD方法考虑了全局和局部位置偏差所带来的影响[9]。POME方法考虑了序列中碱基之间的关联性[10]。为了考虑更复杂的偏差,大量概率生成式模型被提出,其直接模拟读段的随机采样过程。Cufflinks方法设计了不同的模型来消除序列偏差和位置偏差的影响,从而更加准确地描述读段随机采样过程[11]。BitSeq和PBSeq方法采用了与Cufflinks同样的偏差估计模型[12-13]。RSEM方法考虑了读段匹配的不确定性因素,并且使用了读段起始位置的经验分布来表示读段在基因上的非均匀分布特征,但是其未考虑序列偏差这个重要因素[14]。上述方法采用不同的偏差估计模型来模拟读段的非均匀分布特征,都能提高剪切异构体表达水平的估计准确程度。
由于数据噪声和偏差的影响,异构体表达水平的准确性仍然有较大提高的空间[15-16]。常规的RNA-Seq测序实验通常会设置不同的实验条件,比如:同一个细胞组织下参照组和对照组,不同时间点下胚胎发育状况等。此外为了避免实验中的技术性误差,同一个实验条件下会进行多次重复性技术性实验。这使得一次测序实验获得的RNA-Seq数据集是一个多条件多样本的数据集。但是上述方法都是假设RNA-Seq数据集中各个样本之间是相互独立,因此都是单独逐个处理每个数据样本。这导致样本之间的相关性没有得到充分利用。因此有少量工作开始探索联合多样本RNA-Seq数据进行异构体表达水平估计[17-18]。Sequgio方法能从多样本数据中自动获取位置偏差和局部序列影响,再通过对联合统计模型添加一个光滑的正则化项,来控制读段在多样本的一致性[19]。MSIQ方法考虑多样本之间的异质性所导致的结果不稳定性,首先将同质性相近的样本归为同一组,然后在贝叶斯框架模型下,给同一组之内的样本赋予较高的权重,从而获得更加鲁棒的异构体表达水平[20]。XAEM方法采用双线性模型同时估计异构体表达水平和数据偏差,该模型能够自动对潜在的未知偏差进行经验校正[21]。但是上述方法所处理的多样本数据,仅仅是针对单条件下的多样本,比如同一个组织细胞的对照组或者同一个时间点状态。当处理多条件多样本数据时,这些方法都是假设各个条件之间不相关,把多条件多样本数据拆分为多个单条件多样本数据集来进行异构体表达水平计算。但是基因读段分布在不同条件下同样具有高度相似性[22]。为了充分利用数据信息,PGSeq 方法采用泊松分布和伽玛分布的混合模型联合估计基因和异构体表达水平,其伽玛分布用来模拟基因读段分布在多条件多样本下的偏差信息[23]。但PGSeq方法未考虑到基因和异构体表达水平之间的稀疏特性,易受到数据噪声的影响。
基于上述问题,本文提出了一个多条件多样本RNA-Seq测序数据异构体表达水平估计方法,MCMS-Seq(multi-condition multi-sample RNA-Seq)。该模型考虑了基因读段分布在不同条件下的样本具有高度相似性,设计一个联合多条件多样本数据的偏差估计模型,同时考虑了基因读段分布受全局偏差和局部偏差的影响。此外,MCMS-Seq方法增加了
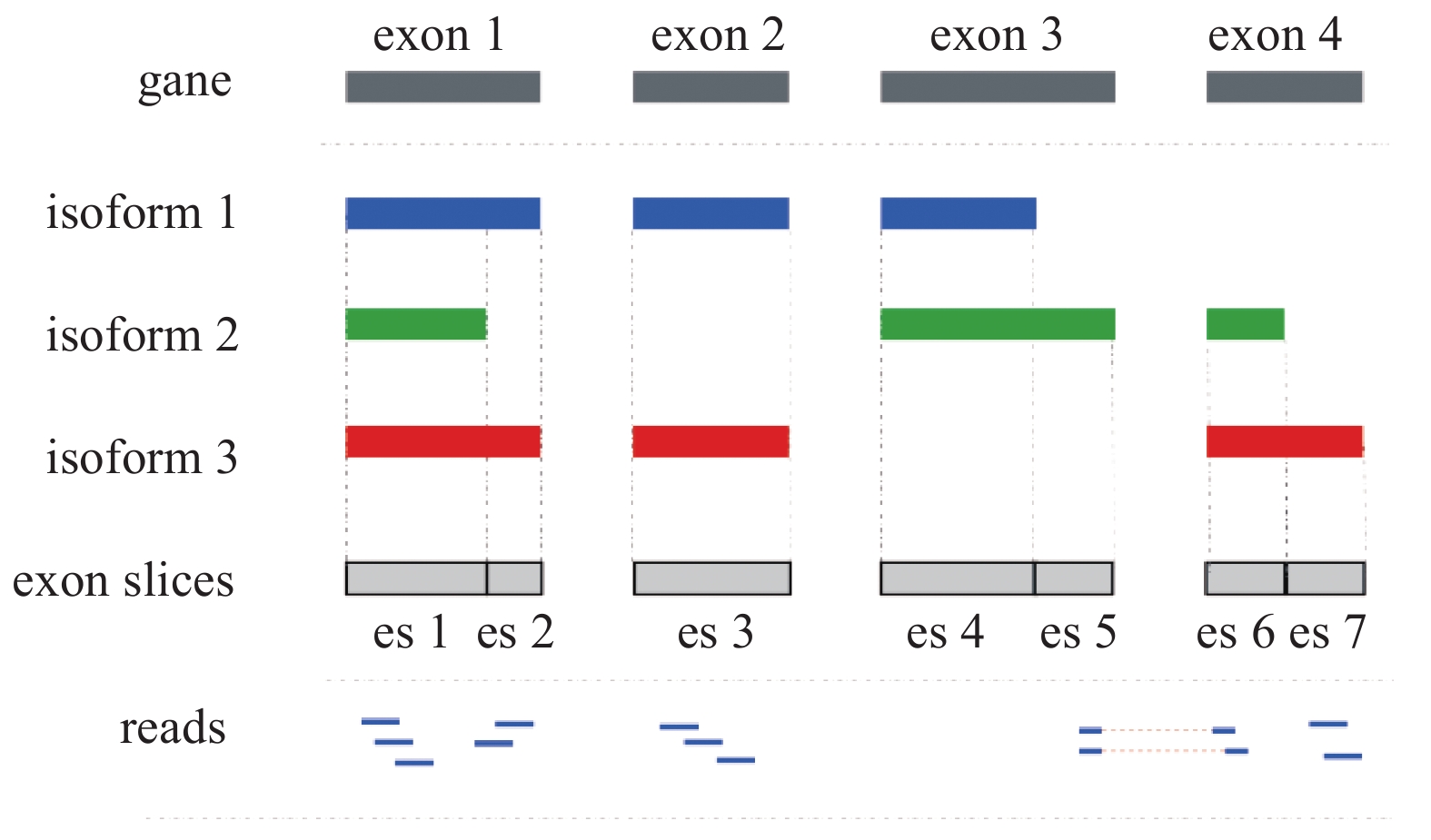
由于选择性剪切事件在真核生物中普遍存在,这给计算剪切异构体表达水平带来了一个最大问题,即如何定量确定匹配到共享外显子上的读段来自哪个剪接异构体。图1中显示的基因包含4个外显子(Exon)和3个剪切异构体。其中一个外显子可以同时被多个剪切异构体共享,比如外显子1被3个剪切异构体共享,但是剪切异构体2仅共享了外显子1的部分序列。针对这类部分共享情况,可将外显子1分割为2个不重叠的外显子片段。因此该基因的4个外显子被分割成7个完全不重叠的外显子片段。映射矩阵A表示图1中剪切异构体与外显子片段的关系,其中矩阵元素
|
Download:
|
| 图 1 剪切异构体中外显子片段划分示例 Fig. 1 Example of exon segmentation in an isoform | |
| $ {\boldsymbol{A}} = \left[ {\left. \begin{array}{l} 1\;\;1\;\;1\;\;1\;\;0\;\;0\;\;0\\ 1\;\;0\;\;0\;\;1\;\;1\;\;1\;\;0\\ 1\;\;1\;\;1\;\;0\;\;0\;\;1\;\;1 \end{array} \right]} \right.\quad{\boldsymbol{D}} = \left[ {\left. \begin{array}{l} 2\;\;\;1\;\;\;2\;\;0\;\;1\;\;1\;\;2\\ 4\;\;\;1\;\;\;2\;\;0\;\;2\;\;2\;\;1\\ 8\;\;10\;\;1\;\;8\;\;1\;\;6\;\;8\\ 9\;\;11\;\;1\;\;7\;\;0\;\;7\;\;8 \end{array} \right]} \right. $ |
假设测序实验获得RNA-Seq数据包含C个条件,每个条件包含N个样本。对于基因g,该基因包含K个剪切异构体和M个外显子片段,其与外显子片段的映射关系由映射矩阵
| $ {y_{cij}} = {w_{ci}}{l_j}\sum\limits_{k = 1}^K {{a_{jk}}{x_{cik}}} $ | (1) |
式中:
式(1)模型是基于基因读段是均匀分布假设的前提,但是实际数据中,基因读段分布呈现明显的非均匀特征。由于基因读段分布模式在不同条件不同样本下具有高度相似性,因此假设
| $ {y_{cij}} = {w_{ci}}{l_j}{b_j}\sum\limits_{k = 1}^K {{a_{jk}}{x_{cik}}} $ | (2) |
对于多条件多样本的RNA-Seq数据集,基因g所包含的K个剪切异构体的表达水平X可以通过回归模型计算,其公式如下:
| $ {{\boldsymbol{X}}^*} = \arg {\min _x}\sum\limits_{c = 1}^C {\sum\limits_{j = 1}^N {\sum\limits_{i = 1}^M {\left( {\frac{{{y_{cij}}}}{{{w_{ci}}{l_j}{b_j}}} - \sum\limits_{k = 1}^K {{a_{jk}}{x_{cjk}}} } \right)} } } $ | (3) |
所有剪切异构体在不同样本中的表达水平都要求
| $ {{\boldsymbol{X}}^*} = \arg {\min _x}\left\| {{\boldsymbol{D - AX}}} \right\|_F^2 $ | (4) |
式中D表示归一化后的数据矩阵。
一个基因虽然包含多个剪切异构体,但是在不同条件下,少数剪切异构体的表达水平决定了该基因的表达。因此基因和剪切异构体表达水平之间具有稀疏特性。通过对剪切异构体表达水平X增加
| $ {{\boldsymbol{X}}^*} = \arg {\min _x}\left\| {{\boldsymbol{D - AX}}} \right\|_F^2 + \lambda {\left\| {\boldsymbol{X}} \right\|_1} $ | (5) |
虽然模型增加了
| $ \begin{gathered} {{\boldsymbol{X}}^*} = \arg {\mathop {\min }\limits_x }\left\| {{\boldsymbol{D - AX}}} \right\|_F^2 + {\lambda _1}{\left\| {\boldsymbol{X}} \right\|_{2,1}} + {\lambda _2}{\left\| {\boldsymbol{X}} \right\|_1} \hfill \\ \quad\quad\quad\quad \quad {\rm{s.t.}}\;{x_{cjk}} \geqslant 0 \hfill \\ \end{gathered} $ | (6) |
式中
|
Download:
|
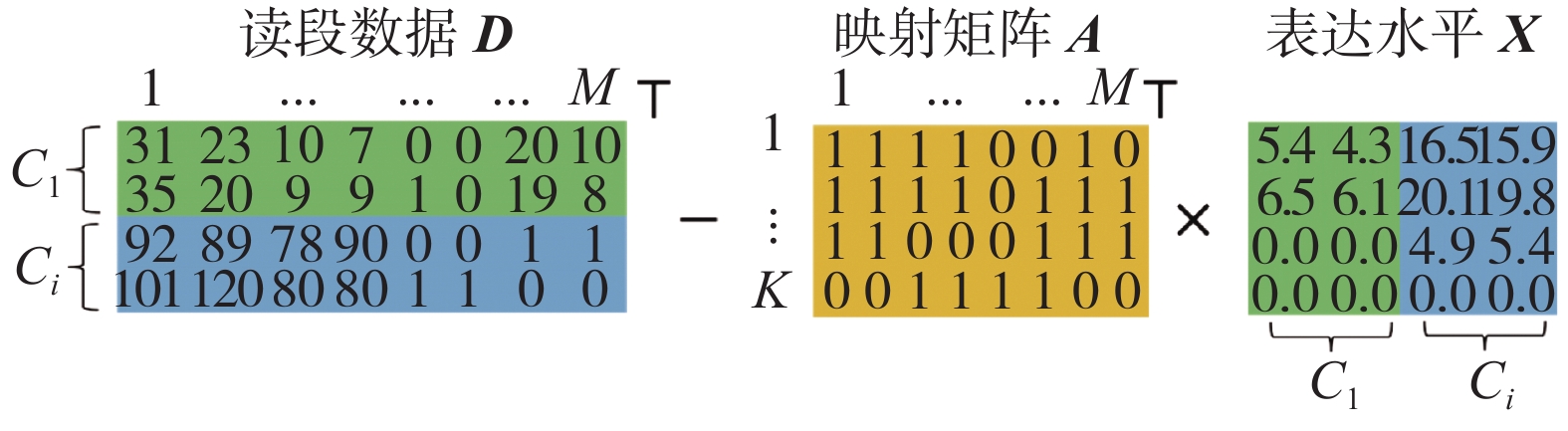
| 图 2 MCMS-Seq方法的优化问题 Fig. 2 Optimization problem of MCMS-Seq method | |
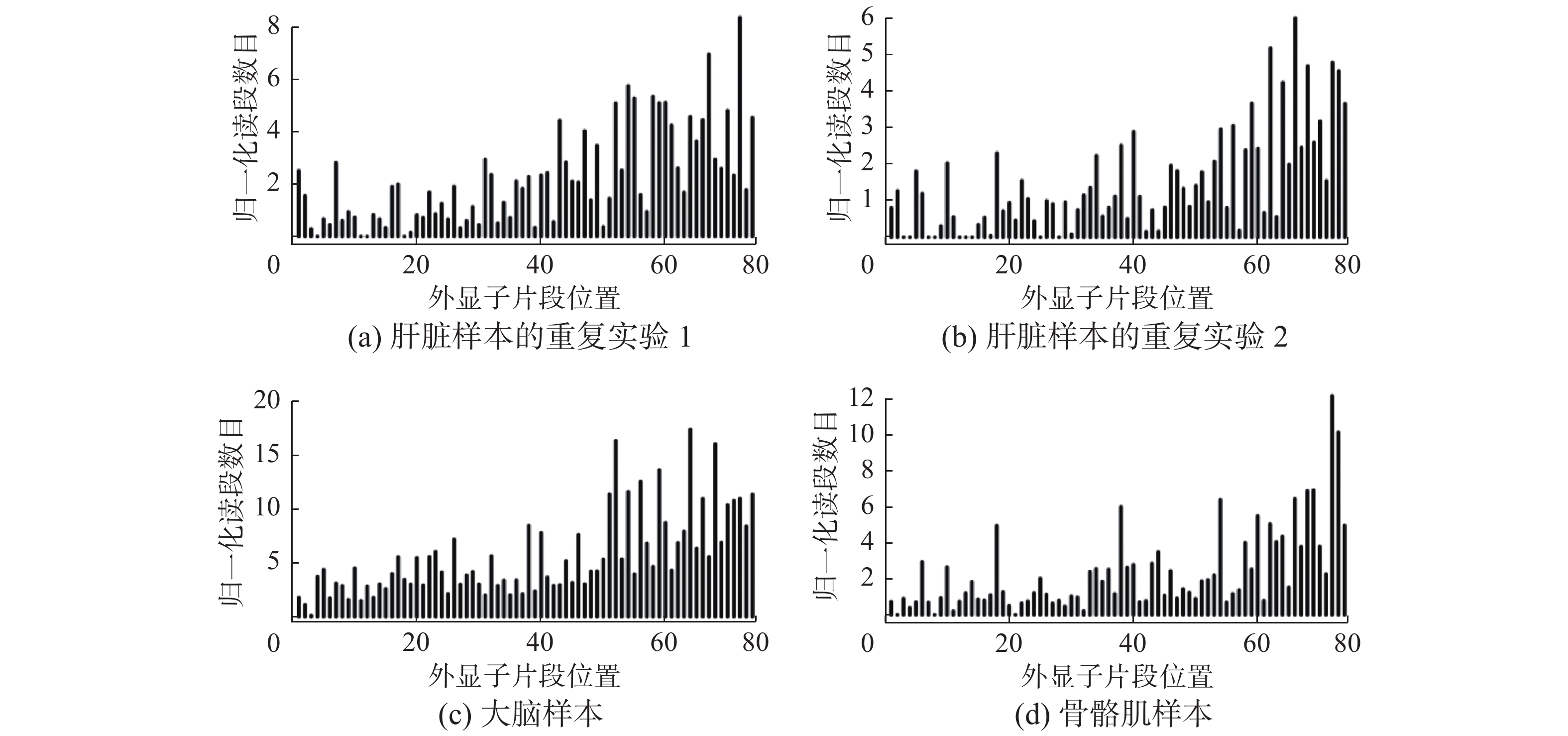
在多条件多样本数据中,图3显示了基因的读段分布无论在不同条件下,还是在同一个条件的重复样本中,其分布模式具有高度相似性。MCMS-Seq方法提出了一个基于多条件多样本的读段非均匀偏差估计模型。该偏差估计模型由两部分构成:全局偏差
|
Download:
|
| 图 3 小鼠数据集中基因Utrn读段分布 Fig. 3 Read distributions of gene Utrn in the mouse dataset | |
一旦获得数据集的全局偏差曲线和单个基因的局部偏差特性,便可以计算出基因上每个外显子片段的偏差值:
| $ {b_j} = \alpha {\beta _{{\rm{global}}}} + (1 - \alpha ){\beta _{{\rm{local}}}} $ | (7) |
式中:
MCMS-Seq方法的实现可以分为3个部分:读段数据预处理、基因偏差估计和表达水平估计。
1) 读段数据预处理,是从匹配成功的读段数据中统计基因每个外显子片段的读段计数,以及从注释文件中获得外显子片段和剪切异构体之间的映射关系矩阵。
2) 基因偏差估计,是计算数据集的全局偏差和基因的局部偏差,从而获得基因每个外显子片段的基因偏差值。
3) 剪切异构体表达水平估计,由于模型是针对多条件多样本数据集,同时模型包含
MCMS-Seq方法的详细流程如算法1所示,采用Python和MATLAB混合编程实现。
算法1 MCMS-Seq方法
输入 多条件多样本数据,注释文件;
输出 每个基因的剪切异构体表达水平。
1)数据预处理:统计外显子片段读段数目矩阵D,构建映射关系矩阵A。
2)基因偏差估计:计算外显子片段偏差值。
3)表达水平估计:计算所有基因的
为了方便用户使用MCMS-Seq方法,本文提供了一个多条件多样本RNA-Seq测序数据分析通道,如图4所示。当获得RNA-Seq测序数据样本后,使用经典读段匹配软件Bowtie[26],将每个数据样本的读段匹配到参考转录组参考序列上。每个样本匹配结果作为输入数据一并输入到MCMS-Seq分析通道中,从而可获得剪切异构体在不同样本中的表达水平。一旦获得剪切异构体的表达水平,可提供给高层次的后续分析使用。

|
Download:
|
| 图 4 多条件多样本RNA-Seq数据分析通道 Fig. 4 Analysis pipeline of multi-condition multi-sample RNA-Seq data | |
本文选择了经典方法Cufflinks(v.2.2.1)和PGSeq(v.1.0),以及最新方法XAEM(v.0.1.1), 分别在 3 个数据集上与MCMS-Seq 方法进行比较,用来验证剪切异构体表达水平的性能。针对多条件多样本数据集,Cufflinks是每个样本单独处理,而PGSeq、XAEM和MCMS-Seq都是多个样本联合处理。
2.1 数据集3个多条件多样本的RNA-Seq数据集被用来验证MCMS-Seq方法估计剪切异构体表达水平的准确性。3个数据集分别是小鼠数据集、人类大脑的SEQC和MAQC-II数据集,它们都来自Illumina/solexa 测序平台。
小鼠数据集包含3个条件,分别是肝脏、大脑和骨骼肌3个组织,其中每个组织分别包含了 2 个重复实验样本。使用 RefSeq 数据库的基因注释信息(GRCm38/mm10),总共包含 33608 个剪切异构体,主要用来验证同条件下重复样本之间剪切异构体表达水平的可重复性[27]。
MAQC(micorarray quality control)来自美国药品监管局的生物芯片质量控制项目。该项目分为三期实施,即MAQC-I、MAQC-II和MAQC-III,其产生的数据集被广泛应用于评估不同测序平台下不同方法的性能。本文主要利用了MAQC-II和MAQC-III两期项目提供的数据。MAQC-III也被称为SEQC(sequencing quality control)。SEQC包括两个实验条件UHRR(universal human reference rna)和HBRR(human brain reference RNA),每个条件分别有8个重复实验样本。SEQC数据集提供了两万多个经qRT-PCR实验验证的剪切异构体。与Ensembl注释信息(GRCh37/hg19)相匹配后,最终得到16603个剪切异构体。这些剪切异构体的qRT-PCR值被当作真实表达水平值,可用来评估模型计算剪切异构体表达水平的准确性[28]。
基因表达水平是由其包含的剪切异构体所构成,因此基因表达水平可用来进一步验证剪切异构体表达水平的准确性。MAQC-II数据集同样包含UHRR和HBRR两个实验条件,每个条件下包含7个重复性实验。该数据提供了1000个经qRT-PCR实验验证的基因。根据与Ensembl注释信息(GRCh37/hg19)相匹配,最终获得838个基因。这些基因的qRT-PCR值被当作真实基因表达水平值,用来间接评估模型计算剪切异构体表达水平的准确程度[29]。
2.2 多条件多样本偏差估计模型验证MCMS-Seq方法提出了一个基于多条件多样本偏差估计模型,同时考虑了读段分布受到全局偏差和局部偏差的影响,用来获取读段分布在样本之间的高度相似性特征。SEQC数据集被用来验证偏差估计模型的有效性。图5显示使用该模型对SEQC数据集的偏差估计流程。从图5(a)中可以看出,在SEQC数据集中,基因的读段分布呈现明显的非均匀分布特征,特别是在基因的两端。这个现象符合基因的

|
Download:
|
| 图 5 MCMS-Seq方法的偏差估计流程 Fig. 5 Bias estimation process of the MCMS-Seq method | |
|
Download:
|
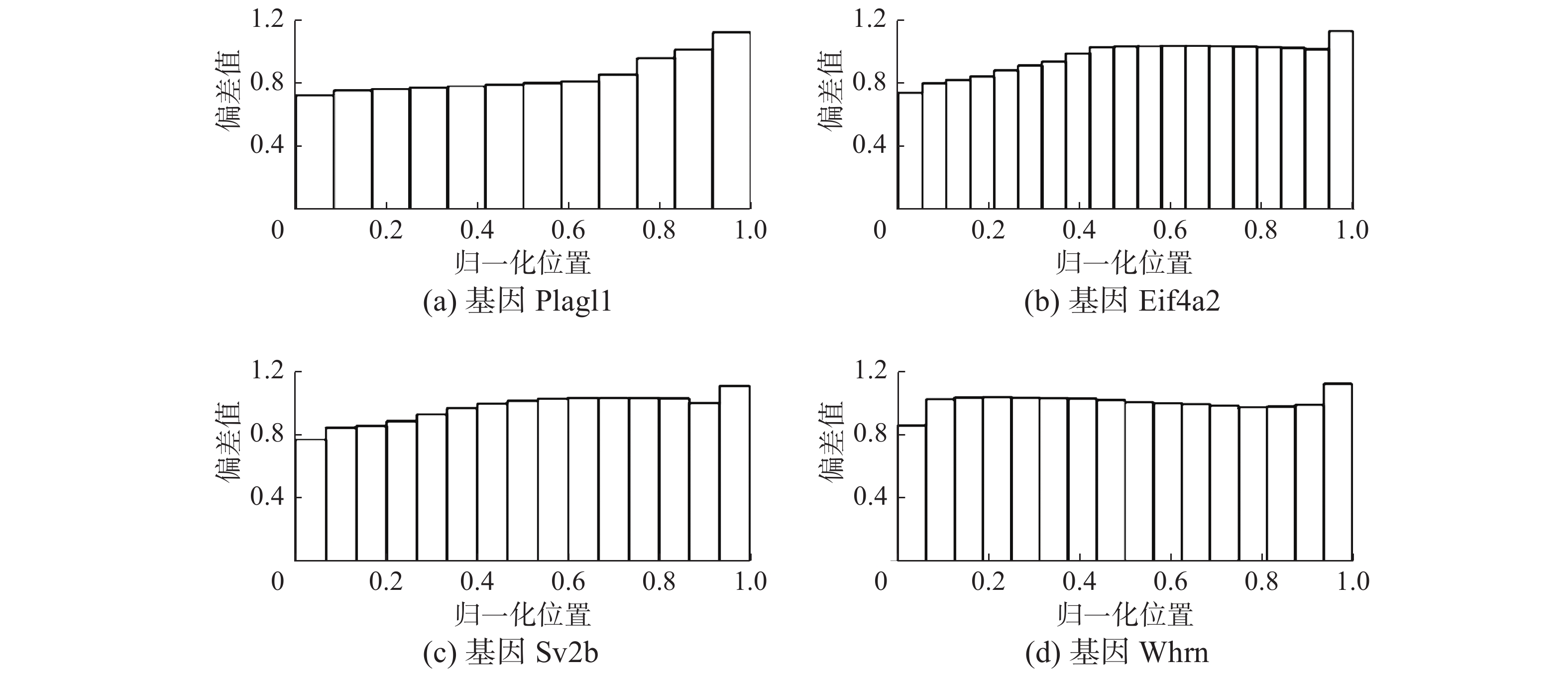
| 图 6 基因的局部偏差分布 Fig. 6 Local bias distribution of genes | |
MCMS-Seq方法处理多条件多样本数据集时是联合所有样本同时处理,通过增加稀疏约束,不仅可以消除数据噪声的影响,同时也能体现基因和剪切异构体之间存在的稀疏特性。选择小鼠数据集的基因Nph2来验证,该基因包含3个剪切异构体。
在小鼠数据集中,同一个剪切异构体在同一个条件下的多个重复样本中,其表达水平应该是相近的。若一个剪切异构体在重复样本中零散地出现低表达,则此剪切异构体的表达水平受到数据噪声的影响。传统方法Cufflinks都是每个样本依次单独处理,其表达水平值如表1所示。NM_001364736表达水平在Muscle条件两个重复样本中就可能受到数据噪声的影响,NM_157294在Liver条件下也存在同样的情况。表2 中XAEM方法获得的NM_001364736和NM_157294表达水平都是极低值,极大可能是受到数据噪声的干扰。MCMS-Seq方法联合处理多条件多样本数据集。从表3中可以看出,NM_001364736在3个组织条件下都未表达,NM_157294在大脑和骨骼肌组织条件下具有真实的低表达,而在肝脏组织条件下未表达,能有效消除数据噪声的影响。
| 表 1 Cufflinks估计基因Nhp2中3个剪切异构体表达水平 Tab.1 Expression level of three isoforms in Nph2 gene estimated using cufflinks |
| 表 2 XAEM估计基因Nhp2中3个剪切异构体表达水平 Tab.2 Expression level of three isoforms in Nph2 gene estimated using XAEM |
| 表 3 MCMS-Seq估计基因Nhp2中3个剪切异构体表达水平 Tab.3 Expression level of three isoforms in Nph2 gene estimated using MCMS-Seq |
此外,基因外在表现通常是由其包含的少数剪切异构体决定的,因此基因和剪切异构体之间存在稀疏特性。在表4中,PGSeq方法得到的3个剪切异构体表达水平都存在较高的表达值,无法体现稀疏特性。而Cufflinks和XAEM受数据噪声影响,同样很难体现出该数据特性。MCMS-Seq方法增加了
| 表 4 PGSeq估计基因Nhp2中3个剪切异构体表达水平 Tab.4 Expression level of three isoforms in Nph2 gene estimated using PGSeq |
在多条件多样本测序实验中,同一个条件下设计多重复性样本是为了避免技术性误差所带来的影响。这使得同一个剪切异构体在同一个条件下的重复样本之间的表达水平是相近的。小鼠数据集被用来验证剪切异构体表达水平在样本之间的可重复性。采用Person 相关系数来评估可重复性,其值越高说明能更加有效地消除技术性误差所造成的偏差。由于RNA-Seq测序技术得到表达水平其幅度跨度很大,Person相关系数易受到少数高表达的剪切异构体影响。因此在计算相关系数之前,对所有剪切异构体表达水平进行对数转换,从而避免上述问题。表5中显示不同方法在小鼠数据集上不同条件下的相关系数值。从表中可以看出,MCMS-Seq方法在肝脏、大脑和骨骼肌3个条件下都获得了比其他3个方法更好的结果。尽管MCMS-Seq方法是面向处理多条件多样本数据集,但仍然可以保证剪切异构体在同一个条件中下样本之间具有高度的可重复性。这也符合RNA-Seq测序实验中设计重复实验的目的。
| 表 5 在小鼠数据集上不同方法估计的剪切异构体表达水平在样本之间的相关系数 Tab.5 Correlation coefficients between isoform expression levels estimated using various methods in the mouse dataset |
SEQC数据集被用来验证不同方法估计剪切异构体表达水平的准确性。该数据集提供了16 603个经过qRT-PCR验证的剪切异构体,这些剪切异构体被当作基准数据。计算不同方法得到剪切异构体表达水平与qRT-PCR值之间的相关系数。从表6中结果可以看出,MCMS-Seq方法在UHRR条件上稍微优于PGSeq方法,而在HBRR条件上获得较为明显的提升。尽管XAEM方法是多样本处理,但获得最差的性能,其可能是该方法对数据偏差考虑得不够。整体上说,MCMS-Seq方法估计的剪切异构体表达水平能取得较为准确的结果。
| 表 6 在 SEQC 数据集上不同方法与 qRT-PCR 验证剪切异构体之间的相关系数 Tab.6 Correlation coefficients between qRT-PCR values and isoform expression levels estimated using various methods in SEQC dataset |
现实中包含qRT-PCR验证的剪切异构体数据集很少,而基因的表达水平是由其所包含的剪切异构体所决定的,因此可以通过验证qRT-PCR验证基因的表达水平来间接验证剪切异构体表达水平的准确性。MAQC-II数据集被广泛地应用于评估不同方法估计基因表达水平的性能。MAQC-II数据集提供了838个qRT-PCR验证的基因,这些基因总共包含了6927个剪切异构体。Cufflinks和PGSeq方法提供了基因的表达水平,XAEM和MCMS-Seq方法的基因表达水平由所对应的剪切异构体表达水平求和得到。表7显示了不同方法得到的基因表达水平与qRT-PCR值之间的相关系数。从表7中可以看出,相比其他方法,MCMS-Seq方法得到了更好的准确性。
| 表 7 在 MAQC-II 数据集上不同方法与 qRT-PCR 验证基因之间的相关系数 Tab.7 Correlation coefficients between qRT-PCR values and isoform expression levels estimated using various methods in the MAQC-II dataset |
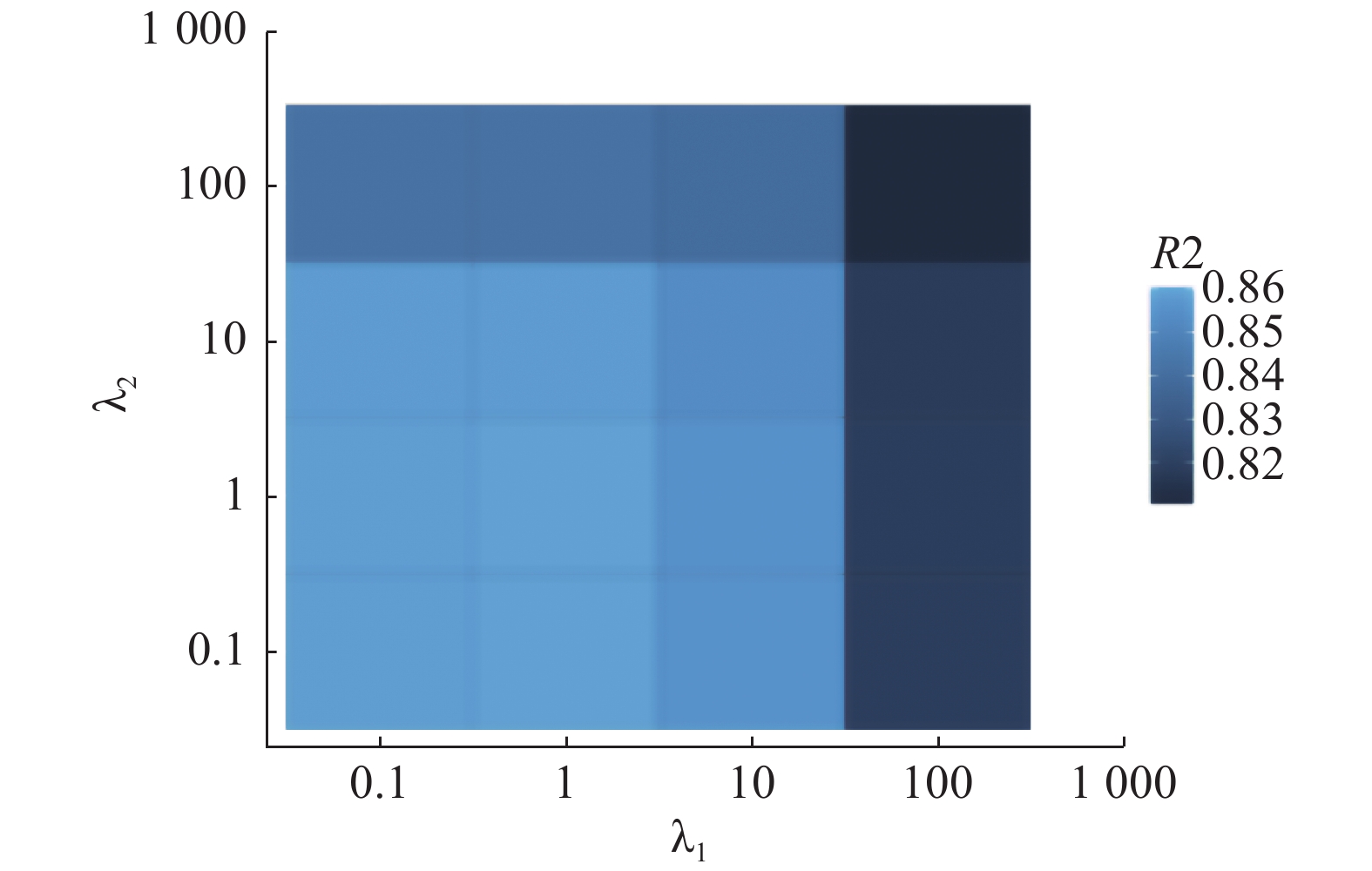
MCMS-Seq方法包含了
|
Download:
|
|
图 7 参数
|
|
本文提出了一个基于多条件多样本RNA-Seq测序数据的剪切异构体表达水平估计方法。为了考虑基因读段分布在不同条件下的高度相似性,MCMS-Seq方法设计一个联合多条件多样本的偏差估计模型,同时考虑了基因读段分布的全局偏差和局部偏差所带来的影响。从数据分析可以看出,该偏差估计模型能较为准确地描述出基因读段非均匀分布特性。此外,MCMS-Seq方法增加了
由于大量多条件多样本数据集是时序数据集,蕴含了时间信息,但是MCMS-Seq模型未考虑到数据中的时间信息。在未来的研究中,可以考虑在模型中融入时间信息,从而进一步提高剪切异构体的表达水平的准确性。此外,可将MCMS-Seq模型推广到单细胞测序数据分析,可提供更好的生物解释性。
| [1] |
MARIONI J C, MASON C E, MANE S M, et al. RNA-Seq: an assessment of technical reproducibility and comparison with gene expression arrays[J]. Genome research, 2008, 18(9): 1509-1517. DOI:10.1101/gr.079558.108 ( 0) 0)
|
| [2] |
周晓光, 任鲁风, 李运涛, 等. 下一代测序技术: 技术回顾与展望[J]. 中国科学: 生命科学, 2010, 40(1): 23-37. ZHOU Xiaoguang, REN Lufeng, LI Yuntao, et al. The next-generation sequencing technology: A technology review and future perspective[J]. Scientia sinica (vitae), 2010, 40(1): 23-37. (  0) 0)
|
| [3] |
王曦, 汪小我, 王立坤, 等. 新一代高通量RNA测序数据的处理与分析[J]. 生物化学与生物物理进展, 2010, 37(8): 834-846. WANG Xi, WANG Xiaowo, WANG Likun, et al. A review on the processing and analysis of next-generation RNA-seq data[J]. Progress in biochemistry and biophysics, 2010, 37(8): 834-846. DOI:10.3724/SP.J.1206.2009.00151 (  0) 0)
|
| [4] |
ZHANG Li, LIU Xuejun. A comprehensive review on RNA-Seq data analysis[J]. Transactions of Nanjing University of Aeronautics and Astronautics, 2016, 33(3): 339-361. ( 0) 0)
|
| [5] |
MONIER B, MCDERMAID A, WANG Cankun, et al. RIS-EDA: an integrated RNA-Seq interpretation system for gene expression data analysis[J]. PLoS computational biology, 2019, 15(2): e1006792. DOI:10.1371/journal.pcbi.1006792 ( 0) 0)
|
| [6] |
王凯莉, 张礼, 刘学军. 融合多平台表达数据的转录组差异表达分析[J]. 计算机学报, 2018, 41(6): 1415-1430. WANG Kaili, ZHANG Li, LIU Xuejun. Differential expression analysis based on integrating transcriptome expression data from multiple platforms[J]. Chinese journal of computers, 2018, 41(6): 1415-1430. DOI:10.11897/SP.J.1016.2018.01415 (  0) 0)
|
| [7] |
王凯莉, 张礼, 刘学军. 多实验平台下基因及异构体表达分析综述[J]. 中国生物医学工程学报, 2017, 36(2): 211-218. WANG Kaili, ZHANG Li, LIU Xuejun. A review of gene and isoform expression analysis across multiple experimental platforms[J]. Chinese journal of biomedical engineering, 2017, 36(2): 211-218. DOI:10.3969/j.issn.0258-8021.2017.02.012 (  0) 0)
|
| [8] |
JIANG Hui, WONG W H. Statistical inferences for isoform expression in RNA-Seq[J]. Bioinformatics, 2009, 25(8): 1026-1032. DOI:10.1093/bioinformatics/btp113 ( 0) 0)
|
| [9] |
WU Zhengpeng, WANG Xi, ZHANG Xuegong. Using non-uniform read distribution models to improve isoform expression inference in RNA-Seq[J]. Bioinformatics, 2011, 27(4): 502-508. DOI:10.1093/bioinformatics/btq696 ( 0) 0)
|
| [10] |
HU Ming, ZHU Yu, TAYLOR J M G, et al. Using poisson mixed-effects model to quantify transcript-level gene expression in RNA-Seq[J]. Bioinformatics, 2012, 28(1): 63-68. DOI:10.1093/bioinformatics/btr616 ( 0) 0)
|
| [11] |
TRAPNELL C, WILLIAMS B A, PERTEA G, et. al. Transcript assembly and quantification by RNA-Seq reveals unannotated transcripts and isoform switching during cell differentiation[J]. Nature biotechnology, 2010, 28(5): 511-515. DOI:10.1038/nbt.1621 ( 0) 0)
|
| [12] |
GLAUS P, HONKELA A, RATTRAY M. Identifying differentially expressed transcripts from RNA-Seq data with biological variation[J]. Bioinformatics, 2012, 28(13): 1721-1728. DOI:10.1093/bioinformatics/bts260 ( 0) 0)
|
| [13] |
ZHANG Li, LIU Xuejun. PBSeq: modeling base-level bias to estimate gene and isoform expression for RNA-Seq data[J]. International journal of machine learning and cybernetics, 2017, 8(4): 1247-1258. DOI:10.1007/s13042-016-0497-z ( 0) 0)
|
| [14] |
LI Bo, DEWEY C N. RSEM: accurate transcript quantification from RNA-Seq data with or without a reference genome[J]. BMC bioinformatics, 2011, 12: 323. DOI:10.1186/1471-2105-12-323 ( 0) 0)
|
| [15] |
LI W V, LI J J. Modeling and analysis of RNA-seq data: a review from a statistical perspective[J]. Quantitative biology, 2018, 6(3): 195-209. DOI:10.1007/s40484-018-0144-7 ( 0) 0)
|
| [16] |
LIU Siyun, JIANG Yuan, TAO Yu. Modelling RNA‐Seq data with a zero-inflated mixture Poisson linear model[J]. Genetic epidemiology, 2019, 43(7): 786-799. DOI:10.1002/gepi.22246 ( 0) 0)
|
| [17] |
ZHANG Chi, ZHANG Baohong, LIN L L, et al. Evaluation and comparison of computational tools for RNA-Seq isoform quantification[J]. BMC genomics, 2017, 18(1): 1-11. DOI:10.1186/s12864-017-4002-1 ( 0) 0)
|
| [18] |
LI Song, SABUNCIYAN S, YANG Guangyu, et al. A multi-sample approach increases the accuracy of transcript assembly[J]. Nature communications, 2019, 10(1): 1-7. DOI:10.1038/s41467-019-12990-0 ( 0) 0)
|
| [19] |
SUO Chen, CALZA S, SALIM A, et al. Joint estimation of isoform expression and isoform-specific read distribution using multisample RNA-Seq data[J]. Bioinformatics, 2014, 30(4): 506-513. DOI:10.1093/bioinformatics/btt704 ( 0) 0)
|
| [20] |
LI W V, ZHAO Anqi, ZHANG Shihua, et al. MSIQ: joint modeling of multiple RNA-Seq samples for accurate isoform quantification[J]. The annals of applied statistics, 2018, 12(1): 510-539. ( 0) 0)
|
| [21] |
DENG Wenjiang, MOU Tian, KALARI K R, et al. Alternating EM algorithm for a bilinear model in isoform quantification from RNA-Seq data[J]. Bioinformatics, 2020, 36(3): 805-812. ( 0) 0)
|
| [22] |
AGUIAR D, CHENG Lifang, DUMITRASCU B, et al. Bayesian nonparametric discovery of isoforms and individual specific quantification[J]. Nature communications, 2018, 9(1): 1-12. DOI:10.1038/s41467-018-03402-w ( 0) 0)
|
| [23] |
LIU Xuejun, ZHANG Li, CHEN Songcan. Modeling exon-specific bias distribution improves the analysis of RNA-Seq data[J]. PLoS one, 2015, 10(10): e0140032. DOI:10.1371/journal.pone.0140032 ( 0) 0)
|
| [24] |
焦李成, 赵进, 杨淑媛, 等. 稀疏认知学习、计算与识别的研究进展[J]. 计算机学报, 2016, 39(4): 835-852. JIAO Licheng, ZHAO Jin, YANG Shuyuan, et al. Research advances on sparse cognitive learning, computing and recognition[J]. Chinese journal of computers, 2016, 39(4): 835-852. DOI:10.11897/SP.J.1016.2016.00835 (  0) 0)
|
| [25] |
JENATTON R, MAIRAL J, OBOZINSKI G, et al. Proximal methods for sparse hierarchical dictionary learning[C]//Proceedings of the 27th International Conference on International Conference on Machine Learning. Haifa, Israel, 2010: 487−494.
( 0) 0)
|
| [26] |
LANGMEAD B, SALZBERG S L. Fast gapped-read alignment with Bowtie 2[J]. Nature methods, 2012, 9(4): 357-359. DOI:10.1038/nmeth.1923 ( 0) 0)
|
| [27] |
MORTAZAVI A, WILLIAMS B A, MCCUE K, et al. Mapping and quantifying mammalian transcriptomes by RNA-Seq[J]. Nature methods, 2008, 5(7): 621-628. DOI:10.1038/nmeth.1226 ( 0) 0)
|
| [28] |
SEQC/MAQC-III Consortium. A comprehensive assessment of RNA-Seq accuracy, reproducibility and information content by the sequencing quality control consortium[J]. Nature biotechnology, 2014, 32(9): 903-914. DOI:10.1038/nbt.2957 ( 0) 0)
|
| [29] |
BULLARD J H, PURDOM E, HANSEN K D, et al. Evaluation of statistical methods for normalization and differential expression in mRNA-Seq experiments[J]. BMC bioinformatics, 2010, 11(1): 1-13. DOI:10.1186/1471-2105-11-94 ( 0) 0)
|
 2021, Vol. 16
2021, Vol. 16


