Fast multiview clustering network combining landmark points and autoencoder
-
摘要: 针对目前存在的多视图聚类方法大多是对聚类准确性进行研究而未着重于提升算法效率，从而难以应用于大规模数据的现象，本文提出一种结合地标点和自编码的快速多视图聚类算法。利用加权
$ \mathrm{P}\mathrm{a}\mathrm{g}\mathrm{e}\mathrm{R}\mathrm{a}\mathrm{n}\mathrm{k} $ 排序算法选出每个视图中最具代表性的地标点。使用凸二次规划函数从数据中直接生成多个视图的相似度矩阵，求得多个视图的共识相似度矩阵以有效利用多个视图包含的具有一致性和互补性的聚类有效信息，将获得的具有低存储开销性能的共识相似度矩阵输入自编码器替代拉普拉斯矩阵特征分解，在联合学习框架下同时更新自编码器参数和聚类中心从而在降低计算复杂度的同时保证聚类精度。在5个多视图数据集上的实验证明了本文算法相对于其他多视图算法在运行时间上的优越性。Abstract: Currently, most existing multiview clustering methods only focus on the accuracy of clustering and pay little attention to the improvement of the efficiency of the algorithm, which makes it difficult to apply them to large-scale datasets. This paper proposes a fast multiview clustering algorithm combining landmarks and autoencoder. The weighted PageRank algorithm is adopted to select the most representative landmark points in each view. The similarity matrix of multiple views is directly generated through the convex quadratic programming function. To effectively use the consistent and complementary clustering effective information contained in multiple views, the consensus similarity matrix of multiple views is obtained. The obtained consensus similarity matrix with low storage overhead performance is inputted to the autoencoder to replace the Laplacian matrix eigendecomposition. The proposed algorithm updates the autoencoder parameters and clustering centers under the framework of joint learning to ensure clustering accuracy while reducing computational complexity. Experiments in five multiview datasets show that the proposed algorithm is better than other multiview algorithms in terms of running time. -
聚类作为一种无监督的学习方法可将给定的数据集根据数据的内在联系划分成多个集内相似度高而集间相似度低的子集，获得了数据挖掘、模式识别、图像分割等诸多领域的关注[1]。并且由于现实世界中多视图数据的普遍存在，例如，文档可以由不同语言来编写，基因可由不同技术来测量[2]。充分利用多视图数据以探索到更丰富、全面的数据特征从而获得更好的性能也成为聚类发展的方向。
多视图子空间聚类由于其优越的性能和丰富的可扩展性得到了飞速发展[3]。例如，Cao等[4]在各个视图之间利用希尔伯特施密特独立性准则(HSIC)进行视图间相互约束，从而捕获到更丰富的数据关系。Wang等[5]通过新颖的位置感知准则来利用多个视图的互补信息，同时通过一致性约束来获得多个视图的通用聚类指示矩阵。Brbic等[6]在生成多个视图的联合亲和度矩阵时利用低秩稀疏进行约束，并将方法扩展到核空间以适用于非线性数据。Nie等[7]通过避免引入超参数的完全自动加权方案来为每个视图分配不同的权重以区分不同视图的重要性。Wang等[8]试图通过整合编码的补充信息，利用具有最大依赖性的空间学习技术来形成多视图的信息丰富的完整感知相似性。Li等[9]通过将潜在表示强制构造为最大程度接近多个视图的形式从而能够灵活地编码来自不同视图的互补信息。随着科技迅速发展，网络数据量也随之剧烈膨胀并越发呈现纷繁复杂状态。例如，Facebook每月约报告60亿张新照片，YouTube每分钟约上传72小时的视频。而聚类分析的主要任务之一就是对大规模数据集进行无监督分类[10]。虽然上述多视图聚类方法相较于单视图聚类方法在聚类精度方面有了质的提升，但是它们都呈现出较高的计算复杂度，从而在大规模数据集上的使用具有局限性[11]。
为了提升面向大规模数据集的可扩展性，亟需找到一种优质的能降低计算复杂度的聚类算法，为了解决这一问题，He等[12]利用随机傅里叶特征来显式表示内核空间中的数据，显式特征映射可显著加快特征向量近似，从而提高谱聚类预测速度。Tian等[13]发现自编码器和谱聚类本质上都是在保留原始数据最重要数据特征的同时实现降维处理，因此运用自编码器来替代谱聚类中的拉普拉斯矩阵特征分解，对于大规模数据集来说，这一处理极大地减少了内存消耗，但此方法仍需要直接处理规模庞大的数据。因此Yin等[14]提出了一种具有局部相似性表示的基于地标的光谱聚类方法，该方法首先通过使用给定的相似度函数对原始数据点的“最相似”地标进行编码，然后对编码数据点进行奇异值分解以得到频谱嵌入数据点，再利用传统聚类方法例如K-means对嵌入数据点进行划分。Banijamali等[15]将地标表示与非线性低维映射相结合，同时避免了直接处理大规模数据集与拉普拉斯矩阵特征分解步骤，实现了更精确的快速聚类方法。虽然上述基于谱聚类的扩展算法十分有效地降低了谱聚类的计算量，但它们都是针对单视图谱聚类进行的，对于多视图学习场景显然无能为力。
综上所述，本文提出一种结合地标点和自编码的快速多视图聚类方法。为了提取大规模数据集中的强代表性点以降低存储开销，首先利用加权PageRank排序算法在每个视图中选取原始数据中权重较高的数据点作为每个视图的地标点，为了避免传统的手工生成相似度矩阵中指数函数与近邻点个数的选择，本文利用凸二次规划函数直接从数据中获得每个视图的相似度矩阵，融合多视图信息，将生成的多视图共识相似度矩阵作为自编码器的输入，利用自编码器替代拉普拉斯矩阵特征分解获得多视图数据的联合嵌入表示，最后利用K-means算法进行最后的聚类划分。为了避免微调环节覆盖之前所得最优参数从而获得更精确的聚类结果，本文将自编码器的重建损失和聚类损失放在同一学习框架下从而能够对自编码器的参数和聚类中心进行联合更新。
1. 相关算法理论
1.1 多视图子空间聚类
鉴于融合多视图数据以捕获到更全面的聚类有效信息是十分有必要的，多视图子空间聚类最近获得了大量关注。给出多视图数据
$${\boldsymbol{X}}=[{\boldsymbol{X}}^{1}\;{\boldsymbol{X}}^{2}\;\cdots \; {\boldsymbol{X}}^{v}]\in {\bf{R}}^{\sum\limits_{i = 1}^v {{d_i}} \times n}$$ 根据自表示思想通过一个稀疏系数矩阵重构原始数据，则多视图子空间聚类网络的目标函数为
$$\begin{aligned} \underset{{{S}}^{i}}{\rm{min}}\sum _{i=1}^{v}{‖{\boldsymbol{X}}^{i}-{\boldsymbol{X}}^{i}{\boldsymbol{S}}^{i}‖}_{F}^{2}+\alpha f\left({\boldsymbol{S}}^{i}\right) \\ {\rm{s.t.}}\quad{\boldsymbol{S}}^{i}\geqslant 0,{\boldsymbol{S}}^{i}{\bf{1}}=1 \quad\quad \end{aligned}$$ (1) 式中：
${\boldsymbol{S}}^{i}$ 为第$ i $ 个视图的相似度矩阵，不同形式的$f(\cdot)$ 可以给出不同性质的解。例如，文献[4]利用HSIC鼓励图对之间的差异性，文献[6]利用低秩稀疏对相似度矩阵${\boldsymbol{S}}^{i}$ 进行约束，文献[9]生成了一个潜在的表示空间以灵活编码多视图信息。但是所有这些多视图子空间聚类方法每个视图的相似度矩阵${\boldsymbol{S}}^{i}$ 的大小都为$ n\times n $ ，从而都至少需要$ O\left({n}^{2}k\right) $ 的时间，且都涉及拉普拉斯矩阵特征分解，因此具有计算效率以及存储空间上的劣势，使其很难扩展到样本点$ n $ 数量庞大的大规模数据集上。1.2 锚图构造
相似度矩阵的构造对于谱聚类来说非常重要，对于构造大规模数据集的相似度矩阵，锚图是一种十分有效的方法[16]。
利用K-means或随机选择等方法从含有
$ n $ 个样本点的数据集中提取出具有$ m\left(m\ll n\right) $ 个样本点的子集，每个子集中的点作为地标点来逼近原数据集，引入$ k $ 近邻点来度量点对之间的局部亲和力。利用地标点与原数据来构造一个稀疏相似度矩阵${\boldsymbol{Z}}\in {\bf{R}}^{n\times m}$ :$$ {{\boldsymbol{Z}}_{ij}} = \left\{ \begin{array}{l} \dfrac{{{K_\delta }\left( {{{\boldsymbol{x}}_i},{{\boldsymbol{a}}_j}} \right)}}{{\displaystyle\sum_{j' \in \left\langle i \right\rangle } {{K_\delta }}{\left({{\boldsymbol{x}}_{i}},{{\boldsymbol{a}}_{j'}} \right)} }},\quad j \in \left\langle i \right\rangle \\ 0,\quad{其他} \end{array} \right.$$ (2) 式中：
$\left\langle i \right\rangle$ 表示$ {\boldsymbol{x}}_{i} $ 的$ r(r < m) $ 个最近邻地标点；${K}_{\delta }\left(\cdot \right)= $ $ {\rm{exp}}\left(-{\rho }^{2}({\boldsymbol{x}}_{i},{\boldsymbol{a}}_{j})/2{\delta }^{2}\right)$ 是带宽参数为$ \delta $ 的常用高斯核函数；$ \delta $ 控制每个数据点的局部邻域大小。然而此启发式策略存在一个总是被忽略的固有缺点，即所构建的图形质量很大程度依赖于指数函数和近邻点个数
$ r $ 的选择，因此，下游任务可能会受到负面影响。2. 结合地标点与自编码的快速多视图聚类算法
2.1 图形构造
大规模数据集中存在很多冗余数据，少量样本完全满足重建子空间的需求。传统的地标点选择方法有文献[15]中的随机抽样和使用
$ {K} $ 均值中心点作为地标点的方法。但是随机抽样可能导致地标点彼此过于靠近，这可能导致邻域重叠。而采用$ {K} $ 均值中心作为地标点的方法运行时间过长且当数据规模极大，超出系统的内存时，${K} $ 均值聚类算法需要不断地执行读取操作[17]。因此，本文采用文献[18]中的加权$ \rm{P}\rm{a}\rm{g}\rm{e}\rm{R}\rm{a}\rm{n}\rm{k} $ 算法来为每个视图选择$ {\rm{wpr}} $ 值最高的$ m $ 个样本点作为地标点。为了避免式(2)形式生成相似度矩阵的不足之处，本文在多视图聚类框架下采取直接从数据生成相似度矩阵的方法，该方法不仅能揭示数据低维结构，还对噪声和数据规模有着极强的鲁棒性。在多视图思想下利用重构误差和约束项建立采用地标点的多视图聚类模型目标函数：
$$\begin{aligned} \underset{{Z}^{v}}{\rm{min}}\sum _{v=1}^{V}{‖{\boldsymbol{X}}^{v}-{\boldsymbol{A}}^{\boldsymbol{v}}{\left({\boldsymbol{Z}}^{v}\right)}^{\rm{T}}‖}_{F}^{2}+\alpha {‖{\boldsymbol{Z}}^{v}‖}_{F}^{2}\\ {\rm{s.t.}} \quad0 \leqslant {\boldsymbol{Z}}^{v},{\left({\boldsymbol{Z}}^{v}\right)}^{\rm{T}}1=1.\quad\quad \end{aligned}$$ (3) 式中：
$ V $ 为从不同来源或者利用不同收集方式获取到的视图总个数；$ {\boldsymbol{X}}^{{v}} $ 、${\boldsymbol{A}}^{{v}}$ 、${\boldsymbol{Z}}^{{v}} $ 分别为第$ v $ 个视图的原始数据矩阵、地标点矩阵、相似度矩阵。因为无需设置近邻点，该形式生成的相似度矩阵不再受困于只能捕获到数据的局部分布这一桎梏，并能完整感知数据从而保留数据的全局结构。可以看出，与式(2)相比，对于每个视图，本方法只需在$ mn $ 个数据点之间计算相似度矩阵而非传统子空间聚类中的$ {n}^{2} $ 个数据点。对于大规模数据集来说，此举可在利用多视图一致性与互补性确保聚类精度的同时使复杂度显著降低。由于现实世界中数据的固有结构呈现出普遍非线性状态[19]，将式(3)扩展到核空间中进行。定义
$ \varphi :{\mathcal{R}}^{D}\to \mathcal{H} $ 为从原始输入空间到核希尔伯特空间$ \mathcal{H} $ 的映射，对于每个包含$ n $ 个样本点的视图${\boldsymbol{X}}^{\boldsymbol{v}}=[{x}_{1}^{v}\;{x}_{2}^{v}\;\cdots \;{x}_{n}^{v}]$ ，其变换后形式为$$\varphi \left({\boldsymbol{X}}^{\boldsymbol{v}}\right)=[\varphi \left({\boldsymbol{x}}_{1}^{v}\right)\; \varphi \left({\boldsymbol{x}}_{2}^{v}\right)\; \cdots \; \varphi \left({\boldsymbol{x}}_{n}^{v}\right)]$$ 由
$ m $ 个地标点构成的强代表性数据矩阵${\boldsymbol{A}}^{\boldsymbol{v}}=[{\boldsymbol{a}}_{1}^{v}\;{\boldsymbol{a}}_{2}^{v}\;\cdots \;{\boldsymbol{a}}_{m}^{v}]$ 的变换后形式为$$\varphi \left({\boldsymbol{A}}^{\boldsymbol{v}}\right)= \left[\varphi \right({\boldsymbol{a}}_{1}^{v})\; \varphi ({\boldsymbol{a}}_{2}^{v})\;\cdots \; \varphi ({\boldsymbol{a}}_{m}^{v}\left)\right]$$ 核函数定义为
$${K}_{\left({\boldsymbol{x}}_{i},{\boldsymbol{x}}_{j}\right)}= < \varphi \left({\boldsymbol{x}}_{i}\right), \varphi \left({\boldsymbol{x}}_{j}\right) > $$ 则式(3)可转变为
$$\begin{aligned} \underset{{Z}^{v}}{\rm{min}}{\rm{tr}}\left({\boldsymbol{K}}^{v}-2{\boldsymbol{K}}^{v}{\boldsymbol{Z}}^{v}+{{\boldsymbol{Z}}^{v}}^{\rm{T}}{\boldsymbol{K}}^{v}{\boldsymbol{Z}}^{v}\right)+{\alpha ‖{\boldsymbol{Z}}^{\boldsymbol{v}}‖}_{F}^{2}\\ {\rm{s.t.}}\quad{{\boldsymbol{Z}}^{v}}^{\rm{T}}1=1,0\leqslant {\boldsymbol{Z}}^{v}\leqslant 1 \quad\quad\quad \end{aligned}$$ (4) 通过求解式(4)可以捕获到
$ \varphi \left(\boldsymbol{x}\right) $ 与$ \varphi \left(\boldsymbol{a}\right) $ 间的线性稀疏关系，即样本点$ \boldsymbol{x} $ 与地标点$ \boldsymbol{a} $ 间的非线性关系。将式(4)按列重新写出：$$\begin{aligned} \underset{{\boldsymbol{Z}}_{i}^{v}}{\rm{min}}{\boldsymbol{K}}_{ii}^{v}-2{\boldsymbol{K}}_{i,:}^{v}{\boldsymbol{Z}}_{i}^{v}+{{\boldsymbol{Z}}_{i}^{v}}^{\rm{T}}{\boldsymbol{K}}^{v}{\boldsymbol{Z}}_{i}^{v}+\alpha {{\boldsymbol{Z}}_{i}^{v}}^{\rm{T}}{\boldsymbol{Z}}_{i}^{v}\\ {\rm{s.t.}}\quad{{\boldsymbol{Z}}_{i}^{v}}^{\rm{T}}1=1, 0 \leqslant {\boldsymbol{Z}}_{i}^{v}\leqslant 1 \quad\quad\quad \end{aligned}$$ (5) 进而式(5)可转变成为二次型形式(6)，从而能直接通过凸二次规划函数求解得到各个视图的由数据直接生成的相似度矩阵
$ {\boldsymbol{Z}}^{v} $ ：$$\begin{aligned} \underset{{\boldsymbol{Z}}_{i}^{v}}{\rm{min}}{{\boldsymbol{Z}}_{i}^{v}}^{\rm{T}}\left(\alpha \boldsymbol{I}+{\boldsymbol{K}}^{v}\right){\boldsymbol{Z}}_{i}^{v}-2{\boldsymbol{K}}_{i,:}^{v}{\boldsymbol{Z}}_{i}^{v}\\ {\rm{s.t.}}\quad{{\boldsymbol{Z}}_{i}^{v}}^{\rm{T}}1=1, 0\leqslant {z}_{ij}\leqslant 1 \quad \end{aligned}$$ (6) 因为所获得的
$ {\boldsymbol{Z}}^{\boldsymbol{v}} $ 的大小不为$ n\times n $ ，不能直接对$ {\boldsymbol{Z}}^{\boldsymbol{v}} $ 进行后续谱聚类操作，在每个视图上求取双随机相似度矩阵${\boldsymbol{S}}^{{v}}={\hat{\boldsymbol{Z}}}^{v}{{\hat{\boldsymbol{Z}}}^{v{\rm{T}}}}$ ，该形式比$ {\boldsymbol{Z}}^{\boldsymbol{v}} $ 能更多地保留数据局部结构，然而利用传统方法计算度矩阵$ {\boldsymbol{D}}^{\boldsymbol{v}} $ 需消耗${ O}\left({n}^{2}m\right)$ 时间，很难负担大规模数据集的运行。为此采用文献[20]中方法进行快速度矩阵计算${{D}}^{{v}}={\rm{diag}}\left({{\hat{\boldsymbol{Z}}}^{v{\rm{T}}}}{\hat{\boldsymbol{Z}}^{{vs}}}\right)$ ，其中${{\hat{{Z}}}^{{vs}}}$ 是第k个元素为${\hat{\boldsymbol{Z}}}^{v}$ 第k行元素之和的$ m\times 1 $ 向量，该计算度矩阵的时间复杂度为${ O}\left(nm\right)$ ，相比${O}\left({n}^{2}m\right)$ 有了巨大提升。拉普拉斯矩阵表示为$$ {\boldsymbol{L}}^{v}={{\boldsymbol{D}}^{v}}^{-1/2}{{\hat{{Z}}}^{{v}{\rm{T}}}}{\hat{\boldsymbol{Z}}}^{v}{{\boldsymbol{D}}^{v}}^{-1/2} $$ (7) 得到
$ {\boldsymbol{S}}^{v}={\widehat{\boldsymbol{Z}}}^{v}{{\boldsymbol{D}}^{v}}^{-1/2} $ ，再联合各个视图以获得具有互补性与一致性的多视图蕴涵的丰富信息：$$ \overline{\boldsymbol{S}}=\frac{\displaystyle\sum\limits_v{\boldsymbol{S}}^{\boldsymbol{v}}}{v} $$ (8) 2.2 联合优化框架
由于对
$ \overline{\boldsymbol{S}} $ 进行特征向量分解而获得类指示矩阵需要花费至少$ { O}\left({n}^{2}k\right) $ 的时间，当面临样本数$ n $ 极为庞大的大规模数据集时，特征分解步骤将耗时巨大从而降低算法可用性。由文献[21]可知谱聚类的本质是寻求样本空间标准相似度矩阵的最小重构误差的过程，这与自编码器的核心思想高度一致，且利用自编码器替代拉普拉斯矩阵特征分解只需消耗样本数$ n $ 的线性次方时间。因此将$ \overline{\boldsymbol{S}} $ 作为自编码器的输入来替代特征分解，通过编码和解码重构学习低维嵌入形式数据。自编码器是一种利用非线性变换函数
$ {f}_{i} $ 将原始输入$ {\boldsymbol{x}}_{i} $ 映射到低维嵌入空间，获得嵌入表示$ {\boldsymbol{h}}_{i} $ ，再通过另一映射函数$ {g}_{{w}^{\text{'}}} $ 对$ {\boldsymbol{h}}_{i} $ 进行解码重构，通过最小化原始输入$ {\boldsymbol{x}}_{i} $ 与嵌入表示$ {\boldsymbol{h}}_{i} $ 的重构输出$ {\boldsymbol{y}}_{i} $ 之间的重构损失$ {L}_{r} $ 来迭代更新的人工神经网络[14]，其均值误差测量形式目标函数为$$ {L}_{r}=\sum _{i=1}^{n}{‖{\boldsymbol{x}}_{i}-{g}_{{w}^{\rm{\text{'}}}}\left({f}_{i}\right)‖}_{2}^{2} $$ (9) 文献[15]同样利用自编码器来配合聚类，然而其仅在聚类步骤前简单叠加无监督深度学习框架，这样形成的低维嵌入空间可能反而会损坏聚类分配效果。为此本文将聚类步骤和表示学习统一到一个基于KL散度的利用损失函数迭代更新自编码器参数
$\{{M}_{1}、{M}_{2}；{\theta }_{1}、{\theta }_{2}\}$ 和聚类中心$ {\boldsymbol{c}}_{j} $ 的联合学习框架中，从而能联合优化聚类标签的分配和特征的学习，也使位于自编码器隐藏层的低维特征能够最大限度的保留原始数据的固有局部结构。将聚类损失目标函数定义为$$ {L}_{c}={\rm{KL}}\left(P\right|\left|Q\right)=\sum _{i}\sum _{j}{p}_{ij}{\rm{log}}\frac{{p}_{ij}}{{q}_{ij}} $$ (10) 式中：
$ Q $ 为由t-SNE测量的软标签的分布；${P}$ 为由$ Q $ 导出的目标分布。KL散度衡量了两种不同分布之间的差异性，若对其进行最小化则能使得目标分布${P}$ 能够尽可能接近聚类输出分布${Q}$ 。$ {q}_{ij} $ 表示根据t-SNE测量得到的嵌入表示$ {\boldsymbol{h}}_{i} $ 与聚类中心$ {\boldsymbol{c}}_{j} $ 的相似程度[14]，其表达式如下：$$ {q}_{ij}=\frac{{(1+‖{\boldsymbol{h}}_{i}-{\boldsymbol{c}}_{j}‖)}^{-1}}{\displaystyle\sum _{j}{(1+{‖{\boldsymbol{h}}_{i}-{\boldsymbol{c}}_{j}‖}^{2})}^{-1}} $$ (11) $ {p}_{ij} $ 则是由$ {q}_{ij} $ 确定的目标分布：$$ {p}_{ij}=\frac{{q}_{ij}^{2}/\displaystyle\sum _{i}{q}_{ij}}{\displaystyle\sum _{j}({q}_{ij}^{2}/{\displaystyle\sum }_{i}{q}_{ij})} $$ (12) 因此，总体的优化目标函数为
$$ L={L}_{c}+\lambda {L}_{r} $$ (13) 其中，
$ \lambda (0 < \lambda < 1) $ 为控制嵌入空间失真程度的平衡参数。则根据mini-batch随机梯度算法反向传播逐层训练网络后计算出的聚类损失$ {L}_{c} $ 关于嵌入表示$ {\boldsymbol{h}}_{i} $ 和聚类中心$ {\boldsymbol{c}}_{j} $ 的梯度计算公式为$$ \frac{\partial {L}_{c}}{\partial {\boldsymbol{h}}_{i}}=2\sum _{j=1}^{k}{\left(1+{‖{\boldsymbol{h}}_{i}-{\boldsymbol{c}}_{j}‖}^{2}\right)}^{-1}\left({p}_{ij}-{q}_{ij}\right)\left({\boldsymbol{h}}_{i}-{\boldsymbol{c}}_{j}\right) $$ (14) $$ \frac{\partial {L}_{c}}{\partial {\boldsymbol{c}}_{j}}=2\sum _{j=1}^{k}{\left(1+{‖{\boldsymbol{h}}_{i}-{\boldsymbol{c}}_{j}‖}^{2}\right)}^{-1}\left({q}_{ij}-{p}_{ij}\right)\left({\boldsymbol{h}}_{i}-{\boldsymbol{c}}_{j}\right) $$ (15) 给定
$ m $ 为小批量样本数，$ \eta $ 为学习速率，编码器权重$ {M}_{1} $ 、译码器权重$ {M}_{2} $ 、聚类中心$ {\boldsymbol{c}}_{j} $ 的更新公式分别为$$ {M}_{1}={M}_{1}-\frac{\eta }{m}\sum _{i=1}^{m}\left(\frac{\partial {L}_{c}}{\partial {{M}}_{1}}+\lambda \frac{\partial {L}_{r}}{\partial {{M}}_{1}}\right) $$ (16) $$ {M}_{2}={M}_{2}-\frac{\eta }{m}\sum _{i=1}^{m}\left(\frac{\partial {L}_{r}}{\partial {{M}}_{2}}\right) $$ (17) $$ {\boldsymbol{c}}_{j}={\boldsymbol{c}}_{j}-\frac{\eta }{m}\sum _{i=1}^{m}\left(\frac{\partial {L}_{c}}{\partial {\boldsymbol{c}}_{j}}\right) $$ (18) 当连续两次更新的类标签分配之间的变化率小于给定的阈值
$ \rm{\delta } $ 时迭代停止。2.3 算法流程图
结合地标点与自编码的快速多视图聚类网络算法流程如图1所示。
图 1 所提算法流程图Fig. 1 Flow chart of the proposed algorithm
下载:
全尺寸图片
2.4 算法复杂度分析
当有
$ v $ 个视图，每个视图有$ n $ 个样本点，每个视图的地标点个数为$ m $ 时：1)利用加权$ \rm{P}\rm{a}\rm{g}\rm{e}\rm{R}\rm{a}\rm{n}\rm{k} $ 算法为每个视图进行地标点选择，因此本文地标点选择步骤的时间复杂度为$ O\left(vtmn\right) $ ，$ t $ 为生成每个样本点的wpr的迭代次数；2)构造多个视图的相似度矩阵，DiMSC和FMR等多视图子空间聚类方法由于未进行1)地标点选择，在2)中DiMSC和FMR算法构造的每个视图的自表示矩阵图形大小均为$ n\times n $ ，二者的计算复杂度分别为$ O(Tv{n}^{3}+vd{n}^{2}) $ 、$O\left(T\right(L+1\left)\right) \left({n}^{3}+k{n}^{2}\right)$ ，其中$ L $ 表示FMR算法中涉及的梯度下降法的迭代次数，$ T $ 为DiMSC、FMR算法总迭代次数。当数据规模$ n $ 很大时，$ L$ 、$T\ll n $ ，因此DiMSC和FMR算法步骤2)的计算复杂度均可视为$ O\left({n}^{3}\right) $ ，这远远高于本文算法的$ m\times n $ ($ m\ll n $ )图形的计算复杂度$ O\left(vn{m}^{3}\right) $ 。3)聚类步骤，DiMSC和FMR算法的步骤3)采用常规谱聚类，涉及到$ {n}^{2} $ 图的拉普拉斯矩阵特征分解，需要消耗$ O\left({n}^{3}\right) $ 的时间复杂度，且存储开销极大。而所提算法采用自编码器替代拉普拉斯矩阵特征分解步骤，自编码器参数和聚类中心联合更新，仅需$ O\left(n{D}^{2}+ndk\right) $ 的时间，其中$ D $ 为自编码器隐藏层的最大单元数，$ d $ 为自编码器中间层的维数，$ k $ 为簇数，与此同时存储开销也被大大降低。因为通常$ k\ll d\ll D $ ，所以本文所提算法的总体时间复杂度为$ O\left(vtpn+vn{m}^{3}+n{D}^{2}\right) $ 。可以看出，本文提出的采用地标点的快速多视图聚类网络的总体时间复杂度为样本点数$ n $ 的线性次方，而DiMSC和FMR聚类算法的总体时间复杂度为样本点数$ n $ 的三次方。表1给出了所提算法与多视图聚类算法DiMSC、FMR的时间复杂度对比结果。与通常的多视图聚类算法相比本文算法的效率大大提升，且所需的存储开销显著降低，从而可更适用于大规模数据集。表 1 不同方法时间复杂度对比Table 1 Complexity analysis of different methods算法 步骤1 步骤2 步骤3 总体 DiMSC — $ O(Tv{n}^{3}+vd{n}^{2}) $ $ O\left({n}^{3}\right) $ $ O\left({n}^{3}\right) $ FMR — $ O\left(T\right(L+1\left)\right)\left({n}^{3}+k{n}^{2}\right) $ $ O\left({n}^{3}\right) $ $ O\left({n}^{3}\right) $ 本文 $ O\left(vtmn\right) $ $ O\left(vn{m}^{3}\right) $ $ O\left(n{D}^{2}+ndk\right) $ $ O\left(n\right) $ 3. 实验与结果分析
3.1 实验环境及评价指标
为了证明本文所提方法对大规模多视图数据的适用性，选取100leaves、Handwritten（HW）、Caltech101-7/20、NUS-WIDE-Object (NUS) 五个大规模的多视图数据集进行实验，每个数据集样本点数都在1000以上，表2为5个大规模多视图数据集的详细介绍，其中
$ {V} $ 为多视图数据集的视图编号。本文算法实验是在python3.7运行，计算机配置为Intel Core i5CPU 1.6 GHz、4 GB内存，操作系统为macOS Catalina。表 2 数据集介绍Table 2 Description of the datasetsV 100leaves Handwritten Caltech101-7/20 NUS 1 64 216 48 65 2 64 76 40 226 3 64 64 254 145 4 — 6 1984 74 5 — 240 512 129 6 — 47 928 — n 1600 2000 1474/2386 30000 k 100 10 7/20 31 将本文方法所得聚类结果与样本真实标签进行比较，利用聚类准确率(ACC)、标准化互信息(NMI)和运行时间(Time)来作为性能评估指标，ACC和NMI取值均在0~1，值越大说明聚类性能越佳，运行时间越短说明算法越具有普遍适用性，即越适用于大规模数据集。
3.2 数据集及对比算法
为证明本文提出的算法的有效性，将其分别与单视图聚类算法和多视图聚类算法进行对比，对比单视图聚类算法分别为文献[21]中的传统单视图谱聚类算法SC和文献[15]中的使用K均值进行地标点选择后利用嵌入表示替代拉普拉斯矩阵分解步骤的SCAL-K，同时与4个近期出现的性能优异的多视图聚类算法DiMSC[4]、MLRSSC[6]、MSC_IAS[8]、FMR[10]进行对比。
为保证算法对比的公平性，所有对比算法都遵从算法原论文的实验设置，并调试参数获得其最优值。文献[15]中的SCAL-K算法及本文算法的自编码器部分的编码器维度设置为p-500-500-2000-10，解码器部分为编码器的镜像，最小批量样本数设置为256，初始学习速率
$ \eta $ 设为$ 0.1 $ ，停止阈值设置为$ h={10}^{-3} $ ，并把控制嵌入空间失真程度的平衡参数$ \lambda $ 设置为$ 0.1 $ 。对于两个单视图聚类算法，在数据集的每个视图上运行实验后取多个视图里的最佳结果展示。3.3 实验结果分析
各个算法在5个数据集上的实验结果如表3~7所示。实验结果ACC和NMI中的性能最优异项被加黑标出。
表 3 不同算法在100leaves数据集上的表现Table 3 Performance of different algorithms on the 100leaves dataset表 4 不同算法在Handwritten数据集上的表现Table 4 Performance of different algorithms on the Handwritten dataset表 5 不同算法在Caltech101-7数据集上的表现Table 5 Performance of different algorithms on the Caltech101-7 dataset本文算法主要针对多视图聚类算法运行效率进行研究，可以看出，本文所提算法在表3~6的4个大规模多视图数据集上的运行速度均快于多视图聚类算法MLRSSC、MSC_IS、DiMSC、FMR，在表7的NUS数据集上同样快于多视图聚类算法MSC_IS。并且可以看出，在越大型的数据集上本文所提算法在运行时间上的优越性愈加明显，甚至可以达到相较于传统多视图聚类算法快几个数量级的效果，例如在NUS数据集上MSC_IS算法需要36 749.39 s运行时间而本算法仅需586.61 s。因为执行时间的波动主要受选取的地标点个数
$ m $ 的影响，而100leaves数据集取得最佳聚类结果时采用的地标点个数在几个数据集中为最小值，因此所提算法在100leaves数据集上的运行时间最短。并且，同时采用了地标点与深度嵌入的单视图聚类算法SCAL-K(best)在多个数据集上的速度也快于SC(best)。上述现象均说明了采用地标点和嵌入表示替代矩阵分解对提升聚类算法运行速度的有效性。此外，当面对例如NUS等每个视图的样本点数$ n $ 超过10000的数据集时，多种多视图聚类算法例如MLRSSC、DiMSC、FMR会由于超出存储空间而无法得到实验结果，因此表7仅给出了SC(best)、SCAL-K(best)、MSC_IS的对比实验结果，与之相反的是本文所提算法在5个多视图数据集上均能得到实验结果，这证明了本文所提算法需要相较于传统多视图聚类算法更低的存储开销与计算复杂度。上述现象均证明了本算法较传统多视图聚类算法对大规模数据集具有更强的适用性。表 6 不同算法在Caltech101-20数据集上的表现Table 6 Performance of different algorithms on the Caltech101-20 dataset本文所提算法的性能在ACC方面始终具有明显的优越性，均取得了所有实验算法结果ACC中的最大值，分别在100leaves、HW、Caltech101-7、Caltech101-20、NUS上超过了第二佳算法1.3%、1.27%、21.3%、4.0%、1.75%。而NMI方面本文算法同样可实现与其他多视图聚类算法相当甚至更好的性能，这证明了本文算法的一致性与稳定性。可以得出，本文所提出的采用地标点的快速多视图聚类算法在大幅度提升聚类速度的同时仍能够保持较好的聚类精确度。
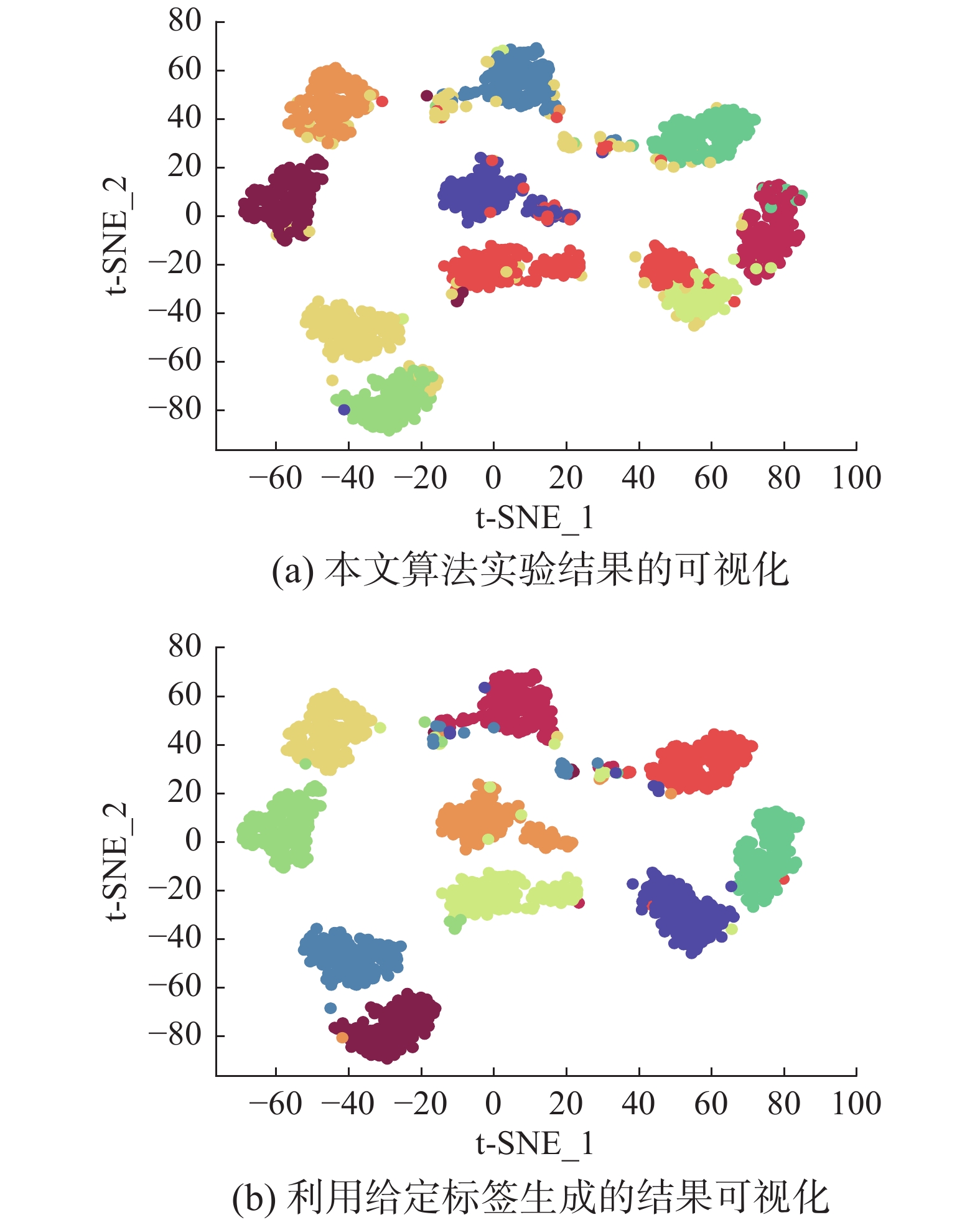
为了进一步研究改进，本文在Handwritten数据集上使用t-SNE进行了二维可视化对比研究。图2(a)为本文算法的聚类结果视图，图2(b)为对比的利用给定标签生成的可视化结果，其中t-SNE_1、t-SNE_2代表分别采用经t-SNE方法降维后的二维数据的第1列和第2列数据作为可视化呈现的
$ x $ 轴和$ y $ 轴。可以看出，虽然仍有少部分数据点未进行正确的聚类划分，但总体上本文算法可以良好地反映聚类结构，从而进一步证明本文算法可以在提升大规模数据集算法效率的同时保持较好的聚类精确度。
图 2 Handwritten数据集实验结果t-SNE可视化Fig. 2 Visualization of experimental results on the Handwritten dataset with t-SNE下载:
全尺寸图片
由于所提方法采用地标点进行原数据重建，地标点个数
$ m $ 越少所提算法的运行时间就越短，但算法的精度却不一定和地标点个数$ m $ 呈线性关系。因此本文作了敏感分析实验，以100leaves、Handwritten、Caltech101-7等3个数据集的ACC为例，调整地标点个数$ m $ ，图3给出了模型对地标点个数的敏感性。可以看出，地标点个数$ m $ 太少时难以完整代表原数据所有特征，而当地标点个数$ m $ 过多时会使其本身的代表性降低并引入额外的错误从而导致性能变差。
图 3 地标点敏感实验结果Fig. 3 Results of landmark sensitive experiments下载:
全尺寸图片
4. 结束语
本文提出了一种结合地标表示和自编码器的多视图快速聚类方法，在多视图的框架下利用了加权
$ \rm{P}\rm{a}\rm{g}\rm{e}\rm{R}\rm{a}\rm{n}\rm{k} $ 方法选择地标点以减少存储开销，通过所选择的地标点重构原始多视图数据直接得到多视图共识相似度矩阵，在降低了计算复杂度的同时充分利用了多个视图中具有互补性与一致性的聚类有效信息，利用自编码器替代拉普拉斯矩阵特征分解，联合更新自编码器参数以及聚类中心，以保证聚类精度。在5个多视图数据集上的实验证明本文所提算法拥有良好的性能。但是本文中多个视图的信息仅是通过简单的相加来融合而并未进行视图差异区分，在未来，致力于进一步研究如何在保证计算速度的情况下更好将多个视图的信息具有区分性地融合，以更好地提升聚类性能。 -
图 1 所提算法流程图
Fig. 1 Flow chart of the proposed algorithm
下载:
全尺寸图片
图 2 Handwritten数据集实验结果t-SNE可视化
Fig. 2 Visualization of experimental results on the Handwritten dataset with t-SNE
下载:
全尺寸图片
图 3 地标点敏感实验结果
Fig. 3 Results of landmark sensitive experiments
下载:
全尺寸图片
表 1 不同方法时间复杂度对比
Table 1 Complexity analysis of different methods
算法 步骤1 步骤2 步骤3 总体 DiMSC — $ O(Tv{n}^{3}+vd{n}^{2}) $ $ O\left({n}^{3}\right) $ $ O\left({n}^{3}\right) $ FMR — $ O\left(T\right(L+1\left)\right)\left({n}^{3}+k{n}^{2}\right) $ $ O\left({n}^{3}\right) $ $ O\left({n}^{3}\right) $ 本文 $ O\left(vtmn\right) $ $ O\left(vn{m}^{3}\right) $ $ O\left(n{D}^{2}+ndk\right) $ $ O\left(n\right) $ 表 2 数据集介绍
Table 2 Description of the datasets
V 100leaves Handwritten Caltech101-7/20 NUS 1 64 216 48 65 2 64 76 40 226 3 64 64 254 145 4 — 6 1984 74 5 — 240 512 129 6 — 47 928 — n 1600 2000 1474/2386 30000 k 100 10 7/20 31 表 3 不同算法在100leaves数据集上的表现
Table 3 Performance of different algorithms on the 100leaves dataset
表 4 不同算法在Handwritten数据集上的表现
Table 4 Performance of different algorithms on the Handwritten dataset
表 5 不同算法在Caltech101-7数据集上的表现
Table 5 Performance of different algorithms on the Caltech101-7 dataset
表 6 不同算法在Caltech101-20数据集上的表现
Table 6 Performance of different algorithms on the Caltech101-20 dataset
-
[1] 何清, 李宁, 罗文娟, 等. 大数据下的机器学习算法综述[J]. 模式识别与人工智能, 2014, 27(4): 327–336. doi: 10.3969/j.issn.1003-6059.2014.04.007 HE Qing, LI Ning, LUO Wenjuan, et al. A survey of machine learning algorithms for big data[J]. Pattern recognition and artificial intelligence, 2014, 27(4): 327–336. doi: 10.3969/j.issn.1003-6059.2014.04.007 [2] KUMAR A, DAUME III H. A co-training approach for multi-view spectral clustering[C]//Proceedings of the 28th International Conference on Machine Learning. Washington, USA, 2011: 393−400. [3] 何雪梅. 多视图聚类算法综述[J]. 软件导刊, 2019, 18(4): 79–81,86. https://www.cnki.com.cn/Article/CJFDTOTAL-RJDK201904019.htm HE Xuemei. A survey of multi-view clustering algorithms[J]. Software guide, 2019, 18(4): 79–81,86. https://www.cnki.com.cn/Article/CJFDTOTAL-RJDK201904019.htm [4] CAO Xiaochun, ZHANG Changqing, FU Huazhu, et al. Diversity-induced multi-view subspace clustering[C]//Proceedings of 2015 IEEE Conference on Computer Vision and Pattern Recognition. Boston, USA, 2015: 586−594. [5] WANG Xiaobo, GUO Xiaojie, LEI Zhen, et al. Exclusivity-consistency regularized multi-view subspace clustering[C]//Proceedings of 2017 IEEE Conference on Computer Vision and Pattern Recognition. Honolulu, USA, 2017: 1−9. [6] BRBIĆ M, KOPRIVA I. Multi-view low-rank sparse subspace clustering[J]. Pattern recognition, 2018, 73: 247–258. doi: 10.1016/j.patcog.2017.08.024 [7] NIE Feiping, LI Jing, LI Xuelong, et al. Self-weighted multiview clustering with multiple graphs[C]//Proceedings of the Twenty-Sixth International Joint Conference on Artificial Intelligence. Melbourne, Australia, 2017: 2564−2570. [8] WANG Xiaobo, LEI Zhen, GUO Xiaojie, et al. Multi-view subspace clustering with intactness-aware similarity[J]. Pattern recognition, 2019, 88: 50–63. doi: 10.1016/j.patcog.2018.09.009 [9] LI Ruihuang, ZHANG Changqing, HU Qinghua, et al. Flexible multi-view representation learning for subspace clustering[C]//Proceedings of the Twenty-Eighth International Joint Conference on Artificial Intelligence. Macao, China, 2016: 2916−2922. [10] CAI Xiao, NIE Feiping, HUANG Heng, et al. Heterogeneous image feature integration via multi-modal spectral clustering[C]//Proceedings of the CVPR 2011. Colorado Springs, USA, 2011: 1977−1984. [11] CAI Xiao, NIE Feiping, HUANG Heng. Multi-view K-means clustering on big data[C]//Proceedings of the Twenty-Third International Joint Conference on Artificial Intelligence. Beijing, China, 2013: 2598−2604. [12] HE Li, RAY N, GUAN Yisheng, et al. Fast large-scale spectral clustering via explicit feature mapping[J]. IEEE transactions on cybernetics, 2019, 49(3): 1058–1071. doi: 10.1109/TCYB.2018.2794998 [13] TIAN Fei, GAO Bin, CUI Qing, et al. Learning deep representations for graph clustering[C]//Proceedings of the Twenty-Eighth AAAI Conference on Artificial Intelligence. Québec, Canada, 2014: 1293−1299. [14] YIN Wanpeng, ZHU En, ZHU Xinzhong, et al. Landmark-based spectral clustering with local similarity representation[C]//Proceedings of the 35th National Conference of Theoretical Computer Science. Wuhan, China, 2017: 198-207. [15] BANIJAMALI E, GHODSI A. Fast spectral clustering using autoencoders and landmarks[C]//Proceedings of the 14th International Conference Image Analysis and Recognition. Montreal, Canada, 2017: 380−388. [16] CHEN Xinlei, CAI Deng. Large scale spectral clustering with landmark-based representation[C]//Proceedings of the Twenty-Fifth AAAI Conference on Artificial Intelligence. San Francisco, USA, 2011: 7−11. [17] 叶茂, 刘文芬. 基于快速地标采样的大规模谱聚类算法[J]. 电子与信息学报, 2017, 39(2): 278–284. https://www.cnki.com.cn/Article/CJFDTOTAL-DZYX201702004.htm YE Mao, LIU Wenfang. Large scale spectral clustering based on fast landmark sampling[J]. Journal of electronics & information technology, 2017, 39(2): 278–284. https://www.cnki.com.cn/Article/CJFDTOTAL-DZYX201702004.htm [18] RAFAILIDIS D, CONSTANTINOU E, MANOLOPOULOS Y. Landmark selection for spectral clustering based on Weighted PageRank[J]. Future generation computer systems, 2017, 68: 465–472. doi: 10.1016/j.future.2016.03.006 [19] ZHANG Guangyu, ZHOU Yuren, HE Xiaoyu, et al. One-step kernel multi-view subspace clustering[J]. Knowledge-based systems, 2020, 189: 105126. doi: 10.1016/j.knosys.2019.105126 [20] LI Xinning, ZHAO Xiaoxiao, CHU Derun, et al. An autoencoder-based spectral clustering algorithm[J]. Soft computing, 2020, 24(3): 478–487. [21] XIE Junyuan, GIRSHICK R, FARHADI A. Unsupervised deep embedding for clustering analysis[C]//Proceedings of the 33rd International Conference on Machine Learning. New York, USA, 2016: 478−487.
