Classification method of cost-sensitive three-way decision boundary region for hybrid data
-
摘要: 针对现有三支决策模型的研究对象多为单一性数据的决策系统,对于混合数据边界域样本处理的研究相对较少,本文面向混合数据提出了基于核属性的代价敏感三支决策边界域分类方法。该方法基于正域约简计算混合邻域决策系统的核属性集,在此基础上计算混合邻域类,并利用三支决策规则分别将对象划分到各决策类的正域、边界域和负域;提出了一种基于代价敏感学习的三支决策边界域分类方法,并构造了误分类代价的计算方法,以此划分边界域中的对象。通过对UCI上的10个数据集进行实验对比与分析,进一步验证了本文方法,为处理边界域样本提供了一种可行有效的方法。Abstract: The research objects of existing three-way decisions models are mostly decision-making systems with single data. Relatively few studies on the boundary region sample processing of mixed data have been conducted. To address this issue, a classification method of a cost-sensitive three-way decision boundary region based on core attributes for hybrid data is proposed in this study. This method computes the core attribute set of the hybrid neighborhood decision system based on positive domain reduction. On this basis, the hybrid neighborhood class is calculated, and the objects are divided into the positive, boundary, and negative regions of each decision-making class through three-way decision rules. The classification method of the three-way decision boundary region based on cost-sensitive learning is proposed. Then, a calculation method of the misclassification cost is constructed to divide the objects in the boundary region. Experiments and analyses are performed on 10 datasets of UCI, which show the feasibility and the effectiveness of the proposed method for the processing of boundary region samples.
-
三支决策是加拿大学者Yao[1-2]提出的一种“化繁为简”决策理论,它从粒计算视角将论域划分为三个互不相交的论域子空间,并对其分别采取不同的应对策略,这种分而治之的思想,可有效提高决策准确度,降低误分类代价。三支决策理论模拟人类认知、学习和决策的过程,可处理决策过程中出现的不确定性问题。近年来,三支决策理论引起了许多研究者的关注,已成为了粒计算和知识发现领域中的一个重要研究方向。目前,三支决策在众多应用领域中得到广泛的应用,如人脸识别[3]、推荐系统[4-5]、决策系统[6]和邮件过滤[7]等;为了处理复杂的应用场景,提出了不同的计算模型,如序贯三支决策[3,8] 、优化三支决策[9]、前景三支决策[10]、三支模糊集[11]和三支约简[12]等。
在实际应用中,代价是影响三支决策划分的重要因素之一。代价敏感学习能够有效缓解分类过程中的数据不平衡问题,其主要作用是处理决策过程和结果产生的各类代价问题。代价敏感学习主要研究两种代价:误分类代价(结果代价)和测试代价,两者互相关联,呈负相关。如在医疗诊断中,患者想要获得更高的诊断准确率(即决策代价越低),就需要做更多的检查(即测试代价越高)。由于代价是数据的内在特征,将其与知识发现结合会使得问题更具有普适性,目前,代价敏感学习已经应用到现实生活中的许多领域,如:人脸识别[13]、价格预测[14]和客户信用评价[15]等。
因此,基于代价敏感的三支决策算法与模型引起了许多学者的关注和研究,已取得重要的研究成果。Fang等[8]将信息粒度纳入决策分析过程,同时考虑决策过程和决策结果的代价,分别设计了两种不同的算法以最小化决策过程和决策结果代价。Fang等[16]提出了一种三支决策和可分辨矩阵的框架,在此框架下分别设计了基于删除和增加的代价敏感近似属性约简算法。Jia等[17]构造了一种可以直接应用于传统的代价敏感学习问题的三支决策模型,在此基础上,提出基于多类三支决策模型的多阶段代价敏感学习方法。Li等[18]为从输入图像中顺序提取分层粒度结构,提出了一种基于DNN的顺序粒度特征提取方法,在此基础上,提出一种代价敏感的序贯三支决策模型。Yang等[19]考虑了用户需求, 提出一种基于模糊粗糙集的序贯三支决策模型的优化机制,用来实现对代价敏感的最优粒度选择。Ma等[20]定义了三支特定类的最低代价约简,分别设计了基于添加−删除策略和删除策略来构建特定类的最小代价约简算法。以上算法与模型能够最小化结果代价或过程代价。而在许多应用领域中往往需要从代价敏感视角来分析三支决策边界域样本,目前三支决策的研究对象多为单一性数据的决策系统,对于混合数据边界域样本处理的研究相对较少。
为此,本文提出了一种面向混合数据的代价敏感三支决策边界域分类方法。首先,基于正域约简,提出了面向混合数据的属性约简模型;然后,提出了一种基于代价敏感的三支决策边界域样本处理方法,在贝叶斯最小风险的基础上构造误分类代价公式,划分边界域中的对象。最后,对UCI上的10个数据集进行实验,结果表明该方法能够降低误分类代价,而且能较准确地划分边界域中的对象;这为三支决策的边界域样本处理提供了一种可借鉴的方法。
1. 基本知识
1.1 邻域粗糙集
在粗糙集理论[21]中,给定一个四元组决策系统:
$${\rm{DS}} = \left\{ {U,A_t = C \cup D,\left\{ {{V_a}{\text{|}}a \in A_t} \right\},\left\{ {{I_a}{\text{|}}a \in A_t} \right\}} \right\} $$ 其中
$U = \left\{ {{x_1},{x_2},\cdots,{x_n}} \right\}$ 表示有限非空的对象全集,称为论域或者对象空间;$A_t$ 表示有限非空的属性全集,由条件属性和决策属性共同组成;$C = \{ {a_1}, $ $ {a_2},\cdots, {a_n} \}$ 表示有限非空的条件属性全集;$D$ 表示决策属性;${V_a}$ 表示$ a \in C $ 的属性值集;${I_a}{\text{|}}U \times A_t \to V$ 是一个信息函数,能给每个对象的每个属性赋值,即$ {I_a}(x) \to {V_a} $ 。定义1[22] 给定混合邻域决策系统
${\rm{DN}} = \left\{ {U,} \right.$ $ \left. {{F^D} \cup {F^C},D,{V_a},{I_a},\delta } \right\} $ ,距离度量函数$ \Delta N:U \times U $ ,给定属性子集$ B \subseteq C $ 和邻域参数$ \delta $ ,则对象$x$ 和$y$ 基于$B$ 的邻域关系为$$ {{\rm{NR}}^\delta }(B) = \left\{ {(x,y) \in U \times U{\text{|}}\Delta {N_B}(x,y) \leqslant \delta } \right\} $$ 对
$ \forall x \in U $ ,$x$ 的邻域粒度可表示为$$ {\delta _B}(x) = \left\{ {y|x,y \in U,\Delta {N_B}(x,y) \leqslant \delta } \right\} $$ 式中:
${F^D}$ 为离散属性集合;${F^C}$ 为连续属性集合;$\delta $ 是邻域参数。1.2 三支决策粗糙集
三支决策粗糙集[23]通过2个状态集和3个动作集来描述其决策过程。其中,状态集
$ S = \left\{ {X,\neg X} \right\} $ 分别表示对象属于概念$X$ 和不属于概念$X$ ,动作集$ A = \left\{ {{a_P},{a_B},{a_N}} \right\} $ 表示对于不同状态分别采取接受、延迟和拒绝3种不同的动作。由于采取不同动作会产生不同的损失,记${\lambda _{PP}}、{\lambda _{BP}}、{\lambda _{NP}}$ 表示当$x \in X$ 时,分别采取动作$ {a_P}、{a_B} $ 和$ {a_N} $ 产生的风险损失值;同样地,记$ {\lambda _{PN}}、{\lambda _{BN}}、{\lambda _{NN}} $ 表示当$x \in \neg X$ 时,分别采取动作$ {a_P}、{a_B} $ 和$ {a_N} $ 产生的风险损失值;损失之间的关系满足:${\lambda _{PP}} < {\lambda _{BP}} < {\lambda _{NP}}$ ,${\lambda _{NN}} < {\lambda _{BN}} < {\lambda _{PN}}$ 。在实际应用中,这些损失值通过专家的经验获取。定义2[1] 在决策系统
${\rm{DS}} = \left\{ {U,C \cup D,{V_a},{I_a}} \right\}$ 中,令$X$ 为论域$U$ 基于决策属性$D$ 的划分,$\alpha $ 和$\beta $ 为三支决策的阈值,$ P(X|[x]) $ 表示对象$x$ 的条件概率,对于$\forall x \in U$ ,根据贝叶斯决策过程,计算得到最小成本准则的三支决策规则:$$ {\rm{POS}}(X) = \left\{ {x \in U{\text{|}}\alpha \leqslant P(X\left| {\left[ x \right]} \right.) \leqslant 1} \right\} $$ $$ {\rm{BND}}(X) = \left\{ {x \in U{\text{|}}\beta \leqslant P(X\left| {\left[ x \right]} \right.) \leqslant \alpha } \right\} $$ $$ {\rm{NEG}}(X) = \left\{ {x \in U{\text{|}}0 \leqslant P(X\left| {\left[ x \right]} \right.) \leqslant \beta } \right\} $$ 其中,
$P(X{\text{|}}\left[ x \right]) = \dfrac{{\left| {X \cap \left[ x \right]} \right|}}{{\left| {\left[ x \right]} \right|}}$ ,$ \left| \cdot \right| $ 表示对象的个数;$$ \alpha = \frac{{({\lambda _{PN}} - {\lambda _{BN}})}}{{({\lambda _{PN}} - {\lambda _{BN}}) - ({\lambda _{BP}} - {\lambda _{PP}})}} $$ $$ \beta = \frac{{({\lambda _{BN}} - {\lambda _{NN}})}}{{({\lambda _{BN}} - {\lambda _{NN}}) - ({\lambda _{NP}} - {\lambda _{BP}})}} $$ 其中,正域
${\rm{POS}}(X)$ 、负域${\rm{NEG}}(X)$ 和边界域${\rm{BND}}(X)$ 分别对应三支决策规则中的接受、拒绝和不承诺规则,且满足:${\rm{POS}}(X) \cup {\rm{BND}}(X) \cup$ ${\rm{NEG}}(X) = X$ ;仅当$ X = U $ 时,${\rm{POS}}(X) \cup {\rm{BND}}(X)$ $\cup {\rm{NEG}}(X) = U$ 。1.3 代价敏感学习
代价敏感学习主要研究误分类代价和测试代价,由于本文中考虑了其误分类代价,误分类代价表示对对象错误划分后的一种惩罚。用
${{\boldsymbol{C}}_{k \times k}}$ 表示误分类代价矩阵,其中$ k $ 表示$ k $ 分类问题。为方便理解,以二分类代价矩阵${{\boldsymbol{C}}_{2 \times 2}}{\text{ = }}\left[ {\begin{array}{*{20}{c}} {{c_{11}}}\;{{c_{12}}} \\ {{c_{21}}}\;{{c_{22}}} \end{array}} \right]$ 为例;其中$ {c_{11}} $ 表示将类别为1的对象划分到类别1中,因此$ {c_{11}} $ 的值为0,同理$ {c_{22}} $ 的值也为0;$ {c_{12}} $ 表示将类别为1的对象划分到类别2中,此时属于误分类,在划分中需付出惩罚代价,因此$ {c_{12}} > 0 $ ,同理$ {c_{21}} > 0 $ 。2. 基于正域约简的代价敏感三支决策边界域分类方法
2.1 面向混合邻域决策系统的正域约简
由于基于三支决策的粒计算方法大多是处理连续型数据或离散型数据等单一型数据,但是在现实生活的应用领域中数据类型通常是既含有连续型数据又含有离散型数据的混合数据,为此需对混合数据的三支决策模型展开研究。
定义3 给定混合邻域决策系统
${\rm{DN}} = \left\{ {U,}{F^D} \cup \right.$ $\left. {F^C}, {D,{V_a},{I_a},\delta } \right\}$ ,$ {V_a}(x) $ 表示对象$x$ 在属性$a$ 上的属性值:对于
$ \forall x,y \in U,\forall a \in {F^D} $ ,则$x$ 和$y$ 基于${F^D}$ 的距离为$$ \Delta {N_{{F^D}}}(x,y) = \left\{ {\begin{array}{*{20}{c}} {0,\;\;\;{V_a}(x) = {V_a}(y)} \\ {1,\;\;\;{V_a}(x) \ne {V_a}(y)} \end{array}} \right. $$ 对于
$ \forall x,y \in U,\forall a \in {F^C} $ ,则$x$ 和$y$ 基于${F^C}$ 的距离为$$ \Delta {N_{{F^C}}}(x,y) = \left( {\sum\limits_{k = 1}^m {{\text{|}}{V_a}(x) = {V_a}{\text{(}}y{\text{)}}{{\text{|}}^p}} } \right)^{\frac{1}{p}} $$ 其中,当
$ p = 1 $ 时,$ \Delta {N_{{F^C}}}(x,y) $ 为曼哈顿距离;当$ p = 2 $ 时,$ \Delta {N_{{F^C}}}(x,y) $ 为欧氏距离;当$ p \to \infty $ 时,$ \Delta {N_{{F^C}}}(x,y) $ 为切比雪夫距离。定义4 给定混合邻域决策系统
${\rm{DN}} = \left\{ {U,} {F^D} \cup\right.$ ${F^C},\left. {D,{V_a},{I_a},\delta } \right\}$ ,令${D_i}$ 为论域$U$ 基于决策属性$D$ 的划分,则混合邻域决策系统的上下近似表示为:$$ \underline {{\rm{AN}}} (D) = \left\{ {x \in U{\text{|}}{\delta _C}(x) \subseteq {D_i}} \right\} $$ $$ \overline {\rm{AN}} (D) = \left\{ {x \in U{\text{|}}{\delta _C}(x) \cap {D_i} \ne \text{Ø} } \right\} $$ 通过上下近似集,可知特征子集
$B$ 上的正域如下:$$ {{\rm{POS}}_C}(D) = \underline {\rm{AN}} (D) = \left\{ {x \in U{\text{|}}{\delta _C}(x) \subseteq {D_i}} \right\} $$ 定义5 给定混合邻域决策系统
${\rm{DN}} = \left\{ {U,} \right.$ $ {F^D} \cup {F^C},\left. {D,{V_a},{I_a},\delta } \right\} $ ,令属性${a_i} \in C$ ,则混合邻域决策系统中基于三支决策的核属性集定义为:$$ {\rm{CORE}}(C) = \left\{ {{a_i}{\text{|}}|{{\rm{POS}}_C}(D)| - |{{\rm{POS}}_{C - \left\{ {{a_i}} \right\}}}(D)| > 0} \right\} $$ 以表1为例,给出一个混合邻域决策系统,其中,
$U = \left\{ {{x_1},{x_2},\cdots,{x_{10}}} \right\}$ 为对象集,$C = \left\{ {{a_1},{a_2},\cdots,{a_6}} \right\}$ 为条件属性集,决策类${U \mathord{\left/ {\vphantom {U D}} \right. } D} = \left\{ {{D_1},{D_2}} \right\}$ ,分别为${D_1} = \left\{ {{x_1},{x_3},{x_5},{x_6},{x_7},{x_9}} \right\}$ ,${D_2} = \left\{ {{x_2},{x_4},{x_8},{x_{10}}} \right\}$ 。表 1 混合邻域决策系统DNTable 1 Hybrid neighborhood decision system DN$U$ ${a_1}$ ${a_2}$ ${a_3}$ ${a_4}$ ${a_5}$ ${a_6}$ $D$ ${x_1}$ 1 0 0.93 0.73 0.80 0.68 ${d_1}$ ${x_2}$ 1 1 0.64 0.50 0.33 0.48 ${d_2}$ ${x_3}$ 1 1 0.58 0.39 0.38 0.29 ${d_1}$ ${x_4}$ 0 1 0.21 0.12 0.11 0.18 ${d_2}$ ${x_5}$ 1 0 0.63 0.80 0.48 0.58 ${d_1}$ ${x_6}$ 0 0 0.74 0.78 0.42 0.62 ${d_1}$ ${x_7}$ 1 0 0.85 0.80 0.50 0.73 ${d_1}$ ${x_8}$ 1 1 0.50 0.62 0.38 0.44 ${d_2}$ ${x_9}$ 0 0 0.42 0.62 0.49 0.50 ${d_1}$ ${x_{10}}$ 0 0 0.39 0.58 0.29 0.50 ${d_2}$ 根据定义5可计算出混合邻域决策系统的核属性集,具体的计算过程为:首先,根据定义3,利用
$ p = 2 $ 时的欧氏距离计算全体对象的混合邻域粒度,再根据定义5计算出${{\rm{POS}}_C}(D) = \left\{ {{x_1},{x_4},{x_5},} \right.{x_6},$ $\left. {{x_7}} \right\}$ ,同理可计算出${{\rm{POS}}_{C - \left\{ {{a_1}} \right\}}}(D) = \left\{ {{x_1},{x_4},{x_5},{x_6},} \right.\left. {{x_7}} \right\}$ ,因为${{\rm{POS}}_C}(D) = {{\rm{POS}}_{C - \left\{ {{a_1}} \right\}}}(D)$ ,所以属性${a_1} \notin $ ${\rm{CORE}}(C)$ ,同理可求出$\left\{ {{a_2},{a_3},{a_5},{a_6}} \right\} \notin {\rm{CORE}}(C)$ ,只有属性${a_4} \in {\rm{CORE}}(C)$ 。由此可知核属性集为${\rm{CORE}}(C) = $ $ \left\{ {{a_4}} \right\}$ 。下面将在此基础上,提出了代价敏感下的三支决策边界域分类方法。2.2 基于核属性集的代价敏感三支决策边界域分类方法
定义6 给定混合邻域决策系统
${\rm{DN}} = \left\{ {U,} \right.$ $ {F^D} \cup {F^C},\left. {D,{V_a},{I_a},\delta } \right\} $ ,设属性子集$ B \subseteq C $ ,$\alpha $ 和$\beta $ 为三支决策的阈值,${D_i}$ 表示不同的决策属性,则不同属性子集下的三支决策规则定义为:$$ {{\rm{POS}}_B}({D_i}) = \left\{ {x \in U{\text{|}}\alpha \leqslant P({D_i}\left| {{\delta _B}(x)} \right.) \leqslant 1} \right\} $$ $$ {{\rm{BND}}_B}({D_i}) = \left\{ {x \in U{\text{|}}\beta < P({D_i}\left| {{\delta _B}(x)} \right.) < \alpha } \right\} $$ $$ {{\rm{NEG}}_B}({D_i}) = \left\{ {x \in U{\text{|}}0 \leqslant P({D_i}\left| {{\delta _B}(x)} \right.) \leqslant \beta } \right\} $$ 其中,
$P({D_i}{\text{|}}{\delta _B}(x)){\text{ = }}\dfrac{{\left| {{D_i} \cap {\delta _B}(x)} \right|}}{{\left| {{\delta _B}(x)} \right|}}$ 。以表1为例,可给出混合邻域决策系统代价矩阵,如表2所示。结合定义2和表2,可求出三支决策的阈值
$\alpha {\text{ = }}{7 \mathord{\left/ {\vphantom {7 9}} \right. } 9},\beta = {1 \mathord{\left/ {\vphantom {1 3}} \right. } 3}$ 。表 2 误分类代价矩阵Table 2 Misclassification cost matrix状态/动作 $X(P)$ $\neg X(N)$ ${a_P}$ ${\lambda _{PP}}{\text{ = }}0$ ${\lambda _{PN}}{\text{ = }}8$ ${a_B}$ ${\lambda _{BP}}{\text{ = }}2$ $ {\lambda _{BN}}{\text{ = }}1 $ ${a_N}$ ${\lambda _{NP}}{\text{ = }}4$ ${\lambda _{NN}}{\text{ = }}0$ 令
$B = {\rm{CORE}}(C) = \left\{ {{a_4}} \right\}$ ,根据定义3可计算出核属性子集$ B $ 下的对象之间的邻域粒度;再根据定义6计算出核属性集下决策类$ {D_1} $ 的的正域、负域和边界域,具体的计算过程为:由定义3可计算出核属性集$ B $ 下$ {x_1} $ 的邻域粒度$ {\delta _B}({x_1}) = $ $\left\{ {{x_1},{x_2},{x_5},} {x_6},{x_7},\right. $ $ \left. {x_8},{x_9},{x_{10}} \right\}$ ,由此求出$ {x_1} $ 的条件概率$P({D_1}\left| {{\delta _B}({x_1})} \right.){\text{ = }} {5 \mathord{\left/ {\vphantom {5 8}} \right. } 8} < $ $ \alpha$ ,所以${x_1} \in {{\rm{BND}}_B}({D_1})$ ,同理$\left\{ {x_2},{x_4},{x_5},{x_6},{x_7},{x_8},{x_9},{x_{10}} \right\} \in $ $ {{\rm{BND}}_B}({D_1})$ ,即${{\rm{BND}}_B}({D_1})$ ${\text{ = }}\left\{ {x_1},{x_2},{x_4},{x_5},{x_6},{x_7},{x_8},{x_9},{x_{10}} \right\}$ 。通过相同的计算可求出:$$ {{\rm{POS}}_B}{\text{(}}{D_1}{\text{) = }}\text{Ø} {\text{,}} {{\rm{NEG}}_B}{\text{(}}{D_1}{\text{) = }}\left\{ {{x_3}} \right\}$$ 定义7 在混合邻域决策系统
${\rm{DN}} = \left\{ {U,} {F^D} \cup \right.$ ${F^C},\left. {D,{V_a},{I_a},\delta } \right\}$ 中,${D_i}$ 为论域$U$ 基于决策属性$D$ 的划分,给定属性子集$B \subseteq C$ ,为了简化公式,用${{\rm{CP}}^r}$ 和${(1 - {\rm{CP}})^r}$ 分别代替$ {1 \mathord{\left/ {\vphantom {1 {P({D_i}\left| {{\delta _B}({x_j})} \right.)}}} \right. } {P({D_i}\left| {{\delta _B}({x_j})} \right.)}} $ 和$ {1 \mathord{\left/ {\vphantom {1 {(1 - P({D_i}\left| {{\delta _B}({x_j})} \right.))}}} \right. } {(1 - P({D_i}\left| {{\delta _B}({x_j})} \right.))}} $ ,对于$\forall {x_j} \in {{\rm{BND}}_B}\left( {{D_i}} \right)$ ,样本简化后的误分类代价计算公式如下:$$ {{\rm{PC}}_B}({D_i}{\text{|}}{x_j}) = \frac{{{{\rm{CP}}^r} \times {\lambda _{PN}}}}{{({{\rm{CP}}^r} \times {\lambda _{PN}}) + ({{(1 - {\rm{CP}})}^r} \times {\lambda _{NP}})}} $$ $$ {{\rm{NC}}_B}({D_i}{\text{|}}{x_j}) = \frac{{{{(1 - {\rm{CP}})}^r} \times {\lambda _{NP}}}}{{({{(1 - {\rm{CP}})}^r} \times {\lambda _{NP}}) + ({{\rm{CP}}^r} \times {\lambda _{PN}})}} $$ 其中,
${{\rm{PC}}_B}({D_i}{\text{|}}x)$ 表示在决策类${D_i}$ 下将对象$ x $ 划分到正域产生的误分类代价,同理,${{\rm{NC}}_B}({D_i}{\text{|}}x)$ 表示在决策类${D_i}$ 下将对象$ x $ 划分到负域产生的误分类代价。$ {\lambda _{NP}} $ 和$ {\lambda _{PN}} $ 是代价矩阵中的风险损失值,$ P({D_i}{\text{|}}{\delta _B}(x)) $ 表示在决策类${D_i}$ 下对象$ x $ 的条件概率。性质1 在混合邻域决策系统
${\rm{DN}} = \left\{ {U,}{F^D} \cup \right.$ ${F^C},\left. {D,{V_a},{I_a},\delta } \right\}$ 中,${D_i}$ 是对决策属性$D$ 的划分,假设属性子集$B \subseteq C$ ,对于$\forall x \in {{\rm{BND}}_B}({D_i})$ ,可得出如下推论:1)如果
${{\rm{PC}}_B}({D_i}{\text{|}}x) > {{\rm{NC}}_B}({D_i}{\text{|}}x)$ ,则$ x \in $ ${{\rm{NEG}}_B}({D_i})$ ;2)如果
${{\rm{PC}}_B}({D_i}{\text{|}}x) \leqslant {{\rm{NC}}_B}({D_i}{\text{|}}x)$ ,则$ x \in $ ${{\rm{POS}}_B}({D_i})$ 。以表1为例,令
$B = {\rm{Core}}(C) = \left\{ {{a_4}} \right\}$ ,已知${D_1} = $ $\left\{ {{x_1},{x_3},{x_5},{x_6},{x_7},{x_9}} \right\}$ 和${ {\rm{BND}}_B}{\text{(}}{D_1}{\text{) = }}\left\{ {{x_1},{x_2},{x_4},{x_5},} \right.{x_6},{x_7},{x_8},$ $\left. {{x_9},{x_{10}}} \right\}$ ,根据定义7和性质1可将边界域中的对象划分到正域和负域,具体的计算过程如下:对于
$\forall x \in {{\rm{BND}}_B}({D_1})$ ,根据定义7可求出划分对象$ {x_1} $ 产生的两种误分类代价${{\rm{PC}}_B}({D_1}{\text{|}}{x_1}) = {6 \mathord{\left/ {\vphantom {6 {11}}} \right. } {11}}$ ,${{\rm{NC}}_B}({D_1}{\text{|}}{x_1}) = {5 \mathord{\left/ {\vphantom {5 {11}}} \right. } {11}}$ ,因为${{\rm{PC}}_B}({D_1}{\text{|}}{x_1}) > {{\rm{NC}}_B}({D_1}{\text{|}}{x_1})$ ,所以${x_1} \in {{\rm{NEG}}_B}({D_1})$ ,同理可得$\left\{ {{x_2},\,{x_4},\,{x_6},\,{x_8},\,{x_9},\,{x_{10}}} \right\} \in$ ${{\rm{NEG}}_B}({D_1})$ 和$\left\{ {{x_5},{x_7}} \right\} \in {{\rm{POS}}_B}({D_1})$ 。由此可知,该混合邻域决策系统的正域为${{\rm{POS}}_B}{\text{(}}{D_1}{\text{) = }}\left\{ {{x_5},{x_7}} \right\}$ ,负域为${{\rm{NEG}}_B}{\text{(}}{D_1}{\text{) = }}\left\{ {{x_1},} \right.\left. {{x_2},{x_3},{x_4},{x_6},{x_8},{x_9},{x_{10}}} \right\}$ 。3. 算法描述及复杂度分析
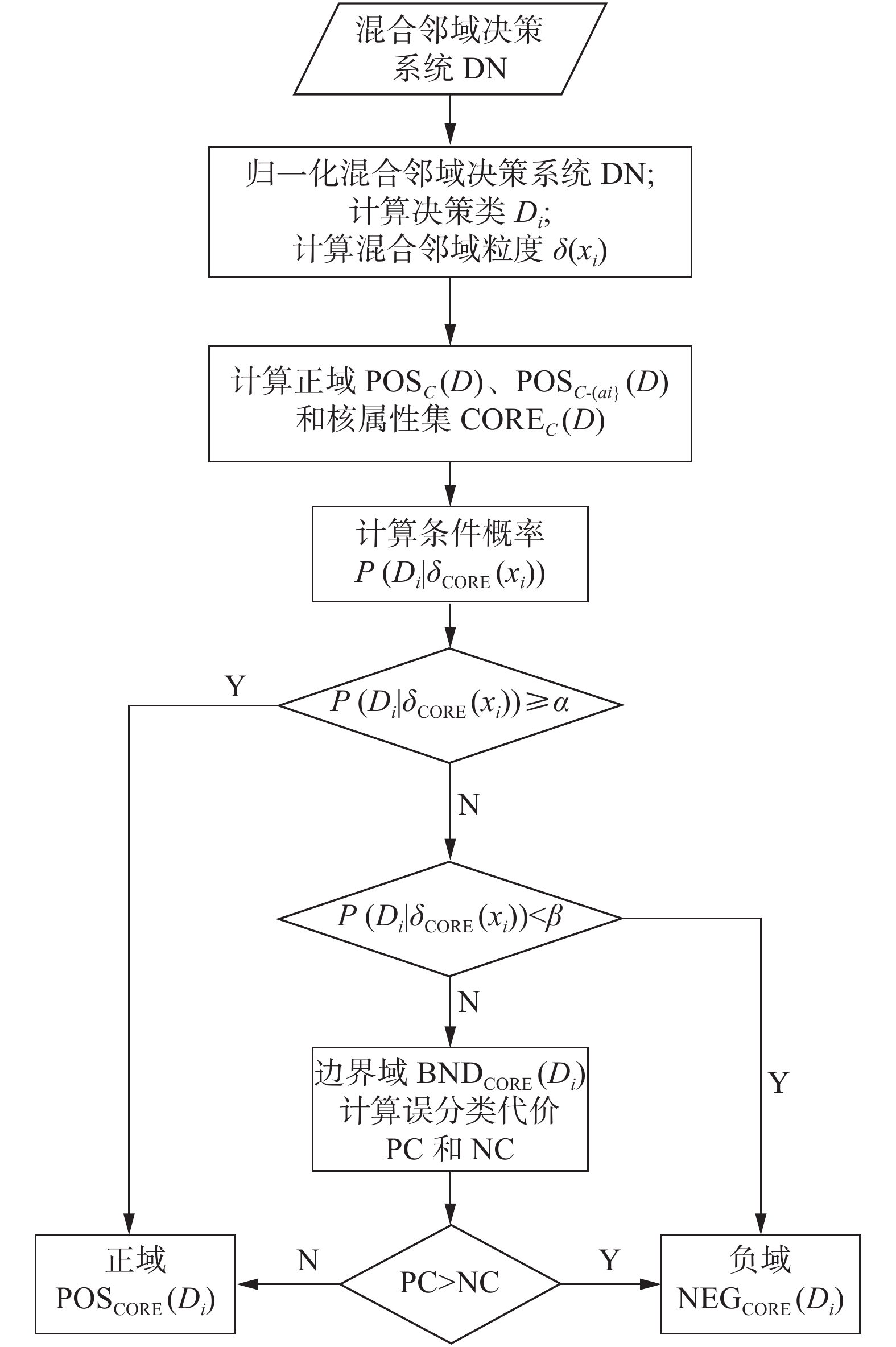
针对混合邻域决策系统,为了有效划分其三支决策边界域中的对象,本文提出了一种面向混合数据的代价敏感三支决策边界域分类方法,该算法主要分为三个部分。首先,针对混合邻域决策系统中的数据,通过混合邻域计算公式计算每个对象的混合邻域粒度,得到混合邻域决策表的正域对象集合,由此基于启发式策略计算核属性集。其次,在此基础上,计算混合邻域决策表中每个对象的邻域粒度,从而计算出每个对象属于不同决策类的条件概率,利用三支决策规则将对象分别划分到不同决策类的正域、边界域和负域中;最后,针对边界域中的对象,分别计算其划分到正域和负域所产生的误分类代价,通过比较这两种代价的大小,将边界域中的对象划分到正域或负域中,为此,算法的流程图1所示。
算法 面向混合数据的代价敏感三支决策边界域分类方法
输入 混合邻域决策系统
${\rm{DN}}$ ,邻域参数$\delta $ 和阈值$\alpha $ ,$\beta $ ;输出 核属性集下对不同决策类的正域和负域。
1)对混合邻域决策系统
${\rm{DN}}$ 做归一化处理;2)计算决策类
$ {D_i} \subseteq {U \mathord{\left/ {\vphantom {U D}} \right. } D} $ ;3)计算邻域粒度
${\delta _C}(x)$ ,初始化${{\rm{CORE}}_C}(D)$ $=\text{Ø}$ ;4)对于
$ \forall x \in U $ ,若满足${\delta _C}(x) \subseteq {D_i}$ ,则将对象$ x $ 存入到正域${{\rm{POS}}_C}(D) \leftarrow {{\rm{POS}}_C}(D) \cup \left\{ x \right\}$ ;5)对于
$ \forall {a_i} \in C $ ,分别计算去除每个对象之后的特征子集的正域集合${{\rm{POS}}_{C- \left\{ {{a_i}} \right\}}}(D)$ ,若满足${{\rm{POS}}_C}(D) \ne {{\rm{POS}}_{C - \left\{ {{a_i}} \right\}}}(D)$ ,则将属性${a_i}$ 存入到核属性集${{\rm{CORE}}_C}(D) \leftarrow {{\rm{CORE}}_C}(D) \cup \left\{ {{a_i}} \right\}$ ;6)基于核属性集
${{\rm{CORE}}_C}(D)$ ,计算对象的邻域粒度${\delta _{{{\rm{CORE}}_C}\left( D \right)}}(x)$ ;7)对于
$ \forall x \in U $ ,计算对象$ x $ 属于决策类$ {D_i} $ 的条件概率$P({D_i}{\text{|}}{\delta _{{{\rm{CORE}}_C}\left( D \right)}}(x))$ :①若
$\alpha \leqslant P({D_i}{\text{|}}{\delta _{{{\rm{CORE}}_C}\left( D \right)}}(x)) \leqslant 1$ ,则将对象$ x $ 划分到决策类$ {D_i} $ 的正域${{\rm{POS}}_{{{\rm{CORE}}_C}}}({D_i})$ ;②否则,若
$0 \leqslant P({D_i}{\text{|}}{\delta _{{{\rm{CORE}}_C}\left( D \right)}}(x)) \leqslant \beta$ ,则将对象$ x $ 划分到决策类$ {D_i} $ 的负域${{\rm{NEG}}_{{{\rm{CORE}}_C}}}({D_i})$ ;③否则将对象
$ x $ 划分到决策类$ {D_i} $ 的边界域${{\rm{BND}}_{{{\rm{CORE}}_C}}}({D_i})$ ;8)对于
$\forall {x_b} \in {{\rm{BND}}_{{{\rm{CORE}}_C}}}({D_i})$ 计算${{\rm{PC}}_{{{\rm{CORE}}_C}}}({D_i}{\text{|}}{x_j})$ 和${{\rm{NC}}_{{{\rm{CORE}}_C}}}({D_i}{\text{|}}{x_j})$ :①若满足
${{\rm{PC}}_{{{\rm{CORE}}_C}}}({D_i}{\text{|}}{x_j}) > {{\rm{NC}}_{{{\rm{CORE}}_C}}}({D_i}{\text{|}}{x_j})$ ,则将对象$ {x_j} $ 划分到决策类$ {D_i} $ 的负域${{\rm{NEG}}_{{{\rm{CORE}}_C}}}({D_i})$ ;②否则将对象
$ {x_b} $ 划分到决策类$ {D_i} $ 的正域${{\rm{POS}}_{{{\rm{CORE}}_C}}}({D_i})$ ;9)输出划分结果正域
${{\rm{POS}}_{{{\rm{CORE}}_C}}}({D_i})$ ,负域${{\rm{NEG}}_{{{\rm{CORE}}_C}}}({D_i})$ 。//算法结束。算法时间复杂度分析:
1)算法的时间复杂度为
$ O(|U||C|) $ ;2)划分决策类所需的时间复杂度为$ O(|U|) $ ;3)在属性全集下,通过混合邻域计算公式得出每个对象的混合邻域粒度,其时间复杂度为$ O(|U{|^2}|C|) $ ;4)计算正域对象的时间复杂度为$ O(|U|) $ ;5)计算核属性集的时间复杂度为$ O(|U{|^2}|C|) $ ;6)在核属性集${\rm{CORE}}$ 下,计算每个对象的混合邻域粒度,其时间复杂度为$O({\text{|}}U{|^2}|{{\rm{CORE}}_C}{\text{(}}{D_i}{\text{)|}})$ ;7)计算各决策类正域、边界域和负域,其时间复杂度为$ O(|U|) $ ;8)结合代价敏感划分边界域中的对象,其时间复杂度为$O(|{{\rm{BND}}_{{{\rm{CORE}}_C}}}\left( {{D_i}} \right)|)$ 。综上所述,算法最坏情况下的时间复杂度是$ O(|U{|^2}|C|) $ ;由于存储空间主要用于存放数据,因此算法的空间复杂度为$ O(|U||C|) $ 。4. 实验比较与分析
为了验证本文方法对边界域对象划分的可行性和有效性,实验从UCI中选取了10个混合数据集进行实验测试与分析;选用分类准确率、权衡因子、误分类损失和时间作为评价指标,对实验结果进行对比与分析。
4.1 数据集与实验设置
为了更好地说明所提出算法的普适性,本文根据数据集的来源和规模两个方面,从国际公开的机器学习UCI数据库中选取了10个数据集进行实验结果的对比和分析,数据集的信息描述如表3所示。表中Speaker Accent和Ionosphere数据集中包含连续型数据,Phishing Websites和Student Evaluation数据集中包含离散型数据;其余数据集均包含连续型和离散型数据;这些数据集来自欺诈分析、医学诊断、信号处理和教育评价等应用领域。 同时为了消除量纲的影响,对所有数据集中的连续型数据进行归一化处理。本次实验的运行环境为:Win10, Intel(R)Core(TM), i5-6500 CPU @ 3.20 GHz 3.19 GHz和8 GB内存,用Python编程语言实现算法设计。
4.2 评价指标
实验将从准确率、权衡因子、误分类损失和运行时间4种度量指标[24]对划分结果进行分析,定义如下:
准确率:
${\rm{Acc}} = \dfrac{{{\rm{POS}}({D_i}) \cap {D_i}}}{{{\rm{POS}}({D_i})}}$ 权衡因子:
$F = 2 \times \dfrac{{{\rm{Acc}} \times {\rm{Cov}}}}{{{\rm{Acc}}+ {\rm{Cov}}}}$ 误分类损失:
${\rm{Cost}} = {n_b} \times {\lambda _{bp}} + {n_n} \times {\lambda _{np}}$ 式中:
${\rm{POS}}({D_i})$ 和$ {D_i} $ 表示正域和决策类,$ {n_b} $ 和$ {n_n} $ 分别表示边界域、负域中的对象个数;$ {\lambda _{bp}} $ 和$ {\lambda _{np}} $ 分别表示将属于某一决策类的对象错误划分到该类别的边界域和负域中产生的损失;由于本文算法的输出只包含正域和负域,因此${\rm{Cov}}{\text{ = }}1$ 。本实验的风险损失参数为$ {\lambda _{bp}}{\text{ = }}0.3 $ ,$ {\lambda _{np}}{\text{ = }}0.7 $ 。4.3 实验结果与分析
4.3.1 参数
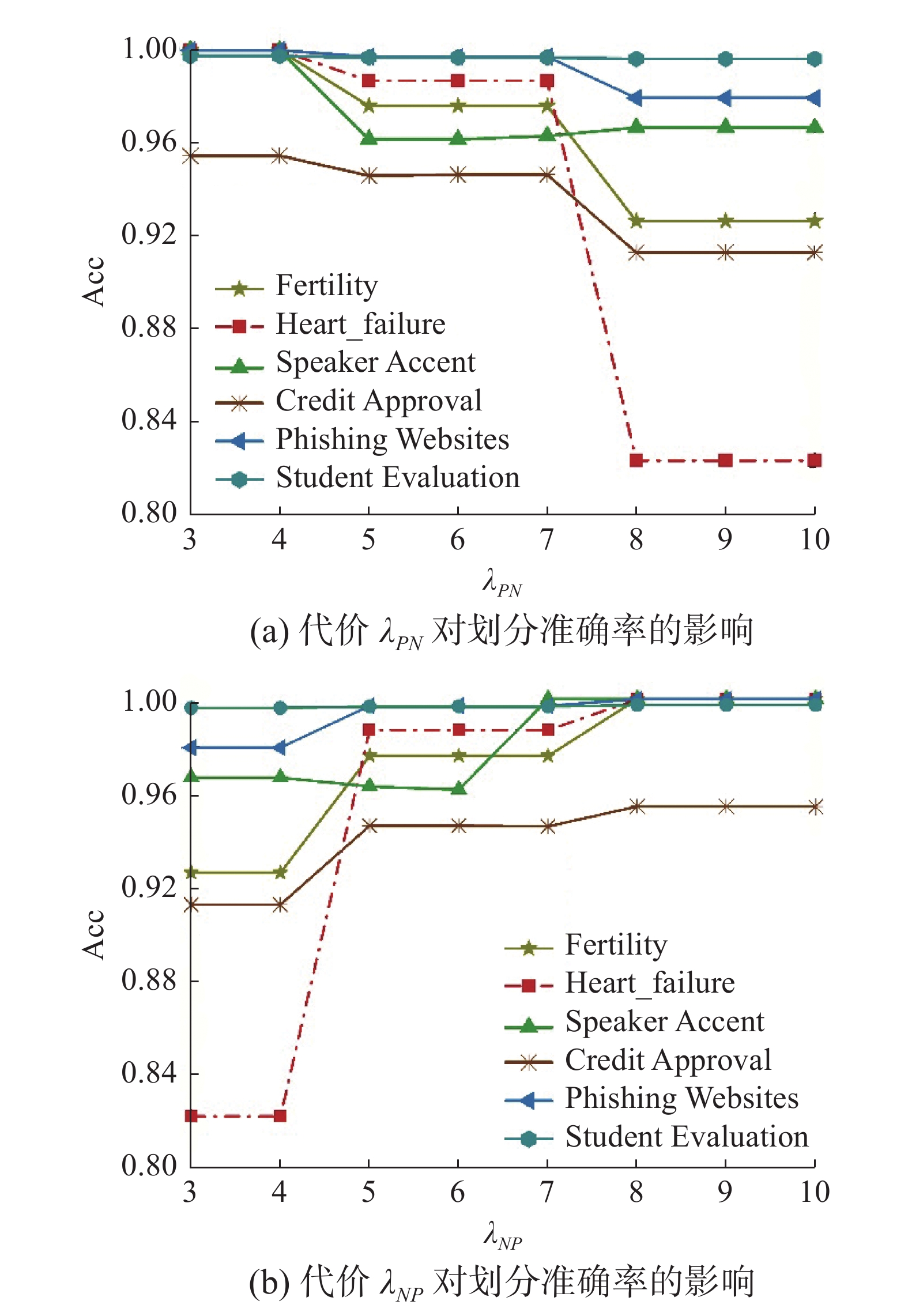
$ {\lambda _{PN}} $ 和$ {\lambda _{NP}} $ 对划分结果的影响在混合邻域决策系统中,参数
$ {\lambda _{PN}} $ 和$ {\lambda _{NP}} $ 通过影响阈值对$\left( {\alpha ,\beta } \right)$ 的大小来影响三支决策的划分。因此,为了详细分析参数$ {\lambda _{PN}} $ 和$ {\lambda _{NP}} $ 的值对划分准确度的影响。本小节中,为了一般性,从上述数据集中选取6个作为代表进行实验分析,分别将$ {\lambda _{PN}} $ 和$ {\lambda _{NP}} $ 的值从3到10,且每次步长变化1进行实验。实验结果如图2所示。表 3 数据集的基本信息Table 3 Basic information of the data set数据集 样本 属性类别 决策类 决策类的样本数 连续属性 离散属性 Fertility 100 2 7 2 {88, 12} Heart failure 299 7 5 2 {96, 203} Speaker Accent 329 12 0 6 {29, 30, 30, 30, 45, 165} Ionosphere 351 34 0 2 {225, 126} Thoraric Surgery 470 2 14 2 {400, 70} Credit Approval 690 7 8 2 {307, 383} Audit Data 773 11 15 2 {305, 468} Diabetic 1151 16 3 2 {540, 611} Phishing Websites 2456 0 30 2 {1094, 1362} Student Evaluation 5820 0 33 5 {812,560,1612,1695,1141} 在图2(a)中,当
$ {\lambda _{PN}} $ 的取值区间在$ \left[ {4,5} \right] $ 时,Credit Approval等5个数据集的准确率随代价的增加而下降,且变化趋势较为平缓;当$ {\lambda _{PN}} $ 的取值区间在$ \left[ {7,8} \right] $ 时,这些数据集的准确率随代价的增加而下降,且变化趋势较为显著。在图2(b)中,当$ {\lambda _{NP}} $ 的取值区间在$ \left[ {4,5} \right] $ 时,Credit Approval等5个数据集的准确率随代价的增加而上升,且变化趋势较为显著;当$ {\lambda _{NP}} $ 的取值在$ \left[ {6,7} \right] $ 区间时,数据集Speaker Accent的准确率随代价的增加而升高,进而达到平稳状态;当$ {\lambda _{NP}} $ 的取值在$ \left[ {7,8} \right] $ 时,Credit Approval等个5数据集的准确率随代价的增加而升高,且变化趋势较为平缓;当代价$ {\lambda _{PN}} $ 和$ {\lambda _{NP}} $ 的取值在[8,10]时,准确率达到平稳状态,所有数据集的准确率不再随着代价的变化而变化。综上所述,从整体上看,代价
$ {\lambda _{PN}} $ 和$ {\lambda _{NP}} $ 对分类准确度的影响呈负相关,数据集的准确率随着代价$ {\lambda _{PN}} $ 的增加,呈现出整体下降的趋势;而随着代价$ {\lambda _{NP}} $ 的增加,整体呈现上升的趋势。从局部上看,当代价的取值在$ \left[ {4,5} \right] $ 和$ \left[ {7,8} \right] $ 这两个区间时,数据集的准确率随着代价的增加而发生变化,当代价的取值在其他区间时,数据集的准确率趋于稳定的状态。由此,在实际的决策过程中,可结合上述分析的结论,并根据数据集的分布和代价敏感学习构造合适的代价矩阵。4.3.2 本文模型与不同三支决策模型的对比分析
本节主要分析不同三支决策模型对分类性能的影响,表4~7给出了3种粗糙集模型下准确率Acc、权衡因子F、误分类损失Cost和运行时间Time的实验结果。其中,NCTM (neighborhood rough set based cost-sensitive three-way decision boundary region processing model)是基于邻域粗糙集[25]设计考虑了代价敏感的三支决策边界域处理模型,PCTM (pawlak rough set based cost-sensitive three-way decision boundary region processing model)是基于经典粗糙集[22]设计考虑了代价敏感的三支决策边界域处理模型,MCTM (mixed-neighborhood rough set based cost-sensitive three-way decision boundary region processing model)代表本文基于混合邻域粗糙集的代价敏感三支决策边界域处理模型。在PCTM模型中对数据集进行离散化预处理,在NCTM和MCTM模型中对数据集进行了归一化预处理,另外,为了使距离处于同一量纲下,在NCTM模型中采取平均距离度量,同时Acc、F、Cost和Time的值均为数据集所有决策类的平均值。实验结果如表4~7所示,其中,符号
$ \uparrow $ 表示度量指标的值越大越好,符号$ \downarrow $ 表示度量指标的值越小越好,加粗字体表示算法在所对应的数据集上的最优值。表 4 三种粗糙集模型的准确率Acc$\left( \uparrow \right)$ 对比Table 4 Comparison of accuracy Acc$\left( \uparrow \right)$ under three kinds of rough set models数据集 NCTM PCTM MCTM Fertility 0.9318 0.9385 1.0000 Heart_failure 0.8863 0.9646 1.0000 Speaker Accent 1.0000 0.8558 1.0000 Ionosphere 0.9241 0.9884 0.9241 Thoraric Surgery 0.9314 0.9345 0.9962 Credit Approval 0.9144 0.9326 0.9620 Audit Data 0.9370 0.9870 0.9750 Diabetic 0.8582 0.8965 0.8590 Phishing Websites 0.9709 0.9897 0.9996 Student Evaluation 0.6582 0.9257 0.9979 如表4所示,使用本文模型的分类准确率高于其他2种模型,例如,其在数据集Credit Approval上的准确率比NCTM和PCTM模型分别提高了4.8%和2.9%,由于MCTM能够针对不同的数据类型采取不同的分类方法,且具有更低的错误率,因此其划分准确率能整体上高于NCTM和PCTM。此外,在数据集Ionosphere上,PCTM模型的优势更加明显,而在数据集Speaker Accent上,本文模型和NCTM模型的准确率相同,由此可知,本文模型能有效地提高分类准确率,且在数据集上整体表现良好。
如表5所示,对权衡因子而言,由其度量公式可知,权衡因子由准确率和覆盖率共同决定,由于本文中的三支决策最终转换成二支决策,因此覆盖率
${\rm{Cov}}{\text{ = }}1$ ,在本文中权衡因子F很大程度上取决于准确率Acc的值。对比表4和表5的实验结果可知,权衡因子F的值略高于准确率Acc的值,但是整体上的变化趋势和Acc相同。表 5 3种粗糙集模型的权衡因子$ F\left( \uparrow \right) $ 对比Table 5 Comparison of trade-off factor$ F\left( \uparrow \right) $ under three kinds of rough set models数据集 NCTM PCTM MCTM Fertility 0.9647 0.9676 1.0000 Heart_failure 0.9393 0.9819 1.0000 Speaker Accent 1.0000 0.9220 1.0000 Ionosphere 0.9602 0.9941 0.9602 Thoraric Surgery 0.9632 0.9661 0.9981 Credit Approval 0.9553 0.9651 0.9806 Audit Data 0.9664 0.9935 0.9872 Diabetic 0.9174 0.9448 0.9234 Phishing Websites 0.9852 0.9948 0.9998 Student Evaluation 0.7616 0.9599 0.9989 如表6所示,使用本文模型的误分类损失整体上明显低于其他2种模型,例如,在数据集Student Evaluation中,本文模型的误分类损失比NCTM和PCTM分别降低了478.1和287.0。从不同的模型角度分析,针对混合邻域决策系统,PCTM对划分的要求较为苛刻,而NCTM对划分的要求较于放松,容错率低,导致划分错误率提高;本文模型MCTM可灵活应用于不同类型的决策系统,容错率高,所以具有更低的误分类代价。
表 6 3种粗糙集模型的误分类损失Cost$ \left( \downarrow \right) $ 对比Table 6 Comparison of misclassification loss Cost$\left( \downarrow \right) $ under three kinds of rough set models数据集 NCTM PCTM MCTM Fertility 4.2000 1.4000 0.0000 Heart_failure 20.3000 7.0000 0.0000 Speaker Accent 0.0000 23.8000 0.0000 Ionosphere 13.3000 3.5000 13.3000 Thoraric Surgery 44.1000 21.7000 2.1000 Credit Approval 33.6000 28.7000 16.8000 Audit Data 46.2000 7.0000 14.7000 Diabetic 13.3000 23.8000 32.2000 Phishing Websites 42.0000 16.8000 0.7000 Student Evaluation 485.1000 294.0000 7.0000 如表7所示,从整体上看,3种粗糙集粒计算模型所消耗的时间较少且随着数据规模的增大而增多;从部分上看,NCTM模型耗时相对较长,主要是由于NCTM是用邻域关系计算邻域类,每两个对象之间都要计算,导致其时间复杂度较高。而PCTM模型和MCTM模型在耗时方面差异性不大,且差异性随数据规模的增大而减小。
综上所述,与其他2种不同的粗糙集模型进行实验对比和分析可知,本文模型总体上具有较高的分类准确度和较低的误分类损失,因此,用其对混合邻域决策系统进行划分较为合理。
表 7 3种粗糙集模型的运行时间 Time$ \left( \downarrow \right) $ 对比Table 7 Comparison of operation hours Time$ \left( \downarrow \right) $ under three kinds of rough set models数据集 NCTM PCTM MCTM Fertility 0.1467 0.0185 0.1112 Heart_failure 1.4253 0.1860 1.1989 Speaker Accent 1.5592 0.2207 1.5177 Ionosphere 1.6507 0.2217 1.4853 Thoraric Surgery 3.9171 0.9209 2.7756 Credit Approval 7.9367 1.1905 6.7061 Audit Data 9.0060 1.6071 6.6358 Diabetic 30.0278 10.4657 26.6360 Phishing Websites 135.5500 16.6810 14.1239 Student Evaluation 868.6762 82.2837 73.5983 4.3.3 本文模型和序贯三支决策模型的边界域分类方法对比
为了进一步验证本文模型的有效性,本小节将本文模型与序贯三支决策的方法进行实验对比和分析。其中,MSTM (mixed-neighborhood rough set based sequential three-way decision boundary region processing model) 是基于经典序贯三支决策[8]改造的基于混合邻域粗糙集的序贯三支决策边界域处理模型。实验结果如表8所示,分别给出了MCTM 和 MSTM的分类准确度、权衡因子、误分类损失和时间的对比。
由表8的实验结果可知,在数据集Ionosphere和Audit Data上,本文模型MCTM的分类性能与MSTM相同,而在另外8个数据集上,本文模型MCTM的分类性能要优于序贯三支决策模型MSTM。从理论上分析,由于MSTM直接由代价矩阵计算的阈值划分边界域对象,而本文在此基础上进一步考虑条件概率和误分类代价来划分边界域中的对象,因此本文模型MCTM在Acc、F、Cost和Time上表现较优。为此,在同等条件下,对于混合邻域决策系统,本文基于属性约简的混合代价敏感三支决策边界域分类方法为处理边界域对象提供了一种可借鉴的分析方法。
表 8 不同边界域处理模型的实验结果对比Table 8 Comparison of experimental results of different boundary domain processing models数据集 ${\rm{Acc}}\left( \uparrow \right)$ $ F\left( \uparrow \right) $ ${\rm{Cost}}\left( \downarrow \right)$ ${\rm{Time}}\left( \downarrow \right)$ MCTM MSTM MCTM MSTM MCTM MSTM MCTM MSTM Fertility 1.0000 0.9880 1.0000 0.9939 0.0000 1.4000 0.1112 0.1092 Heart_failure 1.0000 0.9854 1.0000 0.9926 0.0000 2.8000 1.1989 1.2184 Speaker Accent 1.0000 0.9889 1.0000 0.9943 0.0000 0.7000 1.5177 1.5807 Ionosphere 0.9241 0.9241 0.9602 0.9602 13.3000 13.3000 1.4853 1.50835 Thoraric Surgery 0.9962 0.9924 0.9981 0.9962 2.1000 4.2000 2.7756 2.6520 Credit Approval 0.9620 0.9540 0.9806 0.9764 16.8000 20.9999 6.7061 6.9013 Audit Data 0.9750 0.9750 0.9872 0.9872 14.7000 14.7000 6.6358 6.7636 Diabetic 0.8590 0.8408 0.9234 0.9131 32.2000 42.0000 26.6360 24.9780 Phishing Websites 0.9996 0.9979 0.9998 0.9989 0.7000 3.5000 14.1239 14.3478 Student Evaluation 0.9979 0.9971 0.9989 0.9985 7.0000 9.1000 73.5983 74.0003 5. 结束语
近年来三支决策理论成为热点研究问题,其研究对象多为单一型决策系统,然而,在许多的应用领域中,数据往往呈现混合类型的特点,目前三支决策对混合数据边界域样本处理的研究相对较少。为划分混合决策系统中的边界域对象,本文提出了基于混合数据的属性约简方法;并在此基础上,提出了一种基于核属性的代价敏感三支决策边界域分类方法。通过在不同的数据集上进行实验对比与分析,验证了本文方法的可行性和有效性,获得了一种相对合理的边界域对象的划分方法。由于序贯三支决策更加符合现实生活中的决策过程及人类的认知,下一步工作将研究基于代价敏感的序贯三支决策的粒化问题。
-
表 1 混合邻域决策系统DN
Table 1 Hybrid neighborhood decision system DN
$U$ ${a_1}$ ${a_2}$ ${a_3}$ ${a_4}$ ${a_5}$ ${a_6}$ $D$ ${x_1}$ 1 0 0.93 0.73 0.80 0.68 ${d_1}$ ${x_2}$ 1 1 0.64 0.50 0.33 0.48 ${d_2}$ ${x_3}$ 1 1 0.58 0.39 0.38 0.29 ${d_1}$ ${x_4}$ 0 1 0.21 0.12 0.11 0.18 ${d_2}$ ${x_5}$ 1 0 0.63 0.80 0.48 0.58 ${d_1}$ ${x_6}$ 0 0 0.74 0.78 0.42 0.62 ${d_1}$ ${x_7}$ 1 0 0.85 0.80 0.50 0.73 ${d_1}$ ${x_8}$ 1 1 0.50 0.62 0.38 0.44 ${d_2}$ ${x_9}$ 0 0 0.42 0.62 0.49 0.50 ${d_1}$ ${x_{10}}$ 0 0 0.39 0.58 0.29 0.50 ${d_2}$ 表 2 误分类代价矩阵
Table 2 Misclassification cost matrix
状态/动作 $X(P)$ $\neg X(N)$ ${a_P}$ ${\lambda _{PP}}{\text{ = }}0$ ${\lambda _{PN}}{\text{ = }}8$ ${a_B}$ ${\lambda _{BP}}{\text{ = }}2$ $ {\lambda _{BN}}{\text{ = }}1 $ ${a_N}$ ${\lambda _{NP}}{\text{ = }}4$ ${\lambda _{NN}}{\text{ = }}0$ 表 3 数据集的基本信息
Table 3 Basic information of the data set
数据集 样本 属性类别 决策类 决策类的样本数 连续属性 离散属性 Fertility 100 2 7 2 {88, 12} Heart failure 299 7 5 2 {96, 203} Speaker Accent 329 12 0 6 {29, 30, 30, 30, 45, 165} Ionosphere 351 34 0 2 {225, 126} Thoraric Surgery 470 2 14 2 {400, 70} Credit Approval 690 7 8 2 {307, 383} Audit Data 773 11 15 2 {305, 468} Diabetic 1151 16 3 2 {540, 611} Phishing Websites 2456 0 30 2 {1094, 1362} Student Evaluation 5820 0 33 5 {812,560,1612,1695,1141} 表 4 三种粗糙集模型的准确率Acc
$\left( \uparrow \right)$ 对比Table 4 Comparison of accuracy Acc
$\left( \uparrow \right)$ under three kinds of rough set models数据集 NCTM PCTM MCTM Fertility 0.9318 0.9385 1.0000 Heart_failure 0.8863 0.9646 1.0000 Speaker Accent 1.0000 0.8558 1.0000 Ionosphere 0.9241 0.9884 0.9241 Thoraric Surgery 0.9314 0.9345 0.9962 Credit Approval 0.9144 0.9326 0.9620 Audit Data 0.9370 0.9870 0.9750 Diabetic 0.8582 0.8965 0.8590 Phishing Websites 0.9709 0.9897 0.9996 Student Evaluation 0.6582 0.9257 0.9979 表 5 3种粗糙集模型的权衡因子
$ F\left( \uparrow \right) $ 对比Table 5 Comparison of trade-off factor
$ F\left( \uparrow \right) $ under three kinds of rough set models数据集 NCTM PCTM MCTM Fertility 0.9647 0.9676 1.0000 Heart_failure 0.9393 0.9819 1.0000 Speaker Accent 1.0000 0.9220 1.0000 Ionosphere 0.9602 0.9941 0.9602 Thoraric Surgery 0.9632 0.9661 0.9981 Credit Approval 0.9553 0.9651 0.9806 Audit Data 0.9664 0.9935 0.9872 Diabetic 0.9174 0.9448 0.9234 Phishing Websites 0.9852 0.9948 0.9998 Student Evaluation 0.7616 0.9599 0.9989 表 6 3种粗糙集模型的误分类损失Cost
$ \left( \downarrow \right) $ 对比Table 6 Comparison of misclassification loss Cost
$\left( \downarrow \right) $ under three kinds of rough set models数据集 NCTM PCTM MCTM Fertility 4.2000 1.4000 0.0000 Heart_failure 20.3000 7.0000 0.0000 Speaker Accent 0.0000 23.8000 0.0000 Ionosphere 13.3000 3.5000 13.3000 Thoraric Surgery 44.1000 21.7000 2.1000 Credit Approval 33.6000 28.7000 16.8000 Audit Data 46.2000 7.0000 14.7000 Diabetic 13.3000 23.8000 32.2000 Phishing Websites 42.0000 16.8000 0.7000 Student Evaluation 485.1000 294.0000 7.0000 表 7 3种粗糙集模型的运行时间 Time
$ \left( \downarrow \right) $ 对比Table 7 Comparison of operation hours Time
$ \left( \downarrow \right) $ under three kinds of rough set models数据集 NCTM PCTM MCTM Fertility 0.1467 0.0185 0.1112 Heart_failure 1.4253 0.1860 1.1989 Speaker Accent 1.5592 0.2207 1.5177 Ionosphere 1.6507 0.2217 1.4853 Thoraric Surgery 3.9171 0.9209 2.7756 Credit Approval 7.9367 1.1905 6.7061 Audit Data 9.0060 1.6071 6.6358 Diabetic 30.0278 10.4657 26.6360 Phishing Websites 135.5500 16.6810 14.1239 Student Evaluation 868.6762 82.2837 73.5983 表 8 不同边界域处理模型的实验结果对比
Table 8 Comparison of experimental results of different boundary domain processing models
数据集 ${\rm{Acc}}\left( \uparrow \right)$ $ F\left( \uparrow \right) $ ${\rm{Cost}}\left( \downarrow \right)$ ${\rm{Time}}\left( \downarrow \right)$ MCTM MSTM MCTM MSTM MCTM MSTM MCTM MSTM Fertility 1.0000 0.9880 1.0000 0.9939 0.0000 1.4000 0.1112 0.1092 Heart_failure 1.0000 0.9854 1.0000 0.9926 0.0000 2.8000 1.1989 1.2184 Speaker Accent 1.0000 0.9889 1.0000 0.9943 0.0000 0.7000 1.5177 1.5807 Ionosphere 0.9241 0.9241 0.9602 0.9602 13.3000 13.3000 1.4853 1.50835 Thoraric Surgery 0.9962 0.9924 0.9981 0.9962 2.1000 4.2000 2.7756 2.6520 Credit Approval 0.9620 0.9540 0.9806 0.9764 16.8000 20.9999 6.7061 6.9013 Audit Data 0.9750 0.9750 0.9872 0.9872 14.7000 14.7000 6.6358 6.7636 Diabetic 0.8590 0.8408 0.9234 0.9131 32.2000 42.0000 26.6360 24.9780 Phishing Websites 0.9996 0.9979 0.9998 0.9989 0.7000 3.5000 14.1239 14.3478 Student Evaluation 0.9979 0.9971 0.9989 0.9985 7.0000 9.1000 73.5983 74.0003 -
[1] YAO Yiyu. Three-way decisions with probabilistic rough sets[J]. Information sciences, 2010, 180(3): 341–353. doi: 10.1016/j.ins.2009.09.021 [2] YAO Yiyu. Three-way decision and granular computing[J]. International journal of approximate reasoning, 2018, 103: 107–123. doi: 10.1016/j.ijar.2018.09.005 [3] LI Huaxiong, ZHANG Libo, HUANG Bing, et al. Sequential three-way decision and granulation for cost-sensitive face recognition[J]. Knowledge-based systems, 2016, 91: 241–251. doi: 10.1016/j.knosys.2015.07.040 [4] ZHANG Hengru, MIN Fan, SHI Bing, et al. Regression-based three-way recommendation[J]. Information sciences, 2017, 378: 444–461. doi: 10.1016/j.ins.2016.03.019 [5] HUANG Jiajin, WANG Jian, YAO Yiyu, et al. Cost-sensitive three-way recommendations by learning pair-wise preferences[J]. International journal of approximate reasoning, 2017, 86: 28–40. doi: 10.1016/j.ijar.2017.03.005 [6] CHEN Yufei, YUE Xiaodong, FUJITA H, et al. Three-way decision support for diagnosis on focal liver lesions[J]. Knowledge-based systems, 2017, 127: 85–99. doi: 10.1016/j.knosys.2017.04.008 [7] ZHOU Bing, YAO Yiyu, LUO Jigang. Cost-sensitive three-way email spam filtering[J]. Journal of intelligent information systems, 2014, 42(1): 19–45. doi: 10.1007/s10844-013-0254-7 [8] FANG Yu, GAO Cong, YAO Yiyu. Granularity-driven sequential three-way decisions: a cost-sensitive approach to classification[J]. Information sciences, 2020, 507: 644–664. doi: 10.1016/j.ins.2019.06.003 [9] LIU Jiubing, LI Huaxiong, ZHOU Xianzhong, et al. An optimization-based formulation for three-way decisions[J]. Information sciences, 2019, 495: 185–214. doi: 10.1016/j.ins.2019.05.010 [10] WANG Tianxing, LI Huaxiong, ZHOU Xianzhong, et al. A prospect theory-based three-way decision model[J]. Knowledge-based systems, 2020, 203: 106129. doi: 10.1016/j.knosys.2020.106129 [11] YAO Yiyu, WANG Shu, DENG Xiaofei. Constructing shadowed sets and three-way approximations of fuzzy sets[J]. Information sciences, 2017, 412-413: 132–153. doi: 10.1016/j.ins.2017.05.036 [12] MA Xi’ao, YAO Yiyu. Three-way decision perspectives on class-specific attribute reducts[J]. Information sciences, 2018, 450: 227–245. doi: 10.1016/j.ins.2018.03.049 [13] WAN Jianwu, WANG Yi. Cost-sensitive label propagation for semi-supervised face recognition[J]. IEEE transactions on information forensics and security, 2019, 14(7): 1729–1743. doi: 10.1109/TIFS.2018.2885252 [14] MA Chao, LIU Zhenbing, CAO Zhiguang, et al. Cost-sensitive deep forest for price prediction[J]. Pattern recognition, 2020, 107: 107499. doi: 10.1016/j.patcog.2020.107499 [15] XIAO Jin, ZHOU Xu, ZHONG Yu, et al. Cost-sensitive semi-supervised selective ensemble model for customer credit scoring[J]. Knowledge-based systems, 2020, 189: 105118. doi: 10.1016/j.knosys.2019.105118 [16] FANG Yu, MIN Fan. Cost-sensitive approximate attribute reduction with three-way decisions[J]. International journal of approximate reasoning, 2019, 104: 148–165. doi: 10.1016/j.ijar.2018.11.003 [17] JIA Xiuyi, LI Weiwei, SHANG Lin. A multiphase cost- sensitive learning method based on the multiclass three-way decision-theoretic rough set model[J]. Information sciences, 2019, 485: 248–262. doi: 10.1016/j.ins.2019.01.067 [18] LI Huaxiong, ZHANG Libo, ZHOU Xianzhong, et al. Cost-sensitive sequential three-way decision modeling using a deep neural network[J]. International journal of approximate reasoning, 2017, 85: 68–78. doi: 10.1016/j.ijar.2017.03.008 [19] YANG Jie, WANG Guoying, ZHANG Qinghua, et al. Optimal granularity selection based on cost-sensitive sequential three-way decisions with rough fuzzy sets[J]. Knowledge-based systems, 2019, 163: 131–144. doi: 10.1016/j.knosys.2018.08.019 [20] MA Xi’ao, ZHAO Xuerong. Cost-sensitive three-way class-specific attribute reduction[J]. International journal of approximate reasoning, 2019, 105: 153–174. doi: 10.1016/j.ijar.2018.11.014 [21] PAWLAK Z, SKOWRON A. Rough sets: some extensions[J]. Information sciences, 2007, 177(1): 28–40. doi: 10.1016/j.ins.2006.06.006 [22] HU Qinghua, YU Daren, XIE Zhongxia. Neighborhood classifiers[J]. Expert systems with applications, 2008, 34(2): 866–876. doi: 10.1016/j.eswa.2006.10.043 [23] YAO Y Y, WONG S K M. A decision theoretic framework for approximating concepts[J]. International journal of nan-machine studies, 1992, 37(6): 793–809. [24] XU Yi, TANG Jingxin, WANG Xusheng. Three sequential multi-class three-way decision models[J]. Information sciences, 2020, 537: 62–90. doi: 10.1016/j.ins.2020.05.079 [25] HU Qinghua, YU Daren, LIU Jinfu, et al. Neighborhood rough set based heterogeneous feature subset selection[J]. Information sciences, 2008, 178(18): 3577–3594. doi: 10.1016/j.ins.2008.05.024



























































































































































































































































 下载:
下载: