Parameter self-tuning and optimization algorithm based on reinforcement learning
-
摘要: 传统PID控制算法在非线性时滞系统的应用中，存在参数整定及性能优化过程繁琐、控制效果不理想的问题。针对该问题，提出了一种基于强化学习的控制器参数自整定及优化算法。该算法引入系统动态性能指标计算奖励函数，通过学习周期性阶跃响应的经验数据，无需辨识被控对象模型的具体数据，即可实现控制器参数的在线自整定及优化。以水箱液位控制系统为实验对象，对不同类型的PID控制器使用该算法进行参数整定及优化的对比实验。实验结果表明，相比于传统的参数整定方法，所提出的算法能省去繁琐的人工调参过程，有效优化控制器参数，减少被控量的超调量，提升控制器动态响应性能。Abstract: To achieve better control performance in the nonlinear time-delay system, the traditional Proportional-Integral-Derivative (PID) control algorithm requires tuning and optimization, which complicates the controller design. First, we propose a new self-tuning and optimization algorithm for controller parameters based on reinforcement learning. Then, a reward function based on the system dynamic performance index is introduced by this algorithm. This function can learn the empirical data of periodic step response and realize the online optimization of controller parameters without identifying the model data of the controlled object. Finally, the algorithm is tested through experiments on a water tank level control system with different types of PID controllers. Experimental results show that, in contrast to the traditional parameter tuning method, the manual process is eliminated by the proposed algorithm, effectively optimizing the controller parameters, reducing the overshoot of the controlled quantity, and improving the dynamic response performance of the controller.
-
Keywords:
- reinforcement learning /
- tuning /
- optimization /
- learning algorithm /
- time delay /
- controller /
- level control /
- dynamic response
-
在现代工业控制系统研究中，对控制性能指标进行优化是研究控制算法的首要任务之一。常见的工业控制系统一般具有非线性、含时滞、多变量等复杂特性，研究人员提出了模糊PID控制[1]、分数阶PID控制[2-3]、自抗扰控制[4-5]等算法，提升控制算法的性能。工程实践中，此类控制算法和控制器的参数整定及优化过程需要工程师大量的实践经验，或通过观察被控对象的响应逐步调整，或通过辨识模型推理计算。参数优化过程繁琐耗时、常有重复性工作。随着人工智能技术的发展，深度学习[6-7]、强化学习[8]等人工智能理论及技术被广泛应用于图像识别[9]、智能推荐[10]、机器人控制[11]等领域。由于控制理论的反馈概念与强化学习的奖励概念的相似性，为了增强控制算法性能、减少人工成本，许多学者也尝试在控制理论与控制工程领域引入强化学习[12-14]。但目前这类研究大多处于理论证明和仿真实验阶段[15]，少有工程实践的验证。
本文针对上述问题，首先提出了一种基于强化学习的控制参数优化算法，将参数整定问题近似为求解约束优化问题，通过结合强化学习的奖励、经验回放机制和控制系统的动态性能指标评价模块对控制器参数进行在线自整定及优化。然后，以水箱液位控制系统为实验对象，对上述算法进行实物对比测试。最后，设计了一种动态变参数PID控制算法，验证基于强化学习的参数自整定及优化算法的可行性、有效性和普适性。
1. 强化学习
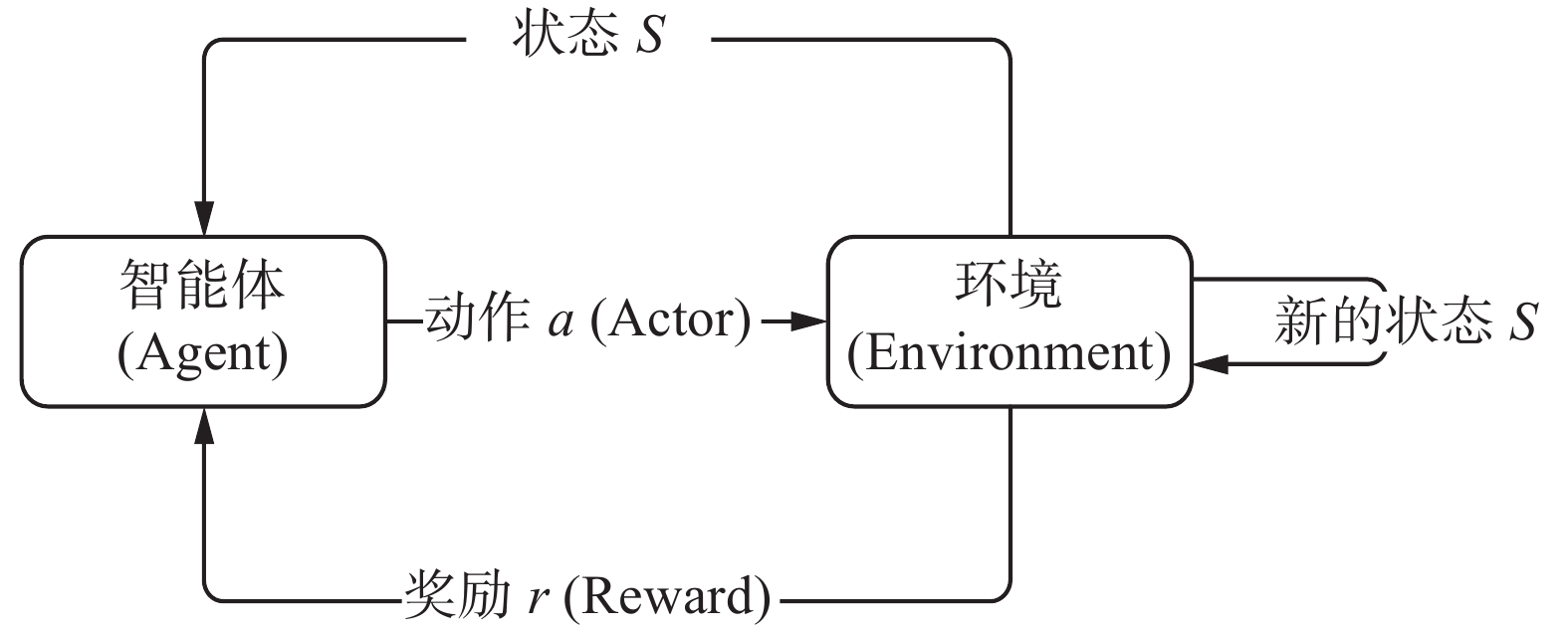
作为一种重要的机器学习方法，强化学习(reinforcement learning, RL)采用了人类和动物学习中的“尝试与失败”机制，强调智能体在与环境的交互过程中学习，利用评价性的反馈信号实现决策的优化。由于强化学习在学习过程中不需要给定各种状态的监督信号，因此其在求解复杂的优化决策问题方面有广泛的应用前景。强化学习的基本框架[16]如图1所示。
图 1 强化学习的基本框架Fig. 1 Basic framework of reinforcement learning
下载:
全尺寸图片
与环境Environment交互过程中，智能体Agent根据当前状态，选择并执行一个动作，环境接受动作后变为新的状态，并把奖赏信号反馈给智能体，根据奖赏信号智能体更新决策单元，选择后续动作，直至获得期望的最大奖励值。
智能体与环境的交互过程中, 在每个周期T会经历如下步骤[17]：
1) 智能体Agent获取环境Environment在当前周期T的状态
$ {S}_{T} $ ；2) 智能体Agent依据状态
$ {S}_{T} $ 和策略$ {P}_{T} $ ，选择并执行动作$ {a}_{T} $ ，作用于当前环境；3) 环境由状态
$ {S}_{T} $ 变为新的状态$ {S}_{T+1} $ ，并反馈当前策略的评价函数$ {r}_{T} $ ；4) 智能体Agent根据评价函数
$ {r}_{T} $ 更新策略，即$ {P}_{T}\to {P}_{T+1} $ ，$T \to T + 1$ ；5) 返回步骤1)，重复上述步骤，直至满足目标要求。
算法流程中，评价函数r是关于环境的状态S和智能体的执行动作a的函数，是决定强化学习训练结果策略P性能好坏的关键性因素。
2. 算法设计
在控制系统控制器性能分析中，系统阶跃响应对应的超调量
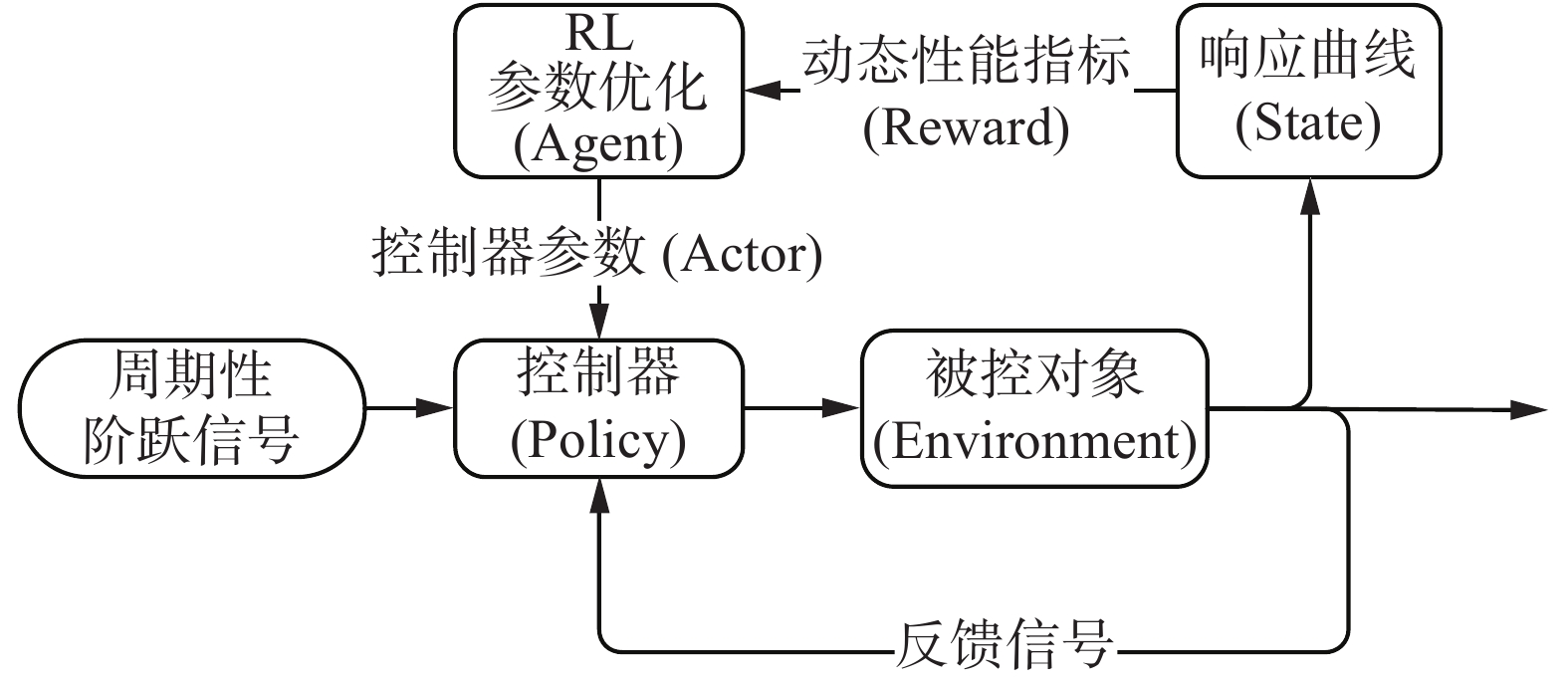
$ \delta $ 、上升时间$t_r$ 、调节时间$t_s$ 等动态性能指标是关于控制器参数矢量X的非线性函数，评价控制器设计优劣的关键性因素。(本文研究中，以稳态值的±2%作为平衡状态误差范围)结合强化学习理论和控制理论知识，本文提出一种基于强化学习(reinforcement learning, RL)的控制器参数自整定及优化算法。算法将控制参数矢量X作为智能体的动作，控制系统的响应结果作为状态，引入动态性能指标计算奖励函数，通过在线学习周期性阶跃响应数据、梯度更新控制器参数的方式改变控制器的控制策略，直至满足优化目标，实现参数的自整定及优化。算法原理如图2所示。
图 2 基于强化学习的控制器参数优化算法原理图Fig. 2 Schematic diagram of controller parameter optimization algorithm based on reinforcement learning下载:
全尺寸图片
根据原理图2，本文提出的参数自整定及优化算法将控制器参数整定问题定义为，求解满足下列不等式约束条件的可行解：
$$\left\{ {\begin{aligned} &{\delta \left( {\boldsymbol{X}} \right) \leqslant {\varOmega _1}}\\ &{t_r\left( {\boldsymbol{X}} \right) \leqslant {\varOmega _2}}\\ &{t_s\left( {\boldsymbol{X}} \right) \leqslant {\varOmega _3}}\\ &{{\rm{s.t.}}{\rm{ }}{\boldsymbol{X}} \in {\boldsymbol{Z}}} \end{aligned}} \right.$$ (1) 式中：Z为待优化的参数矢量X的取值范围；
$ {\varOmega }_{i}\left(i={1,2},3\right) $ 为优化目标的约束值。基于控制系统动态性能指标超调量$ \delta $ 、上升时间$ t_r $ 、调节时间$ t_s $ ，算法定义奖励函数$ R $ 为$$R({\boldsymbol{X}}) = \frac{1}{{\delta {{({\boldsymbol{X}})}^2} + t_r{{({\boldsymbol{X}})}^2} + t_s{{({\boldsymbol{X}})}^2}}}$$ (2) 本文算法的参数整定及优化流程如下（算法1）：
1) 根据实际条件和需求设定优化目标
$ {\varOmega }_{i} $ 和参数X的搜索范围Z，随机初始化参数X；2) 获得系统在参数X下的周期阶跃响应数据，计算动态性能指标
$ \delta $ 、$t_r$ 、$t_s$ 和奖励函数R；若满足优化目标，则终止迭代，输出参数X；3) 从经验回放集S中随机批量抽取m个经验样本，将2)中数据
$\{{\boldsymbol{X}},\delta ,t_r,t_s,R\}$ 存入经验回放集S；4) 计算m个样本的参数平均梯度
$\nabla {\boldsymbol{X}}$ ；5)
$ \sigma $ 为高斯白噪声，$ \alpha $ 为自适应学习率，利用梯度下降法更新参数：${\boldsymbol{X}}={\boldsymbol{X}}+\alpha \cdot \nabla {\boldsymbol{X}}+\sigma$ 6) 返回步骤2)，重复上述步骤。
为了尽可能获得全局最优的参数，本文的参数自整定及优化算法在更新参数的过程中引入高斯白噪声，增加参数的探索度。同时，算法利用经验回放技术，对过去的经验样本进行随机批量抽样，减弱经验数据的相关性和不平稳分布的影响，增加优化过程的准确性和收敛速度。实践试验中，为避免算法陷入局部死循环，当可行解的变异系数小于一定阈值时，即认为算法已获得局部收敛(近似全局)的相对最优解，保留当前结果并重新搜索。
3. 算法实验与对比分析
为了验证上述基于强化学习的参数自整定及优化算法的可行性和有效性，本文选择常见的水箱控制系统作为实物实验对象，对水箱液位控制器进行算法验证实验。实验设备如图3所示。
图 3 水箱控制系统实验设备Fig. 3 Experimental equipment of water tank control system下载:
全尺寸图片
3.1 控制系统模型定性分析
工程实际中的控制系统具有非线性，精准辨识其模型及参数较为困难，而本文所设计的控制器参数整定及优化算法是无需具体分析被控对象模型的无模型算法。因此，为了贴合工程实际条件，本文只对控制系统模型作定性分析，而不对其参数进行详细辨识。
由控制器、变频器(磁力泵)、水箱组成的水箱液位控制系统原理图如图4所示。其中，变频器模块的输出(流量Q)与控制器模块的输出(占空比U)的传递函数可近似为
$$\frac{{Q(s)}}{{U(s)}} = \frac{{{K_1}}}{{({T_1}s + 1)}} \cdot {{\rm{e}}^{( - {\tau _1}s)}}$$ (3) 
图 4 水箱液位控制系统原理Fig. 4 Schematic diagram of liquid control system for tank下载:
全尺寸图片
考虑对象的滞后时间，根据物料平衡方程，水箱液位H与流量Q的传递函数为
$$\frac{{H(s)}}{{Q(s)}} = \frac{{{K_2}}}{{({T_2}s + 1)}} \cdot {{\rm{e}}^{( - {\tau _2}s)}}$$ (4) 综上，本文实验中的水箱液位被控对象为具有二阶传递函数的时滞系统。其传递函数为
$$\frac{{H(s)}}{{U(s)}} = \frac{{{K_1}{K_2}}}{{({T_1}s + 1)({T_2}s + 1)}} \cdot {{\rm{e}}^{ - ({\tau _1}{\rm{ + }}{\tau _2})s}}$$ (5) 实物实验中，因实验装置部件设置的不同，部分模型参数范围为：
${T_1} \in [5,12],{T_2} \in [30,56]$ 。3.2 增量式PID控制器的参数优化
工业过程控制系统通常使用PID控制作为控制器，增量式PID算法表达式为
$$\begin{array}{l} \vartriangle u(k) = {K_{\rm{p}}}[e(k) - e(k - 1)] + {K_{\rm{i}}}e(k) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;{K_{\rm{d}}}[e(k) - 2e(k - 1) + e(k - 2)] \end{array} $$ (6) $$u(k) = u(k - 1) + \vartriangle u(k)$$ (7) 式中:
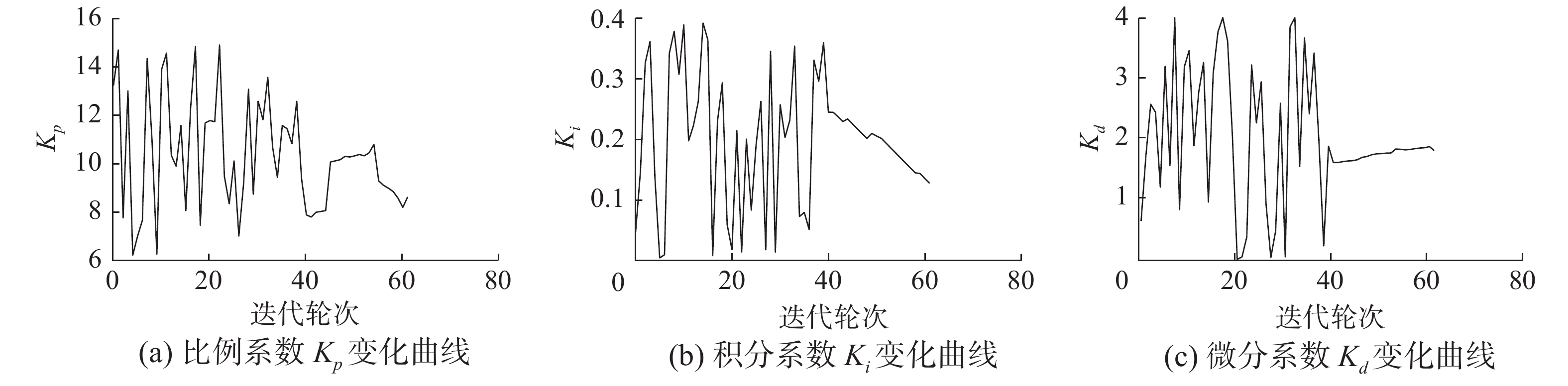
$ e\left(k\right) $ 、$ ∆u\left(k\right) $ 、$ u\left(k\right) $ 分别为采样k时刻的误差信号、输出增量和输出；${K}_{\rm p}$ 、${K}_{\rm i}$ 、${K}_{\rm d}$ 为PID控制器待整定的比例系数、积分系数和微分系数。使用本文提出的基于强化学习的参数自整定及优化算法对水箱实验设备的增量式PID控制器进行参数优化实验，算法参数设定如下：随机样本数
$ m=10 $ ，学习率$ \alpha =0.02 $ 。考虑系统性能实际可行性，设定优化约束如下：系数范围${K}_{\rm p}\in \left[{6,15}\right]$ ，${K}_{\rm i}\in \left[{0,0.4}\right]$ ，${K}_{\rm d}\in \left[{0,4}\right]$ ；超调量阈值$ {\varOmega }_{1}=2{\%} $ ，上升时间阈值${\varOmega }_{2}=20\;{\rm{s}}$ ，调节时间阈值${\varOmega }_{3}=38\;{\rm{s}}$ 。算法训练过程中，PID控制器的系数随迭代轮次的变化曲线如图5所示。由图5可以看出，算法在学习过程的前期，利用较大范围的参数变化增加了参数的探索度，然后通过在线学习经验数据，使得控制器参数逐渐收敛至优化目标。
图 5 PID控制器参数的变化曲线Fig. 5 Change curves of PID controller parameters下载:
全尺寸图片
为了测试所得参数的实际控制性能，将上述参数与传统的Ziegler-Nichols(Z-N)法[18]、基于遗传算法的参数优化方法[19-20]所得参数进行实物实验对比。即在相同输入条件下，对比不同方法所得控制器参数的阶跃响应性能，对比数据如表1和图6所示。由对比数据可以看出，本文提出的基于强化学习的参数自整定及优化算法可以有效地优化常规PID控制器的参数，其实验结果在超调量、调节时间性能指标上明显优于传统的Z-N参数整定法，且省去人工整定参数的繁琐过程。此外，相比于基于遗传算法的参数优化算法，基于强化学习的参数优化算法使用更少的计算机资源，获得了性能相近的结果。
图 6 不同方法所得参数对应的PID控制器阶跃响应曲线Fig. 6 PID controllers dynamic input response tracking curve of parameters obtained by different methods下载:
全尺寸图片
表 1 不同方法所得控制器参数在相同阶跃输入下的对比数据Table 1 Comparison data of controller parameters obtained by different methods with the same step input算法 控制器参数 动态性能指标 优化过程数据计算量 ${K}_{\rm p}$ ${K}_{\rm i}$ ${K}_{\rm d}$ 超调量/% 上升时间/s 调节时间/s Ziegler-Nichols法 8.40 0.180 1.6 9.01 16.9 56.3 人工经验 基于遗传算法的算法 8.67 0.128 2.2 1.10 19.7 35.8 大于300 基于强化学习的算法 8.74 0.132 1.8 0.84 19.7 36.6 小于100 3.3 变参数PID控制器的参数优化
为了进一步验证基于强化学习的参数自整定及优化算法的普适性，提升控制器的动态性能。结合模糊控制理论[21]，本文设计了一种动态变参数的PID控制算法，动态PID系数的计算公式为
$$\left\{ \begin{split} &{K_{\rm{p}}} = {K_0} + 2 \times ({P_1} \cdot e + {P_2} \cdot {d_e} + {P_3} \cdot {e^3}) \\ &{K_{\rm{i}}} = {I_0} + 0.03 \times ({I_1} \cdot e + {I_2} \cdot {d_e} + {I_3} \cdot {e^3}) \\ &{K_{\rm{d}}} = {D_0} + ({D_1} \cdot e + {D_2} \cdot {d_e} + {D_3} \cdot {e^3}) \end{split} \right.$$ (8) 式中：e为经过处理的误差信号；de为误差信号e的变化率；
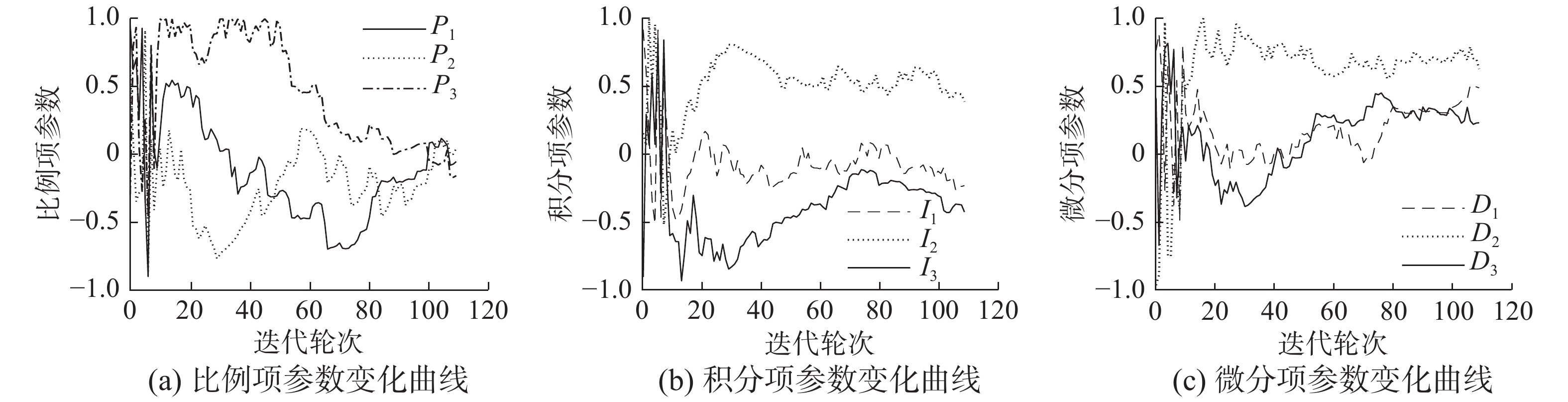
$ {K}_{0} $ 、$ {I}_{0} $ 、$ {D}_{0} $ 是PID系数的偏置量；$ {P}_{i} $ 、$ {I}_{i} $ 、$ {D}_{i} $ ($ i={1,2},3 $ )是待确定的参数。此时，传统的经验方法难以整定这类改进PID控制器的参数；使用遗传算法等最优化方法优化参数所需的计算机资源过多，实际应用较为困难。使用本文算法对上述控制器待确定的参数进行整定和优化。算法参数设定如下：随机样本数
$ m=15 $ ，学习率$ \alpha =0.001 $ 。基于表1的结果，令系数偏置量$ {K}_{0}=8.7 $ ，$ {I}_{0}=0.14 $ ，$ {D}_{0} $ =2.2。优化约束设定如下：$ {P}_{i},{I}_{i},{D}_{i}\in \left[-{1,1}\right],\left(i={1,2},3\right) $ ，超调量阈值$ {\varOmega }_{1}=2{\%} $ ，上升时间阈值${\varOmega }_{2}=19\;{\rm{s}}$ ，调节时间阈值${\varOmega }_{3}=33\;{\rm{s}}$ 。变参数PID控制器的各项参数随迭代轮次的变化曲线如图7所示。本文算法的参数优化结果如表2所示，对应控制系统的阶跃响应动态性能指标如下：超调量为0.896%、上升时间为17.9 s、调节时间为31 s。3.4 对比实验及结果分析
为了进一步测试本文参数优化算法所得控制参数的动态性能，将表1中的Z-N法和基于强化学习(RL)的算法获得的固定参数PID控制器与表2的动态变参数PID控制器进行性能对比。对比测试分为两个部分：动态输入下的响应性能对比和稳定状态下的抗干扰性能对比。
图 7 优化过程的参数变化曲线Fig. 7 Data curves of parameter optimization process下载:
全尺寸图片
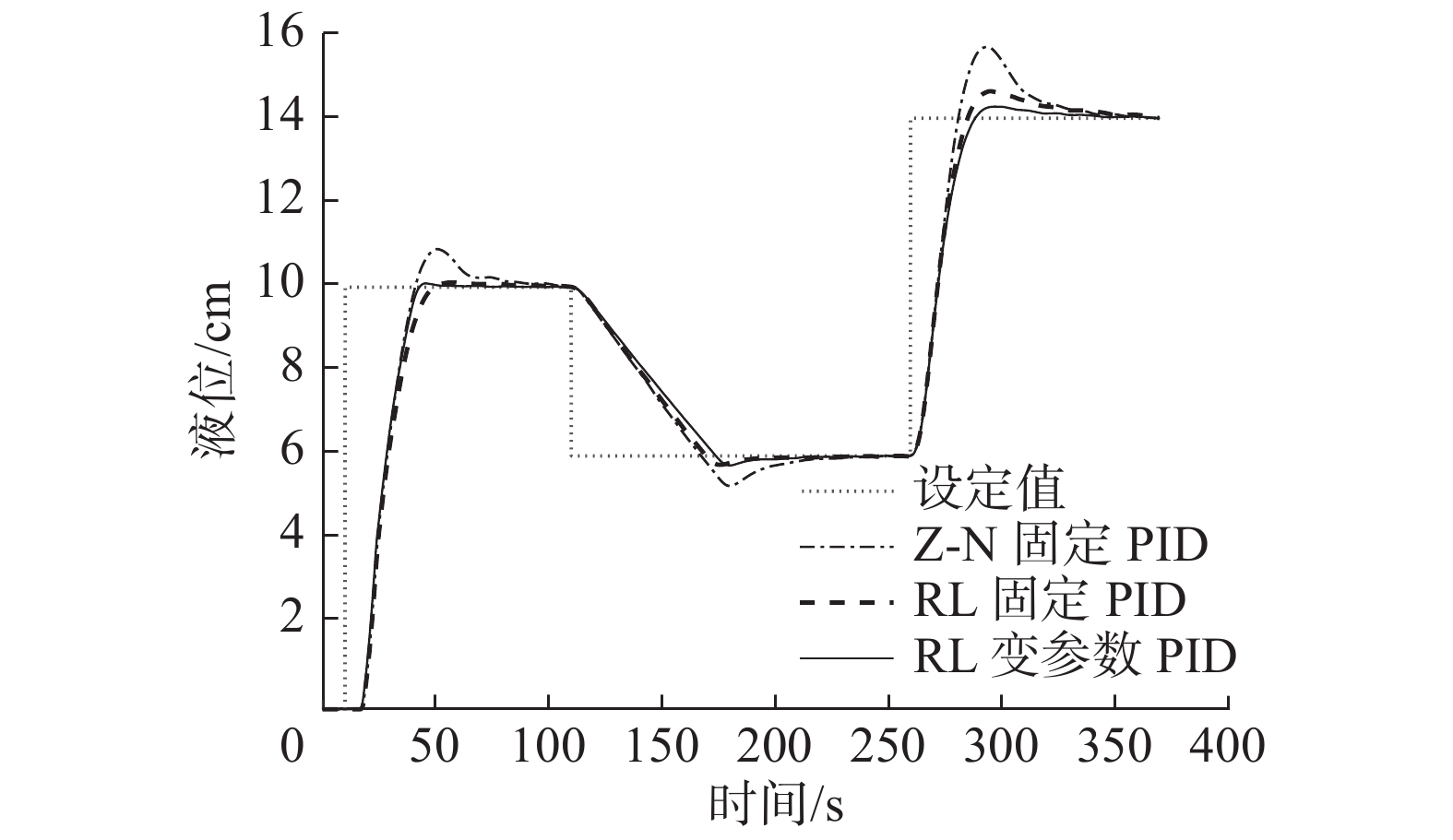
表 2 变参数PID控制器的参数优化结果Table 2 Parameter optimization results of variable parameter PID controller参数名 数值 $P_1$ −0.052 $P_2$ 0.046 $P_3$ −0.156 $I_1$ −0.231 $I_2$ 0.387 $I_3$ −0.426 $D_1$ 0.488 $D_2$ 0.628 $D_3$ 0.231 1)动态输入下的响应性能对比。控制系统在给定相同的动态阶跃输入条件下，3种控制器的响应性能对比如图8所示。由图8可以看出，相比Z-N法的参数，本文算法所得参数具有更小的超调量、更好的响应跟踪性能。同时，本文算法优化后的动态变参数PID控制器具有最小的超调量、最优的响应跟踪性能，验证了本文算法应用于不同类型控制器的有效性和普适性。
图 8 不同控制器的动态输入跟踪曲线Fig. 8 Dynamic input tracking curves for different controllers下载:
全尺寸图片
2)稳定状态下的抗干扰性能对比。控制系统进入稳定状态后，在t=10 s时刻，对被控系统施加一定的干扰，3种控制器在相同扰动条件下的对比曲线如图9所示。
图 9 不同控制器的抗扰动曲线Fig. 9 Anti-disturbance curves of different controllers下载:
全尺寸图片
由图9可以看出，3种控制器受到扰动影响后，被控量恢复至稳定状态所用的时间相近，Z-N法整定的PID控制器恢复时间相对最短，但其恢复过程中的超调量最大，变参数PID控制器的抗干扰综合性能最优。
4. 结束语
本文针对传统PID算法在含时延、非线性的控制系统应用过程中，参数整定繁琐、控制效果较差等问题[22]，提出了一种基于强化学习的参数自整定及优化算法，可以实现在线整定和优化控制器参数。水箱液位控制系统实验的结果表明，基于强化学习的参数自整定及优化算法省去了依赖经验且耗时较长的人工调参过程，比遗传算法等最优化方法使用了更少的计算机资源，获得近似最优的控制器参数，提升控制系统的动态性能。与固定参数的PID控制器相比，经本文算法优化的变参数PID控制器具有超调量小、响应跟踪性能好的优点。本文所提出的算法有望应用于工业过程控制系统的控制器参数整定及控制优化等相关问题。
本文提出的算法是基于PID控制算法进行优化和改进，虽能在一定程度上保证控制系统的控制稳定性，但其控制效果也因此受限于传统的PID算法。在非PID原理的控制器参数优化应用过程，算法无法确定控制器输出的安全性。同时，本文未在优化算法的评价函数中考虑扰动恢复性能等指标，无法从理论上确保优化所得参数的整体性能最优性。
因此，增加奖励函数的评估因素，或改变控制算法的底层策略结构，是今后的研究方向。例如，结合预测控制算法[23-24]或由深度神经网络[25]组成的“黑盒”模型，取代PID算法框架，使用基于深度强化学习[26-27]的优化算法进一步优化控制系统的性能等。
-
图 1 强化学习的基本框架
Fig. 1 Basic framework of reinforcement learning
下载:
全尺寸图片
图 2 基于强化学习的控制器参数优化算法原理图
Fig. 2 Schematic diagram of controller parameter optimization algorithm based on reinforcement learning
下载:
全尺寸图片
图 3 水箱控制系统实验设备
Fig. 3 Experimental equipment of water tank control system
下载:
全尺寸图片
图 4 水箱液位控制系统原理
Fig. 4 Schematic diagram of liquid control system for tank
下载:
全尺寸图片
图 5 PID控制器参数的变化曲线
Fig. 5 Change curves of PID controller parameters
下载:
全尺寸图片
图 6 不同方法所得参数对应的PID控制器阶跃响应曲线
Fig. 6 PID controllers dynamic input response tracking curve of parameters obtained by different methods
下载:
全尺寸图片
图 7 优化过程的参数变化曲线
Fig. 7 Data curves of parameter optimization process
下载:
全尺寸图片
图 8 不同控制器的动态输入跟踪曲线
Fig. 8 Dynamic input tracking curves for different controllers
下载:
全尺寸图片
图 9 不同控制器的抗扰动曲线
Fig. 9 Anti-disturbance curves of different controllers
下载:
全尺寸图片
表 1 不同方法所得控制器参数在相同阶跃输入下的对比数据
Table 1 Comparison data of controller parameters obtained by different methods with the same step input
算法 控制器参数 动态性能指标 优化过程数据计算量 ${K}_{\rm p}$ ${K}_{\rm i}$ ${K}_{\rm d}$ 超调量/% 上升时间/s 调节时间/s Ziegler-Nichols法 8.40 0.180 1.6 9.01 16.9 56.3 人工经验 基于遗传算法的算法 8.67 0.128 2.2 1.10 19.7 35.8 大于300 基于强化学习的算法 8.74 0.132 1.8 0.84 19.7 36.6 小于100 表 2 变参数PID控制器的参数优化结果
Table 2 Parameter optimization results of variable parameter PID controller
参数名 数值 $P_1$ −0.052 $P_2$ 0.046 $P_3$ −0.156 $I_1$ −0.231 $I_2$ 0.387 $I_3$ −0.426 $D_1$ 0.488 $D_2$ 0.628 $D_3$ 0.231 -
[1] 赵新华, 王璞, 陈晓红. 投球机器人模糊PID控制[J]. 智能系统学报, 2015, 10(3): 399–406. https://www.cnki.com.cn/Article/CJFDTOTAL-ZNXT201503014.htm ZHAO Xinhua, WANG Pu, CHEN Xiaohong. Fuzzy PID control of pitching robots[J]. CAAI transactions on intelligent systems, 2015, 10(3): 399–406. https://www.cnki.com.cn/Article/CJFDTOTAL-ZNXT201503014.htm [2] YANG Bo, YU Tao, SHU Hongchun, et al. Perturbation observer based fractional-order PID control of photovoltaics inverters for solar energy harvesting via Yin-Yang-Pair optimization[J]. Energy conversion and management, 2018, 171: 170–187. doi: 10.1016/j.enconman.2018.05.097 [3] JAISWAL S, CHILUKA S K, SEEPANA M M, et al. Design of fractional order PID controller using genetic algorithm optimization technique for nonlinear system[J]. Chemical product and process modeling, 2020, 15(2): 20190072. [4] 陈增强, 黄朝阳, 孙明玮, 等. 基于大变异遗传算法进行参数优化整定的负荷频率自抗扰控制[J]. 智能系统学报, 2020, 15(1): 41–49. https://www.cnki.com.cn/Article/CJFDTOTAL-ZNXT202001008.htm CHEN Zengqiang, HUANG Zhaoyang, SUN Mingwei, et al. Active disturbance rejection control of load frequency based on big probability variation’s genetic algorithm for parameter optimization[J]. CAAI transactions on intelligent systems, 2020, 15(1): 41–49. https://www.cnki.com.cn/Article/CJFDTOTAL-ZNXT202001008.htm [5] WEI Wei, CHEN Nan, ZHANG Zhiyuan, et al. U-model-based active disturbance rejection control for the dissolved oxygen in a wastewater treatment process[J]. Mathematical problems in engineering, 2020: 3507910. [6] 胡越, 罗东阳, 花奎, 等. 关于深度学习的综述与讨论[J]. 智能系统学报, 2019, 14(1): 1–19. https://www.cnki.com.cn/Article/CJFDTOTAL-ZNXT201901001.htm HU Yue, LUO Dongyang, HUA Kui, et al. Review and discussion on deep learning[J]. CAAI transactions on intelligent systems, 2019, 14(1): 1–19. https://www.cnki.com.cn/Article/CJFDTOTAL-ZNXT201901001.htm [7] SILVER D, HUANG A, MADDISON C J, et al. Mastering the game of Go with deep neural networks and tree search[J]. Nature, 2016, 529(7587): 484–489. doi: 10.1038/nature16961 [8] 李超, 张智, 夏桂华, 等. 基于强化学习的学习变阻抗控制[J]. 哈尔滨工程大学学报, 2019, 40(2): 304–311. https://www.cnki.com.cn/Article/CJFDTOTAL-HEBG201902013.htm LI Chao, ZHANG Zhi, XIA Guihua, et al. Learning variable impedance control based on reinforcement learning[J]. Journal of Harbin Engineering University, 2019, 40(2): 304–311. https://www.cnki.com.cn/Article/CJFDTOTAL-HEBG201902013.htm [9] 王念滨, 何鸣, 王红滨, 等. 适用于水下目标识别的快速降维卷积模型[J]. 哈尔滨工程大学学报, 2019, 40(7): 1327–1333. https://www.cnki.com.cn/Article/CJFDTOTAL-HEBG201907021.htm WANG Nianbin, HE Ming, WANG Hongbin, et al. Fast dimensional-reduction convolution model for underwater target recognition[J]. Journal of Harbin Engineering University, 2019, 40(7): 1327–1333. https://www.cnki.com.cn/Article/CJFDTOTAL-HEBG201907021.htm [10] 黄立威, 江碧涛, 吕守业, 等. 基于深度学习的推荐系统研究综述[J]. 计算机学报, 2018, 41(7): 1619–1647. doi: 10.11897/SP.J.1016.2018.01619 HUANG Liwei, JIANG Bitao, LYU Shouye, et al. A review of recommendation systems based on deep learning[J]. Chinese journal of computers, 2018, 41(7): 1619–1647. doi: 10.11897/SP.J.1016.2018.01619 [11] GHEISARNEJAD M, KHOOBAN M H. An intelligent non-integer PID controller-based deep reinforcement learning: implementation and experimental results[J]. IEEE transactions on industrial electronics, 2021, 68(4): 3609–3618. doi: 10.1109/TIE.2020.2979561 [12] BUSONIU L, DE BRUIN T, TOLIĆ D, et al. Reinforcement learning for control: performance, stability, and deep approximators[J]. Annual reviews in control, 2018, 46: 8–28. doi: 10.1016/j.arcontrol.2018.09.005 [13] 袁兆麟, 何润姿, 姚超, 等. 基于强化学习的浓密机底流浓度在线控制算法[J]. 自动化学报, 2021, 47(7): 1558–1571. https://www.cnki.com.cn/Article/CJFDTOTAL-MOTO202107008.htm YUAN Zhaolin, HE Runzi, YAO Chao, et al. Online reinforcement learning control algorithm for concentration of thickener underflow[J]. Acta automatica sinica, 2021, 47(7): 1558–1571. https://www.cnki.com.cn/Article/CJFDTOTAL-MOTO202107008.htm [14] NIAN R, LIU J, HUANG B. A review on reinforcement learning: introduction and applications in industrial process control[J]. Computers and chemical engineering, 2020: 106886. [15] PANG B, JIANG Z P, MAREELS I. Reinforcement learning for adaptive optimal control of continuous-time linear periodic systems[J]. Automatica, 2020, 118: 109035. doi: 10.1016/j.automatica.2020.109035 [16] 殷昌盛, 杨若鹏, 朱巍, 等. 多智能体分层强化学习综述[J]. 智能系统学报, 2020, 15(4): 646–655. https://www.cnki.com.cn/Article/CJFDTOTAL-ZNXT202004003.htm YIN Changsheng, YANG Ruopeng, ZHU Wei, et al. A survey on multi-agent hierarchical reinforcement learning[J]. CAAI transactions on intelligent systems, 2020, 15(4): 646–655. https://www.cnki.com.cn/Article/CJFDTOTAL-ZNXT202004003.htm [17] 高瑞娟, 吴梅. 基于改进强化学习的PID参数整定原理及应用[J]. 现代电子技术, 2014, 37(4): 1–4. doi: 10.3969/j.issn.1004-373X.2014.04.001 GAO Ruijuan, WU Mei. Principle and application of PID parameter tuning based on improved reinforcement learning[J]. Modern electronics technique, 2014, 37(4): 1–4. doi: 10.3969/j.issn.1004-373X.2014.04.001 [18] ALDEMIR A, HAPOĞLU H. Comparison of PID tuning methods for wireless temperature control[J]. Journal of polytechnic, 2016, 19(1): 9–19. [19] 蔡聪仁, 向凤红. 基于遗传算法优化PID的板球系统位置控制[J]. 电子测量技术, 2019, 42(23): 97–101. https://www.cnki.com.cn/Article/CJFDTOTAL-DZCL201923016.htm CAI Congren, XIANG Fenghong. Position control of cricket system based on genetic algorithm optimized PID[J]. Electronic measurement technology, 2019, 42(23): 97–101. https://www.cnki.com.cn/Article/CJFDTOTAL-DZCL201923016.htm [20] 么洪飞, 王宏健, 王莹, 等. 基于遗传算法DDBN参数学习的UUV威胁评估[J]. 哈尔滨工程大学学报, 2018, 39(12): 1972–1978. https://www.cnki.com.cn/Article/CJFDTOTAL-HEBG201812015.htm YAO Hongfei, WANG Hongjian, WANG Ying, et al. UUV threat assessment based on genetic algorithm DDBN parameter learning[J]. Journal of Harbin Engineering University, 2018, 39(12): 1972–1978. https://www.cnki.com.cn/Article/CJFDTOTAL-HEBG201812015.htm [21] 胡勤丰, 陈威振, 邱攀峰, 等. 适用于连续加减速的永磁同步电机模糊增益自调整PI控制研究[J]. 中国电机工程学报, 2017, 37(3): 907–914. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGDC201703030.htm HU Qinfeng, CHEN Weizhen, QIU Panfeng, et al. Research on fuzzy self-tuning gain PI control for accelerating and decelerating based on permanent magnet synchronous motor[J]. Proceedings of the CSEE, 2017, 37(3): 907–914. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGDC201703030.htm [22] 叶政. PID控制器参数整定方法研究及其应用[D]. 北京: 北京邮电大学, 2016. YE Zheng. Research on PID controller parameter tuning method and its application [D]. Beijing: Beijing University of Posts and Telecommunications, 2016. [23] 刘志林, 李国胜, 张军. 有横摇约束的欠驱动船舶航迹跟踪预测控制[J]. 哈尔滨工程大学学报, 2019, 40(2): 312–317. https://www.cnki.com.cn/Article/CJFDTOTAL-HEBG201902014.htm LIU Zhilin, LI Guosheng, ZHANG Jun. Predictive control of underactuated ship track tracking with roll constraint[J]. Journal of Harbin Engineering University, 2019, 40(2): 312–317. https://www.cnki.com.cn/Article/CJFDTOTAL-HEBG201902014.htm [24] 朱芮, 吴迪, 陈继峰, 等. 电机系统模型预测控制研究综述[J]. 电机与控制应用, 2019, 46(8): 1–10,30. https://www.cnki.com.cn/Article/CJFDTOTAL-ZXXD201908001.htm ZHU Rui, WU Di, CHEN Jifeng, et al. A review of model predictive control for motor systems[J]. Electric machines and control application, 2019, 46(8): 1–10,30. https://www.cnki.com.cn/Article/CJFDTOTAL-ZXXD201908001.htm [25] PU Z , WANG Y , CHANG N , et al. A deep reinforcement learning framework for optimizing fuel economy of hybrid electric vehicles[C]//2018 23rd Asia and South Pacific Design Automation Conference. Jeju Island , Korea, 2018. [26] 张法帅, 李宝安, 阮子涛. 基于深度强化学习的无人艇航行控制[J]. 计测技术, 2018, 38(A01): 5. https://www.cnki.com.cn/Article/CJFDTOTAL-HKJC2018S1061.htm ZHANG Fashuai, LI Baoan, RUAN Zitao. Navigation control of unmanned vehicle based on deep reinforcement learning[J]. Metrology and measurement technology, 2018, 38(A01): 5. https://www.cnki.com.cn/Article/CJFDTOTAL-HKJC2018S1061.htm [27] 唐振韬, 邵坤, 赵冬斌, 等. 深度强化学习进展: 从AlphaGo到AlphaGo Zero[J]. 控制理论与应用, 2017, 34(12): 18. https://www.cnki.com.cn/Article/CJFDTOTAL-KZLY201712001.htm TANG Zhentao, SHAO Kun, ZHAO Dongbin, et al. Progress in deep reinforcement learning: from AlphaGo to AlphaGo Zero[J]. Control theory and applications, 2017, 34(12): 18. https://www.cnki.com.cn/Article/CJFDTOTAL-KZLY201712001.htm
