System fault pattern recognition based on the connection number and attribute polygon
-
摘要: 为综合考虑多因素影响下根据系统故障标准模式对系统故障样本模式进行识别,定义了属性多边形并提出基于联系数和属性多边形的系统故障样本模式识别方法。首先,建立了故障模式识别系统,利用特征函数确定单因素的故障模式联系度,确定属性多边形结构。其次,利用属性多边形的同异反分量面积确定多因素联合影响的故障模式联系度。最终,根据故障标准模式的最大隶属原则对故障样本模式进行识别。使用简单电气系统作为实例,实施了识别方法,得到多因素联合影响下的各故障样本模式的识别结果。实验结果表明,通过两阶段联系度的计算可综合考虑单因素和多因素影响下的故障模式特征,进而识别系统故障样本模式。Abstract: To identify the system fault sample patterns under the influence of multiple factors, an attribute polygon is defined, and the system fault sample pattern recognition method is proposed based on the connection number and the attribute polygon. First, the fault pattern recognition system is established, the connection degree of a single factor is determined by the characteristic function, and the structure of the attribute polygon is determined. Second, the area with an identical difference, contrary to the attribute polygon, is used to determine the fault pattern connection degree affected by multiple factors. Finally, the fault sample pattern is identified according to the maximum membership principle of the fault standard pattern. Taking a simple electrical system as an example, the recognition method is implemented, thereby obtaining the recognition results of each fault sample pattern synergistically influenced by multiple factors. The results show that via the two-stage connection degree calculation, the fault pattern characteristics can be comprehensively considered under the influence of a single factor and multiple factors, thereby identifying the system fault sample pattern.
-
故障模式识别主要是利用已有故障模式来识别新出现的样本故障模式。作为识别基础的故障标准模式应是已知的、重要的、具有一定代表性的故障特征。在已出现的众多故障中选择少量的故障标准模式对故障识别和预防治理非常重要。对这些标准模式可进行详细分析,了解故障发生机理,并对该机理采取适合的预防和治理措施。这些研究工作显然不能大量进行,而只能针对被选择的故障标准模式进行。故障标准模式确定后,另一问题是如何将众多新发生的故障样本模式与标准模式对应,以使用标准模式的预防治理措施。这是模式的相似性研究,或称为模式识别,即基于标准模式特征识别样本模式。模式识别需要考虑很多问题,基础数据的获得、故障数据的表示、影响因素的作用和故障发生的机理等。目前这些问题仍缺乏有效方法解决。
故障的模式识别或聚类分析研究正在迅速增加。较新的研究包括:利用改进经验小波变换与压缩感知联合降噪结合导联卷积神经网络进行轴承故障诊断[1],利用网络搜索优化序列最小支持向量机的滚动轴承故障诊断[2],小波包和神经网络的行星齿轮箱故障模式识别[3],配电网选线保护的功角聚类分析[4],滚动轴承变量模态分解能量熵与概率神经网络故障模式识别[5],装备维修性数据挖掘的定量分析[6],基于分形理论与聚类分析的小电阻接地系统故障分析[7],智能电能表故障数据云模型分析[8],卷积神经网络图像分类轴承故障模式识别[9],多维高斯贝叶斯的故障智能诊断[10],卫星姿态控制系统(ACS)系统执行机构与传感器故障识别[11],集成多策略改进模糊C均值算法的旋转机械故障聚类分析[12],基于完备集合经验模态分解–深度信念网络的超低速滚动轴承故障诊断[13]等。这些研究各具优势,使用了不同方法解决了各自领域相关的故障模式识别等问题。正如前述,基础数据获得,故障数据表示,影响因素作用和故障发生机理等方面的分析仍存在问题;而且针对专业背景的故障模式识别方法缺乏系统层面的抽象和分析,导致方法的通用性不佳。
针对这些问题笔者以集对分析联系数和空间故障树特征函数为基础,提出了属性多边形来研究多因素影响下,根据故障标准模式识别故障样本模式的方法。
1. 联系数和属性多边形
集对分析理论是中国学者赵克勤在1992年提出的[14-18]。联系数是集对分析理论的核心,表示了两事物之间的联系关系。联系数的种类从二元联系数到多元联系数有所不同,但基本思想类似。二元联系数表示为μ=a+bi,a和b分别表示确定性分量和不确定分量,i为不确定性系数,表示两者联系的不确定性程度。三元联系数为μ=a+bi+cj,a、b和c分别表示同分量、异分量和反分量,i表示异分量系数,j表示反分量系数,表示两者同异反关系。进一步的,同和反是联系中的确定部分,而异则是联系中的不确定部分。因此三元联系数仍然保持了确定性与不确定性的关系表示,只是对确定性部分进行了细化。之后的四元联系数到多元联系数都可看作对异状态的细化和高阶拆分。例如:安全评价过程中的安全等级,安全和不安全对应着同和反状态,而中间的过渡等级如较安全、一般安全和较不安全则是异状态。其中的安全评价表是根据故障标准模式确定的,而被评价对象则是故障样本模式,因此安全评价也是故障模式识别的特例之一。借助联系数的同异反表示能力,即可了解故障标准模式与故障样本模式的联系程度,达到模式识别的目的。
解决另一问题,即故障数据表示和多因素影响作用。空间故障树理论是作者提出的用于系统可靠性及故障演化与影响因素关系的研究理论体系,包括空间故障树基础理论[19]、智能化空间故障树[20-22]、空间故障网络[23-27]、系统运动空间与系统映射论[28]。其基础源于特征函数对系统故障概率与影响因素关系的表示。本文中修改特征函数进而表示故障发生数量与影响因素的关系。以此表示单因素影响下,因素变化与故障数量变化的关系。多因素对模式识别的影响需通过可表示多个因素同时作用故障模式时的变化予以表示,即多因素的变化差异与故障数量变化差异的对应关系。在空间故障树中曾提出属性圆[29-30]的概念来衡量类似情况。但属性圆是相对的归一化空间,并不适合具有绝对数量的故障发生数和考虑权重不同的因素影响程度。因此提出属性多边形的概念,在属性圆基础上不再限制因素的变化范围,以此来更加明确地表示多个因素影响下标准模式和样本模式的变化差异。另外对于故障机理的研究归属于空间故障网络,进一步的结合有待后继研究。
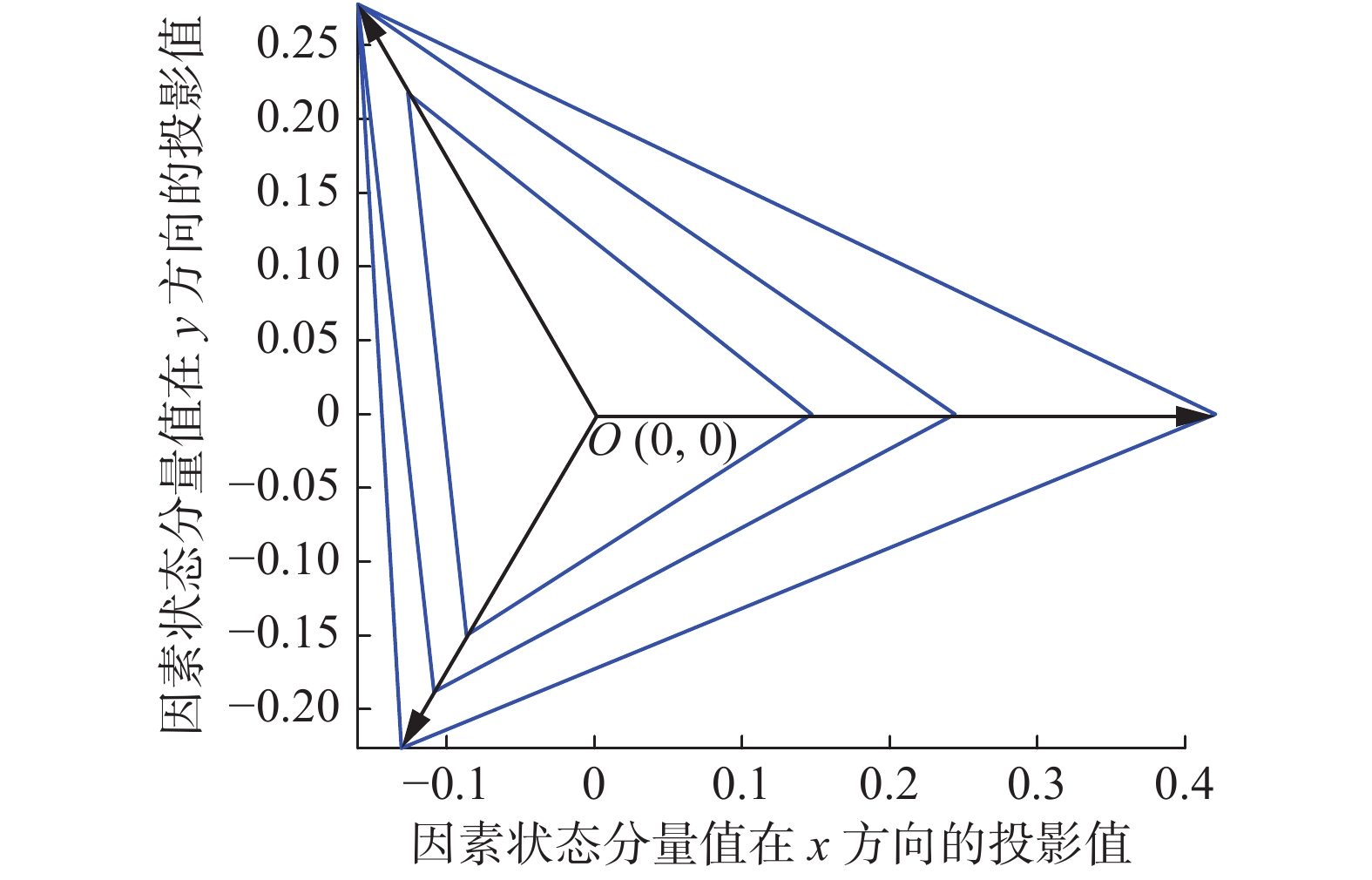
属性多边形是基于属性圆建立的多因素影响下对象相似性对比方法。在二维平面内建立多因素坐标体系。坐标原点为O,由该点以各因素为轴,且各轴之间的夹角相同,进而建立坐标系统,如图1所示。
图1显示了属性多边形,坐标系的中心(0,0)是点O。射线
$ O{A_1} $ ~$ O{A_Q} $ 代表Q个因素在坐标系中的坐标轴。相邻坐标轴之间的夹角,称为属性角,如$ O{A_1} $ 和$ O{A_2} $ 的夹角表示为$ {\alpha _1} = \angle {A_1}O{A_2} $ ,进而$ {\alpha _q} = \angle {A_q}O{A_{q + 1}} $ ,因此属性角的总和为$\displaystyle\sum\limits_{q = 1}^Q {{\alpha _q}} = $ $ \displaystyle\sum\limits_{q = 1}^{Q - 1} {\angle {A_q}O{A_{q + 1}}} = 360^\circ$ 。为表示联系数的同异反关系,将属性多边形划分为3个区域。对于单一因素fq的坐标轴Aq上,将属性值对应坐标上的长度作为划分点。同状态分量值为$ L_q^a $ ,异状分量值为$ L_q^{ab} $ ,反状态分量为$ L_q^{abc} $ 。在坐标轴Aq上分别与圆心O的对应的坐标点为$ (o_{xq}^a,o_{yq}^a) $ 、$ (o_{xq}^{ab},o_{yq}^{ab}) $ 和$ (o_{xq}^{abc}, $ $ o_{yq}^{abc}) $ 。综上构建了表示多因素影响下的属性多边形。方法使用了两次联系数来计算联系度(通过联系数表示)。第一次基于特征函数表示故障数量变化,对单因素影响下标准和样本模式进行同异反分量计算,建立属性多边形。第二次是利用属性多边形的同异反分量面积,对多因素影响下标准和样本模式进行同异反分析,最终完成识别。可见两种理论的结合是有效的。
2. 多因素故障模式的识别方法构建
本文提出的故障模式识别方法是基于集对分析联系数和空间故障树特征函数实现的,设故障模式识别系统T为
$$ \left\{ \begin{aligned} &T = \{ {R_S},R,F,X,W\} \\ &{R_S} = {\rm{\{ }}{r_{{S_1}}},{r_{{S_2}}}{\rm{,}} \cdots {\rm{,}}{r_{{S_M}}}{\rm{\} ,}}\quad m = {\rm{1,2,}} \cdots {\rm{,}}M\\ &R = {\rm{\{ }}{r_1}{\rm{,}}{r_2}{\rm{,}} \cdots {\rm{,}}{r_N}{\rm{\} ,}}\quad n = {\rm{1,2,}} \cdots {\rm{,}}N\\ &F = {\rm{\{ }}{f_1}{\rm{,}}{f_2}{\rm{,}} \cdots {\rm{,}}{f_Q}{\rm{\} ,}}\quad q = 1,2, \cdots ,Q\\ &X = \{ {x_1},{x_2}, \cdots ,{x_Q}\} \\ &W = \{ {w_1},{w_2}, \cdots ,{w_Q}\} \end{aligned} \right. $$ (1) 式中:
$ {R_S} $ 为故障标准模式集合,模式数量为M;$ R $ 为故障样本模式集合,模式数量为N;F为因素集合,因素数量为Q;X为因素值集合;W为因素权重集合。对比故障标准模式
$ {r_{{S_m}}} $ 和故障样本模式$ {r_n} $ ,将故障数量作为函数值,将单一因素值作为参数构建特征函数。用$ P_{}^{{r_{{S_m}}}}({x_q}) $ 和$ P_{}^{{r_n}}({x_q}) $ 分别代表因素fq影响下$ {r_{{S_m}}} $ 和$ {r_n} $ 的特征函数,$ {x_q} $ 是fq的因素值。$ p_{}^{{r_{{S_m}}}}({x_q}) $ 和$ p_{}^{{r_n}}({x_q}) $ 表示$ {x_q} $ 对应的$ {r_{{S_m}}} $ 和$ {r_n} $ 的故障发生数。特征函数的构建可使用空间故障树方法,例如拟合法[19]、因素投影拟合法[31]、模糊结构元[32]或云模型[33]等。特征函数是针对单因素建立的,因素值作为变量,考虑$ {r_{{S_m}}} $ 和$ {r_n} $ 的特征函数值的差与$ {r_{{S_m}}} $ 特征函数值的比,确定各因素影响下$ {r_{{S_m}}} $ 和$ {r_n} $ 的同异反状态数量。如果该比值在[0,30%]为同状态,Na加1;在(30%,70%]为异状态,Nb加1;在(70%,+∞)为反状态,Nc加1。Na、Nb和Nc为$ {r_{{S_m}}} $ 和$ {r_n} $ 的同异反状态数量,循环该过程直到所有比例值遍历统计完成,如式(2)所示:$$\begin{aligned} [{N_a},{N_b},{N_c}] =\quad\quad\quad \quad\quad\quad\quad\quad\\ \left\{ {\begin{aligned} &{{N_a} = {N_a} + 1,\begin{array}{*{20}{c}} {} \end{array}\dfrac{{\left| {{p^{{r_{{S_m}}}}}({x_q}) - {p^{{r_n}}}({x_q})} \right|}}{{\left| {{p^{{r_{{S_m}}}}}({x_q})} \right|}} \in [0,30{\text{%}} ]} \\ &{{N_b} = {N_b} + 1,\begin{array}{*{20}{c}} {} \end{array}\dfrac{{\left| {{p^{{r_{{S_m}}}}}({x_q}) - {p^{{r_n}}}({x_q})} \right|}}{{\left| {{p^{{r_{{S_m}}}}}({x_q})} \right|}} \in (30{\text{%}}} ,70{\text{%} ]} \\ & {{N_c} = {N_c} + 1,\begin{array}{*{20}{c}} {} \end{array}\dfrac{{\left| {{p^{{r_{{S_m}}}}}({x_q}) - {p^{{r_n}}}({x_q})} \right|}}{{\left| {{p^{{r_{{S_m}}}}}({x_q})} \right|}} \in (70{\text{%}}, + \infty )} \end{aligned}} \right. \\ \end{aligned} $$ (2) 根据式(2)得到Na、Nb和Nc,进而计算在因素fq影响下
$ {r_{{S_m}}} $ 和$ {r_n} $ 的联系数系数aq、bq和cq,因此$ {r_{{S_m}}} $ 和$ {r_n} $ 的联系度$ {\mu _{{f_q}}}({r_n} \to {r_{{S_m}}}) $ ,如式(3)所示:$$ \left\{\begin{aligned} &{\mu _{{f_q}}}({r_n} \to {r_{{S_m}}}) = {a_q} + {b_q}{i_q} + {c_q}{j_q} \\ &{a_q} = \dfrac{{{N_a}}}{{{N_a} + {N_b} + {N_c}}}\\ &{b_q} = \dfrac{{{N_b}}}{{{N_a} + {N_b} + {N_c}}} \\ &{c_q} = \dfrac{{{N_c}}}{{{N_a} + {N_b} + {N_c}}} \\ &{a_q} + {b_q} + {c_q} = 1\\ &{i_q} = \dfrac{{{a_q} - {c_q}}}{{{a_q} + {b_q} + {c_q}}}\\ &{j_q} = - 1 \end{aligned} \right. $$ (3) 可同理分析f1−Q的联系度
${\mu _{{f_{1{{ - }}Q}}}}({r_n} \to {r_{{S_m}}})$ 。因素
$ F = {\text{\{ }}{f_1}{\text{,}}{f_2}{\text{,}} \cdots {\text{,}}{f_Q}{\text{\} }} $ 的权重$ W = \{ {w_1},{w_2},...,{w_Q}\} $ 可采用层次分析法[34]或熵权法等确定,这里不作详述。当存在Q个因素时,属性角为360°/Q。在代表fq因素的Aq坐标上,考虑该因素的权重wq,同状态分量值$ L_q^a = {w_q}{a_q} $ ,异状态分量值$L_q^{ab} = $ $ {w_q}({a_q} + {b_q})$ ,反状态分量值$ L_q^{abc} = {w_q}({a_q} + {b_q} + {c_q}) $ 。从而求得各因素各状态分量值对应的坐标点$ (o_{xq}^a,o_{yq}^a) $ 、$ (o_{xq}^{ab},o_{yq}^{ab}) $ 和$ (o_{xq}^{abc},o_{yq}^{abc}) $ ,确定属性多边形的基本结构。上述过程如式(4)所示:$$ \left\{ \begin{split} &\angle {A_1}O{A_2} = \angle {A_2}O{A_3} = \cdots = \angle {A_Q}O{A_1} = 360^\circ /Q\\ &L_q^a = {w_q}{a_q}\\ &L_q^{ab} = {w_q}({a_q} + {b_q})\\ &L_q^{abc} = {w_q}({a_q} + {b_q} + {c_q}),\begin{array}{*{20}{c}} {} \end{array}q = 1,2, \cdots ,Q\\ &(o_{xq}^a,o_{yq}^a) = \left(\cos \left(\displaystyle\sum\limits_{k = 1}^q {{\alpha _k}} \right) \times L_q^a,\sin \left(\displaystyle\sum\limits_{k = 1}^q {{\alpha _k}} \right) \times L_q^a\right)\\ &(o_{xq}^{ab},o_{yq}^{ab}) = \left(\cos \left(\displaystyle\sum\limits_{k = 1}^q {{\alpha _k}} \right) \times L_q^{ab},\sin \left(\displaystyle\sum\limits_{k = 1}^q {{\alpha _k}} \right) \times L_q^{ab}\right)\\ &(o_{xq}^{abc},o_{yq}^{abc}) = \left(\cos \left(\displaystyle\sum\limits_{k = 1}^q {{\alpha _k}} \right) \times L_q^{abc},\sin \left(\displaystyle\sum\limits_{k = 1}^q {{\alpha _k}} \right) \times L_q^{abc}\right) \end{split} \right.$$ (4) 由图1所示,表示
$ {r_{{S_m}}} $ 和$ {r_n} $ 在因素F组成的属性多边形中,同状态分量面积为由坐标点$ (o_{xq}^a,o_{yq}^a) $ ,$ q=1,2,\cdots ,Q $ ,按照逆时针顺序构成的属性多边形面积表示,即$ {S^a}({r_n} \to {r_{{S_m}}}) $ ;异状态分量面积为由坐标点$ (o_{xq}^{ab},o_{yq}^{ab}) $ ,$ q=1,2,\cdots ,Q $ ,按照逆时针顺序构成的属性多边形面积与$ {S^a}({r_n} \to {r_{{S_m}}}) $ 的差表示,即$ {S^b}({r_n} \to {r_{{S_m}}}) $ ;反状态分量面积为由坐标点$ (o_{xq}^{abc},o_{yq}^{abc}) $ ,$ q=1,2,\cdots ,Q $ ,按照逆时针顺序构成的属性多边形面积与$ {S^b}({r_n} \to {r_{{S_m}}}) $ 的差表示,即$ {S^c}({r_n} \to {r_{{S_m}}}) $ ,可得同异反分量面积。确定联系度的关键是获得联系数中a、b和c参数值。由于使用了属性多边形,进而可用不同状态分量面积表示各参数,确定多因素的$ {r_{{S_m}}} $ 和$ {r_n} $ 联系度,如式(5)所示:$$ \left\{\begin{split} &{\mu _F}({r_n} \to {r_{{S_m}}}) = {a_F} + {b_F}{i_F} + {c_F}{j_F} \\ &{a_F} = \dfrac{{{S^a}({r_n} \to {r_{{S_m}}})}}{{{S^a}({r_n} \to {r_{{S_m}}}) + {S^b}({r_n} \to {r_{{S_m}}}) + {S^c}({r_n} \to {r_{{S_m}}})}} \\ &{b_F} = \dfrac{{{S^b}({r_n} \to {r_{{S_m}}})}}{{{S^a}({r_n} \to {r_{{S_m}}}) + {S^b}({r_n} \to {r_{{S_m}}}) + {S^c}({r_n} \to {r_{{S_m}}})}} \\ &{c_F} = \dfrac{{{S^c}({r_n} \to {r_{{S_m}}})}}{{{S^a}({r_n} \to {r_{{S_m}}}) + {S^b}({r_n} \to {r_{{S_m}}}) + {S^c}({r_n} \to {r_{{S_m}}})}} \\ &{a_F} + {b_F} + {c_F} = 1,{i_F} = \dfrac{{{a_F} - {c_F}}}{{{a_F} + {b_F} + {c_F}}},{j_F} = - 1 \\ \end{split} \right. $$ (5) 根据式(5)可获得
$ {r_n} $ ,$n\text{=1,2},\cdots \text{,}N$ ,对于$ {r_{{S_m}}} $ ,$m\text{=1,2},\cdots \text{,}M$ ,的隶属关系,基于最大联系度原则识别系统故障样本模式$ {r_n} $ ,如式(6)所示:$$\begin{array}{l} [n,m] = \{ (n,m)|{\text{Max}}\{ \mu _F^{}({r_n} \to {r_{{S_1}}}), \\ \mu _F^{}({r_n} \to {r_{{S_2}}}), \cdots ,\mu _F^{}({r_n} \to {r_{{S_M}}})\} ,m \in [1,M]\} \end{array} $$ (6) 进而对所有系统故障样本模式根据所有故障标准模式进行识别。
3. 实例分析
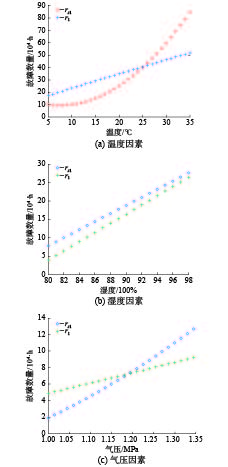
设影响某电器系统故障的主要因素F={f1=温度,f2=湿度,f3=气压}。系统运行环境:x1∈[5,35]℃,取样间隔为1 ℃;x2∈[80, 98]%,取样间隔为1%;x3∈[1.00,1.35]MPa,取样间隔为0.015 MPa。故障标准模式集合为
$ {R_S} = {\text{\{ }}{r_{{S_1}}}{\text{,}}{r_{{S_2}}}{\text{\} }} $ ,故障样本模式集合$ R = {\text{\{ }}{r_1}{\text{,}}{r_2}{\text{,}}{r_3}{\text{\} }} $ 。由专家直接确定各因素的权重W={w1=0.42,w2=0.32,w3=0.26}。识别R中样本模式与RS中标准模式的归属关系,详细给出r1与RS的识别过程,其余略。根据该系统故障数据获得各影响因素对于$ {r_{{S_1}}} $ 和$ {r_1} $ 的特征函数,如式(7)所示:$$ \left\{ {\begin{aligned} &{{f_1}:\left\{ {\begin{aligned} &{{P^{{r_{{S_1}}}}}({x_1}) = \frac{{{({x_1} - 4.9)}^2} - 5.03 \times ({x_1} - 5)}{10.1}+ 9.81} \\ &{{P^{{r_1}}}({x_1}) =\frac{ 9.91{x_1} + 6.78\sqrt {{x_1}}}{9.3 }+ 10.2} \end{aligned}} \right.} \\ &{{f_2}:\left\{ {\begin{aligned} &{{P^{{r_{{S_1}}}}}({x_2}) = 1.1{x_2} - 80.25}/{9.3} \\ &{{P^{{r_1}}}({x_2}) = 1.25{x_2} - 96.1} \end{aligned}} \right.} \\ &{{f_3}:\left\{ {\begin{aligned} &{{P^{{r_{{S_1}}}}}({x_3}) = 9.8{x_3}^{2.5} - 7.9} \\ &{{P^{{r_1}}}({x_3}) = 10.1{x_3}^{1.2} - 5.2} \end{aligned}} \right.} \end{aligned}} \right. $$ (7) 根据式(2)和式(7)统计得到各因素单独影响下
$ {r_{{S_1}}} $ 和$ {r_1} $ 的同异反状态数量如图2所示。从图2可知:
$ {r_{{S_1}}} $ 和$ {r_1} $ 的同异反状态数量,对于温度因素,Na=11、Nb=7、Nc=13;湿度,Na=15、Nb=4、Nc=0;气压,Na=16、Nb=4、Nc=4。根据式(3)和同异反状态数量得到各因素单独影响下$ {r_{{S_1}}} $ 和$ {r_1} $ 的联系度,如式(8)所示:$$ \left\{\begin{aligned} &{\mu _{{f_1}}}({r_1} \to {r_{{S_1}}}) = 0.35 + 0.23i + 0.42j \\ &{\mu _{{f_2}}}({r_1} \to {r_{{S_1}}}) = 0.79 + 0.21i + 0j \\ &{\mu _{{f_2}}}({r_1} \to {r_{{S_1}}}) = 0.66 + 0.17i + 0.17j \\ \end{aligned} \right. $$ (8) 各因素权重为W={w1=0.42,w2=0.32,w2=0.26}。根据式(4)确定属性多边形结构,如式(9)所示:
$$ \left\{ \begin{aligned} &\angle {A_1}O{A_2} = \angle {A_2}O{A_3} = \angle {A_3}O{A_1} = 360^\circ /3 = 120^\circ \\[-0.6pt] &L_1^a = 0.42 \times 0.35 = 0.147\\[-0.6pt] &L_1^{ab} = 0.42 \times (0.35 + 0.23) =0.244\\[-0.6pt] &L_1^{abc} = 0.42 \times (0.35 + 0.23 + 0.42) = 0.42\\[-0.6pt] &(o_{x1}^a,o_{y1}^a) = (0.147,0)\\[-0.6pt] &(o_{x1}^{ab},o_{y1}^{ab}) = (0.244,0)\\[-0.6pt] &(o_{x1}^{abc},o_{y1}^{abc}) = (0.42,0)\\[-0.6pt] &L_2^a = 0.32 \times 0.79 = 0.252 \\[-0.6pt] &L_2^{ab} = 0.32 \times (0.79 + 0.21)= 0.32\\[-0.6pt] &L_2^{abc} = 0.32 \times (0.79 + 0.21) = 0.32\\[-0.6pt] &(o_{x2}^a,o_{y2}^a) = ( - 0.126,0.218)\\[-0.6pt] &(o_{x2}^{ab},o_{y2}^{ab}) = ( - 0.16{\rm{,}}0.277\;1)\\[-0.6pt] &(o_{x2}^{abc},o_{y2}^{abc}) = ( - 0.16{\rm{,}}0.277\;1)\\[-0.6pt] &L_2^a = 0.26 \times 0.66 = 0.172\\[-0.6pt] &L_2^{ab} = 0.26 \times (0.66 + 0.17)= 0.216\\[-0.6pt] &L_2^{abc} = 0.26 \times 1 = 0.26\\[-0.6pt] &(o_{x2}^a,o_{y2}^a) =( - 0.086, - 0.149)\\[-0.6pt] &(o_{x2}^{ab},o_{y2}^{ab}) = ( - 0.108, - 0.187)\\[-0.6pt] &(o_{x2}^{abc},o_{y2}^{abc}) = ( - 0.13, - 0.225) \end{aligned} \right. $$ (9) 根据式(9)计算
$ {r_{{S_1}}} $ 和$ {r_1} $ 的同异反分量面积,如图3所示。结合图1对图3进行分析。图3中有3个嵌套的三角形,使用MATLAB计算它们的面积,由外向内分别为0.1414、0.0865和0.0457。三个三角形由内到外分割的区域依次代表同异反状态的面积区域,即分量面积。那么
$ {S^a}({r_1} \to {r_{{S_1}}}) $ =0.0457,$ {S^b}({r_1} \to {r_{{S_1}}}) $ =0.0865−0.0457=0.0408,$ {S^c}({r_1} \to {r_{{S_1}}}) $ =0.1414−0.0865=0.0549。根据式(5)确定多因素的$ {r_{{S_1}}} $ 和$ {r_1} $ 联系度,如式(10)所示:$$ \left\{\begin{aligned} &{a_F} = \frac{{0.045\;7}}{{0.141\;4}} = 0.323\\ &{b_F} = \frac{{0.040\;8}}{{0.141\;4}} = 0.289 \\ &{c_F} = \frac{{0.054\;9}}{{0.141\;4}} = 0.389 \\ &{i_F} = -0.066\\ &{j_F} = - 1 \\ &{\mu _F}({r_1} \to {r_{{S_1}}}) =0.323 + 0.289 \times (-0.066) + \\ &\quad\quad 0.389 \times ( - 1) = - 0.085 \\ \end{aligned} \right. $$ (10) 同理得到
${\mu _F}({r_1} \to {r_{{S_2}}})$ =0.0132。根据式(6)和${\mu _F}({r_1} \to {r_{{S_2}}})$ =0.0132及${\mu _F}({r_1} \to {r_{{S_1}}})$ =−0.085确定识别结果,如式(11)所示:$$\begin{array}{l} [1,m] = \{ (1,m)|{\text{Max}}\{ \mu _F^{}({r_1} \to {r_{{S_1}}}) = - 0.085, \\ \quad \quad\quad\mu _F^{}({r_1} \to {r_{{S_2}}}) = 0.013\;2\} \} \\ \end{array} $$ (11) 由式(11)可知,m=2,因此
$ {r_1} $ 被识别为$ {r_{{S_2}}} $ ,即$ {r_1} $ 与$ {r_{{S_2}}} $ 的符合性更高。其余故障样本模式识别过程同理,这里不再给出。本文所提方法使用了两次联系数,第一次表示识别过程的确定性和不确定性,第二次表示两种模式的联系度,进而选择最大联系度确定识别结果。基于空间故障树的特征函数表示故障数据变化,进而确定第一次联系数的各参数值。基于属性圆提出属性多边形用于描述因素共同作用的两模式同异反分量之间的关系。将不同因素的相同分量组成多边形,并计算多边形面积从而确定第二次联系数的各参数数值。研究是集对分析联系数和空间故障树的特征函数及属性多边形的综合应用,为系统故障模式的识别提供有效方法。
4. 结束语
本文利用集对分析的联系数和空间故障树的特征函数及属性多边形对系统故障样本模式进行识别。主要结论如下:
1)介绍了集对分析联系数与空间故障网络相结合的可能性,同时重点论述了属性多边形的构造方法和基本性质。
2)构建了多因素影响下的故障模式识别方法。根据系统故障背景建立故障模式识别系统,构造特征函数;统计各因素单独影响下两模式的同异反状态数量;计算单因素的故障模式联系度;确定因素权重;确定属性多边形结构;计算同异反分量面积;计算多因素的故障模式联系度;识别系统故障样本模式。分析过程可总结为两次联系度的计算:第一次为确定单因素下的故障模式联系度,利用特征函数表示故障数据进而计算联系数系数;第二次确定多因素联合影响的故障模式联系度,利用属性多边形的同异反分量面积计算联系数系数。最终确定适合的联系度进行识别。
3)以用简单的电气系统为例对方法流程进行说明。实施了两阶段的联系数计算。通过详细的计算过程得到了系统故障样本模式与故障标准模式的关联程度,最终根据最大联系度原则对故障样本模式进行了识别。
-
-
[1] 陈志刚, 杜小磊, 张楠, 等. IEWT-CS和LCNN在轴承故障诊断中的应用[J]. 哈尔滨工程大学学报, 2020, 41(3): 463–472. CHEN Zhigang, DU Xiaolei, ZHANG Nan, et al. Application of IEWT-CS and LCNN in bearing fault diagnosis[J]. Journal of Harbin Engineering University, 2020, 41(3): 463–472. [2] 周超, 曹春平, 孙宇. 利用GS优化SM-SVM的滚动轴承故障诊断方法研究[J]. 机械设计与制造, 2020(6): 16–19. doi: 10.3969/j.issn.1001-3997.2020.06.005 ZHOU Chao, CAO Chunping, SUN Yu. Research on rolling bearing fault diagnosis method based on GS optimized SM-SVM[J]. Machinery design and manufacture, 2020(6): 16–19. doi: 10.3969/j.issn.1001-3997.2020.06.005 [3] 罗佳, 黄晋英. 基于小波包和神经网络的行星齿轮箱故障模式识别技术[J]. 火力与指挥控制, 2020, 45(4): 178–182. doi: 10.3969/j.issn.1002-0640.2020.04.033 LUO Jia, HUANG Jinying. Fault diagnosis recognition technique of planetary gearbox based on wavelet packet and neural network[J]. Fire control & command control, 2020, 45(4): 178–182. doi: 10.3969/j.issn.1002-0640.2020.04.033 [4] 史泽兵, 丁晓兵, 余江, 等. 基于功角聚类分析的配电网选线保护方法[J]. 电力科学与技术学报, 2020, 35(3): 29–35. SHI Zebing, DING Xiaobing, YU Jiang, et al. A method of line selection protection based on power angle fuzzy clustering analysis[J]. Journal of electric power science and technology, 2020, 35(3): 29–35. [5] 王育炜, 韩秋实, 王红军, 等. 滚动轴承VMD能量熵与PNN故障模式识别研究[J]. 组合机床与自动化加工技术, 2020(4): 47–50. WANG Yuwei, HAN Qiushi, WANG Hongjun, et al. Research on VMD energy entropy and PNN fault pattern recognition of rolling bearings[J]. Modular machine tool & automatic manufacturing technique, 2020(4): 47–50. [6] 魏国东, 朱石坚, 罗忠, 等. 基于数据挖掘的装备维修性定量分析与研究[J]. 海军工程大学学报, 2020, 32(2): 87–91. doi: 10.7495/j.issn.1009-3486.2020.02.015 WEI Guodong, ZHU Shijian, LUO Zhong, et al. Quantitative analysis and research of equipment maintainability based on data mining[J]. Journal of naval university of engineering, 2020, 32(2): 87–91. doi: 10.7495/j.issn.1009-3486.2020.02.015 [7] 曹文思, 吴擎, 徐铭铭, 等. 基于分形理论与聚类分析的小电阻接地系统高阻接地保护方法[J]. 电力自动化设备, 2020, 40(4): 204–209,224. CAO Wensi, WU Qing, XU Mingming, et al. Protection method based on fractal theory and cluster analysis for grounding fault with high resistance of low resistance grounding system[J]. Electric power automation equipment, 2020, 40(4): 204–209,224. [8] 江剑峰, 张垠, 田书欣, 等. 基于云理论的智能电能表故障数据分析[J]. 电力科学与技术学报, 2020, 35(2): 163–169. JIANG Jianfeng, ZHANG Yin, TIAN Shuxin, et al. Fault data analysis of smart electricity meter based cloud theory[J]. Journal of electric power science and technology, 2020, 35(2): 163–169. [9] 张安安, 黄晋英, 冀树伟, 等. 基于卷积神经网络图像分类的轴承故障模式识别[J]. 振动与冲击, 2020, 39(4): 165–171. ZHANG An’an, HUANG Jinying, JI Shuwei, et al. Bearing fault pattern recognition based on image classification with CNN[J]. Journal of vibration and shock, 2020, 39(4): 165–171. [10] 朱建新, 陈学东, 吕宝林, 等. 基于多维高斯贝叶斯的机械设备失效/故障智能诊断及参数影响分析[J]. 机械工程学报, 2020, 56(4): 35–41. doi: 10.3901/JME.2020.04.035 ZHU Jianxin, CHEN Xuedong, LYU Baolin, et al. Smart failure/fault diagnosis and influence analysis for mechanical equipment with multivariate gaussian bayesian method[J]. Journal of mechanical engineering, 2020, 56(4): 35–41. doi: 10.3901/JME.2020.04.035 [11] 程月华, 江文建, 杨浩, 等. 基于深度森林的卫星ACS执行机构与传感器故障识别[J]. 航空学报, 2020, 41(S1): 195–205. CHENG Yuehua, JIANG Wenjian, YANG Hao, et al. Fault identification of actuators and sensors of satellite attitude control systems based on deep forest algorithm[J]. Acta aeronautica et astronautica sinica, 2020, 41(S1): 195–205. [12] 邓林峰, 张爱华, 赵荣珍. 集成多策略改进FCM算法的旋转机械故障数据聚类分析研究[J]. 振动工程学报, 2019, 32(5): 918–926. DENG Linfeng, ZHANG Aihua, ZHAO Rongzhen. Clustering analysis of rotating machine fault data based on improved fuzzy C-means algorithm with integrated multi-strategy[J]. Journal of vibration engineering, 2019, 32(5): 918–926. [13] 张鹏林, 徐桃萍, 马小东, 等. 基于CEEMDAN-深度信念网络的超低速滚动轴承故障诊断[J]. 组合机床与自动化加工技术, 2019(9): 77–80,84. ZHANG Penglin, XU Taoping, MA Xiaodong, et al. Ultra low speed rolling bearing faults based on CEEMDAN -deep belief network[J]. Modular machine tool & automatic manufacturing technique, 2019(9): 77–80,84. [14] 蒋云良, 赵克勤. 人工智能集对分析[M]. 北京: 科学出版社, 2003. [15] 赵克勤. 集对分析对不确定性的描述和处理[J]. 信息与控制, 1995, 24(3): 162–166. ZHAO Keqin. Disposal and description of uncertainties based on the set pair analysis[J]. Information and control, 1995, 24(3): 162–166. [16] 赵森烽, 赵克勤. 几何概型的联系概率(复概率)与概率的补数定理[J]. 智能系统学报, 2013, 8(1): 11–15. doi: 10.3969/j.issn.1673-4785.201208025 ZHAO Senfeng, ZHAO Keqin. Contact probability (complex probability) of the geometry probability and the complement number theorem of probability[J]. CAAI transactions on intelligent systems, 2013, 8(1): 11–15. doi: 10.3969/j.issn.1673-4785.201208025 [17] 赵森烽, 赵克勤. 概率联系数化的原理及其在概率推理中的应用[J]. 智能系统学报, 2012, 7(3): 200–205. doi: 10.3969/j.issn.1673-4785.201112014 ZHAO Senfeng, ZHAO Keqin. The principle of a connection number in probability and its application in probabilistic reasoning[J]. CAAI transactions on intelligent systems, 2012, 7(3): 200–205. doi: 10.3969/j.issn.1673-4785.201112014 [18] 赵克勤. 集对分析与熵的研究[J]. 浙江大学学报, 1992, 6(2): 68–75. ZHAO Keqin. Set pair analysis and entropy[J]. Journal of Zhejiang University, 1992, 6(2): 68–75. [19] 崔铁军, 马云东. 多维空间故障树构建及应用研究[J]. 中国安全科学学报, 2013, 23(4): 32–37,62. CUI Tiejun, MA Yundong. Research on multi-dimensional space fault tree construction and application[J]. China safety science journal, 2013, 23(4): 32–37,62. [20] 崔铁军, 马云东. 基于因素空间的煤矿安全情况区分方法的研究[J]. 系统工程理论与实践, 2015, 35(11): 2891–2897. doi: 10.12011/1000-6788(2015)11-2891 CUI Tiejun, MA Yundong. Research on the classification method about coal mine safety situation based on the factor space[J]. Systems engineering-theory and practice, 2015, 35(11): 2891–2897. doi: 10.12011/1000-6788(2015)11-2891 [21] 李莎莎, 崔铁军, 马云东. 基于云模型的变因素影响下系统可靠性模糊评价方法[J]. 中国安全科学学报, 2016, 26(2): 132–138. LI Shasha, CUI Tiejun, MA Yundong. Research on method for evaluating fuzzily reliability of variable factors influenced system based on cloud model[J]. China safety science journal, 2016, 26(2): 132–138. [22] 崔铁军, 李莎莎, 王来贵. 完备与不完备背景关系中蕴含的系统功能结构分析[J]. 计算机科学, 2017, 44(3): 268–273,306. doi: 10.11896/j.issn.1002-137X.2017.03.055 CUI Tiejun, LI Shasha, WANG Laigui. System function structure analysis in complete and incomplete background relationship[J]. Computer science, 2017, 44(3): 268–273,306. doi: 10.11896/j.issn.1002-137X.2017.03.055 [23] 崔铁军. 系统故障演化过程描述方法研究[J]. 计算机应用研究, 2020, 37(10): 3006–3009. CUI Tiejun. Research on description method of system fault evolution process[J]. Application research of computers, 2020, 37(10): 3006–3009. [24] CUI Tiejun, LI Shasha. Research on complex structures in space fault network for fault data mining in system fault evolution process[J]. IEEE access, 2019, 7: 121881–121896. doi: 10.1109/ACCESS.2019.2937641 [25] 崔铁军, 李莎莎. 空间故障树与空间故障网络理论综述[J]. 安全与环境学报, 2019, 19(2): 399–405. CUI Tiejun, LI Shasha. Revision of the space fault tree and the space fault network system[J]. Journal of safety and environment, 2019, 19(2): 399–405. [26] 崔铁军, 李莎莎, 朱宝艳. 含有单向环的多向环网络结构及其故障概率计算[J]. 中国安全科学学报, 2018, 28(7): 19–24. CUI Tiejun, LI Shasha, ZHU Baoyan. Multidirectional ring network structure with one-way ring and its fault probability calculation[J]. China safety science journal, 2018, 28(7): 19–24. [27] 崔铁军, 李莎莎. 少故障数据条件下SFEP最终事件发生概率分布确定方法[J]. 智能系统学报, 2020, 15(1): 136–143. CUI Tiejun, LI Shasha. Determination method of target event occurrence probability in SFEP under the condition of less fault data[J]. CAAI transactions on intelligent systems, 2020, 15(1): 136–143. [28] 崔铁军, 李莎莎. 系统运动空间与系统映射论的初步探讨[J]. 智能系统学报, 2020, 15(3): 445–451. CUI Tiejun, LI Shasha. Preliminary study of system movement space and system mapping theory[J]. CAAI transactions on intelligent Systems, 2020, 15(3): 445–451. [29] 崔铁军, 马云东. 因素空间的属性圆定义及其在对象分类中的应用[J]. 计算机工程与科学, 2015, 37(11): 2169–2174. doi: 10.3969/j.issn.1007-130X.2015.11.026 CUI Tiejun, MA Yundong. Definition of attribute circle in factor space and its application in object classification[J]. Computer engineering and science, 2015, 37(11): 2169–2174. doi: 10.3969/j.issn.1007-130X.2015.11.026 [30] 崔铁军, 马云东. 基于因素空间中属性圆对象分类的相似度研究及应用[J]. 模糊系统与数学, 2015, 29(6): 56–63. CUI Tiejun, MA Yundong. Research on the similarity of object classification of attribute circular and application based on factors space[J]. Fuzzy systems and mathematics, 2015, 29(6): 56–63. [31] 崔铁军, 马云东. DSFT中因素投影拟合法的不精确原因分析[J]. 系统工程理论与实践, 2016, 36(5): 1340–1345. doi: 10.12011/1000-6788(2016)05-1340-06 CUI Tiejun, MA Yundong. Inaccurate reason analysis of the factors projection fitting method in DSFT[J]. Systems engineering-theory and practice, 2016, 36(5): 1340–1345. doi: 10.12011/1000-6788(2016)05-1340-06 [32] 崔铁军, 马云东. DSFT下模糊结构元特征函数构建及结构元化的意义[J]. 模糊系统与数学, 2016, 30(2): 144–151. CUI Tiejun, MA Yundong. The construction of fuzzy structured element characteristic function and the significance of structure elemented in DSFT[J]. Fuzzy systems and mathematics, 2016, 30(2): 144–151. [33] 张启明, 董国胜. 综合预报中各手段权重的层次分析确定法[J]. 地震, 1993(5): 62–67. ZHANG Qiming, DONG Guosheng. Deriving weight of various means in comprehensive prediction by layer analysis method[J]. Earthquake, 1993(5): 62–67. [34] 程启月. 评测指标权重确定的结构熵权法[J]. 系统工程理论与实践, 2010, 30(7): 1225–1228. doi: 10.12011/1000-6788(2010)7-1225 CHENG Qiyue. Structure entropy weight method to confirm the weight of evaluating index[J]. Systems engineering-theory and practice, 2010, 30(7): 1225–1228. doi: 10.12011/1000-6788(2010)7-1225


 下载:
下载: