System fault-pattern recognition based on set pair analysis with multiple factors
-
摘要: 为研究多因素影响下系统故障模式识别，根据已有故障标准模式对故障样本模式进行分析，提出基于集对分析联系数和故障分布的系统故障模式识别新方法。根据故障背景建立故障模式识别系统，分析故障样本模式与故障标准模式，确定联系度各联系分量，计算联系度和识别度，最后通过确定故障样本模式与故障标准模式关系完成识别。对某电气系统实例分析给出了方法流程，获得了模式识别结果，从而为有针对性的采取预防和治理措施提供了决策支持。Abstract: To study system fault-pattern recognition under the influence of multiple factors, a sample fault pattern was analyzed according to the existing standard fault patterns. A system fault-pattern recognition method based on the set pair analysis connection number and fault distribution is proposed. On the basis of the fault data, we developed the fault-pattern recognition system, analyzed the fault sample and standard fault patterns, determined the relating components and their connection degrees, and calculated the connection and recognition degrees. Finally, the relationship between fault sample and standard fault patterns was determined to complete the identification. An example based on an electrical system analysis showed the process of the method by achieving efficient pattern recognition and proving its effectiveness. This study provides targeted decision-making support for taking preventive and governance measures.
-
故障模式识别是安全科学领域，特别是安全系统工程领域研究的重点内容之一。目前各行各业的安全都以预防为主，而预防的前提是了解系统、影响系统安全的因素、以及系统本身的结构等[1]。这些研究的结果是为预防故障而提供的系统基本情况，因此预防才是所有前期工作的核心。对各种系统制定的安全检查制度和应急预案都是保障系统安全的具体形式。显然在人力、财力和物力有限的情况下这些预案不可能是无限的。因此实际情况必将是针对重点系统故障采取对应的措施，但同时也面临另一问题，即系统在故障状态下表现出来的特征具有多样性。即使两个故障原因大体相同，也有可能由于自然因素或是人关心的方面不同导致表现出的现象不同。那么如何将具有多样性的系统故障样本模式归类为已知的有限的已具有预防治理措施的系统故障标准模式，成为在多因素情况下系统故障识别的关键。
系统故障模式识别是智能科学和安全科学的重点研究领域之一。这些研究包括：中压直流系统故障识别方法研究[2]，机器学习的风电机组变桨系统故障分析[3]，船舶动力装置智能故障诊断技术[4]，频图纹理特征的供输弹系统故障诊断[5]，混合多端直流输电系统故障识别[6]，分布式光纤扰动传感系统故障模式识别[7]，电力系统故障全信息诊断模型研究[8]，光纤通信系统故障诊断[9]，参数缺失时的核动力系统故障诊断[10]，齿轮传动系统故障诊断技术[11]，复杂网络聚类的提升机主轴系统故障诊断[12]等。这些研究在各自领域具有良好的效果，但这些前人的工作也存在一些不足。这些不足可总结为三点：1)系统故障可能受到很多因素影响，而且各故障的影响因素可能是相关甚至相同的。所以这些故障具有内在的相关性，传统方法难以区分。2)影响因素的分析同样难以得到单因素与系统故障的影响关系。相对的，一般可得到几个重点因素联合对故障的影响关系。因此这些数据的有效利用成为关键，而不纠结于必须获得单因素影响关系。3)系统故障本身是难以确定的，影响因素和系统故障的对应关系具有确定性和不确定性共存的特点，该特点通过已有方法仍难以表示。
为解决上述问题，基于集对分析的联系数和空间故障树的故障分布建立系统故障模式识别方法。方法将导致系统故障的直接原因和基本背景因素分开，利用故障分布表示多因素联合影响的系统故障特征，利用集对分析联系数表示故障发生的确定性和不确定性叠加。最后通过一实例说明了分析过程，并给出了方法的优点。
1. 集对分析基本原理
集对分析理论是赵克勤教授在1989年提出的研究系统确定性和不确定性的数学理论，其基础是联系数学的联系数[13]。目前该理论已经用于多个领域，但仍在发展之中[14-17]。
集对分析的核心是联系数，联系数包括二元联系数直到多元联系数。二元联系数可表示为
$$\mu = a + bi $$ 式中：a为确定性分量；b为不确定性分量；i为不确定性系数。其表达了任何系统故障都可表示为确定与不确定的叠加。三元联系数μ=a+bi+cj，这时a仍然是确定性分量，表示同类的概念；b是不确定性分量，表示异类的概念；c是确定性分量，表示反类的概念。即根据定义可将集合中的对象分为同类、异类和反类3种情况。对多元联系数，确定性分量是恒定存在的，而不确定分量“异”可进一步划分。例如在系统安全分析中，“同”代表系统安全，“反”代表系统不安全，而“异”代表良、中、差等级别。因此联系数代表在已有定义下系统安全状态的同异反特征，同和反为确定，异为不确定。
2. 集对分析与空间故障树的耦合
系统故障包括很多，一般是直接的，例如实例中给出的电气系统漏电和短路故障。实例中漏电与温度和湿度有关，而短路与温度、湿度和气压等有关。这说明系统的直接故障与更为基础的背景因素相关。因此至少要对影响系统故障的因素进行两层次划分。一是直接故障，定义为直接因素；二是基础的环境背景因素，定义为背景因素。
确定单一背景因素与直接因素的关系显然是困难的。一般在实际或是实验中取得的数据都是多因素耦合作用的结果。所以使用该结果的分析更为合理，可通过空间故障树理论实现。该理论包括4部分，空间故障树理论基础[1]、智能化空间故障树[18-20]、空间故障网络[21-25]、系统运动空间与系统映射论[26]。主要研究的问题是系统可靠性与影响因素关系，及系统故障演化过程的内在机制。理论中多个影响因素与系统故障概率组成了多维空间，具体的数据组成了空间曲面，即故障概率分布。为解决多因素耦合作用的表示问题，可同样利用该思路将各因素条件影响下的系统故障数量组成故障空间分布，简称故障分布。但在此之前得到的不同因素时的系统故障数量可能是不完整的，存在冗余或遗漏。因此可对这些数据在故障空间内进行拟合得到故障分布曲面，以方便故障识别方法使用。
综上，将集对分析的联系数和空间故障树的故障分布结合使用可有效地对系统故障样本模式进行识别。
3. 故障模式识别方法构建
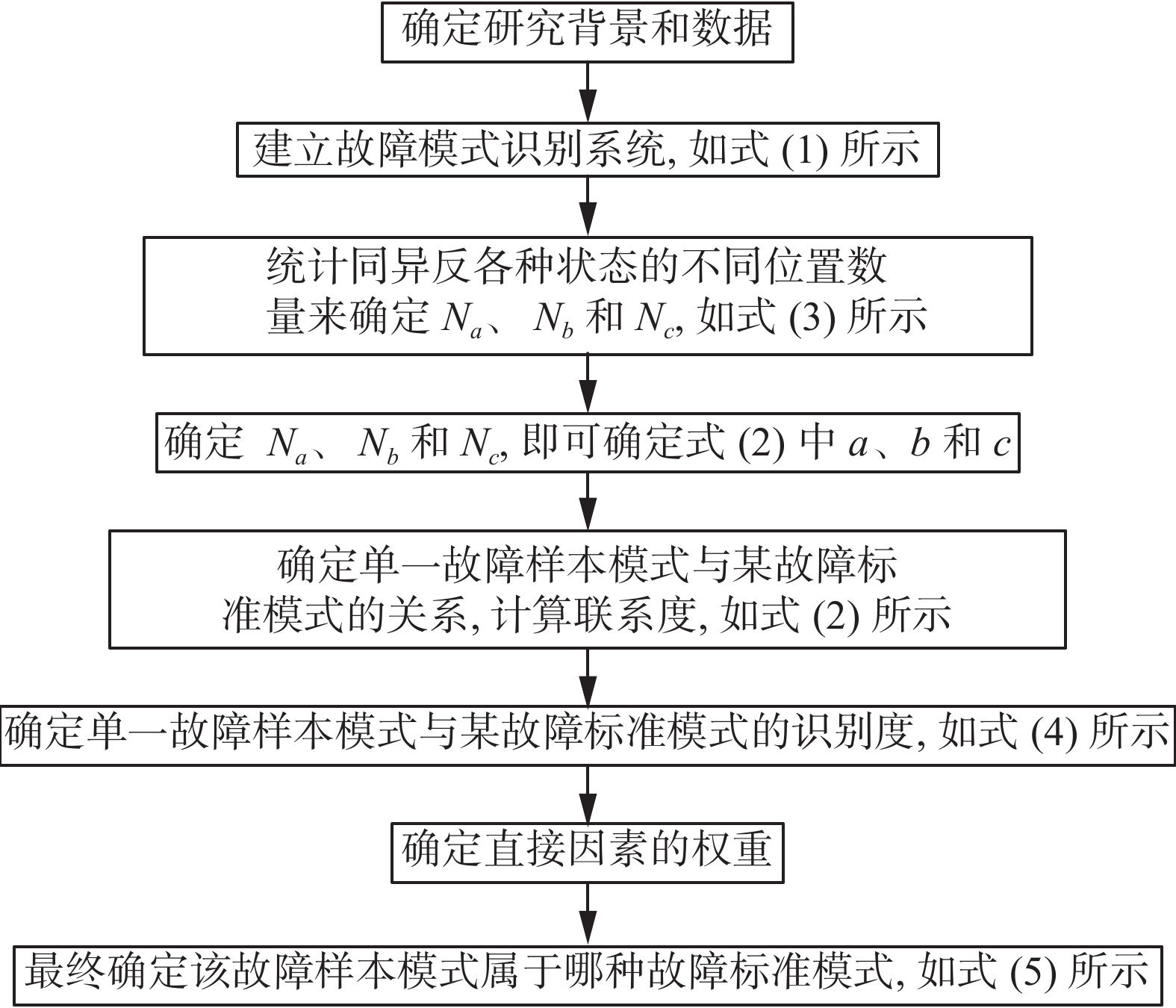
故障模式识别系统的建立是基于集对分析的联系数和空间故障树的故障分布。设故障模式识别系统如式(1)所示。
$$\left\{\begin{array}{l} T = \{{R_S},R,F,X,W\} \\ {R_S} = \{{r_{{S_1}}},{r_{{S_2}}}, \cdots ,{r_{{S_M}}}\} ,m = 1,2, \cdots ,M \\ R = \{{r_1},{r_2}, \cdots ,{r_N}\} ,n = 1,2, \cdots ,N \\ F = \{{f_1},{f_2}, \cdots ,{f_Q}\} ,q = 1,2, \cdots ,Q \\ X = \{{x_1},{x_2}, \cdots ,{x_L}\} ,l = 1, 2,\cdots ,L;{X^{'}},{X^{''}}, \cdots ,{X^{(Q)}} \subseteq X \\ W = \{{w_1},{w_2}, \cdots ,{w_Q}\} \end{array} \right.$$ (1) 式中：
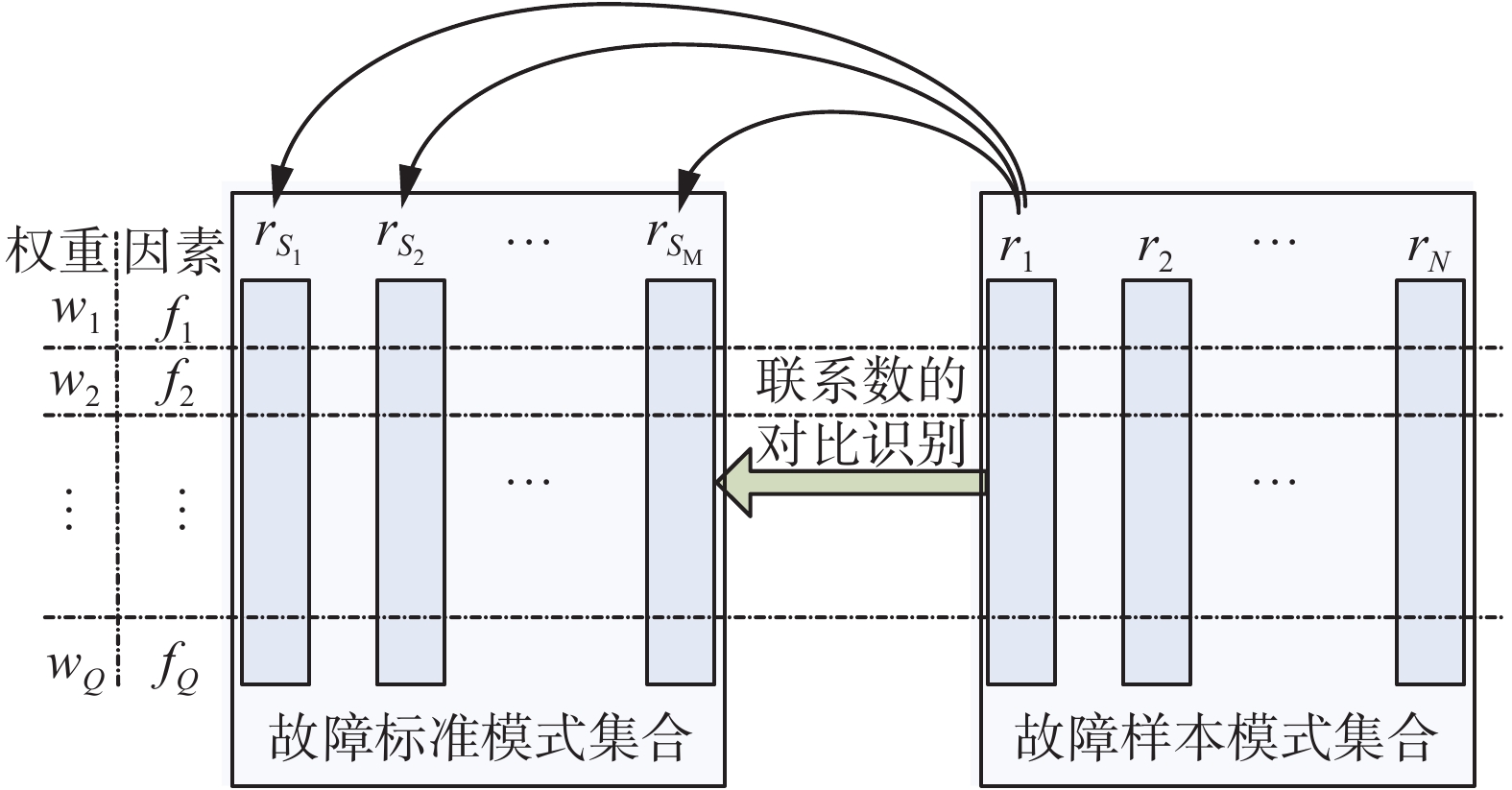
${R_S}$ 为故障标准模式集合；M为标准模式数；$R$ 为故障样本模式集合；N为样本模式数；F为直接因素(可理解为指标)；Q为直接因素数量；X为背景因素集合；L为背景因素数量；${X^{'}},{X^{''}}, \cdots ,{X^{(Q)}}$ 为某直接因素相关的背景因素集合，${X^{'}},{X^{''}}, \cdots , $ $ {X^{(Q)}}$ $ \subseteq $ X，当其作为参数时表示因素集合的各因素具体数值；W为直接因素的权重集合。图1给出了依据故障标准模式识别故障样本模式的方法，具体给出识别的过程。
图 1 故障模式识别过程Fig. 1 Fault pattern recognition process
下载:
全尺寸图片
首先分析单一故障样本模式
${r_n}$ 与某故障标准模式${r_{{S_m}}}$ 的关系。过程中，只考虑单一直接因素${f_q}$ ，与其相关的背景因素集合为${X^{(q)}}$ 。那么${r_n}$ 与${r_{{S_m}}}$ 的联系度$\mu _{{f_q}}^{{X^{(q)}}}({r_n} \to {r_{{S_m}}})$ 表示为$$\left\{\begin{array}{l} \mu _{{f_q}}^{{X^{(q)}}}({r_n} \to {r_{{S_m}}}) = a + bi + cj \\ a = \dfrac{{{N_a}}}{{{N_a} + {N_b} + {N_c}}},b = \dfrac{{{N_b}}}{{{N_a} + {N_b} + {N_c}}},c = \dfrac{{{N_c}}}{{{N_a} + {N_b} + {N_c}}} \\ a + b + c = 1,i = \dfrac{{a - c}}{{a + b + c}},j = - 1 \end{array} \right.$$ (2) 式(2)展示了使用联系数(
$a + bi + cj$ )计算联系度($\mu _{{f_q}}^{{X^{(q)}}}({r_n} \to {r_{{S_m}}})$ )的方法。联系数是集对分析中的重要概念，是联系度概念具体化的方式，这里使用三元联系数表达${r_n}$ 与${r_{{S_m}}}$ 的同异反关系[13]。联系度越大，说明${r_n}$ 与${r_{{S_m}}}$ 越一致。采用相似比法确定i和j的具体数值[13]。研究的联系度使用联系数表示。其次确定式(2)中的Na、Nb和Nc，它们是统计得到的数量，是在背景因素构建的故障空间中，
${r_n}$ 与${r_{{S_m}}}$ 对应${X^{(q)}}$ 状态下取值的距离统计。由于假设${r_n}$ 与${r_{{S_m}}}$ 关于fq(${X^{(q)}}$ 的故障空间)是变化的，所以当考虑${r_n}$ 与${r_{{S_m}}}$ 的同异反状态时，通过${r_n}$ 与${r_{{S_m}}}$ 在故障空间不同位置的对应值的距离进行同异反分析。根据不同位置得到的${r_n}$ 与${r_{{S_m}}}$ 相对距离划分同异反状态，进而统计每种状态的不同位置数量来确定Na、Nb和Nc。这里设距离在[0,30%]为同状态，(30%,70%]为异状态。(70%,+∞)为反状态。因此Na、Nb和Nc的确定如式(3)所示。$$\begin{array}{l} \quad\quad\quad\quad\quad\quad\quad [{N_a},{N_b},{N_c}] = \\ \left\{\begin{array}{l} {N_a} = {N_a} + 1,\dfrac{{|v_{{f_q}}^{{r_{{S_m}}}}({X^{(q)}}) - v_{{f_q}}^{{r_n}}({X^{(q)}})|}}{{|v_{{f_q}}^{{r_{{S_m}}}}({X^{(q)}})|}} \in [0,30\% ] \\ {N_b} = {N_b} + 1,\dfrac{{|v_{{f_q}}^{{r_{{S_m}}}}({X^{(q)}}) - v_{{f_q}}^{{r_n}}({X^{(q)}})|}}{{|v_{{f_q}}^{{r_{{S_m}}}}({X^{(q)}})|}} \in (30\% ,70\% ] \\ {N_c} = {N_c} + 1,\dfrac{{|v_{{f_q}}^{{r_{{S_m}}}}({X^{(q)}}) - v_{{f_q}}^{{r_n}}({X^{(q)}})|}}{{|v_{{f_q}}^{{r_{{S_m}}}}({X^{(q)}})|}} \in (70\% , + \infty ] \\ \bigcup {v_{{f_q}}^{{r_{{S_m}}}}({X^{(q)}})} = V_{{f_q}}^{{r_{{S_m}}}}({X^{(q)}}),\bigcup {v_{{f_q}}^{{r_n}}({X^{(q)}})} = V_{{f_q}}^{{r_n}}({X^{(q)}}) \end{array} \right. \end{array} $$ (3) 式中：
$V_{{f_q}}^{{r_{{S_m}}}}({X^{(q)}})$ 表示${r_{{S_m}}}$ 在${X^{(q)}}$ 内的所有背景因素值排列组合时对应fq值的集合$v_{{f_q}}^{{r_{{S_m}}}}({X^{(q)}})$ 表示该集合中任意一个元素，所有的$v_{{f_q}}^{{r_{{S_m}}}}({X^{(q)}})$ 组成$V_{{f_q}}^{{r_{{S_m}}}}({X^{(q)}})$ 。$V_{{f_q}}^{{r_n}}({X^{(q)}})$ 和$v_{{f_q}}^{{r_n}}({X^{(q)}})$ 的关系同上。确定Na、Nb和Nc即可确定式(2)中a、b和c，从而确定
$\mu _{{f_q}}^{{X^{(q)}}}({r_n} \to {r_{{S_m}}})$ 。因此可同理分析f1-Q的联系度$\mu _{{f_{1\sim Q}}}^{{X^{(q)}}}({r_n} \to {r_{{S_m}}})$ 。进一步确定在X内，
${r_n}$ 与${r_{{S_m}}}$ 的识别度，则需要判断F内各直接因素的权重。因素$F = {\rm{\{}}{f_1}{\rm{,}} $ $ {f_2}{\rm{,}} \cdots {\rm{,}}{f_Q}{\rm{\} }}$ 的权重确定不是重点，可采用专家法或熵权法等确定，这里不做详述，进而确定权重$W = $ $ \{{w_1},{w_2}, \cdots ,{w_Q}\} $ 。那么X内${r_n}$ 与${r_{{S_m}}}$ 的识别度为$$\begin{array}{c} S_F^X({r_n} \to {r_{{S_m}}}) = {[{w_1}\;{w_2}\; \cdots \;{w_Q}]^{\rm{T}}} \times \left[\mu _{{f_1}}^{X'}({r_n} \to {r_{{S_m}}}) \right.\\ \left.\mu _{{f_2}}^{X''}({r_n} \to {r_{{S_m}}})\; \cdots \;\mu _{{f_Q}}^{{X^{(Q)}}}({r_n} \to {r_{{S_m}}})\right] \end{array} $$ (4) 通过式(4)即可得到在背景因素X(直接因素F)组成的故障空间中，各故障标准模式
${r_{{S_{1\sim M}}}}$ 和各故障样本模式${r_{1\sim N}}$ 的分别识别度。识别度越大，证明该识别的对应关系越正确。最终对某一故障样本模式${r_n}$ 属于哪种故障标准模式${r_{{S_{1\sim M}}}}$ 可由式(5)确定：$$\begin{array}{c} [n,m] = \left\{(n,m)|{\rm{MAX}}\left\{S_F^X({r_n} \to {r_{{S_1}}}),S_F^X({r_n} \to {r_{{S_2}}}) ,\right.\right.\\ \left. \left. \cdots ,S_F^X({r_n} \to {r_{{S_M}}})\right\} ,m \in [1,M]\right\} \end{array} $$ (5) 由式(5)可得到
${r_{1\sim N}}$ 隶属于哪种故障标准模式，从而达到多因素影响下不同故障样本模式的识别。4. 实例分析
举一个简单例子说明方法的计算过程，以免复杂例子的结构对方法理解造成影响。设一电气系统，主要关注的直接因素为F={f1=漏电，f2=断路}；其背景因素为X={x1=温度，x2=湿度，x3=气压}；
$X' $ (f1)={x1, x2}，$X'' $ (f2)={x1, x2, x3}；x1∈[0,30]℃，取样间隔为1 ℃；x2∈[80,95]%，取样间隔为1%；x3∈[1.05,1.35]MPa，取样间隔为0.05 MPa；${R_S} = $ $ {\rm{\{}}{r_{{S_1}}}{\rm{,}}{r_{{S_2}}}{\rm{\} }}$ ，M=2，故障标准模式为2个；$R = {\rm{\{}}{r_1}{\rm{,}}{r_2}{\rm{,}}{r_3}{\rm{\} }}$ ，N=3，故障样本模式为3个。由于这里主要论述联系度及识别度的确定方法，而直接因素F导致系统故障的权重W不是重点，因此只通过专家确定简单的权重，W={w1=0.63,w2=0.37}。最终建立故障模式识别系统T，如下进行故障模式识别。目的是得到R中样本模式与RS中标准模式的归属关系。由于过程复杂，这里只详细给出r1与RS的识别度确定过程。首先计算r1与
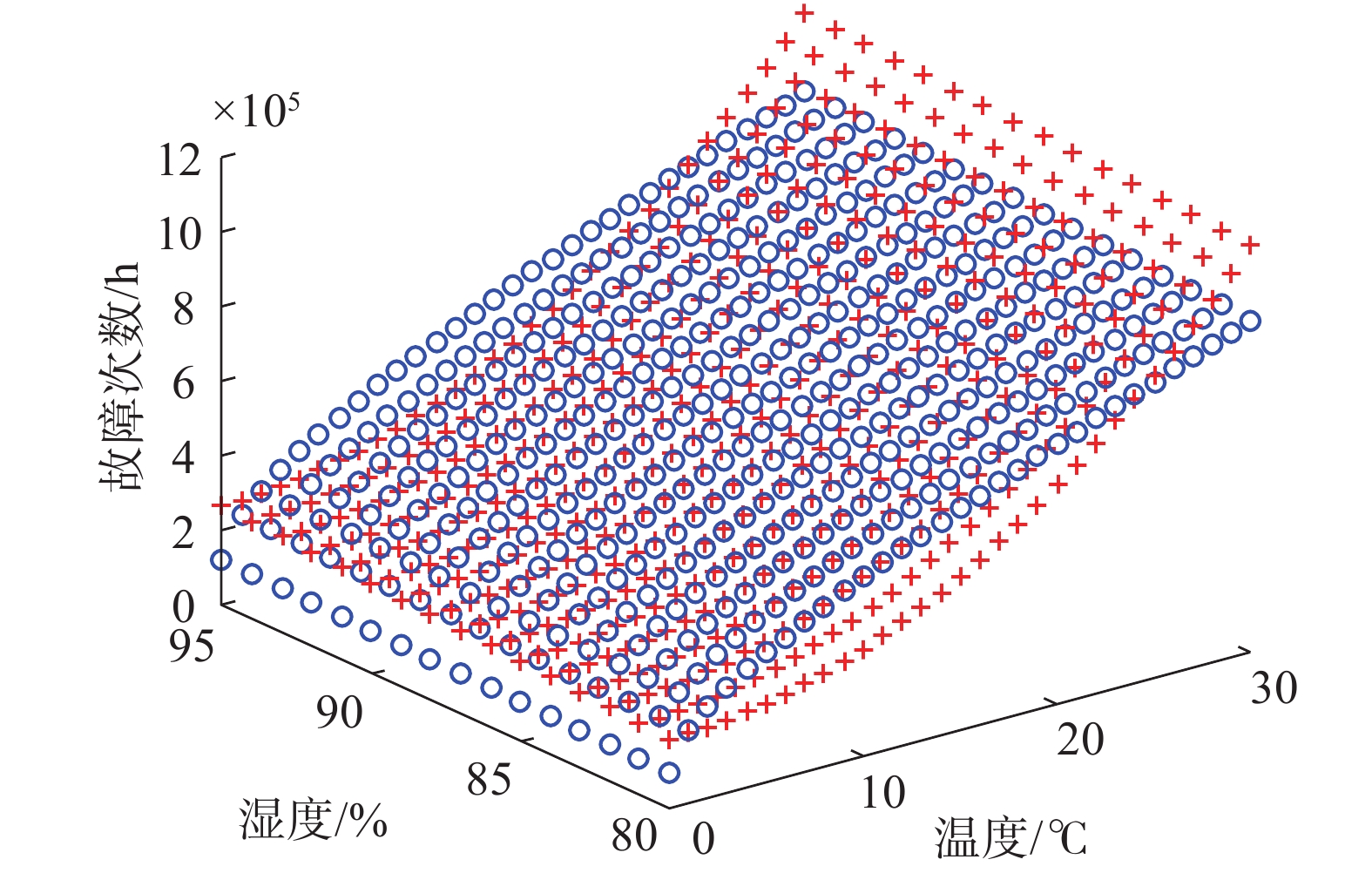
${r_{{S_1}}}$ 的识别度。由系统介绍可知，r1的F={f1=漏电,f2=断路}，$X' $ (f1)={x1, x2}，$X'' $ (f2)={x1, x2, x3}。根据式(4)计算$\mu _{{f_1}}^{X'}({r_1} \to {r_{{S_1}}})$ 中的Na、Nb和Nc。$V_{{f_1}}^{{r_{{S_1}}}}(X')$ 、$v_{{f_1}}^{{r_{{S_1}}}}(X')$ 、$V_{{f_1}}^{{r_1}}(X')$ 和$v_{{f_1}}^{{r_1}}(X')$ 使用图进行表示，如图2所示。
图 2 故障空间与故障分布Fig. 2 Fault space and fault distribution下载:
全尺寸图片
图2显示了
$X' $ 条件下r1与${r_{{S_1}}}$ 的故障数据统计情况。“+”为r1的故障分布特征；“O”为${r_{{S_1}}}$ 的故障分布特征。$V_{{f_1}}^{{r_{{S_1}}}}(X')$ 表示所有“O”点的集合，$v_{{f_1}}^{{r_{{S_1}}}}(X')$ ∈$V_{{f_1}}^{{r_{{S_1}}}}(X')$ ；$V_{{f_1}}^{{r_1}}(X')$ 表示所有“+”点的集合，$v_{{f_1}}^{{r_1}}(X')$ ∈$V_{{f_1}}^{{r_1}}(X')$ 。当然实际的数据统计图并不是这样的，因为实际过程中的数据有冗余和遗漏，造成两个分布的对应位置没有对应的可分析数据。所以这里将各自数据进行曲面拟合，再进行网格化的曲面绘制，从而满足分析要求。这两种分布的曲面方程为$$\left\{{\begin{aligned} &{{r_{{s_1}}}({x_1},{x_2}) = {x_1} + {x_2}/8 + \sqrt {{x_1}{x_2}} } \\ &{{r_1}({x_1},{x_2}) = {x_1}^2 + {x_2}/2 - 21} \end{aligned}} \right.$$ (6) 根据式(3)统计得Na=338、Nb=142、Nc=16，代入式(2)得到a=0.68、b=0.28、c=0.03、j=−1、i=0.68−0.03=0.65，那么
$\mu _{{f_1}}^{X'}({r_1} \to {r_{{S_1}}})$ =0.68+0.28×0.65−0.03=0.832。再计算
$\mu _{{f_1}}^{X''}({r_1} \to {r_{{S_1}}})$ ，由于$X'' $ (f2)={x1, x2, x3}，因此分布需要四维图表示，这里从略。但给出故障分布曲面方程，如式(7)所示。$$\left\{{\begin{aligned} &{{r_{{s_1}}}({x_1},{x_2},{x_3}) = {x_1}/2 + {x_2}\sqrt {{x_1}{x_2}} - {x_3}} \\ &{{r_1}({x_1},{x_2},{x_3}) = {x_1}^2/8 + {x_2}^2/2 + 1.4\sqrt {{x_3}} } \end{aligned}} \right.$$ (7) 根据式(3)进行统计Na=1 953、Nb=609、Nc=910，代入式(2)得到a=0.56、b=0.18、c=0.26、j=−1、i=0.56−0.26=0.3，那么
$\ \mu _{{f_1}}^{X''}({r_1} \to {r_{{S_1}}})$ =0.56+0.18×0.3−0.26=0.354。根据式(4)，
$S_F^X({r_1} \to {r_{{S_1}}}) = {[0.63\;0.37]^{\rm{T}}} \times [0.832\; $ $ 0.354] = 0.655$ 。同理可以得到$S_F^X({r_1} \to {r_{{S_2}}}) = 0.549$ 。那么继续根据式(5)可得，$[1,m] = \{(1,m)|{\rm{MAX}} $ $ \{S_F^X({r_1} \to {r_{{S_1}}}) = 0.655,S_F^X({r_1} \to {r_{{S_2}}}) = 0.549\} \}$ ，这是n=1，m=1。最终故障样本模式r1属于故障标准模式${r_{{S_1}}}$ 。同理可判断r2和r3与${R_S}$ 中各标准模式的归属，从而对样本模式进行识别。总结上述过程的计算步骤如图3所示。
图 3 算法实现的步骤Fig. 3 Steps of algorithm下载:
全尺寸图片
上述方法的特点：1)将因素分为直接因素和背景因素，直接因素是引起系统故障的直接原因，但这些直接原因可能受到多种更为基本的因素影响，因此将因素分层更为合理。2)模式识别是通过联系度确定的，而联系度的系数则是通过故障数据在故障空间中的分布统计确定的。因为无论是实际数据还是实验数据都难以完全独立地得到单因素对故障发生的影响。多因素的联合分布更为准确。3)利用三元联系数表示了故障发生的确定性和不确定性。
上述研究是集对分析理论与空间故障树理论的结合，应用于系统故障模式识别。根据故障标准模式识别故障样本模式，从而分析故障原因，采取对应的故障标准模式预防和治理措施对故障样本模式进行处理。
5. 结束语
1)建立了多因素影响下的系统故障识别方法。首先根据背景材料建立故障模式识别系统；分析故障样本模式与故障标准模式的关系；确定关系联系度的各系数值，通过故障分布统计确定；计算联系度；计算识别度；最终确定故障样本模式与故障标准模式的归属关系。完成故障样本识别。
2)通过实例分析展示了方法流程，并获得了故障样本识别结果。研究一电气系统，主要故障原因为漏电和短路，相关因素为温度、湿度和气压。已具有两个故障标准模式，并获得3个故障样本模式。经过分析得到故障样本模式的联系度和识别度，结果表明故障样本模式r1属于故障标准模式
${r_{{S_1}}}$ 。3)给出了该方法的优点。将因素分为直接因素和背景因素；通过联系度确定关系，联系度系数通过故障在故障空间中的分布进行确定；联系数可表示系统故障发生的确定性和不确定性。
-
图 1 故障模式识别过程
Fig. 1 Fault pattern recognition process
下载:
全尺寸图片
图 2 故障空间与故障分布
Fig. 2 Fault space and fault distribution
下载:
全尺寸图片
图 3 算法实现的步骤
Fig. 3 Steps of algorithm
下载:
全尺寸图片
-
[1] 崔铁军, 马云东. 多维空间故障树构建及应用研究[J]. 中国安全科学学报, 2013, 23(4): 32–37, 62. https://www.cnki.com.cn/Article/CJFDTOTAL-ZAQK201304007.htm CUI Tiejun, MA Yundong. Research on multi-dimensional space fault tree construction and application[J]. China safety science journal, 2013, 23(4): 32–37, 62. https://www.cnki.com.cn/Article/CJFDTOTAL-ZAQK201304007.htm [2] 王盼宝, 孙红梅, 郝鑫, 等. 基于线路电流二阶导数的中压直流系统故障识别方法[J]. 电力系统保护与控制, 2020, 48(13): 1–13. https://www.cnki.com.cn/Article/CJFDTOTAL-JDQW202013001.htm WANG Panbao, SUN Hongmei, HAO Xin, et al. DC line fault identification scheme for a medium-voltage DC power system based on the second derivative of line current[J]. Power system protection and control, 2020, 48(13): 1–13. https://www.cnki.com.cn/Article/CJFDTOTAL-JDQW202013001.htm [3] 熊中杰, 邱颖宁, 冯延晖, 等. 基于机器学习的风电机组变桨系统故障研究[J]. 太阳能学报, 2020, 41(5): 85–90. https://www.cnki.com.cn/Article/CJFDTOTAL-TYLX202005013.htm XIONG Zhongjie, QIU Yingning, FENG Yanhui, et al. Fault analysis of wind turbine pitch system based on machine learning[J]. Acta energiae solaris sinica, 2020, 41(5): 85–90. https://www.cnki.com.cn/Article/CJFDTOTAL-TYLX202005013.htm [4] 蒋佳炜, 胡以怀, 方云虎, 等. 船舶动力装置智能故障诊断技术的应用与展望[J]. 中国舰船研究, 2020, 15(1): 56–67. https://www.cnki.com.cn/Article/CJFDTOTAL-JCZG202001007.htm JIANG Jiawei, HU Yihuai, FANG Yunhu, et al. Application and prospects of intelligent fault diagnosis technology for marine power system[J]. Chinese journal of ship research, 2020, 15(1): 56–67. https://www.cnki.com.cn/Article/CJFDTOTAL-JCZG202001007.htm [5] 潘宏侠, 张玉学. 基于SST时频图纹理特征的供输弹系统故障诊断[J]. 振动与冲击, 2020, 39(6): 132–137, 175. https://www.cnki.com.cn/Article/CJFDTOTAL-ZDCJ202006019.htm PAN Hongxia, ZHANG Yuxue. Fault diagnosis of the ammunition supply system based on the texture features of SST time-frequency distribution image[J]. Journal of vibration and shock, 2020, 39(6): 132–137, 175. https://www.cnki.com.cn/Article/CJFDTOTAL-ZDCJ202006019.htm [6] 刘倪铭, 宁联辉, 高亮, 等. 混合多端直流输电系统故障线路识别方法[J]. 智慧电力, 2020, 48(3): 1–6. doi: 10.3969/j.issn.1673-7598.2020.03.001 LIU Niming, NING Lianhui, GAO Liang, et al. Fault line identification method for multi-terminal hybrid DC transmission system[J]. Smart power, 2020, 48(3): 1–6. doi: 10.3969/j.issn.1673-7598.2020.03.001 [7] 杨健, 杨力, 盛武. 分布式光纤扰动传感系统故障模式识别仿真[J]. 计算机仿真, 2020, 37(1): 444–447. doi: 10.3969/j.issn.1006-9348.2020.01.092 YANG Jian, YANG Li, SHENG Wu. Simulation of fault pattern recognition method for distributed optical fiber disturbance sensing system[J]. Computer simulation, 2020, 37(1): 444–447. doi: 10.3969/j.issn.1006-9348.2020.01.092 [8] 屈子程, 高亮, 康保林, 等. 基于多源数据的电力系统故障全信息诊断模型[J]. 电力系统保护与控制, 2019, 47(22): 59–66. https://www.cnki.com.cn/Article/CJFDTOTAL-JDQW201922008.htm QU Zicheng, GAO Liang, KANG Baolin, et al. A power system fault full information diagnosis model based on multi-source data[J]. Power system protection and control, 2019, 47(22): 59–66. https://www.cnki.com.cn/Article/CJFDTOTAL-JDQW201922008.htm [9] 巫健, 禹宁, 江冰. 一种基于模式识别的光纤通信系统故障诊断方法[J]. 半导体光电, 2019, 40(4): 581–584, 589. https://www.cnki.com.cn/Article/CJFDTOTAL-BDTG201904026.htm WU Jian, YU Ning, JIANG Bing. A fault diagnosis method for optical fiber communication system based on pattern recognition[J]. Semiconductor optoelectronics, 2019, 40(4): 581–584, 589. https://www.cnki.com.cn/Article/CJFDTOTAL-BDTG201904026.htm [10] 赵鑫, 蔡琦, 王晓龙. 基于DTW算法的参数缺失时的核动力系统故障诊断技术[J]. 原子能科学技术, 2019, 53(6): 1070–1077. doi: 10.7538/yzk.2018.youxian.0546 ZHAO Xin, CAI Qi, WANG Xiaolong. Fault diagnosis of nuclear power system based on DTW algorithm for incomplete parameter[J]. Atomic energy science and technology, 2019, 53(6): 1070–1077. doi: 10.7538/yzk.2018.youxian.0546 [11] 王靖岳, 王浩天, 郭立新. 齿轮传动系统故障诊断技术的研究进展[J]. 机械传动, 2016, 40(8): 185–192. https://www.cnki.com.cn/Article/CJFDTOTAL-JXCD201608041.htm WANG Jingyue, WANG Haotian, GUO Lixin. Research progress of fault diagnosis technology of gear transmission system[J]. Journal of mechanical transmission, 2016, 40(8): 185–192. https://www.cnki.com.cn/Article/CJFDTOTAL-JXCD201608041.htm [12] 董磊, 石瑞敏, 曾志强. 基于复杂网络聚类的提升机主轴系统故障诊断[J]. 振动、测试与诊断, 2016, 36(4): 688–693. https://www.cnki.com.cn/Article/CJFDTOTAL-ZDCS201604013.htm DONG Lei, SHI Ruimin, ZENG Zhiqiang. Fault diagnosis for spindle system of hoist based on complex network clustering[J]. Journal of vibration, measurement & diagnosis, 2016, 36(4): 688–693. https://www.cnki.com.cn/Article/CJFDTOTAL-ZDCS201604013.htm [13] 蒋云良, 赵克勤. 人工智能集对分析[M]. 北京: 科学出版社, 2017. [14] 赵克勤. 集对分析对不确定性的描述和处理[J]. 信息与控制, 1995, 24(3): 162–166. https://www.cnki.com.cn/Article/CJFDTOTAL-XXYK503.005.htm ZHAO Keqin. A unified algebraic parameterization or stabilizing controllers for linear discrete-time systems[J]. Information and control, 1995, 24(3): 162–166. https://www.cnki.com.cn/Article/CJFDTOTAL-XXYK503.005.htm [15] 赵森烽, 赵克勤. 几何概型的联系概率(复概率)与概率的补数定理[J]. 智能系统学报, 2013, 8(1): 11–15. doi: 10.3969/j.issn.1673-4785.201208025 ZHAO Senfeng, ZHAO Keqin. Contact probability (complex probability) of the geometry probability and the complement number theorem of probability[J]. CAAI transactions on intelligent systems, 2013, 8(1): 11–15. doi: 10.3969/j.issn.1673-4785.201208025 [16] 赵森烽, 赵克勤. 概率联系数化的原理及其在概率推理中的应用[J]. 智能系统学报, 2012, 7(3): 200–205. doi: 10.3969/j.issn.1673-4785.201112014 ZHAO Senfeng, ZHAO Keqin. The principle of a connection number in probability and its application in probabilistic reasoning[J]. CAAI transactions on intelligent systems, 2012, 7(3): 200–205. doi: 10.3969/j.issn.1673-4785.201112014 [17] 赵克勤. 集对分析与熵的研究[J]. 浙江大学学报, 1992, 6(2): 65–72. https://www.cnki.com.cn/Article/CJFDTOTAL-ZJDX199202010.htm ZHAO Keqin. Set pair analysis and entropy[J]. Journal of Zhejiang University, 1992, 6(2): 65–72. https://www.cnki.com.cn/Article/CJFDTOTAL-ZJDX199202010.htm [18] 崔铁军, 马云东. 基于因素空间的煤矿安全情况区分方法的研究[J]. 系统工程理论与实践, 2015, 35(11): 2891–2897. doi: 10.12011/1000-6788(2015)11-2891 CUI Tiejun, MA Yundong. Research on the classification method about coal mine safety situation based on the factor space[J]. Systems engineering-theory & practice, 2015, 35(11): 2891–2897. doi: 10.12011/1000-6788(2015)11-2891 [19] 李莎莎, 崔铁军, 马云东. 基于云模型的变因素影响下系统可靠性模糊评价方法[J]. 中国安全科学学报, 2016, 26(2): 132–138. https://www.cnki.com.cn/Article/CJFDTOTAL-ZAQK201602025.htm LI Shasha, CUI Tiejun, MA Yundong. Research on method for evaluating fuzzily reliability of variable factors influenced system based on cloud model[J]. China safety science journal, 2016, 26(2): 132–138. https://www.cnki.com.cn/Article/CJFDTOTAL-ZAQK201602025.htm [20] 崔铁军, 李莎莎, 王来贵. 完备与不完备背景关系中蕴含的系统功能结构分析[J]. 计算机科学, 2017, 44(3): 268–273, 306. doi: 10.11896/j.issn.1002-137X.2017.03.055 CUI Tiejun, LI Shasha, WANG Laigui. System function structure analysis in complete and incomplete background relationship[J]. Computer science, 2017, 44(3): 268–273, 306. doi: 10.11896/j.issn.1002-137X.2017.03.055 [21] 崔铁军. 系统故障演化过程描述方法研究[J]. 计算机应用研究, 2020, 37(10): 3006–3009. doi: 10.19734/j.issn.1001-3695.2019.05.0194 CUI Tiejun. Research on description method of system fault evolution process[J]. Application research of computers, 2020, 37(10): 3006–3009. doi: 10.19734/j.issn.1001-3695.2019.05.0194 [22] CUI Tiejun, LI Shasha. Research on complex structures in space fault network for fault data mining in system fault evolution process[J]. IEEE access, 2019, 7: 121881–121896. doi: 10.1109/ACCESS.2019.2937641 [23] 崔铁军, 李莎莎. 空间故障树与空间故障网络理论综述[J]. 安全与环境学报, 2019, 19(2): 399–405. https://www.cnki.com.cn/Article/CJFDTOTAL-AQHJ201902007.htm CUI Tiejun, LI Shasha. Revision of the space fault tree and the space fault network system[J]. Journal of safety and environment, 2019, 19(2): 399–405. https://www.cnki.com.cn/Article/CJFDTOTAL-AQHJ201902007.htm [24] 崔铁军, 李莎莎, 朱宝艳. 含有单向环的多向环网络结构及其故障概率计算[J]. 中国安全科学学报, 2018, 28(7): 19–24. https://www.cnki.com.cn/Article/CJFDTOTAL-ZAQK201807004.htm CUI Tiejun, LI Shasha, ZHU Baoyan. Multidirectional ring network structure with one-way ring and its fault probability calculation[J]. China safety science journal, 2018, 28(7): 19–24. https://www.cnki.com.cn/Article/CJFDTOTAL-ZAQK201807004.htm [25] 崔铁军, 李莎莎. 少故障数据条件下SFEP最终事件发生概率分布确定方法[J]. 智能系统学报: 2020, 15(1): 136−143. CUI Tiejun, LI Shasha. Determination method of target event occurrence probability in SFEP under the condition of less fault data[J]. CAAI transactions on intelligent systems: 2020, 15(1): 136−143. [26] 崔铁军, 李莎莎. 系统运动空间与系统映射论的初步探讨[J]. 智能系统学报, 2020,15(3):445−451 CDATA[CUI Tiejun, LI Shasha. Preliminary study of system movement space and system mapping theory[J]. CAAI transactions on intelligent systems, 2020, 15(3): 445−451
