粗糙集理论是当今知识发现领域的一个研究热点，决策粗糙集模型^[1-2]是粗糙集理论的重要研究分支，由于决策粗糙集在处理噪声数据方面具有较好的泛化性能^[2]，因此目前已广泛应用于机器学习^[3-4]、图像处理^[5]和数据挖掘^[6]等诸多领域。

早期的决策粗糙集建立在完备离散型的信息系统上，在其基础上，学者们进一步地提出了多种扩展的粗糙集模型，例如Liu等^[7]将决策粗糙集推广至不完备信息系统，提出一种改进的不完备决策粗糙集模型；Sun等^[8]在粗糙模糊集下提出了相应的决策粗糙集模型；Dou等^[9]基于多个代价的策略，提出了多代价的决策粗糙集模型；在数值型的数据集方面，Li等^[10]将邻域关系融入决策粗糙集模型中，提出了邻域决策粗糙集模型，该模型进一步提升了决策粗糙集的适用范围。

然而现实环境下的数据不总是静止不变的，而是时刻处于动态更新之中，为了提高粗糙集模型在动态数据下的处理效率，学者们对其提出了多种增量式的模型和算法^[11-13]。在决策粗糙集等模型中，学者们同样提出了多种增量式更新算法。例如，Zhang等^[14]针对属性值动态变化情形提出了相应的增量式更新算法；针对流计算环境，Xu等^[15]提出了对象在线增加和减少时的增量式更新算法；Chen等^[16]利用集合更新的方法设计出了决策粗糙集的增量式更新算法；赵小龙等^[17]针对数值型信息系统，研究了邻域粒化条件熵随对象增加和减少时的增量式更新，并进一步地提出了对应的增量式属性约简算法；杨臻等^[18]研究了混合型信息系统下对象变化时概率的增量式更新，并进一步地提出了变精度粗糙集模型的增量式更新；Luo等^[19]通过矩阵方法构造出了决策粗糙集的增量式更新算法。然而所提出的这些增量式更新算法仅局限于离散数据环境下的决策粗糙集模型，针对邻域型的决策粗糙集还未有相关研究。

论域中对象的增加和减少是信息系统最为常见的一种变化形式，本文将针对这类问题进行邻域决策粗糙集的增量式更新研究。邻域决策粗糙集通过邻域关系来对数值型数据进行信息粒化^[10]，而对其进行增量式计算时必然涉及邻域类的更新计算，邻域关系不同于传统的等价关系和容差关系，其增量式计算的复杂程度要更高。在文献[18]中，杨臻等通过单个对象逐步迭代的方式去处理混合型信息系统变精度粗糙集模型的增量式更新，使得问题的处理方式简便高效。由于决策粗糙集与变精度粗糙集有一定的相似性，因此本文将借鉴文献[18]中关于变精度粗糙集模型的增量式更新研究思路与方法，构造出邻域决策粗糙集的增量式更新模型。文中首先分别研究论域中增加和减少一个对象时，近似集与邻域类之间概率的变化规律，然后根据这种规律来构造单个对象变化时模型上下近似集的增量式更新，最后在单个对象变化的基础上，通过逐步迭代的方式设计了对象批量变化时的增量式更新算法。实验分析表明，所提出的算法具有较高的增量式更新性能，适用于动态数据环境下邻域决策粗糙集模型的动态更新。

1 邻域决策粗糙集模型

粗糙集理论中，数据集表示为信息系统 ${\rm{IS}} = (U,{\rm{AT}})$ 的形式，其中 $U$ 为信息系统的对象集，称为论域。 ${\rm{AT}}$ 称为信息系统的属性集，若属性集 ${\rm{AT}}$ 可分为条件属性集 $C$ 和决策属性集 $D$ ，即 ${\rm{AT}} = C \cup D$ ，那么该信息系统又称为决策信息系统。对于 $\forall x \in U$ 和 $\forall a \in {\rm{AT}}$ ， $a(x)$ 表示对象 $x$ 在属性 $a$ 下的属性值。当条件属性集 $C$ 中的每个属性都为数值型属性时，此信息系统又称之为邻域型信息系统。

Yao等^[1-2]提出的决策粗糙集仅应用于离散型的信息系统，Li等将邻域关系引入传统的决策粗糙集模型中，提出了邻域决策粗糙集^[10]。

定义1^[10] 　设邻域型信息系统 ${\rm{IS}} = (U,{\rm{AT}})$ ，对于属性集 $A \subseteq {\rm{AT}}$ 确定的邻域关系 $N_A^\delta $ 定义为

$N_A^\delta = \{ (x,y) \in U \times U\left| {{\Delta _A}(x,y) \leqslant \delta } \right.\} $

式中： $\delta $ 称为邻域半径，是一个非负常数； ${\Delta _A}(x,y)$ 表示对象 $x$ 与对象 $y$ 之间的闵可夫斯基距离，定义为

${\Delta _A}(x,y) = {\left( {\sum_{\forall a \in A} {|a(x) - a(y){|^k}} } \right)^{{1 / k}}}$

给定邻域信息系统的邻域关系，可以进一步得到每个对象在该邻域关系下的邻域类。

定义2^[10] 　设邻域型信息系统 ${\rm{IS}} = (U,{\rm{AT}})$ ，属性集 $A \subseteq {\rm{AT}}$ 确定的邻域关系为 $N_A^\delta $ ，邻域半径为 $\delta $ 。那么对于 $\forall x \in U$ 在邻域关系 $N_A^\delta $ 下的邻域类定义为

${\delta _A}(x) = \{ y \in U|(x,y) \in N_A^\delta \} $

可以看出，对象 $x$ 的邻域类表示与 $x$ 相近对象的集合，其中 $\delta $ 体现了相近的程度。基于邻域的思想，Li等^[10]提出了邻域决策粗糙集。

在邻域决策粗糙集中，给定状态集 $\varOmega = {\rm{\{ }}X{\rm{,}}{X^c}{\rm{\} }}$ ，其中 $X$ 和 ${X^c}$ 分别表示对象 $x$ 隶属于 $X$ 和 ${X^c}$ 的两种情形，那么对象 $x$ 隶属于 $X$ 的程度可通过概率 $P(X|\delta (x)) = \dfrac{{|X \cap \delta (x)|}}{{|\delta (x)|}}$ 来表示，则对象 $x$ 隶属于 ${X^c}$ 的程度可表示为 $P({X^c}|\delta (x)) = 1 - P(X|\delta (x))$ 。给定对象 $x$ 划分入 $X$ 和 ${X^c}$ 时的3种动作 $\varGamma = {\rm{\{ }}{a_P}{\rm{,}}{a_B}{\rm{,}}{a_N}{\rm{\} }}$ ，其中 ${a_P}$ 、 ${a_B}$ 和 ${a_N}$ 分别表示划分入类别的正区域、边界域和负区域。这里令 ${\lambda _{ * P}}( * \in \{ P,B,N\} )$ 分别表示对象 $x$ 实际属于 $X$ 时采取 ${a_P}$ 、 ${a_B}$ 和 ${a_N}$ 动作时所产生的决策代价， ${\lambda _{ * N}}( * \in \{ P,B,N\} )$ 分别表示对象 $x$ 实际属于 ${X^c}$ 时采取 ${a_P}$ 、 ${a_B}$ 和 ${a_N}$ 动作时所产生的决策代价。因此对于对象 $x$ 进行不同决策动作时所产生的的代价为：

1) ${R_P} = R({a_P}|\delta (x))$ $= {\lambda _{PP}} \cdot P(X|\delta (x)) + {\lambda _{PN}} \cdot P({X^c}|\delta (x))$ ;

2) ${R_B} = R({a_B}|\delta (x))$ $ = {\lambda _{BP}} \cdot P(X|\delta (x)) + {\lambda _{BN}} \cdot P({X^c}|\delta (x))$ ;

3) ${R_N} = R({a_N}|\delta (x))$ $= {\lambda _{NP}} \cdot P(X|\delta (x)) + {\lambda _{NN}} \cdot P({X^c}|\delta (x))$

基于最小化决策代价的原则，那么有

1) ${R_P} \leqslant {R_B}$ 且 ${R_P} \leqslant {R_N}$ 时， $x \in {\rm{POS}}(X)$ ;

2) ${R_B} \leqslant {R_P}$ 且 ${R_B} \leqslant {R_N}$ 时， $x \in {\rm{BUN}}(X)$ ;

3) ${R_N} \leqslant {R_P}$ 且 ${R_N} \leqslant {R_B}$ 时， $x \in {\rm{NEG}}(X)$ 。

通常决策代价满足关系 ${\lambda _{PP}} \leqslant {\lambda _{BP}} < {\lambda _{NP}}$ ， ${\lambda _{NN}} \leqslant {\lambda _{BN}} < {\lambda _{PN}}$ ，那么可以得到

1)当 $P(X|\delta (x)) \geqslant \alpha $ 且 $P(X|\delta (x)) \geqslant \gamma $ 时， $x \in {\rm{POS}}(X)$ ；

2)当 $P(X|\delta (x)) \leqslant \alpha $ 且 $P(X|\delta (x)) \geqslant \beta $ 时， $x \in {\rm{BUN}}(X)$ ；

3)当 $P(X|\delta (x)) \leqslant \beta $ 且 $P(X|\delta (x)) \leqslant \gamma $ 时， $x \in {\rm{NEG}}(X)$ ；

这里的 $\alpha $ 、 $\beta $ 和 $\gamma $ 计算分别为

$\alpha = \frac{{{\lambda _{PN}} - {\lambda _{BN}}}}{{({\lambda _{PN}} - {\lambda _{BN}}) + ({\lambda _{BP}} - {\lambda _{PP}})}}$

$\beta = \frac{{{\lambda _{BN}} - {\lambda _{NN}}}}{{({\lambda _{BN}} - {\lambda _{NN}}) + ({\lambda _{NP}} - {\lambda _{BP}})}}$

$\gamma = \frac{{{\lambda _{PN}} - {\lambda _{NN}}}}{{({\lambda _{PN}} - {\lambda _{NN}}) + ({\lambda _{NP}} - {\lambda _{PP}})}}$

进一步地，若 $\dfrac{{{\lambda _{NP}} - {\lambda _{BP}}}}{{{\lambda _{BN}} - {\lambda _{NN}}}} > \dfrac{{{\lambda _{BP}} - {\lambda _{PP}}}}{{{\lambda _{PN}} - {\lambda _{BN}}}}$ ，则

1)当 $P(X|\delta (x)) > \alpha $ 时，那么 $x \in {\rm{POS}}(X)$ ；

2)当 $\beta \leqslant P(X|\delta (x)) \leqslant \alpha $ 时，那么 $x \in {\rm{BUN}}(X)$ ；

3)当 $P(X|\delta (x)) < \beta $ 时， $x \in {\rm{NEG}}(X)$ 。

因此基于上述决策判别条件，我们可以进一步得到邻域决策粗糙集的上下近似集的定义。

定义3^[10] 　设邻域型信息系统 ${\rm{IS}} = (U,{\rm{AT}})$ ，邻域半径为 $\delta $ ，属性集 $A \subseteq {\rm{AT}}$ 确定的邻域关系为 $N_A^\delta $ ，为了简便，这里简单表示为 ${N_A}$ 。那么对象集 $X \subseteq U$ 关于邻域关系 ${N_A}$ 的 $(\alpha ,\beta )$ 邻域决策粗糙下近似和上近似分别定义为

$\underline N _A^{(\alpha ,\beta )}(X) = \{ x \in U|P(X|{\delta _A}(x)) > \alpha \} $

$\overline N _A^{(\alpha ,\beta )}(X) = \{ x \in U|P(X|{\delta _A}(x)) \geqslant \beta \} $

式中： $0 \leqslant \beta < \alpha \leqslant 1$ , $P(X|{\delta _A}(x))$ 表示对象 $x$ 的邻域关于 $X$ 的概率，定义为

$P(X|{\delta _A}(x)) = \dfrac{{|{\delta _A}(x) \cap X|}}{{|{\delta _A}(x)|}}$

2 邻域决策粗糙集模型的增量式更新

由于现实环境下数据集的动态性，传统的模型和算法不再有效，针对该问题，本节将提出一种论域变化时邻域决策粗糙集模型的增量式更新方法。

定义3已经表明，当信息系统的决策代价已经确定时，则邻域决策粗糙集中的阈值 $\alpha $ 和 $\beta $ 也就确定，因此对于邻域决策粗糙集的研究只需考虑概率 $P(X|\delta (x))$ 与阈值 $\alpha $ 和 $\beta $ 的关系即可。

数据集论域中对象的增加和减少往往都是批量的，而这些批量的变化可以分解成对象的一个一个依次变化，每次只考虑数据集中一个对象增加或减少时的增量式更新问题，然后逐步对多个对象进行迭代，这样可以简化问题的处理^{[12, 17-18]}。根据这一思想，构造了本文模型的增量式更新方法。

2.1 论域中对象增加时模型的增量式更新

在邻域决策粗糙集中，研究增量式更新的关键是上下近似区域的更新问题，由于阈值 $\alpha $ 和 $\beta $ 已经确定，因此主要涉及到对象与对象集之间的概率计算，首先探讨论域对象增加时概率的增量式更新。

定理1^[18] 　设邻域型信息系统 ${\rm{IS}} = (U,{\rm{AT}})$ ，邻域半径为 $\delta $ 且属性集 $A \subseteq {\rm{AT}}$ 。当信息系统论域 $U$ 增加对象 ${x^ + }$ ，新的邻域型信息系统表示为 ${{\rm{IS}}^ + } = ({U^ + } = U \cup \{ {x^ + }\} ,{\rm{AT}})$ 。令 $\delta _A^U(x)$ 表示对象 $\forall x \in {U^ + }$ 在论域 $U$ 下的邻域类，令 $\delta _A^{{U^ + }}(x)$ 表示对象 $\forall x \in {U^ + }$ 在论域 ${U^ + }$ 下的邻域类。对于 $X,Y \subseteq U$ ，若 ${X^ + },{Y^ + } \subseteq {U^ + }$ 且 ${X^ + } = X \cup \{ {x^ + }\} $ ， ${Y^ + } = Y$ 。那么满足：

1) $\forall x \in \delta _A^{U{}^ + }(x{}^ + ) - \{ x{}^ + \}$ ，有

$P({X^ + }|\delta _A^{{U^ + }}(x)) \geqslant P(X|\delta _A^U(x));$

$P({Y^ + }|\delta _A^{{U^ + }}(x)) < P(Y|\delta _A^U(x)).$

2) $\forall x \in {U^ + } - \delta _A^{{U^ + }}({x^ + })$ ，有

$P({X^ + }|\delta _A^{{U^ + }}(x)) = P(X|\delta _A^U(x));$

$P({Y^ + }|\delta _A^{{U^ + }}(x)) = P(Y|\delta _A^U(x)).$

定理1给出信息系统论域 $U$ 增加一个对象后，论域对象在近似集下的概率变化关系，有了这种变化作为基础，接下来可以很容易得到邻域决策粗糙集上下近似的增量式更新。

定理2　设邻域型信息系统 ${\rm{IS}} = (U,{\rm{AT}})$ ，邻域半径为 $\delta $ 。对于 $X,Y \subseteq U$ 关于属性集 $A \subseteq {\rm{AT}}$ 的邻域决策粗糙下近似分别为 $\underline N _A^{(\alpha ,\beta )}(X)$ 和 $\underline N _A^{(\alpha ,\beta )}(Y)$ 。当信息系统论域 $U$ 增加对象 ${x^ + }$ ，新的邻域型信息系统表示为 ${{\rm{IS}}^ + } = ({U^ + } = U \cup \{ {x^ + }\} ,{\rm{AT}})$ 。若 ${X^ + },{Y^ + } \subseteq {U^ + }$ 且 ${X^ + } = X \cup \{ {x^ + }\} $ ， ${Y^ + } = Y$ ，那么 ${X^ + },{Y^ + }$ 关于属性集 $A \subseteq {\rm{AT}}$ 的邻域决策粗糙下近似增量式更新为

$ \begin{aligned} 1)\underline N _A^{(\alpha ,\beta )}&({X^ + }) = \underline N _A^{(\alpha ,\beta )}(X) \cup \\ &\{ x \in \delta _A^{{U^ + }}({x^ + }) - \underline N _A^{(\alpha ,\beta )}(X)|P({X^ + }|\delta _A^{{U^ + }}(x)) > \alpha \} \end{aligned} $

$ \begin{aligned} 2)\underline N _A^{(\alpha ,\beta )}&({Y^ + }) = (\underline N _A^{(\alpha ,\beta )}(Y) - \\ &\{ x \in \underline N _A^{(\alpha ,\beta )}(Y) \cap \delta _A^{{U^ + }}({x^ + })|P({Y^ + }|\delta _A^{{U^ + }}(x)) \leqslant \alpha \} ) \cup \\ &\{ x \in \{ {x^ + }\} |P({Y^ + }|\delta _A^{{U^ + }}(x)) > \alpha \} \end{aligned} $

证明　1)对于 $\forall x \in \underline N _A^{(\alpha ,\beta )}(X)$ ，要么 $x \in \delta _A^{{U^ + }} ({x^ + }) - $ $ \{ {x^ + }\}$ ，要么 $x \in {U^ + } - \delta _A^{{U^ + }}({x^ + })$ 。对于 $\forall x \in \underline N _A^{(\alpha ,\beta )}(X)$ 且满足 $x \in \delta _A^{{U^ + }}({x^ + }) - \{ {x^ + }\} $ ，那么由定理1可以得到 $P({X^ + }|\delta _A^{{U^ + }}(x)) \geqslant P(X|\delta _A^U(x)) > \alpha $ ，则有 $x \in \underline N _A^{(\alpha ,\beta )}({X^ + })$ 。

对于 $\forall x \in \underline N _A^{(\alpha ,\beta )}(X)$ 且满足 $x \in {U^ + } - \delta _A^{{U^ + }}({x^ + })$ ，那么由定理1可以得到

$P({X^ + }|\delta _A^{{U^ + }}(x)) = P(X|\delta _A^U(x)) > \alpha $

同样有 $x \in \underline N _A^{(\alpha ,\beta )}({X^ + })$ 。所以对于 $\forall x \in \underline N _A^{(\alpha ,\beta )}(X)$ 都有 $x \in \underline N _A^{(\alpha ,\beta )}({X^ + })$ ，即 $\underline N _A^{(\alpha ,\beta )}(X) \subseteq \underline N _A^{(\alpha ,\beta )}({X^ + })$ 。

对于 $\forall x \in U - \underline N _A^{(\alpha ,\beta )}(X)$ ，若 $x \in {U^ + } - \delta _A^{{U^ + }}({x^ + })$ ，由定理1可得 $P({X^ + }|\delta _A^{{U^ + }}(x)) = P(X|\delta _A^U(x)) \leqslant \alpha $ 。那么此时 $x \notin \underline N _A^{(\alpha ,\beta )}({X^ + })$ 。

若 $x \in \delta _A^{{U^ + }}({x^ + }) - \{ {x^ + }\} $ ，根据定理1可得

$P({X^ + }|\delta _A^{{U^ + }}(x)) \geqslant P(X|\delta _A^U(x))$

而 $P(X|\delta _A^U(x)) \leqslant \alpha $ ，因此 $P({X^ + }|\delta _A^{{U^ + }}(x))$ 与 $\alpha $ 的大小无法确定，只有当 $P({X^ + }|\delta _A^{{U^ + }}(x)) > \alpha $ 时 $x \in \underline N _A^{(\alpha ,\beta )}({X^ + })$ 。也就是说，只需对 $x \in \delta _A^{{U^ + }}({x^ + }) - \underline N _A^{(\alpha ,\beta )}(X)$ 中的对象进行具体的计算便可以完成最终的下近似更新，因此

$\begin{split} \underline N _A^{(\alpha ,\beta )}({X^ + }) = \underline N _A^{(\alpha ,\beta )}(X) \cup \quad\quad\quad\\ \{ x \in \delta _A^{{U^ + }}({x^ + }) - \underline N _A^{(\alpha ,\beta )}(X)|P({X^ + }|\delta _A^{{U^ + }}(x)) > \alpha \} \\ \end{split} $

即1)成立。

2)对于 $\forall x \in U - \underline N _A^{(\alpha ,\beta )}(Y)$ ，都有 $P(Y|\delta _A^U(x)) \leqslant $ $ \alpha$ 。那么根据定理1，当 $x \in \delta _A^{{U^ + }}({x^ + }) - \{ {x^ + }\} $ 时，有

$P({Y^ + }|\delta _A^{{U^ + }}(x)) < P(Y|\delta _A^U(x)) \leqslant \alpha $

当 $x \in U{}^ + - \delta _A^{U{}^ + }(x{}^ + )$ 时，有

$P({Y^ + }|\delta _A^{{U^ + }}(x)) = P(Y|\delta _A^U(x)) \leqslant \alpha $

因此 $\forall x \in U - \underline N _A^{(\alpha ,\beta )}(Y)$ 都满足 $P({Y^ + }|\delta _A^{{U^ + }}(x)) \leqslant \alpha $ ，即 $x \notin \underline N _A^{(\alpha ,\beta )}({Y^ + })$ 。

对于 $\forall x \in \underline N _A^{(\alpha ,\beta )}(Y)$ ，都有 $P(Y|\delta _A^U(x)) > \alpha $ 。根据定理1，当 $x \in \delta _A^{{U^ + }}({x^ + }) - \{ {x^ + }\} $ 时，有

$P({Y^ + }|\delta _A^{{U^ + }}(x)) < P(Y|\delta _A^U(x))$ ， $P(Y|\delta _A^U(x)) > \alpha $ 。

因此 $P({Y^ + }|\delta _A^{{U^ + }}(x))$ 与 $\alpha $ 的大小无法确定。

当 $x \in U{}^ + - \delta _A^{U{}^ + }(x{}^ + )$ 时，有

$P({Y^ + }|\delta _A^{{U^ + }}(x)) = P(Y|\delta _A^U(x)) > \alpha $

即 $x \in \underline N _A^{(\alpha ,\beta )}({Y^ + })$ ，则需要对 $x \in \delta _A^{{U^ + }}({x^ + }) - \{ {x^ + }\} $ 中的对象计算 $P({Y^ + }|\delta _A^{{U^ + }}(x))$ 可得到新的下近似结果，即

$\begin{split} \underline N _A^{(\alpha ,\beta )}({Y^ + }) = (\underline N _A^{(\alpha ,\beta )}(Y) - \quad\quad\quad\quad \\ \{ x \in \underline N _A^{(\alpha ,\beta )}(Y) \cap \delta _A^{{U^ + }}({x^ + })|P({Y^ + }|\delta _A^{{U^ + }}(x)) \leqslant \alpha \} ) \cup \\ \{ x \in \{ {x^ + }\} |P({Y^ + }|\delta _A^{{U^ + }}(x)) > \alpha \} \quad\quad \quad \\ \end{split} $

定理2证明完毕。

定理2表明，当信息系统增加一个对象后，新的邻域决策粗糙下近似集变化呈现一定的规律，例如从 $\underline N _A^{(\alpha ,\beta )}(X)$ 更新至 $\underline N _A^{(\alpha ,\beta )}({X^ + })$ ，其近似集是增大的，并且增加的对象集只来源于对象集 $\delta _A^{{U^ + }}({x^ + }) - $ $ \underline N _A^{(\alpha ,\beta )}(X)$ ，因此只需对这里面的对象进行概率 $P({X^ + }|\delta _A^{{U^ + }}(x))$ 计算，便可得到最终的更新结果，这样大幅度减小了计算量。同样地对于 $\underline N _A^{(\alpha ,\beta )}(Y)$ 更新至 $\underline N _A^{(\alpha ,\beta )}({Y^ + })$ ，只需对 $\underline N _A^{(\alpha ,\beta )}(Y) \cap \delta _A^{{U^ + }}({x^ + })$ 中的对象进行相关计算便可以完成最终更新，所以定理2所示的下近似集增量式更新具有较高的计算效率。

类似于定理2的研究方法，接下来可以进一步得到上近似集的增量式更新。

定理3　设邻域型信息系统 ${\rm{IS}} = (U,{\rm{AT}})$ ，邻域半径为 $\delta $ 。对于 $X,Y \subseteq U$ 关于属性集 $A \subseteq {\rm{AT}}$ 的邻域决策粗糙上近似分别为 $\overline N _A^{(\alpha ,\beta )}(X)$ 和 $\overline N _A^{(\alpha ,\beta )}(Y)$ 。当信息系统论域 $U$ 增加对象 ${x^ + }$ ，新的邻域型信息系统表示为 ${{\rm{IS}}^ + } = ({U^ + } = U \cup \{ {x^ + }\} ,{\rm{AT}})$ 。若 ${X^ + },{Y^ + } \subseteq {U^ + }$ 且 ${X^ + } = X \cup \{ {x^ + }\} $ ， ${Y^ + } = Y$ ，那么 ${X^ + },{Y^ + }$ 关于属性集 $A \subseteq {\rm{AT}}$ 的邻域决策粗糙上近似增量式更新为

$\begin{split} 1)\overline N _A^{(\alpha ,\beta )}&({X^ + }) = \overline N _A^{(\alpha ,\beta )}(X) \cup \\ &\{ x \in \delta _A^{{U^ + }}({x^ + }) - \overline N _A^{(\alpha ,\beta )}(X)|P({X^ + }|\delta _A^{{U^ + }}(x)) \geqslant \beta \} \\ \end{split} $

$\begin{split} 2)\overline N _A^{(\alpha ,\beta )}&({Y^ + }) = (\overline N _A^{(\alpha ,\beta )}(Y) - \\ &\{ x \in \overline N _A^{(\alpha ,\beta )}(Y) \cap \delta _A^{{U^ + }}({x^ + })|P({Y^ + }|\delta _A^{{U^ + }}(x)) < \beta \} ) \cup \\ &\{ x \in \{ {x^ + }\} |P({Y^ + }|\delta _A^{{U^ + }}(x)) \geqslant \beta \} \\ \end{split} $

证明　证明过程同定理2。

定理3类似于定理2，更新上近似集时也只需要针对部分对象集进行计算便可完成，例如从 $\overline N _A^{(\alpha ,\beta )}(X)$ 更新至 $\overline N _A^{(\alpha ,\beta )}({X^ + })$ ，只需计算 $\delta _A^{{U^ + }}({x^ + }) - \overline N _A^{(\alpha ,\beta )}(X)$ 内的对象，从 $\overline N _A^{(\alpha ,\beta )}(Y)$ 更新至 $\overline N _A^{(\alpha ,\beta )}({Y^ + })$ ，只需计算 $\overline N _A^{(\alpha ,\beta )}(Y) \cap \delta _A^{{U^ + }}({x^ + })$ 中的对象，因此定理3同样具有很高的更新计算效率。

定理2和定理3分别给出当邻域信息系统增加一个对象时，邻域决策粗糙上下近似的增量式更新问题，当信息系统通过增加多个对象，可以根据定理2和定理3逐步进行迭代，直至完成最终的更新。

2.2 论域中对象减少时模型的增量式更新

类似于第2.1节中研究方法，本节将进一步提出论域中对象减少时模型的增量式更新，首先分析对象减少时概率的变化关系。

定理4^[18] 　设邻域型信息系统 ${\rm{IS}} = (U,{\rm{AT}})$ ，邻域半径为 $\delta $ 且属性集 $A \subseteq {\rm{AT}}$ 。当信息系统论域 $U$ 移除对象 ${x^ - }$ ， ${x^ - } \in U$ ，新的邻域型信息系统表示为 ${{\rm{IS}}^ - } = ({U^ - } = U - \{ {x^ - }\} ,{\rm{AT}})$ 。令 $\delta _A^U(x)$ 表示对象 $\forall x \in U$ 在论域 $U$ 下的邻域类，令 $\delta _A^{{U^ - }}(x)$ 表示对象 $\forall x \in U$ 在论域 ${U^ - }$ 下的邻域类。对于 $X,Y \subseteq U$ ,若 ${X^ - },{Y^ - } \subseteq {U^ - }$ 且 ${X^ - } = X - \{ {x^ - }\} $ ， ${Y^ - } = Y$ 。那么满足

1) $\forall x \in \delta _A^U(x{}^ - ) - \{ x{}^ - \}$ ,有

$P({X^ - }|\delta _A^{{U^ - }}(x)) \leqslant P(X|\delta _A^U(x))$

$P({Y^ - }|\delta _A^{{U^ - }}(x)) > P(Y|\delta _A^U(x))$

2) $\forall x \in U - \delta _A^U({x^ - })$ ,有

$P({X^ - }|\delta _A^{{U^ - }}(x)) = P(X|\delta _A^U(x))$

$P({Y^ - }|\delta _A^{{U^ - }}(x)) = P(Y|\delta _A^U(x))$

定理4给出信息系统论域 $U$ 移除一个对象后，近似集在不同对象下的概率变化关系，有了这种变化作为基础，接下来可以很容易得到邻域决策粗糙集上下近似的增量式更新。

定理5　设邻域型信息系统 ${\rm{IS}} = (U,{\rm{AT}})$ ，邻域半径为 $\delta $ 。对于 $X,Y \subseteq U$ 关于属性集 $A \subseteq {\rm{AT}}$ 的邻域决策粗糙下近似分别为 $\underline N _A^{(\alpha ,\beta )}(X)$ 和 $\underline N _A^{(\alpha ,\beta )}(Y)$ 。当信息系统论域 $U$ 移除对象 ${x^ - }$ 且 ${x^ - } \in U$ ，新的邻域型信息系统表示为 ${{\rm{IS}}^ - } = ({U^ - } = U - \{ {x^ - }\} ,{\rm{AT}})$ 。若 ${X^ - },{Y^ - } \subseteq {U^ - }$ 且 ${X^ - } = X - \{ {x^ - }\} $ , ${Y^ - } = Y$ ，那么 ${X^ - },{Y^ - }$ 关于属性集 $A \subseteq {\rm{AT}}$ 的邻域决策粗糙下近似增量式更新为

$\begin{split} 1)\underline N _A^{(\alpha ,\beta )}&({X^ - }) = \underline N _A^{(\alpha ,\beta )}(X) - \{ x \in \underline N _A^{(\alpha ,\beta )}(X) \cap \\ &(\delta _A^U({x^ - }) - \{ {x^ - }\} )|P({X^ - }|\delta _A^{{U^ - }}(x)) \leqslant \alpha \} \quad\quad\quad\quad\quad \\ \end{split} $

$\begin{split} 2)\underline N _A^{(\alpha ,\beta )}&({Y^ - }) = \underline N _A^{(\alpha ,\beta )}(Y) \cup \\ &\{ x \in \delta _A^U({x^ - }) - \{ {x^ - }\} - \underline N _A^{(\alpha ,\beta )}(Y)|P({Y^ - }|\delta _A^{{U^ - }}(x) > \alpha \} \\ \end{split} $

证明　1)对于 $\forall x \in \underline N _A^{(\alpha ,\beta )}(X)$ ，要么 $x \in \delta _A^U({x^ - })$ ，要么 $x \in U - \delta _A^U({x^ - })$ 。若对象满足 $x \in \delta _A^U(x{}^ - ) - \{ x{}^ - \} $ ，那么由定理4可以得到

$P({X^ - }|\delta _A^{{U^ - }}(x)) \leqslant P(X|\delta _A^U(x))$

由于 $P(X|\delta _A^U(x)) > \alpha $ ，则无法直接确定 $P({X^ - }|\delta _A^{{U^ - }} (x))$ 与 $\alpha $ 的关系。即 $\forall x \in \underline N _A^{(\alpha ,\beta )}(X)$ 且 $x \in \delta _A^U(x{}^ - ) - \{ x{}^ - \} $ ，需要计算 $P({X^ - }|\delta _A^{{U^ - }}(x))$ 的值。

若对象满足 $x \in U - \delta _A^U({x^ - })$ ，那么由定理4可以得到 $P({X^ - }|\delta _A^{{U^ - }}(x)) = P(X|\delta _A^U(x)) > \alpha $ ，因此 $\forall x \in \underline N _A^{(\alpha ,\beta )}(X)$ 且 $x \in U - \delta _A^U({x^ - })$ 都有 $x \in \underline N _A^{(\alpha ,\beta )}({X^ - })$ 。

对于 $\forall x \in U - \underline N _A^{(\alpha ,\beta )}(X)$ ，若对象满足 $x \in \delta _A^U (x{}^ - ) - $ $ \{ x{}^ - \} $ ，那么由定理4可以得到

$P({X^ - }|\delta _A^{{U^ - }}(x)) \leqslant P(X|\delta _A^U(x)) \leqslant \alpha .$

因此 $\forall x \in U - \underline N _A^{(\alpha ,\beta )}(X)$ 且 $x \in \delta _A^U(x{}^ - ) - \{ x{}^ - \} $ 都有 $x \notin \underline N _A^{(\alpha ,\beta )}({X^ - })$ .

若对象满足 $x \in U - \delta _A^U({x^ - })$ ，那么由定理4可以得到 $P({X^ - }|\delta _A^{{U^ - }}(x)) = P(X|\delta _A^U(x)) \leqslant \alpha $ 。因此 $\forall x \in U - \underline N _A^{(\alpha ,\beta )} (X)$ 且 $x \in U - \delta _A^U({x^ - })$ 都有 $x \notin \underline N _A^{(\alpha ,\beta )}({X^ - })$ 。综合起来 $\forall x \in U - \underline N _A^{(\alpha ,\beta )}(X)$ 都满足 $x \notin \underline N _A^{(\alpha ,\beta )}({X^ - })$ ，则(1)成立。

2)对于 $\forall x \in \underline N _A^{(\alpha ,\beta )}(Y)$ ，若对象满足 $x \in \delta _A^U(x{}^ - ) - $ $ \{ x{}^ - \}$ ，那么由定理4可以得到

$P({Y^ - }|\delta _A^{{U^ - }}(x)) > P(Y|\delta _A^U(x)) > \alpha $

若对象满足 $x \in U - \delta _A^U({x^ - })$ ，那么由定理4可以得到

$P({Y^ - }|\delta _A^{{U^ - }}(x)) = P(Y|\delta _A^U(x)) > \alpha $

因此 $\forall x \in \underline N _A^{(\alpha ,\beta )}(Y)$ 都有 $x \in \underline N _A^{(\alpha ,\beta )}({Y^ - })$ 。

对于 $\forall x \in U - \underline N _A^{(\alpha ,\beta )}(Y)$ ，若对象满足 $x \in \delta _A^U(x{}^ - ) - $ $ \{ x{}^ - \}$ ，那么由定理4可以得到

$P({Y^ - }|\delta _A^{{U^ - }}(x)) > P(Y|\delta _A^U(x)),P(Y|\delta _A^U(x)) \leqslant \alpha $

此时不能直接确定 $P({Y^ - }|\delta _A^{{U^ - }}(x))$ 与 $\alpha $ 之间的关系。

若对象 $x \in U - \delta _A^U({x^ - })$ ，那么由定理4可得到

$P({Y^ - }|\delta _A^{{U^ - }}(x)) = P(Y|\delta _A^U(x)) \leqslant \alpha $

即 $x \notin \underline N _A^{(\alpha ,\beta )}({Y^ - })$ 。

因此只需要计算对象集 $(U - \underline N _A^{(\alpha ,\beta )}(Y)) \cap $ $ (\delta _A^U({x^ - }) - \{ {x^ - }\} )$ 中的对象便可以完成近似集的增量式更新，即计算 $x \in \delta _A^U({x^ - }) - \{ {x^ - }\} - \underline N _A^{(\alpha ,\beta )}(Y)$ ，因此2)成立。

定理5证明完毕。

定理5表明，当邻域型信息系统移除一个对象 ${x^ - }$ 后，新的邻域决策粗糙下近似集变化也呈现一定的规律，例如从 $\underline N _A^{(\alpha ,\beta )}(X)$ 更新至 $\underline N _A^{(\alpha ,\beta )}({X^ - })$ ，其近似集是减小的，并且减少的对象只来源于一小部分对象集，因此只需对这里面的对象进行概率 $P({X^ - }|\delta _A^{{U^ - }}(x))$ 的计算，便可得到最终的更新结果。同样地对于 $\underline N _A^{(\alpha ,\beta )}(Y)$ 更新至 $\underline N _A^{(\alpha ,\beta )}({Y^ - })$ ，也只需对一小部分对象进行相关计算便可以完成最终更新。所以定理5所示的下近似集增量式更新方法具有较高的计算效率。类似于定理5的研究方法，接下来可以进一步得到上近似集的增量式更新。

定理6　设邻域型信息系统 ${\rm{IS}} = (U,{\rm{AT}})$ ，邻域半径为 $\delta $ 。对于 $X,Y \subseteq U$ 关于属性集 $A \subseteq {\rm{AT}}$ 的邻域决策粗糙上近似分别为 $\overline N _A^{(\alpha ,\beta )}(X)$ 和 $\overline N _A^{(\alpha ,\beta )}(Y)$ .当信息系统论域 $U$ 移除一个对象 ${x^ - }$ ， ${x^ - } \in U$ ，新的邻域型信息系统表示为 ${{\rm{IS}}^ - } = ({U^ - } = U - \{ {x^ - }\} ,{\rm{AT}})$ 。若 ${X^ - },{Y^ - } \subseteq {U^ - }$ 且 ${X^ - } = X - \{ {x^ - }\} $ , ${Y^ - } = Y$ ，那么 ${X^ - }$ 、 ${Y^ - } $ 关于属性集 $A \subseteq {\rm{AT}}$ 的邻域决策粗糙上近似增量式更新为

$\begin{split} 1)\overline N _A^{(\alpha ,\beta )}({X^ - }) = &\overline N _A^{(\alpha ,\beta )}(X) - \{ x \in \overline N _A^{(\alpha ,\beta )}(X) \cap \\ &(\delta _A^U({x^ - }) - \{ {x^ - }\} )|P({X^ - }|\delta _A^{{U^ - }}(x)) < \beta \} \quad\quad \\ \end{split} $

$\begin{split} 2)\overline N _A^{(\alpha ,\beta )}&({Y^ - }) = \overline N _A^{(\alpha ,\beta )}(Y) \cup \\ &\{ x \in \delta _A^U({x^ - }) - \{ {x^ - }\} - \overline N _A^{(\alpha ,\beta )}(Y)|P({Y^ - }|\delta _A^{{U^ - }}(x) \geqslant \beta \} \\ \end{split} $

证明　1)根据定理5的证明结果，对于 $\forall x \in U - \overline N _A^{(\alpha ,\beta )}(X)$ 都满足 $x \notin \overline N _A^{(\alpha ,\beta )}({X^ - })$ 。而对于 $\forall x \in \overline N _A^{(\alpha ,\beta )}(X)$ 且 $x \in U - \delta _A^U({x^ - })$ 都有 $x \in \overline N _A^{(\alpha ,\beta )}({X^ - })$ ，只有当 $\forall x \in \overline N _A^{(\alpha ,\beta )}(X)$ 且 $x \in \delta _A^U(x{}^ - ) - \{ x{}^ - \} $ 时， $P({X^ - }|\delta _A^{{U^ - }}(x))$ 与 $\alpha $ 之间的大小关系不能直接确定，因此定理6中的1)得到证明。

2)根据定理5的证明结果，对于 $\forall x \in \overline N _A^{(\alpha ,\beta )}(Y)$ 都有 $x \in \overline N _A^{(\alpha ,\beta )}({Y^ - })$ 。对于 $\forall x \in U - \overline N _A^{(\alpha ,\beta )}(Y)$ 且 $x \in U - \delta _A^U({x^ - })$ 时，都有 $x \notin \overline N _A^{(\alpha ,\beta )}({Y^ - })$ ，只有当 $\forall x \in U - \overline N _A^{(\alpha ,\beta )}(Y)$ 且 $x \in \delta _A^U(x{}^ - ) - \{ x{}^ - \} $ 时，不能直接确定 $P({Y^ - }|\delta _A^{{U^ - }}(x))$ 与 $\alpha $ 之间的大小关系，因此定理6中的2)得到证明。

定理6与定理5类似，只需要在原先上近似集 $\overline N _A^{(\alpha ,\beta )}(X)$ 和 $\overline N _A^{(\alpha ,\beta )}(Y)$ 的结果上，进一步对 $\delta _A^U({x^ - })$ 中的对象计算概率便可完成最终的更新，因此上近似集的增量式更新同样具有很高的计算效率。

定理5和定理6分别给出当邻域型信息系统移除一个对象时上下近似集的增量式更新问题，当信息系统同时移除多个对象时，可以根据定理5和定理6逐步进行迭代，直至完成最终的更新。

3 邻域决策粗糙集更新算法

根据本文所提出的增量式更新方法，接下来将进一步提出对应的邻域决策粗糙集增量式更新算法，具体如算法1和算法2所示。

算法1　论域增加时邻域决策粗糙集的增量式更新算法

输入　1)邻域型信息系统 ${\rm{IS}} = (U,{\rm{AT}})$ ，邻域半径为 $\delta $ ，阈值 $(\alpha ,\beta )$ 。近似对象集 $X$ 关于属性子集 $A \subseteq {\rm{AT}}$ 的近似集 $\underline N _A^{(\alpha ,\beta )}(X)$ 和 $\overline N _A^{(\alpha ,\beta )}(X)$ 。

2)信息系统增加对象集 $\Delta {U^ + } = \{ x_1^ + ,x_2^ + , \cdots ,x_s^ + \} $ ，新的邻域型信息系统为 ${{\rm{IS}}^ + } = ({U^ + } = U \cup \Delta {U^ + },{\rm{AT}})$ ，新的近似对象集为 ${X^ + }$ 。

输出　新的近似集 $\underline N _A^{(\alpha ,\beta )}({X^ + })$ 和 $\overline N _A^{(\alpha ,\beta )}({X^ + })$ 。

1)将初始时的信息系统 ${\rm{IS}} = (U,{\rm{AT}})$ 记为 ${{\rm{IS}}^{(0)}} = ({U^{(0)}},{\rm{AT}})$ ， $X$ 记为 ${X^{(0)}}$ ，近似集 $\underline N _A^{(\alpha ,\beta )}(X)$ 和 $\overline N _A^{(\alpha ,\beta )}(X)$ 分别记为 $\underline N _A^{(\alpha ,\beta )}({X^{(0)}})$ 和 $\overline N _A^{(\alpha ,\beta )}({X^{(0)}})$ 。

2)对于 $x_i^ + \in \Delta {U^ + }(1 \leqslant i \leqslant s)$ ，将 $x_i^ + $ 加入邻域型信息系统 ${{\rm{IS}}^{(i - 1)}} = ({U^{(i - 1)}},{\rm{AT}})$ 中，新的信息系统表示为 ${{\rm{IS}}^{(i)}} = ({U^{(i)}},{\rm{AT}})$ ，其中 ${U^{(i)}} = {U^{(i - 1)}} \cup \{ x_i^ + \} $ ，此时新的近似对象集为 ${X^{(i)}}$ 。

3)计算对象 $x_i^ + $ 的邻域类 $\delta _A^{{U^{(i)}}}(x_i^ + )$ ，然后根据定理2和定理3在 $\underline N _A^{(\alpha ,\beta )}({X^{(i - 1)}})$ 和 $\overline N _A^{(\alpha ,\beta )}({X^{(i - 1)}})$ 的基础上增量式计算 $\underline N _A^{(\alpha ,\beta )}({X^{(i)}})$ 和 $\overline N _A^{(\alpha ,\beta )}({X^{(i)}})$ 。

4)重复迭代计算步骤2）~3）。

5)令

$ \begin{array}{l} \underline N _A^{(\alpha ,\beta )}({X^ + }) = \underline N _A^{(\alpha ,\beta )}({X^{(s)}});\\ \overline N _A^{(\alpha ,\beta )}({X^ + }) = \overline N _A^{(\alpha ,\beta )}({X^{(s)}}). \end{array} $

返回 $\underline N _A^{(\alpha ,\beta )}({X^ + })$ 和 $\overline N _A^{(\alpha ,\beta )}({X^ + })$ 。

算法2　论域减少时邻域决策粗糙集的增量式更新算法

输入　1)邻域型信息系统 ${\rm{IS}} = (U,{\rm{AT}})$ ，邻域半径为 $\delta $ ，阈值 $(\alpha ,\beta )$ 。近似对象集 $X$ 关于属性子集 $A \subseteq {\rm{AT}}$ 的近似集 $\underline N _A^{(\alpha ,\beta )}(X)$ 和 $\overline N _A^{(\alpha ,\beta )}(X)$ 。

2)信息系统减少对象集 $\Delta {U^ - } = \{ x_1^ - ,x_2^ - , \cdots ,x_t^ - \} $ ，新的邻域型信息系统为 ${{\rm{IS}}^ - } = ({U^ - } = U - \Delta {U^ - },{\rm{AT}})$ ，新的近似对象集为 ${X^ - }$ 。

输出　新的近似集 $\underline N _A^{(\alpha ,\beta )}({X^ - })$ 和 $\overline N _A^{(\alpha ,\beta )}({X^ - })$ 。

1)将初始时的信息系统 ${\rm{IS}} = (U,{\rm{AT}})$ 记为 ${{\rm{IS}}^{(0)}} = ({U^{(0)}},{\rm{AT}})$ ， $X$ 记为 ${X^{(0)}}$ ，近似集 $\underline N _A^{(\alpha ,\beta )}(X)$ 和 $\overline N _A^{(\alpha ,\beta )}(X)$ 分别记为 $\underline N _A^{(\alpha ,\beta )}({X^{(0)}})$ 和 $\overline N _A^{(\alpha ,\beta )}({X^{(0)}})$ 。

2)对于 $x_i^ - \in \Delta {U^ - }(1 \leqslant i \leqslant t)$ ，将 $x_i^ - $ 从邻域型信息系统 ${ {\rm{IS}}^{(i - 1)}} = ({U^{(i - 1)}},{\rm{AT}})$ 中移除，新的信息系统表示为 ${{\rm{IS}}^{(i)}} = ({U^{(i)}},{\rm{AT}})$ ，其中 ${U^{(i)}} = {U^{(i - 1)}} - \{ x_i^ - \} $ ，此时新的近似对象集为 ${X^{(i)}}$ 。

3)计算对象 $x_i^ - $ 的邻域类 $\delta _A^{{U^{(i)}}}(x_i^ - )$ ，然后根据定理5和定理6在 $\underline N _A^{(\alpha ,\beta )}({X^{(i - 1)}})$ 和 $\overline N _A^{(\alpha ,\beta )}({X^{(i - 1)}})$ 的基础上增量式计算 $\underline N _A^{(\alpha ,\beta )}({X^{(i)}})$ 和 $\overline N _A^{(\alpha ,\beta )}({X^{(i)}})$ 。

4)重复迭代计算步骤2)~3)

5)令

$ \begin{array}{l} \underline N _A^{(\alpha ,\beta )}({X^ - }) = \underline N _A^{(\alpha ,\beta )}({X^{(t)}});\\ \overline N _A^{(\alpha ,\beta )}({X^ - }) = \overline N _A^{(\alpha ,\beta )}({X^{(t)}}). \end{array} $

返回 $\underline N _A^{(\alpha ,\beta )}({X^ - })$ 和 $\overline N _A^{(\alpha ,\beta )}({X^ - })$ 。

在算法1所示的增量式计算过程中，每次在更新前信息系统的上下近似基础上进一步计算新的上下近似集，并且定理2和定理3已经表明，只需要计算新增对象的邻域类，便可以完成最终的更新，而不必去计算其他对象的邻域类，这样大大减少了重复的计算量，提高了更新的效率，因此整个算法1和算法2的时间复杂度可表示为 $O(|A| \cdot |U| \cdot |\Delta U|)$ 。

4 实验分析

为了验证所提出增量式更新算法的有效性，将通过实验比较的方式进行验证。本实验主要将文中所提出的增量式更新算法与传统的非增量更新算法对同一组数据集进行动态更新计算，通过比较他们的动态更新效率来验证算法的有效性，其中表1所示的是实验中所使用的数据集，这些数据集均来源于UCI数据集库，其中数据集的各个属性均为数值类型。整个实验所运行的硬件环境为Intel Core G4560 3.5 GHz处理器和DDR4 8 GB内存。

表1所示的均为静态的数据集，为了模拟数据集动态变化的情形，本实验采用其他学者常用的处理方法^{[11-12, 17-18]}，即让数据集按照论域平均分成多个对象集，然后通过将这些对象集逐渐进行合并，达到了数据集论域动态增加的效果，将原始论域逐渐对这些对象集进行移除，便达到了数据集论域动态的减少。本实验将论域平均分成9个部分，这样可以构造出数据集的8次动态更新。实验中将数据集的决策类作为邻域决策粗糙集的近似对象集，即计算数据集每个决策类的上下近似增量式更新。实验中每个数据集的属性值均进行归一化处理，并且统一设定邻域半径 $\delta = 0.15$ ，阈值 $\alpha = 0.75$ ， $\beta = 0.55$ 。

图1为各个数据集论域增加时增量式更新算法(算法1)与非增量式更新算法计算邻域决策粗糙集的时间比较结果，非增量式更新算法采用文献[10]提出的算法。

在图1所示的实验结果中，增量式算法的更新用时大幅度低于非增量式算法，并且随着数据集更新次数的增多，两类算法的差距不断增大。这主要是由于非增量式更新算法在进行模型的更新时，每次均基于完整的论域进行计算，产生的时间会越来越多。对于增量式更新算法，随着数据集论域的增大，更新所需的时间较少且增长的速率较为缓慢，这主要是由于增量式更新算法采用增量式的方法进行更新计算，每次均在前一次更新的结果上进行进一步更新，这样避免了原有对象的重复计算，大幅度提高更新效率，因此增量式算法更加高效。

图2展示的是各个数据集论域减少时，增量式更新算法(算法2)与非增量式更新算法计算邻域决策粗糙集的时间比较结果，非增量式更新算法同样采用文献[10]提出的算法。

在图2所示的实验结果中，可以发现增量式更新算法的更新用时同样大幅度低于非增量式更新算法，对于非增量式更新算法，随着数据集论域的逐渐减少，其更新模型的用时也是逐渐减小，这主要是由于非增量式更新算法在进行更新时，对完整论域进行计算，因此随着论域的减少，非增量式算法的计算量也大幅度减小，产生的时间会越来越少，但是整体还是高于增量式算法。对于增量式更新算法，随着数据集论域的减小，其整体更新用时始终处于一个较低的水平，并且随着更新次数增加，更新用时也是逐渐减小的。这主要是由于增量式更新算法采用增量式的方法进行更新计算，在前一次更新结果的基础上计算后一次结果，由于论域逐渐减少，则更新时间会更加的少，从而效率远高于非增量式算法。

综合图1和图2的实验结果，可以看出本文所提出的增量式更新算法的更新效率均大幅度高于传统的非增量式算法，并且所提出的算法随数据集论域变化的影响较小，这说明了本文所提出的增量式更新算法具有很高的优越性。

另一方面，在本文所提出的邻域决策粗糙集增量式更新算法中，有3个重要的参数，分别为邻域半径 $\delta $ ，和一对阈值 $(\alpha ,\beta )$ 。由于阈值 $(\alpha ,\beta )$ 可以通过不同的评价方式进行确定，因此阈值 $(\alpha ,\beta )$ 可认定为是固定的值，那么接下来将直接探究邻域半径 $\delta $ 对所提算法更新效率的影响。

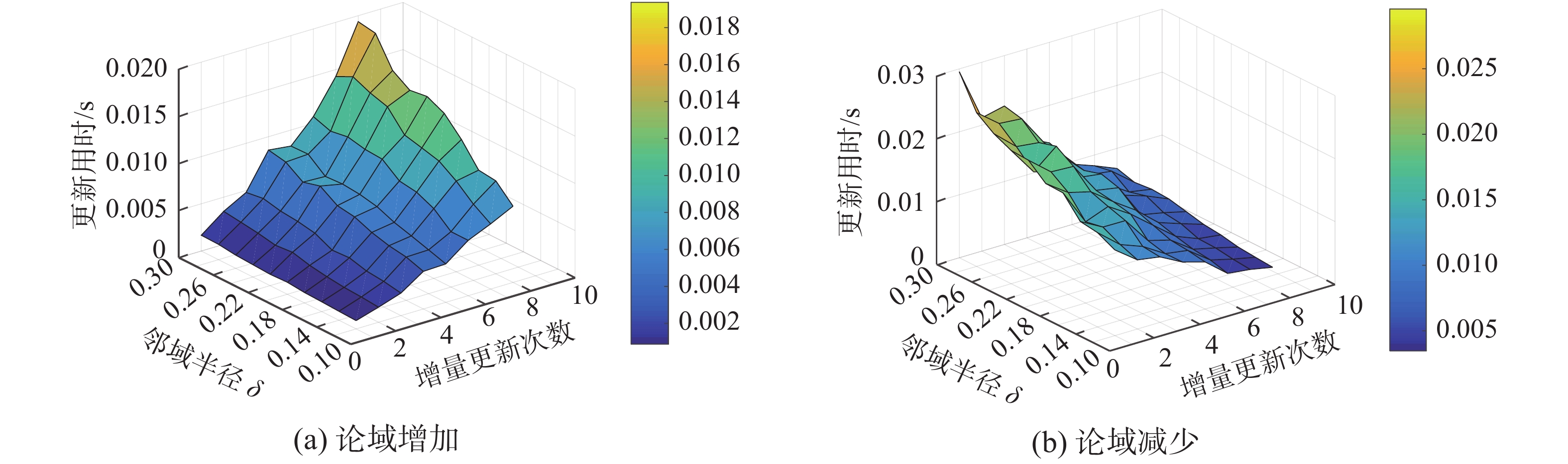
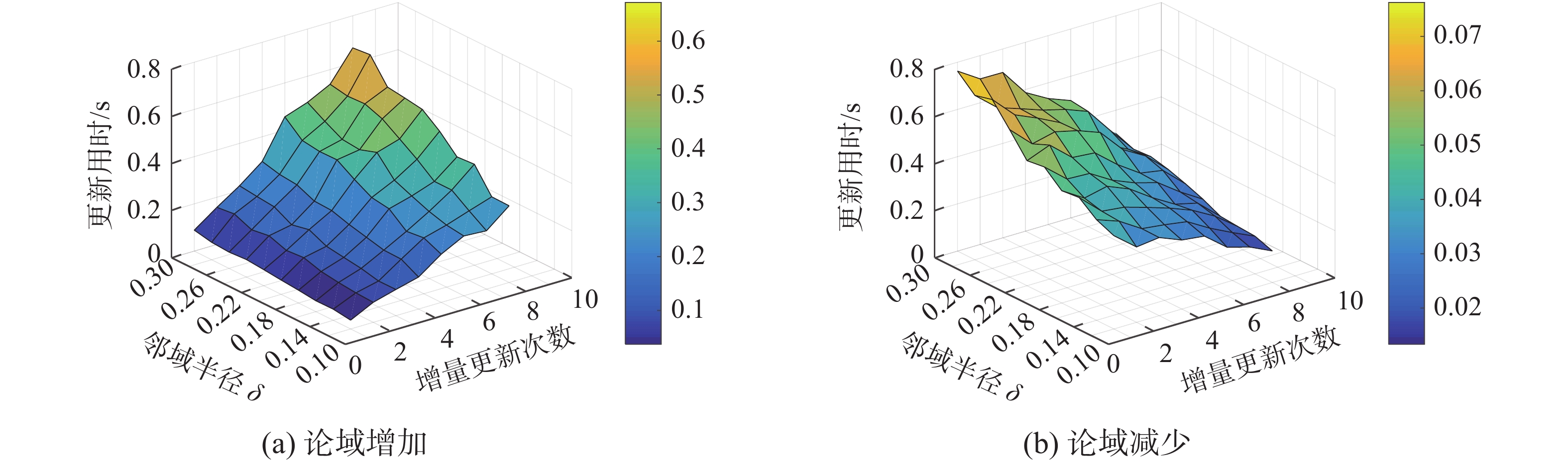
图3～6所示的是部分数据集在不用邻域半径 $\delta $ 下增量式更新用时比较结果，其中包含了论域增加和论域减少的两种情形，这里设定邻域半径 $\delta $ 在[0.1,0.28]内以0.02为间隔分别进行取值。

通过图3~6的结果可以看出，随着邻域半径的逐渐增大，增量式更新算法的更新用时是逐渐增大的，这主要是由于本文所提出的增量更新算法，计算新论域下的模型时，需要计算变化对象的邻域类，并基于这些邻域类进行更新计算，而邻域半径的增大无疑会增加邻域类中对象的数量，因此计算量会增加，从而展现出了图3~6的结果，但是对比图1和图2，这种增量式算法的用时仍然大幅度小于非增量式算法。

5 结束语

邻域决策粗糙集是传统决策粗糙集的重要拓展，针对现实环境下数据集的动态性，本文提出一种论域动态变化时的邻域决策粗糙集增量式更新算法。本文首先研究了论域中单个对象变化时，模型的增量式更新问题，然后以单个对象变化为基础，通过迭代方式完成对象批量变化时的增量式更新问题，实验分析表明，所提出的增量式算法在更新动态数据时，其效率大幅度高于非增量式算法，且增量式算法的更新时间受论域对象变化的影响较小，因此说明了所提出的增量式更新算法具有很高的优越性，从而也进一步推动了决策粗糙集在实际环境下的应用。在本文研究成果的基础上，接下来可以进一步在邻域决策粗糙集的增量式属性约简问题上进行探索。