现实生活中的问题往往会涉及多个优化目标，且它们可能彼此冲突、相互制约，这类问题被称为多目标优化问题(multi-objective optimization problem, MOP)^[1]。而多模态多目标优化问题(multimodal multi-objective optimization problem, MMOP)是其中一类较特殊的问题。相比于传统的多目标优化问题，它在决策空间的多个解可能会有相同的目标值。故多模态多目标优化问题不仅要找到多样性好和逼近性好的近似帕累托前沿(pareto front, PF)，而且要在决策空间找到尽可能多的等价解^[2]。

由于多模态多目标问题在近几年才受到学者们的重视和研究，故相比于多目标优化算法的研究，其成果相对较少。基于Li^[3]提出的无参数小生境算法，Yue等^[4]在此基础上提出基于环形拓扑结构的粒子群算法(multi-objective particle swarm optimizer using ring-topology，MO_Ring_PSO_SCD)来解决多模态多目标问题，该算法除引入基于索引的环形拓扑结构外，还在决策空间和目标空间中设计一种新的特殊的拥挤距离来进行粒子选择与更新。结果表明，该算法能定位和保持大量的等价解；Liang等^[5]提出一种自组织多模态多目标粒子群算法(self-organizing multi-objective particle swarm optimization algorithm，SMPSO-MM)。该算法使用自组织映射网络构建粒子间的邻域关系并进行邻域间信息交流；另外引入精英策略避免算法陷入停滞。实验结果表明该算法能够定位到更多等价解，决策空间解的分布也较均匀；Li等^[6]提出一种基于适应度排序与强化学习的多模态多目标算法(differential evolution based on reinforcement learning with fitness ranking，DE-RLFR)，该算法首先使用适应度函数联合排序值确定种群中每个个体的分层状态，再根据分层状态确定进化方向和变异策略，最后利用强化学习来引导种群搜索。实验证明该算法可以显著提高决策空间中种群搜索效率，在解决多模态多目标问题时有较好表现；Fan等^[7]则使用分区的概念来提高种群在决策空间中的多样性和降低问题的求解复杂度。研究表明，该方法能够辅助MO-Ring-SO-SCD找到更多等价解。Zhang等^[8]提出一种基于聚类的多模态多目标粒子群算法(cluster based PSO with leader updating mechanism and ring-topology，MMO-CLR-PSO)。该算法使用决策变量聚类方法划分子种群，利用带有领导粒子更新机制的全局粒子群算法独立地更新每一个子种群的粒子，并在子种群之间建立环形结构探索未被开发的区域以搜索更多的非支配解。实验结果证明该算法在决策空间与目标空间的解集都能维持较好的多样性；Liang等^[9]提出一种多模态多目标差分进化优化算法(multimodal multi-objective differential evolution optimization algorithm，MMODE)。该算法使用预选择机制将所有个体进行适应度值排序后再根据决策空间中的拥挤距离选择个体进行变异，同时引入新的边界处理方法将停留在边界的个体重新调整。实验结果证明利用 MMODE算法获得的Pareto解在决策空间和目标空间中都有一个较好的表现；Liu等^[10]提出一种基于归档和重组策略的多模态多目标算法(multimodal multi-objective evolutionary algorithm using two-archive and recombination strategies，TriMOEA-TA&R)。该算法使用决策变量分析技术将种群个体分别归入多样性存档和收敛性存档中，各自从两个存档中选择父代进行交叉复制。此外，多样性存档中使用聚类算法及清除策略来保证目标空间多样性。最终将两个存档的解重组以形成最终解集。实验结果证明，两个存档的分工减少了环境选择的难度，且算法的整体性能明显优于比较算法；Lin等^[11]提出一种决策空间和目标空间双重聚类的多模态多目标进化算法(multimodal multi-objective evolutionary algorithm with dual clustering in decision and objective spaces，MMOEA/DC)。该算法在决策空间和目标空间均采用聚类算法来保持两个空间的多样性。在决策空间根据邻域关系将父代与子代结合并划分为多个类别，将这些类中获得的非支配解及其他收敛性好的解对应在目标空间中的解重新划分为多个类。实验结果表明该算法能够有效定位到全局Pareto解和局部Pareto解，并且在两个空间中都有较好的多样性。Zhang等^[12]提出一种改进的粒子群算法(modified particle swarm optimization, MPSO)求解多模态多目标问题。该算法引入一种基于邻域的动态学习策略代替全局学习策略，并使用子代竞争机制来提高算法的多样性。实验结果证明该算法在多数测试函数上的表现都优于其他比较算法。Li等^[13]提出一种基于高斯采样(multi objective particle swarm optimization based on gaussian sampling, GS-MOPSO)的多目标粒子群优化算法以求解多模态多目标问题。该算法在搜索前期利用全局高斯采样方法来进行全局搜索，在搜索后期则采用局部高斯采样来寻找有潜力解的邻域。此外，GS-MOPSO算法采用一种新的外部存档策略来储存历史解。实验结果表明，该算法能够找到更多Pareto解。

虽然诸多学者对多模态多目标进化算法进行改进，但如何保持/提高种群多样性和提高局部搜索能力来找到更多等价解仍需得到进一步研究。为提高多模态多目标进化算法的性能，本文提出一种融合分区和局部搜索的多模态多目标粒子群算法(multimodal multi-objective particle swarm optimization combining zoning search and local search, ZLS-SMPSO-MM)。在ZLS-SMPSO-MM算法中，整个决策空间首先被划分成多个子空间；然后在各个子空间内，自组织映射网络被用来构建各个子空间的邻域，并使用协方差矩阵自适应算法(covariance matrix adaptation evolutionary strategies, CMA-ES)来增强算法的局部搜索能力；最后对所有子空间得到的解集进行合并选择。为验证所提算法性能，本文选取5种知名多模态多目标进化算法和14个多模态多目标问题进行比较与测试。所得实验结果表明，ZLS-SMPSO-MM不仅能够维持种群多样性以找到更多的等价解，而且能够在较短时间内找到高质量的解。

1 预备知识 1.1 多目标优化问题

不失一般性，多目标优化问题(以最小化问题为例)的数学形式表示如下^[13-14]:

$\begin{array}{l} \min \;\;{\boldsymbol{y}}{\rm{ = }}F({\boldsymbol{x}}) = ({f_1}({\boldsymbol{x}}),{f_2}({\boldsymbol{x}}),\cdots ,{f_m}({\boldsymbol{x}})) \\ {\rm{s.t.}}\;\;\;\;{\boldsymbol{x}} = ({x_1},{x_2}, \cdots ,{x_D}) \in {\boldsymbol{X}} \subseteq {R^D} \end{array} $

(1)

式中： ${\boldsymbol{x}}$ 为D维的决策矢量；X为D维的决策空间； ${\boldsymbol{y}} = ({{\boldsymbol{y}}_{\boldsymbol{1}}},{{\boldsymbol{y}}_{\boldsymbol{2}}}, \cdots {{\boldsymbol{y}}_{\boldsymbol{m}}}) \in {\boldsymbol{Y}} \subseteq {R^m}$ 为m维的目标矢量；Y为m维的目标空间。其他一些相关概念如下^[15]：

定理1　支配关系：向量p支配另一个向量q(记作 ${\boldsymbol{p}} \prec {\boldsymbol{q}}$ )的条件是：如果 $\forall \theta \in \{ 1,2, \cdots ,\varphi \} , $ $ {p_\theta } \leqslant {q_\theta }$ ，并且 ${\boldsymbol{p}} \ne{\boldsymbol{q}}$ 。

定理2　Pareto最优解集(pareto set，PS)：一个向量 ${{\boldsymbol{x}}^*} \in {\boldsymbol{X}}$ ，若不存在其他向量 ${\boldsymbol{x}} \in {\boldsymbol{X}}$ ，使得 $F\left( {\boldsymbol{x}} \right) \succ F\left( {{{\boldsymbol{x}}^ * }} \right)$ ，就称 ${{\boldsymbol{x}}^ * }$ 为Pareto解，所有Pareto解构成的集合(记作 ${{\boldsymbol{X}}^ * }$ )被称为Pareto解集。

定理3　Pareto前沿：在多目标优化问题中，Pareto解集对应目标空间中的目标向量被称为Pareto前沿，表示为 ${\rm{PF}} = \{ F\left( {{{\boldsymbol{x}}^ * }} \right)|{{\boldsymbol{x}}^ * } \in {\boldsymbol{X}} * \}$ 。

1.2 多模态多目标优化问题及评价指标

多模态多目标优化问题是一种特殊的多目标优化问题，其主要表现为两种情况：1)决策空间中每个解都有多个等价解；2)决策空间中部分解有多个等价解^[7]。由于多模态多目标优化问题不仅需要在目标空间获得逼近性及多样性较好的PF逼近，也需要在决策空间中获得足够多等价解。因此，本文引入帕累托解集近似(pareto set proximity，PSP)^[4]和超体积值(hypervolume，HV)^[16]这两种评价指标来评价多模态多目标优化算法的性能。

1)PSP

${\rm{PSP}} = \frac{{{\rm{CR}}}}{{{\rm{IGDx}}}}$

(2)

${\rm{IGDx}}({{\rm{PS}}^*},{\rm{PS}}) = \frac{{\displaystyle\sum_{b \in {\rm{PS}}}d(b,{{\rm{PS}}^*}) }}{{\left| {{\rm{PS}}} \right|}}$

(3)

${\rm{CR}} = {\left(\prod\limits_j^D {{{\rm{\delta}} _j}} \right)^{1/2D}}$

(4)

$ {\rm{\delta }}_{j}=\left\{ \begin{split}&1,\quad{B}_{j}^{\rm{max}}={B}_{j}^{\rm{min}}\\ &0,\quad{b}_{j}^{\rm{min}}\geqslant {B}_{j}^{\rm{max}}\left|\right|{b}_{j}^{\rm{max}}\leqslant {B}_{j}^{\rm{min}}\\ &\dfrac{{\rm{min}}({b}_{j}^{\rm{max}},{B}_{j}^{\rm{min}})-{\rm{max}}({b}_{j}^{\rm{min}},{B}_{j}^{\rm{max}})}{{B}_{j}^{\rm{max}}-{B}_{j}^{\rm{min}}},\quad{\text{其他}}\end{split} \right.$

(5)

式中：CR (cover rate)表示所得解集中解个数与真实PS中解个数的比值，也称为解的覆盖率；IGDx表示决策空间中的反向世代距离^[14]； $b_j^{\max }$ 和 $b_j^{\min } $ 是算法获得的解集PS^*中第j个变量的最大值和最小值； $B_j^{\max }$ 和 $B_j^{\min }$ 是PS中第j个变量的最大值和最小值；d(b, PS^*)是b与PS中最近点的欧几里得距离；|PS|表示PS中解的数量。PSP主要评价得到的解集PS^*与PS之间的相似性。PSP的值越大，表示算法得到的等价解越多，算法的性能就越好。

2)HV

$\begin{array}{l} {\rm{HV}}({{\rm{PS}}^*}) = {\rm{VOL}}\Big(\mathop \cup \limits_{x \in P{S^*}} \left[ {{f_1}({\boldsymbol{x}}),{\boldsymbol{r}}_1^*} \right] \times \left[ {{f_2}({\boldsymbol{x}}),{\boldsymbol{r}}_2^*} \right]\times \cdots \times \\ \;\;\;\; \left[ {{f_m}({\boldsymbol{x}}),{\boldsymbol{r}}_m^*} \right]\Big) = [({f_1}({\boldsymbol{x}}) - {\boldsymbol{r}}_1^*){({f_1}({\boldsymbol{x}}) - {\boldsymbol{r}}_1^*)^{\bf{T}}}] + [({f_2}({\boldsymbol{x}}) -\\ {\boldsymbol{r}}_2^*)({f_2}({\boldsymbol{x}}) - {\boldsymbol{r}}_2^*)^{\bf{T}}] \cdots + [({f_m}({\boldsymbol{x}}) - {\boldsymbol{r}}_m^*){({f_m}({\boldsymbol{x}}) - {\boldsymbol{r}}_m^*)^{\bf{T}}}] \end{array} $

(6)

式中：VOL()是勒贝格测度； ${{\boldsymbol{r}}^ * } = \left( {{\boldsymbol{r}}_1^ * ,{\boldsymbol{r}}_2^ * , \cdots ,{\boldsymbol{r}}_m^ * } \right)$ 是选择的参考点，该参考点被目标空间中所有获得的PF逼近中的个体所支配。HV可以用来衡量PF^*的收敛性和多样性。HV的值越大，代表算法获得的PF逼近越接近真实PF，多样性也越好。

2 融合分区和局部搜索的多模态多目标粒子群算法 2.1 分区搜索

对于求解多模态多目标优化问题来说，提高/维持种群多样性是影响其最后结果的一个重要因素。同时，降低问题求解复杂度也能辅助算法找到质量更好的解。鉴于文献[7]中所提方法能够实现以上两个目标，故所提算法使用分区搜索(zoning search，ZS)来求解多模态多目标优化问题。搜索空间分割步骤：首先从决策空间X的D维优化问题中随机选取h(1≤h≤D)个变量，将每个变量都分割成l(l>1)段，最终，整个决策空间被分为l^h个子空间。

2.2 自组织多模态多目标粒子群算法

在所提算法中，选取自组织多模态多目标粒子群算法^[5] (self-organizing multi-objective particle swarm optimization algorithm for multimodal multi-objective problems，SMOPSO)为基本的搜索算法，其主要步骤如下：

1)构建自组织映射网络(self-organizing maps，SOM)。该步骤主要利用SOM网络为粒子群算法中的粒子构建邻域关系，并在根据邻域关系获得的神经元集合中选取合适的引导粒子指导种群进化。SOM网络构建邻域关系主要有以下几步^[5,17-18]：

①判断获胜神经元。

SOM网络中输入的数据维度为 $D$ ，将种群的位置信息 ${\boldsymbol{x}} = \left( {{x_1},{x_2}, \cdots {x_D}} \right)$ 输入网络，隐藏层中的每个神经元与输入层是全连接的结构，所以神经元的权值矩阵的行秩与输入空间的维度相同，神经元权值矩阵的列秩则与神经元个数相同。因此，整个隐藏层的权值矩阵表示为

${\boldsymbol{w}} = \left[ {\begin{array}{*{20}{c}} {{w_{11}}}&{{w_{12}}}& \cdots &{{w_{1D}}} \\ {{w_{21}}}&{{w_{22}}}& \cdots &{{w_{2D}}} \\ \vdots & \vdots & {\;} & \vdots \\ {{w_{\varepsilon 1}}}&{{w_{\varepsilon 2}}}& \cdots &{{w_{\varepsilon D}}} \end{array}} \right]$

(7)

其中 $\varepsilon $ 代表SOM网络中神经元个数。

竞争过程就是找到与输入向量x最佳匹配的权值向量，等价于找到与向量x欧几里得距离最小的权值向量，该权值向量所对应的神经元也被称之为获胜神经元。其主要公式为

${d^2}({\boldsymbol{x}},{{\boldsymbol{w}}_{{u_\rho }}}) = {({\boldsymbol{x}} - {{\boldsymbol{w}}_{{u_\rho }}})^{\rm{T}}}({\boldsymbol{x}} - {{\boldsymbol{w}}_{{u_\rho }}})$

(8)

式中： $\rho \in \left( {1,\varepsilon } \right)$ ； $u_{\rho}$ 代表获胜神经元编号； ${{\boldsymbol{w}}_{{u_\rho }}} = $ $ {\left[ {{w_{\rho 1}}\;\;{w_{\rho 1}}\;\; \cdots\;\; {w_{\rho D}}} \right]^{\rm{T}}}$ 。

用索引 $I({u_\rho })$ 来标识与输入向量x最佳匹配的权值向量，其公式为

$I({u_\rho }) = {\rm{argmin}}\left\| {{\boldsymbol{x}} - {{\boldsymbol{w}}_{{u_\rho }}}} \right\|$

(9)

②获取邻域神经元信息并更新权值。

根据竞争过程产生的获胜神经元的索引确定获胜神经元在隐藏层中的位置，并根据邻域半径确定其邻域神经元。根据已获得的获胜神经元的信息更新邻域神经元的权值信息，权值更新为

${{\boldsymbol{w}}^{g + 1}} = {{\boldsymbol{w}}^g} + {\eta ^g}({\boldsymbol{x}} - {{\boldsymbol{w}}^g})$

(10)

${\eta ^{g + 1}} = {\eta ^g} \times\left(1 - \frac{g}{{1 - G}}\right)$

(11)

式中：g为当前代数；G为最大迭代代数； $\eta$ 为学习率。

2)获得合适的引导粒子。根据1)中构建的SOM网络，记录种群内每个粒子对应的获胜神经元及每个获胜神经元的邻域神经元，将获胜神经元及其邻域神经元对应的粒子组成引导粒子的备选库，并采用非支配排序法选择排序在第一位的粒子作为当前的引导粒子。

3)粒子速度和位置更新。

$\begin{array}{l} {{\boldsymbol{v}}_i}^{g + 1} = {w'} \times {{\boldsymbol{v}}_i}^g + {c_1}{r_1}({x_{{\rm{pbest}}}} - {{\boldsymbol{x}}_i}^g)+\\ \;\;\;\;\;\;\;\;\;\;\;\;\; {c_2}{r_2}({x_{{\rm{nbest}}}} - {{\boldsymbol{x}}_i}^g) \end{array}$

(12)

${{\boldsymbol{x}}_i}^{g + 1} = {{\boldsymbol{x}}_i}^g + {{\boldsymbol{v}}_i}^{g + 1}$

(13)

式中： ${\boldsymbol{v}} = \left( {{v_1},{v_2}, \cdots {v_D}} \right)$ 表示粒子速度； $w'$ 为惯性权重；r₁和r₂是在(0，1)区间正态分布间的随机数；c₁和c₂是两个加速因子； ${x_{{\rm{pbest}}}}$ 是个体历史最优； ${x_{{\rm{nbest}}}}$ 是个体邻域最优。

4)粒子速度和位置超出临界值修正。在进行粒子速度和位置更新时，若粒子速度超出临界值，则将其设置为临界值；若粒子位置超出临界值，则将粒子位置设置为临界值并将该点粒子的速度设置为当前速度的相反数。

5)当g≥G时，算法停止。否则回到1)。

2.3 协方差矩阵自适应策略搜索

协方差矩阵自适应策略(covariance matrix adaptation evolutionary strategies，CMA-ES)主要步骤如下^[19]：

1)对种群内所有粒子进行采样。采样即利用正态分布得到粒子的 $ \lambda $ 个新搜索点作为进入下一代进化的候选解，其采样公式为

${{\boldsymbol{x}}_k}^{g + 1} = {{\boldsymbol{e}}^g} + {\sigma ^g}N(0,{{\boldsymbol{C}}^g}),$

(14)

${{\boldsymbol{e}}^g} = \sum\limits_{{\rm{1}} \leqslant i \leqslant \lambda }^\lambda {{w_i}{{\boldsymbol{x}}_i}^g}, $

(15)

$\sum\limits_{i = 1}^\lambda {{w_i} = 1,} {w_1} \geqslant {w_2} \geqslant {w_3}\geqslant \cdots \geqslant {w_\lambda } > {\rm{0}},$

(16)

式中： $ \lambda \geqslant 2$ ^[20]；k代表第g+1代中第k个个体； ${{\boldsymbol{e}}^g} \in {{\bf{R}}^n}$ 是已被挑选入第g代种群的所有个体的加权平均位置； ${\sigma ^g} \in {{\bf{R}}^ + }$ 是第g代种群进化的步长； ${{\boldsymbol{C}}^g} \in {{\bf{R}}^{D \times D}}$ 是第g代种群进化的协方差矩阵； $ N\left( {0,{{\boldsymbol{C}}^g}} \right)$ 是均值为0，协方差矩阵为 $ {{\boldsymbol{C}}^g}$ 的多元正态分布； ${w_i}$ 是采样后产生的个体的权值。

采样完成后，重新计算 $ {e^{g + 1}}$ 并设置每个个体的权值，使质量更好的个体有更大概率进行下一步操作。

2)协方差矩阵更新。使用秩- $ \mu$ 更新模式来计算连续进化代之间的变异步长，并调整协方差矩阵。协方差矩阵的更新分为两个部分，第1部分是对进化路径进行更新，公式为

$\begin{array}{l} {\boldsymbol{P}}_c^{g + 1} = {h_\sigma }\sqrt {{c_c}(2 - {c_c}){\mu _w}} ({{\boldsymbol{e}}^{g + 1}} - {{\boldsymbol{e}}^g})/{\sigma ^g} {\rm{+ }}(1 - {c_c}){\boldsymbol{P}}_c^g \end{array} $

(17)

${h_\sigma }(c) = \left\{\begin{aligned} {1,\quad c \geqslant 0}\\ {0,\quad c < 0}\end{aligned} \right.$

(18)

${\mu _w} = \frac{1}{{\displaystyle\sum\limits_i^\lambda {{w_i}^2} }}$

(19)

式中： $ {h_\sigma }$ 为Heaviside函数； $ c_c$ 为权值系数； $ {\mu _w}$ 为方差有效选择质量^[20]。第2部分是对协方差矩阵进行更新，公式为

${{\boldsymbol{C}}^{g + 1}} = (1 - {c_\gamma }){{\boldsymbol{C}}^g} + {c_\gamma }{\boldsymbol{P}}_c^{g + 1}{({\boldsymbol{P}}_c^{g + 1})^{\rm{T}}}$

(20)

其中 $ {c_\gamma }$ 是协方差矩阵的学习率。

3)全局步长控制。全局步长控制进化路径更新与2)的进化路径相似，公式为

$\begin{array}{l} {\boldsymbol{P}}_\sigma ^{g + 1} = \sqrt {{c_\sigma }(2 - {c_\sigma }){\mu _{{\rm{eff}}}}} ({{\boldsymbol{e}}^{g + 1}} - {{\boldsymbol{e}}^g})/{\sigma ^g} {\rm{+ }}(1 - {c_\sigma }){\boldsymbol{P}}_\sigma ^{(g)} \end{array} $

(21)

式中： $ {c_\sigma }$ 为进化路径的学习率； ${\mu _{{\rm{eff}}}}$ 为方差有效选择质量，计算方式与 $ {\mu _{w}}$ 一致^[20]。

全局步长更新公式为

${\sigma ^{g + 1}} = {({\sigma ^g})^{\frac{1}{{{{\rm d}_\sigma }}}\left(\frac{{\left\| {{{\boldsymbol{p}}_\sigma }^{g + 1}} \right\|}}{{E\left\| {N(0,{\boldsymbol{I}})} \right\|}} - 1\right)}}$

(22)

其中 $ {d_\sigma }$ 是接近阻尼1的系数。

4)停止准则。当算法消耗评价次数大于CMA-ES算法最大评价次数时，算法停止。否则，回到2)。

2.4 融合分区和局部搜索的多模态多目标进化算法

基于2.1~2.3节，融合分区和局部搜索的多模态多目标算法的具体实现步骤如下：

输入　种群规模NP；算法最大评价次数A；分区数量z_n；粒子群参数w、r₁、r₂、c₁、c₂；子空间外部存档容量Q；CMA-ES算法参数 $c_\gamma $ 、 $c_c$ 、 ${c_\sigma }$ 、局部搜索步长 $\sigma $ 、单个个体进行CMA-ES搜索消耗的最大评价次数A₁；单个个体进行CMA-ES搜索消耗的累计评价次数A₂；CMA-ES算法加入时消耗的算法总评价次数A₃；算法累计评价次数A₄。

输出　PS^*和PF^*。

1)初始化种群 ${\boldsymbol{x}} = \left( {{x_1},{x_2}, \cdots {x_{{\rm{NP}}}}} \right)$ ，子空间外部存档Q，A₁=12，A₂=0，A₃=0，A₄=0；CMA-ES算法其他参数与文献[19]保持一致。

2)根据2.1节对决策空间进行分割，得到4个子空间。

3)在各个子空间中使用2.2节的多模态多目标进化算法进行搜索。

4)当A₃=0时，分别对各个子空间中得到的非支配解使用2.3节的局部搜索算法。当单个粒子消耗的累计评价次数大于A₁时，该粒子的局部搜索过程结束。下一粒子继续进行局部搜索。直到NP个粒子完成局部搜索，或者A₄≥A时局部搜索结束。

5)每个参与局部搜索的粒子与其产生的子代均使用基于特殊拥挤距离的非支配排序法^[4]进行排序，排在第一位的粒子取代原本参与局部搜索的粒子进入粒子群，其余非支配解均加入外部存档。当外部存档内的非支配解个数大于外部存档容量Q时，继续使用基于特殊拥挤距离的非支配排序法进行排序，将前Q个解保留。若外部存档内非支配解个数小于Q，则全部保留。

6)循环3)~5)，直到A₄≥A₁时跳出循环。

7)将每个子空间内最后一代粒子群与子空间外部存档合并，使用基于特殊拥挤距离的非支配排序法选出每个子空间的非支配解。将4个子空间的解集合并后使用环境选择得到最终解集 ${{\rm{PS}}^*} = {\rm{selection}}({{\rm{PS}}_1}^* \cup {{\rm{PS}}_2}^* \cup {{\rm{PS}}_3}^* \cup {{\rm{PS}}_4}^*)$ 和近似帕累托前沿 ${{\rm{PF}}^*} = {\rm{selection}}({{\rm{PF}}_1}^* \cup {{\rm{PF}}_2}^* \cup {{\rm{PF}}_3}^* \cup {{\rm{PF}}_4}^*)$ 。

3 实验结果与分析 3.1 测试函数

为验证ZLS-SMPSO-MM的性能，本文选取14个多模态多目标优化问题对其进行测试。其中，8个MMF问题^[4]、3个SYM-PART问题^[21]、3个OMNI问题^[22]，详情见表1。所有优化问题的目标个数均为2，MMF问题与SYM-PART问题的空间维度为2，OMNI问题的空间维度分别为3、4、5。PSs的数量表示决策空间中的不同PS对应目标空间同一个PF的数量，PSs的数量越大，问题的求解难度也会相应增大。最后一列表示的是PSs在决策空间的每一维度是否重叠，一般情况下，PSs在决策空间的重叠会增加问题的复杂度。

3.2 实验设置

为验证ZLS-SMPSO-MM的性能，本文选取5种多模态多目标进化算法来进行比较。其分别是DN-NSGA-II^[2]、Omni-optimizer^[22]、MO-Ring-PSO-SCD^[4]、SMPSO-MM^[5]、Zoning-MO-Ring-SCD-PSO^[7]。同时，所有比较算法的参数设置与原文献一致。本实验中所有测试函数均为2目标问题，所有测试函数的种群数量均设置为800，最大评价次数为80000，单个粒子使用CMA-ES算法的评价次数设置为12。外部存档容量设置为800。每种算法在测试函数上均独立运行20次。为保证实验结果分析的可靠性，采用Wilcoxon^[23]和Friedman^[24]非参数检验方法对实验结果进行统计分析，显著性水平设置为5%。其中“+”、“−”分别表示所提算法优于、劣于相比较算法；“≈”表示所提算法与相比较的算法性能相近。

3.3 结果对比

ZLS-SMPSO-MM与其他5种比较算法所得PSP值的平均值和标准方差见表2。同时，由Wilcoxon得到的统计分析结果也在表2中显示。从表2可以看出，所提算法在14个测试函数上所得结果都要显著好于DN-NSGA-II、Omni-optimizer、MO-Ring-PSO-SCD、ZS-MO-Ring-SCD-PSO。相比于SMPSO-MM，除在MMF₃函数上取得相似的结果，ZLS-SMPSO-MM在其他测试函数上都能得到更好的结果。同时，这6种算法得到的PSP值排序结果如下表3，在该表中，利用Friedman非参数检验方法对实验结果进行统计分析时，将所有算法得到的测试函数的PSP值均取为其相反数，故排序值越小，算法性能越佳。根据表3结果可得，ZLS-SMPSO-MM在所有比较算法中性能最佳。这是因为使用多模态多目标进化算法进行搜索前先使用分区策略划分了决策空间。在各个互不重叠的子空间区域使用相同规模的粒子群分别进行空间搜索，提升种群多样性的同时也降低了各个子空间的搜索难度；每个子空间内都引入局部搜索算法，在每次全局搜索后的潜力区域用局部搜索能力强的CMA-ES算法进行精细搜索，因此能够找到更多高质量的解。

ZLS-SMPSO-MM与其他5种比较算法所得HV值的平均值和标准方差见表4。同时，由Wilcoxon得到的统计分析结果也在表4中显示。从表4中可以看出，ZLS-SMPSO-MM只在MM7、SYM-I、SYM-II、SYM-III和OMNI-I这5个测试函数中得到较好的结果，Omni-optimizer则在剩余的9个测试函数中占优势，但它们之间的数值差异并不是很显著。这6种比较算法得到的HV值排序结果见表5，ZLS-SMPSO-MM排在第二位。主要原因是ZLS-SMPSO-MM中采取的分区策略和局部搜索只能改变算法在决策空间的性能，对目标空间的影响十分有限。目标空间中仍旧采取了之前的选择策略，因此性能提升效果不明显，但相对于除Omni-optimizer外的其他算法，所提算法在目标空间的表现还是要优于其他4种算法。因此，若是想提升算法在目标空间的性能就必须在目标空间中使用合适的多目标处理技术。

综合各算法的PSP值和HV值实验结果，所提ZLS-SMPSO-MM算法获得的帕累托解集能够较好地逼近真实帕累托前沿，相比于其他算法具有更好的收敛性和多样性。

3.4 算法分析 3.4.1 分区搜索与局部搜索对算法的影响

为验证分区搜索与局部搜索的有效性，该部分实验分别选取没有分区搜索和局部搜索的SMPSO-MM、有分区搜索但没有局部搜索的SMPSO-MM(命名为ZS-SMPSO-MM)来和所提算法进行性能比较。同时，所有算法参数设置与3.2节一致；并挑选3.2节14个测试函数进行实验，所得结果见表6。

从ZLS-SMPSO-MM和ZS-SMPSO-MM的结果来看，除MMF₁、MMF₄、MMF₆、MMF₅、MMF₇这5个测试函数外，ZLS-SMPSO-MM在其余测试函数上得到的PSP值均明显优于ZS-SMPSO-MM，尤其是在较复杂的SYM函数与OMNI函数上。这说明局部搜索策略能够有效辅助多模态多目标进化算法找到更高质量和更多的等效解。从ZLS-SMPSO-MM与SMPSO-MM的结果来看，除MMF₃测试函数外，所提算法能够在所有测试函数上取得更佳效果。这表明分区搜索和局部搜索能够有效帮助SMPSO-MM算法找到更多的等价解。主要是由于分区搜索能够维持算法种群多样性和降低问题求解难度，而局部搜索能够提高搜索精度。另外，从ZS-SMPSO-MM与SMPSO-MM的结果来看，除MMF₃、SYM-I、SYM-II这3个测试函数外，其余测试函数的PSP值均显著优于SMPSO-MM，从实验结果可知，分区搜索能够帮助SMPSO-MM算法定位到更多的等效解，该结论与文献[7]一致。

由于测试函数的帕累托解在整个决策空间并非均匀分布，因此均衡的分区策略会浪费一些计算资源，如测试函数MMF₃，SMPSO-MM加入分区搜索后，其PSP值反而下降。但总体来说，同时使用分区搜索与局部搜索能够提高算法求解多模态多目标问题的能力。

3.4.2 局部搜索评价次数A₁敏感值分析

由于局部搜索会消耗一定的计算量，局部搜索过多消耗计算资源可能使算法全局求解能力下降，而过少消耗计算资源则可能导致局部搜索算法能力发挥不足。故本部分对单个粒子进行局部搜索使用的评价次数进行分析，并用PSP性能指标来对实验结果进行评价。选取3.1节的14个测试函数进行实验，并将单个粒子进行局部搜索使用的评价次数A₁设定为4、8、12、16，其他参数设定同3.2节。

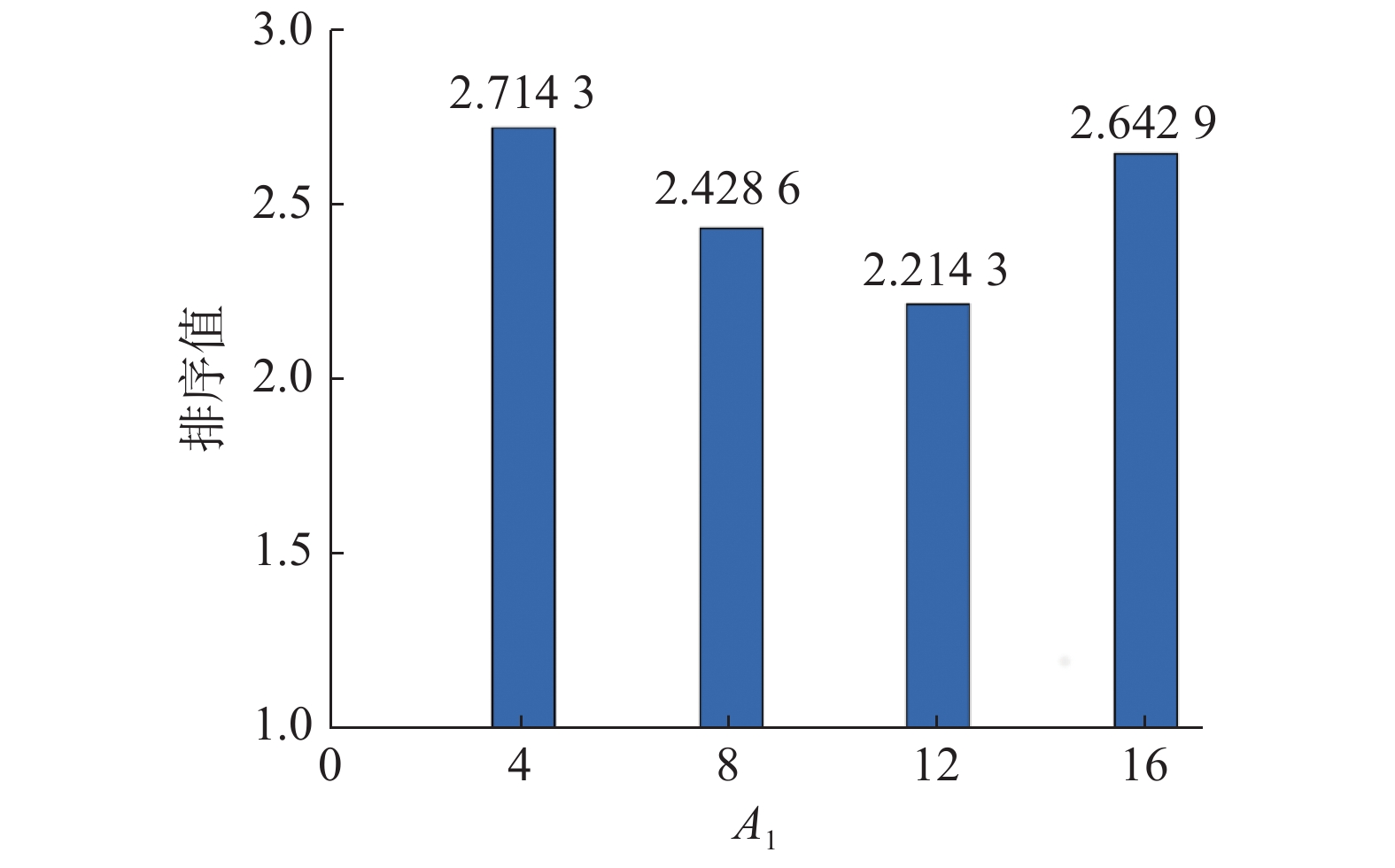
所得结果使用Friedman测试来进行性能排序，见图1。从图1中可以看出，一开始随着局部搜索评价次数的增加，算法的性能也会得到相应的提升，但随着评价次数增加到一定的程度，算法的性能反而会降低。这是因为合适的局部搜索评价次数能平衡局部搜索能力与全局搜索能力。另外，根据图1的结果显示，当 $ A_1=12$ 时，算法的性能表现最佳，因此在所提算法中将 $ A_1$ 设置为12。

3.4.3 局部搜索评价次数A₃敏感值分析

使用局部搜索的时间对算法性能会产生影响。直观来看，过早使用局部搜索会因为所寻得的区域潜力不足而浪费计算资源，过晚使用则可能无法发挥局部搜索的真正作用。因此，本节对局部搜索的使用时间进行分析，并用PSP性能指标来对实验结果进行评价。选取3.1节的14个测试函数进行实验。将局部搜索的使用时间设置为算法已消耗的评价次数。使用时间分为 $ A_3=0$ 、 $A_3=2\;000$ 、 $A_3=4\;000$ 和 $A_3=6\;000$ 。除该参数外其余实验参数设置同3.2节。

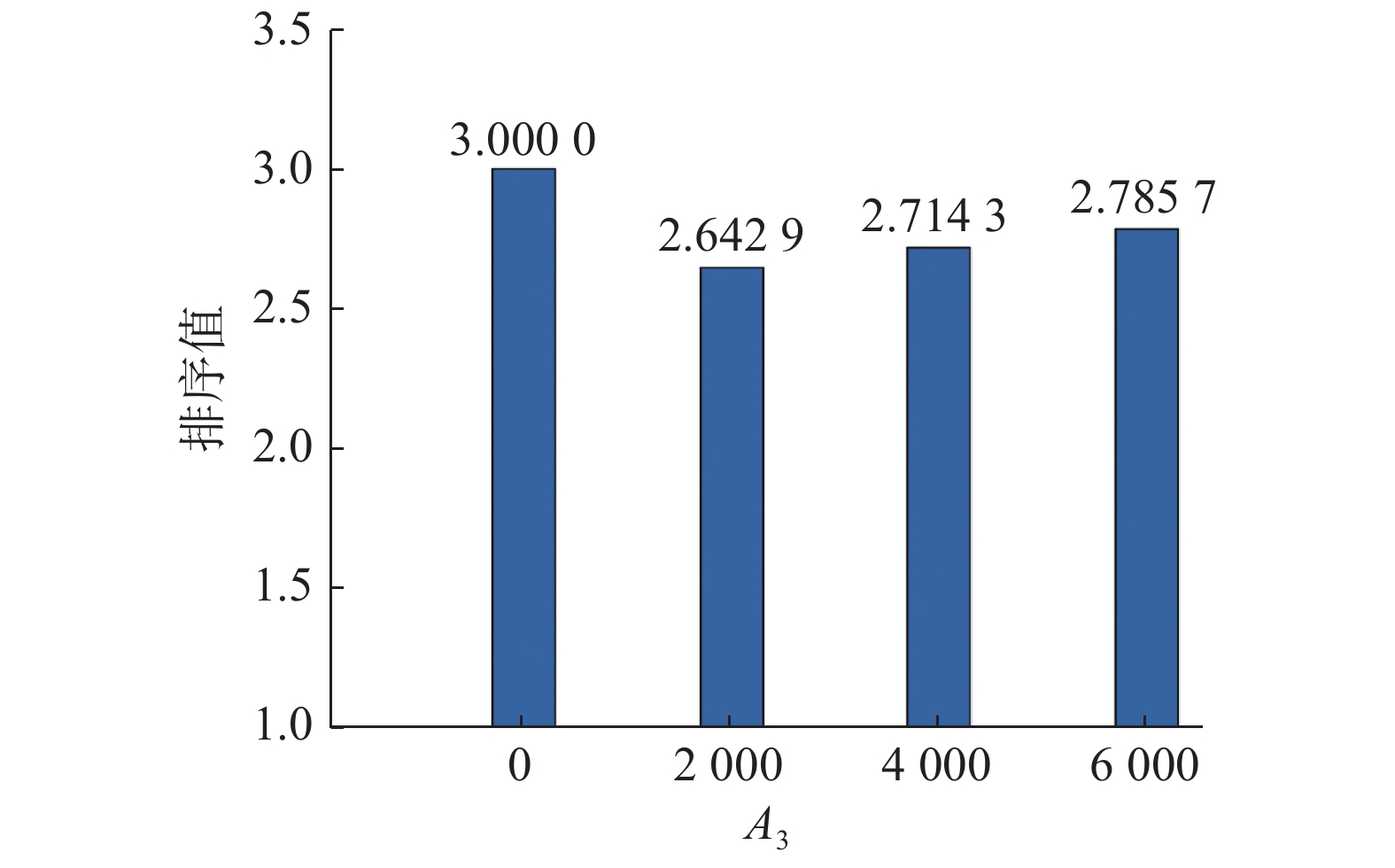
所得结果使用Friedman测试来进行性能排序，见图2。从图2中可以看出，在种群进化前期加入局部搜索能够更加有效帮助算法找到更多的等效解。其主要原因是局部搜索能够在较短时间内辅助多模态多目标进化算法找到高质量的解。当然，这完全取决于算法能否在进化前期就能找到有潜力的搜索区域。另外，图2表示当算法已消耗评价次数不小于2 000时，其能使所提算法性能达到最佳，因此在所提算法中设置 $A_3=2\;000$ 。

3.4.4 种群规模敏感值分析

为分析种群规模对算法的影响，本实验选取第3.1节的14个测试函数；使用PSP作为算法性能评价指标；并将种群规模分别设定为400、800、1 200、1 600，其他参数设定同第3.2节。最大评价次数均为80 000。

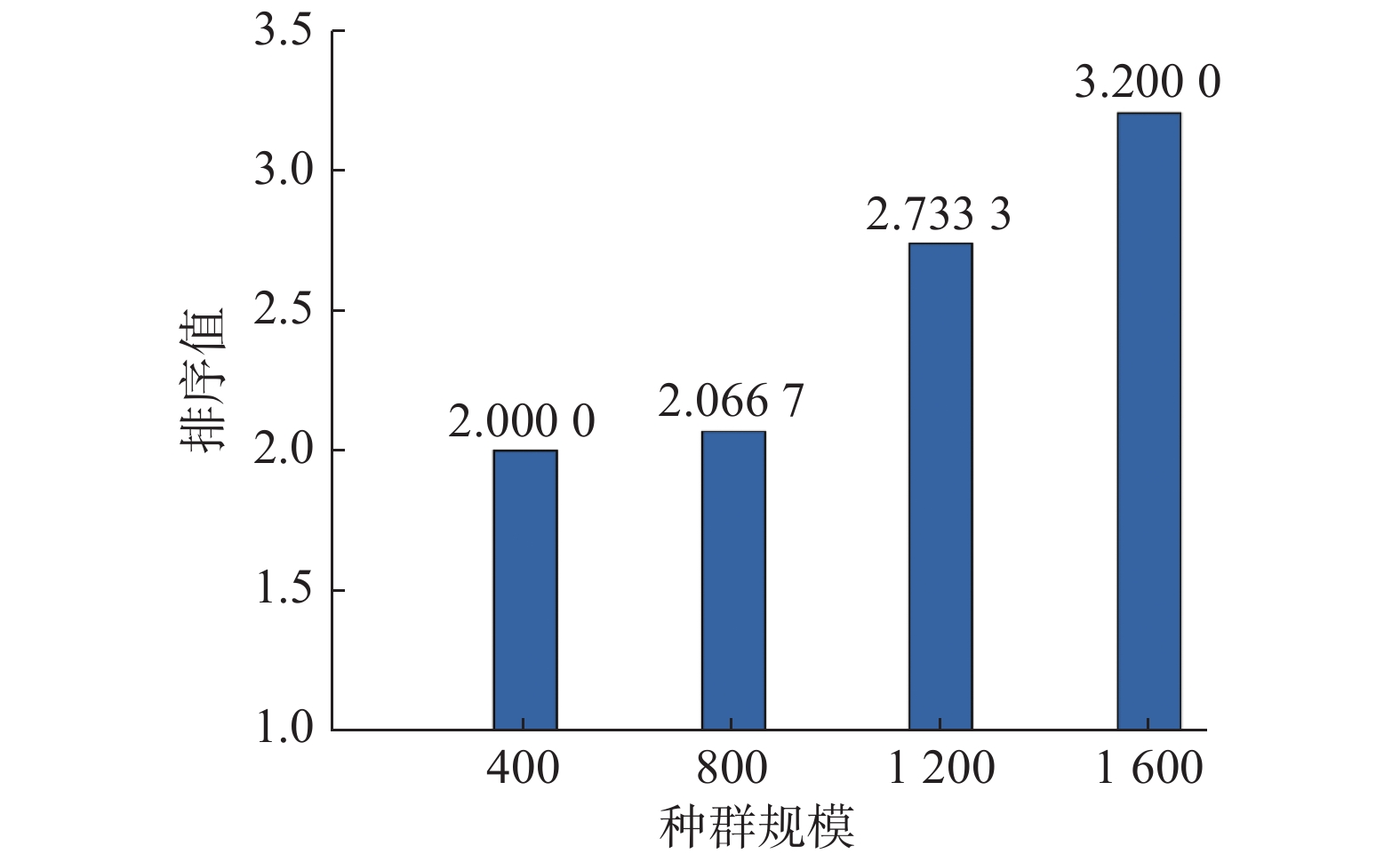
所得结果使用Friedman测试来进行性能排序，见图3。从图3中可以看出，随着种群规模的增加，算法的性能逐渐降低。其主要原因是，虽然大的种群规模可以提高各个分区的种群多样性，但在计算资源有限的情况下，搜索代数会减小，这将直接影响算法的搜索效率。同时，当算法种群规模在400时，算法的性能最佳。但为与第3.2节中比较算法的种群规模保持一致，所提算法的种群规模仍设置为800。

4 结束语

为提高多模态多目标进化算法在搜索过程中的种群多样性和搜索等价解的能力，本文提出一种融合分区和局部搜索的多模态多目标粒子群算法ZLS-SMPSO-MM。在该算法中，首先将整个搜索空间分成多个子空间，然后使用多模态多目标粒子群算法对各个子空间进行搜索，并使用局部搜索来提高算法的搜索效率，最后将各个子空间所得解集进行合并选择。为验证ZLS-SMPSO-MM算法的性能，选取14个多模态多目标优化问题，并将其与DN-NSGA-II、Omni-optimizer、MO-Ring-PSO-SCD、SMPSO-MM、ZS-MO-Ring-SCD-PSO等多模态多目标算法进行比较。实验结果表明，分区搜索和局部搜索能够有效帮助SMPSO-MM找到更多的等价解。