2. 鹏城实验室,广东 深圳 518000
2. Peng Cheng Laboratory, Shenzhen 518000, China
生物学家研究发现,经过数亿年的演变,许多动物都进化出了感知外界环境信息并将其用于导航的奇异能力[1-3]。与人类依赖高科技和精密设备不同,自然界中的生物通过其特有的生理结构,仅依赖环境信息就可以实现精确导航,从而实现觅食、归巢及长途迁徙等行为。人类至今难以制造出仅依赖环境信息导航的装置,但对于生物导航功能的模拟,却是当前仿生学的研究重点之一[4-6]。仿生导航技术是通过模仿自然界生物体某些感知能力,并将感知的信息转化与处理得到导航参数的一种技术。仿生导航具备不依赖卫星导航系统、高性能、高自主、抗干扰等优势。
信鸽在放飞之后成功安全归巢的能力在所有动物中名列前茅,同时由于信鸽长久以来被人类驯养,其可控性高、数目多且较易观察,具有较高的研究价值。同时,生物学家通过Clock-Shift实验、外加磁场干扰实验、脑电波响应等行为学、神经学研究,验证了鸽子对于太阳、地磁场及地面景观的依赖性。无人机已经成体系地发展出全球定位系统(global positioning system,GPS)导航、惯性导航等导航方式,但GPS信号易受复杂任务环境干扰,惯性导航系统存在严重的累计误差,并且2种导航方式均缺少场景感知能力,相比于生物导航系统智能性较低。信鸽的智能导航归巢行为与无人机视觉自主导航技术需求十分吻合,如果能够将信鸽导航归巢过程中涌现出的行为机制应用于无人机自主导航,无疑具有广阔的应用前景。
1 信鸽归巢导航行为信鸽从遥远而陌生的地方成功归巢的能力在所有动物中名列前茅,现有的生物学研究得到许多鸟类导航知识均来自信鸽实验。利用信鸽作为实验对象优势突出:信鸽早在4000多年前被人类驯养,数量足够多;鸽子有可靠的且强烈的归巢动机,为生物学家提供了一个坚实的实验基础;由于长期驯养,它们习惯于被处理,所以其归巢行为可以很容易评估。
1.1 信鸽地图罗盘导航行为机制对鸽子导航的系统分析始于20世纪中叶,得益于Kramer等研究人员的2个重要发现:一是迁徙鸟类更倾向于自然的迁徙方向;二是非迁徙的鸟类被释放时,大多向着离家方向不远的方位出发[2]。当鸽子从陌生地方归巢时,通常是远离鸽房且远远超出了任何直接的感官接触的范围。然而,鸽子仍然能够成功地朝那个方向飞行并到达它。这意味着鸽子借助于外部参照物——罗盘,间接地与目标建立联系,而并不需要知道目标的具体位置。Kramer[3]首次提出“Map-and-Compass”模型,该模型是鸽子导航的核心模型之一,它把鸽子归巢行为描述为2个步骤:1) 鸽子确定它们相对于鸽房的位置,并将归巢方向作为罗盘航向。这相当于人类使用地图获得方向信息,用人类的话,类似于“在南边”这样的描述;2) 通过查阅罗盘来定位这个航向,获得诸如“这条路”或“去那里”之类的信息,指出它们实际飞行的方向[4-5]。
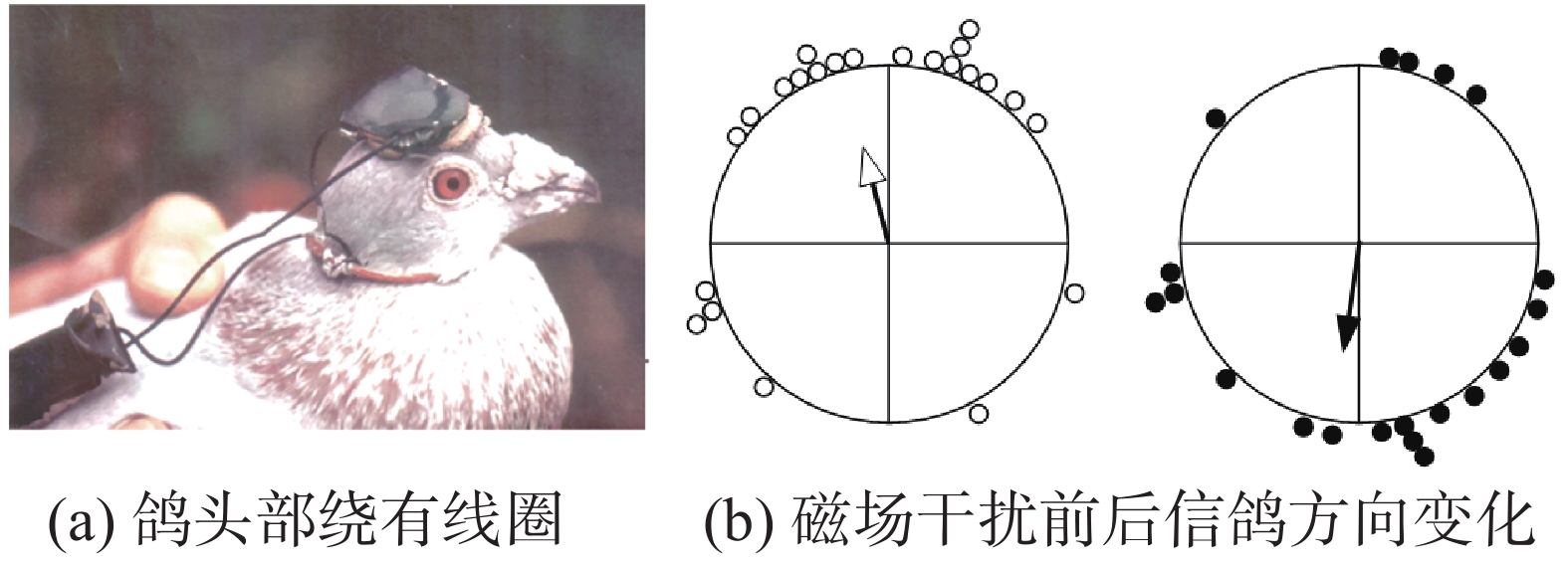
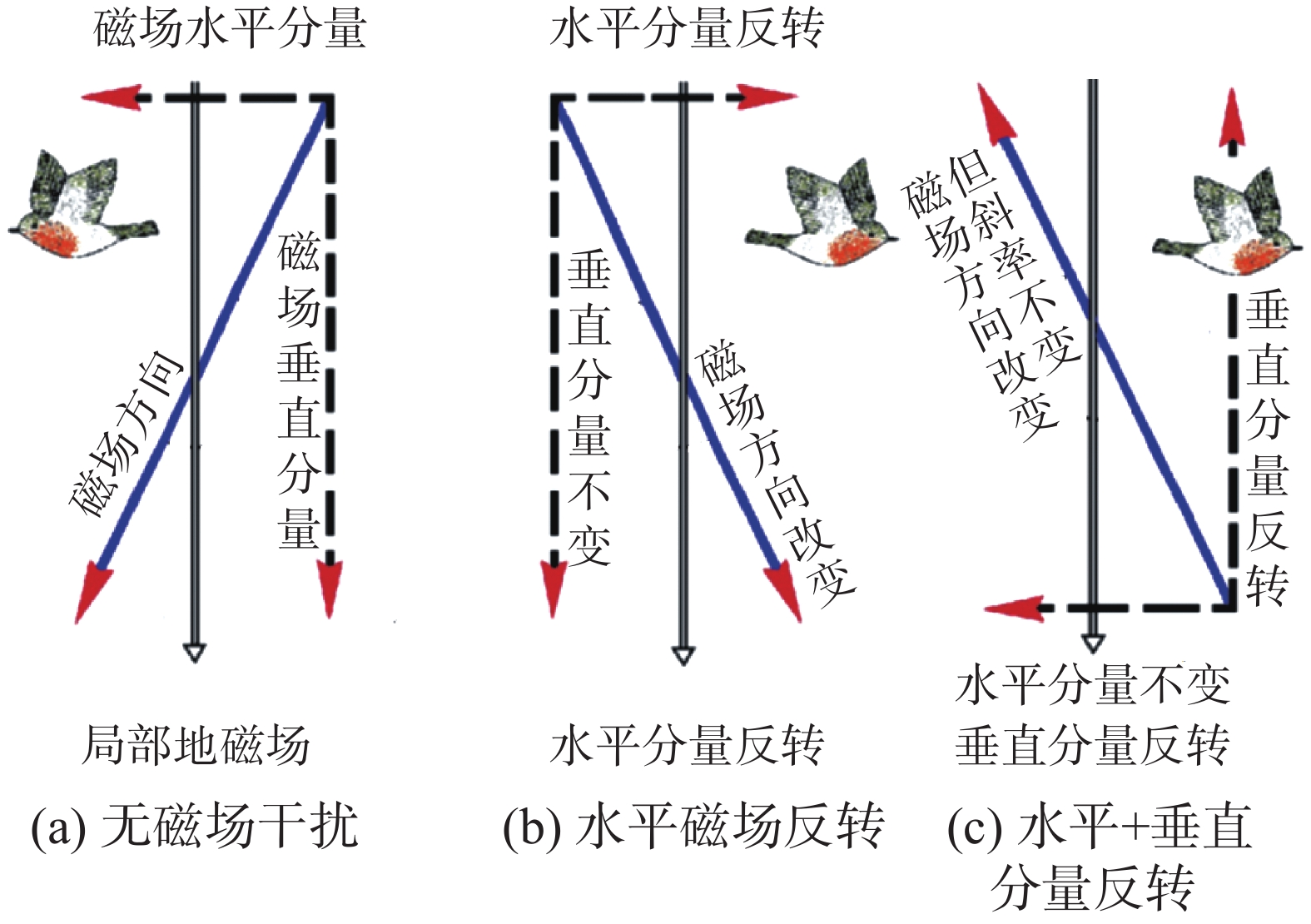
鸽子在地磁场中的定向能力在20世纪60年代首次在候鸟身上得到证实。这得益于在迁徙季节,鸟类在圈养时也表现出对季节适宜的迁徙方向的强烈偏好,这些定向趋势可以通过一种漏斗形的定向笼中记录,Emlen [6]设计了这种定向笼,首先验证了欧洲罗宾鸟的罗盘依赖性。这种笼子的有限空间可以比较方便地改变环境磁场条件,使用亥姆霍兹线圈干扰周围磁场,使其水平分量偏移,而倾角和强度保持不变。该行为学实验的意义在于:如果欧洲罗宾鸟依赖磁罗盘,它们应该跟随磁北的移动并改变其飞行方向。鸽子虽然是非迁徙鸟类,缺乏与迁徙相关的方向偏好,但有强烈的归巢的倾向,会在释放后朝着鸽房的方向飞行。1974年,Walcott等[7]采用定向笼验证了鸽子的磁盘依赖性,如图1所示,图1(a)为鸽子头上绕着一线圈,图1(b)是在阴天释放的鸽子消失方位,感应磁场的S极向上,N极向下,通过控制线圈的极向控制磁场方向,箭头表示平均向量。结果表明,当磁极被翻转时,鸽子跟随这种转变改变了飞行方向,这表明它们在磁场的帮助下定向。此后,Wiltschko发现鸽子的磁罗盘是一种倾角罗盘,其导航特性与磁性无关。如图2所示,在北半球地磁场的垂直分量指向下方;当垂直分量倒转指向上方时,技术指南针仍然指向北方,但鸽子却反向飞行。2001年,Åkesson等发现鸟类在北极附近,磁罗盘在与垂直方向略微偏离小于3°的倾角仍然能够定向。2015年,Lefeldt等[8]在Åkesson实验的基础上,通过实验室验证,得到了相应的结果,进一步确认了鸽子磁罗盘是倾角罗盘。
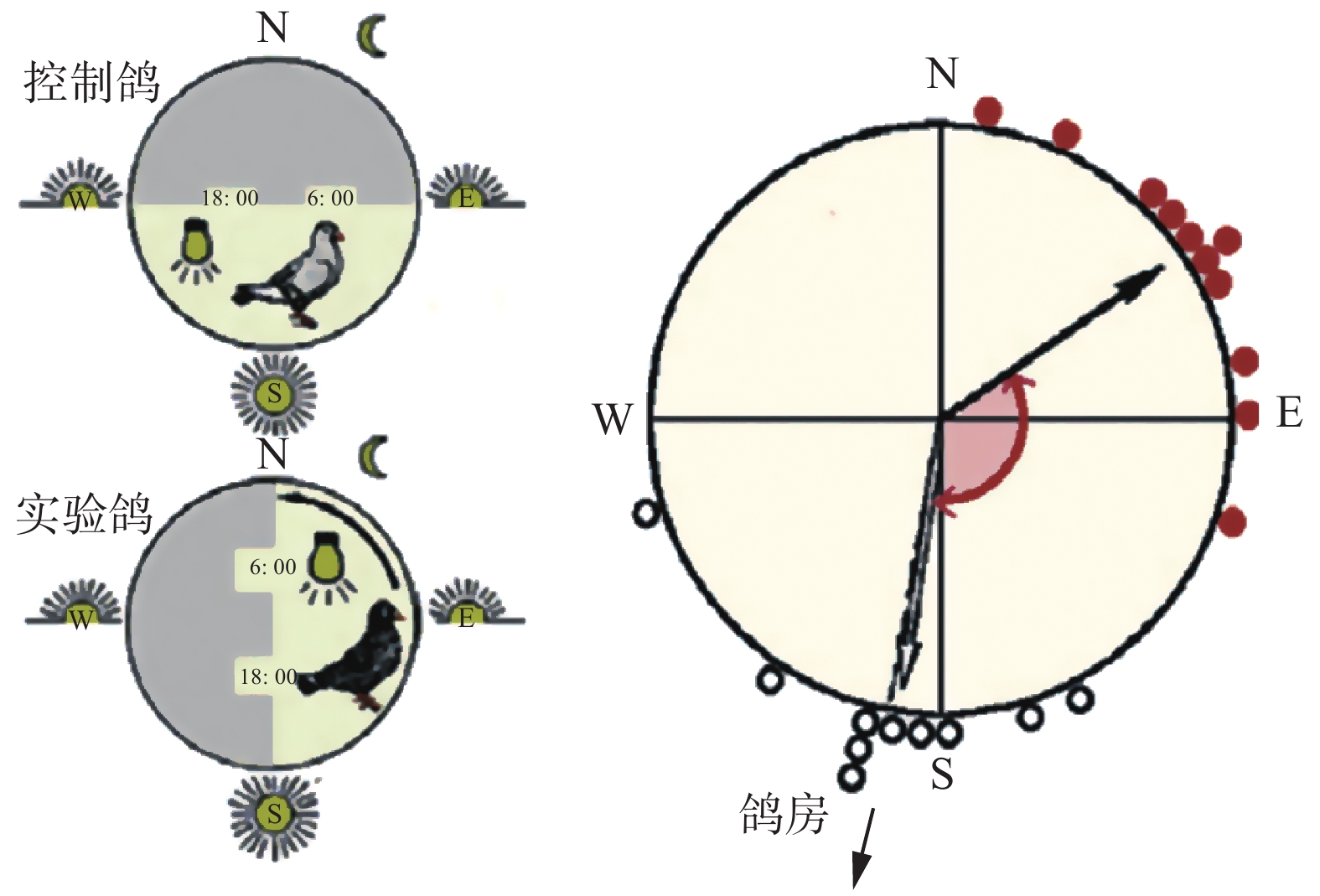
为了验证太阳罗盘的作用,Koeing等[9]在 1958 年设计了著名的 Clock-Shift 对照实验。测试鸽被关在一个封闭的房间,通过自然日出前6 h开始和日落前6 h结束的光周期,将鸽子内部时钟的设置前移6 h,并连续至少5 d,重置其内部时钟;对照组鸽子则不作处理,即按照正常的时间处置。然后对所有鸽子进行释放实验,观察并统计其飞行方向,来判断太阳的罗盘的作用。结果表明,测试鸽在晴天里释放后,与对照鸽比较,它们对太阳的位置判断出现误差。如图3所示。测试鸽误判了太阳的位置,例如,早上6:00放出的鸽子把东方的朝阳解释为南方的中午太阳,如果打算朝南飞行,则改为朝东飞行。这种典型的逆时针偏转,表明鸽子使用太阳罗盘。
基于Clock-shift实验的结果,早期的研究人员认为鸽子已通过太阳的角度判断方向,并假设太阳的平均前进速度为15°/h,预计6 h的时钟偏移中会出现大约90°的偏转。这样的假设看似能够解释鸽子方向的转变,但实际上太阳方位角的变化不是线性的。日出和日落前太阳方位角几乎没有变化,而中午左右太阳方位角变化较大。同时,太阳弧的具体形式在很大程度上取决于地理纬度和季节:在高纬度地区,太阳弧相对平坦,在低纬度地区,太阳弧要陡得多。2000年,德国工程院院士Wolfgang Wiltschko和他的学生通过在新西兰奥克兰附近的一系列Clock-Shift实验对这个问题进行了验证[10]和他的学生通过在新西兰奥克兰附近的一系列 Clock-Shift 实验对这个问题进行了验证。因为地处南纬37°,夏季太阳方位角变化率的差异是相当大的:在日出后的第一个小时内和日落前的最后一个小时内,太阳的前进速度小于10°,而在中午的一个小时内,其速度超过40°。鸽子被释放时,内部时钟基于太阳方位角移动了4 h。观察到鸽子能够分辨不同时间太阳方位角的不同变化率,并对它们进行了补偿。鸽子在归巢的过程中,导航能力会因为太阳高度改变而改变。
1.2 信鸽视觉地标导航行为机制除了依赖太阳和磁场这种自然因素,研究表明鸽子同样依赖视觉线索。2004年,Vyssotski等[11]利用 GPS 设备,对 50 km范围内记录的 216 只信鸽轨迹进行了分析。实验发现通往鸽房的公路和铁路对有经验的鸽子有显著的吸引力,它们通常会自主地沿着道路飞行,并使用路上的交叉口作为转折点校正方向。Vyssotski认为在飞行的早期和中期,沿着大而清晰的道路飞行很可能反映出罗盘航向的稳定性,而不需要导航地图;当鸽子接近鸽房区域时,更可能依赖认知地图,通过重复穿越熟悉地形点实现导航。但GPS对鸽子飞行轨迹的分析只能揭示地形特征对鸽子飞行轨迹的影响,对于视觉标志如何影响鸽子飞行无法说明,记录反映注意力处理的脑电波活动可以表明感兴趣的物体是否引起飞行路径的变化。因此,2009年,Vyssotski[12]又通过在鸽子飞行过程中携带记录 GPS 位置和脑电波(electroencephalogram,EEG)的记录器,分析了鸽子在海上和陆地上释放时,不同频带的变化。通过记录鸽子的脑电波发现,鸽子对于身下几百米的特殊地标会出现脑电波激活响应。
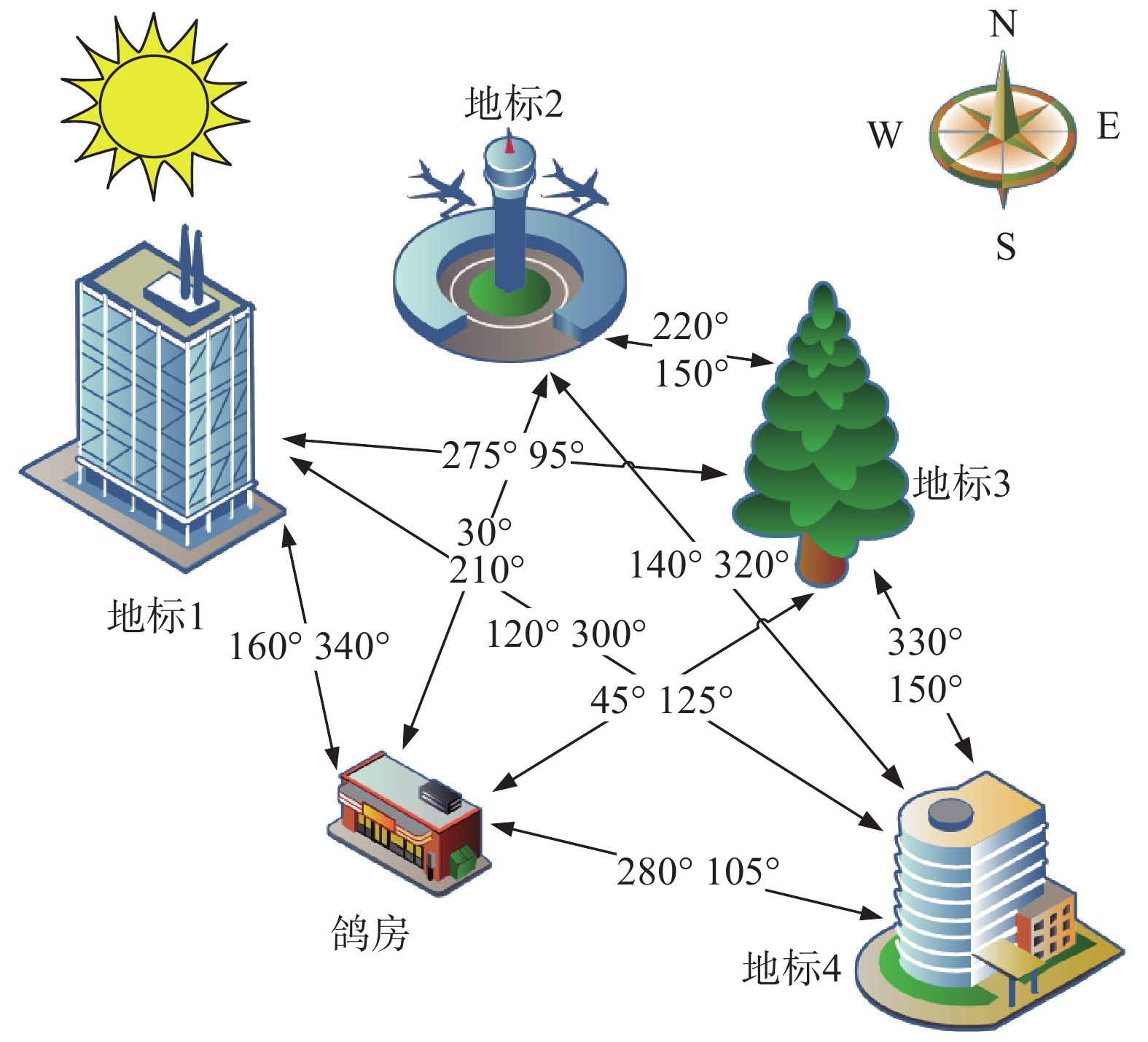
在接近鸽房的区域,本地环境梯度值和鸽房的梯度值之间的差异会低于可检测的阈值,因此在该区域鸽子必须依赖环境梯度以外的线索[13-14]。Wallraff在1974年提出了“马赛克地图(mosaic map)”是对鸽房附近区域突出地标分布的定向心理表征。马赛克地图的范围真实大小至今没有定论,并不是一个固定的值,通常估计其值在5~10 km。2011年,Schiffer等对法兰克福鸽房周围记录的鸽子足迹进行了数学分析,粗略估计了导航过程中涉及的因素数量;分析表明当鸽子接近鸽房时,除了依赖环境梯度之外,还包括地标。Wiltschko提出在鸽房附近一定范围内,鸽子可以直接以最优路径归巢,并将该区域为称为即时归巢区域(immediate home area)。2012年,她提出特殊地标组成 “马赛克地图”解释即时归巢区域,即鸽子能够记忆鸽房附近显著地标相对于鸽房及相互之间的相对位置关系。Wiltschko认为,马赛克地图的大小主要取决于2种情况:1) 鸽子能够区分梯度值差异的距离;2) 在鸽房区域是否有合适的特征性标志。这表明罗盘导航区域与即时归巢区域存在重叠,即使是在即时归巢区域,鸽子同样会受罗盘因素的影响。在即时归巢区域,鸽子可以依赖视觉识别鸽房附近的特殊地标,并利用其给出的方位信息辅助导航。如图4所示。
|
Download:
|
| 图 4 即时归巢机制示意 Fig. 4 Sketch map of immediate home mechanism | |
牛津大学的Biro等[14]通过GPS记录并跟踪了多只信鸽归巢路径,进行了一系列实验,研究鸽子的认知机制在归巢中的作用,发现鸽子不仅依赖于本地区内高度定型但效率低的路线,而且会被熟悉的路线吸引,进一步的研究证实了路径重演现象。这种精确的路径重演显示了整个飞行过程中对熟悉的地标的依赖,从而验证了熟悉的飞行路线对于信鸽视觉引导的作用[15]。2014年,Nagy等[16]利用GPS 设备获取鸽群的飞行轨迹,发现鸽群中的个体除头鸽外,其余跟随者也存在相应的飞行领导等级,位于低级的个体其行为不仅会受到头鸽的影响,也会受到其等级之上个体的影响,而往往来自于临近上级个体的影响更为直接迅速。这表明信鸽在集群飞行时通过视觉进行飞行速度和方向调整,这样做的明显优势在于,信息传递更高效迅速。
2 典型信鸽归巢导航模型为探索信鸽归巢多种复杂行为学实验的内在机理,研究其涌现出的智能导航行为的机制,半个多世纪以来,相关研究者尝试建立信鸽归巢导航的计算机仿真模型和数学分析模型,以描述信鸽导航行为特性。其中,对于影响信鸽归巢导航环境因素即导航罗盘的仿真建模方面的研究,开始的较早,最为人熟知的是Kramer在1957年提出的经典的“Map-and-Compass”模型。“Map-and-Compass”模型将鸽子归巢描述为两步走的过程:1) Compass步骤,即鸽子确定其相对于鸽房的位置并得到鸽房的方向作为罗盘方向;2) Map步骤,鸽子锁定这个方向并在导航地图的帮助下转为飞行方向。
然而在三维空间中飞行,单一罗盘无法确定鸽子的准确位置和方向;不考虑飞行高度的前提下,鸽子至少需要2个方向才能完成导航和定位。根据Map-and-Compass模型,Wallraff[17]提出为了确定罗盘方向,需要依赖在释放地点收集的信息,进行双坐标导航。鸽子获取特定地点的信息,利用环境梯度的局部标量值来确定其相对于鸽房的位置,然后借助导航地图来解释这些梯度值。这种利用双坐标导航的理论受地图网格系统的启发提出,环境场的两个几何参数即强度和斜率共同构成双坐标。1974年,Wallraff提出了双坐标导航的概念模型,认为鸽子至少需要2个参数确定其位置,并且参数值在空间中连续变化。
在“Map-and-Compass”模型和双坐标导航概念的基础上,Ulrich Nehmzow等[18]在 2001 年提出了一种鸽子导航的计算机仿真模型。该模型假设鸽子在具有2个相交梯度的环境中导航飞行,并且鸽子具有罗盘感知能够据此确定环境场的方向,具有梯度感知能够感知本地环境梯度。同时,该模型假设鸽子具有“导航地图”,可以据此确定环境梯度,并理解本地梯度与鸽房附近梯度的差异。该模型能够基本上实现与观测结果对应的仿真效果。
Wiltschko等[19]通过大量鸽子释放归巢实验的数据分析,提出了Nehmzow模型改进的版本,二者具有相似的假设,即两相交的环境梯度,鸽子具有梯度感知、罗盘感知能力,鸽子具有导航地图能够获取本地梯度并能理解本地与鸽房的梯度差异。二者的区别在于:1) 通过对大量鸽子释放实验的数据进行分析总结,得到了更加精确的仿真模型参数,对原始模型进行了修正;2) 考虑了更加复杂的模拟环境,即不单调或不正交的相交梯度情况;3) 提出“即时归巢区域”的概念,在该区域,鸽子将采用视觉线索辅助导航。
2011年,Postlethwaite等[20]提出一种几何模型模拟鸽子导航初始误差的生成过程,通过带有系统的误差的环境刺激轮廓包线,模型模拟鸽子导航开始时会导致对称方向误差,如图5所示,其中H为home点,R为释放点。该模型成功地预测了从信鸽行为学实验数据中发现的误差模式,但低估了误差的幅度。随后,Postlethwaite[21]对模型进行了扩展,考虑了3种包含更复杂的环境信号轮廓线畸变的情况,并计算了在每种情况下参数变化时的方位误差,最后讨论了这些结果对预测鸽子在它们用来导航的任何环境信号中遇到复杂扭曲时的影响。
除了对信鸽导航因素的模拟,研究人员对于信鸽导航状态和导航策略变化,也进行了建模分析。牛津大学的Guilford团队[22-23]利用小型GPS采集设备记录鸽子飞行轨迹,并根据飞行轨迹观测飞行行为中大的变化,推断可能的导航策略变化。Guilford假设鸟类复杂的导航行为可能是围绕一组定义不同导航策略的原型行为状态建模的,这种策略需要形成一组隐藏策略状态。然后利用GPS设备采集的鸽子个体的飞行轨迹数据,构成一个时间演化动力系统,采用混沌系统分析方法分析其复杂性,并采用隐马尔可夫模型对系统建模,建立了一个基于时空熵和概率隐马尔可夫模型的数学模型。最终,Guilford发现鸽子的归巢轨迹数据呈现一种鲁棒的三态结构。随后,Guilford进一步研究了实验结果和细节的行为学原因,着重研究视觉场景对信鸽导航策略切换的影响,提出了位置熵表征导航不确定性的假设,结合三态结构将熟悉区域导航分解为3种导航置信状态。
受Guilford的研究启发,Duan等提出了一种新的仿生智能优化算法——鸽群优化(Pigeon-inspired Optimization, PIO)算法[24]提出了一种仿生智能优化算法−鸽群优化 (pigeon-inspired optimization, PIO) 算法。PIO算法将影响鸽群归巢的关键原因分为2大类:1) 罗盘,包括太阳和地球的磁场;2) 地貌景观,而鸽子在飞行的过程中,根据不同的情况会使用不同的巡航工具。首先通过地磁场来对一个大概的方向进行辨别,然后利用地貌景象对目前的方向实施修正,直到到达精确的目的地。所以 PIO 算法中鸽子归巢有2个基本算子组成:罗盘算子和地标算子。通过模仿鸽子寻找目的地的导航机制,设计目标向量寻求全局最优解的迭代过程。
3 仿信鸽归巢行为的无人机自主导航 3.1 动态切换三阶段信鸽归巢导航模型现有的鸽子归巢导航模型大部分是基于行为学实验的分析和对观测结果的模拟,并且都集中在对自然因素如太阳和磁罗盘的研究,而对于视觉因素的建模则较少。Guilford基于位置熵提出的三态模型,从数据上推论出信鸽归巢过程呈现3种导航置信状态,但这是一种抽象模型,并没有具体到信鸽的导航行为。结合以上2个方面的研究,针对信鸽归巢导航所涌现出的地图罗盘导航、飞行中重定向和鸽房区域快速归巢的行为机制,并借鉴现有信鸽导航模型和位置熵理论,本文提出一种动态切换三阶段信鸽归巢导航模型。本模型将信鸽归巢过程具体化为3个阶段,分别为Map-and-Compass阶段、Leg Length阶段和Immediate Home阶段,并给出建模过程。
1) Map-and-Compass阶段
Map-and-Compass阶段对应信鸽依赖地图罗盘导航行为,此时鸽子处于高熵状态,对自己的位置最不确定,需要依赖自然罗盘收集与导航有关的信息。高熵状态包括2个时期:1) 释放后立即出现的典型时期,即信鸽依赖太阳或磁罗盘确定罗盘方向,并在“认知地图”的帮助下,确定目标方向;2) 信鸽在飞行一定距离后,且没有发现与归巢路线相关的显著标志性特征,会引发对位置的重新评估,从而导致回家方向的重新评估的时期。此时信鸽需要重新校正方向,这也与已有的研究现象相符合。这一过程与Kramer的“Map-and-Compass”模型是一致的。
假设鸽子具备罗盘感知与梯度感知,其感知精度受分别受参数CN和CN控制,并且罗盘读数与梯度值服从以真值为均值的标准正态分布,定义为
| $\varphi = {\varphi _{{\rm{true}}}} + {\rho _1} C_N$ | (1) |
| $\alpha = {\alpha _{{\rm{true}}}} + {\rho _2} C_N$ | (2) |
式中:
鸽子的导航地图是通过反复学习罗盘和环境梯度得到的,因此它也有噪声,但应比罗盘或梯度感知更精确。将地图的角度误差和陡度误差分别设置为CN和GN的25%,可以构建地图模型:
| ${\varepsilon _A} = 0^\circ + {\rho _3} C_N/4$ | (3) |
| ${\varepsilon _B} = {90^ \circ } + {\rho _4} C_N/4$ | (4) |
| ${\sigma _A} = 1 + {\rho _5} C_N/4$ | (5) |
| ${\sigma _B} = 1 + {\rho _6} C_N/4$ | (6) |
式中:
2) Leg Length阶段
Leg Length阶段是飞行中重定向期间的导航行为,即鸽子在飞行一定距离后,重新校正方向。在Leg Length阶段,鸽子处于中熵状态,此时鸽子对自己的归航方向有了合理的信心。按照Guilford的研究,此时使用鸽子导航行为的主要输入可能是以中间目标朝向精度的导航策略,因此可进行频繁调整。一种策略可能是使用视觉航路点,在航路点之间使用其他自我中心机制,如航位推算。本模型将Leg Length阶段定义为一种航位推算行为,此时鸽子不需要维护其飞行方向,而只需要维护其飞行距离;当飞行距离达到或超过Leg Length时,则再次进入Map-and-Compass阶段调整方向。因此,中熵状态可进行频繁调整。
对鸽子的Clock-shift实验的飞行轨迹的记录表明,“Leg Length”值应当在2~7 km,不是一个确定值。本文建模时假设“Map-and-Compass”过程不稳定,这意味着鸽子无法按照固定距离重新确定航向,导致变化的“Leg Length”和非周期性检查的变化。将“Leg Length”更新方式定义为
| $L_L = {\rm{rand}}[2,7]$ | (7) |
式中rand表示在固定区间内均匀取值。在“Leg Length”阶段,鸽子会保持当前航向,只受微小误差影响,但整体方向基本维持不变。
3) Immediate Home阶段
Immediate Home阶段,对应鸽子在鸽房附近区域快速归巢的行为。本模型中,当信鸽进入鸽房附近区域后,将进入低熵状态,此时鸽子对自己的飞行路线最有信心,它们将依赖外部输入地标特征,获取直达鸽房的方向信息。Guilford提出了2种驱动鸟类进入低熵状态的机制,这2种机制都涉及到外部输入视觉特征。因此,本文假设在即时归巢区域,鸽子将采用“马赛克地图”导航方式,通过识别特殊地标,得到鸽房相对于地标的方位。
按照鸽子归巢行为学实验观测结果,即时归巢区域的真实大小无法确定得到,但估计其值在5~10 km,在这个区域内都属于“即时归巢区域”,可以表示为
| ${\rm{IHA}}\_{\rm{R}} = 5$ | (8) |
式中
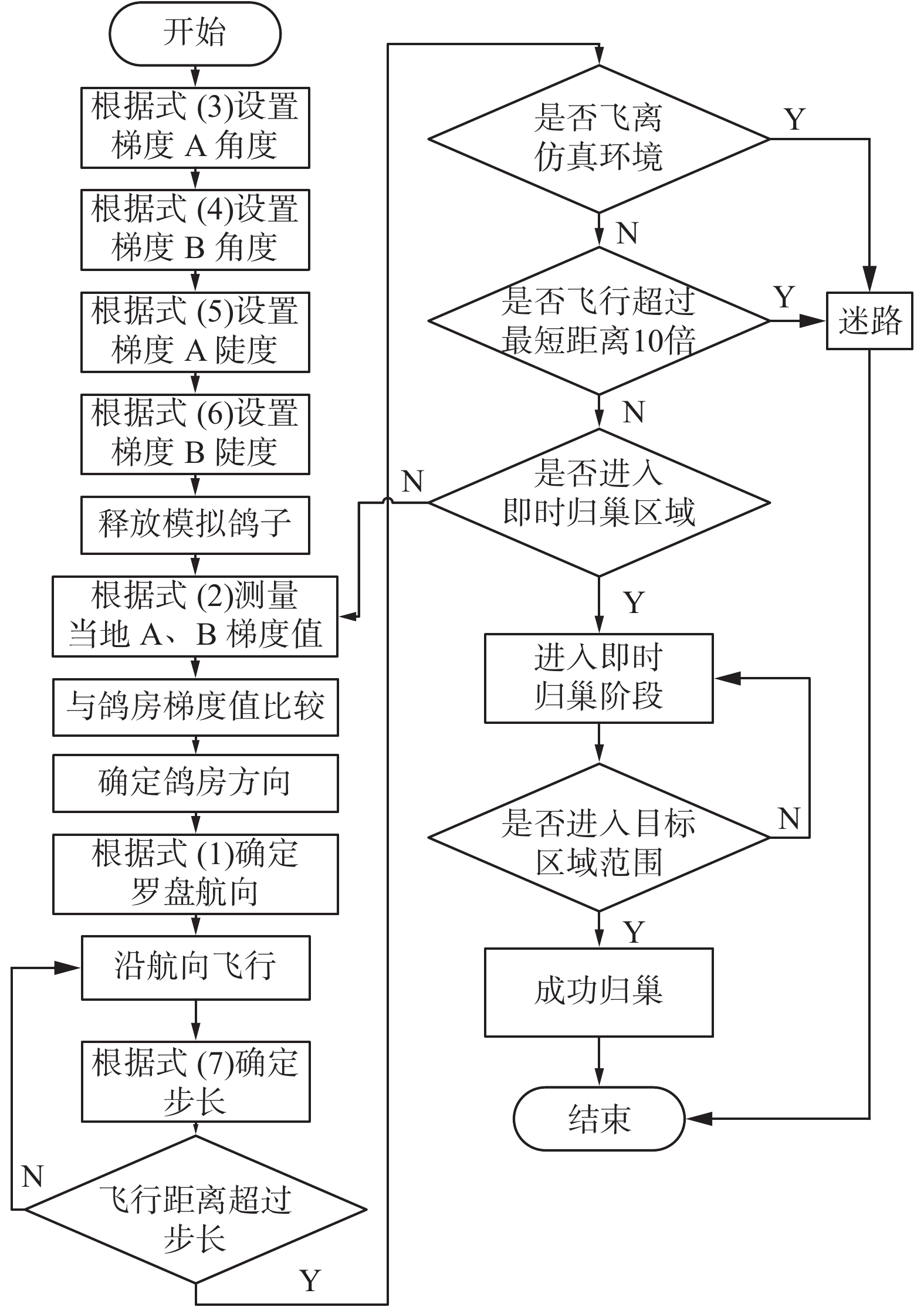
根据上节建立的鸽子归巢行为模型,本节通过模型仿真模拟鸽子归巢飞行结果。当信鸽释放后,首先进入Map-and-Compass阶段依靠罗盘和地图确定航向;然后进入Leg Length阶段,只需要维护其相对于出发点的位置,而不需要再考虑罗盘因素;当飞行距离达到Leg Length后,再次进入Map-and-Compass阶段校正方向;当信鸽进入鸽房区域范围时,通过识别熟悉地标,快速获取鸽房方位;由于导航地图与该区域存在重叠,信鸽同时会受罗盘因素的影响。因此,本文提出的动态切换3阶段鸽子归巢导航模型各阶段之间存在耦合,状态可切换。
仿真环境为的
|
Download:
|
| 图 6 鸽子归巢行为模型仿真流程 Fig. 6 Flow chart of pigeon homing model | |
图 7(a)给出了模型仿真的飞行轨迹,鸽子成功归巢并且飞行轨迹与行为学实验记录的信鸽飞行轨迹近似,表明本文模型的可行性。图7(a)中每个箭头指示的位置为鸽子重定向的位置,中间的距离即Leg Length,由于Leg Length按照式(7)随机更新,因此箭头间的飞行距离不同。在“即时归巢区域”设置了4个模拟的视觉地标,当鸽子到达“即时归巢区域”边界(图 7(b)绿色虚线区域)时,识别距离最近的地标,并首先飞行至地标位置,然后按照最优路径直接归巢,如图 7(b)轨迹所示。

|
Download:
|
| 图 7 鸽子归巢导航仿真飞行轨迹 Fig. 7 Simulation flight trajectory of homing pigeon | |
信鸽归巢导航行为与无人机自主导航在任务环境和任务需求上存在着较大的相似性,因此信鸽导航行为机制对于无人机在高动态/强干扰环境下自主导航具有很多借鉴意义:首先,因任务环境相似,未来无人机所受到的干扰因素比如陆海空天电一体化的复杂作战环境,卫星导航受到恶意干扰和破坏,城市高楼、山底、峡谷间等环境,无人飞行器面临的威胁类型复杂多变,作战模式将呈现多样化,导航信号可能会被拒止、削弱,甚至被欺骗等;而信鸽可以在复杂的环境中飞行并归巢,只依赖自然环境提供的罗盘和地面场景信息,其导航机制对于这类特性环境噪声的抗干扰性恰恰也是设计无人机自主导航系统所需要的。同时,也因二者的任务需求类似,信鸽导航需要依赖太阳或地磁场提供的罗盘,以及通过视觉获取的地面场景和特殊地标信息等;而现有的机载设备具备罗盘和惯导系统,能够满足航向信息需求,机载光电吊舱系统能够实时获取高分辨率图像,满足视觉信息需求。
本文在建立信鸽归巢行为模型时,已经考虑了信鸽归巢行为机制与无人机自主导航任务之间的相似性,因此可以方便地将信鸽导航行为机制映射到无人机自主导航中。本文提出的由于本文提出的动态切换3阶段鸽子归巢导航模型,是基于信鸽归巢导航过程建立的,并且基于位置熵理论对于各阶段依赖的导航策略有明确的结论,更便于与无人机自主导航建立映射关系。在此基础上,可以分别建立从Map-and-Compass模型到无人机基于太阳/磁罗盘定向算法,从Leg Length模型到无人机基于视觉的航位推算算法和从Immediate Home模型到基于马赛克地图的快速导航的算法映射关系,进而实现仿信鸽归巢导航行为机制的无人机自主导航。如图8所示。

|
Download:
|
| 图 8 信鸽归巢归巢行为与无人机自主导航机制映射 Fig. 8 Mechanism mapping from pigeon homing behavior to autonomous navigation of UAV | |
从可行性上考虑,对于Map-and-Compass模型,现有的仿生导航技术包括仿生偏振光导航和仿生地磁导航,分别依赖太阳和地磁场实现导航,已经取得较大的研究进展,并已经开发出了相应的导航装置,表明通过太阳和地磁场导航的可行性。利用已有的仿生偏振导航和仿生地磁导航技术,可以模拟信鸽的Map-and-Compass行为,实现罗盘定向。Leg Length行为实际上是一种典型的“航位推算”行为,信鸽在飞行过程中利用产生的运动信息更新其相对于出发点的位置。由于每次的Leg Length只需要计算其相对于更新航向时的相对位置,基于同时定位与建图(simultaneous localization and mapping, SLAM)技术的视觉导航为解决这个问题提供了可能。SLAM的前端视觉里程计(visual odometry, VO),通过采集序列图像可以实现相对位姿估计,完全符合Leg Length计算的需求[25];并且视觉导航具有场景信息丰富、抗干扰能力强、精度高以及成本低等优点,已经成为无人机导航技术研究的新方向。最后对于Immediate Home模型的实现,其关键在于建立认知地图,即建立孤立的地标之间及其与鸽房之间的相对位置关系,通常采用拓扑地图来模拟生物认知地图。拓扑地图是地图导航的一种,在拓扑地图中,不同位置之间的关系由邻接图表示,因此,通过建立一个拓扑图来表示位置关系是一种有效的方法,并且已有大量关于拓扑建图的方案[26-27]。
4 研究展望目前关于生物导航机制及其相关应用的研究方兴未艾,然而现有的仿生导航技术主要集中在2个方向,即仿生偏振光导航和仿生地磁导航,分别利用太阳光和地磁场实现了相应的导航技术。仿生偏振光导航系统是受昆虫奇特偏振光导航能力的启发,已经有大量的研究,并且国内外均已经开发出基于生物偏振光导航定位机制的新型仿生导航传感器和装置。仿生地磁导航具有全区域、全天候、抗干扰能力强及无积累误差的优点;研究人员从生物地磁导航现象、地磁导航机理,仿生地磁导航定位方法进行了大量的研究,仿生地磁导航方法作为一种重要的辅助性导航方式,在卫星、导弹、航海等领域均有广泛应用。
对于信鸽导航机制研究,尽管近半个多世纪以来有着众多突破性的研究进展,但仍停留在生理学、神经学和行为学实验研究层面,并且目前为止对于信鸽依赖何种机制进行导航还未有定论;对于信鸽导航行为机制的应用的研究,也都还处于建模仿真层面,距离实际应用还很遥远。基于信鸽归巢导航行为机制的无人机自主导航方面的研究,据笔者所知,国内外还未有相关的研究。而信鸽导航行为融合了太阳、地磁场、视觉等多种信息,导航能力优于绝大部分生物,因此仿信鸽归巢导航行为实现无人机自主导航无疑有广泛的应用前景,作者认为还有许多问题有待进一步深入研究:
1)对现有仿生导航系统的应用。现有的研究已经表明信鸽可以依赖太阳和地磁罗盘实现导航,并且已经在鸽子体内发现了光感应和磁感应受体。因此,可以借鉴仿生偏振光导航和仿生地磁导航的研究,将其应用到仿信鸽导航系统中,实现“Map-and-Compass”模型到导航定向算法跨越。
2)信鸽视觉通路建模。随着生理学研究的不断深入,鸽子视觉系统及其神经系统将更为清晰准确地被描绘,鸽子视觉信息处理技术将会变得更加完善,从模拟某个视觉组织或神经通路向更深入或更广泛的区域发展,利用信鸽视觉神经回路机制建立仿鸽子视觉信息处理模型,通过软硬件结合的方式模拟鸽子视觉系统,进而模拟其视觉导航行为。
3)仿信鸽脑海马结构的认知地图导航。基于生物认知机理的导航是智能导航领域的一个重要研究方向。信鸽在即时归巢区域,可以建立认知地图,通过识别熟悉地标实现快速导航,是一种典型的认知导航行为。鸽脑内的海马结构在认知地图的构建方面有重要作用,因此模拟鸽脑海马结构实现认知建图和导航具有重要的理论研究价值和实际意义。
随着无人机在侦察、搜救和测绘等方面应用的日益广泛和深入,无人机的自主导航技术理论和应用研究均有着巨大的发展潜力,基于信鸽导航行为机制的无人机自主导航技术民用和军用领域都将有着更大的发展空间和需求。
5 结束语目前对于仿鸽子智能导航技术的研究已经成为一个研究热点,今年来该领域不断涌现出新的研究成果,但不论是鸽子视觉系统的生理研究,还是其机制的建模分析即仿生学的研究,仍存在一些不完善的部分,尤其是关于应用方面的研究还处于空白。仿鸽子智能导航的应用研究还处于刚刚起步状态,还需要不断丰富自身理论,在更多应用中予以实践。将鸽子智能导航机制映射到无人机自主导航层面,并进一步实现实际无人机导航应用,还任重道远,因此对于仿鸽子智能机制的研究与应用工作具有重要的意义。作者未来的研究重点将放在对信鸽导航模型的算法实现,仿鸽视觉−脑信息处理导航机制研究,建立完整的仿信鸽归巢行为机制的无人机自主导航系统。
| [1] |
褚金奎, 张然, 王志文, 等. 仿生偏振光导航传感器研究进展[J]. 科学通报, 2016, 61(23): 2568-2577. CHU Jinkui, ZHANG Ran, WANG Zhiwen, et al. Progress on bio—inspired polarized skylight navigation sensor[J]. Chinese science bulletinl, 2016, 61(23): 2568-2577. (  0) 0)
|
| [2] |
WILTSCHKO W, WILTSCHKO R. Homing pigeons as a model for avian navigation?[J]. Journal of avian biology, 2017, 48(1): 66-74. DOI:10.1111/jav.01270 ( 0) 0)
|
| [3] |
KRAMER G. Experiments on bird orientation and their interpretation[J]. IBIS, 1957, 99(2): 196-227. ( 0) 0)
|
| [4] |
WILTSCHKO R, WILTSCHKO W. Avian magnetic compass: its functional properties and physical basis[J]. Current zoology, 2010, 56(3): 265-276. DOI:10.1093/czoolo/56.3.265 ( 0) 0)
|
| [5] |
WILTSCHKO R. Navigation without technical aids: how pigeons find their way home[J]. European journal of navigation, 2012, 10(2): 22-31. ( 0) 0)
|
| [6] |
EMLEN S T, EMLEN J T. A technique for recording migratory orientation of captive birds[J]. The auk, 1966, 83(3): 361-367. DOI:10.2307/4083048 ( 0) 0)
|
| [7] |
WALCOTT C, GREEN R P. Orientation of homing pigeons altered by a change in the direction of an applied magnetic field[J]. Science, 1974, 184(4133): 180-182. DOI:10.1126/science.184.4133.180 ( 0) 0)
|
| [8] |
LEFELDT N, DREYER D, SCHNEIDER N L, et al. Migratory blackcaps tested in emlen funnels can orient at 85 but not at 88 degrees magnetic inclination[J]. Journal of experimental biology, 2014, 218(2): 206-211. ( 0) 0)
|
| [9] |
WILTSCHKO W, WILTSCHKO R. The role of outward journey information in the orientation of homing pigeons[M]. PAPI F, WALLRAFF H G. Avian Navigation. Berlin, Heidelberg, Germany: Springer, 1982: 239–252.
( 0) 0)
|
| [10] |
WILTSCHKO R, WALKER M, WILTSCHKO W. Sun-compass orientation in homing pigeons: compensation for different rates of change in azimuth?[J]. The journal of experimental biology, 2000, 203(5): 889-894. DOI:10.1242/jeb.203.5.889 ( 0) 0)
|
| [11] |
LIPP H P, VYSSOTSKI A L, WOLFER D P, et al. Pigeon homing along highways and exits[J]. Current biology, 2004, 14(14): 1239-1249. DOI:10.1016/j.cub.2004.07.024 ( 0) 0)
|
| [12] |
VYSSOTSKI A L, DELL'OMO G, DELL'ARICCIA G, et al. EEG responses to visual landmarks in flying pigeons[J]. Current biology, 2009, 19(14): 1159-1166. DOI:10.1016/j.cub.2009.05.070 ( 0) 0)
|
| [13] |
WILTSCHKO R, WILTSCHKO W. Avian navigation: a combination of innate and learned mechanisms[J]. Advances in the study of behavior, 2015, 47(1): 229-310. DOI:10.1016/j.jtbi.2003.07.003 ( 0) 0)
|
| [14] |
BIRO D, MEADE J, GUILFORD T. Familiar route loyalty implies visual pilotage in the homing pigeon[J]. Proceedings of the national academy of sciences, 2004, 101(50): 17440-17443. DOI:10.1073/pnas.0406984101 ( 0) 0)
|
| [15] |
BIRO D, FREEMAN R, MEADE J, et al. Pigeons combine compass and landmark guidance in familiar route navigation[J]. Proceedings of the national academy of sciences of the United States of America, 2007, 104(18): 7471-7476. DOI:10.1073/pnas.0701575104 ( 0) 0)
|
| [16] |
NAGY M, VÁSÁRHELYI G, PETTIT B, et al. Context-dependent hierarchies in pigeons[J]. Proceedings of the national academy of sciences of the United States of America, 2013, 110(32): 13049-13054. DOI:10.1073/pnas.1305552110 ( 0) 0)
|
| [17] |
WILTSCHKO R, WILTSCHKO W. Avian navigation: a combination of innate and learned mechanisms[J]. Advances in the study of behavior, 2015, 47(1): 229-310. ( 0) 0)
|
| [18] |
NEHMZOW U, WILTSCHKO R. Computer modelling of pigeon navigation according to the “map and compass” model[J]. Orientation and navigation-birds, humans and other animals, 2001: 49-51. ( 0) 0)
|
| [19] |
WILTSCHKO R, NEHMZOW U. Simulating pigeon navigation[J]. Animal behaviour, 2005, 69(4): 813-826. DOI:10.1016/j.anbehav.2004.07.007 ( 0) 0)
|
| [20] |
POSTLETHWAITE C M, WALKER M M. A geometric model for initial orientation errors in pigeon navigation[J]. Journal of theoretical biology, 2011, 269(1): 273-279. DOI:10.1016/j.jtbi.2010.10.036 ( 0) 0)
|
| [21] |
POSTLETHWAITE C M, WALKER M M. A model for navigational errors in complex environmental fields[J]. Journal of theoretical biology, 2014, 363(1): 134-144. ( 0) 0)
|
| [22] |
ROBERTS S, GUILFORD T, REZEK I, et al. Positional entropy during pigeon homing I: application of bayesian latent state modelling[J]. Journal of theoretical biology, 2004, 227(1): 39-50. DOI:10.1016/j.jtbi.2003.07.002 ( 0) 0)
|
| [23] |
GUILFORD T, ROBERTS S, BIRO D, et al. Positional entropy during pigeon homing Ⅱ: navigational interpretation of bayesian latent state models[J]. Journal of theoretical biology, 2004, 227(1): 25-38. DOI:10.1016/j.jtbi.2003.07.003 ( 0) 0)
|
| [24] |
DUAN Haibin, QIAO Peixin. Pigeon-inspired optimization: a new swarm intelligence optimizer for air robot path planning[J]. International journal of intelligent computing and cybernetics, 2014, 7(1): 24-37. DOI:10.1108/IJICC-02-2014-0005 ( 0) 0)
|
| [25] |
FORSTER C, PIZZOLI M, SCARAMUZZA D. SVO: fast semi-direct monocular visual odometry[C]//Proceedings of the IEEE International Conference on Robotics and Automation. Hong Kong, China, 2014: 15–22.
( 0) 0)
|
| [26] |
LOWRY S, SÜNDERHAUF N, NEWMAN P, et al. Visual place recognition: a survey[J]. IEEE transactions on robotics, 2015, 32(1): 1-19. ( 0) 0)
|
| [27] |
ULRICH I, NOURBAKHSH I. Appearance-based place recognition for topological localization[C]//Proceedings of IEEE International Conference on Robotics and Automation. San Francisco, USA, 2000: 1023–1029.
( 0) 0)
|
 2021, Vol. 16
2021, Vol. 16