自闭症(autism spectrum disorder, ASD)是一种广泛性发展障碍类疾病，也是一种具有生物基础的发育障碍类疾病。该病症发病时间不等，大部分发病于儿童时期并伴随一生。其主要症状表现在社会交流障碍、语言交流障碍、情感缺陷等方面。这就导致了患者在日常的生活、交流和学习中有很大的障碍。因此，自闭症的预测分类研究一直备受广大研究者的关注。研究者已经发现ASD患者与正常人(typically developing individuals, TD)在大脑的功能连接上有明显的差异^[1]。

静息态功能磁共振成像(resting state functional magnetic resonance image，rs-fMRI)通过在静息状态下采集血氧水平依赖信号, 对信号去噪^[2]后，使用多层同时扫描技术^[3]对功能磁共振全脑影像快速采集，以此来获得时间分辨率和空间分辨率较高的图像，获得rs-fMRI后，关键问题是如何从中有效提取特征。对于传统的特征提取方法，以相关分析法为例，即选取ROI种子点并计算它的平均时间序列，然后与全脑所有体素的时间序列进行计算，或者两个脑区之间的平均时间序列计算，得到相关系数，以此来反映不同脑区神经活动模式之间的时间相关性^[4]。作为图像的预处理阶段，该方法对ROI异常敏感，种子点选取的位置、大小差异都可能导致较大的数据分析结果差异。

近年来，卷积神经网络(convolutional neural networks, CNN)在医学图像分类任务中取得了非常好的效果，随着结构的不断优化，诞生了多种成熟的网络模型。2017年，Dvornek等^[5]使用具有Long Short-Term Memory的递归神经网络直接从静态fMRI的时间序列上对具有ASD的个体进行分类。但是，从fMRI的感兴趣区域中提取平均时间序列作为输入数据无法兼顾全局信息，易造成信息缺失；2018年，Yu等^[6]开发了一种全自动的3D卷积神经网络框架，用以识别和分类不同类型的功能性脑网络。但是，脑网络在训练前需要花费大量的时间进行手动标记，不可避免地会出现人工标签错误和标签间的差异；2018年，Li等^[7]为了在fMRI中同时利用空间和时间信息，研究了使用滑动窗口随时间测量时间统计量(均值和标准差)以及使用3D卷积神经网络(CNN)捕获空间特征的潜在好处。模型虽然在高维数据上获得了良好的空间识别性能，但是在时间维度上的表现并不明显；2019年，Khosla等^[8]提出了一种新颖的3D卷积神经网络(CNN)方法来实现集成学习策略，提出的CNN方法利用了rs-fMRI数据的全分辨率3D空间结构，并拟合了非线性预测模型。但是，将rs-fMRI预处理后的多通道3D图像作为CNN的输入忽视了隐含在时间轴上的信息。对于以上提出的深度学习方法，网络只能处理维数小于或等于3的灰度或RGB图像，并且在对图像进行预处理过程中，很可能会丢失部分信息，使得出的结果不具有全局性。对于功能磁共振图像而言，如果将每个时间点上的3D图像视为一个通道进行3D卷积，那么根据预处理后的数据集特性，网络生成的通道数目会随着时间的推移而增多，从而使得网络宽度过大，可能会造成传播过程中信息丢失，影响网络的表达能力^[9]。另一方面，可以将每个样本多个时间点上的3D图像视为一个图像立方体输入到3D-CNN中，但是这种处理会增加大量的参数，忽略静息态功能像随时间变化的趋势信息，并且性能表现不佳。总而言之，有必要寻找一种有效的方法从rs-fMRI的时间和空间信息中提取特征。

本文提出了4D卷积神经网络，通过rs-fMRI对ASD进行分类，所提出的4D卷积操作从功能磁共振图像中提取空间和时间上的特征，可以得到功能磁共振图像随时间变化的信息。与几个流行的网络相比，例如AlexNet^[10]、3D-CNN^[11]、2CC3D^[7]、T3D^[12]，所提出的网络能够有效地从功能磁共振图像中提取与ASD密切相关的时间空间特征，较之以往的3D卷积神经网络，4D-CNN对含有时空特性的数据具有更好的适应性，可以实现更好的分类效果。

1 卷积神经网络概述

深度学习是一类通过多层处理，逐渐将初始的低层特征表示转化为高层特征表示的特征学习方法。这样的方法可以被训练用于监督或无监督学习，由此产生的复杂模型已经被广泛用于视觉物体识别、人类行为识别、自然语言处理、音频分类、脑机交互、人体跟踪、图像恢复、去噪、分割等任务。卷积神经网络是一种深度模型，在这种模型中，输入层、隐藏层和输出层组成基本的网络结构，其中隐藏层通常包括卷积层、池化层和全连接层。卷积层中卷积核相当于特征提取器，每个卷积核对整幅图像数据进行有规律地扫描并依次计算各局部区域的特征值以匹配某种模式；池化层对卷积层结果进行特征选择和信息过滤，实现一定程度的平滑压缩；全连接层通常搭建在隐藏层的最后，对卷积层和池化层的结果进行分类。

1998年，纽约大学的Lecun等^[13]正式提出了卷积神经网络LeNet-5，确立了CNN的现代结构，并在图像处理领域获得了极大成功。之后研究人员发现当神经网络饱和之后模型会产生过拟合现象，直到2012年，Krizhevsky等^{[10, 14]}在提出的Alexnet中采用Dropout和数据增强的方法来防止网络过拟合，并使用非线性激活函数ReLU(rectified linear unit)提高网络收敛速度。2014年，Simonyan等^[15]采用小卷积堆叠的方式搭建VGGNet，证明了更深的网络能更好地提取特征，值得一提的是，虽然VGGNet比AlexNet的参数多，但只需要更少的迭代次数就能收敛。此外，在设计网络结构时，除了考虑网络的深度，还会考虑网络的宽度。同年，Szegedy等^[16]提出的Inception v1网络，通过改变传统的卷积层设计思路，在加大网络深度和宽度的同时减少了参数量，并且增加了网络对尺度的适应性。随后，通过对Inception v1网络结构的不断改进，诞生了Inception v2^[17]、Inception v3^[18]、Inception v4^[19]。在VGG网络中，当网络深度达到一定界限的时候，就会产生梯度消失现象，2016年，He等^[20]在提出的ResNet中引入了跳跃连接结构来解决梯度消失的问题，进而可以进一步加大网络深度。2017年，Huang等^[21]受ResNet和Inception的影响，提出了DenseNet，不同于ResNet的是，DenseNet模型建立的是前面所有层与后面层的密集连接，通过特征重用和旁路设置，既缓解了梯度消失问题，又大幅度减少了网络的参数量，实现了比ResNet更优的性能。

根据卷积核结构的不同，CNN可分为一维卷积、二维卷积与三维卷积。一维卷积通常用于序列数据分析，如从rs-fMRI的感兴趣区域中提取时间序列矩阵并输入到一维卷积神经网络中对自闭症进行分类^[22]；二维卷积被广泛用于计算机视觉的图像数据分析,如具有代表性的网络LeNet-5识别手写数字图片^[13]；而三维卷积则可用于时空数据的分析，如3D-CNN识别视频中的人类动作^[11]。CNN的卷积层通过卷积操作提取输入的特征，低层卷积提取低级特征，随着网络结构的加深，更高层的卷积层提取更高级的特征。在卷积层中每个卷积核在对输入图像进行扫描时，仅处理其投影在图像上的感受野的数据，且卷积核权重保持不变，此即为卷积核的局部连接性与权值共享性。由于卷积核的局部连接特性，模型可以计算区域特征，充分利用局部区域内的空间信息；由于卷积核的权值共享特性，在模型训练时卷积层所需参数要远小于全连接层。因此CNN适用于特征维度较大、具有位置信息的图像数据的分析。

本文研究了4D-CNN在医学图像分类任务中对自闭症的功能核磁共振图像进行分类的应用，通过用4D卷积核将多个连续的三维图像堆叠在一起，可实现4D卷积。在降采样层中，通过在上一层特征图上的局部领域上合并来降低特征图的分辨率，从而去除冗余信息，提高网络效率。最后通过全连接层将特征映射到样本标记空间实现分类任务。

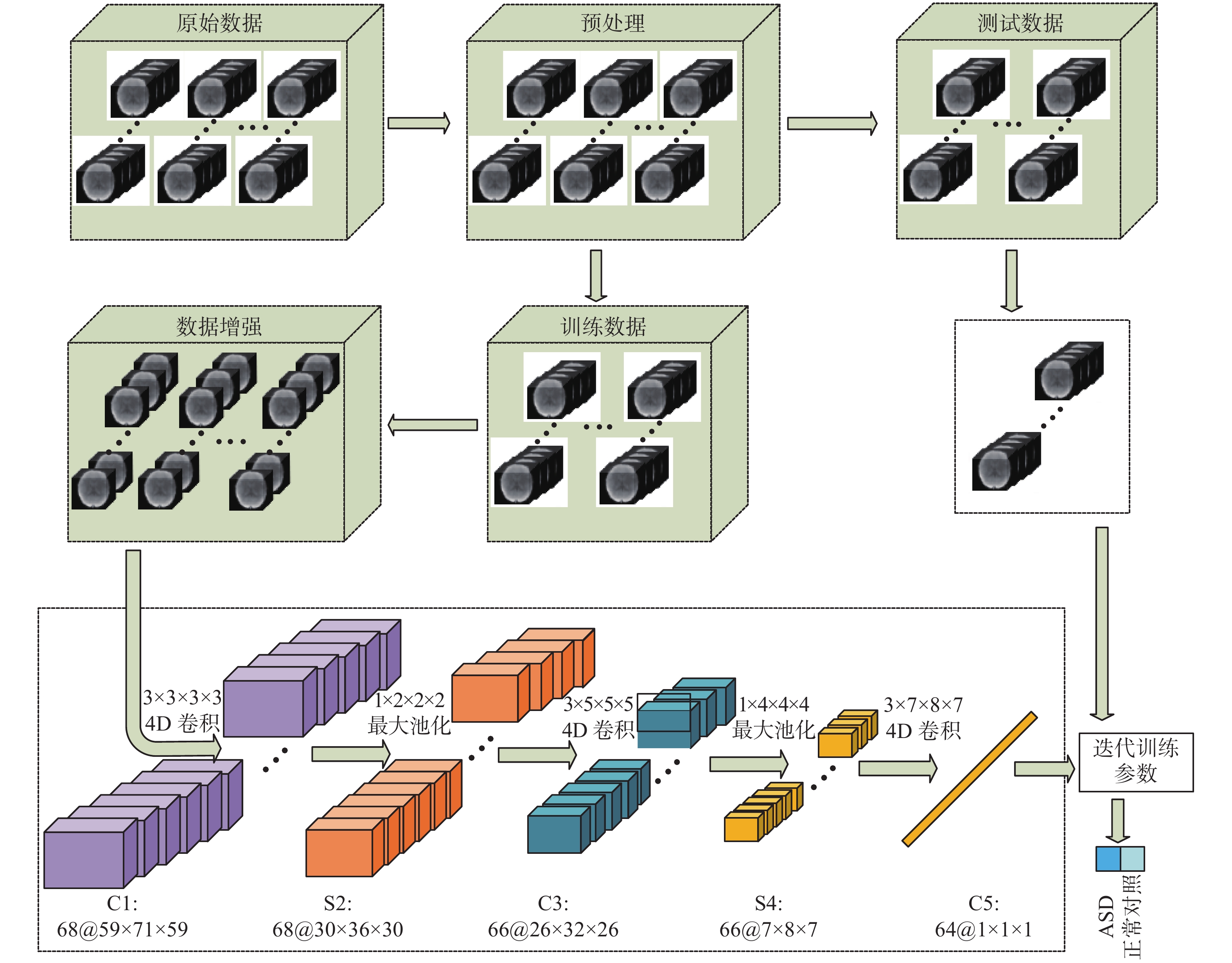
2 基于fMRI数据的4D卷积神经网络

本文的技术路线如图1所示，其中涉及原始数据的预处理、数据增强、模型训练和使用训练好的模型进行测试。

2.1 数据预处理

本文实验基于ABIDE(autism brain imaging data exchange)数据库，其中包括来自多个数据中心的1112名ASD患者和TD的rs-fMRI数据。在本文中，考虑从ABIDE的NYU、UM_1和USM这3个成像中心中获得rs-fMRI，其中各个数据中心的ASD组和TD组样本数如表1所示。使用DPARSF^[23]对rs-fMRI数据进行预处理。具体而言，将每个受试者的前10个获得的rs-fMRI丢弃。然后，执行时间层校正(slice timing)和头部运动校正(realign)。每个人的大脑尺寸大小、形状和位置差异较大，无法将结果按照统一的标准进行分析，因此需要把不同人的大脑影射在同一空间内，本文使用EPI(echo-planar image)模板将数据统一到蒙特利尔神经学研究所(montreal neurological institute,MNI)制定的标准空间中，从而完成对功能性进行空间标准化(normalize)处理。为了提高配准效果和增大图像的信噪比，需要对图像进行空间平滑(smooth)。经过预处理后，本文得到了每个被试在单个时间点上尺寸大小为 $61\times 73\times $ $ 61$ 的rs-fMRI数据。为了验证模型的泛化能力，在数据预处理后将其分为训练集和测试集，在不同成像中心下的具体数据分布如表2所示。

2.2 数据增强

由于每个被试采集的图像具有不同的时间长度，同时，也为了扩大数据集的规模，避免因训练样本过少而引发的模型过拟合问题，本文对训练集应用数据增强策略。具体而言，针对每个被试的rs-fMRI，在保证时间序列的前提下，对时间点上的图像进行随机选取。为了保证数据的有效性和一致性，选取70个时间点上的图像作为一个时间序列，每个被试随机生成5组，并标上相应的标签。通过把所有被试原始训练集中的rs-fMRI经过上述过程的处理，得到了一个新的训练集。

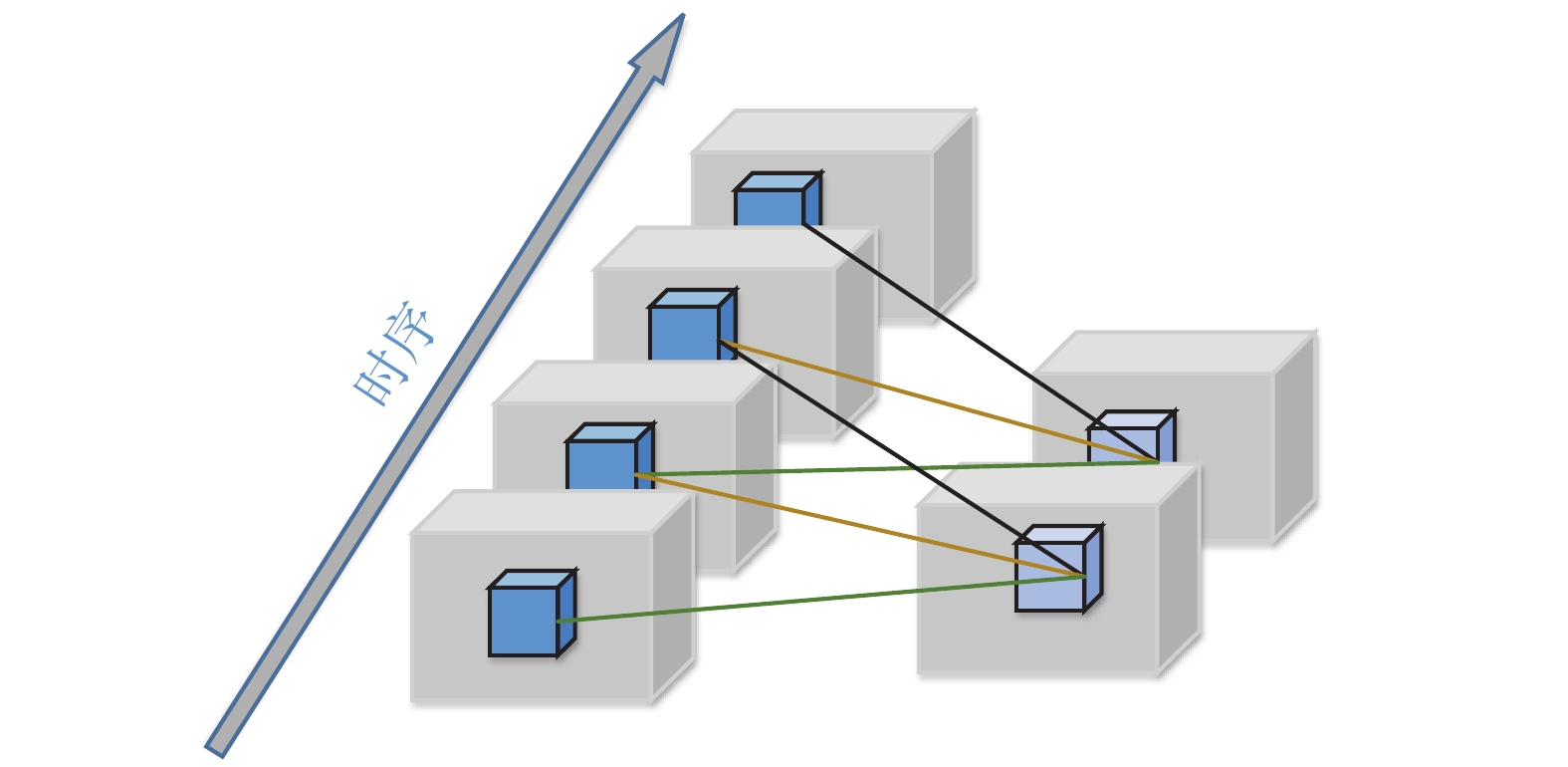
2.3 4D卷积神经网络分类模型

在三维卷积神经网络中，当应用于时间序列上连续的二维特征图时，三维卷积从空间和时间两个维度计算特征，通过将1个三维核与多个相邻二维图叠加而成的立方体进行卷积来实现的，在这种构造中，卷积层中的特征图被连接到前一层中的多个相邻图像，从而获得二维特征图的连续信息。在功能磁共振图像数据中，时间序列上呈现的是三维空间结构，本文应用四维卷积核与多个相邻的三维图叠加而成的四维特征进行卷积，用于处理在时间序列上呈现三维空间结构的数据，从而在空间和时间两个维度上计算特征。四维卷积过程如图2所示。其中，卷积核在时间维度上的大小为3，连接采用颜色编码，相同的颜色权重共享。将相同的4D内核应用于连续的3D立方块中，通过移动步长提取前一层整个时间序列上的特征。

图1给出了用于rs-fMRI的4D-CNN结构，它由1个输入层、3个卷积层、1个全连接层和1个输出层组成。最后使用softmax函数将输出结果转换为概率表示，以便更好地实现分类。每个卷积层由1个大小为 $ P \times Q \times R \times T $ (空间维度为 $ P \times $ $ Q \times R $ ，时间维度为 $ T $ )的四维过滤器内核，1个激活单元和1个池化单元组成。卷积操作通过在输入图像或前一层卷积层的输出中对内核进行卷积来生成特征图，并设置ReLU作为激励函数拟合网络的非线性映射，防止网络梯度消失和加快训练速度。池化单元起到二次提取特征的作用，经过最大池化采样，将高维特征转换成低维代表性特征，有利于在连续多层的网络中进行更深层次的表示。最后，通过反向传播算法^[24]，使来自损失函数的信息通过网络传递，计算梯度来训练网络。

具体而言，由于数据集中每个样本采集图像的时间长短有所差异，为了获得相同的输入规模，本文将统一选取每个被试的前 $ M $ 个时间点，每一个时间点上特征图大小为 $ X\times Y\times Z $ 的fMRI作为特征输入到4D-CNN中。该网络由6层结构组成，每层都包括可训练的参数。输入层包含 $ M $ 个通道，每个通道大小为 $ X\times Y\times Z $ 的四维fMRI数据。对输入层应用大小为 $ 3\times 3\times 3\times 3 $ (空间维度为 $ 3\times 3\times 3 $ ，时间维度为3)的核进行4D卷积，卷积完成后得到 $ {M}_{1} $ 个特征图，每个特征图大小为 $ {X}_{1}\times {Y}_{1}\times {Z}_{1} $ 。S2层是由 $ {M}_{1} $ 个大小为 $ {X}_{2}\times {Y}_{2}\times {Z}_{2} $ 的特征图组成的降采样层，由C1层经过 $ 2\times 2\times 2\times 1 $ 的最大池化得到。卷积层C3是用大小为 $5\times 5\times $ $ 5\times 3$ (空间维度为 $ 5\times 5\times 5 $ ，时间维度为3)的4D卷积核对S2层进行卷积得到，规模为 ${X}_{2}\times {Y}_{2}\times {Z}_{2}\times $ $ {M}_{2}$ (空间维度为 $ {X}_{2}\times {Y}_{2}\times {Z}_{2} $ ，时间维度为 $ {M}_{2} $ )。S4层是由 $ {M}_{2} $ 个大小为 $ {X}_{3}\times {Y}_{3}\times {Z}_{3} $ 的特征图组成的降采样层，由C3层经过 $ 4\times 4\times 4\times 1 $ 的最大池化得到。根据S4层数据规模，采用 $ 7\times 8\times 7\times 3 $ (空间维度为 $ 7\times 8\times 7 $ ，时间维度为3)的卷积核对S4层进行卷积，得到了C5层，规模为 $ {X}_{4}\times {Y}_{4}\times {Z}_{4}\times {M}_{3} $ (空间维度为 $ {X}_{4}\times {Y}_{4}\times {Z}_{4} $ ，时间维度为 $ {M}_{3} $ )。输出层由与分类任务类别数量相同的特征组成，每个特征都与C5层中的 $ {X}_{4}\times {Y}_{4}\times {Z}_{4}\times {M}_{3} $ 个特征完全连接。通过多层卷积和池化，将一个被试在时间序列上连续的功能磁共振图像转换为一个 ${X}_{4}\times {Y}_{4}\times $ $ {Z}_{4}\times {M}_{3}$ 维的特征向量。相比较以往处理功能磁共振图像的方法，在卷积的过程中，蕴含着连续的时间信息。在本设计中，本文最终在 ${X}_{4}\times {Y}_{4}\times {Z}_{4}\times {M}_{3}$ 维特征向量上应用一个线性分类器进行分类。本文设计并评估了其他在不同阶段结合多个信息通道的4D-CNN架构，结果表明该架构的性能最佳。

3 实验与分析

在本节中，在ASD数据集上验证本文提出的4D-CNN模型，通过对影响模型性能的超参数进行寻优，来获得最佳的网络结构。为了验证4D-CNN在ASD分类上的优越性，进一步在ASD的多个成像中心上比较了多种对比方法。

为了体现测试数据集上分类模型的有效性，选取精确度(ACC)、AUC值、敏感度(SEN)和特异性(SPE)作为实验的性能指标。表3和式(1)~(3)用于计算相应的性能指标：

$\mathrm{A}\mathrm{C}\mathrm{C}=\frac{\mathrm{T}\mathrm{P}+\mathrm{T}\mathrm{N}}{\mathrm{T}\mathrm{P}+\mathrm{F}\mathrm{P}+\mathrm{T}\mathrm{N}+\mathrm{F}\mathrm{N}} $

(1)

$ \mathrm{S}\mathrm{E}\mathrm{N}=\frac{\mathrm{T}\mathrm{P}}{\mathrm{T}\mathrm{P}+\mathrm{F}\mathrm{N}} $

(2)

$ \mathrm{S}\mathrm{P}\mathrm{E}=\frac{\mathrm{T}\mathrm{N}}{\mathrm{T}\mathrm{N}+\mathrm{F}\mathrm{P}} $

(3)

3.1 超参数寻优

在本节中，通过4D-CNN来执行ASD诊断，将预处理后的rs-fMRI作为网络的输入数据。本文将ASD组标记为1，将健康对照组标记为0，将ASD诊断视为二分类问题。为了找到适合ASD诊断的4D-CNN的最佳架构，本文进行了架构搜索^[25]策略，即探索基于4D-CNN架构的最佳超参数配置。

对于卷积神经网络，输入帧序列的时间深度在活动识别任务中起着关键作用^[12]，为了实现新架构的最佳配置，本文对网络输入数据的时间深度进行了一系列测试，表4列出了在不同时间深度下模型的测试性能。为寻求4D-CNN的最佳配置，基于上述研究的结果进行了实验，并采用4D卷积核(多个连续的三维权值矩阵)在卷积层之间建立更有效的时空连接，便于最大限度地从fMRI中传递与自闭症相关的时间、空间特征，以此改善网络提取特征的能力。其中，为了选取使4D-CNN具有最佳性能的卷积核，本文对4D卷积核在时间维度上的深度进行了验证。根据前一层特征图的规模，选取不同尺寸的参数矩阵作为单个时间点上的权值矩阵，并默认卷积过程中卷积核的平移步长为1，表5列出了在不同卷积核规模下4D-CNN的测试性能。

在训练阶段，使用随机梯度下降(SGD)进行误差反向传播更新参数，经过验证，将学习率设置为0.01，可避免在训练过程中收敛速度过慢或陷入局部最优。此外，将最大迭代次数设置为150。

结果显示，卷积核规模过小，只能提取单个时间点或单个时间段上的特征；随着卷积核时间维度加深，网络需要训练的参数量呈指数上升，迭代更新参数速度减缓，并出现过拟合现象，带来的后果就是网络的泛化能力大大降低。所以，本文选取时间维度上深度为3的卷积核作为4D-CNN架构的特征提取器。

3.2 方法比较

将提出的网络与基于ROI(regions of interest)构建脑功能网络(ROI-net)方法进行ASD分类性能比较，此外，几个经典的网络对本文中用到的数据集进行诊断，包括T3D、AlexNet、2CC3D、3D-CNN以验证4D-CNN的有效性。表6将对比方法进行了介绍。

本文所用的数据集具有四维特性，无法直接将数据集用于比较的三维卷积神经网络方法中，因此采用系统抽样的方式对数据集进行处理，以便对比方法能更好地适用于本文中的数据集。具体而言，对每个被试的功能磁共振图像在时间轴上进行等距划分，即从第一个时间点开始，每连续10个时间点上的图像为一组，故前50个时间点上的图像随之分为5组，然后每组随机选出一个时间点上的图像作为卷积网络的输入，以此，每个被试选出5个图像分别进行3D卷积处理，输出5个分类结果，并将结果中占比高的类别作为本次输出结果。

3.3 分类结果及分析

表7、8、9分别展示了提出的4D-CNN与其他方法在NYU、UM_1和USM数据集上的分类结果。可以看出，4D-CNN使用四维卷积核对自闭症的功能磁共振图像进行时空特征学习，可以取得比T3D、AlexNet、2CC3D及3D-CNN等经典的三维卷积神经网络更好的性能。表7的实验结果表明提出的4D-CNN在NYU数据集上的表现明显优于其他方法，分类精度达到了70.49%，并且呈现出良好的敏感性和特异性。归结原因在于，本文所提出的4D卷积神经网络结构直接从预处理后的功能磁共振图像中提取时空特征，既充分保留了图像的全局信息，又很好地避免了图像经传统方法预处理后带来的误差和冗余信息。进一步验证了从fMRI中提取四维特征对自闭症分类任务的有效性。在多个数据集上的实验结果说明了本文所提的网络对含有时间和空间特性的数据具有适用性。

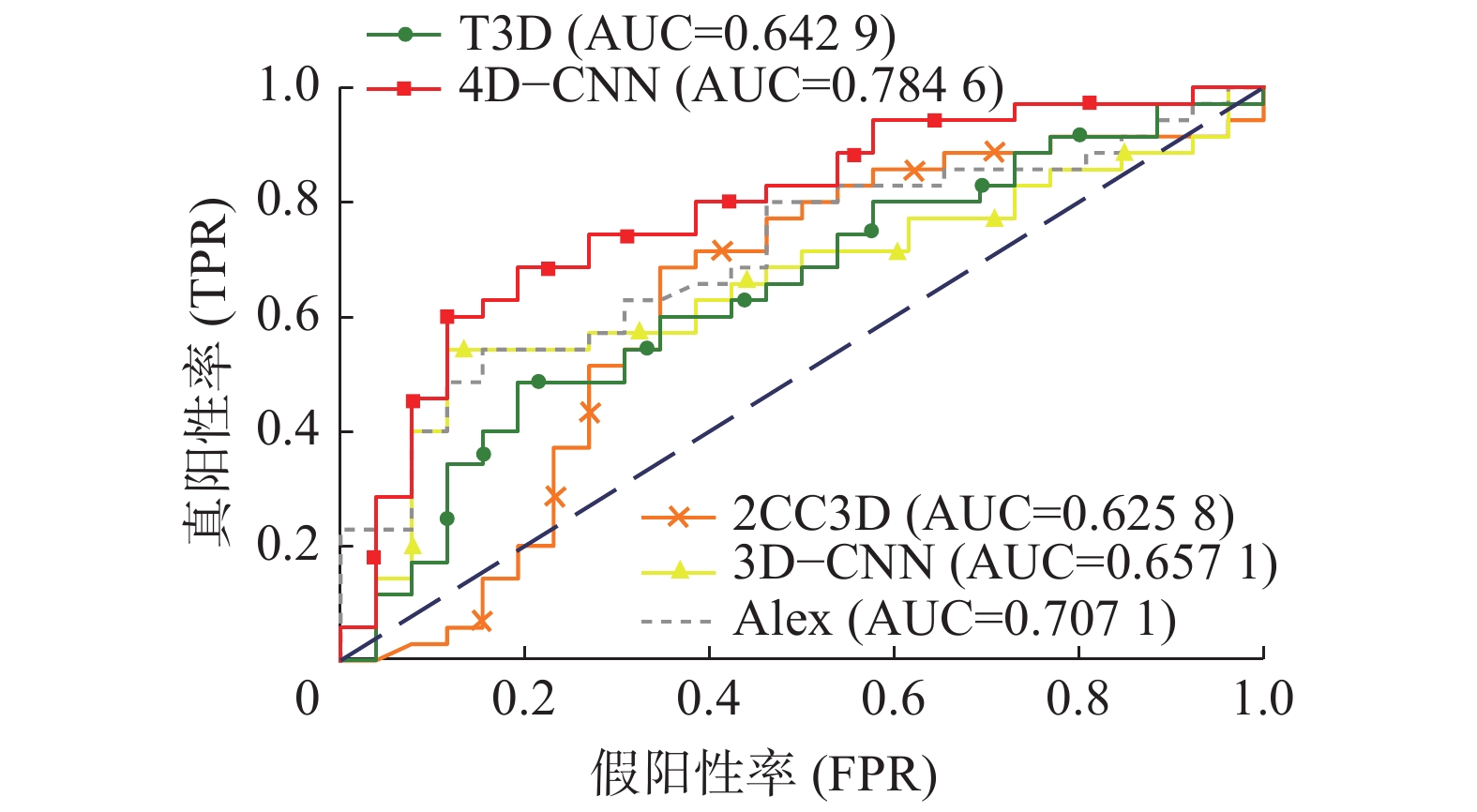
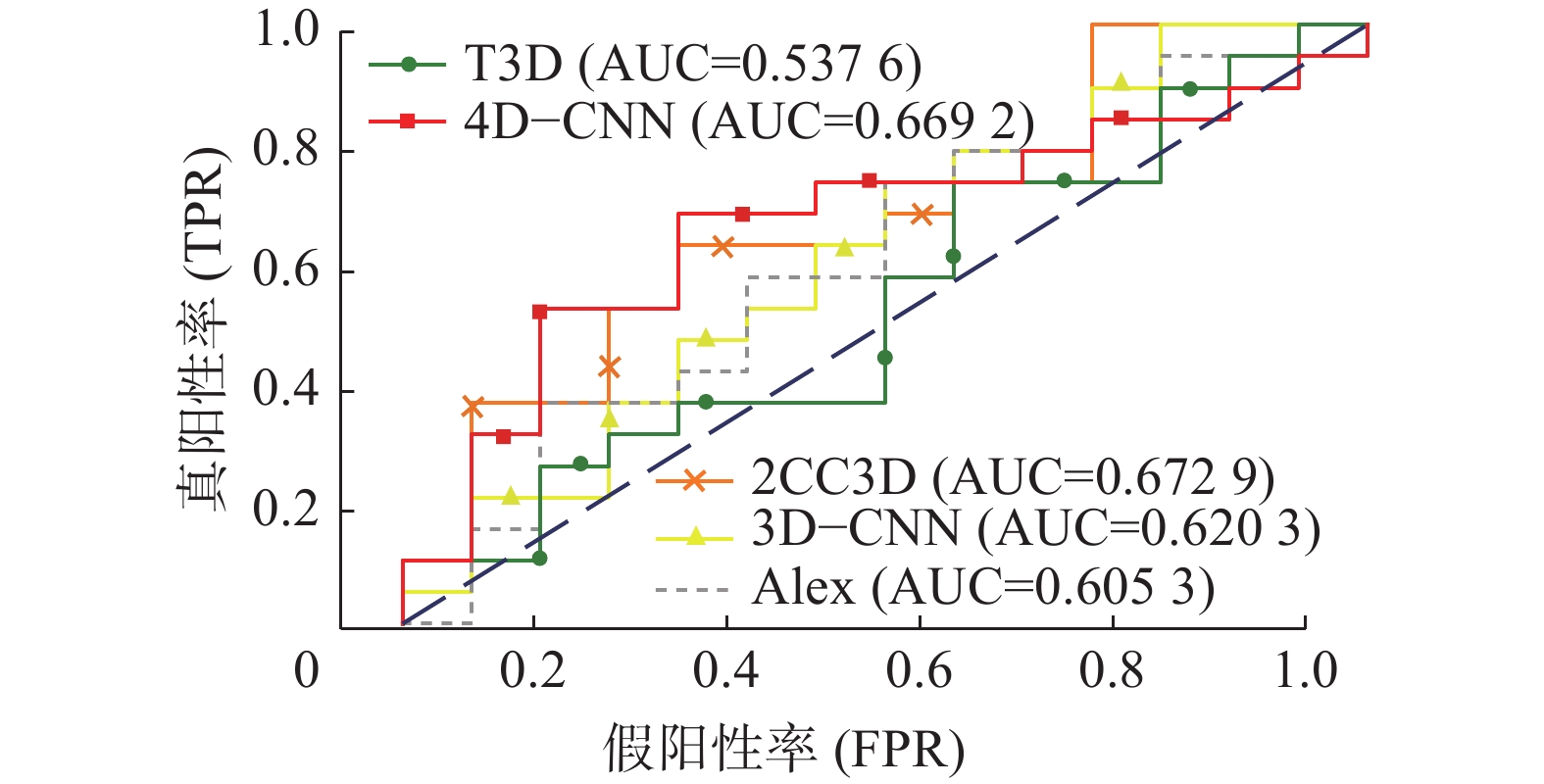
此外，用ROC曲线来更加直观地鉴别模型优劣，ROC曲线能很容易地查出任意界限值时模型对疾病的识别能力，图3、4、5分别显示了在NYU、UM_1和USM这3个数据集上不同方法所获得的ROC曲线。可以看出，4D-CNN的ROC曲线在整体上优于其他方法，说明本文的方法对自闭症有更好的识别能力。ROC曲线下的面积即为AUC值，AUC值能很好地描述模型整体性能的高低，从图3可以看出，在NYU数据集上4D-CNN的AUC值为0.7846，明显高于其他方法。在图4、5中，4D-CNN的AUC值也高于大多数方法。

4 结束语

本文提出了一个四维的卷积神经网络对自闭症的功能磁共振图像进行分类。具体来说，首先对所有的fMRI进行预处理，然后通过提出的模型直接对图像进行训练。根据不断的迭代更新参数，得到了一个具有显著识别能力的4D-CNN。在提出的网络中，训练过程完全保留了受试者的全局特征和连续的时间特征，从而获得了较好的实验结果。对来自不同数据集的受试者实验表明，所提出的4D-CNN方法可以使用fMRI数据有效地对脑疾病进行诊断。