由于风电机组所处运行环境恶劣，受气象、设备老化等多种不确定因素的影响，容易出现性能与运行状态劣化，从而造成关键部件失效。风电机组主轴承连接着轮毂与齿轮箱，作为重要的机械传动部件之一，其可靠性要求较高，但主轴承内部结构和受力较复杂，且常常运行在重负荷、强冲击的工作状态下，容易发生磨损、不对中、不平衡等问题^[1]。风电机组主轴承一旦损坏，受限于维修过程的复杂，其维修费用高、周期长，严重影响风电场的经济效益。

风电机组故障诊断研究目前主要集中在振动信号分析法方法、SCADA数据分析方法、视频图像检测方法、润滑油检测方法、声发射信号检测方法、应变传感信号检测方法等^[2]。数据挖掘方法能够在大量数据中发现隐含的知识或潜在规律，因此近年来在各行业中具有广泛的研究和应用。随着数据挖掘算法的不断发展，一些算法逐渐被应用到故障预警和故障辨识中^[3]。目前基于数据挖掘的风电机组的状态监测研究主要基于采集与监视控制系统(supervisory control and data acquisition, SCADA) 时序数据，利用相关智能学习算法建立设备部件的正常运行模型，通过分析正常模型预测值与实际观测值之间的残差进行状态监测。文献[4]利用深度置信网络建立发电机同步定子故障预警模型，对残差设定故障阈值进行状态监测。文献[5]利用BOX-COX变换和相对熵对残差进行分析，对齿轮箱进行状态监测。文献[6]利用数据分类重建和提取衰退指标的方法对齿轮箱进行状态监测。文献[7]将DS证据理论应用于SCADA警报分析对风电机组进行故障诊断。文献[8]通过提取风电机组SCADA系统中的实际运行数据，采用双向递归神经网络建立风电机组运行预测模型，根据滑动窗口的实际值与实测值之间的残差，利用莱特准则实现故障预警。

以上方法对残差进行分析时需要人为设定故障预警阈值，所述方法适用于某一特定风电场，其泛化性有待提升。文献[9]利用SCADA数据提出了基于工况辨识的Bi-RNN神经网络，建立预警模型对风电机组主轴承运行状态进行监测，该方法在故障决策方面引入随机森林算法避免人为设定故障阈值，但由于故障发生前SCADA数据不全是表征故障的数据，所建立的状态决策模型精度有待提升。

上述研究在不同程度上对风电机组关键核心部件的状态监测和故障预警起到了推动作用，但是普遍存在泛化性弱，故障决策受主观因素影响、缺乏理论支撑等问题，限制了状态监测模型的工程实用性。

因此，本文以风电机组主轴承温度为研究对象，提出了一种基于辅助分类生成对抗网络(auxiliary classifiergenerative adversarial networks, AC-GAN)数据重构的风电机组主轴承状态监测方法对其运行状态进行监测。

1 建模方法设计

温度是风电机组运行数据中较为重要的观测指标，具有很强的抗干扰性，不会轻易因环境或工况变化产生剧烈跳跃变化。正常情况下，轴承温度随着轴承开始运行缓慢上升，后续达到稳定运行状态。风电机组主轴承温度随着热容量、散热速度、转速和负载而发生变化。但机械传动设备在运行过程中产生的磨损、润滑不良、屏蔽不良等问题往往会导致温度数据异常，如果主轴承长期在高温下运行，其运行寿命将会大大缩短，甚至会引起更为严重的故障事故^[10]。因此，本文重点分析风电机组主轴承温度参数的变化，监测并实时掌握主轴承运行状态，发现其潜在隐患。风电机组主轴承温度预测模型的准确度、泛化能力以及状态决策模型的准确度决定着主轴承状态监测的精准度。建模流程如图1所示。

首先，利用SCADA时序数据建立基于轻型梯度增强学习器(light gradient boosting machine, LightGBM)的主轴承温度预测模型，定义模型预测输出温度与实际观测温度之差为残差。相较于其他算法，LightGBM算法无需通过计算所有样本信息增益，其内置的特征降维技术具有较高的预测精度和较快的训练速度，比较适合于工程实现。

其次，通过滑动窗口和统计过程控制(statistical process control, SPC)方法将异常主轴承残差中的正常残差和异常残差进行有效区分。利用AC-GAN 辅助分类生成对抗网络生成与主轴承异常残差分布相似的残差数据集，用来替换异常主轴承残差分布中的正常残差数据集。由于风电机组异常主轴承的残差特征不全表征为异常状态，无法统一进行标记。因此，利用AC-GAN将温度残差特征进行数据重构，得到异常主轴承下的残差特征，从根本上解决了异常样本数据的标记问题，进而提高了后续主轴承状态决策模型的预测精度。

最后，建立基于自然梯度提升(natural gradient boosting, NGBoost)的状态决策模型对风电机组主轴承状态进行判断。NGBoost算法利用自然梯度进行概率预测，解决了传统状态决策方法中采用单一固定阈值或人为主观设定阈值进行风电机组运行状态监测的问题，提高了状态决策模型的预测精度和泛化性。

2 数据预处理 2.1 SCADA数据说明

本文所采用的SCADA数据是河北某风电场1.5 MW双馈式风力发电机组的运行数据。该风电场的风电机组切入风速为3 m/s，切出数据为25 m/s。SCADA数据每10 min记录一条，为了消除偶发性的故障对主轴温度预测模型的影响，本文共选取该风电场1.5 MW机组共36台机组，包括23台主轴承正常机组，13台主轴承异常机组。这36台风电机组生产厂家和型号相同，并且都是同一个风电场的风电机组，因此所利用的风资源和地理环境相似，能够表征该风电场的所有运行工况。SCADA时序数据包括时间、风速、风向、有功功率、发电机转速、叶轮转速、偏航角度、环境温度、齿轮箱油温等百余个有效观测数据。表1为部分SCADA有效数据。

2.2 数据清洗

由于风电机组本身和SCADA系统在运行过程中掉电、传感器损坏、系统宕机、通信设备故障等因素造成SCADA数据中夹杂着很多异常噪声数据。在建模前首先对数据进行清洗，其过程如下：

1)采用分区间方法按风速0.5 m/s划分子工况区间；

2)将小于切入风速、大于切出风速、有功功率小于或等于0的数据剔除；

3)采用统计学中的四分位原理^[11]对每个子工况区间的SCADA数据进行清洗。

为说明去除异常噪声数据的效果，本文对2.1节提到的风电机组历史SCADA数据进行了异常噪声数据去除，如图2所示。图2(a)为该风电机组历史SCADA数据过滤前的风速功率曲线图，图2(b)为过滤后的风速功率曲线图。

2.3 特征数据提取

风电机组SCADA数据中并非所有的时序数据均与风电机组主轴承温度相关，为提高风电机组主轴承温度预测模型精度，同时降低模型训练时长，选取与风电机组主轴承运行状态相关的特征子集。传统的特征筛选方式为利用皮尔森相关系数或根据工程师相关经验进行确定，皮尔森相关系数对数据的要求必须服从正态分布，但风电机组由于弃风、限电等运行工况的变化导致SCADA数据并不符合正态分布，且皮尔森相关系数受到数据异常值的影响较大，仅适用于某些特定场合下的风电场或风电机组。鉴于此，本文选取相关系数收敛快、可解释性好且对数据分布没有特殊要求的斯皮尔曼相关性分析方法提取直接或者间接反映风电机组主轴承温度特征的参数集^[12]，斯皮尔曼相关系数的计算步骤为：

1)SCADA数据特征中主轴承温度定义为 $ Y $ ，其他特征定义为 $ X{}_i $ ，将 $ X{}_i $ 和 $ Y $ 列所对应的数据转换为各自列向量的排名，记为 $ R(X{}_i) $ 和 $ R(Y) $ 。

2)两个列向量中对应数据 $ R(X{}_i) $ 和 $ R(Y) $ 之间的差异 $ d $ 为

$ d = {\sum_{i = 1}^N} {|R(X{}_i) - R(Y){|^2}} $

两个列向量之间的相关性 $ {R_{\text{s}}} $ 为

$ {R_{\text{s}}} = 1 - \frac{{6 \times d}}{{N({N^2} - 1)}} $

式中： $ i $ 为每一列SCADA特征数据； $ N $ 为SCADA数据特征的长度。斯皮尔曼系数高于0.5时特征之间的相关性为强相关，因此，通过斯皮尔曼相关性系数分析，得到SCADA数据中与主轴承温度相关性较高的特征，见表2所示。因此，选取发电机转速、叶轮转速、机舱温度等10个特征。

提取的特征数据中往往具有不同的量纲和量纲单位，为了消除特征数据之间的量纲影响，将数据归一化处理，计算公式为

$ {{\boldsymbol{x}}_{{n}}} = \frac{{{\boldsymbol{x}} - {x_{{\text{mean}}}}}}{{{x_{\max }} - {x_{\min }}}} $

式中： ${\boldsymbol{x}}$ 为每一个SCADA特征数据； $ {x_{{\text{mean}}}} $ 为特征数据的均值； $ {x_{\max }} $ 为特征数据的最大值； $ {x_{\min }} $ 为特征数据的最小值； ${{\boldsymbol{x}}_{{n}}}$ 为归一化以后的特征数据。

3 基于LightGBM的风电机组主轴承温度预测 3.1 LightGBM算法

极限梯度提升(eXtreme gradient boosting, XGBoost)算法是在自适应增强(adaptive boosting, adaBoost)算法和梯度提升迭代决策树(gradient boosting decision tree,GBDT)算法基础上优化形成的算法^[13]，具有良好的预测精度和分类准确率，在众多领域得到了广泛的应用。但XGBoost算法普遍存在训练耗时长、内存占比大等缺点。针对这些缺点，Ke等^[14]做了相应的改进，并在2017年提出了LightGBM算法。LightGBM算法无需计算所有样本信息增益，具有训练效率高、低内存、高准确率、并行化学习等优势，较适合于工程实践。

LightGBM使用直方图算法替换了GBDT的预排序，能够在不损害准确率的前提下加快GBDT模型的训练速度^[15]。为保证结果准确性，算法使用梯度单边采样技术过滤大部分小梯度数据，在计算信息增益的时候只利用具有高梯度的数据信息；为大幅度减少占用内存，采用独立特征合并技术实现互斥特征的捆绑，减少样本特征数据^[16]。

假设训练一个具有 $ T $ 棵树的LightGBM模型，给定数据集为 $D = \{ ({{\boldsymbol{x}}_i},{{\boldsymbol{y}}_i})|i = 1,2, \cdots ,n,{{\boldsymbol{x}}_i} \in {{\bf{R}}^m}, $ $ {{\boldsymbol{y}}_i} \in {\bf{R}}\}$ ，其中给定的数据集共有 $ n $ 个样本，每个样本 $ {x_i} $ 对应 $ m $ 个特征和一个标签值 ${{\boldsymbol{y}}_i}$ 。LightGBM算法在迭代过程中，假设在前一轮迭代中得到的强学习器是 ${f_{t - 1}}({\boldsymbol{x}})$ ，损失函数为 $L({\boldsymbol{y}},{f_{t - 1}}({\boldsymbol{x}}))$ ，为了让本轮迭代的损失函数最小，本轮迭代的目的是找到分类回归树模型的弱学习器 ${h_t}({\boldsymbol{x}})$ ，如式(1)所示：

$ L({\boldsymbol{y}},{f_t}({\boldsymbol{x}})){\text{ = }}L({\boldsymbol{y}},{f_{t - 1}}({\boldsymbol{x}}){\text{ + }}{h_t}({\boldsymbol{x}})) $

(1)

利用损失函数负梯度拟合本轮损失函数近似值，从而拟合一个树模型。第 $ t $ 轮的第 $ i $ 个样本的损失函数 $ L({y_i},f({x_i})) $ 的负梯度 $ {r_{ti}} $ 为

$ {r_{ti}}{\text{ = }} - \frac{{\partial L({y_i},{f_{t - 1}}({{\boldsymbol{x}}_i}))}}{{\partial f({{\boldsymbol{x}}_i})}}{\Big|_{f(x) = {f_{t - 1}}(x)}} $

利用 $({{\boldsymbol{x}}_i},{{\boldsymbol{x}}_{ti}})$ 拟合一个CART回归树，进而得到 $ t $ 棵回归树所对应的叶子节点的范围为 ${{\bf{R}}_{ti}}$ ， $i = 1,2, \cdots ,J$ 。其中 $ J $ 为叶子节点的样本，当损失函数最小时拟合叶子节点输出值 $ {c_{tj}} $ 为

$ {c_{tj}}{\text{ = }}\underbrace {\arg \min }_c\sum\limits_{{{\boldsymbol{x}}_i} \in {{\bf{R}}_{tj}}} {L({{\boldsymbol{y}}_i},{f_{t - 1}}({{\boldsymbol{x}}_i}) + c)} $

式中： $ c $ 是损失函数最小化时的常数值； ${{\boldsymbol{x}}_i} \in {{\bf{R}}_{tj}}$ 表示样本 ${{\boldsymbol{x}}_i}$ 属于第 $ t $ 棵树下的第 $ j $ 个叶子节点。本轮的决策树拟合函数为

$ {h_t}({\boldsymbol{x}}) = \sum\limits_{j = 1}^J {{c_{tj}}I({{\boldsymbol{x}}_i} \in {{\bf{R}}_{tj}})} $

式中： $I({{\boldsymbol{x}}_i} \in {{\bf{R}}_{tj}})$ 是指示函数，当 ${{\boldsymbol{x}}_i} \in {{\bf{R}}_{tj}}$ 时，指示函数的值为1，反之为0^[17]。进而本轮最终得到的强学习器的表达式为

$ {f_t}({\boldsymbol{x}}) = {f_{t - 1}}({\boldsymbol{x}}) + \sum\limits_{j = 1}^J {{c_{tj}}I,\quad{{\boldsymbol{x}}_i} \in {{\bf{R}}_{tj}}} $

3.2 温度预测模型建立

选用10台主轴承正常机组的历史SCADA数据共38955组，按上述方法进行预处理后得到共25946组数据。将数据集80%作为训练集，数据集20%作为测试集。本文所有试验运行环境均为：操作系统为Windows10、python版本为3.7.1、集成开发运行环境为anaconda3，LightGBM算法、XGBoost算法和随机森林算法调用sklearn的API。后续使用的AC-GAN生成对抗神经网络调用kears深度学习框架API，NGBoost算法调用斯坦福的NGBoost框架。

对比分析LightGBM算法、XGBoost算法、CatBoost(categorical boosting)算法在风电机组训练主轴承温度预测模型的精度，如表3所示。

采用模型训练时间、均方根误差RMSE和决定系数 $ {r^2} $ 指标对建模精度进行评价，计算公式为

$ {\rm{RMSE}} = \sqrt {\frac{1}{n}\sum\limits_{i = 1}^n {{{({y_i} - {{\hat y}_i})}^2}} } $

$ {r^2} = 1 - \left[\sum\limits_{i = 1}^n {{{({y_i} - {{\hat y}_i})}^2}}\right]/{\left[\sum\limits_{i = 1}^n {({y_i} - \bar y} )^2\right]} $

式中： $ {y_i} $ 为第 $ i $ 个主轴承温度的真实测量值； $ {\hat y_i} $ 为第 $ i $ 个主轴承温度的预测值； $ \bar y $ 为主轴承温度的真实测量值的均值。LightGBM算法在均方根误差RMSE、决定系数 $ {r^2} $ 指标和训练时间上均优于XGBoost算法和CatBoost算法。表4为LightGBM、XGBoost和CatBoost这3种算法在测试集样本中残差特征对比。LightGBM算法在测试集上的残差最大值为0.129，残差均值为0.022，基于LightGBM的风电机组主轴承温度预测在测试集上具有较高的预测精度。

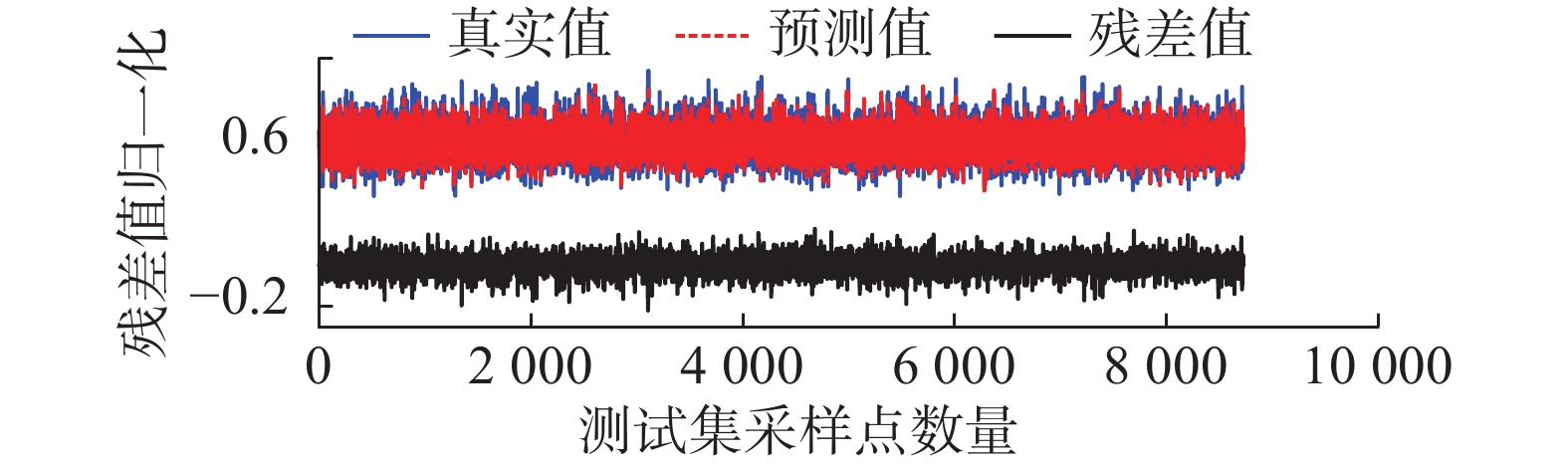
基于LightGBM算法的主轴承温度预测模型在测试集上的残差见图3所示。

4 基于AC-GAN的主轴承温度残差重构

基于AC-GAN的主轴承温度残差重构方法具体步骤为：首先，采用SPC方法将主轴承异常机组残差在控制范围内的正常残差数据剔除；其次，将控制范围之外的异常残差数据作为训练数据，采用AC-GAN生成对抗网络生成与真实数据分布相似的数据替换被剔除的数据。

4.1 基于SPC的残差特征提取

SPC方法最初主要用来监测生产产品中的质量问题，如果生产过程中出现随机质量问题说明此过程处于统计过程当中，如果出现故障问题说明此过程处于失控状态^[18]。

假设某产品在生产过程中的质量特征没有显著的非正态因素，而是由很多随机原因导致，则认为该质量特性服从正态分布^[19]。其质量特征 $ X $ 服从均值为 $ \mu $ ，标准差为 $ \sigma $ 的正态分布，则概率密度分布函数为

$f(x) = \frac{1}{{\sigma \sqrt {2{\text{π}}} }}{{\text{e}}^{ - (x - \mu )/2{\sigma ^2}}}$

$ \begin{array}{l} P(\mu - 3 \sigma \leqslant x \leqslant \mu + 3 \sigma ) \hfill = \displaystyle\int_{\mu - 3 \sigma }^{\mu + 3 \sigma } {f(x)} {\rm{d}}x = 0.9973 \hfill \end{array} $

质量特征在 $[\mu - 3\sigma ,\mu + 3\sigma ]$ 的概率为0.9973，则认为在该范围内的数据是可控的，范围之外为不可控。因此，本文主轴承异常机组温度残差中设定 $ [\mu - 3\sigma ,\mu + 3\sigma ] $ 的范围，范围内的残差为正常残差，范围之外为异常残差，其中 $ \mu $ 和 $ \sigma $ 为主轴承正常机组测试集温度残差的均值和标准差。利用SPC方法可以提取主轴承异常机组残差中的特征，将残差中正常残差进行剔除。

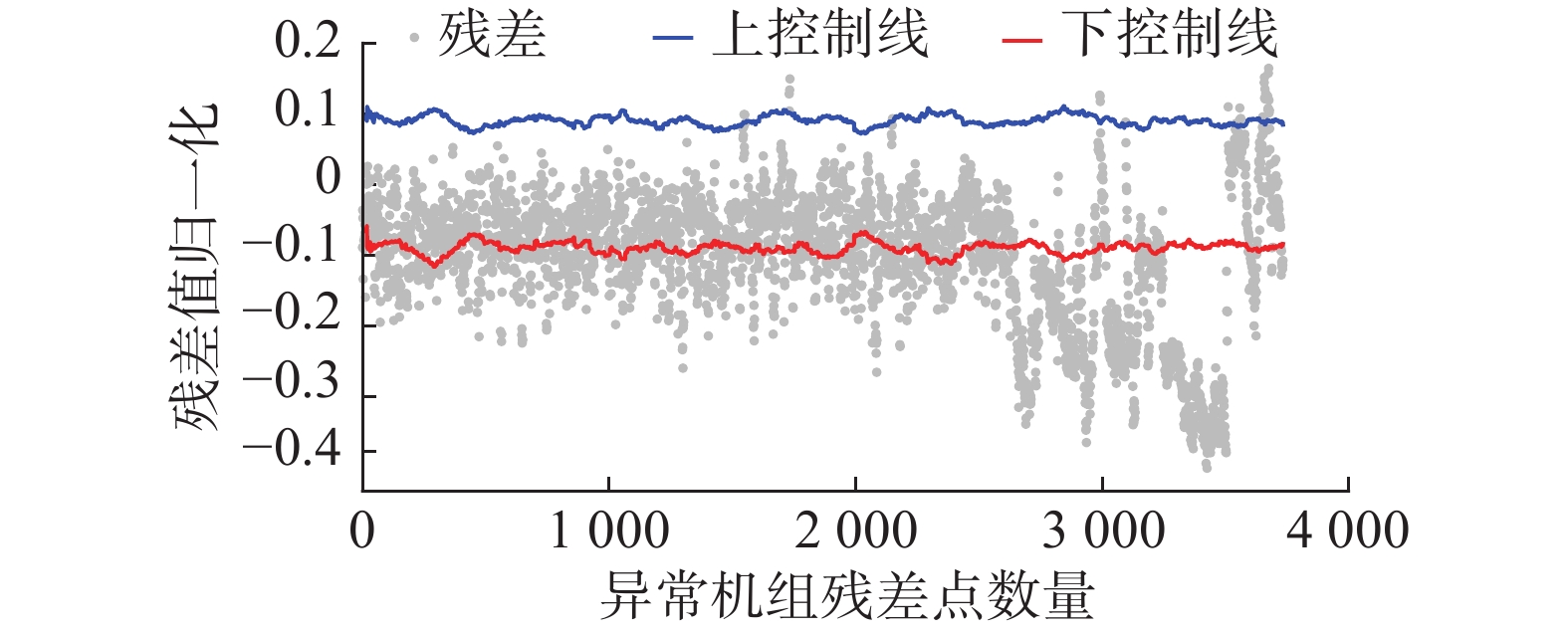
由文献[20]研究得知，轴承类故障在发生故障前一个月会有明显的劣化趋势，因此选取风电机组主轴承故障发生前一个月的SCADA数据进行试验。图4为某机组主轴承故障发生前一个月的温度残差，红线为 $ \mu - 3\sigma $ 下控制线，蓝线为 $ \mu + 3\sigma $ 上控制线，由图可知故障发生前并不是所有的残差都超出控制线范围。采用AC-GAN生成对抗网络重构主轴承异常机组温度残差序列，得到异常主轴承下的残差特征，解决异常样本数据的标记问题，进而提高了后续主轴承状态决策模型的预测精度。

4.2 AC-GAN算法介绍

生成对抗网络(generative adversarial networks, GAN)是一种无监督学习方法，包含生成器G(generator)和判别器D(discriminator)两部分。

将噪声信号 ${\boldsymbol{z}}$ 映射到样本空间，通过生成器 $ G $ 得到生成样本数据 ${{\boldsymbol{X}}_{{\text{fake}}}} = G({\boldsymbol{z}})$ ，将生成样本 ${{\boldsymbol{X}}_{{\text{fake}}}}$ 或真实样本数据 ${{\boldsymbol{X}}_{{\text{real}}}}$ 输入判别器 $ D $ 进而判定概率 $P({\boldsymbol{S}}\left| {\boldsymbol{X}} \right.) = D(X)$ ，表示判别样本 ${\boldsymbol{X}}$ 属于 ${\boldsymbol{S}}$ 的概率。由于 ${{\boldsymbol{X}}_{{\text{real}}}}$ 是真实数据，所以判别器判定概率接近于1， ${{\boldsymbol{X}}_{{\text{fake}}}}$ 是经生成器生成的数据并经过判别器判定是否真实。GAN 的目标函数为

$ \begin{array}{l} \mathop {\min }\limits_G \mathop {\max }\limits_D V(D,G) = {\rm{E}}[{\rm{ln}}P({\boldsymbol{S}} = {\rm{real}}\left| {{{\boldsymbol{X}}_{{\rm{real}}}}} \right.)] + \\ \quad\quad\quad {\rm{E}}[{\rm{ln}} P({\boldsymbol{S}} = {\rm{fake}}\left| {{{\boldsymbol{X}}_{{\rm{fake}}}}} \right.)] \end{array} $

目标函数包含生成器目标函数和判别器目标函数，其中生成器目标函数为

$ \mathop {\min }\limits_G V(G) = {\rm{E}}[{\rm{ln}} P({\boldsymbol{S}} = {\rm{fake}}\left| {{{\boldsymbol{X}}_{{\rm{fake}}}}} \right.)] $

判别器的目标函数为

$ \begin{array}{l} \mathop {\max }\limits_D V(D) = {\rm{E}}[{\rm{ln}}P(S = {\rm{real}}\left| {{X_{{\rm{real}}}}} \right.)]+ \\ \quad\quad {\rm{E}}[{\rm{ln}} P({\boldsymbol{S}} = {\rm{fake}}\left| {{{\boldsymbol{X}}_{{\rm{fake}}}}} \right.)] \end{array} $

GAN 训练过程中，G和D二者交替训练，相互博弈，最终使G生成的样本符合真实样本概率分布，达到纳什均衡。GAN在训练过程中无需先验概率即能学习真实样本的分布，但同时GAN对初始参数极其敏感，输入G的随机噪声信号无约束，导致生成数据概率分布与真实数据差异大，训练过程难以收敛，使整个训练过程出现震荡，发生模式崩溃^[21-22]。为了解决上述问题，文献[23]提出了带标签辅助分类器的生成对抗网络AC-GAN，在传统GAN基础上增加了噪声数据对应的标签 $ c $ ，使用两者来生成 ${{\boldsymbol{X}}_{{\text{fake}}}} = G({\boldsymbol{c}},{\boldsymbol{z}})$ ，判别器计算生成数据的概率分布 $P({\boldsymbol{S}}\left| {\boldsymbol{X}} \right.)$ 和类标签上的概率分布 $P({\boldsymbol{c}}\left| {\boldsymbol{X}} \right.)$ 分别为

$ \left\{\begin{aligned} &P({\boldsymbol{S}}\left| {\boldsymbol{X}} \right.)= D(X)\\ &P({\boldsymbol{c}}\left| {\boldsymbol{X}} \right.) = D(X)\end{aligned}\right. $

式中： ${\boldsymbol{c}} = \{ 0,1,2, \cdots ,n\}$ ， $ n $ 表示样本类数。真实样本数据标记为正常温度残差( ${\boldsymbol{c}} = 0$ )和异常温度残差( ${\boldsymbol{c}} = 1$ )，AC-GAN通过内部博弈，最终实现主轴承异常机组温度残差的重构。

4.3 基于AC-GAN的温度残差重构

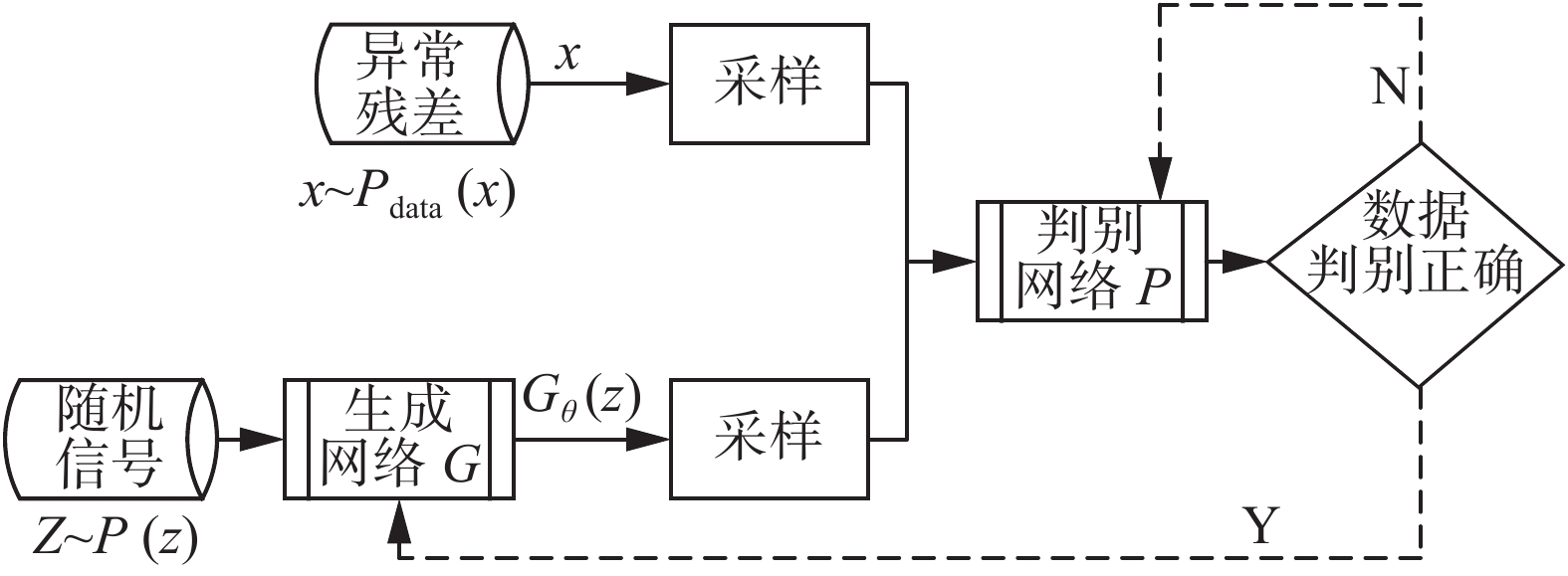
AC-GAN生成器和判别器均采用RNN神经网络，输入层为32个神经单元，隐含层有3层神经单元，输出层为1个神经单元，激活函数为sigmoid，损伤函数为均方误差。AC-GAN生成对抗网络的基本框架见图5。

温度残差重构具体步骤为：

1)将主轴承发生故障前一个月的SCADA特征数据输入至基于LightGBM的主轴承温度预测模型，计算得到一个月内的主轴承异常机组温度残差。

2)采用SPC控制图将主轴承异常机组残差在控制范围内的正常温度残差数据剔除。

3)定义控制线之外的残差数据为训练样本数据，采用AC-GAN算法生成与真实样本数据分布相似的残差数据，用来重构剔除的正常温度残差2)中剔除的正常温度残差。

5 基于NGBoost的主轴承运行状态决策

NGBoost算法由斯坦福吴恩达团队在2019年10月提出的，最初是用于预测不确定性估计的天气预测和医疗保健等领域^[24]。该算法使用自然梯度的Boosting方法，这种方法可直接在输出空间中得到全概率分布，用于预测量化不确定性。NGBoost算法区别于其他Boosting算法是因为该算法可以返回每个预测的概率分布，NGBoost通过预测参数θ，产生概率密度为 $ {P_\theta }(y|x) $ 的概率预测。NGBoost使用自然梯度来学习参数，使得优化问题不受参数化的影响，随后在GBM的框架下让每个基学习器去拟合自然梯度，最后经过放缩和加权组合，得到一个集成模型的参数，由此可以学习最终条件分布参数，从而达到概率预测的目的。NGBoost作为一种梯度提升算法，使用自然梯度(natural gradient)解决现有梯度提升方法难以处理的通用概率预测的技术难题，NGBoost在不确定性估计和传统指标上的预测能力具有相当大的优势^[25]。

对于自然梯度，首先定义得分规则为 $ S $ ，这个得分规则与概率分布 ${\boldsymbol{P}}$ 和输出值 ${\boldsymbol{y}}$ 相关，记为 $S({\boldsymbol{P}},{\boldsymbol{y}})$ 。对于正确的概率分布，并期望取得最佳值，概率预测越准确，损失越小，故有

$ {E_{y \sim Q}}[S({\boldsymbol{Q}},{\boldsymbol{y}})] \leqslant {E_{y \sim Q}}[S({\boldsymbol{P}},{\boldsymbol{y}})],\quad \forall {\boldsymbol{P}},{\boldsymbol{Q}} $

式中： ${\boldsymbol{Q}}$ 为正确的概率分布； ${\boldsymbol{P}}$ 为预测的概率分布。定义得分规则的散度：

$ {D_S}({\boldsymbol{Q}}||{\boldsymbol{P}}) = {E_{y \sim Q}}[S({\boldsymbol{P}},{\boldsymbol{y}})] - {E_{y \sim Q}}[S({\boldsymbol{Q}},{\boldsymbol{y}})] $

得分规则定义需要使得散度非负，并且能够测量分布间的距离。如果得分规则定义为MIF，则

$ S = L(\theta ,{\boldsymbol{y}}) = - \ln {P_\theta }({\boldsymbol{y}}) $

最大似然估计函数 $\displaystyle\sum {\ln ({P_\theta }({\boldsymbol{y}}))}$ 取得最大值，同时使得散度变为KL散度，即

$ {D_L}({\boldsymbol{Q}}||{\boldsymbol{P}}) = {E_{y \sim Q}}\left[\ln\dfrac{{{\boldsymbol{Q}}({\boldsymbol{y}})}}{{{\boldsymbol{P}}({\boldsymbol{y}})}}\right] = {D_{{\rm{KL}}}}({\boldsymbol{Q}}||{\boldsymbol{P}}) $

如果得分规则定义为CRPS(连续概率排位分数)，则

$ C(\theta ,{\boldsymbol{y}}) = \int_{ - \infty }^y {{F_\theta }{{(z)}^2}{\rm{d}}z + } \int_y^\infty {{{(1 - {F_\theta }(z))}^2}{\rm{d}}z} $

式中 $ F $ 为累计概率分布函数。本来定义CRPS为

$ {C^{{\rm{real}}}}(\theta ,{\boldsymbol{y}}) = \int_{ - \infty }^\infty {({F_\theta }(z) - } {F^Q_\theta} (z){)^2}{\rm{d}}z $

式中： ${F^Q_\theta} (z)$ 为真实的累计概率分布，当预测分布与真实分布完全一致时，CRPS为零。预测分布过于集中，过于分散，或者偏离观测值太远时都会导致CRPS增大。但是，真实概率分布未知，只能通过一系列观察数据的累计分布来定义，故有 $ C(\theta ,y) $ ，对应的散度为

$ \begin{array}{l} {D_C}(\theta ,{\boldsymbol{y}}) = {E_{y \sim Q}}[C({\boldsymbol{P}},{\boldsymbol{y}})] - {E_{y \sim Q}}[C({\boldsymbol{Q}},{\boldsymbol{y}})] = \\ \;\;\quad\quad \displaystyle\int_{ - \infty }^\infty {({F_\theta }(x) - } {F_P}(x){)^2}{\rm{d}}x \end{array} $

CRPS对于真实概率，其值最小，散度非负，度量分布距离符合规则的定义要求。对于选择的得分规则 $ S(\theta ) $ ,满足 ${\rm{E}}[\nabla S(\theta )] = 0$ ,对 $ L $ 关于 $ \theta $ 求导有

$ \nabla S(\theta ,{\boldsymbol{y}}) + {\rm{E}}[{\nabla ^2}S(\theta )] = 0 $

最终的梯度为

$ \tilde \nabla S(\theta ,{\boldsymbol{y}}){\text{ = (}}{\rm{E}}[{\nabla ^2}S]{)^{ - 1}}\nabla S(\theta ) $

对于MIF，有

$ \tilde \nabla L(\theta ,{\boldsymbol{y}}){\text{ = }}{\rm{E}}[ - \nabla _\theta ^2L(\theta ,{\boldsymbol{y}})]{^{ - 1}}\nabla S(\theta ,{\boldsymbol{y}}) $

对于CRPS,有

$ \tilde \nabla C(\theta ,{\boldsymbol{y}}){\text{ = }}{\left[2\int_{ - \infty }^\infty {{\nabla _\theta }} {F_\theta }(z){\nabla _\theta }{F_\theta }{(z)^{\rm{T}}}{\rm{d}}z\right]^{ - 1}}\nabla C(\theta ,{\boldsymbol{y}}) $

风电机组的主轴承温度残差同样是一种不确定估计，对主轴承状态监测实质也是一种故障发生不确定性的概率预测，因此可利用该算法建立主轴承运行状态决策模型。

为使降低故障决策中单点误报，获得较高的预测准确度，本文按天提取主轴承温度残差的最大值、最小值、均值、偏度、峰度、中位数、方差、标准差8个特征，将主轴承正常机组的温度残差标签设置为0，主轴承异常机组重构的温度残差标签设置为1。

6 实例应用验证

本实验所采用的SCADA数据为河北某风电场的历史数据。选取机组编号为07#、09#、23#、31#、32#、41#、14#、11#、71#、81#，10台主轴承正常机组，选取编号为69#、37#、84#、88#、99#、15#、96#、86#、13#、70#的10台主轴承异常机组，共计20台机组。通过基于LightGBM的主轴承温度预测模型计算各机组主轴承温度残差，对于异常机组通过AC-GAN算法重构残差值。提取主轴承正常机组和主轴承异常机组8个温度残差特征作为状态决策模型输入，预测的主轴承正常或异常的概率值作为状态决策模型输出。由于主轴承正常机组标签设置为0，异常机组标签设置为1，因此，输出概率在0.5以上可判断为异常状态，0.5以下判断为正常状态。温度残差特征80%用于训练状态决策模型，剩余20%用于测试模型的准确度。按上述流程提取残差特征后共得到938组数据。对比分析NGBoost、XGBoost和随机森林3种算法在残差重构前后测试样本中的准确性。

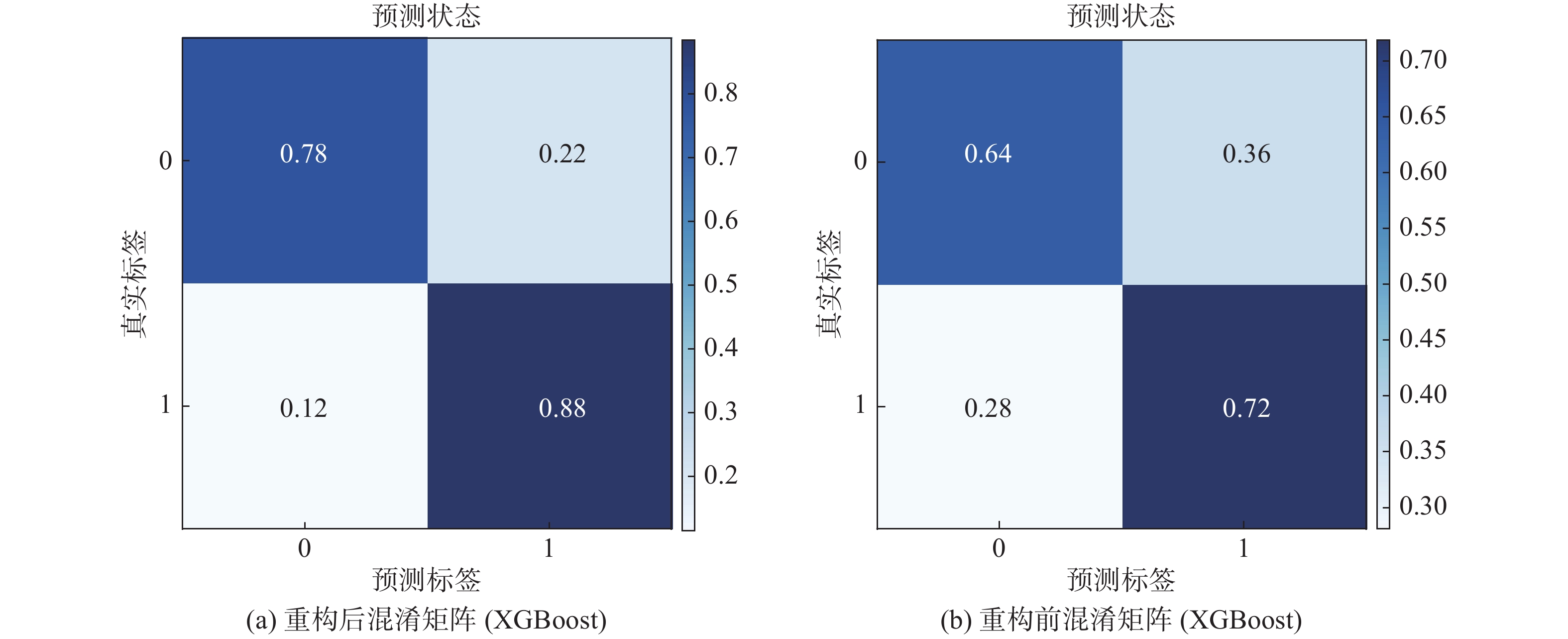
NGBoost算法在测试集上的准确为0.875，混淆矩阵见图6(a)。采用同样的特征提取方法提取没有经过残差重构的特征，在测试集上的准确度为0.660，混淆矩阵见图6(b)。XGBoost算法在测试集上的准确为0.843，混淆矩阵见图7(a)。采用同样的特征提取方法提取没有经过残差重构的特征，在测试集上的准确度为0.651，混淆矩阵见图7(b)。

随机森林算法在测试集上的准确为0.750，混淆矩阵见图8(a)。采用同样的特征提取方法提取没有经过残差重构的特征，在测试集上的准确度为0.642，混淆矩阵见图8(b)。

实验结果表明：在同等条件下，NGBoost算法在风电机组主轴承状态决策模型中优于XGBoost算法和随机森林算法。而且NGBoost、XGBoost和随机森林3种算法经过残差重构的状态决策模型的准确度分别提高了21.5%、19.2%、10.8%，说明基于AG-GAN的数据重构对风电机组主轴承运行状态具有良好的预测准确度。

下一步，选取未参与模型训练和测试的6台机组用来验证基于残差重构和NGBoost算法下的准确性和泛化性。选取主轴承正常机组编号为08#、65#、66#，主轴承异常机组编号为10#、85#、91#。

10#机组在2019年3月28号巡检时发现该机组主轴承振动过大，需要更换主轴承，选取2019年3月1号到2019年3月30号的数据。85#机组在2019年4月1号巡检时有异常响声，经厂家检查发现该机组主轴承电腐蚀严重，因振动导致平衡环境存在轻微开裂迹象，选取2019年3月8号到4月4号的数据。91#机组在2019年10月13号发生主轴承开裂故障，选取2019年9月16号到10月16号的数据。正常机组随机选取一个月的数据。

对比分析表5、6，正常机组编号为08#的机组在经过残差重构后预测的准确率提升了28%，65#机组的准确率提升了3%，66#机组的准确率提升了1%。对比分析表7、8，异常机组编号为10#的机组在经过残差重构后预测的准确率提升了17%，85#机组的准确率提升了15%，91#机组的准确率提升了7%。

7 结束语

本文以风电机组主轴承为研究对象，针对状态监测和故障预警中人为设定阈值的相关问题，提出了基于AC-GAN数据重构的风电机组主轴承状态监测方法，得到如下结论：

1)采用LightGBM算法建立主轴承温度残差预测模型，并将XGBoost算法、CatBoost算法与之对比分析，在同等条件下，LightGBM算法在主轴承温度建模中综合性能优于XGBoost算法和CatBoost算法。

2)采用滑动窗口提取主轴承异常机组残差，利用SPC方法对主轴承异常温度残差在控制线范围内进行筛选，并利用AC-GAN算法对残差序列进行重构，解决了人为设定阈值的相关问题，提升了主轴承异常和正常数据标签标注的准确率。

3)在同等条件下，NGBoost算法在风电机组主轴承状态决策模型中优于XGBoost算法和随机森林算法。而且，NGBoost、XGBoost和随机森林3种算法经过残差重构的状态决策模型的准确度分别提高了21.5%、19.2%、10.8%，选择6台机组进行测试分析(3台主轴承正常机组，3台主轴承异常机组)，均能够判断正确。基于NGBoost的状态决策模型的平均准确率从60.5%(无残差序列重构)提升至72.3%(利用残差数据重构)。