2019年12月，新型冠状病毒肺炎疫情(corona virus disease 2019, COVID-19)在中国湖北省武汉市爆发。新型冠状病毒传染速度极快，短时间内即造成多人感染。为控制疫情，武汉市于2020年1月23日实施封城管理，此后全国多个省市相继启动突发公共卫生事件Ⅰ级响应机制。2020年1月31日，世界卫生组织宣布COVID-19疫情构成“国际关注的突发公共卫生事件”，后于当地时间2020年3月11日宣布COVID-19疫情成为全球大流行。一时之间，疫情的发展趋势成为全国乃至世界人民共同关注的问题。通过对疫情发展趋势的有效预测可对人们提前制定应对措施提供帮助。从疫情爆发初期开始，世界范围内就有诸多学者对疫情情况进行了预测^[1-3]。

SIR模型^[4-5]和SEIR模型^[6-7]都是常用的传染病模型，被用来对传染病传播情况进行模拟和预测。文献[8]使用SEIR模型对武汉当时的疫情规模以及武汉和全国其余地区的疫情峰值进行了预测。文献[9]考虑到人口的流动情况，对SEIR模型进行改进，使用改进后的模型对国内疫情趋势进行预测。文献[10]使用基于年龄的SEIR模型对美国的疫情感染人数和死亡人数进行了预测。传统SIR模型和SEIR模型的局限性在于模型参数都是常数，无法随着现实世界中真实情况的变化而改变。在以往的工作中，模型参数的计算通常需要人为划分时间段，使用不同时间段的数据进行分段计算，以实现动态预测。针对此问题，文献[11]基于启发式算法^[12]，对SEIR模型中的参数不断进行随机采样并通过均方根误差最小的约束原则，获得参数的最优解，从而对武汉的疫情拐点进行预测。文献[13]则在SIR模型的基础上，将模型与机器学习中的极限学习机^[14]相结合，提出了极限IR模型，将疫情发展趋势预测模型的构建转化为对模型参数预测模型的构建，对全国疫情趋势进行了预测。

近年来随着深度学习的不断发展，其以优秀的实验性能在多个领域中脱颖而出，包括计算机视觉领域^[15-17]、自然语言处理领域^[18-20]和语音识别领域^[21-23]等。在时序预测问题中，最常见的神经网络是循环神经网络^[24-25](recurrent neural network, RNN)。RNN可学习到历史输入与当前输入的关联信息，从而进行时序预测。但当时间序列过长时，传统RNN容易出现梯度消失现象，无法处理具有长期依赖关系的问题。为解决这一问题，出现了长短期记忆网络^[26-27](long short-term memory network, LSTM)。在此次疫情中，疫情的变化和发展会受到前期各项措施的影响，因此疫情趋势预测可看作具有长期依赖关系的时序预测问题。文献[11]除使用改进后的SEIR模型之外，也使用了LSTM对疫情的发展趋势进行模拟和预测。

本文将疫情趋势预测看作一个长期且动态变化的时序预测问题，受文献[11, 13]启发，借助传统SEIR模型的数学方法与人工智能方法在时序预测问题上的优越性，从SEIR模型参数入手，针对新冠病毒的传播特点，提出了基于LSTM的病毒传染率预测方法，并将其与SEIR模型结合，提出新冠肺炎疫情趋势预测模型(LSTM-SEIR network, LS-Net)。LS-Net借助LSTM优良的时序信息学习能力对病毒传染率进行实时预测。最后将实时更新的病毒传染率应用到SEIR模型中，实现对疫情发展趋势的智能动态预测。

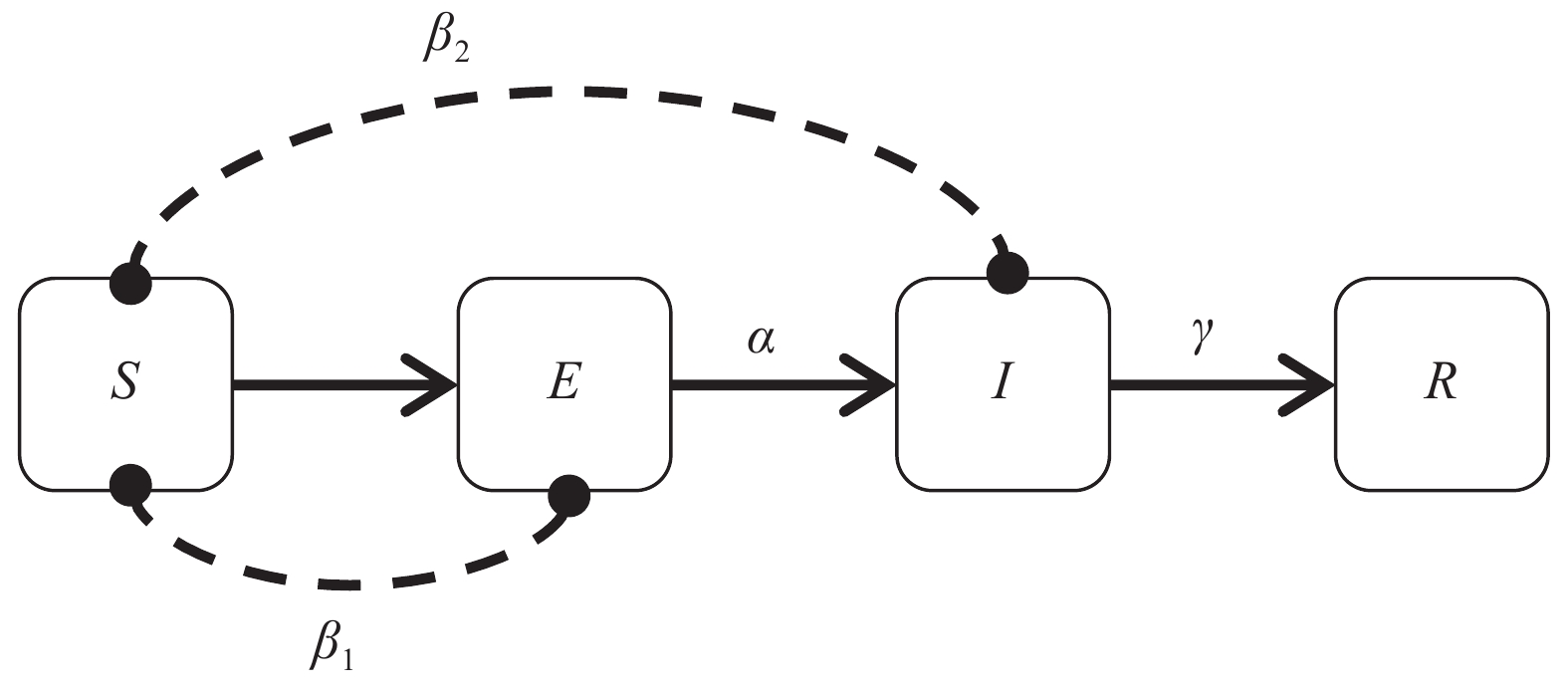
1 基于传统SEIR模型的疫情趋势预测模型 1.1 传染病传播模型——SEIR

SEIR模型是经典的传染病模型，它将人群分为4类：易感者(susceptible)，健康但有可能感染病毒的人，总人数为S；潜伏者(exposed)，已感染病毒但仍未出现病症的人，总人数为E；感染者(infected)，已感染病毒并出现病症的确诊患者，总人数为I；移除者(removed)，感染病毒后因病死亡或成功治愈的人，总人数为R。在COVID-19疫情中，SEIR模型中4类人群的转化关系如图1所示，图中， ${\beta _1}$ 为潜伏者将病毒传染给易感者的概率， ${\beta _2}$ 为感染者将病毒传染给易感者的概率, $\alpha $ 为潜伏者转化为感染者的概率， $\gamma $ 为感染者转化为移除者的概率。SEIR的动力学方程为

$\left\{ \begin{aligned} &\dfrac{{{\rm{d}} S}}{{{\rm{d}} t}} = - \dfrac{{{b_1}SE}}{N} - \dfrac{{{b_2}SI}}{N} \\ &\dfrac{{{\rm{d}} E}}{{{\rm{d}} t}} = \dfrac{{{b_1}SE}}{N} + \dfrac{{{b_2}SI}}{N} - aE \\ &\dfrac{{{\rm{d}} I}}{{{\rm{d}} t}} = aE - gI \\ &\dfrac{{{\rm{d}} R}}{{{\rm{d}} t}} = gI \end{aligned} \right.$

(1)

式中：t为时间步长；N=S+E+I+R为人群总数。

1.2 病毒传染率 ${\beta _1}$ 、 ${\beta _2}$ 的计算方法

根据文献[11]， ${\beta _1}$ 和 ${\beta _2}$ 由式(2)计算得到：

$\left\{ \begin{array}{l} {\beta _1} = {k_1}b \\ {\beta _2} = {k_2}b \end{array} \right.$

(2)

式中： ${k_1}$ 、 ${k_2}$ 分别为平均每潜伏者和每感染者每天接触的人数； $b$ 为病毒的传播率，可由SIR模型计算得到。SIR模型与SEIR模型类似，其将人群分为易感者、感染者、移除者3类，在SIR模型中，病毒传染初期由于感染人数较少，所以 $N \approx S$ ，则

$\frac{{{\rm{d}} I}}{{{\rm{d}} t}} = \frac{{\beta SI}}{N} - \gamma I \approx (\beta - \gamma )I$

(3)

由式(3)可得：

${{I}} ({{t}}) = {\rm{exp}}[(kb - \gamma )I]$

(4)

由式(4)可计算出 $b$ ，将其代入式(2)即可计算出SEIR模型中的 ${\beta _1}$ 和 ${\beta _2}$ 。

在传统SEIR模型中， ${\beta _1}$ 和 ${\beta _2}$ 常是由数据统计得出的常数。而在现实情下，病毒的传染能力很大程度上会受到外界的影响，所以 ${\beta _1}$ 和 ${\beta _2}$ 应是不断变化的。且在上述方法中， ${\beta _1}$ 和 ${\beta _2}$ 均由SIR模型计算得出，没有考虑到潜伏期患者的病毒传染情况。

2 新冠肺炎疫情趋势预测模型——LS-Net

针对传统SEIR模型中的病毒传染率无法实现自动动态预测和没有考虑到潜伏期患者的传染情况的问题，本文基于LSTM和SEIR模型提出LS-Net。

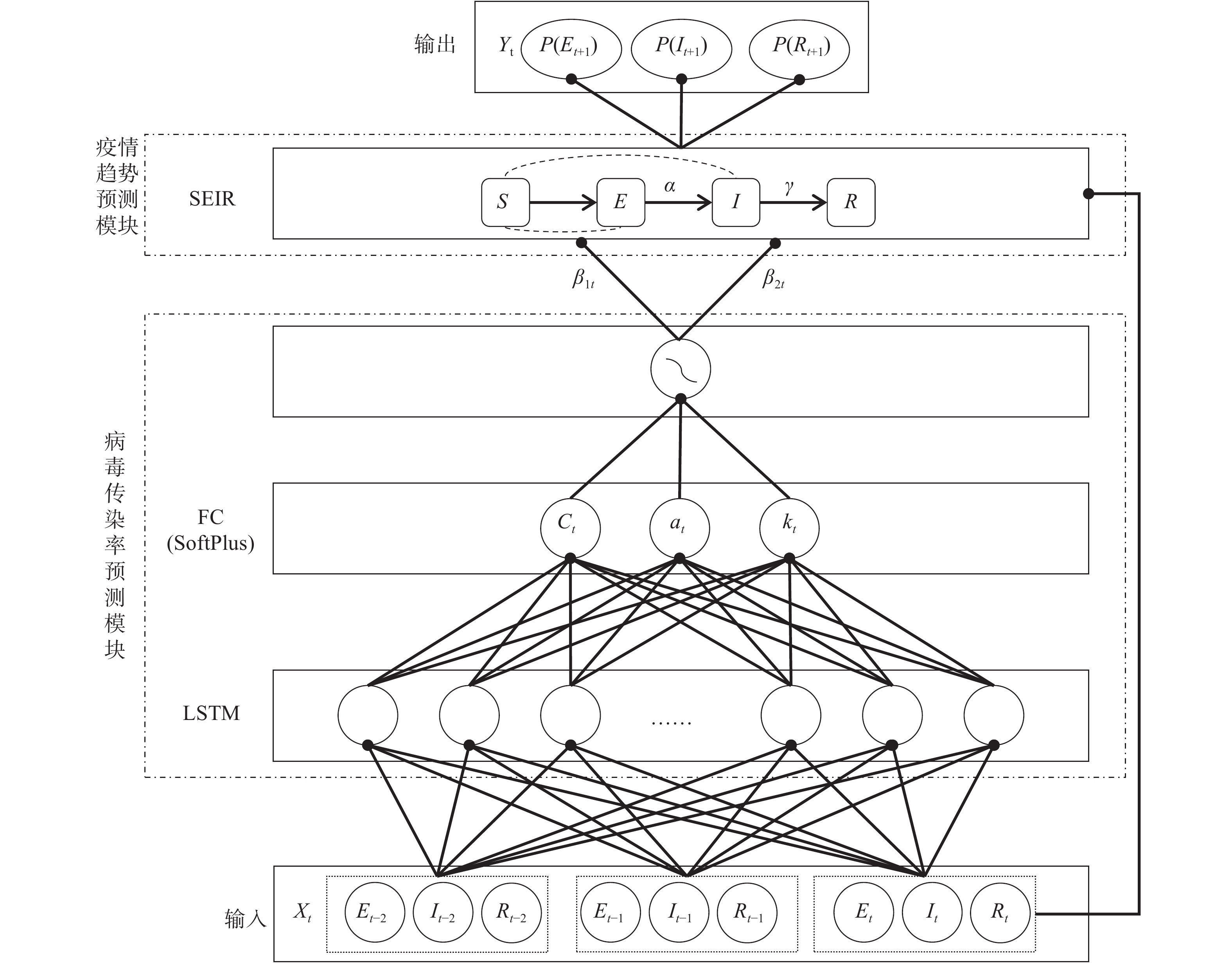
2.1 LS-Net的网络结构与数学模型

LS-Net的总体结构如图2所示，其包括2个模块：病毒传染率预测模块和疫情趋势预测模块。病毒传染率预测模块包括LSTM层、全连接层(fully connection layer，FC)和非线性变换层，实现对新冠病毒传染率 ${\beta _1}$ 和 ${\beta _2}$ 的预测。疫情趋势预测模块包括SEIR模型层，实现对新冠疫情趋势的预测。

2.1.1 病毒传染率预测模块

病毒传染率后期的变化与疫情前期的防控和诊治措施息息相关，因此病毒传染率的预测需要结合历史信息与当前信息共同分析得出。病毒传染率预测模块以LSTM为基础，结合病毒的传播规律对传染率进行预测。为更好地学习到时序数据间的关联信息，LS-Net使用3天的潜伏期、感染者、移除者数量作为输入。

LSTM可学习并生成包含历史信息与当前信息的数据，其包含3类门：输入门 ${i_{{t}}}$ 、遗忘门 ${{{f}}_t}$ 、输出门 ${{{o}}_t}$ 。LSTM更新过程如式(5)所示：

$\left\{ \begin{aligned} & {i_t} = s({W_{ii}}{X_t} + {b_{ii}} + {W_{hi}}{h_{t - 1}} + {b_{hi}}) \\ & {f_t} = s({W_{if}}{X_t} + {b_{if}} + {W_{hf}}{h_{t - 1}} + {b_{hf}}) \\ &{{\tilde c}_t} = s({W_{i{\tilde c}}}{X_t} + {b_{i\tilde c}} + {W_{h{\tilde c}}}{h_{t - 1}} + {b_{h\tilde c}}) \\ &{o_t} = s({W_{io}}{X_t} + {b_{io}} + {W_{ho}}{h_{t - 1}} + {b_{ho}}) \\ &{c_t} = {f_t}{c_{t - 1}} + {i_t}{{\tilde c}_t} \\ &{h_t} = {o_t}\tanh ({c_t}) \end{aligned} \right.$

(5)

式中： ${X_{{t}}}$ 为t时刻的输入。

将 ${{{h}}_t}$ 输出的包含时序信息的特征输入到FC层。FC层计算过程如式(6)所示：

$\left\{ \begin{aligned} &{C_{{t}}} = \lg (1 + \exp ({W_C}{h_t})) \\ &{a_{{t}}} = \lg (1 + \exp ({W_a}{h_t})) \\ &{k_{{t}}} = \lg (1 + \exp ({W_k}{h_t})) \end{aligned} \right.$

(6)

式中： ${C_{{t}}}$ 、 ${{{a}}_{{t}}}$ 、 ${{{k}}_{{t}}}$ 均为预测 $ t $ 时刻 ${\beta _1}$ 和 ${\beta _2}$ 的控制参数。

随着政府和社会管控力度以及人们自身防控意识的不断增强， ${\beta _1}$ 、 ${\beta _2}$ 会逐渐下滑，且后期 $ {\beta }_{1} $ 、 $ {\beta }_{2} $ 相较前期会大幅下降。由于确诊患者会被严密地隔离起来并进行医治，与之接触的医护人员也会采取完备的防护措施，而潜伏期患者相对行动更加自由，所以实际上确诊患者的病毒传播能力相较于潜伏期患者更弱。据此本文为新冠病毒传染创建了式(7)所示的非线性变换函数，由此计算得到 ${\beta _1}$ 和 ${\beta _2}$ 。

$\left\{ \begin{array}{l} {\beta _{{1_{{t}}}}} = {C_t}\exp \left( - \dfrac{1}{{{a_t}}}\right) \\ {\beta _{{{\rm{2}}_t}}} = {k_t}{\beta _{1_t}} \end{array} \right.$

(7)

2.1.2 疫情趋势预测模块

该模块由1.1节所述的SEIR模型构成。SEIR层具有参数S、 $\alpha $ 和 $\gamma $ ，结合病毒传染率预测模块得到的 ${\beta _{{1_{{t}}}}}$ 和 ${\beta _{{2_{{t}}}}}$ 及输入数据 ${E_t}$ 、 ${I_t}$ 、 ${R_t}$ 对类数据进行预测。其计算过程为

$ \left\{ \begin{aligned} & P{(S)_{t + 1}} = {S_{t }} - \dfrac{{{\beta _{{1_t}}}{S_t}{E_t}}}{N} - \dfrac{{{\beta _{{2_t}}}{S_t}{I_t}}}{N} \\ & P{(E)_{t + 1}} = {E_{t }} + \dfrac{{{\beta _{{1_t}}}{S_t}{E_t}}}{N} + \dfrac{{{\beta _{{2_t}}}{S_t}{I_t}}}{N} - \alpha {E_t} \\ & P{(I)_{t + 1}} = {I_{t }} + \alpha {E_t} - \gamma {I_t} \\ & P{(R)_{t + 1}} = {R_{t}} + \gamma {I_t} \end{aligned} \right. $

(8)

式中： $P{(S)_{t + 1}}$ 、 $P{(E)_{t + 1}}$ 、 $P{(I)_{t + 1}}$ 、 $P{(R)_{t + 1}}$ 分别为第t+1天易感者、潜伏者、感染者和移除者数量的预测值。

2.2 模型训练算法

LS-Net训练时使用前3天的数据预测第4天的数据，并使用平均平方误差(mean square error, MSE)作为损失函数。由于现实中感染者和移除者的数据更易收集，且人们对感染者情况更关注，本文在训练时给3类数据的MSE分配了不同的权重。具体如式(9)所示：

$\left\{ \begin{array}{l} {\rm{Loss}} = 0.1{{\rm{MSE}} _E} + 0.5{{\rm{MSE}} _I} + 0.4{{\rm{MSE}} _R} \\ {{\rm{MSE}} _E} = \dfrac{1}{T}\displaystyle\sum\limits_{t = 1}^T {{{({E_t} - P{{(E)}_t})}^2}} \\ {{\rm{MSE}} _I} = \dfrac{1}{T}\displaystyle\sum\limits_{t = 1}^T {{{({I_t} - P{{(I)}_t})}^2}} \\ {{\rm{MSE}} _R} = \dfrac{1}{T}\displaystyle\sum\limits_{t = 1}^T {{{({R_t} - P{{(R)}_t})}^2}} \end{array} \right.$

(9)

式中： ${{\rm{MSE}} _E}$ 、 ${{\rm{MSE}} _I}$ 、 ${{\rm{MSE}} _R}$ 分别为由潜伏者、感染者、移除者的真实值和预测值计算得到的MSE； ${E_t}$ 、 ${I_t}$ 、 ${R_t}$ 为真实值； $P{(E)_t}$ 、 $P{(I)_t}$ 、 $P{(R)_t}$ 为预测值。

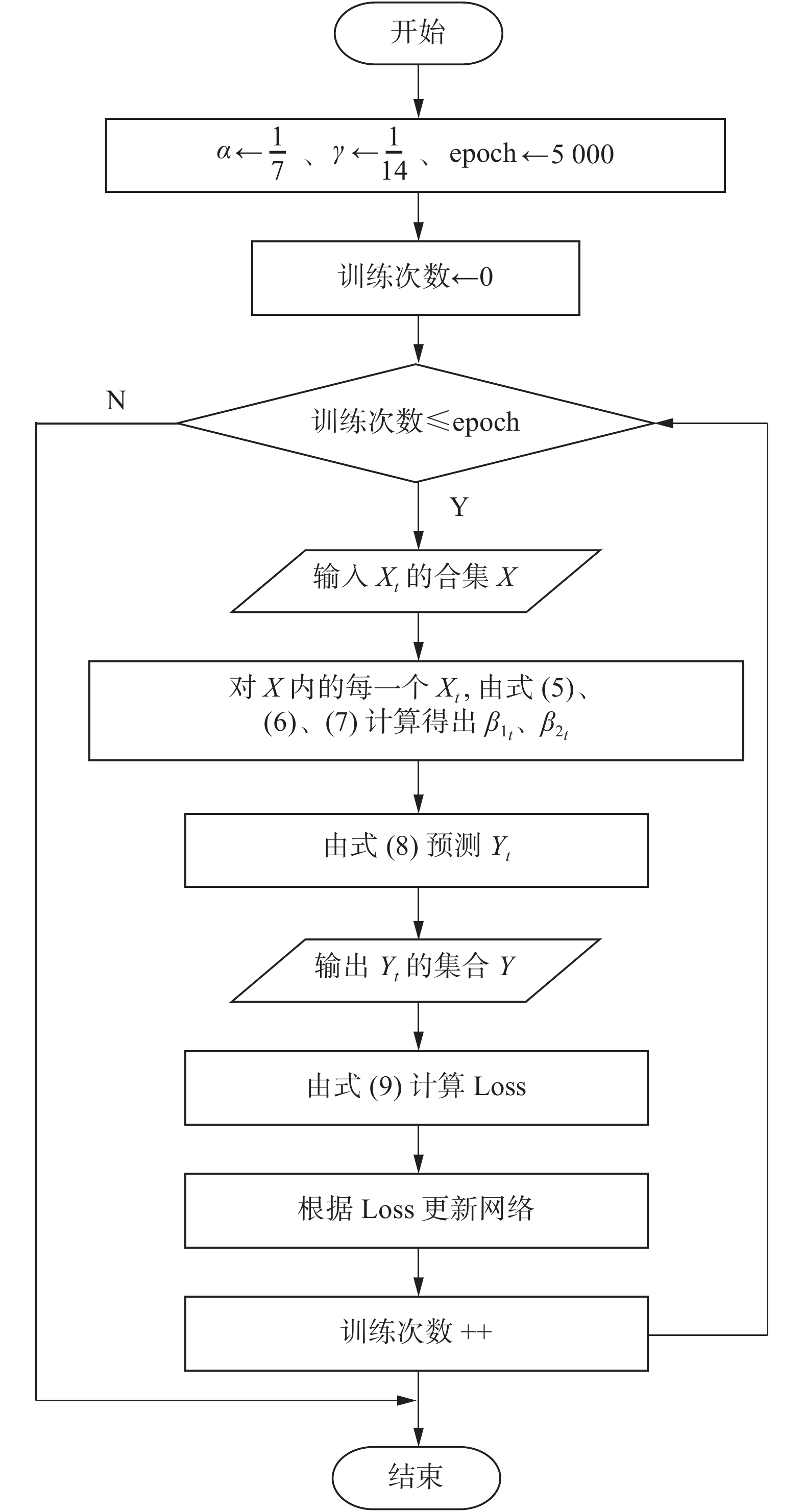
模型训练流程如图3所示。该训练算法见算法1。

算法1　模型训练

输入　训练集样本 $X = \{ {X_2}, \cdots ,{X_{{t}}}, \cdots, {X_T}\}$ ，其中 ${X_t} = \{ {E_{t - 2}},{I_{t - 2}},{R_{t - 2}},{E_{t - 1}},{I_{t - 1}},{R_{t - 1}},{E_t},{I_t},{R_t}\} $ ， ${{t}} \in [2,T]$ ；

输出　模型预测结果 $Y = \{ {Y_2},{Y_3}, \cdots ,{Y_t}\}$ ，其中 ${Y_t} = \{ {E_{t + 1}},{I_{t + 1}},{R_{t + 1}}\} $ ， ${{t}} \in [2,T]$ 。

参数epoch：训练的总次数。

1) While 训练次数 $ \leqslant $ epoch do

2) for each ${X_t} \in X$ do

3)由式(5)、(6)、(7)计算病毒传染率 ${\beta _{{1_{{t}}}}}$ 、 ${\beta _{{2_{{t}}}}}$

4)由式(8)计算新冠肺炎疫情趋势 ${Y_{{t}}}$

5) End for

6)由式(9)计算Loss

7)根据Loss更新LSTM参数

9)End while

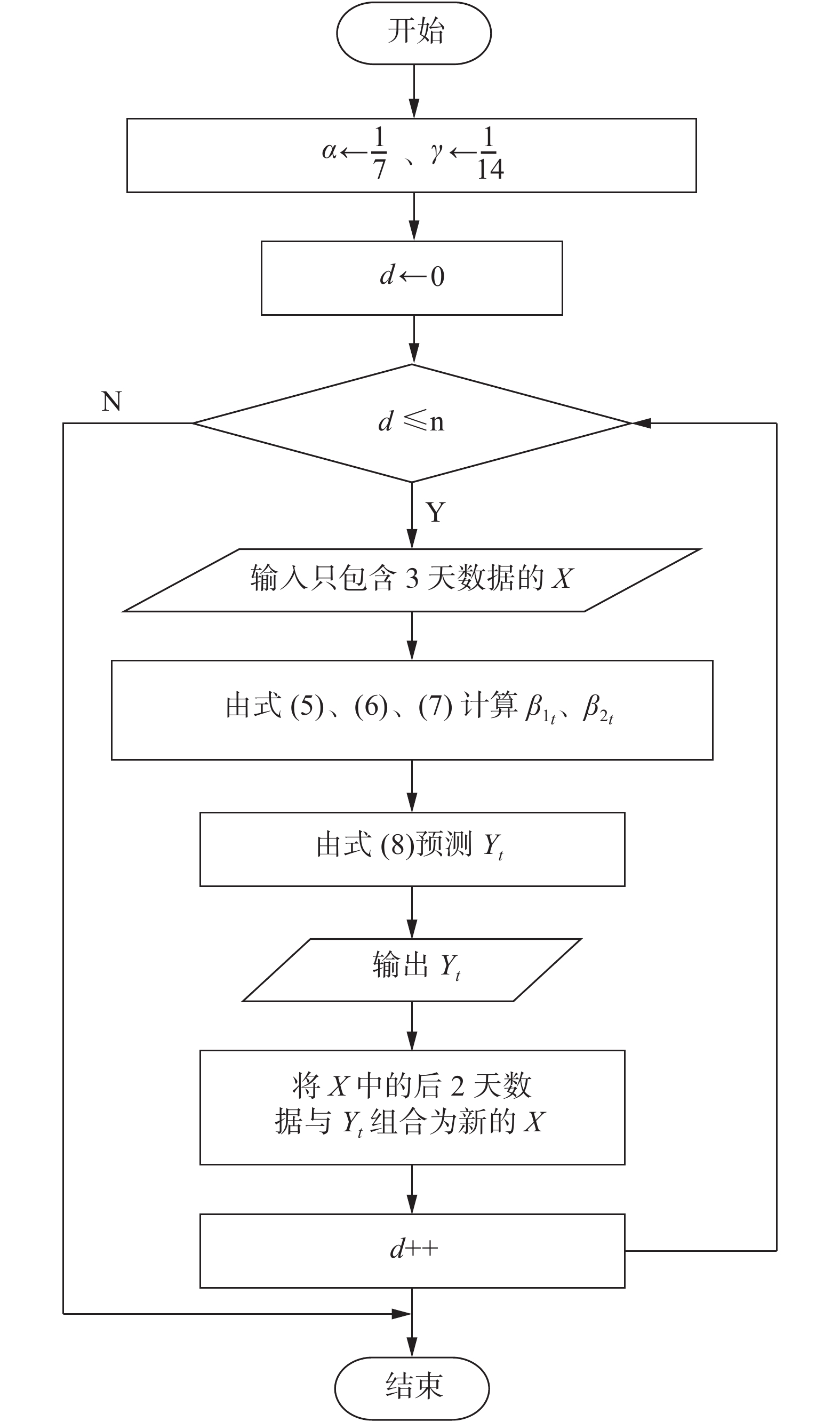
2.3 模型测试算法

LS-Net测试时同样使用前3天的数据预测第4天的数据。但由于疫情趋势预测是对疫情在未来较长时间段内的发展趋势进行预测，而当下无法获得未来时间下的E、I、R具体数据，因此本文将模型的输出与上一组输入中的后2天数据相结合，组成新的输入数据再次输入到模型中进行计算。若对未来n天的疫情趋势进行预测，则测试算法流程如图4所示，测试算法见算法2。

算法2　模型测试

输入　测试集初始输入 $X = \{ {X_{T{\rm{ + }}1}}\} $ ， ${X_T} = \{ {E_{T - 1}}, $ $ {I_{T - 1}},{R_{T - 1}},{E_T},{I_T},{R_T},{E_{T + 2}},{I_{T + 2}},{R_{T + 2}}\}$ 。

输出　模型预测结果 $Y = \{ {Y_{T + 1}},{Y_{T + 2}}, \cdots , {Y_{T + {{d}}}}\}$ ，其中 ${Y_{{{T + d}}}} = \{ {E_{{{T + d}} + 1}}, {I_{{{T + d}} + 1}},{R_{{{T + d}} + 1}}\}$ ， ${{d}} \in [1,n]$ 。

参数d：已测试的天数。

1)While d $ \leqslant $ n do

2)由式(5)、(6)、(7)计算病毒传染率 ${\beta _{{1_{{{t + d}}}}}}$ 、 ${\beta _{{2_{{{t + d}}}}}}$

3)由式(8)计算新冠肺炎疫情趋势 ${Y_{t + d}}$

4) ${{d}} \leftarrow d + 1$ //更新已测试天数

5) ${X_{t + d}} \leftarrow {\rm{concat}}\;( {E_{t + d - 2}},\;{I_{t + d - 2}},\;{R_{t + d - 2}},\;{E_{t + d - 1}},\;{I_{t + d - 1}},\;$ ${R_{t + d - 1}},\; {Y_{t + d - 1}})$ //更新输入数据

6)End while

3 实验及结果

为验证LS-Net的效果，本文使用Pytorch深度学习框架和Python语言搭建预测模型。Python版本为3.6。使用云南省、上海市和陕西省3个地区的疫情数据创建数据集进行实验并与传统SEIR模型进行对比。本节将对实验数据集、实验参数设置进行介绍并对实验结果进行分析。

3.1 数据收集及整理

1)数据来源：2019年12月8日—2020年3月28日全国各省市卫生健康委员会公布的疑似病例、确诊病例、治愈和死亡病例(后文简称移除病例)数据。

2)数据选取：LS-Net没有考虑不同地区之间人员流动的因素，因此选取了武汉实施全面封城后的2020年1月24日—2020年3月28日的数据进行实验，以尽量减少人员流动对实验结果带来的影响。在全国的总体数据中，确诊病例和移除病例大部分来自于湖北省。而早期由于检测手段跟不上，湖北省存在大量患者不能及时得到确诊和无法对疑似病例进行排查的情况，所以早期全国总体数据与现实情况有较大差距。为此本文没有使用全国总体数据进行实验，而是从除湖北省外同时记录有疑似病例、确诊病例和移除病例的省市中挑选了云南省、上海市和陕西省3个地区的数据进行实验。

3)数据集准备：早期无法对人群的病毒感染情况进行排查，还未出现感染症状的潜伏期患者数据难以被记录，因此，本文使用现存疑似病例(已出现病毒感染临床症状但还未得到核酸检测结果的病例)数作为E，现存确诊病例数作为I(现存确诊病例数=累计确诊病例数−累计移除病例数)，移除病例数作为R，各地区2019年常住人口数作为N。将第t~t+2天的数据作为输入，第t+3天的数据作为对应标签来进行整理，共得到62份数据。

4)数据集划分：将3)得到的数据按训练集规模大小的不同分别整理出4个数据集，即Set_10、Set_20、Set_30、Set_40。其中Set_10划分规则: 前10份数据作为训练集，后52份数据的标签作为测试集的标签，第11份输入数据作为测试集的初始输入数据。Set_20、Set_30、Set_40划分规则同理。

3.2 实验参数设置

模型参数：根据文献[5]，设 $\alpha {\rm{ = }}\dfrac{1}{7}$ ，取潜伏期平均值的倒数； $\gamma {\rm{ = }}\dfrac{1}{{14}}$ ，取从成为感染者到成为移除者平均时长的倒数。对传统SEIR模型的 ${\beta _1}$ 、 ${\beta _2}$ 进行计算时，设 ${{{k}}_1}{\rm{ = }}15$ ， ${{{k}}_2}{\rm{ = }}3$ 。

各地区人口总数：N_云南省=4858.3万人^[28]、N_上海市=2824.14万人^[29]、N_陕西省=3876.21万人^[30]。

LSTM的隐层数量为1，维度为22。

3.3 实验结果及分析

本文在不同的数据集上分别对E、I、R进行预测。LS-Net的实验结果如图5所示，传统SEIR模型的实验结果如图6所示。LS-Net和传统SEIR模型对现存确诊人数峰值的预测结果如表1所示。

从图5和表1可看出，在Set_10的测试集上LS-Net能大致预测出I的峰值及达到峰值的时间，且曲线走势与真实情况大致相同。但由于训练集样本较少，3类人群的预测结果均高于真实数据，尤其在R的预测上误差较大。由在Set_10、Set_20、Set_30、Set_40测试集上的预测结果的纵向对比可知，随着训练集样本的增加以及疫情后期发展趋于稳定，预测结果与真实值的误差逐渐减小。图5(e)实验结果中，I后期有反弹趋势，可预测结果却趋于平稳下降，这或许与数据集中的中期至后期E均为0有关。在SEIR模型中，感染者由潜伏者转化而来，因此E对I、R和E本身的最终预测结果都会产生影响。从图5(a)、(d)、(g)可看出3个地区只在前10天左右有疑似病例，而在疑似病例清零的14天之后感染者仍有新增，说明以疑似病例数作为E与真实的潜伏期人数有较大差异。

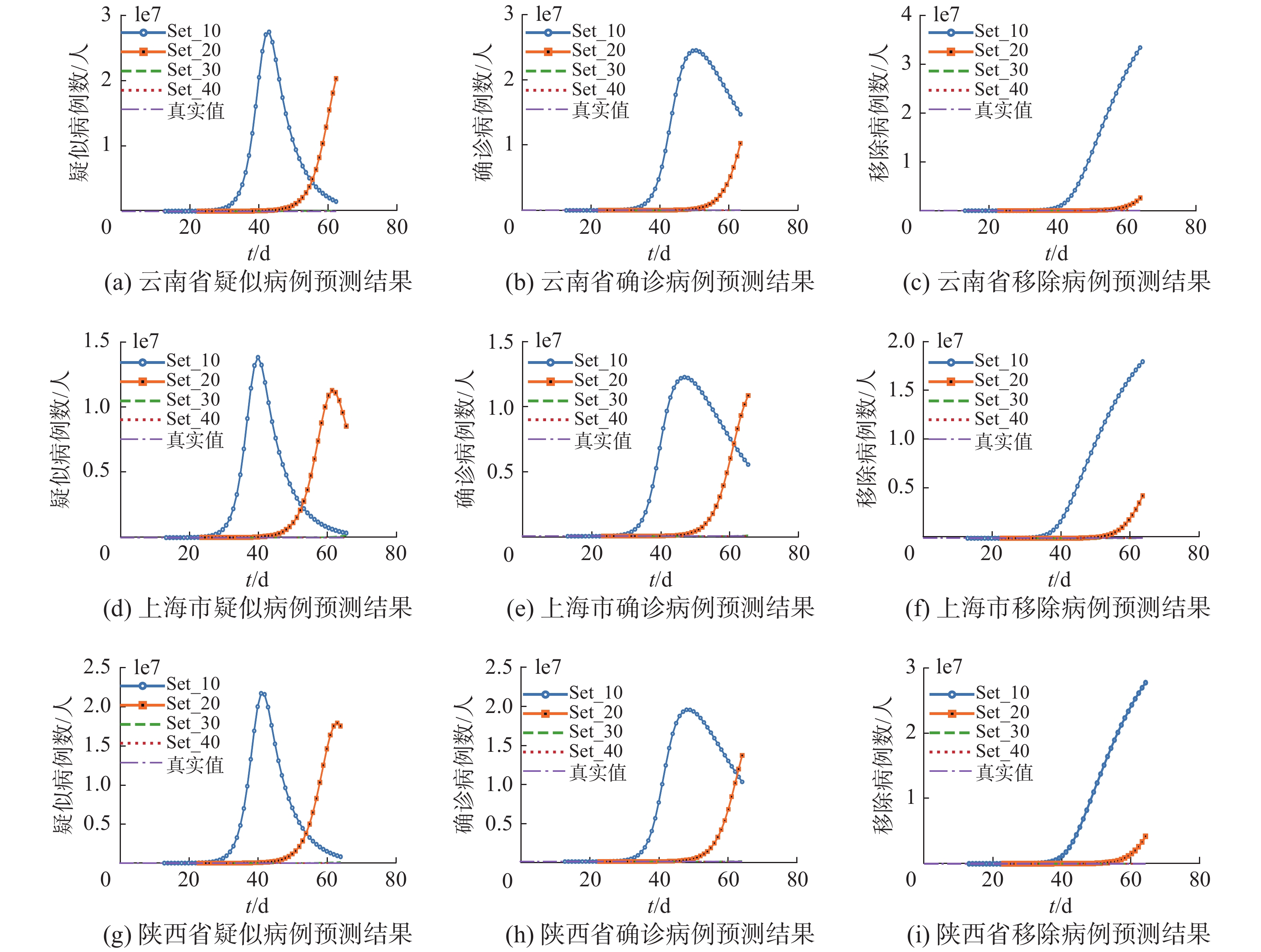
从图6和表1可看出，传统SEIR模型的预测结果与现实情况相差巨大。这是因为，传统SEIR模型中 ${\beta _1}$ 、 ${\beta _2}$ 为定值，难以模拟真实情况。且由图5(b)、(e)、(h)可知疫情前期感染人数急剧增加，此时间段内 ${\beta _1}$ 、 ${\beta _2}$ 较大。所以在不添加任何约束条件的情况下，仍使用前期的 ${\beta _1}$ 、 ${\beta _2}$ 对后期疫情进行预测会有较大误差。

在以上使用包含了云南省、上海市、陕西省的感染人数由急剧增加、到达峰值至逐渐降低趋于稳定几个阶段的实验数据的实验中，LS-Net使用LSTM和式(7)对 ${\beta _1}$ 、 ${\beta _2}$ 进行实时动态预测，而传统SEIR则将 ${\beta _1}$ 、 ${\beta _2}$ 设为定值，结果表明在使用相同的训练数据和约束条件的情况下，LS-Net的预测效果远优于传统SEIR模型。且在E与实际情况存在较大偏差的情况下，LS-Net依然能够大致预测出I达到峰值的日期，以及在E=0的情况下疫情趋势预测曲线基本能与实际数据拟合。

4 结束语

本文结合LSTM和传统SEIR模型提出了LS-Net。实验结果表明，LS-Net可省去人工拆分时段进行动态计算的繁琐过程，使用少量的训练数据即可对疫情中现存确诊病例的峰值进行预测，在一定程度上可为人们在当前的防控措施下对疫情的发展趋势预测提供参考。为使LS-Net成为一个更通用的传染病疫情趋势预测模型，未来工作将会基于现有模型从以下几点进行改进：1)考虑各地人口的流动情况；2)提出可合理地估算潜伏期人群数量的方法。潜伏者数量由于还未出现感染症状，因此难以被统计。从已有数据中准确地估算出潜伏期人群的数量将大大提高模型预测的准确率。