异常事件检测是指通过图像处理、模式识别和计算机视觉等技术，分析视频中的有效信息，判断异常事件。作为智能视频监控系统的重要应用之一，异常事件检测受到了国内外学者的广泛关注。因光照、背景和视角等因素的影响以及缺少异常数据，异常事件检测仍是一项具有挑战性的任务^[1-2]。

异常事件检测通常包含特征提取和建立检测模型。特征分为底层和深度学习特征。底层特征主要有方向梯度直方图^[3]、三维时空梯度^[4]、光流直方图^[5]等。近年来，部分学者提出基于深度学习的检测算法^[6-9]。Zhou等^[8]设计了一个特征提取网络，包含运动混合和特征迁移两个模块。检测模型主要有分类和聚类^[10-11]、误差值^[12-13]和稀疏表示^[14-17]。Lu等^[16]取消稀疏约束，提出稀疏组合学习算法，检测速度可达150 f/s。文献[17]提出将稀疏参数映射到层叠循环神经网络中，提高了检测速度。

本文针对异常检测输入通常为视频帧或图像块的局限性，利用混合高斯算法提取运动前景像素，以滑动窗口方式根据前景像素点占比获取运动前景块，并设计3个自动编码器，分别以灰度图和梯度作为输入，学习前景块的时空特征。最后，采用改进的稀疏组合算法对特征建模，进行异常检测。

1 相关工作 1.1 背景建模

视频中的运动前景检测方法主要有：光流法、帧间差分法和背景差分法3种^[18]。自适应混合高斯算法是常用的前景提取方法，可自适应地确定高斯数量，减少光照、噪声等带来的影响。本文采用Zivkovic^[19]提出的自适应混合高斯算法，提取视频的运动前景。图1为运动前景提取结果图。可以看到，即使光照不均、树叶轻微浮动，运动前景区域分割效果依然很好。

1.2 异常事件检测中的特征学习

特征学习是异常检测的基础和关键。Lee等^[10]考虑速度、方向和群体效应3种因素，采用Farneback算法^[20]提取光流特征，并构建区域运动影响矩阵。

近年来，深度学习在计算机视觉领域取得了巨大成功。Xu等^[6]首次将深度学习应用在异常检测任务，采用叠加去噪编码器提取特征。Hasan等^[12]设计了两个编码器，分别为全连接自动编码器和三维全卷积前馈网络。此外，一些方法使用预训练网络提取表观特征。如文献[21]采用ImageNet^[22]数据集预训练的卷积网络提取特征。该类方法受限于相关任务类型和模型跨领域问题，检测准确率偏低。

与上述方法不同的是，本文提出采用卷积自动编码器学习运动前景块的时空特征，过滤冗余背景信息。

1.3 基于稀疏编码的异常检测

基于稀释编码的异常检测^[13-16]在训练阶段从正常特征数据 ${{X}} = \{ {{{x}}_1},{{{x}}_2}, \cdots ,{{{x}}_n}\} $ 中学习稀疏约束的字典D。在测试阶段，给定测试样本x，计算稀疏重构误差值：

$ \mathop {\min }\limits_\beta \left\| {{{x}} - {{D }}\beta} \right\|_2^2, \;\;{\rm{s.t.}}\;\;{\left\| {\rm{\beta }} \right\|_0} \leqslant s $

式中：β为稀疏编码；s用于控制稀疏度。稀疏编码的优化较为耗时，文献[14]减小字典大小来提升检测效率。Zhao等^[15]改用更快速的求解器，但单帧检测仍需数秒时间。文献[16]提出取消稀疏约束学习多个小字典，作者称之为稀疏组合学习，可达到150 f/s的检测效率。本文在此基础上提出了一种自更新的稀疏组合学习方法，以权值的方式加入先验知识，并在线更新，提高稀疏组合的灵活性。

2 基于运动前景快的特征表示 2.1 构建运动前景块

采用Zivkovic^[19]方法，获取视频运动前景区域。以滑动窗口方式遍历视频帧，前景像素个数占比超过阈值的窗口块为运动前景块。由于前景检测结果中存在噪声点，通过该方式可过滤掉部分噪声，还可保留前景像素点的空间相对位置关系。

具体方法为，假定窗口内的前景像素个数为 $b$ ，计算前景像素点的占比：

$p = \frac{b}{{w \times w}}$

式中：w为窗口大小，本文为64。若p大于阈值则当前窗口为运动前景块，否则为背景或噪声块。

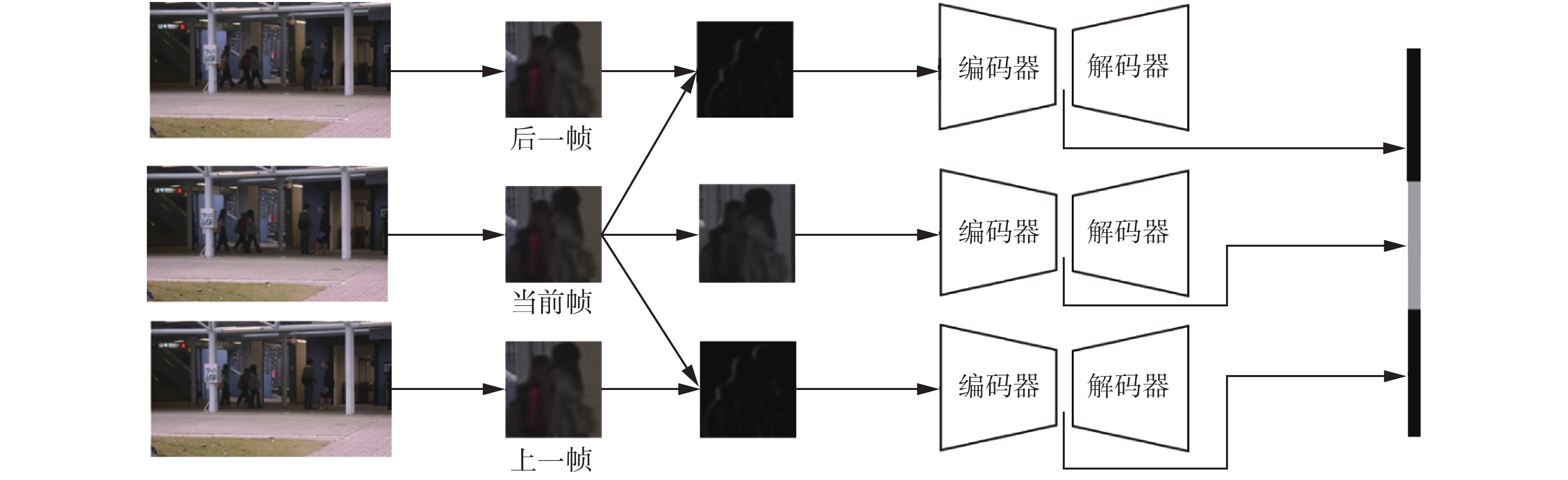
2.2 基于卷积自动编码器的特征提取

本文构建的3个卷积自动编码器提取时空特征，如图2所示。位于中间的自动编码器以灰度图作为输入，学习表观特征。另外两个的输入均为梯度，分别学习前后运动特征。3个自动编码器采用相同的结构，其中编码器由3个卷积层和3个最大池化层构成，解码器为3个上采样层和3个卷积层，以及输出层，具体参数如表1所示。卷积自动编码器的输入输出均为 $64 \times 64 \times {\rm{1}}$ 。卷积层采用 $3 \times 3$ 滤波器，除输出层外均使用ReLU激活函数。编码器的卷积层分别设有32、16、8个滤波器，池化层的步长为2。解码器的第一个卷积层为8个滤波器，随后两层设为16和32，上采样层将输入大小扩大一倍。

采用Adam方法^[21]对网络的参数进行优化，损失函数为

$L({{I}},{{O}}) = \frac{1}{{h,w}}\sum\limits_{i = 1}^h {\sum\limits_{j = 1}^w {{{\left( {{{{I}}_{ij}} - {{{O}}_{ij}}} \right)}^2}} } $

式中：I和O分别为输入输出运动前景块；h、w为运动前景块的高宽。训练数据为正常视频，自动编码器学习正常运动目标的时空特征。将自动编码器的隐特征拼接作为运动前景块的时空特征。因每个卷积编码器的隐特征为 $8 \times 8 \times 8$ ，故运动前景块的时空特征为1536维( $8 \times 8 \times 8 \times 3$ )。

3 基于自更新稀疏组合异常检测算法

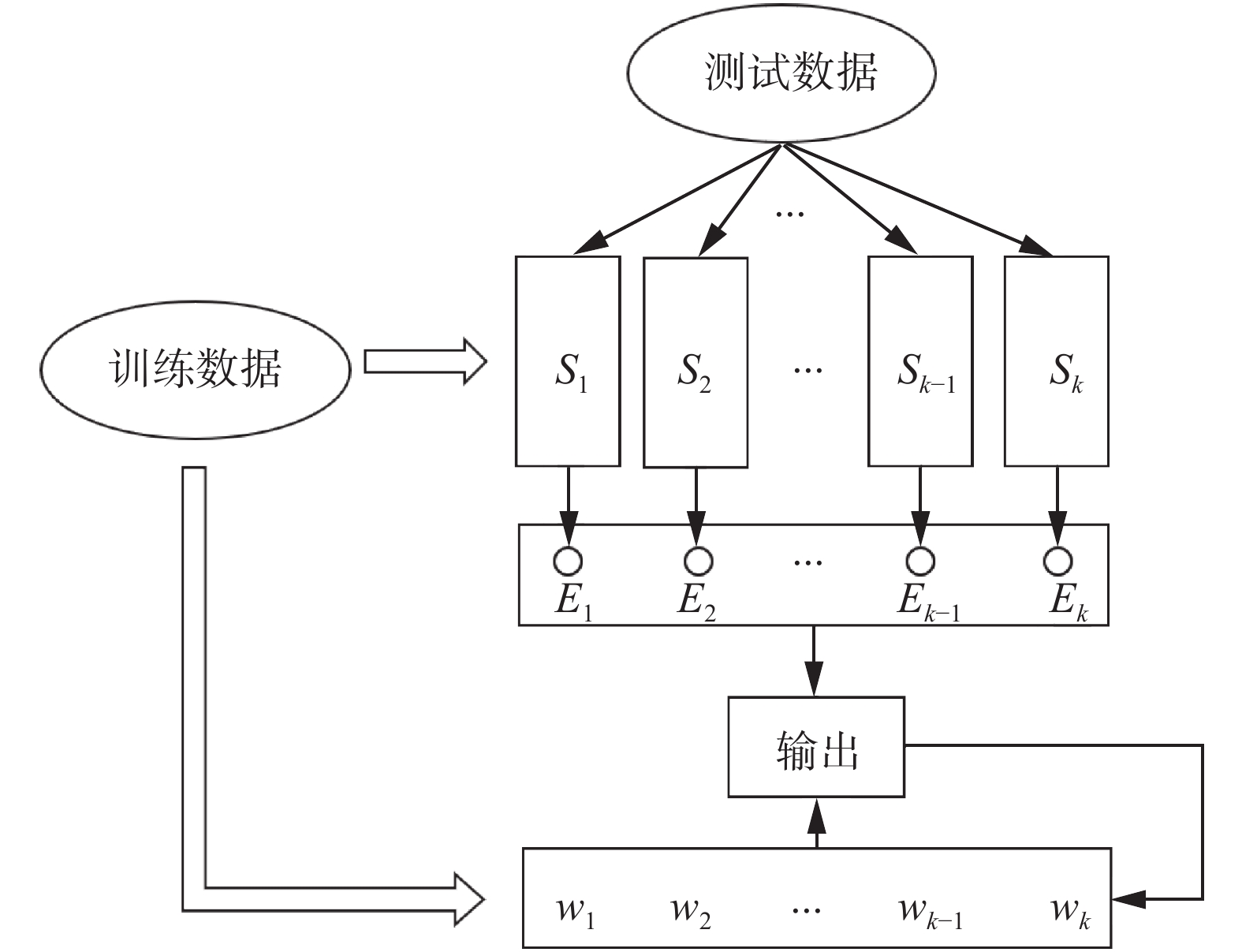
自更新稀疏组合检测算法流程图如图3所示，从训练数据中学习稀疏组合集合 ${{S}} = \{ {{{S}}_1}, $ $ {{{S}}_2}, \cdots ,{{{S}}_k} \}$ ，设定初始权值。给定测试数据，计算加权最小二乘误差，选取最小值作为结果输出。根据输出值大小判断是否为异常，同时选择置信度较高的测试样本对权值进行更新。

3.1 模型构造

稀疏组合学习假定训练样本均可在稀疏组合集合中找出能够以较小误差进行线性重构的组合，表示为

$ \begin{array}{l} t = \mathop {\min }\limits_{{{S}},{{\gamma }},{{\beta }}} \displaystyle\sum\limits_{j = 1}^n {\displaystyle\sum\limits_{i = 1}^k {{{\gamma }}_j^i\left\| {{{{x}}_j} - {{{S}}_i}{{\beta }}_j^i} \right\|_2^2} }\\ {\rm{s.t.}}\;\;\;\displaystyle\sum\limits_{i = 1`}^k {{{\gamma }}_j^i = 1},\;\;\gamma _j^i = \left\{ {0,1} \right\} \end{array} $

(1)

式中：S_i为稀疏组合；x_j为运动前景块的特征；n为训练样本的总数；k为稀疏组合的个数； ${{\gamma }} = \{ {{{\gamma }}_1}, {{{\gamma }}_2}, \cdots ,{{{\gamma }}_n}\} $ ， ${{{\gamma }}_j} = \{ {{\gamma }}_j^1, {{\gamma }}_j^2, \cdots ,{{\gamma }}_j^k\} $ ， ${{\gamma }}_j^i$ 表示S_i是否为特征x_j的最优稀疏组合； $\;{{\beta}} _j^i$ 是稀疏组合S_i用于表示x_j的系数。

3.2 模型参数求解

为了提高检测效率，k值应尽可能小。引入超参λ，当训练数据的重构误差小于该值时，训练结束。式(1)更新为

$ \begin{array}{c} {t_j} = \displaystyle\sum\limits_{i = 1}^k {{{\gamma}} _j^i\left\{ {\left\| {{{{x}}_j} - {{{S}}_i}{{\beta}} _j^i} \right\|_2^2 - \lambda } \right\}} \leqslant 0\\ {\rm{s.t.}}\;\;\displaystyle\sum\limits_{i = 1`}^k {{{\gamma}} _j^i = 1} ,\;\;{{\gamma}} _j^i = \left\{ {0,1} \right\}\;\;\forall j \in \left\{ {1,2, \cdots ,n} \right\} \end{array} $

(2)

采用迭代方式求解式(2)，可快速找到表征大多数正常特征的稀疏组合。具体方法为，对于第i轮，更新S_i。式(2)转化为

$ \begin{array}{l} \mathop {\min }\limits_{{{{S}}_i},{{\gamma }},{{\beta }}} \displaystyle\sum\limits_{j \in {{\mathit{\Omega}} _c}} {{{\gamma }}_j^i\left( {\left\| {{{{x}}_j} - {{{S}}_i}{{\beta }}_j^i} \right\|_2^2 - \lambda } \right)} \\ \;\;\;{\rm{s.t.}}\;\;\displaystyle\sum\limits_{i = 1`}^k {{{\gamma}} _j^i = 1}, \;\;{{\gamma}} _j^i = \left\{ {0,1} \right\} \end{array} $

(3)

式中 ${{\mathit{\Omega}} _c}$ 为当前训练数据 ${{{X}}_c} \in {{X}}$ 的下标集合。同样采用迭代方式求解式(3)，分两步进行：

1) 固定 ${{\gamma}} $ ，更新 ${{{S}}_i}$ 和β。式(3)简化为二次方程：

$L({{\beta }},{{{S}}_i}) = \displaystyle\sum\limits_{j \in {{\mathit{\Omega}} _c}} {{{\gamma }}_j^i} \left\| {{{{x}}_j} - {{{S}}_i}{{\beta }}_j^i} \right\|_2^2$

(4)

对所有 ${{\gamma}} _j^i \ne 0$ ，可求得最优β。β的闭式解为

${{\beta }}_j^i = {\left( {{{S}}_i^{\rm{T}} {{{S}}_i}} \right)^{ - 1}}{{S}}_i^{\rm{T}} {{{x}}_j}$

(5)

通过块坐标下降法求得 ${{{S}}_i}$ 的最优解为

${{{S}}_i} = \Pi \left[ {{{{S}}_i} - {\delta _t}{\nabla _{{S_i}}}L({{\beta }},{{{S}}_i})} \right]$

(6)

式中 ${\delta _t}$ 设置为0.0001。

2) 根据{S_i, β}，更新 ${{\gamma }} $ 。对x_j求解函数为

$ \mathop {\min }\limits_{{{\gamma }}_j^i} {{\gamma }}_j^i\left\| {{{{x}}_j} - {{{S}}_i}{{\beta }}_j^i} \right\|_2^2 - \lambda {{\gamma }}_j^i,\;\;{\rm{s.t.}}\;\;{{\gamma}} _j^i = \left\{ {0,1} \right\} $

(7)

易得 ${{\gamma}} _j^i$ 的闭式解为

$ {{\gamma }}_j^i = \left\{ \begin{array}{l} {1,}\quad{\left\| {{{{x}}_j} - {{{S}}_i}{{\beta }}_j^i} \right\|_2^2 < \lambda }\\ {0,}\quad{{\text{其他}}} \end{array} \right. $

(8)

重复上述两个步骤，直至式(3)收敛，则第i轮结束。x_c为空时，整个训练结束。

3.3 权值初始化和自更新

出现频率越高的稀疏组合所表示事件为正常的概率越高。为每个稀疏组合设定权值，值越高重要性越大。在3.2节每轮训练结束后，统计 ${{\gamma}} _j^i = 1$ 的总数，记为τ_i。对S_i的权值进行初始化：

$w_i^0 = \frac{{\tau _i^0}}{n}$

测试阶段，选择重构误差值小于阈值 $\mu $ 的样本对权值进行更新。给定测试特征 ${{x}} \in {{{\bf{R}}}^p}$ ，计算稀疏组合的加权重构误差：

${e_i} = (1 - {w_i}) \times {E_i}$

式中 $1 \leqslant i \leqslant k$ 。若 $\min \left( {e{}_1,{e_2}, \cdots ,{e_k}} \right) \leqslant \mu $ ，则对权值进行更新，公式为

$ \begin{array}{*{20}{c}} {\tau _i^{t + 1} = \left\{ \begin{array}{l} {\tau _i^t + 1,}\quad{{e_i} = \min ({e_1},{e_2}, \cdots ,{e_k})}\\ {\tau _i^t,}\quad{{\text{其他}}} \end{array} \right.}\\ {w_i^{t + 1} = \dfrac{{\tau _i^{t + 1}}}{{\displaystyle\sum\limits_{j = 1}^k {\tau _j^{t + 1}} }}} \end{array} $

(9)

3.4 自更新稀疏组合检测

给定测试数据x，计算稀疏组合的最小二乘误差：

$\mathop {\min }\limits_{{\beta }} \left\| {{{x}} - {{{S}}_i}{{{\beta }}^i}} \right\|_2^2$

式中： $1 \leqslant i \leqslant k$ ；β的闭式解为

${{{\hat{{\beta }}}}^i} = {({{S}}_i^{\rm{T}} {{{S}}_i})^{ - 1}}{{S}}_i^{\rm{T}} {{x}}$

则x与S_i的加权重构误差为

$\left( {1 - {w_i}} \right)\left\| {{{x}} - {{{S}}_i}{{{\beta }}^i}} \right\|_2^2 = \left( {1 - {w_i}} \right)\left\| {\left( {{{{S}}_i}{{\left( {{{S}}_i^{\rm{T}} {{{S}}_i}} \right)}^{ - 1}}{{S}}_i^{\rm{T}} - {{{{I}}}_p}} \right){{x}}} \right\|_2^2$

式中I_p为 $p \times p$ 的单位矩阵。为每个稀疏组合定义一个辅助矩阵H_i：

${{{H}}_i} = {{{S}}_i}{({{S}}_i^{\rm{T}} {{{S}}_i})^{ - 1}}{{S}}_i^{\rm{T}} - {{{I}}_p}$

最终只需对测试数据x，按照式(10)即可计算出其与每个稀疏组合的加权重构误差：

$\left\{ \begin{array}{l} {E_i} = \left\| {{{{H}}_i}{{x}}} \right\|_2^2\\ {e_i} = (1 - {w_i}){E_i}\end{array} \right.$

(10)

若存在 ${e_i} < T$ ( $1 \leqslant i \leqslant k$ )，x为正常，否则为异常。如果 ${e_i} < \mu $ ，则根据式(9)对权值进行更新，完成权值的在线更新。

4 实验与分析 4.1 数据集

本文在数据集Avenue^[15]和UCSD^[23]上进行了大量实验。Avenue数据集中共16个训练视频，21个测试视频。训练视频仅为正常事件，测试视频包含异常和正常事件。异常事件包含快速奔跑、抛掷物品和蹦跳等，如图4所示。

UCSD数据集分为2个场景Ped1和Ped2。训练数据为正常事件，测试数据涉及多种异常行为，如行人道上骑车、出现货车、轮滑等，如图4所示。Ped1有34段训练视频和36段测试视频; Ped2视频包含16段训练视频和12段测试视频。

4.2 实验设置

对于卷积自动编码器，每个数据集都进行200轮训练，前100轮学习率设为0.001，后100轮学习率设为0.0001，采用小批量方法训练。式(2) 中的λ设置为0.04，表示误差上限。实验均在Ubuntu16.04、NVIDIA CUDA 8.0、PyTorch1.0、OpenCVs 3.0、Python环境下完成。

4.3 评价指标

采用异常检测常用的帧级AUC评价指标^[24]。对于检测结果为异常的样本，若其标注中存在异常像素，则认为检测正确。AUC值为接收者操作特性曲线(receiver operating characteristic, ROC)下包含的面积。

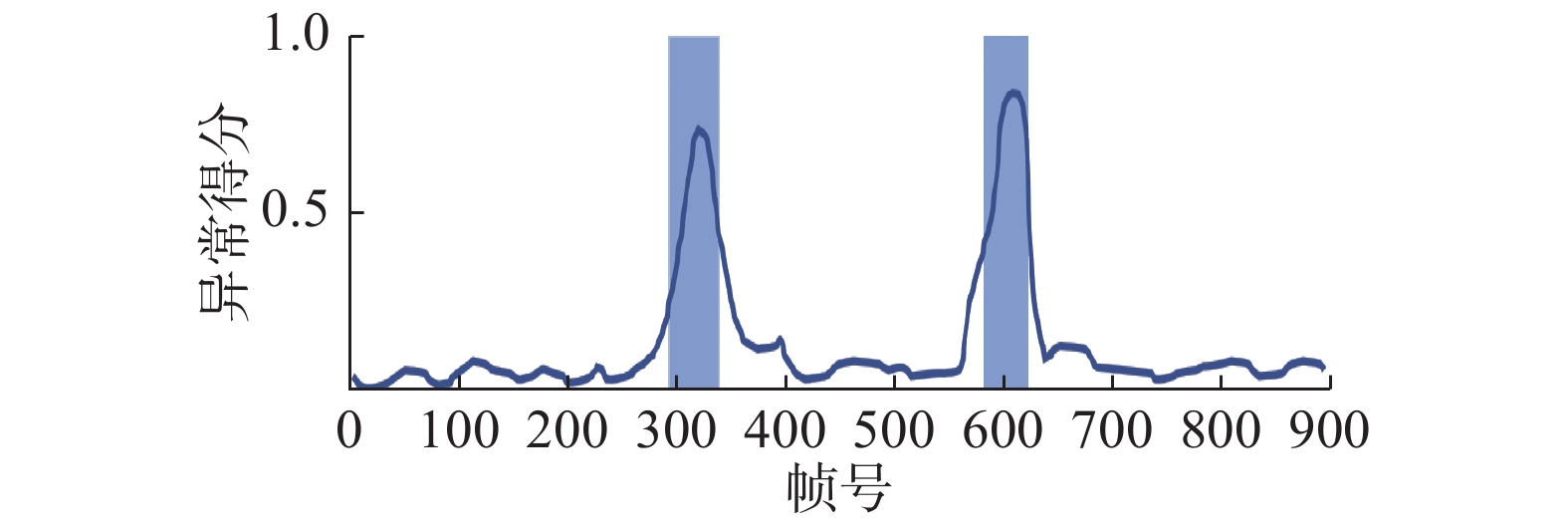
4.4 结果与分析 4.4.1 Avenue数据集

图5为Avenue数据集测试视频03的异常得分。图中灰色部分为标注的异常帧，横轴为帧序号，纵轴为异常得分。可以看到灰色区间内的得分较高而其他区域则偏小。说明本文方法可以检测出这两个异常事件。

表2列出了Avenue测试数据的检测结果，由于篇幅所限只列出了部分结果，所给结果中包含最好与最差情况。最高检测率为视频03，包含两个快速奔跑异常。视频07的异常为行人蹦跳，识别率为90.2%，是21个测试视频中的最低值。对比两段视频，发现虽然两者都是速度上的异常，但视频03中的运动状态变化远大于视频07，造成两者识别率差异较大。

为了进一步验证本文算法的有效性，与其他算法进行了比较，如表3所示。可以看到，相较于经典的稀疏组合算法^[16]，本文算法提升了6.4%，相较于最近的方法^[25]，也有2.9%的提升。

4.4.2 UCSD数据集

表4给出了本文算法与其他算法在UCSD数据集上的AUC值。本文算法AUC为87.3%，比Conv-AE^[12]提高了6.3%，与SC^[15]相比提升了1.05%；在数据集Ped2上，本文算法比SC^[15]提高了11.01%。说明基于运动前景块的特征提取方法有效，滤除了背景冗余信息。所构建的卷积自动编码器可学到更高语义层次的特征，与手工提取特征相比，鲁棒性更强。

图6给出了UCSD数据集上正确检测的异常帧和未检测出的异常帧。图中左侧为部分正确检出的异常帧，可以看到本文算法可将骑行、轮滑以及巡逻车检出；右侧为未检测出的异常帧，异常区域用红色圈标出，异常目标存在遮挡或与周围行人产生交互的情况，算法未能将其识别为异常。

4.4.3 运行时间

表5中所列为本文算法和经典稀疏组合学习算法^[15]在数据集上每帧检测所需时间。本文算法虽慢于稀疏组合学习算法，但根据表3和表4的结果，本文算法检测效果更优。监控视频帧率通常为25 f/s，而本文算法平均能达到100 f/s，完全可以满足实时检测的要求。

5 结束语

本文提出了一种以无监督方式学习运动前景块的深度特征方法和自更新稀疏组合异常检测算法。主要贡献包括4个方面：

1) 提出了以无监督方法基于自动编码器提取运动前景块的时空特征，过滤冗余背景信息，同时保留运动前景像素点的空间相对位置关系；

2) 针对经典的稀疏组合学习缺乏灵活性的问题，通过加入先验知识，提出了一种自更新稀疏组合学习算法；

3) 将深度学习与改进的稀疏组合学习进行结合，提出了一个新的异常检测框架；

4) 一系列监控场景数据的实验结果表明，本文提出的异常检测算法可以准确高效地检测视频中的异常事件。